A comparison of thin-plate spline deformation and finite element modeling to compensate for brain shift during tumor resection

Abstract

Purpose

Brain shift during tumor resection can progressively invalidate the accuracy of neuronavigation systems and affect neurosurgeons’ ability to achieve optimal resections. This paper compares two methods that have been presented in the literature to compensate for brain shift: a thin-plate spline deformation model and a finite element method (FEM). For this comparison, both methods are driven by identical sparse data. Specifically, both methods are driven by displacements between automatically detected and matched feature points from intraoperative 3D ultrasound (iUS). Both methods have been shown to be fast enough for intraoperative brain shift correction (Machado et al. in Int J Comput Assist Radiol Surg 13(10):1525–1538, 2018; Luo et al. in J Med Imaging (Bellingham) 4(3):035003, 2017). However, the spline method requires no preprocessing and ignores physical properties of the brain while the FEM method requires significant preprocessing and incorporates patient-specific physical and geometric constraints. The goal of this work was to explore the relative merits of these methods on recent clinical data.

Methods

Data acquired during 19 sequential tumor resections in Brigham and Women’s Hospital’s Advanced Multi-modal Image-Guided Operating Suite between December 2017 and October 2018 were considered for this retrospective study. Of these, 15 cases and a total of 24 iUS to iUS image pairs met inclusion requirements. Automatic feature detection (Machado et al. in Int J Comput Assist Radiol Surg 13(10):1525–1538, 2018) was used to detect and match features in each pair of iUS images. Displacements between matched features were then used to drive both the spline model and the FEM method to compensate for brain shift between image acquisitions. The accuracies of the resultant deformation models were measured by comparing the displacements of manually identified landmarks before and after deformation.

Results

The mean initial subcortical registration error between preoperative MRI and the first iUS image averaged 5.3 ± 0.75 mm. The mean subcortical brain shift, measured using displacements between manually identified landmarks in pairs of iUS images, was 2.5 ± 1.3 mm. Our results showed that FEM was able to reduce subcortical registration error by a small but statistically significant amount (from 2.46 to 2.02 mm). A large variability in the results of the spline method prevented us from demonstrating either a statistically significant reduction in subcortical registration error after applying the spline method or a statistically significant difference between the results of the two methods.

Conclusions

In this study, we observed less subcortical brain shift than has previously been reported in the literature (Frisken et al., in: Miller (ed) Biomechanics of the brain, Springer, Cham, 2019). This may be due to the fact that we separated out the initial misregistration between preoperative MRI and the first iUS image from our brain shift measurements or it may be due to modern neurosurgical practices designed to reduce brain shift, including reduced craniotomy sizes and better control of intracranial pressure with the use of mannitol and other medications. It appears that the FEM method and its use of geometric and biomechanical constraints provided more consistent brain shift correction and better correction farther from the driving feature displacements than the simple spline model. The spline-based method was simpler and tended to give better results for small deformations. However, large variability in the spline results and relatively small brain shift prevented this study from demonstrating a statistically significant difference between the results of the two methods.

Introduction

Neuronavigation systems (e.g., [1–4]) can be used to map preoperative anatomical, structural and functional imaging into patient coordinates during brain tumor resections, thereby helping to guide surgeons toward planning optimal surgical approaches and achieving more complete resections. However, brain shift decreases the validity of neuronavigation registration as surgery progresses. Brain shift is composed of brain deformation (caused by changes in intracranial pressure, osmolarity, CSF levels, air pockets, head position, etc.), tissue retraction and tumor resection. It begins when the craniotomy is performed, increases when the dura mater is opened and as tumor tissue is removed and has been measured to be as large as 20–30 mm at the brain cortex [5]. As reviewed in [6–9], brain shift has been measured and modeled for more than 20 years. It can be mitigated by navigating from intra-operative imaging such as intraoperative MRI (iMRI) [5, 10, 11] or intraoperative ultrasound (iUS) [12, 13] instead of preoperative imaging. However, iMRI requires specialized equipment and personnel and can significantly disrupt and extend the duration of surgery. iUS can be hard for surgeons to interpret and cannot provide the high-quality anatomical, structural [e.g., diffusion MRI tractography (dMRI)] and functional [e.g., functional MRI (fMRI)] imaging [14, 15] that can be acquired preoperatively.

An alternative to navigating directly from intraoperative imaging is to derive a model of brain shift from intraoperative imaging and use the model to compensate for brain shift. The model is applied to preoperative image data (e.g., anatomical imaging, dMRI, fMRI, segmented structures or the surgical plan) to fit it to the shape of the brain after brain shift. One common approach is to model brain shift as a non-rigid registration from preoperative anatomical MRI to iMRI [16–19] or preoperative MRI to iUS [20–28]. The nonrigid registration can be derived directly from 2D or 3D images (e.g., [29]), or it can be derived from sparse measurements of the cortical surface [30, 31] or sparse features in the image data [32]. Previously, we have shown that displacements of the cortical surface can be used to drive an FEM model of the brain to achieve accurate representations of brain shift [33]. We recently presented a method using the SIFT-Rank algorithm [34] to automatically detect and match features in pairs of iUS images and validated the feature quality and feature matching accuracy across multiple clinical iUS datasets [32]. This work presented preliminary results showing that the automatically detected features could be used to drive a simple thin-plate spline deformation that accurately modeled brain shift.

In this paper, we compare two brain shift compensation methods both driven by the same sparse features derived from clinical data. Specifically, matched feature points were automatically generated in pairs of iUS images acquired at multiple time points during brain tumor resections in 15 clinical cases for a total of 24 iUS to iUS image pairs. The automatic features were used to drive both a simple, fast and readily available thin-plate spline deformation and a patient-specific FEM model that incorporates physical and geometric constraints and heterogeneous material properties but requires significant preprocessing. For comparison, the accuracy of each method was measured using a set of landmarks that were manually identified in each iUS image pair.

Methods

Data acquisition

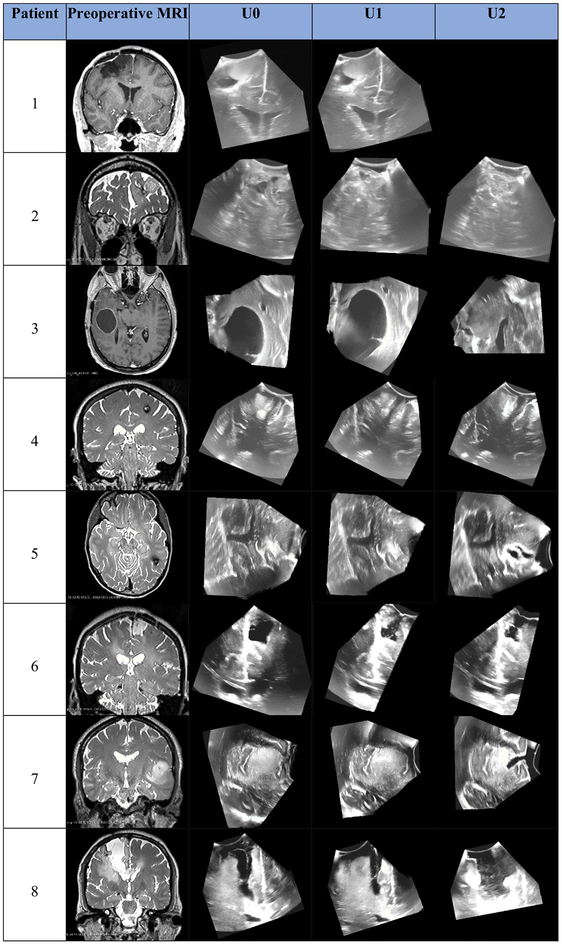
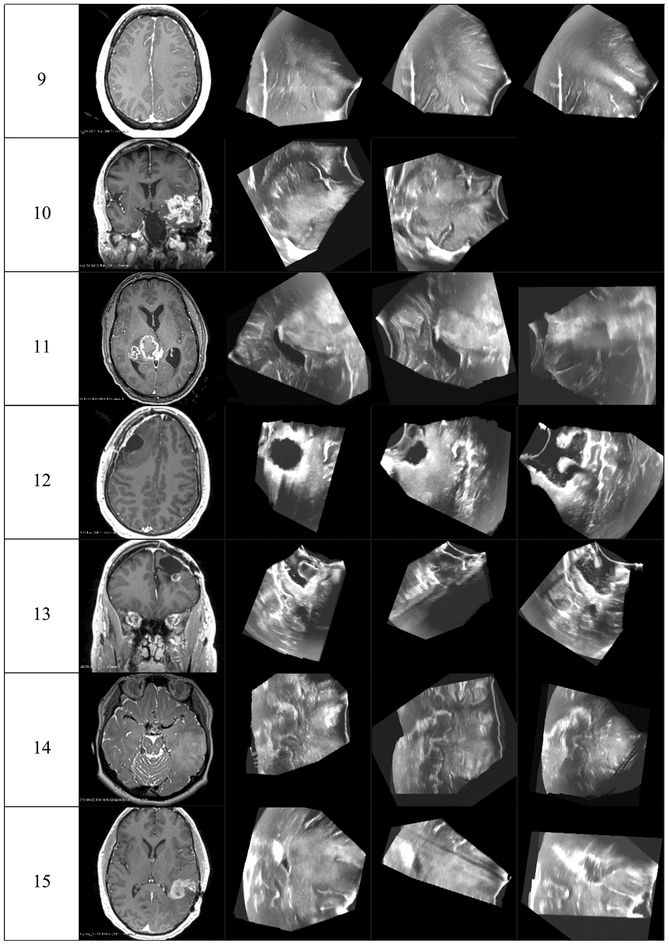
This study was performed on data acquired during 19 sequential tumor resections performed in the Advanced Multi-modal Image-Guided Operating (AMIGO) Suite at Brigham and Women’s Hospital (BWH) in Boston, MA, between December 2017 and October 2018. Patient consent was obtained prior to data acquisition for this IRB-approved study. Each patient underwent preoperative imaging including, as clinically indicated, T1, T2, dMRI and fMRI. During surgery, iUS was acquired at multiple time points: typically, immediately after performing the craniotomy but before opening the dura mater (U0); immediately after opening the dura mater (U1); and after significant resection (frequently immediately before acquiring iMRI) (U2). Because 3D iUS had only recently been introduced into the neurosurgical workflow in AMIGO at the time of this study, some iUS scans were incomplete or missing. Thus, four of the 19 patients and six additional iUS to iUS image registration pairs were excluded from the study because one or more of the iUS images were missing or had insufficient quality for automatic feature detection and matching and/or for manually identifying landmark points. Table 1 summarizes the tumor type, location, size, craniotomy size, iUS images acquired and relevant surgical notes for the 15 patients whose data were used in this study.

Table 1.

Tumor/lesion type, location and volume, the preoperative MRI and iUS images available for retrospective analysis, the craniotomy size measured from intraoperative MRI and relevant surgical notes for each patient

Patient	Tumor			Imaging		Craniotomy size (mm2)	Notes
	Type	Location	Volume (ml)	MRI	iUS
1	Grade III Anaplastic Astrocytoma	Right frontal lobe	10	T1	U0, U1	60 × 30	Repeat surgery
2	Grade II Oligodendroglioma	Left frontal, supratentorial	3.9	T1 MPRAGE T2 SPACE	U0, U1, U2	25 × 40
3	Grade IV Glioblastoma Multiforme	Right temporal lobe	23	T1 with gadolinium	U0, U1, U2	60 × 60	Repeat surgery Large cystic component
4	Cavernous Malformation	Left parietal lobe	0.20	T1 with gad T1 SPACE	U0, U1, U2	25 × 25
5	Cavernous Malformation	Left temporal lobe	0.72	T1 with gad T2 SPACE	U0, U1, U2	33 × 33
6	Grade IV Glioblastoma Multiforme	Left language cortex	2.8	T1 with gad T2 SPACE	U0, U1, U2	60 × 30	Repeat surgery Large cystic component
7	Grade II Diffuse Astrocytoma	large temporal lobe	13	T1 with gad T2 SPACE	U0, U1, U2	38 × 38	Partial resection. First of two stages
8	Grade II Oligodendroglioma	Right frontal lobe	84	T1 with gad T2 SPACE	U0, U1, U2	50 × 25	Repeat surgery
9	Grade III Anaplastic Astrocytoma	Left parietal lobe	3.9	T1 with gad	U0, U1, U2	25 × 30
10	Grade IV Glioblastoma Multiforme	Left temporal lobe	56	T1 with gad	U0, U1	26 × 20	Partial resection
11	Grade IV Diffuse Midline Glioma	Right thalamic region	36	T1 with gad	U0, U1, U2	44 × 46
12	Grade III Anaplastic Astrocytoma	Left frontal lobe	47	T1 with gad	U0, U1, U2	57 × 57	Repeat surgery for more complete resection
13	Grade III Anaplastic Oligodendroglioma	Left frontal lobe	0.68	T1 with gad	U0, U1, U2	30 × 40	Repeat surgery for small enhancing nodule
14	Grade II Oligodendroglioma	Left posterior tem-poral	33	T1 with gad T2 SPACE	U0, U1, U2	25 × 40
15	Grade IV Glioblastoma Multiforme	Left temporal-parietal lobe	22	T1 with gad	U0, U1, U2	45 × 50	Repeat surgery

Tumor types are listed using W.H.O. grading. Volumes were measured from lesion segmentations performed using the Brainlab system

Preoperative MRI was acquired in one of several Siemens 3T scanners used clinically at BWH. Anatomical MRI acquisition type (e.g., T1 FLAIR, MPRAGE, T1 with gadolinium-enhanced contrast or T2 SPACE for nonenhancing lesions) was selected based on clinical and radiologic factors. iUS imaging was performed using a neuro-cranial probe from BK Medical [35] with a BK3000 system for patients 1 and 2 and a BK5000 system for the remaining patients. The 2D US probe was tracking using the Brainlab Curve system [1]. For each iUS image acquisition, Brainlab software was used to reconstruct a 3D US volume from the tracked 2D analog US image stream output from the BK system. Figure 1 shows, for each patient, a representative 2D cross section through the tumor/lesion and corresponding 2D slice from each iUS image acquired for that patient. These images illustrate the variation in iUS image quality and coverage as well as the variation in brain tumor/lesion size, location and imaging properties which makes automatic image registration, tumor segmentation and feature detection so challenging for neurosurgical applications.

Fig. 1.

A representative 2D cross section through the tumor/lesion in preoperative MRI images and corresponding slices through 3D iUS volumes acquired at the indicated time points for each patient whose data were used in this study

Data processing

Initial registration from MRI to U0

The sparse data used to drive both deformation methods were derived from iUS image pairs. Brain shift was measured relative to U0, i.e., the iUS image aquired immediately after the craniotomy and before the dura was opened. Because the FEM model was initialized from preoperative MRI, we performed an initial rigid registration from preoperative MRI to U0 for each patient so that FEM modeling was performed relative to U0. This initial registration compensated for two factors: (1) any initial rigid registration error in the neuronavigation system between the preoperative MRI and the patient’s head at the beginning of surgery and (2) brain shift that occurred before the dura was opened (e.g., during the craniotomy or from medications administered to control intracranial pressure). To perform the rigid registration, we manually identified 5–6 landmarks in the preoperative MRI and U0 images and used 3D Slicer’s [36] Fiducial Registration Module to compute a rigid transform that minimized the mean squared distance between corresponding landmarks in the two images.

We note that while the above rigid registration method is labor-intensive, it was used in this study for the sole purpose of being able to drive both methods with identical features so that a fair comparison could be made. This step is not required by the FEM method, and small errors in the initial rigid registration in this study do not impact the ability of the FEM method to accurately model brain shift between iUS image acquisitions.

Manually identified landmarks in iUS

To provide a ground truth for assessing the accuracy of the brain shift compensation methods, we manually identified ten corresponding landmarks in each iUS images for each patient. Landmarks were selected as image features that could be spatially localized in 3D, visible in all the patients’ iUS images and as dispersed as possible throughout the iUS volumes. These landmarks were identified by a computer image processing expert (first rater, R1) and validated by two MDs (raters R2 and R3). Given landmarks identified by R1 in U0, R2 and R3 each located corresponding landmarks in U1 and U2 for each patient, thus providing three locations for each landmark in U1 and U2. In addition, each location was reviewed by an independent rater and assigned a confidence score of very high, high, acceptable, low or no confidence, which roughly corresponded to a perceived error of less than 1 mm, 3 mm, 5 mm, 10 mm or greater than 10 mm. Each rater located and rated 250 landmarks. Of these, 16, 36 and 24 points located by raters R1, R2 and R3, respectively, were assigned a confidence score that was less than acceptable. After excluding these points from the data, it was found that the average of the distances from each landmark to the mean location of that landmark across the three raters was 1.3 ± 0.6 mm.

Automatic detection of matched features

A set of matched features was automatically generated for each pair of iUS to iUS images. These features were generated and matched using the SIFT-Rank method [34]. A detailed description of this approach and a validation of the quality and accuracy of the automatic features in clinical iUS acquired during neurosurgery are provided in [32]. Features detected by this method are typically dark or light regions of roughly spherical shape. In this study, we used the same SIFT-Rank parameters detailed in [32] and did not attempt to modify parameters when the method failed to generate valid features, often due to poor US quality, as occurred in eight of 32 possible iUS to iUS image pairs. Instead, those pairs were excluded from this study. The number of automatic features for each iUS to iUS pair is identified in square brackets in Table 3.

Table 3.

Brain shift for each patient before and after brain shift compensation for each pair of iUS images

Patient	Brain shift: iUS to iUS
		(1) Mean distance between automatic features (SD) [#features] (mm)		(2) Mean distance between manual landmarks (SD) [#land marks] (mm)
	iUS to iUS pair	Initial	After FEM	Initial	After thin-plate spline	After FEM
1	U0–U1	1.71 (0.79) [46]	1.89 (0.73)	1.53 (0.87) [10]	1.31 (0.67)	1.76 (0.64)
2	U0–U1	4.20 (0.81) [19]	1.43 (0.72)	3.16 (0.06) [10]	1.34 (0.68)	1.71 (0.83)
	U0–U2	2.51 (1.08) [7]	1.63 (0.79)	2.00 (0.93) [10]	2.80 (1.61)	1.67 (0.78)
3	U0–U1	1.55 (0.86) [26]	1.52 (0.81)	1.28 (0.43) [8]	0.67 (0.31)	1.13 (0.51)
	U0–U2	9.29 (1.59) [5]	7.48 (2.95)	7.66 (5.18) [10]	13.8 (8.57)	7.17 (4.38)
4	U0–U1	1.59 (0.77) [112]	1.16 (0.64)	1.77 (1.22) [10]	1.29 (0.75)	1.53 (0.79)
	U0–U2	2.85 (1.53) [16]	1.67 (0.93)	2.93 (1.05) [10]	1.88 (1.00)	1.38 (0.56)
5	U0–U1	0.81 (0.63) [363]	0.81 (0.64)	0.77 (0.40) [10]	0.84 (0.50)	0.82 (0.50)
	U0–U2	2.13 (0.72) [87]	1.16 (0.67)	2.33 (1.12) [10]	1.54 (1.37)	1.46 (1.06)
6	U0–U1	2.22 (1.25) [8]	1.16 (0.39)	2.08 (0.80) [9]	2.58 (1.15)	2.06 (1.01)
7	U0–U1	1.34 (0.66) [67]	0.99 (0.61)	1.96 (1.22) [10]	1.72 (0.75)	1.64 (0.86)
	U0–U2	2.60 (1.39) [41]	1.33 (1.04)	3.25 (0.99) [9]	2.10 (1.20)	1.27 (0.62)
8	U0–U1	2.68 (0.95) [32]	2.59 (0.94)	2.19 (0.86) [10]	1.61 (0.67)	2.07 (0.60)
9	U0–U1	3.15 (0.60) [67]	2.19 (0.87)	2.97 (0.84) [10]	0.80 (0.40)	2.14 (0.89)
	U0–U2	2.97 (0.98) [14]	1.81 (1.00)	3.15 (1.15) [10]	2.66 (1.35)	2.12 (0.96)
10	U0–U1	2.31 (0.89) [10]	1.58 (0.75)	2.08 (0.77) [9]	2.53 (1.47)	2.44 (0.82)
	U0–U2	1.79 (1.55) [46]	1.70 (1.56)	1.64 (0.78) [10]	1.57 (0.64)	1.62 (0.85)
11	U0–U1	2.75 (0.92) [39]	2.15 (0.83)	2.82 (0.96) [10]	2.05 (1.12)	2.46 (1.31)
12	U0–U1	2.00 (0.54) [6]	2.00 (0.45)	2.21 (2.17) [10]	5.12 (3.67)	2.14 (2.09)
	U0–U2	1.34 (0.66) [48]	1.28 (0.67)	1.75 (1.27) [10]	1.49 (0.92)	1.56 (1.14)
13	U0–U1	1.58 (0.77) [13]	1.50 (0.68)	2.10 (0.89) [9]	2.17 (1.12)	2.41 (1.02)
	U0–U2	2.45 (0.80) [12]	1.60 (0.86)	2.64 (1.12) [10]	1.92 (0.78)	2.10 (0.98)
14	U0–U2	2.12 (0.83) [4]	1.70 (0.51)	2.21 (1.75) [10]	2.48 (1.46)	1.81 (1.01)
15	U0–U2	1.71 (0.79) [46]	1.89 (0.73)	1.53 (0.87) [10]	1.31 (0.67)	1.76 (0.64)
Mean		2.52 (1.65)	1.84 (1.30)	2.46 (1.30)	2.44 (2.63)	2.02 (1.18)

Brain shift is measured as the mean distance between (1) automatically generated features and (2) manually identified landmarks

Sparse displacement data

A set of displacement vectors between matched automatic features was computed for each iUS to iUS image pair. These displacement vectors, which represent a sparse set of brain shift measurements, were then used to drive both the thin-plate spline deformation and the FEM-based model of brain shift.

Thin-plate spline deformation modeling

A thin-plate spline is a function of piecewise polynomials defining a deformation that maps one set of points onto a set of corresponding points [37]. In our case, we seek a deformation D that maps automatic features from U0 to matched automatic features in U1 or U2. For a set of K automatic features P_i, i ∈ [1, K] in U0 and corresponding matched automatic features Q_i in U1 or U2, the thin-plate spline deformation D minimizes the energy function

$$E(D)={\displaystyle \sum _{i=1}^K\Vert D\left(P_i\right)-Q_i^2\Vert }$$ (1)

The thin-plate spline is known as an ‘interpolating spline’ because the optimal D maps each point P_i directly onto its corresponding point Q_i. For this reason, distances between corresponding automatic features after spline-based deformation are approximately zero. This was verified and not reported in Table 3. A thin-plate spline algorithm is implemented in the 3D Slicer’s Landmark Registration Module and used to generate a thin-plate spline deformation for each iUS to iUS image pair.

In this study, for each iUS to iUS image pair, we generated a thin-plate spline deformation in 3D Slicer using automatically detected and matched features and applied the deformation to the manually identified landmarks of the iUS to iUS image pair. A good deformation forces distances between corresponding automatic features to zero and reduces distances between corresponding manually identified landmarks.

Finite element method (FEM) for deformation modeling

We used a biophysical computation finite element method (FEM) of brain shift that we have presented previously [33, 38, 39]. This method precomputes an atlas of possible brain shift deformations from an FEM model of the brain, subject to a range of contributing factors such as gravity-induced shift and osmotic agent-induced shift. It uses sparse measurements of brain shift and an inverse problem approach to minimize the least squared error between the sparse measurements and the model prediction, where the model prediction is a linear combination of solutions from the deformation atlas. To initialize the FEM model, each patient’s brain, tumor and dural reflections (i.e., falx and tentorium) were segmented in the preoperative MRI images via a combination of manual and automatic methods and used to generate surface models of these neuro-anatomical structures. A custom mesh generator was then used to generate a biphasic biomechanical FEM model for each patient. The approach and parameters that we used in this study are detailed in [33].

For each pair of iUS to iUS images, we generated an FEM deformation model from the sparse measurements of brain shift (i.e., distances between the automatically detected and matched features) and applied the deformation model to the manually identified landmarks for the same iUS to iUS image pair. A good deformation model reduces distances between automatic features and between corresponding manually identified landmarks.

Results

Results are presented in Tables 2, 3 and 4. Table 2 presents initial registration errors and residual registration errors after rigid registration. Table 3 shows brain shift between iUS acquisitions and brain shift correction using sparse data from intraoperative ultrasound for both the thin-plate spline method and the FEM method described above. Table 4 presents the brain shift before and after brain shift compensation averaged over all patients and iUS–iUS image pairs.

Table 2.

Initial registration error for each patient is presented as the mean distance between corresponding manually identified landmarks in preoperative MRI and the first iUS image (U0)

Patient	Initial registration error: MRI to U0
	Mean initial distance between landmarks (SD) [#landmarks] (mm)	Mean distance between landmarks after rigid registration (mm)
1	3.74 (0.75) [5]	1.98 (0.96)
2	6.78 (3.40) [6]	3.65 (1.29)
3	9.89 (1.30) [6]	2.02 (0.65)
4	3.14 (1.24) [6]	1.81 (1.20)
5	3.20 (0.65) [5]	2.02 (1.14)
6	4.96 (0.40) [6]	1.61 (0.30)
7	2.42 (1.40) [6]	1.84 (0.46)
8	4.12 (0.80) [6]	1.75 (0.87)
9	6.27 (1.11) [6]	1.38 (0.39)
10	5.99 (1.76) [6]	1.51 (1.03)
11	7.05 (0.61) [6]	1.20 (0.55)
12	6.50 (0.51)[6]	2.10 (0.93)
13	6.04 (1.16) [6]	2.21 (0.50)
14	6.98 (1.61) [6]	1.49 (0.55)
15	2.49 (0.65) [6]	1.52 (0.71)
Mean	5.26 (0.75)	1.87 (0.57)

Table 4.

Average brain shift for automatic features and manual landmarks before and after brain shift correction

Registration pairs	Average brain shift: iUS to iUS
	Average distance (SD) between automatic features (mm)		Average distance (SD) between manual landmarks (mm)
	Initial	After FEM	Initial	After thin-plate spline	After FEM
U0–U1	2.11 (0.91)	1.57 (0.52)	2.00 (0.68)	1.52 (0.60)	1.76 (0.47)
U0–U2	3.05 (2.23)	2.19 (1.87)	3.05 (1.68)	3.64 (3.69)	2.35 (1.73)
U0–U1 and U1–U2	2.52 (1.65)	1.84 (1.30)	2.46 (1.30)	2.44 (2.63)	2.02 (1.18)

Brain shift results are reported for all iUS to iUS pairs (U0–U1 and U0–U2) and separately for U0–U1 and U0–U2

Initial registration error

The initial registration error was measured, for each patient, as the average distance between corresponding manually identified landmarks in preoperative MRI and the first iUS image (U0). This initial registration error ranged from 2.42 to 9.89 mm for the 15 patients in our study. The initial registration error averaged across all 15 patients was 5.26 mm with a standard deviation of 0.75 mm.

Displacements between corresponding manual landmarks were used to compute a rigid, affine registration from the preoperative MRI to U0 for each patient using 3D Slicer’s Fiducial Registration Module. After applying this rigid registration, the residual registration error between manual landmarks ranged from 1.29 to 3.83 mm and the residual registration error averaged across all 15 patients was reduced to 1.87 mm with a standard deviation of 0.57 mm. Table 2 details the initial registration errors and residual registration errors after rigid registration and the mean results for all 15 patients.

Brain shift

Brain shift between iUS acquisitions before and after brain shift compensation is presented in Tables 3 and 4. Brain shift between iUS pairs is measured as the average initial distance between corresponding manually identified landmarks in the iUS images. For all patients, these measurements correlate closely with the average initial distance between corresponding automatic features, providing independent validation that the automatic features provide an accurate representation of brain shift and were thus a good source of sparse data to drive the thin-plate spline and FEM methods.

The average brain shift ranged from 0.77 to 7.66 mm using manual landmarks and 0.81 to 9.29 mm using automatic features. These results are detailed in Table 3. The largest brain shifts (7.66 and 9.29 mm) were both observed between U0 and U2 in patient 3, whose lesion included a large cystic component that was drained during resection (see Fig. 1).

The initial average measured brain shift across all iUS to iUS pairs was 2.42 mm for manual landmarks and 2.52 mm for automatic features. When subgrouped by surgical interval, the average brain shift across all patients was 2.00/2.11 mm (landmarks/features) from U0 to U1 and 3.05/3.05 mm (landmarks/features) from U0 to U2, showing an increase in brain shift as surgery progressed, as expected.

For most patients, the average brain shift was reduced after applying both the thin-plate spline and FEM deformations, with smaller improvements for smaller initial brain shifts. Typically, FEM provided larger improvements than thin-plate splines for larger initial brain shifts. In some cases, one or both methods reduced the registration accuracy slightly. In two iUS to iUS pairs, the thin-plate spline method reduced registration accuracy by a relatively large amount (e.g., patient 3, U0 to U2 and patient 12, U0 to U1). As shown in Table 4, when averaged over all iUS to iUS pairs, both thin-plate spline and FEM provide only small improvements, with thin-plate spline showing slightly better results when modeling initial deformations between U0 and U1 and FEM showing better results in the presence of resection (i.e., between U0 and U2). The FEM method provided more consistent results (i.e., less variance in the amount of brain shift correction) than the spline-based method. Statistical analysis shows that the FEM method produced statistically significant brain shift correction using a one-sided t test paired for two sample means (initial landmark displacements vs. landmark displacements after FEM) assuming unequal variances (p = 0.002 which is significant at the 0.05 level). However, because of the relatively large variance in spline-based method results, our study did not find evidence that the spline-based method provided statistically significant brain shift correction nor did it find a statistically significant difference between the FEM and spline-based results.

Discussion and conclusions

This study showed that brain shift occurring between iUS acquisitions was typically smaller than the initial registration error. It showed that thin-plate splines tended to be better than FEM at compensating for small initial brain shifts that occur when opening the dura. This is consistent with our previous results [39] where we reported the best results for our FEM method when brain shift was greater than 3 mm. This study also showed that the FEM method performed better than thin-plate splines in the presence of significant resection. The thin-plate spline method fared poorly in two of the 24 iUS to iUS pairs, increasing the registration error by a factor of nearly two or more. This failure occurred when there were larger brain shifts (i.e., patient 3 where the mean brain shift was greater than 9 mm) and when the automatically detected features used to drive the spline model were located far away from the manually identified landmarks (i.e., patient 12).

We observed smaller brain shifts in the 15 brain tumor resections reported in this study than previously reported [6–8]. There are several possibilities for this discrepancy. It is possible, e.g., due to smaller craniotomies and better control of intracranial pressure with the use of mannitol and other medications, that there is less brain shift today than in the past. It is possible that the patient population in this study was different than in studies reported in the literature since patients in this study were selected solely because their surgeries were performed in AMIGO and not because there was risk of large brain shifts. Some patients, e.g., patients 4, 5, and 9, had particularly small lesions where little brain shift would have been expected. Other significant factors include the way in which brain shift was measured in this study. First, we report measurements of brain shift at deep structures in the brain while the literature mostly reports shifts at the cortical surface. Second, by performing an initial rigid registration from preoperative MRI to U0 before measuring brain shift, we removed a relatively large component that is often included in measurements of brain shift. Third, it was often challenging to find landmarks and features in the iUS images. The most easily identified landmarks tend to be located in the falx and sulcal folds, and these structures tend to shift less than brain parenchyma and tend to be relatively remote from the tumor margin. Thus, it is likely that our measurements of brain shift were smaller than actual shift at tumor margins due to the location of our manual landmarks and automatic features. We are currently investigating new methods for identifying both landmarks and features at or near tumor margins and resection boundaries.

This study shows that FEM methods, which incorporate patient-specific physical and geometric constraints, may provide better modeling of brain shift as tumor resection progresses during surgery than thin-plate spline deformation. Although the FEM method used in this study requires time-consuming preprocessing to build the initial FEM model from preoperative MRI and generate the deformation atlas used during surgery, both methods can compute brain shift correction within a few minutes and are thus suitable for interactive brain shift compensation in the operating room. This study suggests that iUS could be used to correct for initial registration errors caused by misregistration and/or brain shift that occurs before the craniotomy. Finally, it suggests that accurate modeling of brain shift at tumor margins and resection boundaries will require developing algorithms that can measure brain shift at those locations.