Abstract
Single particle analysis for structure determination in cryo-electron microscopy is traditionally applied to samples purified to near homogeneity as current reconstruction algorithms are not designed to handle heterogeneous mixtures of structures from many distinct macromolecular complexes. We extend on long established methods and demonstrate that relating two-dimensional projection images by their common lines in a graphical framework is sufficient for partitioning distinct protein and multiprotein complexes within the same data set. The feasibility of this approach is first demonstrated on a large set of synthetic reprojections from 35 unique macromolecular structures spanning a mass range of hundreds to thousands of kilodaltons. We then apply our algorithm on cryo-EM data collected from a mixture of five protein complexes and use existing methods to solve multiple three-dimensional structures ab initio. Incorporating methods to sort single particle cryo-EM data from extremely heterogeneous mixtures will alleviate the need for stringent purification and pave the way toward investigation of samples containing many unique structures.
Introduction
Cryo-electron microscopy (cryo-EM) has undergone a revolutionary shift in the past few years. Increased signal in electron micrographs, as a result of direct electron detectors, has allowed for the near-atomic resolution structure determination of many macromolecules of various shapes and sizes (Kühlbrandt, 2014). These new detectors combined with automated data collection software and improvements in image processing suggest that cryo-EM could be utilized as a high-throughput approach to structural biology. One emerging field in single particle cryo-EM that seeks to take advantage of these advances is the direct investigation of macromolecules from cellular extracts (Doerr, 2018; Kyrilis et al., 2019). Such an approach is motivated by many observations that fractions from chromatographically separated cell extracts combined with mass spectrometry can be mined for a wealth of information including the organization of macromolecules into larger assemblies (Wan et al., 2015). A natural complement to this information would be direct structural analysis of the macromolecular assemblies from the same fractions of cell extract. Single particle cryo-EM is a promising tool for this goal. Although spatial context is lost when compared to tomography, single particle approaches are more successful at producing high-resolution structures. However, one major obstacle remains: sorting through the immense heterogeneity that is present in a mixture of tens to hundreds of macromolecular assemblies.
We and others have shown that cellular extracts contain rich structural information which can be used for the identification of multiple structures using conventional single particle analysis (Kastritis et al., 2017; Verbeke et al., 2018). More recently, we extended this approach to reconstruct macromolecular machines from the lysate of a single C. elegans embryo (Yi et al., 2018). These studies were limited to the identification of only the most abundant and easily identifiable protein and protein–nucleic acid complexes due to a lack of methods to efficiently categorize which two-dimensional (2D) projection images derive from which three-dimensional (3D) assemblies on the basis of their structural features. While a number of 3D classification schemes exist, all failed to produce reliable reconstructions for the majority of particles in these complicated mixtures. This obstacle emphasizes the long-standing need to sort mixtures of structures in addition to their conformational and compositional heterogeneity.
Several methods have been successfully implemented for sorting heterogeneity in cryo-EM data when there are conformational landscapes or variations in the subunit stoichiometry. These approaches generally fall into three categories. Currently, the most popular approach for sorting heterogeneity in cryo-EM data utilizes a maximum likelihood estimation to optimize the correct classification of particles into multiple structures (Scheres, 2012; Sigworth, 1998; Sigworth et al., 2010). Another approach is to estimate the covariance in cryo-EM data to search for regions of variability between the models and the data (Katsevich et al., 2015; Liao et al., 2015; Penczek et al., 2006). The last approach, and most relevant to this paper, involves computing similarities between projection images in the data before applying clustering methods to separate the data into homogenous subsets (Aizenbud and Shkolnisky, 2019; Herman and Kalinowski, 2008; Shatsky et al., 2010). All of these approaches have been demonstrated on samples containing a primary structure with multiple conformations or variable subunits. However, little work has been done for sorting heterogeneous samples containing multiple distinct structures.
In particular, this work uses the principle of common lines to score the similarity between many otherwise disparate 2D projection images. The central section theorem states that the Fourier transform of any 2D projection of a 3D object is a 2D section through the center of the 3D Fourier transform of the 3D object. Additionally, the 2D central section is perpendicular to the direction of the projection. It follows a dimension lower that a 1D projection (line projection) of a 2D object is a 1D central section through the 2D Fourier transform of the 2D object. Stated in real space: any two 2D projections of the same 3D object must share a 1D line projection in common (i.e. common lines) (Van Heel, 1987). The central section theorem was initially used for ab initio 3D reconstructions but has largely been abandoned in favor of projection matching strategies due to a poor sensitivity to noise (Penczek et al., 1994). For our purposes of investigating structures from lysates, projection matching is largely ineffective because we do not have initial 3D structures or even know how many structures might be present in the data and therefore cannot bootstrap from the models. However, common lines still contain significant information that can be exploited to discriminate 2D projections from a heterogeneous mixture prior to 3D reconstruction by conventional methods.
Here, we develop a pipeline for building 3D reconstructions from rich mixtures of distinct particles by first grouping aligned and averaged 2D projections into discrete, particle-specific classes using the principles of common lines and a novel graphical clustering framework. We demonstrate our method by partitioning reprojections from 35 previously solved structures into their correct groups. Furthermore, we applied this pipeline to an experimental set of cryo-EM micrographs containing a mixture of several macromolecular complexes. We were able to reconstruct multiple 3D structures after our clustering, improving on 3D classification of all particles simultaneously using current 3D reconstruction software. This work adds a new layer to the conventional classification schemes and is a necessary step for moving cryo-EM towards single particle structural biology from samples containing mixtures of many structures.
Results
Classifying projection images from multiple structures
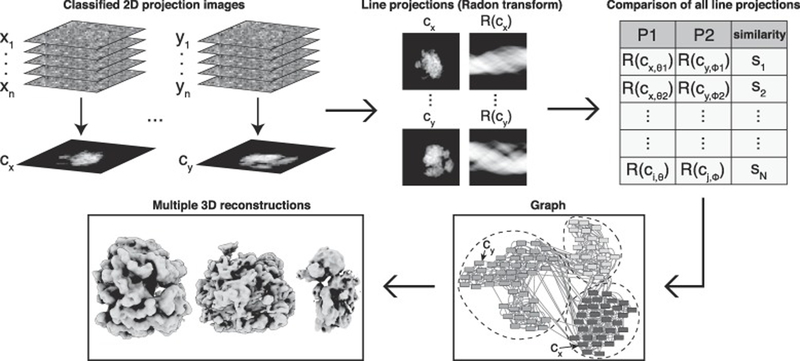
A major challenge facing “shotgun”-style cryo-EM is to reconstruct models from projection images arising from multiple distinct structures present in a mixture. To overcome this obstacle, we sought a method to computationally group heterogeneous projection images into discrete clusters that each derive from the same structure. In order to partition 2D projections into homogenous subsets, we developed an algorithm for detecting Shared Lines In Common Electron Maps (SLICEM). Using this algorithm, we score the similarity of 1D line projections between sets of aligned, classified and averaged 2D projection images (referred to as 2D class averages) without knowledge of the number of underlying 3D objects, or what they look like. Subsequently, these similarity scores can be put into a graphical framework and clustering algorithms can be applied to group related 2D projection images for subsequent 3D reconstructions (Figure 1).
Figure 1. Computational pipeline for SLICEM.
Individual particle images are averaged after reference-free 2D alignment and classification. Using a Radon transform, 1D line projections are created from the 2D class averages (referred to as 2D projections). Each 1D line projection from every 2D projection is then scored for similarity. The top scores between 2D projections are then used to create edges connecting 2D projections that have a similar 1D line projection, forming a graph. 2D projection images are then partitioned into groups belonging to the same putative structure using a community detection algorithm. Individual particle images belonging to each 2D projection within a community are subjected to ab initio 3D reconstruction.
Synthetic data
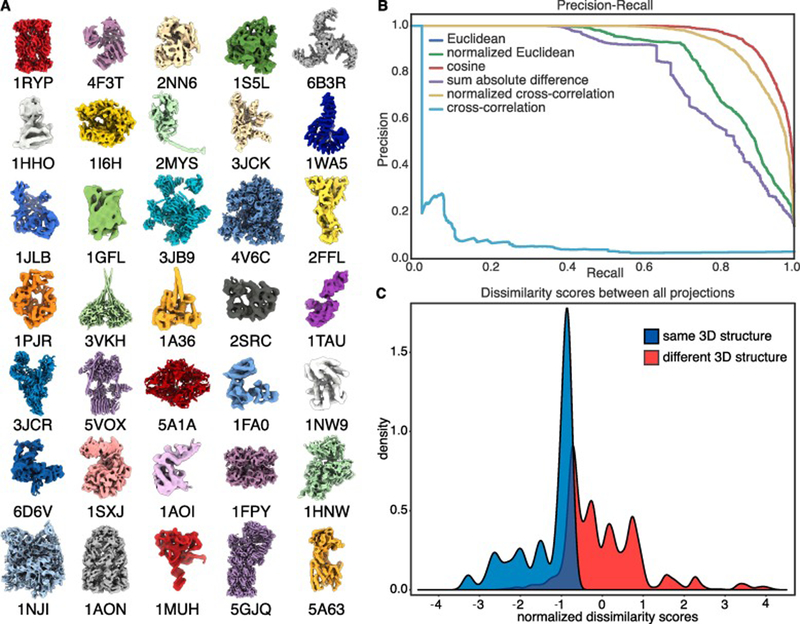
To test our approach using SLICEM, we generated synthetic reprojections from 35 previously solved structures deposited in the PDB (see Methods). The structures ranged in molecular weight from ~30 – 3000 kDa (Figure 2A). Each PDB structure was low-pass filtered to 9 Å and uniformly reprojected to create 12 2D projection images, forming an initial set of 420 reprojections simulating 2D class averages from a mixture of structures (Ludtke et al., 1999) (Figure S1). Although these reprojections do not perfectly reflect experimentally determined 2D class averages, failure of this test would indicate little power for real data. Each 2D projection is in turn projected down to 1D in 5 degree increments over 360 degrees.
Figure 2. Separating mixtures of synthetic 2D reprojections.
Synthetic reprojections were generated from 35 distinct PDB structures low-pass filtered to 9 Å from protein and protein assemblies ranging in molecular weight from ~30 – 3000 kDa, prior to separation using SLICEM. (A) Low-pass filtered models of each PDB structure. (B) Precision-recall plot ranking 6 different metrics at scoring the similarity between 1D line projections from each 2D reprojection. (C) Distribution of scores calculated using Euclidean distance for reprojections belonging to the same structure and reprojections belonging to different structures.
The similarity between all 1D line projections from every 2D reprojection was then scored using different metrics to evaluate their performance for identifying common line projections. The metrics evaluated were Euclidean distance (Eq. 1), sum of the absolute difference (Eq. 2), cross-correlation (Eq. 3) and cosine similarity (Eq. 4) (see Methods). We additionally tested the performance of the Euclidean distance and cross-correlation after a Z-score normalization of each 1D line projection. Scoring common lines depends heavily on the centering of 2D class averages. We address this in two ways in our algorithm. As an additional layer of image processing, the particle in each class average is centered by encompassing it in a minimal bounding box. Next, as part of the scoring, if there is a difference in length between a given pair of 1D projections, the smaller of the two vectors is translated pixel-wise relative to the other vector and scored at each position to account for class averages that might be offset relative to other similar class averages. The optimum score during translations is then used as the similarity between the two 1D line projections.
The precision and recall of correctly pairing 2D class averages from the same 3D structures was then computed in order to determine the performance of each metric, and cosine similarity was determined to be the top performing metric (Figure 2B). Euclidean distance and normalized Euclidean distance had identical performance and are overlaid on the plot. Not surprisingly, cross-correlation was the worst performing metric as the dot product between two vectors scales with their magnitude. Thus, 1D projections from larger protein assemblies are more likely to score higher even if there is no true similarity between the 1D projections.
In order to identify sets of 2D projection images from the same 3D particles, we constructed a network from the comparisons between 2D reprojections, or class averages, as follows: Each 2D class average was represented as a node in a directed graph, with each node connected by edges to the nodes corresponding to the 5 most closely-related 2D class averages based on the similarity of their 1D line projections. While the top-scoring metric in our precision/recall analysis was cosine similarity, the network generated from the Euclidean distance similarity most clearly showed communities (clusters of 2D class averages) correctly partitioned by 3D structure (Figure S2). This result is reflected by the well separated distributions of scores for reprojections belonging to the same structure and scores for reprojections belonging to different structures (Figure 2C). We additionally applied a traditional hierarchical clustering scheme and show the block structure present in the similarity scores between reprojections (Figure S2). These results show that partitioning 2D projection images by scoring the similarity of their 1D line projections is a powerful, unsupervised approach for sorting cryo-EM data from distinct 3D structures within a heterogeneous mixture.
We additionally tested the following cases that are often present in cryo-EM datasets: (1) uneven angular distribution and number of projections (i.e. non-uniform sampling of the structure), (2) molecular symmetry in the structure, and (3) conformational and subunit heterogeneity. In the first test, performance of the algorithm was only slightly diminished over the case of uniform projections (Figure S3). Preferential orientation negatively impacts 3D reconstruction, but has significantly less effect when simply searching for common lines. Our algorithm was also able to effectively distinguish synthetic 2D reprojections for the latter two cases (Figure S4). In the competitive graphical framework, similar but lower scoring projections (e.g. due to a change in conformation) are outcompeted by higher scoring projections in the same conformation. Molecular symmetries may also be beneficial as they increase the chance of finding a common line between structures. Thus, scoring by common lines provides a powerful approach for ranking the similarity of 2D projections in a mixture.
Cryo-EM on a mixture of protein complexes
After validating our SLICEM algorithm on a synthetic dataset, we performed cryo-EM on an experimental mixture of structures and tested our approach as a proof-of-principle. Our experimental mixture consisted of 40S, 60S and 80S ribosomes at 75 nM, 150 nM and 50 nM, respectively, and apoferritin and β-galactosidase each at 125 nM. We collected ~2,400 images and used a template-based particle picking scheme to select ~523,000 particles from the entire data set (Roseman, 2004). Raw micrographs showed a mixture of disperse particles with varying size and shape (Figure S5). We then performed 2D classification on the entire set of particles using RELION (Scheres, 2012). After 1 round of filtering junk particles, the remaining ~203,000 particles were sorted into 100 classes using RELION. The class averages contained many characteristic ribosome projections and had distinct structural features (Figure S5). We were unable to identify any β-galactosidase particles in our collected images.
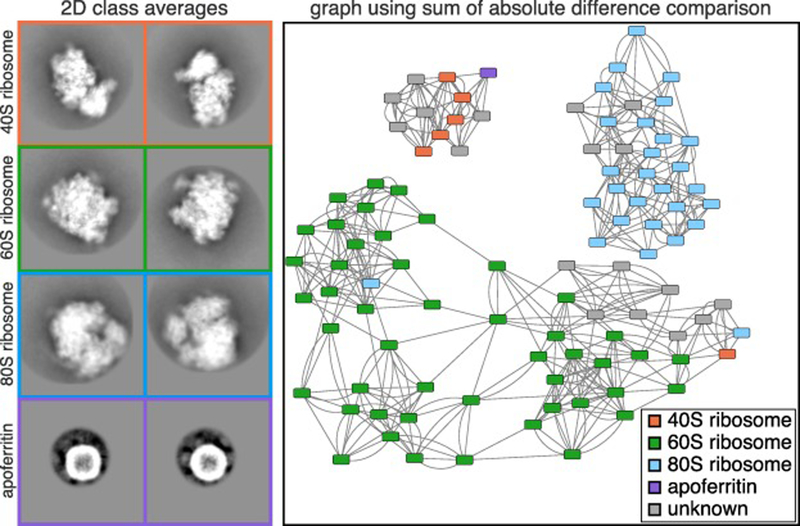
We then applied our SLICEM algorithm to the 100 2D class averages. The identity of each 2D class average was manually annotated, where it was easily recognizable, to assess whether our algorithm was correctly separating the 2D projection images from our heterogeneous mixture (Figure 3). Based on these manual annotations, we again tested the 6-different metrics in a precision-recall framework to determine which metric performed better on experimental data (Figure S6). The Euclidean distance and sum of the absolute difference scoring metrics significantly outperformed the cosine similarity. Using the sum of the absolute difference scoring metric, the network naturally partitioned into 3 distinct communities, one for each ribosome, prior to employing any community detection algorithms (Figure 3).
Figure 3. Experimental 2D class averages and resulting network.
Cryo-EM data was collected on a mixture of 5 protein and protein-nucleic acid complexes. Representative 2D class averages of the 4 complexes identified in the mixture are shown on the left. The identity of each class average was manually annotated were it could be easily identified. The class average corresponding to apoferritin was further subdivided into multiple classes for visualization. Each box corresponds to a width of 422 Å. The network displayed was generated after using SLICEM on the 100 2D class averages scored using the sum of the absolute difference metric. Nodes representing each 2D class averages are colored by their putative structural identity and are connected to their 5 most similar class averages.
As part of our algorithm, we evaluated two community detection methods, edge betweenness and walktrap, to determine if the network should be further subdivided (Newman and Girvan, 2004; Pons and Latapy, 2005). We chose to use community detection algorithms to prevent biasing the data by choosing a specific number of output clusters we expected. Briefly, the algorithms work as follows: For edge betweenness, edges with the highest “betweenness” score in a network are iteratively removed and the betweenness recalculated. At some iteration, the network is separated into separate components (i.e. communities). For walktrap, random walks on a graph tend to stay in the same community if they are densely packed. A similarity score between nodes can then be calculated and used for partitioning of the graph. Both approaches have advantages and disadvantages for our purpose here and the best choice for clustering is largely empirical.
As part of our processing pipeline, we note that the initial choice for the number of 2D class averages, computed here using RELION, can have an effect on the performance of our algorithm. We tested K = 80, 100, 120 and 200 classes to assess the effect on the performance of our algorithm (Figure S7). Despite varying the number of classes, the resulting networks still show correct grouping of 2D class averages from the same 3D structure. At all K values, performance measured by precision and recall is substantially better than random assignment of class averages. However, these results also suggest that moving forward, a more quantitative approach should be taken for selecting the number of 2D class averages. Using our SLICEM algorithm, we demonstrate that it is possible to correctly separate 2D projection images from 3 large, asymmetric macromolecular complexes in the same mixture.
Summed pixel intensity as an additional filtering step
Apart from partitioning 2D projection images into homogenous subsets for 3D reconstruction, one additional goal of shotgun-EM is to determine the identity of each projection image. In previous studies, we and others have leveraged mass spectrometry data to help identify electron microscopy reconstructions from a heterogeneous mixture, such as cell lysate, where the architecture of every protein or protein complex is not known (Kastritis et al., 2017; Verbeke et al., 2018). However, this combined MS-EM approach was only useful for identifying highly abundant and easily recognizable structures.
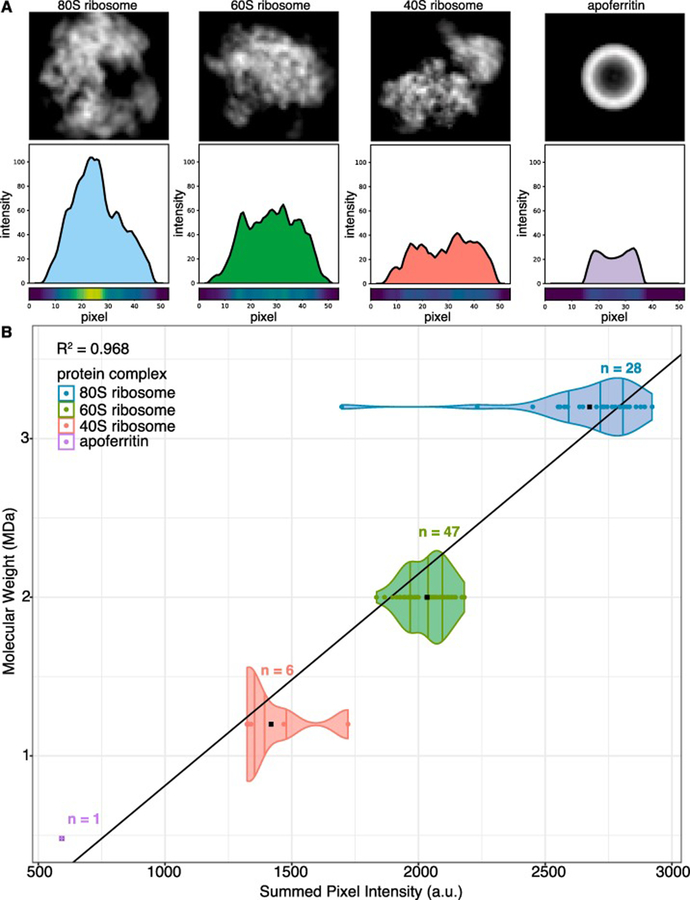
To provide evidence of macromolecular identity from the electron maps, we calculated the sum of pixel intensities for each manually annotated 2D class average as a proxy for molecular weight (Figure 4). The summed pixel intensities of each annotated 2D class average is plotted as a point on the violin plot to show the distribution of summed pixel intensities between projections of the same structure and between projections of different structures. We found that each of the three ribosomes and apoferritin had unique summed pixel intensities that could be used to distinguish their class averages. Although these values do not directly correspond to molecular weight, and the values will depend on microscope settings or specimen variation, such as ice thickness, class averages belonging to the same structure should have similar values that can be ranked relative to external data (e.g. mass spectrometry data). A least-squares fit to the mean of the summed pixel intensities showed a linear relationship between summed pixel intensity and molecular weight.
Figure 4. Summed pixel intensities of 2D class averages correlate to molecular weight.
(A) 2D to 1D projections (projection angle orthogonal to the x-axis) for representative 2D class averages of each structure present in the mixture. 1D projection plots show the line profile for a single 1D projection of each 2D class average. Pixel heat maps show the intensity of the line profile at each pixel. (B) Distribution of the summed pixel intensities calculated for each 2D class average. Summed pixel intensities for each manually identified 2D class average are plotted against their respective molecular weight. Black points are the mean summed pixel intensity for each structure and n indicates the number of 2D classes for each structure.
The summed pixel intensities were therefore used as an additional filtering step by removing nodes in communities whose summed pixel intensities were outliers in that community. Using this filtering step, the apoferritin class average was removed from the community containing predominantly 40S ribosome reprojections. Our data suggest that, given an appropriate set of standards, summed pixel intensity can be correlated to molecular weight. Thus, summed pixel intensity could be useful in narrowing down the possible identities for a set of electron density maps, when combined with sequence information from mass spectrometry.
3D classification of a mixture of protein complexes
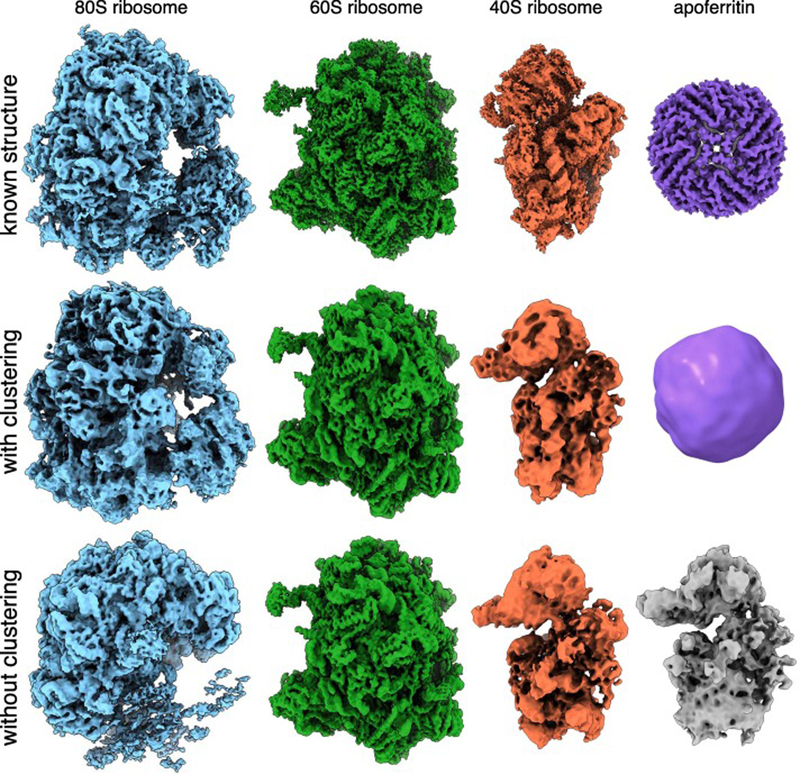
The ultimate goal of our pipeline is to reconstruct multiple 3D models from our output of clustered 2D projection images. We chose to use cryoSPARC for 3D reconstructions because it can perform heterogeneous reconstruction without a priori information on structure or identity (Punjani et al., 2017). We used the particles from each of our 3 distinct communities in addition to the isolated apoferritin node for ab initio reconstruction in cryoSPARC (Figure 5). The cluster containing primarily 40S ribosome particles was split into two classes to filter the additional junk particles present in the community. Comparison of our models reconstructed after clustering to the models produced using the entire data set as input for ab initio reconstruction in cryoSPARC with 4 classes (one for each protein complex in the mixture) showed our pre-sorting procedure improved the resulting structures (Figure 5). In particular, we were able to build an apoferritin model that was missed in the 3D classification of all particles from cryoSPARC. Our 80S model also shows a more complete density for the small subunit than its counterpart in the model created without clustering. We also observe that changing the number of classes using ab initio reconstruction in cryoSPARC had a substantial impact on the quality of classification (Figure S8).
Figure 5. Ab initio structures from an experimental mixture.
(Top) High-resolution structures of the 80S ribosome EMD-2858 (Cianfrocco and Leschziner, 2015), 60S ribosome EMD-2811 (Shen et al., 2015), 40S ribosome EMD-4214 (Scaiola et al., 2018) and apoferritin EMD-2788 (Russo and Passmore, 2014). (Middle) 3D models of the 80S ribosome, 60S ribosome, 40S ribosome and apoferritin generated by sorting particles using SLICEM prior to ab initio 3D reconstruction in cryoSPARC. (Bottom) 3D models generated using ab initio reconstruction to generate 4 classes in cryoSPARC without pre-sorting particles using SLICEM.
Each model was refined and evaluated using the gold-standard 0.143 Fourier shell correlation criterion (Figure S9). We obtained easily identifiable 40S, 60S, and 80S ribosome structures at 12, 4, and 5.4 Å resolution, respectively. We were also able to reconstruct the smaller, more compact apoferritin at 19 Å resolution. The ratio of particle numbers for each model was also compared to the input concentrations and shows a bias towards 60S particles (Figure S9). Notably, the 40S and 80S models contain streaks in one dimension, indicating that we are missing several orientations of the particles. We attribute this to preferential orientation of the particles in ice, rather than an inability of our algorithm to properly sort particles into correct communities. Together, these results demonstrate a functioning pipeline for sorting 2D projection images from a heterogeneous mixture of 3D structures, allowing for single particle EM to be applied to samples containing multiple proteins or protein complexes. Importantly, aside from choosing the most appropriate similarity measure, our approach is fully unsupervised, requiring no user defined estimate of the number of existing 3D classes.
Discussion
As cryo-EM continues to rapidly advance, one potential application would be to perform high-throughput single particle structural biology of the cell. In particular, our goal is to survey macromolecular structures directly from cell lysates. The ability to correctly sort and classify heterogeneous mixtures will become a necessary feature. One advantage of this approach would be to study closer-to-native proteins directly from cells without the need to purify or alter the sample. Currently, handling compositional and conformational heterogeneity is a major challenge for the EM field, usually requiring expert, time-consuming steps. For our purposes of samples containing many structures, the more sophisticated projection matching algorithms currently used are not effective by themselves as they require an estimate for the number of 3D models expected. Additionally, chromatographic separation of cell lysate is often done on the basis of size, ruling out using the size of 2D projections as a means for separating them.
In this study, we present an unsupervised algorithm, SLICEM, which extends on previous methods and demonstrates that scoring the similarity between 2D class averages based on their 1D line projections contains sufficient information to correctly cluster 2D class averages of the same 3D structure from a mixture of protein and protein-nucleic acid complexes. Using the principal of common lines in a competitive graphical framework provides auxiliary information which can enhance traditional classification. Additionally, as we are not using the common lines to define a relative angle about a tilt axis between 2D projections, many of the pitfalls previously observed with using common lines for 3D reconstruction do not apply. We first demonstrate that the algorithm successfully sorts a synthetic dataset of reprojections created from 35 unique macromolecular structures. Next, we show the same algorithm can successfully partition 2D class averages from an experimental data set containing multiple macromolecular complexes. Pre-sorting 2D projection images prior to 3D classification can allow for current reconstruction algorithms to be employed on datasets containing many unique structures.
Although we demonstrated the feasibility of our approach on synthetic and experimental data, we acknowledge that there are several limitations. In particular, our algorithm relies on the quality of upstream 2D alignment, classification and averaging. One possible approach to better quantify the 2D class averages input to our algorithm would be to sweep multiple values of 2D classes and compare their Fourier ring correlations to see which number of classes has the most similar, high-resolution classes. There will likely be a tradeoff between picking enough classes to cover the heterogeneity present in the data and still having enough signal for accurate common line detection. However, our intent with this algorithm is simply to pre-sort 2D projections belonging to the same structure allowing for more robust 3D classification schemes. As we observed during 2D classification of our cryo-EM data, all apoferritin particles were grouped into a single class average. However, during our network generation step, each class average is given multiple edges to the most similar classes, forcing the single apoferritin class average to have multiple spurious edges. This error will occur any time the number of class averages of a given structure is less than the number of edges used in the graph. Future modifications to the algorithm could include searching for symmetric class averages, where this error is more likely to occur, and removing them prior to community detection.
As we move cryo-EM towards structural determination from complicated mixtures, several other technical challenges will emerge, such as universal freezing conditions. In our mixture of 5 macromolecular complexes, we were unable to easily find freezing conditions that accommodated all proteins. The result was a mixture missing β-galactosidase and containing orientation preferences for the 40S and 80S ribosome. However, previous work has produced e.g. high-resolution structures of fatty-acid synthase from fractionated cell lysate, suggesting it is possible to find suitable cryo-conditions for solutions containing many macromolecular species (Kastritis et al., 2017). An additional challenge will be developing particle picking algorithms specifically for mixtures, where the particle shape may be unknown and, perhaps more importantly, non-uniform. While in this study we used a template picking scheme, future studies with mixtures of unknown composition will require more sophisticated approaches.
An expert might be able to manually sort the class averages from our cryo-EM data set; however, as mixtures grow in complexity, manual sorting will certainly become infeasible. Introducing algorithms such as SLICEM will provide an unbiased way to group 2D projection images and can be easily implemented in conjunction with a variety of image processing and 3D reconstruction packages. One additional utility of this algorithm could be to remove junk class averages from data in a semi-supervised manner by removal of communities of projection images that do not appear to have structural features. Our approach for sorting mixtures of structures combined with previous approaches for sorting conformational heterogeneity could be a powerful tool for deep classification. Development of methods to sort mixtures of structures in single particle cryo-EM will allow us to solve more structures in parallel and alleviate time-consuming protein purification and sample preparation.
Materials and Methods
Synthetic data generation
The following list of PDB entries were used to create the dataset of synthetic reprojections (1A0I, 1HHO, 1NW9, 1WA5, 3JCK, 5A63, 1A36, 1HNW, 1PJR, 2FFL, 3JCR, 5GJQ, 1AON, 1I6H, 1RYP, 2MYS, 3VKH, 5VOX, 1FA0, 1JLB, 1S5L, 2NN6, 4F3T, 6B3R, 1FPY, 1MUH, 1SXJ, 2SRC, 4V6C, 6D6V, 1GFL, 1NJI, 1TAU, 3JB9, 5A1A). Each PDB entry was low-pass filtered to 9 Å and converted to a 3D EM density using ‘pdb2mrc’ in EMAN (Ludtke et al., 1999). These densities were then uniformly reprojected using ‘project3d’ in EMAN to create 12 2D reprojections for each structure (Ludtke et al., 1999). Reprojections were centered in 350 Å boxes.
Purification of apoferritin and β-galactosidase
Size-exclusion chromatography was performed at 4 °C on an AKTA FPLC (GE Healthcare). Approximately 10 mg of apoferritin (Sigma A3660–1VL) and 5 mg of β-galactosidase G5635–5KU were independently applied to a Superdex 200 10/300 GL analytical gel filtration column (GE Healthcare) equilibrated in 20 mM HEPES KOH, 100 mM potassium acetate, 2.5 mM magnesium acetate, pH 7.5 at a flow rate of 0.5 mL min-1. Fractions were collected every 0.5 mL.
SLICEM Algorithm
Our algorithm consists of five main steps: (1) Extracting 2D class average signal from background, (2) Generating 1D line projections from the extracted 2D projection images, (3) Scoring the similarity of all pairs of 1D line projections, (4) Building a nearest-neighbors graph of the 2D class averages and (5) Partitioning communities within the graph.
(1) Extracting 2D class averages from background
The input to our algorithm is a set of centered and normalized 2D class averages. The images are normalized according to the RELION conventions of setting particles to a mean value of zero and a standard deviation of one for all pixels in the background area. We then extract the centered region of positive pixels values from the zero-mean normalized images to remove background signal and extra densities that might be present in a class average. This step also serves to re-center the class average by surrounding it with a minimal bounding box.
(2) Generating 1D line projections from extracted 2D projection images
Each newly extracted class average is then projected into 1D over 360 degrees in 5 degree intervals by summing the pixel values along the projection axis. The 1D line projections are then ready to be scored or are independently zero-mean normalized if the normalized cross-correlation or normalized Euclidean distance scoring metric are selected.
(3) Scoring the similarity of all pairs of 1D line projections
To score the similarity of the 1D line projections we consider 6 different scoring metrics. The metrics evaluated were Euclidean distance (Eq. 1), sum of the absolute difference (Eq. 2), cross-correlation (Eq. 3) and cosine similarity (Eq. 4). We additionally consider Euclidean distance and cross-correlation after a Z-score normalization of each 1D line projection. For two 1D line projection vectors p and q, the difference d between the vectors can be calculated as follows:
| (1) |
| (2) |
| (3) |
| (4) |
The similarity of the 1D line projections is calculated for all pixel-wise translations of the smaller 1D projection across the larger 1D projection if there is a difference in projection size, analogous to the ‘sliding’ feature of standard cross-correlations. The optimum score during the translations is kept for each pair of 1D projections. After pairwise scoring of all 1D line projections from all 2D class averages, the similarity between each pair of 2D class averages is defined by their respective best scoring 1D line projections.
(4) Building a nearest-neighbors graph of the 2D class averages
SLICEM then constructs a directed graph using the similarity scores calculated for each pair of 2D class averages. Each node (2D class average) is connected to the 5 most similar (top scoring) 2D class averages. Each edge is assigned a weight computed as a Z-score relative to all scores for a given 2D class average.
(5) Partitioning communities within the graph.
The resulting graph is then subdivided using a community detection algorithm. Specifically, we evaluated the edge-betweenness and walktrap algorithms to define clusters in the graph. The default parameters for each clustering method implemented in iGraph were used in our algorithm, however we note that different similarity metrics and ‘clustering strengths’ can be applied. For edge-betweenness, the dendrogram is cut at the level which maximizes the modularity and for walktrap, the length of the random walks is set to 4. Then, the median absolute deviation of summed pixel intensities for each node is calculated to remove outliers from clusters. Finally, for each community, the individual raw 2D particles corresponding to the now-grouped 2D class averages are then used as input for 3D reconstruction in cryoSPARC.
Cryo-EM grid preparation and data collection
C-flat holey carbon grids (CF-1.2/1.3, Protochips Inc.) were pre-coated with a thin layer of freshly prepared carbon film and glow-discharged for 30 seconds using a Gatan Solarus plasma cleaner before addition of sample. 2.5 μl of a mixture of 75 nM 40S ribosome, 150 nM 60S ribosome, 50 nM 80S ribosome, 125 nM apoferritin and 125 nM β-galactosidase were placed onto grids, blotted for 3 seconds with a blotting force of 5 and rapidly plunged into liquid ethane using a FEI Vitrobot MarkIV operated at 4 °C and 100% humidity. Data were acquired using an FEI Titan Krios transmission electron microscope (Sauer Structural Biology Laboratory, University of Texas at Austin) operating at 300 keV at a nominal magnification of ×22,500 (1.1 Å pixel size) with defocus ranging from −2.0 to −3.5 μm. The data were collected using a total exposure of 6 s fractionated into 20 frames (300 ms per frame) with a dose rate of ~8 electrons per pixel per second and a total exposure dose of ~40 e− Å−2. A total of 2,423 micrographs were automatically recorded on a Gatan K2 Summit direct electron detector operated in counting mode using the MSI Template application within the automated macromolecular microscopy software LEGINON (Suloway et al., 2005).
Cryo-EM data processing
All image pre-processing was performed in Appion (Lander et al., 2009). Individual movie frames were aligned and averaged using ‘MotionCor2’ drift-correction software (Zheng et al., 2017). These drift-corrected micrographs were binned by 8, and bad micrographs and/or regions of micrographs were removed using the ‘manual masking’ command within Appion. A total of 522,653 particles were picked with a template-based particle picker using a reference-free 2D class average from a small subset of manually picked particles as templates. The contrast transfer function (CTF) of each micrograph was estimated using CTFFIND4 (Rohou and Grigorieff, 2015). Selected particles were extracted from micrographs using particle extraction within RELION (Scheres, 2012) and the EMAN2 coordinates exported from Appion. Two rounds of reference free 2D classification with 100 classes for each sample were performed in RELION to remove junk particles, resulting in a clean stack of 202,611 particle images.
Supplementary Material
Highlights.
Single particle cryo-EM can be performed on mixtures containing multiple distinct macromolecular assemblies
Developed an algorithm using common lines in a graphical framework to classify 2D projection images
Using this algorithm, we separate a mixture of synthetic data and a mixture of experimental data
Acknowledgements
We thank S. Musalgaonkar and A. Johnson for providing 40S and 60S yeast ribosomes; A. Dai for expert cryo-EM assistance at the Sauer Structural Biology Laboratory at UT Austin; and members of the Taylor and Marcotte laboratories for helpful discussions. This work was supported in part by Welch Foundation Research Grants F-1938 (to D.W.T.) and F-1515 (to E.M.M.), Army Research Office Grant W911NF-15-1-0120 (to D.W.T.), a Robert J. Kleberg, Jr. and Helen C. Kleberg Foundation Medical Research Award (to D.W.T.), and grants from the National Institutes of Health (GM122480, DK110520, HD085901) to E.M.M.. D.W.T is a CPRIT Scholar supported by the Cancer Prevention and Research Institute of Texas (RR160088) and an Army Young Investigator supported by the Army Research Office (W911NF-19–1-0021).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Data Availability
The cryo-EM reconstructions of the 40S, 60S, 80S, and apoferritin have been deposited in the Electron Microscopy Databank with accession codes EMD-20109, EMD-20110, EMD-20111 and EMD-20112, respectively. The motion-corrected sum micrographs have been deposited into EMPIAR with accession code EMPIAR-10268. Computer code for SLICEM is available at https://github.com/marcottelab/SLICEM.
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper
References
- Aizenbud Y, and Shkolnisky Y. (2019). A max-cut approach to heterogeneity in cryo-electron microscopy. J. Math. Anal. Appl 479, 1004–1029. [Google Scholar]
- Cianfrocco MA, and Leschziner AE. (2015). Low cost, high performance processing of single particle cryo-electron microscopy data in the cloud. ELife 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doerr A. (2018). Taking inventory with shotgun EM. Nat. Methods 15, 649–649. [DOI] [PubMed] [Google Scholar]
- Herman GT, and Kalinowski M. (2008). Classification of heterogeneous electron microscopic projections into homogeneous subsets. Ultramicroscopy 108, 327–338. [DOI] [PubMed] [Google Scholar]
- Kastritis PL, O’Reilly FJ, Bock T, Li Y, Rogon MZ, Buczak K, Romanov N, Betts MJ, Bui KH, Hagen WJ, et al. (2017). Capturing protein communities by structural proteomics in a thermophilic eukaryote. Mol. Syst. Biol 13, 936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katsevich E, Katsevich A, and Singer A. (2015). Covariance Matrix Estimation for the Cryo-EM Heterogeneity Problem. SIAM J. Imaging Sci 8, 126–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kühlbrandt W. (2014). The resolution revolution. Science 343, 1443–1444. [DOI] [PubMed] [Google Scholar]
- Kyrilis FL, Meister A, and Kastritis PL. (2019). Integrative biology of native cell extracts: a new era for structural characterization of life processes. Biol. Chem 400, 831–846. [DOI] [PubMed] [Google Scholar]
- Lander GC, Stagg SM, Voss NR, Cheng A, Fellmann D, Pulokas J, Yoshioka C, Irving C, Mulder A, Lau P-W, et al. (2009). Appion: An integrated, database-driven pipeline to facilitate EM image processing. J. Struct. Biol 166, 95–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao HY, Hashem Y, and Frank J. (2015). Efficient Estimation of Three-Dimensional Covariance and its Application in the Analysis of Heterogeneous Samples in Cryo-Electron Microscopy. Structure 23, 1129–1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludtke SJ, Baldwin PR, and Chiu W. (1999). EMAN: Semiautomated Software for High-Resolution Single-Particle Reconstructions. J. Struct. Biol 128, 82–97. [DOI] [PubMed] [Google Scholar]
- Newman MEJ, and Girvan M. (2004). Finding and evaluating community structure in networks. Phys. Rev. E 69. [DOI] [PubMed] [Google Scholar]
- Penczek PA, Grassucci RA, and Frank J. (1994). The ribosome at improved resolution: new techniques for merging and orientation refinement in 3D cryo-electron microscopy of biological particles. Ultramicroscopy 53, 251–270. [DOI] [PubMed] [Google Scholar]
- Penczek PA, Frank J, and Spahn CMT. (2006). A method of focused classification, based on the bootstrap 3D variance analysis, and its application to EF-G-dependent translocation. J. Struct. Biol 154, 184–194. [DOI] [PubMed] [Google Scholar]
- Pons P, and Latapy M. (2005). Computing Communities in Large Networks Using Random Walks In Computer and Information Sciences - ISCIS 2005, pInar Yolum, Güngör T, Gürgen F, and Özturan C, eds. (Berlin, Heidelberg: Springer Berlin Heidelberg; ), pp. 284–293. [Google Scholar]
- Punjani A, Rubinstein JL, Fleet DJ, and Brubaker MA. (2017). cryoSPARC: algorithms for rapid unsupervised cryo-EM structure determination. Nat. Methods 14, 290–296. [DOI] [PubMed] [Google Scholar]
- Rohou A, and Grigorieff N. (2015). CTFFIND4: Fast and accurate defocus estimation from electron micrographs. J. Struct. Biol 192, 216–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roseman A. (2004). FindEM—a fast, efficient program for automatic selection of particles from electron micrographs. J. Struct. Biol 145, 91–99. [DOI] [PubMed] [Google Scholar]
- Russo CJ, and Passmore LA. (2014). Ultrastable gold substrates for electron cryomicroscopy. Science 346, 1377–1380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scaiola A, Peña C, Weisser M, Böhringer D, Leibundgut M, Klingauf-Nerurkar P, Gerhardy S, Panse VG, and Ban N. (2018). Structure of a eukaryotic cytoplasmic pre-40S ribosomal subunit. EMBO J. 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheres SHW. (2012). RELION: Implementation of a Bayesian approach to cryo-EM structure determination. J. Struct. Biol. 180, 519–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shatsky M, Hall RJ, Nogales E, Malik J, and Brenner SE. (2010). Automated multi-model reconstruction from single-particle electron microscopy data. J. Struct. Biol 170, 98–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen PS, Park J, Qin Y, Li X, Parsawar K, Larson MH, Cox J, Cheng Y, Lambowitz AM, Weissman JS, et al. (2015). Rqc2p and 60S ribosomal subunits mediate mRNA-independent elongation of nascent chains. Science 347, 75–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigworth FJ. (1998). A Maximum-Likelihood Approach to Single-Particle Image Refinement. J. Struct. Biol 122, 328–339. [DOI] [PubMed] [Google Scholar]
- Sigworth FJ, Doerschuk PC, Carazo J-M, and Scheres SHW. (2010). An Introduction to Maximum-Likelihood Methods in Cryo-EM In Methods in Enzymology, (Elsevier; ), pp. 263–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suloway C, Pulokas J, Fellmann D, Cheng A, Guerra F, Quispe J, Stagg S, Potter CS, and Carragher B. (2005). Automated molecular microscopy: The new Leginon system. J. Struct. Biol 151, 41–60. [DOI] [PubMed] [Google Scholar]
- Van Heel M. (1987). Angular reconstitution: A posteriori assignment of projection directions for 3D reconstruction. Ultramicroscopy 21, 111–123. [DOI] [PubMed] [Google Scholar]
- Verbeke EJ, Mallam AL, Drew K, Marcotte EM, and Taylor DW. (2018). Classification of Single Particles from Human Cell Extract Reveals Distinct Structures. Cell Rep. 24, 259–268.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan C, Borgeson B, Phanse S, Tu F, Drew K, Clark G, Xiong X, Kagan O, Kwan J, Bezginov A, et al. (2015). Panorama of ancient metazoan macromolecular complexes. Nature 525, 339–344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi X, Verbeke EJ, Chang Y, Dickinson DJ, and Taylor DW. (2018). Electron microscopy snapshots of single particles from single cells. J. Biol. Chem jbc.RA118.006686. [DOI] [PMC free article] [PubMed]
- Zheng SQ, Palovcak E, Armache J-P, Verba KA, Cheng Y, and Agard DA. (2017). MotionCor2: anisotropic correction of beam-induced motion for improved cryo-electron microscopy. Nat. Methods 14, 331–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.