Abstract
Time-resolved decays of fluorescence anisotropy were obtained from frequency-domain measurements of the phase angle difference between the parallel and perpendicular components of the polarized emission and the ratio of the modulated amplitudes. These data were measured at modulation frequencies ranging from 1 to 200 MHz. To demonstrate the general applicability of this method, we describe the resolution of both simple and complex decays of anisotropy. In particular, we resolved single, double, and triple exponential decays of anisotropy and the hindered rotational motions of fluorophores within lipid bilayers. The ease and rapidity with which these results were obtained indicate that frequency-domain measurements are both practical and reliable for the determination of complex decays of anisotropy.
Registry No. DPH, 1720-32-7; DMPC, 18194-24-6; DPPC, 63-89-8; DOPC, 4235-95-4; perylene, 198-55-0; fluorescein, 2321-07-5; propylene glycol, 57-55-6; cholesterol, 57-88-5
Time-resolved decays Of fluorescence anisotropy reveal the time-dependent rotational motions of fluorophores on the nanosecond time scale. These motions are generally dependent upon the fluorophore and its surrounding environment. For instance, time-resolved anisotropies can reveal the torsional motions of tryptophan and tyrosine residues in proteins (Ichiye & Karplus, 1983; Levy & Szabo, 1982; Lipari & Szabo 1980; Munro et al., 1979; Ross et al., 1981a,b), which in turn may reflect the extent of structural fluctuations within the protein matrix. Additionally, time-resolved anisotropies have provided valuable information about the dynamics and order of lipid bilayers (Kinosita et al., 1984; Stubbs et al., 1981; Chen et al., 1977) and about the overall flexibility of large proteins such as the immunoglobulins (Hanson et al., 1981). Such measurements have been the subject of several recent reviews (Steiner, 1983; Lakowicz, 1983).
Information about the time-dependent decays of anisotropy can also be obtained from steady-state measurements in the lifetime domain. For instance, by the use of quenching, one can reveal in an approximate manner the nature of the anisotropy decay law (Lakowicz et al., 1983; Lakowicz & Maliwal, 1983; Lakowicz & Knutson, 1980). Additionally, by use of phase fluorometry at one or two modulation frequencies, it has been possible to determine that the rotational motions of fluorophores in solvents and lipid bilayers are hindered and/or anisotropic (Mantulin & Weber, 1977; Lakowicz et al., 1979). However, the information content of these measurements is limited. In the case of quenching the information is limited by the range of lifetimes obtainable by quenching. In the case of phase fluorometry, the resolution has been limited by the few fixed modulation frequencies obtainable with commercially available instrumentation. With the construction of continuously variable frequency phase fluorometers (Gratton & Limkeman, 1983; Lakowicz & Maliwal, 1984) it is now possible to assess the true potential of frequency-domain measurements in determining the decays of fluorescence anisotropy. In this initial report we used two newly developed phase-modulation fluorometers which operate at modulation frequencies from 1 to 200 MHz. We measured the phase angle difference between the parallel and perpendicular polarized components of the emission and the ratio of the polarized modulated fluorescence intensities. We used these data and fitting by a nonlinear least-squares method (Bevington, 1969; Lakowicz et al., 1984a) to resolve complex anisotropy decay laws. A complete description of the theory and potential resolution has been derived (J. R. Lakowicz, B.P. Maliwal, and H. Cherek, unpublished results). To illustrate this application of the frequency-domain fluorometry, we now describe the analysis of single, double, and triple exponential decays of anisotropy, as well as analysis of the hindered rotators diphenylhexatriene (DPH)1 and perylene in lipid bilayers (Stubbs et al., 1981; Dale et al., 1977; Veatch & Stryer, 1977). Our model system for an isotropic rotator is fluorescein in propylene glycol, and an anisotropically rotating fluorophore was provided by perylene in propylene glycol (Mantulin & Weber, 1977; Barkley et al., 1981). A still more complex decay of anisotropy was observed for perylene in lipid vesicles, for which three rotational correlation times were needed to account for the measurements. It was not our intention to perform an extensive study of these systems. Rather, these systems were chosen to illustrate the diverse anisotropy decays which can be determined by using frequency-domain fluorescence spectroscopy.
Theory
Fluorescence Lifetimes.
Determination of time-resolved anisotropies from the frequency-domain data can be accomplished by using the frequency-dependent values of Δω and Λω (see below) and the fluorescence lifetime. For the present report we selected fluorophores whose intensity decays are mainly a single exponential. However, a single-exponential intensity decay is not necessary for our analysis procedures. The decay times were determined by using 6–10 modulation frequencies and the nonlinear least-squares method (Bevington, 1969; Lakowicz et al., 1984a). The calculated phase angles (ϕωc) and demodulation factors (mωc) at each modulation frequency ω are fit to the measured values (ϕω and mω by using
| (1) |
where σϕω and σmω are the estimated standard deviations of the measured phase and modulation data, as described by Gratton et al. (1984). For a single exponential decay of fluorescence intensity with a lifetime τ the calculated values are given by (Weber, 1977)
| (2) |
| (3) |
where
| (4) |
| (5) |
Decays of Fluorescence Anisotropy.
Time-resolved anisotropies were determined from the phase angle difference (Δω) between the perpendicular (ϕ⊥) and parallel (ϕ‖) component of the modulated emission (Δω = ϕ⊥ − ϕ‖) and from the ratio of the amplitudes (Λω) of the parallel (m‖) and the perpendicular (m⊥) components of the modulated emission (Λω = m‖/m⊥). Assume the decay of intensity is described by I(t) = I0e−t/τ. Then, the decay of the parallel (‖) and perpendicular (⊥) components of the decay are given by
| (6) |
| (7) |
where r(t) is the time-resolved decay of anisotropy. The form of r(t) depends upon the assumed model. Generally, r(t) can be described as a multiexponential decay
| (8) |
where r0 is the limiting anisotropy in the absence of rotational diffusion. The rotational correlation times (θi,) and the fraction of the total anisotropy loss associated with each correlation time (gi) depend upon the fluorophore, the excitation wavelength (r0), and the nature of the environment surrounding the fluorophore. We will consider three types of anisotropy decay: isotropic, anisotropic, and hindered. Irrespective of the assumed model the expected values of Δω (Δcω) and Δω (Λcω) can be calculated from the sine and cosine transforms of the individual polarized decays (Weber, 1977; Lakowicz, 1983).
| (9) |
| (10) |
The frequency-dependent values of Δω and Λω are given by
| (11) |
| (12) |
where the Ni and Di are individually calculated at each frequency. The parameters describing the anisotropy decay are obtained by minimizing the weighted squared deviations between measured and calculated values
| (13) |
In this expression and σΔω and σΛω are the estimated experimental uncertainties in the measured quantities.
We used three models to describe the decay of anisotropy. For an isotropic rotator we used
| (14) |
For the anisotropic rotator model we used a anisotropy decay law with two correlation times
| (15) |
with g1 + g2 = 1 To model a fluorophore whose motions are hindered, we used
| (16) |
In this expression r∞ is the anisotropy that would be observed at times much longer than the rotational correlation time of the fluorophore. The expressions describing Δcω and Λcω for each of these models are given in the Appendix. For all least-squares fits we used an independently measured value of r0. In most cases this restriction was not necessary, and the same results (θi, and gi) were obtained with or without this restriction. Unless indicated otherwise the errors in Δω were estimated to be 0.2 deg and in Λω to be 0.02. These values of the uncertainties (σΔω and σΛω) were chosen after examining a large number of least-squares fits. With these values the phase and modulation data appear to be weighted approximately equally, and the values of reduced χR2 are reasonably close to unity. The value of σΛω is somewhat larger than expected from previous measurements performed on mixtures of fluorophores (Lakowicz et al., 1984a; Gratton et al., 1984) and may represent some systematic error in measurement of the ratio of the modulated amplitudes. One possible source of error is that the sensitivity of the emission detector is slightly different for the parallel and perpendicular components of the emission.
Experimental Procedures
Frequency-domain measurements were obtained from 1 to 200 MHz by using either of two instruments. A variable-frequency phase modulation fluorometer was recently described in detail (Gratton & Limkeman, 1983). Some measurements were performed with this instrument using a Argon ion laser (351 nm) and an electrooptic modulator from Lasermetrics (LMA-1). Measurements of perylene in DMPC vesicles and of DPH in mineral oil were performed by using a newly constructed instrument (Lakowicz & Maliwal, 1984). This instrument uses an Inrad 102–020 electrooptic modulator, frequency synthesizers from Product Test Sources (500 MHz), and a helium-cadmium laser (Liconix) for excitation at 325 and 442 nm. All experiments were performed at least in duplicate, typically using both of the instruments described above. The experimental conditions varied slightly between these experiments, and only one of the experiments was chosen for presentation in this paper. The uncertainties in the parameters were estimated from the diagonal elements of the covariance matrix (Bevington, 1969), as was described previously for analysis of mixtures of fluorophores (Lakowicz et al, 1984a; Gratton et al., 1984). With one exception (perylene in DMPC at 5 °C) we did not present the uncertainty estimates. While the derived correlation times agreed well with the expected results, the uncertainties in the correlation times and amplitudes seemed unreasonably small. We are still investigating this topic.
Data adequate to calculate the time-resolved anisotropies were obtained by first measuring the lifetime of the sample by using about 6–10 modulation frequencies. For these measurements the excitation was vertically polarized and the emission detected through a polarizer oriented 54.7° relative to the vertical orientation. The emission was observed through a liquid filter of 1 M NaNO3 (2 mm thickness) and a Corning 3–73 filter, which served to remove scattered light at the excitation wavelength. The phase angle difference between the vertically and horizontally polarized components of the emission and the modulated amplitude ratio were directly measured by rotation of the emission polarizer. Control measurements with horizontally polarized excitation revealed no difference between these quantities. However, a small but undetected difference in sensitivity to each polarized component may have contributed to larger than expected values of σΛω.
The computer programs for the nonlinear least-squares fits were written in Basic, to operate on a MINC 11/23 under either MINC Basic or RT-11 (J. R. Lakowicz et al., unpublished results). (These programs are available from J.R.L. on request.) These programs were tested extensively by using simulated data with an without random error, and analysis of the simulated data returned the expected values for the parameters. The simulations will be the subject of a subsequent paper (J. R. Lakowicz et al., unpublished results).
Lipid vesicles were prepared as described previously (Lakowicz et al, 1979). Small unilamellar vesicles were prepared by using a probe-type sonicator followed by centrifugation at 50000g for 1 h to remove metal particles and large lipid aggregates. For all the vesicle suspensions and fluorophores in solvents the background fluorescence from the unlabeled solutions was less than 0.1% of the solutions containing fluorophore. Limiting anisotropies (r0) were determined at −65 °C in propylene glycol. These values are given in the tables.
Results
Fluorescein in Propylene Glycol, an Isotropic Rotator.
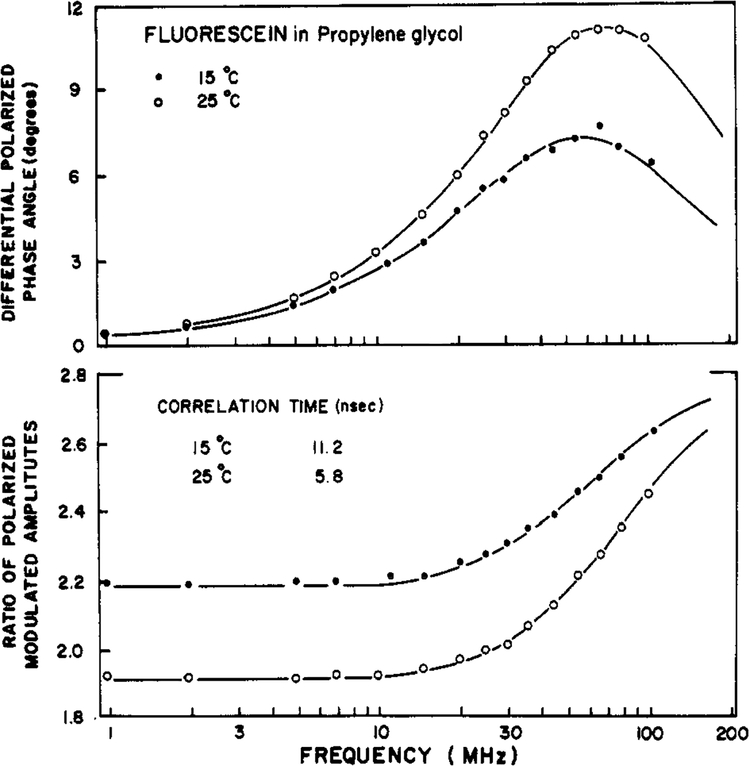
Differential polarized phase angles and modulated amplitude ratios for fluorescein in propylene glycol are shown in Figure 1. As the modulation frequency is increased one notices that the value of Δω passes through a maximum and A increases monotonically. At higher temperature (25 °C vs. 15 °C) this maximum of Δω occurs at higher frequency, reflecting the faster rotational rate of fluorophore. In this figure the solid line indicates the calculated values of Δω by using the parameters which yield the minimum value of reduced χ2 (χ2 = χ2/v, where v is the number of degrees of freedom). This theoretical curve is for the single correlation time model, which provides a satisfactory fit between the measured and the calculated data. This fact is evident from the randomly distributed deviations between Δω and Δω and between Λω and Λcω (data not shown). If the single correlation time model were not adequate, then the deviations would systematically deviate from zero (J. R. Lakowicz et al., unpublished results). This will be seen below for the anisotropic rotator perylene. For fluorescein in this solvent the inclusion of hindrance (a nonzero value of r∞) or the inclusion of a second correlation time did not result in any improvement in the value of χR2 (Table I).
FIGURE 1:
Differential polarized phase angles (top) and modulated amplitude ratio (bottom) for fluorescein in propylene glycol. Data are shown at 15 (●) and 25 (○) °C.
Table I:
Anisotropy Decay Parameters for Fluorophores in Solvents
| samples | temp (°C) | τ (ns) | r0 | fita | θ1 (ns) | θ2 (ns) | r∞ | g1 | χR2 b |
|---|---|---|---|---|---|---|---|---|---|
| fluorescein/propylene glycol | 15 | 3.7 | 0.375 | θ | 11.2 | 0.8 | |||
| θ, r∞ | 11.6 | −0.009 | 0.08 | ||||||
| 2θ | 11.9c | 27 ± 13 | 1.09 | 0.9 | |||||
| 25 | 3.7 | 0.375 | θ | 5.8 | 0.6 | ||||
| θ, r∞ | 6.3 | −0.019 | 0.4 | ||||||
| 2θ | 3.2c | 5.3 | −0.22 | 0.5 | |||||
| perylene/propylene glycol | −9 | 4.8 | 0.312 | θ | 4.09 | 25.0 | |||
| θ, r∞ | 2.64 | 0.058 | 1.8 | ||||||
| 2θ | 2.03 | 12.6 | 0.616 | 0.7 |
This indicates the floating parameters. For instance, the entry (θ, r∞) means both θ and are r∞ floating parameters. In all cases the gi, values are also floating.
In all cases both phase and modulation data were used σp = 0.2 deg and σm = 0.02.
These fits are variable and are only shown to indicate that the use of the more complex model is not supported by the data.
Perylene in Propylene Glycol, an Anisotropic Rotator.
The resolution of the correlation times of asymmetric molecules is a difficult problem (Weber, 1973). To date, only a few such resolutions have appeared. The existence of anisotropic rotations for perylene and other nonpolar molecules was shown by using differential phase fluorometry by Mantulin & Weber (1977). Subsequently, the individual rotational rates of perylene were determined by time-correlated single photon counting using mineral oil (Zinsli, 1977) and glycerol (Barkley et al., 1981) as solvents.
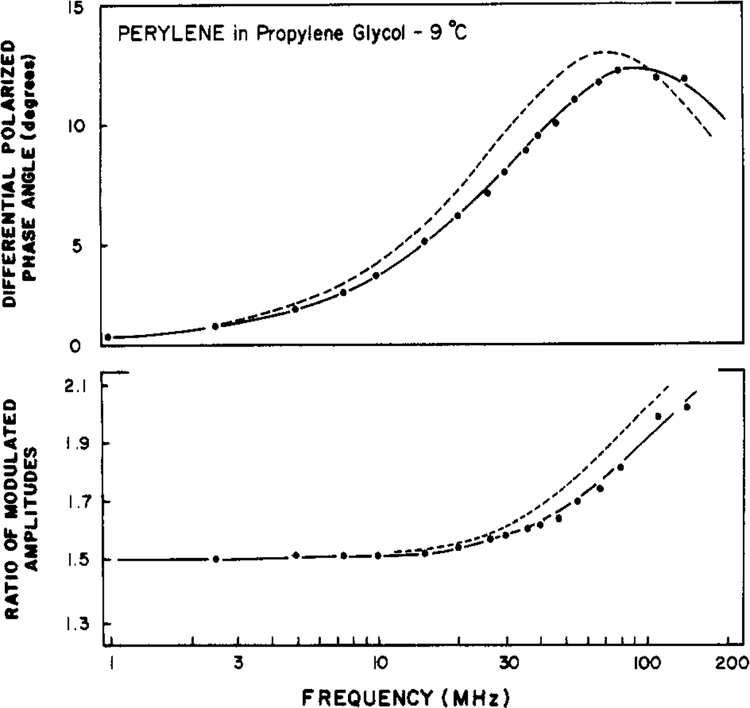
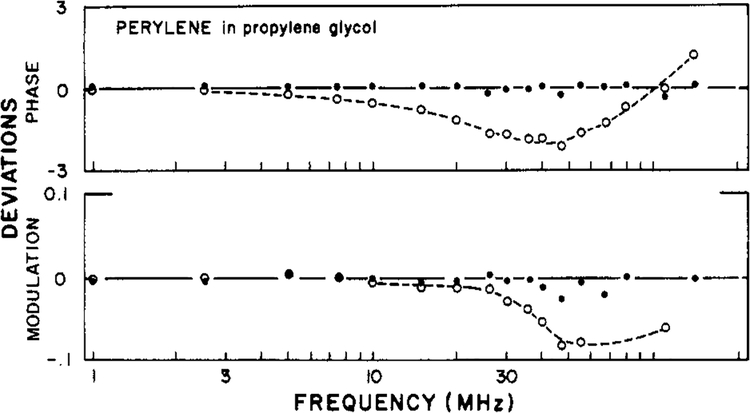
In Figure 2 we show the first resolution of a double-exponential anisotropy decay from frequency-domain data. For perylene in propylene glycol the best fit was obtained by using the two-correlation time model (eq 15). Using this model, we obtained correlation times of 2 and 12 ns (Table I) and random deviations between the measured and calculated values (Figure 3). In contrast, the data were not adequately described by a single exponential decay of anisotropy, as is evident from the systematic deviations between the measured and calculated values of Δω and Λω (Figure 3), and by the increased value of χ2R (Table I). The approximate 6-fold ratio of the correlation times of perylene is in excellent agreement with that found in the time domain by Barkley and co-workers (1981). The presence of two correlation times increases the width of the Δω vs. frequency plot (J. R. Lakowicz et al., unpublished results). This effect is modest for the closely spaced correlation times of perylene. Evidently, the currently available precision is adequate to detect this subtle difference between the data resulting from an isotropic and those from an anisotropic rotator and is also adequate to determine the individual correlation times. We note that the application of frequency-domain fluorescence is just beginning and that the experience with time-resolved methods is more extensive. One must conclude that the potential resolving power of the frequency-domain measurements is at least equivalent to that currently possible by using time-resolved measurements.
FIGURE 2:
Differential polarized phase angles (top) and modulated amplitude ratio (bottom) for perylene in propylene glycol at −9 °C. The solid line shows the best fit to the data (●) obtained by using two correlation times, χR2 = 0.7. The dashed line is the best fit obtained by using a single correlation time, χR2 = 25.
FIGURE 3:
Deviation between the measured and calculated data for perylene in propylene glycol at −9 °C. Deviations are shown for the best fits obtained by using a single correlation time (○) and two correlation times (●). In both cases r0 was held constant at the measured value of 0.312.
In Table I we also list the anisotropy decay parameters for perylene obtained by using the hindered rotator model (eq 16), whose complexity is intermediate between the one- and two-correlation time models. The hindered model provides a superior fit to the single correlation time model (eq 14) but inferior to that found by using two correlation times (eq 15). The distinction between these fits is modest, which is not an unexpected result. In all fitting procedures that employ several floating parameters one must ultimately rely on other information for selecting between models that predict similar data. For instance, there is no reason to suspect any limit to the angular displacements of perylene in propylene glycol. Hence, one is inclined toward the two-correlation time model over the hindered model. The 2-fold lower value of χR2 which is obtained by using this model strongly supports this choice.
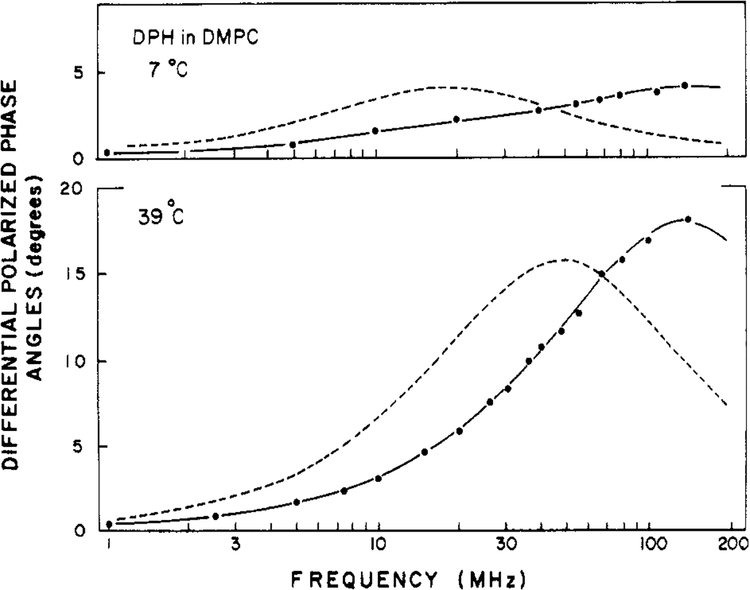
Diphenylhexatriene in Mineral Oil and Lipid Bilayer.
The probe DPH was initially suggested as an indicator of the microviscosity of cell membranes (Shinitzky & Barenholz, 1974). Subsequently, it was realized that the anisotropy decay of DPH in bilayers is complex, and considerable attention has been given to the interpretation of the r∞ values in terms of the order parameters of the bilayers (Kinosita et al., 1977; Heyn, 1979; Jahnig, 1979). To further illustrate the general usefulness of the frequency-domain measurements, we chose to examine DPH in the reference solvent mineral oil and in lipid bilayers.
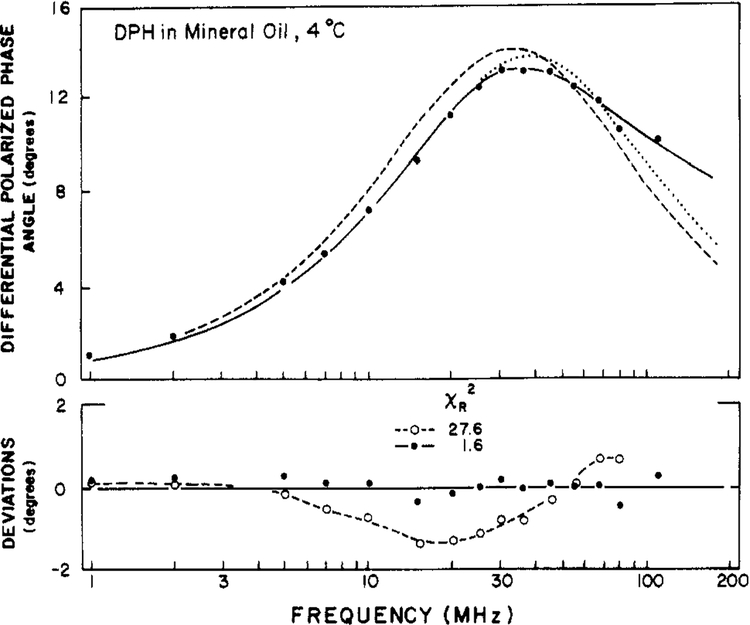
Differential polarized phase angles for DPH in mineral oil are shown in Figure 4. To our surprise the single correlation time model (broken line) did not seem adequate. Consequently, we used the more complex models with hindrance or two correlation times (Table II). The best results, as indicated by the minimum values of χR2, were obtained with the two-correlation time model (eq 15). However, it would be misleading to indicate that the data are adequate to unambiguously distinguish these comparable models. Upon examination of the results from Dale and co-workers (1977) we noticed that the time-resolved results also indicated a multiexponential anisotropy decay for DPH in mineral oil.
FIGURE 4:
Differential polarized phase angles for DPH in mineral oil at 4 °C. Data (●) and theoretical curves are shown for the models by using two correlation times (—), a single correlation time with a nonzero r∞ (⋯), and a single correlation time with r∞ = 0 (---). The lower panel shows the deviations between the measured and calculated values for the two correlation time model [(●) χR2 = 1.6] and the single correlation time model with r∞ = 0 [(○) χR2 = 27.6].
Table II:
Anisotropy Decay Parameters for Diphenylhexatriene in Mineral Oil and in Lipid Vesicles
| solvent or lipid | temp (°C) | τ (ns) | fit | θ1 (ns) | θ2 (ns) | g1 | r∞ | χR2 |
|---|---|---|---|---|---|---|---|---|
| mineral oil | 4 | 9.8 | 1θ | 10.0 | 1.0 | 27.6 | ||
| θ, r∞ | 7.3 | 0.06 | 8.6a | |||||
| 2θ | 0.76 | 9.7 | 0.16 | 1.6 | ||||
| 20b | 10.3 | 1θ | 5.27 | 81 | ||||
| θ, r∞ | 3.85 | 0.051 | 1.1 | |||||
| 2θ | 3.62 | 56.7 | 0.83 | 0.5 | ||||
| DMPC | 7 | 10.2 | 1θ | 62 | 87.5 | |||
| θ, r∞ | 1.9 | 0.31 | 5.6 | |||||
| 2θ | 1.1 | 192 | 0.15 | 0.4 | ||||
| 39 | 7.8 | 1θ | 6.2 | 547 | ||||
| θ, r∞ | 1.5 | 0.094 | 2.5 | |||||
| 2θ | 1.4 | 71 | 0.74 | 1.3 | ||||
| DPPC | 7 | 9.3 | θ | 72 | 50.8 | |||
| θ, r∞ | 2.53 | 0.311 | 3.5 | |||||
| 2θ | 1.41 | 196 | 0.14 | 0.6 | ||||
| 39 | 8.5 | θ | 9.2 | 696 | ||||
| θ, r∞ | 1.4 | 0.11 | 6.1 | |||||
| 2θ | 1.15 | 48 | 0.696 | 1.6 | ||||
| DOPC | 8 | 8.3 | 1θ | 7.0 | 104 | |||
| θ, r∞ | 3.7 | 0.083 | 7.0 | |||||
| 2θ | 2.3 | 15.5 | 0.55 | 0.9 | ||||
| 40 | 7.0 | 1θ | 0.89 | 17.1 | ||||
| θ, r∞ | 1.2 | 0.04 | 2.4 | |||||
| 2θ | 0.8 | 3.9 | 0.85 | 0.4 | ||||
| DMPC/cholesterol | 8 | 10.2 | 1θ | 66 | 117 | |||
| θ, r∞ | 1.4 | 0.31 | 3.0 | |||||
| 23θ | 1.0 | 315 | 0.18 | 0.86 | ||||
| 40 | 9.3 | 1θ | 23 | 663 | ||||
| θ, r∞ | 1.0 | 0.16 | 1.8 | |||||
| 2θ | 1.0 | 440 | 0.57 | 1.7 |
Phase only data, σp = 0.2 deg.
r0 = 0.380, 325 nm.
We also examined DPH in lipid bilayers of varied phospholipid composition (Table II). Typical results for DPH in DPPC vesicles are shown in Figure 5. Clearly, it was not possible to account for these data by using a single correlation time with no hindrance (broken line). This is particularly evident from the deviations between the measured and calculated values (Figure 6). These values are large and strongly systematic for the single correlation time model (open circle) but random for the two-correlation time model (filled circle). The data are reasonably close to those predictable for a hindered rotator, but still better agreement was obtained when two correlation times were used (Table II and Figure 6). Close examination of the deviations (not shown) reveals that these are systematic when the hindered model is used but random when a two-correlation time fit is used. One of the correlation times is typically quite long (50–200 ns). The data are probably just adequate to distinguish these two models. Nonetheless, our results are in close agreement with the time-resolved studies on the same systems with respect to both the correlation times and the values of r∞ or g1 (Lakowicz et al., 1979; Chen et al., 1977; Kawato et al., 1977). In the time-resolved studies it was also possible to obtain suitable fits using either model, but somewhat superior results were obtained if instead of r∞ a second long correlation time was used. Our results for a number of lipid vesicles are summarized in Table II. In general, the data require the conclusion of either hindrance (r∞ > 0) or a second long correlation time. The two-correlation time model generally resulted in a superior fit, as judged by comparison of the deviations and the relative values of χR2 (Table II).
FIGURE 5:
Differential polarized phase angles for DPH in DPPC vesicles. The solid line represents the best fit to the data (●) by using the model with two correlation times. The dashed line represents the best fit by using a single correlation time and r∞ = 0.
FIGURE 6:
Deviations between the measured and calculated differential phase angles for DPH in DMPC vesicles. Deviations are shown for the two correlation time model (●) and for the single correlation time model with r∞ = 0 (○).
Perylene in Lipid Vesicles.
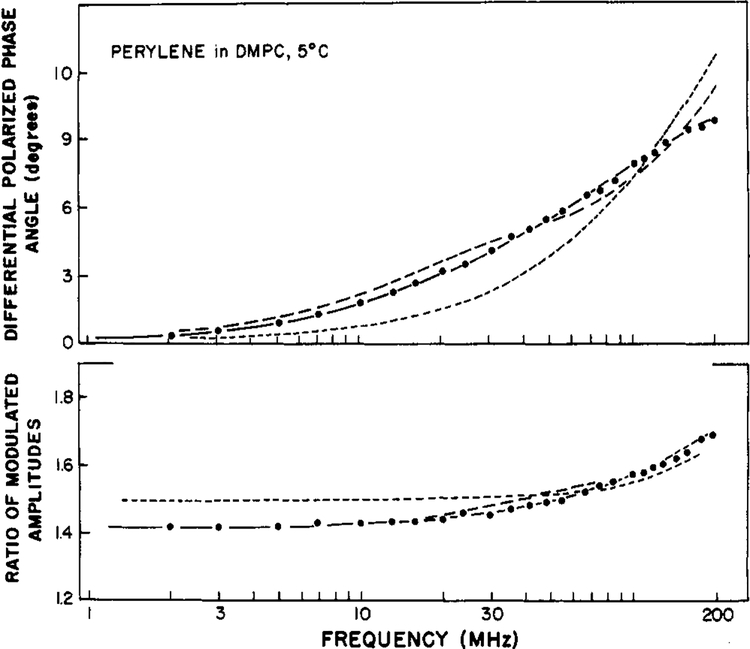
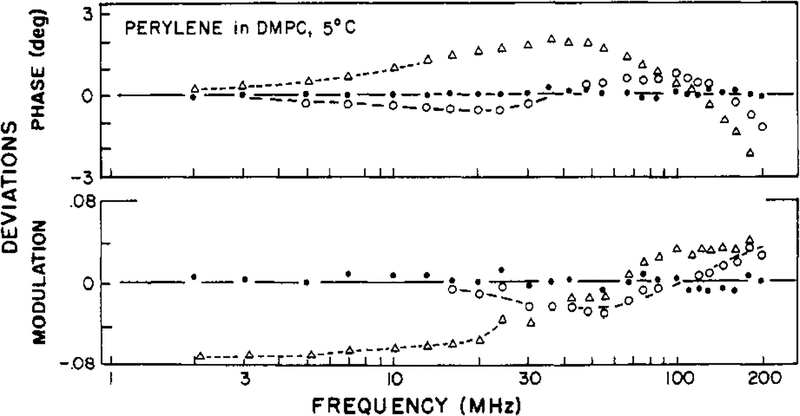
Finally, we examined perylene in vesicles of DMPC at 5 °C, and these results illustrate the considerable resolving power of the frequency-domain measurements for complex decay laws. For these measurements we used the newly constructed instrument (Lakowicz & Maliwal, 1984) with an excitation wavelength of 442 nm. Previous studies in the lifetime domain (Lakowicz & Knutson, 1980) indicated that at temperatures below the phase transition of DMPC (<25 °C) perylene behaves as a hindered rotator. Differential polarized phase and modulation ratios from 2 to 200 MHz are shown in Figure 7. The hindered model (one θ and r∞ is completely inadequate to account for the measurements (Table III; χR2 = 106). Even the more complex model with two correlation times is inadequate (χR2 = 14.4). The inadequacy of these fits is illustrated by the poor agreement between the measured and best-fit calculated values (Figure 7) and by the systematic deviations between these values (Figure 8). For DMPC-bound perylene we required three-correlation times to provide an adequate fit of the data (χR2 = 0.5). It seems probable that the anisotropy decay of perylene is even more complex than a triple exponential (Kinosita et al., 1977; Lipari et al., 1981; Zannoni et al., 1983). Nonetheless, it is reasonable to expect a three-component anisotropy decay for perylene in DMPC bilayers. Perylene is an anisotropic molecule, and its rotational motions can be hindered by the acyl side chains of the membrane. One of these correlation times is rather long, 46.7 ns, which may be regarded as a hindered motion with an amplitude of r0 × 0.343 or 0.12. The degree of hindrance observed in the present investigation compares favorably with that obtained by oxygen quenching experiments (Lakowicz & Knutson, 1980). The fact that the amplitude of the hindered motion may exceed0.10 may indicate that both the in-plane and out-of-plane motions of perylene are hindered to some extent. For instance, fixing the amplitude of the out-of-plane motion (presumed to be the 1.46-ns correlation time) to 0.10 increases the minimum value of χR2 by 56%, from 0.50 to 0.76. Alternatively, fixing the amplitude of the faster motion (0.20 ns) to 0.25 results in lack of convergence. These results seem to indicate that both the in-plane and out-of-plane motions of perylene are hindered to some extent. Additional experimentation and analysis are needed to clarify this point. The two shorter correlation times (0.2 and 1.46 ns) are in the ratio of 7 to 1, which is the value found for perylene in propylene glycol (Table I). These results are one of the most complex anisotropy decays which have been resolved to date.
FIGURE 7:
Differential polarized phase angles and modulated amplitude ratios for perylene in DMPC vesicles at 5 °C. The best fits are shown to the data (●) by using the three-correlation time model (—), two-correlation time model (--), and a single correlation time with a nonzero r∞(---).
Table III:
Anisotropy Decay Parameters for Perylene in DMPC Vesicles at 5 °Ca
| fit | θi (ns) | gi | r∞ | χR2 |
|---|---|---|---|---|
| θ | 6.51 | 3208 | ||
| θ, r∞ | 0.41 | 0.129 | 106 | |
| 2θ | 0.31 | 0.584 | 14.4 | |
| 22.5 | 0.416 | |||
| 3θ | 0.20 (±0.3)b | 0.451 (±0.01) | 0.5 | |
| 1.46 (±0.05) | 0.206 (±0.01) | |||
| 46.7 (±0.001) | 0.343 |
r0 was held constant at 0.35 (442-nm excitation). The estimated errors were σm = 0.1 deg and σm = 0.01. The measured lifetime was 6.81 ns.
The values in parentheses are the estimated uncertainties, for uncorrelated parameters, obtained from the diagonal terms of the covariance matrix (Bevington, 1969).
FIGURE 8:
Deviations between the measured and calculated frequency-domain data for perylene in DMPC vesicles at 5 °C. Deviations are shown for the three-correlation time model (●), the two-correlation time model (○) and the hindered model (Δ).
Discussion
Our experience with frequency-domain measurements of anisotropy decays yields several general observations. The measurements are rapid. Typically, acquisition of data for a single decay of anisotropy can be completed in less than 1 h. With the present instruments, which are not automated, most of this time is expended in adjustment of the instrument rather than in actual data acquisition. Also, calculation of the anisotropy decay parameters can be accomplished in minutes, even when programs written in the interpretive language Basic are used. If necessary, automated data acquisition could further reduce the time for data acquisition, but this hardly seems warranted. At present, data for a number of anisotropy decays can be obtained and analyzed in a single day, which is adequate for most purposes.
Second, the ability of the frequency-domain measurements to resolve complex decay laws appears to be substantial. This is especially evident from the results for the anisotropic rotator perylene. We found two correlation times for perylene in propylene glycol and three correlation times for this fluorophore in DMPC vesicles. One of these times was long (46 ns) and probably reflects hindered motions of an anisotropic rotator. The results presented in this paper represent essentially our first attempts. Given the precise quantitative and qualitative agreement with the available time-domain results, we conclude that no special precautions and/or precedures are required to resolved complex decays comparable to those shown in this report. Also, these results indicate the apparent absence of systematic errors which could hinder the resolution of the anisotropy decay parameters. It seems that the resolution is limited mainly by the random errors in the measured values of Δω and Λω and the spectral properties of the fluorophore. A more complete analysis of this problem will be presented elsewhere (J. R. Lakowicz et al., unpublished results).
Finally, we note that the frequency-domain measurements can also be used to determine time-resolved emission spectra (Lakowicz et al., 1984b), as well as the less demanding problem of resolving multiexponential decays of intensity (Gratton et al., 1984). We conclude that the resolution of anisotropy decay laws possible from the frequency-domain data is at least equivalent to that possible by using time-do main measurements.
Acknowledgments
We thank the referees for their constructive comments.
Supported by National Science Foundation Grants PCM 80-41320, 81-06910, and 82-10878 to J.R.L. and PCM 79-18646 to E.G.
Appendix
Here we summarize the expressions for Ni and Di for the various anisotropy decay models. For convenience we used Γ = τ−1 and 6R = θ−1
Isotropic Rotators.
For an unhindered isotropic rotator, and a single exponential decay of intensity, application of eq 9 and 10 to eq 6–8 yields
| (A1) |
| (A2) |
| (A3) |
| (A4) |
In our fitting procedure we used analytical derivatives and the Marquardt nonlinear least-squares algorithm (Bevington, 1969). We held r0 constant at the measured value. These expressions have been described (J. R. Lakowicz et al., unpublished results).
Hindered Rotators.
Suppose the anisotropy decay is described by eq 16. Then the needed expressions are
| (A5) |
| (A6) |
| (A7) |
| (A8) |
Double-Exponential Decay of Anisotropy.
Suppose the anisotropy from a single fluorophore decays with two correlation times. Then
| (A9) |
| (A10) |
The expressions for N and D can be obtained by substitution of −(l/3)r0 for (2/3)r0 in eq A9 and A10.
Footnotes
Abbreviations: DPH, diphenylhexatriene; DOPC, DMPC, and DPPC, dioleoyl-, dimyristoyl-, and dipalmitoyl-l-α-phosphatidylcholine, respectively.
References
- Barkley MD, Kowalczyk AA, & Brand L (1981) J.Chem. Phys 75, 3581–3593. [Google Scholar]
- Bevington PR (1969) Data Reduction and Error Analysis in the Physical Sciences, McGraw Hill, New York. [Google Scholar]
- Chen LA, Dale RE, Roth S, & Brand L (1977) J. Biol. Chem 252, 2319–2324. [PubMed] [Google Scholar]
- Dale RE, Chen LA, & Brand L (1977) J. Biol. Chem 252, 7500–7510. [PubMed] [Google Scholar]
- Gratton E, & Limkeman M (1983) Biophys. J 44, 315–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gratton E, Lakowicz JR, Maliwal B, Cherek H, Laczko G, & Limkeman M (1984) Biophys. J 46, 479–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanson DC, Yguerabide J, & Schumaker VN (1981)Biochemistry 20, 6842–6852. [DOI] [PubMed] [Google Scholar]
- Heyn MP (1979) FEBS Lett 108, 359–369. [DOI] [PubMed] [Google Scholar]
- Ichiye T, & Karplus M (1983) Biochemistry 22, 2884–2893. [DOI] [PubMed] [Google Scholar]
- Jahnig F (1979) Proc. Natl. Acad. Sci. U.S.A 76, 6361–6365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawato S, Kinosita K, & Ikegami A (1977) Biochemistry 16, 2319–2324. [DOI] [PubMed] [Google Scholar]
- Kinosita K, Kawato S, & Ikegami A (1977) Biophys. J 20, 289–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinosita K, Kawato S, & Ikegami A (1984) Adv. Biophys 17, 147–203. [DOI] [PubMed] [Google Scholar]
- Lakowicz JR (1983) Principles of Fluorescence Spectroscopy, Plenum Press, New York. [Google Scholar]
- Lakowicz JR, & Knutson JR (1980) Biochemistry 19,905–911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakowicz JR, & Maliwal B (1983) J. Biol. Chem 258, 4794–4801. [PubMed] [Google Scholar]
- Lakowicz JR, & Maliwal B (1984) Biophys. Chem (in press). [DOI] [PubMed] [Google Scholar]
- Lakowicz JR, Prendergast FG, & Hogen D (1979) Biochemistry 18, 508–519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakowicz JR, Maliwal B, Cherek H, & Balter A (1983) Biochemistry 22, 1741–1752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakowicz JR, Gratton E, Laczko G, Cherek H, & Limekeman M (1984a) Biophys. J 46, 463–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakowicz JR, Cherek H, Maliwal B, Laczko G, & Gratton E (1984b) J. Biol. Chem 259, 10967–10972. [PubMed] [Google Scholar]
- Levy RM, & Szabo A (1982) J. Am. Chem. Soc 104, 2073–2075. [Google Scholar]
- Lipari G, Szabo A (1980) Biophys. J 30, 489–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipari G, & Szabo A (1981) J. Chem. Phys 75, 2971–2976. [Google Scholar]
- Mantulin WW, & Weber G (1977) J. Chem. Phys 66, 4092–4099. [Google Scholar]
- Munro I, Pecht L, & Stryer L (1979) Proc. Natl. Acad. Sci. U.S.A 76, 56–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross JAB, Rousslang KW, & Brand L (1981a) Biochemistry 20, 4361–4369. [DOI] [PubMed] [Google Scholar]
- Ross JAB, Schmidt CJ, & Brand L (1981b) Biochemistry 20, 4369–4377. [DOI] [PubMed] [Google Scholar]
- Shinitzky M, & Barenholz Y (1974) J. Biol. Chem 249, 2652–2657. [PubMed] [Google Scholar]
- Shinitzky M, Dianorex AC, Gitler C, & Weber G (1971) Biochemistry 10, 2106–2113. [DOI] [PubMed] [Google Scholar]
- Steiner RF (1983) in Excited States of Biopolymer (Steiner RF, Ed.) pp 117–162, Plenum Press, New York. [Google Scholar]
- Stubbs CD, Kauyama T, Kinosita K, & Ikegami A (1981) Biochemistry 20, 4257–4262. [DOI] [PubMed] [Google Scholar]
- Veatch WA, & Stryer L (1977) J. Mol. Biol 117, 1109–1113. [DOI] [PubMed] [Google Scholar]
- Weber G (1973) in Fluorescence Techniques in Cell Biology (Thaes AA, & Sernetz M, Eds.) pp 5–13, Springer-Verlag, New York. [Google Scholar]
- Weber G (1977) J. Chem. Phys 66, 4081–4091. [Google Scholar]
- Zannoni C, Arcioni A, & Cavatorta P (1983) Chem. Phys. Lipids 32, 179–250. [Google Scholar]
- Zinsli PE (1977) Chem. Phys 20, 299–309. [Google Scholar]