Decision Making in Numeracy Tasks with Spatially Continuous Scales

Abstract

A diffusion model of decision making on continuous response scales is applied to three numeracy tasks. The goal is to explain the distributions of responses on the continuous response scale and the time taken to make decisions. In the model, information from a stimulus is spatially continuously distributed, the response is made by accumulating information to a criterion, which is a 1D line, and the noise in the accumulation process is continuous Gaussian process noise over spatial position. The model is fit to the data from three experiments. In one experiment, a one or two digit number is displayed and the task is to point to its location on a number line ranging from 1–100. This task is used extensively in research in education but there has been no model for it that accounts for both decision times and decision choices. In the second task, an array of dots is displayed and the task is to point to the position of the number of dots on an arc ranging from 11 to 90. In a third task, an array of dots is displayed and the task is to speak aloud the number of dots. The model we propose accounts for both accuracy and response time variables, including the full distributions of response times. It also provides estimates of the acuity of decisions (standard deviations in the evidence distributions) and it shows how representations of numeracy information are task-dependent. We discuss how our model relates to research on numeracy and the neuroscience of numeracy, and how it can produce more comprehensive measures of individual differences in numeracy skills in tasks with continuous response scales than have hitherto been available.

Much of our interaction with the world involves making decisions on continuous scales but laboratory research has focussed mainly on two-choice tasks. There are several reasons for this-- data are easier to collect with binary responses, interpretations of them can be relatively simple, and models of performance are well established and tractable so that application of them is relatively straightforward. In this article we present choice and response time (RT) data collected on continuous response scales from three tasks that have been used (or are similar to those that have been used) in the numerical cognition literature. The aim is to provide data for testing the spatially continuous diffusion model (SCDM; Ratcliff, 2018) in a new application to tasks that have been of central importance in numerical cognition.

Along with the SCDM, there is another new model that accounts for choice and RT on continuous scales, the circular diffusion model (Smith, 2016). Both this model and the SCDM provide theoretical accounts of processes that give rise to responses made on continuous scales with stimuli represented on continuous scales. In this article, we use only the SCDM because, at this point, the circular diffusion model has not been extended to apply to responses on the straight lines or arcs that we use for the tasks reported here (though there is certainly the potential for competitive model testing).

We present data from three tasks that allow the SCDM be validated in new applications to the numeracy domain. The stimuli for our first task were one- and two-digit numbers and subjects were asked to indicate where on a number line from 1 to 100 a number would fall (the number-line task). For the second task, the stimuli were arrays of dots and subjects were asked to indicate where on an arc from 11 to 90 the number of dots would fall (the dots-arc task). The third task also used arrays of dots between 11 and 90, but subjects were asked to speak aloud their estimates of the numbers of dots (the spoken-dots task). These tasks were chosen to represent, first, a symbolic stimulus and continuous response, second, a nonsymbolic stimulus and continuous response, and third, a nonsymbolic stimulus and a symbolic response, but on a scale that has a number of options. As noted later, we started with a response scale with all the numbers from 11 to 90, but we found that the last digit was meaningless, so we moved to having responses as 10’s. These tasks allow us to examine differences in both stimulus and response modes.

The SCDM offers an account for both accuracy and RT across the continuous response scale. This provides information about biases, precision, and amount of evidence needed to make a decision. The results indicate that number representations can be assumed to be on an analog scale, which explains faster responses in the first two tasks which require a motor response on an analog scale. However, the third task requires a categorical/symbolic verbal response to be produced from this analog representation and responses are considerably slower. The results are discussed in relation to the nature of number representation in the numeric cognition literature.

Continuous Scale Tasks in Numerical Cognition

The number-line task is typical of those often used in practical applications and in research on numeracy with children (Fazio, Bailey, Thompson, & Siegler, 2014; Schneider et al., 2018; Siegler, 2016; Siegler & Booth, 2004; Siegler & Opfer, 2003). The recent meta-analysis by Schneider et al. (2018) of number-line tasks found a correlation of 0.44 between number-line estimation and mathematical competence (over 263 effect sizes from studies with 10,576 subjects with mean ages from 4 to 14 years). Our other two tasks are similar to ones that have been used infrequently in the numerical cognition domain.

This task has been used extensively to understand how children’s knowledge of numeracy develops with age. Typically, results show a transition from a non-linear function for young children to a linear function for older children and adults (with the range of numbers 1–100; Siegler & Opfer, 2003; for a review, see Siegler, Thompson, & Opfer, 2009). The most prominent view is that the form of the non-linear function is logarithmic, though as we discuss below, this view has been challenged.

Responses to the number-line task are made on continuous scales but there are other often-used tasks for which subjects are asked to make two-choice discriminations. For example, the stimuli might be two arrays of dots displayed side by side and subjects are asked which array has the most dots. Like number-line tasks, discrimination tasks are predictive of later math skills for children (e.g., Halberda, Mazzocco, & Feigenson, 2008; Halberda et al., 2012; Park & Brannon, 2013).

For two-choice numeracy discrimination tasks, numerosity information is argued to be represented in a system that is called the “Approximate Number System” (ANS), where numerosity is represented by a Gaussian distribution over number. Two models have been proposed for how this function changes as numerosity increases. In one, the mean of the distribution and its standard deviation (SD) increase linearly with numerosity (Gallistel & Gelman, 1992). In the second, the mean of the distribution increases logarithmically and its SD is usually assumed to be constant (sometimes implicitly) over numerosity (Dehaene & Changeux, 1993). For older children and adults, it might be thought that the linear function seen with the number-line task is related to the linear ANS model. However, SDs change little in the number-line task as number increases, which is not consistent with increasing SDs in the linear ANS model. Or it might be thought that the logarithmic (non-linear) function observed for young children is related to the logarithmic ANS model. But the increasing variability in children’s number line estimates is not consistent with the constant SD in the logarithmic ANS model.

Two explanations have been proposed for the nonlinear function that has been observed with young children and claimed to be logarithmic. For the first, the function is not logarithmic but bilinear. Lower numbers (e.g. 1 – 10) are well-learned, which gives a slope higher than that of larger numbers. Larger numbers (e.g., 11–100) are less well-learned and so have a lower slope.

Young and Opfer (2011) fit the logarithmic and bilinear functions to several data sets and concluded that the logarithmic model provided a better and more parsimonious account of the data. However, straight comparisons of the two models are somewhat problematic because the bilinear function tended to fit data from the logarithmic function better than a logarithmic function fit data from a bilinear function and so the bilinear model appears more flexible for these data.

This means that model comparison needs to take into account the flexibility of the two functions (see Wagenmakers et al., 2004, for detailed discussion of these model-comparison issues and methods to evaluate them). Another problem with flexibility is that if the bilinear model were correct, it is unlikely that the transition point on the number line from one linear function to the other would be at the same point for all children. If that transition point were variable, then integrating over a distribution of transition points would produce a function that was even less discriminable from the logarithmic model. As we discuss at length below, the other dependent variable, RT, may be better able to separate the different interpretations: If there is a large difference in RTs between the small and large number ranges, this might support a bilinear interpretation, but if RTs were constant or increased continuously (by not too much), a single function might be supported.

The second alternative to the logarithmic function is one that assumes there are anchor points on the number line (e.g., at 0, 100 and sometimes halfway at 50) at which responses are more accurate and less variable. Slusser, Santiago, and Barth (2013) and Rouder and Geary (2014) examined a simple power function model with an anchor point at zero for the youngest children and two or more anchor points for older children. For first-grade children, a power function or more generally a compressed scale model (e.g., a power function or a logarithmic function) fit best with increasing variability as number increased. For older children, models with anchor points fit better. Rouder and Geary pointed out that the models become more constrained when realistic variance assumptions are included in the modeling so that the variance decreases near the ends of the ranges of possible responses and near anchor points. (If constant variances are assumed, then the model can produce nonsensical estimates less than 0 or greater than 100.) Slusser et al. argued that one cannot interpret results from these kinds of number-line tasks as being a direct reflection of the representation of numerical information. The representations map through perceptual processes to the response scale. We might go one step further and argue that the representation used in these tasks is determined by an interaction between numerical knowledge and task demands, as we demonstrate in the modeling presented below.

The Spatially Continuous Diffusion Model

The core of the SCDM is conceptually simple: It is a sequential sampling model in which evidence from a stimulus is represented on a continuous line or plane and evidence from it is accumulated over time up to a decision criterion, which is also a continuous line or plane. Distributions of evidence from stimuli are assumed to be Gaussian and the parameters are the mean location of the distribution, the height of the distribution, and the spread of the distribution. Key to the model’s success is that there is variability over time in the accumulation process, specifically random Gaussian process noise that is continuously, spatially distributed.

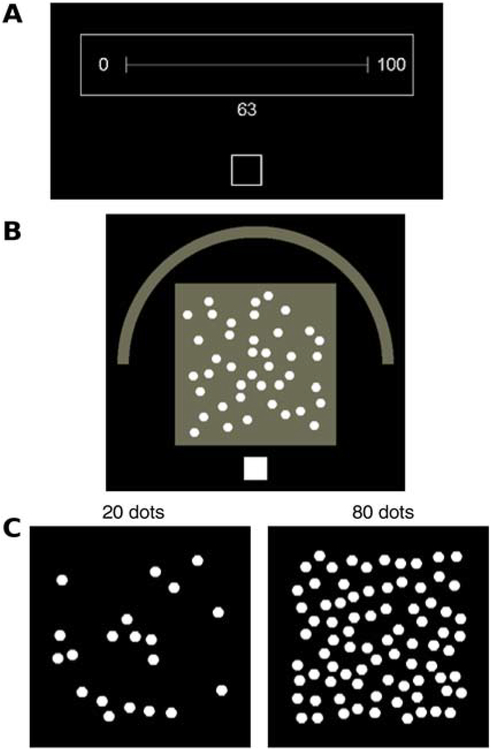
To ground the discussion, we briefly describe the three experiments we conducted and the data from them that are used in testing the SCDM model. Figure 1 shows examples of the stimulus displays. In Experiment 1 (Figure 1A), a standard number-line task, one- and two-digit numbers were presented on a CRT touch screen and a subject’s task was to move his or her index finger from a resting box at the bottom of the screen to the location of that number on a horizontal line extending from 1 to 100 (though “100” was never presented). In Experiment 2 (Figure 1B), the stimuli were displays of between 11 and 90 dots and a subject’s task was to move his or her index finger from a resting box to the location of that number on a 180 degree arc extending from 11 to 90. In Experiment 3 (Figure 1C), the stimuli were the same as those for Experiment 2 but the task was to call out the number of dots in the display; responses were made in 10’s (i.e., a subject called out 10, 20, 30, ‥, or 90). RTs were recorded as the time at which the finger was lifted from the resting box for Experiments 1 and 2 and from the onset of the vocal response for Experiment 3.

Figure 1.

Examples (screen shots) of the experimental displays for the experiments. A: Experiment 1, the number-line task. Subjects rested their index finger on the bottom square, the number appears, then subjects lift their finger and move it to the position on the line that corresponds to the number. Response time is measured from when the finger lifts from the square. B: Experiment 2. Subjects rested their index finger on the bottom white square, the array of dots appears, then subjects lift their finger and move it to the position on the arc that corresponds to the number. C: Experiment 3. This shows two examples of numbers of dots for the experiment. The array appears and subjects respond by calling out the nearest 10 to the number in the array.

For all three experiments, we show that the model, the Spatially Continuous Diffusion Model (SCDM), can explain the representations of stimulus information, how decisions are expressed on continuous scales, and how decisions evolve over the time between onset of a stimulus and execution of a response. The SCDM also provides a new tool for examining how individual components of processing are used in number-line tasks.

The SCDM can be seen as an extension of one of the more successful models of simple decision making, the sequential sampling, diffusion decision model for two-choice decisions (Ratcliff, 1978; Ratcliff & McKoon, 2008; Ratcliff, Smith, Brown, & McKoon, 2016). That model explains the choices individuals make and the time taken to make them by assuming that noisy evidence from a stimulus is accumulated over time to one of two decision criteria, at which point a response is executed. This and related models have been influential in many domains, including clinical research (Ratcliff & Smith, 2015; White, Ratcliff, Vasey, & McKoon, 2010), neuroscience, and neuroeconomics (Gold & Shadlen, 2001, 2007; Krajbich, Armel, & Rangel, 2010; Smith & Ratcliff, 2004). There is also a growing body of evidence that diffusion models provide a reasonable account of the mappings between behavioral measures and neurophysiological measures (e.g., EEG, fMRI, and single-cell recordings in animals; see the review by Forstmann, Ratcliff, & Wagenmakers, 2016). The model is also being used as a psychometric tool in studies of differences among individuals (e.g., Ratcliff, Thapar & McKoon, 2010, 2011; Ratcliff, Thompson, & McKoon, 2015; Schmiedek et al., 2007; Pe, Vandekerckhove, & Kuppens, 2013). There are also close relationships between the SCDM and models of confidence judgments and multichoice decision-making.

Historically, the earliest models for two-choice decisions were random walk and counter models (LaBerge, 1962; Laming, 1968; Link & Heath, 1975; Stone, 1960; Smith & Vickers, 1988; Vickers, Caudrey, & Willson, 1971) in which evidence entered the decision process at discrete times (see Ratcliff & Smith, 2004, for an evaluation of model architectures). The advance from evidence entering at discrete times to evidence entering over continuous time contributed to the explosion of theoretical and applied research (much of it in the last 15 to 20 years). We believe that the advance from modeling the time course of discrete decisions to the time course of decisions in continuous space might have the same theoretical and applied impact over time.

The SCDM applied to the numeracy tasks assumes a stimulus is represented on a continuous line as a Gaussian drift rate distribution and evidence from it is accumulated up to a decision criterion, which is also a continuous line. Variability in the evidence accumulation process is represented by Gaussian process noise, which is continuously and spatially distributed. Gaussian process noise has two properties, first that at any spatial position, successive samples of noise have a Gaussian distribution, and second, values at nearby locations are correlated with each other. The rate at which the correlation falls off over spatial position is determined by a parameter of the model.

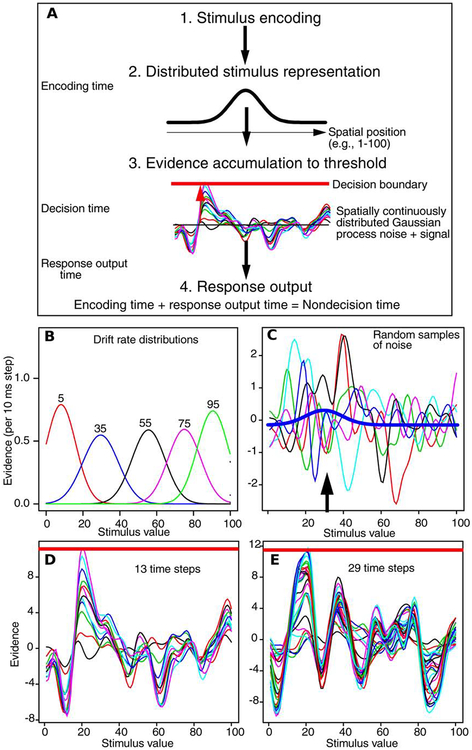
Figure 2 shows the overall time course of a decision from encoding to evidence accumulation to response output with time progressing from top to bottom of the figure. The representation of a stimulus is assumed to be normally distributed over the spatial response scale (e.g., 1–100) and it is this representation, called the drift-rate distribution, that drives the accumulation of evidence. The representation plus samples of noise are accumulated up to a decision criterion and when a process hits the criterion, a response is initiated. Because of the noise in the accumulation process, the time it takes for evidence to reach the criterion varies and sometimes the accumulated evidence reaches the wrong location on the criterion, producing errors. Because responses are distributed over locations, the transition from correct to error responses over spatial position is gradual. Errors vary from being close to the correct response to being quite far from it; there is no identifiable cutoff point between correct and error responses as there is for two-choice tasks.

Figure 2.

A: An illustration of processes in the SCDM. The stimulus is encoded to produce a drift-rate distribution, this along with samples of noise is accumulated to the decision threshold, then the point at which the process terminates is used to generate a response. The black arrows represent the progression of processing over time. B: Five example drift-rate distributions. The parameters used for these distributions were the means and SDs from fits to Experiment 1 (from Table 1). C: The drift-rate distribution (solid blue line) and samples of Gaussian process noise, all to the same scale. The black arrow points to the peak of the drift-rate distribution. D and E: These show two examples of a single trial with a drift-rate distribution mean of 20. The decision criterion line (solid red line at the top of each figure) differs because of trial to trial variability in the setting.

This model provides measures of bias and variability that are represented in the drift rate distributions. The model also provides measures related to time course of processing. Any of the measures of the stimulus representation and decision processes represented in the model parameters may be related to mathematical competence and related to the development of decision making competence in numeracy discussed in the introduction.

In the SCDM, it is assumed that at each point in time, the total evidence is normalized to zero (e.g., Audley & Pike, 1965; Bogacz, Brown, Moehlis, Holmes, & Cohen, 2006; Ditterich, 2006; Niwa & Ditterich, 2008; Ratcliff & Starns, 2013; Roe, Busemeyer, & Townsend, 2001; Shadlen & Newsome, 2001). This is accomplished by making the drift-rate distribution and each sample of Gaussian process noise have mean height of zero. In practice, the mean height of the drift rate distribution is computed and subtracted from the unnormalized distribution and the mean height of Gaussian process noise is computed and subtracted to produce a normalized sample of noise. We also thought about using short-range lateral inhibition, but there was no evidence of a short-range decrease in choice probability followed by a rise further away from the correct location.

The assumption of zero total evidence at each point in time is the same as that for a two-accumulator (two-choice) model with a step up in one accumulator corresponding to an equal-sized step down in the other. This means that accumulated evidence is normalized at each time step in a manner that is directly analogous to the SCDM model. In confidence-judgment tasks, Ratcliff and Starns (2013) showed that normalization allowed their RTCON2 model to account for shifts in RT distributions that occurred for about half of the subjects in their experiments.

Figure 2A labels the encoding time for a stimulus, decision time (the time to reach criterion), and response output time. Encoding time and response output time are added together in one parameter of the model, nondecision time. It is important to understand that stimulus encoding time includes the time taken to process the raw perceptual representation into decision-relevant evidence, the evidence that will drive the accumulation of evidence, i.e., the drift-rate distribution. For example, for an array of dots, stimuli could vary on a number of dimensions and decisions could be made on any of those dimensions, such as the total area covered by the dots, their color, their shape, and so on. For the tasks used in the experiments here, it is evidence about number that must be extracted.

Although the accumulation process is assumed to be continuous in space and time, it must be simulated in discrete time steps and with discrete spatial locations, as must be done for any simulation of a continuous process on a digital computer. Later in this section, a discussion of how to change the step size in time to approach continuous processes is presented (increasing the number of points in space is discussed in Ratcliff, 2018).

A Gaussian process is a stochastic process, where u is a random variable and the values of u(x) (the random variable at spatial position x) are normally distributed. The parameters of the Gaussian process are:

$$\text{ mean, }\mu =\text{E}\left\{u(x)\right\}$$

$$\text{covariance, }K\left(x,x^{\prime }\right)=Cov\left(u(x),u\left(x^{\prime }\right)\right).$$

We use the Gaussian covariance (kernel) function in the implementation of the SCDM (Ratcliff, 2018),

$$K\left(x,x^{\prime }\right)=exp(-{\left(x-x^{\prime }\right)}^2/\left(2r^2\right),$$

where x and x′ are two points and r is the (kernel) length parameter that determines how smooth the function is. The closer x and x′ are together, the greater the correlation between the random variables u(x) and u(x′).

To obtain random numbers from the Gaussian process, the square root (R) of the kernel matrix, K (K=R′R, where R is an upper triangular matrix), is multiplied by a vector of independent Gaussian-distributed random numbers (with SD 1) to produce the smooth random function (Lord et al., 2014). If r is relatively small, the matrix R will have only a few values off the diagonal and only points close together in the random vector will be smoothed together, resulting in a jagged Gaussian process function. If r is relatively large, the matrix R will have many off-diagonal elements that are not small and the Gaussian process function will be smooth with few peaks and troughs.

The equation for the update of evidence, y, at any spatial position x and time t is:

$$dy(x,t)=\xi (x)dt+\sigma dw(x,t),$$

where w represents Gaussian process noise and σ represents the size of the Gaussian process noise. In the SCDM, it is assumed that evidence for one location in space is evidence against all the other locations. As noted earlier, this is accomplished by making the drift rate distribution and the Gaussian process noise have zero mean. For the discrete approximation to the continuous process used in simulating the process, at each time step, the equation is:

$$\Delta y(x,t)=\xi (x)\Delta t+\sigma \Delta \text{w}(\text{x},\text{t}).$$

The assumptions that there is noise in the process of accumulating evidence and that the total amount of accumulated evidence is constant across time are shared with the two-choice diffusion model. There are two other shared assumptions: One is that the value of a criterion is under an individual’s control; setting it higher means longer RTs and higher accuracy and setting it lower means shorter RTs and lower accuracy (e.g., Ratcliff, 2018, Experiment 8). For two-choice tasks, it is usually found that drift rate and criterion setting are independent across individuals (e.g., Ratcliff et al., 2010, 2011; Ratcliff et al., 2015). This means that an individual can set the criteria to value speed over accuracy or accuracy over speed, no matter what his or her drift rate. And an individual with higher drift rate (or lower drift rate) can respond more or less quickly, depending on where he or she sets the criteria.

The other shared assumption is that there is variability across trials in the distributions of drift rates, the setting of the criterion, and nondecision time, reflecting individuals’ inability to hold processing exactly constant from one trial of a stimulus class to another (or even from one stimulus to an identical one presented later, Ratcliff, Voskuilen, & McKoon, 2018). Variability in drift rate is represented by uniformly-distributed random variation in the height of the drift-rate distribution in Ratcliff (2018), but in the applications for Experiments 1, 2, and 3 here, the best fits were obtained with the variability in height set to zero.

The distributions of variability in the decision criterion and nondecision time are assumed to be uniform. Ratcliff (2013) showed that the two-choice model was not sensitive to the precise forms of these distributions (and the drift-rate distribution) because modest to moderate changes in the distribution shapes led to about the same predicted values of RT and accuracy. The intuition is that within-trial variability washes out the effects of the precise distributional shape of these distributions. We believe the same will be true of the distributional assumptions in the SCDM.

The most important feature of the SCDM is that the stimulus representation that determines drift rate, the noise in the accumulation of evidence, and the response criteria are all continuous in space. That the stimulus representations have a Gaussian distribution is straightforward, but the assumption about noise is less familiar because theoretical assumptions about continuously distributed noise across space during the time course of evidence accumulation have received almost no attention in psychology.

Figure 2A illustrates the model as it applies to the number-line task used in Experiment 1. The response scale ranged from 1 to 100. In analyses of the data, both stimuli and responses were grouped into bins of width 10. Figure 2B shows the corresponding drift-rate distributions for five of them. Each is a continuous normal distribution and the area under the five distributions is the same. The lowest and highest distributions, 5 and 95, are cut off at the lower and upper ends respectively, but the distributions are normalized so that their areas are the same as that of the other distributions.

Figure 2C shows random samples of noise from a single trial with 35 as the stimulus value. The distribution for 35 is shown by the bold line. As is typical in fits of the SCDM, the height of the stimulus distribution is much lower than most of the vertical excursions of noise. This means that when a single stimulus distribution is added to a single noise sample, the combination is not discriminable by eye from noise samples. This provides the intuition for why signal plus noise must be accumulated over samples (i.e., time) for the signal to emerge from the noise.

Figures 2D and 2E each show an example of the evidence-accumulation process. The stimulus is the number 20 and at each time step the drift-rate distribution for that number along with a Gaussian-process noise sample (e.g., those in Figure 2C) is accumulated until some point on the criterion is reached. Each line on the figures represents the accumulated evidence at each time step; Figure 2D has 13 steps (13 lines) and Figure 2E has 29. The two examples were constructed using mean parameter values from Experiment 1.

The examples show what appear to be quite systematic peaks and troughs in addition to the one that produces the criterion crossing at around 20. These peaks and troughs are the result of accumulating Gaussian-process noise and they are not systematic between the two examples. For example, there is a large peak at around a stimulus value of 40 and a large trough around 30 for Figure 2D; these are missing from Figure 2E. Furthermore, there are some very large excursions up and down on individual steps. For example, in the trough in Figure 2D at a stimulus value of 12, two of the lines are at −2 and −4 and then most of the others are below −6 with the lowest value at −7.5. This means that 2 of the 13 time steps have large negative excursions, at this stimulus value, and the rest move the function much less. Peaks and troughs like these are the usual result of random variation in the accumulation process, i.e., they occur as the result of accumulating random samples of Gaussian-process noise. Note that the criterion is different in the two examples because of the across-trial variability in it.

The smooth continuous Gaussian-process functions across the x-axis are generated from Gaussian random numbers smoothed by the kernel function presented above where the kernel length parameter r determines how smooth the function is. The precise form of the kernel function is likely to be unimportant as long as it is unimodal, because samples are accumulated in the decision process and central-limit-like behavior likely applies.

The parameters of the model, as applied to the experiments in this article, are as follows: For drift rate distributions, for all three experiments, the stimuli and responses were divided into groups. For the number-line task, the groups were 1–10, 11–20, 21–30, …, 91–99 and for the two dots tasks, the groups were 11–20, 21–30, ‥, 81–90. This means that the data form 10×10 groups for the number-line task (for each of the 10 stimulus groups, responses can occur in each of the 10 response groups), 8×8 groups for the dots task with manual responses, and 8×9 groups for the dots task with spoken responses. For each stimulus group, there is a mean of the (Gaussian) drift-rate distribution and a SD. For example, for the number-line task this gives 10 means and 10 SDs. These means and SDs provide measures of the stimulus representation, but there is no model for how they should behave or relate to each other. If such a model is developed, it could be fit to these values, or better still, integrated into the model to provide drift rate distributions for the model as for numerosity in the integrated diffusion models for numerosity discrimination (Ratcliff & McKoon, 2018, see discussion later).

The other parameters of the model are nondecision time (T_er), the range of nondecision times (s_t, uniformly distributed), the criterion setting (a), the range of the criterion setting (s_a, uniformly distributed), the Gaussian process kernel parameter (r), and a parameter that represents the height of the drift-rate distribution (v_h) that multiplies the density of all of the drift-rate distributions. We set the size of the SD in within-trial (Gaussian process) noise at 1.

In fitting the model to data, as for most models of continuous processes that have to be implemented and fit using numerical methods, continuous space and time has to be approximated by discrete values with small time and space increments. The values of the SCDM parameters are defined in terms of 10 ms time steps and one unit (number) steps in numerosity. Ratcliff (2018) described which model parameters must be scaled to change the size of time steps and spatial distances. These changes can be understood by examining the units of the various model parameters. For example, drift rate is evidence per unit time so changes in time steps will require changes in drift rate. The diffusion coefficient (σ²) has units of evidence per unit time and so σ has units of (time)^−1/2. Thus the value of σ will be changed if the time step is changed. The kernel parameter has units of spatial distance and so changes in the number of spatial divisions will change this parameter.

For example, to change the time step by a factor of t, these parameters are adjusted:

1. Drift rate peak and range in the peak (d and s_d) are divided by t.

2. The SD in noise added on each time step (σ) in the accumulation process is divided by the square root of t.

3. The criterion and range in the criterion parameters, SD in the drift-rate distribution and the SD in Gaussian process noise (the kernel parameter) all remain the same.

Fitting the SCDM Model to Data

We do not know of any exact solutions for the probabilities of responses at the criterion line or for the distributions of RTs so we must use simulations. Predictions are generated from simulations with discrete steps in time and location with many more simulated trials than in the data, e.g., 4000 per condition. These are compared to empirical data and the parameters used to generate the simulated data are adjusted with a SIMPLEX minimization routine to obtain the best match between simulated and empirical data. The data for all the conditions of an experiment are fit to the model simultaneously and the data for each subject are fit individually.

We fit the model using 10 ms time steps and single integer spatial divisions (e.g., 10, 11, 12, …), so the model parameters are given in terms of 10 ms time steps and integer spatial divisions. The equation for the update to a spatial position at each 10 ms time step is the standard Δx_i=v_iΔt + ση_i √Δt, where σ(=1) is the SD in within-trial noise, v_i is the height of the drift-rate distribution at spatial position i, x_i is the amount of evidence, and η_i is a normally-distributed random variable with mean zero and SD 1.

For fitting the model and for displaying empirical data and the model’s predictions, RT distributions for the stimulus and response groups are represented by 5 quantiles, the .1, .3, .5, .7, and .9 quantiles. The quantiles and the probabilities of responses for each response group for each stimulus condition of the experiment are entered into the SIMPLEX minimization routine and given these quantile RTs, and the model is used to generate the predicted cumulative probability of a response occurring by each quantile RT. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the proportion of responses between adjacent quantiles. For a G-square computation, these are the expected proportions, to be compared to the observed proportions of responses between the quantiles (i.e., the proportions between 0, .1, .3, .5, .7, .9, and 1.0, which are .1, .2, .2, .2, .2, and .1). The proportions for the observed (p_o) and expected (p_e) frequencies and summing over 2Np_olog(p_o/p_e) for all conditions gives a single G-square (log multinomial likelihood) value to be minimized (where N is the number of observations).

For the number-line task and the two tasks with dots, any stimulus will have a drift-rate distribution that spreads across all or most of the whole range of stimuli. For example, the distribution for a stimulus of 20, while centered at 20, would have probability density across the whole range, although the farthest will be close to zero. In consequence, many of the 10×10, 8×8, and 8×9 stimulus/response groups in Experiments 1, 2, and 3, respectively, have relatively few observations in them, often zero, and so quantile RTs can not be reliably estimated or estimated at all. To deal with this, when the number of observations in a category was less than 8, only a single value based on the overall probability contributed to G-square (2Np_olog(p_o/p_e). When the number of observations was 8 or greater, six proportions from the six bins between quantiles were used (as above). Therefore, the number of degrees of freedom for each stimulus group was 6 times the number of response groups for which quantiles were used, plus the number without quantiles with more than zero observations, minus 1 (as proportions have to add to 1).

The fitting process often entered a part of the space in which moderate changes to a parameter had little effect on G-square. Part of the reason for this is because the function being minimized was generated by simulation and produced predicted values that fluctuated from simulation to simulation (even if the parameter values were the same). This means that smooth descent was not possible near the best fitting parameter values, especially when changes in parameters produced only small changes in G-square. To lessen this problem (and the possibility that the fitting process might end up in a local minimum), the SIMPLEX routine was restarted 35 times with 10 iterations per run with an initial simplex that had a range for each parameter that was 10% of the parameter value. After the 35 runs, SIMPLEX was run with 200 iterations. Usually for the last 100 to 150 iterations, there was little or no change in the parameter values.

In addition to the possibility of local minima and parts of the parameter space in which changes had little effect on the value of G-square, there were some other problems. If nondecision time was large and across-trial variability in nondecision time was small, it was possible that there was no overlap between the predicted and data distributions at the lower quantiles. This means that a probability cannot be assigned to the lower quantile RTs and this produces numerical overflow in the programs we use. To deal with this, a value of nondecision time at the low end of the range for successful fits to data was selected along with a large value of across-trial variability in it. These were fixed for the first two runs of the SIMPLEX routine. This allowed other parameters to move to values nearer their best-fitting values. For the third iteration, all the parameters were free to vary, which allowed nondecision time to move to a value near the best-fitting value for those data. The fourth iteration started with the across-trial range in nondecision time divided by 2.5 to counteract the large value used in the initial runs (without this adjustment, it took a lot more restarts of the SIMPLEX routine for this parameter to move to a stable lower value). Additionally, nondecision time was not allowed to become shorter than 165 ms for Experiments 1 and 2 because a value lower than this is implausible given the neurophysiology of neural transmission times for encoding and response output processes and translations between the raw stimulus representation and the representation of the decision variable processes that drives the decision process. Initial values of the parameters were set to the mean over subjects of those from a first exploratory run of the model-fitting program and they were the same for each subject. Overall, the fitting method was robust to moderate changes in the initial values (e.g., a 30–50% change in them).

Because the predictions are generated by simulation, even with exactly the same parameter values, the predictions will differ from one set of simulations to another. This means that the fitting method has this additional source of variability not present in models that can produce exact predictions. Given this variability in predictions and the way we group data and represent RT distributions as quantiles, there may be better ways of estimating parameters. Our focus is on model development and new applications; at this point, we have not yet explored additional methodological issues in fitting this model. However, the method we use is robust and the important point is that the model fits the data at least as well as is shown in the figures.

This model provides measures of bias and variability that are represented in the drift rate distribution as well as measures related to time. All of these provide measures of the stimulus representation and decision processes, any of which may be related to mathematical competence and development of decision making competence in this kind of task that were discussed in the introduction. To foreshadow the results, we find that the representations derived from the number-line, dot-arc, and spoken-dots tasks are inconsistent with the representations derived from numerosity discrimination experiments (in Ratcliff & McKoon, 2018). We argue this is because the experimental tasks determine the representation used in making decisions. However, it is an open question whether individual differences in ability correlate across tasks, so that it may be that these different representations are based on the same underlying abilities.

Experiments

The stimuli were displayed on touch-screen CRTs, one- and two-digit numbers for Experiment 1 and arrays of dots for Experiments 2 and 3. For Experiments 1 and 2, subjects moved their index fingers from a resting box at the bottom of the screen to the location on a number line (Experiment 1) or an arc (Experiment 2) that they believed matched the stimulus. In Experiment 3, they called out the number of dots in 10’s (e.g., for a stimulus of 24 dots, they could call out 10, 20, 30, 40 and so on). The number line ranged from 1 to 100 (though 100 was never presented) and the arcs from 11 to 90. Response times were measured from stimulus onset to the time at which the finger lifted from the box for the touch screen tasks or the time at which a microphone detected the initiation of a vocal response for Experiment 3. Examples of the stimuli and displays are shown in Figure 1.

Experiments 1 and 2 were similar to standard tasks for which responses are made on continuous scales but with constraints (adapted from Ratcliff, 2018). These were designed to encourage subjects to make their decisions before lifting their fingers from the resting box and then to move in as ballistic a manner as possible directly to the location they chose on the line or arc. In all three experiments subjects were instructed to use the whole scale and were told what the largest and smallest stimuli were and that these corresponded to the ends of the scale.

All of the subjects were Ohio State University students in an introductory psychology class who participated for class credit. There were 16 subjects in each experiment and each experiment took about 45 minutes to complete.

Experiment 1

On each trial, a one- or two-digit number was displayed and subjects moved their fingers from the resting box to the point on the number line that they believed best matched the displayed number. As discussed earlier, this task is often used in the numerical cognition literature to measure an individual’s abilities to make use of symbolic numeracy and to examine the development of numeracy in children.

Method

The touch screen (CRT) was a 17 inch ELO Entuitive 1725C with dimensions 40 cm. wide and 30 cm. high. Because there is considerable arm fatigue in using a touch screen vertically on a desk, a mount was constructed so that the screen was almost horizontal and located between the knees of subjects. This eliminated arm fatigue. Calibration studies (discussed in Ratcliff, 2018) showed that there was a 110 ms delay in detecting a finger lift and a 48 ms delay in detecting the finger touching the response line. These were subtracted from the lifting and movement-initiation times, respectively.

The resolution of the screen was 640×480 pixels. At a standard viewing distance, 55.8 cm., 1 cm. subtends one degree of visual angle and 20 pixels is 1 cm. in length. The number line was 320 pixels wide (16 cm. and 16 degrees of visual angle), the one- or two-digit number was 60 pixels below the number line and the two-digit number dimensions were roughly 24×17 pixels. The resting box was 140 pixels below the number line and its dimensions were 40×40 pixels.

Subjects began each trial by placing their index fingers on the resting box. Then a plus sign was displayed for 500 ms, then the screen was cleared for 250 ms, and then the stimulus number was presented. When the finger lifted from the box, the number was cleared from the screen. After the subject touched the number line, they returned their finger to the resting box. Then either there was a 250 ms delay before the plus sign for the next trial or feedback was given: if the finger lifted earlier than 220 ms after stimulus presentation, “Too fast lifting” was displayed for 1500 ms; if the finger lifted later than 1500 ms after stimulus presentation, “Too slow lifting” was displayed for 500 ms; if the movement took longer than 360 ms “Too slow movement” was displayed for 500 ms. All these messages were presented 60 pixels above the number line. After feedback, the plus sign appeared for the next trial.

There were 10 blocks of trials, 99 trials each, 1 trial for each possible stimulus number (1–99), presented in random order. Each block began with a message to press a square in the upper left of the screen when ready to begin each block of trials (to allow subjects to take a short break between blocks of trials). There were also 16 practice trials, the same as those in the blocks, except that if the finger was moved to a location away from the target number by 8 or more, the message “ERROR” was given for 250 ms.

Results

As mentioned earlier, RTs were lift-off times from the resting box. RTs less than 150 ms and greater than 2000 ms were eliminated. This eliminated about 2% of the data.

The mean movement time over subjects (the time from lift-off to response) was 263 ms and the median was 251 ms. This speed suggests that subjects were doing what they were asked to do, that is, move their fingers only after they had made their decision and move them directly to the location they chose on the number line.

There was a mean (computed for each subject then averaged over subjects) correlation between movement time and RT of −0.10 (and correlation was +0.13 in Experiment 2). If subjects were computing their decisions during movement on some moderate to large proportion of the trials, then a large negative correlation would be expected because computation of the decision in the movement duration would have produced a long movement time and this would have been accompanied by a shorter RT measured by the lift time. Histograms of movement times are shown at the end of the results sections.

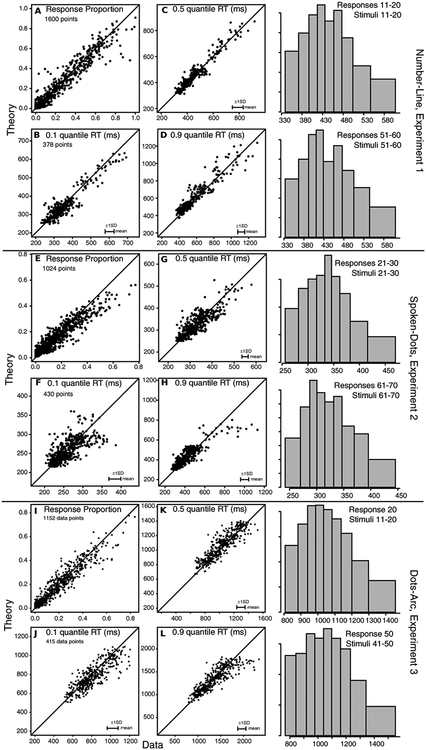
The data and predictions of the model are displayed in two ways. The first is to plot predictions of the model against the data for each subject and each condition (e.g., Ratcliff et al., 2010). Figure 3A shows the probabilities of responses and Figures 3B, 3C, and 3D show the 0.1, 0.5, and 0.9 quantile RTs. For response probabilities, there were 1600 data points: 16 subjects by 10 stimulus groups by 10 response groups (note that many of the values for both data and predictions were near zero). The data and predictions fall around the straight line, indicating a reasonably good fit of the model to the data. There were a few misses as large as 10%, but misses of this size are expected from the size of the SDs in the values. Approximate values of the SDs in the proportions can be computed as follows. A typical value of the number of observations in a stimulus group is 100, then for a proportion of responses of 0.4, the SD is sqrt(.4*.6/100)=0.05 and for a proportion of 0.1, the SD is sqrt(.1*.9/100)=0.03. This means that 2SDs are plus or minus 0.1 and plus or minus 0.06 respectively. These are about the range of misses between data and theory for the plotted points except a few of the most extreme misses.

Figure 3.

Model predictions plotted against data for, A, the proportion of responses, B, C, and D, the 0.1, 0.5 (median) and 0.9 quantile RTs respectively for the number-line task, Experiment 1. The points show the values for all the stimulus and response groups (10×10) for data from each individual subject. All 1600 are shown for proportions of responses, but only those conditions with greater than 10 responses are shown for RT quantiles. The horizontal error bars in the bottom right corner represent the mean 1 SDs in the quantile RTs derived from a bootstrap analysis. E, F, G, and H: the same as A, B, C, and D but for Experiment 2 with smaller numbers of points in the plots because of the smaller stimulus range. I, J, K, and L: The same as E, F, G, and H but for Experiment 3. On the right hand side are some group RT distributions formed by averaging quantile RTs across subjects and drawing equal area rectangles between them (Ratcliff & McKoon, 2008, Figure 5; Ratcliff, 1979).

There was also a reasonably good fit of the model to the 0.1, 0.5, and 0.9 quantile RTs (Figures 3B, 3C, and 3D) with no systematic deviations between the data and predictions. There are only 378 points in these plots because only data for which there were more than 10 observations per condition per response category are plotted. The mean SDs across conditions and subjects are shown in the bottom right corner of each plot, horizontally (because the data are on the x-axis). To construct the error bars, a bootstrap method was used. For each condition and response category for each subject, a bootstrap sample was obtained by sampling with replacement from all the responses for that condition. This was repeated for 100 samples and then the SDs in the RT quantiles were obtained for that subject, condition, and response category from the 100 bootstrap data sets. The error bars represent the means across subjects and conditions. For all three quantiles, the data lie mainly within 2 SDs of the predictions.

We believe that this method of presenting the data and model fits to the data is about as transparent as can be done (especially in these days in which openness is being promoted heavily). Many ways of presenting fits of models to data in the literature are quite inadequate and can hide serious misfits between theory and data - if the quality of fits is presented at all. The method presented here shows whether there are systematic deviations between theory and data for any single subject or single condition (a consistent set of misses would suggest that these possibilities need to be examined). It also shows the quality of fits to the RT distributions in the leading edge (the 0.1 quantile) and the tail (the 0.9 quantile) as well as the center (the median, 0.5 quantile).

To show the shapes of the RT distributions, group RT distributions (Ratcliff & McKoon, 2008, Figure 5; Ratcliff, 1979) are presented in the right hand column of Figure 3. In these plots, the .05, .15, .25, …, .95 RT quantiles are computed and averaged over subjects. Then equal area rectangles are drawn between the quantiles as shown in the plots. Conditions were selected with the largest number of responses, one near the beginning of the range and one in the middle. The distributions are right skewed, as for two-choice tasks, but there is more probability density in the middle of the distribution.

Figure 5.

The same plots for Experiment 2 (dots-arc task) as in Figure 4 but for 8 stimulus groups and 8 response groups.

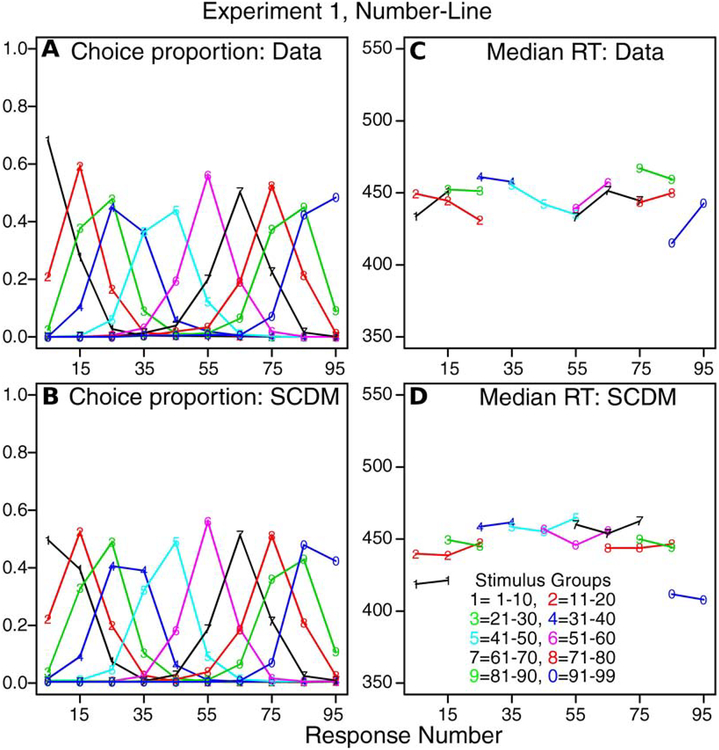
The second way the data and the predictions of the model were compared is shown in Figure 4. The stimuli and responses were grouped into the 10×10 categories described above. Then, for each stimulus category, the probability of a response for each response group was plotted. Figure 4A shows results for the data and Figure 4B for the model. The data were averaged over subjects and the predictions given by the model’s best-fitting parameter values were averaged over subjects (i.e., predictions and data were averaged in the same way).

Figure 4.

A: Values of choice proportions from experimental data from Experiment 1 (number-line task) for 10 stimulus groups and 10 response groups averaged over subjects. B: Predicted values of choice proportions from the SCDM for the same grouping as in A and averaged over subjects in the same way. C: Values of median RTs for the same groups as in panel A. Only values are shown when all subjects contribute values to the medians. D: Values of median RTs matching those in panel C.

The data and model predictions show regular distance effects with responses with highest probability close to their stimulus values. As would be expected from the results in Figure 4A, there is a good correspondence between the predictions and the data for the probabilities. The median RTs are shown in Figures 4C and 4D and these also show reasonable matches between predictions and data. However, there are two deviations that warrant discussion. First, RTs to the stimuli at the ends of the ranges (1–10 and 91–99) are predicted shorter than for the interior stimuli by about 10–30 ms. The data do not show consistent decreases of this size. In the model, these end effects may be accommodated by higher decision criteria at the ends or some other end effect that is not addressed by the model. (Experiment 2 shows a similar pattern.) Second, the probability of a response in the 1–10 bin for a stimulus in the 1–10 bin is about 18% lower for the model than the data. Again this is an end effect not addressed by the model. A raised decision criterion on the end of the range to accommodate the shorter RTs might need more probability density in the distribution at the end of the ranges. The assumption we have used, namely a constant decision criterion across the spatial range, is the simplest. To examine other more complicated assumptions such as a non-constant criterion, we believe that data from single subjects with multiple sessions should be used, i.e., data with much higher reliability than data from single sessions.

Table 1 shows the means of the model parameters that produced the best fits of the model to the data for all of the experiments, averaged over subjects. Discussion of the parameter values and comparisons across experiments are presented after the results from all the experiments are presented.

Table 1:

Mean SCDM model parameters for the three experiments.

Experiment	Ter	st	a	sa	vh	r	G2	df	χ2(crit)
1: Number-line	218.3	43.5	12.2	5.1	14.4	5.83	326	108	133
2: Dots-arc	173.5	39.0	9.9	4.5	13.8	1.40	479	154	184
3: Spoken-dots	614.2	532.6	18.1	2.6	15.6	1.72	315	137	165
	s5	s15	s25	s35	s45	s55	s65	s75	s85	s95
1: Number-line	11.9	11.9	10.5	11.1	10.9	10.4	10.6	10.2	10.7	9.9
2: Dots-arc		15.3	15.5	17.8	22.5	17.5	15.5	15.9	15.1
3: Spoken-dots		17.7	16.9	18.6	18.3	18.3	18.1	16.2	14.1
	v5	v15	v25	v35	v45	v55	v65	v75	v85	v95
1: Number-line	10.6	15.9	22.8	29.8	42.5	55.3	65.7	74.9	81.1	89.5
2: Dots-arc		19.8	29.1	38.6	52.6	63.8	71.8	77.6	82.5
3: Spoken-dots		19.2	33.2	42.7	52.6	61.7	69.5	75.3	82.2

T_er is nondecision time, s_t is the range in nondecision time, a is the boundary setting, s_a is the range in the boundary setting, r is the Gaussian process kernel parameter, v_h multiplies the density for each the drift rate distribution, the v values are the means of the drift rate distributions, the s values are the SDs of the drift rate distributions, the and G² is the multinomial maximum likelihood statistic.

Experiment 2

Arrays of dots (Figure 1B) were presented to subjects and they were asked to point to the location of the number of dots on an arc. This task has been used relatively infrequently (see Fazio, Bailey, Thompson, & Siegler, 2014; and Sasanguie & Reynvoet, 2013) and, as far as we know, RTs have not been examined for this task.

Method

The touch-screen CRT and its dimensions were the same as for Experiment 1. The arcs were displayed in gray against a black background square, which we call the display box. The resting box and dots were white. The arc, display box and resting box remained on the screen throughout the experiment.

The arc went from 0 degrees to 180 degrees (the central radius was 5.75 cm. or 230 pixels) and was 0.5 cm. wide (20 pixels). The 0 and 180 degree ends were located halfway between the top and bottom of the display. The display box was 7×7 cm. (280×280 pixels) and the center of the box was at the origin of the response arc. The resting box was 1 cm. square. It was centered on the bottom of the display, 4.5 cm. below the center of the display box. The dots were 0.4 cm. in diameter and could not be closer to the edge of the display box than 0.35 cm. and could not be closer to each other than 0.125 cm.

The number of dots varied from 11 to 90. There were 16 blocks of 80 trials, with all the numbers of dots displayed in random order for each block, preceded by 16 practice trials (that were not used in the data analyses). Subjects began each block by pressing a square in the upper left corner of the screen, after which the resting block, response arc and display box were displayed.

A subject began each trial by placing his or her right index finger on the resting box. 250 ms later, the dots appeared and then, when the finger lifted from the resting box, the dots disappeared. As before, RTs were measured from stimulus onset to the finger leaving the resting box. Touches less than 6 digits on either side of the correct location on the arc were considered correct responses and a “1” appeared at the correct location on the arc immediately after the touch. Responses further away were considered errors (for the purpose of feedback) and a “0” was presented at the correct location on the arc. These messages were presented for 250 ms.

As for Experiment 1, there was feedback: if the RT was shorter than 200 ms, “Too fast lifting” was displayed, if the RT was longer than 1000 ms, “Too slow lifting” was displayed, and if the movement time from lift off to touching the arc was longer than 300 ms, “Too slow moving” was displayed. These messages were located 200 pixels above the top of the arc and were displayed for 500 ms following which the message was cleared. If none of these messages was displayed, then the next trial began with a finger touch in the resting box.

Results

The data show a mean movement time of 240 ms and a median movement time of 221 ms. These movements are fast enough to assume that decisions were not being made during the movement to the response arc. RTs shorter than 200 ms or longer than 2000 ms were eliminated from analyses (about 3.7% of the data).

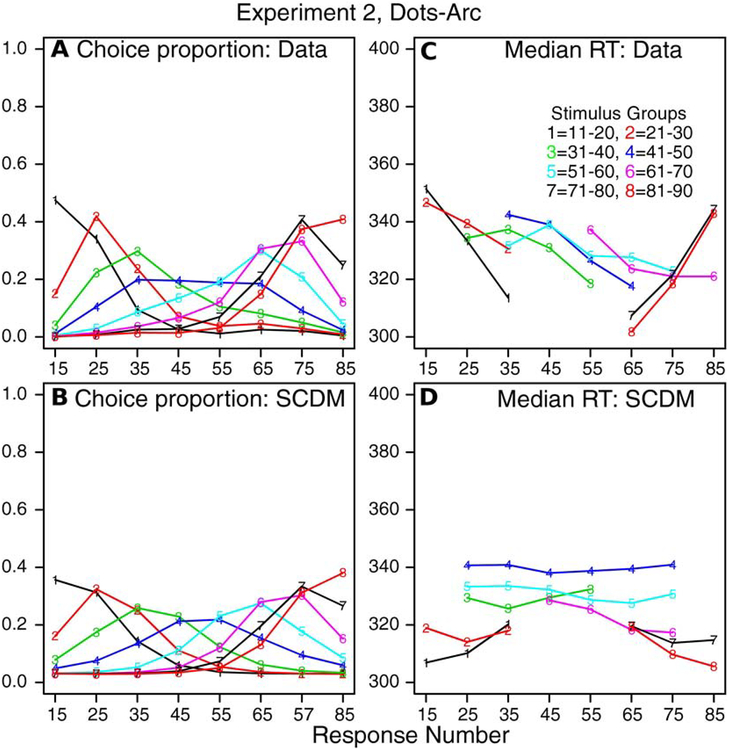
The numbers of dots were grouped into 10’s to make 8 stimulus groups and 8 response groups (11–20, 21–30, …, 81–90). Results are shown in the same ways as for Experiment 1. Figure 3E shows data and predictions plotted against each other for the probabilities of responses with 1024 data points (16 subjects by 8 stimulus groups by 8 response groups) and the other panels show plots of data and predictions for quantile RTs. There are only 430 points in the quantile plots because only data for which there were more than 10 observations per condition per response category are plotted.

For response probabilities, there were some moderately large misses for larger probabilities, with the data having larger values than the predictions (misses at the top right of Figure 3E). Many of these come from misses at the lower end of the stimulus and response range, that is, for 11–20 dots and responses. Typical numbers of observations per stimulus group were about 150 per subject per group. Thus, for a probability of 0.4, the SD is 0.04 and for probability 0.1, the SD is 0.024 (see examples for Experiment 1). This means that plus or minus 2SDs are 0.16 and 0.10, respectively. These 2SD ranges cover most of the values close to the line of equality but there are about 20 or 30 misses below the line of equality, especially for probabilities greater than 0.1. These misses could be examined to determine whether they are systematic using data sets with more observations per subject. If they do replicate, then they can be a focus for model evaluation and model comparison.

For the quantile RTs, the data and predictions fall around the straight line. Plus or minus 1 SD error bars are shown in the bottom right corners as they were for Experiment 1. For the 0.1 quantiles, there are some misses but given the relatively large SD in the quantiles relative to the spread in the data, the number of significant misses is not that large. The 0.5 and 0.9 quantiles show good fits, with only a few 0.9 quantile RTs missed by the model.

Figure 5 shows the second way of presenting the data and model fits. Figure 5A and 5B show plots of the proportions of responses for the 8 stimulus categories for the 8 response groups with data and predictions averaged over subjects. The data and predictions show regular distance effects with responses with highest probability close to their stimulus values. As would be expected from the results in Figure 5, there are some systematic deviations. Response proportions at the ends of the ranges are higher in the data than the model. Figures 5C and 5D show median RTs for the same combinations as for Figures 5A and 5B but, as for Experiment 1, only for conditions in which all subjects produced responses. The data are not as regular as might be hoped especially for the end categories. The model predicts lower RTs by 20–30 ms for the ends of the ranges (stimuli 11–20 and 81–90) relative to the middle of the ranges. As for Experiment 1, relaxing the assumption that the criterion is flat might produce better fits, but larger data sets with more observations per subject might produce more regular data and would allow exploration of deviations between model and data with more certainty.

Experiment 3

Subjects saw arrays of dots just as in Experiment 2, but they conveyed their decisions with vocal responses. This extends application of the model from manual response modes (finger, eye and mouse movements; Ratcliff, 2018) to vocal responses. This is similar to the position to number task in which a position on a line is presented and subjects have to report the corresponding number (e.g., Ashcraft & Moore, 2012; Iuculano & Butterworth, 2011; Siegler & Opfer, 2003; Slusser & Barth, 2017). Results have shown that performance on the position to number task matches that of the number to position in that the same anchor point models account for the results.

In our initial experiment, subjects were asked to produce an exact number of dots (e.g., 74, 23) but this led to extremely long RTs and more symmetric RT distributions than are typically observed. We believe this to have occurred because subjects could not meaningfully distinguish, for example, 31 from 27 or 66 from 69. A quick pilot experiment in which subjects produced both the tens and units digits on some blocks of trials, as in the initial experiment, and produced only the tens digits on the other blocks showed RTs 200–400 ms shorter when only tens were required. Given this, Experiment 3 asked subjects to produce only tens (for example, the response for numbers of dots between 26 to 34 should be 30). With the 9 response categories, the response scale became discrete, not continuous, but in the model, we assumed that subjects were producing responses on an internal continuous scale but then reading out their responses to the nearest tens digit.

Method

Subjects spoke their responses into a microphone, which drove a voice key that detected the onset of sound. RTs were measured from the onset of the arrays of dots to the beginning of the vocalization. The numbers each subject spoke were recorded by a research assistant sitting next to the subject.

The displays had the same range of number of dots as in Experiment 2 and were the same size and displayed in a similar way to those in Experiment 2. The monitor had a 1280×960-pixel 17-inch diagonal screen and was used in standard vertical position (not between the legs as for the touch screens in Experiments 1 and 2). The dot arrays were displayed on a black background and examples are presented in Figure 1C. The dots were presented in a rectangle of size 256×256 pixels in the middle of the screen. The dots had diameters of 16 pixels and they could touch the edge of the 256×256 pixel box. The circles could not be closer to each other than 0.125 cm.

On each trial, an array was presented for 250 ms and then the screen was cleared. Subjects were instructed to call out the number of dots to the nearest 10. If the RT was between 300 and 2500 ms, the next trial began 1500 ms after the response (this accommodated the length of time to produce the whole sound). If the RT was shorter than 300 ms or longer than 1800 ms, “Too fast” or “Too slow” appeared for 1500 ms or 800 ms, respectively, one quarter of the way down the screen (above the position of the dot array). Then the screen was cleared for 1500 ms and then the next trial began.

There were 32 blocks of 40 trials. For each block, the numbers of dots were randomly selected without replacement from the 80 possible numbers. At the beginning of the experiment, there were 10 trials and, for each, a two-digit number showing the number of dots was displayed simultaneously with the array of dots in order to allow the subjects to calibrate themselves. These were followed by 20 more practice trials each with the correct number of dots displayed in the center of the screen after the vocal response. For this task, pilot data showed that subjects could lose their calibration so that responses for the largest stimuli drifted to lower numbers (because there was no feedback). To reduce this drift, we presented five further calibration trials for which the dots and their number were displayed simultaneously after blocks 1, 2, 4, 8, and 16.

Results

Trials with RTs shorter than 200 ms and greater than 3000 ms were eliminated from analyses (about 1.4% of the data). The model was applied in the same way as for the other tasks except that there was one additional assumption: when the evidence accumulation process hit the decision criterion, the ten’s number nearest to that location was produced as the response.

Plots of response probabilities and the 0.1, 0.5, and 0.9 RT quantiles for which there were more than 10 responses are shown in Figure 3I–3L. There are a few misses in the response probabilities that are larger than would be expected by chance (1SD at a probability of 0.4 and with 90 observations is sqrt(.4*.6/90)=0.052). There are also a few misses for some of the 0.1 quantile RTs, but these are close to within 2SDs of the corresponding data.

The difference between the RTs for Experiment 3 and those for Experiments 1 and 2 was large. The median RT for Experiment 3 was around 1000 ms whereas the medians for Experiments 1 and 2 were around 450 ms and 350 ms, respectively. (The pilot experiment in which subjects had to call out a 2-digit number had median RTs around 1300 ms.) Model parameters responsible for this difference will be discussed later.

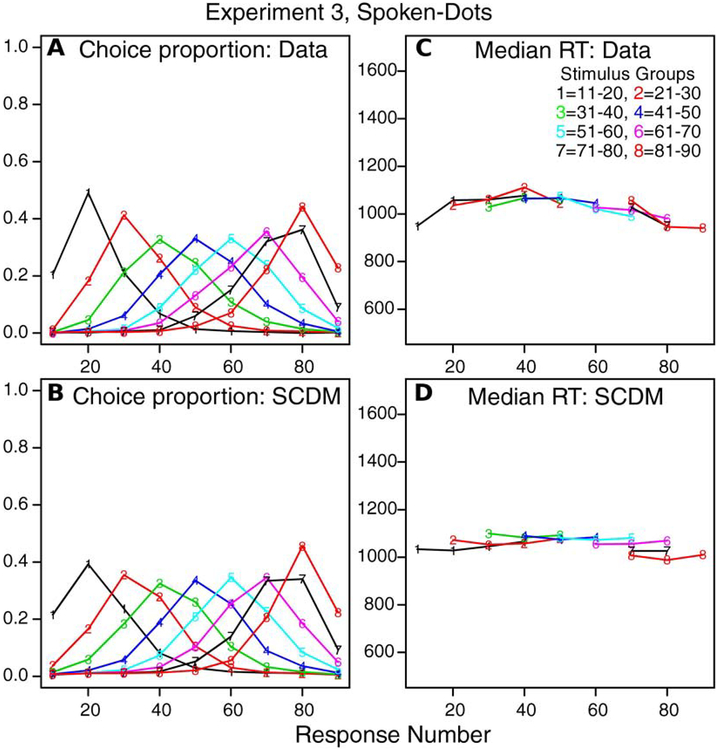
As for Experiments 1 and 2, Figures 6A and 6B show plots of response proportions for the 9 response groups for each of the 8 stimulus groups for data and model fits. As for the other experiments, the theory and data match quite well with the exception that the model predicts smaller choice proportions at the left extreme. Figures 6C and 6D show median RTs for response groups with all subjects providing at least 10 responses for the different stimulus and response groups as before. The match between theory and data is quite reasonable with the single exception of a modest decrease in RT for the 11–20 stimulus group for 10’s responses in the data relative to the prediction from the model fit (the effect is the opposite for Experiments 1 and 2 in which the theory predicted a larger fall than is seen in the data).

Figure 6.

The same plots for Experiment 3 (spoken-dots task) as in Figure 4 but for 8 stimulus groups and 9 response groups.

Comparison of Model Parameters and Fits Across Tasks

Table 1 shows the mean values of the best-fitting parameters of the model across subjects. First, nondecision time was similar for the number-line task and the dots task with manual responses, around 170–220 ms, but it was considerably longer for the dots task with spoken responses, around 600 ms. This suggests that the process of translating from a number or an array of dots to a position on a line or arc is highly automated and does not require much time to translate from the stimulus to the scale but that vocalizing the number of dots is much less direct. The across-trial variability in nondecision time was much larger for the vocal-response task than the other two, about 40 ms for the two manual tasks and about 500 ms for the vocal task, as might be expected from the mean RTs of the tasks.

Second, the mean criterion setting was largest for the spoken-dots task, next largest for the number-line task, and smallest for the dots-arc task, but the size of the range in across-trial variability had a different ordering, namely number-line, dots-arc, then spoken-dots.

Third, the Gaussian-process kernel parameter had values 5.8, 1.4, and 1.7 for Experiments 1, 2, and 3 respectively. These values are smaller than the SDs in the drift-rate distributions, showing more spatial variability in the noise than the drift-rate distributions.

Generally, the G-square goodness of fit values were reasonable (Table 1), with mean values about 2–3 times the critical value of the chi-square statistic. This is consistent with Ratcliff and Starns’ confidence judgment model and the SCDM applied to perceptual tasks (Ratcliff, 2018; Ratcliff & Starns, 2013; Ratcliff, Thapar, Gomez, & McKoon, 2004).

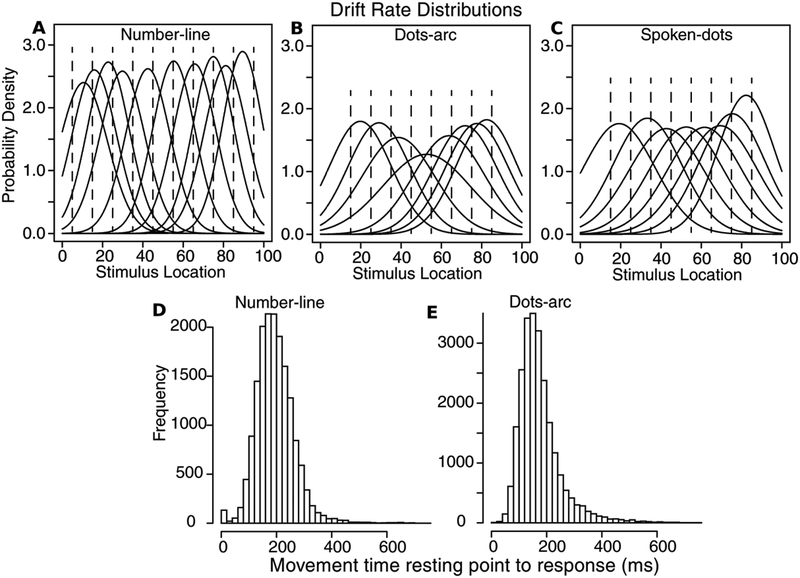
The parameters that represent the stimulus representation driving the decision process are the means and SDs in the drift-rate distributions and these are shown in Table 1 and Figures 7A, 7B, and 7C (the dashed lines represent the stimulus values corresponding to the distribution means). Biases in representations are represented by biases in the means of the drift-rate distributions. For the number-line task, there is little bias apart from the ends of the distribution, for example, for drift rate for stimulus 5, the mean was at 10.6 (Table 1). For the dots-arc and spoken-dots task, there was a bias towards larger numbers so the means of the distributions were larger than stimulus values except at the extreme end of the distribution. The SDs in the distributions showed similar values across the whole range for the number-line task. But for the dots-arc task, the distribution of SDs was narrower at the ends of the ranges and larger in the middle, that is, less precision or acuity in the middle. These lower SDs at the ends of the range can be seen as anchor effects. For the dots-spoken experiment, the SDs hardly change except for a smaller SD at the right-hand end (showing a slight anchor effect for larger numbers of dots).

Figure 7.

A, B, C: Drift rate distributions for Experiments 1, 2, and 3, respectively, from the SCDM using parameter values averaged over subjects that are shown in Table 1. D and E: Movement time distributions averaged over all subjects and all conditions for Experiments 1 and 2 respectively. The distribution for Experiment 1 is a little wider than that for Experiment 2 because of longer travel times for Experiment 1 for the ends of the number line (see Figure 1A and 1B).

As discussed in the introduction, in the numerical cognition literature, anchor effects have received a lot of attention (e.g., Rouder & Geary, 2014), especially with regard to development of numeracy abilities (Ansari, 2008; Case, Okamoto, Henderson, McKeough, & Bleiker, 1996; Dehaene, 1997; Geary, 2011; Siegler & Booth, 2004; Siegler, Thompson, & Opfer, 2009; Slusser, Santiago, & Barth, 2013; Thompson & Siegler, 2010). The drift rate distributions in our experiments show only small anchor effects (except for Experiment 2), and show no anchor effects for the middle of the range (stimuli near 50). This may be due to the practice and feedback we gave the subjects. Because the effects are small and there are no center effects, we believe that there would be little benefit in using these data for examining or testing models about anchor effects, especially for Experiments 1 and 3.

Finally, movement time histograms for Experiments 1 and 2 are shown in Figures 7D and 7E. In the experiments, subjects are instructed to make their decision before moving their finger to make the response. These distributions show that subjects largely complied with the instructions. Because these tasks required subjects to lift their fingers and move them to the response line or arc, we do not have the paths they travel as we might have with mouse movements or eye movements. In new experiments in our laboratory, we have subjects slide (swipe) their fingers to make their response and this provides tracks. This allows subjects with paths that are not straight lines (or close to straight lines) to be identified and so instructions can be given to change behavior or their data might be eliminated.

Discussion

The three experiments used a symbolic task and two non-symbolic tasks, two with manual responses and one with vocal responses. The fits of the model to data produced choice proportion distributions that have relatively little bias in the locations of the means. The spreads of these distributions (SDs) show small changes across the number line for the number-line and spoken-dots tasks, but with an increase in the spreads from both ends towards the middle for the dots-arc task (Figure 4A, 4E, and 4I).

For RTs, there was almost no change across positions on the response scale (Figures 4C, 5C, and 6C). Although this was one possible outcome, before we obtained the data we believed it possible that RTs would increase from lower numbers to larger numbers because of higher familiarity with low numbers. In addition, there was almost no change in RTs from the peak responding area for a stimulus value to surrounding areas. Responses in the surrounding areas can be thought of as errors and so RTs to them might have been predicted to be similar to those from two-choice data: faster or slower than RTs for correct responses depending on the particular conditions of an experiment. Further, the RT distributions have the standard right-skewed shape, which provides strong constraints on model architectures (Ratcliff, 1978; Ratcliff & Smith, 2004). The SCDM accounts for the right-skewed shape at the same time that it accounts for the finding that RTs differ little across positions.

Mean RTs for Experiments 1 and 2 were quite short, shorter than two-choice tasks using similar stimuli. The leading edges of the RT distributions, as measured by the 0.1 quantile RTs, were also shorter than those for two-choice tasks. For example, for conditions (groups of numbers or numerosities) with proportions of responses greater than 0.3, the mean 0.1 quantile RT for the number-line task was 346 ms and for the dots-arc task, it was 289 ms (cf. Figures 3B and 3F). In comparison, for a number discrimination task (is this one-digit or two-digit number greater or less than 50; Ratcliff, Thompson, & McKoon, 2015), the 0.1 quantile RT was 400 ms and for a dots discrimination task (are there more or fewer dots than 25, Ratcliff & McKoon, 2018), the 0.1 quantile RT was 375 ms. The difference between the continuous-response and two-choice tasks is important because it suggests that the mapping from a number or array of dots to a line or arc involves less processing than deciding if a number is greater or less than a standard. Thus, such continuous tasks with manual responses may be a more direct measure of the representations of symbolic and nonsymbolic numeracy than the two-choice tasks. RTs for the spoken-dots task were much slower than for the number-line and dots-arcs tasks, in fact, over 500 ms slower, suggesting a time-consuming process that maps from the internal representation of the number of dots to the estimate of the number to be spoken.

These differences in RTs and leading edges of RT distributions for the number-line and dots-arc tasks relative to the two-choice tasks to which they are similar are not due to differences in the apparatus used or the procedures. Gomez, Ratcliff, and Childers (2015) used the same apparatus as the experiments presented here and found similar RTs for keyboard responses and touch-screen responses for two-choice tasks that were identical except for the response mode. In their experiments, RTs for responses were measured from finger lift time in the touch screen task in the same way as in the number-line and dots-arc tasks here. The leading edges of the RT distributions for the key-press and lifting responses had quite similar RTs.

The SCDM gave a good account of all the data from the three tasks; it matched the data with either 22 or 26 parameters for between 135 and 177 degrees of freedom in the data, with only a few systematic deviations in RTs at the ends of the response ranges. The model accounted for the probabilities of responses for 8 or 10 stimulus groups crossed with 8, 9, or 10 response groups. It accounted for RT distributions across subjects and across the conditions in the experiments (except for conditions in which there were too few observations to reliably estimate the quantiles of the distributions).

The model has 6 parameters that are common across all the stimulus and response groups for each experiment. These are nondecision time and the range of across-trial variability in it, the setting of the response criterion and the range of across-trial variability in it, the Gaussian-process kernel parameter for the Gaussian-process noise, and the drift-rate height parameter that multiplies the density of all the distributions of drift rates. In addition, for each numerosity group, there is a parameter for the mean location of its drift-rate distribution and one for the SD in the distribution.

The model’s misses in RTs at the ends of the response scales might be addressed in three ways. One is that the criterion setting might be adjusted higher at the ends so that more evidence is required before a decision. The second is that the range of the response scale might be extended. For example, for Experiment 2, instead of using the 11–90 range, the range 1–100 might be used. Then any decision at a location higher than 90 would be relocated to the 81–90 bin and any decision lower than 11 would be relocated to 11–20 bin. This might increase RTs at the ends of the scale and so give a better match between model and data. Third, the drift-rate distributions might have different sizes (densities) at different locations and so the distributions at the extremes could be higher. This latter possibility would produce greater probability of responding at the extremes, but the greater drift rate might produce shorter RTs, which would make the misses in RTs between theory and data at the ends greater (a higher decision criterion might alleviate this problem). These assumptions and combinations of them need to be explored with experiments that have more sessions per subject and more practice with the tasks.

An important point to be made about our analyses for the number-line task is that the plots in Figures 4A, 4E, and 4I show both location and spread of responses, something that has rarely been reported (if at all) for previous number-line experiments. The choice proportions plotted in Figure 4A show acuity (i.e., the spreads of the distributions of responses) and biases in the distributions of responses away from the position corresponding to the correct location, two aspects of the data that are not separated in some measures of performance. For example, a measure of ability to perform the number-line task that has been used extensively is the mean absolute deviation of the choice-proportion data from the correct response position (summed over stimulus positions). However, this measure can be large for two reasons. First, responses can be biased away from the correct values even with small variability around the biased value, or second, the SD in the spread around the correct value can be large even with no bias away from the correct value. Thus, the plots we show give a more detailed measure of all facets of the data than reporting only response proportions.

The distributions of responses around the correct response location (Figures 4A, 5A, and 6A) are consistent with the idea that representations of number are distributed over position. For example, if the stimulus is, say, 45, then the location corresponding to 45 would have a lot of density around 45, less around 40 and 50, and much less further out (Figure 4A), which can be interpreted as a distributed representation. This is also consistent with the assumptions of distributed representations in the widely used ANS models.

The model used in our experiments assumes that the response scale has equal divisions and that all deviations from linearity are represented in the stimulus distributions. However, we have recently collected data from older adults and a few of them (5%) produced very few responses in the middle of the arc in the dots-arc task (i.e., an “anti-anchor” point). To accommodate this, we might have to make the response scale nonlinear with points on the scale being parameters of the model. For example, the region of the scale corresponding to, say 46–55, would be very narrow. These regions would act like regions between confidence criteria in confidence models which can be narrow to accommodate few responses in that category. This means that the numbers on the x-axis in Figures 7A-7C would not be uniformly distributed. In fitting the model, we group responses into 10’s and so with this grouping, this scheme would add 10 parameters to define the response regions. Another alternative would be to have the decision criterion vary over number as opposed to being constant over all numbers as it is in the fits to Experiments 1–3. Both of these assumptions are implemented in the RTCON2 confidence model (Ratcliff & Starns, 2013) in which confidence is represented as a distribution, confidence criteria are parameters of the model, and decision criteria differ across confidence judgment categories. In the RTCON2 model, changes in the confidence criteria and changes in the decision criteria make different predictions about RT distributions. These will also have different predictions about RT distributions in the SCDM and fitting the model will allow us to determine which assumptions are needed. For the experiments in this article, neither is needed (apart from the small misses between theory and data discussed above).

As discussed in the introduction, in the numerical cognition literature, there are two popular ANS models (Dehaene, 1997, 2003; Gallistel & Gelman, 1992) that have been used to explain two-choice numerosity discrimination tasks. In one, numerosity is represented on a linear scale with the SD in the distribution increasing linearly with number. In the other, numerosity is represented on a logarithmic scale with a distribution around the mean that is typically assumed to have a constant SD as numerosity increases. These models have been mainly aimed at understanding how judgments are made about numerosity discrimination tasks that ask which of two arrays of dots has the most dots. They have been used to explain why the probability with which responses are made decreases as the total number of dots increases (the “magnitude effect”) and why it increases as the distance between the numbers of dots in the two arrays increases (the “distance effect”).

These models have rarely been used to address RTs. When Ratcliff and McKoon (2018) integrated the two ANS models with the two-choice diffusion model, results from both accuracy and RTs showed that the two models produced qualitatively different patterns of RT predictions and that which model best fit data was different for different tasks. When the task was to decide whether there were more blue or yellow dots in an array in which the dots were intermingled, RTs decreased with magnitude for constant differences between the two kinds of dots and the linear model fit best. When the task was to decide which of two side-by-side arrays of dots had the most dots, RTs increased with magnitude for constant differences between the two kinds of dots and the logarithmic model fit best. Results similar to those from the task with intermingled dots (in Ratcliff & McKoon, 2018) have also been obtained for perceptual tasks, namely brightness and motion discrimination, and the linear model has fit data from those tasks well (Ratcliff, Voskuilen, & Teoderescu, 2018).

Some of the model components that are extracted from fits to numerosity discrimination tasks appear to be similar to those extracted from fits of the SCDM in this article. However, the model components are not exactly the same. For the number-line task, Experiment 1, numbers are overlearned and the linearity of the scale (certainly for numbers 1–99) is well-learned and understood. Drift-rate distributions had only a little bias away from the center of the number range, their means increased linearly, and the SDs in the distributions hardly differed across the whole stimulus range (Figure 7A). For adults, these results are different from results from numerosity discrimination tasks and the ANS-diffusion model fits which show either a compressed scale or increasing variability with numerosity. Thus, for the number-line task, the representations derived from the data are inconsistent with the representations from the numerosity discrimination tasks.

For the dots-arc task, Experiment 2, we might have expected that the results might match those from numerosity discrimination tasks and that one of the ANS representation models would apply (either the scale would be non-linear or the SD in the drift-rate distributions would increase with numerosity). However, the means did not show non-linear compression or increasing SDs at the upper end of the range (they were roughly symmetric, Figure 7B) and results showed anchor points at the ends of the scales with SDs increasing from 11 to 50 dots but also with SDs decreasing as the number of dots increases from 50 to 90 (Figure 7B). Thus, these results do not match those from the ANS-diffusion models.

For the spoken-dots task, Experiment 3, we might have expected from the ANS models that the scale might be compressed or the SDs in the drift-rate distributions might increase with numerosity. However, as for Experiment 1, the means of the distributions increased linearly and the SDs hardly differed with numerosity. Again, this is not what would be expected from either of the ANS models. With the SCDM, the experimental tasks reported here determined the stimulus representations, not a common representation across tasks. The findings here generalize the task dependency observed by Ratcliff and McKoon (2018) from the numerosity discrimination tasks to these continuous scale tasks.

The SCDM has been applied to a number of perceptual tasks that are different from the numeracy tasks presented above. These perceptual tasks used a variety of perceptual stimuli and response modes (Ratcliff, 2018). The stimuli were black and white and colored arrays of pixels, arrays of arrows, and arrays of moving dots, with static and dynamic displays. Responses were made by eye, finger, or mouse movements. In each experiment, there were several levels of difficulty. The SCDM accounted for accuracy and RT distributions for the data from the experiments quite well, with relatively few deviations between theory and data for experiment. The model captured the spatial distributions of responses and the full distributions of RTs. The results from the experiments here and SCDM’s successful account of the data show that the SCDM can be applied to the numeracy domain as well as to perceptual tasks.

Even though the representations we derive from these number-line, dot-arc, and spoken-dots tasks are inconsistent with the representations derived from the numerosity discrimination experiments, it is likely that parameters representing ability show similar individual differences. If someone performs well on one numeracy task, it is likely that they will perform well on other numeracy tasks. However, what model components might correlate between tasks is hard to guess. Nondecision time and boundary parameters (which are determined more by RT data than accuracy data in estimation) arise from somewhat different structures in the models and so it is hard to guess whether they will correlate. Drift rate coefficients and SD coefficients in the numerosity discrimination models (Ratcliff & McKoon, 2018) represent ability while the drift rate distribution heights, SDs, and the biases away from the correct location represent ability. Thus, there are several possible relationships between the two classes of models. These kinds of tasks have been shown to provide individual differences that relate to achievement in children, but so far we have no data for children that are appropriate for modeling. Such data would allow achievement to be related to these various components of the model.

Relationships to Neuroscience and Other Research Domains

The SCDM can be seen as an implementation of population code models in neuroscience (e.g., Beck et al., 2008; Deneve, Latham, & Pouget, 1999; Jazayeri & Movshon, 2006; Liu & Wang, 2008; McMillen, Simen, & Behseta, 2011; Nichols & Newsome, 2002; Pouget, Beck, Wei, & Latham, 2013). In these models, populations of neurons that respond to different values on the stimulus dimension drive decisions. Thus, the SCDM can offer the possibility for interactions to advance modeling between psychology and neuroscience. However, because most of these population code models have been developed with the architecture of the oculomotor system as the target system, our experiments with motor responses with fingers and spoken outputs will require significant modification of the models to make them compatible with the neuroscience of the motor system for manual responses or the motor system for spoken responses.

In much previous research in decision-making neuroscience with animals, areas in motor cortex or oculomotor systems (such as LIP, FEF, or SC) include a motor or retinotopic map such that activity in regions of the map corresponds to motor or eye movements to locations in space. In experiments with monkeys, a great deal of time (many hours over weeks) is needed to train the mapping between, for example, a perceptual variable and the oculomotor response to produce decision-related activity in decision-related areas such as LIP, FEF, or SC. In a typical experiment using a motion discrimination task, the left vs. right stimulus motion has to be trained so that the monkeys move their eyes to one target location for right motion and a different location for left motion. This means that the mapping between the output of perceptual processes and the decision-related areas is to some degree arbitrary, but the mapping must be trainable. In contrast, human day-to-day functioning shows the ability to arbitrarily map from cognitive and perceptual operations to motor outputs. Furthermore, such mapping can be acquired very quickly, in one trial with verbal instructions. Perhaps the speed of acquiring such a mapping is the same for monkeys for their natural tasks and behaviors.

We know of only one experiment in which monkeys were trained to respond on a continuum (Nicols & Newsome, 2002 - training was apparently so difficult that such training has not been done again, at least in published reports). The stimuli were moving dots and motion was coherently in one direction and responses were made on a circle corresponding to the motion direction. Results from this study showed responses distributed over spatial position just as in the tasks reported here (Figures 4A, 5A, and 6A and in the perceptual experiments in Ratcliff (2018). The manipulation of most interest in the study was microstimulation to see how responses were biased as a function of angular distance between the location of microstimulation and the motion direction. Neural recordings in decision-making areas were not reported.

If neural recordings were collected from an experiment like this, once a stimulus-to-response mapping was trained, neural responses from the monkeys would provide data to guide theories aimed at connecting neural and behavioral processes in decision-making on continuous scales. The buildup of neural activity would correspond to the accumulation of evidence in the SCDM and other population code models such as Beck et al. (2008).

Experiment 3 suggests that the mapping between internal representations and spoken motor output is much more complicated than the simple spatial mappings between stimuli and responses that are trained in most experiments that examine two-choice decision-making with animals. Systems for spoken responses are very unlikely to have simple spatial mappings for number words in the tens as in Experiment 3. The size of a typical vocabulary is many tens of thousands of words and everything we know suggests that there are not spatially distributed representations (e.g., grandmother cells or small populations of grandmother cells) for words, where each word is located at a different location on part of the cortex, for example. Furthermore, the architecture of the vocal system does not have a spatial representation in the way that the oculomotor systems has. If the SCDM application to Experiment 3 is correct, then for spoken responses, the decision process must be carried out earlier in the processing stream than the final mapping onto the motor areas responsible for producing the spoken response. For example, it might be carried out on a more abstract numerosity scale from which a signal would be generated to guide the spoken output.

In the numerosity domain, there is evidence for localized, spatially distributed tuning curves for numerosity in the prefrontal cortex of monkeys. Nieder and Miller (2003) presented such evidence for tuning curves for numerosities in the range of 2–6 and Nieder and Merton (2007) extended this to numerosities up to 30. However, these tasks used a match-to-sample procedure in which responses were made as to whether the numerosity of a stimulus array of dots matched the numerosity of a second or third array of dots. It has not been demonstrated that these representations would be used in a task similar the dots-arc task (for animals) with numbers up to 90.

There is also evidence from fMRI for representations of numerosity in humans in the bilateral intraparietal sulci. The task used in the studies providing such evidence involved passive viewing of arrays of dots with most having the same number, but with an occasional deviation (Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004) or with numbers and spoken numbers mixed in with the dot arrays (Piazza, Pinel, Le Bihan, & Dehaene, 2007). fMRI responses increased with the size of the change in the number which suggests that this area is involved in processing numerosity. However, these experiments do not show the kind of spatially distributed tuning curves as for monkeys and so how these pieces of evidence (monkey single cell recordings and fMRI results) relate to each other is unclear. At this point, we believe that there are no neurophysiological data that can give clear guidance on how numerosity is represented and processed in tasks like the number-line task.

The results above and the results in Ratcliff and McKoon (2018) suggest that representations are task dependent and so in neurophysiology, representations would have to be built in response to task demands. These representations would then have to map into the decision-related evidence (drift rates) that is to be used in the decision-making task, in flexible and dynamic ways.

Conclusions

Application of the SCDM to the simple numeracy tasks used in Experiments 1, 2, and 3 gives a view of processing through a model-based framework. Previous research has been largely empirical. Measures of accuracy have been used to test simple hypotheses about representations and to examine individual differences in ability. The accuracy measure most often used is based on the mean deviation between the responses and the correct response location (though some analyses have examined biases as well as variability in responses).

In contrast, the SCDM gives clearer and more direct information about cognitive representations of numeracy-- the strength of numerosities (the parameter representing the height of the distributions, v_h), biases away from the correct numerosity (the means of the distributions relative to the correct value), and acuity, represented by the SDs in the distributions. Along with these aspects of performance are parameters that represent the time course of processing, namely nondecision time and criterion setting and their associated variability parameters. Any or all of these quantities may be useful in understanding the representation and processing of numerosity in decision-making.

The number-line task has been used extensively in the developmental domain. However, it is important not to apply the SCDM to data from children who have not yet automated the decision process but rather may be performing slow (perhaps serial) computations to work out an answer. Such slow processing would add components that are not part of the SCDM evidence accumulation process and so would require a different kind of model or additional components to the SCDM. Examination of RT distributions would provide clues to whether the model should be applied to the data from a particular population.

The SCDM provides a different analysis of performance on numeracy tasks from what is currently available. It accounts for the distributions of choices and the variability in those choices around the mean value. Unlike most other research using these tasks, SCDM is a model of the time course of evidence accumulation and it accounts for the distributions of RTs. For modeling, RTs provide a powerful constraint and also provide additional measures for use in examining individual differences in subject populations.

Highlights.

• This is the first modeling of RT and accuracy for number line tasks

• The SCDM fits data from tasks in which responses are made on continuous scales

• RT and accuracy data are presented for symbolic and non-symbolic number line tasks

• Model parameters represent acuity, strength, bias, and decision processes

• The SCDM provides parameters potentially useful for individual difference studies