Abstract
A positron emission tomography (PET) scanner with submillimeter spatial resolution, capable of in vivo imaging of murine extremities was built based on two dual ended readout, hybrid depth of interaction (DOI) PET detectors. Each was composed of a 36 × 36 array of 0.43 mm × 0.43 mm × 8 mm unpolished lutetium oxyorthosilicate crystals separated by a 50 μm white diffuse reflector. The array was coupled to a position-sensing photomultiplier tube at one end and to an avalanche photodiode at the other end. The detector characterization included crystal identification accuracy, DOI, energy, and timing resolution measurements. The scanner was characterized in terms of its spatial resolution and its sensitivity and mouse images were acquired of a mouse paw injected with 18-F-NaF. Out of the 36 × 36 crystals only 33 × 33 crystals were identified. The coincidence timing, DOI, and energy resolution of the scanner was measured to be 2.8 ns, 1.4 mm, and 27%, respectively. The scanner’s spatial resolution was measured with a line source and determined from an ordered subsets expectation maximization reconstruction to be 0.56 mm. The sensitivity of the scanner was measured to be 0.6% at the center of the field of view.
Index Terms—: Depth of interaction (DOI), high resolution imaging, hybrid DOI detector, mouse paw imaging, positron emission tomography (PET) detectors, preclinical PET
I. Introduction
THE QUANTITATIVE assessment of disease status in rheumatoid arthritis (RA) is difficult and the common approach is to serologically test for C-reactive protein levels and erythrocyte sedimentation rate, which are nonspecific markers of inflammation [1], [2]. Molecular imaging of synovial inflammation with 18F-FDG positron emission tomography (PET) has been demonstrated in humans [3]–[7]; it has the potential to provide quantitative evidence of disease progression before X-ray-based radiographic progression can be observed. The use of PET for inflammation imaging is well documented [8] and RA treatment aims at minimizing inflammation. However, questions remain about the effectiveness of the treatment methodology and the underlying inflammatory process, that is, responsible for the pathogenesis of the disease [4], [9]. Such questions are being addressed with preclinical RA models [10], [11]. For example, the collagen induced arthritic mouse model has been used to study the role of tumor necrosis factor alpha in the pathogenesis of RA [12] and for documenting RA pathogenesis [13].
The current gold standard for assessing inflammation in animal studies is ex vivo histopathology imaging [14]. This precludes longitudinal studies using fewer animals. As in the clinic, PET imaging can serve as a tool for longitudinal in vivo assessment of disease status in the arthritic mouse [13]. However, the quantitative accuracy of PET degrades when imaging objects that are smaller than the spatial resolution of the system, as is the case when imaging a mouse paw with a commercially available animal PET scanner [13], [15]. A typical mouse phalangeal joint has a diameter of approximately 1 mm and the typical system spatial resolution of commercial animal scanners is approximately 1.5 mm [16]. Ideally, to achieve accurate quantitative mouse paw imaging, a resolution of a quarter mouse paw joint diameter is needed, therefore, an ultra high resolution (submillimeter) PET scanner is proposed [17].
Generally, high image spatial resolution is achieved by selecting the optimal PET scanner design parameters: scintillation crystal width, the depth of interaction (DOI) resolution, the accuracy of the crystal decoding process, and the detector separation distance. Additional factors that influence spatial resolution are the positron range, and the image reconstruction technique. The contribution of these parameter on the PET system spatial resolution has been analyzed in detail elsewhere [18], [19] and are usually determined within the detector design.
Trends in high-resolution detector design have been to couple arrays of fine, high aspect ratio, scintillation crystals to position sensing photodetectors [20]–[24]. Monolithic scintillator detectors have also been designed for high resolution imaging in animals [25]. High-resolution detectors that are DOI encoding capable have been typically single ended readout [26], [27] or dual ended readout [28]–[30]. The ultra high-resolution scanner presented in this paper is a scanner based on a hybrid dual ended readout DOI detector [31]–[33]. The dual ended configuration was selected as it achieves better DOI and energy resolution (ER) compared to other configurations.
Yang et al. [34] was able to achieve 0.6 mm spatial resolution in a prototype scanner designed for mouse brain imaging based on a dual ended readout detector with avalanche photodiodes (APD). The scanner used 16 detectors arranged in a ring geometry with a 30 mm transaxial and 7 mm axial field of view (FOV). The axial FOV was not long enough to scan the full mouse hind paw from metatarsus to calcaneus in a single acquisition [35]. The scanner’s coincidence electronics processed 128 × 32 energy signals and was capable of recording coincidence events between two detectors at a time. The scanner proposed in this paper uses two detectors which are readout by a scaled down version of the same coincidence electronic system. The detectors configured in this paper have a larger array of crystals and take the timing properties and spatial positioning accuracy from a photomultiplier tube (PMT) opposite to an APD, resulting in a compact DOI capable detector with similar detector performance.
In this paper, the performance of the ultra high-resolution scanner intended for mouse extremities is presented in terms of the scanner’s spatial resolution evaluated with phantoms. The characterization of the ultra high-resolution hybrid DOI PET detector is also reported.
II. Material and Methods
A. Hybrid Detector Design
Two detectors, where fabricated, each composed of a 36 × 36 array of 0.43 mm × 0.43 mm × 8 mm unpolished lutetium oxyorthosilicate (LSO) crystals separated with 50 μm white diffuse reflector (Toray Industries Inc., Tokyo, Japan) achieving a crystal pitch of 0.5 mm and array outer dimensions of 18 mm × 18 mm (Fig. 1). The arrays, where manufactured by Agile Engineering Inc. (Knoxville, TN, USA) using a method described in [23]. A position sensing PMT (PSPMT) (H7546A, Hamamatsu Corporation, Japan) was coupled to the proximal end of the crystal array and an APD (Radiation Monitoring Devices Inc., Watertown, USA) to the distal end [Fig. 1(a)]. Both photodetectors were coupled to the array using optical grease (BC-630, Saint-Gobain Crystals, Hiram, OH, USA). The PSPMT had a 18 mm × 18 mm active area and its 64 anodes were multiplexed to 4 output channels by a resistive network and preamps described in [36] and operated at −900 V. The APD output channel was taken at the anode pin after amplification with a charge sensitive preamp (CR-110, Cremat Inc., USA) and was operated at −1700 V. All five channels, four from the PSPMT and 1 from the APD, were processed with nuclear instrumentation module electronics as described in (34) and all data were acquired using a data acquisition board (PD2-MFS-8–500k/14, UEI, Inc., Canton, MA, USA). To improve gain and reduce noise the APD was cooled to 10°C for all measurements. Cooling was achieved by flowing chilled dryair (XR401 Air-Jet, FTS Systems, SP Industries, Stone Ridge, NY, USA) into the closed plastic detector housing.
Fig. 1.
(a) Photograph of the detector module with components shown. The PSPMT, crystal array, and APD are marked by a, b, c, respectively. (b) Photograph of the LSO crystal array and a regional microscopic image (black arrow shows the width of a crystal).
B. Scanner Design and Fabrication
The scanner was designed to rotate with two single modular detectors [Fig. 2(a)]. Each module consisted of a PSPMT, APD, and crystal array housed in a plastic case, which was 3-D printed [Fig. 2(b)]. The module case was designed in solid modeling software (Inventor, Autodesk, San Rafael, CA, USA) and the 3-D output files, in STL format, were printed using a 3-D printer (Object Eden 260V, Stratasys Ltd., USA). Guide features were designed into each module case to allow proper alignment and positioning of the crystal arrays on the rotating gantry. A cooling port was also designed in the module case to cool the APD [Fig. 2(b)]. The gantry was made of a 12.7 mm thick aluminum plate machined on a computer numerical control mill with features to ensure proper detector module positioning. The gantry was mounted onto a rotating table (Velmex Inc., Bloomfield, NY, USA) with the axis of rotation parallel to the horizontal, capable of 180° rotation [Fig. 2(a)]. A small acrylic table was built on the gantry for positioning the mouse during imaging. A 4 mm thick lead shield was mounted on the table in front of the rotating detectors to reduce the impact of activity from outside the FOV. The transaxial FOV was 16 mm in diameter, but the object is restricted to an effective 9 mm diameter FOV because of the space needed for the APD readout board and cooling duct. The axial FOV was 16 mm.
Fig. 2.
(a) PawPET assembled after fabrication front view. (b) Detector module assembly, made with 3-D printer.
C. Mouse Paw Imaging
All experiments were performed in compliance with the guide for the care and use of laboratory animals and were conducted under protocols approved by the Institutional Animal Care and Use Committee at the University of California at Davis. A normal BaLB/c female mouse weighing 27 g was injected with 74 MBq of 18-F-NaF. The tracer was allowed a 2 h uptake period in the awake mouse. After the uptake period the mouse was euthanized by cervical dislocation under general anesthesia then a hind limb was removed. The removed limb was placed in a counting well and the activity was measured to be 0.703 MBq. Additionally, the mouse limb was scanned for 4.5 h. A CD-1 female mouse weighing 54 g was imaged in vivo. A dose of 48 MBq of 18-F-NaF was injected in the tail vein and a 3 h uptake period was allowed while awake. The mouse was then scanned while under anesthesia for 2 h. After imaging the mouse was returned to its cage and was not sacrificed.
D. Data Acquisition and Image Reconstruction
In each scan the scanner gantry stepped through 40 angular steps covering 180°. Images were reconstructed using ordered subsets expectation maximization (OSEM). The DOI system matrix was generated using the multiray tracing method [37]. The image size was 51 × 51 × 33 voxels. The voxel size was 0.25 mm × 0.25 mm × 0.5 mm. During the system matrix generation, the DOI resolution was set to be 1.4 mm for a total of four DOI bins. During image reconstruction, the OSEM algorithm was used with ten subsets. Since there were 40 angles in total ten subsets was a reasonable choice. A component-based normalization of the line of response efficiencies was implemented. The crystal efficiency and geometrical profile was estimated from a plane phantom scan. The plane phantom was made of plastic acrylic with inner thickness of 5 mm and was scanned for 8 h with an initial activity of 7.4 MBq. The phantom was refilled after three half-lives to maintain the coincidence count rate.
E. Crystal ID, Energy, and DOI Resolution
The measurement of the detector performance parameters was accomplished by selectively irradiating the crystal array from a lateral side at seven positions in the direction perpendicular to the detector face, starting at 1 mm from the PSPMT and stepping toward the APD in 1 mm intervals. The depth selection was performed using electronic collimation (30) of a sealed 22-Na point source with 1.2 MBq of activity and a diameter of 0.25 mm. The collimating detector was composed of a single channel PMT (Hamamatsu, R580) coupled to a 0.6 mm × 32 mm × 20 mm LSO slab. The point source was positioned to achieve a beam width of 0.6 mm at the array. Flood histograms, where obtained at each sampled depth and the resolved crystals were counted. The ER was measured for the entire array at each sampled depth. The total event energy was calculated as the sum of the PSPMT four channel sum and the scaled (with a gain calibration constant) APD channel value. A gain calibration constant, k, was calculated to match the photodetector’s gain. The constant was determined by the ratio of the individual photodetector’s full energy peaks measured at the middle of the crystal length. The DOI was estimated from the individual photodetector’s signals as
| (1) |
the ratio R of the PSPMT energy (the sum of the four PSPMT output channels) EPSPMT to the total energy sum of the PSPMT energy and APD energy EAPD for any detected prompt event. For each sampled depth a histogram was created and the peak of R was recorded. The R for each counted event was then calibrated to units of millimeters with a calibration curve, obtained by fitting a straight line to the plot of the mean R value versus the depth position in millimeters, where it was measured. The DOI resolution was measured as the full width at half maximum (FWHM) after fitting a Gaussian curve to the histogram of DOI estimation (in millimeters) for each sampled depth.
F. Coincidence Timing Resolution
The timing resolution was measured with the detectors in coincidence. The 22-Na point source described above, was placed in between and coincidence events were qualified with a constant fraction discriminator (CFD). The delay on the CFD was set to 80% of the PSPMT rise time. This values was determined empirically to optimize for timing and ER. The CFD output from a detector was fed into a time to amplitude converter (TAC) as the start signal and the other detector CFD output was set as the stop signal. The amplitude of the TAC output signal was sampled and digitized. The timing resolution was measured as the FWHM, determined from a Gaussian curve fit to a histogram of the TAC data. The measured FWHM was scaled to units of nanoseconds by adding a known delay time to the stop signal creating a second peak in the histogram, where the scaling factor was the ratio of the known time delay to the peak’s separation value.
G. Intrinsic Spatial Resolution
A 0.25 mm diameter point source of 22-Na, described above, was positioned midway between the detectors, 30 mm apart, and was stepped parallel to the face of the detectors in 0.1 mm intervals using a motorized linear actuator. Starting at the edge of the array and ending near the center. The counts per source position of several crystals near the edge and several near the center were plotted. The intrinsic spatial resolution (ISR) was taken as the FWHM of the resulting profiles using linear interpolation between points.
H. Image Spatial Resolution
A dual line phantom was utilized to measure the image spatial resolution in the FOV. Two 27-gauge steel syringe needles with inner diameter of 200 μm and wall thickness of 100 μm were filled with 2.4 MBq of 18-F-FDG. The line sources were placed in the FOV parallel to the axis of rotation; one needle was placed near the transaxial isocenter and the other with a radial offset of 3.6 mm. The outer line source was offset by 1.8 mm in x and 3.4 mm in the y direction of the transaxial plane. They were scanned at the same time for the duration of 4 h, acquired in 25 min frames. OSEM with 40 iterations and ten subsets was used. During the dual line phantom reconstruction a uniform background image was forward projected and added to the dual line sinogram. After image reconstruction, the background value was subtracted and the FWHM was measured on the dual-line-only image. This was used to reduce the effect of non-negative constraint on the resolution measurement [38]. The contrast ratio of the dual-line-only image to the added background was 4.5:1.
I. Coincidence Sensitivity
The system sensitivity was measured using a 22-Na point source moved along the axial direction constantly held at the center of the transaxial FOV. Random coincidence events, where measured by the delayed coincidence method and subtracted from the prompts at each source position.
J. Count Rate Performance
The count rate performance was measured with 14.3 MBq of activity placed in the FOV and timing measurements were taken as the source decayed. The coincidence dead-time and random coincidence rate was measured. A nonparalyzable model was fit to the coincidence data to determine the dead-time. The random coincidence rates were measured using the delayed-channel coincidence method. An estimation of the random coincidence rate, r, was calculated from the measured singles from detector 1, S1, and from detector 2, S2 by r = 2τS1S2, where τ is the detector coincidence time window. The singles-based random coincidence rate estimate was compared to that measured with the delayed-channel method.
K. Phantom Imaging
The system image spatial resolution was qualitatively tested using a miniature Derenzo phantom. The phantom was designed in a solid modeling suite and printed on the 3-D printer. The rod diameters in millimeters were 0.42, 0.50, 0.63, 0.72, 0.90, respectively. The phantom was filled with 18-FFDG with an activity of 5.0 MBq. The miniature Derenzo phantom was scanned for 1 half-life without refilling. The image reconstruction was done with and without DOI information and included. OSEM with 40 iterations and ten subsets was used.
III. Results
A. Crystal Identification
The flood histograms used to identify crystals on the face of the PSPMT are shown in Fig. 3. At 1 mm, 33 × 33 of the 36 × 36 crystals in the array were identified. This loss was mainly due to the degradation in positioning performance at the edges of the PSPMT [39]. Potential crystal misidentification at the array edges was addressed by masking out two rows of edge crystals in the reconstruction, resulting in a masked array size of 32 × 32 crystals. The crystal numbering was 0–31 in the axial and transaxial sampling planes. Based on a line profile across the flood histogram at 4 mm the average peak-to-valley ratio was 3.17 and the peak distance-to-FWHM ratio was 1.6. At 7 mm the average peak-to-valley ratio was 1.2. The peak distance-to-FWHM ratio could not be determined. Also evident was the intensity gradient from left to right in the flood histograms. This was a result of illuminating the crystal array from the side.
Fig. 3.
Crystal identification maps for depth positions measured from the PSPMT end at 1 mm, 4 mm, and 7 mm from left to right, respectively.
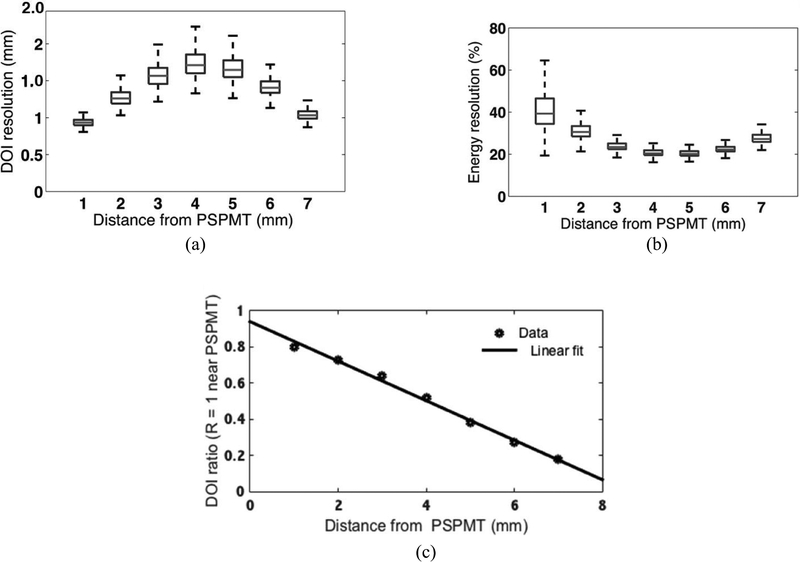
B. Energy, DOI, and Coincidence Timing Resolution
The ER measured for each crystal as a function of DOI is shown in Fig. 4. The per-crystal ER mean (-/− standard deviation) was 27% +/− 10%, with a range of 20%–65%. Fig. 4 shows the ER progressively degrades as the photodetectors are approached from the middle. It can also be seen that the ER was worst near the PSPMT. In a central crystal, the APD ER at the nearest and farthest DOI position was 33% and 39%, respectively. The PSPMT ER at the nearest and farthest DOI position was 39% and 51%, respectively.
Fig. 4.
(a) DOI resolution and (b) ER measured for each crystal in the array are plotted in box plot form. (c) Calibration curve averaged from all crystals.
The DOI measurement results for the entire array at all seven positions and the DOI calibration curve are shown in Fig. 4. The per-crystal DOI resolution mean was 1.4 mm +/− 0.6 mm with a range of range 0.9–2.5 mm. The coincidence timing resolution was measured to be 2.8 ns for the entire array.
C. Intrinsic and Image Spatial Resolution
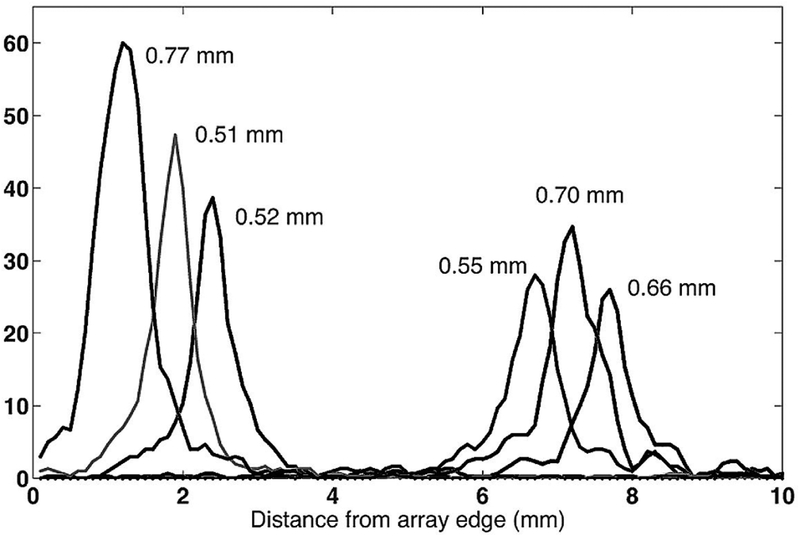
The profiles for selected crystals are shown in Fig. 5. Three crystals were selected from the edge and three from the center of the array. The average ISR was 0.62 mm and with a range of 0.51–0.77 mm.
Fig. 5.
Intrinsic positioning profiles for six crystals, three at the edge of the array, and three at the center.
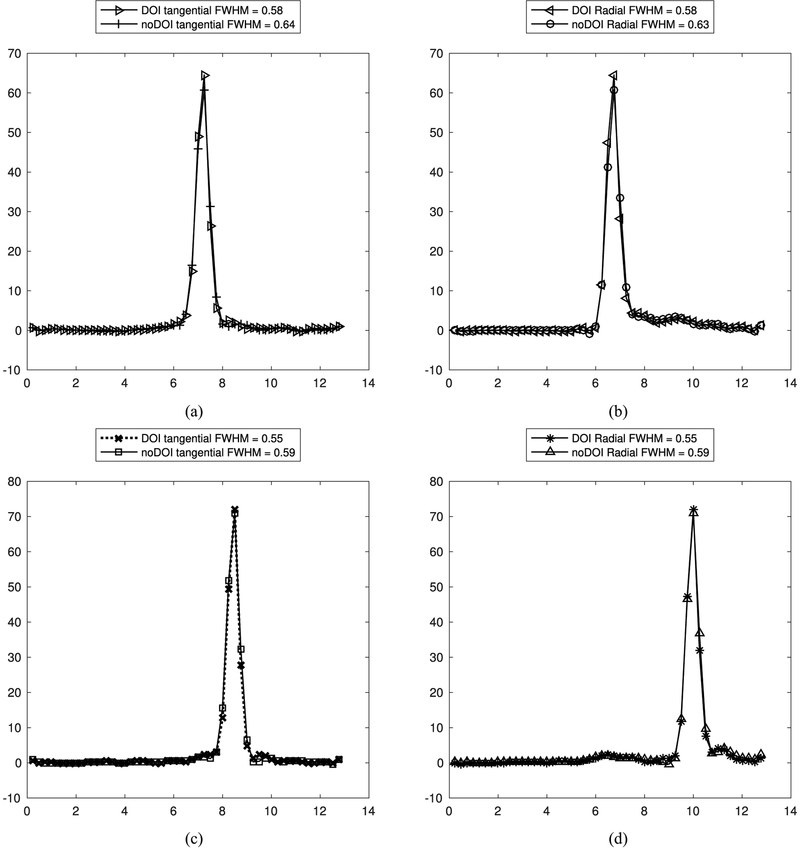
The image spatial resolution average between the center and edge lines in the phantom measured with DOI was 0.56 mm (range of 0.55–0.58 mm) and 0.61 mm (range of 0.59–0.64 mm) measured with no DOI. The radial and tangential direction spatial resolution measurements are shown in Table I for the DOI and no DOI case. In the DOI case there was a 5.2% resolution loss at the center compared to the edge. In the no DOI case there was a 6.3% resolution loss at the center compared to the edge (Fig. 6). The resolution improvements from having DOI information were more pronounced at the center than at the edges. The radial resolution at the center improved by 8.6% with DOI, while a 7.2% improvement was observed at the edge. This result is supported by the fact that the density of oblique lines of response is greater at the FOV center than the edge. The total number of events used in the image reconstruction was 32 132 942 counts.
TABLE I.
Measured FWHM From Profiles Through the Middle Axial Slice of Line Source Placed at the Center and Edge of the FOV
| DOI | no DOI | |||
|---|---|---|---|---|
| Location | Radial | Tangential | Radial | Tangential |
| Center | 0.58 mm | 0.58 mm | 0.63 mm | 0.64 mm |
| Edge | 0.55 mm | 0.55 mm | 0.59 mm | 0.59 mm |
Fig. 6.
Tangential and radial line profiles through center and edge reconstructed line phantoms. (a) Tangential profile of center line. (b) Radial profile of center line phantom. (c) Tangential profile of edge line phantom. (d) Radial profile of edge line phantom.
D. Miniature Derenzo Phantom
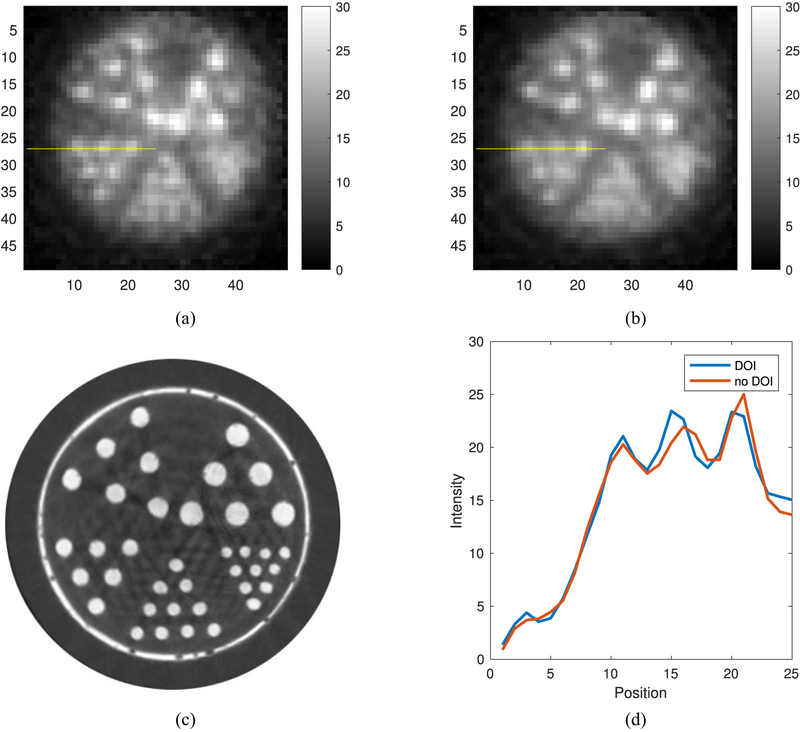
A miniature Derenzo phantom was imaged with the prototype PET scanner using 18-F-FDG and the images were reconstructed with a voxel size of 0.25 mm × 0.25 mm × 0.5 mm, with 15 center slices summed. The smallest rod that was resolved was the 0.6 mm diameter rod with or without DOI information in the reconstruction. However, with DOI the rods appear sharper and more intense as seen in Fig. 7. The 0.5 mm and 0.4 mm diameter rods were not resolved. Some of the rods were not seen in the image because of air bubbles in the rod.
Fig. 7.
(a) FDG PET image reconstructed with DOI information. (b) Same FDG PET image but reconstructed without DOI information. (c) Micro CT of miniature Derenzo phantom with rod diameters: 0.42 mm, 0.50 mm, 0.63 mm, 0.72 mm, and 0.90 mm. (d) Plot of the line profile through the row of 0.63 mm rods on both Derenzo images.
E. Coincidence Sensitivity
The maximum sensitivity at the center of the FOV was 0.6% without any energy cut-off. All events that would have been used in the reconstruction were included.
F. Count Rate Performance
The coincidence dead-time was measured to be 10.45 μs. This large dead-time was attributed to the 10.0 μs trigger guard used in the electronics required to compensate for the time delay of the APD signal. The average percent error between the calculated singles-based randoms rate compared to the measured delayed-channel rates was 4% at 2.59 MBq and above. The range of values for the measured delayed-channel rates was 80 cps to 2713 cps, at 2.59 MBq to 14.32 MBq, respectively.
Singles-based random coincidence rates estimates were typically slightly lower than delayed-window randoms rates and linear regression analysis showed a slope of 0.963 (R2 > 0.996). Greatest differences were seen at the lowest rates (average of 21% difference with less than 2.59 MBq in the FOV), where randoms were less than 1% of the prompts.
G. Mouse Paw Imaging
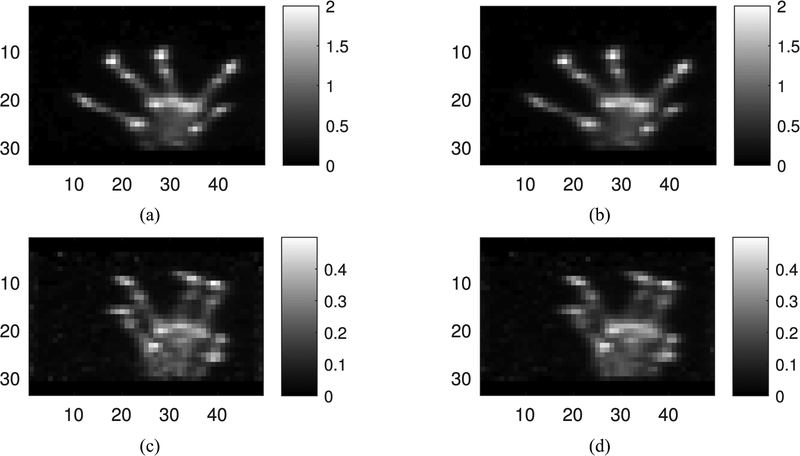
Mouse maximum intensity projection images of the ex vivo paw are shown in Fig. 8(a) and (b) in the coronal view. The anatomy of the paw was visible; the individual digits were seen. The in vivo mouse images are shown in Fig. 8(c) and (d). The image quality was poorer than the ex vivo image, mainly as a result of 68% fewer counts in the image reconstruction (669 627 counts in vivo and 2 060 584 ex vivo), however, anatomical structure was still resolved.
Fig. 8.
Maximum intensity projection images of ex vivo and in vivo with or without DOI. Images are coronal views reconstructed with OSEM ten iterations and ten subsets, (a) DOI, ex vivo, (b) no DOI, ex vivo, (c) DOI, in vivo, and (d) no DOI, in vivo.
H. Discussion
The majority of crystals at 1–6 mm depths were identified by the PSPMT. At the 7 mm depth the crystals were not resolved with the same sharpness, however, the reconstructed images do not seem to be highly affected by this. This can be explained by noting that about 82% of all recorded events interacted outside the front 1 mm of crystal, where the majority of the crystals can be resolved.
The ER of the detector averaged 27%, higher than that reported in the previous work using APDs [30]. The APDs used in this paper were larger and also the aspect ratio of the crystals was greater. Larger APDs have increased capacitance, which increases shot noise, reducing the signal-to-noise ratio. The high crystal aspect ratio increases the potential for photon trapping and the unpolished crystal surface increases the potential for photons to escape detection. Both effects are expected to degrade the ER. The use of silicon PMs (SiPM) can greatly improve ER. SiPM have come a long way and have been promising better performance, and SiPM arrays of the proper size and compactness have recently become possible [40], [41]. However, decoding small crystals remains a challenge.
The dependence of ER with interaction position may be explained as follows. since the crystal surface treatment and reflector material combination was lossy, the amount of light collected by either photodetector decreases as the interaction point to photodetector distance increases. Superior performance in the middle may be explained if noise from the distal photodetector dominates the measurements taken at the ends of the array. The poorest ER performance seen for interactions close to the PSPMT may similarly be explained if the lower signal to noise ratio of the APD (compared to the PSPMT) dominates the measurement.
The scanner uses the hybrid DOI detector for imaging at a resolution of 0.5 mm. This value was slightly smaller than the measured mean ISR, suggesting that crystal pitch was not the dominant limiting factor for ISR, since theoretically the ISR with decoding error would be expected to be close to two-fifths the crystal pitch [42]. However, there may be an underestimation of the ISR performance given that the source used for the measurement was 0.25 mm across and that the array was irradiated with a fan-beam geometry. Furthermore the ISR varied across the crystal face and we did not measure all the crystals. It is therefore possible that our reported average ISR value was somewhat biased toward larger values. Misidentification of crystals does not seem to be a major factor degrading the ISR since crystal peaks were separated by more than the FWHM (peak distance-to-width ratio of 1.6). It is possible that intercrystal Compton scatter may also be a limiting factor for ISR for this detector design. It is possible that a crystal pitch larger than 0.5 mm may improve the detector performance in terms of ER and crystal ID, without substantial impairment of spatial resolution.
A shortcoming of the current scanner design was its poor photon detection sensitivity and count-rate performance. A way of improving the sensitivity is to increase the number of detectors and the length of their crystals. A way to improve count-rate performance is to use faster electronics, thereby reducing dead-time and pileup effects.
Another way to improve sensitivity is to reduce the detector-to-detector separation. However, it is expected that moving the detectors closer to each other will place a stronger demand on DOI resolution. The available DOI resolution averaging 1.4 mm (four DOI bins) may be sufficient since It has been shown that even a coarse DOI resolution (two DOI bins) can have a significant improvement in image resolution (33). The resolution uniformity in the sampled locations can potentially be explained by the fact that the effective FOV was only 9 mm in diameter compared to the 16 mm width of the array, and the line sources were spaced out 3.6 mm apart. Hence, both locations contain similar degrees of oblique radiation. Nonetheless, the benefits of DOI correction were visually appreciable, as seen in Fig. 7, and in the image spatial resolution.
In the count rate measurements, singles-based randoms estimates agreed closely with delayed-channel randoms estimates at higher rates. At lower rates, differences become apparent and these difference are larger than can be explained purely by Poisson variations. However, since the contribution of randoms to prompts was very small under these conditions (less than 1%), these differences are considered negligible.
The preclinical imaging capability of the scanner was examined ex vivo and in vivo using 18-F-NaF. This tracer was selected to demonstrate the scanner’s ability to resolve fine anatomical structure of the mouse paw. The ex vivo scan showed that the scanner was capable of resolving the anatomy of the mouse paw. However, significant image degradation was observed when comparing the in vivo to ex vivo images, mainly as a result of reduced counts. In its current standing the scanner may not be suitable for in vivo imaging in low signal applications. However, there is a clear path to improve the sensitivity in future designs, which may counter these effects.
Since the quantification accuracy of a PET system is decreased by increased partial volume blurring, the gain in spatial resolution shown in this paper should result in a more quantitatively accurate device [43]. However, the count limitations may counter this gain in quantitative accuracy by increasing variation in the image. Scatter rates are another factor influencing accuracy, which were not characterized in this paper. This system still needs to be improved to compete quantitatively with commercial systems. Nonetheless, headway was achieved in terms of spatial resolution.
IV. Conclusion
An ultrahigh resolution PET scanner using hybrid depth encoding detectors was built and characterized. Results show that the scanner can perform with a submillimeter image spatial resolution. Mouse paw imaging showed that the scanner was capable of resolving the paw anatomy.
Acknowledgment
The authors would like to thank N. Bauer for help in handling animals, J. Fung for help in handling animals and scanning them, and Dr. E. Roncali for helpful discussions and commentary.
This work was supported in part by the National Institutes of Health under Grant NCI F31 CA157213 and Grant NCI R01 CA129561, and in part by the University of California at Davis Chancellor’s Post-Doctoral Fellowship under Grant K12 HD051958.
Contributor Information
Felipe Godinez, Department of Perinatal Imaging, King’s College London, London SE1 7EH, U.K..
Kuang Gong, Department of Biomedical Engineering, University of California at Davis, Davis, CA 95616 USA..
Jian Zhou, Toshiba Medical Research Institute, USA, Inc., Vernon Hills, IL 60061 USA..
Martin S. Judenhofer, Department of Biomedical Engineering, University of California at Davis, Davis, CA 95616 USA..
Abhijit J. Chaudhari, Department of Biomedical Engineering, University of California at Davis, Davis, CA 95616 USA..
Ramsey D. Badawi, Department of Biomedical Engineering, University of California at Davis, Davis, CA 95616 USA..
References
- [1].Amos RS, Constable TJ, Crockson RA, Crockson AP, and McConkey B, “Rheumatoid arthritis: Relation of serum C-reactive protein and erythrocyte sedimentation rates to radiographic changes,” Brit. Med. J, vol. 1, no. 6055, pp. 195–197, 1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Plant MJ et al. , “Relationship between time-integrated C-reactive protein levels and radiologic progression in patients with rheumatoid arthritis,” Arthritis Rheumatism, vol. 43, no. 7, pp. 1473–1477, 2000, doi: . [DOI] [PubMed] [Google Scholar]
- [3].Beckers C et al. , “Assessment of disease activity in rheumatoid arthritis with 18F-FDG PET,” J. Nucl. Med, vol. 45, no. 6, pp. 956–964, 2004. [Online]. Available: http://jnm.snmjournals.org/content/45/6/956.abstract [PubMed] [Google Scholar]
- [4].Brenner W, “18F-FDG PET in rheumatoid arthritis: There still is a long way to go,” J. Nucl. Med, vol. 45, no. 6, pp. 927–929, 2004. [Online]. Available: http://jnm.snmjournals.org/content/45/6/927.short [PubMed] [Google Scholar]
- [5].Bruijnen STG, Gent YYJ, Voskuyl AE, Hoekstra OS, and Van Der Laken CJ, “Present role of positron emission tomography in the diagnosis and monitoring of peripheral inflammatory arthritis: A systematic review,” Arthritis Care Res, vol. 66, no. 1, pp. 120–130, 2014. [DOI] [PubMed] [Google Scholar]
- [6].Chaudhari AJ et al. , “High-resolution 18 F-FDG PET with MRI for monitoring response to treatment in rheumatoid arthritis,” Eur. J. Nucl. Med. Mole. Imag, vol. 37, no. 5, p. 1047, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Palmer WE et al. , “Quantification of inflammation in the wrist with gadolinium-enhanced mr imaging and PET with 2-[F-18]-fluoro-2-deoxy-d-glucose,” Radiology, vol. 196, no. 3, pp. 647–655, 1995. [DOI] [PubMed] [Google Scholar]
- [8].Rennen HJJM, Boerman OC, Oyen WJG, and Corstens FHM, “Imaging infection/inflammation in the new millennium,” Eur. J. Nucl. Med, vol. 28, no. 2, pp. 241–252, 2001, doi: 10.1007/s002590000447. [DOI] [PubMed] [Google Scholar]
- [9].Firestein GS, “Evolving concepts of rheumatoid arthritis,” Nature, vol. 423, no. 6937, pp. 356–361, 2003. [DOI] [PubMed] [Google Scholar]
- [10].Bendele AM, “Animal models of rheumatoid arthritis,” J. Musculoskelet. Neuronal Interact, vol. 1, no. 4, pp. 377–385, 2001. [PubMed] [Google Scholar]
- [11].Brand DD, Latham KA, and Rosloniec EF, “Collagen-induced arthritis,” Nat. Protocols, vol. 2, no. 5, pp. 1269–1275, 2007. [DOI] [PubMed] [Google Scholar]
- [12].Williams R, Feldmann M, and Maini RN, “Anti-tumor necrosis factor ameliorates joint disease in murine collagen-induced arthritis,” Proc. Nat. Acad. Sci. USA, vol. 89, no. 20, pp. 9784–9788, 1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Kundu-Raychaudhuri S, Mitra A, Datta-Mitra A, Chaudhari AJ, and Raychaudhuri SP, “In vivo quantification of mouse autoimmune arthritis by PET/CT,” Int. J. Rheumatic Diseases, vol. 19, no. 5, pp. 452–458, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Camps M et al. , “Blockade of PI3Kγ suppresses joint inflammation and damage in mouse models of rheumatoid arthritis,” Nat. Med, vol. 11, no. 9, pp. 936–943, 2005. [DOI] [PubMed] [Google Scholar]
- [15].Irmler IM et al. , “In vivo molecular imaging of experimental joint inflammation by combined 18F-FDG positron emission tomography and computed tomography,” Arthritis Res. Ther, vol. 12, no. 6, pp. 1–9, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Visser EP et al. , “Spatial resolution and sensitivity of the inveon small-animal PET scanner,” J. Nucl. Med, vol. 50, no. 1, pp. 139–147, 2009. [DOI] [PubMed] [Google Scholar]
- [17].Soret M, Bacharach SL, and Buvat I, “Partial-volume effect in PET tumor imaging,” J. Nucl. Med, vol. 48, no. 6, pp. 932–945, 2007. [DOI] [PubMed] [Google Scholar]
- [18].Moses WW, Virador PRG, Derenzo SE, Huesman RH, and Budinger TF, “Design of a high-resolution, high-sensitivity PET camera for human brains and small animals,” IEEE Trans. Nucl. Sci, vol. 44, no. 4, pp. 1487–1491, August 1997. [Google Scholar]
- [19].Stickel JR and Cherry SR, “High-resolution PET detector design: Modelling components of intrinsic spatial resolution,” Phys. Med. Biol, vol. 50, no. 2, pp. 179–195, 2005. [Online]. Available: http://stacks.iop.org/0031-9155/50/i=2/a=001 [DOI] [PubMed] [Google Scholar]
- [20].Chatziioannou A, Tai YC, Doshi N, and Cherry SR, “Detector development for microPET II: A 1 μl resolution PET scanner for small animal imaging,” Phys. Med. Biol, vol. 46, no. 11, pp. 2899–2910, 2001. [DOI] [PubMed] [Google Scholar]
- [21].Doshi NK, Shao Y, Silverman RW, and Cherry SR, “Design and evaluation of an LSO PET detector for breast cancer imaging,” Med. Phys, vol. 27, no. 7, pp. 1535–1543, 2000. [DOI] [PubMed] [Google Scholar]
- [22].Song TY, Wu H, Komarov S, Siegel SB, and Tai Y-C, “A sub-millimeter resolution PET detector module using a multi-pixel photon counter array,” Phys. Med. Biol, vol. 55, no. 9, pp. 2573–2583, 2010. [Online]. Available: http://stacks.iop.org/0031-9155/55/i=9/a=010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Stickel JR, Qi J, and Cherry SR, “Fabrication and characterization of a 0.5-mm lutetium oxyorthosilicate detector array for high-resolution PET applications,” J. Nucl. Med, vol. 48, no. 1, pp. 115–121, 2007. [PubMed] [Google Scholar]
- [24].Yamaya T et al. , “A SiPM-based isotropic-3D PET detector X’tal cube with a three-dimensional array of 1 mm3 crystals,” Phys. Med. Biol, vol. 56, no. 21, pp. 6793–6807, 2011. [DOI] [PubMed] [Google Scholar]
- [25].España S, Marcinkowski R, Keereman V, Vandenberghe S, and Van Holen R, “DigiPET: Sub-millimeter spatial resolution small-animal PET imaging using thin monolithic scintillators,” Phys. Med. Biol, vol. 59, no. 13, pp. 3405–3420, 2014. [DOI] [PubMed] [Google Scholar]
- [26].Ito M, Lee JS, Park MJ, Sim KS, and Hong SJ, “Design and simulation of a novel method for determining depth-of-interaction in a PET scintillation crystal array using a single-ended readout by a multi-anode PMT,” Phys. Med. Biol, vol. 55, no. 13, pp. 3827–3841, 2010. [DOI] [PubMed] [Google Scholar]
- [27].Seidel J, Vaquero JJ, Siegel S, Gandler WR, and Green MV, “Depth identification accuracy of a three layer phoswich PET detector module,” IEEE Trans. Nucl. Sci, vol. 46, no. 3, pp. 485–490, June 1999. [Google Scholar]
- [28].Dokhale PA et al. , “Intrinsic spatial resolution and parallax correction using depth-encoding PET detector modules based on position-sensitive APD readout,” IEEE Trans. Nucl. Sci, vol. 53, no. 5, pp. 2666–2670, October 2006. [Google Scholar]
- [29].James SS et al. , “Experimental characterization and system simulations of depth of interaction PET detectors using 0.5 mm and 0.7 mm LSO arrays,” Phys. Med. Biol, vol. 54, no. 14, pp. 4605–4619, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Yang Y et al. , “Depth of interaction resolution measurements for a high resolution PET detector using position sensitive avalanche photodiodes,” Phys. Med. Biol, vol. 51, no. 9, pp. 2131–2142, 2006. [DOI] [PubMed] [Google Scholar]
- [31].Chaudhari AJ et al. , “PSPMT/APD hybrid DOI detectors for the PET component of a dedicated breast PET/CT system—A feasibility study,” IEEE Trans. Nucl. Sci, vol. 55, no. 3, pp. 853–861, June 2008. [Google Scholar]
- [32].Godinez F, Chaudhari AJ, Yang Y, Farrell R, and Badawi RD, “Characterization of a high-resolution hybrid DOI detector for a dedicated breast PET/CT scanner,” Phys. Med. Biol, vol. 57, no. 11, pp. 3435–3449, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Moses WW, Derenzo SE, Melcher CL, and Manente RA, “A room temperature LSO/PIN photodiode PET detector module that measures depth of interaction,” IEEE Trans. Nucl. Sci, vol. 42, no. 4, pp. 1085–1089, August 1995. [Google Scholar]
- [34].Yang Y et al. , “A prototype high-resolution small-animal PET scanner dedicated to mouse brain imaging,” J. Nucl. Med, vol. 57, no. 7, pp. 1130–1135, 2016. [Online]. Available: http://jnm.snmjournals.org/content/57/7/1130.abstract [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Wong J, Bennett W, Ferguson MWJ, and McGrouther DA, “Microscopic and histological examination of the mouse hindpaw digit and flexor tendon arrangement with 3D reconstruction,” J. Anat, vol. 209, no. 4, pp. 533–545, October 2006. [Online]. Available: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2100351/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Tai Y-C et al. , “MicroPET II: Design, development and initial performance of an improved microPET scanner for small-animal imaging,” Phys. Med. Biol, vol. 48, no. 11, pp. 1519–1537, 2003. [DOI] [PubMed] [Google Scholar]
- [37].Zhou J and Qi J, “Efficient fully 3D list-mode TOF PET image reconstruction using a factorized system matrix with an image domain resolution model,” Phys. Med. Biol, vol. 59, no. 3, pp. 541–559, February 2014. [Online]. Available: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC4182441/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Gong K, Cherry SR, and Qi J, “On the assessment of spatial resolution of PET systems with iterative image reconstruction,” Phys. Med. Biol, vol. 61, no. 5, pp. N193–N202, 2016. [Online]. Available: http://stacks.iop.org/0031-9155/61/i=5/a=N193 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Shao Y, Silverman RW, and Cherry SR, “Evaluation of Hamamatsu R5900 series PMTs for readout of high-resolution scintillator arrays,” Nucl. Instrum. Methods Phys. Res. A Accelerators Spectrometers Detectors Assoc. Equipment, vol. 454, nos 2–3, pp. 379–388, 2000. [Google Scholar]
- [40].Kang HG et al. , “A dual-ended readout detector using a meantime method for SIPM TOF-DOI PET,” IEEE Trans. Nucl. Sci, vol. 62, no. 5, pp. 1935–1943, October 2015. [Google Scholar]
- [41].Zhang H, Zhou R, and Yang C, “A PET detector module with monolithic crystal, single end readout, SIPM array and high depth-of-interaction resolution,” J. Instrum, vol. 11, no. 8, 2016, Art. no. P08020. [Online]. Available: http://stacks.iop.org/1748-0221/11/i=08/a=P08020 [Google Scholar]
- [42].Moses WW, “Fundamental limits of spatial resolution in PET,” Nucl. Instrum. Methods Phys. Res. A Accelerators Spectrometers Detectors Assoc. Equipment, vol. 648, pp. S236–S240, August 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Harri M, Mika T, Jussi H, Nevalainen OS, and Jarmo H, “Evaluation of partial volume effect correction methods for brain positron emission tomography: Quantification and reproducibility,” J. Med. Phys. Assoc. Med. Physicists India, vol. 32, no. 3, pp. 108–117, Jul-Sep 2007. [Online]. Available: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3000501/ [DOI] [PMC free article] [PubMed] [Google Scholar]