Elimination of pseudo-negative conductance by coercive steady state in perm-selective ion transportation

Abstract

Ion concentration polarization (ICP) has drawn unprecedented attention due to its new underlying physics and engineering applications such as biomolecular preconcentrator and electrofluidic desalination. Typically, the current-voltage characteristic of ICP has three distinctive regimes with a positive slope in all regimes, but an unintentional negative slope (“overshoot current”) was often observed in the Ohmic/limiting regime. This phenomenon impeded an exact estimation of electrokinetic properties of the ICP platform. Therefore, in this work, we eliminated overshoot current by limiting the length of the diffuse layer using a coercive injection of a fresh electrolyte solution. Both the visualization of ICP layer propagation and the measurement of current-voltage characteristics verifying the time for reaching the steady state within an effective length of a microchannel played a critical role. The most relevant parameter was shown to be the diffusion relaxation time which was directly correlated with the sweep rate of an external voltage. Using this new measurement platform, one can significantly reduce the time and labor for the electrokinetic studies and applications based on them.

I. INTRODUCTION

In recent years, perm-selective ion transportation through the nanoporous membrane has been extensively studied due to its utility in various fields such as sensors,¹ separation,² water desalination,³ and fuel cells.⁴ One of the major phenomena that occur near the nanoporous membrane is ion concentration polarization (ICP), which has received tremendous attention among theoretical^5–8 and experimental researchers.^9–12 Because it provides the differential platform of the perm-selective migration near the membrane, one can deeply comprehend the mechanism behind the movement using in situ visualization of flow field/concentration distribution^13,14 and direct numerical simulation.^15,16 Based on these findings, one can precisely control the nanoelectrokinetic environment of such systems for better engineering efficiency.^17–20

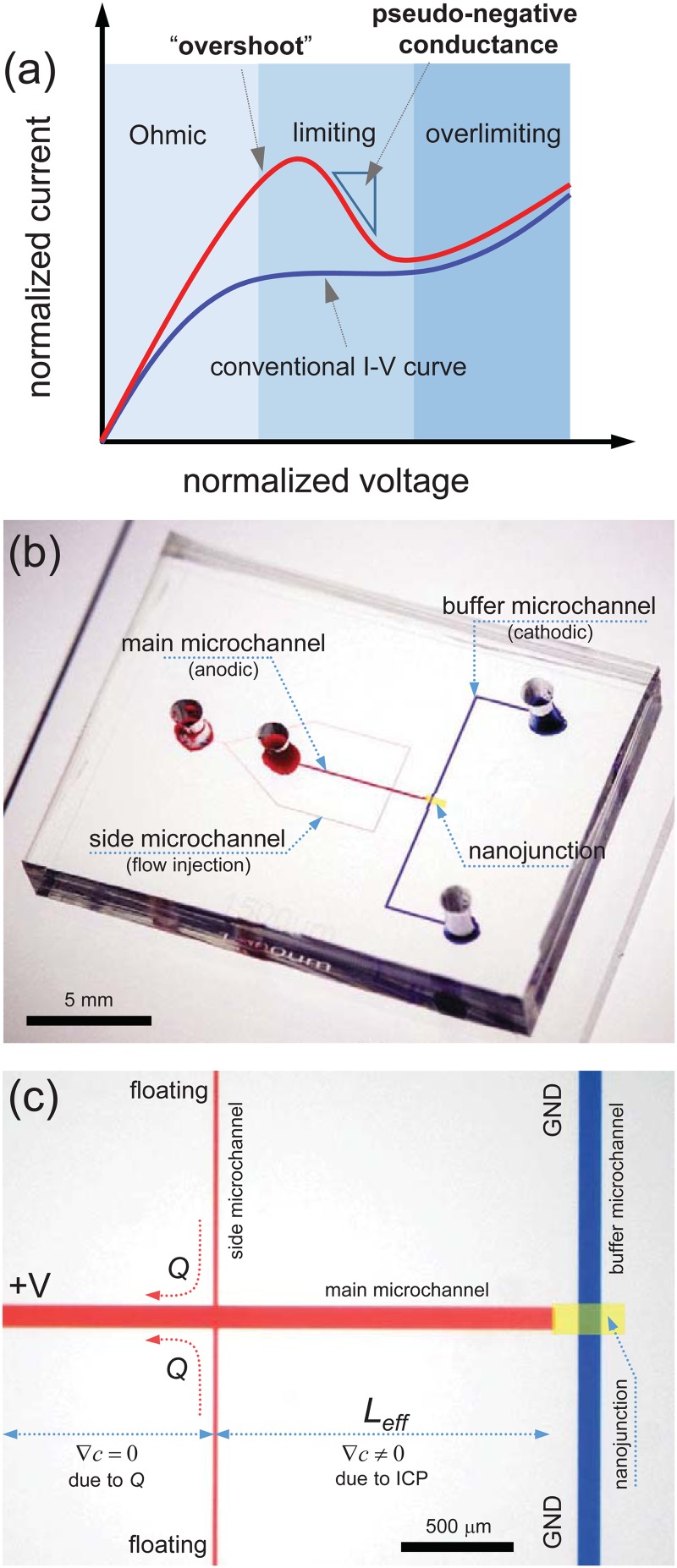
ICP resulting from unbalanced ion transportation through the membrane can be directly characterized by the formation of an ion depletion zone and an ion enrichment zone at the anodic and the cathodic side of the membrane, respectively, in the case of the cation-selective membrane.^21,22 Furthermore, the current-voltage (I-V) curve is the most representing fingerprint of ICP because of its distinctive transitions as a function of the applied voltage. In a voltammetric measurement, the I-V curve has 3 distinguishable regimes (i.e., Ohmic, limiting, and overlimiting regimes).^6,11,23–25 Due to the lowest concentration inside the ion depletion zone, the ionic current was mainly determined by the properties of the ion depletion zone. In a micro-/nanofluidic platform, however, an overshoot phenomenon (i.e., pseudonegative conductance) was easily observed at the transition from the Ohmic regime to the limiting regime, as shown in Fig. 1(a).^26–28 The overshoot is a nuisance for the accurate estimation of electrical performance in the electrochemical membrane system. Moya and Sistat have theoretically reported that a overshoot current in the electrodialysis system can be eliminated by slowing the sweep rate of the voltammetric measurement.²⁹ They also suggested that the required time to reach the steady state was decided by the length of the diffuse layer. However, in a micro-/nanofluidic system, the length of a microchannel was usually ∼O(10) mm so that the required time to flatten the overshoot current was over 10 h, which significantly impeded the nanoelectrokinetic study. Therefore, an alternative approach was demanded for measuring the proper I-V curve within a short time, even with a microfluidic channel.

FIG. 1.

(a) Conventional (blue line) I-V curve vs “overshoot” phenomenon that possessed a pseudonegative conductance. (b) Overview of a micro-/nanofluidic device. It had side microchannels to inject a fresh electrolyte to the vicinity of a nanojunction. (c) Microscopic image of the device. Due to the fresh electrolyte injection, the electrolyte concentration should be uniform by L_eff away from the nanojunction.

In this work, we fabricated the ICP device composed of two microchannels and a nanoporous membrane, as shown in Fig. 1(b). The effective length (L_eff) of the main microchannel was coercively shortened by pumping fresh electrolyte solution through the side microchannels. As a result, electrolyte concentration can be uniform along the main microchannel from the left reservoir to the interconnected point with the side microchannels. In this manner, the ICP layer can be formed only in the range from the interconnection to the nanojunction. Thus, we can achieve a coercive steady state for complete diffusion within the range of L_eff. By this mean, we demonstrated that the diffusion relaxation time played a deterministic role in eliminating an overshoot phenomenon. Therefore, this simple but effective measurement platform would be a highly practical method to characterize the electrokinetic properties of perm-selective ion transportation because it can significantly save time and labor.

II. EXPERIMENTAL METHODS

Micro-/nanofluidic devices were fabricated using soft-lithography with poly(dimethylsiloxane) (PDMS, Sylgard 184 Silicon Elastomer Kit, Dow Corning, USA). A negative photoresist (SU8 2015, Microchem, USA) was coated on a 4 in. wafer to form a 15 μm thick film for the device and 50 μm for the Nafion patterning microchannel. Soft bake was processed at 95 °C for 3 min to remove the organic solvent. Proper UV irradiation with a predesigned mask was performed, and the channels were developed using a SU8 developer. Then, the mixture of PDMS base and curing agent (10:1 ratio) was poured on the top of the wafers and was then solidified at 70 °C for 4 h. Meanwhile, the blank microchannel (50 μm thickness, 100 μm width, and 1 cm length) was reversibly attached to a glass slide. Then, the microchannel was filled with Nafion solution (20 wt. % resin solution, Sigma-Aldrich) by capillary force or negative pressure, and the PDMS block was detached from the glass, referred to as a surface patterning method.²² After curing the glass at 95 °C for 5 min, the solidified Nafion resin remained on the glass substrate. The fabricated PDMS microchannel and the Nafion coated glass substrate were irreversibly bonded using a plasma bonder (CuteMP, Femto Science, Korea). Main and buffer microchannels shown in Fig. 1(c) had the dimensions of 100 μm width and 15 μm depth.

The most important feature in this work was the connection of the side microchannels. Electrically floated side microchannels were able to replenish a fresh electrolyte through a pump (PHD2000, Harvard). The dimensions of the side microchannel were 20 μm width and 15 μm depth. Therefore, the electrolyte concentration varied due to ICP in the range from the nanojunction to the injection point (i.e., within L_eff), while the concentration was expected to be uniform out of the range as shown in Fig. 1(c). We fabricated a number of devices for different L_eff = 150, 300, 500, 650, 750, 1000, 1500, and 2000 μm.

For the initiation of ICP, the external voltage (source measure unit, Keithley 236, USA) was applied through the Ag/AgCl electrode connected to reservoirs [Fig. 1(c)]. I-V responses were measured by voltage sweep enabled by the customized LabView program. The sweep rate of voltage was 0.05 V/30 s from 0 V to 1.5 V for the main experiment and 0.05 V/1.5 s to 0.05 V/60 s for the sweep rate effect experiment. In the meantime, the propagation of the ICP layer was visualized using an inverted fluorescent microscope (IX-51, Olympus, Japan) and a charge-coupled device (CCD) camera (DP73, Olympus, Japan). The obtained images were then postprocessed with CellSense (Olympus). For the fluorescent emission, 1 mM KCl solution (Sigma-Aldrich, USA) with sulforhodamine B (SRB) (2 nM, Sigma-Aldrich, USA) was continuously injected from the side microchannels.

III. RESULTS AND DISCUSSIONS

A. Electrokinetic response depending on L_eff

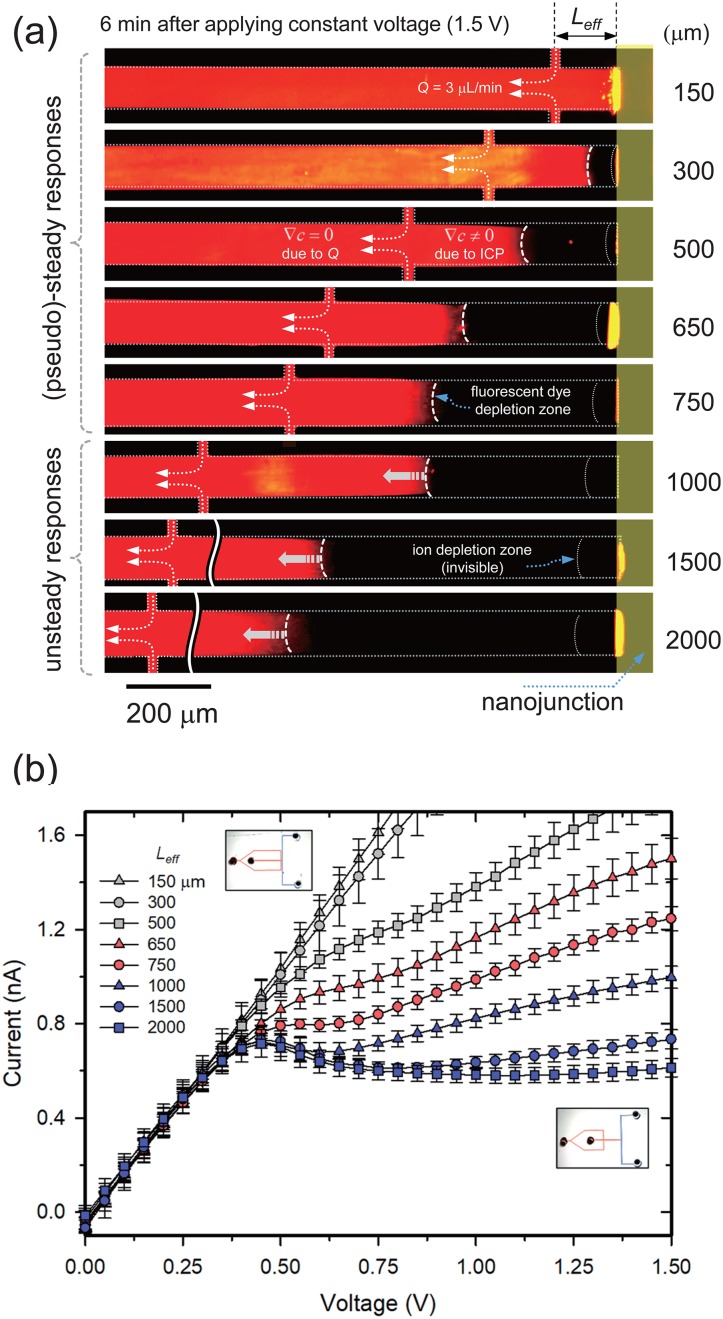
The main experiments were conducted by varying the position (L_eff) of the interconnection where a fresh electrolyte was continuously injected. Since the main microchannel was a dead-end configuration, the infused solution flowed only from the side microchannels to the anodic reservoir as shown in Fig. 2(a). The flow rate was 3 μl/min. Therefore, the concentration profile of the main microchannel would have two distinctive parts. One from side channels to the reservoir kept constant concentration (i.e., ∇c = 0) due to the injected flow, and the other from the nanojunction to the side microchannels had a change of concentration (i.e., ∇c ≠ 0) as ICP was generated. The snapshots in Fig. 2(a) were captured after 6 min applying 1.5 V, which was the highest voltage in this study, in order to certify whether the depletion zone would be suppressed between the nanojunction and the intersection. A black region represented the depletion zone of the fluorescent dye. With L_eff being under 750 μm, the depletion zone merely expanded, which was considered the pseudosteady state, while it slowly expanded but was bounded by the side channels over L_eff = 1000 μm.

FIG. 2.

(a) Experimental visualization of the propagation of the ICP layer as a function of L_eff. A constant voltage of 1.5 V was applied and the snapshot was captured after 6 min of applying the voltage. (b) Experimental measurement of I-V responses as a function of L_eff. The sweep rate was 0.05 V/30 s. The overshoot phenomenon was eliminated when L_eff = 650 and 750 μm. Over the range, I-V has a significant overshoot.

Under this circumstance, one needs to measure the electrical response of each configuration. Figure 2(b) demonstrates the I-V characteristic from 0 V to 1.5 V with varying L_eff. When L_eff was 150 μm, the I-V curve remained in the Ohmic regime until the voltage reached 1.5 V. When L_eff was 300 μm and 500 μm, the I-V curve was changed from the Ohmic regime to the overlimiting regime without the limiting regime. Since hydraulic convection caused by injected flow from the side microchannel completely (or largely) suppressed the propagation of the ICP layer, the I-V response had a long Ohmic regime and a direct jump to the overlimiting regime without the limiting current response.²⁷

Interestingly, the I-V curve had three distinctive regimes without overshoot current when L_eff was 650 and 750 μm. Under the steady-state assumption, we can compare the experimental limiting current value with an analytical expression¹⁰ of i_lim = 2FDc₀A/δ, where F is the Faraday constant, A is the cross-sectional area of the microchannel, and c₀ is the bulk concentration as shown in Table I. The difference between i_lim,theo and i_lim,exp was under 7% when L_eff was 650 and 750 μm. When L_eff exceeded over 1000 μm, the overshoot was generated and i_lim,exp was much higher than i_lim,theo, leading to erroneous electrokinetic responses when there is an overshoot phenomenon.

TABLE I.

Theoretically calculated and experimentally measured limiting current value depending on L_eff.

Leff	ilim,theo (nA)	ilim,exp (nA)
650	0.89	0.90–0.95
750	0.77	0.76–0.80
1000	0.58	0.68–0.72
1500	0.39	0.61–0.73
2000	0.29	0.58–0.72

B. Diffusion relaxation time in a microchannel of L_eff

The diffusion relaxation time of ions in the occurrence of overshoot current in voltammetry was reported to have a close relationship with the response of ion flux in the main channel.²⁹ In Ohmic and limiting regimes, all of the convection was negligible and most of the electromigration affected the small portion of the microchannel [i.e., the ion depletion zone which is invisible in Fig. 2(a)]. Therefore, we only considered the relaxation time of diffusion for characterizing the overshoot effect. The analytical expression for the diffusion relaxation time, τ_D, is δ²/D, where δ is the length of the diffuse layer in the steady state and D is the diffusion coefficient of the ion. As L_eff increased, the diffuse layer at the steady state and the diffusion relaxation time would also be longer.

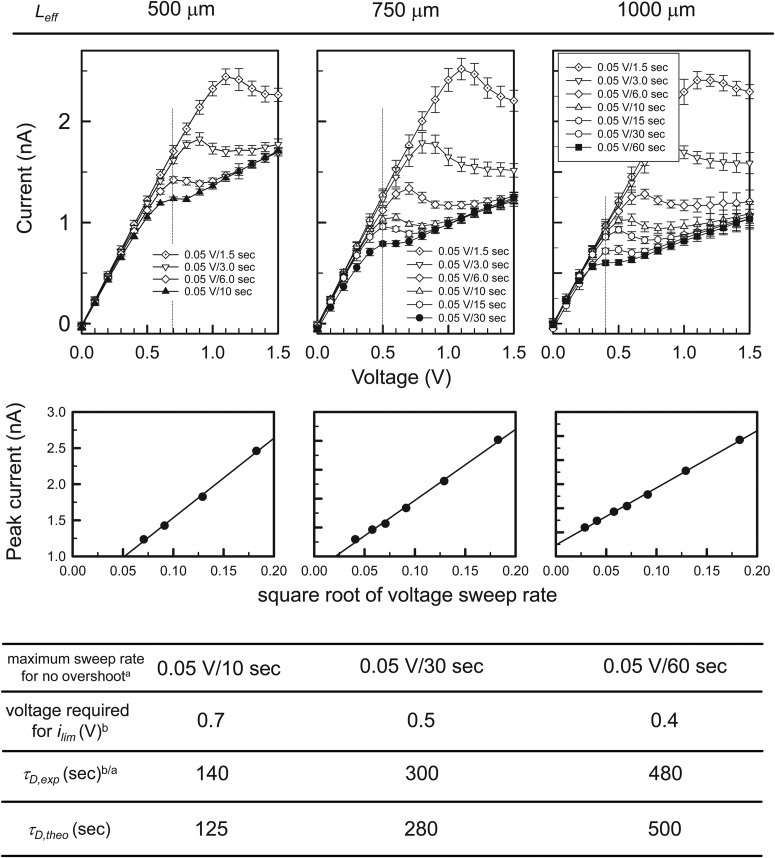
To verify this scenario, we conducted the I-V measurement as a function of various sweep rates of voltage, as shown in Fig. 3. I-V curves with a fast sweep rate had a higher current value and an overshoot phenomenon on the whole. This relationship can be explained by classical cyclic voltammetry theory.³⁰ The peak current at the overshoot scales as the square root of the voltage sweep rate.²⁹ Note that the scaling (RT/zFs, where s is the sweeping rate) in classical cyclic voltammetry theory is off by a factor of 20 or so to our diffusion time. The factor of 20 actually comes from the fact that the characteristic voltage for the diffusion time is not (RT/zF) ∼ 24 mV but rather the voltage of the experiment for depletion by a membrane. RT/zF is a typical voltage drop for electrochemical reactions in cyclic voltammetry but not so for membrane depletion. In fact, if one uses the voltage at limiting current listed in the response, 0.4–0.7 V, these voltages are about 20 times RT/zF. Thus, the overshoot is due to the advancement of the depletion front, which is quite analogous to the advancement of a diffusion front in cyclic voltammetry. The only difference is the characteristic voltage used. This would be a nice connection between an ion-selective membrane and an ion-selective electrode. In this work, however, as the sweep rate slowed, peak currents tended to decrease and overshoot was diminished. The maximum sweep rates to eliminate the overshoot was 0.05 V/10 s, 0.05 V/30 s, and 0.05 V/60 s for L_eff = 500, 750, and 1000 μm, respectively. Without the occurrence of the overshoot, the voltages required for initiating limiting current were 0.7, 0.5, and 0.4 V, respectively. Thus, it took 140, 300, and 480 s to reach these voltage values in the experiments. These values matched well with theoretically estimated τ_D, which is summarized in Fig. 3. Therefore, one needs to set the sweep rate as the ions can diffusively transport only within the effective length of the microchannel, not the entire length of the microchannel, which dramatically reduces I-V measurement time and labor.

FIG. 3.

Table of I-V responses for varying L_eff and the sweep rate. From the plots, one can estimate the maximum sweep rate for the disappearance of the overshoot. Also, the peak currents were proportional to the square root of the voltage sweep rate. The rate has a close relationship with the diffusion time of ions in a microchannel.

IV. CONCLUSION

In this work, we developed a new measurement platform for I-V characteristics of perm-selective ion transportation. It has been reported that an overshoot phenomenon impeded the correct electrokinetic responses in a micro-/nanofluidic device, because it represented a pseudonegative conductance. In the light of the fact that the fast transition to the steady state can eliminate the overshoot, we coercively shortened the effective length of the microchannel using a continuous injection of a fresh electrolyte through the side microchannels. The effect of the device was confirmed in both visualization and I-V measurements. The conventional micro-/nanofluidic device has a centimeter long microchannel so that it takes 14 h to get the I-V response without overshoot. Using the presenting idea, however, it takes only 2 min to obtain the I-V response without overshoot. Considering the repeatability verifications for solid research results (usually 5 times for each 3 different devices), our device can significantly save experimental time and labor.