An evaluation of supervised methods for identifying differentially methylated regions in Illumina methylation arrays

Abstract

Epigenome-wide association studies (EWASs) have become increasingly popular for studying DNA methylation (DNAm) variations in complex diseases. The Illumina methylation arrays provide an economical, high-throughput and comprehensive platform for measuring methylation status in EWASs. A number of software tools have been developed for identifying disease-associated differentially methylated regions (DMRs) in the epigenome. However, in practice, we found these tools typically had multiple parameter settings that needed to be specified and the performance of the software tools under different parameters was often unclear. To help users better understand and choose optimal parameter settings when using DNAm analysis tools, we conducted a comprehensive evaluation of 4 popular DMR analysis tools under 60 different parameter settings. In addition to evaluating power, precision, area under precision-recall curve, Matthews correlation coefficient, F1 score and type I error rate, we also compared several additional characteristics of the analysis results, including the size of the DMRs, overlap between the methods and execution time. The results showed that none of the software tools performed best under their default parameter settings, and power varied widely when parameters were changed. Overall, the precision of these software tools were good. In contrast, all methods lacked power when effect size was consistent but small. Across all simulation scenarios, comb-p consistently had the best sensitivity as well as good control of false-positive rate.

Introduction

DNA methylation (DNAm) is one of the most studied epigenetic mechanisms, which are stable heritable traits that cannot be explained by DNA sequences [1]. The most widely characterized DNAm process is the addition of the methyl group at the 5-carbon of the cytosine ring, which results in 5-methylcytosine (5-mC). When located in a gene promoter, DNAm typically acts to repress gene transcription. The gold standard for measuring methylation status is the whole-genome bisulfite sequencing (WGBS). However, the high cost of WGBS limits its use in large epidemiology studies.

Currently, most of the epigenome-wide association studies (EWASs) conducted utilize array-based technologies, which provides an economical, high-throughput and comprehensive alternative. For example, the HumanMethylation450 BeadChip (Infinium, Illumina, San Diego, California, USA) methylation microarray (450K) [2] targets 485577 cytosine positions in the human genome, distributed across gene promoters (within 200 or 1500 bp upstream of transcription start sites), 5′ untranslated region (UTRs), first exon, gene bodies, 3′ untranslated region (UTRs) and intergenic regions. Alternatively, these positions can also be classified by their relation to CpG islands (CGIs), which are regions in the genome where there are more CG dinucleotides than expected by chance. The CpG positions can be classified into CGIs, shores (2 kb region flanking CGIs) and shelves (2 kb region flanking shores) [3]. More recently, the MethylationEPIC BeadChip (Infinium) microarray (850K) was developed [4]. This newer array includes more than 90% of the 450K array probes, as well as an additional 333 265 probes targeting sites in regulatory regions recently identified by the ENCODE [5, 6] and FANTOM5 [7] projects.

Recently, it has been observed that contiguous regions in the epigenome with differentially methylated regions (DMRs) are associated with various diseases [8–11]. For example, hyper-methylation of promoter regions of several candidate genes is important in neoplastic development and contributes to colon cancer carcinogenesis [12]. In neurodevelopmental dis-orders, Ladd-Acosta et al. [13] identified and replicated three genomic regions with significant DNAm changes in postmortem brain tissues from patients with autism spectrum disorder. Similarly, Liu et al. [14] identified two clusters within the major histocompatibility complex region whose differential methylation potentially mediates genetic risk for rheumatoid arthritis.

A number of tools have been developed for the analysis of DMRs [15–19]. Methods for DMR identification can be classified into supervised and unsupervised methods. The unsupervised methods first group the CpG probes into genomic regions (e.g. CGIs, CGIs shores, TSS200) based on array annotation information, and then test each genomic region for association with phenotype information. In contrast, in supervised methods aP-value or corresponding t-statistic is computed at each CpG first, then the regions in the genome with consecutive small P-values or t-statistics are identified based on user-specified criteria (such as the minimum number of CpGs for the region). Note that because of the large number of probes included in the array (almost half a million), when scanning for small P-values, these methods typically compute multiple comparison adjusted P-values for each probe first and then scans the genome for regions enriched with significant adjusted P-values. Two previous studies [20, 21] compared unsupervised DMR analysis methods that test for predefined genomic regions. However, there is currently a lack of systematic evaluation of supervised DMR identification methods.

In this study, we conduct a comprehensive evaluation of the most popular software tools for supervised DMR analysis, including DMRcate [17], Probe Lasso [19], bump hunting [15] and comb-p [16]. We chose these tools based on the following several criteria: (i) They can be used to analyze Illumnina methylation arrays. (ii) They use the supervised approach to identify DMRs. (iii) The software has open source code with implementation in the R or Python programming languages, the most commonly used computing languages for epigenetic studies, and the implementations can be scaled up to analyze an EWAS with moderate sample size in a reasonable amount of time.

In practice, we find the algorithms underlying these methylation analysis tools typically have multiple parameters that need to be specified. However, directions for specifying the parameters are often missing from the user guides, and the performance of the tools under different parameter settings are often unclear. To help users understand and choose best parameter settings for DNAm analysis tools, we conduct a comprehensive evaluation of the tools under multiple parameter settings. In addition to evaluating power, precision, area under precision-recall curve (AuPR), Matthews correlation coefficient (MCC), F1 score (F1) and type I error rate, we also compare several additional characteristics of the analysis results by these different methods, including the size of the DMRs and overlap between the methods. We discuss details of the simulation study scheme in the Methods section, and we discuss the results of the simulation study and a real data set in the Results section. In the last section, we provide a brief summary on our main findings and also highlight future directions in this important research area.

Methods

To preserve correlation patterns in real data sets, we generated simulation data by using a real data set as input. Figure 1 shows the workflow of our simulation study, which involved the following several steps:

1. First, we obtained a publicly available methylation data set. The GEO data set GSE41169 from Horvath et al. [22] included DNAm profiles of whole blood samples of 62 patients with schizophrenia and 33 healthy controls from the Dutch population. The Illumina Infinium 450k Human DNA methylation Beadchip v1.2 was used to measure the methylation status of 485 577 CpGs. For our study, we selected a total of 14 samples that satisfied two conditions, (i) these are all healthy male samples and (ii) the age of the patients ranged from 20 to 30 years. The sample IDs of the 14 selected samples are GSM1009666, GSM1009667, GSM1009668, GSM100 9681, GSM1009688, GSM1009695, GSM1009742, GSM1009743, GSM1009744, GSM1009745, GSM1009746, GSM1009748, GSM10 09892 and GSM1009893.

2. Next, we performed Adjacent Site Clustering (A-clustering) [22] to obtain 3063 clusters of adjacent CpG probes (A-clusters), see details in the section ‘Simulating clusters of CpGs with differential methylation’ below.

3. We then simulated differentially methylated clusters of CpGs by randomly selecting 500 A-clusters and adding treatment effects to selected samples in the data sets. This process was repeated for five times for each effect size 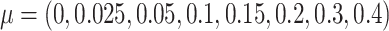. This gave us 40 simulation data sets.

4. We applied four DMR finding methods (DMRcate, bumphunter, Probe Lasso, comb-p) to the simulation data sets generated in step 3.

5. Finally, we compared results of these methods on precision, power, AuPR, MCC, F1, type I error rate, size of the DMRs, execution time as well as overlap of DMRs identified by different methods.

Figure 1.

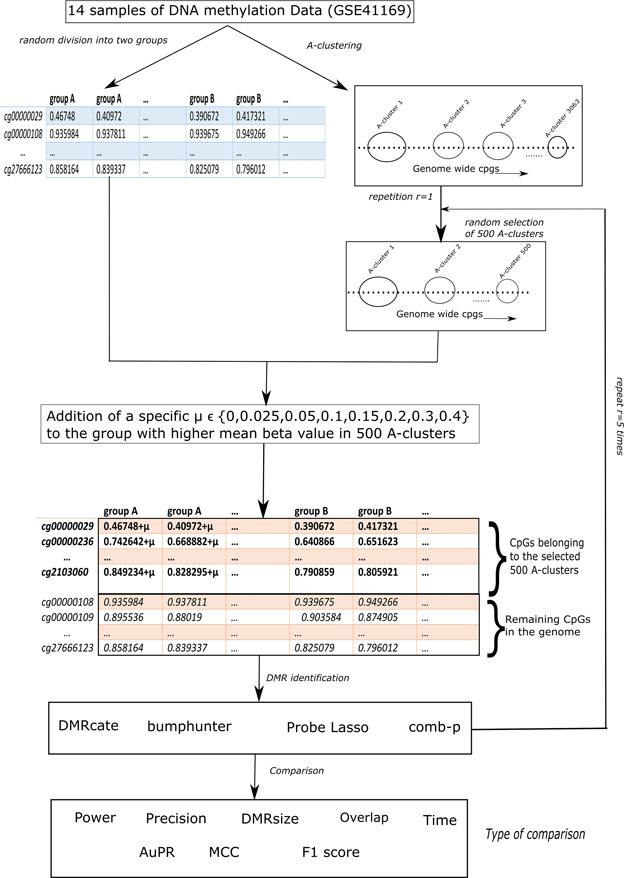
Overall workflow of the analysis.

We discuss these steps in details next. The analysis scripts used for this study can be accessed at https://github.com/gabriel odom/DMRcomparePaper.

Simulating clusters of CpGs with differential methylation

Before clustering analysis, we used the DMRcate [17] function rmSNPandCH to remove CpGs that are close to single-nucleotide polymorphisms (SNPs) or CpGs that cross-hybridize with locations on sex chromosomes. We also removed those CpGs with little variations across all the samples, i.e. those CpGs with beta values <0.05 or beta values >0.95 in all samples.

Next we used Adjacent Site Clustering (A-clustering) [22] to group neighboring CpG sites that are correlated with each other into clusters. We applied A-clustering to the 14 samples selected above to obtain a total of 3063 clusters, each consisting of at least five adjacent CpGs. The parameters we used are assign.to.clusters(betas = beta.value, dist.thresh = 0.5, bp.merge = 200, dist.type = "spearman", method = "complete") from the Aclust R package (https://github.com/tamartsi/Aclust), which corresponded to merging two CpGs with Spearman correlation greater than 0.5 and are within 200 bp into a cluster. Figure 2 shows an example of an A-cluster with 5 CpGs.

Figure 2.

An example cluster with 5 CpGs.

The 14 methylation samples were randomly divided into two groups. Differential methylation of a small subset (i.e. 500) of the clusters were simulated by adding a small treatment effect 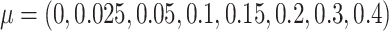to beta values in the group with higher average beta value. For each value of 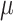, we repeated the process five times. This yielded a total of 40 simulation data sets (8 values of 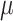× 5 repetitions).

On the methylation arrays, beta values are computed based on the ratios of the methylated signal intensity to the sum of both methylated and unmethylated signals after background subtraction, so they range from 0 (completely unmethylated) to 1 (fully methylated). To ensure the added treatment effects do not cancel out existing differences in beta values, for each CpG probe in the methylation cluster, we first compared the group means of the two groups and then added treatment effects to the group with higher mean beta values. After adding treatment effects, if a beta value was larger than 1, it was set to 1.

Methods for identifying DMRs

DMRcate

The DMRcate [17] method is implemented in the Bioconductor package DMRcate. The DMRcate method first fits a linear model at each CpG using the empirical Bayesian methodology from the limma R package. In our study, this model included methylation M value as the outcome variable and group status as independent variable. M values are logit transformation of beta values, that is 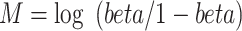, these values have been shown to have better statistical properties such as homoscedasticity [23] in methylation data analysis. The statistic Y = t² is then calculated for each position, where t is the t-statistic from the linear model corresponding to the group effect. In the second step, DMRcate applies kernel smoothing using a Gaussian smoother with bandwidth 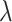scaled by a scaling factor C. The P-values at each position are then computed by moment-matching using the method of Sattererthwaite [24]. The CpG sites with multiple-comparison-corrected P-values (via the method of Benjamini and Hochberg [25]) are then selected as significant CpGs. Regions for DMRs are identified by collapsing contiguous significant CpGs that are within 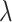nucleotides from each other. The P-value for DMR is computed using Stouffer’s method [26]. We studied the effect of 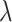and C on the performance of DMRcate in our simulation study.

Bumphunter

Bumphunter [15] is implemented in the Bioconductor packages bumphunter and minfi. In the bumphunter method, first a linear regression model regressing the M value on group is applied to model differential methylation between case and control groups at each CpG site. Candidate regions (bumps) are then identified, these are clusters of consecutive probes for which all the t-statistics exceed a user-defined threshold (argument cutoff in the bumphunter function). Permutation tests, which permute sample labels to create the null distribution of candidate regions, are then conducted to estimate statistical significance of the candidate regions separated by at least maxgap base pairs. In the identification of regions, spatial correlation structures are used to model correlations of methylation levels between neighboring CpGs. We studied the effect of the parameters maxGap, pickCutoffQ and B (the number of resamples) used to estimate DMR P-values, on performance of bumphunter in the simulation study.

Probe Lasso

Probe Lasso [19] is implemented in the Bioconductor package ChAMP. In the Probe Lasso method, first a linear model regressing beta value on group is applied to model differential methylation between case and control groups at each CpG site. Next, because the probe spacing on the methylation arrays are not uniform (e.g. probes located in promoter regions are more densely spaced, while those located in intergenic regions are more spread out), Probe Lasso defines flexible boundaries around each probe depending on the type of genomic feature the probe is located in (e.g. TSS200, 3′UTR). Much like a real lasso, the Probe Lasso algorithm ‘throws’ a lasso around each probe with the dynamic boundaries, centered at the target probe. A region around the target probe is selected if the number of significant probes captured within the Probe Lasso boundary is higher than the user-specified threshold (argument minProbes in the champ.DMR function). For each region, Probe Lasso then computes a correlation matrix of normalized beta values within that region and then uses Stouffer’s method to compute a P-value for the region by weighting individual probes by the inverse sum of its squared correlation coefficient in the correlation matrix. We studied the effect of parameters adjPvalProbe (significance threshold for probes to be included in DMRs), meanLassoRadius (radius around each significant probe to detect a DMR) and minDmrSep (the minimum separation in base pairs between neighboring DMRs) on the performance of Probe Lasso.

Comb-p

Comb-p [16] is a command-line tool and a Python library [16]. In contrast to the three methods described above, it does not support calculation of P-values for individual CpGs. Instead, the input of comb-p is a .BED file with P-values and chromosome locations of the CpG sites. The comb-p tool then computes correlations at varying distance lags (auto-correlation), which are used to compute corrected P-values at each CpG site using the Stouffer–Liptak–Kechris correction [27]. The corrected P-value at a CpG site will be smaller than the original P-value if the neighboring CpG sites also have comparatively small P-values. On the other hand, the corrected P-value at a CpG site will remain large if neighboring P-values are also large. The false discovery rate [25] is then calculated at each CpG site and a peak-finding algorithm is then used to find regions enriched with small P-values. Once the regions are identified, the final P-value for each region is computed based on the Stouffer–Liptak correction. We compared the performance of comb-p when parameters seed (P-value significance threshold to start a region) and dist (extend a region if there is another P-value lower than seed within this distance) were varied.

Evaluation criteria

To compare the sensitivity and specificity of the four DMR finding methods, we assessed their performances on the 40 simulation data sets generated in step (3) of ‘Methods’ section above. For all methods, we considered detected regions with DMR P-values less than 0.05 that also contained five or more CpGs as significant DMRs. For each simulation data set with 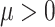, there were a subset of regions (clusters of CpGs) to which we added treatment effect 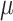. In Table 3, a true-positive (TP) DMR is defined as a significant DMR declared by a method that overlaps with a region, which we added treatment effects to methylation beta values (section ‘Simulating clusters of CpGs with differential methylation’ above). A false-positive (FP) DMR is defined as a significant DMR that does not overlap with any of the regions with added treatment effects. A false negative (FN) is defined as a region with added treatment effect that does not overlap with any significant DMRs.

Table 3.

TP, FP, FN, Power, Precision, AuPR, MCC, F1 and Elapsed Time (in Second) for the different DMR detection tools based on simulation data sets. For each method, shown are the mean (standard deviation) of the performance measures under the best performing parameter setting for five repetitions of the simulation study at each simulation scenario

Mu	Method	TP	FP	FN	Power	Precision	AuPR	MCC	F1	Time (seconds)
0.025	Bumphunter	144 (7.87)	69 (3.27)	356 (7.87)	0.29 (0.02)	0.63 (0.02)	0.36 (0.02)	0.38 (0.02)	0.44 (0.02)	157 (4.42)
0.025	Comb-p	198 (8.11)	12 (2.86)	302 (8.11)	0.4 (0.02)	0.95 (0.02)	0.55 (0.01)	0.57 (0.02)	0.55 (0.02)	55 (0.58)
0.025	DMRcate	32 (4.34)	0 (0.45)	468 (4.34)	0.06 (0.01)	0.99 (0.01)	0.25 (0.01)	0.23 (0.02)	0.12 (0.02)	21 (0.24)
0.025	Probe Lasso	0 (0)	0 (0)	500 (0)	0 (0)	NA	NA	NA	NA	7 (0.42)
0.05	Bumphunter	248 (10.92)	68 (3.36)	252 (10.92)	0.5 (0.02)	0.75 (0.02)	0.56 (0.02)	0.58 (0.02)	0.63 (0.02)	160 (3.88)
0.05	Comb-p	352 (10.55)	13 (3.58)	148 (10.55)	0.7 (0.02)	0.97 (0.01)	0.78 (0.02)	0.8 (0.02)	0.81 (0.02)	56 (0.37)
0.05	DMRcate	178 (9.63)	3 (1.22)	322 (9.63)	0.36 (0.02)	0.98 (0.01)	0.52 (0.02)	0.55 (0.02)	0.52 (0.02)	20 (0.43)
0.05	Probe Lasso	212 (10.92)	21 (5.03)	288 (10.92)	0.42 (0.02)	0.93 (0.01)	0.57 (0.02)	0.58 (0.02)	0.57 (0.02)	17 (0.83)
0.1	Bumphunter	280 (11.73)	66 (2.88)	220 (11.73)	0.56 (0.02)	0.79 (0.02)	0.64 (0.02)	0.65 (0.02)	0.7 (0.02)	163 (6.92)
0.1	Comb-p	448 (3.11)	16 (4.36)	52 (3.11)	0.9 (0.01)	0.97 (0.01)	0.91 (0.01)	0.92 (0.01)	0.93 (0)	57 (0.53)
0.1	DMRcate	326 (9.29)	8 (3.35)	174 (9.29)	0.65 (0.02)	0.98 (0.01)	0.75 (0.01)	0.77 (0.01)	0.78 (0.01)	21 (1.69)
0.1	Probe Lasso	362 (7.02)	36 (7.36)	138 (7.02)	0.72 (0.01)	0.93 (0.01)	0.79 (0.01)	0.79 (0.01)	0.81 (0.01)	18 (0.16)
0.15	Bumphunter	281 (11.95)	63 (2.86)	219 (11.95)	0.56 (0.02)	0.8 (0.02)	0.66 (0.02)	0.65 (0.02)	0.7 (0.02)	160 (10.11)
0.15	Comb-p	465 (4.16)	17 (4.6)	35 (4.16)	0.93 (0.01)	0.97 (0.01)	0.93 (0.01)	0.94 (0.01)	0.95 (0.01)	57 (0.47)
0.15	DMRcate	376 (6.69)	10 (3.03)	124 (6.69)	0.75 (0.01)	0.98 (0.01)	0.82 (0.01)	0.83 (0.01)	0.85 (0.01)	20 (0.47)
0.15	Probe Lasso	406 (7.6)	40 (8.53)	94 (7.6)	0.81 (0.02)	0.93 (0.01)	0.85 (0.01)	0.84 (0.01)	0.86 (0.01)	18 (0.09)
0.2	Bumphunter	280 (11.78)	62 (3.16)	220 (11.78)	0.56 (0.02)	0.81 (0.02)	0.67 (0.02)	0.66 (0.02)	0.71 (0.02)	157 (6.39)
0.2	Comb-p	471 (4.06)	18 (5.13)	29 (4.06)	0.94 (0.01)	0.97 (0.01)	0.94 (0)	0.94 (0)	0.95 (0)	57 (0.47)
0.2	DMRcate	385 (5.79)	10 (2.86)	115 (5.79)	0.77 (0.01)	0.97 (0.01)	0.83 (0.01)	0.84 (0.01)	0.86 (0.01)	20 (1.43)
0.2	Probe Lasso	415 (9.31)	41 (7.45)	85 (9.31)	0.83 (0.02)	0.93 (0.01)	0.86 (0.02)	0.85 (0.01)	0.87 (0.01)	19 (1.92)
0.3	Bumphunter	280 (11.78)	57 (5.15)	220 (11.78)	0.56 (0.02)	0.82 (0.02)	0.68 (0.02)	0.67 (0.02)	0.71 (0.02)	155 (9.56)
0.3	Comb-p	476 (2.61)	19 (4.67)	24 (2.61)	0.95 (0.01)	0.96 (0.01)	0.95 (0.01)	0.95 (0)	0.96 (0)	56 (0.36)
0.3	DMRcate	398 (1.79)	10 (2.59)	102 (1.79)	0.8 (0)	0.98 (0.01)	0.85 (0)	0.86 (0)	0.88 (0)	21 (1.2)
0.3	Probe Lasso	425 (8.56)	42 (7.48)	75 (8.56)	0.85 (0.02)	0.93 (0.01)	0.87 (0.01)	0.87 (0.01)	0.89 (0.01)	18 (0.06)
0.4	Bumphunter	280 (11.83)	52 (6.15)	220 (11.83)	0.56 (0.02)	0.84 (0.03)	0.68 (0.02)	0.68 (0.03)	0.72 (0.02)	156 (12.24)
0.4	Comb-p	478 (2.7)	19 (4.32)	22 (2.7)	0.96 (0.01)	0.96 (0.01)	0.95 (0.01)	0.95 (0)	0.96 (0)	57 (0.77)
0.4	DMRcate	401 (2.86)	10 (4.44)	99 (2.86)	0.8 (0.01)	0.98 (0.01)	0.85 (0.01)	0.87 (0.01)	0.88 (0.01)	20 (0.95)
0.4	Probe Lasso	427 (8.04)	42 (7.48)	73 (8.04)	0.85 (0.02)	0.93 (0.01)	0.88 (0.01)	0.87 (0.01)	0.89 (0.01)	19 (0.22)

To compare the four DMR methods, we considered the following criteria:

1. Power (sensitivity, recall): This is defined as Probability (predicted positive | actual positive), which was estimated by the number of TP DMRs over the total number of regions with treatment effects added (i.e. 500).

2. Precision: This is defined as Probability (actual positive | predicted positive), which was estimated by dividing the number of TP DMRs over the total number of DMRs declared by a method.

3. AuPR: Because the data sets we analyzed in this study are highly imbalanced—the proportion of true-negative regions in the genome are much higher than the proportion of TP regions—we evaluated the performance of the methods using AuPR, which is robust against class skewness. The precision-recall curve shows the tradeoff between precision and recall (or power, sensitivity) as the significance cutoff is varied. The AuPR represents the overall discriminatory ability of the methods at determining whether a given region is associated with the disease over all possible cutoffs. Higher values of AuPR indicates better performance for a method, we selected the best-performing parameter setting for each method based on largest AuPR.

4. MCC: This is essentially the correlation coefficient between observed and predicted binary classification. It is also robust against different sizes of the positive and negative classes. MCC is computed as 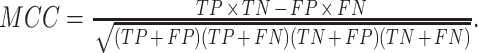An MCC of +1, 0 and −1 correspond to perfect prediction, no better than random prediction and total disagreement between predicted and actual status, respectively.

5. F1: This is another measure of a test’s accuracy. It is computed as 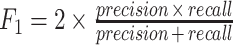. F1 ranges from 0 (worst prediction) to 1 (perfect precision and recall).

6. DMR size: Since the probes on the arrays are not distributed uniformly, we estimated DMR sizes by the number of CpG sites a detected DMR has.

7. DMR overlap: The agreement between the DMR detection methods were assessed by the number of common DMRs detected by them. We used the makeVennDiagram function in the ChIPpeakAnno R package to draw the Venn diagrams.

8. Time: The elapsed time measured in seconds for each DMR detection method was recorded on a Lenovo Thinkstation, 1009 Think Place Morrisville, NC 27560 United States, P910 server with 64 GB 2400 MHz, DDR4 RAM, Dual Core Intel Xeon E5-2643 V4 (3.4 GHz) CPU and the Windows 10 Operating System (for bumphunter, Probe Lasso and DMRcate); and a Dell Precision Tower Linux server, Dell Inc. One Dell Way Round Rock, TX 78682, with 64 GB of 2133 DDR4 RAM and Intel Xeon E5-2640 v3 (2.60 GHz) CPU (for comb-p). When comparing computing times used for different algorithms, we did not use parallel computing for the results in Table 3.

Results

Table 1 lists the parameter settings that were compared for the four DMR finding methods.

Table 1.

Parameter settings for the DMR identification methods. Default settings are underlined and in bold font.

Method	Implementation	Input Parameters	Statistics for computing DMR P-value	DMR P-value label in output table
Bumphunter	R/BioC package bumphunter v1.20.0	pickCutoffQ = (0.95, 0.99), maxGap = (200, 250, 500, 750, 1000), nullMethod ="permutation", B=10	permutation distribution based on permuting sample labels	P-value area
Comb-p	Python library comb-p v0.48	--seed (0.001, 0.01, 0.05) --dist (200, 250, 500, 750, 1000)	Stouffer–Liptak statistic	z_p
DMRcate	R/BioC package DMRcate v1.14.0	lambda = (200, 250, 500, 750, 1000), C = (1,2,3,4,5)	Stouffer’s method	Stouffer
Probe Lasso	R/BioC package ChAMP v2.9.10	method = “ProbeLasso”, adjPvalProbe = (0.001, 0.01, 0.05) meanLassoRadius = (375, 700, 1000) minDmrSep = (200, 250, 500, 750, 1000)	Stouffer’s method	dmrP

Type I error

The results of our simulation study showed all methods had well-controlled type I error rates (Supplementary Table 1). When no treatment effects were added to the methylation data sets, DMRcate and Probe Lasso (under all parameter settings) detected no significant DMRs. Comb-p detected between 1 and 12 significant DMRs, and bumphunter detected between 17 (0.57%) and 106 (3.49%) of 3063 significant DMRs with 5 CpGs or more in different parameter settings. However, these FP rates are still well below the expected 5% type I error rate for the total of 3063 methylation clusters identified by A-clustering with no added treatment effect in this type I error rate simulation study.

AuPR, MCC, F1

For each method, we selected the parameter settings that performed best (Table 2) based on largest AuPR value. Table 3 shows the number of TP, FP DMRs, missed regions (FN) as well as power, precision, AuPR, MCC and F1 for each simulation scenario for the four methods under the parameter settings that performed best. Similar information for all tested parameter settings are shown in Supplementary Tables S2–S5. Shown in these tables are the mean and standard deviations of the metrics averaged over five simulation repetitions. We note that the results were highly consistent between AuPR and MCC and F1, the best models with largest AuPR also had the highest MCC and F1.

Table 2.

Parameter settings that achieved best performance (AuPR) for each method

Method	Parameter setting with best performance
bumphunter	cuttoffQ = 0.95, maxGap = 250
comb-p	seed = 0.05, dist = 750
DMRcate	lambda = 500, C = 5
ProbeLasso	adjPval = 0.05, mLassoRad = 1000, minDmrSep = 1000

Precision

Figure 3A shows under the best performing parameter setting (largest AuPR); all four methods had good precision or positive predictive value. In fact, this hold true for all methods under all parameter settings. In Supplementary Tables S3–S5 and Figure SF1, comb-p, DMRcate and Probe Lasso achieved precision of 90% or more under all parameter settings in all simulation scenarios. That is, given that a DMR is identified by a method, it’s almost certain that the DMR is a TP. Bumphunter achieved better precision when the parameter cutoff = 0.99 (instead of 0.95), 80% or more precision was achieved when effect 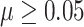under this parameter setting. On the other hand, varying the parameter maxGap had little effect on precision, especially when the effect is at least moderate with 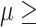0.1. However, at small effect size, bumphunter’s precision dropped significantly. For example, at effect size 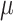= 0.025, precision for bumphunter ranged from 0.66 to 0.80 across different settings. None of the Probe Lasso parameter settings identified any significant DMRs when 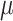= 0.025, so precision estimates were not available (NA) for these particular instances.

Figure 3.

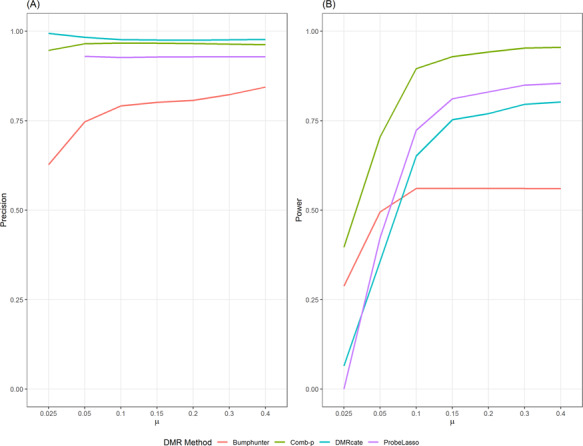
Precision (A) and power (B) of the methods under best performing parameter setting when different treatment effects where added to simulation data sets.

Power

Figure 3B shows power of the four methods under best-performing (largest AuPR) parameter setting. We note that when effect size is consistent but small across treated samples (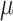 = 0.025), none of the currently available methods had acceptable power over 50% (Figure 3). At 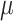= 0.05, only comb-p achieved more than 50% power. Across all simulation scenarios, comb-p consistently had the highest power, followed by Probe Lasso and DMRcate.

Supplementary Tables S2–S5 and Figure SF2 show the power of all the methods under all parameter settings. We found power varied widely when parameter settings were changed for all methods. For example, when 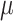= 0.1, power for bumphunter ranged from 44% to 56%; power for DMRcate ranged from 26% to 65%; power for Probe Lasso ranged from 30% to 72%; power for comb-p ranged from 69% to 91%. We found that none of the methods yielded highest power under default parameter settings for any effect size (Table 2, Supplementary Tables S2–S5).

For bumphunter, decreasing the number of resamples used when computing null distribution (parameter B) from 1000 to 10 or changing the maxGap parameter resulted in similar power (Supplementary Table S6, Figure SF2). However, decreasing parameter cutoffQ from the default of 0.99–0.95 improved power, especially when effect size was small (Supplementary Figure SF2, Table S2). For comb-p, power improved when the dist parameter was increased. Power also improved when the seed parameter was increased, but only when effect size was small (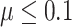; Figure SF2, Table S3). For DMRcate, power improved when parameter lambda was decreased or when the parameter C was increased (Figure SF2, Table S4). For Probe Lasso, power was similar when the parameter minDMrSep was changed, but power improved substantially when the parameter meanLassoRadius was increased from default value of 375 to 1000 or when adjPval was increased from 0.001 to 0.05 (Figure SF2, Table S5).

Precision-recall curves

Figure 4 and Supplementary Figure SF4 show precision-recall curves for the four methods under the parameter configurations, which yielded the highest AuPR. Curves for methods that perform better are closer to the upper-right corner. These results showed that comb-p consistently performed best across all simulation scenarios. For small effect size (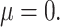05), when power (recall) approaches 80%, all methods exhibited poor precision. When effect size was increased to 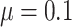, both comb-p and Probe Lasso had excellent precision (over 80%), while precision for DMRcate and bumphunter remained poor. For large effect size ( 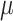= 0.4), when power (recall) approaches 80%, all methods except bumphunter had good precision.

Figure 4.

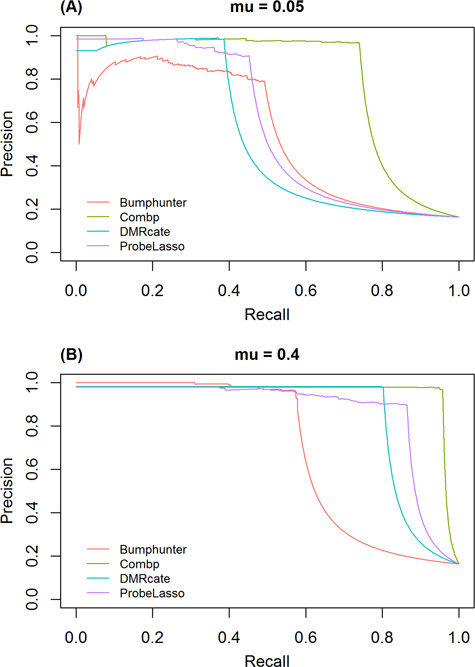
Precision-recall curve of the four methods under best performing parameter settings, (A) for small effect size (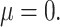05) and (B) large effect size (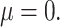4).

DMR sizes

Figure 5 shows distribution of the sizes of significant DMRs identified by each method. For each method, the size of significant DMRs remained stable across different effect sizes. The median DMR sizes for bumphunter, comb-p and DMRcate were 6, 7 and 7, respectively. Significant DMRs identified by Probe Lasso were larger with median DMR size around 9. We also note that the sizes of the DMRs identified by Probe Lasso tended to have larger variabilities in the simulation data sets than those from other methods.

Figure 5.

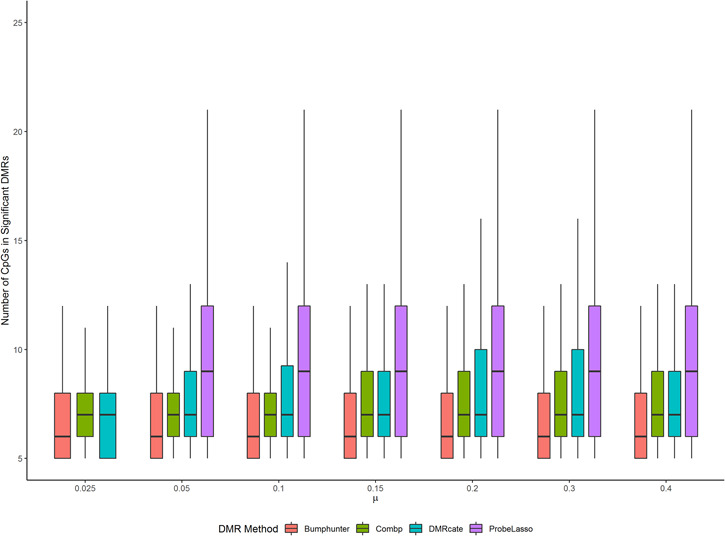
DMR sizes of the four methods under best performing parameter settings for each of the four methods.

Overlap of DMRs by different methods

Figure 6 and Supplementary Figure SF5 show the overlap of significant DMRs identified by the four methods under best parameter settings. We observed an increase in agreement among the methods when effect size was increased. There was substantial overlap in the significant DMRs identified by comb-p, DMRcate and Probe Lasso. Overall, comb-p and bumphunter identified the most unique DMRs not found by other methods, followed by Probe Lasso. Almost all DMRs identified by DMRcate were also identified by comb-p.

Figure 6.

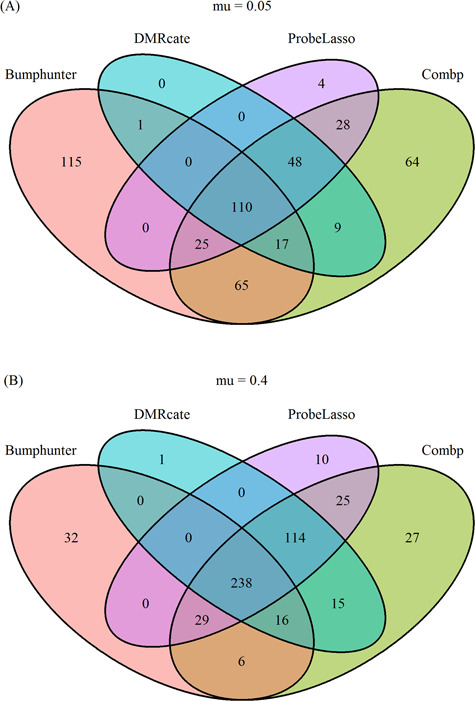
Overlap of the four methods under best performing parameter settings, (A) for small effect size (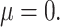05) and (B) large effect size (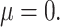4).

Execution time

The last column in Table 3 shows execution time for each of the methods under different simulation scenarios. We found analysis using all software can be finished within a reasonable amount of time. All methods completed calculation in less than 1 min per simulation data set, except for the bumphunter method. We believe this may be because bumphunter relies on permuting sample labels rather than approximation based on statistical distribution to estimate P-values. Both bumphunter and Probe Lasso support parallelization on all major operating systems, while DMRcate supports parallelization in Unix environment.

Results of real data analysis

In addition to simulated data sets, we also applied the four software tools under best parameter settings (Table 2) to a real methylation data set from The Cancer Genome Atlas (TCGA) project [28]. Yuan et al. (2016) [29] conducted a comprehensive study on the molecular basis for sex disparities in 13 cancer types and identified 1 group of cancers with a small number of sex-affected genes and another group with more extensive sex-based molecular signatures. In this study, we compared DNAm profiles between colon cancer samples from male and female subjects in the TCGA database.

First, we downloaded TCGA level 3 methylation data, which were measured by Illumina 450K arrays, for the colon cancer cohort (COAD) from the UCSC Xena Public Data Hubs (http://xena.ucsc.edu/public-hubs/). Level 3 data consists of calculated methylation beta values mapped to genome per sample (https://cancergenome.nih.gov/abouttcga/aboutdata/datalevelst ypes#9). We used beta values for 325 independent tumor samples for comparison, including 174 male and 151 female samples. First, we removed confounding effects by fitting a linear regression model with methylation M values (logit-transformed beta values) as the outcome variable and patient stage and age at initial pathologic diagnosis as independent variables. We then used the residuals from this model for further analysis. We compared the four DMR identification methods at their best performing parameter settings as identified in the simulation study.

In real DNAm data, precision and recall cannot be assessed because the true DMRs are not known. Nevertheless, we compared the patterns of significant DMRs by each method. Overall, we found the results of the real data analysis were largely in agreement with results from the simulation study. We compared the number of significant DMRs with P-values less than 0.05 that also included at least 5 CpGs identified by each method (Figure 7). The results showed that comb-p identified 70 significant DMRs, bumphunter identified 72 significant DMRs, DMRcate identified 10 significant DMRs and Probe Lasso identified no significant DMRs. Yuan et al. showed that COAD belongs to the group of cancers with a weak sex effect, so we expected small effect sizes for the differences between male and female samples in COAD cohort. The results from our COAD sex-differences comparison agreed well with the results from our simulation study (shown in Table 3; 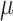= 0.025). In Table 3, the number of significant DMRs is indicated by the sum of TP and FP columns. In particular, both real data analysis and simulation study results showed that comb-p and bumphunter identified the most significant DMRs, followed by DMRcate, while Probe Lasso lacked power when effect size is small.

Figure 7.

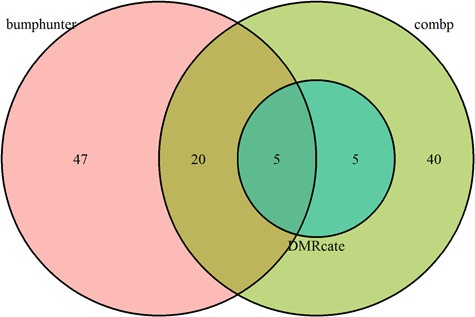
Significant DMRs identified by the four methods under best performing parameter settings for the comparison between male and female tumor samples in the TCGA COAD cohort.

Discussion

Most complex diseases are likely caused by a combination of genetic and environmental factors. Although many genetic variants have been identified, typically, they only explain a small proportion of variance in disease susceptibility. Epigentic variations, such as DNAm, hold promise in detecting new regulatory mechanisms that may be susceptible to modification by environmental factors, which in turn modify the risk of disease. However, exactly how DNAm contributes to disease risk and progression remains poorly defined for many diseases. The development of genome-wide methylation profiling techniques has led to the increased popularity of EWASs for characterizing methylation patterns across the genome.

While some aspects of the analyses in EWAS are similar to those for genome wide association studies (GWAS), such as the need to properly control for multiple comparisons and correction for batch effects, EWAS presents several additional challenges [30]. First, while genetic variants studied in GWAS are static, epigenetic marks such as DNAm are tissue specific. Therefore, selecting appropriate tissues would have important implications for studying disease-relevant variations. Second, it’s important to control factors that are known to influence the methylome, such as age [31], gender [32], smoking [33] and cellular heterogeneity [34]. Third, the dynamic nature of methylation changes means these changes can also be caused by the disease itself. Therefore, the results of methylation study need to be interpreted carefully, and additional experimental approaches are needed to prove functional relevance. Finally, while methylation of specific cytosines can be important, recent research has gradually shifted to the analysis of DMRs, as it has been observed that differential methylation between different tissue and cell types [35], in malignant cells [3] and in response to environmental factors [36] often extends across genomic regions.

To this end, critical evaluation of tools used to identify DMRs in EWASs becomes an important issue. In contrast to studies that rely on simulated data generated from specific statistical distributions, we conducted our simulation study by generating simulation data sets from a real methylation data set and added treatment effects to selected samples. We believe this approach, which previously has been successfully applied to methylation [22] and gene expression data sets [37, 38], can better emulate the correlation patterns in real omics data sets and enable more unbiased comparison of the methylation analysis methods.

Our study compared four popular DMR analysis methods under 60 different parameter settings. We found all methods performed well in terms of precision. In terms of power, all tools varied widely depending on parameter settings. Overall, comb-p showed the best sensitivity as well as good control of FP rate across all simulation scenarios. Although a large number of significant DMRs were identified by all methods, comb-p identified substantially more TP DMRs than other methods, especially when effect sizes were small. We also examined the overlap of significant DMRs between the software tools, and we found that the results from the different methods agreed more when effect size was increased. On the practical side, computation from all algorithms can be finished in a reasonable amount of time.

However, all methods lacked adequate power to detect small but consistent changes across all samples. Therefore, currently available tools would likely perform well for disease studies that are known to have large effect sizes (such as various cancers), but can be problematic when studying for phenotypes with smaller effect sizes (such as neurological or developmental diseases). The research field will likely benefit from future development of methods that can detect small but consistent changes in DNAm data. Integrating with functional annotations or additional omics data types such as pathway-based analysis [39–41] and integrative GWA-eQTL analysis [42–44], which have been successful for GWAS data, are also likely to improve power in EWAS.

Furthermore, as we have shown, performance of the software tools varied widely depending on different parameter settings. We would therefore encourage future software developers to include in-depth discussion and experience-based recommendations in the package vignettes on how users should choose parameter settings.

In summary, we have studied the effect of different parameter settings on performance of the methods including power, AuPR, MCC, F1, and type I error rate, as well as additional characteristics such as computation time, overlap of the methods and size of the DMRs. For each method, we have also identified the best parameter setting that had highest overall discriminatory ability based on AuPR. A summary of the conclusions for our study is shown in Table 4. We hope that our study results, based on both simulation and real methylation data sets, will help investigators to better understand and select the most appropriate methods and parameter settings for their studies.

Table 4.

Summary of comparison results for the four DMR identification methods

	Small effect size		Large effect size
Method	Precision	Power	Precision	Power	Speed	Can model covariate variable
bumphunter	-	-	+	-	+	Yes
combp	++	-	++	++	+	Yes
DMRcate	++	--	++	+	++	Yes
Probe Lasso	+	--	++	+	++	No

A ‘--’ and ‘-’ indicate very unsatisfactory and unsatisfactory results for the given criterion, respectively. A ‘+’ and ‘++’ indicate good and very good results for the given criterion, respectively.

Key Points

• The identification of DMRs is an important analytical task in the analysis of EWASs.

• All DMR analysis tools had well-controlled type I error rate and good precision.

• Power of all supervised DMR analysis tools (bumphunter, comb-p, DMRcate and Probe Lasso) varied widely depending on parameter settings.

• None of the methods had good power to detect small but consistent changes.

• Overall, comb-p performed best in terms of precision and recall across all simulation scenarios.

Funding

National Institutes of Health / National Cancer Institute R01 CA158472; NIH/NCI R01 CA200987; NIH/NCI U24 CA210954.

Saurav Mallik is a postdoctoral fellow at the Division of Biostatistics, Department of Public Health Sciences, University of Miami, Miller School of Medicine.

Gabriel J. Odom is a postdoctoral fellow at the Division of Biostatistics, Department of Public Health Sciences, University of Miami, Miller School of Medicine.

Zhen Gao is an associate scientist at the Sylvester Comprehensive Cancer Center.

Lissette Gomez is a biostatistician at the John P. Hussman Institute for Human Genomics, University of Miami, Miller School of Medicine.

Xi Chen is an associate professor at the Division of Biostatistics, Department of Public Health Sciences, University of Miami, Miller School of Medicine.

Lily Wang is an associate professor at the Division of Biostatistics, Department of Public Health Sciences, and Dr. John T. Macdonald Foundation, Department of Human Genetics at University of Miami, Miller School of Medicine.