Same fold, different properties: polarizable molecular dynamics simulations of telomeric and TERRA G-quadruplexes

Abstract

DNA and RNA sequences rich in guanine can fold into noncanonical structures called G-quadruplexes (GQs), which exhibit a common stem structure of Hoogsteen hydrogen-bonded guanine tetrads and diverse loop structures. GQ sequence motifs are overrepresented in promoters, origins of replication, telomeres, and untranslated regions in mRNA, suggesting roles in modulating gene expression and preserving genomic integrity. Given these roles and unique aspects of different structures, GQs are attractive targets for drug design, but greater insight into GQ folding pathways and the interactions stabilizing them is required. Here, we performed molecular dynamics simulations to study two bimolecular GQs, a telomeric DNA GQ and the analogous telomeric repeat-containing RNA (TERRA) GQ. We applied the Drude polarizable force field, which we show outperforms the additive CHARMM36 force field in both ion retention and maintenance of the GQ folds. The polarizable simulations reveal that the GQs bind bulk K⁺ ions differently, and that the TERRA GQ accumulates more K⁺ ions, suggesting different ion interactions stabilize these structures. Nucleobase dipole moments vary as a function of position and also contribute to ion binding. Finally, we show that the TERRA GQ is more sensitive than the telomeric DNA GQ to water-mediated modulation of ion-induced dipole-dipole interactions.

INTRODUCTION

G-quadruplexes (GQs) are noncanonical nucleic acid folds that can arise in guanine-rich sequences in DNA and RNA with a consensus sequence of G_xN_yG_xN_yG_xN_yG_x, where N is any nucleotide, x ≥ 3, and 1 < y ≤ 7 (1). Sequences between the guanine repeats are variable and dictate loop conformation and the overall GQ topology as a function of their length and composition (2,3). GQs may be intramolecular, forming within one oligonucleotide strand or intermolecular, forming among two or four strands (4). Putative and confirmed GQ-forming sequences are enriched in regulatory sequences, such as gene promoters (5,6), origins of replication (7–9), 5′- and 3′-untranslated regions of mRNA (10–12), and at the ends of chromosomes in telomeres to promote chromosomal stability (13). Thus, GQs are believed to be relevant in regulating transcription, DNA replication, translation and genomic maintenance.

Telomeres are nucleoprotein complexes that form at the 3′-overhangs of chromosomes to protect them against premature degradation that would otherwise arise from semiconservative replication (14), and also mediate chromosomal synapsis and recombination during meiosis (15). Telomeric DNA is enriched in guanine, and the repeat telomeric DNA sequence in humans is d(TTAGGG). As such, these genomic regions are capable of forming GQs, and previous studies have found that telomeric DNA GQs can exhibit a variety of folds, as reviewed in (16), including bimolecular (17) and unimolecular, intrastrand structures (18,19). Telomeric GQs are the substrate for telomerase (13), the enzyme that elongates chromosomal DNA and is overactive in numerous cancer subtypes. Stabilization of telomeric GQs inhibits telomerase activity, leading to chromosomal shortening and cell death, thus designing small molecules that stabilize telomeric GQs is a potential avenue for developing novel chemotherapeutics (16,20–25).

Transcription of the C-rich strand of subtelomeric regions in chromosomes produces telomeric repeat-containing RNA (TERRA), which have a characteristic repeat sequence of r(UUAGGG) (26). TERRA functions in regulating telomerase activity, heterochromatin formation, homologous recombination, and in suppressing the DNA damage response that would otherwise lead to telomere degradation (27). Montero et al. recently demonstrated that the human 20q subtelomeric locus is the production site of TERRA that are critical to suppressing the DNA damage response (28). This conclusion suggests that regulating TERRA expression is critical to genomic integrity and expression of these transcripts may occur at specific loci rather than at all subtelomeric regions, despite the subtelomere and telomere sequence similarity across all chromosomes. The characteristic TERRA sequence gives rise to the possibility that these transcripts can also form G-quadruplexes. Collie et al. determined the structure of a human TERRA GQ using X-ray crystallography (29), finding that it adopted a bimolecular, parallel architecture reminiscent of the telomeric DNA GQ structure determined by Parkinson et al. (17). Thus, available experimental evidence suggests that both d(TTAGGG)_n and r(UUAGGG)_n sequences can adopt bimolecular GQs.

Molecular dynamics (MD) simulations are a useful method of investigating biomolecular structure and dynamics at the atomistic scale. Many MD simulation studies have been carried out on GQs towards a greater understanding of the factors influencing their stability and the dynamics of loop regions. Islam et al. carried out an extensive series of MD simulations on human telomeric DNA GQs including structures that feature propeller (30) and lateral or diagonal loops (31). These investigations revealed considerable structural plasticity in the loop regions, which adopted a variety of folds and exhibited many different base orientations. To complement the determination of their bimolecular TERRA GQ structure, Collie et al. performed short (20-ns) MD simulations of both the TERRA GQ and the telomeric DNA GQ structure determined by Parkinson et al. Collie et al. observed that the UUA propeller loops were stable and remained stacked during the simulations, but the DNA TTA propeller loops became disordered. Moreover, they observed that the TERRA GQ deviated less from its starting structure than the telomeric DNA GQ. Caution is warranted in interpreting these results, as the simulations were very short, though the disordering of the TTA propeller loop in the telomeric DNA GQ is consistent with the more exhaustive sampling described above by Islam et al. (30).

A principal challenge in performing robust MD simulations of GQs is the modeling of ion-ion and ion-GQ interactions. GQs with three or more tetrads will coordinate at least two monovalent ions (K⁺ or Na⁺) along the stem axis of the tetrad core. The close proximity of these ions can lead to aberrant ion-ion repulsion if the force field used is not sufficiently accurate in describing these interactions. A quantum mechanical (QM) study by Gkionis et al. concluded that ion-ion repulsion is overestimated by nonpolarizable force fields (32), contributing to ion expulsion often seen in MD simulations of GQs (33–35). Loss of coordinated ions can contribute to structural distortions in the tetrad stems of GQs, undermining the accuracy of the MD simulation results. Some studies have shown that a judicious combination of ion parameters and water models can mitigate this aberrant behavior (35,36), or that non-transferable, system-specific reparametrization will improve ion retention (34), but Gkionis et al. concluded that to robustly describe ion-ion interactions in GQ simulations will require the explicit representation of electronic polarization to capture dipole-dipole and ion-dipole interactions that contribute to the stabilization of monovalent ions in GQ stems.

In the classical Drude oscillator model, electronic degrees of freedom are represented by explicit particles carrying partial negative charges, attached to their parent atoms via harmonic springs. The specific details of the Drude polarizable force field used in the present work have recently been reviewed (37), but a brief description is appropriate here. In the Drude oscillator model, charges are assigned to each Drude oscillator according to the atomic polarizability, α, of each non-hydrogen atom:

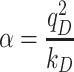(1)

where q_D is the charge on the Drude oscillator and k_D is the spring constant between the parent atom and the Drude oscillator. In the Drude force field, k_D is fixed at 1000 kcal mol⁻¹ Å⁻² for all atom-Drude pairs. All Drude oscillators are ascribed a mass of 0.4 amu, which is subtracted from the mass of the parent atom such that the atom-Drude pair has the total atomic mass of the element. Doing so allows for the Drude oscillators to have their positions integrated on the same footing as the atoms via an extended Lagrangian algorithm (38). Induced dipole interactions are explicitly included in the energy function for all first- and second-neighbor bonded pairs via a screening function described by Thole (39). Such interactions are normally excluded in pairwise-additive (nonpolarizable) force fields. The Drude force field also includes anisotropic treatment of polarizability for all hydrogen bond acceptors (40).

The first Drude polarizable force field for DNA, called ‘Drude-2013,’ was published by Savelyev and MacKerell (41). This model was shown to accurately model ion competition around duplex DNA (42), predicted ion-specific modulation of DNA structure (43), and more accurately modeled the free energy differences of base-flipping than the additive CHARMM36 force field (44). Subsequent refinement of this force field improved base stacking interaction energies, backbone conformational energetics, and sugar puckering, leading to stable A-, B-, and Z-DNA simulations on the microsecond time scale (45,46). This force field was designated ‘Drude-2017,’ and was subsequently extended to include RNA (47).

We recently applied the Drude-2017 force field to the c-kit1 promoter GQ, finding that explicit polarization was required to maintain K⁺ ion coordination in the GQ stem (48). Further, we observed the unbiased binding of a K⁺ ion to Thy12, an event that strengthened the interaction energy between the structured ions with the guanine bases in the tetrad stem via dipole-dipole interactions. Building upon these observations, in the present work, we simulated a bimolecular telomeric DNA GQ (17) and the analogous TERRA GQ (29). We sought to determine if (i) binding of bulk K⁺ ions is a generic feature of GQs, (ii) such binding is relevant to bimolecular GQs and (iii) the ion distributions around DNA and RNA GQs differ. Towards understanding the factors governing GQ structure and stability, we also sought to compare the conformational sampling, hydration, and nucleobase electronic properties of DNA and RNA GQs with the same fold, which can be done systematically in the case of telomeric DNA and TERRA GQs. The simulations of the TERRA GQ presented here are the first of their kind in applying the Drude-2017 force field to an RNA GQ.

MATERIALS AND METHODS

System construction

Initial coordinates for the telomeric DNA and TERRA GQs were taken from PDB entries 1K8P (17) and 3IBK (29), respectively. Both GQs have a bimolecular, parallel architecture and exhibit a similar folded topology (Figure 1). The sequence of the telomeric DNA GQ is 5′-d(TAGGGTTAGGGT)-3′ and for the TERRA GQ it is 5′-r(UAGGGUUAGGGU)-3′. K⁺ ions coordinated in each GQ tetrad stem were retained. Missing hydrogen atoms were constructed using the CHARMM program (49). Each GQ was centered in a cubic box with a minimum GQ-box distance of 10 Å, which was subsequently filled with TIP3P water (50) and 150 mM KCl, including neutralizing counterions. Each system was relaxed via 500 steps of steepest descent minimization, followed by 500 steps of adopted-basis Newton-Raphson minimization. Energy minimization was performed in CHARMM. The CHARMM36 nucleic acid force field (51–54) was applied to the GQs, and the TIP3P water molecules included the CHARMM modification to assign Lennard-Jones parameters to the hydrogen atoms (55,56). Standard CHARMM ion parameters (57) were applied to K⁺ and Cl⁻ ions.

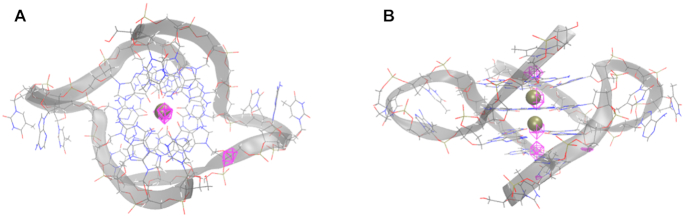
Figure 1.

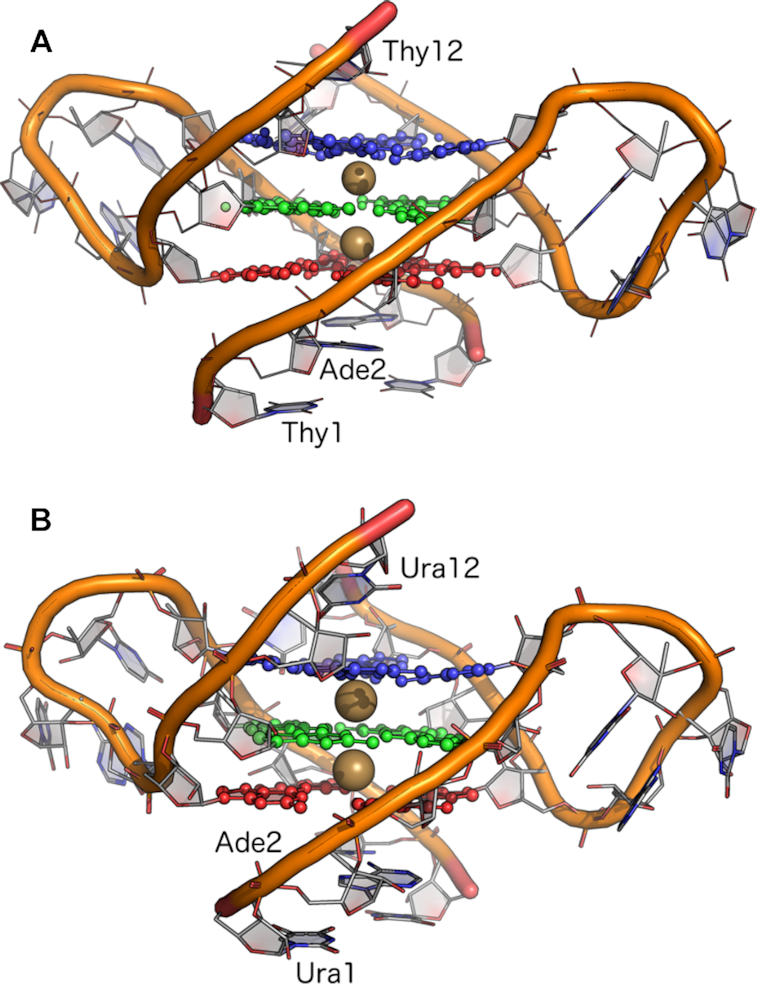
Rendering of the crystal structures of the (A) telomeric DNA GQ from PDB entry 1K8P (17) and (B) TERRA GQ from PDB entry 3IBK (29). Nucleobase atoms in guanine tetrads 1 (red, Gua3 and Gua9 in each oligonucleotide strand), 2 (green, Gua4 and Gua10), and 3 (blue, Gua5 and Gua11) are shown in ball-and-stick. The two K⁺ ions coordinated along the tetrad axis are shown as gold spheres. The 5′-3′ sense of the oligonucleotide strands is indicated by the labeling of Thy1/Ura1, Ade2 and Thy12/Ura12.

Additive MD simulations

Following energy minimization, three independent simulations were initiated to equilibrate each GQ system by assigning different, random velocities to each atom. Equilibration was performed under an NPT ensemble at 298 K and 1 atm of pressure in NAMD (58). Harmonic restraints were applied to all non-hydrogen atoms in the GQs and the bound K⁺ ions in each structure, with a force constant of 5.0 kcal mol⁻¹ Å⁻². Water molecules and bulk ions were free to move during equilibration. Temperature was maintained via a Langevin thermostat with a friction coefficient of 5.0 ps⁻¹. Pressure was regulated using a Langevin piston (59) with a decay time of 100 fs and an oscillation period of 200 fs. Short-range Lennard-Jones forces were switched smoothly to zero from 10 to 12 Å. Electrostatic forces were calculated with the particle mesh Ewald method (PME) (60), with a real-space cutoff of 12 Å. Nonbonded neighbor lists were maintained within 16 Å. Periodic boundary conditions were applied in all dimensions. Bonds to hydrogen atoms were constrained with SHAKE (61) and water molecules were kept rigid with SETTLE (62), allowing an integration time step of 2 fs.

The equilibration protocol yielded three separate systems for both the telomeric and TERRA GQs. Unrestrained MD simulations using the CHARMM36 force field were then carried out in OpenMM, version 7.1 (63), under the same NPT ensemble described above, except that temperature was regulated using the Andersen thermostat (64) with a collision frequency of 1.0 ps⁻¹, and pressure was maintained at 1 bar with a Monte Carlo barostat, attempting box scaling every 25 time steps. Production simulations were performed for 1 μs, saving coordinates every 10 ps for subsequent analysis.

Polarizable MD simulations

Drude systems were prepared by taking the equilibrated CHARMM36 coordinates and constructing Drude oscillators and lone pairs in CHARMM. Doing so also converted TIP3P water to the polarizable SWM4-NDP model (65). The Drude-2017 force field for DNA (45,46) and RNA (47) was applied to the GQs. Ion parameters were taken from Yu et al. (66) with specific nonbonded parameter modifications by Savelyev and MacKerell for interactions with nucleic acid moieties (67). After converting the GQ systems to the Drude model, the Drude oscillators were relaxed via energy minimization in CHARMM, employing 1000 steps of steepest descent minimization, followed by 2000 steps of adopted-basis Newton-Raphson minimization.

Drude systems were equilibrated in NAMD, using the extended Lagrangian integration scheme, implemented in NAMD as Langevin dynamics (68). The real atoms of the system were coupled to a thermostat at 298 K and the Drude oscillators were coupled to a low-temperature, relative thermostat at 1 K, thereby approximating the Born-Oppenheimer surface (38). The friction coefficients applied to real atoms and Drude oscillators were 5.0 and 20.0 ps⁻¹, respectively. Pressure was maintained at 1 atm using the same Langevin piston method described above. The short-range Lennard Jones potential was switched smoothly to zero from 10 to 12 Å. PME was employed to calculate electrostatic forces, with a real-space cutoff of 12 Å. Bonds to hydrogen were constrained via SHAKE (61) and SWM4-NDP water molecules were kept rigid with SETTLE (62). A ‘hard wall’ constraint (69) was enforced at 0.2 Å to prevent polarization catastrophe. The integration time step was set to 1 fs and equilibration was performed for 1 ns. As in the CHARMM36 simulations, non-hydrogen GQ atoms and bound K⁺ ions were harmonically restrained with a force constant of 5.0 kcal mol⁻¹ Å⁻².

Production MD simulations for Drude systems were carried out in OpenMM, which has recently been extended to perform extended Lagrangian integration for Drude polarizable systems (70). The same NPT ensemble was maintained as in equilibration using dual Langevin thermostats, but pressure was regulated at 1 bar using a Monte Carlo barostat, attempting box scaling every 25 integration steps. Production MD simulations were performed for 1 μs, saving coordinates every 10 ps. Simulation performance is given in Supplementary Table S1.

Single-stranded DNA and RNA simulations

One of the goals of this study was an examination of nucleobase dipole moments as a function of oligonucleotide conformation. While reference data for nucleobase dipole moments from duplex DNA and RNA are available from previous simulations using the Drude-2017 force field (45–47), a comparison to nucleobase properties in single-strand oligonucleotides is also appropriate, particularly since most cellular RNA is single-stranded. To this end, a single oligonucleotide chain was taken from each of the GQ crystal structures and solvated as described above in a cubic box with 150 mM KCl. Bound K⁺ ions from the crystal structure were not retained; the only ions present in the simulations were in bulk solution. After an initial 1-ns NPT equilibration using the CHARMM36 force field as described above, each system was heated to 500 K and simulated for 100 ns under an NVT ensemble to denature the GQ oligonucleotide strand. The snapshot with the largest radius of gyration in each system was converted to the Drude-2017 model in CHARMM, equilibrated for 1 ns under an NPT ensemble as described above, and unrestrained simulations were performed for 1 μs in OpenMM at 298 K.

RESULTS AND DISCUSSION

Stability of the G-Quadruplexes with CHARMM36 and Drude-2017

GQ structures are challenging to model using empirical force fields because they are stabilized by interactions that differ from canonical nucleic acids, and GQ backbone structures often adopt noncanonical conformations. As such, the appropriateness of the force field used for the simulation is an essential first step in interpreting MD simulation outcomes for GQs. We previously demonstrated that the polarizable Drude-2017 force field is superior to the nonpolarizable CHARMM36 in the case of the unimolecular c-kit1 GQ (48), but given the relatively recent introduction of Drude-2017, it is important to assess its ability to model other GQs accurately. Here, we began by investigating the stability of each GQ fold in terms of its deviation from published structures, noncanonical base pairing above and below the tetrad core, and the conformational ensemble of the loops that connect the tetrad core. A full description of the analyses that were performed is given in the Supplementary Information but will be briefly summarized here. The root-mean-square deviation (RMSD) of each structure was slightly lower with Drude-2017 than CHARMM36 (Supplementary Tables S2 and S3), indicating that the Drude-2017 force field produced ensembles that were more consistent with experimental structures. The greatest deviations were in the loop nucleotides (Supplementary Figure S1), which is reasonable given that the crystal structures are influenced by extensive crystal packing effects that induce intramolecular base stacking (Supplementary Figures S2 and S3). A previous MD simulation study by Islam et al. noted that these propeller loops rapidly disordered with the AMBER force field (30), and the NMR structure of the TERRA GQ shows no ordered base stacking (71). Backbone and glycosidic dihedral sampling was similar between the two force fields, though the Drude-2017 model yielded improved agreement with the experimental structures in a few instances (Supplementary Figures S4 and S5). One notable difference between the force fields was their ability to retain the K⁺ ions coordinated in the tetrad stem. In each of the CHARMM36 simulations, one K⁺ ion was expelled from the stem within 30 ns (Supplementary Figure S6). Thus, the CHARMM36 simulations suffer from a defect in ion retention that undermines confidence in their results. Thus, in this work, we will focus on the results of the Drude-2017 simulations, which retained both coordinated K⁺ ions, and will make comparisons to CHARMM36 outcomes only when relevant in the context of understanding important differences that arose in the polarizable simulations.

2′-Hydroxyl dihedral sampling and water properties in GQ grooves

Nucleic acids bind water molecules in their grooves, and those bound in the minor groove are highly structured (72–76). In RNA, the 2′-hydroxyl groups contribute to this organization as a function of the conformations they adopt (77). Given the relationship between 2′-hydroxyl dynamics and water structure, we analyzed the conformational sampling of the TERRA GQ 2′-hydroxyl groups along with the structure and dipole properties of water molecules in the GQ grooves, which are formed at the interface of the 5′-terminal nucleotides (U₁A₂G₃G₄) of one chain and the 3′-terminal nucleotides (G₉G₁₀G₁₁U₁₂) of the other chain. For the telomeric DNA GQ, since there are no 2′-hydroxyl groups, we analyzed only the structure and dipole properties of the groove water molecules and compared those features to the TERRA GQ, as crystallographic evidence suggests that the extent of structuring induced by each GQ is different (29).

In RNA, the 2′-hydroxyl group primarily samples one of three orientations, as characterized by the C1′-C2′-O2′-H2′ dihedral angle: base (60–120°), O3′ (190–270°), and O4′ (280–330°) (77). The nomenclature of these orientations derives from the atom or moiety to which the 2′-hydroxyl hydrogen (H2′) points. In the base orientation, which is the dominant mode in canonical, duplex A-RNA, the 2′-hydroxyl group engages in a water-mediated hydrogen bond to a nitrogen atom in the nucleobase. Such positioning imposes rigidity on the structure and promotes the organization of water molecules in the broad, minor groove (77). The O3′ and O4′ orientations are associated with flexibility; with the 2′-hydroxyl group having moved away from the base and liberating the water molecule that was hydrogen-bonded to the nucleobase, the RNA becomes more flexible.

The results of the 2′-hydroxyl dihedral analysis are shown in Figure 2. In the Drude-2017 simulations, the 2′-hydroxyl groups of the TERRA GQ primarily sampled base orientations at the higher end of the range (∼120°) and occasionally sampled orientations that fell between the base and O3′ regions. Persistence of base sampling agrees well with the prevalence of canonical backbone dihedral conformations throughout the GQ structure (Supplementary Figure S5) and also suggests the structure is fairly rigid. In the CHARMM36 simulations, the 2′-hydroxyl groups tended to sample orientations between base and O3′, particularly among the first four nucleotides, which form one face of each groove between the two oligonucleotide chains. The 2′-hydroxyl orientations adopted by nucleotides 5–12 were similar between both force fields, given the magnitudes of the error estimates in these quantities (Figure 2).

Figure 2.

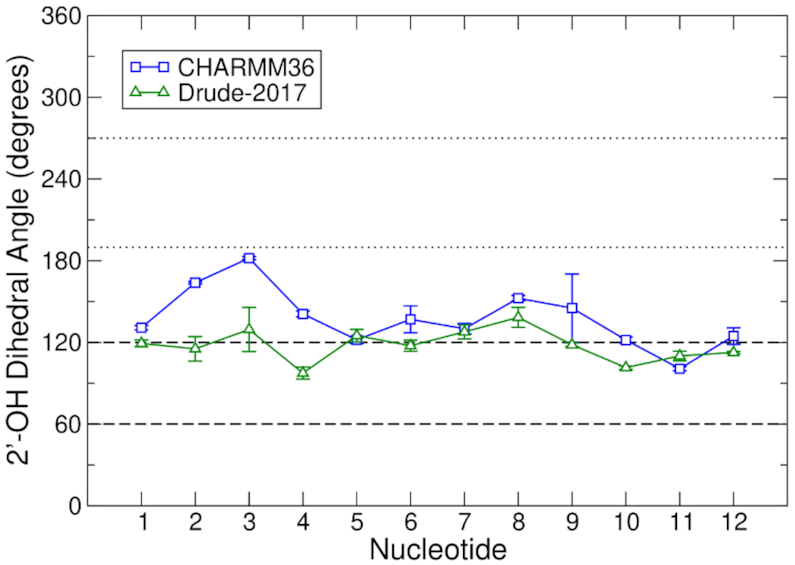
2′-Hydroxyl sampling in the TERRA GQ for CHARMM36 and Drude-2017. Data from the simulations are the averages of the three pooled replicates. Error bars represent the root-mean-square fluctuation of the combined time series. Horizontal, dashed and dotted lines represent the boundaries of base (60–120°) and O3′ (190–270°) orientations of the 2′-hydroxyl group, respectively, as characterized by the C1′-C2′-O2′-H2′ dihedral.

Intramolecular hydrogen bonding between the 2′-hydroxyl group of nucleotide n to the O4′ atom of nucleotide n+1 has been proposed as a mechanism by which fewer water molecules are coordinated in the groove of the TERRA GQ relative to the telomeric DNA GQ (29). To assess this possibility, we defined a hydrogen bond between consecutive nucleotides as having an O2′_n-O4′_n+1 distance of ≤3.5 Å and an O2′_n-H2′_n-O4′_n+1 angle of ≥150°. This analysis was performed only for groove-defining nucleotides (U₁A₂G₃G₄ of one chain and G₉G₁₀G₁₁U₁₂ of the other chain). In the CHARMM36 simulations, 21.6% of all the 2′-hydroxyl configurations exhibited such hydrogen bonding. In contrast, in the Drude-2017 simulations, the existence of such hydrogen bonds was only 9.8%. This outcome is likely related to the tendency of the Drude-2017 2′-hydroxyl groups to favor base orientations (Figure 2), thus occupying the 2′-hydroxyl group with other interactions instead of hydrogen bonding to the O4′ atom of the next nucleotide in the chain. Regardless, neither force field predicted prevalent hydrogen bonding between consecutive nucleotides in the same chain.

To characterize the structured waters in the grooves of each of the two GQs, we considered a water molecule to be bound in a groove if either of its hydrogen atoms satisfied the standard cutoff distance for a hydrogen bond with any acceptor atom (2.4 Å) (78) of the groove-defining nucleotides of both oligonucleotide chains, simultaneously. An angular criterion was not imposed, as structured water molecules in nucleic acid grooves may engage in a complex network of interactions. As such, it was not appropriate to enforce a specific, ideal geometry for hydrogen bonding; counting water molecules in contact with both grooves was sufficient for this analysis and water molecules that were identified were visually confirmed as residing in the grooves to verify the integrity of the approach. Additionally, we calculated the number of water molecules that bridged other water molecules via hydrogen bonding. The water molecules that satisfied either of these criteria were considered those that were structured in the grooves of the two GQs.

In our simulations, the grooves of both GQs were hydrated to similar extents using both force fields. Analysis of the 1K8P and 3IBK crystal structures by Collie et al. suggested that the TERRA GQ grooves coordinated fewer water molecules (6 per groove, 12 total) than the telomeric DNA GQ (9 per groove, 18 total), a behavior that was attributed to intramolecular 2′-hydroxyl hydrogen bonding in the TERRA GQ (29). As noted above, we observed few such hydrogen bonds. Consequently, the hydration of the DNA and RNA grooves was similar. With CHARMM36, the TERRA GQ accumulated three more water molecules (14 ± 3) than the telomeric DNA GQ (11 ± 3), though this difference is within error. With Drude-2017, the difference was even smaller, with only one additional water molecule in the TERRA GQ (13 ± 3) relative to the telomeric DNA GQ (12 ± 3). These findings suggest that both force fields predict similar groove hydration, though the difference between DNA and RNA was slightly smaller with Drude-2017 than with CHARMM36. The difference in hydration is smaller than what is observed in the case of duplex DNA and RNA melting; RNA duplexes are hydrated by one additional water molecule per nucleotide relative to DNA (74). Each GQ groove was defined by four base-pairs, so the increase in hydration in the TERRA GQ versus the telomeric DNA GQ was less pronounced than in the case of duplexes.

Finally, we examined the dipole properties of water molecules bound in GQ grooves. Previous work on duplex DNA suggests that confinement of water molecules in the major and minor grooves of these canonical structures imposes different dipole properties (41). Given the unique topologies of GQs, an examination of this behavior is appropriate here to understand if structuring of these water molecules induces changes to water molecular dipole moments that contribute to the stabilization of the GQ folds via perturbations in the local electric field. This analysis was only carried out for the Drude-2017 simulations, as in the CHARMM36 simulations, the rigid TIP3P water model was employed. By definition, the TIP3P dipole moment (2.35 D) cannot vary. In both of the GQ structures, groove waters had dipole moments that were identical to those of bulk water, 2.46 D for bulk SWM4-NDP water (65). In the telomeric DNA GQ, water molecules had an average dipole moment of 2.46 ± 0.16 D whereas in the TERRA GQ, the average was 2.44 ± 0.15 D. Thus, binding of water molecules in these GQ grooves does not perturb the electronic structure of water.

Sugar puckering dynamics

Examination of sugar puckering dynamics in the GQ simulations revealed an important difference in the outcomes of the CHARMM36 and Drude-2017 simulations. For the telomeric DNA GQ, the magnitude of the sugar puckering pseudorotation angle was systematically higher in the Drude-2017 simulations than the CHARMM36 simulations, with the exception of the 3′-terminal Thy12 (Figure 3A). The crystal structure (PDB 1K8P) is dominated by South/C2′-endo conformations of the sugars, with the exceptions of Thy1 and Thy7 (Figure 3A), both of which are in the North pucker region. Neither force field sampled these North conformations during the MD simulations. The remaining nucleotides sampled South pucker conformations, in agreement with the experimental values, though the pseudorotation angles in the Drude-2017 simulations were generally in better quantitative agreement than those produced by CHARMM36.

Figure 3.

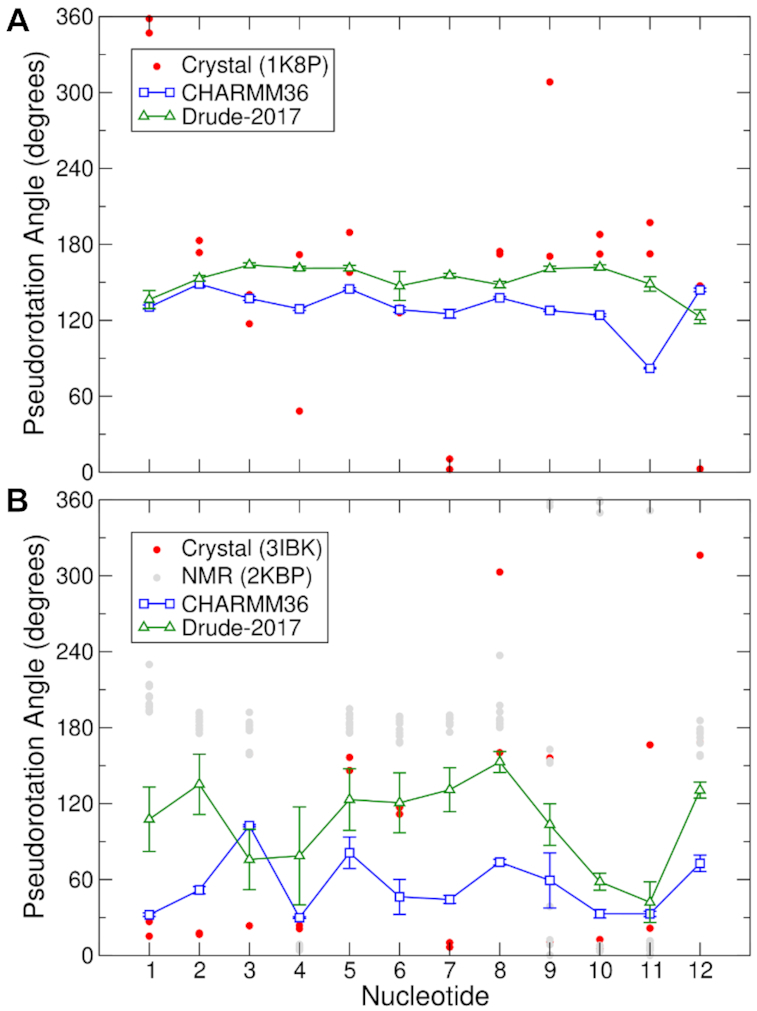
Sugar pucker in (A) the telomeric DNA GQ and (B) TERRA GQ. Data for CHARMM36 and Drude-2017 reflect the average values from the pooled trajectories, with error bars representing the root-mean-square fluctuation of the combined time series.

In the TERRA GQ, sugar puckering differs between the crystal structure (PDB 3IBK) and the NMR ensemble (PDB 2KBP), similar to what was observed in the context of backbone dihedral angles (Supplementary Figure S5). Whereas North/C3′-endo sugar puckering dominates in the crystal structure as is typical for RNA, the NMR ensemble reflects considerable sampling of South/high-South (C2′-endo/C3′-exo) sugar puckering, particularly in tetrad guanines 3 and 5, as well as the U₆U₇A₈ loop (Figure 3B). Here, the CHARMM36 and Drude-2017 force fields produced very different results. With CHARMM36, North/C3′-endo puckering dominated, except in the case of Gua3, which sampled O4′-endo and C1′-exo states. In the Drude-2017 simulations, the TERRA GQ sugars sampled more C1′-exo and C2′-endo states, in better agreement with the NMR ensemble, as well as Gua5, Ura6 and Ade8 in the crystal structure, which were primarily C2′-endo in the simulations. The accuracy of Ura7 sugar puckering is difficult to determine, as the Drude-2017 simulations are in reasonable agreement with the NMR ensemble (C1′-exo and C2′-endo) while the CHARMM36 simulations agree better with the crystal (C3′-endo) at this position. As noted above, the RMSD of tetrad guanine nucleotides in the Drude-2017 simulation ensemble was larger than that of CHARMM36 (Supplementary Table S3) as a result of using the 3IBK crystal structure as a reference, since the sugar puckering behavior is very different from the crystal structure.

Ultimately, given the discrepancies in sugar puckering between the experimental methods for the TERRA GQ, it is difficult to determine which force field is more accurate in this regard. Both force fields produce sugar puckering pseudorotation angles that fall within the range of values observed in the crystal structure and NMR ensemble, though Drude-2017 is clearly superior for Gua5 and the UUA propeller loop, the dynamics of which are important for the stability of the GQ fold. It is important to note that the Drude-2017 force field is not biased towards South puckering in RNA. Analysis of duplex RNA structures simulated as part of the Drude-2017 RNA force field validation shows that the expected canonical North puckering dominates (Supplementary Figure S7). We also previously demonstrated the agreement of RNA sugar puckering with NMR experiments on a duplex RNA with a G•A mismatch and a stem-loop structure (47). In those systems, the conformational sampling of both North and South pucker was in good agreement, indicating robust performance of Drude-2017 in this regard. Thus, the polarizable model may represent an important improvement in the representation of sugar puckering dynamics, particularly in simulations of RNA.

Ion interactions

A persistent challenge in the simulation of GQs is accurate modeling of ion-ion and ion-GQ interactions. A previous QM study concluded that explicit electronic polarization is required to correctly model the ion-ion interactions that occur along GQ stems (32). Indeed, extensive MD simulations of GQ systems have found that ion retention in GQ stems is generally not modeled correctly (33,34), such that ions are expelled from the GQ stem with subsequent structural distortion. Some studies have reported that ions remain stably bound with careful choice of water model and ion parameters (36) or by reparametrizing nucleobase partial charges to implicitly polarize the force field (34).

To examine the interactions of K⁺ ions with the telomeric DNA and TERRA GQs, we analyzed the interatomic distance between the two structured K⁺ ions, the spatial distribution of K⁺ ions around the GQs, and computed volume Jacobian-normalized radial distribution functions (RDFs) around the GQs to describe the ion atmosphere around each structure. In the Drude-2017 simulations, both the telomeric DNA and TERRA GQs retained both of their structured ions over the entirety of each 1-μs simulation. For the telomeric DNA GQ, the average inter-K⁺ distance was 3.6 ± 0.2 Å, and for the TERRA GQ, this distance was 3.5 ± 0.2 Å. These results demonstrate that the polarizable force field more accurately models ion retention in the GQ stem, unlike simulations with the CHARMM36 force field, in which one K⁺ ion was rapidly expelled in each simulation (Supplementary Figure S6).

To further characterize the sampling of ions around the GQs, we computed occupancy maps over the GQ surfaces. To do so, for each frame in the trajectory, the simulation box was divided into a grid with 1-Å spacing in all three spatial dimensions. Each K⁺ ion (including both bulk and structured ions) was assigned to the nearest grid point. The results of this analysis are presented in Figure 4 for the telomeric DNA GQ and in Figure 5 for the TERRA GQ. The occupancy maps are shown with an isosurface cutoff value of 1% occupancy, meaning that an ion was present in those regions of space for ≥1% of the trajectory. Even with such a low threshold, discrete regions of K⁺ sampling are obvious in both systems, suggesting highly specific binding, rather than diffuse, nonspecific sampling over the GQ surfaces.

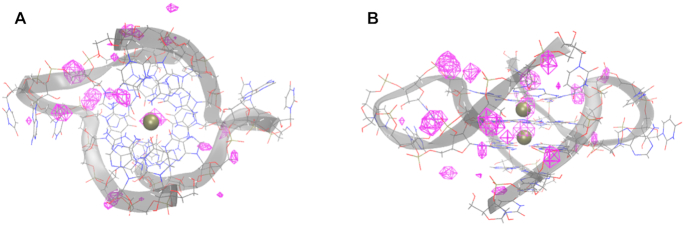
Figure 4.

K⁺ occupancy maps around the telomeric DNA GQ in the Drude-2017 simulations. (A) View along the GQ tetrad axis. (B) Side view. The crystal structure of the DNA GQ is shown as lines and colored by element, with a cartoon overlay of the backbone to illustrate the fold. Crystallographic K⁺ ions are shown as gold spheres.

Figure 5.

K⁺ occupancy maps around the TERRA GQ in the Drude-2017 simulations. (A) View along the GQ tetrad axis. (B) Side view. The crystal structure of the TERRA GQ is shown as lines and colored by element, with a cartoon overlay of the backbone to illustrate the fold. Crystallographic K⁺ ions are shown as gold spheres.

In the Drude-2017 simulations of the telomeric DNA GQ, both structured K⁺ ions were retained and bulk K⁺ ions tended to only sample the regions above and below the tetrad stem (Figure 4). As such, we investigated the binding of bulk K⁺ ions to the outer faces of tetrads 1 and 3 in the Drude-2017 simulations. A bulk K⁺ ion was considered aligned if it fell within the distance range sampled by the structured ions already in the GQ stem (3.6 ± 0.2 Å). That is, if a bulk K⁺ ion was within 3.8 Å of a structured K⁺ ion, it was considered coordinated. From this analysis, we found that a bulk K⁺ ion was aligned above tetrad 3 in 18.5% of all trajectory frames, and a bulk K⁺ ion was aligned below tetrad 1 in 14.4% of all frames. In 2.5% of all frames, ions were simultaneously in both locations such that four K⁺ ions were coordinated to the telomeric DNA GQ stem. Coordination of additional ions from the bulk solution was aided by Thy12 bases via their O2 and O4 atoms, and by Ade2 bases via their N1 atoms. Reversible binding of K⁺ to Thy12 was observed in all three replicate simulations, but binding to Ade2 was observed in only one simulation. In our Drude-2017 simulations, Thy1 bases from each strand were only weakly hydrogen-bonded, base-pairing for only 25.1% of the total simulation time (Supplementary Figure S8). Ade2 bases from each strand engaged in strong N6-N1 hydrogen bonding; these interactions were formed in 95.5% of trajectory frames. In the few instances in which these interactions were broken, a K⁺ ion could bind to N1 of both Ade2 and was subsequently sandwiched between the outer face of tetrad 1 (interacting with guanine O6 atoms) after the Ade2 bases re-formed their hydrogen bonds. Thy12 from each strand in the bimolecular GQ were base-paired 50.4% of the time (Supplementary Figure S9), equally occluding the open face of tetrad 3 from ion binding and opening to allow for ion binding.

As with the telomeric DNA GQ, we investigated the binding of bulk K⁺ ions to the TERRA GQ, considering bulk ions to be aligned if they fell within 3.7 Å of a structured ion (based on the average interatomic distance between structured K⁺ of 3.5 ± 0.2 Å). The results in this system were different from the telomeric DNA GQ. For the TERRA GQ systems, bulk K⁺ ions showed a strong preference for occupancy above tetrad 3 (68.6% of all frames), and only 0.8% occupancy below tetrad 1 (Figure 5B). Given this asymmetric occupancy, the simultaneous alignment of two bulk K⁺ ions was only observed in 0.5% of all frames, lower than in the case of the telomeric DNA GQ. The persistence of K⁺ ions above tetrad 3 is due to the absence of hydrogen bonding between Ura12 in opposing strands in the TERRA GQ. Unlike in the telomeric DNA GQ, in which inter-strand Thy12 hydrogen bonding occurred in half the simulation frames, Ura12 never formed hydrogen bonds between strands in any of our simulations (Supplementary Figure S9), exposing O2 and O4 atoms to bulk K⁺ ions and helping to coordinate them along the GQ stem. This phenomenon was observed in all three replicate simulations of the TERRA GQ. In contrast, the near absence of K⁺ ions below tetrad 1 in the TERRA GQ is due to strong hydrogen bonding between Ura1 in each oligonucleotide strand (Supplementary Figure S8), with hydrogen bonds formed 63.6% of the simulation time. Additionally, Ade2-Ade2 hydrogen bonding was observed less frequently in the TERRA GQ as compared to the telomeric DNA GQ, only forming N6-N1 hydrogen bonds in 58.9% of all simulation frames. Whereas Thy1–Thy1 hydrogen bonding was comparatively weak in the telomeric DNA GQ, allowing for ions to sample close to Ade2, in the TERRA GQ, Ura1–Ura1 hydrogen bonding was stronger, occluding this space. Additionally, the lower tendency of Ade2 to form hydrogen bonds in the TERRA GQ precluded the formation of an organized complex to which K⁺ ions could bind. Thus, the binding of ions to the telomeric and TERRA GQs is intrinsically different, in part, as a function of different properties of the constituent bases and their propensities to engage in non-canonical hydrogen bonding interactions.

In addition to this bulk K⁺ ion coordination, the TERRA GQ bound a greater number of ions than the telomeric DNA GQ. To quantify the extra accumulation of ions around each of the GQs, we computed volume Jacobian-normalized RDFs. This technique has been successfully applied in previous studies of ion accumulation and competition around duplex DNA with the Drude force field (42,67). To distinguish bulk ions from those bound to the nucleic acid, a very large system size is necessary. The simulations performed here were not conducted in such large simulation boxes, so it is not possible to quantitatively describe the ionic atmosphere around the GQs. Instead, we provide a qualitative assessment. The volume Jacobian-normalized RDFs for the telomeric DNA and TERRA GQs using the Drude-2017 force field are shown in Supplementary Figure S10. The RDFs indicate that the TERRA GQ accumulates many more ions than the telomeric DNA GQ, consistent with the observations from the ion maps in Figures 4 and 5. A recent study by Gebala and Herschlag found that RNA duplexes accumulate cations more readily than DNA duplexes of equivalent length and composition due to a stronger electrostatic field (79); our results suggest that this property extends to GQs.

Nucleobase dipole moments and K⁺ interaction energies

To form bimolecular GQs, each strand of the structure must exist as a single-stranded oligonucleotide, at least transiently. As such, it is interesting to investigate the nucleobase dipole moments as a function of existence in duplex DNA or RNA, single-stranded GQ sequences, and in the GQs themselves. The nucleobase dipole moment data for duplex DNA and RNA are from previous simulations performed as part of the validation of the Drude-2017 force field (45–47). The ssDNA and ssRNA data are from 1-μs simulations performed here as described in the Materials and Methods. Results of this analysis are shown in Figure 6 for Ade, Thy, and Ura. Guanine bases were analyzed separately and are discussed below.

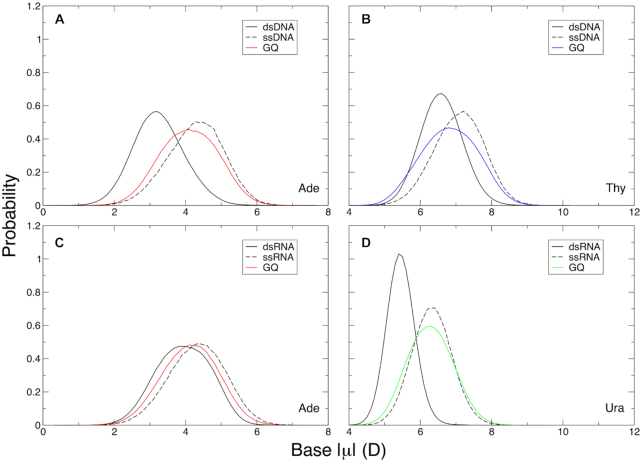
Figure 6.

Adenine, thymine, and uracil base dipole moments relative to duplex and single-stranded DNA and RNA. (A) Adenine in the telomeric DNA GQ, (B) thymine in the telomeric DNA GQ, (C) adenine in the TERRA GQ, and (D) uracil in the TERRA GQ. In panels (A) and (B), dsDNA dipole moments were computed from 1-μs MD simulations of the six duplex, B-DNA structures used in the validation of the Drude-2017 force field (45,46). In panels (C) and (D), the dsRNA dipole moments were calculated from 1-μs MD simulations of two duplex, A-RNA structures used in the validation of the Drude-2017 force field (47). Dipole moments in ssDNA and ssRNA were calculated from 1-μs trajectories of a single strand of the telomeric DNA and TERRA GQ, respectively (see Materials and Methods).

Adeine bases in both GQs had similar properties, with an average base dipole moment of 4.1 ± 0.8 D, falling between duplex and single-stranded DNA and RNA (Figure 6A). Adenine bases in both the ssDNA and ssRNA simulations had the same average dipole moments (4.3 ± 0.8 D). Interestingly, adenine base dipole moments in dsDNA and dsRNA were different 3.2 ± 0.7 D in DNA and 3.9 ± 0.8 D in RNA. Thus, adenine bases in GQs have properties similar to those found in single-stranded oligonucleotides, but the change in polarization response differs based on the nature of the nucleic acid. In DNA, the electronic structure of adenine bases changes more dramatically (Δ|μ| = 0.9 D) than in RNA (Δ|μ| = 0.2 D). These observations suggest that conformational changes between duplex, single-stranded, and GQ forms of a given oligonucleotide sequence may impact adenine bases differently depending on whether the sequence is DNA or RNA. Intrinsic differences in nucleobase properties in duplex DNA and RNA are beyond the scope of this work but will be explored in greater depth in future studies.

As with adenine, the dipole moments of thymine bases were different in dsDNA and ssDNA (6.6 ± 0.6 and 7.0 ± 0.7 D, respectively) and the thymine bases in the telomeric DNA GQ fell between these two values (6.8 ± 0.8 D). The GQ thymine bases had different properties depending on their position within the GQ. These data are summarized in Table 1. While Thy1 and Thy6 had base dipole moments that reflected the average over all thymine bases, Thy7 in the T₆T₇A₈ propeller loop had an elevated dipole moment and Thy12, which engaged in hydrogen bonding throughout the majority of the frames in the simulations, had a much lower base dipole moment. The Thy12 dipole moment was lower than both the dsDNA and ssDNA values, suggesting that non-canonical base-pairing depolarizes the base relative to canonical Watson-Crick A:T pairing or solvent exposure. The elevated base dipole moment of Thy7 is a result of being largely solvent-exposed during the simulations and occasionally interacting with K⁺ ions.

Table 1.

Thymine and uracil base dipole moments (D) as a function of nucleotide position in the telomeric DNA and TERRA GQs. Shown are the averages over the replicate simulations, with the error bars representing the root-mean-square fluctuations of the pooled time series.

Nucleotide	Telomeric DNA (Thy)	TERRA (Ura)
1	6.9 ± 0.7	6.0 ± 0.6
6	6.9 ± 0.7	6.4 ± 0.6
7	7.2 ± 0.7	6.4 ± 0.6
12	6.2 ± 0.7	6.4 ± 0.7

Uracil bases generally had lower dipole moments than thymine bases. In dsRNA and ssRNA, the average uracil base dipole moments were 5.5 ± 0.4 D and 6.3 ± 0.6 D, respectively. Thus, both thymine and uracil manifest higher base dipole moments upon transitioning from duplex to single-stranded states. We observed a similar phenomenon in DNA base-flipping of thymine (44), though the change in base dipole moment in that context was much larger (∼1.5 D), likely as a function of proximity to the negatively charged phosphodiester backbone in the flipped state. Nevertheless, it appears that an increase in base dipole moment upon transition from Watson-Crick to extrahelical or single-stranded forms triggers a pronounced increase in base dipole moment in thymine and uracil. In the TERRA GQ, uracil bases had an average base dipole moment of 6.3 ± 0.6 D, and a per-nucleotide analysis of this quantity revealed that most of the bases had dipole moments around this average, unlike in the case of thymine, which was more variable as a function of nucleotide position (Table 1). Ura1 had a slightly lower base dipole moment than the other three uracil bases, which may be a function of noncanonical base-pairing as we propose with Thy12 in the telomeric DNA GQ.

In our previous simulations of the c-kit1 DNA GQ (48), we observed that guanine base dipole moments varied as a function of their position along the GQ stem and their interaction with a third K⁺ ion that bound to the outer face of one tetrad. As such, we explored the same behavior here. Guanine base dipole moment distributions are plotted in Figure 7 and listed in Table 2. Interestingly, guanine bases in duplex DNA and RNA had different dipole moments, with bases in DNA more polarized than those in RNA (Table 2), the opposite of what was observed in the case of adenine (see above). However, guanine bases in both ssDNA and ssRNA had the same average dipole moment of 8.7 D. All tetrad base dipole moments were larger than this single-stranded value, indicating that the guanine bases polarize upon dimerization of the oligonucleotides that comprise the telomeric DNA and TERRA GQs.

Figure 7.

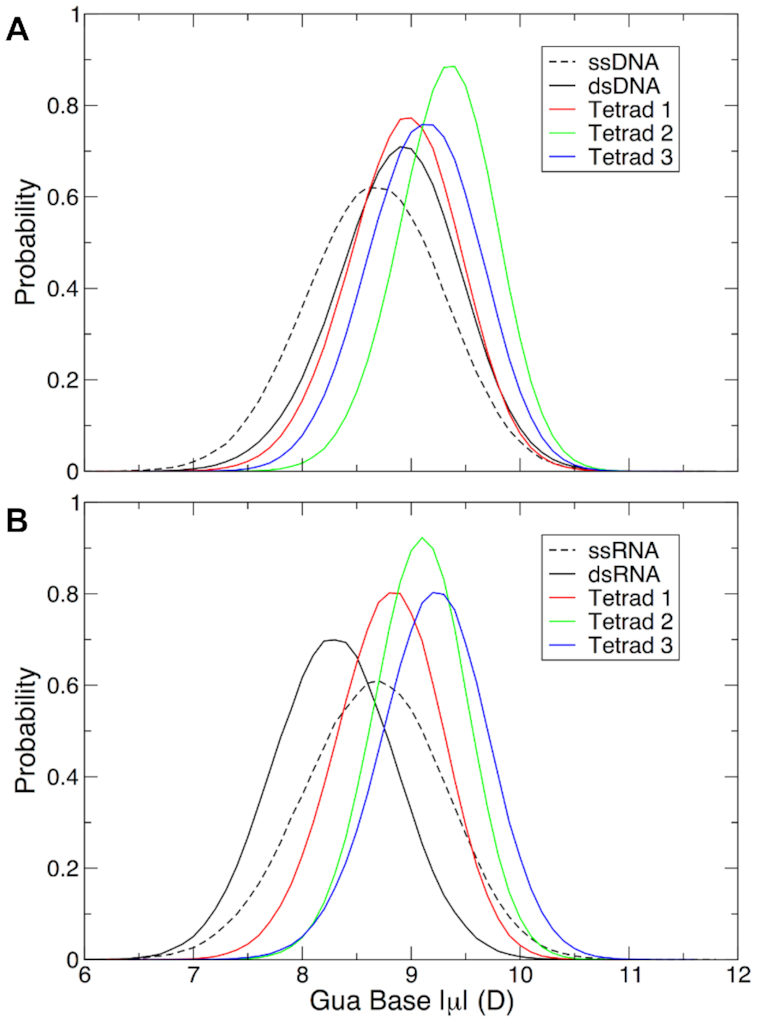
Guanine base dipole moments in each of the three tetrads in (A) the telomeric DNA GQ and (B) the TERRA GQ relative to duplex and single-stranded DNA and RNA. Values of guanine base dipole moments in dsDNA and dsRNA in panels (A) and (B) were calculated from trajectories in the six B-DNA duplexes (45,46) and the two A-RNA duplexes (47) simulated in the validation of the Drude-2017 force field. Dipole moments in ssDNA and ssRNA were calculated from 1-μs trajectories of a single strand of the telomeric DNA and TERRA GQ, respectively (see Materials and Methods).

Table 2.

Guanine base dipole moments (D) in DNA and RNA. ‘Duplex’ values come from canonical B-DNA and A-RNA duplexes simulated previously (45–47). ‘Single-stranded’ refers to a single strand of the telomeric DNA and TERRA GQ structures modeled here. GQ tetrads 1, 2, and 3 are the guanine bases in each specified tetrad in the telomeric DNA and TERRA GQs. Error bars are the root-mean-square fluctuations of the respective time series.

	DNA	RNA
Duplex	8.9 ± 0.6	8.3 ± 0.6
Single-stranded	8.7 ± 0.6	8.7 ± 0.7
GQ tetrad 1	8.9 ± 0.5	8.8 ± 0.5
GQ tetrad 2	9.3 ± 0.5	9.1 ± 0.4
GQ tetrad 3	9.1 ± 0.5	9.2 ± 0.5

In the telomeric DNA GQ, guanine bases in tetrad 2 had the largest base dipole moments (Figure 7 and Table 2). We attribute this behavior to the fact that these bases always interacted with two K⁺ ions (the structured ions in the GQ stem). Tetrads 1 and 3 were slightly less polarized than tetrad 2, reflecting the fact that these bases always coordinated one K⁺ ion each, and each tetrad infrequently interacted with an additional K⁺ ion from the bulk solvent. Binding of a bulk ion to tetrad 3 was observed slightly more frequently than binding to tetrad 1 (see above), a phenomenon that is reflected in the base dipole moments, with tetrad 3 guanine bases being slightly more polarized than those of tetrad 1, but still lower than those of tetrad 2. This behavior is similar to what we observed in the case of the c-kit1 promoter GQ, which had only one binding site for a bulk ion, leading to a similar pattern of tetrad base dipole moments (48).

The guanine base dipole moments in the TERRA GQ showed different behavior from those in the telomeric DNA GQ. In contrast to the DNA GQ, in the TERRA GQ, guanine bases in tetrad 3 were the most polarized, though their dipole moments were only ∼0.1 D larger than those of tetrad 2. While tetrad 2 bases always coordinated two K⁺ ions and tetrad 3 frequently coordinated a third ion to the GQ stem (see above), we attribute this property to the base dipole moments of Ura12 and the greater solvent accessibility of this site. Whereas in the telomeric DNA GQ, Thy12 had the lowest dipole moment of each of the thymine bases in the structure (Table 2),n the TERRA GQ, Ura12 had a larger dipole moment, the only such instance in which the dipole moment of a uracil base was greater than that of the thymine base at the same position in the oligonucleotide chain. The combination of a more polarized base and greater solvent accessibility combined for greater ion occupancy above tetrad 3 and larger dipole moments for these guanine bases. Tetrad 1 infrequently bound a bulk K⁺ ion, so the constituent base dipole moments were the lowest of any tetrad (DNA or RNA) simulated here.

To examine the energetic implications of bulk K⁺ ion binding to the GQ stems, we calculated the nonbonded interaction energy (E_int) between the two structured K⁺ ions as a function of the number of ions bound to the GQ stem. Interaction energy is the nonbonded potential energy (sum of van der Waals and electrostatic interactions) between two defined species, and reflects the energy required to bring the two species to a defined geometry from an infinite distance (80). We computed this E_int directly from the trajectory snapshots saved in the simulations (‘with solvent’) and after removal of solvent and subsequent dipole relaxation via reoptimization of Drude oscillator positions. The latter quantity was computed by holding the positions of the GQ atoms and ions fixed and allowing the Drude oscillators to relax via energy minimization. Doing so allows us to (i) determine how ion binding to the external faces of tetrads 1 and 3 influences the stability of structured ions via dipole-dipole interactions and (ii) directly quantify the multibody contribution of water to these E_int values. Results of this analysis are shown in Table 3 for the telomeric DNA GQ and in Table 4 for the TERRA GQ. Since the binding of a third K⁺ ion to each GQ can occur at one of two locations, results are presented throughout this section by breaking down these data into frames in which a K⁺ ion was coordinated below tetrad 1 or above tetrad 3. By doing so, it is possible to describe geometry-specific effects on the strength of ion coordination.

Table 3.

Interaction energies (E_int, kcal mol⁻¹) between the two coordinated K⁺ ions and the guanine bases in each tetrad of the telomeric DNA GQ in the Drude-2017 simulations. Each column represents the total number of K⁺ ions coordinated to the stem, with 2 K⁺ corresponding to only the ions between the tetrads, and 3 and 4 K⁺ indicating frames in which 1 or 2 bulk ions bound to the tetrad stem, respectively.

	With solvent			After in vacuo Drude reoptimization
	2 K+	3 K+	4 K+	2 K+	3 K+	4 K+
Tetrad 1	−28.7 ± 2.4	−35.0 ± 2.4a	−35.5 ± 2.8	−25.7 ± 2.8	−32.8 ± 3.3a	−33.9 ± 4.0
		−25.4 ± 4.3b			−22.1 ± 5.0b
Tetrad 2	−66.3 ± 3.6	−66.9 ± 4.5a	−69.1 ± 3.9	−62.5 ± 4.8	−64.2 ± 6.2a	−68.1 ± 6.8
		−66.5 ± 3.9b			−64.2 ± 5.5b
Tetrad 3	−33.8 ± 2.1	−32.9 ± 4.0a	−36.7 ± 3.5	−29.4 ± 2.6	−27.7 ± 5.1a	−33.7 ± 4.9
		−36.1 ± 3.1b			−32.7 ± 4.0b

^a E _int when the bulk ion was coordinated below tetrad 1.

^b E _int when the bulk ion was coordinated above tetrad 3.

Table 4.

Interaction energies (E_int, kcal mol^-1) between the two coordinated K⁺ ions and the guanine bases in each tetrad of the TERRA GQ in the Drude-2017 simulations. Each column represents the total number of K⁺ ions coordinated to the stem, with 2 K⁺ corresponding to only the ions between the tetrads, and 3 and 4 K⁺ indicating frames in which 1 or 2 bulk ions bound to the tetrad stem, respectively.

	With solvent			After in vacuo Drude reoptimization
	2 K+	3 K+	4 K+	2 K+	3 K+	4 K+
Tetrad 1	−32.5 ± 3.6	−37.3 ± 3.2a	−37.7 ± 3.3	−27.7 ± 4.0	−35.1 ± 4.0a	−35.7 ± 4.3
		−30.2 ± 4.7b			−25.3 ± 4.0b
Tetrad 2	−64.7 ± 3.9	−65.9 ± 3.9a	−67.7 ± 3.9	−60.8 ± 4.4	−64.0 ± 5.4a	−67.5 ± 5.9
		−63.6 ± 4.4b			−61.6 ± 5.0b
Tetrad 3	−31.7 ± 3.1	−29.8 ± 4.7a	−35.1 ± 3.3	−27.4 ± 4.0	−25.6 ± 6.1a	−33.4 ± 4.4
		−34.4 ± 3.1b			−32.0 ± 3.6b

^a E _int when the bulk ion was coordinated below tetrad 1.

^b E _int when the bulk ion was coordinated above tetrad 3.

In the case of the telomeric DNA GQ, coordination of a bulk K⁺ on either external face affected the E_int between the structured ions and tetrad 2 equivalently (Table 3). Unsurprisingly, E_int between the ions and tetrads 1 and 3 became more favorable when a bulk ion was coordinated by these respective tetrads. In contrast, the E_int with these tetrads became less favorable when an ion bound at the opposite tetrad; that is, interactions between structured ions and tetrad 1 became less favorable when a bulk ion was coordinated above tetrad 3, and vice versa (Table 5). E_int analysis on ‘with solvent’ snapshots in the TERRA GQ system (Table 4) revealed similar results to those of the telomeric DNA GQ, though it is notable that the magnitudes of E_int were smaller. We attribute these differences to the fact that the guanine bases in the TERRA and telomeric DNA GQ stems have different dipole moments (Table 2), thus different electronic structures that modulate permanent electrostatic and induced dipole interactions with the two structured K⁺ ions.

Table 5.

Differences in interaction energies (ΔE_int, kcal mol⁻¹) between ‘with solvent’ trajectory frames with 3 or 4 K⁺ ions bound and only 2 K⁺ ions bound in the GQ stems.

	Telomeric GQ		TERRA GQ
	3 K+	4 K+	3 K+	4 K+
Tetrad 1	−6.3 ± 3.4a	−6.8 ± 3.7	−4.8 ± 4.8a	−5.2 ± 4.9
	3.3 ± 4.9b		2.3 ± 5.9b
Tetrad 2	−0.6 ± 5.8a	−2.8 ± 5.3	−1.2 ± 5.5a	−3.0 ± 5.5
	−0.2 ± 5.3b		1.1 ± 5.9b
Tetrad 3	0.9 ± 4.5a	−2.9 ± 4.1	1.9 ± 5.6a	−3.4 ± 4.5
	−2.3 ± 3.7b		−2.7 ± 4.4b

^aΔE_int when the bulk ion was coordinated below tetrad 1.

^bΔE_int when the bulk ion was coordinated above tetrad 3.

As discussed above, the telomeric DNA GQ exhibited bulk K⁺ ion binding on the outer faces of tetrads 1 and 3 with roughly equal probability, whereas the TERRA GQ manifested a distinct asymmetry, strongly preferring K⁺ binding above tetrad 3. We assessed whether this directional preference was a result of ion-dipole and/or dipole-dipole interactions between K⁺ ions. ΔE_int values for snapshots with three or four K⁺ bound versus those with only the two K⁺ ions indicate that the structured ions became more strongly bound in the telomeric DNA GQ than in the TERRA GQ, suggesting a larger induced dipole effect. As such, the interactions among the K⁺ ions do not rationalize ion binding asymmetry. Instead, the intrinsic dynamics of the GQ structures must drive this ion binding preference. Stronger Thy12–Thy12 hydrogen bonding in the telomeric DNA GQ occluded the open face of tetrad 3 to a greater extent in the TERRA GQ, which lacked Ura12–Ura12 hydrogen bonding. The result in the TERRA GQ was simply that the open face of tetrad 3 was more sterically accessible to ion binding.

We previously observed that water modulated the values of ΔE_int in the c-kit1 GQ, screening the interactions of K⁺ ions with the guanine tetrads (48). That is, the ΔE_int values in vacuo (after Drude reoptimization in the absence of water) were of greater magnitude than those directly from the MD trajectory. Whereas the c-kit1 GQ only bound a third K⁺ ion at one location (on the outer face of tetrad 1 and coordinated by a thymine base), as we have discussed here, the telomeric DNA and TERRA GQs bound a third K⁺ ion in one of two locations and occasionally bound four K⁺ along the GQ stems. In the case of four bound K⁺ ions, we observed the same behavior as in the case of c-kit1 in both the telomeric DNA and TERRA GQs; water generally damped the polarization response between K⁺ and guanine bases such that ΔE_int values in vacuo (Table 6) were more favorable than when water was present across ion interactions with all tetrads (Table 5).

Table 6.

Differences in interaction energies (ΔE_int, kcal mol⁻¹) between trajectory frames with 3 or 4 K⁺ ions bound and only 2 K⁺ ions bound in the GQ stems after in vacuo Drude reoptimization.

	Telomeric GQ		TERRA GQ
	3 K+	4 K+	3 K+	4 K+
Tetrad 1	−5.1 ± 4.3a	−8.2 ± 4.9	−7.4 ± 5.7a	−8.0 ± 5.9
	3.6 ± 5.7b		2.4 ± 5.7b
Tetrad 2	−1.7 ± 7.8a	−5.6 ± 8.3	−3.2 ± 7.0a	−6.7 ± 7.4
	−1.7 ± 7.3b		−0.8 ± 6.7b
Tetrad 3	1.7 ± 5.7a	−4.3 ± 5.5	1.8 ± 7.3a	−6.0 ± 5.9
	−3.3 ± 4.8b		−4.6 ± 5.4b

^aΔE_int when the bulk ion was coordinated below tetrad 1.

^bΔE_int when the bulk ion was coordinated above tetrad 3.

Calculation of ΔΔE_int (by subtracting data in Table 6 from data in Table 5) quantifies the extent to which water screens the polarization response upon ion binding in each GQ system. We computed ΔΔE_int to determine if there are fundamental differences in the way water modulates ion binding to DNA and RNA GQs. Interestingly, ΔΔE_int was different for the telomeric DNA and TERRA GQs (Table 7). The TERRA GQ exhibited a more pronounced response, such that water had a greater effect in damping the K⁺ interaction energy upon binding of bulk K⁺ ions. Binding of a third or fourth K⁺ ion to the tetrad stem of the TERRA GQ was generally made less favorable by water, on the order of 2–4 kcal mol⁻¹, except in the instances of a third ion binding to the opposite face of the stem (i.e. the interaction energy between coordinated K⁺ ions with tetrad 1 when the third ion bound above tetrad 3, and vice versa). In these cases, the ΔΔE_int was negligible (±0.1 kcal mol⁻¹). Values of ΔΔE_int were systematically smaller for the telomeric DNA GQ, on the order of 1–3 kcal mol⁻¹, with several notable exceptions. Binding of a third ion below tetrad 1 led to more favorable interactions between the two coordinated K⁺ ions in the stem as a function of being solvated by water, –1.2 kcal mol⁻¹ with tetrad 1 and –0.8 kcal mol⁻¹ with tetrad 3. Water made the interaction energy between structured ions and tetrad 1 more favorable upon binding of a K⁺ ion above tetrad 3 by only 0.3 kcal mol⁻¹, less than k_BT (0.592 kcal mol⁻¹), therefore this quantity is also negligible. Together, these findings indicate that the DNA and RNA GQs have different energetic responses to ion binding and hydration, which are a function of the differences in their nucleobase electronic structure (Figures 6 and 7) and accumulation of ions (Figures 4 and 5) noted above.

Table 7.

ΔΔE_int (kcal mol⁻¹) between coordinated K⁺ – tetrad guanine base interaction energy in water and in vacuum after Drude reoptimization.

	Telomeric GQ		TERRA GQ
	3 K+	4 K+	3 K+	4 K+
Tetrad 1	−1.2 ± 5.5a	1.4 ± 6.1	2.6 ± 7.5a	2.8 ± 7.7
	−0.3 ± 7.5b		−0.1 ± 8.2b
Tetrad 2	1.1 ± 9.7a	2.8 ± 9.8	2.0 ± 8.9a	3.7 ± 9.2
	1.5 ± 9.0b		1.9 ± 8.9b
Tetrad 3	−0.8 ± 7.3a	1.4 ± 6.9	0.1 ± 9.2a	2.6 ± 7.4
	1.0 ± 6.1b		1.9 ± 7.0b

^aΔΔE_int when the bulk ion was coordinated below tetrad 1.

^bΔΔE_int when the bulk ion was coordinated above tetrad 3.

CONCLUSIONS

Here, we have investigated two bimolecular GQs with the same overall architecture, differing only in the fact that one is DNA and the other is RNA. Our results suggest that the telomeric DNA and TERRA GQs are intrinsically different in important ways. Having demonstrated that the Drude-2017 polarizable force field leads to better overall agreement with structural properties than CHARMM36, particularly in retention of bound ions in the GQ stems, we observed that the TERRA GQ accumulated more bulk K⁺ ions than the telomeric DNA GQ. This phenomenon implies that the RNA GQ has greater affinity for cations and therefore may be additionally stabilized by indirect ion interactions. Beyond these indirect interactions, K⁺ ions bound to the outer faces of the guanine tetrads in each GQ stem. Whereas the telomeric DNA GQ coordinated ions roughly equally at either face, the TERRA GQ manifested a preference for binding ions at tetrad 3, owing to the greater tendency of the Ura12–Ura12 base pair to remain open. In the telomeric DNA GQ, Thy12–Thy12 interactions were stronger and thus precluded ion coordination; these outcomes are reflected in different nucleobase dipole moment properties, an observation that can only be made using a polarizable force field. Finally, the interaction energy of the two initially coordinated K⁺ ions was found to vary as a function of bulk ion alignment to the outer faces of tetrads 1 and 3. Water modulated this response, with the TERRA GQ showing a greater sensitivity than the telomeric DNA GQ. Together, these findings imply that each GQ has different electronic properties, which means that folding pathways and interactions of cognate binding proteins may also differ. Such properties will be explored in future studies.

DATA AVAILABILITY

Simulation trajectories and corresponding topologies in PSF format are supplied via the Open Science Framework at https://osf.io/2pfj8/.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health [R35GM133754]; Thomas F. and Kate Miller Jeffress Memorial Trust (Bank of America, Trustee), USDA-NIFA [VA-160092]; Virginia Tech Office of the Provost, College of Agriculture and Life Sciences, and Department of Biochemistry; Computing time and resources were provided by Virginia Tech Advanced Research Computing. Funding for open access charge: NIGMS [R35GM133754] and the Thomas F. and Kate Miller Jeffress Memorial Trust.

Conflict of interest statement. None declared.