Abstract
Motivation: Metabolomics involves studies of a great number of metabolites, which are small molecules present in biological systems. They play a lot of important functions such as energy transport, signaling, building block of cells and inhibition/catalysis. Understanding biochemical characteristics of the metabolites is an essential and significant part of metabolomics to enlarge the knowledge of biological systems. It is also the key to the development of many applications and areas such as biotechnology, biomedicine or pharmaceuticals. However, the identification of the metabolites remains a challenging task in metabolomics with a huge number of potentially interesting but unknown metabolites. The standard method for identifying metabolites is based on the mass spectrometry (MS) preceded by a separation technique. Over many decades, many techniques with different approaches have been proposed for MS-based metabolite identification task, which can be divided into the following four groups: mass spectra database, in silico fragmentation, fragmentation tree and machine learning. In this review paper, we thoroughly survey currently available tools for metabolite identification with the focus on in silico fragmentation, and machine learning-based approaches. We also give an intensive discussion on advanced machine learning methods, which can lead to further improvement on this task.
Keywords: mass spectrometry, machine learning, substructure prediction, substructure annotation
Introduction
Metabolites are small molecules, which are used in, or created by, the chemical reactions occurring in every cell of living organisms [64]. They play lots of important roles including signaling, building block of cells, energy transport, etc. Interpreting biochemical characteristics of the metabolites is an essential part of the metabolomics to extend the knowledge of biological systems. It is also the key to the development of many applications in areas such as biotechnology, biomedicine or pharmaceuticals.
In order to better understand metabolites, various techniques, most commonly used Mass Spectrometry (MS) and Nuclear Magnetic Resonance (NMR), have been employed to measure them in a high-throughput manner with different approaches [65]. Both are quite complementary and promising in the area, but neither has been shown to be clearly preferred over the other, because different techniques might also be used, depending on various factors such as the type and quality of sample to be analyzed, as well as the concentration and molecular properties of the metabolites. In general, NMR allows for a detailed characterization of the chemical structure of the compound, and it is opted for unambiguous identification of a chemical structure. However, a disadvantage of NMR is that it requires abundant and pure samples, yielding low sensitivity. By contrast, MS is more sensitive and specific, requiring fewer amount of samples, but providing less information regarding the chemical structures, namely its elemental composition and some structural fragments. We focus on the use of MS rather than NMR throughout the rest of this paper.
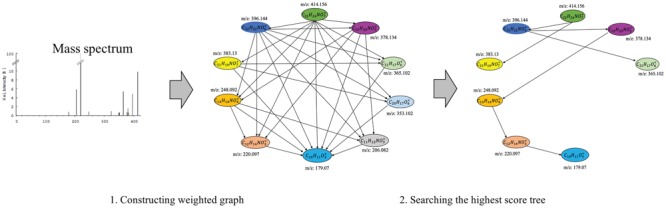
MS is a commonly used technique in analytical chemistry [14, 22, 37]. A mass spectrometer analyzes a chemical sample to determine the mass-to-charge ratios (m/z) of its substructures. The resulting mass spectrum is represented by a graph with m/z on the x-axis and the relative abundance of ions with m/z values on the y-axis (Figure 1). Another way to represent a mass spectrum is as a list of peaks, each of which is defined by its m/z and intensity value (top-right corner of Figure 1). The intensity values are often normalized such that the highest peak has a relative intensity of 100 for the subsequent processing stages.
Figure 1.
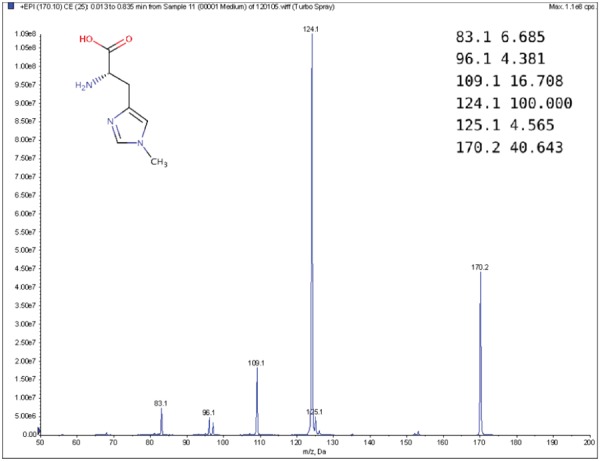
Example MS spectrum from the public Human Metabolome Database for 1-Methylhistidine (HMBD00001) [66], with its corresponding chemical structure (top left) and peak list (top right).
The main components of a mass spectrometer are as follows: an ionization source, a mass analyzer and a detector (Figure 2). The ion source is to make the input molecules become charged ions. The mass analyzer is to physically separate ions according to their m/z (mass). Once the ions have been separated according to their m/z, they are subsequently detected and quantified by the detector. Two usual forms of ionization are Electron Ionization (EI) and Electrospray Ionization (ESI), while the commonly used mass analyzer types include quadrupole, time-of-flight and orbitrap devices. The details of these devices can be found in [13, 14, 36]. As a preprocessing step, complex biological mixtures are often separated by a chromatographic step to provide pure or near pure compounds to the mass spectrometer [14, 37]. There are two common forms of chromatography: gas chromatography (GC) and liquid chromatography (LC). While GC, often coupled with EI method (known as GC-EI-MS), requires the input to be in the gaseous phase, LC, often coupled with ESI (known as LC-ESI-MS), uses liquid mobile phase.
Figure 2.
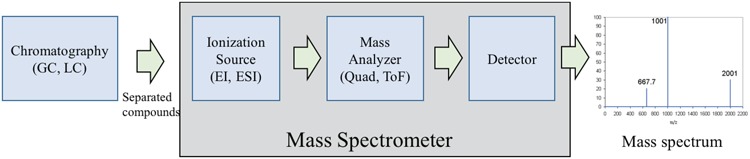
Main components of a mass spectrometer: ionization source, mass analyzer and detector.
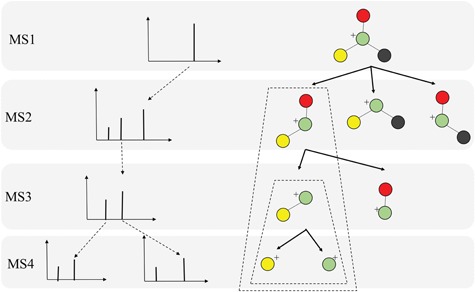
In practice, tandem mass spectrometry (or MS/MS) is widely used to provide more information about the chemical structures of compounds. Once samples are ionized (by ESI, EI, etc.) to generate a mixture of ions, precursor ions of a specific m/z are chosen (namely MS1) and then fragmented to generate product ions for detection (MS2). This selection–fragmentation–detection process can be further extended. For example, selected product ions in MS2 can be further fragmented to produce another group of product ions (MS3) and so on. Finally, all mass spectra with different levels are collected to make a mass spectral tree as illustrated in Figure 3.
Figure 3.
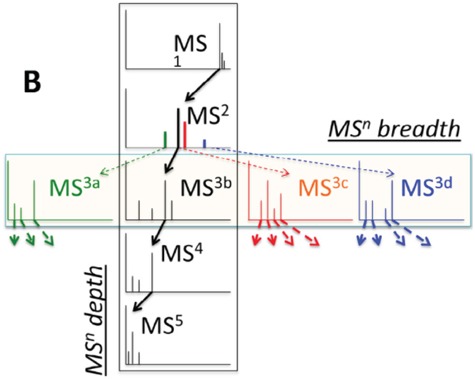
A mass spectral tree with nodes corresponding to individual mass spectra with different levels. Mass spectral trees are characterized by depth ( level) and breadth (the number of product ions chosen for the subsequent fragmentation). The figure is adapted from [61].
level) and breadth (the number of product ions chosen for the subsequent fragmentation). The figure is adapted from [61].
Identification of metabolites from MS or MS/MS spectra is an important step for further chemic-biological interpretation of metabolomics samples and modeling. In practice, this process is presumed to be one challenging and also the most time-consuming task in metabolomics experiments. Different from peptides and protein where the fragmentation is generally simple due to the repetition of their structures, the fragmentation process of metabolites under varying fragmentation energies is a more complicated stochastic process. Therefore, the interpretation of mass spectra is cumbersome and requires expert knowledge. There have been lots of computational techniques/software proposed and developed to deal with the task of metabolite identification. The primary purpose of this survey is not only to summarize the proposed techniques in the literature, but also to systematically organize them into groups according to their methodology and approaches. It would be beneficial in making researchers comprehend the key differences between techniques as well as the rationale behind their groupings. In general, we grouped computational techniques for the task into the following categories: (1) mass spectra library; (2) in silico fragmentation; (3) fragmentation tree and (4) machine learning. Given a query MS/MS spectrum of an unknown compound, mass spectral library is to compare the query spectrum against a database of MS/MS spectra of reference compounds and rank the candidates based on their similarity to the query spectrum. In contrast, in silico fragmentation attempts to generate simulated spectra from the chemical structures of reference compounds in a database and compare them to the query MS/MS spectrum. Fragmentation trees are constructed from MS/MS spectra by optimization techniques and can be used to cluster compounds into groups. Machine Learning (ML) is to learn and predict an intermediate representation between spectra and compound structures and then use such representation for matching or retrieval. The details these approaches and their difference will be presented in the following sections.
In this paper, we focus on the above (2) and (4), which are in silico fragmentation and machine learning for metabolite identification. The structure of the paper is organized as follows: mass spectra library will be briefly introduced in section 2; in section 3, we present methods to generate in silico fragments from chemical structures of compounds, which can be further divided into three subgroups including rule-, combinatorial- and machine learning-based. Prior to the focus of approaches using machine learning for identifying metabolites in section 5, algorithms to construct fragmentation trees directly from MS/MS spectrum as well as its benefits for the metabolite identification task will be briefly described in section 4. Finally, a thorough discussion about using advanced machine learning approaches will be given in section 6.
Mass spectra library
A traditional approach to identifying metabolites is to compare a given unknown MS or MS/MS spectrum (query spectrum) of an unknown compound against a database of a number of reference MS or MS/MS spectra [16, 51, 58]. The candidate molecules from the database are ranked based on the similarity of their spectra and the query spectrum and the best matching candidates are returned. In order to do that, various similarity or distance function have been proposed, from simple weighted counts of matching peaks [57], to more complicated probability-based measures [42].
However, the main disadvantage of these methods is that, the reference database is often incomplete and represents merely a small fraction of molecules in reality, leading to unreliable matching results if the reference spectrum of the targeted compound is not contained in the database. For example, the public Human Metabolome Database [66] consists of MS/MS spectrum for only approximately 2000 compounds, compared to more than 40 000 known human metabolites. The Metlin database [54] contains MS/MS spectra for more than 13 000, compared to over 240 000 endogenous and exogenous metabolites. The Global Natural Products Social Networking Library [62] contains MS/MS spectra for around 4000 compounds. As a result, alternative approaches for identifying metabolites have been devised to deal with the unavailability of measured reference spectra.
In silico fragmentation tools to aid metabolite identification
Due to the lack of MS/MS data of compounds in mass spectral databases, the ability to identify unknown compounds through search in these databases is limited as mentioned in the previous section. Therefore, the advent of software tools for predicting fragments and their abundance from the molecular structures of compounds can fill the gap between spectral and structural databases. This strategy has been successfully applied in protein studies to construct databases containing data on trypsin-associated cleavage and MS/MS spectra of peptides, such as MASCOT [12] and SEQUEST [17]. It is noted that the prediction of the fragmentation mechanism for peptides and protein is pretty simple due to the repetition in their structures. In contrast, the fragmentation of product ions of metabolites in a tandem mass spectrometer is a much more complicated stochastic process and depends on various factors including the detailed 3D structures of metabolites, the amount of energy to break several certain bonds to obtain the product ion, the probabilities of different dissociation reactions and so on. Nowadays, many in silico fragmentation software tools have been developed and used to identify MS/MS spectra when the reference spectrum is not available. In this section we survey different tools/methods using various algorithms for in silico fragmentation. The algorithms differ in the way that they deploy different strategies to generate in silico fragments from the chemical ‘structures/graphs’ of the candidate compounds. We can divide them into three subgroups, which are as follows: rule-, combinatorial- and machine learning-based fragmentation tools (Figure 4).
Figure 4.
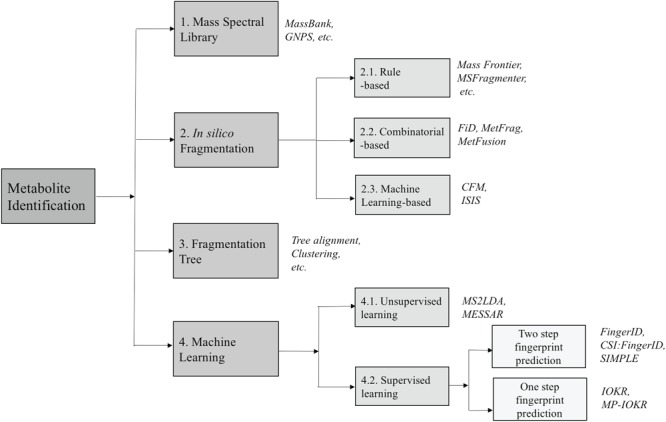
The overview of approaches for metabolite identification. The numbers show the corresponding (sub)sections for each category.
Rule-based methods
The rule-based in silico fragmentation tools are used to predict/generate theoretical spectra from chemical structures/graphs of compounds in the database using a set of rules. This set of rules is a collection of general and heuristic rules of fragmentation processes extracted from data sets of elucidated MS/MS spectra. The predicted spectra of candidate compounds from the database will be compared with the queried spectrum [25, 32].
A typical commercial software tool, Mass Frontier [40], developed by HighChem, can generate fragments according to general rules or to specific rule libraries. The libraries can be defined by users or provided by HighChem or combination of both. ACD/MS Fragmenter (available at: http://www.acdlabs.com), another commercial tool, also uses a comparable set of rules to generate fragments. MOLGEN-MSF [52], developed by the University of Bayreuth, uses general fragmentation rules and also is able to accept additional rules as an optional input file when calculating fragments. Besides, non-commercial rule-based software tools, like MASSIS [9] and MASSIMO [18] adopted different ways. In particular, structure-specific cleavage rules contained in MASSIS are divided into 26 different molecular classes. A molecule is classified into one or some of these classes and the corresponding fragmentation rules are applied to obtain a set of fragments. MASSIMO uses a small set of general fragmentation reactions parameterized with reaction probabilities drawn from a collection of determined fragmentations.
In fact, these rule-based methods are not preferred in practice due to several disadvantages, which are as follows: (1) the fragmentation process can significantly be variant due to small changes in the structure of a molecule. Hence, a fragmentation rule collected from a known fragmentation of a molecule may not be applied to another, even though they have very similar chemical structures; (2) It is empirically shown that a set of general rules is insufficient to identify some observed fragments with reasonably high accuracy. Although specific rules are constantly added to rule databases, they do not need to be applied to a new undiscovered compound in many cases and (3) The product ions of generated spectra have the same intensities because the bond cleavage rates are ignored. In reality, different molecules can generate the same product ions and the relative intensities can play a meaningful role in distinguishing these molecules.
Combinatorial-based methods
Different from the above software tools, which rely on fragmentation rule databases, combinatorial-based methods are to generate a graph of substructures from the chemical structure of a candidate compound in the database (Figure 5), then find the most likely subset of the substructures or the so-called fragmentation trees that best matches the query spectrum by solving optimization problems. An advantage offered by this approach is in situations where MS/MS spectra of compounds with less known fragmentation rules are queried. Some typical methods are reviewed in this subsection. In general, methods belonging to this subsection differ in the way of how they find the fragmentation tree best matches to the query spectra to produce a similarity score.
Figure 5.
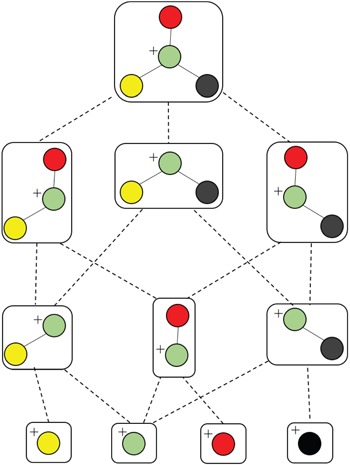
An illustration of generating all connected subgraphs of the precursor graph.
FiD (Fragment iDentificator, [23]) performs a search over all potential fragmentation paths and outputs a ranked list of alternative structures. More specifically, given a graph structure of a precursor ion and its MS/MS spectrum, FiD first generates all potential connected subgraphs by a depth-first graph traversal (Figure 5), then computing the masses of productions corresponding to the generated subgraphs to match with observed peak masses in the spectrum. After that, a list of candidate fragments is obtained then each of which is assigned a cost, namely, the standard bond energy required to cleave bonds from the precursor ion. Obviously, the candidate fragment with smaller cost will be preferred. Finally, a combinatorial optimization method, such as mix integer linear programming (MILP) is used to assign candidate fragments to measured peaks with minimal cost. Their experimental results show that, the product ions predicted by FiD agree better with the manual identification produced by domain experts than those of the rule-based fragment identification tools mentioned in the previous section. However, the main drawback of FiD is the computational expensiveness due to the following reasons: (1) rapid increase in the number of connected subgraphs; (2) the computational complexity of MILP to explain peaks with most likely candidate fragments. For these reasons, FiD can be applied to only small-sized molecules.
Another combinatorial based method is MetFrag [67] using heuristic strategies, such as the breadth-first search algorithm with a maximum tree depth parameter or removing duplicated subgraphs, to limit the search space of candidate fragments, overcoming the computational difficulty of FiD which employs depth-first graph traversal to generate subgraphs, as illustrated in Figure 5. Hence, it is much faster than FiD and can be applied to a full structure database to find the compound that explains best the spectrum. MetFrag uses bond dissociation energies for the cost of cleaving bonds. The candidate fragments are then used to rank the candidate molecules in the database without finding the most likely fragments corresponding to the spectrum. In the same vein, MAGMA, introduced in [49], is an extended version to multistage spectral trees 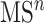 . Different from MetFrag, when a substructure is considered to explain an
. Different from MetFrag, when a substructure is considered to explain an 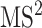 product ion which is the precursor ion of
product ion which is the precursor ion of 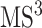 spectrum, in addition to its substructure score, the resulting
spectrum, in addition to its substructure score, the resulting 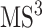 spectrum is also taken into account. This spectrum is temporarily annotated with a subset of the substructures, similarly to
spectrum is also taken into account. This spectrum is temporarily annotated with a subset of the substructures, similarly to 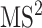 level fragmentation spectrum. Then, the substructure scores obtained at level 3 are added to the sore at level 2 and this total core is for ranking substructure candidates for MS/MS peak and its fragmentation spectrum. This procedure is applied recursively to handle
level fragmentation spectrum. Then, the substructure scores obtained at level 3 are added to the sore at level 2 and this total core is for ranking substructure candidates for MS/MS peak and its fragmentation spectrum. This procedure is applied recursively to handle 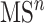 with any level, as illustrated in Figure 6.
with any level, as illustrated in Figure 6.
Figure 6.
An illustration of MAGMA to recursively rank structure candidates with multiple levels.
Gerlich and Neumann [19] presented a system, namely MetFusion, to combine the results from MassBank (search in the spectral database) and MetFrag as illustrated in Figure 7. The aim of this combination is to take advantage of complementary approaches to improve the compound identification. That is, the vast coverage of the structural databases queried by MetFrag and reliable matching results achieved by search in spectral libraries if similar spectra are available. The experimental results [19] show that a combination of an in silico fragmentation based method with curated reference measurements can improve compound identification and achieve the best of two approaches.
Figure 7.
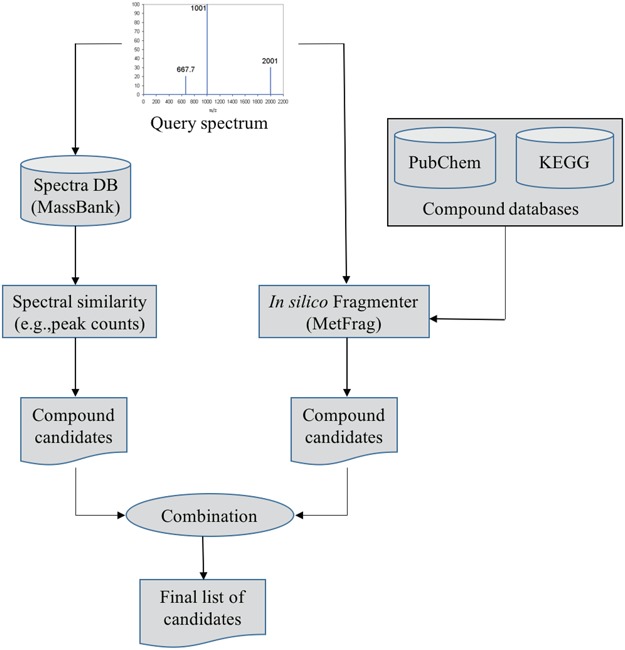
The flowchart of MetFusion: MassBank and MetFrag process the query spectrum and return two individually ranked list of compound candidates. The lists are then combined into a single integrated list of re-ranked candidates by calculating the similarity between candidate structures.
A drawback of this approach is that the above methods are mainly based on a bond disconnection approach to generate fragments from molecules, e.g., standard bond energy and bond dissociation energy used by FiD and MetFrag, respectively. However, these are solely approximate estimates and bond dissociation energies are much more complicated in reality. These limitations have been tackled with some methods based on learning models, which are presented the following subsections.
Machine learning-based methods
Besides the above approaches to generate in silico fragments from graph structure of compounds, there are a few works proposed to use machine learning models to learn the fragmentation process from the training data and have shown great promise in generating in silico spectra for the structural identification purpose. To avoid the confusion of the content in section 5, we clarify here that machine learning methods are used to learn and predict the presence of certain fragments (e.g., whether a bond between two atoms is broken or not) to generate in silico spectra from chemical structures. In a different sense, methods in section 5 are to learn and perform classification or clustering from spectra (Figure 8 for illustration).
Figure 8.
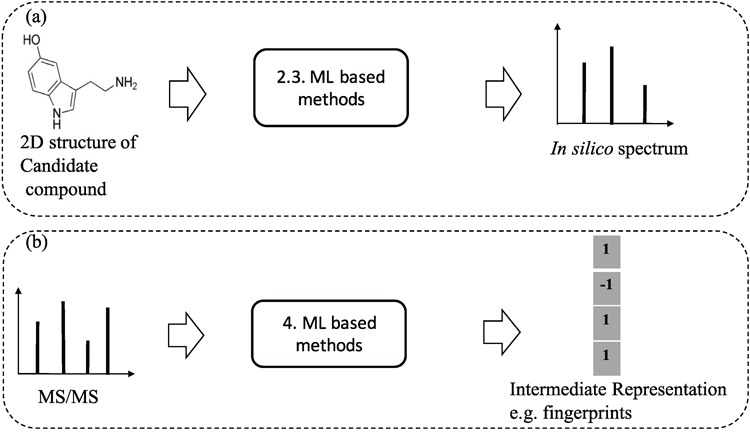
An illustration to clarify the difference between ML-based methods for learning and predicting in silico spectra from 2D structures of compounds (a) and ML based methods for learning and predicting substructures or chemical properties from MS/MS spectra (b). The numbers indicate the (sub)sections for each category.
The previously mentioned methods to generate in silico fragments from the chemical structures of compounds are based on either chemical reaction equations or approximate bond strength. None of them have shown sufficient accuracy in generating in silico spectra for enabling automated and correct identification of metabolites. To overcome the difficulty, [29] presented a method, named ISIS, using machine learning to generate in silico MS/MS spectra for lipids solely from chemical structures of compounds without fragmentation rules and no need to define bond dissociation energy. The main idea is that, for every bond in the molecular structure, one artificial neural network (ANN) is designed to predict bond cleavage energy from which bond cleavage rates can be calculated to determine the relative intensities; another is to predict which side of the bond is charged and captured by the detector in the mass spectrometer. These ANNs are iterated over all bonds within a molecule to find bond cleavage energies and charged ions. For the leaning process, the weights of the former ANN are trained by genetic algorithm to better predict the bond cleavage energies that produce ions and their corresponding intensities in the in silico spectra. The objective of GA is to have the in silico spectra match those in the experimental spectra using a Pearson 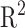 correlation. The latter ANN is trained by backpropagation algorithm in which the labels can be found by comparing the fragment masses to the experimental spectra.
correlation. The latter ANN is trained by backpropagation algorithm in which the labels can be found by comparing the fragment masses to the experimental spectra.
Allen, Greiner and Wishart [1] proposed a probabilistic generative model, namely competitive fragmentation mode (CFM), for the fragmentation process. They assume that each peak in the spectrum is generated by a fixed length sequence of random fragment states. It consists of the following two models: transition model to define the probability of each fragment leads to another at one step in the process and an observation model to map the final intermediate fragment state to the given peak. The parameter estimation for the transition and observation models is performed by an Expectation Maximization-like algorithm. The trained CFM can be used to predict peaks in the spectrum and for metabolite identification. The results showed that, CFM obtained substantially better ranking for the correct candidate than MetFrag and FingerID. However, like other above methods, this method is limited to small molecules due to the combinatorial enumeration of fragmentation possibilities. It is noteworthy that, while ISIS is based on supervised machine learning, CFM is based on unsupervised learning to predict spectra.
Fragmentation tree
Fragmentation tree (FT) plays an important role in interpreting the structure of molecules since it is usually assumed that only MS/MS spectra are not sufficient to describe the fragmentation process. It is noteworthy that these FTs are constructed from spectra while the trees mentioned in subsection 3.2 are generated from chemical structures of candidate compounds. This section is devoted to review the benefits of the use of FTs for metabolite identification and summarize methods to construct them directly from the MS/MS spectra.
Unlike proteins and glycans, where molecules are only fragmented at specific chemical bonds and thus the fragmentation process can be well understood, this process for small metabolites can happen at almost any bonds, hence, being difficult to predict and interpret MS/MS data. Böcker and Rasche [5] proposed using FTs for interpretation of MS/MS spectra. The FT as shown in Figure 9 can bring several benefits such as: they can be used to identify the molecular formula of a molecule, also to interpret the fragmentation process of a precursor ion by MS/MS spectrum (see [46]). Because of this reason, there are some efforts [6, 53] to use FTs combined with MS/MS spectra in identifying metabolites, which will be discussed later. Moreover, we can align FTs of two unknown compounds to compare them based on their corresponding trees, by which, useful information about unknown compounds that cannot be identified also can be derived such as a clustering (see [47, 50] for more details).
Figure 9.
Noscapine and the corresponding hypothetical fragmentation tree computed by the method introduced in [46].
The FT is represented by a set of vertexes, each of which corresponds to a fragment or precursor ion, and is annotated with its molecular formula. Edges connecting pairs of vertexes represent fragmentation reactions and are annotated with the molecular formulas of neutral loss. Briefly, FT computation is performed in the following two main steps: (1) Construction of weighted fragmentation graph containing all possible trees corresponding to the given MS/MS data; (2) Searching for the highest-score tree inside the graph. More specifically, the fragmentation graph is constructed as follows: each peak in the MS/MS spectra is assigned to one or more molecular formulas with mass sufficiently close to the peak mass. These resulting molecular formulas are vertexes of a directed acyclic graph (DAG). Two vertexes 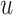 and
and  are connected by an edge
are connected by an edge  if the molecular formula of
if the molecular formula of 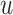 is sub-formula of the formula of
is sub-formula of the formula of 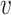 and that edge is assigned a score using the annotated neutral loss (i.e. the fragment not being captured by the device) and/or other properties such as peak intensities, mass deviation, representing how likely the neutral loss is. Also, vertexes in the graph are colored so that two vertices with the same color correspond to the same peak. To avoid the case that, there are two vertexes in the FT to represent the same peak, another constraint is added, that is, any two vertexes in the tree have different colors, (or so-called colorful tree) must be imposed, leading to ‘the Maximum Colorful Subtree problem’ (MCS).
and that edge is assigned a score using the annotated neutral loss (i.e. the fragment not being captured by the device) and/or other properties such as peak intensities, mass deviation, representing how likely the neutral loss is. Also, vertexes in the graph are colored so that two vertices with the same color correspond to the same peak. To avoid the case that, there are two vertexes in the FT to represent the same peak, another constraint is added, that is, any two vertexes in the tree have different colors, (or so-called colorful tree) must be imposed, leading to ‘the Maximum Colorful Subtree problem’ (MCS).
MCS problem: Given a vertex-colored DAG 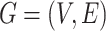 with a set of colors
with a set of colors 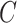 and weights
and weights 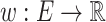 . Find the induced colorful subtree
. Find the induced colorful subtree  of
of  of maximum weight
of maximum weight  .
.
Despite the fact that finding MCS is an NP-hard problem, proved in [47], many algorithms have been proposed to solve this, being categorized into the following two main groups: exact algorithms and heuristics. While a dynamic programming algorithm solving the MSC problem is an exact algorithm, a simple greedy heuristic is to consider the edges in descending order of their weights [5]. Besides, [5] presented a hybrid method that constructs a preliminary subtree (or backbone) with a small number of vertices by the dynamic programming and completes the subtree by the greedy approach.
It has been shown that for small molecules, exact algorithms (e.g. dynamic programming) can quickly find the optimal solution [5]. Especially, for tasks requiring the construction of accurate FTs, such as tree-alignment for MS/MS spectra [50], it is advised that exact algorithms should be used. In the case of dealing with a huge number of molecules, to decrease the running time, a heuristic in combination with an exact algorithm (e.g. tree completion heuristic, [48]) may be preferred.
Machine learning-based metabolite identification
Recently, several machine learning frameworks have been introduced to deal with the task of metabolite identification. Besides identifying chemical compounds by searching in structural databases as presented in the previous sections, there are some methods proposed to predict structural substructures or general chemical properties, e.g. [6, 15, 24]. Another direction is to automatically discover substructures from a set of MS/MS spectra from which we can identify the candidate compounds from the database based on their substructures, e.g. [41, 60]. In this section, we cover machine learning frameworks for this task, which can be divided into the following two subgroups: supervised learning for substructure prediction and unsupervised learning for substructure annotation. The difference between the two subgroups can be intuitively illustrated asin Figure 10.
Figure 10.
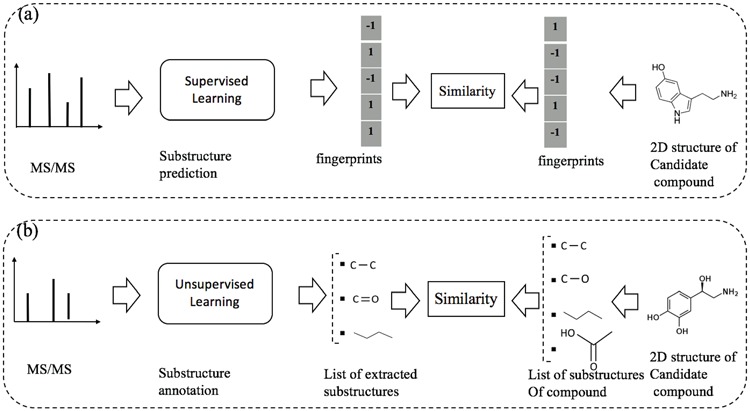
An illustration to clarify the difference between supervised and unsupervised learning for metabolite identification: (a) substructure prediction using supervised learning to map a given MS/MS spectrum to an intermediate representation (e.g. fingerprints), which is subsequently used to retrieve candidate metabolites in the database. (b) substructure annotation using unsupervised learning to extract biochemically relevant substructures with certain confidence from the given spectrum. Then, the similarity between the MS/MS spectrum and a chemical structure of a metabolite is estimated according to their common substructures. Note that the output of supervised learning (e.g. fingerprints) may indicate the presence/absence of all ‘predefined’ substructures whereas that of unsupervised learning may be a list of substructures frequently occurring in the database.
Supervised learning for substructure prediction
The task of supervised learning for metabolite identification is that, given a set of MS/MS spectra, one may want to learn a map from a MS/MS spectrum to a molecule. Instead of learning this mapping directly, fingerprint-based approach has been used in many systems. This can be called a two-step approach in many publications. A molecular fingerprint is a feature vector, which is used to encode the structure of a molecule. In general, the values of this vector are binary indicating the presence or absence of certain substructures or more general chemical properties. Methods using fingerprint prediction for metabolite identification generally consist of two main steps, which are as follows: (1) from a set of MS/MS spectra of known molecules, learn a model to predict the corresponding fingerprints with supervised ML; (2) use the predicted fingerprints to retrieve candidate molecules from the database with retrieval techniques (Figure 11). The 1st step can be dealt with by classification tools such as linear discriminative analysis (LDA), partial least squares discriminative analysis [70] or decision tree [26]. A notable method is FingerID [24], which uses support vector machine (SVM, [8]) with kernels to predict fingerprint. The kernels for pairs of mass spectra were defined, including integral mass kernel and probability product kernel (PPK, [27]). It is noteworthy that the above methods are mainly based on the information from individual peaks present in the spectra while ignoring their interactions. In fact, such information is proved to be useful in predicting fingerprint.
Figure 11.
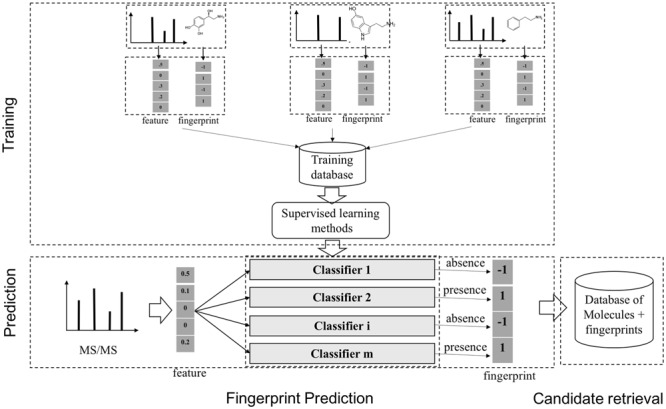
A general scheme to identify unknown metabolites based on the molecular fingerprint vectors. There are two main stages, which are as follows: (1) learning a mapping from a molecule to the corresponding binary molecular fingerprint vector by classification methods, given a set of MS/MS spectra and fingerprints; (2) using the predicted fingerprints to retrieve candidate molecules from the databases of known metabolites.
CSI:FingerID [15, 53], an extended version of FingerID, jointly takes MS/MS spectra and corresponding FTs as input to improve the predictive performance since FTs, reviewed in the previous section, can be used to provide prior knowledge about the structure of compounds (i.e. dependencies between peaks in spectra), which was ignored in the previous system. For this purpose, kernels for FTs have to be defined, which range from simple ones for nodes including node binary and node intensity; for edges including loss binary, loss count, loss intensity to more complicated ones like common paths counting, common subtree counting, etc. Subsequently, multiple kernel learning (MKL, [20]) is used to combine these kernels using several methods including centered alignment (ALIGNF, [11]), quadratic combination [33] and  -norm regularized combination [31]. The combined kernel is then used in learning the final model for fingerprint prediction. CSI:FingerID presented improved scores against other benchmarked tools but has the current limitation of processing MS/MS spectra one at a time due to the need of computationally heavy conversion of spectra into FTs. Additionally, in spite of accurate prediction, kernel-based methods are often not desirable to deal with sparse data and lack of interpretation, especially, for MS/MS spectra where each spectrum is composed of a number of few peaks and each fingerprint value (or chemical property in general) is mainly determined by a sparse subset of peaks.
-norm regularized combination [31]. The combined kernel is then used in learning the final model for fingerprint prediction. CSI:FingerID presented improved scores against other benchmarked tools but has the current limitation of processing MS/MS spectra one at a time due to the need of computationally heavy conversion of spectra into FTs. Additionally, in spite of accurate prediction, kernel-based methods are often not desirable to deal with sparse data and lack of interpretation, especially, for MS/MS spectra where each spectrum is composed of a number of few peaks and each fingerprint value (or chemical property in general) is mainly determined by a sparse subset of peaks.
To alleviate those limitations, [44] recently proposed two learning models that are able to explicitly incorporate peak interactions to improve the performance of fingerprint prediction without FTs in prediction stage. The 1st is also based on kernel learning in which kernels are defined for not only individual peaks but also interactions between them, and then combine the kernels through MKL. The 2nd one, named SIMPLE, is more computationally efficient and interpretable for this problem. More specifically, given an MS/MS spectrum, represented by a feature vector, 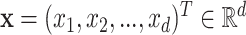 , SIMPLE is to predict a fingerprint value by computing the prediction function
, SIMPLE is to predict a fingerprint value by computing the prediction function
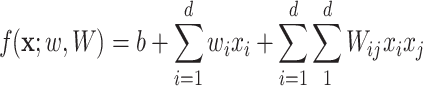 |
(1) |
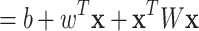 |
(2) |
where 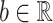 ,
, 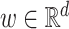 and
and 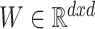 correspond to the fingerprint value (note that fingerprint values are separately trained). The prediction function consists of a bias
correspond to the fingerprint value (note that fingerprint values are separately trained). The prediction function consists of a bias 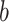 and two terms, which are as follows: main effect term parameterized by the weight vector
and two terms, which are as follows: main effect term parameterized by the weight vector 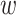 and interaction term parameterized by the weight matrix
and interaction term parameterized by the weight matrix 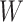 . The former capture information about the peaks, while the latter captures information about peak interactions. Since the task is classification, which predicts the presence or absence of properties in fingerprint vector, the output of the model can be computed by
. The former capture information about the peaks, while the latter captures information about peak interactions. Since the task is classification, which predicts the presence or absence of properties in fingerprint vector, the output of the model can be computed by 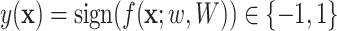 . For the purpose of interpretation, they impose
. For the purpose of interpretation, they impose 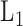 -norm [59] and nuclear norm [56] regularizations on main effect and interaction terms to induce sparsity in
-norm [59] and nuclear norm [56] regularizations on main effect and interaction terms to induce sparsity in 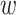 and low-rankness in
and low-rankness in 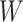 after training. The training stage is performed by minimizing a convex objective function, guaranteeing that the obtained solution is globally optimal. In addition, an obvious advantage of SIMPLE in comparison with kernel-based methods is prediction speed. Indeed, the prediction of SIMPLE is proportional to the number of peaks in the testing spectrum while the prediction of kernel methods depends definitely on the number of training examples.
after training. The training stage is performed by minimizing a convex objective function, guaranteeing that the obtained solution is globally optimal. In addition, an obvious advantage of SIMPLE in comparison with kernel-based methods is prediction speed. Indeed, the prediction of SIMPLE is proportional to the number of peaks in the testing spectrum while the prediction of kernel methods depends definitely on the number of training examples.
Different from fingerprint prediction based approaches, Input Output Kernel Regression (IOKR, [6]) is used to learn mappings between MS/MS spectra (as a structured input set 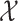 ) and molecular structures (as a structured output set
) and molecular structures (as a structured output set 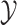 ). The idea behind this method is the definitions of two kernels
). The idea behind this method is the definitions of two kernels 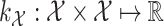 and
and 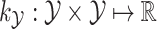 to encode similarities in input space (e.g., spectra and/or FT ) and output space (e.g. molecular fingerprint or graph structure), respectively. The following two novel points can be observed: (1) unlike previous methods, it can handle the structured output space such as the fingerprint or molecular structure space; (2) two steps are combined into one, that is more efficient in running time.
to encode similarities in input space (e.g., spectra and/or FT ) and output space (e.g. molecular fingerprint or graph structure), respectively. The following two novel points can be observed: (1) unlike previous methods, it can handle the structured output space such as the fingerprint or molecular structure space; (2) two steps are combined into one, that is more efficient in running time.
In brief, this spectra-metabolite mapping problem can be decomposed into the following two tasks:
- Estimation of the output feature map, involving approximating the feature map
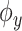 associated with the kernel
associated with the kernel 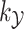 by learning the function
by learning the function 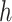 between the input set
between the input set 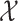 and the Hilbert output space
and the Hilbert output space 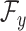 . More specifically, given a set S of
. More specifically, given a set S of  training examples
training examples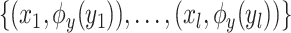 , where
, where 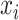 and
and 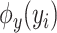 denote spectrum and the corresponding fingerprint vector of the
denote spectrum and the corresponding fingerprint vector of the 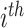 example in the task of metabolite identification, the goal is to learn a function
example in the task of metabolite identification, the goal is to learn a function 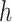 that minimize the following regression objective function:
that minimize the following regression objective function:
where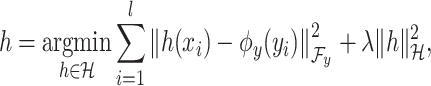
(3) 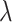 is the regularization parameter. IOKR uses the representer theorem [38] devoted to vector-valued function to obtain the closed-form solution of (3).
is the regularization parameter. IOKR uses the representer theorem [38] devoted to vector-valued function to obtain the closed-form solution of (3). - Computation of the pre-image problem, involving mapping back the predicted feature vector
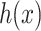 to the output space
to the output space  by solving the following pre-image problem: given the predicted feature vector
by solving the following pre-image problem: given the predicted feature vector 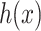 , the goal is to find the molecules in databases (structured output) with minimal distances to
, the goal is to find the molecules in databases (structured output) with minimal distances to 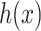 , that is,
, that is,
By using the representer theorem for vector-output space and replacing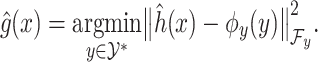
(4) 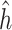 of the solution in (3), the following solution for (4) can be obtained:
of the solution in (3), the following solution for (4) can be obtained:
where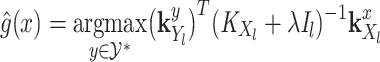
(5) 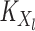 is the operator-valued kernel of the following form:
is the operator-valued kernel of the following form: 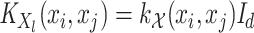 .
. 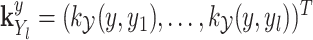 and
and 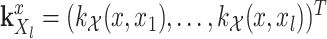 .
.
The overview of this method can be seen in Figure 12. Some advantages of this method over fingerprint prediction -based methods can be observed as follows: (1) the kernel trick in the output space  allows us to evaluate the function
allows us to evaluate the function 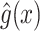 in (5) through kernels even in the case that the output feature map
in (5) through kernels even in the case that the output feature map 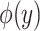 is not explicitly defined, suggesting that there is no need to predict fingerprint vectors as the intermediate step. That is why it is called one-step method for metabolite identification. (2) the closed form solution in (3) make the training process much more efficient in terms of the training time and testing time.
is not explicitly defined, suggesting that there is no need to predict fingerprint vectors as the intermediate step. That is why it is called one-step method for metabolite identification. (2) the closed form solution in (3) make the training process much more efficient in terms of the training time and testing time.
Figure 12.
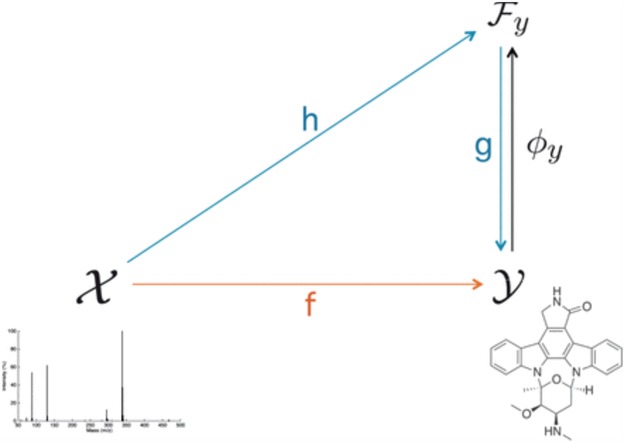
The overview of IOKR. The figure is adapted from [6].
In above IOKR approach, the pre-image problem reduces to the ranking problem, in which the candidate molecules are ordered according to their distances to the predicted output feature vectors. However, the ranking problem was not taken into consideration in the learning phase. In the training set, each input sample or MS/MS spectrum is associated with a list of candidate molecules (candidate set). Magnitude-preserving IOKR (MP-IOKR, [7]), a variant of IOKR, is recently proposed so that the information on the candidate ranking of the candidate sets can be incorporated in the learning phase, instead of the prediction phase only. The main idea behind this method is to preserve the discrepancy between the training output and candidates in the output space. This extends the magnitude-preserving ranking approach proposed by [10] for learning to rank. That is, the considered targets are vectors in the output space rather than scalar values, e.g. ratings, and the magnitude are considered between a training sample and each of its candidates. The details of this method can be summarized as follows: given a set of  training examples
training examples 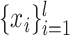 , each of which
, each of which 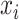 is associated with a candidate set
is associated with a candidate set 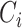 , the objective function (6) is considered to be minimized;
, the objective function (6) is considered to be minimized;
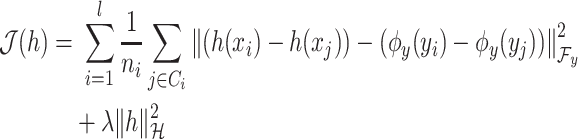 |
(6) |
where 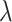 is the regularization parameter to prevent overfitting.
is the regularization parameter to prevent overfitting. 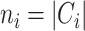 corresponds to the number of candidates for
corresponds to the number of candidates for 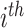 -training example. The 1st term is to minimize discrepancy between the pairwise differences of the predicted output vectors
-training example. The 1st term is to minimize discrepancy between the pairwise differences of the predicted output vectors 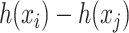 and the pairwise differences of the ground truth
and the pairwise differences of the ground truth 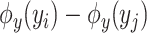 , while the 2nd term is for regularization. Similarly, minimization of this objective function can be done by applying the representer theorem. It is empirically shown that MP-IOKR consistently obtains better top-k accuracies compared to IOKR on the tasks of metabolite identification and document retrieval as well [7].
, while the 2nd term is for regularization. Similarly, minimization of this objective function can be done by applying the representer theorem. It is empirically shown that MP-IOKR consistently obtains better top-k accuracies compared to IOKR on the tasks of metabolite identification and document retrieval as well [7].
Unsupervised learning for substructure annotation
Metabolites may have common substructures, yielding similar product ions in their MS/MS spectra. Many substructures among them contain information pertaining to the biochemical processes present. Therefore, extraction of such biochemically relevant substructures allows metabolites to be grouped based on their shared substructures regardless of classical spectral similarity. Also, this can be used to improve the accuracy of metabolite identification.
One of the typical software tools for chemical substructure exploration is MS2Analyzer [35], which is a library-independent tool, allowing to exploit the potential structure information contained in MS spectra. It was developed to elucidate substructures of small molecules from accurate MS/MS spectra. The main function of this tool is to search mass spectral features including neutral loss, precursor, fragment ions mass and mass differences in a large number of mass spectra. By combining the searching results and substructures/compound class relationship knowledge, compounds can be identified. However, MS2Analyzer can find all molecules sharing a specific set of mass spectral features provided by users and sample-specific features are likely to be ignored. Another technique, namely molecular networking [62, 63, 69], groups parent ions i.e. MS1 peaks, based on their MS2 spectral similarity, e.g. cosine score, such that metabolites which are structurally annotated in a cluster can be used to annotate their neighbors. However, a drawback of molecular networks is that only MS1 peaks with high similarity are grouped and spectral features specifying the clusters have to be manually extracted. Thus, it may fail to cluster molecules sharing small substructures with low MS2 spectral similarity.
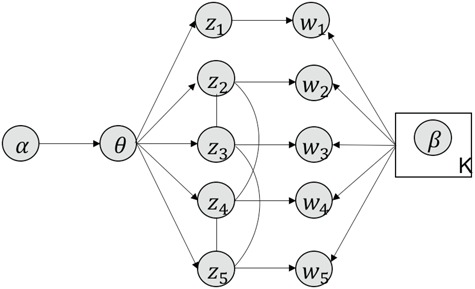
MS2LDA, presented in [60], is a software tool offering benefits of both methods while overcoming their disadvantages. It can automatically extract relevant substructures in molecules based on their co-occurrence of mass fragments and neutral losses, and cluster the molecules accordingly. Based on the assumption that, each observed MS/MS spectrum is composed of one or more substructures, MS2LDA adopts Latent Dirichlet Allocation (LDA, [4]) initially developed for text mining for extracting such substructures. LDA is a Bayesian version of probabilistic latent semantic analysis. In standard setting for text mining, LDA models each of 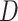 documents as a discrete distribution over
documents as a discrete distribution over 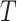 latent topics, each of which is a discrete distribution over a vocabulary of
latent topics, each of which is a discrete distribution over a vocabulary of 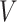 words. For document
words. For document 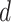 , the distribution over topics, denoted by
, the distribution over topics, denoted by 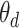 , is drawn from a Dirichlet distribution
, is drawn from a Dirichlet distribution 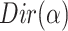 , and for each topic
, and for each topic 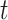 , the distribution over words, denoted by
, the distribution over words, denoted by 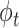 , is drawn from a Dirichlet distribution
, is drawn from a Dirichlet distribution 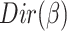 . A generative process in LDA is defined on document
. A generative process in LDA is defined on document 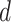 as follows (note that the index
as follows (note that the index 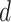 for document
for document 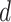 is omitted for simplification):
is omitted for simplification):
Choose
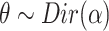 .
.-
For each word
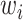 in document
in document 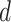 :
:(a) Choose a topic
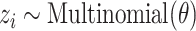 .
.(b) Choose a word
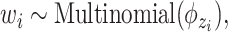
where latent variable 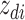 is a topic assignment for
is a topic assignment for 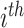 word
word 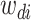 in the document
in the document 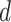 . The parameters to be learned include
. The parameters to be learned include 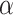 and
and 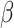 . The graphical representation of this process is illustrated in Figure 13.
. The graphical representation of this process is illustrated in Figure 13.
Figure 13.
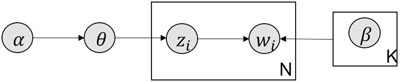
Simplified graphical representation of LDA.
The correspondence between text documents and fragmentation spectra can be obviously observed from machine learning perspective. LDA decomposes a document into topics based on the co-occurring words, while MS2LDA decomposes MS/MS spectra into patterns of co-occurring fragments and losses. Learning LDA (MS2LDA) is to extract these topics (patterns or so-called (Mass2) Motifs) as illustrated in Figure 12. For reference, either collapsed Gibb sampling [21] or Variational Bayes [4] can be used to assign topics (Mass2Motifs) to words (peaks). This step applied to mass spectra is called substructure annotation. By MS2LDA, each metabolite can be explained by one or more Mass2Motifs by which we can partly identify unknown metabolites via their spectra. Also, It can be used to quickly classify metabolites into functional classes without knowing the complete structures.
A drawback of the aforementioned MS2LDA is that, the extracted motifs still need to be structurally annotated based on expert knowledge, which is a complex process and time-consuming. To overcome this difficulty, [41] introduced an automated method named MESSAR for substructure recommendation from mass spectra, motivated by frequent set mining. Similarly to MS2LDA, this method is also capable of capturing recurring patterns from mass spectra. In brief, molecular substructures are first generated from chemical structures/graphs of metabolites in a database, which consists of both MS/MS spectra and corresponding molecular structures of known metabolites. Then, they are associated with fragment ions (i.e. peaks) and mass differences between peaks to construct a single data set in the transactional format. Subsequently, frequent set mining techniques are applied to this set to extract rules of the following format: peaks 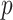 (or mass difference
(or mass difference 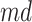 ) can be associated with substructure
) can be associated with substructure 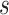 with support
with support 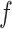 and confidence
and confidence 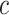 . Such rules can be used to annotate substructures with calculated scores of support and confidence for mass spectra in which, the given peaks and mass differences are observed. Moreover, the recommended substructures can also be used to rank candidate metabolites retrieved from a database by the similarity between recommended substructures and candidate molecular structures. Metabolites with a high number of substructures with high confidence are assigned a higher rank.
. Such rules can be used to annotate substructures with calculated scores of support and confidence for mass spectra in which, the given peaks and mass differences are observed. Moreover, the recommended substructures can also be used to rank candidate metabolites retrieved from a database by the similarity between recommended substructures and candidate molecular structures. Metabolites with a high number of substructures with high confidence are assigned a higher rank.
It is noteworthy that the aim of the aforementioned methods are similar, i.e. substructure annotation. While MS2LDA only needs a set of unlabeled MS/MS spectra for learning without prior information about the molecular structures, MESSAR utilizes both experimental spectra and the corresponding structures, hence, providing an automated substructure recommendation as opposed to expert-driven substructure annotation by MS2LDA. To end this section, we give a brief comparison of methods in both supervised and unsupervised approaches for substructure prediction and substructure annotation in Table 1.
Table 1.
Comparison of main representative methods for supervised and unsupervised learning approaches. The performance of supervised methods is evaluated by the accuracy of the returned list of candidates, whereas that of unsupervised methods is evaluated by their capability of substructure annotation
| Approaches | Methods | Info. type for learning | Performance | Training cost | Prediction cost |
|---|---|---|---|---|---|
| Supervised | FingerID [24] | spectra | low | low | low |
| CSI:FingerID [15] | spectra + trees | high | high | high | |
| SIMPLE [44] | spectra | high | low | low | |
| IOKR [6] | spectra + trees | high | medium | medium | |
| MP-IOKR [7] | spectra + trees + ranking | high | medium | medium | |
| Unsupervised | MS2Analysis [35] | user-specific features | low | N/A | N/A |
| MolecularNetwork [69] | spectra | low | N/A | N/A | |
| MS2LDA [60] | spectra | high | N/A | N/A | |
| (expert-driven) | |||||
| MESSAR [41] | spectra + molecular graph | high | N/A | N/A | |
| (automation) |
Discussion
It is obvious that machine learning techniques are key to recent progress in metabolite identification such as [1, 6, 15, 60]. However, emerging developments of advanced learning models in both supervised and unsupervised approaches have not been taken into consideration in the existing frameworks for this task. Our aim in this section is to raise some key drawbacks of ML methods for metabolite identification and discuss possible solutions to deal with them.
In supervised learning-based frameworks for prediction of molecular substructures, there are some points to be considered, which are as follows: (1) high-dimensional feature vector of mass spectra due to the need of fine-grained discretization of the m/z range. (2) The existence of high-order interactions of subset of peaks due to probably consecutive fragmentation processes from product ions and precursor ions (fragments). (3) Introduction of sparsity into learning models because each fingerprint representing a chemical property may be determined by a subset of few peaks (features). These have been partially taken into account in several research work (see [53], [6], [44]).
The standard data preprocessing converts spectra into high-dimensional feature vectors by dividing m/z range into bins and taking accumulated intensity within each bin as a feature value. However, the width of bins is hard to determine. While wide bins can cause noise, too narrow bins can induce alignment errors due to mass error. This can be circumvented by using the kernel, say PPK, as previously mentioned. Although machine learning-based frameworks [15, 53] used SVMs with kernel functions as the main component achieved significant improvement in metabolite identification task, feature selection was not considered for MS/MS spectra. It is due to the fact that SVMs produce sparse solutions in only dual space, not primal space as known as support vectors in the literature [8], leading to lack of the interpretability in these kernel-based methods. A popular approach in supervised learning problem to deal with high-dimensional data is to use regularization, such as adding an additional penalty term of the form 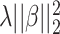 (Ridge) or
(Ridge) or 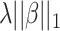 (LASSO, [59]) to the loss function, where
(LASSO, [59]) to the loss function, where 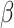 is a coefficient vector to be learned and
is a coefficient vector to be learned and 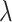 is the hyperparameter controlling the amount of regularization, with larger values implying more regularization. The latter type of penalty, called LASSO, has attracted a lot of attention in both machine learning and statistics. One reason for its popularity is that it does feature selection; it sets some coefficients
is the hyperparameter controlling the amount of regularization, with larger values implying more regularization. The latter type of penalty, called LASSO, has attracted a lot of attention in both machine learning and statistics. One reason for its popularity is that it does feature selection; it sets some coefficients 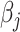 exactly to zero, meaning that the corresponding features are excluded from the model. The merit of this feature selection is to stabilize the parameter estimates with sparsity while leading to interpretable models (e.g. ability to explain which peaks determine a certain property of the metabolite).
exactly to zero, meaning that the corresponding features are excluded from the model. The merit of this feature selection is to stabilize the parameter estimates with sparsity while leading to interpretable models (e.g. ability to explain which peaks determine a certain property of the metabolite).
It is also noted that sparsity alone may not be sufficient to achieve a stable estimate due to the high-order interaction of peaks in the spectra. From a biological point of view, it can be explained that, a number of groups of peaks (or substructures) define some certain properties of molecules. Additionally, peaks in a mass spectra have a hierarchical relationship due to probably consecutive fragmentation processes from product ions and precursor ions, e.g. in multistage MS or tandem mass spectrum where a product ion can be further fragmented into new ions. Exploiting interactions among features is an area of active research. For example, methods in [28, 71, 72] produce structured sparsity. These made use of the group lasso penalty, given pre-determined groups of coefficients, inducing the whole groups of coefficients to be set to zero. In particular, given a set of groups of variables, 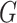 , group-lasso [71] generalizes the lasso by adding
, group-lasso [71] generalizes the lasso by adding 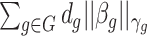 to the loss function, where
to the loss function, where 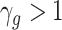 ,
, 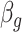 is
is 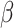 projected onto the coordinates in
projected onto the coordinates in 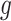 , and
, and 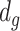 is a nonnegative weight (e.g. size of group
is a nonnegative weight (e.g. size of group 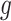 ). This penalty induces a very few number of groups of coefficients to be selected (or so-called group selection). Composite absolute penalties (CAP, [72]) express both group and hierarchical selection. The CAP penalty assumes a known hierarchical structure on the feature (such as fragmentation process of mass spectra where a peak is generated from its precursor ion). The hierarchical structured sparsity is obtained by considering the penalty:
). This penalty induces a very few number of groups of coefficients to be selected (or so-called group selection). Composite absolute penalties (CAP, [72]) express both group and hierarchical selection. The CAP penalty assumes a known hierarchical structure on the feature (such as fragmentation process of mass spectra where a peak is generated from its precursor ion). The hierarchical structured sparsity is obtained by considering the penalty: 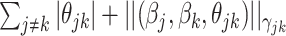 , where
, where 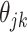 is the coefficient for the interaction between
is the coefficient for the interaction between  and
and  features. Different from the above penalties, where pre-determined groups and hierarchical structures are needed (e.g. FT constructed from mass spectra), methods introduced in [3, 34] are to learn 1st order interactions of features without knowing the group or hierarchical structures in advance. Likewise, these methods use versions of group lasso to select interactions and enforce hierarchy via regularizations. The interested readers can refer to the paper and references therein. To incorporate high-order interactions between peaks into the learning model, the use of FTs along with mass spectra through MKL to combine kernels corresponding to these data types may be a reasonable choice, see [6, 15]. As earlier mentioned, using FTs might be similar to considering peak interactions. However, if FTs are used as input features, spectra must be converted to such trees not only in training but also in prediction, which needs a heavy computation. In fact, the number of such interaction is very few, compared to a possible number of interactions among peaks. Again, advanced sparse models for learning such interactions should be considered.
features. Different from the above penalties, where pre-determined groups and hierarchical structures are needed (e.g. FT constructed from mass spectra), methods introduced in [3, 34] are to learn 1st order interactions of features without knowing the group or hierarchical structures in advance. Likewise, these methods use versions of group lasso to select interactions and enforce hierarchy via regularizations. The interested readers can refer to the paper and references therein. To incorporate high-order interactions between peaks into the learning model, the use of FTs along with mass spectra through MKL to combine kernels corresponding to these data types may be a reasonable choice, see [6, 15]. As earlier mentioned, using FTs might be similar to considering peak interactions. However, if FTs are used as input features, spectra must be converted to such trees not only in training but also in prediction, which needs a heavy computation. In fact, the number of such interaction is very few, compared to a possible number of interactions among peaks. Again, advanced sparse models for learning such interactions should be considered.
Similarly, for unsupervised learning methods for substructure annotation, a key limitation of the existing probabilistic topic models including LDA in subsection, is that, words (peaks) are assumed to be uncorrelated or so-called bag-of-word assumption, meaning that the topic assignment for each word (peak) is irrelevant to all other words (peaks). This assumption results in losing rich information about the word (peak) dependencies and incoherent learned topics (motifs). Some methods have been proposed to incorporate external knowledge regarding the word correlation, such as WordNet [39], which can be considered to learn more coherent topics. Andrzejewski, Zhu and Craven [2] proposed an approach to incorporate such knowledge into LDA by imposing Dirichlet Forest Prior, replacing the Dirichlet prior over topic-word multinomial to encode the Must-links and Cannot-links between words. Words having Must-links are imposed to have similar probabilities within all topics while those with Cannot-links are not allowed to have high probabilities in any topics simultaneously. In a similar fashion, [43] proposed a quadratic regularizer and a convolved Dirichlet over the topic-word distribution to incorporate the dependencies between words. One point is that these methods ignored the fact that there are some words correlated depending on the topic they appear in. Xie, Yang and Xing [68] proposed to use a Markov random field for regularization of LDA to encourage words similarly labeled to share the same topic label (Figure 14). Under this model, the topic assignment of each word is not independent, but depends on the topic labels of its correlated words. This model can be represented as in Figure 15. Motivated by these advanced learning models designed for text applications, FTs constructed directly from mass spectra can be used as a source of external knowledge to provide rich information about peak correlations, making the learned motifs more coherent.
Figure 14.
The correspondence between LDA for text and MS2LDA for mass spectra: LDA finds topics based on the co-occurrence of words while MS2LDA finds substructures based on the co-occurrence of mass fragments and neutral losses. This figure is adapted from [60].
Figure 15.
Graphical representation of Markov random field regularized LDA; if two words are correlated according to the external knowledge, an undirected edge between their topic labels is created. Finally, a graph in which nodes are latent topic labels and edges connect topic labels of semantically related words. In this example, the graph contains five nodes  ,
,  ,
,  ,
, 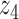 ,
, 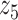 and four edges (
and four edges (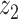 ,
, 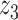 ), (
), (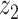 ,
, 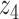 ), (
), (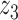 ,
, 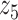 ) and (
) and (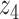 ,
, 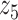 ).
).
One step approach has been shown promising supervised machine learning methods for the task, without predicting fingerprints as the intermediate step. The main scheme is to map the structured input to images in the output feature vector space and rank the candidate compounds by calculating their distances to the predicted image in the output space. Both IOKR and MP-IOKR use fingerprints as the output feature vectors and consider equally the present substructures in the fingerprints. It would be more reasonable to take the importance of substructures into account in calculating the distance between two feature vectors for ranking. Indeed, considering a compound 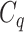 and its two candidates
and its two candidates 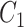 and
and 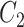 . While
. While 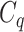 and
and 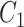 have very few common substructures but biochemically important,
have very few common substructures but biochemically important, 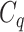 and
and 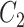 have many common ones but less important. In many cases,
have many common ones but less important. In many cases, 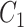 should be ranked higher than
should be ranked higher than 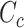 with respect to
with respect to 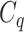 . The above argument encourages that the distance between two output feature vectors should be adaptable to the importance of substructures present in the compound, suggesting learning distance directly from the data, e.g. Mahalanobis-based metric learning.
. The above argument encourages that the distance between two output feature vectors should be adaptable to the importance of substructures present in the compound, suggesting learning distance directly from the data, e.g. Mahalanobis-based metric learning.
Besides fingerprints, the other information on compounds is not taken into account in the learning phase. For example, in the training data set used by [6, 7], graph structures of the compounds are available along with their corresponding fingerprints. We argue that the structures can be useful to provide extra information about metabolites in both the learning and prediction phases. In the literature, a lot of kernels have been proposed to define similarity between two compounds from their corresponding graph structures, e.g. labeled-pair graph kernels [45], Marginalized Graph Kernels [30] and Tree kernels [55], to name a few. Incorporation of the kernels for the output space by learning to combine them into a single one has not been addressed in the existing methods. It might improve the performance of the task and will be considered in our future work.
It is suggested in this survey that statistical machine learning-based methods should be a reasonable choice for the task of metabolite identification. Especially, when the amount of spectra and molecular structure data is increasing over time, the ability of machine learning algorithms to learn and predict relationships inherent in the data will be more enhanced. For example, (MP-)IOKR (Table 1) are currently best kernel-based tools/methods for automatic candidate molecule ranking in competitions (e.g. CASMI 2016, 2017). Additionally, we also emphasize that the combination of different approaches should be also taken into account, by which we can take advantages of them for significant improvement. For example, (MP-)IOKR and CSI:FingerID are using machine learning and fragmentation trees. Another is MetFusion, mentioned in subsection 3.2, combines the results from MassBank (mass spectral library) and MetFrag (in silico fragmentation) to take advantages of complementary approaches.
Key Points
Metabolite identification is an essential and important part in metabolomics to enlarge the knowledge of biological systems. However, it is still a challenging task with a huge number of potentially interesting but unknown metabolites.
We review many techniques/software with different approaches to deal with the task of metabolite identification, which can be divided into the following four groups: mass spectra library, in silico fragmentation, fragmentation tree and machine learning. We mainly focus on machine learning-based methods (used in in silico fragmentation and machine learning approaches) for the task, which are the key to the recent progress in metabolite identification.
We conclude by discussing on advanced machine learning methods, which can lead to further improvement on this task.
Dai Hai Nguyen is currently a PhD student at the Bioinformatics Center in Kyoto University. His current research interest focus on machine learning and bioinformatics.
Canh Hao Nguyen is an assistant professor at the Bioinformatics Center, Institute for Chemical Research, Kyoto University, working on machine learning for graph data, with applications to biological networks.
Hiroshi Mamitsuka is a professor at the Bioinformatics Center, Institute for Chemical Research, Kyoto University, and a FiDiPro professor at the Department of Computer Science, Aalto University, working on machine learning, data mining and application to biology and chemistry.
Funding
This work was partially supported by MEXT KAKENHI Grant Number 16H02868, Grant Number JPMJAC1503 ACCEL JST, FiDiPro Tekes (currently Business Finland) and AIPSE Academy of Finland.
References
- [1]. Allen F, Greiner R, Wishart D. Competitive fragmentation modeling of ESI-MS/MS spectra for putative metabolite identification. Metabolomics 2015;11(1):98–110. [Google Scholar]
- [2]. Andrzejewski D, Zhu X, Craven M.. Incorporating domain knowledge into topic modeling via dirichlet forest priors. In: Proceedings of the 26th Annual International Conference on Machine Learning, 2009. pp. 25–32. Montreal, QC, Canada: ACM. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3]. Bien J, Taylor J, Tibshirani R. A lasso for hierarchical interactions. Ann Statist 2013;41(3):1111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Blei DM, Ng AY, Jordan MI. Latent dirichlet allocation. J Mach Learn Res 2003;3(Jan):993–1022. [Google Scholar]
- [5]. Böcker S, Rasche F. Towards de novo identification of metabolites by analyzing tandem mass spectra. Bioinformatics 2008;24(16):i49–55. [DOI] [PubMed] [Google Scholar]
- [6]. Brouard C, Shen H, Dührkop K, et al Fast metabolite identification with input output kernel regression. Bioinformatics 2016;32(12):i28–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Brouard C, Bach E, Böcker S, Rousu J. Magnitude-preserving ranking for structured outputs. In: Asian Conference on Machine Learning, 2017. pp. 407–22. Seoul, South Korea: ACM. [Google Scholar]
- [8]. Burges CJ. A tutorial on support vector machines for pattern recognition. Data Min Knowl Discov 1998;2(2):121–67. [Google Scholar]
- [9]. Chen H, Fan B, Xia H, et al Massis: a mass spectrum simulation system. 1. principle and method. Eur J Mass Spectrom 2003;9(3):175–86. [DOI] [PubMed] [Google Scholar]
- [10]. Cortes C, Mohri M, Rastogi A. Magnitude-preserving ranking algorithms. In:Proceedings of the 24th International Conference on Machine Learning, 2007. pp. 169–76. Corvallis, OR, USA: ACM. [Google Scholar]
- [11]. Cortes C, Mohri M, Rostamizadeh A.. Algorithms for learning kernels based on centered alignment. J Mach Learn Res 2012; 13(Mar):795–828. [Google Scholar]
- [12]. Cottrell JS, London U. Probability-based protein identification by searching sequence databases using mass spectrometry data. Electrophoresis 1999;20(18):3551–67. [DOI] [PubMed] [Google Scholar]
- [13]. Dass C. Fundamentals of Contemporary Mass Spectrometry, Vol. 16 Hoboken, New Jersey, USA: John Wiley & Sons, 2007. [Google Scholar]
- [14]. De Hoffmann E, Stroobant V. Mass Spectrometry: Principles and Applications. John Wiley & Sons, 2007. [Google Scholar]
- [15]. Dührkop K, Shen H, Meusel M, et al Searching molecular structure databases with tandem mass spectra using CSI: FingerID. Proc Natl Acad Sci 2015;112(41):12580–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16]. Dunn WB, Ellis DI. Metabolomics: current analytical platforms and methodologies. TrAC Trends Analytic Chem 2005; 24(4):285–94. [Google Scholar]
- [17]. Eng JK, McCormack AL, Yates JR. An approach to correlate tandem mass spectral data of peptides with amino acid sequences in a protein database. J Amer Soc Mass Spectrom 1994;5(11):976–89. [DOI] [PubMed] [Google Scholar]
- [18]. Gasteiger J, Hanebeck W, Schulz K-P. Prediction of mass spectra from structural information. J Chem Inf Comput Sci 1992;32(4):264–71. [Google Scholar]
- [19]. Gerlich M, Neumann S. Metfusion: integration of compound identification strategies. J Mass Spectrom 2013;48(3):291–8. [DOI] [PubMed] [Google Scholar]
- [20]. Gönen M, Alpaydın E. Multiple kernel learning algorithms. J Mach Learn Res 2013;12(Jul):2211–68. [Google Scholar]
- [21]. Griffiths TL, Steyvers M. Finding scientific topics. Proc Natl Acad Sci 2004;101(suppl 1):5228–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22]. Gross JH. Mass Spectrometry: A Textbook, 2006. Berlin/Heidelberg, Germany: Springer Science & Business Media. [Google Scholar]
- [23]. Heinonen M, Rantanen A, Mielikäinen T, et al Fid: a software for ab initio structural identification of productions from tandem mass spectrometric data. Rapid Commun Mass Spectrom 2008;22(19):3043–52. [DOI] [PubMed] [Google Scholar]
- [24]. Heinonen M, Shen H, Zamboni N, Rousu J. Metabolite identification and molecular fingerprint prediction through machine learning. Bioinformatics 2012;28(18):2333–41. [DOI] [PubMed] [Google Scholar]
- [25]. Hill DW, Kertesz TM, Fontaine D, et al Mass spectral metabonomics beyond elemental formula: chemical database querying by matching experimental with computational fragmentation spectra. Analyt Chem 2008;80(14):5574–82. [DOI] [PubMed] [Google Scholar]
- [26]. Hummel J, Strehmel N, Selbig J, et al Decision tree supported substructure prediction of metabolites from GC-MS profiles. Metabolomics 2010;6(2):322–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Jebara T, Kondor R, Howard A.. Probability product kernels. J Mach Learn Res 2004;5(Jul):819–44. [Google Scholar]
- [28]. Jenatton R, Audibert J-Y, Bach F.. Structured variable selection with sparsity-inducing norms. J Mach Learn Res 2011;12(Oct): 2777–824. [Google Scholar]
- [29]. Kangas LJ, Metz TO, Isaac G, et al In silico identification software (ISIS): a machine learning approach to tandem mass spectral identification of lipids. Bioinformatics 2012;28(13): 1705–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30]. Kashima H, Tsuda K, Inokuchi A.. Marginalized kernels between labeled graphs. In: Proceedings of the 20th International Conference on Machine Learning (ICML-03), 2003. pp. 321–28. Atlanta, GA, USA: ACM. [Google Scholar]
- [31]. Kloft M, Brefeld U, Sonnenburg S, Zien A.. Lp-norm multiple kernel learning. J Mach Learn Res 2011;12(Mar):953–97. [Google Scholar]
- [32]. Kumari S, Stevens D, Kind T , et al Applying in-silico retention index and mass spectra matching for identification of unknown metabolites in accurate mass GC-TOF mass spectrometry. Analyt Chem 2011;83(15):5895–902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33]. Li J, Sun S. Nonlinear combination of multiple kernels for support vector machines. In 20th International Conference on Pattern Recognition (ICPR), 2010. pp. 2889–92. Istanbul, Turkey: IEEE. [Google Scholar]
- [34]. Lim M, Hastie T.. Learning interactions via hierarchical group-lasso regularization. J Comput Graph Stat 2015;24(3): 627–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35]. Ma Y, Kind T, Yang D , et al MS2Analyzer: a software for small molecule substructure annotations from accurate tandem mass spectra. Analyt Chem 2014;86(21): 10724–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Makarov A. Electrostatic axially harmonic orbital trapping: a high-performance technique of mass analysis. Analyt Chem 2000; 72(6):1156–62. [DOI] [PubMed] [Google Scholar]
- [37]. McLafferty FW, Turecek F. Interpretation of Mass Spectra, 3rd edn Mill Valley, CA: University Science Books, 1993. [Google Scholar]
- [38]. Micchelli CA, Pontil M.. On learning vector-valued functions. Neural Comput 2005;17(1):177–204. [DOI] [PubMed] [Google Scholar]
- [39]. Miller GA. Wordnet: a lexical database for English. Commun ACM 1995;38(11):39–41. [Google Scholar]
- [40]. Mistrik R. A new concept for the interpretation of mass spectra based on a combination of a fragmentation mechanism database and a computer expert system. In: Ashcroft AE, Brenton G, Monaghan JJ (eds). Advances in Mass Spectrometry. Amsterdam: Elsevier. [Google Scholar]
- [41]. Mrzic A, Meysman P, Bittremieux W, Laukens K. Automated recommendation of metabolite substructures from mass spectra using frequent pattern mining. 2017. bioRxiv, p. 134189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42]. Mylonas R, Mauron Y, Masselot A , et al X-rank: a robust algorithm for small molecule identification using tandem mass spectrometry. Analyt Chem 2009;81(18):7604–10. [DOI] [PubMed] [Google Scholar]
- [43]. Newman D, Bonilla EV, Buntine W.. Improving topic coherence with regularized topic models. In: Advances in Neural Information Processing Systems, 2011. pp. 496–504. [Google Scholar]
- [44]. Nguyen DH, Nguyen CH, Mamitsuka H.. Simple: sparse interaction model over peaks of molecules for fast, interpretable metabolite identification from tandem mass spectra. Bioinformatics 2018;34(13):i323–i332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45]. Ralaivola L, Swamidass SJ, Saigo H, Baldi P.. Graph kernels for chemical informatics. Neural Netw 2005;18(8):1093–110. [DOI] [PubMed] [Google Scholar]
- [46]. Rasche F, Svatoš A, Maddula RK , et al Computing fragmentation trees from tandem mass spectrometry data. Anal Chem 2010;83(4):1243–51. [DOI] [PubMed] [Google Scholar]
- [47]. Rasche F, Scheubert K, Hufsky F, et al Identifying the unknowns by aligning fragmentation trees. Anal Chem 2012; 84(7):3417–26. [DOI] [PubMed] [Google Scholar]
- [48]. Rauf I, Rasche F, Nicolas F, Böcker S.. Finding maximum colorful subtrees in practice. J Comput Biol 2013;20(4):311–21. [DOI] [PubMed] [Google Scholar]
- [49]. Ridder L, Hooft JJ, Verhoeven S, et al Substructure-based annotation of high-resolution multistage MSn spectral trees. Rapid Commun Mass Spectrom 2012;26(20):2461–71. [DOI] [PubMed] [Google Scholar]
- [50]. Rojas-Cherto M, Peironcely JE, Kasper PT, et al Metabolite identification using automated comparison of high-resolution multistage mass spectral trees. Anal Chem 2012; 84(13):5524–34. [DOI] [PubMed] [Google Scholar]
- [51]. Scheubert K, Hufsky F, Böcker S.. Computational mass spectrometry for small molecules. J Cheminform 2013;5(1):12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52]. Schymanski EL, Meringer M, Brack W.. Matching structures to mass spectra using fragmentation patterns: are the results as good as they look? Anal Chemistry 2009;81(9):3608–17. [DOI] [PubMed] [Google Scholar]
- [53]. Shen H, Dührkop K, Böcker S, Rousu J.. Metabolite identification through multiple kernel learning on fragmentation trees. Bioinformatics 2014;30(12):i157–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54]. Smith CA, O’Maille G, Want EJ, et al Metlin: a metabolite mass spectral database. Ther Drug Monit 2005;27(6): 747–51. [DOI] [PubMed] [Google Scholar]
- [55]. Smola AJ, Vishwanathan S.. Fast kernels for string and tree matching. In: Advances in Neural Information Processing Systems, 2003. pp. 585–92. [Google Scholar]
- [56]. Srebro N, Shraibman A.. Rank, trace-norm and max-norm. In: International Conference on Computational Learning Theory, 2005. pp. 545–60. Bertinoro, Italy: Springer. [Google Scholar]
- [57]. Stein SE, Scott DR.. Optimization and testing of mass spectral library search algorithms for compound identification. J Amer Soc Mass Spectrom 1994;5(9):859–66. [DOI] [PubMed] [Google Scholar]
- [58]. Tautenhahn R, Cho K, Uritboonthai W, et al An accelerated workflow for untargeted metabolomics using the metlin database. Nat Biotechnol 2012;30(9):826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59]. Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc Series B Methodol 1996;58(1):267–288. [Google Scholar]
- [60]. van Der Hooft JJJ, Wandy J, Barrett MP, et al Topic modeling for untargeted substructure exploration in metabolomics. Proc Natl Acad Sci 2016;113(48):13738–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61]. Vaniya A, Fiehn O.. Using fragmentation trees and mass spectral trees for identifying unknown compounds in metabolomics. TrAC Trends Analyt Chem 2015;69:52–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62]. Wang M, Carver JJ, Phelan VV, et al Sharing and community curation of mass spectrometry data with global natural products social molecular networking. Nat Biotech 2016;34(8):828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63]. Watrous J, Roach P, Alexandrov T, et al Mass spectral molecular networking of living microbial colonies. Proc Natl Acad Sci 2012;109(26):E1743–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64]. Wishart DS. Current progress in computational metabolomics. Brief Bioinformatics 2007;8(5):279–93. [DOI] [PubMed] [Google Scholar]
- [65]. Wishart DS. Computational strategies for metabolite identification in metabolomics. Bioanalysis 2009;1(9):1579–96. [DOI] [PubMed] [Google Scholar]
- [66]. Wishart DS, Feunang YD, Marcu A, et al HMDB 4.0: the human metabolome database for 2018. Nucleic Acids Res 2017;46(D1):D608–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67]. Wolf S, Schmidt S, Müller-Hannemann M, Neumann S.. In silico fragmentation for computer assisted identification of metabolite mass spectra. BMC Bioinformatics, 2017; 11(1):148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68]. Xie P, Yang D, Xing E.. Incorporating word correlation knowledge into topic modeling. InProceedings of the 2015 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 2015. pp. 725–34. Denver, Colorado, USA. [Google Scholar]
- [69]. Yang JY, Sanchez LM, Rath CM, et al Molecular networking as a dereplication strategy. J Nat Products 2013;76(9): 1686–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70]. Yoshida H, Leardi R, Funatsu K, Varmuza K. Feature selection by genetic algorithms for mass spectral classifiers. Anal Chim Acta 2001;446(1–2):483–92. [Google Scholar]
- [71]. Yuan M, Lin Y.. Model selection and estimation in regression with grouped variables. J R Stat Soc Series B Stat Method 2006; 68(1):49–67. [Google Scholar]
- [72]. Zhao P, Rocha G, Yu B.. The composite absolute penalties family for grouped and hierarchical variable selection. Ann Stat, 2009;3468–97. [Google Scholar]


