Smart computational exploration of stochastic gene regulatory network models using human-in-the-loop semi-supervised learning

Abstract

Motivation

Discrete stochastic models of gene regulatory network models are indispensable tools for biological inquiry since they allow the modeler to predict how molecular interactions give rise to nonlinear system output. Model exploration with the objective of generating qualitative hypotheses about the workings of a pathway is usually the first step in the modeling process. It involves simulating the gene network model under a very large range of conditions, due to the large uncertainty in interactions and kinetic parameters. This makes model exploration highly computational demanding. Furthermore, with no prior information about the model behavior, labor-intensive manual inspection of very large amounts of simulation results becomes necessary. This limits systematic computational exploration to simplistic models.

Results

We have developed an interactive, smart workflow for model exploration based on semi-supervised learning and human-in-the-loop labeling of data. The workflow lets a modeler rapidly discover ranges of interesting behaviors predicted by the model. Utilizing that similar simulation output is in proximity of each other in a feature space, the modeler can focus on informing the system about what behaviors are more interesting than others by labeling, rather than analyzing simulation results with custom scripts and workflows. This results in a large reduction in time-consuming manual work by the modeler early in a modeling project, which can substantially reduce the time needed to go from an initial model to testable predictions and downstream analysis.

Availability and implementation

A python-package is available at https://github.com/Wrede/mio.git.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

A substantial level of single-cell variability both between cell-lines but also between individual cells in the same cell-line has long been a prediction of both stochastic simulations in systems biology (Elowitz et al., 2002; Fange and Elf, 2006; Lawson et al., 2013; McAdams and Arkin, 1999; Sturrock et al., 2013, 2014) and experimental observations (Chubb et al., 2006; Raj et al., 2006). Single-cell transcriptomics such as scRNA-Seq (Haque et al., 2017) and single-cell proteomics (Budnik et al., 2018) have offered snapshots of this variability in RNA and protein expression for a large number of genes. Comparative studies overlaying such transcriptomics and proteomics data have also recently highlighted how protein expression may or may not be correlated with the expression of its mRNA both in E.coli (Taniguchi et al., 2010) and recently in mouse embryonic stem cells (Budnik et al., 2018), hinting to the complexity in regulation arising from non-linearly interacting pathways. While single-cell omics and modern analysis pipelines make it possible to quantify differentially expressed genes across a population (Perkel, 2017), these techniques do not enable direct study of the precise mechanisms that give rise to the observed variability. Quantitative, stochastic and dynamic models of these gene regulatory networks (GRN), on the other hand, can be used to predict how such nonlinear interactions result in observed gene expression profiles and how they can explain cell–cell variability. Discrete stochastic simulation of the spatial and temporal dynamics of intracellular biochemical reaction networks has thus become a central tool to study GRNs in system biology (Drawert et al., 2016b; Elowitz et al., 2002; Sturrock et al., 2013, 2014; Vilar et al., 2002). These simulation methods capture intrinsic noise due to low copy numbers of the involved molecular species (Gillespie et al., 2013), and can be used to make predictions about both the system dynamics and the variability in behaviors across a cell population.

However, the use of modeling to generate predictions in the absence of prior knowledge about system behavior is challenging due to the large uncertainty in the reaction network interactions and the large amounts of unknown kinetic rate parameters. To explore models under this uncertainty with the objective of obtaining a qualitative understanding of the type of interesting behavior the model suggest about the underlying system, the modeler uses parameter sweeps in which the parameters are varied over a large range and the simulation results are analyzed in postprocessing steps. There are two main problems with this approach. First, in order to encode the criteria for postprocessing analysis, the modeler needs to have prior hypotheses about model behavior. Thus, there is a substantial risk to miss interesting dynamics that was not already anticipated. Second, due to the curse of dimensionality global parameter sweeps become very large and will require massive computations and time-consuming manual work by the modeler to inspect output time series data and manually fine-tune sampling of the parameter space. Related work concerning parameter sweeps of stochastic biomolecular networks have been conducted in the past in the area of statistical model checking, a subarea within formal verification (Bortolussi and Silvetti, 2018; Ceccarelli et al., 2015; Clarke et al., 2008; Češka et al., 2017; Jha et al., 2009). These methods infer parameter regions by statistically evaluating temporal logics directly on the discrete states of the Markov process underlying the stochastic simulations. While these methods are elegant approaches to quantitatively assess different properties and feasible regions of a model they remain challenging for biologists to interpret due to the lack of knowledge in formal verification methods. Further, the user of the methods need to explicitly define which logics to be evaluated which can be burdensome if the user simply wants to get an initial understanding of the behavior of the model. We suggest a simpler approach using summary statistics or time series features that can be automatically generated and evaluated on the full trajectory paths of the molecular species. Since summary statistics have been extensively used and engineered for likelihood-free parameter inference (such as Approximate Bayesian Computation) and Monte Carlo analyses, they are remain reproducible and familiar to the systems biology community. Further, to the best of our knowledge we have not seen any statistical model checking tools which enables the user to interactively propose what might be an interesting behavior and accordingly adjust the parameter sweep to those preferences.

In this paper we have developed a smart workflow framework based on human-in-the-loop semi-supervised learning and black-box stochastic models with the objective to greatly reduce both the manual work involved in going from an initial model to insight about the principle behavior of the model. The main contribution of our smart workflow tools is to greatly reduce the amount of manual work required by the modeler by (i) automating the process of generating features (e.g. which can be used to engineer summary statistics) in the absence of prior information, and (ii) replacing model-specific manual postprocessing with large-scale autonomous analysis enabled by user interactivity.

We demonstrate the methodology of our workflow using a GRN model of a circadian clock based on positive and negative regulatory elements. The model, which has 9 species, 18 reactions and 15 reaction rate parameters involves two genes with the translated transcription factors acting as positive and negative regulatory elements, respectively. This model was developed in one of the first studies highlighting the importance of intrinsic molecular noise in systems biology. The model can give rise to robust oscillations in the presence of noise, and the parameter values and the initial condition to achieve robust oscillations with a period of 24 h is well known (Vilar et al., 2002). However, for demonstration purposes, here we assume no a priori knowledge about the system dynamics and demonstrate how our interactive workflow lets us efficiently explore the high-dimensional parameter space, discover oscillatory dynamics as the principal behavior and interactively label such behavior as interesting. The exploration process for this model example can be divided into three logical phases; (i) the initial exploration and labeling, (ii) semi-supervised label propagation and (iii) zooming in on region of interest (ROI) and engineer summary statistics.

2 Materials and methods

2.1 A smart workflow for model behavior discovery for high-dimensional models

The developed methodology is a smart computational workflow for screening and exploring for different behavioral properties of a black-box candidate model based on globally searching in the parameter space. The proposed workflow is a heuristic approach for getting an initial understanding of qualitative behaviors in a model. It does not guarantee to find all behaviors and neither is there any robustness analyses of behaviors involved, for this substantial work has to be contributed to smart experimental designs involving adaptive sampling of parameter space which we will save for future work. Figure 1 outlines the basic approach of our workflow.

Fig. 1.

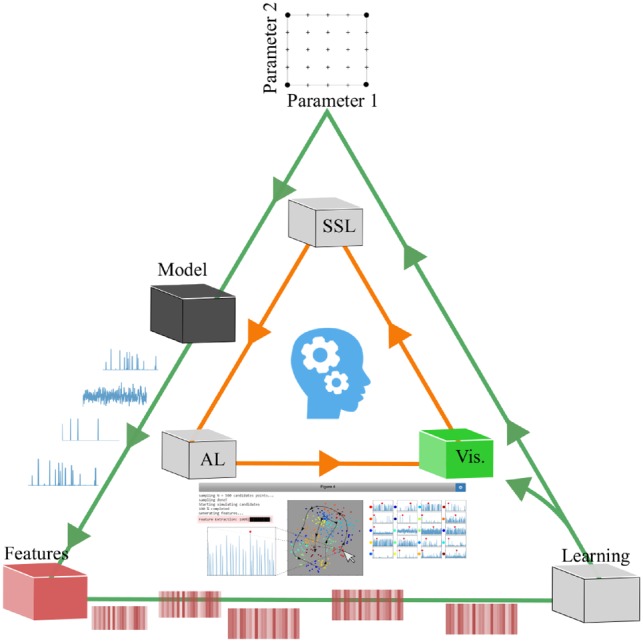
Smart Exploration workflow. The workflow starts with the user defining a parameter experimental design (top) to build a first batch of different parameter settings. Each parameter point is then realized in the model and corresponding simulator (black), which will output the trajectories for each realization. The raw trajectories (time series) are then converted to feature arrays (red) based on time series analysis. The data from the sweep will then enter a learning cycle (white), where the modeler will be able to visualize and interact with the data points (which corresponds to a parameter point) in a reduced 2D or 3D feature space using a dimension reduction method where points in proximity to each other are assumed to have similar qualitative behavioral properties. Clicking on the scatter points will show the raw simulation output trajectory of a user specified molecular species (green). While exploring, the modeler can give feedback to the system by labeling data points. Only a few labeled data points are needed since the data will then be fed into a semi-supervised learning algorithm (SSL). Using the semi-supervised model to infer labels of unlabeled data points, the system will also be able to evaluate the label uncertainty. This uncertainty can be used by active learning (AL) to ultimately suggest data points that the modeler might not yet have discovered or to simply improve the semi-supervised model. Once the modeler is satisfied with the current labeling of data points the experimental design can be fine-tuned to include new parameter points, e.g. zoom in on ROIs of points according to the predictions of the semi-supervised model

Using a transductive semi-supervised approach enables the modeler to change their preferences, and thus the labeling, at any time during the workflow and only requires subset of points to be labeled. As the model exploration continues and more parameter points are added, the modeler is able to focus on particular ROIs, either according to the predictions of the semi-supervised model or by manual inspection. This in turn enables hierarchy of the exploration workflow. By neglecting points that are predicted as non-interesting we can solely turn our focus to the interesting points generated by our simulator. This interactive human-in-the-loop machine learning approach is at the core of our workflow, and illustrated further in Supplementary Video S1. In the higher level exploration, the modeler will be able to tweak and engineer new summary statistics to fine-tune the separations of interesting and non-interesting trajectories. In the following paragraphs we will outline the specifics of each individual unit of the smart exploration workflow which are included in Figure 1.

2.2 Parameter experimental design

To initiate the workflow we need an experimental design of the model parameter space. This involves defining global bounds for each parameter to define the search space in which parameter points (candidates) will be drawn following some density or picked in a deterministic manner using, e.g. factorial design. In case of little a priori knowledge of the model, one might for example start with a very simple exhaustive approach involving a uniform density bounded by minimum and maximum values for each parameter. Once a first batch has been processed by the workflow and we have gained more knowledge about the model behavior, these designs can be redefined according to the modelers preferences, e.g. by mapping interesting realizations to parameter space and centralizing new designs around these corresponding parameter points. In practice, this range can be defined based on biophysical arguments, but it can be quite large (order of magnitudes). The experimental design step in the workflow is very critical for the efficiency of parameter sweep studies. Therefore, we plan to dedicate substantial future work on this step. Currently, If another experimental design than random uniform sampling, factorial design or Latin hypercube sampling is desired, the user needs to implement those.

2.3 Stochastic simulation of gene regulatory networks

The most commonly employed mathematical framework for discrete stochastic simulations of chemical kinetics is continuous-time discrete-space Markov processes (Gillespie, 1992; Van Kampen, 1992). The Stochastic Simulation Algorithm (SSA) (Gillespie, 1976), commonly referred to as the Gillespie algorithm, generates statistically exact realizations from such processes. In our workflow the SSA will be treated as a black-box simulator, evaluated on a realization of the parameter points

$$S_j:=\mathit{Model}({\theta }_j,T)\hspace{1em}\mathit{for} j=1,2,\mathrm{..},N$$ (1)

where T is the simulation time and θ_j a parameter point. Each realization of the model will contain the copy number evolution over T for all molecular species. We use the GillesPy2 (Abel et al., 2017) package for simulations. GillesPy2 is part of the StochSS (Drawert et al., 2016b) suite of tools, and wraps StochKit2 (Sanft et al., 2011).

2.4 High-throughput generation of summary statistics using comparative time series analysis

To represent simulation results in feature space rather than the raw simulation output, each batch of realizations passes a feature generating process where it is possible to generate several hundreds of features based on time series analysis. Each individual simulation result S_j corresponding to a particular realization of θ_j results in a feature vector

$$F_{j,s}:=[f_1(S_{j,s}),f_2(S_{j,s}),\dots ,f_n(S_{j,s})]\in {\mathbb{R}}^n\hspace{1em}\forall \hspace{0.17em}j,s$$ (2)

for a particular species s contains features f based on time series analysis, such as different moments, autocorrelation, Fast Fourier Transform (FFT) and many more. The system supports a minimal set of features to be generated for an initial large scale sweep design. We use the python package TSFRESH (Christ et al., 2018) (Time Series Feature extraction based on scalable hypothesis tests) for automatic time series feature extraction. TSFRESH have a large library of time series feature functions, which ease the process of engineering features for various time series classification problems. The set of features used in the workflow can be manipulated to contain any feature set supported in TSFRESH as well as user defined functions such as correlations between molecular species.

2.5 Visualization and interactivity

Once the feature generation is finished the system will present the feature space in a reduced feature space using a specified dimension reduction (DR) method. Here, we currently support PCA (Pearson, 1901), kernel-based PCA (Schölkopf et al., 1998), t-SNE (Maaten and Hinton, 2008) and UMAP (McInnes and Healy, 2018). The support of several DR methods is useful for getting different perspectives of the data due to each method’s individual properties. The non-linear methods support different kernels and different distance metrics in case of high-dimensional features spaces. Using interactive Jupyter notebooks (Ragan-Kelley et al., 2014) as illustrated in Supplementary Video S1, the modeler can then navigate and explore different parameter points in a 2D or 3D scatter plot which is a mapping of the full feature space based on the dataset ${\left\{F_{j,s}\right\}}^N$ for a specified species s. By clicking on points in the scatter plot, a specified trajectory of a particular species will show up next to the scatter plot. By using the assumption that data points in close proximity to each other have similar behavior, the effort needed to locate different or similar behaviors of the model is greatly reduced. The modeler will then have the opportunity to give feedback to the system about preferences over different model behaviors seen in the data by labeling individual points.

2.6 Semi-supervised label propagation and active learning

The labeling feedback can be used in a semi-supervised fashion for learning the preferred behaviors of unlabeled parameter points. This involves fitting a model to the data which models the associated labels (model behaviors) to parameter points which has not yet been looked at in the interactive exploration. If the model is probabilistic, we can infer some parameter points as being more uncertain than others. This enables us to: (i) direct the modelers attention to points that might not have been noticed by the modeler and (ii) query the labels of these uncertain realizations to improve the accuracy of the model. The latter is commonly referred as active learning. Our current semi-supervised approach is label propagation by Gaussian Random Fields (GFR) (Zhu et al., 2003b). In a semi-supervised setting, only a few points in the dataset are given a label, while the others remain unknown. GFR together with the properties of harmonic functions propagate the information of labeled instances to their neighbors. This follows from the assumption that nearby points (neighbors) have similar label information. By constructing a graph from the data, where nodes represent instances and edges the similarity between them, we can propagate the label information along the graph edges. The graph is represented by the NxN weight matrix W which measure the similarity between points. Using the Gaussian Radial Basis Function (RBF) as the similarity measure we get

$$w_{\mathit{ij}}=\text{exp}\hspace{0.17em}\left(-\sum _{k=1}^n\frac{{(x_{\mathit{ik}}-x_{\mathit{jk}})}^2}{{\sigma }_k^2}\right)$$ (3)

where $x\in {\mathbb{R}}^n$ can either be the full feature vector F_j belonging to parameter point θ_j for a specified species s or the same point represented in the reduced feature space. σ_k is the length scale hyperparameter for feature k. We use the reduced dimensional space to propagate our labels, since this is the visual space that we explore during labeling. We also use the same length scale for both dimensions in this space, i.e. an isotropic RBF. By partitioning W and the label vector f into partitions of labeled versus unlabeled instances, the label propagation over the unlabeled instances y_u corresponds to solving the linear system

$$y_u={(D_{\mathit{uu}}-W_{\mathit{uu}})}^{-1}{W}_{\mathit{ul}}{y}_l={(L_{\mathit{uu}})}^{-1}{W}_{\mathit{ul}}{y}_l$$ (4)

where L is the graph Laplacian and D is the diagonal matrix with entries $d_i=\sum _j{w}_{\mathit{ij}}$. We use the normalized graph Laplacian and remove clamping of labeled points, i.e. labeled points can change their labels to some degree (Zhou et al., 2004). There is an elegant probabilistic interpretation of the label propagation above. Namely, it can be seen as a random walk procedure over the graph. The equation above can be expressed by the normalized transition matrix $P=D^{-1}W$. Starting a random walk from an unlabeled node i, P_ij is the probability of walking (transitioning) to node j after one step. The walk will continue until a labeled node has been reached. y_i then becomes the probability of node i reaching a node of a particular label. The probabilistic framework enables the usage of active learning based on uncertainty of propagated labels over the graph. One simple way of measuring the uncertainty is by calculating the entropy

$$H(y_i)=-y_{i}l\mathit{og}(y_i)-(1-y_i)\mathit{log}(1-y_i)$$ (5)

where a high entropy would correspond to high uncertainty. Thus, by arranging $H(y_u)$ we can query the modeler to label uncertain points, which will decrease uncertainty in the model and can also give new insight about the exploration. The average label entropy will also be used as the loss function to fit the length scale parameter using a global optimizer such as basin hopping (Wales and Doye, 1997). To enforce a smoothness over the graph edges and avoiding overfitting we will add a ridge penalty to the loss.

2.7 Hierarchical exploration by zooming in on ROIs to engineer summary statistics

At any stage after initiation of the workflow it is possible to ‘zoom in’ on particular ROIs in the reduced feature space or in parameter space. Here we refer the ‘zoom in’ as a way to isolate an ROI and explore it in more detail. This opens up the opportunity to fine-tune and engineer ad hoc summary statistics for the purpose of separating the interesting parameter points versus the non-interesting. This can either be done by manually adding new features using knowledge about suitable features, or to naively generate many features which then can be used for feature selection.

2.8 Interactive parallel computing in clouds using Dask and MOLNs

The simulation (using SSA) and the feature generation are both embarrassingly parallel, and is well suited for parallelism in cloud computing infrastructure. We use the MOLNs (Drawert et al., 2016a) orchestration software part of the StochSS suite of tools to deploy virtual clusters. For this work we have extended MOLNs with support for Dask, a framework for parallel computing in Python (Dask Development Team, 2016). Apart from deploying Dask and Jupyter notebook, MOLNs installs the tools needed for scalable stochastic computational experiments of biochemical reaction networks. MOLNs is able to dynamically deploy clusters in a range of public and private clouds. This approach makes our software and workflow require minimal effort on setting up and configuring software, and allows for highly scalable parallel computing. For the experiments in this paper we made use of the SNIC Science Cloud, a community cloud based on OpenStack, provided by the Swedish National Infrastructure for computing.

3 Results

3.1 Phase 1: an initial exploration reveals oscillations as a principal behavior of the model

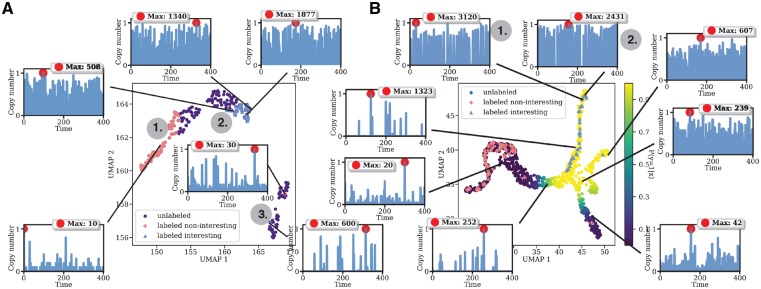
Figure 2A illustrates the first initial phase of the smart model exploration workflow. Using Jupyter interactive notebooks, the modeler has a central role to guide the workflow during exploration. Assuming that the model contains high diversity in the model behavior, a global sampling of parameter space, with an initial small batch size, can ease the process of identifying interesting behaviors for the modeler by keeping the visual information at a comprehensible level. Here we chose an initial batch size of 1000 realizations which span the entire initial sweep design (Supplementary Table S1), which is provided by the modeler. Further, each parameter point is simulated in parallel with the stochastic simulation algorithm (SSA). A natural bottleneck in the simulator when using a wide span of parameter values is the possibility of parameter combinations that leads to uncontrolled growth, or explosion, of some chemical species. This will cause the simulation time to become very large. To avoid this we set a user defined timeout (here 50 s/realization) for the simulation time, effectively filtering our bio-physically unrealistic, exploded trajectories. Once the simulation batch has completed, each simulated trajectory of the species passes through a summary statistics, or feature, generation process using TSFRESH. A minimal set of summary statistics comprising of extreme values, mean, median, standard deviation, variance and the sum are initially generated, converting the raw time series trajectory into an array of features. To visualize and interact with the data, a dimensional reduction (DR) of the feature space corresponding to a particular species is performed. In this example we use UMAP with Euclidean distance as our metric (McInnes and Healy, 2018). At this point, the modeler is able to interact with each individual parameter point in a low dimensional representation of the feature space. By clicking on a parameter point, the corresponding trajectory of a specified species is shown and points in close proximity to each other have similar behavior, which aids the modeler in initial exploration (see Supplementary Video S1). Observe that the modeler has to tune and play with the hyperparameters of the DR method as part of the exploration. Figure 2A shows the reduced feature space on the Activator protein using UMAP. In our example, the first batch resulted in 244 out of 1000 realizations completing within the threshold used (50 s/realization), the remainder resulting in unphysical explosion of one or more species. As the modeler explore the data she will be able to label interesting clusters or individual parameter points according to her preference. Here, we observed that the left hand side of the reduced feature space corresponds to trajectories with consistent low copy numbers of the transcription factors (Fig. 2A ①), and they are labeled as non-interesting. The upper right cluster on the other hand have more reasonable copy numbers and a bursting behavior of high frequency (Fig. 2A ②), a phenomena which can (with parameter tweaking) result in oscillations. As the cluster elongates to the right of the feature space, the higher the copy number becomes. With our preferences these were labeled as interesting. Further, we observe two outlier clusters, where the labeling become more uncertain. One parameter point from each cluster was labeled. (Fig. 2A ③). Phase 1 of the workflow can be repeated as many times as desired to add more data and support for individual classes. We conducted three batches of the same size as the first batch and following the same uniform sampling of the parameter space. A few more samples was added to the interesting and non-interesting class, respectively.

Fig. 2.

(A) First phase of the smart model exploration workflow. After an initial, coarse parameter sampling, and after generating summary statistics using a minimal set of time series features, the simulation output (here represented in feature space of the Activator protein) is embedded into a lower dimensional representation using UMAP. This plot is then presented to the modeler as an interactive plot in a Jupyter Notebook and the modeler quickly inspects a few representative samples in the data clusters. The modeler will be able to label samples according to their preferences. ① Non-interesting behavior with very low copy numbers. ② Bursty behavior and potentially interesting. ③ Outliers. (B) More samples added to the parameter sweep (947 points in total), a few more points has been labeled. Using label propagation gives predictions of unlabeled points. Yellow color of unlabeled points corresponds to a high probability of belonging to the interesting class (y = 1). Two trajectories of particular interest were found (① and ②)

3.2 Phase 2: Semi-supervised learning to propagate labels to unlabeled time series

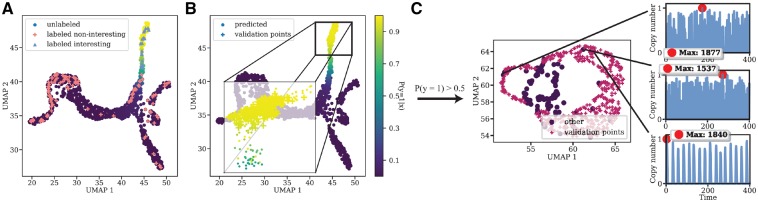
Phase 1 results in the modeler gaining an initial understanding of the model’s behavioral diversity, and in some few initial labeled parameter points representing this diversity. After simulating more data and performing a new dimension reduction on the data, the workflow uses a semi-supervised learning algorithm to predict labels of the unlabeled realizations. Here, we use label propagation in the reduced dimensional space, which uses the properties of Gaussian Random Fields and harmonic functions (Zhou et al., 2004). After propagating the labels, every single parameter point in the current state of the exploration will have an associated probability of belonging to a label (Fig. 2B). Since label propagation uses the notion that similar data points have similar labels, the modeler can use this information to ‘guide the eye’ in an otherwise very cluttered dataset, which can markedly reduce manual work. Further, the modeler will be able to map out points with high label uncertainty by directly observing the probability (green color in Fig. 2B). Usually the highest uncertainty is at the boundary of two labels in feature space or in the outliers. One way of measuring the uncertainty or information gain associated with groups or individual realizations can for example be entropy-based or based on the generalization error (Zhu et al., 2003a). By letting the modeler label a few of the realization with the highest e.g. entropy, we will efficiently gain more information about the preferred label distributions and thus get a better semi-supervised model. This is commonly referred as active learning. It is straightforward for the modeler to also map the gained label propagation information to parameter space. This can be used to fine tune the parameter sweep to particular ROIs. In our example, we were able to locate two trajectories of particular interests (Fig. 2B ① and ②) which gave a high probability of belonging to the interesting class. Observe that the modeler is able to change their preferences at any time. This is one of the advantages of using a transductive semi-supervised approach such as label propagation. Once we found these two interesting trajectories, our preference was changed to focus on this particular ROI (Fig. 3A). Once the modeler have reached the point where she is satisfied with the current state of the system (i.e. she have found some interesting trajectories and would like to find more of them) she can ‘freeze’ the current state, i.e. use the current dimension reduction mapping and labels to project new parameter points onto the same space and let the label propagation predict the outcome of these points. If new points get a low probability of belonging to the interesting class we will neglect them, thus the predictions from the label propagation will act as filter to filter out non-interesting realizations. To demonstrate this, we consciously sampled parameter points known to result in robust oscillations with a period of 24 h and with copy numbers ranging between 1200 and 1500 for the Activator protein. Figure 3B, show that all these parameter points become projected onto our ROI. Further, using a predictive probability threshold of 0.5, the label propagation will classify all of them as interesting.

Fig. 3.

(A) The parameter sweep continues. Here a total of 1553 samples are being observed. Label propagation enables the modeler to change and add labels to points as the sweep continues. Here, the focus and thus the preferences has been directed to the upper part of the data blob. A new label propagation is performed yielding new probabilities of unknowns. (B) To simulate the process of a massive parameter sweep and the robustness of the current state of the system, we sample parameter points associated with robust oscillations. These points become mapped directly to our ROI. To reduce the uncertainty in the prediction model, the modeler can be queried to label points with high uncertainty using e.g. entropy based measures. (C) Zooming in on ROIs by neglecting points with low probability of belonging to the interesting class. We observe some non-robust outliers in the ROI. This suggest that we need other features than the minimal set to separate these from the robust oscillations

3.2 Phase 3: Zooming in on the ROIs to engineer summary statistics

Phase 2 gave us a ROI which enables us to filter out non-interesting parameter points from the sweep using the dimension reduction mapping and a predictive threshold on the output from label propagation. Obviously, the modeler would like to inspect all points that pass the filter, i.e. ‘zoom in on the ROI’. To do this we simply create a separate projection using a DR method and explore the data (Fig. 3C). At this point in the smart workflow, it becomes more difficult to separate different behaviors within the ROI using only the initial minimal set of summary statistics. Ideally we could like to find new or additional summary statistics which can separate the robust oscillations from all other points in the ROI. To do this, we simply use our knowledge about suitable summary statistics to capture the oscillating properties of a time series, e.g. features based on autocorrelation or Fast Fourier Transform (FFT). After some testing with different combinations of such summary statistics we found three which fitted well (Fig. 4A), namely (i) absolute sum of changes, (ii) mean aggregate of autocorrelation with various lags and (iii) variance aggregate of an autocorrelation with the same lags (see Supplementary Information). This process suggests that we can use sequences of ROIs to ultimately find more of the interesting trajectories and to engineer suitable summary statistics.

Fig. 4.

(A) By using features related to measures of oscillating patterns (e.g. autocorrelation) we are able to separate the outliers in the ROI. This can be seen as a feature engineering for robust oscillations. Here we added ‘absolute sum of changes’ feature and aggregates of autocorrelation features which clearly contribute to the separation from outliers. (B) The complete sweep dataset with newly found features to separate noise from robust oscillations. Possible objective for classifiers, Monte Carlo estimation and likelihood-free parameter inference

4 Discussion

Using features to measure similarity between simulations results instead of the raw time series gives us several advantages. Mainly it opens up the opportunity for the smart system to be highly generalized to different models and objectives. The simulator itself can be regarded as a black-box and thus easily interchangeable. Further, it enables a wide range of machine learning techniques to be applied in the system, which do not have to be specialized for temporal data. Secondly, using features associated with time series analysis can be more informative and descriptive than raw time series and can further be used as summary statistics in complementary analysis such as likelihood-free parameter inference.

In this paper we exemplified the new tools on a model of a genetic oscillator. We would like to point out that the methodology is designed for generality, to be able to discern between different types of new behavior. In the Supplementary Material, we give a complementary example where the workflow discerns between different states in bistable systems, and in which a downstream classifier is used to map out regions in parameter space giving rise to the discovered behaviors.

The proposed smart workflow and its current state is the first version towards a greater toolkit designed for model exploration. The focus of this paper has been on the human-in-the-loop interaction and semi-supervised learning. We have not considered the mapping of qualitative behaviors to parameter space. In future work we plan to implement adaptive sampling using active learning to conduct robustness analyses of the interesting regions.

One downside of our workflow is the computational burden of computing features if they are many. However, for the purpose of later large-scale downstream analysis of a model, a subset of features can be used. Note that, in our example we used our knowledge to test different summary statistics in a manual manner. However, in cases where this is not possible we can use feature selection techniques on a larger set of features which we have plan to add support for in out toolkit. For example, the similarity matrix used in the label propagation is computed by the pairwise distance using the radial basis function (RBF). A feature selection approach could be to learn the weights (corresponding to the length-scale hyperparameter per summary statistics) for an anisotropic RBF. An important note is to be cautious of overfitting when using a large set of summary statistics and performing feature selection, since we want our predictions to be generalized for new and unseen behaviors.

In this work we have used the Gillespy2 Python Package to simulate the gene regulatory models. It should be noted that the smart workflow methodology is agnostic to the solver used – popular packages such as PySB (Lopez et al., 2013), BioNetGen (Arora et al., 2016) or COPASI (Lee et al., 2006) could be integrated easily.

The current state of the system support automatic features to be generated via the TSFRESH package. However, in future releases we want to use our own feature functions designed specifically for different qualitative behaviors. The idea is that the modeler should be able to preselect possible interesting behaviors, and features should be chosen accordingly in an automatic fashion. In the same manner it should filter out physically unrealistic realization based on appropriate features or events.

Our future objective also involves to build inductive classifiers which can predict newly generated realizations in a downstream process for massive parameter sweeps. Here, the classifier would act as filter which can structure the simulation results into qualitative interesting behaviors (see Supplementary Information Toggle example where we use the label propagation model as transductive downstream classifier) and e.g. be used to save those realization into prioritized storage. This classifier would then be easily interchangeable between modelers and different models which contain similar qualitative behaviors. As an example, using the engineered features (Results: Phase 3) on the complete dataset we are clearly able to linearly separate interesting points from non-interesting in the reduced dimensional space (Fig. 4B). This suggests that we can use a linear classifier as a compact model for filtering out robust oscillations in massive parameter sweeps. Moreover, a classifier like that could be used for more sophisticated and automatic approaches for sampling parameter points. By using sampling algorithms which utilizes both exploration (e.g. space filling) and exploitation (i.e. ‘zooming’ in on ROIs or classified as interesting by a classifier) we would greatly reduce the effort needed to fine-tune parameter space searches. Such algorithms are often based on sequential Monte Carlo techniques (Bortolussi and Silvetti, 2018; Zamora-Sillero et al., 2011).

5 Conclusion

Using techniques from semi-supervised machine learning, we have deviced a workflow for exploring high-dimensional stochastic models of gene regulatory networks (here conducted on a genetic oscillator) that greatly reduce time to go from an initial prototype model to qualitative insights and predictions. Our human-in-the-loop exploration workflow effectively removes the need for hand-crafted analysis scripts based on prior information or hypotheses. This work has been conducted in the context of the StochSS project (Drawert et al., 2016b). StochSS, or Stochastic Simulation Service, is a cloud-native software as a service for constructing gene regulatory network models and to scale their simulations in public or private clouds (Drawert et al., 2016a). In future work we plan to use the herein presented methodology to develop a Model Exploration Toolkit (MET); intelligent cloud services with the objective of letting users of StochSS rapidly input various versions of gene regulatory models and semi-automatically exploring them for interesting behavior. By training ensembles of inductive classifiers for different identified behaviors as outlined above, we have the opportunity to further automate identification of interesting dynamics by letting users share and deploy their classifiers. This vision outlines a collaborative modeling support systems that improves in the degree of automation by incorporating the knowledge of the expert modelers using it.

Funding

This work was supported by the Center for Interdisciplinary Mathematics graduate school, the Göran Gustafsson foundation and the NIH National Institute of Biomedical Imaging And Bioengineering (NIBIB) under award no. 2R01EB014877-04A1.

Conflict of Interest: none declared.