Mangroves protect coastal economic activity from hurricanes

Significance

The increasing losses from tropical cyclones in developing countries highlight the importance of understanding how natural habitats can be used to protect assets and economic activity against this hazard. Here, we estimate the relationship between hurricane strength and economic damages in Central America and explore how the presence of mangrove habitats mitigates these losses. We find that hurricanes lead to significant losses in economic activity in the short run and that wide mangrove belts are capable of mitigating these losses. One important implication of these findings is that only large-scale mangrove conservation efforts are likely to provide a benefit in terms of protection.

Abstract

This paper evaluates whether mangroves can mitigate the impact of hurricanes on economic activity. The paper assembles a regionwide panel dataset that measures local economic activity using nightlights, potential hurricane damages using a detailed wind field model, and mangrove protection by mapping the width of mangrove forests on the path to the coast. The results show that hurricanes have negative short-run effects on economic activity, with losses likely concentrated in coastal lowlands that are exposed to both wind and storm surge hazards. In these coastal lowlands, the estimates show that nightlights decrease by up to 24% in areas that are unprotected by mangroves. By comparison, the impact of the hurricanes observed in the sample is fully mitigated in areas protected by mangrove belts of 1 km or more.

More than 1.4 billion people live in coastal areas at risk for tropical cyclones (1). Cyclone damage is expected to increase as a result of more frequent high-intensity storms created by climate change and increased exposure created by the ongoing movement of people and assets to high-risk coastal areas (2–4). While interventions, such as early warning systems, may be cost effective in terms of saving lives (5), coastal defense interventions to protect assets and prevent disruptions to economic activity tend to be expensive to construct and maintain (e.g., seawalls or embankments) and can have adverse ecological side effects (6).

An alternative coastal defense intervention is the conservation and restoration of natural habitats that can provide protection against cyclones (7). Mangrove forests have received considerable attention because their aerial root and canopy structure makes them capable of reducing wave action (8–11), wind velocity (12), and storm surge (13–16). While there is an ongoing debate on whether mangroves are effective at saving lives (5, 17), relatively little is known about their value in terms of protecting assets and mitigating disruptions to economic activity. Recent work in ref. 18 suggests that mangroves can provide protection to coastal communities, but the extent to which mangroves can alter the relationship between cyclone strength and economic damages is still unknown.

Building on the literature that uses wind field models to estimate the damage of hurricanes (19–26), we fill this gap by estimating how mangrove forests change the relationship between cyclone strength and damages. We focus on Central America because hurricanes occur frequently; because its coastline is highly exposed to storm surge (1), which is one of the most damaging features of hurricanes; and because coastal areas have historically sustained mangrove forests (27) capable of providing protection.

Intuitively, because mangrove forests act as barriers to obstruct flow and buffer winds, protection is expected to increase with their density and width (28). Mangroves in Central America may be particularly well suited for providing protection. Specifically, in terms of density, mangroves near the equator are characterized by dense aboveground biomass and by less pronounced seasonal variation in their density (29). Moreover, the dense stilt root systems of the Rhizophora spp., which is commonly found in Central America, have been shown to be effective at dissipating wave energy (11, 15) and withstanding storms (30, 31). In terms of width, mangrove belts are still found in the region despite significant deforestation (32). Wide mangrove belts are likely to be an important feature of protection against storm surge as argued in ref. 15.

To estimate whether mangroves can reduce hurricane damage, we divide Central America into 1-${\mathrm{k}\mathrm{m}}^2$ grid cells and construct a cell–year panel for the 2000 to 2013 period. The panel combines measures of economic activity, potential hurricane damage, and mangrove protection. Specifically, we use remote sensing data on nightlights to measure local economic activity. Nightlights have been shown to be a good proxy of economic activity (reviewed in ref. 33), and their high spatial resolution is ideal because the economic impact of tropical cyclones has been shown to be highly localized (22, 25). We measure potential hurricane damages using predicted wind speed from the wind field model of ref. 34. The model is calibrated for Central America, has been validated with historical data, and provides wind speed at the same spatial resolution as the nightlights data. To translate wind speed into potential destruction, we use the damage function proposed in ref. 3. To measure the degree of mangrove protection, we follow ref. 5 and calculate the width of mangrove, as measured in 2000, along the closest path to the coast.

We estimate the causal impact of hurricanes on our proxy of economic activity by regressing nightlights on our damage index. The identifying assumption is that hurricane strikes are exogenous conditional on cell and year fixed effects. We then explore the heterogeneity in the impact of hurricanes by interacting our damage index with the predetermined width of mangrove on the path to the coast.

Our results fall into 2 categories. The first set of results shows that, consistent with previous literature, hurricanes have negative short-run effects on economic activity (20–25, 35–38). The estimated effect size suggests that a category 3 hurricane in the Saffir–Simpson scale can reduce our proxy of economic activity by 16%. We additionally document a 17% reduction in economic activity for coastal lowlands, which are at risk from both wind and storm surge damage. The second set of results shows that the impact of hurricanes in these storm surge-prone areas decreases as the width of mangrove increases. To ensure that the effect is driven by the mangrove vegetation itself and not by other characteristics of the location of mangrove habitats, we further restrict our sample to cells that have been historically protected by mangrove habitats. Our preferred specification explores the impact of hurricanes in steps of 1-km mangrove width. We find that, in areas with less than 1 km of mangrove width, a category 3 hurricane can decrease nightlights by roughly 24%. By comparison, areas with a mangrove width of 1 km or more are unaffected. To show that these findings are not driven by a mechanical relationship between mangrove width and distance to the coast, we additionally show that, in coastal lowlands, the impact of hurricanes does not decrease with distance to the coast in the absence of wide mangrove belts.

Our findings contribute to the literature on the storm-protective services of mangroves (ref. 39, a review; ref. 18, recent work). We add to this literature by providing empirical estimates of how mangroves moderate the relationship between hurricane strength and local economic damages. In addition to modeling hurricane strength, our approach also extends previous efforts by flexibly estimating the heterogeneous impact of hurricanes across levels of mangrove width. By not assuming a linear relationship, we can show that areas protected by wide mangrove belts drive the reduction in hurricane impact. Our paper also estimates the protective service of mangroves using 1-km cell-level data. By fully exploiting the high spatial resolution of our measure of economic activity, potential hurricane destruction, and mangrove protection, we reduce the risk that our estimates of hurricane impact will be “aggregated out” (ref. 22; ref. 25 has a discussion of aggregation bias). Last, our findings also contribute to the literature on the impact of cyclones on economic activity (19–26, 35–38) by providing additional empirical evidence in favor of hurricanes having short-run negative consequences in Central America.

Description of the Data

Nightlights.

We measure local economic activity using imagery from 4 weather satellites that are part of the US Air Force Defense Meteorological Satellite Program. These satellites record daily cloud formation by measuring the amount of moonlight reflected by clouds at night. On nights with no cloud cover, these satellites measure the light emissions from the earth’s surface. Specifically, we use the annual composites produced by the National Oceanic and Atmospheric Administration (NOAA) (40). These composites predominantly measure human-made lights because they only use information from cloud-free days and because NOAA’s methodology filters transient sources of light (ref. 41 has further details). Nightlights provide a good proxy for economic activity because consumption of lights at night is likely to increase with income. Accordingly, nightlights have been extensively used to measure changes in economic activity (ref. 33 has a literature review), including the downturns generated by hurricanes (22–25).

Our nightlights dataset is composed of 22 satellite–year composites for the period 2000 to 2013. Each composite covers Central America and contains information on 604,473 1-${\mathrm{k}\mathrm{m}}^2$ grid cells. Each cell records the intensity of nightlights on a scale that ranges from 0 (no light) to 63 (maximum light). In years with overlapping satellite coverage, we aggregate nightlights by taking cell-level weighted averages across satellites, where the weights are given by the number of cloud-free days. We restrict the sample to cells that have non-0 nightlights in at least 1 y during our sample period. The resulting cell–year panel is composed of 212,072 cells, which we observe for 13 y. The average value of nightlights in 2000 is 5.1, with an SD of 8.4.

Hurricane Damage.

Hurricane wind field model.

To measure the distribution of surface winds from hurricanes in Central America during our sample period, we use the wind field model developed in ref. 34. This model uses an asymmetric Holland equation that has been calibrated for Central America. The main model output is predicted wind speed in kilometers per hour at the height of 10 m for each cell and tropical cyclone that has since 2000 affected at least 1 of the following countries: Costa Rica, El Salvador, Honduras, Guatemala, Nicaragua, and Panama. SI Appendix, section SI1 has further details, and SI Appendix, Fig. S1 shows the tracks of the 44 tropical storms and hurricanes in our sample.

Hurricane destruction index.

To match the wind speed dataset to our nightlight data, we construct a cell–year panel that uses only observations from the hurricane with the highest recorded wind speed during a given year. Approximately a quarter of the cells in our sample experience non-0 wind speed.

We convert wind speed into potential damage using the transformation and parameters proposed in ref. 3. This transformation imposes a threshold below which damage is unlikely to occur, it guarantees that damage will approach unity for very high wind speeds, and it accounts for the physical property that wind power (the rate of increase of kinetic energy) from a hurricane is proportional to the third power of wind speed. The damage index $f$ is given by

$$f_{it}=\frac{{\left[\frac{max\left(V_{it}-V_T,0\right)}{V_H-V_T}\right]}^3}{1+{\left[\frac{max\left(V_{it}-V_T,0\right)}{V_H-V_T}\right]}^3},$$ [1]

where $V_{it}$ represents wind speed in cell $i$ and year $t$, $V_T$ is the threshold below which damage is unlikely to occur (it is set at 92.6 km/h [50 knots]), and $V_H$ is the wind speed at which half of all structures are expected to be destroyed, 277.8 km/h (150 knots). Additionally, because physical damages may be higher nonlinear functions of wind and water stress, in SI Appendix we show that our results are also robust to an eighth-power relationship between maximum wind speed and damages as suggested in ref. 42.

Storm surge-prone area.

The $f$ damage index provides an informative measure of wind damages and potentially, of overall damages because it is also correlated with damage from excess rainfall and storm surge. Nonetheless, because storm surge is often considered one of the most damaging aspects of hurricanes, we further investigate whether coastal lowlands are disproportionately affected by hurricanes. Specifically, we create a coastal lowland indicator variable identifying contiguous areas along the coast that are less than 10 m above sea level.* This storm surge-prone area is composed of 7,758 cells (3.6% of all cells). For each of these cells, we additionally calculate the shortest path (Euclidean distance) from the centroid of the cell to the coast. The average distance to the coast is 5.41 km.

Mangrove.

Data on the distribution of mangroves come from 2 sources. The first is a collection of harmonized maps, 1960 to 1996, that was assembled for the World Mangrove Atlas (27). We use this map to identify areas that have historically supported mangrove habitats. The second source is ref. 44, which uses 1997 to 2000 Landsat data together with supervised and unsupervised digital image classification to construct a 30-${\mathrm{m}}^2$-resolution map of the global distribution of mangrove. We use this second dataset to precisely measure the presence of mangrove at the beginning of our sample period.

To rule out that any protection benefits of the mangrove are derived because mangroves grow in areas that are naturally more sheltered (for example, areas that lay in a steeper continental shelf), we begin by excluding from the analysis areas that have not historically supported mangrove habitats. Specifically, for every cell in the storm surge-prone area, we exclude cells that have no mangrove as defined by ref. 27 in their shortest path to the coast. We find that there are 3,853 cells (49% of cells in storm surge-prone areas) with mangrove on their path to the coast.

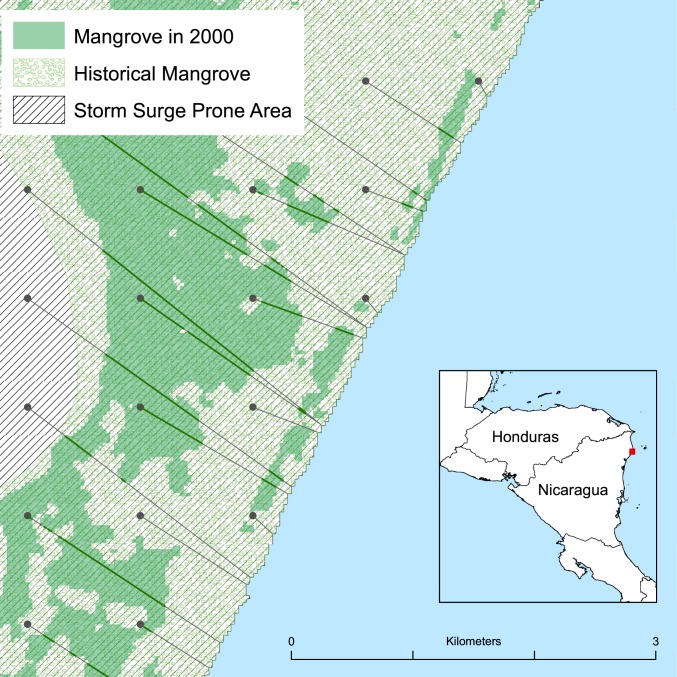
Next, for each of the remaining cells, we calculate mangrove width in 2 steps. First, we identify the line segments along the shortest path to the coast that overlap mangrove forests as defined by ref. 44. Second, we sum the line segments to measure cumulative mangrove width on the shortest path to the coast. Fig. 1 provides a visual representation of the mangrove width calculation in the coast where the largest event in our sample made landfall (Hurricane Felix). We find that in our sample the average mangrove width is 0.9 km, with a minimum of 0 km and a maximum of 10.11 km.

Fig. 1.

Distribution of mangrove in the North Caribbean Coast Autonomous Region, Nicaragua. Dots represent centroids of cells; lines show the shortest path to the coast. The green line segments represent mangrove on the path to the coast.

Method and Results

Impact of Hurricanes on Nightlights.

To estimate the impact of hurricanes on economic activity as measured by nightlights, we use the following 2-way fixed effect specification:

$$N{L}_{it}=\alpha +\beta f_{it}+{\pi }_t+{\mu }_i+{\epsilon }_{it},$$ [2]

where $N{L}_{it}$ represents the nightlight intensity of cell $i$ in year $t$, $f_{it}$ is the damage index, ${\pi }_t$ are year fixed effects, ${\mu }_i$ are cell fixed effects, and ${\epsilon }_{it}$ is the error term. The parameter $\beta$ measures the impact of hurricanes on nightlights under the assumption that these shocks are exogenous. While certain areas of Central America may have a greater historical incidence of hurricanes (for example, leading to investment in damage prevention), we account for this possibility by including cell fixed effects. We also account for time-varying common shocks and address the issue of over time comparability of nightlights by including year fixed effects. Eq. 2 is estimated using ordinary least squares for the sample period 2001 to 2013.^† To allow for arbitrary patterns of correlation among nightlights across cells and over time, we cluster SEs at the administrative level below the state.

Table 1 shows, consistent with previous literature, that hurricanes have considerable short-run negative effects on local economic activity. Column 1 in Table 1 presents the results from the specification in Eq. 2. Our estimate of $\beta$ is negative and statistically significant at the 5% level. The size of the coefficient indicates, for example, that nightlights in cells that experience strong category 3 hurricane winds ($f$ = 0.2, wind speed of 208 km/h) decrease by 0.81 units ($\approx -4.055\times 0.2$).^‡ Since the average nightlight was 5.1 in 2000, this effect roughly corresponds to a 16% decrease in our proxy of economic activity. The most affected cells in our sample experience an $f$ of 0.23; the average $f$ among impacted cells is 0.004.

Table 1.

Impact of hurricanes on nightlights

Variable	(1)	(2)	(3)
$f$	−4.055 (1.693)	−4.046 (1.765)
$f\left(t-1\right)$		0.104 (1.543)
$f$ in nonstorm
surge-prone areas			−2.574 (6.648)
$f$ in storm
surge-prone areas			−4.417 (0.648)

Dependent variable is nightlights. Estimates from ordinary least squares regression, cell, and year fixed effects are included but not reported. Robust SEs clustered at the municipal level are in parentheses (1,056 clusters). The number of observations is 2,757,001, of which 100,854 are in storm surgeprone areas.

Next, in column 2 in Table 1, we investigate whether hurricanes have lasting effects on economic activity by introducing a lag of the $f_{it}$ damage index but find no evidence of effects beyond the year the hurricane occurs. Specifically, the estimated $f$ coefficient is statistically significant and nearly identical to that of column 1 in Table 1, while the lagged coefficient is small and statistically indistinguishable from 0. This result implies a recovery to trend and is in line with previous literature, which has highlighted that the negative effect of hurricanes on economic activity is relatively short lived (20–25, 35–38).

Last, in column 3 in Table 1, we estimate the impact of hurricanes in storm and nonstorm surge-prone areas. Specifically, we create dummy variables for each of these areas, and we interact these variables with our damage index $f$. We then include the variables obtained in the previous step in place of $f$ in Eq. 2. The resulting coefficients can be interpreted as the effect of hurricanes on nightlights for each of these areas. The coefficient for nonstorm surge-prone areas is negative, but noisily estimated, we cannot rule out that it is statistically indistinguishable from 0 or from the coefficient for storm surge-prone areas. By comparison, the coefficient for storm surge-prone areas is sharply estimated and clearly indicates that hurricanes have considerable negative effects in this area. Specifically, nightlights in cells in storm surge-prone areas that experience category 3 hurricane winds ($f=0.2$) are reduced by 0.88 units or 17%.

Mangroves Reduce Hurricane Impact.

We study the effectiveness of mangrove defenses by testing whether the impact of hurricanes on nightlights decreases as the level of mangrove protection increases. Our measure of mangrove protection for each cell is the width of mangrove in 2000 along the shortest path to the coast. We focus on storm surge-prone areas because we have shown that hurricanes generate considerable damage in these areas and because mangroves may be well suited to provide protection against wave action and storm surge. As described in the data section, to rule out that the reduction in damages is generated by the characteristics of the habitat, we further exclude from the sample cells that historically have not had mangrove on their path to the coast.

Because past literature has argued that there may be a nonlinear relationship between mangrove width and the observed reduction in storm surge (29), we begin exploring the heterogeneity of hurricane impact by estimating 3 different models. In each model, we discretize mangrove width into various bins that correspond to its q quantiles. For the first model (q = 2), we create a dummy variable for each bin and interact these variables with the $f$ damage index. We then take the resulting variables and include them in Eq. 2 in place of the $f$ damage index. We repeat this procedure using q = 3 and q = 4. These models allow our estimates of the impact of hurricanes to vary freely across bins and hence, are able to accommodate any nonlinear pattern describing the heterogeneous impact of hurricanes across levels of mangrove width.

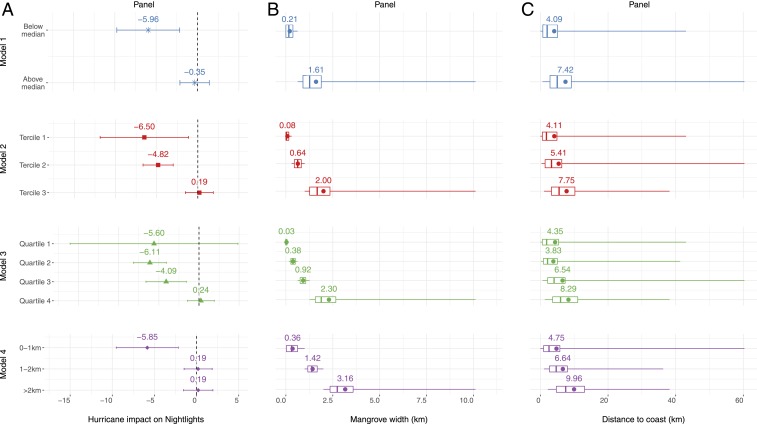
Fig. 2A plots the point estimates and 95% confidence intervals for each of these models. The coefficients can be interpreted as the reduction in nightlights caused by hurricanes for each group. Fig. 2B plots the distribution of mangrove width for each bin, the box represents the interquartile range, the whiskers are the minimum and the maximum, and the dot is the average value.

Fig. 2.

Impact of hurricanes on nightlights by mangrove width. A plots point estimates and 95% confidence intervals for 4 models. In the first 3 models, we discretize the mangrove width variable into various bins that correspond to its q quantiles and estimate the impact of hurricanes on economic activity for each bin: model 1 uses q = 2 and is labeled with stars, model 2 uses q = 3 and is labeled with squares, and model 3 uses q = 4 and is labeled with triangles. Model 4 uses bins representing 1-km steps of mangrove width and is labeled with diamonds. B plots the distribution of mangrove width for each bin, and C plots the distribution of distance to the coast for each bin. In B and C, the box represents the interquartile range, the whiskers are the minimum and the maximum, and the dot is the average value.

In Fig. 2A, model 1 (q = 2), the bins correspond to cells with above- and below-median mangrove width on their path to the coast (0.63 km). We find that in below-median areas (cells with an average mangrove width of 0.21 km) hurricanes considerably reduce nightlights. The estimated coefficient of −5.96 indicates that, when a cell experiences, for example, category 3 hurricane winds ($f$ = 0.2), nightlights decrease by $\approx$1.2 units ($-5.96\times 0.2$) or a 23% reduction. By comparison, the effect in above-median areas (with an average of 1.6-km mangrove width) is small and statistically indistinguishable from 0. We additionally test and confirm that the effect of hurricanes is differential between the groups (P value $<0.001$). Taken at face value, the difference between these coefficients indicates that the reduction in damage from mangroves roughly corresponds to 5.6 nightlight units.

Fig. 2A, model 2 (q = 3) and model 3 (q = 4) show the same decreasing pattern of hurricane damage, with full mitigation of damages taking place in the last bin: that is, for model 2, the third tercile (mangrove width greater than 1 km and average width of 2 km) and for model 3, the fourth quartile (mangrove width greater than 1.26 km and average width of 2.3 km). As before, we additionally test and are able, in both cases, to reject the null hypotheses of equality between the last bin and the previous bin (P value $<0.001$). The estimated reduction in damages from mangroves is of a similar magnitude to that found in model 1.

On the whole, the previous models indicate that cells with 1 km or more of mangrove width along their path to the coast suffer considerably less damage from hurricanes. In Fig. 2A, model 4, we summarize these findings, estimating the impact of hurricanes on nightlights for 3 groups of mangrove width: 0 to 1, 1 to 2, and 2 km or more. The estimated coefficients highlight that the benefits of mangrove protection occur among cells with 1 km or more of mangrove width in their path to the coast. Specifically, while category 3 hurricane winds ($f$ = 0.2) would lead to a 24% decrease in economic activity in cells with less than 1 km of mangrove width, cells with more than 1 km of mangrove width would experience no damage.

This finding is broadly consistent with other estimates of mangrove protection, which indicate that 2 to 7 km of mangrove width would be needed to fully attenuate storm surge for the hurricanes that make up the bulk of our sample (categories 1 to 3).^§ Moreover, our estimates suggest that this effect is economically relevant. A simple counterfactual simulation for coastal Nicaragua reveals that avoided losses from protection by mangroves account for up to 2.5% of the economic activity observed in Nicaragua’s coast in 2000. SI Appendix, section SI2 has a step-by-step description of this counterfactual calculation.

Next, Fig. 2C plots distance to the coast for each model and bin. The figure reveals that, while there are many observations with low values of mangrove width at long distances from the coast, it is still the case that on average a longer mangrove width also implies a longer distance to the coast. An important concern is that our heterogeneity results are not driven by mangrove protection but rather, by factors related to distance to the coast. These include, for example, greater exposure and presence of assets close to the coast or factors not fully captured by our wind field model, such as the decay of storm surge as the hurricane moves inland.

To rule out these alternative explanations, we conduct a placebo exercise where we test whether hurricane damage decreases with distance to the coast after we exclude from the sample cells that are protected by mangrove. SI Appendix, section SI3 shows that, after excluding cells protected by mangrove (mangrove widths of 1 km or more), there is no longer evidence of a decreasing pattern between hurricane damages and distance to the coast. Accordingly, we conclude that in our sample, where 95% of observations are within 18 km of the coastline, the reduction in hurricane impact is not driven by distance to the coast but rather, by the protection provided by the mangrove.

Last, SI Appendix, section SI4 shows that the result from our preferred specification (model 4 of Fig. 2) is robust. Specifically, we show that we find very similar results using a wide range of alternative assumptions for the inference of SEs, the construction of the hurricane damage function, the calculation of mangrove width, and the model specification. We additionally show that our results hold among the sample of most affected countries and that they are not driven by confounding factors that are common within a state in any given year, such as government recovery efforts. Moreover, we also provide supporting evidence against topographic features driving our results by showing that estimates of mangrove protection are unchanged when we rely on within-municipal variation, where coastline features are likely to be similar.

Summary and Conclusions

In this paper, we show that wide mangrove belts in Central America have the potential to mitigate the disruption to economic activity generated by hurricanes. We measure local economic activity using remote sensing data on nightlights, potential hurricane destruction using a damage index derived from a wind field model calibrated for Central America, and mangrove protection by calculating the cumulative width of mangroves along the closest path to the coast. Using these data, we estimate the impact of hurricanes on economic activity under the assumption that hurricane strikes are exogenous conditional on cell and year fixed effects. We then explore using a binning estimator whether there is a negative and plausibly nonlinear relationship between mangroves and hurricane damages.

We find that hurricanes have negative short-run effects on economic activity, with losses likely concentrated in coastal lowlands at risk for both wind and storm surge. Within the coastal lowlands, we further show that the impact of hurricanes declines with mangrove width and specifically, that the effect of hurricanes in our sample is entirely mitigated by 1 km or more of mangrove width. We additionally conduct various robustness checks and rule out that these findings are driven by the physical characteristics of the location of the mangrove habitat or by the distance to the coast.

Our results are important for policy makers because they highlight that mangrove conservation and restoration efforts can be used in coastal lowlands to protect economic activity against tropical cyclones. One important observation from this analysis, however, is that the benefit of protection is only accrued from wide mangrove belts. This observation implies that large-scale efforts will be required to achieve the benefits of mangrove protection.

Last, there are 2 important caveats of this analysis concerning the benefits of mangrove conservation and restoration over a longer time horizon. First, our estimates are likely to underestimate the protective value of mangroves in the long run because mangrove protection may entail benefits on outcomes, such as lives saved, health, and human capital accumulation, which are not well captured by nightlights. Second, while climate change and the resulting intensification of storms may increase the value of conservation for protection purposes, areas designated for conservation or restoration must be carefully chosen given the threat of sea-level rise (46). Consequently, an important avenue for future research is the identification of areas that should be prioritized for conservation or restoration.

Data Availability.

The data and code used in this paper can be found in the open Inter-university Consortium for Political and Social Research repository.