Significance
Glioblastoma (GBM) is the most common and aggressive malignant brain tumor in adults, with one of the most dismal prognoses of all cancers. Yet, the reason why GBM grows so fast and aggressively is not understood. Our study provides an intriguingly simple explanation for the infiltrative behavior of GBM by looking at fluidity—a material property that quantifies the viscous behavior of biological tissues measured in vivo by magnetic resonance elastography. We show that fluidity of neurotumors is anomalous in that it decreases as water content increases, enabling GBM to infiltratively finger into normal surrounding brain matter. Fluidity might thus become an important target for cancer research and opens horizons for the diagnosis and treatment of cancer.
Keywords: neurotumors, in vivo magnetic resonance elastography, invasive growth, glioblastoma, viscous fingering
Abstract
Mechanical properties of biological tissues and, above all, their solid or fluid behavior influence the spread of malignant tumors. While it is known that solid tumors tend to have higher mechanical rigidity, allowing them to aggressively invade and spread in solid surrounding healthy tissue, it is unknown how softer tumors can grow within a more rigid environment such as the brain. Here, we use in vivo magnetic resonance elastography (MRE) to elucidate the role of anomalous fluidity for the invasive growth of soft brain tumors, showing that aggressive glioblastomas (GBMs) have higher water content while behaving like solids. Conversely, our data show that benign meningiomas (MENs), which contain less water than brain tissue, are characterized by fluid-like behavior. The fact that the 2 tumor entities do not differ in their soft properties suggests that fluidity plays an important role for a tumor’s aggressiveness and infiltrative potential. Using tissue-mimicking phantoms, we show that the anomalous fluidity of neurotumors physically enables GBMs to penetrate surrounding tissue, a phenomenon similar to Saffman−Taylor viscous-fingering instabilities, which occur at moving interfaces between fluids of different viscosity. Thus, targeting tissue fluidity of malignant tumors might open horizons for the diagnosis and treatment of cancer.
Glioblastoma (GBM) and meningioma (MEN) are brain tumors which differ markedly in clinical prognosis, outcome, and treatment options (1). MENs originate from meningeal tissue, grow slowly, and very often have sharply demarcated edges (2). In contrast, GBMs (World Health Organization [WHO] grade IV gliomas) grow rapidly and diffusively invade surrounding tissue, resulting in difficult-to-localize lesions without detectable boundaries (3). Therefore, GBMs have an overall poor clinical prognosis with a high risk of short-term local recurrence after resection and adjuvant radiation and chemotherapy, while most MENs are well treatable by surgery (4, 5).
Despite these differences, both tumor entities have similar mechanical properties in terms of stiffness (6–8). Contrary to what the Latin word “tumor” suggests, brain tumors do not always present as rigid, space-occupying masses but can have an even softer behavior than the already very soft brain tissue (9–11). From a biophysical perspective, the infiltrative growth of a soft aggressive mass such as GBM into a more rigid surrounding tissue is a peculiarity that needs to be resolved in order to better understand the physics of cancer in general (12, 13).
A closer look at solid tumors reveals that rigid tumor masses are not just solidified lumped cells but are interspersed with fibrous matrix elements including the surrounding extracellular matrix (ECM) (14). The existence of such a rigid−solid backbone in most tumors led to the notion of palpable stiff masses. Nevertheless, there is increasing evidence for softening of individual cancer cells (15, 16), giving rise to a more detailed picture: Malignant masses include fluid areas of unjammed, motile cells that can escape the tumor (17), while the solid backbone of nonmotile jammed cells provides the physical rigidity a growing tumor needs to displace healthy surrounding tissues and push the microenvironment out of the way.
However, the situation differs in the brain, where cellular networks within an ECM, which is rich in glucosaminoglycans (GAGs), do not develop significant fibrosis (18). As a result, brain tumor ECM is close to that of normal nervous tissue (19). The obvious lack of rigidity of brain tumors suggests that tumor invasion is mechanically promoted not only by stiffness but also by a second important property, which is related to tissue fluidity.
Conceptually, fluidity signifies the transition of a material from a solid to a liquid state. When the storage modulus exceeds the loss modulus, the material is, by definition, a solid. Yet, as the loss modulus increases, the tissue becomes more dissipative, acquiring more and more traits of a fluid, such as plasticity. A viscoelastic fluid responds essentially as an elastic body at time scales shorter than the time scale of structural reorganization within the fluid. The same material responds as a liquid in the opposite case, that is, large time scales such as weeks or months of tumor development. Thus, it makes sense to talk about the fluidity of tumors and to analyze how fluid-like behavior can control the invasiveness of GBMs.
To this end, we use in vivo magnetic resonance elastography (MRE) in patients with brain tumors and quantify the magnitude (|G*|) and phase angle (φ) of the complex shear modulus of apparently normal brain tissue versus GBM and MEN (7, 8). As φ relates to the ratio of loss modulus to storage modulus, it represents—in the context of the above definition—a “pure” measure of fluidity over a range of 0 (elastic solid) to 2π (viscous liquid). At higher values (>π/4), φ indicates fluid properties, irrespective of tissue stiffness |G*| (20). Moreover, as will be shown here, fluidity is not related to water content in the sample and can even increase when the material becomes dryer.
To understand this unexpected behavior of tissue fluidity, we will use MRE to study 3 categories of phantom materials characterized by their largely different water-binding behaviors: agarose, heparin, and tofu—all blended with different amounts of water. While agarose and heparin are hydrated polysaccharides, tofu is composed of soybean proteins aggregated through predominantly hydrophobic interactions (21). Our hypothesis is that the 3 materials undergo different changes in their mechanical fluidity upon dilution, thereby providing insights to guide our interpretation of in vivo fluidity as quantified in neurotumors.
In the following, we will first use MRE to identify “normal” (φ correlates with water content) as opposed to “anomalous” (φ inversely correlates with water content) fluid behavior in phantoms. We will then develop a model of soft-tumor infiltrative behavior based on anomalous fluidity as observed in neurotumors.
Methods
Eighteen patients with GBM (n = 9, 70 ± 7 y, all WHO grade IV) or MEN (n = 9, 57 ± 14 y, all WHO grade I) underwent both standard clinical MRI including T2- and T1-weighted sequences and multifrequency MRE. Patient demographics and data on brain tumor localization and size are given in Table 1. The study was approved by the local ethics boards of Universitätsmedizin Leipzig and Charité – Universitätsmedizin Berlin (Az278-13-07102013, EA1/261/12). All patients gave informed written consent prior to MRE.
Table 1.
Patient data, tumors, and MRE parameters
| No. | Age | Sex | Entity | Location | Size, cm3 | |G*|tumor in kPa | |G*|ref in kPa | φtumor in rad | φref in rad |
| 1 | 61 | M | GBM | left temporal | 26.1 | 1.36 (0.50) | 1.71(0.42) | 0.50 (0.30) | 0.70 (0.29) |
| 2 | 80 | M | GBM | right frontal | 37.5 | 0.80 (0.23) | 1.71 (0.36) | 0.43 (0.24) | 0.61 (0.22) |
| 3 | 72 | F | GBM | left frontal | 21.2 | 0.85 (0.28) | 1.36 (0.31) | 0.33 (0.18) | 0.64 (0.26) |
| 4 | 72 | F | GBM | right parietal + ventricle | 29.3 | 1.52 (0.43) | 1.87 (0.43) | 0.51 (0.24) | 0.69 (0.26) |
| 5 | 60 | F | GBM | left parietooccipital | 14.4 | 1.11 (0.20) | 1.82 (0.58) | 0.33 (0.24) | 0.68 (0.31) |
| 6 | 78 | F | GBM | right frontal | 28.7 | 1.24 (0.17) | 2.16 (0.28) | 0.22 (0.11) | 0.68 (0.21) |
| 7 | 71 | M | GBM | left insular | 27.6 | 1.40 (0.33) | 1.64 (0.32) | 0.34 (0.14) | 0.63 (0.24) |
| 8 | 63 | F | GBM | left parietal + splenium | 19.7 | 0.58 (0.09) | 2.13 (0.34) | 0.23 (0.12) | 0.59 (0.26) |
| 9 | 75 | M | GBM | left parietal | 5.9 | 1.02 (0.11) | 1.91 (0.25) | 0.32 (0.13) | 0.65 (0.23) |
| 10 | 62 | F | MEN | right frontal | 15.4 | 1.34 (0.32) | 1.50 (0.32) | 1.12 (0.26) | 0.54 (0.22) |
| 11 | 50 | M | MEN | right temporal | 42.9 | 1.26 (0.33) | 1.59 (0.23) | 0.84 (0.28) | 0.57 (0.25) |
| 12 | 38 | M | MEN | right frontal | 35.3 | 1.23 (0.26) | 1.46 (0.20) | 1.06 (0.43) | 0.61 (0.30) |
| 13 | 50 | F | MEN | right frontal | 7.7 | 1.36 (0.52) | 1.74 (0.21) | 0.84 (0.25) | 0.72 (0.17) |
| 14 | 36 | M | MEN | right frontal | 27.1 | 1.71 (0.59) | 1.77 (0.36) | 1.02 (0.33) | 0.63 (0.30) |
| 15 | 65 | F | MEN | left/right limbic | 10.9 | 1.90 (0.28) | 1.98 (0.33) | 1.12 (0.20) | 0.54 (0.17) |
| 16 | 69 | F | MEN | left/right frontal | 80.4 | 2.06 (0.70) | 2.32 (0.41) | 1.07 (0.45) | 0.53 (0.12) |
| 17 | 68 | F | MEN | right frontal | 10.4 | 0.96 (0.23) | 1.80 (0.44) | 1.16 (0.32) | 0.60 (0.22) |
| 18 | 75 | F | MEN | left frontal | 52.7 | 1.76 (0.35) | 1.89 (0.50) | 0.78 (0.24) | 0.44 (0.20) |
Note that all GBMs are of WHO grade IV, while all MENs are of WHO grade I. Intratumor SDs indicating heterogeneity are given in brackets. |G*|tumor, |G*|ref: magnitude shear modulus of tumor, reference (nonaffected) tissue; φtumor, φref: phase angle of shear modulus of tumor, reference tissue. M, male; F, female.
Phantom Preparation.
To test the influence of water on MRE-measured viscoelastic parameters, we blended 3 generic phantom materials with different amounts of water and then performed MRE using the protocol specified below.
Heparin–water.
Approximately 100 mL of heparin−water solutions were investigated by MRE in a cylindrical container of 5-cm diameter and 5-cm height at 7 different concentrations (5.1, 4.2, 3.6, 3.2, 2.8, 2.5, and 2.3 wt %). Solid dry heparin sodium was obtained from heparin sodium (Ratiopharm) at 60,000 IU per 100 g unction by fully evaporating the solvent and resolving the dry mass in distilled water.
Agar–water.
One hundred grams of agar−agar-based wirogel (BEGO GmbH & Co. KG) was blended with water to produce 5 samples with 50, 55, 60, 65, and 70 wt % water-to-gel fractions. Dry solid fractions in the 5 samples, determined by evaporation of solvents, were 18.2, 16.4, 14.6, 12.7, and 10.9 wt %. For MRE, the samples were placed in the same cylindrical container previously used for heparin.
Tofu–water.
Two hundred twenty milliliters of soy milk was heated to 90 °C. Then, under continuous stirring, a solution of 25 mL of water and 1 mL of 100% acetic acid was added until complete coagulation of the soy milk was accomplished. The coagulated soy protein−water solution was then transferred into a cylindrical container of 5.4-cm diameter equipped with a metal mesh press to separate excess fluid from the soybean curd and to adjust porosity of the remaining solid tofu matrix. Six samples of different water-to-solid ratios were prepared and investigated by MRE. Dry solid fractions in the samples were 12.3, 13.6, 15.2, 18.7, 16.1, and 20.1%.
MRE.
MRE measures the complex shear modulus of soft tissues based on harmonic shear waves and motion-sensitive MRI (20). Higher spatial resolutions of viscoelastic parameter maps are attainable by using multiple frequencies, usually in the range from 30 to 60 Hz. Our multifrequency MRE setup is described in detail in ref. 8. In brief, all in vivo and phantom experiments were performed on a 3-T MRI scanner (Magnetom Trio) using a 12-channel head coil. Seven stimulation frequencies from 30 to 60 Hz (5-Hz increments) were used to vibrate a head cradle connected to a piezoelectric driver. A stack of 15 slices of 2 × 2 × 2 mm3 resolution was acquired by single-shot spin-echo echo-planar imaging MRE. Further imaging parameters were repetition time 3,000 ms, echo time 71 ms, field of view 256 × 192 mm2, parallel acquisition factor 2, 8 wave dynamics equally spaced over a vibration period, and 30 mT/m amplitude of the motion-encoding gradient. Total acquisition time for a full set of 3-dimensional (3D) multifrequency MRE data was ∼9 min.
Data analysis was based on multifrequency dual elasto-visco (MDEV) inversion as described elsewhere (8). The whole inversion pipeline is publicly available under https://bioqic-apps.charite.de/. Prior to multifrequency inversion, complex MRI data were smoothed using a 2-dimensional (2D) Gaussian filter with a kernel size of 5-pixel edge length and a sigma of 0.65 pixels. Then, data were unwrapped by in-plane first-derivative operators (central derivatives with 3-pixel stencils) for both phase unwrapping and high-pass filtering. Furthermore, temporal Fourier transformation was applied, and first-harmonic wave images were smoothed by a 2D Butterworth low-pass filter with 100 m−1 threshold (8).
MDEV inversion provided 2 independent parameters, the magnitude and the phase angle of the complex shear modulus (|G*| and φ) as frequency-averaged quantities applying to the frequency range of our experiments (30 to 60 Hz). |G*| is directly solved from the Helmholtz equation in magnitude representation, which provides numerically more stable solutions than retrieving the complex shear modulus (storage and loss modulus). φ is retrieved from the scalar product of the displacement vector and its Laplacian, taking into account that the Laplacian operator rotates a complex-valued wave field by angle φ. More details are provided in ref. 22. Based on φ, we defined the parameter “fluid fraction” by the area in which fluid properties dominate (φ > π/4) normalized to the total tumor area. Furthermore, the magnitude of the complex MRI signal (|S*|) from the MRE scan was used as a measure of relative water content. Regions of tumor and healthy reference tissue were manually defined by experienced neuroradiologists (K.-J.S. and M.R.-Z.) on the basis of image contrast in the MRE magnitude images. Healthy reference tissue was selected from normal-appearing white matter within the contralateral hemisphere of the tumor.
Statistical Analysis.
Results are given as arithmetic mean ± SD. Differences between tumor entities and corresponding healthy tissue in |G*|, φ, |S*|, and fluid fraction were analyzed with the 2-tailed unpaired Student’s t test. Possible correlations between viscoelastic properties and water signal were tested using Pearson’s linear correlation analysis. To account for small sample sizes, a P value of <0.01 was considered statistically significant. All calculations were performed using the MATLAB Statistics Toolbox (MathWorks).
Data Availability.
MRE data of all patients will be made available upon reasonable request to the corresponding author.
Results
Phantoms.
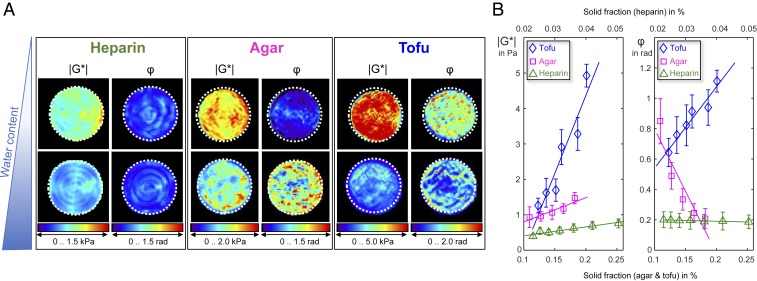
To qualitatively illustrate the anomalous fluidity behavior of tofu, Fig. 1 shows representative maps of |G*| and φ in tofu along with those of heparin and agar for 2 different amounts of water. While similar patterns of decrease in |G*| with higher amounts of water are visible in all 3 materials, φ reflects distinct material properties. For heparin, φ appears to be the same for low and high amounts of water, while φ becomes larger with dilution in agar and smaller in tofu. Quantitative values are plotted in Fig. 1B, where |G*| and φ are shown over dry solid fraction (wt %). All 3 phantom materials display stronger mechanical resistance with increasing solute concentration, reflected by larger |G*| values as the dry mass of the solute increases. The smallest change in |G*| associated with water uptake was encountered in heparin (0.4 kPa/%, R2 = 0.9), followed by agar (7.1 kPa/%, R2 = 0.87) and tofu (43.2 kPa/%, R2 = 0.88). Consistently, heparin displayed almost no change in φ (−0.02 rad/%, R2 = 0.80), while agar (−8.4 rad/%, R2 = 0.86) and tofu (5.3 rad/%, R2 = 0.94) changed markedly in their viscous behavior.
Fig. 1.
MRE of agarose, heparin, and tofu blended with different amounts of water. (A) Maps of magnitude of the complex shear modulus (|G*|) and phase angle of the complex shear modulus (φ) in 3 phantom materials at different states of fluidity resulting from different amounts of water content. Top presents maps for materials with a larger dry solid fraction (heparin, 0.05; agar, 0.18; tofu, 0.2) whereas Bottom shows maps with a smaller dry solid fraction (heparin, 0.02; agar, 0.11; tofu, 0.12). (B) Changes in magnitude shear modulus (|G*|) and phase angle (φ) over dry solid fraction in the 3 phantom materials characterized by different water-binding capacity and polarity. Error bars indicate the SD of values within the sample volumes.
In Vivo Brain Tumors.
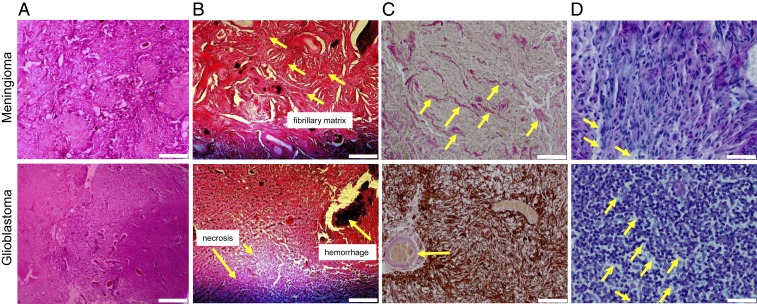
Fig. 2 displays representative histopathological slices of MEN and GBM. Hematoxylin and eosin (H&E) stains demonstrate solid structures such as fibrillary components in MENs and necrotic regions in GBMs (indicated by arrows). Elastica van Gieson staining further reveals that MEN ECM is characterized by an abundance of collagen fibers, which, in GBM, are apparent in the (peri-)vascular space only. Alcian blue stains show a higher content of GAGs in GBM in comparison with MEN.
Fig. 2.
Histological images of 2 representative cases of GBM and MEN with demarcation of structures that potentially influence macroscopic viscoelastic properties. (A and B) H&E stains demonstrate fibrillary structures in MEN and necrotic regions in GBM (arrows). (Scale bar: A, 400 μm; B, 200 μm.) (C) Collagen is further revealed by Elastica van Gieson staining as light red/pink fibrils throughout the ECM in MEN and in the vascular and perivascular spaces in GBM (arrows), while the glial matrix is highlighted with Glial Fibrillary Acidic Protein (GFAP) immunostain. (Scale bar: 100 μm.) (D) Alcian blue staining highlights sulfated GAGs as light blue regions (arrow), showing abundance of GAGs in GBM and lower GAG density in MEN. (Scale bar: 40 μm.)
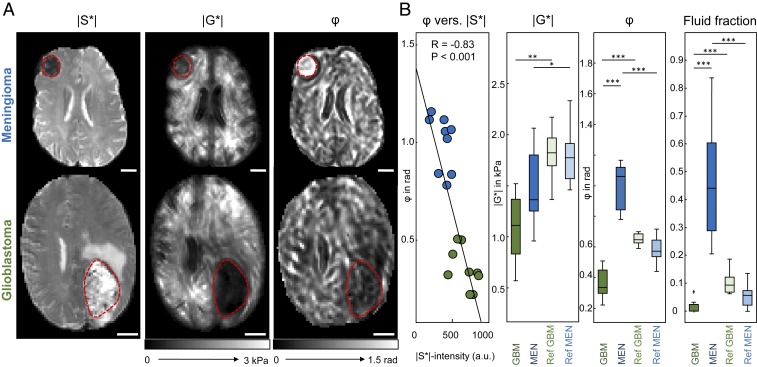
The GAG-related high water content of GBMs is reflected by high signal intensity in T2/T2*-weighted MRI, which is the signal contrast provided by the magnitude signal of the MRE scan (|S*| in Fig. 3). In |S*| images, GBM tumor regions appear hyperintense due to high water content and heterogeneous due to GAG accumulation and necrotic cores. Conversely, the MEN-associated |S*| hypointensity reflects low water content and abundance of solid matter such as the fibrillary structures demarcated in the histological images in Fig. 2. The MRE images in Fig. 3A show that both tumors have softer properties than normal brain tissue (lower |G*| values), while tissue fluidity (φ) is larger in MEN and smaller in GBM compared with healthy reference tissue.
Fig. 3.
In vivo MRE of brain tumors. (A) Two representative cases of MRE in GBM and MEN illustrating basic differences in T2*/T2-weighted MRI signal intensity (magnitude signal of the MRE scan, |S*|), magnitude shear modulus (|G*|), and phase angle of the shear modulus (φ). (Scale bar: 20 mm.) Red dashed lines demarcate tumor regions. (B) Quantitative analysis with correlation analysis of MRE-measured fluidity φ versus T2*/T2-weighted MRI signal intensity (|S*|). |S*| indicates the relative amount of free water inside the tumor, which is negatively correlated with fluidity φ. Group statistical plots of |G*|, φ, and the fluid fraction, that is, the fraction of intratumoral tissue with φ > π/4, are shown for tumors (GBM and MEN) and normal-appearing reference tissue (denoted as Ref GBM and Ref MEN). *P < 0.01, **P < 0.001, ***P < 10−4.
Fig. 3B shows that, in brain tumors, φ is negatively correlated with |S*|, suggesting a negative correlation between tissue fluidity and water content (R = −0.83, P < 0.001), while |G*| does not correlate with |S*| (R = −0.25, P = 0.32). The anomalous behavior of φ in brain tumors (higher fluidity at lower water content) mirrors our observations in tofu. While φ in MEN exceeds π/4—the physical limit of fluid behavior—all φ values in GBM remain below that threshold, suggesting that MEN is a fluid while GBM is a solid. Nevertheless, across the solid−fluid transition, a universal trend is that fluidity increases with lower water content in both malignant and healthy brain tissue.
The other panels in Fig. 3B present statistical plots of |G*| (Left Center), φ (Right Center), and the fluid fraction of tumor tissue, with the latter quantifying the relative proportion of tissue with φ > π/4 (Right). In both tumor entities, mechanical resistance measured by |G*| is lower than in healthy surrounding tissue (Ref), disfavoring the assumption that the tumor mass forcefully pushes surrounding tissue away (MEN vs. Ref: 1.51 ± 0.34 kPa vs. 1.78 ± 0.25 kPa, P = 0.009; GBM vs. Ref: 1.10 ± 0.29 kPa vs. 1.81 ± 0.23 kPa, P < 0.001). The values we obtained in healthy tissue are in the range reported in the literature (23) and were not different in patients with MEN and GBM (|G*|: P = 0.81; φ: P = 0.02). Tumor results for both φ and the fluid fraction strongly confirm that GBM behaves like a soft elastic solid (GBM vs. Ref: 0.36 ± 0.10 rad vs. 0.65 ± 0.04 rad, P < 10−4). For MEN, the average phase angle indicates that the tumor behaves like a fluid (MEN vs. Ref: 1.00 ± 0.13 rad vs. 0.58 ± 0.07 rad, P < 10−4). Nevertheless, the fluid tumor fraction in MEN is less than 50%, which provides a fully percolated solid backbone for the tumor. Overall, fluid fraction of 0.466 ± 0.192 in MEN is much larger than that in GBM (0.013 ± 0.022, zero in 6 of 9 tumors, P < 10−5), allowing full separation of the 2 tumor entities.
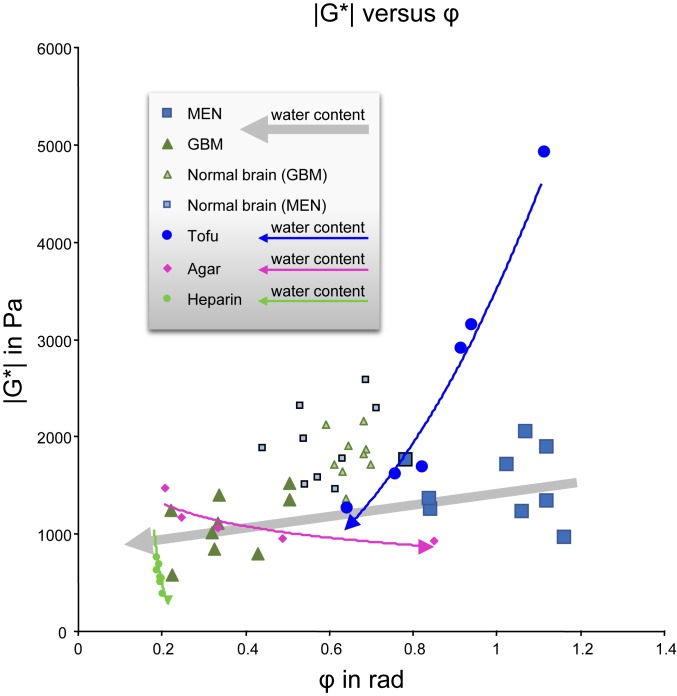
Fig. 4 depicts all |G*| and φ values measured in this study both in vivo and in the phantoms. In vivo data are provided for the 2 tumor entities and normal-appearing brain tissue without tumor. Individual patient MRE data are listed in Table 1. Phantom data are superimposed on in vivo data to illustrate the direction of change of |G*| and φ with increasing water content for normal and anomalous behavior. Agar and heparin show normal behavior, that is, increasing fluidity with increasing water content. Only tofu reflects the rare and unexpected properties of brain tissue, namely, decreasing fluidity with increasing water content.
Fig. 4.
Magnitude shear modulus (|G*|) versus phase angle of the shear modulus (φ) of all tumor values and reference tissues superimposed on phantom data. Arrows indicate the directions of increasing fluidity (in phantoms, measured as the dry solid fraction, and, in tumors, based on |S*|-signal intensities).
Discussion
While genes and signaling pathways exert exquisite control over cell properties, it is increasingly clear that mechanical interactions play an important role in sculpting collections of cancer cells into an aggressive tumor (14, 24). Typically, solid tumors become aggressive by displacing growth, which requires an increase in the tumor’s rigidity, and by metastatic spread, which requires partial fluidification so that cancer cells can move. The results presented here show that this is fundamentally different in aggressive brain tumors. GBMs become softer and more solid, which favors infiltrative growth as predicted by the framework of viscous fingering in fluid mechanics.
Softening of tumors has been considered an obstacle to cancer cell proliferation (25, 26). The traditional notion of stiffness as a tumor promoter has been challenged by our recent in vivo MRE findings in the brain showing the opposite behavior, as we found softer properties at higher tumor grades (6, 8, 10). Moreover, classification of benign MEN (WHO grade I) as being fluid and GBM (WHO grade IV) as being solid is surprising in view of the traditional interpretation of T2-weighted hyperintensity in MRI: Brain tumors, hyperintense on T2, are considered soft and more vascular. In the opposite case of T2-weighted hypointensity, brain tumors tend to have a firmer intraoperative consistency, as classified by surgeons and consistent with the presence of fibrous structures in histology (27, 28).
In our cohort, T2-weighted signal intensity was a poor surrogate for tumor stiffness (P = 0.32) but did inversely correlate with fluidity (P < 0.001). This can be explained by the fact that fluidity directly relates to the mobility of water molecules and to the overall viscous dissipation of the sample. Noteworthy is that, in biological tissues with complex macromolecular networks, motile chains and dangling structures with many eigenmodes are the key components contributing to viscosity, rather than the hydrodynamic friction of water molecules (29). This is why fluidity is sensitive to the composition of tissues as illustrated by our phantom results.
Our phantom data show that hydrophilic polysaccharide networks such as heparin can bind large amounts of water without notable changes in their viscous behavior. By contrast, tofu is predominantly made up of entangled protein networks in which internal hydrophobic bounds are shielded from the polar substrate (21). A larger amount of water promotes longer chains, while solvent drainage leads to coagulated protein clusters with higher friction and enhanced viscous dissipation (21). At low shear rates, water lubricates the motion of protein chains relative to each other, resulting in small stresses. At high shear rates, water might locally be drained out of the pores, so that there is no longer sufficient liquid to prevent direct solid−solid contacts, leading to friction and higher shear stresses through hydrophobic network interactions. As a result, tofu has a large dispersion slope of the complex shear modulus, causing apparent stiffness to rise rapidly as the shear rate increases. The resulting large φ-values in tofu are similar to the situation in MEN. This could explain why surgeons often describe MENs as stiff and palpable solid masses (9, 30), since a fast deforming touch would induce hydrophobic interactions, which are associated with higher intrinsic resistance of the sample.
From the perspective of solid mechanics, MEN and GBM do not generate the mechanical resistance necessary for displacing growth, since both entities can be softer than surrounding healthy tissue. Instead, the difference in fluidity we have quantified here endows GBMs with the infiltrative potential needed for their highly aggressive behavior. Nonlinear dynamics in growing cell populations permits spatiotemporal instabilities, which explains, for example, the folding of the cerebral cortex (31). Similar nonlinear effects could enable GBM to trigger fingering growth, thus overcoming the problem that it cannot grow as a simple displacing tumor mass (32).
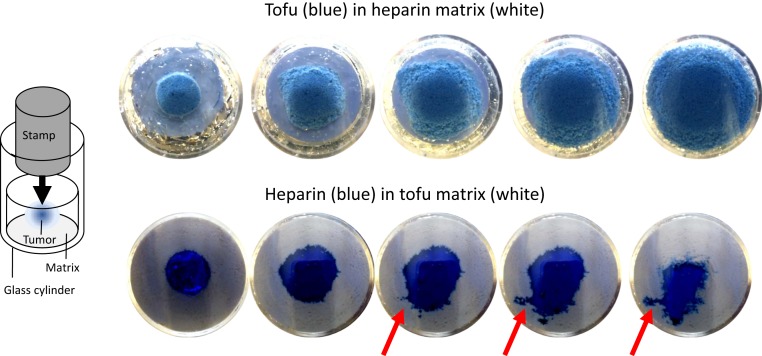
Considering that healthy tissue surrounding a tumor might be a porous medium, we note 2 modes of microinvasive growth: viscous and capillary fingering (33, 34). Both effects could synergistically cause the invasive, interpenetrating growth of GBMs and might explain why no boundary exists to surrounding healthy tissue (35, 36). Our data show that GBM has a 4 times lower viscosity than the surrounding healthy brain tissue, which clearly favors viscous fingering based on Saffman−Taylor instabilities outlined in Appendix: Saffman−Taylor Instabilities in Viscoelastic Solids (37). Slow growth of a tumor may be associated with a small capillary number, which would favor growth dominated by capillary fingering (33). However, the solid behavior of GBM suppresses surface tension at the border of the cell mass, which supports viscous fingering even when the tumor grows slowly. In addition, the formation of folds in the cerebral cortex proves that even slow embryonic growth can trigger instabilities (38). In our phantoms showing the same anomalous behavior as brain tumors, we could reproduce viscous fingering. Fig. 5 illustrates how infiltratively the low-viscous heparin is pushed into the surrounding highly viscous tofu. Vice versa, as predicted by theory, the expanding tofu mass does not generate viscous fingers.
Fig. 5.
Demonstration of viscous fingering in phantoms made of tofu embedded in heparin or, vice versa, heparin embedded in a tofu matrix. The enclosed material (stained blue) is intended to mimic the tumor’s viscous behavior when growing within a less viscous environment (MEN, Top) or within a more viscous environment (GBM, Bottom). The snapshot images were taken from underneath the glass cylinder while pushing a stamp onto the phantom to induce spread. A sketch of the experimental setup is shown on the left-hand side. Red arrows indicate sites of viscous fingering.
Since the mechanical resistance of MEN and GBM alone cannot explain displacing growth, the fluidity behavior we found in our experiments provides a physical explanation for tumor aggressiveness. MENs are, in great parts, fluid with a viscosity higher than the surrounding tissue. MEN ECM has a lower content of GAGs with their solidifying effect (39). GBMs are very soft solids due to an excess of GAGs (19), enabling them to grow by fingering based on a much lower viscosity and surface tension than the surrounding microenvironment (35). Such surface instabilities might also explain why GBMs do not have sharp and distinct boundaries in radiological images (36). However, it should be noted that images acquired by MRI and MRE in the clinical setting have limited spatial resolution. Pixel edge sizes of the order of 2 mm in patients (7, 40) and 100 microns in small animals (41) do not provide the detail resolution necessary to directly depict the infiltrative growth of a tumor at its boundaries as seen by microscopy (42). Instead, our study shows a way to infer from bulk tissue properties quantified in vivo at coarse resolution to the microscopic mechanical interactions, which locally push or stabilize tumor boundaries. Therefore, tissue fluidity might become an important imaging marker in cancer research, as it has the potential to improve the diagnosis and treatment of brain tumors in general and to improve the devastating clinical prognosis of patients with GBM in particular (43).
In summary, the anomalous fluidity behavior induced by different ECM compositions in normal and abnormal brain tissues is an elegant physical explanation for the highly different invasiveness of MENs and GBMs. Regarding the ECM as a possible target of treatments (44) aimed at eliminating the potential of infiltrative growth of soft tumors might open horizons for the diagnostic and therapeutic management of cancer patients.
Appendix: Saffman−Taylor Instabilities in Viscoelastic Solids
Here, we combine the equilibrium equation of viscoelastic flow (45) with the Saffman−Taylor model (37) to analytically predict instabilities at tumor boundaries. The progressive expansion of a growing tumor mass is naturally driven by the proliferation and rearrangement of cells and ECM components (35). This induces mechanical strain in the tumor and surrounding tissue, which resembles flow on large time scales that is governed by fluid viscosity . In a simplified approach, we assume that the tumor expands as a spherical mass and denote the strain tensor in cylindrical coordinates . Since growth velocity v is pointed outward, away from the center of the mass, the radial components of strain and of the strain rate are positive. Hence, we restrict our attention to these radial components of strain and of the strain rate, assuming that no tangential strains (shear strains) are generated. Consequentially, the solid stress is a scalar quantity determined by compression modulus K and radial strain , which we note as tumor pressure . The resulting total stress is
| [1] |
leading to the equilibrium equation of force density
| [2] |
where f expresses the sum of the external forces such as gravitational forces per unit mass, and denotes mass density. In the limit of small velocities and quasi-static deformations , the Navier−Stokes equation (Eq. 2) takes the form
| [3] |
The viscosity term on the left-hand side is the resistance of the medium against fluid flow through a porous medium as specified in Darcy’s law (45). For a basic understanding of instabilities at tumor boundaries, we continue with the assumption of homogenous materials of viscosities and separated by a spherical interface at . Subscripts 1 and 2 stand for tumor and surrounding tissue, respectively. For sufficiently large and no gravitational forces, we readily obtain
| [4] |
According to ref. 37, we introduce a small disturbance of displacement at , which varies in time and space and converges to zero at infinity in case of stable conditions,
| [5] |
The disturbance of the strain rate added to the pressures in Eq. 4 yields
| [6] |
The boundary conditions assert continuity of pressure at , that is, . First-order approximation in omega then leads to
| [7] |
Since in expanding tumors, we always find if (the disturbance fades out over times). This condition reflects larger tumor viscosity compared with surrounding tissue viscosity, causing stable interfaces. This is the case in MEN, while GBM has smaller viscosity than surrounding brain , leading to and instable boundaries.
The relationship between fluidity parameter and viscosity depends on the underlying model of viscoelasticity. Total stress in Eq. 1 is linked to the Kevin−Voigt model, in which solid and fluid stresses are linearly superimposed. In general, viscosity is related to the imaginary part of the complex modulus, that is, the loss modulus. According to the Kevin−Voigt model, the loss modulus is
| [8] |
| [9a] |
| [9b] |
As indicated by our data, the group mean ratio does not significantly differ from one. However, individual variation in the magnitude modulus ratio between tumor and surrounding tissue might indicate the likelihood of viscous fingering. More data from patients with different types of brain tumors are needed to assess the predictive power of Eqs. 9a and 9b for their infiltrative potential.
Acknowledgments
We thank Benjamin Englert from Charité Berlin for help with histopathology. Support from the German Research Foundation (Grants GRK2260 BIOQIC and SFB1340 Matrix-in-Vision) is gratefully acknowledged. The study was further supported by the European Union’s Horizon 2020 Funding Program (ID 668039, EU FORCE – Imaging the Force of Cancer).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
References
- 1.DeAngelis L. M., Brain tumors. N. Engl. J. Med. 344, 114–123 (2001). [DOI] [PubMed] [Google Scholar]
- 2.Oya S., Kim S. H., Sade B., Lee J. H., The natural history of intracranial meningiomas. J. Neurosurg. 114, 1250–1256 (2011). [DOI] [PubMed] [Google Scholar]
- 3.Stupp R., et al. ; European Organisation for Research and Treatment of Cancer Brain Tumor and Radiotherapy Groups; National Cancer Institute of Canada Clinical Trials Group , Radiotherapy plus concomitant and adjuvant temozolomide for glioblastoma. N. Engl. J. Med. 352, 987–996 (2005). [DOI] [PubMed] [Google Scholar]
- 4.Lim M., Xia Y., Bettegowda C., Weller M., Current state of immunotherapy for glioblastoma. Nat. Rev. Clin. Oncol. 15, 422–442 (2018). [DOI] [PubMed] [Google Scholar]
- 5.Preusser M., Brastianos P. K., Mawrin C., Advances in meningioma genetics: Novel therapeutic opportunities. Nat. Rev. Neurol. 14, 106–115 (2018). [DOI] [PubMed] [Google Scholar]
- 6.Simon M., et al. , Non-invasive characterization of intracranial tumors by MR-Elastography. New J. Phys. 15, 085024 (2013). [Google Scholar]
- 7.Reiss-Zimmermann M., et al. , High resolution imaging of viscoelastic properties of intracranial tumours by multi-frequency magnetic resonance elastography. Clin. Neuroradiol. 25, 371–378 (2015). [DOI] [PubMed] [Google Scholar]
- 8.Streitberger K.-J., et al. , High-resolution mechanical imaging of glioblastoma by multifrequency magnetic resonance elastography. PLoS One 9, e110588 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Murphy M. C., et al. , Preoperative assessment of meningioma stiffness using magnetic resonance elastography. J. Neurosurg. 118, 643–648 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schregel K., et al. , Characterization of glioblastoma in an orthotopic mouse model with magnetic resonance elastography. NMR Biomed. 31, e3840 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jamin Y., et al. , Exploring the biomechanical properties of brain malignancies and their pathologic determinants in vivo with magnetic resonance elastography. Cancer Res. 75, 1216–1224 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fritsch A., et al. , Are biomechanical changes necessary for tumour progression? Nat. Phys. 6, 730–732 (2010). [Google Scholar]
- 13.Butcher D. T., Alliston T., Weaver V. M., A tense situation: Forcing tumour progression. Nat. Rev. Cancer 9, 108–122 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Levental K. R., et al. , Matrix crosslinking forces tumor progression by enhancing integrin signaling. Cell 139, 891–906 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Guck J., et al. , Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Biophys. J. 88, 3689–3698 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Plodinec M., et al. , The nanomechanical signature of breast cancer. Nat. Nanotechnol. 7, 757–765 (2012). [DOI] [PubMed] [Google Scholar]
- 17.Oswald L., Grosser S., Smith D. M., Käs J. A., Jamming transitions in cancer. J. Phys. D Appl. Phys. 50, 483001 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rutka J. T., Apodaca G., Stern R., Rosenblum M., The extracellular matrix of the central and peripheral nervous systems: Structure and function. J. Neurosurg. 69, 155–170 (1988). [DOI] [PubMed] [Google Scholar]
- 19.Delpech B., et al. , Hyaluronan and hyaluronectin in the extracellular matrix of human brain tumour stroma. Eur. J. Cancer 29A, 1012–1017 (1993). [DOI] [PubMed] [Google Scholar]
- 20.Hirsch S., Braun J., Sack I., Magnetic Resonance Elastography: Physical Background and Medical Applications (Wiley-VCH, 2017). [Google Scholar]
- 21.Kohyama K., Sano Y., Doi E., Rheological characteristics and gelation mechanism of tofu (soybean curd). J. Agric. Food Chem. 43, 1808–1812 (1995). [Google Scholar]
- 22.Papazoglou S., Hirsch S., Braun J., Sack I., Multifrequency inversion in magnetic resonance elastography. Phys. Med. Biol. 57, 2329–2346 (2012). [DOI] [PubMed] [Google Scholar]
- 23.Gerischer L. M., et al. , Combining viscoelasticity, diffusivity and volume of the hippocampus for the diagnosis of Alzheimer’s disease based on magnetic resonance imaging. Neuroimage Clin. 18, 485–493 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Friedl P., Gilmour D., Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell Biol. 10, 445–457 (2009). [DOI] [PubMed] [Google Scholar]
- 25.Helmlinger G., Netti P. A., Lichtenbeld H. C., Melder R. J., Jain R. K., Solid stress inhibits the growth of multicellular tumor spheroids. Nat. Biotechnol. 15, 778–783 (1997). [DOI] [PubMed] [Google Scholar]
- 26.Delarue M., et al. , Compressive stress inhibits proliferation in tumor spheroids through a volume limitation. Biophys. J. 107, 1821–1828 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Maiuri F., et al. , Intracranial meningiomas: Correlations between MR imaging and histology. Eur. J. Radiol. 31, 69–75 (1999). [DOI] [PubMed] [Google Scholar]
- 28.Chen T. C., et al. , Magnetic resonance imaging and pathological correlates of meningiomas. Neurosurgery 31, 1015–1022 (1992). [DOI] [PubMed] [Google Scholar]
- 29.Doi M., Edwards S. F., The Theory of Polymer Dynamics (Oxford University Press, New York, New York, 1986). [Google Scholar]
- 30.Xu L., et al. , Magnetic resonance elastography of brain tumors: Preliminary results. Acta Radiol. 48, 327–330 (2007). [DOI] [PubMed] [Google Scholar]
- 31.Tallinen T., Chung J. Y., Biggins J. S., Mahadevan L., Gyrification from constrained cortical expansion. Proc. Natl. Acad. Sci. U.S.A. 111, 12667–12672 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mather W., Mondragón-Palomino O., Danino T., Hasty J., Tsimring L. S., Streaming instability in growing cell populations. Phys. Rev. Lett. 104, 208101 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jung J., Jang J., Ahn J., Characterization of a polyacrylamide solution used for remediation of petroleum contaminated soils. Materials (Basel) 9, E16 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chen Y. F., Fang S., Wu D. S., Hu R., Visualizing and quantifying the crossover from capillary fingering to viscous fingering in a rough fracture. Water Resour. Res. 53, 7756–7772 (2017). [Google Scholar]
- 35.Bogdan M. J., Savin T., Fingering instabilities in tissue invasion: An active fluid model. R. Soc. Open Sci. 5, 181579 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Behin A., Hoang-Xuan K., Carpentier A. F., Delattre J. Y., Primary brain tumours in adults. Lancet 361, 323–331 (2003). [DOI] [PubMed] [Google Scholar]
- 37.Saffman P. G., Taylor G., The penetration of a fluid into a porous medium or hele-shaw cell containing a more viscous liquid. Proc. R. Soc. London Ser. A 245, 312–329 (1958). [Google Scholar]
- 38.Markus A., Folding the cortex. Nat. Neurosci. 6, 1249 (2003). [DOI] [PubMed] [Google Scholar]
- 39.Bertolotto A., Giordana M. T., Magrassi M. L., Mauro A., Schiffer D., Glycosaminoglycans (GAGs) in human cerebral tumors. Part 1. Biochemical findings. Acta Neuropathol. 58, 115–119 (1982). [DOI] [PubMed] [Google Scholar]
- 40.Streitberger K. J., et al. , Brain viscoelasticity alteration in chronic-progressive multiple sclerosis. PLoS One 7, e29888 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bertalan G., et al. , Fast tomoelastography of the mouse brain by multifrequency single-shot MR elastography. Magn. Reson. Med. 81, 2676–2687 (2019). [DOI] [PubMed] [Google Scholar]
- 42.Han Y. L., et al. , Cell swelling, softening and invasion in a three-dimensional breast cancer model. Nat. Phys., 10.1038/s41567-019-0680-8 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Aldape K., et al. , Challenges to curing primary brain tumours. Nat. Rev. Clin. Oncol. 16, 509–520 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Solari V., et al. , MYCN-dependent expression of sulfatase-2 regulates neuroblastoma cell survival. Cancer Res. 74, 5999–6009 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sack I., Schaeffter T., Quantification of Biophysical Parameters in Medical Imaging (Springer, Heidelberg, Germany, 2018). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
MRE data of all patients will be made available upon reasonable request to the corresponding author.