Significance
A striking feature in bivalved seashells is that the 2 valves fit together perfectly when closed. This trait has evolved in 2 phyla from a common shell-less ancestor and has been described for hundreds of years. While its functional advantage is clear, there is no understanding of how this feature is generated. A mathematical model of the shell growth process explains how geometry and mechanics conspire to generate an interlocking pattern. This model provides a physical explanation for a prominent example of convergent evolution. By showing how variations in the mechanism create a wide variety of morphological trends the model provides insight into how biophysical processes, probably modulated by genetic factors, are manifest across scales to produce a predictable pattern.
Keywords: morphogenesis, growth, mathematical model, mollusk
Abstract
Brachiopods and mollusks are 2 shell-bearing phyla that diverged from a common shell-less ancestor more than 540 million years ago. Brachiopods and bivalve mollusks have also convergently evolved a bivalved shell that displays an apparently mundane, yet striking feature from a developmental point of view: When the shell is closed, the 2 valve edges meet each other in a commissure that forms a continuum with no gaps or overlaps despite the fact that each valve, secreted by 2 mantle lobes, may present antisymmetric ornamental patterns of varying regularity and size. Interlocking is maintained throughout the entirety of development, even when the shell edge exhibits significant irregularity due to injury or other environmental influences, which suggests a dynamic physical process of pattern formation that cannot be genetically specified. Here, we derive a mathematical framework, based on the physics of shell growth, to explain how this interlocking pattern is created and regulated by mechanical instabilities. By close consideration of the geometry and mechanics of 2 lobes of the mantle, constrained both by the rigid shell that they secrete and by each other, we uncover the mechanistic basis for the interlocking pattern. Our modeling framework recovers and explains a large diversity of shell forms and highlights how parametric variations in the growth process result in morphological variation. Beyond the basic interlocking mechanism, we also consider the intricate and striking multiscale-patterned edge in certain brachiopods. We show that this pattern can be explained as a secondary instability that matches morphological trends and data.
Brachiopods and mollusks are 2 invertebrate phyla that possess calcified shells. Evidence derived from molecular clocks, molecular phylogeny, shell biochemistry, and the fossil record (1–5) suggests, however, that they have diverged from a shell-less common ancestor (Fig. 1). The bivalved condition of the shell in both brachiopods and bivalve mollusks is an evolutionary convergence that led several authors to mistakenly assign brachiopods to mollusks in the early 19th century (6). One of the most remarkable features of the shells of brachiopods and bivalves, readily observed but rarely fully appreciated, is the simple fact that the 2 valves of the shell fit together perfectly when the shell is closed; i.e., throughout the development of the shell the edge of 2 valves meet each other in a commissure that forms a continuous curve with no gaps. At first glance this may not appear as a surprise, as the 2 valves constitute 2 halves of the same organism. Moreover, it is a trait that brings an easily understood functional advantage, providing a protective role against predators and environmental events, and it could be tempting to conclude that this function alone explains why both valves closely interlock. However, the function of a trait does not explain how it is formed during development, which is the goal of the present work.
Fig. 1.
(A) Phylogenetic relationships among brachiopods and mollusks (data from refs. 5, 7, 8, and 37). (B and C) Convergently evolved shell commissures in fossil brachiopods (Septaliphoria orbignyana and Kutchirhynchia obsoleta) and bivalve mollusks (Rastellum sp. and Ctenostreon rugosum). (D) An oyster with irregular interlocking pattern, Lopha sp. (Senonian, Algeria). (E) Xenomorphic oyster, Lopha sp.(Upper Cretaceous, Algeria). The attached valve carries the negative impression of another shell, while the free valve replicates its positive form (indicated by the arrows). (Scale bars: 10 mm.)
The 2 valves of the shell are secreted separately by 2 lobes of a thin elastic organ, the mantle. Also, the 2 valves may grow at different rates and have different shapes, and the pattern of shell edge does not exhibit perfect regularity: It may be more or less perturbed, for instance by external factors such as a patterned substrate on which some species live attached or by environmental events causing shell injuries. Yet, in all cases the interlocking of the 2 shell edges is tightly maintained. These observations imply that the interlocking pattern emerges as the result of epigenetic interactions modulating the behavior of the secreting mantle during shell development.
Here, we provide a geometric and mechanical explanation for this morphological trait based on a detailed analysis of the shell geometry during growth and the physical interaction of the shell-secreting soft mantle with both the rigid shell edge and the opposing mantle lobe. We demonstrate how an interlocking patterned shell edge emerges naturally as the continuation of a biaxially constrained mechanical instability. We demonstrate how significant morphological variation emerges via parametric variation and also demonstrate how a secondary instability accounts for the striking multiscaled oscillatory patterns found on certain brachiopods.
1. Background
Despite some differences in mode of secretions and anatomy between bivalves and brachiopods, the shells of both groups are incrementally secreted at the margin by a thin membranous elastic organ called the mantle that secretes first the periostracum, a thin soft organic layer that serves as a matrix for the deposition of the calcium carbonate of the shell (9, 10). The form of the calcified shell may thus be viewed as a spatiotemporal record of the form taken by the mantle at the shell margin during development. Although recent studies have begun to investigate cellular differential growth patterns underlying left–right asymmetries in gastropods (11) and to identify genetic and molecular bases of shell biomineralization in both mollusks and brachiopods (12, 13), the morphogenetic processes underlying the diversity of shell shapes in both groups remain poorly known. Theoretical models invoking either reaction–diffusion chemical systems (14) or nervous activity in the mantle epithelial cells (15), although successful in capturing the emergence of pigmentation patterns, do not explain the emergence of three-dimensional (3D) forms. A common default assumption in developmental biology is that molecular patterning precedes and triggers 3D morphogenetic processes. While this assumption might partly motivate recent studies of genetic and molecular mechanisms involved in shell development, only two-dimensional (2D) pigmentation patterns (that are molecular in nature) have been shown to map precisely with gene expression patterns (16). Marginal shell growth in bivalves and brachiopods takes place when the valves are open, both mantle lobes being retracted away from the margin of each valve when the shell is tightly closed. In the case of patterned interlocking commissures, it is difficult to conceive of genetic and molecular processes of morphogenetic regulation that would specify that when the margin of a mantle lobe secretes a patterned edge on one valve, the same complex processes must regulate the morphogenesis of the other mantle lobe to generate a perfectly antisymmetric edge on the other valve, both patterned edges closely interlocking when the mantle is retracted and the shell is closed. In other words, supposing that molecular patterning triggers 3D morphogenetic processes raises the question of the nature of the coordinating signal between both mantle lobes and how it could be transmitted. Formulated in that way, the development of closely interlocking edges and the repeated emergence of similar complex commissures during the evolution of 2 different phyla are puzzling problems.
A partial answer to this puzzle comes from oysters that live attached to a substratum. In these oysters, the surface of the attached valve carries the negative impression of the morphology of the substratum, while the free valve replicates in positive the form of the substratum, a phenomenon known as xenomorphism (i.e., “having a foreign form”) (Fig. 1E). No matter the irregular form of the substratum on which the oyster is attached (a stone, another shell, or an artificial substrate), the edge of the free valve closely fits with the edge of the attached valve. As the oyster grows bigger, the mantle margin of the attached valve starts to turn away from the substratum and no longer grows attached. At this stage, the shell attains what is called its idiomorphic form (i.e., “having its own form”) (17) and in some species, a zigzag-shaped commissure is generated at this stage. Our interpretation is that the xenomorphic and idiomorphic parts do not differ fundamentally from the point of view of the growth processes. In the xenomorphic part, the form taken by the mantle margin secreting the attached valve is mechanically imposed by the form of the substratum, and this form is itself mechanically imposed to the mantle lobe secreting the free valve when both mantle lobes are at least temporarily in close contact while secreting the slightly opened shell. Once the shell no longer grows attached to the substratum, the mechanical influence of the substratum is removed and there is only a reciprocal mechanical influence between both lobes. This reciprocal mechanical influence seems to be a general characteristic of the growth of brachiopods and bivalves. For example, in the case of traumatic individuals, the nontraumatic valve adapts its form and interlocks with the traumatic valve, no matter the abnormal form of the shell edge.
Xenomorphic–idiomorphic transition in oysters and trauma mirroring in both bivalves and brachiopods suggest the following hypothesis: Interlocking commissures are created by a combination of the mechanical constraints acting on each lobe and the mechanical influence of the 2 lobes on each other. In this paper, we develop a theoretical model of shell morphogenesis that confirms this hypothesis and we also extract universal morphogenetic rules. We show that the mechanical constraint acting on each lobe during growth imposes the geometric orientation of the morphological pattern while the reciprocal interaction between lobes enforces the antisymmetry of this pattern. Both principles are needed for perfect closure and are universal characteristics of the growth of brachiopods and bivalves.
2. Mathematical Model
A. Base Geometry
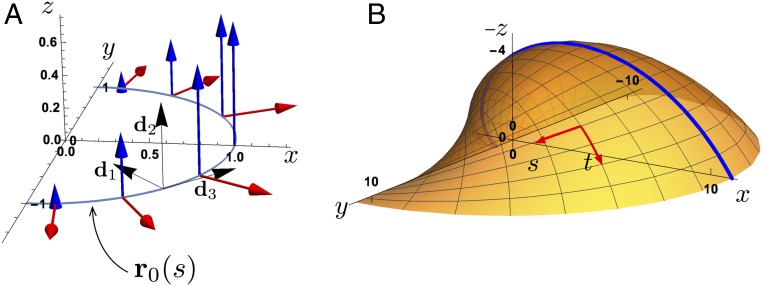
We first describe the general framework for the growth of bivalved shells by using the localized growth kinematics description of refs. 18 and 19. The shell is modeled as a surface , where is a material parameter describing location along the shell edge, and is a growth “time” parameter which need not correspond to actual time but which increases through development. The shell is constructed by defining an initial curve (where is the arclength) and a growth velocity field representing the rate of shell secretion such that (overdot represents time derivative). In the case of bivalved shells, the field requires only 2 components: a dilation rate, denoted , which describes the rate of expansion of the aperture, and a coiling rate, denoted , which is equivalent to the gradient in growth in the binormal direction and dictates how tightly coiled the shell is (Fig. 2). However, since we are interested only in the shape, we can set the dilation rate to without loss of generality, as it is only the ratio of dilation to expansion that is relevant in the shell form.
Fig. 2.
(A) The base geometry for bivalved shells is constructed via a locally defined growth velocity field defined on a base curve equipped with orthonormal basis . The growth consists of dilation (red arrows) and a coiling velocity in the binormal () direction with linear gradient (blue arrows) and hinge along the axis. (B) The resulting surface for one valve of the bivalve shell, with the and directions highlighted as well as the longitudinal midline (the curve ), which forms a logarithmic spiral.
The key to this description is to express the velocity field in a local orthonormal basis attached to each point of the shell edge. Here, we choose to be tangent to the shell edge; i.e., , where the prime denotes the derivative with and is a scale parameter characterizing the degree of total dilation from the base curve. Defining to align with the binormal direction, coiling is generated through a binormal growth velocity component ; i.e., shell coiling requires a linear growth gradient along an axis (taken without loss of generality to be the initial axis). Bivalves also require a hinge; in this formulation the hinge is the axis, where and thus ; see Fig. 2 and further geometric details in SI Appendix, section 1. The benefit of this approach is that the base shape of the shell emerges through a single geometric growth parameter, the coiling rate that can be related to a self-similar process of secretion of shell material and growth of the mantle. We do not assume a symmetry between the 2 valves; i.e., the coiling rates for the 2 halves may be different as seen in brachiopods (Section 3.C). Nevertheless, due to fixed dilation ( for both valves), if both halves have the same initial curve, then the 2 valves (of the smooth shell) will always meet perfectly in the - plane when the base shell is closed.
B. Mechanical Basis of Ornamentation
In bivalves and brachiopods, 3D ornamentations typically consist of an oscillation pattern of the shell edge that is termed antimarginal ornamentation. The basic premise for our investigation is that while the developmental processes underlying the variations of base geometry of the shell remain largely unknown, ornamentations emerge as the result of mechanical deformations of the secreting mantle margin (20). If the mantle grows at the same rate as the shell edge that it is itself secreting, both mantle and shell are in perfect synchrony and the shell will remain smooth. However, if the mantle margin grows faster, it has an excess of length with respect to the shell edge. This leads to a compressive stress that can induce buckling of the mantle, and the buckled pattern will subsequently be calcified in the next secretion of shell edge. If an excess of length is sustained through development, the deformation pattern will evolve and be amplified. In this way, ornamentation patterns are spatiotemporal records of these continued deformation patterns. This basic mechanism underlies the formation of ornamentation in shells and can be elegantly modeled by treating the mantle edge as a growing elastic beam (the mantle) attached to an evolving foundation (the rigid shell edge). Within this framework, one can explain how basic changes in shell geometry, growth, and mechanical properties produce a diverse morphology of ornamentation patterns (21–24). Here, we use the same modeling framework adapted to the growth constraints in bivalved shells.
C. Ornamentation Orientation
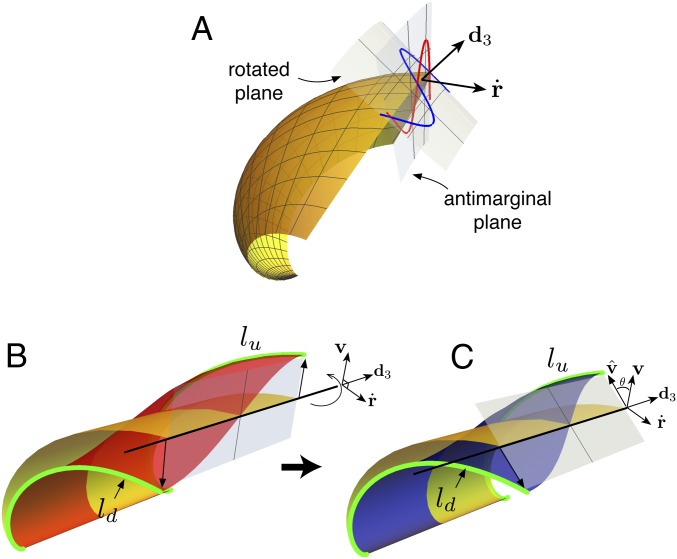
In our model the shell is obtained as the superposition of the morphological pattern of the buckled mantle on the smooth geometric surface generated via the growth velocity field. Antimarginal ornamentation is generally understood as a morphological pattern in the plane orthogonal to the shell margin, i.e., in the plane which has normal vector pointing tangent to the direction of shell growth (the plane with normal vector in the geometric description outlined above). However, close inspection of bivalved seashells shows that ornamentations typically do not form in the orthogonal plane and a natural problem is to determine the orientation of the ornamentation plane. Fig. 3A illustrates an oscillation pattern in the antimarginal plane as well the same pattern in a rotated plane.
Fig. 3.
(A) The difference between a pattern imposed in the antimarginal plane, with normal vector , and a rotation of this plane about the direction. In B, an oscillatory pattern in the antimarginal plane creates an unbalanced strain in the generative zone, as the arclength at the valleys is less than at the peaks. In the schematic, the green curve has shorter length than . This strain creates locally a moment around the axis. (C) This moment is balanced by rotating the plane of ornamentation until the arclengths are made equal and the strain is balanced.
The solution to this problem is the first key component that produces interlocking. The length of shell in the growth direction (i.e., arclength in the direction for fixed material point ) is determined by the rate of secretion. For neighboring material points the rate of secretion and thus arclength in the smooth shell are nearly identical. Once the mantle (and thus the shell edge) deforms, these arclengths may differ, depending on the plane in which the deformed pattern appears, and this will produce a moment of force about the shell edge (the direction) that serves to rotate the plane. The idea is illustrated in Fig. 3 B and C. Fig. 3B shows a portion of a base shell (yellow) and the same shell with a half-mode oscillation pattern imposed on top (red), with the pattern appearing in the antimarginal plane.* Once the mantle deforms, however, the arclengths are no longer equal: The arclength at the point which has deformed “up” is longer than the arclength at the point which has deformed “down”; i.e., as pictured. This difference creates a differential strain in the generative zone, the deformable region that connects the mantle to the already calcified portion of the shell, which induces a moment of force acting on the mantle that rotates the plane of ornamentation. In Fig. 3C, the same mode of deformation is shown in a rotated plane where the arclengths at the up and down points are equal, , so that the differential strain and thus the moment vanish.
The precise degree of rotation that balances the strain depends on the stage of development, the material point along the shell edge, and the growth parameters for the base shell. In particular it is worth noting that the steeper the angle of commissure, which occurs with increased coiling rate , the more rotation is needed. This is intuitive, if one considers that for a perfectly flat shell there is a perfect symmetry between up and down deformations, and thus no rotation is needed. Mathematically, points on the upper and lower side of the pattern are located at , where is the amplitude of deflection of the mantle, the factor accounts for the scaling of the buckling pattern’s amplitude, and is a unit vector to be determined that describes the orientation of the pattern such that the ornamentation appears in the - plane (details in SI Appendix, section 2). Then the balance of moment can be written as a geometric condition
| [1] |
This is a nonlinear differential equation satisfied by the rotation angle, which will depend on both the material point and the development time .
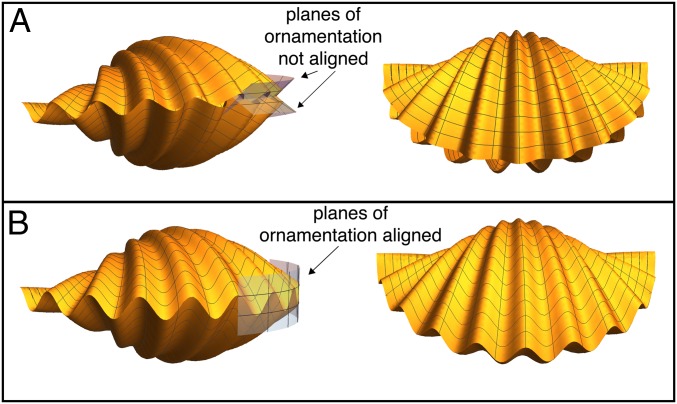
D. Rule 1: Coplanarity of Ornamentation Planes
For perfect interlocking to occur, the pattern on each individual valve must locally occur in the same plane when the valve is closed. We state this as the first rule of interlocking: The ornamentation planes of the 2 opposing valves must be aligned at all points when the valves are closed. This geometric rule is illustrated in Fig. 4, in which we superimpose a sinusoidal ornamentation on a bivalve. In Fig. 4A the ornamentation is truly antimarginal; i.e., there is no rotation of the plane of ornamentation. In this case, even though the pattern on the 2 valves was chosen to coincide, i.e., the sinusoidal curves are in phase, significant gaps and overlaps appear so that the valves do not interlock. Fig. 4B shows the same shell, but with a rotation of the plane of ornamentation. Here, a perfect interlocking is attained. Intuitively, the reason that the 2 valves can interlock is that the rotation imposed by generative zone strain causes both patterns to develop in the same plane.
Fig. 4.
The first rule of interlocking: At the shell level rotating the ornamentation plane is required for interlocking. A nonrotated plane of ornamentation (A) leads to a misalignment of the ornamentation patterns and thus gaps and overlaps appear when the 2 valves are closed. With rotation (B), opposing planes agree and a perfect interlocking is attained.
The argument and calculation in Section 2.C provide a geometric condition for the local orientation of the plane of each valve, although it is to be noted that this condition does not take into account the presence of the other valve. However, when both valves are rotated to meet in the - plane, rule 1 is satisfied. Indeed, the plane of ornamentation for the shell in Fig. 4B was computed according to the calculation described above. In fact, we find that this is a generic feature: For a bivalved shell growing according to the rules outlined above, and with plane of ornamentation defined by the balance of moments Eq. 1, the planes of ornamentation of each valve almost perfectly coincide at all points along the shell edge and at all times throughout development (SI Appendix, section 2).
E. Rule 2: In-Phase Synchrony of Ornamentation Pattern
While the coplanarity of ornamentation planes ensures that the 2 ornamentation patterns will appear in the same plane, it does not in itself guarantee that the 2 valves will interlock. For this to occur, we also require rule 2 of interlocking: The ornamentation patterns must coincide in phase. We now show that this synchrony is born out of the mechanical interaction of the 2 opposing mantle lobes.
Following refs. 22 and 23, we treat each mantle edge as a morphoelastic rod (25) attached elastically via the generative zone to a foundation, the rigid calcified shell (details in SI Appendix, section 3). The 2 mantle edges interact with each other when in contact through a repulsive interaction force ensuring that the 2 mantles cannot interpenetrate.
Since the 2 valves are meeting at a common plane with equivalent length of shell edge, and assuming that the mantle tissue of each valve has the same mechanical properties, given an excess of length that induces a mechanical pattern, the preferred buckling mode for each respective valve will be the same, if considered in isolation. The question then is what form the buckled pattern will take when the 2 mantle edges are not in isolation, but interacting with each other. The problem is greatly simplified by the first rule: Since the 2 planes of ornamentation are locally aligned, we can consider the buckling problem in a single surface. Further assuming that the curvature of the mantle along the edge is small, we “unwrap” the common ornamentation surface and consider a planar problem. For a given excess of length due to mantle growth, we compute the possible modes of deformation for the 2 mantles parametrically given by , , in the - ornamentation plane (SI Appendix, section 3). Once these are found, we consider the total mechanical energy of the system, given by the sum of bending and foundation energies on each side and the interaction energy between the two:
| [2] |
where
| [3] |
Here denotes the half-width of each mantle, is the resultant moment acting on the growing mantle, and describes the strength of the foundation. The interaction between both mantles is modeled by
| [4] |
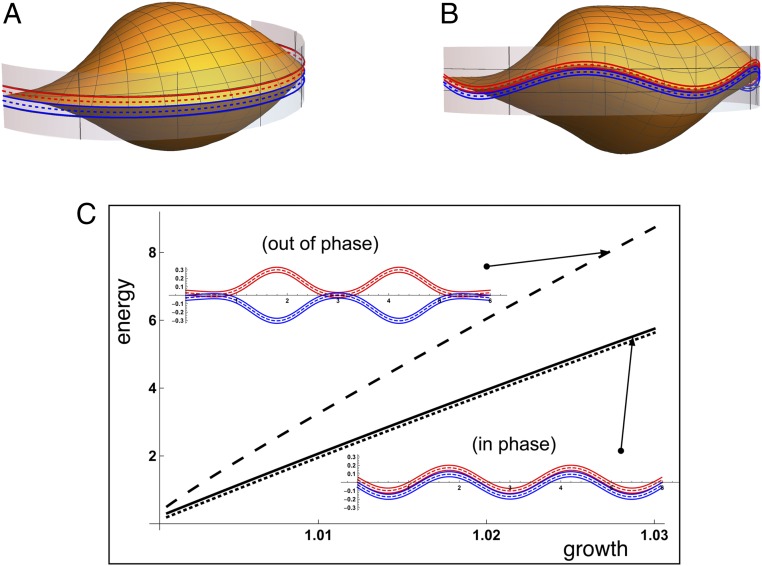
where is a constant that characterizes the strength of the repulsive interaction. We compare the energy in 2 distinct configurations: one in which the opposing mantle edges are “in phase” and one in which they are “out of phase.” These configurations are obtained by first computing the preferred buckling shape of a mantle in isolation. The buckling forms a bifurcation from the trivial straight solution with 2 solution branches of equal energy that are mirror images of each other. Taking both mantles from the same branch forms the in-phase solution while taking them from opposing branches forms the out-of-phase solution. We then compute the energy in the system as a function of mantle growth. The energies are plotted in Fig. 5C, which shows that the energy in the out-of-phase pattern is significantly higher than the in-phase energy. For comparison, we compute the energy of the 2 mantles in the absence of interaction (dashed line), which forms a lower bound on the total energy.
Fig. 5.
The ornamentation pattern emerges as a mechanical instability due to excess growth of the shell secreting mantle and periostracum. In the model, the mantle edge (A) is unwrapped to compute the 2D pattern which is then imposed back on the shell in the plane of ornamentation (B). In C, an energy comparison demonstrates that the in-phase pattern with interlocking edges is energetically favorable and nearly identical to the energy without interaction between the mantles (dotted curve in C).
The complete shell with the energy-minimizing buckling pattern imposed is plotted in Fig. 5B. Physically, the in-phase pattern has lower energy because a large deformation is needed to maintain geometric compatibility in the out-of-phase case, and the contact energy is also much higher. The significant difference in energy between in-phase and out-of-phase deformation modes (almost double at the point of only 3% growth extension) and the close proximity of in-phase energy with the lower-bound “no interaction” energy suggests that the in-phase solution is a global minimizer and the preferred configuration. We conclude that the mechanical interaction of the mantles provides the mechanism for rule 2.
3. Morphological Trends
A. Growth, Accretion, and Secretion
The formation of a shell involves 3 distinct but closely related activities: growth of the mantle, secretion of new shell material by the mantle, and accretion of the shell. The distinction between secretion and accretion is subtle, but if we define accretion as increase of shell length in the growth direction, then it becomes clear that it is possible for shell material to be secreted without actually contributing to accretion, e.g., by thickening the shell as empirical evidence shows in many seashells. To explain the distinction between observed morphologies requires considering the interplay between these activities.
We first consider the link between mantle growth and secretion rate. By mantle growth we refer specifically to longitudinal growth along the mantle edge—the growth that produces the excess of length that drives mantle buckling and thus generates the patterned shell edge. The rate of amplification of the buckling pattern is governed by the rate of mantle growth. Here we make the simple assumption that the mantle growth rate is proportional to the secretion rate . In this way, a shell with higher coiling rate (larger ) will have a higher ornamentation amplitude compared to a shell with lower coiling rate. In particular, the linking of growth with secretion provides a simple mechanism for zigzag commissures (Fig. 1C), which tend to appear in shells with a very steep angle of commissure (high coiling rate): These may be seen as an extreme form of a (smooth) buckling pattern but with a very small wavelength combined with a high amplitude, the latter arising due to high secretion rate.
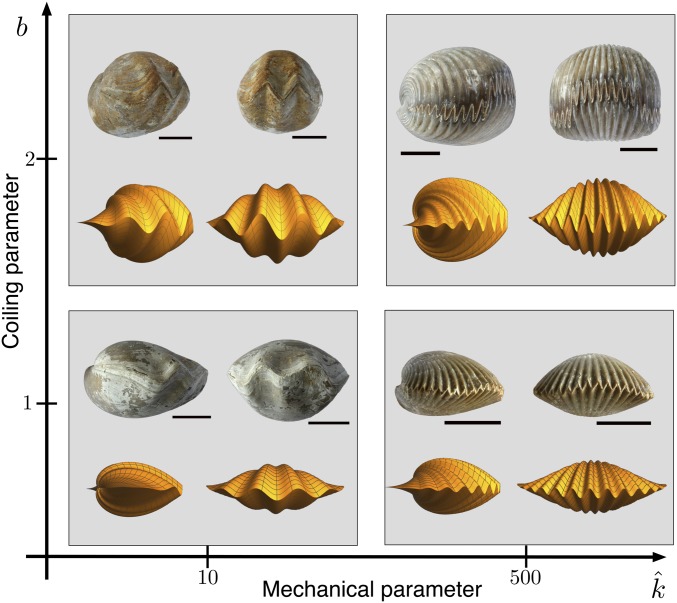
B. A 2D Morphospace
In this construction, there are only 2 main parameters governing the shell morphology: the coiling rate and a single mechanical parameter (SI Appendix, section 3), which governs the mode of buckling and hence the wavelength of the interlocking ornamentation pattern† .
In Fig. 6 we illustrate the range of shell morphologies as a 2D morphospace formed by the parameters and . A low value of results in a long wavelength pattern, and vice versa, while a low coiling rate produces a shallow shell, with high coiling rate producing a steeper shell and more amplified pattern. For comparison, we include 4 representative shells matching the basic characteristics of each corner of the morphospace. Since by construction these shells satisfy both rules of interlocking, the interlocking pattern is perfectly formed.
Fig. 6.
Morphology variety for (symmetric) interlocking bivalved shells and sample shells illustrating the diversity of form (brachiopod species from Upper Left to Lower Right: Cererithyris arkelli; Sphenorhynchia plicatella; Cererithyris intermedia; Kutchirhynchia obsoleta). The simulated shells correspond to the 4 different combinations of a low () and a high () coiling rate and small () and large () mechanical stiffness. The computational procedure is outlined in SI Appendix, section 4. (Scale bars: 10 mm.)
C. Asymmetry and Secondary Ornamentation
An intriguing feature of our findings is that interlocking does not require symmetry between the 2 valves (consider that one’s hands clasp together very nicely, but they also grow as almost perfect mirror images). Indeed, in many shells, notably in brachiopods, the 2 valves have markedly different coiling rates. In our model, rule 1 is accomplished by a rotation of the generative zone that does not rely on the physical interaction of the opposing valve, and thus the 2 base valves need not be mirror images of each other for the planes of ornamentation to align. And once the planes align, rule 2 for antisymmetry of the pattern is accomplished by the mechanical interaction of the 2 mantles.
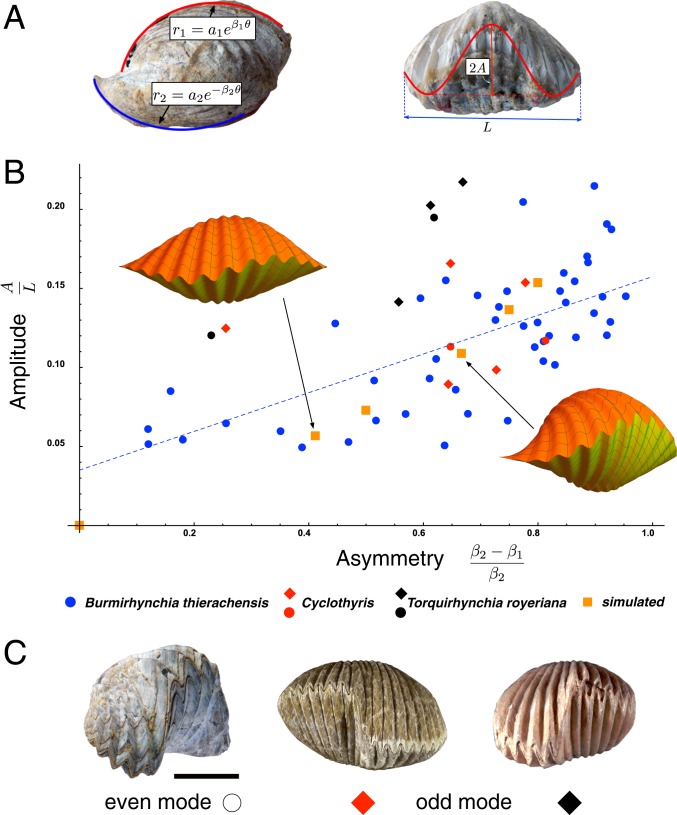
However, by linking mantle growth to secretion rate, an asymmetry in coiling implies also an asymmetry in mantle growth. Therefore, we can put our modeling framework to the test by studying the ornamentation morphology of shells with asymmetric coiling. In particular, we are motivated by a striking feature found in some brachiopod shells, as shown in Fig. 7. These shells exhibit a secondary, long wavelength pattern, on top of which a small wavelength primary pattern can be found‡. Both the long and short wavelength patterns vary significantly between species and specimens, yet remarkably, perfect interlocking is maintained in all cases.
Fig. 7.
Asymmetry and large-scale pattern in brachiopods. (A) For each shell we extract both an asymmetry measure via difference in coiling rates and relative amplitude of the large pattern. (B) These data are collected on a set of shells displaying the large-scale pattern: Burmirhynchia thierachensis (blue), Cyclothyris (red), and Torquirhynchia royeriana (black). Shells displaying the odd mode are marked with a diamond symbol. A linear regression is plotted as the dashed line. The orange squares are produced via a 2-beam mechanical model, and complete shells are simulated at the marked points. (The hollow point at the origin is not simulated; by construction zero asymmetry has zero amplitude.) (C) Large wavelength patterns in brachiopods appear both as an even mode deformation (Left, Septaliphoria orbignyana) and as an odd mode (Center, Cyclothyris sp.; and Right, T. royeriana). In the latter, there is no lateral preference.
To study the impact of asymmetry in the model we suppose that one valve, say valve 1, has a higher secretion rate than the other one, say valve 2. The corresponding mismatch in mantle growth means that mantle 1 will have a greater (unstressed) reference length, but is under the same geometric constraints as mantle 2. This mismatch induces a mechanical stress in the mantle which is relieved by a secondary buckling instability of the entire mantle/periostracum system§ .
C.1. Adaptive accretion.
As a first test of the model, we check that interlocking is maintained within the framework we have developed. In the base case, before any deformation, the coiling rates are constant for each valve, and the 2 valve edges meet at the same midplane when the valves are closed. Once a large-scale deformation occurs, the valve edges no longer meet in a single plane (the - plane as in the base case). Some material points along the edge will have moved in one direction (to , say) while other points will have moved in the other direction (). However, the rotation of each valve about the hinge—increased rotation is needed to accommodate increased material—is a global property. Thus, the geometrical constraint of the presence of the opposing valve locally changes along the shell edge. The local accretion rate, i.e., local coiling rate, must change in response. By analyzing the coiling geometry with such a deformation imposed, we show in SI Appendix, section 5 that the coiling naturally adapts such that the 2 shell edges still perfectly coincide, although no longer in a single plane.
The next step is to reintroduce the small-scale pattern by the same process as before: A generative zone strain is induced by the difference in arclength at the valleys compared to the peaks of the small-scale pattern, and thus the plane of ornamentation is defined such that the arclength is equal at the peaks and valleys. The corresponding nonlinear ODE is then solved for the tilt of mantle that defines the local plane of ornamentation (details in SI Appendix, section 5A). The net result is that the plane of ornamentation rotates nonuniformly at each point along the shell edge compared to the base case, but the orientations still coincide locally between the 2 valves. Thus rule 1 is satisfied even in the presence of asymmetry.
C.2. Synchrony of ornamentation with asymmetry.
The conceptual idea of rule 2 is as before: For interlocking to occur the ornamentation patterns must be antisymmetric, a synchrony we expect to be maintained by the mutual interaction of the mantles. However, the situation is more complicated by the difference in mantle growth rates and requires an extension of the previous mechanical model for 2 mantles geometrically constrained by each other with the additional assumption that they are growing at unequal rates (SI Appendix, section 6).
We find that for moderate asymmetry, the interaction of the mantles is sufficient to enforce synchrony of the pattern. However, as further elucidated in SI Appendix, section 6, for larger asymmetry the mantles eventually separate due to a divergence in their reference lengths. A biomechanical coupling would be necessary in such cases.
C.3. Asymmetry patterns.
We confirm the prediction of our model against basic morphological trends observed in shells with the secondary pattern. In brachiopods the 2 valves cover the dorsal and ventral sides of the animal. Prior to the large-scale deformation, the dorsal side has the higher coiling rate (when there is asymmetry present). Once the large-scale pattern appears, the following characteristics are observed: 1) The large wavelength pattern appears either as an “even mode” or as an “odd mode” (Fig. 7C) and 2) there is a positive correlation between the degree of dorsoventral asymmetry and the size of the large-scale pattern.
Observation 1 is clearly compatible with a mechanical instability, for which different buckling modes will be triggered based on geometric and mechanical parameters. For odd modes, there is no lateral preference; i.e., right- and left-“handed” shells with an odd mode always occur in roughly the same numbers in populations (26) and in the 29 known cases of plants and animals displaying a random direction of bilateral asymmetry, the direction of asymmetry almost always lacks a genetic basis (27). A mechanical origin is consistent with this trend, as there is no lateral preference in the case of an odd mode buckling, by symmetry of the geometry. With even modes, on the other hand, the middle point of the shell edge always deforms toward the dorsal valve. This requires a bias in the buckling direction that impacts only even modes; a plausible mechanism based on the already present coiling asymmetry is described in SI Appendix, section 6.
Observation 2 is also consistent with a mechanical process, as an increase in dorsoventral asymmetry would imply an increase in mechanical stress, which would lead to earlier buckling and an increased amplitude relative to shell size. To quantify this trend, we have studied a sample of 59 brachiopods from different species. For each shell, we extract dorsoventral asymmetry by fitting logarithmic spirals to a side profile and amplitude of the large pattern by fitting a sinusoid to a front view, as shown in Fig. 7A. Amplitude is plotted against asymmetry in Fig. 7B, showing a strong correlation: We compute a Spearman’s rank correlation coefficient of 0.67 and a P value less than 0.0001. The extracted data, as well as an image of every shell sampled with curves overlaid, are available in SI Appendix, section 7. From the mechanical model (SI Appendix, section 6) we extract the equivalent measures by taking the difference in asymmetry to correspond to the difference in mantle growth rates, computing the bifurcation curves following buckling and extracting amplitude relative to length for several different measures of asymmetry. These appear as the orange squares in Fig. 7B, demonstrating that the patterns and trends predicted by the model are consistent with the observed morphological trends.
Moreover, the morphological features are well captured by the model. To illustrate, the computed buckled shape at the 2 marked simulated points in Fig. 7B was fed into the full shell model, with small pattern taken as output of the small-scale mechanical model and plane of ornamentation computed with adapted coiling in combination with base shell geometry; all model components were combined to produce the simulated shells appearing in Fig. 7B, which in both cases exhibit a perfect interlocking.
4. Discussion
In this paper we have shown the key role of mechanics in forming common features of shell sculpture in interlocking bivalved shells. Ornamentation appears as a mechanical instability arising due to a simple developmental change—growth of the mantle outpacing expansion of the aperture—while at the same time shell interlocking is maintained by mechanical forces without requiring specific genetic processes. This biophysical explanation of developmental origins provides a much-needed complementary view to functional considerations. Indeed, during the 20th century most aspects of brachiopod and mollusk shell morphologies have been interpreted within the functional perspective of the neo-Darwinian synthesis. According to this view one may explain how a trait has come into being and has evolved by appealing to its function alone. For instance, Rudwick (28) proposed that zigzag-shaped commissures have evolved as filtering grids to prevent the entry of harmful particles above a certain size in brachiopods and bivalves that feed by filtering tiny food particles from seawater and concluded that this function explains the presence of this trait and the intrinsic probability that zigzags evolved many times independently in these organisms, an interpretation that has since remained unquestioned (29, 30). However, the promotion of traits by natural selection is logically distinct from the mechanisms that generate them during development. While some of the possible functional advantages of interlocking structures are clear, an explanation of the repeated emergence of similar characters in distantly related lineages requires an understanding of the development of these characters that might induce a reproductive bias (i.e., natural selection).
Our study shows that a part of the morphological diversity and evolution of these groups of invertebrates may be understood in light of both the mechanical interactions of the mantle with the rigid shell edge and the reciprocal mechanical influence that both mantle lobes have on each other during shell secretion. Our conclusion is that brachiopods and bivalves have managed to secrete interlocking shells simply as a consequence of a biaxially constrained mechanical instability of the secreting mantle. It is therefore not surprising that the same patterns of interlocking structures have evolved repeatedly among brachiopods and bivalves, an evolutionary trend which is a predictable outcome of the physics of the growth process. It is also worth noting that we have restricted our study to self-similar shell growth (prior to emergence of any large-scale pattern) and with small-scale patterns appearing at right angles to the shell margin. While it is a suitable assumption for most bivalves and brachiopods, there are species that deviate from self-similarity or with ribs appearing oblique to the shell margin. In such shells interlocking is consistently maintained, suggesting that the process we propose is robust with respect to these perturbations as well. Accordingly, we hypothesize that mechanical forces also play the same role in these systems. However, to model these forces explicitly would require introducing an additional torsional component in the generative zone¶ and/or deviating from the self-similar growth that we have utilized in our geometric construction. While such steps are certainly feasible, and conceptually all of the same ideas outlined in our paper would still apply, modeling such cases would introduce additional computational complexity and is left as future work.
There are other striking examples in nature of organisms with matching of body parts, such as the closed mouth of the snapdragon flower (29, 31), the interacting gears of the planthopper insect Issus (30), or dental occlusion in vertebrates (32). The role of mechanics in the morphogenesis of such structures could be the subject of fruitful future inquiries. Among mollusks, the hinge in bivalves is also formed by a series of interlocking teeth and sockets on the dorsal, inner surface of the shell. In this case too, the hinge teeth are secreted by 2 lobes of the mantle which are retracted from the hinge line when the shell is tightly closed and when teeth and sockets interlock in each other. The morphologies of these hinge teeth (e.g., taxodont, heterodont, schizodont …) have traditionally provided the basis of bivalve classifications, but recent molecular phylogenies (33) show that these characters do not always bear a coherent phylogenetic signal, which could be explained by the fact that ahistorical physical processes play an important role in their development.
The fact that physical processes are key in shell morphogenesis does not imply that genetic and molecular processes are irrelevant. For example, both the amplitude and wavelength of ornamentation may vary considerably among oyster species, possibly because of species-specific combinatorial variations in control parameters such as commarginal growth rate or stiffness of the mantle. Given that these parameters may be genetically modulated, our approach might open the door to future studies aiming at understanding how biochemical and biophysical processes across scales could conspire to regulate the development and variations of morphologies among different species. The interplay between predictable patterns and unpredictability of specific outcomes in large part defines biological evolution (34). Cells, tissues, and organs satisfy the same laws of physics as nonliving matter, and in focusing on the noncontingent and predictable rules that physical processes introduce in development and in the trajectories that are open to morphological evolution, we shift the focus from the Darwinian perspective of “the survival of the fittest” to a more predictive one of “the making of the likeliest.”
While buckling and wrinkling instabilities have long been viewed as only detrimental in engineering, an increasing number of studies, often inspired by biology, have shown the potential contribution of this physical phenomenon to smart applications (35). Interlocking structures are ubiquitous in man-made structures where they serve as physical connections between constitutive parts in such diverse areas as building or biomedical engineering, and their presence in nature is a source of inspiration for biomimetic engineering (36). Our study shows that brachiopods and bivalves have made good use of mechanical instabilities to secrete their interlocking shell since about 540 million years ago; in this light perhaps the growth of these invertebrates could be inspirational in biomimetic research for the development of self-made interlocking structures at many scales.
Data Availability.
All materials, methods, and data needed to evaluate the conclusions are present in the main text and/or SI Appendix.
Supplementary Material
Acknowledgments
We thank E. Robert (Université Lyon 1, France) and J. Thomas (Université de Bourgogne, Dijon, France) for providing us an access to paleontological collections. This work was made possible by a visiting position from LGL-TPE, Université Lyon 1.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. S.H.R. is a guest editor invited by the Editorial Board.
*Locally, a small section of shell can be approximated as a cylinder with logarithmic spiral shape and with equal arclength at neighboring points prior to mantle deformation; hence for visual simplicity here we plot portions of the shells as being cylindrical.
†The cross-sectional shape is another degree of freedom, and indeed our approach may be applied to any cross-sectional shape, but we have restricted it to a semicircle here, as this provides the simplest form and is a good model for most bivalved shells.
‡We term the long wavelength pattern as secondary, as this pattern only ever appears later in development, while the small-scale ornamentation appears early and has the same characteristics as the ornamentations we have described thus far in this paper.
§In this view, the small-scale pattern is primarily focused at the thin periostracum while the much thicker mantle remains effectively flat (SI Appendix, section 5 and Fig. 2).
¶In terms of the plane of ornamentation, our model considers a rotation about the tangent direction; an oblique pattern could be produced by also rotating about the direction, which would create a “slant” to the antimarginal ornamentation.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1916520116/-/DCSupplemental.
References
- 1.Kouchinsky A., et al. , Chronology of early Cambrian biomineralization. Geol. Mag. 149, 221–251 (2012). [Google Scholar]
- 2.Peterson K. J., Cotton J. A., Gehling J. G., Pisani D., The Ediacaran emergence of bilaterians: Congruence between the genetic and the geological fossil records. Philos. Trans. R. Soc. Biol. Sci. 363, 1435–1443 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Luo Y. J., et al. , The Lingula genome provides insights into brachiopod evolution and the origin of phosphate biomineralization. Nat. Commun. 6, 8301 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Isowa Y., et al. , Proteome analysis of shell matrix proteins in the brachiopod Laqueus rubellus. Proteome Sci. 13, 21 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Laumer C. E., et al. , Spiralian phylogeny informs the evolution of microscopic lineages. Curr. Biol. 25, 2000–2006 (2015). [DOI] [PubMed] [Google Scholar]
- 6.Williams A., Carlson S. J., Brunton C. H. C., Holmer L. E., Popov L., A supra-ordinal classification of the Brachiopoda. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 351, 1171–1193 (1996). [Google Scholar]
- 7.Kocot K. M., et al. , Phylogenomics reveals deep molluscan relationships. Nature 477, 452–456 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Carlson S. J., The evolution of Brachiopoda. Annu. Rev. Earth Planet Sci. 44, 409–438 (2016). [Google Scholar]
- 9.Simkiss K., Wilbur K. M., Biomineralization: Cell Biology and Mineral Deposition (Academic Press, San Diego, CA, 1989). [Google Scholar]
- 10.Roda M. S., et al. , Calcite fibre formation in modern brachiopod shells. Sci. Rep. 9, 598 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Johnson A. B., Fogel N. S., Lambert J. D., Growth and morphogenesis of the gastropod shell. Proc. Natl. Acad. Sci. U.S.A. 116, 6878–6883 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jackson D. J., Wörheide G., Degnan B. M., Dynamic expression of ancient and novel molluscan shell genes during ecological transitions. BMC Evol. Biol. 7, 160 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jackson D. J., et al. , The Magellania venosa biomineralizing proteome: A window into brachiopod shell evolution. Genome Biol. Evol. 7, 1349–1362 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Meinhardt H., The Algorithmic Beauty of Sea Shells (Springer-Verlag, 1995). [Google Scholar]
- 15.Boettiger A., Ermentrout B., Oster G., The neural origins of shell structure and pattern in aquatic mollusks. Proc. Natl. Acad. Sci. U.S.A. 106, 6837–6842 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jackson D. J., et al. , A rapidly evolving secretome builds and patterns a sea shell. BMC Biol. 4, 40 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Stenzel H. B., “Oysters” in Treatise on Invertebrate Paleontology, Part N, Bivalvia, Moore R. C., Ed. (Geological Society of America, 1971), vol. 3, pp. N953–N1224. [Google Scholar]
- 18.Moulton D. E., Goriely A., Surface growth kinematics via local curve evolution. J. Math. Biol. 68, 81–108 (2014). [DOI] [PubMed] [Google Scholar]
- 19.Goriely A., The Mathematics and Mechanics of Biological Growth (Springer-Verlag, New York, NY, 2017). [Google Scholar]
- 20.Moulton D. E., Goriely A., Chirat R., Mechanical growth and morphogenesis of seashells. J. Theor. Biol. 311, 69–79 (2012). [DOI] [PubMed] [Google Scholar]
- 21.Erlich A., Howell R., Goriely A., Chirat R., Moulton D. E., Mechanical feedback in seashell growth and form. ANZIAM J. 59, 581–606 (2018). [Google Scholar]
- 22.Chirat R., Moulton D. E., Goriely A., Mechanical basis of morphogenesis and convergent evolution of spiny seashells. Proc. Natl. Acad. Sci. U.S.A. 110, 6015–6020 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Moulton D. E., Goriely A., Chirat R., The morpho-mechanical basis of ammonite form. J. Theor. Biol. 364, 220–230 (2015). [DOI] [PubMed] [Google Scholar]
- 24.Erlich A., Moulton D. E., Goriely A., Chirat R., Morphomechanics and developmental constraints in the evolution of ammonites shell form. J. Exp. Zool. B Mol. Dev. Evol. 326, 437–450 (2016). [DOI] [PubMed] [Google Scholar]
- 25.Moulton D. E., Lessinnes T., Goriely A., Morphoelastic rods part 1: A single growing elastic rod. J. Mech. Phys. Solids 61, 398–427 (2012). [Google Scholar]
- 26.Fürsich F. T., Palmer T., Commissural asymmetry in brachiopods. Lethaia 17, 251–265 (1984). [Google Scholar]
- 27.Palmer A. R., Symmetry breaking and the evolution of development. Science 306, 828–833 (2004). [DOI] [PubMed] [Google Scholar]
- 28.Rudwick M. J. S., The function of zigzag deflections in brachiopods. Palaeontology, 7, 135–171 (1964). [Google Scholar]
- 29.Green A. A., Kennaway J. R., Hanna A. I., Bangham J. A., Coen E., Genetic control of organ shape and tissue polarity. PLoS Biol. 8, e1000537 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Burrows M., Sutton G., Interacting gears synchronize propulsive leg movements in a jumping insect. Science 341, 1254–1256 (2013). [DOI] [PubMed] [Google Scholar]
- 31.Cui M. L., Copsey L., Green A. A., Bangham J. A., Coen E., Quantitative control of organ shape by combinatorial gene activity. PLoS Biol. 8, e1000538 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Calamari Z. T., Hu J. K. H., Klein O. D., Tissue mechanical forces and evolutionary developmental changes act through space and time to shape tooth morphology and function. BioEssays 40, 1800140 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Plazzi F., Ceregato A., Taviani M., Passamonti M., A molecular phylogeny of bivalve mollusks: Ancient radiations and divergences as revealed by mitochondrial genes. PLoS One 6, e27147 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Koonin E. V., The Logic of Chance: The Nature and Origin of Biological Evolution (FT Press, 2011). [Google Scholar]
- 35.Hu N., Burgueño R., Buckling-induced smart applications: Recent advances and trends. Smart Mater. Struct. 24, 063001 (2015). [Google Scholar]
- 36.Zhang Y., Yao H., Ortiz C., Xu J., Dao M., Bio-inspired interfacial strengthening strategy through geometrically interlocking designs. J. Mech. Behav. Biomed. Mater. 15, 70–77 (2012). [DOI] [PubMed] [Google Scholar]
- 37.Telford M. J., Budd G. E., Invertebrate evolution: Bringing order to the molluscan chaos. Current Biology, 21, R964–R966 (2011). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All materials, methods, and data needed to evaluate the conclusions are present in the main text and/or SI Appendix.