Accurate and rapid background estimation in single-molecule localization microscopy using the deep neural network BGnet

Significance

Single-molecule localization microscopy has developed from a specialized technique into a widely used method across biological and chemical science. However, to see one molecule, unwanted light from the sample (background) must be minimized. More importantly, nonuniform background can seriously degrade the localization process. So far, addressing this problem has been challenging. We provide a robust, general, and easy-to-implement framework rooted in deep learning to accurately and rapidly estimate arbitrarily structured background so that this interfering structure can be removed. The method works both for conventional microscopes and also for complex 3-dimensional designs based on engineering the point-spread function. Accurate background estimation is a critically useful tool for extracting maximum information from single-molecule images.

Abstract

Background fluorescence, especially when it exhibits undesired spatial features, is a primary factor for reduced image quality in optical microscopy. Structured background is particularly detrimental when analyzing single-molecule images for 3-dimensional localization microscopy or single-molecule tracking. Here, we introduce BGnet, a deep neural network with a U-net-type architecture, as a general method to rapidly estimate the background underlying the image of a point source with excellent accuracy, even when point-spread function (PSF) engineering is in use to create complex PSF shapes. We trained BGnet to extract the background from images of various PSFs and show that the identification is accurate for a wide range of different interfering background structures constructed from many spatial frequencies. Furthermore, we demonstrate that the obtained background-corrected PSF images, for both simulated and experimental data, lead to a substantial improvement in localization precision. Finally, we verify that structured background estimation with BGnet results in higher quality of superresolution reconstructions of biological structures.

In optical microscopy, the term “background” (BG) summarizes contributions to an image that do not arise from the species that is investigated, but from other sources (1, 2). These contributions lower the quality of the image and are, therefore, unwanted. For example, when performing fluorescence microscopy of a cellular protein labeled via immunochemistry, antibodies may bind nonspecifically to other cellular components or to the sample chamber, or the sample itself can exhibit autofluorescence (3).

Often, during camera-based localization within a small region of interest (ROI), the BG structure of an image is considered to be uniform within that region and is accounted for by subtraction of a mean or median fluorescence signal that is extracted from an image area that has no contribution from the fluorescently labeled species of interest (4). The assumption of unstructured (uniform) BG is, however, an oversimplification in most situations. For example, in biological microscopy, a typical specimen such as a cell or a tissue slice features a huge number of different components that are distributed over many different spatial length scales that may be autofluorescent (5). A fluorescent probe introduced to label a component may also bind nonspecifically to other components. Therefore, the resulting fluorescent BG will be composed of many different spatial frequencies. Thus, this type of BG can be termed “structured BG” (sBG) (6).

sBG is especially detrimental when single emitters such as single molecules are detected and imaged to estimate their position on the nanometer scale, as is done in localization-based superresolution microscopy methods (e.g., photoactivated localization microscopy [PALM], stochastic optical reconstruction microscopy [STORM], fluorescence PALM [f-PALM]) or single-molecule tracking (7–9). In these approaches, a BG-free model function of the point-spread function (PSF), i.e., the response function of the microscope when a single emitter is imaged, is fit to the experimentally recorded camera image of the single molecule containing BG (2, 10). In the simplest case, the standard (open aperture) PSF of a typical microscope can be approximated by a 2-dimensional (2D) Gaussian. For 3-dimensional (3D) imaging, more complex PSFs have been developed via PSF engineering in the Fourier plane, and the information about z position is encoded in the more complex image (11). Similar PSF engineering strategies can be used to encode other variables such as emitter orientation, wavelength, etc. (12–14).

While unstructured BG can be easily accounted for in the PSF fitting process as an additive offset, removing sBG is much more challenging: a simple subtraction of some number will just shift the average BG magnitude but not remove the underlying structure. The remaining sBG changes the PSF shape, which can strongly affect the result of the position estimation, regardless of the fitting algorithm used (e.g., least squares or maximum-likelihood estimation [MLE]) (15, 16).

Unfortunately, correction for sBG is not trivial as it can exhibit contributions from various spatial scales. Any approach to remove sBG must be able to differentiate between the spatial information from the PSF alone, which must be retained, and the spatial information in the sBG (17, 18). A recent Bayesian approach estimated background for a specific case (19), but more general background estimation procedures are needed. Methods such as sigma clipping (20, 21) have been developed to account for sBG; however, for more complex PSFs used in 3D imaging, sBG estimation with these approaches is very challenging. Therefore, even though sBG is a prominent feature for experimental datasets, the simple assumption of constant BG is still widely used today. In this work, we address this problem by employing advanced image analysis with deep neural networks (DNNs), using the network to extract the sBG for proper removal.

Results and Discussion

General Workflow and BGnet Architecture.

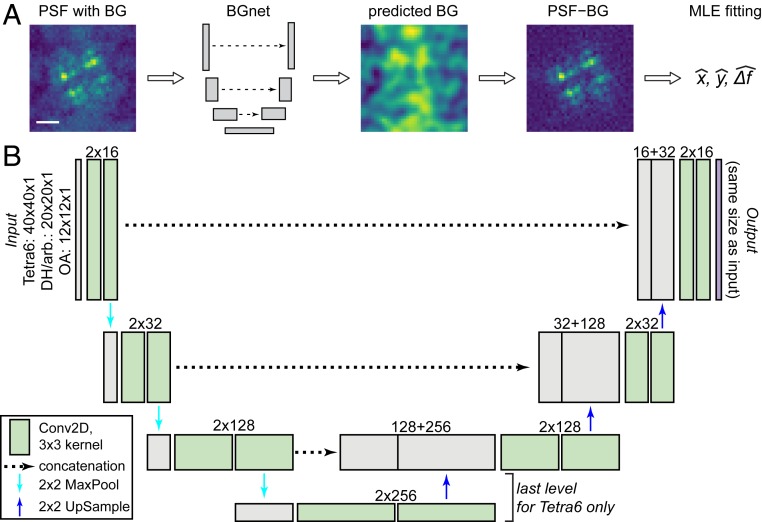
Here, we introduce BGnet, a DNN that allows for rapid and accurate estimation of sBG. DNNs are versatile tools for various applications, among which, image analysis for general purpose feature recognition as well as for optical microscopy are prominent (22–26). Recently, the U-net architecture has been demonstrated to be well suited for image segmentation (27, 28). Fundamentally, image segmentation is similar to sBG estimation: a feature—the PSF without BG—is overlaid with the sBG, which should be identified from the combined image in order to subsequently remove it. Therefore, we suspected that a U-net-type architecture might also be applicable for sBG estimation in optical microscopy, as schematically depicted in Fig. 1A. The architecture of BGnet is depicted in Fig. 1B, illustrating the U-shaped architecture of the network. The fundamental idea is to first condense the spatial size of the input image stepwise while increasing its filter space. Then, stepwise up-sampling is performed until the original spatial scale of the image is obtained, and the filter space is reduced in turn. This is often termed encoder–decoder architecture (22, 29). In U-net-type architectures, the output before each down-sampling (left arm of the U) is concatenated with the result of the up-sampling (right arm of the U) at corresponding spatial scales. This is reminiscent of residual nets where the output of a layer is added to the output of a deeper layer via skipped connections (30).

Fig. 1.

General approach and BGnet architecture. (A) BGnet receives an image of a PSF (here the Tetra6 PSF) with BG. Its output is the predicted BG contribution at each pixel. Thus, the predicted BG can be readily subtracted from the input PSF image. The BG-corrected PSF can subsequently be analyzed, for example via MLE fitting for position estimation in x and y with defocus Δf. (B) The PSF images are supplied to BGnet as single-channel 12 × 12 (OA PSF), 20 × 20 (DH, arbitrary PSF), or 40 × 40 pixel images. After two 2D convolutions with 16 filters, batch normalization and rectified linear unit activation, 2 × 2 MaxPooling is performed. Two 2D convolutions with 32 filters are performed. The output is again subjected to 2 × 2 MaxPooling, followed by two 2D convolutions with 128 filters. An additional 2 × 2 MaxPooling, followed by 2 more 2D convolutional layers with 256 filters, is performed for the Tetra6 PSF only. The output of the 2D convolutional layers with the lowest spatial size is up-sampled (2 × 2) and concatenated with the output of the 2D convolutional layer that was supplied to the final 2 × 2 MaxPooling. Up-sampling, concatenation, and 2D convolution are repeated until the spatial scale of the image is again 12 × 12, 20 × 20, or 40 × 40, respectively. The last layer is a 12 × 12 × 1, 20 × 20 × 1, or 40 × 40 × 1 2D convolutional layer, returning the predicted BG. (Scale bar in A, 1 μm.)

First, we provided BGnet with training data that covers the wide parameter space that sBG estimation poses: A given PSF that should be analyzed can have various shapes and sizes at different axial positions of the emitter; and many different spatial frequencies can combine to form the sBG. Therefore, we turned to accurate PSF simulations of 3 PSFs commonly used for superresolution imaging and single-particle tracking: The standard open aperture (OA) PSF, the double-helix (DH) PSF with 2-μm axial range (15, 31), and the Tetrapod PSF with 6-μm axial range (Tetra6 PSF) (32). Also, we included an arbitrary PSF with a rather chaotic shape to test whether our approach is robust against PSF shapes that do not exhibit a well-defined symmetric structure. See SI Appendix, Fig. S1 for the development of the 4 investigated PSF throughout their respective relevant focal range. As a model for sBG, we chose Perlin noise because it is 1) able to accurately resemble sBG encountered under most experimental conditions and 2) precisely controllable in its spatial frequency composition (see SI Appendix, Fig. S2 for an overview) (33).

PSFs were simulated by means of vectorial diffraction theory (34, 35) using simulation parameters matching typical experimental values and accurately characterized aberrations, determined via phase retrieval as previously published (16). The PSFs were simulated at different focal positions and different distances away from a glass coverslip (n = 1.518) in water (n = 1.33) (see SI Appendix, Tables S1–S4 for simulation parameters). The Perlin noise used for sBG modeling contained spatial frequencies of L/12, L/6, L/4, and L/2 for the OA PSF; L/20, L/10, L/5, and L/2 for the DH and arbitrary PSF; and L/40, L/20, L/10, L/5, and L/2, for the Tetra6 PSF; with the parameter L being the size of the image in pixels (12, 20, or 40, respectively). Notably, the contribution of each individual frequency was not restricted and was chosen randomly to be anywhere between 0 and 100%. Signal and BG photons were simulated across a wide range, dependent on the PSF, to generate training and validation data. Each input PSF was normalized between 0 and 1, and the target, i.e., the true BG that BGnet is trained to return, was scaled identically. Therefore, the BGnet not only predicts the structure of the BG but also its intensity relative to the input PSF image at each pixel.

BGnet was implemented in Keras with Tensorflow backend and trained on a desktop personal computer (PC) equipped with 64-gigabyte random-access memory, an Intel Xeon E5-1650 processor, and an Nvidia GeForce GTX Titan graphics-processing unit (GPU). Convergence was reached after training for approximately 1 h (OA PSF) to approximately 9 h (Tetra6 PSF). Detailed training parameters are listed in SI Appendix, Table S5. All validation experiments were done with an independent dataset that was not part of the training dataset.

BGnet Accurately Estimates sBG from Images of Various PSF Shapes.

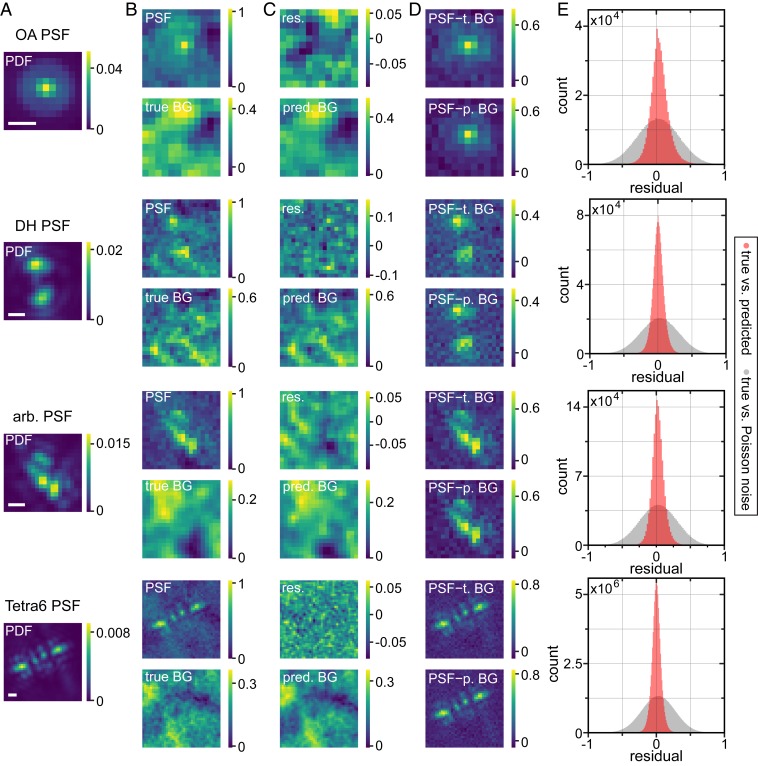
Fig. 2 shows representative examples for the PSF simulation process and the performance of BGnet on validation data. In Fig. 2A, the probability density functions (PDFs) are shown as a reference for one axial position. The PSFs containing BG (Fig. 2 B, top images for each PSF) are supplied to BGnet, which returns the predicted BGs (Fig. 2 C, bottom images). The agreement between true (Fig. 2 B, bottom images) and predicted BGs is excellent, reflected in small residuals (Fig. 2 C, top images).The obtained BGs can then be subtracted from the PSF images for BG correction. The strongly improved quality of the PSF shapes after BG correction is evident. Illustrating the quality of the BG estimation, the images for the PSFs corrected with the true BGs and the PSF corrected with the predicted BGs are very similar (Fig. 2D). For additional representative examples, see SI Appendix, Figs. S3–S6.

Fig. 2.

Representative examples for BG estimation with BGnet and overall performance. (A) Example PDFs for the 4 investigated PSFs. (B) The BG-corrupted input PSFs, normalized between 0 and 1, and the underlying (true) BGs. The signal photon count for the depicted PSFs is 4,723, 5,275, 5,994, and 37,637, and the average BG photon count per pixel is 147, 137, 26, and 127 (from top to bottom). (C) The BG prediction by BGnet on the same intensity scale as the input PSF and the residual (res.) between true and predicted (pred.) BG. (D) The original PSFs corrected for BG using either the true BG (t. BG) or the predicted BG (p. BG). Note that negative pixel values for the BG-corrected PSFs are only a side effect of PSF normalization and originate from Poisson noise fluctuations. (E) Pixelwise residuals for all of the PSFs of the validation dataset. For this analysis, true and predicted BGs were scaled between 0 and 1, such that all residuals ranged from −1 to 1. As a control, we also calculated pixelwise residuals between the true BG and pure Poisson noise, exhibiting the same average photon count per pixel as the true BG, which was also scaled between 0 and 1 for residual calculation. (Scale bar in A, 500 nm.)

To quantify the overall agreement between true and predicted BGs, we normalized each pair of true and predicted BGs between 0 and 1 (otherwise, due to varying signal and background levels, the residuals cannot be directly compared). Then, we calculated the pixelwise difference between true and predicted BGs for all of the PSFs in the validation dataset. The result is depicted in Fig. 2E. Clearly, the residuals, which can range between −1 and 1, form a narrow distribution that is centered at 0. The control, i.e., pixelwise comparison of the true background to pure Poisson noise exhibiting the same average photon count per pixel, forms a significantly broader distribution, as expected. This indicates that the BG is accurately estimated by BGnet. Importantly, this process is very fast; 3,500 to 5,000 PSFs were analyzed in 4 to 30 s on a standard desktop PC (quickest for the OA PSF, slowest for the Tetra6 PSF due to the different image sizes), which corresponds to ∼1 to 6 ms/PSF, suitable for real-time analysis. Using a PC equipped with a dedicated GPU could speed up BG estimation even more if required.

BGnet Strongly Improves Localization Precision of Single Molecules.

The good agreement between predicted and true BGs is promising. However, it is critical to verify that removing the predicted sBGs translates to improved precision of extracted single-molecule parameters compared to conventional BG correction approaches. Therefore, we explored how BG correction with BGnet affects the 3D emitter-localization precision via MLE fitting of the images to the models (Materials and Methods). For this analysis, we simulated PSFs at various distances from the coverslip and various focal positions. Furthermore, we varied the signal photons and the average BG photons per pixel over a wide range, specific to each PSF, and used values typical for experiments, which resulted in 90 different parameter combinations for the OA, the DH, and the arbitrary PSF and in 270 different parameter combination for the Tetra6 PSF (SI Appendix, Table S6). Each parameter combination was realized 100 times with the respective PSF position held constant. However, each of the 100 PSF realizations for a specific parameter combination was corrupted with different BG structures. As the true PSF position is always the same, the “spread” of the localizations (i.e., the mean of the SDs of the position estimates in each spatial dimension x, y, and Δf) directly reports on the effect of BG subtraction.

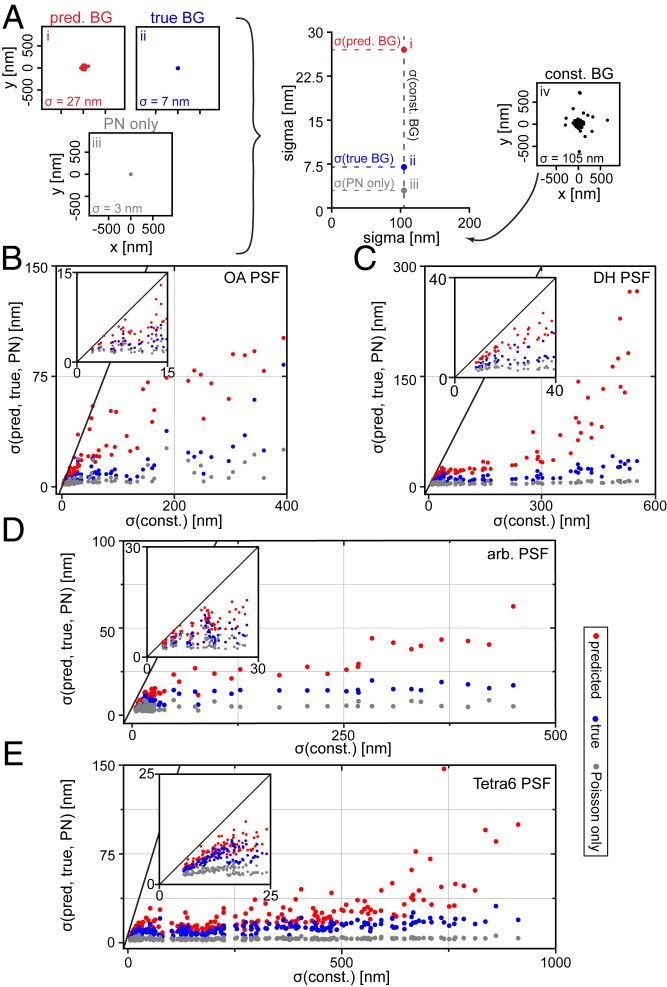
We analyzed 4 different scenarios: 1) BG correction with the predicted BG from BGnet (scenario i); 2) BG correction with the ground-truth, true BG (scenario ii); 3) a BG-free PSF that only exhibits Poisson noise (scenario iii); and 4) conventional BG correction with a constant BG as typically assumed (scenario iv). Scenario iii is a baseline reference that exhibits the best localization precision obtainable in a BG-free scenario for the detected photons assumed. The results are depicted in Fig. 3.

Fig. 3.

Significant improvement in localization precision occurs with MLE fitting when BG correction with BGnet is used. (A) Schematic of data visualization approach and representative x/y scatter plots for a given parameter combination for the OA PSF. The spreads of the position estimates are 105, 27, 7, and 3 nm for scenarios i to iv, respectively, leading to the points placed on the plot in the center. (B–E) The spread of the position estimates for scenarios i, ii, and iii is plotted against the spread of the position estimates for scenario iv, that is, the constant BG estimate is used as a reference. Insets show magnifications. The gray line has a slope of unity and thus indicates equal performance. Points below that line perform better than the reference case (constant BG estimate). Results from simulated data for the OA PSF (B), DH PSF (C), arbitrary PSF (D), and Tetra6 PSF (E). For the OA PSF, only the x/y position estimates are considered; the other cases use 3D spreads. const., constant; pred., predicted.

For each of the 4 scenarios, the MLE fitting of the images with different background structures yields 100 position estimates, the spreads of which can be quantified by an SD. The x/y scatter plots in Fig. 3A show a representative result for the OA PSF (10,000 signal photons, 150 average BG photons/pixel, emitter at 2 μm, focal position for scatter plot at 0.5 μm; for further examples of all investigated PSFs, including x/Δf scatter plots, see SI Appendix, Figs. S7–S10). The spreads of the position estimates for scenarios i, ii, and iii are plotted against the spread of the reference scenario, the constant BG estimate (scenario iv, on the right in Fig. 3A) for each parameter combination. Fig. 3 B–E depicts the OA, DH, arbitrary, and Tetra6 PSF, respectively. The significant improvement in localization precision when using BGnet is evident for all PSFs and any condition: The spread of the position estimates is much smaller when BG correction with BGnet is used. Nearly all points corresponding to BG correction with BGnet are located far below the line with slope unity. This demonstrates that the excellent accuracy with which BGnet extracts the BG from PSF images directly results in improved localization precision.

For many cases, the crude BG correction with a constant BG leads to spreads of hundreds of nanometers, which is considerably reduced when BG correction with BGnet is performed. These extreme cases with large x-axis coordinates correspond to PSFs with high BG and low signal and would likely be hard to detect under experimental conditions. These PSFs would therefore probably not be analyzed in localization microscopy. However, for single-particle tracking, this is not the case. When a fluorescently labeled object gradually bleaches away, one has high confidence in the presence of a dim object within a certain ROI due to the known trajectory from previous frames. Therefore, subtraction of the BG with BGnet can strongly increase the length of the whole trajectory, increasing the statistical strength of a diffusion analysis, for example. Furthermore, for brighter emitters that would be easily detected, BGnet remarkably still improves the localization precision by a factor of approximately 2 to 10 (insets in Fig. 3 B–E). For an additional analysis for the Tetra6 PSF with higher signal photon counts as typical for quantum dots or polystyrene fluorescent beads, see SI Appendix, Figs. S11 and S12.

BGnet Strongly Improves Localization Accuracy of Single Molecules for Various BG Complexities.

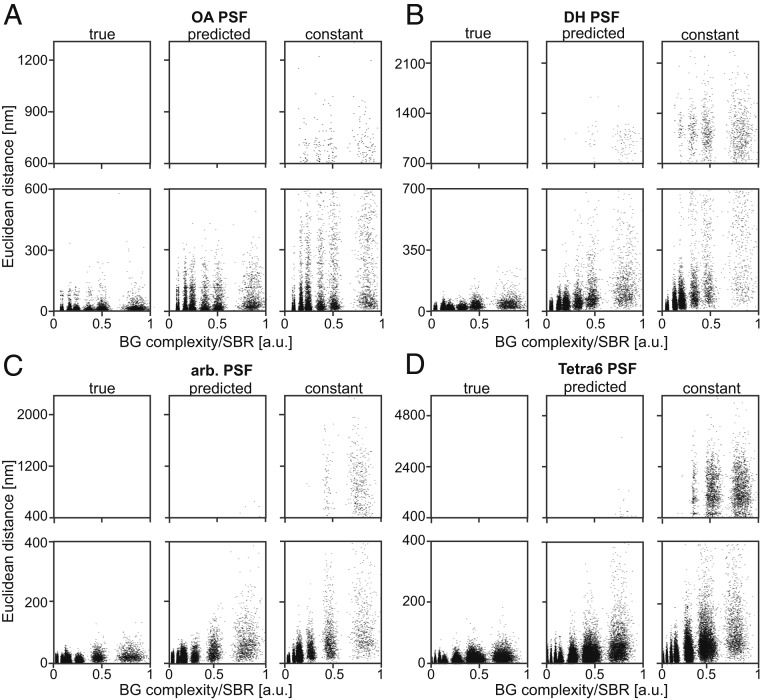
In the approach described above, the 100 PSF realizations were corrupted by different BG structures. The obtained position estimates were subsequently pooled to extract the spread of the localizations. While this method is intuitive, it does not report on the effect of an individual BG structure. To confirm that BG correction with BGnet improves the performance at the level of an individual localization event, we first developed a metric to quantify the complexity of the BG (termed “BG complexity”) in a given PSF image. First, we calculated the spatial Fourier transform (FT) of the sBG alone. Additionally, we calculated the FT of a constant BG with the same average photon count per pixel and Poisson noise. Then, we subtracted the FT of the constant BG from the FT of the sBG to remove the dominant lowest spatial frequency. Next, we calculated the integrated weighted radial distribution. The result was normalized by the signal-to-background ratio (SBR) (see SI Appendix, Fig. S13 for details), yielding the BG complexity metric for the considered sBG, which is larger for BG with higher spatial frequencies or lower SBR. For each localization event, we calculated the Euclidian distance from the known true position (i.e., the accuracy) and plotted it against the respective normalized BG complexity, as depicted in Fig. 4.

Fig. 4.

Relationship between localization accuracy and BG complexity. To account for the influence of the SBR, which trivially has an effect on the localization accuracy, the BG complexity metric was normalized by the SBR. For increasing BG complexity, the accuracy of the localization decreases, but in all cases, the BGnet outperforms constant BG subtraction. (A–D) Results from simulated data for the OA PSF, DH PSF, arbitrary PSF, and Tetra6 PSF, respectively. True, BG correction with true BG; predicted, BG correction with the prediction from BGnet; constant, constant BG estimate. Note that the “streaks” visible arise from the discrete SBRs considered. Also note different y-axis scaling in the top and bottom graphs for each PSF. a.u., arbitrary units.

This analysis confirms that BG correction with BGnet improves the accuracy of each single localization event. As is clearly visible, the differences between the estimated and the true positions are significantly smaller when the BG is corrected with BGnet compared to correction with a constant BG. This is true for all 4 analyzed PSF shapes. As one would expect, the accuracy decreases when the normalized BG complexity increases, regardless of the BG correction method (Fig. 4, bottom graphs for each PSF—the scatter clouds rising from the x axis). However, when the predicted BG from BGnet is used, this trend is clearly dampened. Thus, BG correction with BGnet performs much closer to the ideal case, i.e., BG correction with the true BG. Additionally, the number of significant outliers is strongly reduced compared to BG correction with constant BG (Fig. 4, top graphs for each PSF). In an experimental setting, for example in localization microscopy, this is of high relevance as gross mislocalizations deteriorate image quality 2-fold: first, the number of spurious localizations in the reconstruction increases; and, second, the localizations no longer report on the structure to be imaged, reducing the spatial resolution.

BGnet Enhances Localization Precision and Image Quality for Experimental Datasets.

Finally, we verify the performance of BGnet on experimental data, without retraining the neural net. For this, we first imaged 100-nm fluorescent polystyrene beads in water that were attached to a glass cover slide using either no phase mask (OA), the DH, or the Tetra6 phase mask. sBG was introduced with a continuously moving white light source that illuminated the sample nonhomogenously during data acquisition. Also, a large number of beads was not attached to the glass, but diffused freely in solution. Their emission contributed to the structured BG as well. For each PSF shape, we imaged different immobile beads for 1,000 frames, which were positioned at different regions of the field of view and exhibited different SBRs and BG structures. Then, we performed MLE fitting, either assuming a constant BG or performing BG correction with BGnet.

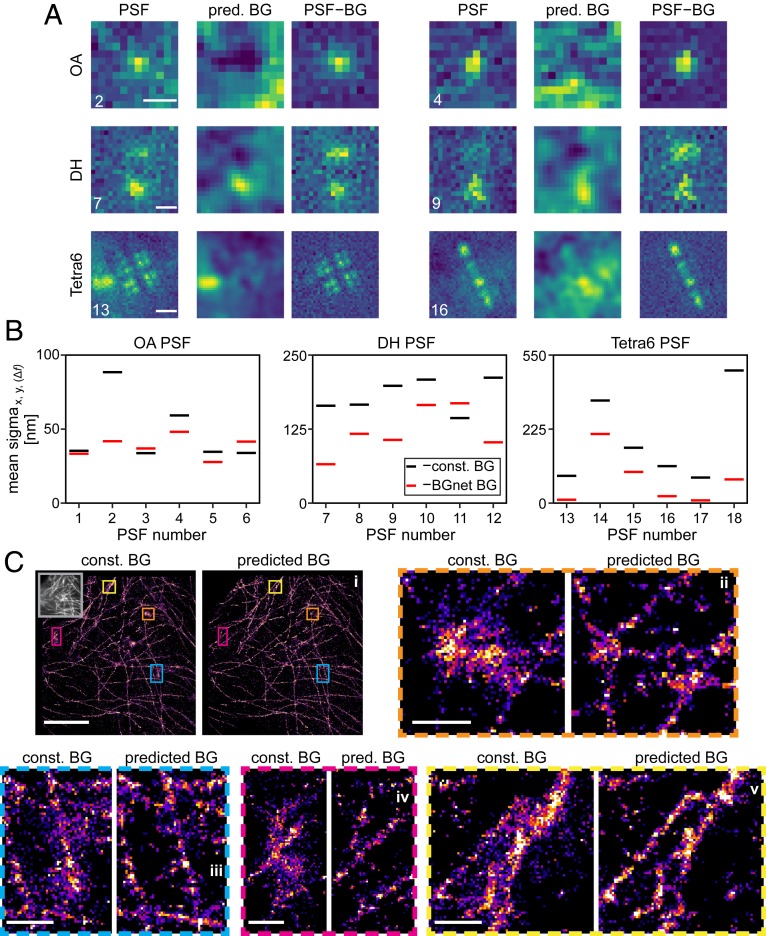
Fig. 5A shows representative frames from the obtained stacks for the 3 PSFs, the corresponding estimated BGs using BGnet, and the resulting BG-corrected PSFs. The results for BGnet are striking. For example, a part of a PSF caused by a diffusing bead is visible for the Tetra6 PSF 13 at the left edge, which is correctly identified by BGnet. Also, sBG with lower spatial frequency, visible from “humps” in the images, is accurately removed, leading to more pronounced PSF images for all 3 investigated PSFs. We also extracted the BG complexity metric using the same approach as for the simulated data and also scaled it identically to provide the same arbitrary units as in Fig. 4. For the ROIs shown in Fig. 5A, the values range from 0.1 to 1.34 (Fig. 5 caption). Compiling the scaled BG complexities for all frames of all beads yielded the histograms shown in SI Appendix, Fig. S14. Importantly, some values are larger than 1, which was the highest value we realized when training BGnet. Nevertheless, BGnet still performed well. This indicates that our approach is robust and does not sharply decrease in performance when the boundary of the training parameter space is exceeded.

Fig. 5.

Performance of BGnet on experimental data. (A) Two representative frames for 3 imaged PSF shapes, predicted BG (pred. BG), and corresponding BG-corrected PSFs (PSF–BG). Contrast settings are not equal between the images. Background complexity values were 0.57 and 1.34 (OA PSF 2 and 4), 0.23 and 0.10 (DH PSF 7 and 9), and 0.34 and 0.35 (Tetra6 PSF 13 and 16), where the scaling is the same as in Fig. 4. (B) Mean SDs of x-, y-, and Δf-position estimates over 1,000 frames for 6 experimental realizations of each PSF shape, either assuming constant BG (const. BG) (black) or using BG correction with BGnet (BGnet BG) (red). Note that the position estimates are shifted to the origin to facilitate comparison. For the OA PSF, only the x- and y-position estimates are considered. Note that the large spread of SDs arises from varying SBRs as well as different BG structures. (C) Superresolution reconstructions of microtubules in fixed BSC-01 cells using the OA PSF and BG correction with a constant BG estimate or with BGnet. Four magnified regions are shown. Contrast settings are equal for each compared region. (Scale bars: 5 μm for the image depicting the entire field of view [C, i]; 500 nm for zoom-ins [C, ii–v].) The gray inset in C, i, Left depicts the corresponding diffraction-limited image. Reconstructions are shown as 2D histograms with 23.4-nm bin width. (Scale bar in A, 500 nm [OA PSF and DH PSF]; 1 μm [Tetra6 PSF].)

The visual impression translates to significantly improved localization precisions when performing MLE fitting. Fig. 5B shows the SD of the position estimates, averaged over x, y, and Δf (Δf only for the DH and Tetra6 PSF) for 6 cases for each PSF (see SI Appendix, Fig. S15 for example scatter plots). The localization precision is evidently increased by BG correction with BGnet. Only very rarely, BGnet performs worse than when constant BG is assumed (PSF 3, PSF 6, and PSF 11). However, in these cases, BGnet also does not strongly reduce the localization precision. Therefore, in the worst case, BG correction with BGnet performs comparable to constant BG subtraction but will, in the majority of cases, greatly improve the localization precision.

While BGnet improves localization precision in a proof-of-concept scenario, a further relevant assessment is to test its capability in a commonly encountered experimental setting. To this end, we investigated how BG correction with BGnet performs in localization-based superresolution microscopy of a biological structure. We labeled microtubules in fixed BSC-01 cells via immunostaining, using AlexaFluor 647 as a fluorescent dye. Then, we acquired STORM superresolution microscopy data and localized the detected single molecules. Also, we acquired an sBG image by illuminating an empty well with a light-emitting diode white-light source. We added this sBG image to each frame of the single-molecule localization data to introduce a strong sBG and thus to perform an assessment of BGnet under truly challenging conditions (see SI Appendix, Fig. S16 for the sBG image and a representative frame). In the localization step, we corrected for BG either by assuming a constant BG or by using the estimate from BGnet (see Materials and Methods). The result is depicted in Fig. 5C. The assumption of constant BG leads to severe artifacts in the reconstructions, evident from spurious localizations, nonstructured regions, and loss of finer details. BG correction with BGnet, in contrast, yields excellent reconstructions of the microtubules (compare magnifications in Fig. 5C). Thus, we have successfully demonstrated the capability of BGnet to improve the image quality of superresolution reconstructions, a result that can be readily transferred to other flavors of single-molecule experiments.

Conclusion

In summary, we have developed a robust and easy-to-implement method to rapidly correct PSF images for sBG. We demonstrate that this approach significantly improves emitter localization of OA, DH, and Tetra6 PSFs both for accurate PSF simulations and for experimental data. BGnet is not restricted to any specific assumptions about the BG characteristics. The method works because the PSF model is known, and it can be obtained accurately using known techniques.

Using single-molecule emitters as point-like markers for localizing nanoscale objects has developed from a specialized technique into a generally available, widely used method across biology, chemistry, and materials science. However, removal of sBG was so far not addressed. In our work, we provide a robust and easy-to-implement method to tackle this problem, and all applications of single-molecule localization microscopy will immediately benefit. Our experimental demonstration of the effectiveness of BGnet in the simplest experimental setting, epifluorescent illumination using the 2D open aperture PSF, underscores the general relevance of our results as this is a widely employed localization microscopy method today. Nevertheless, BGnet is equally powerful when applied to more complex PSFs used, e.g., for 3D imaging.

Our method should improve PSF analysis for a wide range of powerful state-of-the-art techniques such as single-molecule localization microscopy (36–38), single-molecule and single-particle tracking (39), aberration correction with adaptive optics (40), or deep-tissue imaging, where sBG is an especially prominent issue as recently highlighted by a noteworthy study (41). Furthermore, we are confident that our workflow can be readily generalized according to the requirements of other flavors of microscopy (e.g., optical coherence tomography [OCT], scattering microscopy, or stimulated emission-depletion [STED] microscopy) and is not limited to just fluorescence microscopy, providing a broad range of scientific disciplines with a highly versatile resource.

Materials and Methods

Cell Culture.

BSC-01 cells were cultured in phenol red-free Dulbecco’s modified Eagle medium (Thermo Fisher), supplemented with 1 mM sodium pyruvate (Thermo Fisher) and 10% fetal bovine serum (Thermo Fisher), at 37 °C in a humidified 5% CO₂ atmosphere. The cells were seeded into 8-well chambered cover slides (ibidi GmbH) and used 2 d after seeding.

Immunolabeling.

BSC-01 cells were washed with prewarmed phosphate-buffered saline (PBS) plus Ca²⁺/Mg²⁺ (Thermo Fisher) and preextracted with prewarmed 0.2% saponin in citrate-buffered saline (CBS)—10 mM 2-(N-morpholino)ethanesulfonic acid, 138 mM NaCl, 3 mM MgCl₂, 2 mM ethylene glycol bis(2-aminoethyl)tetraacetic acid, 320 mM sucrose (all Sigma-Aldrich)—for 1 min. Then, cells were fixed with 3% paraformaldehyde and 0.1% glutaraldehyde (Sigma-Aldrich) in CBS for 15 min at room temperature (RT). Then, cells were reduced with 0.1% NaBH₄ (Sigma-Aldrich) in PBS for 7 min at RT and rinsed 3 times for 3 min with PBS. Next, cells were blocked and permeabilized with 3% bovine serum albumin (BSA) (Sigma-Aldrich) and 0.2% Triton X-100 (Sigma-Aldrich) in PBS for 30 min at RT. Then, cells were incubated with the primary antibody (1:100 rabbit anti-alpha tubulin; ab18251 [Abcam]) in 1% BSA and 0.2% Triton X-100 in PBS for 1 h at RT, which was followed by washing 3 times for 5 min each with 0.05% Triton X-100 in PBS at RT. Then, cells were incubated with the secondary antibody (1:1,000 donkey anti-rabbit AF647; ab150067 [Abcam]) in 1% BSA and 0.2% Triton X-1900 at RT. Finally, the cells were washed 3 times for 5 min with 0.05% Triton X-100 in PBS at RT and postfixed with 4% paraformaldehyde for 10 min at RT. Finally, cells were washed 3 times for 3 min each with PBS at RT and stored at 4 °C.

Microscopy.

Cells were imaged on a custom epifluorescence microscope using a Nikon Diaphot 200 as core, equipped with an Andor Ixon DU-897 electron-multiplying charge-coupled device camera, a high-NA oil-immersion objective (UPlanSapo 100×/1.40 NA; Olympus), a motorized xy-stage (M26821LOJ; Physik Instrumente), and a xyz-pizeo stage (P-545.3C7; Physik Instrumente). Molecules were excited with a 642-nm, 1-W continuous-wave laser (MPB Communications Inc.). The emission was passed through a quadpass dichroic mirror (Di01-R405/488/561/635; Semrock) and filtered using a ZET642 notch filter (Chroma) and a 670/90 bandpass filter (Chroma). For 3D imaging, DH (Double Helix Optics) and Tetra6 phase masks (described in ref. 42) were inserted into the 4f-system of the microscope as described previously (43).

MLE Fitting Algorithm.

In order to determine the position, signal photon counts, and background photon counts of single-emitter images, a maximum-likelihood fitting algorithm was employed. Under the assumption of Poisson noise statistics, the objective function for MLE is given by ${\displaystyle \sum _i{\mu }_i\left(\theta \right)-n_i\ln \left({\mu }_i\left(\theta \right)\right),}$ where $n_i$ is the photon count measured in pixel $i$ and ${\mu }_i\left(\theta \right)$ is the total photon count predicted in that pixel by a forward model of the PSF for specific values of emitter parameters $\theta$ (position, signal photons, and background photons). Minimizing the objective function with respect to $\theta$ yields the maximum-likelihood parameter estimates $\widehat{\theta }$.

Superresolution Data Acquisition and Image Reconstruction.

For superresolution data acquisition, a reducing and oxygen-scavenging buffer was used (44), consisting of 40 mM cysteamine, 2 μL/mL catalase, 560 μg/mL glucose oxidase (all Sigma-Aldrich), 10% (wt/vol) glucose (BD Difco), and 100 mM tris(hydroxymethyl)aminomethane⋅HCl (Thermo Fisher). The exposure time was 30 ms, and the calibrated EM gain was 186. Single-molecule signals were detected with a standard local maximum-intensity approach. Each single-molecule signal was fitted to a 2D Gaussian, either without BG correction using BGnet or with BG correction using BGnet. In both cases, a constant offset was implemented for the fitting. If no BG correction with BGnet was applied, this translates to an estimated constant BG. For initial BG correction with BGnet, the offset was, expectedly, very close to zero. The position of the maximum of the Gaussian fit was stored as the localization of the single molecule. Drift correction was performed via cross-correlation.

Data Availability Statement.

Data and code supporting the findings of this paper are available from W.E.M. upon reasonable request.