Shaping the learning landscape in neural networks around wide flat minima

Significance

Deep neural networks (DNN) are becoming fundamental learning devices for extracting information from data in a variety of real-world applications and in natural and social sciences. The learning process in DNN consists of finding a minimizer of a loss function that measures how well the data are classified. This optimization task is typically solved by tuning millions of parameters by stochastic gradient algorithms. This process can be thought of as an exploration process of a highly nonconvex landscape. Here we show that such landscapes possess very peculiar wide flat minima and that the current models have been shaped to make the loss functions and the algorithms focus on those minima. We also derive efficient algorithmic solutions.

Abstract

Learning in deep neural networks takes place by minimizing a nonconvex high-dimensional loss function, typically by a stochastic gradient descent (SGD) strategy. The learning process is observed to be able to find good minimizers without getting stuck in local critical points and such minimizers are often satisfactory at avoiding overfitting. How these 2 features can be kept under control in nonlinear devices composed of millions of tunable connections is a profound and far-reaching open question. In this paper we study basic nonconvex 1- and 2-layer neural network models that learn random patterns and derive a number of basic geometrical and algorithmic features which suggest some answers. We first show that the error loss function presents few extremely wide flat minima (WFM) which coexist with narrower minima and critical points. We then show that the minimizers of the cross-entropy loss function overlap with the WFM of the error loss. We also show examples of learning devices for which WFM do not exist. From the algorithmic perspective we derive entropy-driven greedy and message-passing algorithms that focus their search on wide flat regions of minimizers. In the case of SGD and cross-entropy loss, we show that a slow reduction of the norm of the weights along the learning process also leads to WFM. We corroborate the results by a numerical study of the correlations between the volumes of the minimizers, their Hessian, and their generalization performance on real data.

Artificial neural networks (ANN), currently also known as deep neural networks (DNN) when they have more than 2 layers, are powerful nonlinear devices used to perform different types of learning tasks (1). From the algorithmic perspective, learning in ANN is in principle a hard computational problem in which a huge number of parameters, the connection weights, need to be optimally tuned. Yet, at least for supervised pattern recognition tasks, learning has become a relatively feasible process in many applications across domains and the performances reached by DNNs have had a huge impact on the field of machine learning.

DNN models have evolved very rapidly in the last decade, mainly by an empirical trial and selection process guided by heuristic intuitions. As a result, current DNN are in a sense akin to complex physical or biological systems, which are known to work but for which a detailed understanding of the principles underlying their functioning remains unclear. The tendency to learn efficiently and to generalize with limited overfitting are 2 properties that often coexist in DNN, and yet a unifying theoretical framework is still missing.

Here we provide analytical results on the geometrical structure of the loss landscape of ANN which shed light on the success of deep learning (2) algorithms and allow us to design efficient algorithmic schemes.

We focus on nonconvex 1- and 2-layer ANN models that exhibit sufficiently complex behavior and yet are amenable to detailed analytical and numerical studies. Building on methods of statistical physics of disordered systems, we analyze the complete geometrical structure of the minimizers of the loss function of ANN learning random patterns and discuss how the current DNN models are able to exploit such structure, for example starting from the choice of the loss function, avoiding algorithmic traps, and reaching rare solutions that belong to wide flat regions of the weight space. In our study the notion of flatness is given in terms of the volume of the weights around a minimizer that do not lead to an increase of the loss value. This generalizes the so-called local entropy of a minimizer (3), defined for discrete weights as the log of the number of optimal weights assignments within a given Hamming distance from the reference minimizer. We call these regions high local entropy (HLE) regions for discrete weights or wide flat minima (WFM) for continuous weights. Our results are derived analytically for the case of random data and corroborated by numerics on real data. In order to eliminate ambiguities that may arise from changes of scale of the weights, we control the norm of the weights in each of the units that compose the network. The outcomes of our study can be summarized as follows.

• 1)We show analytically that ANN learning random patterns possess the structural property of having extremely robust regions of optimal weights, namely WFM of the loss, whose existence is important to achieve convergence in the learning process. Although these wide minima are rare compared to the dominant critical points (absolute narrow minima, local minima, or saddle points in the loss surface), they can be accessed by a large family of simple learning algorithms. We also show analytically that other learning machines, such as the parity machine, do not possess WFM.
• 2)We show analytically that the choice of the cross-entropy (CE) loss function has the effect of biasing learning algorithms toward HLE or WFM regions.
• 3)We derive a greedy algorithm—entropic least-action learning (eLAL)—and a message passing algorithm—focusing belief propagation (fBP)—which zoom in their search on wide flat regions of minimizers.
• 4)We compute the volumes associated to the minimizers found by different algorithms using belief propagation (BP).
• 5)We show numerically that the volumes correlate well with the spectra of the Hessian on computationally tractable networks and with the generalization performance on real data. The algorithms that search for WFM display a spectrum that is much more concentrated around zero eigenvalues compared to plain stochastic gradient descent (SGD).

Our results on random patterns support the conclusion that the minimizers that are relevant for learning are not the most frequent isolated and narrow ones (which also are computationally hard to sample) but the rare ones that are extremely wide. While this phenomenon was recently disclosed for the case of discrete weights (3, 4), here we demonstrate that it is present also in nonconvex ANN with continuous weights. Building on these results we derive algorithmic schemes and shed light on the performance of SGD with the CE loss function. Numerical experiments suggest that the scenario generalizes to real data and is consistent with other numerical results on deeper ANN (5).

HLE/WFM Regions Exist in Nonconvex Neural Devices Storing Random Patterns

In what follows we analyze the geometrical structure of the weights space by considering the simplest nonconvex neural devices storing random patterns: the single-layer network with discrete weights and the 2-layer networks with both continuous and discrete weights. The choice of random patterns, for which no generalization is possible, is motivated by the possibility of using analytical techniques from statistical physics of disordered systems and by the fact that we want to identify structural features that do not depend on specific correlation patterns of the data.

The Simple Example of Discrete Weights.

In the case of binary weights it is well known that even for the single-layer network the learning problem is computationally challenging. Therefore, we begin our analysis by studying the so-called binary perceptron, which maps vectors of $N$ inputs $\xi \in {\left\{-\mathrm{1,1}\right\}}^N$ to binary outputs as $\sigma \left(W,\xi \right)=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(W\cdot \xi \right)$, where $W\in {\left\{-\mathrm{1,1}\right\}}^N$ is the synaptic weights vector $W=\left(w_1,\hspace{0.17em}{w}_2,\hspace{0.17em}\dots ,\hspace{0.17em}{w}_N\right)$.

Given a training set composed of $\alpha N$ input patterns ${\xi }^{\mu }$ with $\mu \in \left\{1,\dots ,\alpha N\right\}$ and their corresponding desired outputs ${\sigma }^{\mu }\in {\left\{-\mathrm{1,1}\right\}}^{\alpha N}$, the learning problem consists of finding a solution $W$ such that $\sigma \left(W,{\xi }^{\mu }\right)\hspace{0.17em}=\hspace{0.17em}{\sigma }^{\mu }$ for all $\mu$. The entries ${\xi }_i^{\mu }$ and the outputs ${\sigma }^{\mu }$ are random unbiased independent and identically distributed variables. As discussed in ref. 6 (but see also the rigorous bounds in ref. 7), perfect classification is possible with probability 1 in the limit of large $N$ up to a critical value of $\alpha$, usually denoted as ${\alpha }_c$; above this value, the probability of finding a solution drops to zero. ${\alpha }_c$ is called the capacity of the device.

The standard analysis of this model is based on the study of the zero-temperature limit of the Gibbs measure with a loss (or energy) function ${\mathcal{L}}_{\mathrm{N}\mathrm{E}}$ that counts the number of errors (NE) over the training set:

$${\mathcal{L}}_{\mathrm{N}\mathrm{E}}=\sum _{\mu =1}^{\alpha N}\mathrm{\Theta }\left(-{\sigma }^{\mu }\sigma \left(W,{\xi }^{\mu }\right)\right),$$ [1]

where $\mathrm{\Theta }\left(x\right)$ is the Heaviside step function, $\mathrm{\Theta }\left(x\right)\hspace{0.17em}=\hspace{0.17em}1$ if $x>0$ and 0 otherwise. The Gibbs measure is given by

$$P\left(W\right)\hspace{0.17em}=\hspace{0.17em}\frac{1}{Z\left(\beta \right)}\hspace{0.17em}\exp \left(-\beta \sum _{\mu =1}^{\alpha N}\mathrm{\Theta }\left(-{\sigma }^{\mu }\sigma \left(W,{\xi }^{\mu }\right)\right)\right),$$ [2]

where $\beta \ge 0$ is the inverse temperature parameter. For large values of $\beta$, $P\left(W\right)$ concentrates on the minima of ${\mathcal{L}}_{\mathrm{N}\mathrm{E}}$. The key analytical obstacle for the computation of $P\left(W\right)$ is the evaluation of the normalization factor, the partition function $Z\left(\beta \right)$:

$$Z\left(\beta \right)\hspace{0.17em}=\hspace{0.17em}\sum _{\left\{w_i=\pm 1\right\}}\exp \left(-\beta \sum _{\mu =1}^{\alpha N}\mathrm{\Theta }\left(-{\sigma }^{\mu }\sigma \left(W,{\xi }^{\mu }\right)\right)\right).$$ [3]

In the zero-temperature limit ($\beta \to \infty$) and below ${\alpha }_c$ the partition function simply counts all solutions to the learning problem,

$$Z_{\infty }\hspace{0.17em}=\hspace{0.17em}\underset{\beta \to \infty }{lim}Z\left(\beta \right)=\sum _{\left\{W\right\}}{\mathbb{X}}_{\xi }\left(W\right),$$ [4]

where ${\mathbb{X}}_{\xi }\left(W\right)\hspace{0.17em}=\hspace{0.17em}{\prod }_{\mu =1}^{\alpha N}\mathrm{\Theta }\left({\sigma }^{\mu }\sigma \left(W,{\xi }^{\mu }\right)\right)$ is a characteristic function that evaluates to one if all patterns are correctly classified, and to zero otherwise.

$Z_{\infty }$ is an exponentially fluctuating quantity (in $N$), and its most probable value is obtained by exponentiating the average of $\log Z_{\infty }$, denoted by ${⟨\log Z_{\infty }⟩}_{\xi }$, over the realizations of the patterns:

$$Z_{\infty ,\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}\simeq \exp \left(N{⟨\ln Z_{\infty }⟩}_{\xi }\right).$$ [5]

The calculation of ${⟨\log Z_{\infty }⟩}_{\xi }$ was done in the 1980s and 1990s by the replica and the cavity methods of statistical physics and, as mentioned above, the results predict that the learning task undergoes a threshold phenomenon at ${\alpha }_c=0.833$, where the probability of existence of a solution jumps from one to zero in the large $N$ limit (6). This result has been put recently on rigorous grounds by ref. 7. Similar calculations predict that for any $\alpha \in \left(0,{\alpha }_c\right)$, the vast majority of the exponentially numerous solutions on the hypercube $W\in {\left\{-\mathrm{1,1}\right\}}^N$ are isolated, separated by a $O\left(N\right)$ Hamming mutual distance (8). In the same range of $\alpha$, there also exist an even larger number of local minima at nonzero loss, a result that has been corroborated by analytical and numerical findings on stochastic learning algorithms that satisfy detailed balance (9). Recently it became clear that by relaxing the detailed balance condition it was possible to design simple algorithms that can solve the problem efficiently (10–12).

Local Entropy Theory.

The existence of effective learning algorithms indicates that the traditional statistical physics calculations, which focus on the set of solutions that dominate the zero-temperature Gibbs measure (i.e., the most numerous ones), are effectively blind to the solutions actually found by such algorithms. Numerical evidence suggests that in fact the solutions found by heuristics are not at all isolated; on the contrary, they appear to belong to regions with a high density of nearby other solutions. This puzzle has been solved very recently by an appropriate large deviations study (3, 4, 13, 14) in which the tools of statistical physics have been used to study the most probable value of the local entropy of the loss function, that is, a function that is able to detect the existence of regions with an $O\left(N\right)$ radius containing a high density of solutions even when the number of these regions is small compared to the number of isolated solutions. For binary weights the local entropy function is the (normalized) logarithm of the number of solutions $W\prime$ at Hamming distance $D\hspace{0.17em}N$ from a reference solution $W$:

$${\mathcal{E}}_D\left(W\right)\hspace{0.17em}=\hspace{0.17em}-\frac{1}{N}\ln \mathcal{U}\left(W,D\right)$$ [6]

with

$$\mathcal{U}\left(W,D\right)\hspace{0.17em}=\hspace{0.17em}\sum _{\left\{W\prime \right\}}{\mathbb{X}}_{\xi }\left(W\prime \right)\delta \left(W\prime \cdot W,N\left(1-2D\right)\right)$$ [7]

and where $\delta$ is the Kronecker delta symbol. In order to derive the typical values that the local entropy can take, one needs to compute the Gibbs measure of the local entropy:

$$P_{\mathrm{L}\mathrm{E}}\left(W\right)\hspace{0.17em}=\hspace{0.17em}\frac{1}{Z_{\mathrm{L}\mathrm{E}}}\hspace{0.17em}\exp \left(-y{\mathcal{E}}_D\left(W\right)\right),$$ [8]

where $y$ has the role of an inverse temperature. For large values of $y$ this probability measure focuses on the $W$ surrounded by an exponential number of solutions within a distance $D$. The regions of HLE are then described in the regime of large $y$ and small $D$. In particular, the calculation of the expected value of the optimal local entropy

$$\mathcal{S}\left(D\right)\hspace{0.17em}\equiv \hspace{0.17em}{\mathcal{E}}_D^{\mathrm{o}\mathrm{p}\mathrm{t}}=\underset{\left\{W\right\}}{max}\left\{-\frac{1}{N}{⟨\ln \mathcal{U}\left(W,D\right)⟩}_{\xi }\right\}$$ [9]

shows the existence of extremely dense clusters of solutions up to values of $\alpha$ close to ${\alpha }_c$ (3, 4, 13, 14).

The probability measure Eq. 8 can be written in an equivalent form that generalizes to the nonzero errors regime, is analytically simpler to handle, and leads to novel algorithmic schemes (4):

$$P_{\mathrm{L}\mathrm{E}}\left(W\right)\hspace{0.17em}\sim \hspace{0.17em}P\left(W;\beta ,y,\lambda \right)\hspace{0.17em}=\hspace{0.17em}Z{\left(\beta ,y,\lambda \right)}^{-1}{e}^{y\hspace{0.17em}\mathrm{\Phi }\left(W,\beta ,\lambda \right)}.$$ [10]

where $\mathrm{\Phi }\left(W,\beta ,\lambda \right)$ is a “local free entropy” potential in which the distance constraint is forced through a Lagrange multiplier $\lambda$:

$$\mathrm{\Phi }\left(W,\beta ,\lambda \right)\hspace{0.17em}=\hspace{0.17em}\ln \sum _{\left\{W\prime \right\}}{e}^{-\beta {\mathcal{L}}_{\mathrm{N}\mathrm{E}}\left(W\prime \right)-\lambda \hspace{0.17em}d\left(W,W\prime \right)},$$ [11]

where $d\left(\cdot ,\cdot \right)$ is some monotonically increasing function of the distance between configurations, defined according to the type of weights under consideration. In the limit $\beta \to \infty$ and by choosing $\lambda$ so that a given distance is selected, this expression reduces to Eq. 8.

The crucial property of Eq. 10 comes from the observation that by choosing $y$ to be a nonnegative integer, the partition function can be rewritten as

$$Z\left(\beta ,y,\lambda \right)\hspace{0.17em}=\hspace{0.17em}\sum _{\left\{W\right\}}{e}^{y\hspace{0.17em}\mathrm{\Phi }\left(W,\beta ,\lambda \right)}\hspace{0.17em}=\hspace{0.17em}\sum _{\left\{W\right\}}\sum _{{\left\{W\prime a\right\}}_{a=1}^y}{e}^{-\beta {\mathcal{L}}_{\mathrm{R}}\left(W,W\prime a\right)},$$ [12]

where

$${\mathcal{L}}_{\mathrm{R}}\left(W,W\prime a\right)\hspace{0.17em}=\hspace{0.17em}\sum _{a=1}^y{\mathcal{L}}_{\mathrm{N}\mathrm{E}}\left(W\prime a\right)\hspace{0.17em}-\hspace{0.17em}\frac{\lambda }{\beta }\sum _{a=1}^{y}d\left(W,W\prime a\right).$$ [13]

These are the partition function and the effective loss of $y+1$ interacting real replicas of the system, one of which acts as reference system ($W$) while the remaining $y$ ($\left\{W\prime a\right\}$) are identical, each being subject to the energy constraint ${\mathcal{L}}_{\mathrm{N}\mathrm{E}}\left(W\prime a\right)$ and to the interaction term with the reference system. As discussed in ref. 4, several algorithmic schemes can be derived from this framework by minimizing ${\mathcal{L}}_{\mathrm{R}}$. Here we shall also use the above approach to study the existence of WFMs in continuous models and to design message-passing and greedy learning algorithms driven by the local entropy of the solutions.

Two-Layer Networks with Continuous Weights.

As for the discrete case, we are able to show that in nonconvex networks with continuous weights the WFMs exist and are rare and yet accessible to simple algorithms. In order to perform an analytic study, we consider the simplest nontrivial 2-layer neural network, the committee machine with nonoverlapping receptive fields. It consists of $N$ input units, one hidden layer with $K$ units and one output unit. The input units are divided into $K$ disjoint sets of $Ñ=\frac{N}{K}$ units. Each set is connected to a different hidden unit. The input to the $\ell$-th hidden unit is given by $x_{\ell }^{\mu }=\frac{1}{\sqrt{Ñ}}{\sum }_{i=1}^{Ñ}{w}_{\ell i}{\xi }_{\ell i}^{\mu }$, where $w_{\ell i}\in \mathbb{R}$ is the connection weight between the input unit $i$ and the hidden unit $\ell$ and ${\xi }_{\ell i}^{\mu }$ is the $i$-th input to the $\ell$-th hidden unit. As before, $\mu$ is a pattern index. We study analytically the pure classifier case in which each unit implements a threshold transfer function and the loss function is the error loss. Other types of (smooth) functions, more amenable to numerical simulation, will be also discussed in a subsequent section. The output of the $\ell$-th hidden unit is given by

$${\tau }_{\ell }^{\mu }=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(x_{\ell }^{\mu }\right)\hspace{0.17em}=\hspace{0.17em}\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(\frac{1}{\sqrt{Ñ}}\sum _{i=1}^{Ñ}{w}_{\ell i}{\xi }_{\ell i}^{\mu }\right).$$ [14]

In the second layer all of the weights are fixed and equal to one, and the overall output of the network is simply given by a majority vote ${\sigma }_{\mathrm{o}\mathrm{u}\mathrm{t}}^{\mu }=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(\frac{1}{\sqrt{K}}{\sum }_{\ell }{\tau }_{\ell }^{\mu }\right)$.

As for the binary perceptron, the learning problem consists of mapping each of the random input patterns $\left({\xi }_{\ell i}^{\mu }\right)$, with $\ell =1,\dots ,K$, $i=1,\dots ,Ñ$, $\mu =1,\dots ,\alpha N$, onto a randomly chosen output ${\sigma }^{\mu }$. Both ${\xi }_{\ell i}^{\mu }$ and ${\sigma }^{\mu }$ are independent random variables that take the values $\pm 1$ with equal probability. For a given set of patterns, the volume of the subspace of the network weights that correctly classify the patterns, the so-called version space, is given by

$$V=\int \prod _{i\ell }\mathrm{d}{w}_{\ell i}\prod _{\ell }\delta \left(\sum _i{w}_{\ell i}^2-Ñ\right)\prod _{\mu }\mathrm{\Theta }\left({\sigma }^{\mu }{\sigma }_{\mathrm{o}\mathrm{u}\mathrm{t}}^{\mu }\right).$$ [15]

where we have imposed a spherical constraint on the weights via a Dirac $\delta$ in order to keep the volume finite (though exponential in $N$). In the case of binary weights the integral would become a sum over all of the $2^N$ configurations and the volume would be the overall number of zero error assignments of the weights.

The committee machine was studied extensively in the 1990s (15–17). The capacity of the network can be derived by computing the typical weight space volume as a function of the number of correctly classified patterns $\alpha N$, in the large $N$ limit. As for the binary case, the most probable value of $V$ is obtained by exponentiating the average of $\log V$, $V_{\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}\simeq \exp \left(N{⟨\log V⟩}_{\xi }\right)$, a difficult task which is achieved by the replica method (18, 19).

For the smallest nontrivial value of $K$, $K=3$, it has been found that above ${\alpha }_0\simeq 1.76$ the space of solutions changes abruptly, becoming clustered into multiple components.* Below ${\alpha }_0$ the geometrical structure is not clustered and can be described by the simplest version of the replica method, known as replica symmetric solution. Above ${\alpha }_0$ the analytical computation of the typical volume requires a more sophisticated analysis that properly describes a clustered geometrical structure. This analysis can be performed by a variational technique which is known in statistical physics as the replica-symmetry-breaking (RSB) scheme, and the clustered geometrical structure of the solution space is known as RSB phase.

The capacity of the network, above which perfect classification becomes impossible, is found to be ${\alpha }_c\simeq$ 3.02. In the limit of large $K$ (but still with $Ñ\gg 1$), the clustering transition occurs at a finite number of patterns per weight, ${\alpha }_0\simeq 2.95$ (15), whereas the critical capacity grows with $K$ as ${\alpha }_c\propto \sqrt{\ln K}$ (20).

The Existence of WFM.

In order to detect the existence of WFM we use a large deviation measure which is the continuous version of the measure used in the discrete case: Each configuration of the weights is reweighted by a local volume term, analogously to the analysis in Local Entropy Theory. For the continuous case, however, we adopt a slightly different formalism which simplifies the analysis. Instead of constraining the set of $y$ real replicas^† to be at distance $D$ from a reference weight vector, we can identify the same WFM regions by constraining them directly to be at a given mutual overlap: For a given value $q_1\in \left[-\mathrm{1,1}\right]$ , we impose that $W^a\cdot W^b=N{q}_1$ for all pairs of distinct replicas $a,b$. The overlap $q_1$ is bijectively related to the mutual distance among replicas (which tends to 0 as $q_1\to 1$). That, in turn, determines the distance between each replica and the normalized barycenter of the group $\sqrt{N}{\sum }_a{W}^a/∥{\sum }_a{W}^a∥$, which takes the role that the reference vector had in the previous treatment. Thus, the regime of small $D$ corresponds to the regime of $q_1$ close to 1, and apart from this reparametrization the interpretation of the WFM volumes is the same. As explained in Materials and Methods, the advantage of this technique is that it allows to use directly the first-step formalism of the RSB scheme (1-RSB). Similarly to the discrete case, the computation of the maximal WFM volumes leads to the following results: For $K=3$ and in the large $y$ limit, we find‡

$$\begin{array}{ll}\hfill \mathcal{V}\left(q_1\right)& \hspace{0.17em}=\hspace{0.17em}\underset{{\left\{W^a\right\}}_{a=1}^y}{max}\left\{\frac{1}{Ny}{⟨\ln V\left({\left(W^a\right)}_{a=1}^y,q_1\right)⟩}_{\xi }\right\}\hfill \\ \hfill & \hspace{0.17em}=\hspace{0.17em}{G}_S\left(q_1\right)\hspace{0.17em}+\hspace{0.17em}\alpha G_E\left(q_1\right)\hfill \end{array}$$

with

$$\begin{array}{ll}\hfill G_{\mathrm{S}}\left(q_1\right)& \hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\left[1+\ln 2\pi +\ln \left(1-q_1\right)\right]\hfill \\ \hfill G_{\mathrm{E}}\left(q_1\right)& \hspace{0.17em}=\hspace{0.17em}\int \prod _{\ell =1}^{3}D{v}_{\ell }\underset{u_1,u_2,u_3}{max}\left[-\frac{{\sum }_{\ell =1}^3{u}_{\ell }^2}{2}+\right.\hfill \\ \hfill & \hspace{0.17em}+\hspace{0.17em}\left.\ln \left({\stackrel{\sim }{H}}_1{\stackrel{\sim }{H}}_2+{\stackrel{\sim }{H}}_1{\stackrel{\sim }{H}}_3+{\stackrel{\sim }{H}}_2{\stackrel{\sim }{H}}_3-2{\stackrel{\sim }{H}}_1{\stackrel{\sim }{H}}_2{\stackrel{\sim }{H}}_3\right)\right],\hfill \end{array}$$

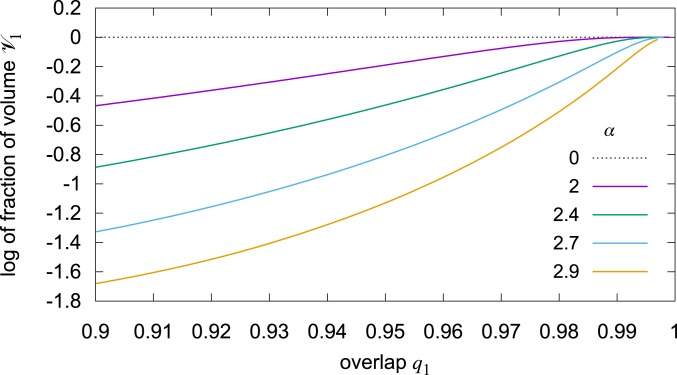
where ${\stackrel{\sim }{H}}_{\ell }\equiv H\left(\sqrt{\frac{d_0}{1-q_1}}{u}_{\ell }+\sqrt{\frac{q_0}{1-q_1}}{v}_{\ell }\right)$, $H\left(x\right)\hspace{0.17em}\equiv \hspace{0.17em}{\int }_x^{\infty }Dv$, $Dv\equiv dv\frac{1}{\sqrt{2\pi }}{e}^{-\frac{1}{2}{v}^2}$, $d_0\equiv y\left(q_1-q_0\right)$ and $q_0$ satisfies a saddle point equation that needs to be solved numerically. $\mathcal{V}\left(q_1\right)$ is the logarithm of the volume of the solutions, normalized by $Ny$, under the spherical constraints on the weights, and with the real replicas forced to be at a mutual overlap $q_1$. In analogy with the discrete case, we still refer to $\mathcal{V}\left(q_1\right)$ as to the local entropy. It is composed by the sum of 2 terms; the first one, $G_{\mathrm{S}}\left(q_1\right)$, corresponds to the log-volume at $\alpha =0$, where all configurations are solutions and only the geometric constraints are present. This is an upper bound for the local entropy. The second term, ${\mathcal{V}}_1\left(q_1\right)\hspace{0.17em}\equiv \hspace{0.17em}\alpha G_{\mathrm{E}}\left(q_1\right)$, is in general negative and it represents the log of the fraction of solutions at overlap $q_1$ (among all configurations at that overlap), and we call it normalized local entropy. Following the interpretation given above, we expect (in analogy to the discrete case at small $D$; see Fig. 3) that in a WFM this fraction is close to 1 (i.e., ${\mathcal{V}}_1$ is close to 0) in an extended region where the distance between the replicas is small, that is, where $q_1$ is close to 1; otherwise, WFMs do not exist in the model. In Fig. 1 we report the values of ${\mathcal{V}}_1\left(q_1\right)$ vs. the overlap $q_1$ for different values of $\alpha$. Indeed, one may observe that the behavior is qualitatively similar to that of the binary perceptron: Besides the solutions and all of the related local minima and saddles predicted by the standard statistical physics analysis (15–17, 20) there exist absolute minima that are flat at relatively large distances. Indeed, reaching such wide minima efficiently is nontrivial, and different algorithms can have drastically different behaviors, as we will discuss in detail in Numerical Studies.

Fig. 3.

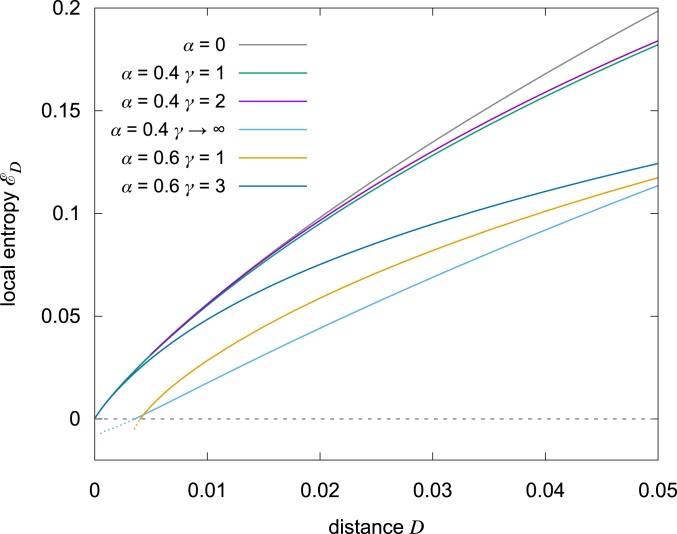
Average local entropy around a typical minimum of the ${\mathcal{L}}_{\mathrm{C}\mathrm{E}}$ loss for various values of $\alpha$ and $\gamma$. The gray upper curve, corresponding to $\alpha =0$, is an upper bound since in that case all configurations are solutions. For $\alpha =0.4$, the 2 curves with $\gamma =1$ and 2 nearly saturate the upper bound at small distances, revealing the presence of dense regions of solutions (HLE regions). There is a slight improvement for $\gamma =2$, but the curve at $\gamma \to \infty$ shows that the improvement cannot be monotonic: In that limit, the measure is dominated by isolated solutions. This is reflected by the gap at small $D$ in which the entropy becomes negative, signifying the absence of solutions in that range. For $\alpha =0.6$ we see that the curves are lower, as expected. We also see that for $\gamma =1$ there is a gap at small $D$, and that we need to get to $\gamma =3$ in order to find HLE regions.

Fig. 1.

Normalized local entropy ${\mathcal{V}}_1$ vs. $q_1$, that is, logarithm of the fraction of configurations of $y$ real replicas at mutual overlap $q_1$ in which all replicas have zero error loss ${\mathcal{L}}_{\mathrm{N}\mathrm{E}}$. The curves are for a tree-like committee machine with $K=3$ hidden units trained on $\alpha N$ random patterns, for various values of $\alpha$, obtained from a replica calculation in the limit of large $N$ and large number of real replicas $y$. When the curves approach 0 as $q_1\to 1$ it means that nearly all configurations are minima, and thus that the replicas are collectively exploring a wide minimum (any $q_1<1$ implies distances of $O\left(N\right)$ between replicas). The analogous figure for the limiting case of a large number of hidden units $K$ can be found in SI Appendix.

The case $K=3$ is still relatively close to the simple perceptron, although the geometrical structure of its minima is already dominated by nonconvex features for $\alpha >1.76$. A case that is closer to more realistic ANNs is $K\gg 1$ (but still $N\gg K$), which, luckily enough, is easier to study analytically. We find

$$\begin{array}{ll}\hfill G_{\mathrm{S}}\left(q_1\right)& \hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\left[1+\ln 2\pi +\ln \left(1-q_1\right)\right]\hfill \\ \hfill G_{\mathrm{E}}\left(q_1\right)& \hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}\int \hspace{0.17em}\hspace{0.17em}Dv\hspace{0.17em}\underset{u}{max}\left[-\frac{u^2}{2}+\ln H\left(\sqrt{\frac{\mathrm{\Delta }{q}_1^e}{1-q_1^e}}u+\frac{q_0^e}{1-q_1^e}v\right)\right],\hfill \end{array}$$

where $\mathrm{\Delta }{q}_1^e=q_1^e-q_0^e$ with $q_1^e\equiv 1-\frac{2}{\pi }\arccos \left(q_1\right)$, $q_0^e\equiv 1-\frac{2}{\pi }\arccos \left(q_0\right)$, and $q_0$ is fixed by a saddle point equation. The numerical results are qualitatively similar to those for $K=3$: We observe that indeed WFM still exist for all finite values of $\alpha$. The analogue of Fig. 1 for this case is reported in the SI Appendix.

The results of the above WFM computation may require small corrections due to RSB effects, which, however, are expected to be very tiny due to the compact nature of the space of solutions at small distances.

A more informative aspect is to study the volumes around the solutions found by different algorithms. This can be done by the BP method, similarly to the computation of the weight enumerator function in error correcting codes (21).

Not All Devices Are Appropriate: The Parity Machine Does Not Display HLE/WFM Regions.

The extent by which a given model exhibits the presence of WFM can vary (see, e.g., Fig. 1). A direct comparison of the local entropy curves on different models in general does not yet have a well-defined interpretation, although at least for similar architectures it can still be informative (22). On the other hand, the existence of WFM itself is a structural property. For neural networks, its origin relies on the threshold sum form of the nonlinearity characterizing the formal neurons. As a check of this claim, we can analyze a model that is in some sense complementary, namely the so-called parity machine. We take its network structure to be identical to the committee machine, except for the output unit, which performs the product of the $K$ hidden units instead of taking a majority vote. While the outputs of the hidden units are still given by sign activations, Eq. 14, the overall output of the network reads ${\sigma }_{\mathrm{o}\mathrm{u}\mathrm{t}}^{\mu }={\prod }_{\ell =1}^K{\tau }_{\ell }$. The volume of the weights that correctly classifies a set of patterns is still given by Eq. 15.

Parity machines are closely related to error-correcting codes based on parity checks. The geometrical structure of the absolute minima of the error loss function is known (20) to be composed of multiple regions, each in one to one correspondence with the internal representations of the patterns. For random patterns such regions are typically tiny and we expect the WFM to be absent. Indeed, the computation of the volume proceeds analogously to the previous case^§ , and it shows that in this case for any distance the volumes of the minima are always bounded away from the maximal possible volume, that is, the volume one would find for the same distance when no patterns are stored. The log-ratio of the 2 volumes is constant and equal to $-\alpha \log \left(2\right)$. In other words, the minima never become flat, at any distance scale.

The Connection between Local Entropy and CE.

Given that dense regions of optimal solutions exist in nonconvex ANN, at least in the case of independent random patterns, it remains to be seen which role they play in current models. Starting with the case of binary weights, and then generalizing the result to more complex architectures and to continuous weights, we can show that the most widely used loss function, the so-called CE loss, focuses precisely on such rare regions (see ref. 23 for the case of stochastic weights).

For the sake of simplicity, we consider a binary classification task with one output unit. The CE cost function for each input pattern reads

$${\mathcal{L}}_{\mathrm{C}\mathrm{E}}\left(W\right)\hspace{0.17em}=\hspace{0.17em}\sum _{\mu =1}^M\hspace{0.17em}{f}_{\gamma }\left(\frac{{\sigma }^{\mu }}{\sqrt{N}}\sum _{i=1}^N{w}_i{\xi }_i^{\mu }\right),$$ [16]

where $f_{\gamma }\left(x\right)\hspace{0.17em}=\hspace{0.17em}-\frac{x}{2}+\frac{1}{2\gamma }\log \left(2\cosh \left(\gamma x\right)\right)$. The parameter $\gamma$ allows one to control the degree of “robustness” of the training (Fig. 2, Inset). In standard machine learning practice $\gamma$ is simply set to 1, but a global rescaling of the weights $W_i$ can lead to a basically equivalent effect. That setting can thus be interpreted as leaving $\gamma$ as implicit, letting its effective value, and hence the norm of the weights, to be determined by the initial conditions and the training algorithm. As we shall see, controlling $\gamma$ explicitly along the learning process plays a crucial role in finding HLE/WFM regions.

Fig. 2.

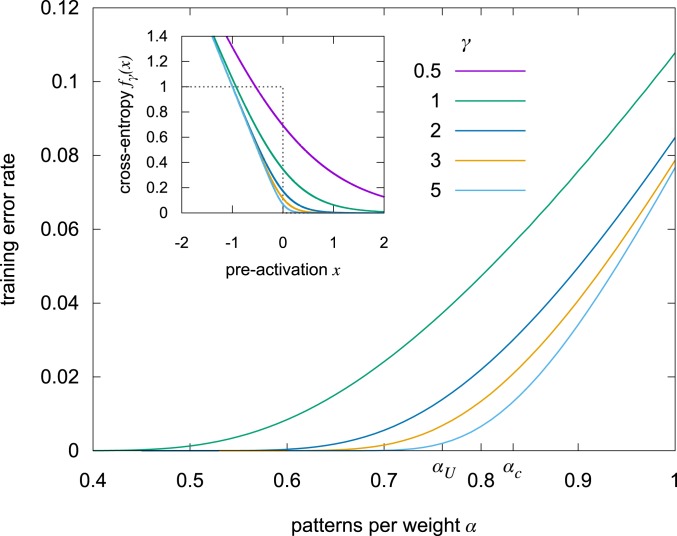
Mean error rate achieved when optimizing the CE loss in the binary single-layer network, as predicted by the replica analysis, at various values of $\gamma$ (increasing from top to bottom). The figure also shows the points ${\alpha }_c\approx 0.83$ (up to which solutions exist) and ${\alpha }_U\approx 0.76$ (up to which nonisolated solutions exist). (Inset) Binary CE function $f_{\gamma }\left(x\right)$ for various values of $\gamma$ (increasing from top to bottom). For low values of $\gamma$, the loss is nonzero even for small positive values of the input, and thus the minimization procedure tends to favor more robust solutions. For large values of $\gamma$ the function tends to $max\left(-x,0\right)$. The dotted line shows the corresponding NE function, which is just 1 in case of an error and 0 otherwise (cf. Eq. 1).

For the binary case, however, the norm is fixed and thus we must keep $\gamma$ as an explicit parameter. Note that since $\underset{\gamma \to \infty }{lim}{f}_{\gamma }\left(x\right)\hspace{0.17em}=\hspace{0.17em}max\left(-x,0\right)$ the minima of ${\mathcal{L}}_{\mathrm{C}\mathrm{E}}$ below ${\alpha }_c$ at large $\gamma$ are the solutions to the training problem, that is, they coincide with those of ${\mathcal{L}}_{\mathrm{N}\mathrm{E}}$.

We proceed by first showing that the minimizers of this loss correspond to near-zero errors for a wide range of values of $\alpha$ and then by showing that these minimizers are surrounded by an exponential number of zero error solutions.

In order to study the probability distribution of the minima of ${\mathcal{L}}_{\mathrm{C}\mathrm{E}}$ in the large $N$ limit, we need to compute its Gibbs distribution (in particular, the average of the $\log$ of the partition function; see Eq. 5) as it has been done for the error loss ${\mathcal{L}}_{\mathrm{N}\mathrm{E}}$. The procedure follows standard steps and it is detailed in SI Appendix. The method requires one to solve 2 coupled integral equations as functions of the control parameters $\alpha$, $\beta$, and $\gamma$. In Fig. 2 we show the behavior of the fraction of errors vs. the loading $\alpha$ for various values of $\gamma$. Up to relatively large values of $\alpha$ the optimum of ${\mathcal{L}}_{\mathrm{C}\mathrm{E}}$ corresponds to extremely small values of ${\mathcal{L}}_{\mathrm{N}\mathrm{E}}$, virtually equal to zero for any accessible size $N$.

Having established that by minimizing the CE one ends up in regions of perfect classification where the error loss function is essentially zero, it remains to be understood which type of configurations of weights are found. Does the CE converge to an isolated point-like solution in the weight space (such as the typical zero energy configurations of the error function)^¶ or does it converge to the rare regions of HLE?

In order to establish the geometrical nature of the typical minima of the CE loss, we need to compute the average value of ${\mathcal{E}}_D\left(W\right)$ (which tells us how many zero energy configurations of the error loss function can be found within a given radius $D$ from a given $W$; see Eq. 6) when $W$ is sampled from the minima of ${\mathcal{L}}_{\mathrm{C}\mathrm{E}}$. This can be accomplished by a well-known analytical technique (24) which was developed for the study of the energy landscape in disordered physical systems. The computation is relatively involved, and here we report only the final outcome. For the dedicated reader, all of the details of the calculation, which relies on the replica method and includes a double analytic continuation, can be found in SI Appendix. As reported in Fig. 3, we find that the typical minima of the CE loss for small finite $\gamma$ are indeed surrounded by an exponential number of zero error solutions. In other words, the CE focuses on HLE regions. The range of $\gamma$ for which this happens is generally rather wide, but neither too-small nor too-large values work well (additional details on this point are provided in SI Appendix). On the other hand, this analysis does not fully capture algorithmic dynamic effects, and in practice using a procedure in which $\gamma$ is initialized to a small value and gradually increased should be effective in most circumstances (4).

As an algorithmic check we have verified that while a simulated annealing approach gets stuck at very high energies when trying to minimize the error loss function, the very same algorithm with the CE loss is indeed successful up to relatively high values of $\alpha$, with just slightly worse performance compared to an analogous procedure based on local entropy (13). In other words, the CE loss on single-layer networks is a computationally cheap and reasonably good proxy for the LE loss. These analytical results extend straightforwardly to 2-layer networks with binary weights. The study of continuous weight models can be performed resorting to the BP method.

BP and fBP

BP, also known as sum-product, is an iterative message-passing algorithm for statistical inference. When applied to the problem of training a committee machine with a given set of input–output patterns, it can be used to obtain, at convergence, useful information on the probability distribution, over the weights of the network, induced by the Gibbs measure. In particular, it allows one to compute the marginals of the weights as well as their entropy, which in the zero-temperature regime is simply the logarithm of the volume of the solutions, Eq. 15, rescaled by the number of variables $N$. The results are approximate, but (with high probability) they approach the correct value in the limit of large $N$ in the case of random uncorrelated inputs, at least in the replica-symmetric phase of the space of the parameters. Due to the concentration property, in this limit the macroscopic properties of any given problem (such as the entropy) tend to converge to a common limiting case, and therefore a limited amount of experiments with a few samples is sufficient to describe very well the entire statistical ensemble.

We have used BP to study the case of the zero-temperature tree-like committee machine with continuous weights and $K\hspace{0.17em}=\hspace{0.17em}3$. We have mostly used $N\hspace{0.17em}=\hspace{0.17em}999$, which turns out to be large enough to produce results in quite good agreement with the replica theory analysis. Our implementation follows standard practice in the field (see, e.g., refs. 4, 10, and 25) and can be made efficient by encoding each message with only its mean and variance (SI Appendix). As mentioned above, this algorithm works well in the replica-symmetric phase, which for our case means when $\alpha \le {\alpha }_0\approx 1.76$. Above this value, the (vanilla) algorithm does not converge at all.

However, BP can be employed to perform additional analyses as well. In particular, it can be modified rather straightforwardly to explore and describe the region surrounding any given configuration, as it allows one to compute the local entropy (i.e., the log-volume of the solutions) for any given distance and any reference configuration (this is a general technique; the details for our case are reported in SI Appendix). The convergence issues are generally much less severe in this case. Even in the RSB phase, if the reference configuration is a solution in a wide minimum, the structure is locally replica-symmetric, and therefore the algorithm converges and provides accurate results, at least up to a value of the distance where other unconnected regions of the solutions space come into consideration. In our tests, the only other issue arose occasionally at very small distances, where convergence is instead prevented by the loss of accuracy stemming from finite size effects and limited numerical precision.

Additionally, the standard BP algorithm can be modified and transformed into a (very effective) solver. There are several ways to do this, most of which are purely heuristic. However, it was shown in ref. 4 that adding a particular set of self-interactions to the weight variables could approximately but effectively describe the replicated system of Eq. 12. In other words, this technique can be used to analyze the local-entropy landscape instead of the Gibbs one. By using a sufficiently large number of replicas $y$ (we generally used $y=10$) and following an annealing protocol in the coupling parameter $\lambda$ (starting from a low value and making it diverge) this algorithm focuses on the maximally dense regions of solutions, thus ending up in WFM. For these reasons, the algorithm was called “focusing BP” (fBP). The implementation closely follows that of ref. 4 (complete details are provided in SI Appendix). Our tests—detailed below—show that this algorithm is the best solver (by a wide margin) among the several alternatives that we tried in terms of robustness of the minima found (and thus of generalization properties, as also discussed below). Moreover, it also achieves the highest capacity, nearly reaching the critical capacity where all solutions disappear.

eLAL

Least-action learning (LAL), also known as minimum-change rule (26–28), is a greedy algorithm that was designed to extend the well-known perceptron algorithm to the case of committee machines with a single binary output and sign activation functions. It takes one parameter, the learning rate $\eta$. In its original version, patterns are presented randomly one at a time, and at most one hidden unit is affected at a time. In case of correct output, nothing is done, while in case of error the hidden unit, among those with a wrong output, whose preactivation was closest to the threshold (and is thus the easiest to fix) is selected, and the standard perceptron learning rule (with rate $\eta$) is applied to it. In our tests we simply extended it to work in mini-batches, to make it more directly comparable with stochastic-gradient-based algorithms: For a given mini-batch, we first compute all of the preactivations and the outputs for all patterns, then we apply the LAL learning rule for each pattern in turn.

This algorithm proves to be surprisingly effective at finding minima of the NE loss very quickly: In the random patterns case, its algorithmic capacity is higher than gradient-based variants and almost as high as fBP, and it requires comparatively few epochs. It is also computationally very fast, owing to its simplicity. However, as we show in Numerical Studies, it finds solutions that are much narrower compared to those of other algorithms.

In order to drive LAL toward WFM regions, we add a local-entropy component to it, by applying the technique described in ref. 4 (see Eq. 13): We run $y$ replicas of the system in parallel and we couple them with an elastic interaction. The resulting algorithm, which we call eLAL, can be described as follows. We initialize $y$ replicas randomly with weights $W^a$ and compute their average $\stackrel{\sim }{W}$. We present mini-batches independently to each replica, using different permutations of the dataset for each of them. At each mini-batch, we apply the LAL learning rule. Then, each replica is pushed toward the group average with some strength proportional to a parameter $\lambda$. More precisely, we add a term $\lambda \eta \left(\stackrel{\sim }{W}-W^a\right)$ to each of the weight vectors $W^a$. After this update, we recompute the average $\stackrel{\sim }{W}$. At each epoch, we increase the interaction strength $\lambda$. The algorithm stops when the replicas have collapsed to a single configuration.

This simple scheme proves rather effective at enhancing the wideness of the minima found while still being computationally efficient and converging quickly, as we show in Numerical Studies.

Numerical Studies

We conclude our study by comparing numerically the curvature, the wideness of the minima, and the generalization error found by different approaches. We consider 2 main scenarios: One, directly comparable with the theoretical calculations, where a tree committee machine with $K=9$ is trained over random binary patterns, and a second one, which allows us to estimate the generalization capabilities, where a fully connected committee machine with $K=9$ is trained on a subset of the Fashion-MNIST dataset (29). The choice of using $K=9$ instead of 3 is intended to enhance the potential robustness effect that the CE loss can have over NE on such architectures (see Fig. 2, Inset): For $K=3$, a correctly classified pattern already requires 2 out for 3 units to give the correct answer, and there is not much room for improvement at the level of the preactivation of the output unit. On the other hand, since we study networks with a number of inputs of the order of $10^3$, an even larger value of $K$ would either make $N/K$ too small in the tree-like case (exacerbating numerical issues for the BP algorithms and straying too far from the theoretical analysis) or make the computation of the Hessians too onerous for the fully connected case (each Hessian requiring the computation of ${\left(NK\right)}^2$ terms).

We compare several training algorithms with different settings (Materials and Methods): stochastic GD with the CE loss (ceSGD), LAL and its entropic version eLAL, and fBP. Of these, the nongradient-based ones (LAL, eLAL, and fBP) can be directly used with the sign activation functions (Eq. 14) and the NE loss. On the other hand, ceSGD requires a smooth loss landscape, and therefore we used $\tanh$ activations, adding a gradually diverging parameter $\beta$ in their argument, since ${lim}_{\beta \to \infty }\tanh \left(\beta x\right)\hspace{0.17em}=\hspace{0.17em}\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(x\right)$. The $\gamma$ parameter of the CE loss (Eq. 16) was also increased gradually. As in the theoretical computation, we also constrained the weights of each hidden unit of the network to be normalized. The NE loss with sign activations is invariant under renormalization of each unit’s weights, whereas the CE loss with $\tanh$ activations is not. In the latter case, the parameters $\beta$ and $\gamma$ can be directly interpreted as the norm of the weights, since they just multiply the preactivations of the units. In a more standard approach, the norm would be controlled by the initial choice of the weights and be driven by the SGD algorithm automatically. In our tests instead we have controlled these parameters explicitly, which allows us to demonstrate the effect of different schedules. In particular, we show (for both the random and the Fashion-MNIST scenarios) that slowing down the growth of the norm with ceSGD makes a significant difference in the quality of the minima that are reached. We do this by using 2 separate settings for ceSGD, a “fast” and a “slow” one. In ceSGD-fast both $\beta$ and $\gamma$ are large from the onset and grow quickly, whereas in ceSGD-slow they start from small values and grow more slowly (requiring much more epochs for convergence).

In all cases—for uniformity of comparison, simplicity, and consistency with the theoretical analysis—we consider scenarios in which the training error (i.e., the NE loss) gets to zero. This is, by definition, the stopping condition for the LAL algorithm. We also used this as a stopping criterion for ceSGD in the “fast” setting. For the other algorithms, the stopping criterion was based on reaching a sufficiently small loss (ceSGD in the “slow” setting), or the collapse of the replicas (eLAL and fBP).

The analysis of the quality of the results was mainly based on the study of the local loss landscape at the solutions. On one hand, we computed the normalized local entropy using BP as described in a previous section, which provides a description of the NE landscape. On the other hand, we also computed the spectrum of the eigenvalues of a smoothed-out version of the NE loss, namely the mean square error (MSE) loss computed on networks with $\tanh$ activations. This loss depends on the parameters $\beta$ of the activations: We set $\beta$ to be as small as possible (maximizing the smoothing and thereby measuring features of the landscape at a large scale) under the constraint that all of the solutions under consideration were still corresponding to zero error (to prevent degrading the performance). For the Fashion-MNIST case, we also measured the generalization error of each solution and the robustness to input noise.

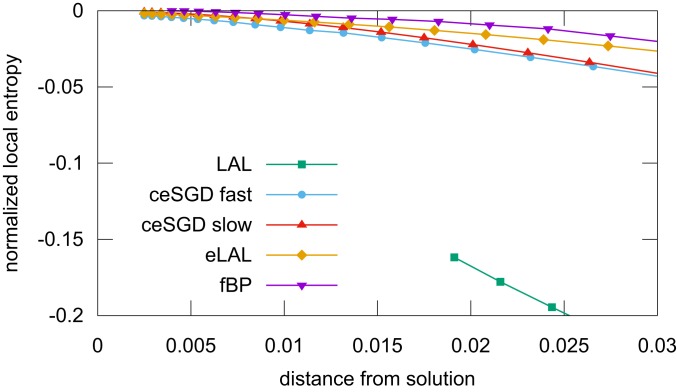
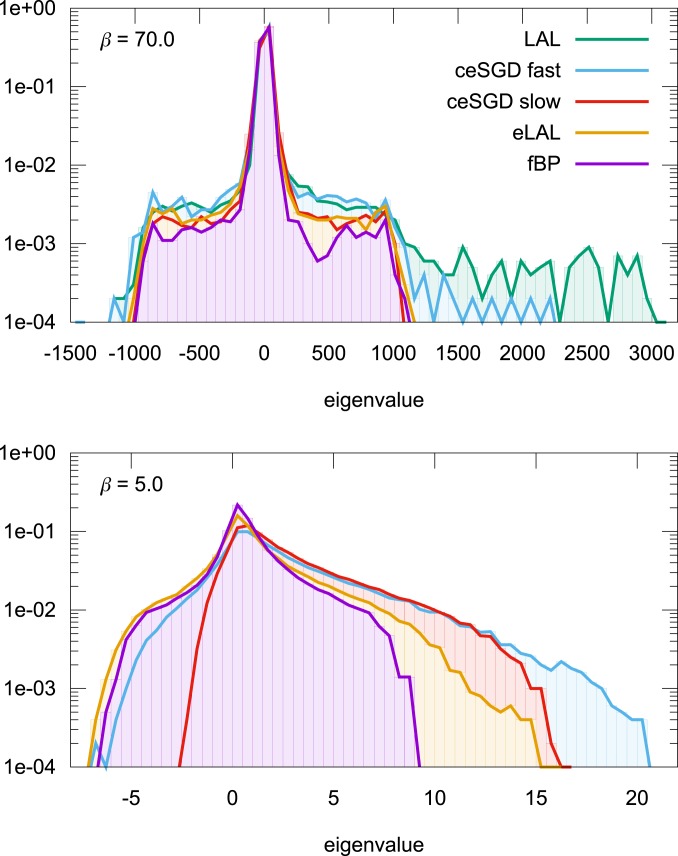
In the random patterns scenario we set $N=999$ and $\alpha =1$ and tested 10 samples (the same for all of the algorithms). The results are presented in Figs. 4 and 5. The 2 analyses allow one to rank the algorithms (for the Hessians we can use the maximum eigenvalue as a reasonable metric) and their results are in agreement. As expected, fBP systematically finds very dense regions of solutions, qualitatively compatible with the theoretical analysis (compare Fig. 4 with Fig. 1) and corresponding to the narrowest spectra of the Hessian at all $\beta$; the other algorithms follow roughly in the order eLAL, ceSGD-slow, ceSGD-fast, and LAL. The latter is a very efficient solver for this model, but it finds solutions in very narrow regions. On the other hand, the same algorithm performed in parallel on a set of interacting replicas is still efficient but much better at discovering WFM. These results are for $y=20$ replicas in eLAL, but our tests show that $y=10$ would be sufficient to match ceSGD-slow and that $y=100$ would further improve the results and get closer to fBP. Overall, the results of the random pattern case confirm the existence of WFM in continuous networks and suggest that a (properly normalized) Hessian spectrum can be used as a proxy for detecting whether an algorithm has found a WFM region.

Fig. 4.

Normalized local entropy as a function of the distance from a reference solution, on a tree-like committee machine with $K=9$ and $N\hspace{0.17em}=\hspace{0.17em}999$, trained on 1,000 random patterns. The results were obtained with the BP algorithm, by averaging over 10 samples. Numerical issues (mainly due to the approximations used) prevented BP from converging at small distances for the LAL algorithm, and additionally they slightly affect the results at very small distances. Qualitatively, though, higher curves correspond to larger local entropies and thus wider minima.

Fig. 5.

Spectra of the Hessian for the same solutions of Fig. 4, for various algorithms. The spectra are directly comparable since they are all computed on the same loss function (MSE; using CE does not change the results qualitatively) and the networks are normalized. (Top) The results with the parameter $\beta$ of the activation functions set to a value such that all solutions of all algorithms are still valid; this value is exclusively determined by the LAL algorithm. (Bottom) The results for a much lower value of $\beta$ that can be used when removing the LAL solutions, where differences between ceSGD-slow, eLAL and fBP that were not visible al higher $\beta$ can emerge (the spectrum of LAL would still be the widest by far even at this $\beta$).

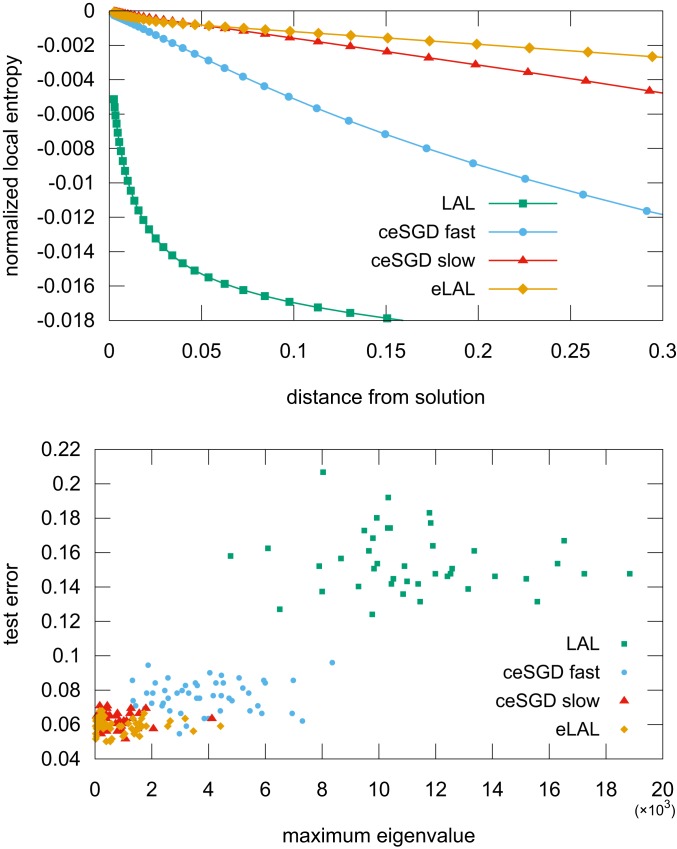
We then studied the performance of ceSGD (fast and slow settings), LAL, and eLAL on a small fully connected network that learns to discriminate between 2 classes of the Fashion-MNIST dataset (we chose the classes Dress and Coat, which are rather challenging to tell apart but also sufficiently different to offer the opportunity to generalize even with a small simple network trained on very few examples). We trained our networks on a small subset of the available examples (500 patterns, binarized to $\pm 1$ by using the median of each image as a threshold on the original grayscale inputs; we filtered both the training and test sets to only use images in which the median was between 0.25 and 0.75 as to avoid too-bright or too-dark images and make the data more uniform and more challenging). This setting is rather close to the one which we could study analytically, except for the patterns statistics and the use of fully connected rather than tree-like layers, and it is small enough to permit computing the full spectrum of the Hessian. On the other hand, it poses a difficult task in terms of inference (even though finding solutions with zero training error is not hard), which allowed us to compare the results of the analysis of the loss landscape with the generalization capabilities on the test set. Each algorithm was run 50 times. The results are shown in Fig. 6, and they are analogous to those for the random patterns case, but in this setting we can also observe that indeed WFM tend to generalize better. Also, while we could not run fBP on this data due to the correlations present in the inputs and to numerical problems related to the fully connected architecture, which hamper convergence, it is still the case that ceSGD can find WFM if the norms are controlled and increased slowly enough, and that we can significantly improve the (very quick and greedy) LAL algorithm by replicating it, that is, by effectively adding a local-entropic component.

Fig. 6.

Experiments on a subset of Fashion-MNIST. (Top) Average normalized local entropies. (Bottom) Test error vs. maximum eigenvalue of the Hessian spectrum at $\beta =90$. The maximum eigenvalue is correlated to the generalization (WFM tend to generalize better), and the quality of the minima varies between algorithms.

We also performed an additional batch of tests on a randomized version of the Fashion-MNIST dataset, in which the inputs were reshuffled across samples on a pixel-by-pixel basis (such that each sample only retained each individual pixel bias while the correlations across pixels were lost). This allowed us to bridge the 2 scenarios and directly compare the local volumes in the presence or absence of features of the data that can lead to proper generalization. We kept the settings of each algorithm as close as possible to those for the Fashion-MNIST tests. Qualitatively, the results were quite similar to the ones on the original data except for a slight degradation of the performance of eLAL compared to ceSGD. Quantitatively, we observed that the randomized version was more challenging and generally resulted in slightly smaller volumes. Additional measures comparing the robustness to the presence of noise in the input (which measures overfitting and thus can be conceived as being a precursor of generalization) confirm the general picture. The detailed procedures and results are reported in SI Appendix.

Conclusions and Future Directions

In this paper, we have generalized the local entropy theory to continuous weights and we have shown that WFM exists in nonconvex neural systems. We have also shown that the CE loss spontaneously focuses on WFM. On the algorithmic side we have derived and designed algorithmic schemes, either greedy (very fast) or message-passing, which are driven by the local entropy measure. Moreover, we have shown numerically that ceSGD can be made to converge in WFM by an appropriate cooling procedure of the parameter which controls the norm of the weights. Our findings are in agreement with recent results showing that rectified linear units transfer functions also help the learning dynamics to focus on WFM (22). Future work will be aimed at extending our methods to multiple layers, trying to reach a unified framework for current DNN models. This is a quite challenging task which has the potential to reveal the role that WFM play for generalization in different data regimes and how that can be connected to the many layer architectures of DNN.

Materials and Methods

1-RSB Formalism to Analyze Subdominant Dense States.

The relationship between the local entropy measure (12) and the 1-RSB formalism is direct and is closely related to the work of Monasson (30). All of the technical details are given in SI Appendix; here we just give the high-level description of the derivation.

Consider a partition function in which the interaction among the real replicas is pairwise (without the reference configuration $\stackrel{\sim }{W}$) and the constraint on the distance is hard (introduced via a Dirac delta function):

$$Z=\hspace{0.17em}\hspace{0.17em}\int \prod _a\mathrm{d}\mu \left(\hspace{0.17em}{W}^a\right)\prod _{\mu }{e}^{-\beta \sum _{a=1}^y\hspace{0.17em}E\left(\hspace{0.17em}{W}^a\right)}\prod _{a>b}\delta \left(\hspace{0.17em}d\left(\hspace{0.17em}{W}^a,W^b\right)-ND\right),$$

where $\mathrm{d}\mu \left(W^a\right)$ is an integration measure that imposes some normalization constraint (e.g., spherical) on the $W$s. Suppose then that we study the average free entropy $⟨\log Z⟩$ (where $⟨\cdot ⟩$ represents the average over the random parameters, the patterns in the specific case of ANN) in the context of replica theory. The starting point is the following small $n$ expansion $Z^n=1+n\log Z+O\left(n^2\right)$. This identity may be averaged over the random parameters and gives the average of the $\log$ from the averaged $n$-th power of the partition function $⟨\log Z⟩={min}_{n\to 0}\frac{⟨Z^n⟩-1}{n}$. The idea of the replica method is to compute the average for integer $n$ and to take the analytic continuation $n\to 0$. Overall we have to deal with $n$ virtual replicas of the whole system (coming from the replica method) and since each system has $y$ real replicas we end up with $ny$ total replicas. Let us use indices $c$, $d$ for the virtual replicas and $a$, $b$ for the real ones, such that a configuration will now have 2 indices, for example $W^{ca}$. Suppose that we manage to manipulate the expression such that it becomes a function, among other order variables, of the overlaps $q^{ca,db}=\frac{1}{N}⟨W^{ca},W^{db}⟩$, where $⟨\cdot ,\cdot ⟩$ represents some scalar product, and that the distance function $d\left(\cdot ,\cdot \right)$ can be expressed in terms of those. Say that $d\left(W,W\prime \right)\hspace{0.17em}=\hspace{0.17em}⟨W,W⟩+⟨W\prime ,W^{\prime }⟩-2⟨W,W\prime ⟩$; then

$$\delta \left(\hspace{0.17em}d\left(\hspace{0.17em}{W}^{ca},W^{cb}\right)-ND\right)=\delta \left(\hspace{0.17em}N\left(\hspace{0.17em}{q}^{ca,ca}+q^{cb,cb}-2q^{ca,cb}-D\right)\right).$$

By assuming replica symmetry, the integral can be computed by saddle point over the following variables:

$$\begin{array}{ll}\hfill q^{ca,ca}& =Q\hfill \\ \hfill q^{ca,cb}& =q_1\hspace{1em}\left(a\ne b\right)\hfill \\ \hfill q^{ca,db}& =q_0\hspace{1em}\left(c\ne d\right)\hfill \end{array}$$

with $Q\ge q_1\ge q_0$. The above expression simplifies to

$$\delta \left(N\left(q^{ca,ca}+q^{cb,cb}-2q^{ca,cb}-D\right)\right)=\delta \left(2N\left(Q-q_1-D\right)\right).$$

Therefore, the order parameter $q_1$ is simply $Q-D$, rather than being fixed by a saddle point. In the cases under our consideration, $Q$ is also fixed a priori by the intergration measure. We are thus left with an expression that depends only on $q_1$, which can be treated as an external parameter. By comparison with the generic 1-RSB formalism applied to the original system (without any real replica), one finds that the only differences in the expressions are that 1) in our setting the parameter $q_1$ is not optimized but rather becomes a control parameter and 2) the so-called Parisi parameter $m$ is replaced by the number of real replicas $y$ and instead of ranging in $\left[\mathrm{0,1}\right]$ it is sent to $\infty$ in order to maximize the local entropy measure. Additional technical details can be found in SI Appendix.

Numerical Experiments.

Here we provide the details and the settings used for the experiments reported in Numerical Studies.

In all of the experiments and for all algorithms except fBP we have used a mini-batch size of 100. The mini-batches were generated by randomly shuffling the datasets and splitting them at each epoch. For eLAL, the permutations were performed independently for each replica. Also, for all algorithms except fBP the weights were initialized from a uniform distribution and then normalized for each unit. The learning rate $\eta$ was kept fixed throughout the training. The parameters $\gamma$ and $\beta$ for the ceSGD algorithm were initialized at some values ${\gamma }_0$, ${\beta }_0$ and multiplied by $1+{\gamma }_1$, $1+{\beta }_1$ after each epoch. Analogously, the parameter $\lambda$ for the eLAL algorithm was initialized to ${\lambda }_0$ and multiplied by $1+{\lambda }_1$ after each epoch. The parameter $\lambda$ for the fBP algorithm ranged in all cases between 0.5 and 30 with an exponential schedule divided into 30 steps; at each step, the algorithm was run until convergence or at most 200 iterations. We used $y=20$ for eLAL and $y=10$ for fBP. The stopping criterion for ceSGD-fast was that a solution (0 errors with $\beta =\infty$) was found; for ceSGD-slow, that the CE loss reached $10^{-7}$; and for eLAL, that the sum of the squared distances between each replica and the average replica $\stackrel{\sim }{W}$ reached $10^{-7}$. We also report here the average and SD of the number of epochs $\overline{T}$ for each algorithm.

Parameters for the case of random patterns.

ceSGD-fast: $\eta =10^{-2}$, ${\gamma }_0=3$, ${\beta }_0=1$, ${\gamma }_1=0$, ${\beta }_1=10^{-3}$ ($\overline{T}=770\pm 150$). ceSGD-slow: $\eta =3\cdot 10^{-3}$, ${\gamma }_0=0.1$, ${\beta }_0=0.5$, ${\gamma }_1=4\cdot 10^{-4}$ ($\overline{T}=\left(1.298\pm 0.007\right)\cdot 10^4$). LAL: $\eta =5\cdot 10^{-3}$ ($\overline{T}=76\pm 15$). eLAL: $\eta =10^{-2}$, ${\lambda }_0=0.5$, ${\lambda }_1=10^{-4}$ ($\overline{T}=861\pm 315$).

Parameters for the Fashion-MNIST experiments.

ceSGD-fast: $\eta =2\cdot 10^{-4}$, ${\gamma }_0=5$, ${\beta }_0=2$, ${\gamma }_1=0$, ${\beta }_1=10^{-4}$ ($\overline{T}=460\pm 334$). ceSGD-slow: $\eta =3\cdot 10^{-5}$, ${\gamma }_0=0.5$, ${\beta }_0=0.5$, ${\gamma }_1=10^{-3}$, ${\beta }_1=10^{-3}$ ($\overline{T}=\left(3.57\pm 0.05\right)\cdot 10^3$). LAL: $\eta =10^{-4}$ ($\overline{T}=61\pm 21$). eLAL: $\eta =2\cdot 10^{-3}$, ${\lambda }_0=30$, ${\lambda }_1=5\cdot 10^{-3}$ ($\overline{T}=190\pm 40$).

Data Availability.

The code and scripts for the tests reported in this paper have been deposited at https://gitlab.com/bocconi-artlab/TreeCommitteeFBP.jl.