Skip to main content
PMC home page
ACS Medicinal Chemistry Letters logoLink to ACS Medicinal Chemistry Letters
. 2019 Dec 11;11(1):77–82. doi: 10.1021/acsmedchemlett.9b00499

Utilizing Grand Canonical Monte Carlo Methods in Drug Discovery

Michael S Bodnarchuk 1,*, Martin J Packer 1, Alexe Haywood 1
PMCID: PMC6956344  PMID: 31938467

Abstract

graphic file with name ml9b00499_0008.jpg

The concepts behind targeting waters for potency and selectivity gains have been well documented and explored, although maximizing such potential gains can prove to be challenging. This problem is exacerbated in cases where there are multiple interacting waters, wherein perturbation of one water can affect the free energy landscape of the remaining waters. Knowing the right modification a priori is challenging, and computational approaches are ideally suited to help answer the key question of which substitution is best to try. Here, we use Grand Canonical Monte Carlo and the recent Grand Canonical Alchemical Perturbation methods to both understand and predict the effect of ligand-mediated water displacement when more than one water molecule is involved, as well as to understand how exploiting water networks can help govern selectivity.

Keywords: water, ATAD2, DPP1, KIT, GCMC, free energy

In recent years there have been a plethora of computational methods described which aim to predict the location of water molecules in protein binding sites, as well as assess their propensity to be displaced or interacted with.1 Molecular-dynamics-based methods such as WaterMap,2,3 grid-based methods such as 3D-RISM,4 SZMAP,5,6 and waterFLAP,7,8 and interaction potential-based approaches such as WarPP9 have all shown great promise10,11 and are ideally suited to complementing crystallographic efforts to find waters. As a result, the medicinal chemist is now able to tailor strategies to interact with water molecules depending on their energetics, such as to displace weakly bound waters, stabilize distal waters, or interact with stable, bound waters.12

It could be argued, however, that two major challenges remain poorly addressed by current methods. The first of these is what to do when there are multiple interacting waters in the binding site. Displacing or interacting with a water molecule in such a network can affect both the position and stability of the others, the energetic consequence of which needs to be known in a lead-optimization context. Molecular-dynamics-based methods can find such networked waters, although they are not always suited to calculating their energy because they typically only apply a first-order entropy term to the free energy calculation. It should be noted that Gilson et al. developed a method for introducing a second-order entropy term to the IFST calculation from which molecular-dynamics-based methods are based upon, although this increases the computational time significantly.13

One solution to this challenge lies in the use of Grand Canonical Monte Carlo (GCMC).14,15 GCMC allows for the number of water molecules to fluctuate during a simulation according to the predefined chemical potential,16 which can then be used to calculate the absolute binding free energy. GCMC captures synergy between water molecules and allows for the solvent occupancy of the pocket to be calculated as a function of the applied potential. The applied potential can be used to create a complete water network, similarly to WaterMap and WaterFLAP, while it can be tuned to observe the effect of removing strongly or weakly bound waters from the network, which may result in reorganization, it can be easily observed.17,18 GCMC can also be performed either upon the entire protein or a specific region such as a binding or allosteric site.

Having identified that a water molecule is deemed suitable for displacement, a critical challenge emerges: which group should the chemist add to the lead compound to displace the water? Techniques such as free energy perturbation (FEP)19 have shown their utility to reliably predict free energy changes relating to ligand modification, although traditionally, they cannot capture water displacement while mutating a ligand “on-the-fly”. As a result, multiple simulations need to be performed to build so-called “free energy cycles” to try and capture the overall change in free energy. While such approaches are rigorous, they are typically time-consuming both to set up and to analyze, while sampling meaningful states of the system, which includes the starting location of water networks, can be challenging. As a result, they are not always suitable for use in lead optimization efforts, although it should be noted that the FEP+ method from Schrodinger has shown promise in combining FEP with GCMC sampling

In 2018, Bruce-Macdonald et al. published a new method called Grand Canonical Alchemical Perturbation (GCAP).20 GCAP allows for ligand modifications to be performed while explicitly sampling the number of waters in the binding site using GCMC. Such a method is ideally suited for use on occluded binding sites where solvent exchange with bulk is not a facile process. The free energy change for displacing multiple waters by a ligand can be easily captured by GCAP, with provisional studies on scytalone dehydratase showing encouraging agreement with experiment.

An alternate approach has been used by Wahl and Smieško.21 Rather than employing GCMC during the alchemical perturbation, they used GCMC to calculate the expected hydration around a set of six congeneric ligands before the simulation was performed. Such an approach was shown to improve the convergence of the free energy simulations, although they highlighted that this approach can suffer from the need for extended sampling time. Another approach by Ben-Shalom et al. uses Metropolis Monte Carlo to enhance water occupancy convergence during free energy simulations.22

In this paper, we use GCMC and GCAP to explore some of the challenges faced by medicinal chemists when dealing with multiple waters in protein binding sites. We hope that these case studies highlight the potential of such Grand Canonical methods to solve a number of different challenges and encourage their uptake in medicinal chemistry projects.

Challenge 1: Displacing Multiple Waters in a Binding Site: A Proxy for Ligandability?

ATAD2 is a type IV bromodomain, sharing close similarity to other bromodomains such as KIAA1240 and BRD-9. Bromodomains are known to have a deep acetyl-lysine pocket (KAc) which can accommodate small molecules, although a network of four highly conserved waters often governs the extent to which small molecules are able to penetrate the pocket.

Aldeghi et al. used GCMC to study the hydration of 35 different bromodomains, including ATAD2.23 They identified ATAD2 as one of the bromodomains with the least stable water networks, and as such waters within this pocket should be more displaceable than other bromodomains.

A previous fragment crystallography campaign at AZ against ATAD2 found an unusual pyrazoloquinazolone hit, N-[3-(dimethylamino)propyl]-9-oxo-4,9-dihydropyrazolo[5,1-b]quinazoline-2-carboxamide 1, which bound in the KAc pocket with pIC50 = 5.4 while being inactive against BRD4. As shown in Figure 1, four water molecules which are found in the apo structure of ATAD2 are displaced. A similar displacement phenomenon in ATAD2 has also recently been disclosed by Bamborough et al. using a phenyl-sulfonamide warhead.24

Figure 1.

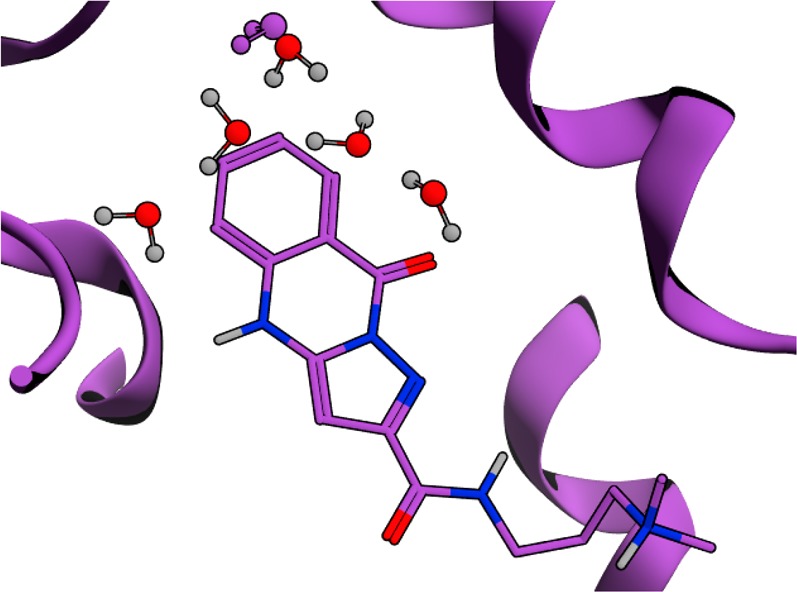
Figure 1

Open in a new tab

X-ray structure of 1 binding to the KAc binding site of ATAD2. Waters observed in the apo structure of ATAD2 are shown in red, while waters observed in the compound 1-ATAD2 holo structure are shown in purple.

We sought to validate and understand this observation using GCMC, following the procedures of Bodnarchuk and Ross et al.16,17 The crystal structure of ATAD2 was aligned against BRD4, BRD9, and TAF-1; all bromodomains which are known not to accommodate ligands deep in the KAc pocket. As shown in Figure 2, we found that the network of four waters in ATAD2 is the least stable of the bromodomains studied, with each water in the network contributing an average binding free energy of >−3 kcal/mol. This result is in good agreement with the Aldeghi study.

Figure 2.

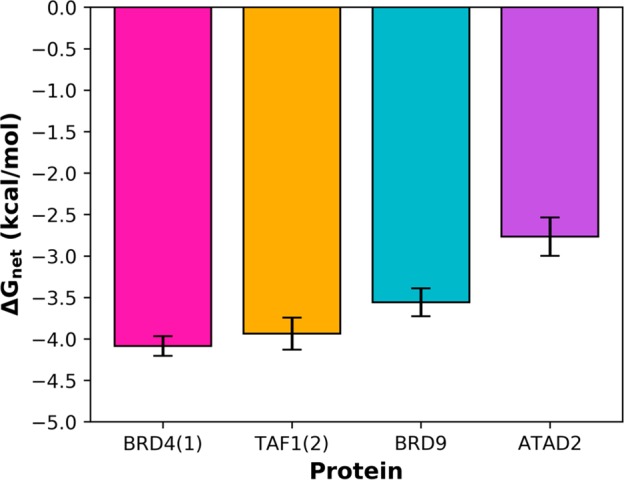
Figure 2

Open in a new tab

Average binding free energies for the four waters in the KAc pocket of BRD4, TAF1, BRD9, and ATAD2. The waters in ATAD2 are significantly less stable than the other bromodomains studied and display free energies which are consistent with them being displaced by a ligand.

Pioneering work by Barillari and coworkers used Bayesian modeling to indicate that displaceable waters typically have binding free energies in the region of −3 kcal/mol and above, which is in excellent agreement with the crystallographic and GCMC evidence.12 Our experience has shown that GCMC can help predict regions of proteins which are weakly hydrated, although rational design of ligands to displace all such waters remains a challenge.

Challenge 2: Understanding Selectivity through Bound Waters

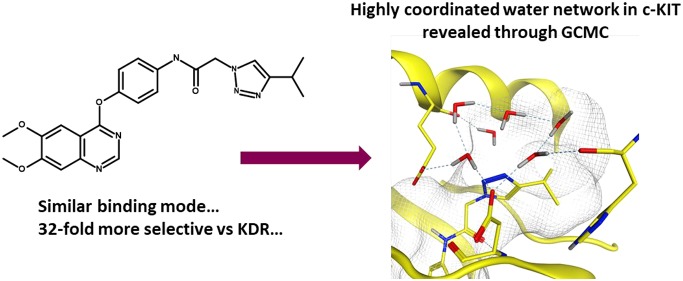
Kettle et al. reported the synthesis and characterization of a series of quinoline and quinazoline inhibitors of c-KIT,25 a key target in the treatment of gastrointestinal stromal tumors (GISTs). A key observation was made wherein the authors identified that the introduction of a 1,2,3 triazole group in the end-group of N-{4-[(6,7-dimethoxy-4-quinazolinyl)oxy]phenyl}-2-(4-isopropyl-1H-1,2,3-triazol-1-yl)acetamide (2) conferred selectivity (32-fold, 2.05 kcal/mol) against KDR, a key off-target, hypothesized due to affecting the solvation patterns relative to other triazole regioisomers. We sought to explain the origins of selectivity using GCMC, with the simulated regions highlighted in Figure 3.

Figure 3.

Figure 3

Open in a new tab

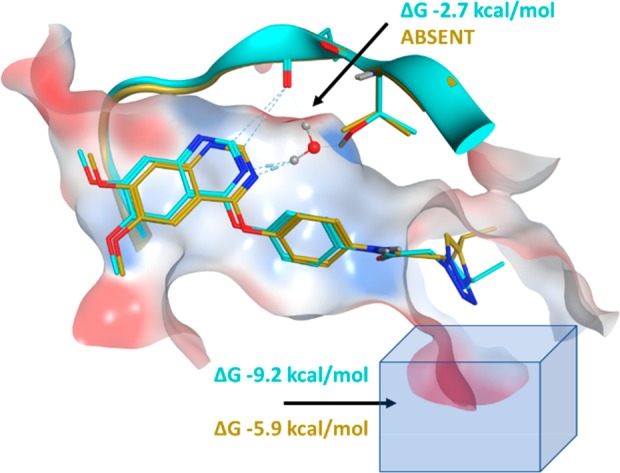
Overlay of crystal structures 6GQL (c-KIT, cyan) and 6GQQ (KDR, gold) showing the position of the crystallographic water near the T670 gatekeeper residue of c-KIT and the triazole region of 2 adjacent to the DFG pocket.

One of the key differences between c-KIT and KDR lies in their gatekeeper residues: Thr670 in c-KIT and Val916 in KDR. Crystallographic evidence suggests that there is a bridging water between the N3-quinazoline and Thr670 in c-KIT, while no water is seen in KDR. GCMC simulations were performed around the gatekeeper region of both KIT and KDR and confirm this observation. The hydrogen-bonding distance and geometry between the water and Thr670 is suboptimal, reflecting the modest affinity of the water at −2.7 kcal/mol, although enough to boost the selectivity profile over two proteins with 56% homology in the kinase domains.

To explore the hypothesis that the solvation around the triazole region of the molecule was contributing to selectivity, a cubic box of size 216 Å3 was placed in proximity to the triazole. GCMC simulations were performed for both c-KIT and KDR and revealed that, although the expected number of water molecules was the same for both proteins, the free energy difference for these networks was significantly different. The c-KIT waters were 3.3 kcal/mol more stable than those in KDR, an effect which arises from the triazole being closer to the solvent-accessible front in c-KIT.

To understand the free energy difference between the two proteins further, the predicted positions of the waters were extracted from the simulations. As shown in Figure 4, the waters in the c-KIT complex form a tightly coupled network between the backbones of Glu640 (1) and His790 (4) and the side chain of Asp810 (4) and the N2-triazole (2). A further weakly coupled water with a binding free energy of 0 kcal/mol is also observed intermittently, shown in yellow. In comparison, significantly fewer hydrogen bonds are seen within the network of KDR. Waters are seen to interact with the side chains of Glu885 (1) and Asp1046 (3), although there are few or weak contacts to the other waters or the ligand. Our experience is that GCMC gives a highly detailed atomistic view of the water networks around protein–ligand interfaces which is complementarity to crystallography.

Figure 4.

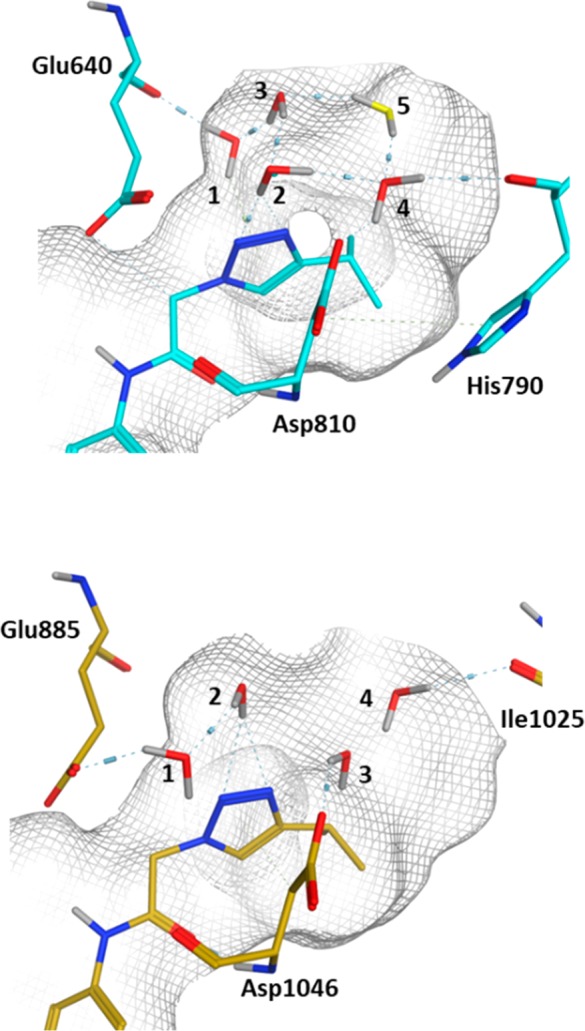
Figure 4

Open in a new tab

Predicted water networks around compound 2 in the presence of c-KIT (upper figure, cyan) and KDR (lower figure, gold). The water network in the presence of c-KIT is highly coordinated and well-positioned to form a hydrogen-bonding network, a factor which is believed to contribute to the selectivity profile.

Challenge 3: Predicting the Effects of Solvent Displacement

As previously highlighted, one of the challenges associated with displacing water molecules is what to displace it with. Techniques such as FEP have shown great utility in predicting the free energy for perturbing one group to another, but they can struggle to converge changes in the number or position of water molecules unless they are solvent facing or GCMC techniques are deployed. Historically, decisions to displace one or more water molecules with a particular functional group are typically driven by either synthetic tractability or non free energy-based approaches such as WSCORE26 or Gameplan. There exists a gap in the medicinal and computational chemist’s arsenal, which has now been addressed through combining GCMC with alchemical perturbations using GCAP or FEP+.

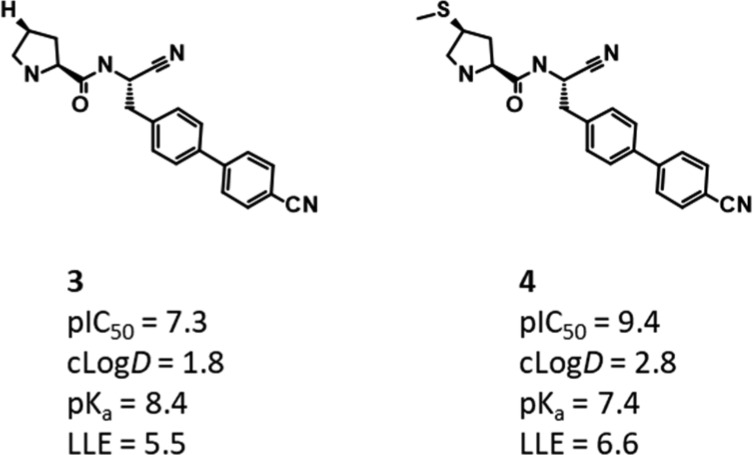
Dipeptidyl peptidase I (DPP1) is a lysosomal cysteine protease which has been implicated in diseases such as chronic obstructive pulmonary disease.27 Inhibition of DPP1 is thought to prevent the activation of neutrophil serine proteases such as cathepsin G and neutrophil elastase, which in turn prevents degradation of the extracellular matrix and inflammation. A series of pyrrolidine amino nitrile DPP1 inhibitors have recently been reported, wherein a network of water molecules has been identified in the deep, occluded part of the S2 pocket (Figure 6). These waters contact a chloride ion in the back of the pocket, which is important for DPP1 activity.28

Figure 6.

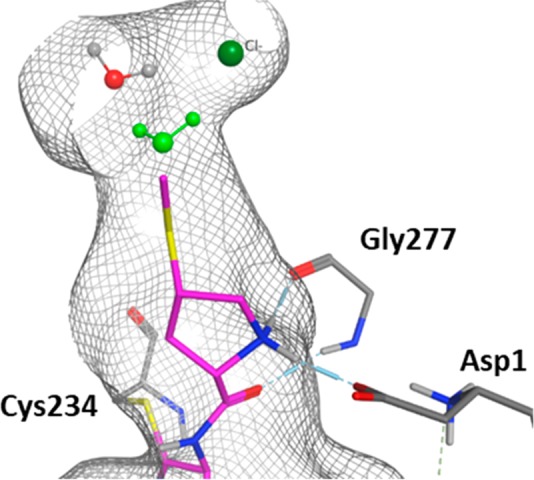
Figure 6

Open in a new tab

Enlarged view of the S2 pocket in DPP1. The SMe group in 4 displaces the green water, which remains present with the hydrogen analogue 3. A 54 Å3 box was placed over the S2 pocket for the GCAP simulations.

GCMC, free energy simulations, and conformational analysis were used to explain much of the structure-activity relationship (SAR) arising from modifications to the pyrrolidine ring in this region of the protein; however, they were unable to satisfactorily describe the effect of displacing a water through the introduction of a thiomethyl group, something which led to a >100-fold boost in potency. This SAR is shown in Figure 5, which highlights that the gain in potency for introducing the SMe group is above that from merely adding lipophilicity.

Figure 5.

Figure 5

Open in a new tab

DPP1 congeneric ligands, highlighting the gain in potency for adding a SMe group to the pyrrolidine. Although the lipophilicity increases, the gain in potency outweighs this, implying an additional effect for introducing the group.

Figure 6 shows the location of this water, which is predicted to have a binding free energy of −3.47 kcal/mol when bound to the unsubstituted pyrrolidine compound 3. This water usually makes a contact to the chloride ion and a highly stable water at the back of the pocket.

DPP1 is a system which is ideally suited for the application of GCAP. Upon switching from H in 3 to SMe in 4, the displaced water could not dissipate into the bulk during the simulation time frame, resulting in an incorrect estimate of the free energy change when traditional alchemical perturbation methods such as FEP were applied. While FEP or TI could be performed in the absence of the waters, the resultant free energy change is unlikely to be of relevance unless GCMC is performed concurrently. We therefore sought to investigate this perturbation using GCAP, following the procedures of Bruce Macdonald et al.20

The GCAP simulation is performed in two parts, akin to traditional free energy methods. First 4 was perturbed to 3 in the presence of DPP1, followed by the analogous transformation in bulk solvent. For the protein-bound leg, GCMC is performed in the S2 pocket to allow for the correct number of waters to be present at the two end-states of the simulation. The difference in free energy between the first simulation and the second is then used to calculate the relative binding free energy between the two ligands. This free energy change can then be compared to the experimental free energy change (H → SMe) of −2.86 ± 0.6 kcal/mol.

Gratifyingly, the free energy change of −3.59 ± 0.50 kcal/mol was in excellent agreement with the experimental value. Previous work on DPP1 using GCMC indicated that the optimal number of waters around compound 3 was two, while the SMe-containing compound 4 preferred a single water. As shown in Figure 7, the correct average number of waters was found for both ligands, highlighting the strength of the GCAP method.

Figure 7.

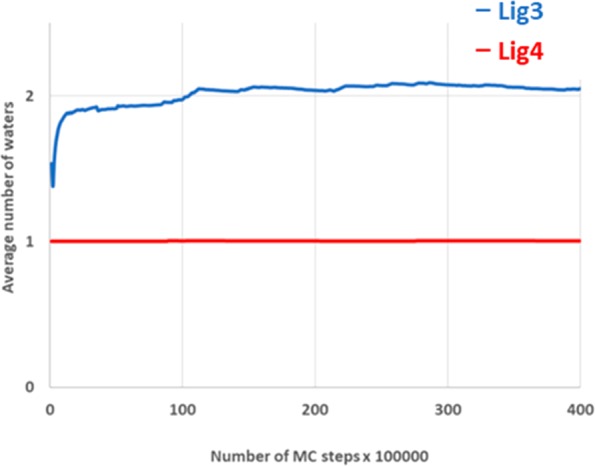
Figure 7

Open in a new tab

Plot showing the number of waters in the S2 pocket as a function of the simulation time. The average number of waters for the SMe containing 4 rapidly equilibrates to 1, while the hydrogen analogue 3 reaches convergence of 2 waters after 20 Monte Carlo steps.

To demonstrate the importance of accurate solvation in the simulations, GCAP simulations were performed in the absence of the S2 waters and without any grand canonical sampling. The free energy change (H→ SMe) under these conditions was found to be −6.88 ± 0.5 kcal/mol, representative of a large overestimation of the free energy change and highlighting the importance of applying GCMC sampling. It is significant to note that the difference between the two sets of conditions, 3.29 kcal/mol, is consistent with the difference in the binding free energy, 3.47 kcal/mol, of the displaced water calculated previously using GCMC. Such an observation indicates that the GCAP simulations were well-converged and demonstrate excellent internal consistency.

Conclusions

With recent developments in force fields, theoretical methods, and computational power, computational chemistry has evolved to help define and refine medicinal chemistry strategy. In this paper, two such methods, Grand Canonical Monte Carlo and Grand Canonical Alchemical Perturbation, have been used to help explain the druggability of a pocket, explain kinase selectivity, and to predict the free energy change upon displacing a water molecule. The three different challenges are representative of ones which are pertinent in medicinal chemistry and highlight the potential of in silico techniques in solving them. These studies, alongside numerous others in the literature, highlight that such methods are rapidly reaching maturity and can aid compound design in both lead identification and lead optimization.1,29

GCMC simulations show promise in assessing the potential ligandability of binding sites. The ATAD2 case study highlights that the waters in the S2 pocket are less stable than those of the other studied bromodomains, an observation backed up by experimental evidence showing the waters can be displaced. GCMC allows a pragmatic approach to be taken to assessing ligandability: there is no need to look at the stability of individual waters because these are naturally incorporated into the network analysis. Such a scheme is likely to be timesaving when analyzing multiple proteins within the same family.

In cases where a water molecule is targeted by ligand modification, such as the DPP1 example, we suggest that these Grand Canonical methods are used to augment the traditional medicinal chemistry process. The addition of a methyl group to a heterocycle or an alkyl chain is rarely trivial and compelling evidence is often needed before a long and challenging synthesis is embarked upon. The DPP1 example clearly demonstrates that incorrect free energies can be obtained if an incorrect number of waters is simulated, which could potentially lead to the wrong compound being prioritized for synthesis. GCAP alleviates this potential source of error and can deliver free energy estimates in good agreement with experiment.

Perhaps the most challenging use of GCMC, but the most impactful, is understanding how selectivity between two off-targets can be explained through water networks. A simple explanation for selectivity would be that ligands make distinct contacts to the different proteins, driven by sequence differences. However, in the case of the c-KIT/KDR pair discussed here, the only difference in direct contact to each protein arises from a mediating water at the gatekeeper residue; otherwise, they make similar contacts, such that visual inspection of the binding modes provides no insight on selectivity. GCMC analysis of the water network in each complex rationalizes selectivity, showing that the network around c-KIT is more stable than in KDR. It is also possible to generate visual feedback in the form of bound water positions which are not visible in the X-ray density. A similar insight was reported by Robinson et al., who explained selectivity between closely related PI3K isoforms using WaterMap.30

The three use cases explored here represent commonly recurring challenges in molecular design: can we displace one or more waters from a pocket, should we treat them as part of the protein–ligand interface, or can we interact with them directly to realize potency gains? Can water networks explain selectivity when direct interactions appear to be conserved, and is it possible to quantify the impact of displacing multiple waters? Grand Canonical techniques provide a rigorous and increasingly accessible means to study the influence of solvent on protein–ligand binding and show promise in their usage within the design process wherever structural information is available.

Acknowledgments

The authors would like to thank Jon Winter-Holt for helpful discussions and insights towards the writing of this manuscript.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsmedchemlett.9b00499.

  • Simulation details (PDF)

Author Contributions

The manuscript was written through contributions of all authors. M.S.B. and M.J.P. designed the simulations, and M.S.B. and A.H. performed the simulations.

The authors declare no competing financial interest.

Supplementary Material

ml9b00499_si_001.pdf (87.9KB, pdf)

References

  1. Bodnarchuk M. S. Water, Water, Everywhere...It’s Time to Stop and Think. Drug Discovery Today 2016, 21 (7), 1139–1146. 10.1016/j.drudis.2016.05.009. [DOI] [PubMed] [Google Scholar]
  2. Young T.; Abel R.; Kim B.; Berne B. J.; Friesner R. A. Motifs for Molecular Recognition Exploiting Hydrophobic Enclosure in Protein–ligand Binding. Proc. Natl. Acad. Sci. U. S. A. 2007, 104 (3), 808–813. 10.1073/pnas.0610202104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Abel R.; Young T.; Farid R.; Berne B. J.; Friesner R. A. Role of the Active-Site Solvent in the Thermodynamics of Factor Xa Ligand Binding. J. Am. Chem. Soc. 2008, 130 (9), 2817–2831. 10.1021/ja0771033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Sindhikara D.; Hirata F. Analysis of Biomolecular Solvation Sites by 3D-RISM Theory. J. Phys. Chem. B 2013, 117 (22), 6718–6723. 10.1021/jp4046116. [DOI] [PubMed] [Google Scholar]
  5. Grant J. A.; Pickup B. T.; Nicholls A. A Smooth Permittivity Function for Poisson-Boltzmann Solvation Methods. J. Comput. Chem. 2001, 22 (6), 608–640. 10.1002/jcc.1032. [DOI] [Google Scholar]
  6. Bayden A. S.; Moustakas D. T.; Joseph-McCarthy D.; Lamb M. L. Evaluating Free Energies of Binding and Conservation of Crystallographic Waters Using SZMAP. J. Chem. Inf. Model. 2015, 55 (8), 1552–1565. 10.1021/ci500746d. [DOI] [PubMed] [Google Scholar]
  7. Bortolato A.; Tehan B. G.; Bodnarchuk M. S.; Essex J. W.; Mason J. S. Water Network Perturbation in Ligand Binding: Adenosine A2A Antagonists as a Case Study. J. Chem. Inf. Model. 2013, 53 (7), 1700–1713. 10.1021/ci4001458. [DOI] [PubMed] [Google Scholar]
  8. Mason J. S.; Bortolato A.; Weiss D. R.; Deflorian F.; Tehan B.; Marshall F. H. High End GPCR Design : Crafted Ligand Design and Druggability Analysis Using Protein Structure, Lipophilic Hotspots and Explicit Water Networks. In Silico Pharmacol 2013, 1 (23), 1–12. 10.1186/2193-9616-1-23.25505646 [DOI] [Google Scholar]
  9. Nittinger E.; Flachsenberg F.; Bietz S.; Lange G.; Klein R.; Rarey M. Placement of Water Molecules in Protein Structures: From Large-Scale Evaluations to Single-Case Examples. J. Chem. Inf. Model. 2018, 58 (8), 1625–1637. 10.1021/acs.jcim.8b00271. [DOI] [PubMed] [Google Scholar]
  10. Bucher D.; Stouten P.; Triballeau N. Shedding Light on Important Waters for Drug Design: Simulations versus Grid-Based Methods. J. Chem. Inf. Model. 2018, 58, 692–699. 10.1021/acs.jcim.7b00642. [DOI] [PubMed] [Google Scholar]
  11. Nittinger E.; Gibbons P.; Eigenbrot C.; Davies D. R.; Maurer B.; Yu C. L.; Kiefer J. R.; Kuglstatter A.; Murray J.; Ortwine D. F.; et al. Water Molecules in Protein–ligand Interfaces. Evaluation of Software Tools and SAR Comparison. J. Comput.-Aided Mol. Des. 2019, 33 (3), 307–330. 10.1007/s10822-019-00187-y. [DOI] [PubMed] [Google Scholar]
  12. Barillari C.; Taylor J.; Viner R.; Essex J. W. Classification of Water Molecules in Protein Binding Sites. J. Am. Chem. Soc. 2007, 129 (9), 2577–2587. 10.1021/ja066980q. [DOI] [PubMed] [Google Scholar]
  13. Nguyen C. N.; Kurtzman T.; Gilson M. K. Spatial Decomposition of Translational Water-Water Correlation Entropy in Binding Pockets. J. Chem. Theory Comput. 2016, 12 (1), 414–429. 10.1021/acs.jctc.5b00939. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Adams D. J. Grand Canonical Ensemble Monte Carlo for a Lennard-Jones Fluid. Mol. Phys. 1975, 29, 307–311. 10.1080/00268977500100221. [DOI] [Google Scholar]
  15. Adams D. J. Chemical Potential of Hard-Sphere Fluids by Monte-Carlo Methods. Mol. Phys. 1974, 28, 1241–1252. 10.1080/00268977400102551. [DOI] [Google Scholar]
  16. Bodnarchuk M. S.; Viner R.; Michel J.; Essex J. W. Strategies to Calculate Water Binding Free Energies in Protein-Ligand Complexes. J. Chem. Inf. Model. 2014, 54 (6), 1623–1633. 10.1021/ci400674k. [DOI] [PubMed] [Google Scholar]
  17. Ross G. A.; Bodnarchuk M. S.; Essex J. W. Water Sites, Networks, and Free Energies with Grand Canonical Monte Carlo. J. Am. Chem. Soc. 2015, 137 (47), 14930–14943. 10.1021/jacs.5b07940. [DOI] [PubMed] [Google Scholar]
  18. Ross G. A.; Bruce Macdonald H. E.; Cave-Ayland C.; Cabedo Martinez A. I.; Essex J. W. Replica-Exchange and Standard State Binding Free Energies with Grand Canonical Monte Carlo. J. Chem. Theory Comput. 2017, 13 (12), 6373–6381. 10.1021/acs.jctc.7b00738. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Zwanzig R. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420–1426. 10.1063/1.1740409. [DOI] [Google Scholar]
  20. Bruce Macdonald H. E.; Cave-Ayland C.; Ross G. A.; Essex J. W. Ligand Binding Free Energies with Adaptive Water Networks: Two-Dimensional Grand Canonical Alchemical Perturbations. J. Chem. Theory Comput. 2018, 14 (12), 6586–6597. 10.1021/acs.jctc.8b00614. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Wahl J.; Smieško M. Assessing the Predictive Power of Relative Binding Free Energy Calculations for Test Cases Involving Displacement of Binding Site Water Molecules. J. Chem. Inf. Model. 2019, 59 (2), 754–765. 10.1021/acs.jcim.8b00826. [DOI] [PubMed] [Google Scholar]
  22. Ben-Shalom I. Y.; Lin C.; Kurtzman T.; Walker R. C.; Gilson M. K. Simulating Water Exchange to Buried Binding Sites. J. Chem. Theory Comput. 2019, 15, 2684–2691. 10.1021/acs.jctc.8b01284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Aldeghi M.; Ross G. A.; Bodkin M. J.; Essex J. W.; Knapp S.; Biggin P. C.. Large-Scale Analysis of Water Stability in Bromodomain Binding Pockets with Grand Canonical Monte Carlo. Commun. Chem. 2018, 1 ( (1), ). 10.1038/s42004-018-0019-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Bamborough P.; Chung C.; Demont E. H.; Bridges A. M.; Craggs P. D.; Dixon D. P.; Francis P.; Furze R. C.; Grandi P.; Jones E. J.; et al. A Qualified Success: Discovery of a New Series of ATAD2 Bromodomain Inhibitors with a Novel Binding Mode Using High-Throughput Screening and Hit Qualification. J. Med. Chem. 2019, 62 (16), 7506–7525. 10.1021/acs.jmedchem.9b00673. [DOI] [PubMed] [Google Scholar]
  25. Kettle J. G.; Anjum R.; Barry E.; Bhavsar D.; Brown C.; Boyd S.; Campbell A.; Goldberg K.; Grondine M.; Guichard S.; et al. Discovery of N-(4-{[5-Fluoro-7-(2-Methoxyethoxy)Quinazolin-4-Yl]Amino}phenyl)-2-[4-(Propan-2-Yl)-1 H-1,2,3-Triazol-1-Yl]Acetamide (AZD3229), a Potent Pan-KIT Mutant Inhibitor for the Treatment of Gastrointestinal Stromal Tumors. J. Med. Chem. 2018, 61 (19), 8797–8810. 10.1021/acs.jmedchem.8b00938. [DOI] [PubMed] [Google Scholar]
  26. Murphy R. B.; Repasky M. P.; Greenwood J. R.; Tubert-Brohman I.; Jerome S.; Annabhimoju R.; Boyles N. A.; Schmitz C. D.; Abel R.; Farid R.; et al. WScore: A Flexible and Accurate Treatment of Explicit Water Molecules in Ligand-Receptor Docking. J. Med. Chem. 2016, 59 (9), 4364–4384. 10.1021/acs.jmedchem.6b00131. [DOI] [PubMed] [Google Scholar]
  27. Guay D.; Beaulieu C.; Percival M. D. Therapeutic Utility and Medicinal Chemistry of Cathepsin C Inhibitors. Curr. Top. Med. Chem. 2010, 10 (7), 708–716. 10.2174/156802610791113469. [DOI] [PubMed] [Google Scholar]
  28. Käck H.; Doyle K.; Hughes S. J.; Bodnarchuk M. S.; Lönn H.; Van De Poël A.; Palmer N. DPP1 Inhibitors: Exploring the Role of Water in the S2 Pocket of DPP1 with Substituted Pyrrolidines. ACS Med. Chem. Lett. 2019, 10, 1222. 10.1021/acsmedchemlett.9b00261. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Spyrakis F.; Ahmed M. H.; Bayden A. S.; Cozzini P.; Mozzarelli A.; Kellogg G. E. The Roles of Water in the Protein Matrix: A Largely Untapped Resource for Drug Discovery. J. Med. Chem. 2017, 60 (16), 6781–6828. 10.1021/acs.jmedchem.7b00057. [DOI] [PubMed] [Google Scholar]
  30. Robinson D.; Bertrand T.; Carry J. C.; Halley F.; Karlsson A.; Mathieu M.; Minoux H.; Perrin M. A.; Robert B.; Schio L.; et al. Differential Water Thermodynamics Determine PI3K-Beta/Delta Selectivity for Solvent-Exposed Ligand Modifications. J. Chem. Inf. Model. 2016, 56 (5), 886–894. 10.1021/acs.jcim.5b00641. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ml9b00499_si_001.pdf (87.9KB, pdf)

Articles from ACS Medicinal Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES