Abstract
Experimental studies of cognitive detriments in mice and rats after proton and heavy ion exposures have been performed by several laboratories to investigate possible risks to astronauts exposed to cosmic rays in space travel and patients treated for brain cancers with proton and carbon beams in Hadron therapy. However, distinct radiation types and doses, cognitive tests and rodent models have been used by different laboratories, while few studies have considered detailed dose-response characterizations, including estimates of relative biological effectiveness (RBE). Here we report on the first quantitative meta-analysis of the dose response for proton and heavy ion rodent studies of the widely used novel object recognition (NOR) test, which estimates detriments in recognition or object memory. Our study reveals that linear or linear-quadratic dose-response models of relative risk (RR) do not provide accurate descriptions. However, good descriptions for doses up to 1 Gy are provided by exponentially increasing fluence or dose-response models observed with an LET dependence similar to a classical radiation quality response, which peaks near 100–120 keV/μm and declines at higher LET values. Exponential models provide accurate predictions of experimental results for NOR in mice after mixed-beam exposures of protons and 56Fe, and protons, 16O and 28Si. RBE estimates are limited by available X-ray or gamma-ray experiments to serve as a reference radiation. RBE estimates based on use of data from combined gamma-ray and high-energy protons of low-LET experiments suggest modest RBEs, with values <8 for most heavy ions, while higher values <20 are based on limited gamma-ray data. In addition, we consider a log-normal model for the variation of subject responses at defined dose levels. The log-normal model predicts a heavy ion dose threshold of approximately 0.01 Gy for NOR-related cognitive detriments.
INTRODUCTION
Health risks including cancer, cataracts and detriments in cognitive performance and other central nervous system (CNS) effects are a concern for astronauts exposed to protons and heavy ions in spaceflight (1), as well as for cancer patients receiving Hadron therapy (2). Due to the absence of heavy ion epidemiology data, except for cataract risks (3, 4), the data from epidemiology studies of photon exposures has been combined with that of experimental studies in small animal and cell culture models to estimate radiation quality and dose-rate modifiers for use in cancer risk assessments (5, 6). Heavy ions produce distinct spatial patterns of ionization at low dose compared to photons, including clusters of ionization in biomolecules and columns of heavily damaged cells (1, 7, 8). Concerns about CNS effects, including detriments in cognition, were raised after Apollo astronauts reported experiencing light flashes, which led to discussions of neuronal cell loss and microlesions from the passage of single heavy ions in brain tissue (9, 10), while CNS risks are not expected for low dose photon exposures (1). These early concerns were not borne out, as cell loss in later studies was found to be minimal at low heavy ion doses [reviewed in (1, 7)]; however, a large number of mechanistic studies and, importantly, various tests of cognitive detriments in mice and rats [reviewed in (1, 7, 8)] continue to suggest the possibility of low-dose risks to the CNS from heavy ion exposure.
Two major problems in the prediction of heavy ion CNS risks for astronauts and patients have been the lack of dose-response data and models in rodent studies, and the development of an approach for extrapolation from animal models to predict human cognitive risks. While numerous cognitive studies in mice and rats have been reported, these studies have used a variety of cognitive tests, a small number of doses (typically one or two), particle types and LET values, and a range of animal ages and postirradiation times. Here we report on a meta-analysis of proton and heavy ion rodent studies in which the widely used novel object recognition (NOR) test was employed; the NOR test provides estimates of detriments in recognition or object memory. We compiled a database from the NOR data collected after photon, proton and heavy ion exposures, and formulated a relative risk (RR) model for use when considering several dose- or fluence-response models, which are fitted to the data and tested for goodness of fit. We explored several dose-response models and the use of linear energy transfer (LET) or the density of a particle track which scales as Z2/β2, where Z is the ion charge number and β is the ion velocity scaled to the speed of light as the model physical descriptors. Because the ions considered are at high kinetic energy (>100 MeV/u), we ignore any differences in effective charge number, Z* and Z, while Z* accounts for atomic screening of particles as they slow down. Results are then discussed and future outlook for meta-analysis of results from rodent studies of other cognitive tests are briefly described. The use of a RR model is a common approach for extrapolation of experimental data to humans, and its application should reflect the strengths or weaknesses of rodent models in representing human cognitive risks.
METHODS
Relative Risk for Novel Object Recognition (RRNOR)
Cognitive performance of learning and memory evaluated using NOR measures the ability of the subject to learn and remember prior interaction with an object after a delay interval. The NOR test can be assessed by the differences in exploration time of novel and familiar object. In this work, we have defined the result of the NOR test as a “familiar” to “novel” object recognition ratio (FNR),
| (1) |
where, in general, a subject animal that spends more time exploring the novel than familiar objects gives a FNR <1. Meanwhile, the effect of radiation on the NOR test is expressed as a relative risk (RR), defined by Eq. (2).
| (2) |
A memory deficit caused by radiation (IR) is evidenced by failure to spend more time exploring the novel object, resulting in FNRIR > FNRcontrol. Therefore, radiation exposures that have no effect on memory gives RRNOR = 1, while radiation-induced memory dysfunction results in RRNOR > 1.
In our analysis, to gather the available experimental data about the effects of radiation exposures on cognition assessed through a NOR test, we performed a PubMed search using the keywords “cognition” and “novel object recognition” with “radiation” or “whole body radiation” or “X-rays” or “gamma rays” or “protons” or “heavy ions”. The number of published articles identified were 42, 12, 2, 3, 2 and 1, respectively. Based on our knowledge of the literature, a few additional articles were identified beyond the PubMed search. Some articles were dismissed, since we limited our considerations to NOR tests involving radiation exposures of male rodents or combination of male and female rodents that gave nonsignificant differences in test results between genders. These data for a variety of radiation types are provided in Table 1 based on references (11–25). The calculated relative risks for each radiation type adjust for differences in subject animal and age; however, other considerations on the impact of such differences are briefly discussed.
TABLE 1.
Published Studies with Experimental Novel Object Recognition Test (NOR) Data for Different Doses and Types of Radiation and Rodent Models
| Radiation type |
Kinetic energy (MeV/u) |
LET (keV/μm) |
Animal type | Sex | Age at irradiation (days) |
Time postirradiation (days) of NOR test |
Refs. |
|---|---|---|---|---|---|---|---|
| 56Fe | 600 | 181 | Sprague-Dawley rats | M | 60 | 90 360 |
(11) |
| C57BL6/J mice | M | 180 | 14 140 |
(12) | |||
| M, F | 60 | 14 | (13) | ||||
| M | 60 | 30 90 |
(14) | ||||
| M | 90 | 150 270 |
(15) | ||||
| 1,000 | 150 | Sprague-Dawley rats | M | 60 | 90 | (16) | |
| 48Ti | 500 | 134 | Sprague-Dawley rats | M | 60 | 90 | (17, 18) |
| 600 | 120 | Tg(Thy1-EGFP) MJrsJ mice | M | 180 | 42 | (19) | |
| 84 168 |
(20) | ||||||
| 1,100 | 106 | Sprague-Dawley rats | M | 60 | 210 510 |
(11) | |
| 28Si | 300 | 69 | C57BL6/J mice | M | 90 | 150 270 |
(15) |
| 375 | 61 | Sprague-Dawley rats | M | 60 | 82.5 | (17, 18) | |
| 380 | 61 | 120 | (11) | ||||
| 380 | 61 | 300 | |||||
| 600 | 51 | 150 | |||||
| 600 | 51 | 270 | |||||
| 1,000 | 44 | 120 | |||||
| 1,000 | 44 | 390 | |||||
| 16O | 600 | 16 | Tg(Thy1-EGFP) MJrsJ mice | M | 180 | 84 168 |
(20) |
| 600 | 16 | Sprague-Dawley rats | M | 60 | 60 300 |
(11) | |
| 1,000 | 14 | 120 360 |
|||||
| 12C | 290 | 13 | Sprague-Dawley rats | M | 60 | 30 | (11) |
| 150 | (17, 18) | ||||||
| 330 | (11) | ||||||
| 4He | 250 | 1.6 | B6D2F1 mice | M, F | 150 | 90 | (21) |
| 1H | 150 | 0.5 | Sprague-Dawley rats | M | 60 | 60 | (22) |
| C57BL6/J mice | M | 60 | 30 | (23) | |||
| 250 | 0.4 | M | 60 | 30 90 |
(24) | ||
| M | 180 | 14 140 |
(25) | ||||
| 1,000 | 0.22 | Sprague-Dawley rats | M | 60 | 60 | (22) | |
| 120 390 |
(11) | ||||||
| C57BL6/J mice | M | 90 | 150 270 |
(15) | |||
| Gamma ray | - | - | C57BL6/J mice | M | 90 | 150 270 |
(15) |
| M | 60 | 90 | (25) | ||||
Models of RRNOR for Different Radiation Type
Based on experimental NOR test results (Table 1), relative risks for novel object recognition (RRNOR) for all radiation types were calculated using Eq. (2) and these computed RRNOR values were made to globally fit to linear-quadratic (LQ) (for all doses) and linear and exponential (for doses ≤1 Gy) dose-response models. Variations of the exponential model (“Exp model”), including LET (L, keV/μm), dose D in Gy and time postirradiation (tpIR, days) dependence, were examined. The functional forms of dose-response models used are as follows:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where RR0 is the “baseline” relative risk or RR computed from control or sham subjects.
Calculated RRNOR values were also globally fitted to a track structure model using particle fluence F (in units of μm–2).
| (8) |
where , with σ0, κ and m possible fitting parameters.
Finally, individual ion data were fitted to a linear (fluence) model with a model coefficient A1 fitted as a Gaussian function of LET or Z2/β2.
| (9) |
| (10) |
Using the relationship of fluence and dose, , with D in Gy and L in keV/μm, the fluence model coefficient A1 can also be expressed in terms of that can be used to compute for the relative biological effectiveness (RBE) as shown below:
| (11) |
| (12) |
Equation (11) uses gamma rays as reference radiation, however because of the scarcity of gamma-ray data Eq. (12) utilizes the average of gamma rays and low-LET protons as reference radiation.
Finally, computed RRNOR values for each radiation dose (independent of radiation type) were fitted to a log-normal distribution as described by Eq. (13):
| (13) |
Parameters of log-normal distribution, D0 and σ, were plotted against radiation dose and fitted to a power and exponential functions, respectively, in the form of:
| (14) |
| (15) |
Data Fitting and Statistical Analysis
All data fitting and statistical analyses were done using STATA/SE version 14.2 (StataCorp LLC, College Station, TX) and MATLAB® R2015a (MathWorks®, Natick, MA). Global fitting across all radiation types was done in Stata using nonlinear least-squares data fitting. The best fit for different models was determined using adjusted R2 and the Akaike information criteria (AIC) and Bayesian information criteria (BIC) that consider the number of model parameters. The model with highest adjusted R2 and lowest AIC and BIC provided the best fit to data. Linear model fitting for each radiation type and log-normal distribution for each radiation dose were also performed using Stata. Nonlinear least-squares fitting of Gaussian function and log-normal distribution parameters were accomplished using MATLAB built-in curve fitting tool. All data fitting was weighted by the inverse of the variance.
RESULTS
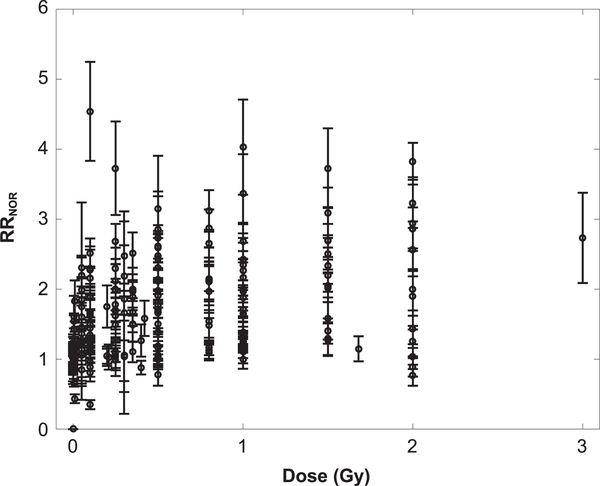
In Table 1, a summary is provided of the available experimental data on NOR tests after whole-body exposures from a variety of radiation types. Figure 1 shows a plot of the RRNOR values versus dose determined from experiments (11–25). These experimental data have utilized different rodent species and strains with irradiations at various ages. Therefore, we have assumed in our analysis that the computed relative risks adjust for differences in subject animal and age. However, if more experimental data are made available that invalidate this assumption, a normalizing factor can be added to the model to accommodate the differences in the aforementioned factors.
FIG. 1.
Dose-response plot of relative risk for novel object recognition (RRNOR) computed from experimental data. Total number of data points is 236 and all error bars are standard error of the mean (SEM).
The RRNOR values were made to globally fit to several dose-response models with results for the LQ and linear models shown in Table 2 and exponential models shown in Table 3. Linear and exponential dose-response and sigma-fluence models used RRNOR values for doses up to 1 Gy only, to focus on the low doses of space radiation exposures or the periphery of a tumor volume, and because of the saturation observed at higher doses for individual ions. The linear and LQ models led to poor fits to the NOR data sets considered, while the exponential and sigma-fluence models provided very good agreement based on the high adjusted R2 and low AIC and BIC values. The Exp model 2, with LQ dependence on LET, improved the fits compared to Exp model 1, which suggests a saturation or declining response at high-LET values (>100 keV/μm).
TABLE 2.
Parameters for Global Fitting of RRNOR
| Parameter | LQ model | Linear model |
|---|---|---|
| RR0 | 1.04 ± 0.03 (<10–4) | 1.06 ± 0.03 (<10−4) |
| α (Gy−1) | 0.60 ± 0.14 (<10–4) | 0.36 ± 0.06 (<10−4) |
| β (Gy−2) | −0.18 ± 0.09 (0.049) | - |
| Adjusted R2 | 0.1650 | 0.1244 |
| AIC | 190.70 | 137.66 |
| BIC | 201.09 | 144.35 |
TABLE 3.
Parameters for Global Fitting of RRNOR in Several Exponential Models
| Exponential models | |||
|---|---|---|---|
| Parameter | Exp model 1 | Exp model 2 | Exp model 3 |
| RR0 | 1.02 ± 0.03 (<10−4) | 1.06 ± 0.03 (<10−4) | 1.03 ± 0.04 (<10−4) |
| α0 (Gy−1) | 0.78 ± 0.15 (<10−4) | 0.22 ± 0.07 (0.002) | 0.22 ± 0.07 (0.002) |
| α1 (Gy-keV/μm)−1 | - | 0.0052 ± 0.0022 (0.019) | 0.0049 ± 0.0022 (0.029) |
| α2 (Gy–1(keV/μm−1)−2) | - | −0.00003 ± 0.00001 (0.013) | −0.00003 ± 0.00001 (0.020) |
| ρ(day−1) | - | - | 0.00022 ± 0.00019 (0.232) |
| Adjusted R2 | 0.9988 | 0.9989 | 0.9989 |
| AIC | 139.17 | 136.65 | 137.25 |
| BIC | 145.86 | 150.02 | 153.96 |
| Sigma-fluence model | |||
| Parameter | m = 2 | m = 3 | m = “fitting parameter” |
| m | 2 | 3 | 1.30 ± 0.14 (<10−4) |
| RR0 | 1.08 ± 0.03 (<10−4) | 1.08 ± 0.03 (<10−4) | 1.06 ± 0.03 (<10−4) |
| σ0 (μm2) | 4.24 ± 1.05 (<10−4) | 3.93 ± 0.85 (<10−4) | 6.01 ± 2.38 (0.012) |
| κ | 130.9 ± 33.2 (<10−4) | 87.88 ± 16.41 (<10−4) | 304.3 ± 174.0 (0.082) |
| Adjusted R2 | 0.9988 | 0.9989 | 0.9989 |
| AIC | 137.72 | 136.65 | 136.38 |
| BIC | 147.75 | 150.02 | 149.75 |
Note. Models that fit the data best are indicated in bold type.
Studies reported have used various postirradiation times, from 14 days to more than one year. We next used the exponential dose-response model to evaluate the model dependence to LET and postirradiation time (tpIR). The use of an exponential dependence on postirradiation time [Eq. (7)] could reflect either an increase or decrease in RRNOR with time after irradiation as determined by the fitted value of ρ. However, Exp model 3 did not lead to a significant dependence on postirradiation time, tpIR (fitting parameter ρ has a P value=0.232) and did not improve the agreement of the model to experiments compared to Exp model 2. Adding a covariate for postirradiation times of 14 days or more did not improve the fits to these data, suggesting that only a weak dependence occurs.
We next considered the sigma-fluence model, which utilizes the track structure parameter Z2/β2 that uses the density of a particle track (26, 27) as the physical descriptor, while the width of the particle track for high-energy particles is much larger than biomolecules or neuronal structures that would likely be considered (28). The sigma-fluence model led to a slightly better fit compared to exponential models with m as “fitting parameter”. In Supplementary Fig. S1 (https://doi.org/10.1667/RR15419.1.S1), comparison of experimental data to sigma-fluence modeling results (with mfit = 1.30) shows a reasonable fit to all ions except titanium (Ti). The value of σ0 of 6 μm2 and low value of mfit of 1.30 suggests a damage mechanism involving ionization clusters in targets with radii of approximately 1.4 μm, while the improvement of the exponential dose-response models compared to linear or LQ models suggests that damage increases as the number of targets damaged increases exponentially. The global fits for both the Exp models and sigma-fluence models provided better fits for ions with Z = 14 and below because of the larger number of data points for these ions compared to the fewer data points for Ti and iron (Fe) ions.
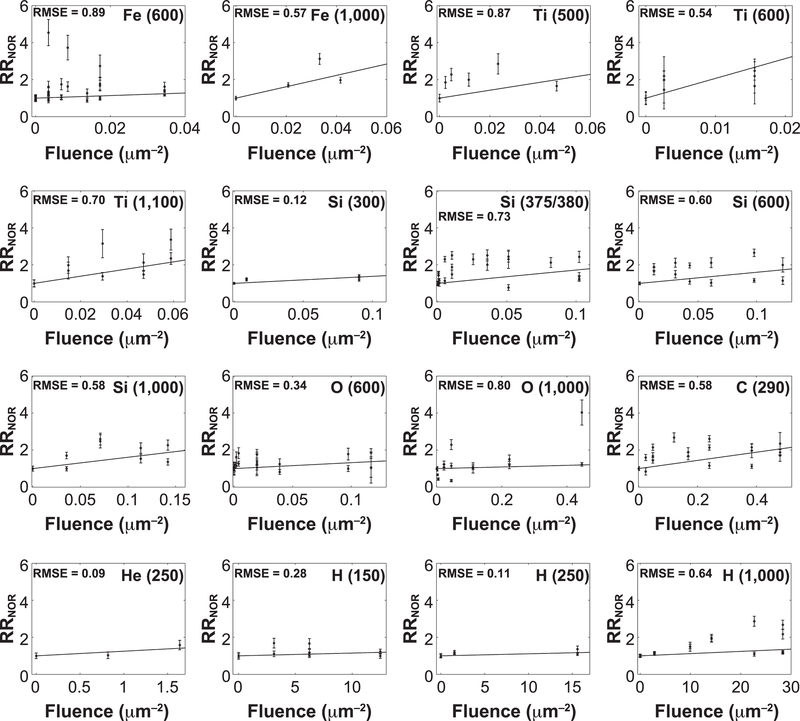
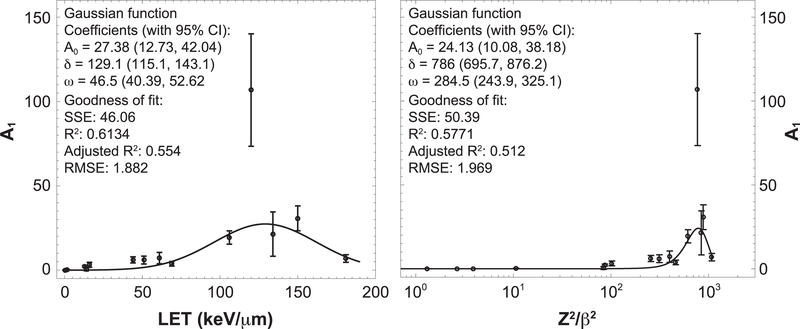
We also performed a separate linear fitting of computed RRNOR values for each radiation type (fluence model) for doses up to 1 Gy. The kinetic energy, LET and Z2/β2 for each radiation type, together with fluence model coefficient A1, including related coefficient A2 and calculated RBE values (RBE1 and RBE2), are presented in Table 4. In the fluence model fitting, we have set RR0 = 1, which led to excellent fits (adjusted R2 = 0.9838 – 1.0) and one less fitting parameter for each radiation type. Figure 2 shows the comparison of modeling results with experimental data, where it can be recognized that the fluence model provides an acceptable fit (RMSE, 1.0) for each radiation type being considered. In Fig. 3, the fluence model coefficient A1 is plotted against LET and Z2/β2, and both are fitted to a Gaussian function. A noticeable outlier at LET ¼ 120 keV/ μm or Z2/β2 = 770.7 that corresponds to 48Ti (600) can be seen in the plot. It is possible that this is due to the large error of individual data and the lack of data for 48Ti (600) at relatively higher fluence values, since available experimental data is only up to 0.015 μm−2 compared to other radiation types with data up to 0.034 – 28 μm−2 (see Fig. 2). In any case, Gaussian fitting of fluence model coefficient A1 as a function of both LET and Z2/β2 give little weight for this particular data point due to its large error.
TABLE 4.
Parameters for Fluence Model of RRNOR for each Radiation Type and Computed Relative Biological Effectiveness (RBE)
| Radiation type | Kinetic energy (MeV/u) |
LET (keV/μm) |
Z2/β2 | A1 (μm2) | A2 (Gy−1) | RBE1 | RBE2 |
|---|---|---|---|---|---|---|---|
| 56Fe | 600 | 181 | 1,076.4 | 6.92 ± 2.23 (0.004) | 0.24 ± 0.22 | 3.61 ± 1.39 | 1.25 ± 0.64 |
| 1,000 | 150 | 882.81 | 30.7 ± 7.38 (0.025) | 1.28 ± 0.73 | 19.4 ± 6.21 | 6.69 ± 3.11 | |
| 48Ti | 500 | 134 | 842.46 | 21.4 ± 13.2 (0.165) | 1.00 ± 1.58 | 15.1 ± 9.81 | 5.21 ± 3.82 |
| 600 | 120 | 770.65 | 106.8 ± 33.4 (0.013) | 5.55 ± 1.86 | 84.2 ± 31.8 | 29.0 ± 14.7 | |
| 1,100 | 106 | 614.08 | 19.4 ± 3.95 (0.001) | 1.14 ± 0.38 | 17.3 ± 5.08 | 5.96 ± 2.67 | |
| 28Si | 300 | 69 | 460.17 | 3.79 ± 1.36 (0.039) | 0.34 ± 0.24 | 5.19 ± 2.16 | 1.79 ± 0.96 |
| 375/380 | 61 | 398.73 | 7.19 ± 3.38 (0.045) | 0.74 ± 0.69 | 11.1 ± 5.75 | 3.84 ± 2.37 | |
| 600 | 51 | 312.08 | 5.39 ± 2.33 (0.023) | 0.73 ± 0.44 | 11.1 ± 4.92 | 3.83 ± 2.13 | |
| 1,000 | 44 | 255.96 | 6.12 ± 1.82 (0.008) | 0.87 ± 0.55 | 13.2 ± 4.80 | 4.54 ± 2.26 | |
| 16O | 600 | 16 | 101.90 | 3.19 ± 1.46 (0.039) | 1.24 ± 0.61 | 18.9 ± 9.51 | 6.50 ± 3.95 |
| 1,000 | 14 | 83.58 | 0.44 ± 0.82 (0.604) | 0.20 ± 0.89 | 2.97 ± 5.57 | 1.03 ± 1.95 | |
| 12C | 290 | 13 | 86.43 | 2.21 ± 0.56 (0.001) | 1.06 ± 0.42 | 16.1 ± 5.31 | 5.55 ± 2.62 |
| 4He | 250 | 1.6 | 10.62 | 0.25 ± 0.11 (0.142) | 0.98 ± 0.74 | 14.8 ± 7.22 | 5.10 ± 3.03 |
| 1H | 150 | 0.5 | 3.90 | 0.015 ± 0.008 (0.100) | 0.19 ± 0.25 | 2.84 ± 1.63 | 0.98 ± 0.65 |
| 250 | 0.4 | 2.66 | 0.011 ± 0.005 (0.068) | 0.17 ± 0.06 | 2.60 ± 1.30 | 0.90 ± 0.54 | |
| 1,000 | 0.22 | 1.31 | 0.012 ± 0.004 (0.016) | 0.34 ± 0.31 | 5.16 ± 2.04 | 1.78 ± 0.93 | |
| Gamma ray | - | - | - | - | 0.066 ± 0.014 | 1.00 ± 0.30 | 0.35 ± 0.16 |
FIG. 2.
Comparison of experimental data with modeling results of separate linear fitting to fluence model. Absolute goodness of fit of data to model is measured by root mean squared error (RMSE).
FIG. 3.
Fluence model coefficient A1 as a function of radiation LET and Z2/β2. Goodness of fit is measured by the sum of the squared errors (SSE), correlation coefficients (R2 and adjusted R2) and root mean square error (RMSE).
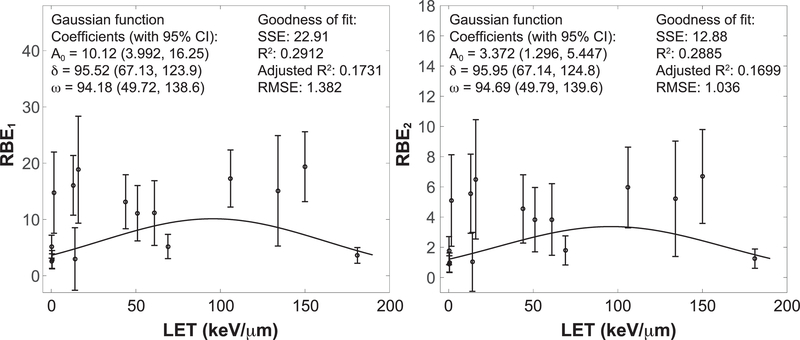
Relative biological effectiveness (RBE) with reference to gamma rays and to average of gamma rays and protons can be computed using Eqs. (11) and (12), respectively. The latter choice was considered because of the scarcity of reports on gamma rays, especially at low to moderate doses (<2 Gy) needed for RBE estimates. These calculated RBE values were plotted against LET, as shown in Fig. 4. The fitting of RBE values to a Gaussian function is done by excluding the titanium outlier data point at LET=120 keV/μm.
FIG. 4.
Relative biological effectiveness (RBE) computed using fluence model with reference to gamma rays (left) and with reference to the average of square error (RMSE).gamma rays and protons (right). Goodness of fit is measured by sum of the squared errors (SSE), correlation coefficients (R2 and adjusted R2) and root mean
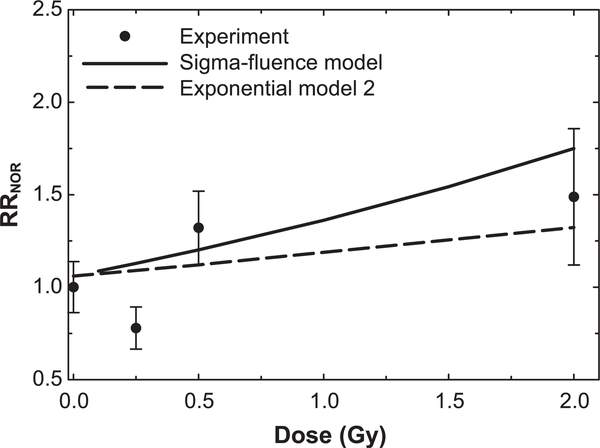
In space, mixed radiation fields of many particle species and kinetic energies occur (29), and mixed fields occur in Hadron therapy due to beam and target fragmentation. Recently, the Raber laboratory has considered mixed component radiation fields comprised of several ion types (14, 30). Raber et al. (30) studied male and female B6D2F1 mice (4 to 6 months old) that received whole-body mixed field irradiation delivered in several minutes of 20%, 20% and 60% of 28Si (263 MeV/u), 16O (250 MeV/u) and protons (1,000 MeV), respectively. We made predictions using the Exp model 2 and sigma-fluence model and compared these to the data for the male mice (Fig. 5). Good agreement of the sigma-fluence model was found, while the Exp model 2 tended to underestimate the experimental RRNOR values. In a second experiment, male C57Bl6/J mice (2 months old) received 0.1 Gy proton irradiation (150 MeV) and 24 h later received 0.5 Gy 56Fe irradiation (600 MeV/u). The NOR test was performed at 30 or 90 days postirradiation, with RRNOR values of 0.987 ± 0.079 and 1.198 ± 0.181, respectively. The Exp model 2 and sigma-fluence model provided predictions of 1.146 and 1.210, respectively, however, they did not include postirradiation time as a variable, as noted above.
FIG. 5.
Comparison of relative risks (RRNOR) from prediction of models to experiment by Raber et al. (30) for male B6D2F1 mice (4 to 6 months old) irradiated with mixed field, delivered in several minutes, of 20%, 20% and 60% of 28Si (263 MeV/u), 16O (250 MeV/u) and protons (1,000 MeV), respectively, to several total doses. The novel object recognition (NOR) test was administered 2 months postirradiation.
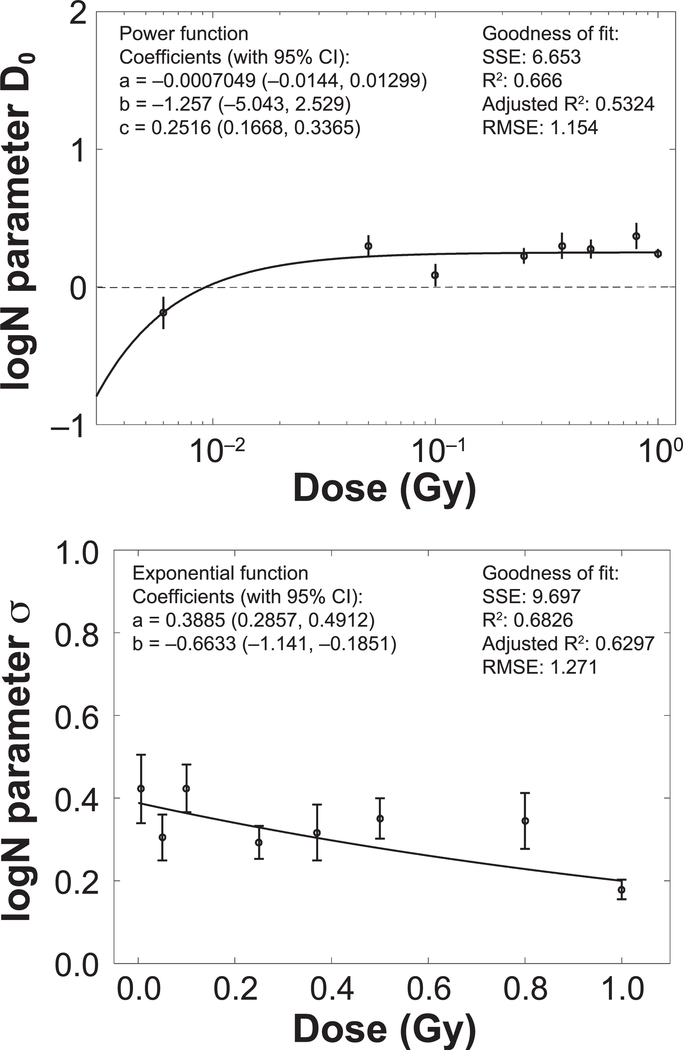
Several published studies have indicated that there are large individual variations in cognitive responses to radiation (31–33). Furthermore, our RBE analysis did not suggest a strong dependence of RRNOR on radiation quality among different heavy ion species. We therefore considered the logN-dose model [Eq. (13)], where the values of the relative risk for novel object recognition (RRNOR) are computed for each radiation dose (independent of radiation type). As shown in Fig. 6, parameters of log-normal distribution of RRNOR values (D0 and σ) are plotted against radiation dose, where power and exponential functions give reasonable fit for D0 and σ, respectively. These analyses suggest a median threshold dose in detriments of novel object recognition of approximately 0.01 Gy (1 rad) for heavy ions, while the log-normal distribution predicts the distribution of values for more and less sensitive subjects.
FIG. 6.
Parameters (D0 and σ) for log-normal distribution as a function of dose. Goodness of fit is measured by the sum of the squared errors (SSE), correlation coefficients (R2 and adjusted R2) and root mean square error (RMSE).
DISCUSSION
To our knowledge, this is the first quantitative analysis of the dose and radiation quality dependence of experimental data reporting on detriments in novel object recognition. NOR tests are used to assess detriments in recognition memory (34–36); memory sensitivity is related to the medial temporal lobe and perirhinal cortex with certain roles for the hippocampus and prefrontal cortex (35, 36). The meta-analysis reported here integrates a large number of studies (11–25) that considered different rodent models, ages, postirradiation times, doses and particle types. There were also differences among laboratories in the application of the NOR test, including differences in training protocols and objects utilized (11–25). Of the over 236 data points identified, only irradiation with 56Fe (600 MeV/u) at 0.1 and 0.5 Gy and 16O (600 MeV/u) at 0.05 Gy were common data points in different experiments reported, although here difference in animal age and time after exposure occurred. This limited the possibility to apply a random effects model. Our approach is essentially a fixed effects model, while using the relative risks between irradiated and control groups as the approach to adjust for experimental differences and to allow a global analysis of the diverse data sets.
Whole-body exposures to radiation occur in space travel, while head-only irradiation involving dose location to the tumor volume occurs in Hadron therapy with proton or carbon beams and for conventional radiation. The data considered herein for mice (12, 13, 19–24) were acquired from whole-body irradiation experiments, while the data of Rabin et al. (16–18, 25) were acquired from head-only (shielded body) irradiations. Recently Rabin et al. have considered differences in whole-body, head-only and body-only irradiations for several cognitive tests in rats using 16O (37) irradiation and differences in whole-body and head-only 4He irradiation (38). No effect on NOR was observed after 16O body-only irradiation (37). The differences in NOR test results were small between head-only- and whole-body-irradiated groups, while larger differences were observed for other cognitive tests. Immune cells are radiosensitive (8, 39), while RBEs for heavy ion damage of hematopoietic cells are generally low (<5) (8, 40). Circulation of damaged immune cells in whole-body irradiation could increase damage to the brain above what is observed in head-only irradiation. However, we expect differences between head-only and whole-body irradiation to be small at low doses (<1 Gy), which was the focus of the current study.
We focused data from irradiated male animals or data sets where male and female results were similar. Data for gamma rays was limited (15, 25) with no detailed dose-response data reported. In another published study (41), 6-month-old female C57BL/6 mice received 2, 5 and 8 Gy irradiation and were subjected to NOR test at 48 h postirradiation; a significant detriment was observed at all doses with the largest effect after 2 Gy. The 48-h time point is expected to be earlier than the onset of an inflammatory response [see (42)] and therefore could involve a distinct mechanism from the data sets considered herein, which are at 14 days postirradiation or longer. Tests for the effects of differences among laboratories due to variable time after irradiation for the NOR test were not significant when comparing Exp model 2 and Exp model 3, and a similar result was found for the sigma-fluence model (result not shown).
The results described suggest that for doses up to 1 Gy of heavy ions or protons, an exponentially increasing dose or fluence response model provides an excellent global fit to the RRNOR reported in heavy ion and proton studies from a variety of rodent models. Linear or LQ models that are often used to fit DNA damage related end points, such as mutation and cell kill, were found to be inadequate to describe these data. We suggest that the exponentially increasing response models reflect the nature of neural networks where dose-dependent damage to an increasing number of synapses, dendrites and neurons increases the severity and probability of the cognitive impairment. The LET dependence of the Exp model 2 leads to a negative coefficient (α2) reflecting that the LET dependence of the response gets weaker at high LET. The track structure related model (sigma-fluence model) includes a saturation effect with the peak effectiveness for ions with Z2/β2 near 300, and suggests a target on the order of 1.4 μm in radii, which would be similar to the size of targets such as synapses including neurotransmitters, or dendrite associated mitochondria.
In conclusion, we developed an accurate model of the dose or fluence response for the relative risks for detriments in novel object recognition. Published studies using mice and rats receiving various heavy ion species and doses have been performed, in which a variety of cognitive tests other than NOR were employed. These include studies of behavioral toxicity (43), hippocampal function and impaired neurogenesis (44) and spatial memory and executive function (32, 45). In future work, the meta-analysis approach used here will be applied to spatial memory data, and we will investigate the variability of the dose response and radiation quality dependence for specific cognitive detriments, including differences in whole-body and partial-body irradiation. Other research will be undertaken with the goal of predicting relative risks for cognitive detriments using full galactic cosmic ray simulations in a variety of space mission scenarios.
Supplementary Material
ACKNOWLEDGMENTS
We thank Drs. Jacob Raber, Bernard Rabin, Charles Limoli and Vipan Parihar for sharing numerical data from their experiments. This research was supported by the National Institutes of Health-National Cancer Institute (NIH-NCI; grant no. 1RO1CA208526–01).
Footnotes
Editor’s note. The online version of this article (DOI: 10.1667/RR15419.1) contains supplementary information that is available to all authorized users.
REFERENCES
- 1.Information needed to make radiation protection recommendations for space missions beyond low-earth orbit. NCRP Report No. 153. Bethesda, MD: National Council on Radiation Protection and Measurements; 2006. [Google Scholar]
- 2.Shulz-Ertner D, Tsujii H. Particle radiation therapy using proton and heavier ion beams. J Clinic Oncol 2007; 25:953–64. [DOI] [PubMed] [Google Scholar]
- 3.Cucinotta FA, Manuel F, Jones J, Izsard G, Murray J, Djojonegoro B, et al. Space radiation and cataracts in astronauts. Radiat Res 2001; 156:460–6. [DOI] [PubMed] [Google Scholar]
- 4.Chylack LT, Peterson LE, Feiveson A, Wear M, Manuel FK, Tung W, et al. NASCA report 1: cross-sectional study of relationship of exposure to space radiation and risk of lens opacity. Radiat Res 172; 2009:10–20. [DOI] [PubMed] [Google Scholar]
- 5.Cucinotta FA. Space radiation risks for astronauts on multiple International Space Station missions. PLoS One 2014; 9:e96099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cucinotta FA, Cacao E. Non-targeted effects models predict significantly higher Mars mission cancer risk than targeted effects models. Sci Rep 2017; 7:1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.National Academy of Sciences. HZE-particles in manned spaceflight. Washington, DC: National Academy of Sciences Press; 1973. [Google Scholar]
- 8.Guidance on radiation received in space activities. NCRP Report No. 98. Bethesda, MD: National Council on Radiation Protection and Measurements; 1989. [Google Scholar]
- 9.Cucinotta FA, Alp M, Sulzman FM, Wang M. Space radiation risks to the central nervous system. Life Sci Space Res 2014; 2:54–69. [Google Scholar]
- 10.Cucinotta FA, Cacao E. Risks of cognitive detriments after low dose heavy ion and proton exposures. Int J Radiat Biol 2019; 95:985–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rabin BM, Shukitt-Hale B, Carrihill-Knoll KL. Effects of age on the disruption of cognitive performance by exposure to space radiation. J Behavioral and Brain Science 2014; 4:298–307. [Google Scholar]
- 12.Impey S, Jopson T, Pelz C, Tafessu A, Fareh F, Zuloaga D, et al. Short- and long-term effects of 56Fe irradiation on cognition and hippocampal DNA methylation and gene expression. BMC Genomic 2016; 17:825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Haley GE, Yeiser L, Olsen RHJ, Davis MJ, Johnson LA, Raber J. Early effects of whole body 56Fe irradiation on hippocampal function in C57BL/6J mice. Radiat Res 2013; 179:590–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Raber J, Allen AR, Sharma S, Allen B, Rosi S, Olsen RH, et al. Effects of proton and combined proton and 56Fe radiation on the hippocampus. Radiat Res 2016; 185:20–30. [DOI] [PubMed] [Google Scholar]
- 15.Patel R, Arakawa H, Radivoyevitch T, Gerson SL, Welford SM. Long-term effects in behavior performances caused by low- and high-linear energy transfer radiation. Radiat Res 2017; 188:752–60. [DOI] [PubMed] [Google Scholar]
- 16.Rabin BM, Carrihill-Knoll KL, Hinchman M, Shukitt-Hake B, Joseph JA, Foster BC. Effects of heavy particle irradiation and diet on object recognition memory in rats. Adv Space Res 2009; 43:1193–9. [Google Scholar]
- 17.Rabin BM, Shukitt-Hale B, Joseph JA, Carrihill-Knoll KL, Carey AN, Cheng V. Relative effectiveness of different particles and energies in disrupting behavioral performance. Radiat Environ Biophys 2007; 46:173–7. [DOI] [PubMed] [Google Scholar]
- 18.Rabin BM, Carrihill-Knoll KL, Shukitt-Hale B. Operant responding following exposure to HZE particles and its relationship to particle energy and linear energy transfer. Adv Space Res 2011; 48:370–7. [Google Scholar]
- 19.Parihar VK, Allen BD, Tran KK, Macaraeg TG, Chu EM, Kwok SF, et al. What happens to your brain on the way to Mars? Sci Adv 2015; 1:e1400256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Parihar VK, Allen BD, Caressi C, Kwok S, Chu EM, Tran KK, et al. Cosmic radiation exposure and persistent cognitive dysfunction. Sci Rep 2016; 6:34774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Raber J, Torres ERS, Akinyeke T, Lee J, Weber Boutros SJ, Turker MS, et al. Detrimental effects of helium irradiation on cognitive performance and cortical levels of MAP-2 in B6D2F1 mice. Int J Mol Sci 2018; 19:1247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rabin BM, Heroux NA, Shukitt-Hale B, Carrihill-Knoll KL, Beck Z, Baxter C. Lack of reliability in the disruption of cognitive performance following exposure to protons. Radiat Environ Biophys 2015; 54:285–95. [DOI] [PubMed] [Google Scholar]
- 23.Parihar VK, Allen BD, Tran KK, Chmielewski NN, Craver BM, Martirosian V, et al. Targeted overexpression of mitochondrial catalase prevents radiation-induced cognitive dysfunction. Antioxid Redox Signal 2015; 22:78–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Impey S, Jopson T, Pelz C, Tafessu A, Fareh F, Zuloaga D, et al. Bi-directional and shared epigenomic signatures following proton and 56Fe irradiation. Sci Rep 2017; 7:10227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rabin BM, Carrihill-Knoll KL, Shukitt-Hale B. Comparison of the effectiveness of exposure to low-LET helium particles (4He) and gamma rays (137Cs) on the disruption of cognitive performance. Radiat Res 2015; 184:266–72. [DOI] [PubMed] [Google Scholar]
- 26.Katz R, Ackerson B, Homayoonfar M, Scharma SC. Inactivation of cells by heavy ion bombardment. Radiat Res 1971; 47:402–25. [PubMed] [Google Scholar]
- 27.Cucinotta FA, Nikjoo H, Goodhead DT. Model for radial dependence of frequency distributions for energy imparted in nanometer volumes from HZE particles. Radiat Res 2000; 153:459–68. [DOI] [PubMed] [Google Scholar]
- 28.Alp M, Cucinotta FA. Biophysics model of heavy ion degradation of neuron morphology in mouse hippocampal granular cell layer neurons. Radiat Res 2019; 189:312–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kim MY, Rusek A, Cucinotta FA. Issues in ground-based GCR simulation for space radiobiology. Front Oncol 2015; 5:122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Raber J, Yamazaki J, Torres ERS, Kirchoff N, Stagamann K, Sharpton T, et al. Combined effects of three high-energy charged particle beams important for space flight on brain behavioral and cognitive endpoints in B6D2F1 female and male mice. Front Phys 2019; 10:179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Davis CM, DeCicco-Skinner KL, Roma PG, Hienz RD. Individual differences in attentional deficits and dopaminergic protein levels following exposure to proton radiation. Radiat Res 2014; 181:258–71. [DOI] [PubMed] [Google Scholar]
- 32.Wyrobek AJ, Britten RA. Individual variations in dose response to spatial memory learning among outbred Wistar rats exposed from 5 to 20 cGy of 56Fe particles. Environ Mol Mut 2016; 57:331–40. [DOI] [PubMed] [Google Scholar]
- 33.Iancu OD, Boutros SW, Olsen RHJ, Davis MJ, Stewart B, et al. Space radiation alters genotype-phenotype correlations in fear learning and memory tests. Front Genet 2018; 9:404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ennaceur A, Delacour J. A new one-trial test for neurobiological studies of memory in rats. 1: Behavioral data. Behav Brain Res 1988; 31:47–59. [DOI] [PubMed] [Google Scholar]
- 35.Antunes M, Biala G. The novel object recognition memory:neurobiology, test procedure, and its modifications. Cogn Process 2012; 13:93–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sivakumaran MH, Mackenzie AK, Callan IR, Ainge JA, O’Connor AR. The discrimination ratio derived from novel object recognition tasks as a measure of recognition memory sensitivity, not bias. Sci Rep 2018; 8:11579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rabin BM, Shukitt-Hale B, Carrihill-Knoll KL, Gomes SM. Comparison of the effects of partial- or whole-boy exposures to 16O particles on cognitive performance on rats. Radiat Res 2014; 181:251–7. [DOI] [PubMed] [Google Scholar]
- 38.Rabin BM, Poulose SM, Bielinski DF, Shukitt-Hale B. Effects of head-only or whole-body exposure to very low doses of 4He(1000 MeV/n) particles on neuronal function and cognitive performance. Life Sci Space Res 2019; 20:85–92. [DOI] [PubMed] [Google Scholar]
- 39.Smirnova O, Hu S, Cucinotta FA. Analysis of the lymphocyte-poiesis dynamics in nonirradiated and irradiated humans: A modeling approach. Radiat Res 2014; 181:240–50. [DOI] [PubMed] [Google Scholar]
- 40.Ainsworth EJ, Kelly LS, Mahlmann LJ, Schooley JC, Thomas RH, Howard EJ, Alpen EL. Response of colony-forming units-spleen to heavy charged particles. Radiat Res 1983; 96:180–97. [PubMed] [Google Scholar]
- 41.Kumar M, Haridas S, Trivedi R, Khushu S, Manda K. Early cognitive changes due to whole body gamma-irradiation: A behavioral and diffusion tensor imaging study in mice. Exp Neurol 2013; 248:360–8. [DOI] [PubMed] [Google Scholar]
- 42.Cacao E, Cucinotta FA. Modeling impaired hippocampal neurogenesis after radiation exposure. Radiat Res 2016; 185:319–31. [DOI] [PubMed] [Google Scholar]
- 43.Rabin BM, Hunt WA, Joseph JA. An assessment of the behavioural toxicity of high-energy iron particles compared to other qualities of radiation. Radiat Res 1989; 119:113–22. [PubMed] [Google Scholar]
- 44.Rola R, Raber J, Rizk A, Otsuka S, VandenBerg SR, Morhardt DR, et al. Radiation-induced impairment of hippocampal neurogenesis is associated with cognitive deficits in young mice. Expt Neurol 2004; 188:316–30. [DOI] [PubMed] [Google Scholar]
- 45.Britten RA, Davis LK, Jewell JS, Miller VD, Hadley MM, et al. Exposure to mission relevant doses of 1 GeV/nucleon 56Fe particles leads to impairment of attentional set-shifting performance in socially mature rats. Radiat Res 2014; 182:292–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.