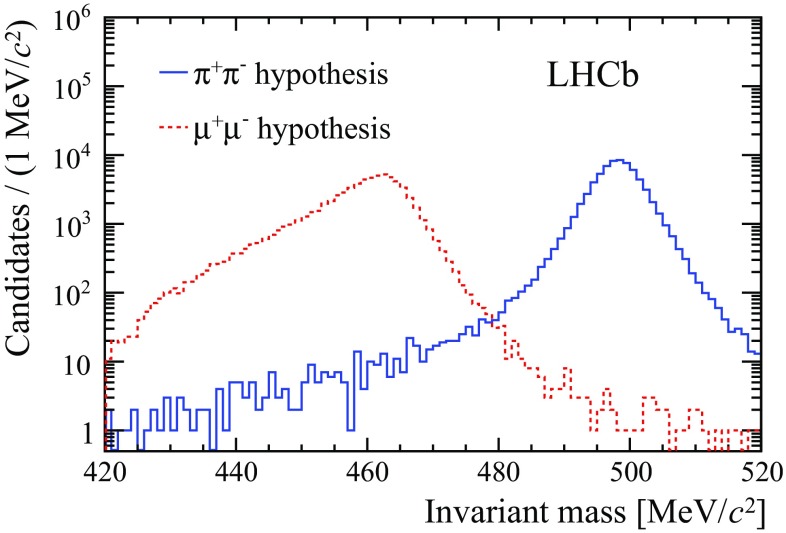
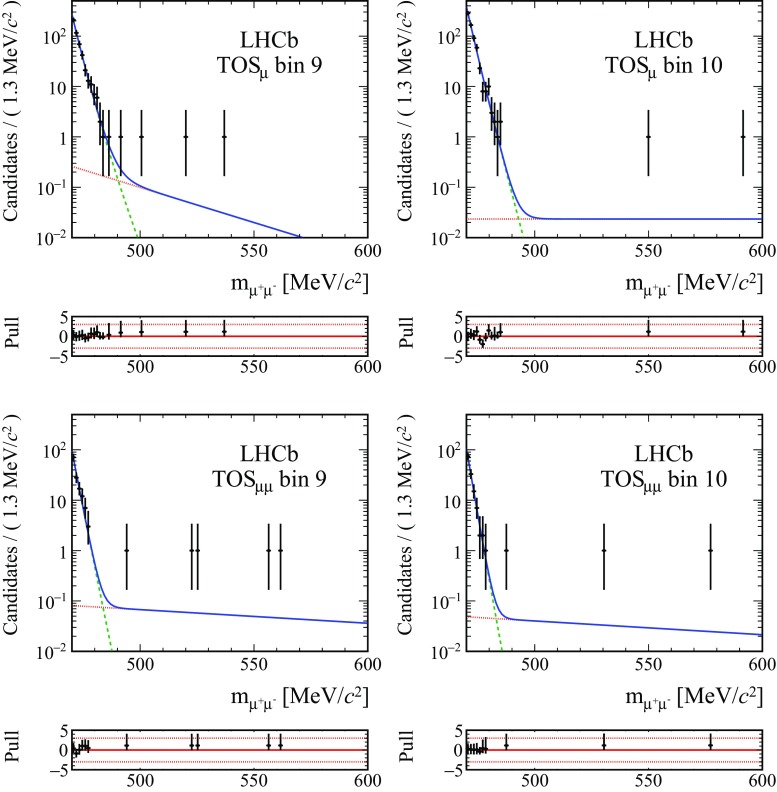
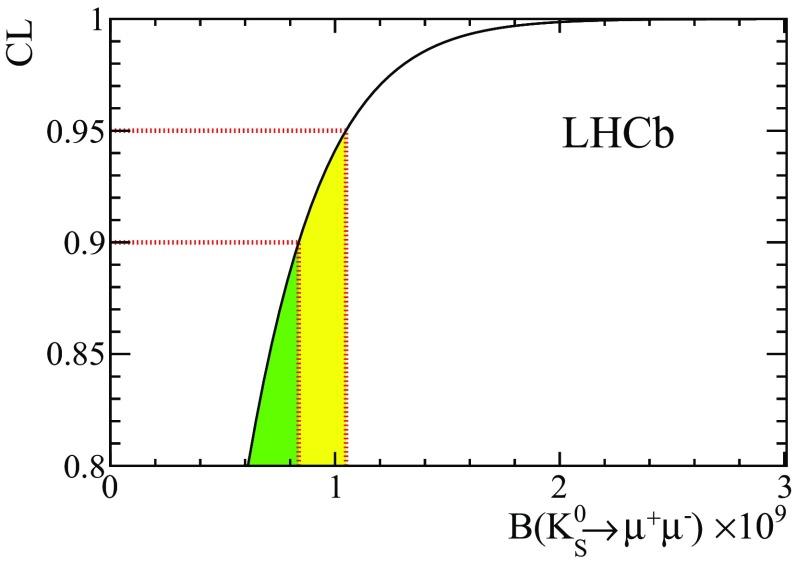
R Aaij
R Aaij
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
B Adeva
B Adeva
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
M Adinolfi
M Adinolfi
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
Z Ajaltouni
Z Ajaltouni
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
S Akar
S Akar
59University of Cincinnati, Cincinnati, OH USA
59,
J Albrecht
J Albrecht
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
F Alessio
F Alessio
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
M Alexander
M Alexander
53School of Physics and Astronomy, University of Glasgow, Glasgow, UK
53,
S Ali
S Ali
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
G Alkhazov
G Alkhazov
31Petersburg Nuclear Physics Institute (PNPI), Gatchina, Russia
31,
P Alvarez Cartelle
P Alvarez Cartelle
55Imperial College London, London, UK
55,
A A Alves Jr
A A Alves Jr
59University of Cincinnati, Cincinnati, OH USA
59,
S Amato
S Amato
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
S Amerio
S Amerio
23Sezione INFN di Padova, Padua, Italy
23,
Y Amhis
Y Amhis
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
L An
L An
3Center for High Energy Physics, Tsinghua University, Beijing, China
3,
L Anderlini
L Anderlini
18Sezione INFN di Firenze, Florence, Italy
18,
G Andreassi
G Andreassi
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
M Andreotti
M Andreotti
17Universita e INFN Ferrara, Ferrara, Italy
17,
J E Andrews
J E Andrews
60University of Maryland, College Park, MD USA
60,
R B Appleby
R B Appleby
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
F Archilli
F Archilli
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
P d’Argent
P d’Argent
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
J Arnau Romeu
J Arnau Romeu
6CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
6,
A Artamonov
A Artamonov
37Institute for High Energy Physics (IHEP), Protvino, Russia
37,
M Artuso
M Artuso
61Syracuse University, Syracuse, NY USA
61,
E Aslanides
E Aslanides
6CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
6,
G Auriemma
G Auriemma
26Sezione INFN di Roma La Sapienza, Rome, Italy
26,
M Baalouch
M Baalouch
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
I Babuschkin
I Babuschkin
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
S Bachmann
S Bachmann
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
J J Back
J J Back
50Department of Physics, University of Warwick, Coventry, UK
50,
A Badalov
A Badalov
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
C Baesso
C Baesso
62Pontifícia Universidade Católica do Rio de Janeiro (PUC-Rio), Rio de Janeiro, Brazil
62,
S Baker
S Baker
55Imperial College London, London, UK
55,
V Balagura
V Balagura
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
W Baldini
W Baldini
17Universita e INFN Ferrara, Ferrara, Italy
17,
A Baranov
A Baranov
35Yandex School of Data Analysis, Moscow, Russia
35,
R J Barlow
R J Barlow
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
C Barschel
C Barschel
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
S Barsuk
S Barsuk
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
W Barter
W Barter
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
F Baryshnikov
F Baryshnikov
32Institute of Theoretical and Experimental Physics (ITEP), Moscow, Russia
32,
M Baszczyk
M Baszczyk
27Henryk Niewodniczanski Institute of Nuclear Physics Polish Academy of Sciences, Kraków, Poland
27,
V Batozskaya
V Batozskaya
29National Center for Nuclear Research (NCBJ), Warsaw, Poland
29,
V Battista
V Battista
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
A Bay
A Bay
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
L Beaucourt
L Beaucourt
4LAPP, Université Savoie Mont-Blanc, CNRS/IN2P3, Annecy-Le-Vieux, France
4,
J Beddow
J Beddow
53School of Physics and Astronomy, University of Glasgow, Glasgow, UK
53,
F Bedeschi
F Bedeschi
24Sezione INFN di Pisa, Pisa, Italy
24,
I Bediaga
I Bediaga
1Centro Brasileiro de Pesquisas Físicas (CBPF), Rio de Janeiro, Brazil
1,
A Beiter
A Beiter
61Syracuse University, Syracuse, NY USA
61,
L J Bel
L J Bel
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
V Bellee
V Bellee
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
N Belloli
N Belloli
21Universita and INFN Milano-Bicocca, Milan, Italy
21,
K Belous
K Belous
37Institute for High Energy Physics (IHEP), Protvino, Russia
37,
I Belyaev
I Belyaev
32Institute of Theoretical and Experimental Physics (ITEP), Moscow, Russia
32,
E Ben-Haim
E Ben-Haim
8LPNHE, Université Pierre et Marie Curie, Université Paris Diderot, CNRS/IN2P3, Paris, France
8,
G Bencivenni
G Bencivenni
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
S Benson
S Benson
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
S Beranek
S Beranek
9I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
9,
A Berezhnoy
A Berezhnoy
33Institute of Nuclear Physics, Moscow State University (SINP MSU), Moscow, Russia
33,
R Bernet
R Bernet
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
A Bertolin
A Bertolin
23Sezione INFN di Padova, Padua, Italy
23,
C Betancourt
C Betancourt
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
F Betti
F Betti
15Sezione INFN di Bologna, Bologna, Italy
15,
M-O Bettler
M-O Bettler
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
M van Beuzekom
M van Beuzekom
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
Ia Bezshyiko
Ia Bezshyiko
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
S Bifani
S Bifani
47University of Birmingham, Birmingham, UK
47,
P Billoir
P Billoir
8LPNHE, Université Pierre et Marie Curie, Université Paris Diderot, CNRS/IN2P3, Paris, France
8,
A Birnkraut
A Birnkraut
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
A Bitadze
A Bitadze
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
A Bizzeti
A Bizzeti
18Sezione INFN di Firenze, Florence, Italy
18,
T Blake
T Blake
50Department of Physics, University of Warwick, Coventry, UK
50,
F Blanc
F Blanc
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
J Blouw
J Blouw
11Max-Planck-Institut für Kernphysik (MPIK), Heidelberg, Germany
11,
S Blusk
S Blusk
61Syracuse University, Syracuse, NY USA
61,
V Bocci
V Bocci
26Sezione INFN di Roma La Sapienza, Rome, Italy
26,
T Boettcher
T Boettcher
58Massachusetts Institute of Technology, Cambridge, MA USA
58,
A Bondar
A Bondar
36Budker Institute of Nuclear Physics (SB RAS), Novosibirsk, Russia
36,
N Bondar
N Bondar
31Petersburg Nuclear Physics Institute (PNPI), Gatchina, Russia
31,
W Bonivento
W Bonivento
16Sezione INFN di Cagliari, Cagliari, Italy
16,
I Bordyuzhin
I Bordyuzhin
32Institute of Theoretical and Experimental Physics (ITEP), Moscow, Russia
32,
A Borgheresi
A Borgheresi
21Universita and INFN Milano-Bicocca, Milan, Italy
21,
S Borghi
S Borghi
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
M Borisyak
M Borisyak
35Yandex School of Data Analysis, Moscow, Russia
35,
M Borsato
M Borsato
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
F Bossu
F Bossu
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
M Boubdir
M Boubdir
9I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
9,
T J V Bowcock
T J V Bowcock
54Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
54,
E Bowen
E Bowen
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
C Bozzi
C Bozzi
17Universita e INFN Ferrara, Ferrara, Italy
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
17,40,
S Braun
S Braun
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
T Britton
T Britton
61Syracuse University, Syracuse, NY USA
61,
J Brodzicka
J Brodzicka
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
E Buchanan
E Buchanan
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
C Burr
C Burr
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
A Bursche
A Bursche
16Sezione INFN di Cagliari, Cagliari, Italy
16,
J Buytaert
J Buytaert
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
S Cadeddu
S Cadeddu
16Sezione INFN di Cagliari, Cagliari, Italy
16,
R Calabrese
R Calabrese
17Universita e INFN Ferrara, Ferrara, Italy
17,
M Calvi
M Calvi
21Universita and INFN Milano-Bicocca, Milan, Italy
21,
M Calvo Gomez
M Calvo Gomez
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
A Camboni
A Camboni
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
P Campana
P Campana
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
D H Campora Perez
D H Campora Perez
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
L Capriotti
L Capriotti
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
A Carbone
A Carbone
15Sezione INFN di Bologna, Bologna, Italy
15,
G Carboni
G Carboni
25Sezione INFN di Roma Tor Vergata, Rome, Italy
25,
R Cardinale
R Cardinale
20Sezione INFN di Genova, Genoa, Italy
20,
A Cardini
A Cardini
16Sezione INFN di Cagliari, Cagliari, Italy
16,
P Carniti
P Carniti
21Universita and INFN Milano-Bicocca, Milan, Italy
21,
L Carson
L Carson
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
K Carvalho Akiba
K Carvalho Akiba
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
G Casse
G Casse
54Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
54,
L Cassina
L Cassina
21Universita and INFN Milano-Bicocca, Milan, Italy
21,
L Castillo Garcia
L Castillo Garcia
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
M Cattaneo
M Cattaneo
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
G Cavallero
G Cavallero
20Sezione INFN di Genova, Genoa, Italy
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
20,40,
R Cenci
R Cenci
24Sezione INFN di Pisa, Pisa, Italy
24,
D Chamont
D Chamont
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
M Charles
M Charles
8LPNHE, Université Pierre et Marie Curie, Université Paris Diderot, CNRS/IN2P3, Paris, France
8,
Ph Charpentier
Ph Charpentier
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
G Chatzikonstantinidis
G Chatzikonstantinidis
47University of Birmingham, Birmingham, UK
47,
M Chefdeville
M Chefdeville
4LAPP, Université Savoie Mont-Blanc, CNRS/IN2P3, Annecy-Le-Vieux, France
4,
S Chen
S Chen
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
S F Cheung
S F Cheung
57Department of Physics, University of Oxford, Oxford, UK
57,
V Chobanova
V Chobanova
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
M Chrzaszcz
M Chrzaszcz
27Henryk Niewodniczanski Institute of Nuclear Physics Polish Academy of Sciences, Kraków, Poland
42Physik-Institut, Universität Zürich, Zurich, Switzerland
27,42,
A Chubykin
A Chubykin
31Petersburg Nuclear Physics Institute (PNPI), Gatchina, Russia
31,
X Cid Vidal
X Cid Vidal
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
G Ciezarek
G Ciezarek
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
P E L Clarke
P E L Clarke
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
M Clemencic
M Clemencic
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
H V Cliff
H V Cliff
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
J Closier
J Closier
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
V Coco
V Coco
59University of Cincinnati, Cincinnati, OH USA
59,
J Cogan
J Cogan
6CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
6,
E Cogneras
E Cogneras
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
V Cogoni
V Cogoni
16Sezione INFN di Cagliari, Cagliari, Italy
16,
L Cojocariu
L Cojocariu
30Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest-Magurele, Romania
30,
P Collins
P Collins
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
A Comerma-Montells
A Comerma-Montells
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
A Contu
A Contu
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
A Cook
A Cook
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
G Coombs
G Coombs
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
S Coquereau
S Coquereau
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
G Corti
G Corti
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
M Corvo
M Corvo
17Universita e INFN Ferrara, Ferrara, Italy
17,
C M Costa Sobral
C M Costa Sobral
50Department of Physics, University of Warwick, Coventry, UK
50,
B Couturier
B Couturier
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
G A Cowan
G A Cowan
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
D C Craik
D C Craik
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
A Crocombe
A Crocombe
50Department of Physics, University of Warwick, Coventry, UK
50,
M Cruz Torres
M Cruz Torres
62Pontifícia Universidade Católica do Rio de Janeiro (PUC-Rio), Rio de Janeiro, Brazil
62,
R Currie
R Currie
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
C D’Ambrosio
C D’Ambrosio
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
F Da Cunha Marinho
F Da Cunha Marinho
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
E Dall’Occo
E Dall’Occo
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
J Dalseno
J Dalseno
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
A Davis
A Davis
3Center for High Energy Physics, Tsinghua University, Beijing, China
3,
K De Bruyn
K De Bruyn
6CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
6,
S De Capua
S De Capua
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
M De Cian
M De Cian
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
J M De Miranda
J M De Miranda
1Centro Brasileiro de Pesquisas Físicas (CBPF), Rio de Janeiro, Brazil
1,
L De Paula
L De Paula
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
M De Serio
M De Serio
14Sezione INFN di Bari, Bari, Italy
14,
P De Simone
P De Simone
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
C T Dean
C T Dean
53School of Physics and Astronomy, University of Glasgow, Glasgow, UK
53,
D Decamp
D Decamp
4LAPP, Université Savoie Mont-Blanc, CNRS/IN2P3, Annecy-Le-Vieux, France
4,
M Deckenhoff
M Deckenhoff
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
L Del Buono
L Del Buono
8LPNHE, Université Pierre et Marie Curie, Université Paris Diderot, CNRS/IN2P3, Paris, France
8,
H-P Dembinski
H-P Dembinski
11Max-Planck-Institut für Kernphysik (MPIK), Heidelberg, Germany
11,
M Demmer
M Demmer
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
A Dendek
A Dendek
28Faculty of Physics and Applied Computer Science, AGH-University of Science and Technology, Kraków, Poland
28,
D Derkach
D Derkach
35Yandex School of Data Analysis, Moscow, Russia
35,
O Deschamps
O Deschamps
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
F Dettori
F Dettori
54Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
54,
B Dey
B Dey
22Sezione di Milano, Milan, Italy
22,
A Di Canto
A Di Canto
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
P Di Nezza
P Di Nezza
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
H Dijkstra
H Dijkstra
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
F Dordei
F Dordei
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
M Dorigo
M Dorigo
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
A Dosil Suárez
A Dosil Suárez
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
A Dovbnya
A Dovbnya
45NSC Kharkiv Institute of Physics and Technology (NSC KIPT), Kharkiv, Ukraine
45,
K Dreimanis
K Dreimanis
54Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
54,
L Dufour
L Dufour
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
G Dujany
G Dujany
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
K Dungs
K Dungs
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
P Durante
P Durante
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
R Dzhelyadin
R Dzhelyadin
37Institute for High Energy Physics (IHEP), Protvino, Russia
37,
M Dziewiecki
M Dziewiecki
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
A Dziurda
A Dziurda
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
A Dzyuba
A Dzyuba
31Petersburg Nuclear Physics Institute (PNPI), Gatchina, Russia
31,
N Déléage
N Déléage
4LAPP, Université Savoie Mont-Blanc, CNRS/IN2P3, Annecy-Le-Vieux, France
4,
S Easo
S Easo
51STFC Rutherford Appleton Laboratory, Didcot, UK
51,
M Ebert
M Ebert
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
U Egede
U Egede
55Imperial College London, London, UK
55,
V Egorychev
V Egorychev
32Institute of Theoretical and Experimental Physics (ITEP), Moscow, Russia
32,
S Eidelman
S Eidelman
36Budker Institute of Nuclear Physics (SB RAS), Novosibirsk, Russia
36,
S Eisenhardt
S Eisenhardt
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
U Eitschberger
U Eitschberger
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
R Ekelhof
R Ekelhof
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
L Eklund
L Eklund
53School of Physics and Astronomy, University of Glasgow, Glasgow, UK
53,
S Ely
S Ely
61Syracuse University, Syracuse, NY USA
61,
S Esen
S Esen
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
H M Evans
H M Evans
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
T Evans
T Evans
57Department of Physics, University of Oxford, Oxford, UK
57,
A Falabella
A Falabella
15Sezione INFN di Bologna, Bologna, Italy
15,
N Farley
N Farley
47University of Birmingham, Birmingham, UK
47,
S Farry
S Farry
54Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
54,
R Fay
R Fay
54Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
54,
D Fazzini
D Fazzini
21Universita and INFN Milano-Bicocca, Milan, Italy
21,
D Ferguson
D Ferguson
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
G Fernandez
G Fernandez
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
A Fernandez Prieto
A Fernandez Prieto
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
F Ferrari
F Ferrari
15Sezione INFN di Bologna, Bologna, Italy
15,
F Ferreira Rodrigues
F Ferreira Rodrigues
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
M Ferro-Luzzi
M Ferro-Luzzi
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
S Filippov
S Filippov
34Institute for Nuclear Research of the Russian Academy of Sciences (INR RAN), Moscow, Russia
34,
R A Fini
R A Fini
14Sezione INFN di Bari, Bari, Italy
14,
M Fiore
M Fiore
17Universita e INFN Ferrara, Ferrara, Italy
17,
M Fiorini
M Fiorini
17Universita e INFN Ferrara, Ferrara, Italy
17,
M Firlej
M Firlej
28Faculty of Physics and Applied Computer Science, AGH-University of Science and Technology, Kraków, Poland
28,
C Fitzpatrick
C Fitzpatrick
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
T Fiutowski
T Fiutowski
28Faculty of Physics and Applied Computer Science, AGH-University of Science and Technology, Kraków, Poland
28,
F Fleuret
F Fleuret
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
K Fohl
K Fohl
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
M Fontana
M Fontana
16Sezione INFN di Cagliari, Cagliari, Italy
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
16,40,
F Fontanelli
F Fontanelli
20Sezione INFN di Genova, Genoa, Italy
20,
D C Forshaw
D C Forshaw
61Syracuse University, Syracuse, NY USA
61,
R Forty
R Forty
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
V Franco Lima
V Franco Lima
54Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
54,
M Frank
M Frank
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
C Frei
C Frei
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
J Fu
J Fu
22Sezione di Milano, Milan, Italy
22,
W Funk
W Funk
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
E Furfaro
E Furfaro
25Sezione INFN di Roma Tor Vergata, Rome, Italy
25,
C Färber
C Färber
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
A Gallas Torreira
A Gallas Torreira
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
D Galli
D Galli
15Sezione INFN di Bologna, Bologna, Italy
15,
S Gallorini
S Gallorini
23Sezione INFN di Padova, Padua, Italy
23,
S Gambetta
S Gambetta
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
M Gandelman
M Gandelman
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
P Gandini
P Gandini
57Department of Physics, University of Oxford, Oxford, UK
57,
Y Gao
Y Gao
3Center for High Energy Physics, Tsinghua University, Beijing, China
3,
L M Garcia Martin
L M Garcia Martin
69Instituto de Fisica Corpuscular, Centro Mixto Universidad de Valencia-CSIC, Valencia, Spain
69,
J García Pardiñas
J García Pardiñas
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
J Garra Tico
J Garra Tico
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
L Garrido
L Garrido
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
P J Garsed
P J Garsed
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
D Gascon
D Gascon
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
C Gaspar
C Gaspar
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
L Gavardi
L Gavardi
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
G Gazzoni
G Gazzoni
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
D Gerick
D Gerick
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
E Gersabeck
E Gersabeck
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
M Gersabeck
M Gersabeck
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
T Gershon
T Gershon
50Department of Physics, University of Warwick, Coventry, UK
50,
Ph Ghez
Ph Ghez
4LAPP, Université Savoie Mont-Blanc, CNRS/IN2P3, Annecy-Le-Vieux, France
4,
S Gianì
S Gianì
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
V Gibson
V Gibson
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
O G Girard
O G Girard
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
L Giubega
L Giubega
30Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest-Magurele, Romania
30,
K Gizdov
K Gizdov
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
V V Gligorov
V V Gligorov
8LPNHE, Université Pierre et Marie Curie, Université Paris Diderot, CNRS/IN2P3, Paris, France
8,
D Golubkov
D Golubkov
32Institute of Theoretical and Experimental Physics (ITEP), Moscow, Russia
32,
A Golutvin
A Golutvin
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
55Imperial College London, London, UK
40,55,
A Gomes
A Gomes
1Centro Brasileiro de Pesquisas Físicas (CBPF), Rio de Janeiro, Brazil
1,
I V Gorelov
I V Gorelov
33Institute of Nuclear Physics, Moscow State University (SINP MSU), Moscow, Russia
33,
C Gotti
C Gotti
21Universita and INFN Milano-Bicocca, Milan, Italy
21,
E Govorkova
E Govorkova
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
R Graciani Diaz
R Graciani Diaz
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
L A Granado Cardoso
L A Granado Cardoso
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
E Graugés
E Graugés
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
E Graverini
E Graverini
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
G Graziani
G Graziani
18Sezione INFN di Firenze, Florence, Italy
18,
A Grecu
A Grecu
30Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest-Magurele, Romania
30,
R Greim
R Greim
9I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
9,
P Griffith
P Griffith
16Sezione INFN di Cagliari, Cagliari, Italy
16,
L Grillo
L Grillo
21Universita and INFN Milano-Bicocca, Milan, Italy
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
21,40,
B R Gruberg Cazon
B R Gruberg Cazon
57Department of Physics, University of Oxford, Oxford, UK
57,
O Grünberg
O Grünberg
67Institut für Physik, Universität Rostock, Rostock, Germany
67,
E Gushchin
E Gushchin
34Institute for Nuclear Research of the Russian Academy of Sciences (INR RAN), Moscow, Russia
34,
Yu Guz
Yu Guz
37Institute for High Energy Physics (IHEP), Protvino, Russia
37,
T Gys
T Gys
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
C Göbel
C Göbel
62Pontifícia Universidade Católica do Rio de Janeiro (PUC-Rio), Rio de Janeiro, Brazil
62,
T Hadavizadeh
T Hadavizadeh
57Department of Physics, University of Oxford, Oxford, UK
57,
C Hadjivasiliou
C Hadjivasiliou
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
G Haefeli
G Haefeli
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
C Haen
C Haen
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
S C Haines
S C Haines
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
B Hamilton
B Hamilton
60University of Maryland, College Park, MD USA
60,
X Han
X Han
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
S Hansmann-Menzemer
S Hansmann-Menzemer
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
N Harnew
N Harnew
57Department of Physics, University of Oxford, Oxford, UK
57,
S T Harnew
S T Harnew
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
J Harrison
J Harrison
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
M Hatch
M Hatch
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
J He
J He
63University of Chinese Academy of Sciences, Beijing, China
63,
T Head
T Head
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
A Heister
A Heister
9I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
9,
K Hennessy
K Hennessy
54Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
54,
P Henrard
P Henrard
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
L Henry
L Henry
69Instituto de Fisica Corpuscular, Centro Mixto Universidad de Valencia-CSIC, Valencia, Spain
69,
E van Herwijnen
E van Herwijnen
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
M Heß
M Heß
67Institut für Physik, Universität Rostock, Rostock, Germany
67,
A Hicheur
A Hicheur
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
D Hill
D Hill
57Department of Physics, University of Oxford, Oxford, UK
57,
C Hombach
C Hombach
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
P H Hopchev
P H Hopchev
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
Z-C Huard
Z-C Huard
59University of Cincinnati, Cincinnati, OH USA
59,
W Hulsbergen
W Hulsbergen
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
T Humair
T Humair
55Imperial College London, London, UK
55,
M Hushchyn
M Hushchyn
35Yandex School of Data Analysis, Moscow, Russia
35,
D Hutchcroft
D Hutchcroft
54Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
54,
M Idzik
M Idzik
28Faculty of Physics and Applied Computer Science, AGH-University of Science and Technology, Kraków, Poland
28,
P Ilten
P Ilten
58Massachusetts Institute of Technology, Cambridge, MA USA
58,
R Jacobsson
R Jacobsson
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
J Jalocha
J Jalocha
57Department of Physics, University of Oxford, Oxford, UK
57,
E Jans
E Jans
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
A Jawahery
A Jawahery
60University of Maryland, College Park, MD USA
60,
F Jiang
F Jiang
3Center for High Energy Physics, Tsinghua University, Beijing, China
3,
M John
M John
57Department of Physics, University of Oxford, Oxford, UK
57,
D Johnson
D Johnson
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
C R Jones
C R Jones
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
C Joram
C Joram
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
B Jost
B Jost
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
N Jurik
N Jurik
57Department of Physics, University of Oxford, Oxford, UK
57,
S Kandybei
S Kandybei
45NSC Kharkiv Institute of Physics and Technology (NSC KIPT), Kharkiv, Ukraine
45,
M Karacson
M Karacson
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
J M Kariuki
J M Kariuki
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
S Karodia
S Karodia
53School of Physics and Astronomy, University of Glasgow, Glasgow, UK
53,
M Kecke
M Kecke
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
M Kelsey
M Kelsey
61Syracuse University, Syracuse, NY USA
61,
M Kenzie
M Kenzie
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
T Ketel
T Ketel
44Nikhef National Institute for Subatomic Physics and VU University Amsterdam, Amsterdam, The Netherlands
44,
E Khairullin
E Khairullin
35Yandex School of Data Analysis, Moscow, Russia
35,
B Khanji
B Khanji
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
C Khurewathanakul
C Khurewathanakul
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
T Kirn
T Kirn
9I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
9,
S Klaver
S Klaver
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
K Klimaszewski
K Klimaszewski
29National Center for Nuclear Research (NCBJ), Warsaw, Poland
29,
T Klimkovich
T Klimkovich
11Max-Planck-Institut für Kernphysik (MPIK), Heidelberg, Germany
11,
S Koliiev
S Koliiev
46Institute for Nuclear Research of the National Academy of Sciences (KINR), Kyiv, Ukraine
46,
M Kolpin
M Kolpin
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
I Komarov
I Komarov
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
R Kopecna
R Kopecna
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
P Koppenburg
P Koppenburg
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
A Kosmyntseva
A Kosmyntseva
32Institute of Theoretical and Experimental Physics (ITEP), Moscow, Russia
32,
S Kotriakhova
S Kotriakhova
31Petersburg Nuclear Physics Institute (PNPI), Gatchina, Russia
31,
M Kozeiha
M Kozeiha
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
L Kravchuk
L Kravchuk
34Institute for Nuclear Research of the Russian Academy of Sciences (INR RAN), Moscow, Russia
34,
M Kreps
M Kreps
50Department of Physics, University of Warwick, Coventry, UK
50,
P Krokovny
P Krokovny
36Budker Institute of Nuclear Physics (SB RAS), Novosibirsk, Russia
36,
F Kruse
F Kruse
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
W Krzemien
W Krzemien
29National Center for Nuclear Research (NCBJ), Warsaw, Poland
29,
W Kucewicz
W Kucewicz
27Henryk Niewodniczanski Institute of Nuclear Physics Polish Academy of Sciences, Kraków, Poland
27,
M Kucharczyk
M Kucharczyk
27Henryk Niewodniczanski Institute of Nuclear Physics Polish Academy of Sciences, Kraków, Poland
27,
V Kudryavtsev
V Kudryavtsev
36Budker Institute of Nuclear Physics (SB RAS), Novosibirsk, Russia
36,
A K Kuonen
A K Kuonen
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
K Kurek
K Kurek
29National Center for Nuclear Research (NCBJ), Warsaw, Poland
29,
T Kvaratskheliya
T Kvaratskheliya
32Institute of Theoretical and Experimental Physics (ITEP), Moscow, Russia
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
32,40,
D Lacarrere
D Lacarrere
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
G Lafferty
G Lafferty
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
A Lai
A Lai
16Sezione INFN di Cagliari, Cagliari, Italy
16,
G Lanfranchi
G Lanfranchi
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
C Langenbruch
C Langenbruch
9I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
9,
T Latham
T Latham
50Department of Physics, University of Warwick, Coventry, UK
50,
C Lazzeroni
C Lazzeroni
47University of Birmingham, Birmingham, UK
47,
R Le Gac
R Le Gac
6CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
6,
J van Leerdam
J van Leerdam
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
A Leflat
A Leflat
33Institute of Nuclear Physics, Moscow State University (SINP MSU), Moscow, Russia
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
33,40,
J Lefrançois
J Lefrançois
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
R Lefèvre
R Lefèvre
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
F Lemaitre
F Lemaitre
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
E Lemos Cid
E Lemos Cid
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
O Leroy
O Leroy
6CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
6,
T Lesiak
T Lesiak
27Henryk Niewodniczanski Institute of Nuclear Physics Polish Academy of Sciences, Kraków, Poland
27,
B Leverington
B Leverington
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
T Li
T Li
3Center for High Energy Physics, Tsinghua University, Beijing, China
3,
Y Li
Y Li
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
Z Li
Z Li
61Syracuse University, Syracuse, NY USA
61,
T Likhomanenko
T Likhomanenko
35Yandex School of Data Analysis, Moscow, Russia
68National Research Centre Kurchatov Institute, Moscow, Russia
35,68,
R Lindner
R Lindner
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
F Lionetto
F Lionetto
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
X Liu
X Liu
3Center for High Energy Physics, Tsinghua University, Beijing, China
3,
D Loh
D Loh
50Department of Physics, University of Warwick, Coventry, UK
50,
I Longstaff
I Longstaff
53School of Physics and Astronomy, University of Glasgow, Glasgow, UK
53,
J H Lopes
J H Lopes
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
D Lucchesi
D Lucchesi
23Sezione INFN di Padova, Padua, Italy
23,
M Lucio Martinez
M Lucio Martinez
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
H Luo
H Luo
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
A Lupato
A Lupato
23Sezione INFN di Padova, Padua, Italy
23,
E Luppi
E Luppi
17Universita e INFN Ferrara, Ferrara, Italy
17,
O Lupton
O Lupton
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
A Lusiani
A Lusiani
24Sezione INFN di Pisa, Pisa, Italy
24,
X Lyu
X Lyu
63University of Chinese Academy of Sciences, Beijing, China
63,
F Machefert
F Machefert
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
F Maciuc
F Maciuc
30Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest-Magurele, Romania
30,
O Maev
O Maev
31Petersburg Nuclear Physics Institute (PNPI), Gatchina, Russia
31,
K Maguire
K Maguire
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
S Malde
S Malde
57Department of Physics, University of Oxford, Oxford, UK
57,
A Malinin
A Malinin
68National Research Centre Kurchatov Institute, Moscow, Russia
68,
T Maltsev
T Maltsev
36Budker Institute of Nuclear Physics (SB RAS), Novosibirsk, Russia
36,
G Manca
G Manca
16Sezione INFN di Cagliari, Cagliari, Italy
16,
G Mancinelli
G Mancinelli
6CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
6,
P Manning
P Manning
61Syracuse University, Syracuse, NY USA
61,
J Maratas
J Maratas
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
J F Marchand
J F Marchand
4LAPP, Université Savoie Mont-Blanc, CNRS/IN2P3, Annecy-Le-Vieux, France
4,
U Marconi
U Marconi
15Sezione INFN di Bologna, Bologna, Italy
15,
C Marin Benito
C Marin Benito
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
M Marinangeli
M Marinangeli
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
P Marino
P Marino
24Sezione INFN di Pisa, Pisa, Italy
24,
J Marks
J Marks
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
G Martellotti
G Martellotti
26Sezione INFN di Roma La Sapienza, Rome, Italy
26,
M Martin
M Martin
6CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
6,
M Martinelli
M Martinelli
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
D Martinez Santos
D Martinez Santos
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
F Martinez Vidal
F Martinez Vidal
69Instituto de Fisica Corpuscular, Centro Mixto Universidad de Valencia-CSIC, Valencia, Spain
69,
D Martins Tostes
D Martins Tostes
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
L M Massacrier
L M Massacrier
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
A Massafferri
A Massafferri
1Centro Brasileiro de Pesquisas Físicas (CBPF), Rio de Janeiro, Brazil
1,
R Matev
R Matev
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
A Mathad
A Mathad
50Department of Physics, University of Warwick, Coventry, UK
50,
Z Mathe
Z Mathe
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
C Matteuzzi
C Matteuzzi
21Universita and INFN Milano-Bicocca, Milan, Italy
21,
A Mauri
A Mauri
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
E Maurice
E Maurice
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
B Maurin
B Maurin
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
A Mazurov
A Mazurov
47University of Birmingham, Birmingham, UK
47,
M McCann
M McCann
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
55Imperial College London, London, UK
40,55,
A McNab
A McNab
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
R McNulty
R McNulty
13School of Physics, University College Dublin, Dublin, Ireland
13,
B Meadows
B Meadows
59University of Cincinnati, Cincinnati, OH USA
59,
F Meier
F Meier
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
D Melnychuk
D Melnychuk
29National Center for Nuclear Research (NCBJ), Warsaw, Poland
29,
M Merk
M Merk
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
A Merli
A Merli
22Sezione di Milano, Milan, Italy
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
22,40,
E Michielin
E Michielin
23Sezione INFN di Padova, Padua, Italy
23,
D A Milanes
D A Milanes
66Departamento de Fisica, Universidad Nacional de Colombia, Bogotá, Colombia
66,
M-N Minard
M-N Minard
4LAPP, Université Savoie Mont-Blanc, CNRS/IN2P3, Annecy-Le-Vieux, France
4,
D S Mitzel
D S Mitzel
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
A Mogini
A Mogini
8LPNHE, Université Pierre et Marie Curie, Université Paris Diderot, CNRS/IN2P3, Paris, France
8,
J Molina Rodriguez
J Molina Rodriguez
1Centro Brasileiro de Pesquisas Físicas (CBPF), Rio de Janeiro, Brazil
1,
I A Monroy
I A Monroy
66Departamento de Fisica, Universidad Nacional de Colombia, Bogotá, Colombia
66,
S Monteil
S Monteil
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
M Morandin
M Morandin
23Sezione INFN di Padova, Padua, Italy
23,
M J Morello
M J Morello
24Sezione INFN di Pisa, Pisa, Italy
24,
O Morgunova
O Morgunova
68National Research Centre Kurchatov Institute, Moscow, Russia
68,
J Moron
J Moron
28Faculty of Physics and Applied Computer Science, AGH-University of Science and Technology, Kraków, Poland
28,
A B Morris
A B Morris
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
R Mountain
R Mountain
61Syracuse University, Syracuse, NY USA
61,
F Muheim
F Muheim
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
M Mulder
M Mulder
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
M Mussini
M Mussini
15Sezione INFN di Bologna, Bologna, Italy
15,
D Müller
D Müller
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
J Müller
J Müller
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
K Müller
K Müller
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
V Müller
V Müller
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
P Naik
P Naik
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
T Nakada
T Nakada
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
R Nandakumar
R Nandakumar
51STFC Rutherford Appleton Laboratory, Didcot, UK
51,
A Nandi
A Nandi
57Department of Physics, University of Oxford, Oxford, UK
57,
I Nasteva
I Nasteva
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
M Needham
M Needham
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
N Neri
N Neri
22Sezione di Milano, Milan, Italy
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
22,40,
S Neubert
S Neubert
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
N Neufeld
N Neufeld
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
M Neuner
M Neuner
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
T D Nguyen
T D Nguyen
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
C Nguyen-Mau
C Nguyen-Mau
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
S Nieswand
S Nieswand
9I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
9,
R Niet
R Niet
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
N Nikitin
N Nikitin
33Institute of Nuclear Physics, Moscow State University (SINP MSU), Moscow, Russia
33,
T Nikodem
T Nikodem
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
A Nogay
A Nogay
68National Research Centre Kurchatov Institute, Moscow, Russia
68,
A Novoselov
A Novoselov
37Institute for High Energy Physics (IHEP), Protvino, Russia
37,
D P O’Hanlon
D P O’Hanlon
50Department of Physics, University of Warwick, Coventry, UK
50,
A Oblakowska-Mucha
A Oblakowska-Mucha
28Faculty of Physics and Applied Computer Science, AGH-University of Science and Technology, Kraków, Poland
28,
V Obraztsov
V Obraztsov
37Institute for High Energy Physics (IHEP), Protvino, Russia
37,
S Ogilvy
S Ogilvy
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
R Oldeman
R Oldeman
16Sezione INFN di Cagliari, Cagliari, Italy
16,
C J G Onderwater
C J G Onderwater
70Van Swinderen Institute, University of Groningen, Groningen, The Netherlands
70,
A Ossowska
A Ossowska
27Henryk Niewodniczanski Institute of Nuclear Physics Polish Academy of Sciences, Kraków, Poland
27,
J M Otalora Goicochea
J M Otalora Goicochea
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
P Owen
P Owen
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
A Oyanguren
A Oyanguren
69Instituto de Fisica Corpuscular, Centro Mixto Universidad de Valencia-CSIC, Valencia, Spain
69,
P R Pais
P R Pais
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
A Palano
A Palano
14Sezione INFN di Bari, Bari, Italy
14,
M Palutan
M Palutan
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
A Papanestis
A Papanestis
51STFC Rutherford Appleton Laboratory, Didcot, UK
51,
M Pappagallo
M Pappagallo
14Sezione INFN di Bari, Bari, Italy
14,
L L Pappalardo
L L Pappalardo
17Universita e INFN Ferrara, Ferrara, Italy
17,
C Pappenheimer
C Pappenheimer
59University of Cincinnati, Cincinnati, OH USA
59,
W Parker
W Parker
60University of Maryland, College Park, MD USA
60,
C Parkes
C Parkes
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
G Passaleva
G Passaleva
18Sezione INFN di Firenze, Florence, Italy
18,
A Pastore
A Pastore
14Sezione INFN di Bari, Bari, Italy
14,
M Patel
M Patel
55Imperial College London, London, UK
55,
C Patrignani
C Patrignani
15Sezione INFN di Bologna, Bologna, Italy
15,
A Pearce
A Pearce
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
A Pellegrino
A Pellegrino
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
G Penso
G Penso
26Sezione INFN di Roma La Sapienza, Rome, Italy
26,
M Pepe Altarelli
M Pepe Altarelli
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
S Perazzini
S Perazzini
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
P Perret
P Perret
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
L Pescatore
L Pescatore
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
K Petridis
K Petridis
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
A Petrolini
A Petrolini
20Sezione INFN di Genova, Genoa, Italy
20,
A Petrov
A Petrov
68National Research Centre Kurchatov Institute, Moscow, Russia
68,
M Petruzzo
M Petruzzo
22Sezione di Milano, Milan, Italy
22,
E Picatoste Olloqui
E Picatoste Olloqui
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
B Pietrzyk
B Pietrzyk
4LAPP, Université Savoie Mont-Blanc, CNRS/IN2P3, Annecy-Le-Vieux, France
4,
M Pikies
M Pikies
27Henryk Niewodniczanski Institute of Nuclear Physics Polish Academy of Sciences, Kraków, Poland
27,
D Pinci
D Pinci
26Sezione INFN di Roma La Sapienza, Rome, Italy
26,
A Pistone
A Pistone
20Sezione INFN di Genova, Genoa, Italy
20,
A Piucci
A Piucci
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
V Placinta
V Placinta
30Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest-Magurele, Romania
30,
S Playfer
S Playfer
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
M Plo Casasus
M Plo Casasus
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
T Poikela
T Poikela
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
F Polci
F Polci
8LPNHE, Université Pierre et Marie Curie, Université Paris Diderot, CNRS/IN2P3, Paris, France
8,
M Poli Lener
M Poli Lener
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
A Poluektov
A Poluektov
36Budker Institute of Nuclear Physics (SB RAS), Novosibirsk, Russia
50Department of Physics, University of Warwick, Coventry, UK
36,50,
I Polyakov
I Polyakov
61Syracuse University, Syracuse, NY USA
61,
E Polycarpo
E Polycarpo
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
G J Pomery
G J Pomery
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
S Ponce
S Ponce
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
A Popov
A Popov
37Institute for High Energy Physics (IHEP), Protvino, Russia
37,
D Popov
D Popov
11Max-Planck-Institut für Kernphysik (MPIK), Heidelberg, Germany
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
11,40,
B Popovici
B Popovici
30Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest-Magurele, Romania
30,
S Poslavskii
S Poslavskii
37Institute for High Energy Physics (IHEP), Protvino, Russia
37,
C Potterat
C Potterat
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
E Price
E Price
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
J Prisciandaro
J Prisciandaro
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
C Prouve
C Prouve
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
V Pugatch
V Pugatch
46Institute for Nuclear Research of the National Academy of Sciences (KINR), Kyiv, Ukraine
46,
A Puig Navarro
A Puig Navarro
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
G Punzi
G Punzi
24Sezione INFN di Pisa, Pisa, Italy
24,
W Qian
W Qian
50Department of Physics, University of Warwick, Coventry, UK
50,
R Quagliani
R Quagliani
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
7,48,
B Rachwal
B Rachwal
28Faculty of Physics and Applied Computer Science, AGH-University of Science and Technology, Kraków, Poland
28,
J H Rademacker
J H Rademacker
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
M Rama
M Rama
24Sezione INFN di Pisa, Pisa, Italy
24,
M Ramos Pernas
M Ramos Pernas
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
M S Rangel
M S Rangel
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
I Raniuk
I Raniuk
45NSC Kharkiv Institute of Physics and Technology (NSC KIPT), Kharkiv, Ukraine
45,
F Ratnikov
F Ratnikov
35Yandex School of Data Analysis, Moscow, Russia
35,
G Raven
G Raven
44Nikhef National Institute for Subatomic Physics and VU University Amsterdam, Amsterdam, The Netherlands
44,
F Redi
F Redi
55Imperial College London, London, UK
55,
S Reichert
S Reichert
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
A C dos Reis
A C dos Reis
1Centro Brasileiro de Pesquisas Físicas (CBPF), Rio de Janeiro, Brazil
1,
C Remon Alepuz
C Remon Alepuz
69Instituto de Fisica Corpuscular, Centro Mixto Universidad de Valencia-CSIC, Valencia, Spain
69,
V Renaudin
V Renaudin
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
S Ricciardi
S Ricciardi
51STFC Rutherford Appleton Laboratory, Didcot, UK
51,
S Richards
S Richards
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
M Rihl
M Rihl
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
K Rinnert
K Rinnert
54Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
54,
V Rives Molina
V Rives Molina
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
P Robbe
P Robbe
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
A B Rodrigues
A B Rodrigues
1Centro Brasileiro de Pesquisas Físicas (CBPF), Rio de Janeiro, Brazil
1,
E Rodrigues
E Rodrigues
59University of Cincinnati, Cincinnati, OH USA
59,
J A Rodriguez Lopez
J A Rodriguez Lopez
66Departamento de Fisica, Universidad Nacional de Colombia, Bogotá, Colombia
66,
P Rodriguez Perez
P Rodriguez Perez
56School of Physics and Astronomy, University of Manchester, Manchester, UK
56,
A Rogozhnikov
A Rogozhnikov
35Yandex School of Data Analysis, Moscow, Russia
35,
S Roiser
S Roiser
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
A Rollings
A Rollings
57Department of Physics, University of Oxford, Oxford, UK
57,
V Romanovskiy
V Romanovskiy
37Institute for High Energy Physics (IHEP), Protvino, Russia
37,
A Romero Vidal
A Romero Vidal
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
J W Ronayne
J W Ronayne
13School of Physics, University College Dublin, Dublin, Ireland
13,
M Rotondo
M Rotondo
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
M S Rudolph
M S Rudolph
61Syracuse University, Syracuse, NY USA
61,
T Ruf
T Ruf
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
P Ruiz Valls
P Ruiz Valls
69Instituto de Fisica Corpuscular, Centro Mixto Universidad de Valencia-CSIC, Valencia, Spain
69,
J J Saborido Silva
J J Saborido Silva
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
E Sadykhov
E Sadykhov
32Institute of Theoretical and Experimental Physics (ITEP), Moscow, Russia
32,
N Sagidova
N Sagidova
31Petersburg Nuclear Physics Institute (PNPI), Gatchina, Russia
31,
B Saitta
B Saitta
16Sezione INFN di Cagliari, Cagliari, Italy
16,
V Salustino Guimaraes
V Salustino Guimaraes
1Centro Brasileiro de Pesquisas Físicas (CBPF), Rio de Janeiro, Brazil
1,
D Sanchez Gonzalo
D Sanchez Gonzalo
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
C Sanchez Mayordomo
C Sanchez Mayordomo
69Instituto de Fisica Corpuscular, Centro Mixto Universidad de Valencia-CSIC, Valencia, Spain
69,
B Sanmartin Sedes
B Sanmartin Sedes
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
R Santacesaria
R Santacesaria
26Sezione INFN di Roma La Sapienza, Rome, Italy
26,
C Santamarina Rios
C Santamarina Rios
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
M Santimaria
M Santimaria
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
E Santovetti
E Santovetti
25Sezione INFN di Roma Tor Vergata, Rome, Italy
25,
A Sarti
A Sarti
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
C Satriano
C Satriano
26Sezione INFN di Roma La Sapienza, Rome, Italy
26,
A Satta
A Satta
25Sezione INFN di Roma Tor Vergata, Rome, Italy
25,
D M Saunders
D M Saunders
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
D Savrina
D Savrina
32Institute of Theoretical and Experimental Physics (ITEP), Moscow, Russia
33Institute of Nuclear Physics, Moscow State University (SINP MSU), Moscow, Russia
32,33,
S Schael
S Schael
9I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
9,
M Schellenberg
M Schellenberg
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
M Schiller
M Schiller
53School of Physics and Astronomy, University of Glasgow, Glasgow, UK
53,
H Schindler
H Schindler
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
M Schlupp
M Schlupp
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
M Schmelling
M Schmelling
11Max-Planck-Institut für Kernphysik (MPIK), Heidelberg, Germany
11,
T Schmelzer
T Schmelzer
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
B Schmidt
B Schmidt
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
O Schneider
O Schneider
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
A Schopper
A Schopper
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
H F Schreiner
H F Schreiner
59University of Cincinnati, Cincinnati, OH USA
59,
K Schubert
K Schubert
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
M Schubiger
M Schubiger
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
M-H Schune
M-H Schune
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
R Schwemmer
R Schwemmer
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
B Sciascia
B Sciascia
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
A Sciubba
A Sciubba
26Sezione INFN di Roma La Sapienza, Rome, Italy
26,
A Semennikov
A Semennikov
32Institute of Theoretical and Experimental Physics (ITEP), Moscow, Russia
32,
A Sergi
A Sergi
47University of Birmingham, Birmingham, UK
47,
N Serra
N Serra
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
J Serrano
J Serrano
6CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
6,
L Sestini
L Sestini
23Sezione INFN di Padova, Padua, Italy
23,
P Seyfert
P Seyfert
21Universita and INFN Milano-Bicocca, Milan, Italy
21,
M Shapkin
M Shapkin
37Institute for High Energy Physics (IHEP), Protvino, Russia
37,
I Shapoval
I Shapoval
45NSC Kharkiv Institute of Physics and Technology (NSC KIPT), Kharkiv, Ukraine
45,
Y Shcheglov
Y Shcheglov
31Petersburg Nuclear Physics Institute (PNPI), Gatchina, Russia
31,
T Shears
T Shears
54Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
54,
L Shekhtman
L Shekhtman
36Budker Institute of Nuclear Physics (SB RAS), Novosibirsk, Russia
36,
V Shevchenko
V Shevchenko
68National Research Centre Kurchatov Institute, Moscow, Russia
68,
B G Siddi
B G Siddi
17Universita e INFN Ferrara, Ferrara, Italy
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
17,40,
R Silva Coutinho
R Silva Coutinho
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
L Silva de Oliveira
L Silva de Oliveira
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
G Simi
G Simi
23Sezione INFN di Padova, Padua, Italy
23,
S Simone
S Simone
14Sezione INFN di Bari, Bari, Italy
14,
M Sirendi
M Sirendi
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
N Skidmore
N Skidmore
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
T Skwarnicki
T Skwarnicki
61Syracuse University, Syracuse, NY USA
61,
E Smith
E Smith
55Imperial College London, London, UK
55,
I T Smith
I T Smith
52School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
52,
J Smith
J Smith
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
M Smith
M Smith
55Imperial College London, London, UK
55,
l Soares Lavra
l Soares Lavra
1Centro Brasileiro de Pesquisas Físicas (CBPF), Rio de Janeiro, Brazil
1,
M D Sokoloff
M D Sokoloff
59University of Cincinnati, Cincinnati, OH USA
59,
F J P Soler
F J P Soler
53School of Physics and Astronomy, University of Glasgow, Glasgow, UK
53,
B Souza De Paula
B Souza De Paula
2Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2,
B Spaan
B Spaan
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
P Spradlin
P Spradlin
53School of Physics and Astronomy, University of Glasgow, Glasgow, UK
53,
S Sridharan
S Sridharan
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
F Stagni
F Stagni
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
M Stahl
M Stahl
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
S Stahl
S Stahl
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
P Stefko
P Stefko
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
S Stefkova
S Stefkova
55Imperial College London, London, UK
55,
O Steinkamp
O Steinkamp
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
S Stemmle
S Stemmle
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
O Stenyakin
O Stenyakin
37Institute for High Energy Physics (IHEP), Protvino, Russia
37,
H Stevens
H Stevens
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
S Stoica
S Stoica
30Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest-Magurele, Romania
30,
S Stone
S Stone
61Syracuse University, Syracuse, NY USA
61,
B Storaci
B Storaci
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
S Stracka
S Stracka
24Sezione INFN di Pisa, Pisa, Italy
24,
M E Stramaglia
M E Stramaglia
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
M Straticiuc
M Straticiuc
30Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest-Magurele, Romania
30,
U Straumann
U Straumann
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
L Sun
L Sun
64School of Physics and Technology, Wuhan University, Wuhan, China
64,
W Sutcliffe
W Sutcliffe
55Imperial College London, London, UK
55,
K Swientek
K Swientek
28Faculty of Physics and Applied Computer Science, AGH-University of Science and Technology, Kraków, Poland
28,
V Syropoulos
V Syropoulos
44Nikhef National Institute for Subatomic Physics and VU University Amsterdam, Amsterdam, The Netherlands
44,
M Szczekowski
M Szczekowski
29National Center for Nuclear Research (NCBJ), Warsaw, Poland
29,
T Szumlak
T Szumlak
28Faculty of Physics and Applied Computer Science, AGH-University of Science and Technology, Kraków, Poland
28,
S T’Jampens
S T’Jampens
4LAPP, Université Savoie Mont-Blanc, CNRS/IN2P3, Annecy-Le-Vieux, France
4,
A Tayduganov
A Tayduganov
6CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
6,
T Tekampe
T Tekampe
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
G Tellarini
G Tellarini
17Universita e INFN Ferrara, Ferrara, Italy
17,
F Teubert
F Teubert
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
E Thomas
E Thomas
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
J van Tilburg
J van Tilburg
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
M J Tilley
M J Tilley
55Imperial College London, London, UK
55,
V Tisserand
V Tisserand
4LAPP, Université Savoie Mont-Blanc, CNRS/IN2P3, Annecy-Le-Vieux, France
4,
M Tobin
M Tobin
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
S Tolk
S Tolk
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
L Tomassetti
L Tomassetti
17Universita e INFN Ferrara, Ferrara, Italy
17,
D Tonelli
D Tonelli
24Sezione INFN di Pisa, Pisa, Italy
24,
S Topp-Joergensen
S Topp-Joergensen
57Department of Physics, University of Oxford, Oxford, UK
57,
F Toriello
F Toriello
61Syracuse University, Syracuse, NY USA
61,
R Tourinho Jadallah Aoude
R Tourinho Jadallah Aoude
1Centro Brasileiro de Pesquisas Físicas (CBPF), Rio de Janeiro, Brazil
1,
E Tournefier
E Tournefier
4LAPP, Université Savoie Mont-Blanc, CNRS/IN2P3, Annecy-Le-Vieux, France
4,
S Tourneur
S Tourneur
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
K Trabelsi
K Trabelsi
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
M Traill
M Traill
53School of Physics and Astronomy, University of Glasgow, Glasgow, UK
53,
M T Tran
M T Tran
41Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
41,
M Tresch
M Tresch
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
A Trisovic
A Trisovic
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
A Tsaregorodtsev
A Tsaregorodtsev
6CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
6,
P Tsopelas
P Tsopelas
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
A Tully
A Tully
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
N Tuning
N Tuning
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
A Ukleja
A Ukleja
29National Center for Nuclear Research (NCBJ), Warsaw, Poland
29,
A Ustyuzhanin
A Ustyuzhanin
35Yandex School of Data Analysis, Moscow, Russia
35,
U Uwer
U Uwer
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
C Vacca
C Vacca
16Sezione INFN di Cagliari, Cagliari, Italy
16,
V Vagnoni
V Vagnoni
15Sezione INFN di Bologna, Bologna, Italy
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
15,40,
A Valassi
A Valassi
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
S Valat
S Valat
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
G Valenti
G Valenti
15Sezione INFN di Bologna, Bologna, Italy
15,
R Vazquez Gomez
R Vazquez Gomez
19Laboratori Nazionali dell’INFN di Frascati, Frascati, Italy
19,
P Vazquez Regueiro
P Vazquez Regueiro
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
S Vecchi
S Vecchi
17Universita e INFN Ferrara, Ferrara, Italy
17,
M van Veghel
M van Veghel
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
J J Velthuis
J J Velthuis
48H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
48,
M Veltri
M Veltri
18Sezione INFN di Firenze, Florence, Italy
18,
G Veneziano
G Veneziano
57Department of Physics, University of Oxford, Oxford, UK
57,
A Venkateswaran
A Venkateswaran
61Syracuse University, Syracuse, NY USA
61,
T A Verlage
T A Verlage
9I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
9,
M Vernet
M Vernet
5Clermont Université, Université Blaise Pascal, CNRS/IN2P3, LPC, Clermont-Ferrand, France
5,
M Vesterinen
M Vesterinen
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
J V Viana Barbosa
J V Viana Barbosa
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
B Viaud
B Viaud
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
D Vieira
D Vieira
63University of Chinese Academy of Sciences, Beijing, China
63,
M Vieites Diaz
M Vieites Diaz
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
H Viemann
H Viemann
67Institut für Physik, Universität Rostock, Rostock, Germany
67,
X Vilasis-Cardona
X Vilasis-Cardona
38ICCUB, Universitat de Barcelona, Barcelona, Spain
38,
M Vitti
M Vitti
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
V Volkov
V Volkov
33Institute of Nuclear Physics, Moscow State University (SINP MSU), Moscow, Russia
33,
A Vollhardt
A Vollhardt
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
B Voneki
B Voneki
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
A Vorobyev
A Vorobyev
31Petersburg Nuclear Physics Institute (PNPI), Gatchina, Russia
31,
V Vorobyev
V Vorobyev
36Budker Institute of Nuclear Physics (SB RAS), Novosibirsk, Russia
36,
C Voß
C Voß
9I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
9,
J A de Vries
J A de Vries
43Nikhef National Institute for Subatomic Physics, Amsterdam, The Netherlands
43,
C Vázquez Sierra
C Vázquez Sierra
39Universidad de Santiago de Compostela, Santiago de Compostela, Spain
39,
R Waldi
R Waldi
67Institut für Physik, Universität Rostock, Rostock, Germany
67,
C Wallace
C Wallace
50Department of Physics, University of Warwick, Coventry, UK
50,
R Wallace
R Wallace
13School of Physics, University College Dublin, Dublin, Ireland
13,
J Walsh
J Walsh
24Sezione INFN di Pisa, Pisa, Italy
24,
J Wang
J Wang
61Syracuse University, Syracuse, NY USA
61,
D R Ward
D R Ward
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
H M Wark
H M Wark
54Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
54,
N K Watson
N K Watson
47University of Birmingham, Birmingham, UK
47,
D Websdale
D Websdale
55Imperial College London, London, UK
55,
A Weiden
A Weiden
42Physik-Institut, Universität Zürich, Zurich, Switzerland
42,
M Whitehead
M Whitehead
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
J Wicht
J Wicht
50Department of Physics, University of Warwick, Coventry, UK
50,
G Wilkinson
G Wilkinson
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
57Department of Physics, University of Oxford, Oxford, UK
40,57,
M Wilkinson
M Wilkinson
61Syracuse University, Syracuse, NY USA
61,
M Williams
M Williams
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
M P Williams
M P Williams
47University of Birmingham, Birmingham, UK
47,
M Williams
M Williams
58Massachusetts Institute of Technology, Cambridge, MA USA
58,
T Williams
T Williams
47University of Birmingham, Birmingham, UK
47,
F F Wilson
F F Wilson
51STFC Rutherford Appleton Laboratory, Didcot, UK
51,
J Wimberley
J Wimberley
60University of Maryland, College Park, MD USA
60,
M A Winn
M A Winn
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
J Wishahi
J Wishahi
10Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
10,
W Wislicki
W Wislicki
29National Center for Nuclear Research (NCBJ), Warsaw, Poland
29,
M Witek
M Witek
27Henryk Niewodniczanski Institute of Nuclear Physics Polish Academy of Sciences, Kraków, Poland
27,
G Wormser
G Wormser
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
S A Wotton
S A Wotton
49Cavendish Laboratory, University of Cambridge, Cambridge, UK
49,
K Wraight
K Wraight
53School of Physics and Astronomy, University of Glasgow, Glasgow, UK
53,
K Wyllie
K Wyllie
40European Organization for Nuclear Research (CERN), Geneva, Switzerland
40,
Y Xie
Y Xie
65Institute of Particle Physics, Central China Normal University, Wuhan, Hubei China
65,
Z Xu
Z Xu
4LAPP, Université Savoie Mont-Blanc, CNRS/IN2P3, Annecy-Le-Vieux, France
4,
Z Yang
Z Yang
3Center for High Energy Physics, Tsinghua University, Beijing, China
3,
Z Yang
Z Yang
60University of Maryland, College Park, MD USA
60,
Y Yao
Y Yao
61Syracuse University, Syracuse, NY USA
61,
H Yin
H Yin
65Institute of Particle Physics, Central China Normal University, Wuhan, Hubei China
65,
J Yu
J Yu
65Institute of Particle Physics, Central China Normal University, Wuhan, Hubei China
65,
X Yuan
X Yuan
61Syracuse University, Syracuse, NY USA
61,
O Yushchenko
O Yushchenko
37Institute for High Energy Physics (IHEP), Protvino, Russia
37,
K A Zarebski
K A Zarebski
47University of Birmingham, Birmingham, UK
47,
M Zavertyaev
M Zavertyaev
11Max-Planck-Institut für Kernphysik (MPIK), Heidelberg, Germany
11,
L Zhang
L Zhang
3Center for High Energy Physics, Tsinghua University, Beijing, China
3,
Y Zhang
Y Zhang
7LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
7,
A Zhelezov
A Zhelezov
12Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
12,
Y Zheng
Y Zheng
63University of Chinese Academy of Sciences, Beijing, China
63,
X Zhu
X Zhu
3Center for High Energy Physics, Tsinghua University, Beijing, China
3,
V Zhukov
V Zhukov
33Institute of Nuclear Physics, Moscow State University (SINP MSU), Moscow, Russia
33,
S Zucchelli
S Zucchelli
15Sezione INFN di Bologna, Bologna, Italy
15;
LHCb Collaboration71
 baryons to are suppressed by removing candidates close to the expected ellipses in the Armenteros–Podolanski (AP) plane [20]. In this plane the of the final-state particles under the pion mass hypothesis is plotted versus the longitudinal momentum asymmetry, defined as , where is the longitudinal momentum of the charged tracks. Both and are considered with respect to the direction of the mother particle. The decays are symmetrically distributed on the AP plane while
baryons to are suppressed by removing candidates close to the expected ellipses in the Armenteros–Podolanski (AP) plane [20]. In this plane the of the final-state particles under the pion mass hypothesis is plotted versus the longitudinal momentum asymmetry, defined as , where is the longitudinal momentum of the charged tracks. Both and are considered with respect to the direction of the mother particle. The decays are symmetrically distributed on the AP plane while  decays produce two ellipses at low and . A kaon veto, based on the response of the RICH detector, is used to suppress decays and other possible final states including a charged kaon.
decays produce two ellipses at low and . A kaon veto, based on the response of the RICH detector, is used to suppress decays and other possible final states including a charged kaon.