Abstract
We have shown that the key state in N2 reduction to two NH3 by the enzyme nitrogenase is the E4(4H), ‘Janus’ intermediate, which has accumulated four [e−/H+] and is poised to undergo reductive elimination of H2 coupled to N2 binding and activation. Initial 1H and 95Mo ENDOR studies of freeze-trapped E4(4H) revealed the catalytic multi-metallic cluster (FeMo-co) binds two Fe-bridging hydrides, [Fe-H-Fe]. However, the analysis failed to provide a satisfactory picture of the relative spatial relationships of the two [Fe-H-Fe]. Our recent density functional theory (DFT) study yielded a lowest-energy form, denoted E4(4H)(a), with two parallel Fe-H-Fe planes bridging pairs of ‘anchor’ Fe on the Fe2,3,6,7 face of FeMo-co. However, the relative energies of structures E4(4H)(b), with one bridging and one terminal hydride, and E4(4H)(c), with one pair of anchor Fe supporting two bridging hydrides, were not beyond the uncertainties of the calculation. Moreover, a structure of V-dependent nitrogenase resulted in a proposed structure analogous to E4(4H)(c), and additional structures have been proposed by DFT studies of others. To resolve the nature of hydride binding to the Janus intermediate, we performed exhaustive, high-resolution CW-stochastic 1H-ENDOR experiments using improved instrumentation, Mims 2H ENDOR, and a recently-developed pulsed-ENDOR protocol (‘PESTRE’) to obtain absolute hyperfine-interaction signs. These measurements are coupled to DFT structural models through an analytical point-dipole Hamiltonian for the hydride electron-nuclear dipolar coupling to its ‘anchoring’ Fe ions, an approach that overcomes limitations inherent in both experimental interpretation and computational accuracy. The result: the freeze-trapped, lowest-energy Janus intermediate structure is E4(4H)(a).
Graphical Abstract

Introduction
The Mo-dependent nitrogenase enzyme system comprises two component proteins. The Fe protein delivers electrons one at a time to the MoFe protein, where they are utilized to reduce substrate at the active-site iron-molybdenum cofactor ([7Fe-9S-Mo-C-R-homocitrate]; FeMo-co, Fig 1).1,2 We have established the proposed Lowe-Thorneley (LT) kinetic model for nitrogenase function, developed in the 1970s and 1980s,1,3,4 which describes the kinetics of transformations among catalytic intermediates, denoted En, where n is the number of electrons delivered from the nitrogenase Fe protein to the catalytic FeMo-co of the MoFe protein (Fig 2). A defining feature of this scheme is the accumulation of 4[e−/H+] before N2 is reduced, and the obligatory formation and release of one mole of H2 per mole of N2 reduced, with a limiting stoichiometry for enzyme-catalyzed nitrogen fixation given by eq 1,
| (1) |
which implies a stoichiometric enzymatic requirement for 8[e−/H+] per N2 reduced, rather than the chemically required 6[e−/H+], a central feature that was both baffling and disputed, and eventually even doubted by those who originally proposed it.1
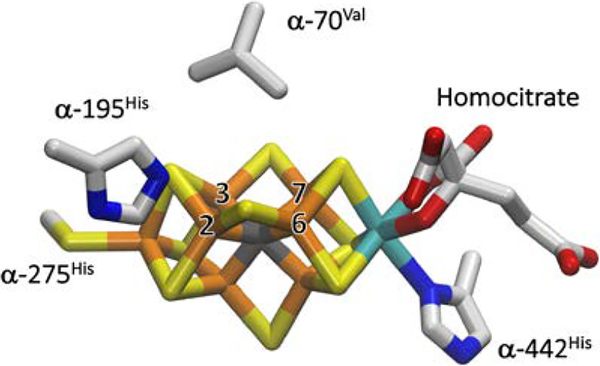
Figure 1.
Crystal structure of FeMo-co. Fe is show in rust, Mo in cyan, S in yellow, carbide in dark grey, carbon in light gray, N in blue and O in red. The Fe atoms of catalytic 4Fe-4S face are labelled as 2, 3, 6, and 7. The α−275Cys and α−442His FeMo-co ligands along with two amino acids, α−70Val and α−195His, that approach the FeMo-co are also shown. The image was created using PDB coordinate 2AFI.
Figure 2.
Simplified kinetic scheme for nitrogen reduction that focuses on the electron-accumulation and FeMo-co activation stages. En notation: n = number of [e−/H+] added to resting-state FeMo-co; in parentheses, stoichiometry of H/N bound to FeMo-co.
The key state in this scheme is E4(4H), the ‘Janus’ intermediate, which has accumulated four of the eight reducing equivalents required by eq 1: E4(4H) sits at a transition in the N2 reduction pathway, Fig 2, poised to ‘fall back’ to the E0 resting state by successive release of two H2,5 but equally poised to eliminate H2 and proceed to the reduction of N2 to two NH3 through the accumulation of four more equivalents, hence we have termed it, ‘Janus’.6 We freeze-trapped and studied the Janus intermediate by EPR/ENDOR spectroscopies, showing that it has accumulated four reducing equivalents stored as two [Fe-H-Fe] bridging hydrides.5,7,8 The location of the hydrides as bridges between Fe atoms plays a central mechanistic role. In a key contribution to catalytic efficiency, bridging hydrides are less susceptible to protonation than terminal hydrides, and so they diminish the tendency of FeMo-co to “fall back” towards the resting state by loss of reducing equivalents through hydride protonation and the formation of H2 (Fig 2). However, opposing this benefit, the bridging mode likewise lowers the reactivity of these hydrides for N2 reduction.9,10
The characterization of E4(4H) led to the experimental confirmation of the proposed stoichiometric requirement of eq 1, and to an understanding of the fundamental mechanistic role of the hydrides through the recognition that the enzyme can only be activated for N≡N binding and triple-bond cleavage through reductive elimination (re) of H2.6,11,12 We showed12 that the triple bond cleavage proceeds through a near-thermoneutral reductive elimination/oxidative addition (re/oa) equilibrium, as pictured in Fig 2. This process was subsequently explored through a computational analysis13 based on broken symmetry (BS) density functional theory (DFT) calculations. These showed how the E4(4H) enzyme state mechanistically couples exothermic H2 formation and release to the endothermic cleavage of the N2 triple bond, to create the near-thermoneutral re/oa equilibrium: re of the hydrides generates an H2 complex, but as inferred from experiment,14 H2 is only lost when displaced by N2, leading to an end-on Fe-N2 complex that proceeds to the diazene-level E4(2N2H) intermediate.6,11,12
These computations are distinguished by their exploration of the size and character of the computational model required to accurately describe the re activation of nitrogenase. They showed that to obtain an accurate picture it is necessary to include all the residues and waters interacting directly with FeMo-co, both via specific H-bond interactions and non-specific electrostatic interactions of FeMo-co with its environment, and that not all of these are evident from a mere inspection of the available crystal structures. However, these DFT calculations revealed the presence of various possible E4 isomers close in energy, which differ on the location of the four cofactor-bound hydrogens of E4(4H),13 and whose ordering is sensitive to the adopted DFT flavor, as highlighted in recent reports.13,15,16 Moreover, notorious issues related to the single-determinant nature of BS DFT, which result in a solution that is a superposition of states with a given secondary spin quantum number mS = S rather than a proper pure spin state S,17,18 add further uncertainties to the energy ordering of computationally identified E4 isomers. In fact, the energies of the proper pure spin states can be quite different from the BS DFT energies.
Because of the central role of E4(4H) as the culmination of the electron-accumulation phase of the nitrogenase cycle and the starting point for the key re of H2 and reduction of N2, it is of the highest importance to characterize its nature. Our original 1H ENDOR study concluded that FeMo-co in E4(4H) binds two metal-bridging hydrides, [Fe-H-M], based on the observation of spin delocalization onto the H and analysis of the anisotropic hydride hyperfine coupling tensors with an analytical description for a nucleus that is located at an arbitrary position relative to two spin-coupled paramagnetic metal ions, and that interacts by a through-space dipolar coupling with each of these ‘anchor’ ions.19,20 When combined with the results of a subsequent 95Mo ENDOR study,21 this treatment ruled out molybdenum as an anchor metal, thus implying the presence of two [Fe-H-Fe] bridging hydrides.21 Since then, this analytical treatment of bridging hydrides has been supported through its successful application to biomimetic inorganic hydrides, both terminal and metal-bridging.22–24
The initial 1H ENDOR study of of E4(4H) showed that the two [Fe-H-Fe] bridges have highly similar electronic properties. It further showed that they are differently oriented relative to the g-tensor of FeMo-co, but the analysis was unable to provide a satisfactory picture of the relative spatial relationships of the two bridging moieties.8 Our DFT study of the re/oa equilibrium yielded as the lowest-energy form of E4(4H) the structure E4(4H)(a) shown in Fig 3 with parallel Fe-H-Fe planes bridging two pairs of ‘anchor’ Fe on the Fe2,3,6,7 face of FeMo-co.13 Slightly higher in energy was structure E4(4H)(b), with one bridging and one terminal hydride, and still higher was E4(4H)(c), in which a single pair of anchor Fe supports two bridging hydrides, a ‘di-hydride15 dibridge’. However, the differences in energy between these states were not beyond the uncertainties of the calculation, and a structure of the VFe protein obtained by Einsle and coworkers indeed led them to propose a dibridge structure analogous to E4(4H)(c).25,26 Finally, a quite different ‘open’ structure, E4(3H;CH), with one [Fe-H-Fe] bridging hydride and a protonated interstitial carbide rather than a second hydride, denoted E4(3H;CH), was found at quite high energy. Other DFT studies proposed this structure to have a critical role in nitrogenase activity.27–30 Siegbahn further suggested that E4(3H;CH) is the precursor of a Fe-bound methyl intermediate where FeMoco has accumulated 7[e−/H+], denoted here as P-7 (referred to28 as E50), which was proposed to be the central catalytic species that undergoes re of H2.27,28
Fig. 3:
Lowest-energy structures of the Janus intermediate as seen in recent density functional theory computations13 E4(4H)(a,b,c), plus a high-energy structure with singly protonated carbide that has been proposed based on other computations, E4(3H;CH)26–29 and the P-7 structure proposed by Siegbahn,26,17 which results from the accumulation of 7 [e-/H+]. The relative electronic energies (ΔE in kJ/mol calculated at DFT/BP86 level) for E4(4H)(a,b,c) and E4(3H;CH) along with selected Fe-H distances (in Angstrom) from Ref. 13 are provided. Fe-H distances for P-7 from Ref. 17 are also given. Note that the Fe-H distances of a [Fe-H-Fe] are not typically equal. Irons are shown in rust, molybdenum in cyan, carbon in gray, sulfurs in yellow, protic hydrogens in green, and hydrides in red.
To resolve the nature of hydride binding to the Janus intermediate, we have carried out extensive, high-resolution 1H ENDOR measurements using the resolution-enhancing ‘stochastic’31 CW-ENDOR protocol performed on instrumentation greatly improved since our original study.8 These are complemented by use of a recently developed pulsed-ENDOR procedure to obtain absolute signs for hyperfine couplings,32 and by Mims pulsed 2H ENDOR measurements. These measurements are coupled to the structural DFT models through use of the analytical point-dipole Hamiltonian for the electron-nuclear dipolar interaction of the hydride to its ‘anchoring’ Fe ions, a powerful approach that overcomes limitations inherent in both experimental interpretation and computational chemistry accuracy. The result of this protocol is the identification of the lowest-energy structure of the Janus intermediate: E4(4H)(a) (Fig. 3).
Materials and Methods
Materials and Protein purifications
All reagents were obtained from SigmaAldrich (St. Louis, MO) or Fisher Scientific (Fair Lawn, NJ) and were used without further purification. Argon, N2, and acetylene gases were purchased from Air Liquide America Specialty Gases LLC (Plumsteadville, PA). The E4(4H) intermediate has been characterized and behaves similarly in three Azotobacter vinelandii MoFe variants: wild-type;33,12 singly-substituted α−70Ile; doubly-substituted α−70Val→Ile/α−195His→Gln MoFe protein.8 As use of the variants permits the freeze trapping of MoFe with higher populations of E4(4H),8 experiments were carried out both with the singly and doubly-substituted MoFe protein. The enzymes were purified and samples were prepared as has been described.34
ENDOR spectroscopy
Q-band CW ENDOR spectra were collected at 2K on a spectrometer with a helium immersion Dewar as previously reported.35 For many systems the original ‘Feher-style’ CW ENDOR protocol36–38 (100 kHz field modulation; phase-sensitive detection of the dispersion, rapid-passage signal; 2 K) and variants give far better signal/noise (S/N) ratios than pulsed ENDOR measurements. However the effects of slow nuclear relaxation on an rf frequency-swept CW ENDOR spectrum can distort the ENDOR responses, cause poor ‘baselines’, suppress some lines while inverting others, and lower the resolution, and such effects were present in the 2005 CW frequency-swept ENDOR spectra of E4(4H) (see Fig S1). These difficulties are overcome here by the use of Stochastic ENDOR, first reported by Brueggeman and Niklas,39 a hybrid method that employs field-modulated CW-EPR but pulsed rf31 In addition, S/N has been improved by the introduction of a low-noise microwave amplifier, The collection of ENDOR spectra employed broadening of the RF to 100 kHz to improve signal-to-noise.40
Q-band pulsed Mims and Davies ENDOR spectra41 were collected at 2K on a spectrometer with a helium immersion Dewar as previously reported42 In the Mims experiment, the ENDOR intensities are modulated by the response factor (R) inherent to the experiment, which is a function of the product of the hyperfine coupling (A) and the time between the second and third microwave pulses in the three-pulse sequence (τ), and given by R ≈ [1 − cos(2πAτ)]. When Aτ = n (n = 0,1,2,…), the ENDOR response is at a minimum, resulting in hyperfine ‘suppression holes’ in the Mims spectra.41
For a single molecular orientation and for nuclei with nuclear spin I = 1/2 (1H), the ENDOR transitions for the mS = ±1/2 electron manifolds are observed, to first order, at frequencies ν± = |νn ± A/2|, where νn is the nuclear Larmor frequency and A is the orientation-dependent hyperfine coupling. Additional quadrupole splittings for 2H (I = 1) are not resolved The 1,2H frequencies are related by νH/νD = AH/AD = gH/gD = 6.51. At the low- and high-field edges of the EPR spectrum (g1 and g3, respectively), ENDOR interrogates only a single molecular orientation (‘single-crystal-like’ position). At intermediate fields, however, ENDOR interrogates a well-defined subset of molecular orientations.43 The complete hyperfine and quadrupole tensor principal values and their orientations relative to g are obtained by analyzing a 2D field-frequency (‘orientation-selective’) pattern of ENDOR spectra taken at numerous fields across the EPR envelope, as described.43–45 ENDOR simulations were performed in MATLAB with the easyspin (v5.0) toolbox.46
Absolute hyperfine sign determination
Signs of the hyperfine couplings (more specifically, the sign of gNucANuc) were obtained by the PESTRE protocol,32 a pulsed-ENDOR multi-sequence comprising multiple Davies ENDOR sequences, carried out in three distinct experimental phases: (I) an EPR saturation phase (RF off) of 100 Davies sequences whose spin-echo intensities quickly converge to the steady-state “baseline” (BSL); (II) 24 sequences, each of which contains a fixed RF frequency; and (III) an EPR recovery phase (RF off) of 388 sequences during which the spin echo intensity of the spin system polarized by the ENDOR transitions induced in II, the ‘dynamic reference level (DRL)’, relaxes to BSL. In the slow-relaxation regime that applies to the E4(4H) intermediate at helium temperatures, the sign of ANuc is unambiguously given by the sign of the decaying difference in echo intensities, (DRL – BSL), as observed in III. When ANuc > 0 (and gNuc > 0), if ν+/ν- is being interrogated, the DRL relaxes to the BSL from below/above. When ANuc < 0, the opposite behavior is observed.
Density functional theory calculations
The structure of the E4 isomers investigated in the present study (Fig. 3) was taken from previous BS-DFT calculations.13 All structures were obtained for an electron count for E0 in the oxidation state [Mo3+3Fe2+4Fe3+].17,18 The adopted structural model of the active site comprises 198 atoms and includes the FeMo-co with truncated modifications of the α−275Cys, α−442His ligands (Azotobacter vinelandii numbering), R-homocitrate, and all of the MoFe protein residues and water molecules that engage hydrogen-bonding interactions with the FeMo-co, or are known to be important of the catalytic activity (α−70Val and α−96Arg).
Results
ENDOR spectroscopy of the hydrides in E4(4H)
The implementation of the stochastic ENDOR protocol, coupled with the improved spectrometer sensitivity, yields spectra of remarkable resolution with strong orientation selection, as illustrated in Fig 4. A full 2D field-frequency 1H stochastic CW ENDOR patterns has been collected across the EPR envelope for E4(4H) in H2O and D2O buffers, and the extent of the improvement is seen by comparison with the 2D pattern reported previously, Fig S1. However, before presenting the new 2D pattern, we first navigate a ‘decision tree’ that leads to assignment of the features within the spectra to one of the two hydrides, H1 and H2. This in turn enables the analysis of the 2D pattern in terms of the magnitudes and relative signs of the two hyperfine coupling tensors. We then describe determination of the absolute signs of these tensors and, central to this report, the relative orientations of the principal axes of the two tensors. Finally, we employ the analytic ‘anchor’ model for the anisotropic coupling tensor of a bridging hydride, which allows us to use the symmetries of the [Fe-H-Fe] hyperfine tensors and their relative orientations for H1 and H2 to distinguish among the proposed structures for the E4(4H) intermediate (Fig 3).
Fig. 4.
35 GHz 1H stochastic-field modulation detected (stochastic CW) ENDOR spectra of E4(4H) acquired at g = 1.991 and 1.964 (Black); simulations generated as described below (Red). The signal with ν0(1H) ± ~3MHz, with both positive and negative features, represents transient responses from weakly coupled, more distant protons.38 Experimental Conditions: Microwave frequency, 35.045 GHz; modulation amplitude, 2.7 G; microwave power, 1 μW; RF power, 10 W; temperature, 2 K; stochastic sequence (sample/delay/RF), 1/3/3 ms; the bandwidth of the RF excitation was broadened to 100 kHz.
Alternative models for 1H ENDOR patterns
As shown in Fig 5A, the single-crystal-like 1H ENDOR spectra of E4(4H) collected at g1 and g3 each shows hyperfine-split doublets from two strongly-coupled protons; the peaks disappear in samples prepared in D2O (not shown), showing these hydrons are exchangeable. The resolution of two signals immediately shows that the two protons are magnetically inequivalent, with different hyperfine-tensor orientations and/or principal values. However, as shown below, at intermediate fields the responses from the two protons spread and overlap strongly. As a first ‘branch-point’ in a decision ‘tree’ for determining the hyperfine tensors, one must correlate the signals denoted H1 and H2 at g1 with the two signals at g3 (Fig. 5A). In one alternative, A(H1) > A(H2) at both g1 and g3, i.e. the signals of the two hydrides at the extremal g-values do not ‘cross’. In the second alternative, the signals do ‘cross’, i.e. A(H1) > A(H2) at g1 but A(H1) < A(H2) at g3.
Fig 5.
A) Single-crystal-like ENDOR spectra collected at g1 and g3 (slight splittings in H1 peaks at g1 indicate the rigorously single-crystal limit has not been reached). The figure illustrates the two possible scenarios by which the hydride signals can evolve across the EPR envelope in a 2D field-frequency pattern of ENDOR spectra collected from g1 to g3. In the first scenario, the patterns of H1 and H2 do not ‘cross’ at intermediate fields, i.e. A(H1) > A(H2) at g1 and A(H1) > A(H2) at g3 (solid lines). In the second scenario, the patterns of H1 and H2 do ‘cross’ at intermediate fields, so that A(H1) > A(H2) at g1 but A(H1) < A(H2) at g3 (dashed lines). B) Alternative models for hydride binding to FeMo-co, where a 4Fe4S face is depicted as an oval. Both hydrides may be terminal (model denoted T/T) or bridging (B/B), or the intermediate may contain one terminal and one bridging hydride, denoted T/B or B/T depending on the assignment to H1 and H2 (compare part A of this Figure). For each of these four models, either of the two ‘crossing’ scenarios illustrated in A can obtain, leading to a total of 8 possible bases for the 2D field-frequency plot.
As a second ‘branch-point’, we re-visit our previous assignment of these two strongly-coupled 1H ENDOR signals to two [Fe-H-Fe] bridging hydrides with rhombic anisotropic coupling tensors, considering all possible assignments of these two signals to terminal and bridging hydrides. Studies of crystallographically characterized inorganic complexes22–24 have thoroughly validated our previous assumption that a terminal hydride yields an approximately axial hyperfine tensor, whereas a bridging hydride is expected to give a hyperfine tensor whose anisotropic component is nearly rhombic. There are four alternative models for assigning binding mode to the two distinct hydridic species bound to FeMo-co (Fig. 5B): Both hydrides may be terminal (denoted T/T) or bridging (B/B); one hydride may be terminal and the other bridging, which itself comprises two cases differing in the assignment to H1 and H2 (T/B or B/T). In addition, for each of these four models, the hydride signals can evolve as the magnetic field is moved across the EPR envelope according to either a ‘crossing’ or ‘non-crossing’ scenario.
To distinguish among the resulting eight alternatives, and then to optimize the hyperfine tensors the two hydrides for the proper alternative, we tested the eight possibilities against the full 2D field-frequency pattern of stochastic CW ENDOR spectra collected across the EPR envelope of E4(4H), Fig 6. A limitation of the 1H stochastic CW ENDOR experiment is that, like Davies pulsed ENDOR, it suppresses the weakly coupled features predicted to appear at fields near g1 and around g2 (Figs. 6 and 7). So as not to lose this information, 2H Mims ENDOR measurements were performed on the intermediate generated during turnover in D2O buffer. After scaling by the ratio of the proton/deuteron nuclear g-values, these spectra are inserted into the figures.
Fig. 6.
Full 35 GHz 1H stochastic CW field-frequency ENDOR pattern for E4(4H). Experimental data (black), and sum of simulations for 1H1 and 1H2 (red), normalized at each g value. Curves running across the 2D plot were added as a guide to the eye, connecting the outer edges of 1H1 (blue) and 1H2 (green) spectral features along the different g values. Simulation parameters (B/B model) are listed in Table 1. At selected g values, a complementary 1H field-swept CW or 2H Mims ENDOR spectrum (thinner line; 2H spectra were collected on D2O turnover samples and scaled to 1H frequencies by factor gN(1H)/gN(2H) = 6.5) is shown to illustrate the match of experiment and simulation in the low-frequency region; for further 2H measurements, Fig S12. Experimental Conditions: 1H stochastic CW ENDOR: same as in Fig. 4. 1H field-swept CW ENDOR: Microwave frequency, 35.036 GHz; modulation amplitude, 0.7 G; microwave power, 1 μW; RF power, 10 W; RF scan speed, 1 MHz/s; temperature, 2 K; the bandwidth of the RF excitation was broadened to 100 kHz. 2H Mims ENDOR: 34.890 GHz; π/2 = 50 ns; τ = 400 ns; tRF = 30 μs; repetition time, 50 ms; temperature, 2 K.
Fig. 7.
Absolute hyperfine sign determination for hydride H1 by PESTRE at g = 1.977. A) 35 GHz 1H stochastic CW (thicker black line) and Davies (thinner black line) ENDOR responses around the ν+ branch of the 1H1 doublet, and sum (red) and separate 1H1 (blue), 1H2 (green) simulations. Simulation parameters (B/B model) are listed in Table 1. B) 1H PESTRE trace collected from the ν+ branch of the 1H1 doublet. Experimental Conditions: A) 1H stochastic CW ENDOR: same as in Fig. 4. 1H Davies ENDOR: Microwave frequency, 34.776 GHz; π = 60 ns; τ = 450 ns; tRF = 35 μs; repetition time, 100 ms; tmix = 5 μs; temperature, 2 K. B) Same as in A (1H Davies) except for: repetition time, 200 ms; RF frequency, 65.5 MHz.
To determine the correct ‘scenario’, we optimized as best as possible simulations of the 2D patterns for each of the models, while constraining the anisotropic component of a ‘T’ hydrogen to have a nearly axial (dipolar) symmetry, and a ‘B’ hydrogen to have a rhombic symmetry (Figs S2–9). Within each model we constrained the calculated spectra at g1 and g3 to match experiment precisely, while varying the principal values and orientations of the hyperfine tensors to optimize the agreement with experiment at intermediate fields. The best simulations for each model are shown in Figs. 5, S9. While all calculated patterns by construction show perfect agreement with experimental frequencies at single-crystal-like fields near the edges of the EPR spectrum, some show poor agreement in those shapes, and for every model but one, the match with experiment is poor at fields away from the edges: only the B/B model with ‘crossing’ H1 and H2 signals at intermediate fields successfully matches our experimental results.
Having established that the hydride 1H spectra obey the ‘crossing’ B/B model, its parameters were further refined. Overlaid on the spectra of Fig 6 are sums of optimized simulation that employ the parameters listed in Table 1. Figure S5 displays the 2D pattern and simulations of Fig 6 as well as the 2D pattern overlain with the individual simulations for the two hydrides. These provide the basis for determining the listed signs of the hyperfine interactions, which are established in the next subsection.
Table 1.
Experimentally determined [Fe-1H-Fe] 1H Hyperfine Coupling Parameters for E4(4H)
| H1 | H2 | |
|---|---|---|
| T | [−13.2, 0.0, +13.2] | +[13.2, −13.2, 0.0] |
| [α, β, γ]b | 0, 20, 20 | 10, 30, 0 |
1H hyperfine tensor component, uncertainties, ~ 0.1 MHz.
Euler angles [α, β, γ] defined according to the zyz convention describe rotation of A eigenframe away from the g reference frame; uncertainties, ≲ 2–30
The two hyperfine tensors have near-equal isotropic components and, both anisotropic (traceless) tensor contributions are not only completely rhombic, namely with one null component and the remaining two components having equal magnitude and opposite signs, but with the non-zero components for the two hydrides being of equal magnitude. Of central importance to this study is the relative orientation of these two tensors, to which we return below. As can be seen in Fig 6, the simulations generated with the hyperfine tensors listed in Table 1 provide a remarkably precise correspondence with the extremely high-resolution experimental stochastic CW spectra across the 2D pattern plus the scaled 2H spectra. For completeness and for use below, Fig S5 shows both the 2D pattern with summed simulations and the same pattern showing the individual simulations for H1 and H2.
Absolute signs of hydride hyperfine couplings
Earlier, it was impossible to obtain absolute signs of the H1 and H2 hyperfine couplings, and thus of aiso, or the relative orientations of the positive/negative components of the two anisotropic interactions. We here do so through use of the PESTRE multi-Davies sequence pulsed ENDOR protocol for determining hyperfine signs32 (see Materials and Methods). This protocol involves monitoring an ENDOR transition from the nucleus in question through application of a Davies ENDOR multi-sequence at a fixed RF frequency, and thus requires measurement at frequencies where the responses of the two hydrides do not overlap. The assignment of ENDOR peaks to H1 and H2 is simple in the spectra collected at the edges of the EPR signal (Figs 6 and S5), but these fields also have the lowest ENDOR signal intensity, and as a result the PESTRE response at these fields is not readily obtained. However, the excellent resolution and precise simulation of the new 1H ENDOR data allows us to identify ENDOR features associated with an individual hydride even in spectra at intermediate g-values, where the overall patterns of the two hydrides overlap extensively (Figs 6, S5 and S10). Thus, at g = 1.977 1H1 exhibits an isolated sharp peak with ν+ = 65.5 MHz whose 1H Davies ENDOR response (Fig. 7A) is strong enough to obtain a 1H PESTRE trace. In the corresponding 1H1 PESTRE trace, shown in Fig. 7B, the ν+ DRLδ intensity in the PESTRE multi-sequence relaxes to the BSL level from below, which for 1H (gN > 0) implies A > 0; as the magnitude of A is governed by aiso, thus means that aiso > 0 for 1H1.
In the 1H ENDOR spectrum at g2, both branches of the ν+/ν- doublet for H2 exhibit features that are isolated from H1 signals, and that have sufficient intensity to yield satisfactory 1H PESTRE traces (Fig. 8). As required, the two branches give opposite DRL responses: the ν- DRLδ relaxes to the BSL from above, whereas the ν+ DRLδ relaxes from below. This again implies that A > 0 and aiso > 0 for the 1H2 nucleus. This result was confirmed by an additional 1H PESTRE measurement of the ν+ = 70.8 MHz signal from 1H2 at g = 1.970 (Fig. S11).
Fig. 8.
Absolute hyperfine sign determination for hydride H2 by PESTRE at g2 = 2.008. A) 35 GHz 1H stochastic CW (thicker black line) and Davies (thinner black line) ENDOR responses around the ν- (black arrow) and ν+ (purple arrow) branch of the 1H2 doublet, and sum (red) and separate 1H1 (blue), 1H2 (green) simulations. Simulation parameters (B/B model) are listed in Table 1. B) 1H PESTRE traces collected from the ν- (black) and ν+ (purple) branch of the 1H2 doublet. Experimental Conditions: A) 1H stochastic CW ENDOR: same as in Fig. 4. 1H Davies ENDOR: Microwave frequency, 34.757 GHz; π = 80 ns; τ = 600 ns; tRF = 35 μs; repetition time, 50 ms; tmix = 5 μs; temperature, 2 K. B) Same as in A (1H Davies) except for: repetition time, 150 ms; RF frequency, 41.1 (ν-) and 64.7 (ν+) MHz.
With the hyperfine signs as determined from the 1H PESTRE measurements, the present ENDOR measurements and analysis provide signed hydride hyperfine tensors with extraordinary precision. The result is hyperfine tensors for 1H1 and 1H2 hyperfine tensors whose anisotropic components T not only are fully rhombic, namely of the form, each exhibiting a null component [t, 0, -t], but also exhibit identical, although permuted, principal values within the precision of these measurements (Table 1). We emphasize that the tabulated couplings naturally arise from the fitting, rather than being imposed as a constraint on the fitting. The hydrides are not, however, chemically identical; the isotropic components, although similar, are not identical: aiso ~ +22, +25 MHz for H1, H2. The availability of both magnitudes and signs of the hydride couplings provides a strong constraint on computations of the geometric and electronic structure of the hydride-bound FeMo-co of E4(4H) as will be seen below.
Relative Orientations of H1/H2 Hyperfine Tensors
The small values for the Euler angles relating the hyperfine tensor of each hydride to the g-tensor axis frame (Table 1) imply that the hyperfine (A), and thus the anisotropic dipole-coupling (T), tensors of both hydrides are essentially coaxial with g and, thus, are themselves coaxial; indeed, Table 2 (below) explicitly shows that each of the three corresponding pairs of principal axes for the hyperfine couplings of the two hydrides subtends an angle of only a few degrees. However, although, the anisotropic tensors for the two hydrides have components with identical values, as noted above, these values are permuted with respect to each other: A3(H1)⇿A1(H2); A1(H1) ⇿A2(H2); A2(H1)⇿A3(H2), as indicated in Chart 1, which shows that the ‘clockwise’ permutation of the tensor components of H1 yield tensor H2, and the counterclockwise permutation of the H2 components yields tensor H1 Stated alternatively, each hydride has dipole-components, [±(t = 13.2 MHz); 0] but the permutation of the tensor components orients the axes of the tensor so that parallel (‖) components are as follows: {–t(H1)‖+t(H2)}, {0(H1)‖-t(H2)}, {+t(H1)‖0(H2)}. The differences in the 2D patterns for H1 and H2, not least the differences in the single-crystal-like spectra at g1 and g3, arise primarily because of this permutation. Of central importance, through an analysis presented below, the permuted relative orientations of the components of the coaxial tensors provide the basis for distinguishing among the possible structures of the Janus intermediate presented in Fig 3.
Table 2.
Angles Between Corresponding H1/H2 Components of the H1, H2 Rhombic Dipolar Tensors(1)
| {−t(H1)‖+t(H2)} | {0(H1)‖−t(H2)} | {+t(H1)‖0(H2)} | {0(H1)‖0(H2)} | |
|---|---|---|---|---|
| Experiment | 13 | 10 | 11 | 85 |
| B3LYP | 16 | 11 | 16 | 81 |
| B3LYP | 54(2) | 46 | 46(2) | 99.7(3) |
| B3LYP | 49 | 46 | 56 | 65 |
Signs in headings for DFT reesults, (−/+) etc, indicate signs of t1 and t2. Estimated uncertainties in experimental angles, ~4–5°. Reversing all signs yields equivalent results.
The calculated angles are the complement; an angle and its complement are experimentally indistinguishable.
Theses angles are fixed by the (−/+) signs to equal the dihedral angle between [Fe-H-Fe] planes.
Chart 1:
1H Tensor Permutations
ENDOR spectroscopy of S-H protons of E4(4H)
According to the kinetic model for nitrogenase catalysis,1,3,4 FeMo-co accumulate a proton as well as an electron at each stage of reduction, the four [e−/H+] at the E4(4H) stage taking the form of the two bridging hydrides and two protons. Based on experimental and theoretical studies of Fe-S-based clusters,47–54 these protons can be reasonably assumed to reside on the sulfurs of FeMo-co, presumably in the vicinity of the bridging hydrides, to form either an (SH)− bridge or a terminal –SH through cleavage of one Fe-S bond.13 We know of only one EPR study to date55 that describes 1H hyperfine couplings for [Fe–(SH)n–Fe] (n = 1, 2) complexes. This reported isotropic 1H hyperfine couplings for complexes composed of low-spin Fe ions, aiso ~ 6 MHz for n = 1 and ~ 4 MHz for n = 2. In contrast to these models, [Fe–(SH)–Fe] bridges in FeMo-co would likely involve high-spin Fe ions, which would reduce the contributions to the net isotropic 1H hyperfine interaction from each Fe ion by a factor of (2S)−1.56 1H hyperfine couplings of bridging (SH)− in the E4(4H) intermediate are thus expected to be dominated by the dipolar interactions with the metal ions bound to the sulfurs. Use of the analytical ‘anchor’ dipolar coupling equations indicates that these should have maximum values approach ~10 MHz, and thus the ENDOR signals could be easily buried within the broad ENDOR intensity around the Larmor frequency.
To directly examine exchangeable proton sites without interference from 1H signals associated with nearby residues, we recorded a 2D field-frequency pattern of 2H Mims ENDOR spectra on the D2O turnover sample (Fig. S12). The g2 spectrum is shown in Fig. 9A. It exhibits a sharp doublet (A(2H) ≈ 1.4 MHz ↔ ~ 9 MHz (1H) associated with the H1 bridging hydride whose coupling increases as the field is moved towards g1 or g3 (Fig. S12). This signal rides on the ‘tail’ of the unresolved 2H signal centered at νD. As shown in the expansion of Fig 10B, this signal has a maximum breadth of Amax(2H) ≈ 1.2 – 1.5 MHz, corresponding to a maximum 1H coupling, proton coupling, Amax(1H) ≈ 8–10 MHz)H1. As the environment of the FeMo-co active face was long-ago shown to be quite ‘dry’, with a few solvent-exchangeable protons having hyperfine couplings A < 3 MHz, these signals can be confidently attributed to a bridging or semi-bridging S-H. We note that an (1H-S−) released from the cluster and moved over ~7 Å away57 would instead give an extremely small 1H coupling, A < 1 MHz.
Fig. 9.
2K 35 GHz1,2H Mims ENDOR spectra of H2O and D2O turnover samples at g2 = 2.008. Experimental data (black and purple), and sum of simulations for1,2H1 and1,2H2 (red). Mims holes in the 2H intensitiy indicated as open triangles show the extent of the 2H+ intensity. Simulation parameters for hydrides (B/B model) are listed in Table 1 and were scaled by factor gN(2H)/gN(1H) = 6.5−1 for 2H spectra. Experimental Conditions: A) Same as in Fig. 6. B) same as A except, microwave frequency, 34.80–34.87 GHz; repetition time, 100 ms; temperature.
Fig 10:
Reduced dipolar tensor components, ai = Ti/t1, calculated as a function of t2/t1 for a hydride bridge with R = 2.52Å, r1 = 1.65,, r2 = 1.69. The two a1 nulls give similar angles, γ.
Analysis of Anisotropic Hyperfine Couplings
Hyperfine Couplings to Metal Hydrides.
Our work with enzymatic intermediates and inorganic complexes with both terminal and bridging hydrides22–24 has taught us the characteristic signatures of hydrides bound to paramagnetic metal centers. (i) They exhibit large isotropic couplings that for the high-spin ions of FeMo-co would primarily arise from spin delocalization into the M-H bond(s), (ii) The anisotropic hyperfine coupling tensor of a terminal hydride exhibits a ‘dipolar’ form, T ≈ [-t, -t, 2t], where the unique direction corresponds to the M-H vector. (iii) The anisotropic coupling to a hydride interacting with two metal ions depends jointly on the distances to the two ‘anchor’ M’s distances and on their spin. When the spin on the ‘second’ metal is small and/or its distance to the hydride is much larger than to the ‘first’, the anisotropic coupling can approach the dipolar form of a terminal M-H. However, in sharp contrast, a rhombic coupling, T ≈ [-t, 0, t] is a definitive signature of a hydride bridge that has significant interactions with both ‘anchor’ metal ions.
Point-Dipole Approaches.
Our recent work has further shown that we can calculate the dipolar tensor of a hydride, T, bound to ions of a multinuclear center with high accuracy by summing the through-space point-dipole interactions with the spins on each of the spin-bearing metal-ions (Fe, Mo) of a paramagnetic center,
| (2a) |
where the 3×3 matrices Mi incorporate the orientation of the Mi-H vector relative to the FeMo-co molecular frame and the weight of an individual [Mi–H] point-dipole interaction is determined by the parameter, ti, whose value is determined by three factors: (1) a dipolar term, which depends on fundamental constants and the inverse-cube of the Mi-H distance, r; (2) the covalency parameter di (0 < di ≤ 1), i.e., the fraction of the unpaired spin density, ρi, of an ion of spin Si that remains on the ion after it undergoes covalent interactions with its ligands, as obtained from a BS-DFT computation, di =|ρi|/2Si; and (3) the vector-coupling coefficient, Ki, for ion i obtained from the spin-coupling model for FeMo-co, in which its total spin is determined by exchange-coupling between metal ions. The point-dipole approach is particularly appropriate for nitrogenase and other enzymes that involve high-spin Fe ions, because to a first approximation they should be spherical ‘balls of spin’ – exactly so for FeIII (S = 5/2) and very nearly so even for FeII (S = 2), and thus behave like point dipoles when interacting with distant nuclei.
For the FeMo-co multimetallic cluster one can numerically diagonalize the full matrix sum over all metal ions, T, to obtain predicted principal values for the observed cluster anisotropic coupling tensor,
| (3) |
plus the orientation of that tensor relative to the molecular frame. The ‘anchor’ approach to the determination of T instead focuses on the dominant contribution to eqs 2 and 3, the interactions of an [Fe-H-Fe] hydride with its two ‘anchoring’ FeMo-co Fe ions. The anchor model is reliable for a multi-metallic cluster such as FeMo-co because the ti exhibit an r−3 dependence on the distance r between metal-ion and hydride: the longer distances between a hydride and the non-anchor metal ions minimizes the interactions with these other ions and, consequently, their contribution to the full sum over ions, eq 2. This expectation was supported by comparison of calculations with the anchor-model equations of eq 4 to an implementation of eq 3 for test-case, spin-projected (S = 1/2) DFT-derived states for the E4(4H)(a).
[Fe-H-Fe] Bridge:
A signal benefit of the ‘anchor’ approach to an [Fe-H-Fe] moiety is that the sum of dipolar interactions between two Fe atoms and a bridging hydride at arbitrary relative position, Chart 2, yields analytic equations for the components of the tensor, T, and the tensor orientation, eqs 4,19,20,58
| (4a) |
| (4b) |
| (4c) |
| (4d) |
The components, T1, T3 lie in the [Fe-H-Fe] plane, rotated away from the Fe-Fe axis by the angle, γ, about the normal to that plane (T2) (T3 lies along that axis for γ = 0). Of particular note, these equations reveal that both the relative magnitudes of the components of the anisotropic coupling tensor and the tensor orientation (eq 4d) depend on the geometry of the center (expressed here in terms of the two internal angles, β1, β2) and a single spin/structure-dependent parameter, the ratio of the ti for the anchor metal ions, t2/t1, while the absolute signs and values of the components scale with the parameter t1.
Chart 2.
It is straightforward to solve the analytical equations for the anchor model for conditions under which the dipolar tensor, T, becomes fully rhombic, namely with one null component. Although this tensor symmetry has been observed in biomimetic di-iron complexes and in E4(4H), such behavior is by no means required. For a typical DFT-determined bridging hydride geometry, the ‘reduced’ tensor components,
as given by eqs 4, are plotted in Fig 10 as a function of t2/t1, which for such a fixed geometry varies with the ratio of the factors, (Kidi), eq 2a. Figure 10 shows that for such a bridging geometry, (i) the tensor is rhombic with the component T2 = 0 if t2/t1 = −1, and (ii) the component T1 = 0 for no more than two values of t2/t1 > 0, and (iii) for highly asymmetric interactions (extremely different ti) there will be no solutions. Thus, there are two distinct scenarios in which the signature rhombic symmetry of the hyperfine tensors of the two (B/B) E4(4H) hydrides (Table 1) can be precisely matched by the tensor arising from the interactions of a hydride bridge with the spins of its two anchor Fe ions.
i) When t1 and t2 have opposite signs and T is rhombic because t1 = -t2 (eq 4c and Fig 10), the null tensor element is T2, oriented along the normal to the [Fe-H-Fe] plane, eq 4c (Chart 3). This imposes an exact constraint on the ratios of the Kidi products in terms of the ratio of the Fe-H distances, ri:
| (5) |
The two non-zero components T2 and T3 have opposite signs and equal magnitudes, and are rotated around the normal/T2 by the angle γ (eq 4d)
Chart 3.
ii) If t1 and t2 have the same sign, t2/t1 > 0, then solving eqs 4 for a null tensor element is often (but not always) possible. For all plausible FeMo-co [Fe-H-Fe] geometries and ratios t2/t1, there are at most two values of t2/t1 that yield nulls (eg. Fig 10), in which cases the null lies in the Fe-H-Fe plane, T1 = 0 (Chart 4). The two non-zero components T2 and T3 have opposite signs and equal magnitudes (eq 4c), T2 = -T3, determined by specifying the value of either ti, and T1, T3 are rotated by the angle γ (eq 4d). Such a situation has been seen for delocalized mixed-valence Fe2 complexes.22,24
Chart 4.
[Fe3-H] ‘Triangle:
The P-7 structure recently proposed by Siegbahn28 has two moieties that have a hydride lying roughly in the plane of three Fe ions, as illustrated in Chart 5. Although we show below that the question of whether this model can describe E4(4H) is ultimately decided by other arguments, for completeness we note that the anchor model can even provide guidance in considering the hyperfine couplings of such a moiety. Thus, if t3 = -(t1+t2), then the dipolar tensor is rhombic with T2 = 0, and if t1, t2 > 0 (as shown), then –T3 = T1 > 0 and 0 ≤ γ ≤ 150, whereas if (t1, t2) are of opposite sign then γ approaches ± 450 depending on which one is greater in magnitude.
Chart 5.
Testing the Janus Structural Models
The central goal of this study is the discrimination among computationally proposed structures of the E4(4H) (S = 1/2) Janus intermediate, Fig 3. We do so by integrating BS-DFT-derived structures with the key characteristics of the E4(4H) intermediate obtained from high-resolution ENDOR experiments. These key characteristics shown in this report are: (i) There are two metal hydrides bound to the FeMo-co cluster, and they exhibit nearly-identical hyperfine tensor components; (ii) The tensors are very closely coaxial (and coaxial with g); (iii) The two hyperfine tensors are dominated by large, nearly-equal isotropic couplings. (iv) The anisotropic hyperfine interaction tensors, T, for the two hydrides are perfectly rhombic within experimental error (B/B 2D ENDOR pattern); (v) Although the components of the two anisotropic tensors have the same magnitudes, the signed tensor components of one hydride are ‘permuted’ with respect to those of the other, with correspondence between the two hydride tensors as summarized in Table 2 and Chart 1.
The analysis presented below focusses primarily on the relative orientations of the signed hyperfine components of the rhombic H1 and H2 hyperfine tensors. With this approach, we need not employ fine details of the BS-DFT spin densities to calculate tensor components, a task that approaches, and indeed likely passes, their limits of reliability. Instead, to determine whether a BS-DFT state with a given arrangement of two hydrides (Fig 3) is capable of reproducing the ‘permuted’ rhombic tensors of experiment, one need only incorporate into the anchor equations the [Fe-H-Fe] geometries for each hydride, which are robustly determined, solve for the ti that yield a rhombic dipolar tensor for each, and then compare the calculated relative orientations with experiment (Fig 10, Table 2).
Calculations with this protocol firstly show that it is robust against quite substantial variations in the structure of the Fe-H-Fe fragment. Secondly, the protocol eliminates any residual uncertainties caused by the limitations of the BS-DFT energetics and the secondary contributions from spins on the other Fe ions: the experimental tensors indeed are rhombic and this procedure reproduces their symmetry by construction. Finally, as noted above, the anchor equations are supported by comparisons with anisotropic ‘DFT-tensors’ obtained by summing the dipolar interactions with all the metal ions. The relevant metrical and electronic-structural parameters of the FeMo-co E4 states visualized in Fig 3 and used in the protocol are listed in Table S1, which includes structural data obtained from DFT calculations using both BP86 and B3LYP exchange and correlation functionals;13 the comparisons with experiment are carried out for structures generated with both functionals.
E4(4H)(a), with parallel hydride bridges.
For both BP86 and B3LYP functionals, the lowest-lying structure is E4(4H)(a), which features two bridging hydrides, [Fe2-H1-Fe6] and [Fe3-H2-Fe7] (Fig 3). In E4(4H)(a) the planes of the [Fe2-H-Fe6] and [Fe3-H-Fe7] hydride bridges are essentially orthogonal to the Fe2,3,6,7 face and nearly parallel to each other, with the angle between their normals (dihedral angle between [Fe-H-Fe] planes) of only τ ~ 10° (Table S1). Both functionals predict a cluster of BS states with essentially the same geometry and only slightly different energy (within 20 kJ/mol from the lowest-energy solution), yet differing in the orientations of the anchor-Fe spins13.
For each functional, there are states within this cluster of BS solutions that cannot satisfy the experimental restrictions on the dipolar interaction tensors of the two hydrides as schematized in Chart 1 (and see, Tables 1, 2). For example, we find anchor spin patterns (t2; t6)(t3; t7) = (−/−)(−/−), where each hydride bridges Fe atoms with parallel spins (as in Chart 4), and (−/+)(+/−), where each hydride bridges Fe atoms with antiparallel spins (as in Chart 3). These BS states yield two nearly identical hydride hyperfine tensors, with positive aiso and coaxial rhombic dipolar tensors, but the corresponding tensor components are nearly parallel, rather than permuted (Chart 1). However, the cluster of low-laying BS solutions also includes states where the [Fe2-H-Fe6] hydride has anti-parallel anchor spins, implying opposite signs of their dipolar coupling parameters, (t2; t6) ⟷ (−/+) while the [Fe3-H-Fe7] hydride has parallel anchor spins, with (t3; t7) ⟷ (+/+), as schematized in Chart 6. The above ‘anchor’ analysis shows that when such a spin arrangement exhibits two hydrides with tensors of rhombic symmetry the [Fe2-H1-Fe6] hydride has its null tensor component normal to its Fe-H-Fe plane (T2 = 0) with T3 < 0; the [Fe3-H2-Fe7] hydride has T1 = 0 and T3 > 0 (both in-plane); the tensors are rotated about the normal to their [Fe-H-Fe] normal (T2 direction) by an angle, γ, that ranges from 31°−54° for the two functionals (Table 2). Thus, by examining the patterns of signs of the interaction parameters ti in combination with DFT-computed E4(4H)(a) geometries as inputs into the anchor equations, we can predict the relative orientations of rhombic [Fe2-H-Fe6]/[Fe3-H-Fe7] hydride tensors that are possible for a structure. In this way we can determine whether a model (Fig 3) exhibits tensors that match the experimentally determined angles between the corresponding tensor components of H1 and H2.
Chart 6.
As can be seen from the results reported in Table 2, tensors for E4(4H)(a) as computed using the structure from either functional and ‘anchor signs’ (−/+) for [Fe2-H1-Fe6], (+/+) for [Fe3-H2-Fe7] accurately reproduce the experimentally observed coaxial, rhombic dipolar coupling tensors with near-parallel ‘permuted components’ and near-orthogonal nulls, as drawn in Chart 6.
E4(4H)(c), ‘di-Hydride, di-bridge’.
E4(4H)(c) (Fig 3) features a di-hydride ‘di-bridge’ with both hydrides anchored by Fe2 and Fe6. Again, both functionals give a cluster of BS solutions with essentially the same geometric structure differing only slightly in energy,13 with members of the cluster exhibiting both parallel [e.g., (+/+)] and antiparallel [e.g., (−/+)] Fe2/Fe6 anchor spins as reflected in the signs of the ti. In the parallel case, a rhombic tensor for each hydride must have the null component lying in its [Fe-H-Fe] plane, while in the anit-parallel case the null is normal to its plane. With both BP86 and B3LYP functionals the anchor-model dipolar tensor for each hydride is rotated around the normal to its [Fe-H-Fe] plane by an angle of γ ~ 450; in the computational models the two planes are rotated relative to each other about the Fe-Fe vector with large dihedral angles, (BP86, 77.7°; B3LYP, 99.7°). As above for the E4(4H)(a) structure, we have calculated the angles between the near-coaxial ‘permuted’ component of the calculated rhombic hydride dipolar tensors, for both parallel (+/+) and antiparallel (−/+) spin orientations (signs of the ti). As can be seen from the results reported in Table 2, the calculated angles between corresponding components of the ‘permuted’ tensors for the E4(4H)(c) structure, whether considering states with (+/+) or (−/+) anchor Fe, strongly disagree with the experimentally determined angles, and in addition, the null components are not orthogonal for the (+/+) configuration. This violation of the experimental constraints on the relative tensor orientations provides strong evidence against such a structure for E4(4H).59
E4(4H)(b).
This structure contains one Fe2-H-Fe6 bridging hydride and one terminal hydride on Fe2 (Fig 3). Application of the ‘anchor’ model to this structure shows that it cannot yield a rhombic tensor for both hydrides: when the bridging hydride does exhibit a rhombic tensor, then the other would exhibit the dipolar-type tensor of a terminal hydride. Thus, this structure spectroscopically would correspond to the T/B, B/T models for the 1H ENDOR patterns, which have been ruled out above. In short, this model is incompatible with experiment and cannot describe the Janus intermediate.
E4(3H;CH).
The E4(3H;CH) structure is no less easily dismissed by comparison to the present experiments. This structure contains only one hydride, in a near-symmetrical bridging [Fe2-H-Fe6] arrangement (average Fe-H distance, 1.65 Å). The central carbide of the resting FeMo-co is protonated, with the resulting C-H fragment near-symmetrically coordinated ‘above’ a square plane of the four Fe atoms, Fe2,6,4,5 on the surface of the ‘exploded’ FeMo-co cluster [Fe4(CH)], with the [Fe2-H-Fe6] hydride roughly lying in this plane.
To begin, the DFT computations show that the C-H fragment bears essentially zero spin density. Thus, this 1H atom would not have the large isotropic coupling associated with H1, H2 seen experimentally (Table 1). The C-1H hydrogen will undergo through-space anisotropic dipolar couplings to the four ‘psuedo-anchor’ Fe ions that bind the carbon. However, consideration of a peudo-anchor model that incorporates only couplings to the Fe of the Fe4 plane (or of the more complete of eq 3) indicates that it would be impossible for the diagonalized sum of these couplings to yield a rhombic tensor whose components are equal to those of the hydride bridge, but permuted. In fact, the dipolar couplings to the C-1H hydrogen will be much less than to the hydride bridge. The [Fe2-1H-Fe6] bridge is nearly symmetric, with average Fe-1H distance of 1.65Å, whereas the average distance between the 1H bonded to the C and the Fe ions of the Fe4 ‘anchor base’ is 2.64Å. Thus, for sets of Fe di spin-coefficients (eq 2a) for the two hydrides with the comparable values needed to achieve rhombic dipolar tensors, the difference in distances would make the magnitudes of the Fe-H dipolar coupling ti parameters for the pseudo-anchors of the C-1H would be much smaller than those for the anchors of the bridging hydride, |ti(Fe4)/tj(bridge)| ≈ 1/4, and the resulting non-zero dipolar tensor components for C-1H would be correspondingly smaller. Indeed, with both a small aiso and small dipolar coupling for such a C-1H moiety, if one were present it would be expected to give ENDOR signals that fall within the signals from the –SH protons, rather than correspond to one of the H1, H2 Fe-bound hydrides.
Thus, we conclude that the 1H of a E4(3H;CH) C-1H fragment cannot give a hyperfine tensor – neither isotropic nor dipolar contributions – that matches that of the hydride bridge as seen in experiment, and that E4(3H;CH) and similar models with a singly-protonated carbide do not describe the Janus E4(4H) intermediate.
P-7.
This model can be dismissed based on the properties of E4(4H) and its reactivities. (i) That E4(4H) has accumulated 4[e−/H+], was cleanly shown by its return to E0 by two sequential steps of hydride protonation with the overall loss of two H2 molecules;5 instead, P-7 has accumulated seven [e−/H+] and cannot return to E0 by loss of two H2 molecules. (ii) E4(4H) is an odd-electron system with S = 1/2 whose EPR spectrum is well established8,12 and whose ENDOR properties we report here in detail; P-7 has an even number of electrons and thus an integer-spin (proposed as S = 0), which is incompatible with the experimental evidence. (iii) E4(4H) undergoes an experimentally observed, kinetically facile, near-thermoneutral conversion to the EPR-active (S = 1/2) E4(2N2H) through re loss of H2 and binding/reaction of N2; re by P-7 would create an even-electron state (also proposed as S = 0), which is again incompatible with experiment.
The relaxation of E4(4H) to E0 needs further elaboration. The proposal that the P-7 state, with seven accumulated [e−/H+], is the Janus intermediate (the state that binds N2 upon re of H2) instead of E4(4H), with four accumulated [e−/H+], is embedded in a mechanism that involves an activation of the true E0 through accumulation of 5 [e−/H+] to generate a state, which we will denote P-5 (referred to as A50 or E30 in Ref.28), after which the enzyme cycles through an 8[e−/H+] catalytic process that begins and ends with P-5 and produces 2NH3. However, no such pre-activation process has been observed in the many pre-steady state measurements carried out over the years.1,3 Moreover, a two-step relaxation of the even-electron P-7 with release of two H2 molecules would produce the even-electron P-3, whereas the measurements of the relaxation of the odd-electron S = 1/2 E4(4H) with release of 2H2 unambiguously show that it relaxes directly to the EPR-active odd-electron E0 (S = 3/2) resting state. The structure of this state has been beautifully revealed as having a trigonal-prismatic Fe6C core with ‘intercalated’ carbide,60 not the EPR-silent (or integer-spin) P-5 state with a peripheral iron-bound methyl group as would be required by such a mechanism. And there is no doubt that E4(4H) indeed relaxes to the E0 state. That the crystalline E0 and the putative E0 formed by E4(4H) relaxation are identical is established by the identity of the EPR spectra of the solution E0 formed by relaxation and that of the crystalline E0, both of which precisely match the long-established EPR spectrum of ‘as-isolated’ Mo-nitrogenase.
Conclusions
Exceptionally high resolution 2D field-frequency 35 GHz 1H ENDOR patterns confirm and highly refine previous reports that the E4(4H) nitrogenase Janus intermediate contains two [Fe-H-Fe] bridging hydrides, and in addition characterize the protons bound to sulfides that accompany the bridging hydrides.
Detailed analysis of the 2D field-frequency ENDOR patterns unequivocally show that there are two hydrogenic species bound to the cluster, which exhibit nearly-identical hyperfine tensor components (Table 1). The tensors are dominated by large, nearly-equal isotropic couplings, and thus these species are associated with metal hydrides, not protons bound to sulfur, which, as expected, have much smaller couplings. The signs of the isotropic couplings have been established for the first time. The components of the anisotropic hyperfine interaction tensors determined here for the two E4(4H) hydrides are identical and perfectly rhombic within experimental error (B/B 2D ENDOR pattern). Such rhombic dipolar interactions are a signature of bridging hydrides, as discussed in our earlier reports, and established in studies of enzyme active sites19 and model studies.22–24 95Mo ENDOR studies showed that the 95Mo hyperfine coupling for this intermediate is about five-fold too small for Mo to be an anchor metal ion of either hydride, leaving two Fe atoms as the only possible anchors for each of two [Fe-H-Fe] hydride bridges. As we show here, the anisotropic tensors of the two hydrides are nearly coaxial and have identical components, but the tensor components of one hydride are ‘permuted’ with respect to those of the other. This property is captured by noting the near-orthogonality of the equivalent tensor components for the two hydrides and corresponding, near-exact coaxiality of the permuted components found in the present, high-precision measurements, Table 2. The determination of the absolute signs of the tensor components for each of the two hydrides, as presented in the table, is of particular importance in relating these tensors to structure.
These experimental findings were complemented by a careful theoretical analysis of structural models of the E4(4H) state. We recently explored possible E4(4H) structures using broken symmetry DFT calculations. Consistent with the experimental evidence, these calculations identified the E4(4H)(a), where two hydrides bridging the Fe2/Fe6 and Fe3/Fe7 pairs of atoms, as the lowest-energy isomer. However, variations between different flavors of DFT exchange and correlation functionals, while having small impact on geometries, can appreciably affect the energy ordering.13,15,16 These considerations, along with the inability of DFT to accurately describe multi-reference electronic systems, such as FeMo-co, makes it difficult to determine the nature of E4(4H) based on DFT-derived relative energies alone. To overcome these limitations, the present spectroscopic properties have been combined with DFT calculations to test five possible structures for the Janus intermediate (Fig 3: E4(4H)(a), E4(4H)(b), E4(4H)(c), E4(3H;CH) and P-7), primarily through use of a model hyperfine Hamiltonian based on point dipolar interaction with the electron-spins of the ‘anchoring’ Fe ions. The spectroscopic signatures for each of these structures have been assessed and compared with experiment.
Of the five structures of Fig 3, three can be dismissed as qualitatively in disagreement with the ENDOR results: P-7, E4(3H;CH) and E4(4H)(b). Indeed, P-7 has the wrong ‘electron count’ (7 not 4[e−/H+]) and is not even an odd-electron, EPR-active state. Neither of the other two contains two bridging hydrides, much less two that can exhibit the signature rhombic, coaxial and permuted, anisotropic hyperfine coupling tensors, while the 1H of the protonated carbide of E4(3H;CH) and other such models would fail to show the large measured isotropic coupling. A third structure, E4(4H)(c), does exhibit two hydrides, both of which bridge the same pair of Fe ions (Fe2 and Fe6), but the resulting relative orientations of the two hydride dipolar tensors are in strong quantitative disagreement with those found experimentally. Only the E4(4H)(a) structure can accurately account for the observed presence of two bridging hydrides with rhombic anisotropic tensors that are coaxial, but with permuted tensor components (Table 2). Taken altogether, these results allow us to assign E4(4H)(a), with [Fe2-H-Fe6] and [Fe3-H-Fe7] hydride bridges whose planes are essentially perpendicular to the Fe2,3,6,7 FeMo-co face and parallel to each other (Fig 3), as the lowest-energy FeMo-co state of the Janus intermediate, trapped during the relatively slow hand-freezing process used to generate the samples for ENDOR measurements. Although these measurements were performed at 2K, EPR spectra indicate that no other isomer of Janus becomes populated by ~25 K12,14 (above which the signal becomes relaxation-broadened). However, as calculations have indicated the presence of isomers, such as E4(4H)(b/c) (Fig 3), very close in energy, we can envision that at ambient temperatures the E4(4H) hydrides may become fluxional, with dynamic population of multiple isomers.
Supplementary Material
Acknowledgments
This work was supported by the National Institutes of Health GM 111097 and the National Science Foundation MCB 1515981 (to B.M.H.), the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), Division of Chemical Sciences, Geosciences, and Bio-Sciences award number DE-AC05-76RL01830/FWP66476 (S.R.), and U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), Physical Biosciences award number DESC0010687 (L.C.S). V.H benefitted from support by a postdoctoral fellowship from the German National Academy of Sciences Leopoldina, LPDS 2013-10. PNNL is operated by Battelle for the U.S. DOE. Calculations were performed using the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility (Contract No. DE-AC02-05CH11231) and the Cascade supercomputer at EMSL, a DOE Office of Science User Facility sponsored by the Office of Biological and Environmental Research.
Footnotes
Supporting Information. Figures S1–S12; Table S1
References
- (1).Burgess BK; Lowe DJ Mechanism of Molybdenum Nitrogenase. Chem Rev 1996, 96, 2983–3012. [DOI] [PubMed] [Google Scholar]
- (2).Seefeldt LC; Hoffman BM; Dean DR Mechanism of Mo-Dependent Nitrogenase. Annu. Rev. Biochem 2009, 78, 701–722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Thorneley RNF; Lowe DJ Kinetics and Mechanism of the Nitrogenase Enzyme System. Metal Ions in Biology 1985, 7, 221–284. [Google Scholar]
- (4).Wilson PE; Nyborg AC; Watt GD Duplication and Extension of the Thorneley and Lowe Kinetic Model for Klebsiella Pneumoniae Nitrogenase Catalysis Using a Mathematica Software Platform. Biophysical Chemistry 2001, 91, 281–304. [DOI] [PubMed] [Google Scholar]
- (5).Lukoyanov D; Barney BM; Dean DR; Seefeldt LC; Hoffman BM Connecting Nitrogenase Intermediates with the Kinetic Scheme for N2 Reduction by a Relaxation Protocol and Identification of the N2 Binding State. PNAS 2007, 104, 1451–1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Hoffman BM; Lukoyanov D; Dean DR; Seefeldt LC Nitrogenase: A Draft Mechanism. Acc. Chem. Res 2013, 46, 587–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Lukoyanov D; Yang ZY; Duval S; Danyal K; Dean DR; Seefeldt LC; Hoffman BM A Confirmation of the Quench-Cryoannealing Relaxation Protocol for Identifying Reduction States of Freeze-Trapped Nitrogenase Intermediates. Inorg. Chem 2014, 53, 3688–3693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Igarashi RY; Laryukhin M; Dos Santos PC; Lee HI; Dean DR; Seefeldt LC; Hoffman BM Trapping H− Bound to the Nitrogenase FeMo-Cofactor Active Site During H2 Evolution: Characterization by ENDOR Spectroscopy. J. Am. Chem. Soc 2005, 127, 6231–6241. [DOI] [PubMed] [Google Scholar]
- (9).Crabtree RH: The Organometallic Chemistry of the Transition Metals; 5th ed.; Wiley: Hoboken, N.J., 2009. [Google Scholar]
- (10).Peruzzini M; Poli R; Editors: Recent Advances in Hydride Chemistry; Elsevier Science B.V.: Amsterdam, Netherlands, 2001. [Google Scholar]
- (11).Hoffman BM; Lukoyanov D; Yang ZY; Dean DR; Seefeldt LC Mechanism of Nitrogen Fixation by Nitrogenase: The Next Stage. Chem Rev 2014, 114, 4041–4062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Lukoyanov D; Khadka N; Yang ZY; Dean DR; Seefeldt LC; Hoffman BM Reductive Elimination of H2 Activates Nitrogenase to Reduce the N≡N Triple Bond: Characterization of the E4(4H) Janus Intermediate in Wild-Type Enzyme. J. Am. Chem. Soc 2016, 138, 10674–10683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Raugei S; Seefeldt LC; Hoffman BM Critical Computational Analysis Illuminates the Reductive-Elimination Mechanism That Activates Nitrogenase for N2; Reduction. Proceedings of the National Academy of Sciences 2018, 115, E10521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Lukoyanov D; Khadka N; Dean DR; Raugei S; Seefeldt LC; Hoffman BM Photoinduced Reductive Elimination of H2 from the Nitrogenase Dihydride (Janus) State Involves a FeMo-Cofactor-H2 Intermediate. Inorg. Chem 2017, 56, 2233–2240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Cao L; Caldararu O; Ryde U Protonation and Reduction of the FeMo Cluster in Nitrogenase Studied by QM/MM Calculations. Journal of Chemical Theory and Computation 2018. [DOI] [PubMed] [Google Scholar]
- (16).Cao L; Ryde U Extremely Large Differences in DFT Energies for Nitrogenase Models. Phys. Chem. Chem. Phys 2019, 21, 2480–2488. [DOI] [PubMed] [Google Scholar]
- (17).Bjornsson R; Lima FA; Spatzal T; Weyhermüller T; Glatzel P; Bill E; Einsle O; Neese F; DeBeer S Identification of a Spin-Coupled Mo(III) in the Nitrogenase Iron–Molybdenum Cofactor. Chemical Science 2014, 5, 3096–3103. [Google Scholar]
- (18).Bjornsson R; Neese F; DeBeer S Revisiting the Mössbauer Isomer Shifts of the FeMoco Cluster of Nitrogenase and the Cofactor Charge. Inorg. Chem 2017, 56, 1470–1477. [DOI] [PubMed] [Google Scholar]
- (19).Willems J-P; Lee H-I; Burdi D; Doan PE; Stubbe J; Hoffman BM Identification of the Protonated Oxygenic Ligands of Ribonucleotide Reductase Intermediate X by Q-Band 1,2H CW and Pulsed ENDOR. J. Am. Chem. Soc 1997, 119, 9816–9824. [Google Scholar]
- (20).Randall DW; Gelasco A; Caudle MT; Pecoraro VL; Britt RD Ese-ENDOR and Eseem Characterization of Water and Methanol Ligation to a Dinuclear Mn(III)Mn(IV) Complex. J. Am. Chem. Soc 1997, 119, 4481–4491. [Google Scholar]
- (21).Lukoyanov D; Yang Z-Y; Dean DR; Seefeldt LC; Hoffman BM Is Mo Involved in Hydride Binding by the Four-Electron Reduced (E4) Intermediate of the Nitrogenase MoFe Protein? J. Am. Chem. Soc 2010, 132, 2526–2527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Kinney RA; Saouma CT; Peters JC; Hoffman BM Modeling the Signatures of Hydrides in Metalloenzymes: ENDOR Analysis of a Di-Iron Fe(μ-NH)(μ-H)Fe Core. J. Am. Chem. Soc 2012, 134, 12637–12647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Kinney RA; Hetterscheid DGH; Hanna BS; Schrock RR; Hoffman BM Formation of {[HIPTN3N]Mo(III)H}- by Heterolytic Cleavage of H2 as Established by EPR and ENDOR Spectroscopy. Inorg. Chem 2010, 49, 704–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Yang H; Rittle J; Marts AR; Peters JC; Hoffman BM ENDOR Characterization of (N2)FeII(M-H)2FeI(N2)-: A Spectroscopic Model for N2 Binding by the Di-μ-Hydrido Nitrogenase Janus Intermediate. Inorg. Chem 2018, 57, 12323–12330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Sippel D; Einsle O The Structure of Vanadium Nitrogenase Reveals an Unusual Bridging Ligand. Nat Chem Biol 2017, 13, 956–960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Rohde M; Sippel D; Trncik C; Andrade SLA; Einsle O The Critical E4 State of Nitrogenase Catalysis. Biochemistry 2018, 57, 5497–5504. [DOI] [PubMed] [Google Scholar]
- (27).Siegbahn PEM Is There Computational Support for an Unprotonated Carbon in the E4 State of Nitrogenase? J. Comput. Chem 2017, 39, 743–747. [DOI] [PubMed] [Google Scholar]
- (28).Siegbahn PEM Model Calculations Suggest That the Central Carbon in the FeMo-Cofactor of Nitrogenase Becomes Protonated in the Process of Nitrogen Fixation. J. Am. Chem. Soc 2016, 138, 10485–10495. [DOI] [PubMed] [Google Scholar]
- (29).McKee ML A New Nitrogenase Mechanism Using a CFe8S9 Model: Does H2 Elimination Activate the Complex to N2 Addition to the Central Carbon Atom? J. Phys. Chem. A 2016, 120, 754–764. [DOI] [PubMed] [Google Scholar]
- (30).Rao L; Xu X; Adamo C Theoretical Investigation on the Role of the Central Carbon Atom and Close Protein Environment on the Nitrogen Reduction in Mo Nitrogenase. ACS Catal. 2016, 6, 1567–1577. [Google Scholar]
- (31).Bruggemann W; Niklas JR Stochastic ENDOR. J. Magn. Reson., Ser. A 1994, 108, 25–29. [Google Scholar]
- (32).Doan PE Combining Steady-State and Dynamic Methods for Determining Absolute Signs of Hyperfine Interactions: Pulsed ENDOR Saturation and Recovery (PESTRE). J. Magn. Reson 2011, 208, 76–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Lukoyanov DA; Khadka N; Yang Z-Y; Dean DR; Seefeldt LC; Hoffman BM Hydride Conformers of the Nitrogenase FeMo-Cofactor Two-Electron Reduced State E2(2H), Assigned Using Cryogenic Intra Electron Paramagnetic Resonance Cavity Photolysis. Inorg. Chem 2018, 57, 6847–6852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Christiansen J; Goodwin PJ; Lanzilotta WN; Seefeldt LC; Dean DR Catalytic and Biophysical Properties of a Nitrogenase Apo-MoFe Protein Produced by a Nifb-Deletion Mutant of Azotobacter Vinelandii. Biochemistry 1998, 37, 12611–12623. [DOI] [PubMed] [Google Scholar]
- (35).Werst MM; Davoust CE; Hoffman BM Ligand Spin Densities in Blue Copper Proteins by Q-Band 1H and 14N ENDOR Spectroscopy. J. Am. Chem. Soc 1991, 113, 1533–1538. [Google Scholar]
- (36).Feher G Electron Spin Resonance Experiments on Donors in Silicon. I. Electronic Structure of Donors by the Electron Nuclear Double Resonance Technique. Physical Review 1959, 114, 1219–1244. [Google Scholar]
- (37).Feher G Observation of Nuclear Magnetic Resonances Via the Electron Spin Resonance Line. Physical Review 1956, 103, 834–835. [Google Scholar]
- (38).Doan PE; Gurbiel RJ; Hoffman BM The Ups and Downs of Feher-Style ENDOR. Appl. Magn. Reson 2007, 31, 649–663. [Google Scholar]
- (39).Brueggemann W; Niklas JR Stochastic ENDOR. Journal of Magnetic Resonance, Series A 1994, 108, 25–29. [Google Scholar]
- (40).Hoffman BM; DeRose VJ; Ong JL; Davoust CE Sensitivity Enhancement in Field-Modulated CW ENDOR Via RF Bandwidth Broadening. J. Magn. Reson 1994, 110, 52–57. [Google Scholar]
- (41).Schweiger A; Jeschke G: Principles of Pulse Electron Paramagnetic Resonance; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- (42).Davoust CE; Doan PE; Hoffman BM Q-Band Pulsed Electron Spin-Echo Spectrometer and Its Application to ENDOR and Eseem. J. Magn. Reson 1996, 119, 38–44. [Google Scholar]
- (43).Hoffman BM; Martinsen J; Venters RA General-Theory of Polycrystalline ENDOR Patterns - G and Hyperfine Tensors of Arbitrary Symmetry and Relative Orientation. J. Magn. Reson 1984, 59, 110–123. [Google Scholar]
- (44).Hoffman BM Electron Nuclear Double Resonance (ENDOR) of Metalloenzymes. Acc. Chem. Res 1991, 24, 164–170. [Google Scholar]
- (45).Doan PE: The Past, Present, and Future of Orientation-Selected ENDOR Analysis: Solving the Challenges of Dipolar-Coupled Nuclei In Paramagnetic Resonance of Metallobiomolecules; Telser J, Ed.; American Chemical Society, 2003; pp 55–81. [Google Scholar]
- (46).Stoll S; Schweiger A Easyspin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR. J. Magn. Reson 2006, 178, 42–55. [DOI] [PubMed] [Google Scholar]
- (47).Shen B; Martin LL; Butt JN; Armstrong FA; Stout CD; Jensen GM; Stephens PJ; La Mar GN; Gorst CM; Burgess BK Azotobacter Vinelandii Ferredoxin I. Aspartate 15 Facilitates Proton Transfer to the Reduced Iron-Sulfur [3Fe-4S] Cluster. J. Biol. Chem 1993, 268, 25928–25939. [PubMed] [Google Scholar]
- (48).Leggate EJ; Bill E; Essigke T; Ullmann GM; Hirst J Formation and Characterization of an All-Ferrous Rieske Cluster and Stabilization of the [2Fe-2S]0 Core by Protonation. Proc. Natl. Acad. Sci. U.S.A 2004, 101, 10913–10918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Henderson RA Mechanistic Studies on Synthetic Fe-S-Based Clusters and Their Relevance to the Action of Nitrogenases. Chem Rev 2005, 105, 2365–2437. [DOI] [PubMed] [Google Scholar]
- (50).Henderson RA Proton Transfer to Synthetic Fe-S-Based Clusters. Coord. Chem. Rev 2005, 249, 1841–1856. [Google Scholar]
- (51).Noodleman L; Peng CY; Case DA; Mouesca JM Orbital Interactions, Electron Delocalization and Spin Coupling in Iron-Sulfur Clusters. Coord. Chem. Rev 1995, 144, 199–244. [Google Scholar]
- (52).Rod TH; Norskov JK Modeling the Nitrogenase FeMo Cofactor. J. Am. Chem. Soc 2000, 122, 12751–12763. [Google Scholar]
- (53).Chen K; Hirst J; Camba R; Bonagura CA; Stout CD; Burgess BK; Armstrong FA Atomically Defined Mechanism for Proton Transfer to a Buried Redox Centre in a Protein. Nature 2000, 405, 814. [DOI] [PubMed] [Google Scholar]
- (54).Hirst J; Duff JLC; Jameson GNL; Kemper MA; Burgess BK; Armstrong FA Kinetics and Mechanism of Redox-Coupled, Long-Range Proton Transfer in an Iron-Sulfur Protein. Investigation by Fast-Scan Protein-Film Voltammetry. J. Am. Chem. Soc 1998, 120, 7085–7094. [Google Scholar]
- (55).Keizer PN; Krusic PJ; Morton JR; Preston KF Thiolato-Bridged and Selenato-Bridged Dinuclear Iron Carbonyl Radicals. J. Am. Chem. Soc 1991, 113, 5454–5456. [Google Scholar]
- (56).Atherton NM: Principles of Electron Spin Resonance; Ellis Horwood: New York, 1993. [Google Scholar]
- (57).Sippel D; Rohde M; Netzer J; Trncik C; Gies J; Grunau K; Djurdjevic I; Decamps L; Andrade SLA; Einsle O A Bound Reaction Intermediate Sheds Light on the Mechanism of Nitrogenase. Science 2018, 1484–1489. [DOI] [PubMed] [Google Scholar]
- (58).Eq 4a was suggested as illuminating by a knowledgeable reviewer; 4b-d are from ref 18, with β2 here being the complement of β2 defined in ref 18. As the tensor-orientation angle, γ, is a function of the two angles, we use this original two-angle formulation of ref 18 in eq 4b–d, noting, however that for a given geometry, one can express tensor components in terms of any two geometric parameters and the law of cosines.
- (59).For completeness, we note that no state in which the two hydrides share a common vertex (cv), such as one bridging Fe2 and Fe6, the second bridging Fe2 and Fe3, has been found in BS-DFT computations even at extremely high energies, so such structures are not considered.
- (60).Spatzal T; Aksoyoglu M; Zhang LM; Andrade SLA; Schleicher E; Weber S; Rees DC; Einsle O Evidence for Interstitial Carbon in Nitrogenase FeMo Cofactor. Science 2011, 334, 940–940. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.