Screening human embryos for polygenic traits has limited utility

Summary

The increasing proportion of variance in human complex traits explained by polygenic scores, along with progress in preimplantation genetic diagnosis, suggest the possibility of screening embryos for traits such as height or cognitive ability. However, the expected outcomes of embryo screening are unclear, which undermines discussion of associated ethical concerns. Here, we use theory, simulations, and real data to evaluate the potential gain of embryo screening, defined as the difference in trait value between the top-scoring embryo and the average embryo. The gain increases very slowly with the number of embryos, but more rapidly with the variance explained by the score. Given current technology, the average gain due to screening would be ≈2.5cm for height and ≈2.5 IQ points for cognitive ability. These mean values are accompanied by wide confidence intervals, and indeed, in large nuclear families, the majority of children top-scoring for height are not the tallest.

Graphical Abstract

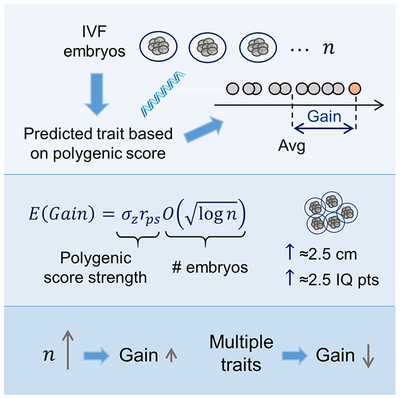
In Brief:

Recent progress in genetic testing of embryos has made it technically feasible to profile IVF embryos for polygenic traits such as height or IQ, but simulations, models, and empirical data show that the gain in trait value when selecting the top-scoring embryo is currently limited and uncertain.

Introduction

The use of biotechnology to influence the genetic composition of human embryos in the absence of specific disease risk raises many ethical concerns, and the recent live births resulting from human embryonic CRISPR editing have heightened global attention to these issues (Coller, 2019; National Academies of Sciences Engineering and Medicine, 2017). Currently, the most practical approach to genetic “enhancement” of embryos is preimplantation genetic screening of IVF embryos. Preimplantation genetic diagnosis and screening (Sullivan-Pyke and Dokras, 2018) have been utilized for years to avoid implantation of embryos harboring monogenic disease-causing alleles or aneuploidies. Recently, it also became technically feasible to generate accurate genome-wide genotypes from single-cell input (Kumar et al., 2015). This development, coupled to recent progress in complex traits genetics, has made it possible to genetically screen embryos for polygenic traits, and has raised the prospect of “designer babies” (The Economist, 2018).

Perhaps the most controversial potential application of polygenic embryo selection would be selection for intelligence, especially given the abhorrent history of the early-20^th century eugenics movement (Tabery, 2015). While most ethicists are deeply troubled by such prospects, at least one prominent scholar has suggested that there is an ethical obligation for parents to “select the best children” (Savulescu, 2001). In our view, any discussion of the ethics of embryo selection would ideally be informed by quantification of the expected utility of polygenic selection, either as of today, or as reasonably projected into the future. In this report, we thus utilize statistical and empirical methods to evaluate the potential effects of human embryo selection for polygenic traits.

Polygenic scores (PS) are derived from large-scale genome-wide association studies (GWAS) of complex traits, which can be quantitative (such as intelligence or height) or categorical (such as disease status, in which case they are often referred to as ‘polygenic risk scores’) (Wray et al., 2013). A PS is the count of effect alleles in an individual’s genome, weighted by each allele’s strength of association with the trait of interest in an independent GWAS (International Schizophrenia Consortium, 2009). The predictive power of a PS is usually represented by $r_{\text{ps}}^2$, or the proportion of variance of the quantitative trait explained by the PS. To date, the largest GWAS of intelligence (Davies et al., 2018; Savage et al., 2018) has demonstrated a relatively modest out-of-sample $r_{\text{ps}}^2$ (≈5%), despite large sample sizes (n≈300,000 individuals). By contrast, recent large-scale GWASs of height have attained $r_{\text{ps}}^2$ of approximately 25%, demonstrating a highly polygenic genetic architecture similar to intelligence (Yengo et al., 2018a). Consequently, in the present report, we analyze height in addition to cognitive ability, which also allows us to exploit several datasets in which height data, but not intelligence data, are available.

PSs are typically evaluated on a cohort basis, and are not used to differentiate one individual from another (although a recent report has demonstrated that, for an extraordinarily tall NBA player, the PS for height was >4 standard deviations above the population mean (Sexton et al., 2018)). In order for polygenic embryo selection to hold potential utility (independent of ethical considerations), PSs must provide sufficient predictive power to differentiate between embryos within the restricted range of genetic variance available in a single family, and with a finite number of embryos. Two reports utilizing only mathematical modeling have suggested that substantial effect sizes for embryonic selection are possible (Branwen, 2016; Shulman and Bostrom, 2014). But to our knowledge, despite the widespread application of polygenic scores to complex traits and precision medicine in the research literature (Torkamani et al., 2018), no published studies have empirically examined the possibilities and limitations of a polygenic approach to embryo selection.

We consider here embryo selection in the context of a hypothetical IVF cycle. Our quantity of interest is the difference between the predicted value of the selected trait (i.e., height or intelligence) when the embryo with the highest PS is selected, compared with the mean across embryos. We term this difference the gain, and we further differentiate between the predicted gain, as determined by the PS, and the realized gain, as observed in the fully-grown offspring. Because no study can be performed in actual embryos, we utilize three sources of data: 1) a quantitative genetic model; 2) simulated embryo genomes generated using realistic parameters from existing genotyped datasets of adults with known phenotypic values; and 3) a unique pedigree dataset of nuclear families with large numbers of offspring (10 on average), now fully-grown adults, with available genotype and phenotype data. In our simulated data, we examine the gain as a function of varying predictive strengths ($r_{\text{ps}}^2$) of the PS, as well as of the number of embryos (n) available; these results are compared against a theoretical model derived for average gain. Although a typical IVF cycle may produce 3-8 viable embryos (median=5; (Sunkara et al., 2011)), we examine the gain across a broad range of values of n, given the possibility of future advances in IVF technology. Particular emphasis is placed on n = 10, representing a plausible upper bound within the foreseeable future.

Results

We first developed a simple quantitative genetic model for the expected gain. The model assumes a polygenic additive trait with no assortative mating, and hence no correlation between the scores of SNPs from homologous chromosomes or chromosomes of spouses. We recognize that statistically significant assortative mating has been demonstrated for genetic variants associated with polygenic traits such as height and educational attainment (Conley et al., 2016); however, the overall magnitude of this effect accounts for <5% of the variance in spousal phenotype (Robinson et al., 2017; Tenesa et al., 2015). Assortative mating would tend to reduce the efficacy of embryo selection due to reduced variance available from which to select and lower within-family score accuracy (Mostafavi et al., 2019), and thus our results described below represent an upper bound on the potential gain.

We assumed a couple has generated n embryos, and computed the distribution of the polygenic scores of these embryos for a trait with phenotypic variance ${\sigma }_z^2$, of which a proportion $r_{\text{ps}}^2$ is explained by the PS. The set of n polygenic scores can be modeled as having a multivariate normal distribution with zero means, all variances equal to ${\sigma }_z^2{r}_{\text{ps}}^2$, and all covariances equal to $\frac{1}{2}{\sigma }_z^2{r}_{\text{ps}}^2$. The gain is formally defined as the difference between the maximal and average PSs among the n embryos. Based on properties of multivariate normal distributions, the mean gain can be shown to be approximately (for details see Methods S1, Sections 1–3)

$$E\left[gain\right]\propto {\sigma }_z{r}_{\mathrm{ps}}\sqrt{\log n,}$$ (1)

where the coefficient of proportion is ≈0.77. A more accurate formula based on extreme value theory can also be derived (Methods S1 Eq. (33)). Most notably for our purposes, the mean gain increases with the square root of the variance explained (or linearly with the correlation coefficient between the PS and the trait), but the effect of n is considerably attenuated, as denoted by the square root and log transformation in Eq. (1).

Next, for our simulations, we used genotypic and phenotypic data from two cohorts. The Longevity cohort contained 102 couples of Ashkenazi Jewish origin with genome-wide genotypes and information on height, drawn from a larger longevity study (Atzmon et al., 2009). The ASPIS cohort (Stefanis et al., 2004) contained 919 young Greek males with genome-wide genotypes and information on general cognitive function. To simulate embryos, we used either actual couples (for the Longevity cohort) or randomly matched couples (for both cohorts), and generated n = 10 or 50 synthetic offspring per couple based on a standard model of recombination (see Methods for details).

To predict the height or IQ of each embryo, we used polygenic scores based on summary statistics derived from recent large-scale GWAS meta-analysis. For height, the most recent meta-analysis contained ≈700,000 individuals (Yengo et al., 2018a) and did not include the subjects in our test (Longevity) cohort. For IQ, we utilized the most recent published meta-analysis (Savage et al., 2018), from which the COGENT set of cohorts (including the ASPIS cohort) had been removed, resulting in a discovery sample size of n = 234,569. We optimized the polygenic scores with respect to imputation, LD-pruning, and the P-value threshold (Methods). Our scores predicted height in the Longevity cohort with $r_{\text{ps}}^2=24.8\%$ and IQ in the ASPIS cohort with $r_{\text{ps}}^2=4.3\%$, both within one percentage point of the maximum out-of-sample predictive power reported in the original GWAS. Using linear regression of the phenotype (age- and sex-corrected for height) on the polygenic scores in each cohort, we predicted the height or IQ of each simulated embryo.

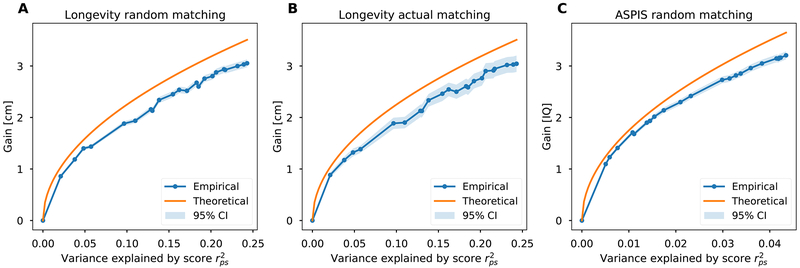
Having calculated the predicted height of each simulated embryo from the Longevity cohort and the predicted IQ of each simulated embryo from the ASPIS cohort, we sought to test the predictions of the mathematical model in Eq. (1). To examine the relationship between predicted gain and the variance accounted for by the PS, we fixed the number of embryos to n = 10, and plotted the mean gain for height against increasing $r_{\text{ps}}^2$. Because polygenic contributions to most complex traits (including height and IQ) are evenly distributed throughout the genome (Shi et al., 2016), we generated PSs that were progressively stronger using PSs derived from growing subsets of the 22 autosomes (e.g., chromosome 1 SNPs only, chromosome 1 + chromosome 2 SNPs only, etc.). As shown in Figure 1, the average gain reaches ≈3cm or ≈3 IQ points when the full genome-wide PS is used (corresponding to ≈0.5 and ≈0.2 standard deviations of the trait, respectively). The average gains obtained from varying $r_{\text{ps}}^2$ are close to the values predicted by the theoretical model (Eq. (1)). Our results did not differ when the actual couples are used as the source of the simulated embryos (Figure 1, panel B), compared to couples randomly matched from the Longevity cohort (Figure 1, panel A), indicating that effects of any assortative mating in this dataset are de minimis.

Figure 1. The mean gain vs the proportion of the variance explained by the PS.

Blue dots and the 95% confidence intervals (light blue bands) represent simulations with 10 embryos per couple. To generate scores with increasing proportions of variance explained, we gradually added chromosomes 1 to 22 to the computed PS. The orange line corresponds to the theoretical model derived in Methods S1 and described in Eq. (1). For each value of $r_{\text{ps}}^2$, dots are averages and 95% confidence intervals are based on ±1.96 the standard error of the mean over the simulated families. (A) Gain in height for random couples: 500 simulated pairings drawn from the Longevity cohort. (B) Gain in height for actual couples: 102 couples from the Longevity cohort. (C) Gain in IQ for random couples: 500 simulated pairings drawn from the ASPIS cohort. See also Figure S3.

The PSs used so far are based on current GWAS results and on a simple LD-pruning and P-value-thresholding strategy. However, GWASs are expected to increase in size (in particular given the rapid growth of the direct to consumer genetic industry (Khan and Mittelman, 2018)), and statistical prediction methods are constantly improving [e.g., (Chung et al., 2019; Lello et al., 2018; Mak et al., 2017; Vilhjálmsson et al., 2015)]. Given that the theoretically predicted relationship of the gain with r_ps was supported by the data in Figure 1, we can forecast the prospects of embryo selection as predictors become increasingly accurate. For example, doubling the proportion of explained variance of height from ≈25% to 50% is expected to increase the mean gain from ≈3 to ≈4.24cm, with a maximum possible gain of ≈5.5cm for $r_{\text{ps}}^2\approx 80\%$ (the upper bound of the heritability of the trait, as derived from twin studies; (Jelenkovic et al., 2016)). Similarly, quadrupling the variance explained for IQ would lead to a doubling of the gain, to ≈6 IQ points (given n = 10 embryos).

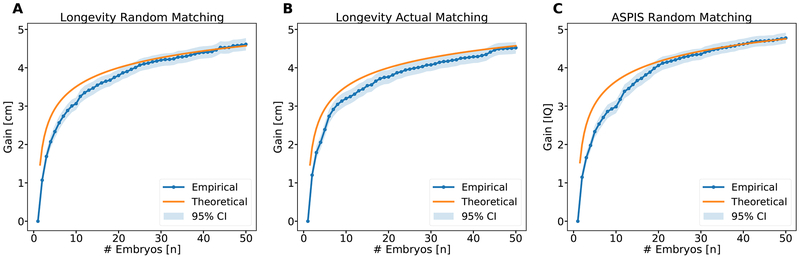
Next, we tested the relationship between the gain and the number of embryos, holding $r_{\text{ps}}^2$ constant. In Figure 2, we show the expected gain vs the number of embryos, for up to 50 embryos. Comparison to the theoretical model again shows good agreement, with an even better fit demonstrated in Figure S1 based on a more accurate approximation (Methods S1 Eq. (33)). Two implications are immediately apparent from Figure 2. First, current reproductive technologies are in the most sensitive area of the curve. With a typical IVF cycle yielding 5 testable, viable embryos (Sunkara et al., 2011), the predicted gain is reduced from ≈3 to ≈2.5 (cm or IQ points); below 5 embryos, the gain drops precipitously. Second, there is a rather slow increase of the mean gain as the number of embryos increases beyond 10. Thus, even with 1000 embryos, the mean gain would be only ≈1.7 times higher compared to selection with 10 embryos. Again, no differences were observed between randomly paired and actually married couples (panels A and B). The pattern for intelligence was roughly equivalent to that observed for height (panel C).

Figure 2. The mean gain vs the number of embryos.

Blue dots are from simulations, and orange lines are for the theoretical prediction (Eq. (1)). All details are as in Figure 1. See also Figures S1 and S2.

Both of the results above demonstrate the average gain expected under varying levels of $r_{\text{ps}}^2$ and n across 102 real couples or 500 simulated couples. However, for any given couple, the predicted gain will further vary around this mean. The distribution of the gain, when choosing the best out of 10 embryos, is shown in Figure 3 for height (for both random and actual couples) and IQ. The gain in height is typically between 1-6cm, with a median of 2.88cm for random couples (SD: 1.03; IQR: 2.34-3.80) and 3.02cm (SD: 0.98; IQR: 2.43-3.84) for actual couples. The gain in IQ was between ≈1-7 points (SD: 1.06; IQR: 2.43 - 3.84), with a median of 3.02 IQ points. Thus, the predicted gain for a given couple may be somewhat higher or lower than suggested by the mean results of our simulations, due to variation across couples and the random assortment of SNPs in the offspring (see Methods S1, Section 4 for a derivation of the variance of the gain). The mean gain itself is affected by the genotypes of the parents, but not by their total scores (Methods S1, Section 5).

Figure 3. The distribution of the predicted gain from embryo selection with 10 embryos per couple.

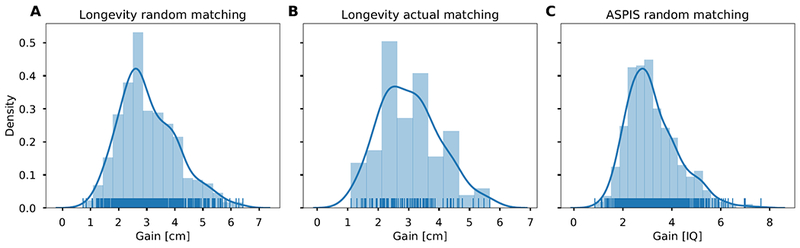
(A) The gain in height by simulating 500 random couples from the Longevity cohort. (B) Same as (A), but with actual spouses (n = 102). (C) The gain in IQ by simulating 500 random couples from the ASPIS cohort. Lines are estimated densities.

Figure 3 demonstrates the variability of the predicted gain across couples, but environmental variance leads to additional and substantial variability in the realized gain, as observed in the phenotype of the offspring. Naively (Methods S1, Section 6), given PS_max ,the score of the top-scoring embryo, the 95% prediction interval for the (zero-centered) trait value is

$$\left[{\mathrm{PS}}_{\max }-1.96{\sigma }_z\sqrt{1-r_{\mathrm{ps}}^2},{\mathrm{PS}}_{\max }+1.96{\sigma }_z\sqrt{1-r_{\mathrm{ps}}^2}\right].$$ (2)

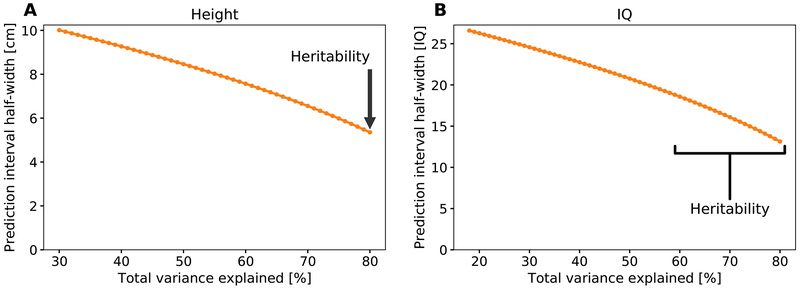
Eq. (2) can be compared to a 95% prediction interval of [−1.96σ_z, 1.96σ_z] without selection. However, prediction intervals can be narrowed based on the parental phenotypic values, which are usually known. For example, it has been long known that mid-parental height can explain ≈40% of the variance in height of the offspring (Aulchenko et al., 2009), or theoretically h⁴/2 ≈ 32% (Visscher et al., 2010). These ≈32% of the variance overlap with the ≈25% explained by the PS, and the combination of both sources of information can never explain more than the heritability. As shown in Figure 4A, even under the extreme scenario where the combination of the PS and the parental values explain the entire heritability of height (≈80%), there would still be ±5cm interval around any predicted gain due to environmental and stochastic factors. Based on either the current PS alone, or based on the parents alone, the interval would be as large as ±9-10cm. For IQ, the 95% prediction interval would be ±13-19 points in case the entire heritability is explained (assuming h² ∈ [0.6,0.8]), or ±24-27 points based on the parents (Figure 4B). Thus, the unexplained variance yields a wide confidence interval around any predicted value for an offspring’s trait, and therefore a considerable uncertainty in the realized gain that any given couple can expect from embryo selection. This would need to be combined with the variability in the predicted gain itself, as depicted in Figure 3, thereby substantially attenuating any guarantees on the potential benefit.

Figure 4. The prediction interval width as a function of the proportion of variance explained by the combination of parental phenotypes and the PS of the child.

If the proportion of variance explained is p, the half-interval width is $1.96{\sigma }_z\sqrt{1-p}$. (A) The prediction interval for height, assuming σ_z = 6cm. The proportion p is unknown, but cannot exceed the heritability, which we assume to be h² ≈ 0.8, and cannot fall under h⁴/2 ≈ 0.32, which is the theoretical variance explained by the mid-parental height. (B) The prediction interval for IQ, with σ_z = 15 points. We assume the heritability is in the range [0.6,0.8], with a minimal variance explained of 0.6²/2 = 0.18.

To give another example, assume there is no variability in the gain, the entire heritability is explained by the combination of the score and the parental phenotypes, and the proportion of variance explained by the PS is 40% for height and 15% for IQ. Selecting out of 10 embryos, a 95% prediction interval for the height of a male child (assuming average parents, 176cm for the population average, and an SD of 6cm) would be approximately 180±5cm (i.e., 175-185cm). This is compared to 176±10cm (166-186cm) without selection (Methods S1, Section 6). For IQ (mean 100 and SD 15, assuming h² = 0.6), the 95% prediction interval would be approximately 106±19 (88-125), compared to 100±27 (73-127) without selection. The future child has a non-negligible probability (≈0.25, assuming a normal distribution) to have an IQ below the population average.

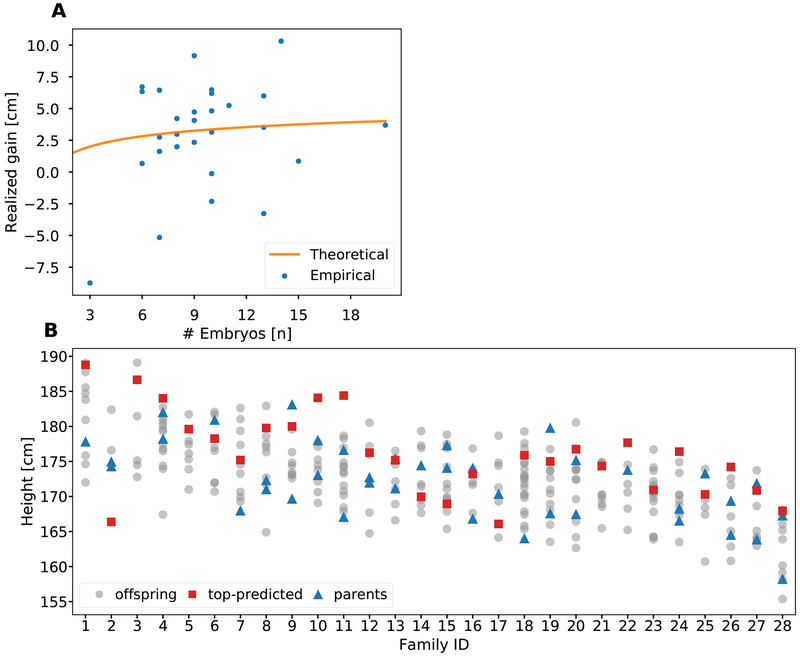
To evaluate the utility of embryo selection in a real-world setting, we examined a unique cohort of 28 large families with up to 20 offspring each (range 3-20; mean=9.6), now grown to adulthood and phenotyped for height. While all these families were the result of traditional means of procreation, we treated the offspring data as if all offspring were simultaneously generated embryos available for selection based on their PSs. Figure 5A depicts the actual difference in height between the offspring with the highest PS, compared to the average height of all the offspring in each family, i.e., the realized gain. (All heights were corrected for age and sex). While the observed values average around the mean gain predicted by the theory, there was substantial variability in the realized gain. Some families realized a gain of up to 10cm, while for 5 of the 28 families, choosing the embryo with the highest PS would have resulted in an offspring with height below the average (i.e., gain < 0).

Figure 5. An analysis of selection for height in 28 real families with up to 20 adult offspring each.

(A) The realized gain in each family, defined as the difference between the actual (age- and sex-corrected) height of the offspring with the highest PS and the average height of all offspring in the family. The theoretical prediction is based on Eq. (1). (B) The actual height (age- and sex-corrected) of all members of all families. The figure demonstrates the effect of the current low-accuracy prediction models, as the tallest-predicted sibling (red squares) is usually not the actual-tallest sibling (only 7/28 times). Siblings are depicted as grey dots, and the parents of each family as blue triangles. In some families only one parent was available.

The inherent uncertainty in PS-based selection is also demonstrated in Figure 5B, which displays the actual height for each family member. It is notable that the offspring with the highest PS (red squares) is the tallest actual offspring in only 7 of the 28 families. Moreover, when repeatedly downsampled to n = 7 children, the offspring with the highest PS was the tallest in ≈31.5% of the families, close to the theoretical prediction (≈33.4%; Methods S1, Section 7). Across all families, the tallest child was on average ≈3.0cm taller than the child with the tallest predicted height, again very close to the theoretical prediction (3.1cm; Methods S1, Section 7).

Finally, embryo selection could be desired or attempted on the basis of scores for multiple traits, some of which may be positively or negatively correlated. We extended our quantitative model to predict the outcome of this selection scheme (Methods S1, Section 8). Specifically, we assumed selection for a weighted average of the scores for T traits, with correlation ρ_ps,ij between the scores of traits i and j. We defined the weight of trait i as λ_i/σ_ps,i, where σ_ps,i = σ_z,ir_ps,i is the standard deviation of the predicted trait (${\sigma }_{z,i}^2$ is the variance of trait i and $r_{\text{ps},i}^2$ is the proportion of variance in trait i explained by the PS). The mean gain in trait i (i.e., the predicted value of trait i of the embryo with the maximal combined score; denoted G_i), is

$$E\left(G_i\right)\propto {\sigma }_{z,i}{r}_{\mathrm{ps},i}\sqrt{\log n}\frac{{\lambda }_i+{\sum }_{j=1,j\ne i}^T{\lambda }_j{\rho }_{\mathrm{ps},ij}}{\sqrt{{\sum }_{j=1}^T{\lambda }_j^2+{\sum }_{j=1}^T{\sum }_{k=1,k\ne j}^T{\lambda }_j{\lambda }_k{\rho }_{ps,jk}}}.$$ (3)

We demonstrate the application of this formula when jointly selecting for height and BMI in the Longevity cohort (Figure S2).

To gain more insight into Eq. (3), consider the case when all trait-trait correlations are equal to ρ, and all weights are equal to λ/σ_ps,i. This corresponds to giving each trait an equal weight, after accounting for the different variance explained by each score. The mean gain per trait is

$$E\left(G_i\right)\propto {\sigma }_{z,i}{r}_{\mathrm{ps},i}\sqrt{\log n}\frac{\sqrt{1+\left(T-1\right)\rho }}{\sqrt{T}}.$$ (4)

If ρ = 1, i.e., all scores are equal after normalization, the gain per trait is the same as the gain achieved when selecting for a single trait, as expected. When ρ = 0, i.e., when selecting for T independent traits, the mean gain per trait is $1∕\sqrt{T}$ smaller compared to selecting for a single trait. When all traits are maximally anti-correlated (ρ = −1/(T − 1)), the mean gain per trait completely vanishes. Thus, when selecting for multiple traits simultaneously, the gain per trait can be much smaller compared to selection for a single trait, in particular if PSs of traits are anti-correlated.

Discussion

In this paper, we explored the expected gain in trait value due to selection of human embryos for height and IQ. We showed that the average gain, with current predictors and with five viable embryos, is around ≈2.5cm and ≈2.5 IQ points. We predicted and confirmed by simulations that the gain will increase proportionally to the square root of the variance explained by the predictor, but much more slowly with the number of embryos. Only two previous studies have addressed this question to date, both of which employed only mathematical modeling. One study has assumed the entire heritability can be explained by the genetic predictor, leading to larger effect sizes than possible with currently available scores (Shulman and Bostrom, 2014). The second study (a blog) used a model similar to ours, but focused on futuristic approaches to increasing the number of available embryos (Branwen, 2016).

In animal breeding, genomics-based selection is usually performed not by selecting embryos but by genotyping young males and using top-scoring animals as sires for the next generation. The recent success of genomic selection is mostly attributed to the shortening of the generation time (Garcia-Ruiz et al., 2016), as the genetic value of an animal can already be determined at birth (Meuwissen et al., 2016; van der Werf, 2013). Beyond generation time, genomic selection is expected to be more powerful than embryo selection, because first, the population variance is double the variance between siblings, increasing the gain by a factor of $\sqrt{2}$, and second, the number of individuals to select from (n) is not limited as in IVF cycles. Indeed, we have identified only one study in animal genetics that has suggested and empirically examined embryo selection (Mullaart and Wells, 2018).

Given that $r_{\text{ps}}^2$ holds the strongest effect on the potential gain from embryo selection, it is worthwhile to consider the potential for increasing $r_{\text{ps}}^2$ in the foreseeable future. Increasing sample sizes of discovery GWASs is the most straightforward means of increasing $r_{\text{ps}}^2$ (Chatterjee et al., 2013). For educational attainment, a trait strongly correlated with IQ (r_g ≈ 0.70; (Hagenaars et al., 2016)), increasing GWAS sample size from ≈300K (Okbay et al., 2016) to ≈1.1M (Lee et al., 2018) resulted in an increase in out-of-sample variance explained from 3.2% to 11%. For height, the out-of-sample $r_{\text{ps}}^2$ increased more modestly, from 17% to 24.6% when GWAS sample size increased from ≈250k (Wood et al., 2014) to ≈700k individuals (Yengo et al., 2018a). The variance explained by the predictor should approximately satisfy $r_{\text{ps}}^2=h_{\text{snp}}^2{\left(1+\frac{M}{N{h}_{\text{snp}}^2}\right)}^{-1}$, where N is the (discovery) GWAS sample size, M is the effective number of markers, and $h_{\text{snp}}^2$ is the SNP-based heritability (Pasaniuc and Price, 2017; Wray et al., 2019). The dependence of the gain on N has an empirical S shape (Figure S3). For IQ, increasing GWAS sample sizes to N ≈ 10⁷ is expected to double the gain, up to ≈7 IQ points (for n = 10 embryos). For height, we are closer to saturation, and using N ≈ 10⁷ will only increase the gain to ≈4.5cm. These limitations are to some extent due to the strict upper bound $r_{\text{ps}}^2\le h_{\text{snp}}^2$.

Further improvement is expected with the use of whole-genome sequencing (WGS), as it was recently shown that WGS data explains the entire heritability of height and BMI (Wainschtein et al., 2019). For cognitive ability, a recent family-based study (Hill et al., 2018a) has demonstrated that more than half of the variation is attributable to rare variation not captured by current GWASs. However, as the effective number of markers in WGS is much larger compared to microarrays and the sample sizes much smaller, the current predictive power is very low (expected gain for height <1cm; Figure S3). Once sample sizes reach N = 10⁷ − 10⁸, the gain for height can reach ≈5.5cm, nearly double the current gain (Figure S3). To incorporate rare variation while overcoming the problem of small WGS sample sizes, imputation is a promising approach (Yang et al., 2015), and as reference panels grow in size and diversity, imputation is expected to accurately assess variants with frequencies down to 0.1% or even lower (Lencz et al., 2018; Taliun et al., 2019).

Finally, statistical approaches to calculating PSs from GWASs are becoming increasingly sophisticated (Khera et al., 2018; Prive et al., 2019a; Torkamani et al., 2018). Most notably, the application of penalized regression methods to the generation of PSs holds a potential for rapid gains in $r_{\text{ps}}^2$ without requiring any additional data collection in either GWAS datasets or imputation reference panels (Mak et al., 2017; Prive et al., 2019b). For example, initial evidence suggests that currently available datasets might be able to explain up to 40% of the variance in height by using LASSO (Lello et al., 2018). Additionally, the use of multiple related phenotypes has been demonstrated to enhance the predictive power of PS (Krapohl et al., 2017); for example, the combination of educational attainment and intelligence GWAS may permit a doubling of cognitive $r_{\text{ps}}^2$ (Allegrini et al., 2019). Finally, it has recently been suggested that enrichment of certain subcategories of functional variation (e.g., coding, conserved, regulatory, and LD-related genomic annotations) in GWAS results can be leveraged to further enhance prediction accuracy (Kichaev et al., 2019; Marquez-Luna et al., 2018).

While it is likely that some combination of the above factors will increase the accuracy of PSs in the near future, substantial limitations to PSs must also be acknowledged (Loos and Janssens, 2017). First, PSs do not account for extremely rare Mendelian variants associated with extreme phenotypes such as short stature (Grunauer and Jorge, 2018) or intellectual disability (Vissers et al., 2016). More broadly, the lower end of the phenotypic distribution is less well predicted from common variant PS than the middle and upper percentiles (Chan et al., 2011); this fact limits the utility of PSs for “reverse” embryonic selection (i.e., to avoid extreme low values). Second, it is well known that PSs lose substantial power, or may even be invalid, when applied across different populations (Coram et al., 2017; Kim et al., 2018; Martin et al., 2017). Moreover, even within a single population, subtle ethnic and geographic stratification effects may result in inflated estimates of $r_{\text{ps}}^2$ (Barton et al., 2019; Haworth et al., 2019), and prediction accuracy may also vary by age and sex (Domingue and Fletcher, 2019). Third, polygenic scores are correlated with parental genotypes and hence with the environment induced by the parents, in particular for education. This leads to lower prediction accuracy within families (Cheesman et al., 2019; Domingue and Fletcher, 2019; Morris et al., 2019; Mostafavi et al., 2019; Selzam et al., 2019), which further limits the utility of embryo screening. Fourth, SNP effects may be environmentally sensitive, and may not be consistent across time and place (Keyes et al., 2015).

Beyond these limitations in PS power and accuracy, several additional constraints on the expected utility of embryo selection are notable. First, we did not explicitly model assortative mating, which likely exists to some extent for traits such as height and cognitive ability (Conley et al., 2016; Yengo et al., 2018b), and is expected to further reduce the potential available variance for embryo selection. While there was no detectable effect of assortative mating in our Longevity cohort, these subjects represented an older birth cohort, and assortative mating on phenotypic traits may be increasing. Second, the number of embryos per IVF cycle is usually less than 10 (Sunkara et al., 2011), and, as can be seen in Figure 2, in this regime the utility drops sharply with a decreasing number of embryos. Third, with the increasing age of childbearing, the proportion of aneuploid embryos increases. For example, the proportion of aneuploid embryos is 35% for women aged 35 and 60% at age 40 (Franasiak et al., 2014). Relatedly, embryos with particularly high polygenic scores are not guaranteed to implant and lead to a live birth. While it is theoretically possible to perform multiple IVF cycles to generate more embryos, IVF is invasive, involves a substantial discomfort to the prospective mother, and requires significant financial means (Teoh and Maheshwari, 2014) (which would often also imply an older age of the prospective parents and fewer viable embryos per cycle). To the best of our knowledge, no upcoming technology is expected to significantly increase the number of oocytes extracted per IVF cycle (Casper et al., 2017; Lin et al., 2013). While it has been suggested that induced pluripotent stem cells may greatly increase the potential number of available embryos (Hikabe et al., 2016; Yamashiro et al., 2018), such technologies are not close to implementation for human reproduction. Either way, even with tens of viable embryos, our simulations show that the gain in trait value would be relatively small (Figure 2). Finally, once IVF and genotyping/sequencing have been performed, couples may attempt to select for multiple phenotypes, and as we have shown, this will lead to smaller gains per each individual trait.

Perhaps more importantly, we have also demonstrated that two sources of variability result in wide confidence intervals for the prediction of final observed phenotypic values: 1) random assortment of SNPs will result in variability of the predicted gain around its mean value; and 2) environmental variation will produce considerable additional uncertainty around the predicted gain. In our empirical dataset, the majority of offspring who were the tallest among their siblings were not those with the highest PS, and a substantial fraction of the top-scoring offspring had lower than average phenotypic values. Regardless of the future accuracy of $r_{\text{ps}}^2$ or the number of available embryos, these uncontrollable sources of variability will limit the appeal of selection for any individual couple.

A final reason for caution over the utility of embryo selection is the widespread pleiotropy across most traits (Bulik-Sullivan et al., 2015; Pickrell et al., 2016; Visscher et al., 2017). For example, while IQ is negatively correlated with most psychiatric disorders (Zheng et al., 2017), it is genetically positively correlated with autism and anorexia (Hill et al., 2018b; Savage et al., 2018). Therefore, selecting an embryo on the basis of higher predicted IQ will increase the risk for autism or anorexia in the offspring. In animal breeding, selection for production and growth traits has resulted in serious health issues in dairy cattle (Oltenacu and Algers, 2005), broiler chickens (Bessei, 2006), and other animals (Rauw et al., 1998; Rodenburg and Turner, 2012), and in plants, it was recently demonstrated that a flavor allele was lost due to human selection (Gao et al., 2019). Thus, negative effects on correlated health traits should be seriously considered.

In addition to practical limitations, there are major ethical and societal concerns with embryo screening, mostly due to associations with ideas of eugenics. Eugenics was originally developed by Galton, who envisioned breeding of humans for higher intelligence (Tabery, 2015). In short order, Galton’s concept was extended in some countries to the forced sterilization of those possessing mental traits deemed as ‘undesirable’ (Hoge and Appelbaum, 2012; Wikler, 1999). The specter of eugenics has accompanied the development of modern reproductive technologies since the development of IVF and preimplantation genetic diagnosis of monogenic diseases (Bonnicksen, 1992). At the same time, application of the term ‘eugenics’ to modern reproductive practices can lead to terminological and conceptual ambiguities that require careful delineation (Cavaliere, 2018). But even when completely removed from the context of state coercion, embryo selection raises ethical concerns of equity and justice in the availability of expensive reproductive technologies (President’s Council on Bioethics (US), 2003), as well as potential conflicts between individual benefits and societal costs (Anomaly et al., 2019). More broadly, embryo selection for non-disease traits raises the possibility of fundamentally altering “the meaning of childbearing” (President’s Council on Bioethics (US), 2003).

The legal and regulatory framework for PGD remains unsettled, especially in the United States. While PGD is legal in most countries, its use is often restricted (European Society of Human Reproduction and Embryology (ESHRE), 2017; Jones and Cohen, 2007; Knoppers et al., 2006). Across much of Europe, PGD is legally allowed only when risk for a serious medical condition is high (Dondorp and de Wert, 2019). In this context, high risk generally refers to highly penetrant (dominant or recessive) alleles for clearly defined diseases; thus, polygenic scores for quantitative traits would fail to meet these requirements. In the UK, the set of permitted conditions is determined by a designated body, which issues explicit guidelines as to which diseases and genes are included, and which mandates genetic counseling in order to access these services (Bayefsky, 2016). In Israel, such decisions are made by institutional review boards, and PGD is not permitted for traits (Israel Ministry of Health, 2013). In China, PGD is regulated and social sex selection and selection for traits are not permitted (Cyranoski, 2017). In contrast, in the USA, the targeted use of PGD is not regulated, and hence, to the best of our knowledge, embryo selection for polygenic traits can be offered to consumers (Bayefsky, 2018, 2016). In such an environment, and given the concerns over pleiotropic effects and given the invasive nature of PGD, it may be desired to introduce oversight over at least the advertised outcomes.

Beyond legal restrictions, an additional concern involves the principle of informed consent (Katz, 1994), which suggests that embryo screening should be offered in the context of appropriate genetic counseling. It is our hope that the present work provides an initial evidence base for professionals and regulators to consider the risks and benefits that are at the heart of the informed consent process.

Finally, in this paper we did not consider the prospects, nor the ethics, of “population-scale” embryo selection for IQ or other traits. While claims were made that population-scale selection could lead to a dramatic increase in trait values at the population level (e.g., the popular article (Hsu, 2016)), we leave a rigorous evaluation of this prediction to future studies.

STAR Methods

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Shai Carmi (shai.carmi@huji.ac.il). This study did not generate new unique reagents.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Cohorts for simulating offspring

Longevity

Our data included 208 individuals from 104 couples who were part of the LonGenity study of longevity and aging in Ashkenazi Jews (the “Longevity” cohort). Genotyping was performed using Illumina HumanOmniExpress array. Genotyping and QC were previously described (Chang et al., 2014; Eny et al., 2014; Roshandel et al., 2016; Sathyan et al., 2018). The number of SNPs was 704,759, with an average missing rate 0.2%. We removed duplicate variants and variants with missingness rate >1%. Height was available for all individuals except two who were discarded along with their spouses. Height was 177±6cm (mean±SD) in males (range 163-191) and 163±6cm in females (range 147-175). BMI was available for 203 individuals. BMI was 26.5±3.9 (kg/m²) (mean±SD) in males (range 15.9-42.9) and 25.4±5.0 (kg/m²) in females (range 18.0-51.2).

ASPIS

The Athens Study of Psychosis Proneness and Incidence of Schizophrenia (Stefanis et al., 2004) (henceforth “ASPIS”) included 1066 randomly selected young male conscripts aged 18 to 24 years from the Greek Air Force in their first two weeks of admission. All participants were free of serious medical conditions. Cognitive measures included: Raven Progressive Matrices Test (Raven Matrices; raw score); Continuous Performance Task, Identical Pairs version (CPT-IP; d-prime score); Verbal N-Back working memory task (Verbal NBack; total accuracy); and Spatial N-Back working memory task (Spatial NBack; total accuracy). General cognitive ability scores (g) were generated using the first principal component. We transformed the scores to IQ points by scaling the mean to 100 and the standard deviation to 15 (range 47-140). We note that this measure of cognitive ability is only an estimate of the IQ as would have been obtained from standard tests (such as the Wechsler Adult Intelligence Scale), and hence the somewhat wide range. Genotyping was performed on Affymetrix 6.0 arrays (Hatzimanolis et al., 2015; Smyrnis et al., 2007; Stefanis et al., 2007). The number of SNPs was 487,126, with an average missingness rate of 0.3%. Out of the 1066 genotyped samples, 147 had their cognitive function scores missing and were discarded from the analysis, leaving 919 individuals.

Nuclear families

We used 28 large nuclear Jewish families with an average of 9.6 adult offspring (full-siblings) per family who have completed their growth. The families were recruited in Israel and in the US after obtaining IRB approvals in both locations. Details on the cohort, measurements, and genotyping appear elsewhere (Zeevi et al., 2019). In short, participants signed a consent form and filled a medical questionnaire (to ensure there were no medical conditions that could have affected their growth), and their heights were measured with four technical repeats at an accuracy of ±0.1cm. All 308 consented participants were genotyped on the Affymetrix Axiom Biobank array (≈630,000 SNPs). One from each of six pairs of monozygotic twins was excluded. Heights were corrected for age and age², then standardized to Z-scores in each sex separately, then reported as 173.0 + 5.6Zcm.

METHOD DETAILS

Phasing

We phased the Longevity and ASPIS cohorts (separately) using SHAPEIT2 (O’Connell et al., 2014). Default parameters were used, except for using 200 states (to improve precision), and an effective population size of 12k, similar to the value suggested for Europeans. The genetic map used was from HapMap (International HapMap 3 Consortium, 2010).

Polygenic score calculation

Longevity cohort: height and BMI

We used summary statistics from (Yengo et al., 2018a), a meta-analysis based on (Wood et al., 2014) and the UK Biobank (Bycroft et al., 2018). Effect sizes were available for 2,334,001 SNPs, of which 1,789,210 were missing from the Longevity panel. Another 241 variants had mismatching alleles, leaving a total of 544,550 for downstream analyses. Scoring of individuals based on the summary statistics was performed in PLINK (Chang et al., 2015) with the no-mean-imputation flag.

Given a polygenic score (PS), we predicted height in a two-step approach. First, the heights of the Longevity individuals were regressed against age and sex. Second, the residuals from the first step were regressed against their PS ($r_{\text{ps}}^2\approx 0.248$, comparable to (Yengo et al., 2018a); Figure S4). The regression line from the second step was used to predict the height of the simulated offspring.

To optimize the PS, we first determined whether imputation had an effect on prediction accuracy. We used IMPUTE2 (Howie et al., 2009) and The Ashkenazi Genome Consortium reference panel (Lencz et al., 2018). Imputed data was post-processed to include only single nucleotide variants present in the summary statistics and with IMPUTE2 INFO-score >0.9. The $r_{\text{ps}}^2$ for height prediction (using all SNPs) was 0.201, which was slightly lower than for the PS generated without imputation, consistent with previous reports (Ware et al., 2017). Since imputation incurs a significant computational and storage burden, we proceeded with the genotyped SNPs only.

Next, we considered the effect of linkage-disequilibrium (LD) pruning and P-value thresholds. LD-clumping was performed in PLINK (Chang et al., 2015) with window size of 250kb and r² threshold of 0.1. LD was estimated based on 574 genomes from The Ashkenazi Genome Consortium (Lencz et al., 2018), reduced to the 657,179 SNPs intersecting with the Longevity study. The number of remaining SNPs after LD-clumping was 93,345. We considered P-value thresholds between 10⁻⁷ to 1 in multiples of 10. We then searched for the parameter combination giving the maximum $r_{\text{ps}}^2$ between predicted and actual phenotypes. Without LD-pruning, the maximal $r_{\text{ps}}^2$ was 0.207 (using a P-value cutoff of 0.1). With LD-pruning, the maximal $r_{\text{ps}}^2$ was 0.248, using a P-value cutoff of 0.001. Thus, our final score used LD-pruning and P<0.001, and included 15,752 SNPs.

We used the same GWAS (Yengo et al., 2018a) to obtain summary statistics for BMI. We regressed BMI on age and sex, and then we regressed the residuals on the PS. We used cross-validation to optimize the r² threshold and the P-value threshold. The optimal parameters were r² = 0.1 and P = 0.1. The score included 15,695 SNPs and explained 3.1% of the variance (Figure S4). This is less than previously reported (≈10% of the variance) but was significantly non-zero. Scores for BMI were only used for the analysis of selection for multiple traits.

Nuclear families: height

We used the set of 15,752 SNPs obtained for the Longevity cohort with the thresholds P<0.001 and LD r² < 0.1. Of these, we used 15,124 SNPs that were present on the array or could be imputed from the AJ reference panel (Carmi et al., 2014). We excluded SNPs homozygous in all participants. The weight of each SNP was its effect size (Yengo et al., 2018a), zero centered for the cohort. Scores were standardized into Z-scores and reported as for the actual heights.

ASPIS: general cognitive ability

We used summary statistics from (Savage et al., 2018), based on a meta-analysis of intelligence (excluding the ASPIS cohort). Out of total of 9,145,263 SNPs, 468,809 intersected with the ASPIS panel. Following the results from height, we did not consider imputation. The optimal LD-clumping threshold and P-value threshold were r² = 0.3 and 1, respectively, leaving 130,199 SNPs and reaching $r_{\text{ps}}^2=0.043$ (Figure S4). For improving the accuracy of LD estimation, we considered the entire 1066 genotyped individuals, including those without phenotypes.

We note that other approaches for genetic prediction may have slightly higher predictive power. However, an extensive benchmarking of methods and thresholds for trait prediction is beyond the scope of this paper. Our quantitative model would allow to approximate the utility of any score, based on its proportion of variance explained.

Simulating embryos

The Longevity cohort included actual couples, and these were used to simulate offspring (“actual matching”). For both the Longevity and the ASPIS cohorts, we also matched parents randomly (“random matching”). Given a pair of parents, we simulated offspring (embryos) by specifying the locations of crossovers in each parent. Recombination was modeled as a Poisson process, with distances measured in cM using the HapMap genetic map (International HapMap 3 Consortium, 2010). For each parent, we drew the number of crossovers in each chromosome from a Poisson distribution with mean equal to the chromosome length in Morgans. Random positions along the chromosome (in Morgans) represented the locations of the crossovers. We mixed the phased paternal and maternal chromosomes of the parent according to the crossovers’ locations, and randomly chose one of the resulting sequences as the chromosome transmitted from that parent. Note that due to phase switch errors, the paternal and maternal chromosomes are each a mixture of both. Nevertheless, phasing is expected to be accurate over short distances (switch error rate around 1%) (Choi et al., 2018), thus correctly representing LD blocks.

We repeated the process to generate either 10 or 50 embryos per couple (whether a true couple or randomly matched). The number of couples for random matches was such that the total number of embryos was 5000 (Table 1). For a number of embryos other than 10 or 50, we downsampled embryos from the n = 50 simulations.

Table 1.

The sets of simulated embryos.

Cohort	Phenotype	Matching	Number of matches	Number of offspring per couple
Longevity	Height/BMI	Random	500	10
Longevity	Height/BMI	Random	100	50
Longevity	Height	Actual	102	10
Longevity	Height	Actual	102	50
ASPIS	Cognitive ability	Random	500	10
ASPIS	Cognitive ability	Random	100	50

To calculate the polygenic scores for the synthetic embryos, we used the same summary statistics as for the parents. To predict the phenotypes of the embryos, we used the regression model that we have generated for the parents. The predicted phenotype is thus in its natural units (cm, kg/m², or IQ points). Adding sex- or age-specific means was unnecessary, as we considered only the differences between embryos attributed to their polygenic scores.

Multiple traits

We used the Longevity cohort, which had data on both height and BMI. We used the same sets of simulated embryos as for height. For each embryo, we computed the scores for height and BMI, and normalized the scores by the standard deviations of the predicted phenotypes (2.89cm for height and 0.78kg/m² for BMI). The combined score per embryo was the normalized height score minus the normalized BMI score (to simulate selection for lower BMI). The gain for height was the predicted height for the embryo with the highest combined score, and similarly for BMI. The correlation between the scores of height and BMI was −0.16, which we used in the equations for the gain ((3) and (4)).

QUANTIFICATION AND STATISTICAL ANALYSIS

Polygenic scores calculations were performed with PLINK (Chang et al., 2015). Other data analyses were performed using custom Python and R scripts.

In Figures 1, 2, S1, and S2, 95% confidence intervals are based on ±1.96 the standard error of the mean (SEM) over the simulated families. Regressions (as in Figure S4) were performed using statsmodels (Seabold and Perktold, 2010). For regression of the trait on PS, The proportion of variance explained was the squared correlation coefficient, and the P-value for a non-zero correlation coefficient was computed with scipy.stats.pearsonr. The mean and 95% confidence bands in Figure S4 were generated by bootstrapping by seaborn.lmplot.

The quantitative genetic model

We modeled the vector of polygenic scores for a set of embryos as a multivariate normal variable with zero means, and derived its covariance matrix. The model implies that the score of each embryo can be represented as a sum of two normal variables, one shared across embryos and one independent, both with variance equal to half the variance in the trait explained by the PS. The maximal score, and thereby the gain, could be written using the maximum of n independent normal variables. We derived formulas for the mean and variance of the gain, and then: the mean gain conditional on the parental scores and phenotypes, a prediction interval for the phenotype, the difference between the maximal-predicted and the actual maximal trait value, and the gain when selecting for multiple traits. Full details are available in Methods S1.

DATA AND CODE AVAILABILITY

Python code implementing the analyses described in this paper is available at https://bitbucket.org/ehudk/embryo-pgs-selection.

R code that implements some of the calculations of the gain under the quantitative genetic model can be found at https://github.com/orzuk/EmbryoSelectionCalculator.

Supplementary Material

1

Methods S1. The quantitative genetic model. Related to STAR Methods.

2

Figure S1. The mean gain in embryo selection vs the number of embryos n. Related to Figure 2.

All details are the same as in Figure 2. The theoretical prediction here is based on extreme value theory, as given in Methods S1 Eq. (33), providing a slightly better fit compared to main text Eq. (1).

3

Figure S2. Selection for multiple traits. Related to Figure 2.

We simulated up to 50 embryos per (random) couple from the Longevity cohort, and calculated PSs for height and BMI. In (A) (height) and (B) (BMI) we show the gain per trait when selecting either for the focal trait (height in (A) and (negative) BMI in (B), blue dots along with their 95% confidence intervals; as in Figure 2 or Figure S1) or when selecting for the sum of the scores for height and negative BMI, after normalizing each score by its standard deviation (green dots along with their 95% confidence intervals). Note that the gain for BMI is negative, since we select for lower values of BMI. As expected, selection for multiple traits leads to lower gains (in absolute value) per trait. The orange lines correspond to Eq. (33) of Methods S1 for the mean gain when selecting for a single trait. The red lines correspond to Eq. (93) of Methods S1, where we used the expression for the mean of the maximum of n normal variables based on extreme value theory (Eq. (33)). In (C) and (D), we plot the gains for height and BMI, respectively, when the (normalized) score of height is weighted by λ and the (normalized) score for BMI is weighted by −(1 − λ). Green dots and 95% confidence intervals are based on simulations, whereas the red lines are based on Eq. (99) of Methods S1. The gain in height increases and the gain in BMI decreases (in absolute value) with λ, as expected. Note that the gain is non-zero even for λ = 0 or λ = 1, due to the correlation between height and BMI.

4

Figure S3. The expected increase in the mean gain with discovery GWAS sample sizes. Related to Figure 1.

To evaluate the expected gain given a GWAS sample size N, we used the relation $r_{\text{ps}}^2=h_{\text{snp}}^2{\left(1+\frac{M}{N{h}_{\text{snp}}^2}\right)}^{-1}$ (Pasaniuc and Price, 2017; Wray et al., 2019). In this equation, $h_{\text{snp}}^2$ is the SNP-based or chip heritability (the variance in the trait explained by all SNPs on the array) and M is the effective number of SNPs. To estimate M for height, we substituted $h_{\text{snp}}^2=0.48$, N ≈ 700 · 10³, and $r_{\text{ps}}^2\approx 0.24$ (Yengo et al., 2018a), which gave M = 328 · 10³. For IQ, $h_{\text{snp}}^2=0.19$, N ≈ 270 · 10³, and $r_{\text{ps}}^2=0.05$ (Savage et al., 2018), which gave M = 136 · 10³. Given these values of M, we calculated the expected $r_{\text{ps}}^2$ for a range of GWAS sample sizes. To compute the expected gain when selecting one embryo out of n = 10, we used an exact numerical solution for the mean of the maximum of independent normal variables (Methods S1 Eq. (28)), and assumed standard deviations of 6cm for height in (A) and 15 points for IQ in (B). The red lines denote the gain with current GWAS sizes. (C) The expected gain in height for scores based on whole-genome sequencing (WGS) data. Based on (Wray et al., 2019), we used a value of M 10x larger compared to that of arrays, giving M = 3.28 · 10⁶. Instead of $h_{\text{snp}}^2$, we used $h_{\text{wgs}}^2=0.79$ (Wainschtein et al., 2019).

5

Figure S4. Height, BMI, and cognitive ability (IQ) vs their polygenic scores. Related to STAR Methods.

Results are shown for the heights and BMI of 204 individuals in the Longevity cohort ((A) and (B), respectively), the heights of 308 individuals from the large nuclear families (C), and the IQ of 919 individuals from the ASPIS cohort (D). Also shown are the regression lines with 95% bootstrap confidence intervals, the proportions of variance explained, and the P-values. The proportions of variance explained by the polygenic scores are ≈25-27% for height, ≈3% for BMI, and ≈4.3% for IQ.

• IVF embryos could be profiled with polygenic scores for traits such as height or IQ

• The top-scoring embryo is expected to be ≈2.5cm or ≈2.5 IQ points above the average

• The adult trait value of the top-scoring embryo would remain widely distributed

• Multiple ethical and other factors impose practical limits on the actual gain