Simulating PFAS Transport Influenced by Rate-limited Multi-process Retention

Abstract

The transport of per- and poly-fluoroalkyl substances (PFAS) in the vadose zone is complicated by the fact that multiple mass-transfer processes can contribute to their retention and retardation. In addition, PFAS transport at some sites can be further complicated by the presence of organic immiscible liquids (OIL). Mass-transfer processes are inherently rate limited and, therefore, have the potential to cause nonideal transport of PFAS. The objectives of this research were to: (1) develop a solute-transport model that explicitly accounts for multiple retention processes, including adsorption at air-water and OIL-water interfaces, adsorption by the solid phase, and diffusive mass-transfer between advective and nonadvective domains, and (2) apply the model to measured transport data to delineate which processes are rate limited and contribute to observed nonideal transport. Breakthrough curves for transport of two PFAS and one hydrocarbon surfactant in sand obtained from prior miscible-displacement experiments exhibited nonideal transport. The multiprocess model effectively simulated the measured transport data. The results of the analyses indicate that adsorption at the air-water and OIL-water interface can generally be treated as effectively instantaneous for transport in porous media. The rate limitations associated with solid-phase adsorption and diffusive mass transfer between advective and nonadvective domains were of greater significance.

Graphical Abstract

1. Introduction

Per- and poly-fluoroalkyl substances (PFAS) are environmental contaminants of critical concern due to their ubiquitous distribution and potential human-health effects. Accurate characterization and risk assessment of PFAS-contaminated sites, as well as effective design and implementation of mitigation and treatment efforts, requires an understanding of PFAS transport and fate in the subsurface. The transport of PFAS in source zones is of particular interest due to the potential presence of relatively large reservoirs of PFAS that can serve as long-term sources of contamination to surface water and groundwater. PFAS transport in source zones is complicated by the fact that multiple processes can contribute to their retention and retardation.

Adsorption by the solid phase is a primary process of potential importance for PFAS transport in porous media. Characterizing the adsorption of PFAS for a wide variety of adsorbents and delineating associated adsorption mechanisms has been a major focus of research for more than the past decade, as reviewed by Du et al. (2014). The transport of sorbing solutes can be influenced by nonlinear and rate-limited adsorption, and prior research has demonstrated this behavior for the transport of hydrocarbon surfactants (e.g., Adeel and Luthy, 1995; Hayworth and Burris, 1997; Smith et al., 1997; Noordman et al., 2000) and for PFAS (Lyu et al., 2018; Lv et al., 2018; Brusseau et al., 2019a, 2019b). In addition, it is well established that the transport of solutes in unsaturated porous media can be influenced by the presence of poorly-advective domains associated with water trapped in drained and dead-end pores, with preferential flow and rate-limited diffusive mass transfer contributing to nonideal transport (e.g., Brusseau and Rao, 1989; Selim and Ma, 1998).

Prior research has indicated that the vadose zone may serve as a significant long-term source of PFAS to groundwater (Shin et al., 2011; Xiao et al., 2015; Weber et al., 2017; Brusseau, 2018; Anderson et al., 2019). The presence of air-water interface in water-unsaturated porous media adds additional complication for PFAS transport in the vadose zone. Recent studies have shown that adsorption at the air-water interface can significantly increase retention of PFAS during transport in unsaturated porous media (Brusseau, 2018, 2019a; Lyu et al., 2018; Brusseau et al., 2019a). This additional retention can influence rates of migration through the vadose zone and also affect mass distribution. PFAS transport at some sites may also be affected by the presence of organic immiscible liquid (OIL) co-contamination. Solid-phase adsorption may be impacted in such cases (Guelfo and Higgins, 2013; McGuire et al., 2014; McKenzie et al., 2015, 2016), and in addition adsorption at OIL-water interfaces may contribute to PFAS retention (Brusseau, 2018; Brusseau et al., 2019a).

Important questions to resolve for any mass-transfer process is what is the characteristic time scale for mass transfer and, is it rate limited with respect to advective transport in porous media. This question has been addressed in numerous prior works for solid-phase adsorption and diffusive mass transfer between advective and nonadvective domains. Conversely, it has not been examined to date for fluid-fluid interfacial adsorption. It is well established that surfactant adsorption to the fluid-fluid (e.g., air-water, OIL-water) interface is rate limited. Attaining equilibrium can require from seconds to many hours or more depending upon the surfactant, the surfactant concentration, and solution conditions (e.g., Eastoe and Dalton, 2000; Loppinet and Monteux, 2016; Miller et al., 2017). A few studies have measured the kinetics of PFAS adsorption to the air-water interface (Gao et al, 2005; Rodriguez-Abreu and Kunieda, 2005; Kuo et al., 2013; Casandra et al., 2018; Noskov et al., 2019), with reported equilibration times ranging from <1 hour to ~3 hours for PFAS concentrations in the 1 mg/L range. These experiments were conducted using tensiometer systems that have unconstrained contact between fluid phases. The occurrence and magnitude of rate-limited fluid-fluid interfacial adsorption have not been investigated for PFAS transport in porous media. The pertinent questions to resolve are: what are the time scales of fluid-fluid interfacial adsorption in porous-media systems, are they consistent with prior tensiometer-based measurements, and are the relevant adsorption time scales of sufficient magnitude to significantly influence PFAS transport in porous media.

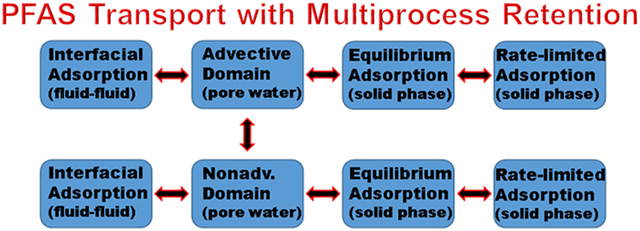
Models developed for surfactant transport in multiphase systems have been focused on simulating the impacts of surfactant on water flow and OIL dissolution and mobilization (e.g., Abriola et al., 1993; Smith and Gilham, 1994; Delshad et al., 1996; Ji and Brusseau, 1998; Karagunduz et al., 2015). As such, the models have not accounted for the influence of fluid-fluid interfacial adsorption on the retention and transport of the surfactant. The effective simulation of PFAS transport in multiphase systems requires a model that explicitly accounts for the multiple retention processes that can affect transport. The solute-transport model developed by Brusseau et al. (1989) accounts explicitly for multiprocess mass transfer and retention, specifically the impacts of rate-limited adsorption and diffusive mass transfer between advective and nonadvective domains. This model is revised in the present work to incorporate adsorption at fluid-fluid interfaces. This revised model provides the means to quantitatively characterize PFAS transport that is influenced by multiple mass-transfer processes.

The objectives of this research are to (1) develop a solute-transport model that explicitly accounts for multiple retention processes including adsorption at air-water and OIL-water interfaces, adsorption by the solid phase, and diffusive mass-transfer between advective and nonadvective domains, and (2) apply the model to measured transport data to delineate which processes are rate limited and contribute to observed nonideal transport. A specific focus is given to characterizing for the first time the potential rate limitations of fluid-fluid interfacial adsorption for PFAS transport in porous media. Breakthrough curves for transport of two PFAS in sand obtained from prior miscible-displacement experiments are used for the investigation. Transport data for a hydrocarbon surfactant are used for comparison.

2. Mathematical Modeling

Transport Model

There are two general approaches to simulating solute transport influenced by multiple retention processes. The first is a simplified approach wherein all retention processes are lumped together into a reduced number of terms. It is well established that the use of these lumped-process models generally produce poor results that are not consistent across different conditions, particularly for systems influenced by nonlinear and/or rate-limited mass transfer (e.g., Brusseau, 1998; Chapelle et al., 2007). The second approach employs process-discrete, distributed-parameter models wherein each transport, mass-transfer, and attenuation process is explicitly and separately represented. The latter approach is used in the present study.

The multiprocess rate-limited mass-transfer (MPMT) model developed by Brusseau et al. (1989) was designed to simulate solute transport influenced by rate-limited solid-phase adsorption and by preferential flow and diffusive mass transfer in systems with nonadvective domains. The two-region (advective-nonadvective) approach was used to represent preferential flow and diffusive mass transfer. Hence, water flow and advective-dispersive transport of solute is assumed to occur only in the advective domain, and diffusive mass transfer occurs between the advective and nonadvective domains. Adsorption was represented by the two-domain approach, with adsorption assumed to be essentially instantaneous for a portion of the sorbent and rate-limited for the remainder. Adsorption may be instantaneous or rate-limited in either of the two porosity domains. The four dimensionless governing equations for the MPMT model are as follows (Brusseau et al., 1989):

$$R_{a1}\frac{\partial C_a^{*}}{\partial T}+k_a^0\left(C_a^{*}-S_a^{*}\right)+\omega \left(C_a^{*}-C_n^{*}\right)=\frac{1}{P}\frac{{\partial }^2{C}_a^{*}}{\partial {\text{X}}^2}-\frac{\partial C_a^{*}}{\partial \text{X}}$$ (1)

Definitions of parameters and variables are provided in the Appendix. Equations 1–2 are the mass

$$R_{n1}\frac{\partial C_n^{*}}{\partial T}+k_n^0\left(C_n^{*}-S_n^{*}\right)=\omega \left(C_a^{*}-C_n^{*}\right)$$ (2)

$$R_{a2}\frac{\partial S_a^{*}}{\partial T}=k_a^0\left(C_a^{*}-S_a^{*}\right)$$ (3)

$$R_{n2}\frac{\partial S_n^{*}}{\partial T}=k_n^0\left(C_n^{*}-S_n^{*}\right)$$ (4)

balances for the advective and non-advective domains, respectively. Equations 3–4 are balances for the rate-limited sorbed-phases in the advective and non-advective domains, respectively. Details on initial and boundary conditions, and methods of solution are provided in Brusseau et al. (1989).

Of special note are the nondimensional parameters represented by β, k⁰, and ω (see Notation). The β terms represent the fraction of retardation associated with each domain, and they sum to unity. Hence they delineate the distribution of solute mass. The k⁰ and ω represent Damkohler Numbers, which are nondimensional mass-transfer rate coefficients comprising ratios of residence time and characteristic times of mass transfer. They serve as an index delineating the degree to which a mass-transfer process is rate limited with respect to advective transport.

The MPMT model developed by Brusseau et al. (1989) has been used successfully to simulate the transport of various sorbing solutes in physically and geochemically homogeneous and heterogeneous porous media (e.g., Brusseau et al., 1989; Brusseau, 1991; Brusseau et al., 1992; Brusseau and Zachara, 1993; Hu and Brusseau, 1996; Johnson et al., 2003a; Leij and Bradford, 2009). A limitation of the bicontinuum approach used to represent rate-limited adsorption and rate-limited diffusive mass transfer between advective and nonadvective domains is the potential inability to accurately simulate extended low-concentration elution tailing that may be present when rate limitations are significant (Chen and Wagenet, 1997; Haggerty and Gorelick, 1998; Johnson et al., 2003b, 2009; Kempf et al., 2009; Russo et al., 2010; Akyol et al., 2011; Brusseau et al., 2012; Akyol, 2015; Brusseau et al., 2019b). So-called multi-rate mass-transfer models that incorporate a continuum of domains and associated rate coefficients described using some form of probability density function have been developed to simulate transport with extended tailing behavior for conditions of inter-domain diffusive mass transfer (e.g., Haggerty and Gorelick, 1995), rate-limited sorption (Chen and Wagenet, 1995, 1997; Culver et al., 1997; Saiers and Tao, 2000; Johnson et al., 2003b), or a combination of both (e.g., Li and Brusseau, 2000). The focus of the current work is to examine the relative degree of rate limitation (i.e., nonequilibrium) of the various mass-transfer processes influencing overall (bulk) PFAS transport. The transport model presented herein is anticipated to be sufficient to accomplish this purpose, similarly to the successful applications cited previously.

Modeling Adsorption at the Fluid-Fluid Interface

The fluid-fluid interfacial adsorption process is generally conceptualized to comprise two steps, (1) diffusion of surfactant monomers from the bulk solution to the boundary layer adjacent to the interface, and (2) transfer into the interface proper (e.g., Eastoe and Dalton, 2000; Loppinet and Monteux, 2016; Miller et al., 2017). The diffusion step is governed by standard diffusive mass transfer and is a function of the aqueous diffusion coefficient of the surfactant, solution properties, and concentration gradient. Transfer into the interface may be rate limited by factors such as an electrostatic barrier in the electrical double layer, the availability of an open space within the interface, and steric constraints governing the reorientation of the monomer in the proximity of the interface and reorganization of adsorbed molecules within the monolayer (e.g., Eastoe and Dalton, 2000; Valkovska et al., 2004). It is important to keep in mind that equilibrium is a dynamic condition with a constant flux of monomer to and from the interface, with the fluxes equal at equilibrium.

It is generally considered that adsorption of surfactant to fluid-fluid interfaces is governed primarily by diffusion at concentrations below the critical micelle concentration (e.g., Loppinet and Monteux, 2016; Miller et al., 2017). Prior research conducted with PFAS support diffusion as the primary control for interfacial adsorption (Sekine et al., 2004; Valkovska et al., 2004; Day et al., 2007). Therefore, for model development, diffusive mass transfer will be considered as the primary factor governing adsorption of PFAS at fluid-fluid interfaces.

The MPMT model can be revised to incorporate retention associated with adsorption at the fluid-fluid interface. To do so, the total retardation factor is redefined as follows:

$$\text{R}=1+{\text{K}}_{\text{d}}{\rho }_{\text{b}}/{\theta }_{\text{w}}+{\text{K}}_{\text{nw}}{\text{A}}_{\text{nw}}/{\theta }_{\text{w}}$$ (5)

where K_nw is the fluid-fluid interfacial adsorption coefficient (L) and A_nw is the specific fluid-fluid interfacial area (L²/L³). The β and ω terms also need to be revised, depending upon which mass-transfer processes are deemed rate limited. For example, one simplified system is the case wherein physical nonideality is absent (either nonadvective pore water is absent or inter-domain mass transfer is not rate limited), solid-phase adsorption is rate limited, and fluid-fluid interfacial adsorption is also rate limited. The β terms for this case are:

$${\beta }_1=\left[1+(\rho /\theta ){\text{FK}}_{\text{d}}\right]/\text{R}$$

$${\beta }_2=\left[(\rho /\theta )(1-\text{F}){\text{K}}_{\text{d}}\right]/\text{R}$$

$${\beta }_3=\left[{\text{K}}_{\text{nw}}{\text{A}}_{\text{nw}}/\theta \right]/\text{R}$$

$${\beta }_4=0$$

A Damkohler Number for rate-limited fluid-fluid interfacial adsorption is defined as ω_nw = α_nwL/q, where α_nw is the first-order mass transfer coefficient for fluid-fluid interfacial adsorption (1/T). For a system with nonadvective domains (and the accompanying inter-domain diffusive mass transfer), rate-limited solid-phase adsorption, and assuming fluid-fluid interfacial adsorption to be effectively instantaneous (as will be discussed in the Results), the β terms are:

$${\beta }_1=\left[\phi +\left(\text{f}(\rho /\theta ){\text{FK}}_{\text{d}}\right)+\left(\phi {\text{K}}_{\text{nw}}{\text{A}}_{\text{nw}}/\theta \right)\right]/\text{R}$$

$${\beta }_2=\left[\text{f}(\rho /\theta )(1-\text{F}){\text{K}}_{\text{d}}\right]/\text{R}$$

$${\beta }_3=\left[(1-\phi )+\left((1-\text{f})(\rho /\theta ){\text{FK}}_{\text{d}}\right)+\left((1-\phi ){\text{K}}_{\text{nw}}{\text{A}}_{\text{nw}}/\theta \right)\right]/\text{R}$$

$${\beta }_4=[(1-\text{f})(\rho /\theta )(1-\text{F}){\text{K}}_{\text{d}}]/\text{R}$$

These two cases represent those that were necessary for simulating the experiment data.

Experiment Data and Parameter Determination

The results of prior miscible-displacement experiments reported by Brusseau and colleagues are used for the study. Data for perfluorooctanoic acid (PFOA) transport in a well-sorted quartz sand were reported by Lyu et al. (2018). Unpublished data from the study reported by Brusseau et al. (2019a) are used for perfluorooctanesulfonic acid (PFOS) transport in well-sorted quartz sand. Data for sodium dodecylbenzenesulfonate (SDBS) transport in the same sand are used for comparison, and were reported in Brusseau et al. (2008) and Brusseau et al. (2015) for OIL-water and air-water systems, respectively. Transport data for both water-saturated and water-unsaturated conditions are available for all three solutes. Pentafluorobenzoate was used as the nonreactive tracer (NRT) for the experiments. Pentafluorobenzoate is not a PFAS, and is useful as an NRT for characterizing PFOS and PFOA transport in part because of its similar aqueous diffusion coefficient to those of PFAS consisting of moderate (e.g., 8-carbon) chain lengths (Brusseau et al., 2019b). The use of similar diffusion coefficients will enhance the representativeness of hydrodynamic characterization provided by the NRT (e.g., Brusseau, 1993). The columns used for the experiments were 7- or 15-cm long and the flow rates were equivalent to pore-water velocities ranging from 20–30 cm/h, providing consistent experimental conditions for the data sets.

For the present application, it will be assumed that the solid-phase adsorption coefficient as well as the F term are the same for advective and nonadvective domains (no significant geochemical heterogeneity). Adsorption of PFOA, PFOS, and SDBS by the sand is weakly nonlinear, with measured Freundlich-n values of 0.9, 0.85, and 0.85, respectively. However, the 95% confidence intervals for n range close to or equal to 1. In addition, as will be discussed in the Results section, the impact of nonlinear solid-phase adsorption is minimal in comparison to rate-limited adsorption for the solutes investigated in this study. Thus, linear adsorption is assumed for the MPMT simulations. As well, prior research has demonstrated that fluid-fluid interfacial adsorption coefficients for PFAS of moderate chain lengths such as PFOA and PFOS attain essentially maximum values at concentrations of approximately 1–10 mg/L (Brusseau, 2019b, Brusseau and Van Glubt, 2019). Given that the concentrations used for the experiments are similar to or less than this concentration, fluid-fluid interfacial adsorption is treated as linear and the interfacial adsorption coefficient is considered a constant.

The value for the Peclet Number is obtained by application of the ideal advection-dispersion equation to the NRT data obtained for water-saturated conditions. The retardation factor and associated K_d are determined by moment analysis of the sorbing-solute breakthrough curves obtained under saturated-flow conditions. Values for input pulse, T₀, bulk density, porosity, water content, pore-water velocity, and column length are measured for each experiment. Of the measured data sets used, the impact of diffusive mass transfer between advective and nonadvective domains was significant only for the unsaturated-flow experiment conducted with the lowest water saturation (the PFOS experiment). The standard two-region model (van Genuchten and Wierenga, 1976) is used to simulate transport of the NRT for this system. The associated f and α variables are determined from calibration of the two-region model to the NRT data. A two-domain model (Hu and Brusseau, 1998) is used to simulate transport of nonlinear, rate-limited sorbing solute in saturated porous media. The values for F and k₂ are determined by calibration to the measured data obtained from the saturated-flow experiments. Values for K_nw and A_nw were obtained from surface-tension measurements and interfacial-area measurements, respectively, as discussed by Brusseau and colleagues (Brusseau, 2018, 2019; Lyu et al., 2018; Brusseau et al., 2019a). The rate data reported in the literature for fluid-fluid interfacial adsorption are used to determine estimates for α_nw. First-order mass-transfer coefficients ranging from approximately 2 to 15 h⁻¹, with a geometric mean of 5, were calculated for PFAS based on the data cited in the Introduction. Morgan et al. (2012) reported the results of experiments conducted to measure air-water interfacial adsorption kinetics for SDBS. A first-order mass-transfer coefficient of 7 h⁻¹ was calculated from their data.

The approach described above provides values for all required input parameters for simulating PFAS and SDBS transport in the water-unsaturated experiments. Thus, the simulations represent independent predictions, rather than calibrations, of the measured data. The use of independent prediction is a more robust method to test model efficacy and characterize critical processes. Of all of the input variables, the mass-transfer rate coefficient for fluid-fluid interfacial adsorption is the only one for which the values were obtained from literature sources. This imparts a degree of uncertainty for the simulations. Hence, a sensitivity analysis is conducted as part of the analyses, with α_nw set to three values as follows (Table 1): (1) equal to the geometric mean of the values obtained from the literature (ω_nw = 8,14), (2) approximately 10 times higher than the mean (ω_nw = 100), and 10 times lower than the mean (ω_nw = 0.8). In addition, model-calibration simulations are conducted wherein the value for ω_nw is optimized by calibration of the model to the measured data. The ω_nw term is the sole parameter optimized in these latter simulations.

Table 1.

Parameter values for simulations

Parameter	PFOA C = 10 μg/L	PFOA C = 100 μg/L	PFOA C = 1 mg/L	PFOA Sw = 0.8	PFOA Sw = 0.87	PFOS C = 10 mg/L	SDBS Air-water	SDBS OIL-water
R	2.8	2.4	2.0	1.85	1.68	3.2	1.8	1.4
β1	0.45	0.51	0.59	0.63	0.68	0.63	0.63	0.77
β2	0.15	0.14	0.14	0.13	0.13	0.16	0.11	0.10
β3	0.40	0.35	0.27	0.24	0.19	0.17	0.26	0.13
β4	-	-	-	-	-	0.04	-	-
ka0	0.9	0.7	0.6	0.6	0.6	0.8	0.3	0.1
kn0	-	-	-	-	-	0.2	-	-
ω	-	-	-	-	-	0.9	-	-
ωnw	0.8, 8, 100	0.8, 8, 100	0.8, 8, 100	0.8, 8, 100	0.8, 8, 100	100	1, 14, 100	0.8, 8, 100

3. Results

Nonideal Transport Behavior

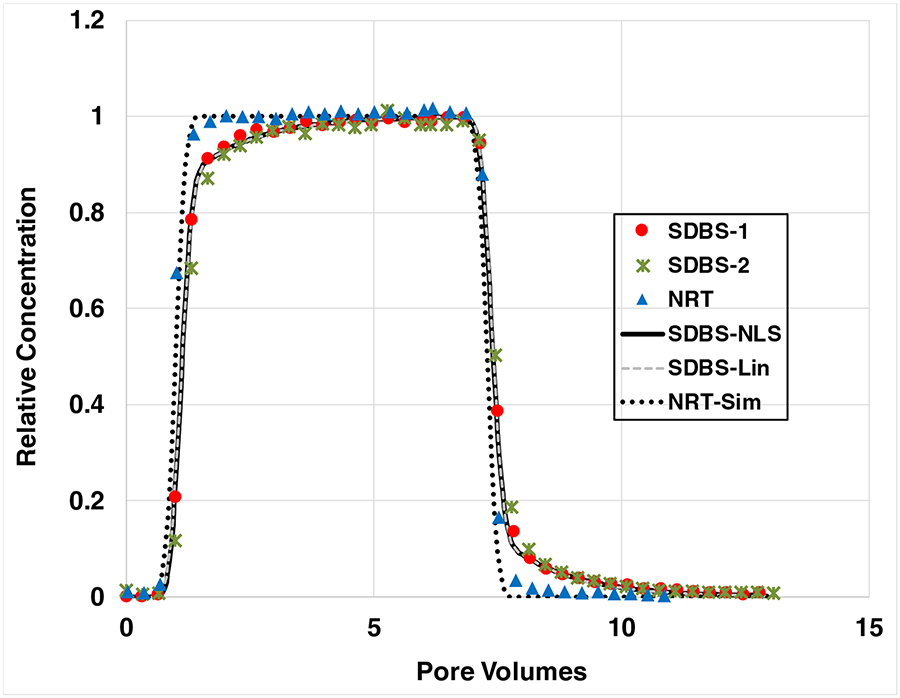
The transport of the nonreactive tracer in the sand under water-saturated conditions was ideal for all packed columns, with sharp and symmetrical breakthrough curves. An illustrative example is provided in Figure 1. The ideal solute-transport model incorporating a homogeneous porous medium and no mass-transfer limitations provides good fits to the measured data. These results indicate that flow and aqueous-phase transport in the packed columns is effectively ideal.

Figure 1.

Breakthrough curves for the nonreactive tracer (NRT) and SDBS transport under water-saturated conditions. The two simulations for SDBS represent solid-phase adsorption as nonlinear (NLS) and linear (Lin). SDBS injection concentration is ~40 mg/L.

Nonideal mass transfer significantly influences SDBS transport in the sand under water-saturated conditions, as evidenced by the asymmetrical breakthrough curves obtained from the miscible-displacement experiments (Figure 1). The solute-transport model incorporating nonlinear, rate-limited adsorption provides good fits to the measured data. The simulated curve assuming linear adsorption is essentially indistinguishable from the curve including nonlinear sorption (Figure 1). This indicates that nonlinear adsorption has minimal impact on SDBS transport compared to that of rate-limited adsorption.

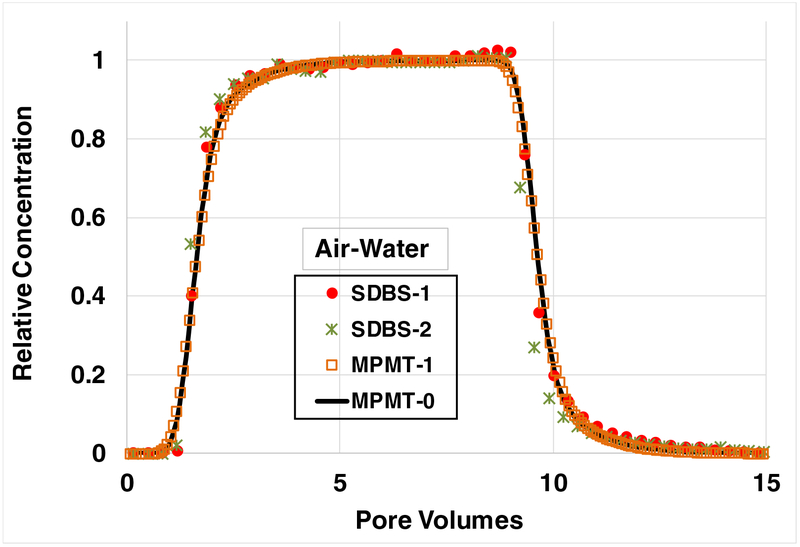
The breakthrough curves for SDBS transport under water-unsaturated conditions are presented in Figure 2. The simulated curve incorporating rate-limited solid-phase adsorption along with an assumption of local equilibrium for air-water interfacial adsorption (MPMT-0) provides a very good prediction of the measured data. The simulation incorporating rate-limited air-water interfacial adsorption (MPMT-1), with the rate coefficient based on the reported literature value, is observed to be essentially identical to the curve produced assuming local equilibrium. As noted above, these simulations represent independent predictions, rather than calibrations, of the measured data. The nondimensional parameter values used for all simulations are presented in Table 1.

Figure 2.

Breakthrough curves for SDBS transport under water-unsaturated conditions, with adsorption at air-water interfaces contributing to retention. Both simulations incorporate rate-limited solid-phase adsorption. Case MPMT-0 represents local equilibrium (e.g., effectively “instantaneous”) air-water interfacial adsorption. Case MPMT-1 incorporates rate-limited air-water interfacial adsorption. SDBS injection concentration is ~40 mg/L; water saturation is 0.8.

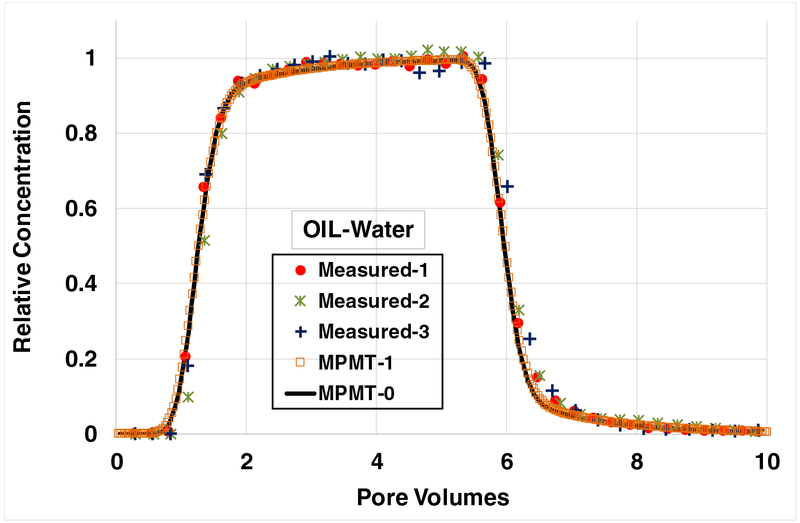
The breakthrough curves for SDBS transport in columns containing trapped residual OIL are presented in Figure 3. The simulated curve incorporating rate-limited solid-phase adsorption along with an assumption of local equilibrium for OIL-water interfacial adsorption (MPMT-0) provides a very good prediction of the measured data. The simulation incorporating rate-limited OIL-water interfacial adsorption (MPMT-1) is observed to be essentially identical to the curve produced assuming local equilibrium. Hence, the results for the OIL-water and air-water systems are consistent.

Figure 3.

Breakthrough curves for SDBS transport in columns containing trapped residual OIL, with adsorption at OIL-water interfaces contributing to retention. Both simulations incorporate rate-limited solid-phase adsorption. Case MPMT-0 represents local equilibrium (e.g., effectively “instantaneous”) OIL-water interfacial adsorption. Case MPMT-1 incorporates rate-limited OIL-water interfacial adsorption. Note that the input pulse was slightly larger for experiment 3, and therefore the simulated curve does not match the measured elution curve. SDBS injection concentration is ~40 mg/L; water saturation is 0.8.

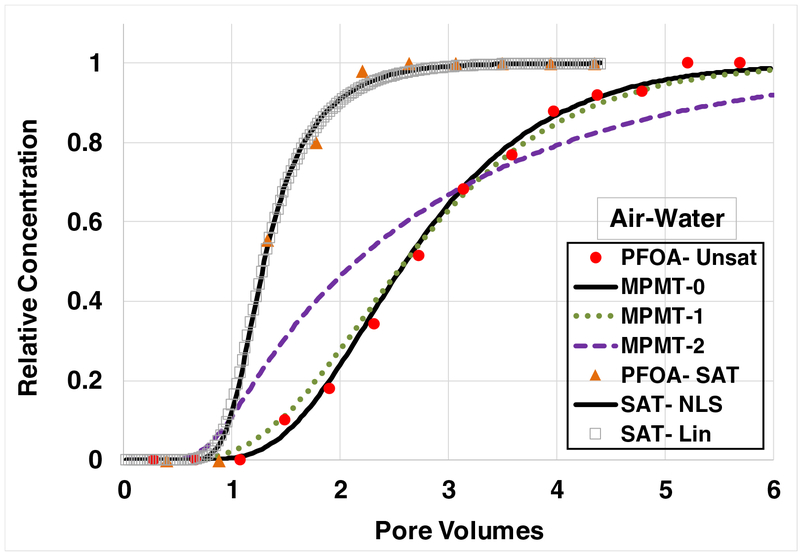
The breakthrough curve for PFOA transport in the sand under water-saturated conditions exhibits some degree of arrival-wave tailing, indicating the impact of rate-limited adsorption (Figure 4). The solute-transport model incorporating nonlinear, rate-limited adsorption provides a good fit to the measured data. As was observed for SDBS, the simulated curve with linear adsorption is essentially indistinguishable from the one incorporating nonlinear adsorption.

Figure 4.

Breakthrough curves for PFOA transport under water-saturated and water-unsaturated conditions, with adsorption at air-water interfaces contributing to retention in the latter system. All simulations incorporate rate-limited solid-phase adsorption. The two simulations for the saturated-flow experiment represent solid-phase adsorption as nonlinear (NLS) and linear (Lin). For the unsaturated-flow experiments, case MPMT-0 incorporates local equilibrium (e.g., effectively “instantaneous”) air-water interfacial adsorption. Case MPMT-1 incorporates rate-limited air-water interfacial adsorption, with the rate coefficient set equal to the geometric mean of literature- reported values. Case MPMT-2 incorporates rate-limited air-water interfacial adsorption, with the rate coefficient set equal to a value 10-times lower than the geometric mean of literature reported values. PFOA injection concentration is 10 μg/L; water saturation is 0.7.

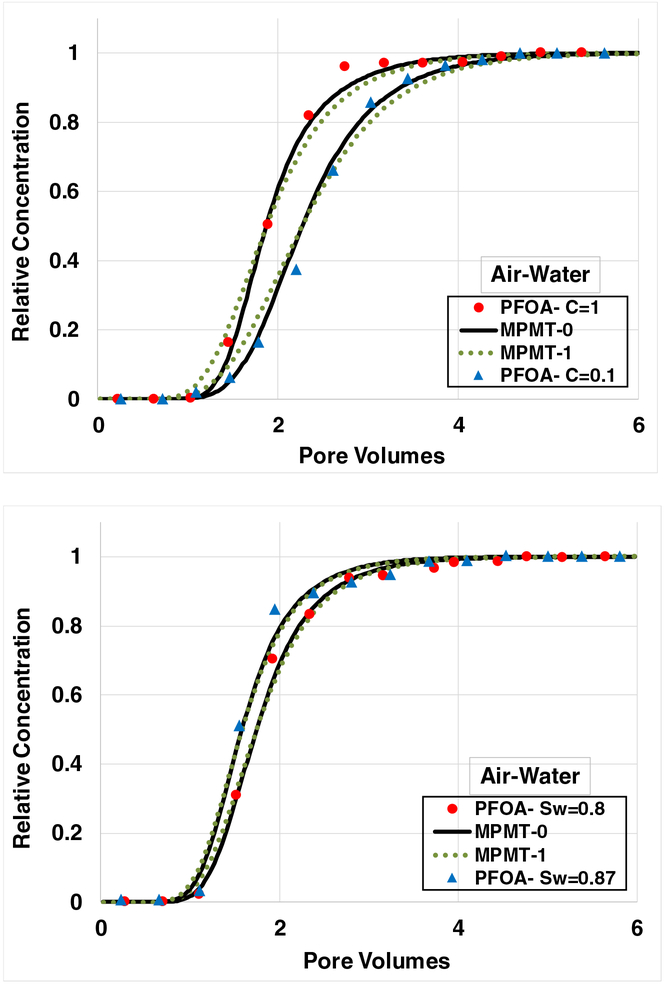
The breakthrough curve for PFOA transport under water-unsaturated conditions, with an injection concentration of 10 μg/L, is presented in Figure 4. The simulated curve incorporating rate-limited solid-phase adsorption along with an assumption of local equilibrium for air-water interfacial adsorption (MPMT-0) provides a very good prediction of the measured data. The simulation incorporating rate-limited air-water interfacial adsorption (MPMT-1), with the rate coefficient based on the geometric mean of the reported literature values, is observed to be similar to the curve produced assuming local equilibrium. Similar results are obtained for PFOA transport with injection concentrations of 100 μg/L and 1000 μg/L (see Figure 5A), and for PFOA transport at different water saturations (Figure 5B).

Figure 5.

Breakthrough curves for PFOA transport under water-unsaturated conditions, with adsorption at air-water interfaces contributing to retention. All simulations incorporate rate-limited solid-phase adsorption. Case MPMT-0 incorporates local equilibrium (e.g., effectively “instantaneous”) air-water interfacial adsorption. Case MPMT-1 incorporates rate-limited air-water interfacial adsorption, with the rate coefficient set equal to the geometric mean of literature- reported values. A. PFOA injection concentration is 0.1 and 1 mg/L; water saturation is 0.7. B. PFOA injection concentration is 1 mg/L; water saturation is 0.8 and 0.87.

The transport of PFOS in the sand under water-saturated conditions is influenced by rate-limited adsorption (Figure 6), similar to PFOA and SDBS transport. The solute-transport model incorporating nonlinear, rate-limited adsorption provides a good fit to the measured data. Consistent with the SDBS and PFOA results, the simulation produced for linear adsorption is indistinguishable from the one with nonlinear adsorption (data not shown). The greater significance of rate-limited adsorption versus nonlinear adsorption for PFOS and PFOA transport observed herein is consistent with the results reported by Brusseau et al. (2019b) for PFOS transport in two soils under water-saturated conditions.

Figure 6.

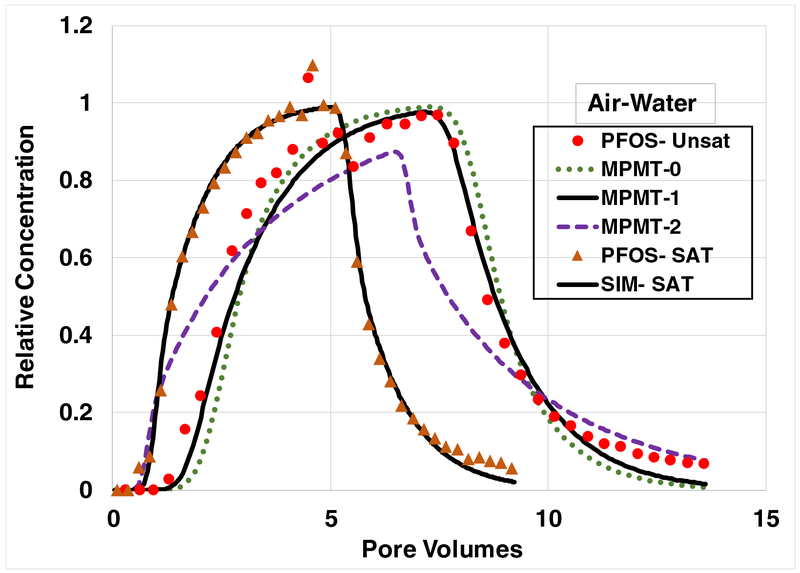
Breakthrough curves for PFOS transport under water-saturated and water-unsaturated conditions, with adsorption at air-water interfaces contributing to retention in the latter system. All simulations incorporate rate-limited solid-phase adsorption. For water-unsaturated conditions, Case MPMT-0 incorporates local equilibrium (e.g., effectively “instantaneous”) air-water interfacial adsorption and effectively instantaneous diffusive mass transfer between advective and nonadvective domains. Case MPMT-1 incorporates rate limited diffusive mass transfer between advective and nonadvective domains, and local equilibrium air-water interfacial adsorption (AWIA). The AWIA is apportioned between the advective and nonadvective domains. Case MPMT-2 incorporates rate limited diffusive mass transfer between advective and nonadvective domains, and local equilibrium air-water interfacial adsorption (AWIA). The AWIA is apportioned fully to the nonadvective domain. PFOS injection concentration is 10 mg/L; water saturation is 0.6.

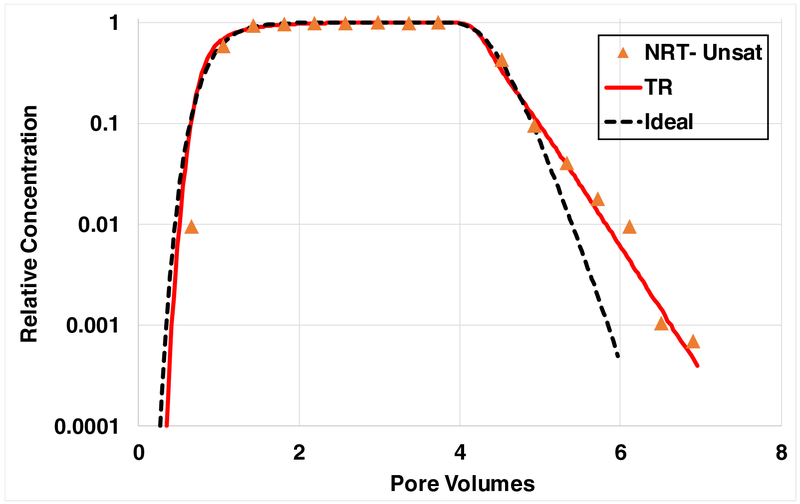
The unsaturated-flow experiment for PFOS was conducted with a lower water saturation (0.6) compared to the PFOA and SDBS experiments. The transport of the NRT for the experiment conducted with a matching lower water saturation was somewhat nonideal due to the presence of poorly-advective domains associated with water trapped in drained and dead-end pores and the impact of rate-limited diffusive mass transfer between the advective and nonadvective domains (Figure 7). A simulation produced with the two-region model incorporating rate-limited diffusive mass transfer between the advective and nonadvective domains provides a better fit to the measured NRT data compared to the simulation produced for ideal transport. The transport of PFOS is likely to also be influenced by rate-limited diffusive mass transfer between the advective and nonadvective domains, and therefore this process will be incorporated into the simulations of PFOS transport.

Figure 7.

Breakthrough curve for transport of the nonreactive tracer (NRT) in sand at a lower water saturation (0.6) matching the PFOS unsaturated-flow transport experiment (data in Figure 6). Simulations are produced assuming ideal conditions or the presence of preferential flow and rate-limited diffusive mass transfer (two-region, TR, model).

The breakthrough curve for PFOS transport under water-unsaturated conditions is presented in Figure 6. The simulated curve incorporating rate-limited solid-phase adsorption, local equilibrium for air-water interfacial adsorption, and local equilibrium for rate-limited diffusive mass transfer between the advective and nonadvective domains (MPMT-0) does not match the measured data. An improved prediction is obtained with case MPMT-1, which adds rate-limited diffusive mass transfer between the advective and nonadvective domains. For this case, air-water interfacial adsorption is apportioned between the advective and nonadvective domains according to the distribution of water between the two domains as determined from the NRT data. The simulation produced with all air-water interfacial adsorption apportioned to the nonadvective domain (MPMT-2) provides a very poor match to the measured data. This indicates that adsorption to the air-water interface is distributed proportionally within both domains. The simulation produced for MPMT-1 does not fully match the lower-concentration portion of the elution curve. A simulation produced with air-water interfacial adsorption treated as rate limited poorly matches the measured data (not shown), consistent with the results for SDBS and PFOA. The simulation produced for the saturated-flow PFOS experiment also underpredicts the latter portion of the elution curve. Hence, it is possible that the two-domain model does not fully capture the impact of rate-limited adsorption for this system.

4. Discussion

A critical aspect to the use of any mathematical model is determination of input parameters. The literature is replete with discussions of parameter determination for equilibrium adsorption coefficients and adsorption rate coefficients. Similarly, determination of parameters for preferential flow and diffusive mass transfer between advective and nonadvective domains has been discussed previously. Hence, the focus of this evaluation will be on fluid-fluid interfacial adsorption.

Determination of Fluid-Fluid Interfacial Adsorption Parameters

Two variables control the magnitude of fluid-fluid interfacial adsorption, K_nw and A_nw. Inspection of equation 5 shows that independent prediction of R requires knowledge of both variables. In turn, determination of K_nw values from the results of miscible-displacement experiments (back-calculation from R) requires independent determination of A_nw (along with the other variables in equation 5). Similarly, determination of A_nw values from the results of miscible-displacement experiments requires independent determination of K_nw.

The standard method to measure K_nw values is via surface/interfacial tension measurements. This measurement method is typically very robust, as illustrated by a comparison of surface-tension measurements conducted for PFOA (Brusseau, 2019b; Brusseau and Van Glubt, 2019). An analysis of several data sets reported in the literature showed remarkable consistency among the measurements even though different investigators conducted the studies over a span of decades using different methods. Values for K_nw determined from miscible-displacement experiments for PFOS and PFOA for systems where the A_nw was known a priori were shown to be consistent with values determined by surface-tension measurement (Lyu et al., 2018; Brusseau et al., 2019a). These results indicate that surface-tension measurements can be considered to provide robust determinations of K_nw for transport experiments, as long as the solution conditions are consistent.

The greatest source of potential uncertainty for characterizing fluid-fluid interfacial adsorption for transport is determining the amount of air-water or OIL-water interfacial area present. The amount of fluid-fluid interface present in a given system is a function of matric potential, fluid saturation and distribution, and properties of the solid such as particle/pore size distribution and solid surface area (e.g., Anwar et al., 2000; Costanza and Brusseau, 2000; Schaefer et al., 2000). Different methods are available to measure A_nw in porous media, with the two primary being high-resolution x-ray microtomography (XMT) and interfacial partitioning tracer tests (IPTT). The different methods produce different magnitudes of interfacial area (Brusseau et al., 2006, 2007, 2008, 2010; Narter and Brusseau, 2010), and therefore the method used can have a significant impact on interpretation of PFAS transport data.

The impact of employing A_nw values determined with the two primary methods is illustrated through comparing K_nw values back-calculated from the retardation factors measured for the SDBS OIL-water miscible-displacement experiments. Values for A_nw were determined with the air-water aqueous-phase IPTT method and by XMT for the sand. The details on the principles and application of these two methods are available in the literature (e.g., Brusseau et al., 2006, 2007, 2008, 2015). The measurements were conducted at S_w = 0.8, matching the S_w of the SDBS OIL-water experiments. Total and capillary interfacial areas of 18 and 11 cm⁻¹ were measured with XMT. A total interfacial area of 41 was measured with the IPTT method. The back-calculated K_nw values are 0.0046, 0.0028, and 0.0012 cm for the XMT-capillary, XMT-total, and IPTT interfacial areas, respectively. A value of 0.0013 cm was measured with the interfacial-tension method. It is observed that the K_nw values determined using the XMT data are more than 2–3 times greater than the measured value. Conversely, the K_nw value determined based on the IPTT-measured A_nw is essentially identical to the measured value. This is consistent with results obtained based on a comparison of independently measured and back-calculated A_nw values (Brusseau, 2019a). These results illustrate the importance of employing appropriate measures of fluid-fluid interfacial area when characterizing PFAS transport in multiphase systems.

Rate Limitations for Fluid-Fluid Interfacial Adsorption

The results presented above are consistent for SDBS, PFOA, and PFOS transport under water-unsaturated conditions. The independently-predicted simulations produced with air-water and OIL-water interfacial adsorption assumed to be under local equilibrium provided very good matches to the measured data. These results suggest that adsorption of all three surfactants to the fluid-fluid interface is effectively instantaneous with respect to advective transport for the conditions of the experiments. This observation is further tested by examining the results of the sensitivity analyses and the model-calibration simulations.

The significance of potential rate limitation for any mass-transfer process is assessed by comparison of the characteristic time of mass transfer to the characteristic transport time, i.e., the residence time. The nondimensional Damkohler Number provides a means to conduct such a comparison. A Damkohler Number of 100 represents the effective upper limiting case wherein mass transfer is sufficiently rapid compared to residence time that it can be treated as effectively instantaneous (e.g., Jennings and Kirkner, 1984; Bahr and Rubin, 1987; Brusseau et al., 1989). Conversely, a value of 0.01 represents the effective lower limiting case for which mass transfer is extremely rate limited with respect to transport.

Damkohler Numbers in the range of 10 (ω_nw in Table 1) were obtained using the first-order mass-transfer coefficients determined from the literature data for air-water interfacial adsorption. The breakthrough curves simulated for this magnitude of ω_nw are observed to exhibit a relatively small degree of deviation from the curves produced with an assumption of local equilibrium (i.e., ω_nw = 100), as observed in Figures 2–5. The potential limits of equilibrium behavior for fluid-fluid interfacial adsorption are illustrated by the simulations conducted with a mass-transfer coefficient that is 10-times lower than the mean of the literature values, which results in a ω_nw = ~1. The breakthrough curves for this case exhibit significantly greater early breakthrough and tailing compared to the measured data. An example is shown in Figure 4 for PFOA transport (case MPMT-2). This simulation clearly provides a poor match to the measured data. This result shows that unrealistically short residence times (e.g., extremely high pore-water velocities) or much smaller diffusive mass-transfer coefficients (e.g., much smaller diffusion coefficient; much larger diffusive path length) are required to produce conditions for which fluid-fluid interfacial adsorption is significantly rate limited with respect to PFAS transport.

In addition to the independent-prediction based simulations, the model was also calibrated to the measured data to obtain optimized values for ω_nw. The optimized ω_nw values were 30 (10–120) and 52 (15–160) for SDBS and PFOA transport, respectively, in the air-water systems. These results are consistent with the results of the sensitivity analysis, and further support the conclusion that fluid-fluid interfacial adsorption was effectively instantaneous for the extant transport conditions. The sensitivity-analysis and calibration results also suggest that the magnitudes of the mass-transfer coefficients for the transport experiments may be somewhat larger than the values determined from the tensiometer-based literature data. The magnitudes of the Damkohler Numbers discussed above can be compared to a value determined with diffusion parameters, employing the diffusion-based equivalency of first-order mass transfer defined as (e.g., van Genuchten, 1985; Parker and Valocchi, 1986):

$${\alpha }_{\text{nw}}=\left(\text{a}\cdot {\text{D}}_0\cdot {\theta }_{\text{w}}\right)/\left(\tau \cdot {\text{l}}^2\right)$$ (6)

where D₀ is the aqueous diffusion coefficient (set to 6 · 10⁻⁶ cm²/s, Sekine et al., 2004; Kuo et al., 2013), a is a shape factor (set to 3 for planar geometry), l is the characteristic diffusion half-length (e.g., half-thickness for a slab), and τ is tortuosity. The median grain size of the sand is 350 μm, and a path length of 100 μm is used based on observations that pore diameters are typically smaller than grain diameters. A second calculation is made using a path length of 350 for comparison. A value of 2 is used for tortuosity (Brusseau and Rao, 1989) and a representative value of 0.25 is used for θ_w based on the measured values of the experiments. The ω_nw determined with these values is greater than 100 for the path length of 100 μm. Assuming a maximum diffusion path length equal to the median grain diameter produces a ω_nw of 40, for which rate-limited mass transfer is essentially insignificant. These estimated Damkohler Numbers are consistent with the measured and simulated transport results. Of particular note, the value of 40 is similar to the ω_nw values obtained from the model-calibration simulations (i.e., 30 and 52). The first-order mass-transfer coefficients for fluid-fluid interfacial adsorption determined using equation 6 are larger than the literature values. This is consistent with the difference in characteristic diffusion path lengths for surface-tension measurement instruments versus columns packed with porous media.

The preceding results indicate that PFOA and PFOS adsorption at the fluid-fluid interface was not rate limited for the transport experiments. However, PFAS comprise a wide range of molecular sizes, and aqueous diffusion coefficients decrease with increasing molecular size. Thus, it is relevant to consider the potential occurrence of rate limitations for larger PFAS. A diffusion coefficient of 2.3 · 10⁻⁶ cm²/s was reported for FC-4, a large PFAS with a molecular weight exceeding 900 (Gao et al., 2005). Using this value as an illustration, the first-order mass-transfer coefficient calculated using equation 6 is ~10 h⁻¹, with a corresponding Damkohler Number of ~15. Thus, adsorption of this larger PFAS at the fluid-fluid interface would be expected to have minimal rate limitation for transport under the conditions used in the experiments. Using equation 6 and the associated parameters, a diffusion coefficient of ~5 · 10⁻⁷ cm²/s is estimated as the value for which fluid-fluid interfacial adsorption would become significantly rate-limited for these conditions.

The results showed that solid-phase adsorption and diffusive mass transfer between advective and nonadvective domains were both rate limited for the miscible-displacement experiments. The respective Damkohler Numbers for these two processes are approximately 0.11 for the former and 1 for the latter for the conditions of the experiments (Table 1). These values are at least 10-times smaller than the values for air-water and OIL-water interfacial adsorption. These differences explain the observed relative significances of rate-limited mass transfer for the three processes.

5. Conclusions

The multiprocess mass-transfer model presented in this study was effective in simulating the observed nonideal transport of PFAS and SDBS. The results indicate that adsorption at air-water and OIL-water interfaces was under equilibrium conditions for the transport experiments. The rate limitations associated with solid-phase adsorption and diffusive mass transfer between advective and nonadvective domains were of greater significance. It is noted that consistent outcomes were obtained for lower-concentration (10 and 100 μg/L) and higher-concentration (140 mg/L) experiments. In addition, consistent results were obtained for a range of water saturations. Hence, the results presented herein are expected to be representative of PFAS transport over a wide range of conditions.

The hydraulic residence times associated with standard laboratory miscible-displacement experiments are typically significantly smaller than field-scale values. Damkohler Numbers for field-scale transport would therefore typically be some orders-of-magnitude greater than the ones reported herein. Hence, potential rate-limitations associated with air-water or OIL-water interfacial adsorption are anticipated to be of even lesser significance for most field-scale transport conditions compared to the results presented herein. The results indicate that adsorption at the air-water and OIL-water interface can be generally treated as effectively instantaneous for PFAS transport in porous media. The ramifications of this scale effect for the diminished impact of rate-limited adsorption on PFAS transport was discussed by Brusseau et al. (2019b). The influence of preferential flow and diffusive mass transfer between advective and nonadvective domains is anticipated to be a function of transient conditions, discussed in the following paragraph.

A number of other factors not considered in this study may influence the transport of PFAS in source zones. These include spatial and possibly temporal variability of geochemical properties of the solids, as well as spatial variability of water and/or OIL saturation. Another relevant factor is the influence of solution chemistry conditions such as ionic composition and the presence of co-contaminants on both solid-phase adsorption (e.g., Du et al., 2014; McKenzie et al., 2015, 2016) and fluid-fluid interfacial adsorption (Brusseau and Van Glubt, 2019). In addition, transient conditions may be present in the vadose zone due to infiltration-redistribution events. Under such conditions, S_w and A_nw will be temporally variable. In addition, such transient conditions can influence advective transport and the extent and distribution of nonadvective domains. Hence, PFAS adsorption at the air-water interface may exhibit apparent nonequilibrium under transient-flow conditions. It is anticipated that time scales for S_w relaxation are likely to be longer than the characteristic times of air-water interfacial adsorption reported in this study. Thus, any apparent nonequilibrium would more likely be a result of the transient-flow conditions rather than inherent mass-transfer limitations to fluid-fluid interfacial adsorption. Similarly, temporally variable S_w and A_nw behavior may be anticipated for systems with OIL present when the OIL undergoes dissolution or mobilization. The influence of transient multiphase flow conditions on PFAS retention and migration in the vadose zone and in OIL-contaminated source zones warrants specific detailed investigation.

Highlights.

The kinetics of air-water and OIL-water interfacial adsorption are examined for PFAS

The impact of rate-limited solid-phase adsorption is investigated

The impact of rate-limited diffusive mass transfer is investigated

The performance of a multiprocess transport model is tested

APPENDIX-NOTATION

• A_nw = specific fluid-fluid interfacial area (L²/L³)

• C₀ = input solute concentration (M/L³)

• C_a = solute concentration in the advective domain (M/L³)

• C_n = solute concentration in the non-advective domain (M/L³)

• C_a* = Ca/C0, dimensionless solute concentration

• C_n* = C_n/C₀, dimensionless solute concentration

• D = hydrodynamic dispersion coefficient (L²/T)

• D₀ = aqueous diffusion coefficient of the solute (L²/T)

• f = mass fraction of sorbent comprising the advective domain, dimensionless

• F_a = fraction of sorbent in the advective domain for which sorption is instantaneous, dimensionless

• F_n = fraction of sorbent in the non-advective domain for which sorption is instantaneous, dimensionless

• k_a2 = first-order desorption rate coefficient in the advective domain (1/T)

• k_n2 = first-order desorption rate coefficient in the non-advective domain (1/T)

• k_a⁰ = k_a2LθR_a2/q, Damkohler number representing contribution of sorption non-ideality in the advective domain, dimensionless

• k_n⁰ = k_n2LθR_n2/q, Damkohler number representing contribution of sorption non-ideality in the non-advective domain, dimensionless

• K_a = equilibrium sorption constant for the advective domain (L³/M)

• K_d = global equilibrium sorption constant (L³/M)

• K_n = equilibrium sorption constant for the non-advective domain (L³/M)

• K_nw = fluid-fluid interfacial adsorption coefficient (L)

• L = length of interest (L)

• n = Freundlich intensity parameter, dimensionless

• P = qL/θ_aD, Peclet Number, dimensionless

• q = Darcy flux (L/T)

• R = R_a1+R_a2+R_n1+R_n2 = 1+(ρ/θ)K_d, the global retardation factor, dimensionless

• R_a1 = [φ+f(ρ/θ)F_aK_a]/R, retardation in the instantaneous sorbed-phase of the advective domain, dimensionless

• R_a2 = [f(ρ/θ)(1-F_a)K_a]/R, retardation in the rate-limited sorbed-phase of the advective domain, dimensionless

• R_n1 = [(1-φ)+(1-f)(ρ/θ)F_nK_n]/R, retardation in the instantaneous sorbed-phase of the non-advective domain, dimensionless

• R_n2 = [(1-f)(ρ/θ)(1-F_n)K_n]/R, retardation in the rate-limited sorbed-phase of the non-advective domain, dimensionless

• S_a2 = mass of sorbate in rate-limited sorbed-phase divided by the mass of sorbent in the advective domain (M/M)

• S_n2 = mass of sorbate in rate-limited sorbed-phase divided by mass of sorbent in the non-advective domain (M/M)

• S_a* = S_a2/[(1-F_a)K_aC₀], dimensionless

• S_n* = S_n2/[(1-F_n)K_nC₀], dimensionless

• T = qt/θL, dimensionless time in pore volumes

• T₀ = input pulse in pore volumes, dimensionless

• v_a = q/θ_a, average pore water velocity in the advective domain (L/T)

• X = x/L, dimensionless length

• α = first-order mass transfer coefficient for diffusion between advective and nonadvective domains (1/T)

• β₁ = R_a1/R, fractional retardation parameter, dimensionless

• β₂ = R_a2/R, fractional retardation parameter, dimensionless

• β₃ = R_n1/R, fractional retardation parameter, dimensionless

• β₄ = R_n2/R, fractional retardation parameter, dimensionless

• θ = θ_a + θ_n, total volumetric water content (L³/L³)

• θ_a = volumetric water content in the advective domain (L³/L³)

• θ_n = volumetric water content in the non-advective domain (L³/L³)

• ρ = bulk density (M/L³)

• φ = θ_a/θ, dimensionless

• ω = αL/q, the Damkohler number representing the contribution of physical non-ideality (diffusive mass transfer between advective and nonadvective domains), dimensionless