Research on an evolutionary game model and simulation of a cluster innovation network based on fairness preference

Chuanyun Li; Xia Cao; Ming Chi

doi:10.1371/journal.pone.0226777

. 2020 Jan 13;15(1):e0226777. doi: 10.1371/journal.pone.0226777

Research on an evolutionary game model and simulation of a cluster innovation network based on fairness preference

Chuanyun Li ¹, Xia Cao ^1,^*, Ming Chi ²

Editor: Luo-Luo Jiang³

PMCID: PMC6957165 PMID: 31929550

Abstract

The cluster innovation network is an important part of regional economic development. In addition, the fairness preference of internal innovators in the processes of investment and benefit distribution are particularly important for curbing "free riding" and other speculative behaviors and for creating a good cooperation environment. Therefore, taking a cluster innovation network constructed by the weighted evolutionary BBV model as the research subject, this paper constructs an evolutionary game model of a cluster innovation network based on a spatial public goods game and the theory of fairness preferences, which involves the processes of investment and payoff allocation. Using simulation analysis, this paper studies the evolution of innovators’ cooperative behaviors and benefits in cluster innovation network under the conditions of a fairness preference and a return intensity. The results show that an increase in the weight coefficient, gain coefficient and degree of differentiation between the previous income and current investment can effectively promote improvements in the level of enterprise cooperation. Indeed, the greater the weight coefficient, the gain coefficient and the degree of differentiation are, the more substantial the improvement in the level of enterprise cooperation will be. Moreover, an improvement in the differentiation of the breadth and depth of enterprise cooperation has an inhibitory effect on enterprise cooperation. Furthermore, whereas increases in regulation and gain coefficients can effectively promote enterprise cooperation. However, the increase in the weight coefficient has a different effect on enterprise benefit in terms of the breadth and depth of cooperation. Finally, we hope to improve the overall cooperation level and cooperation income of the network by deeply understanding the fair preferences of innovators in the processes of investment and benefit distribution, which is helpful for promoting the evolution and development of cluster innovation networks.

1 Introduction

Cluster innovation networks are an innovative organizational form designed to accelerate the development of cooperative innovation and to improve knowledge level and innovation ability, which have become indispensable part of China’s regional innovation system. Since clusters possess the characteristics of geographical proximity and knowledge spillovers[1], the knowledge and technology of innovators exhibit the attributes of "public goods"[2]. In the process of cooperative innovation, speculation[3] such as "hitchhiking" and "betrayal" often occurs, and it seriously damages the cooperative environment of the cluster innovation network. Additionally, the fairness preference[4] and moderate return intensity[5] in the process of investment and the payoff allocation of innovators can effectively inhibit the emergence of these speculative activities. In addition, in the actual network evolution game process, the cooperation behavior of innovators is not only influenced by the network structure but also closely related to the intensity of the cooperative relationship between innovators[6], that is, the connection in the real network has the weight attribute. According to the existing research, a real network with connected weights has both the power-law distribution characteristics of the degree distribution and the power-law distribution characteristics of the strength distribution[7]. The weighted scale-free network constructed based on the weighted evolutionary BBV model can simulate a real network very well [8]. Therefore, we take a weighted scale-free cluster innovation network as the research subject. By considering the interaction between cooperative behavior of innovators and the network structure and analyzing the evolution of the cluster innovation network under the given fairness preferences and return intensity, we can avoid problems such as hitchhiking and cooperation inertia(among others), and improve both overall level of cooperation and the cooperative benefit of the network. This result is very significant for promoting the evolution and development of a cluster innovation network.

From the perspective of game theory, the cooperative game process among innovators in cluster innovation networks can be regarded as a spatial public goods game[9]. Because the betrayer’s income is often higher than the cooperator’s income, the cooperative dilemma of the "tragedy of the commons" occurs[10]. To resolve this dilemma, some scholars have found that volunteer[11], reputation[12], reward[13] and punishment[14] mechanisms can improve the level of cooperation in the network. Some scholars have also found that fixed static network structures such as rule networks[15], small-world networks[16] and scale-free networks[17] can also promote cooperation under certain conditions[18]. Santos et al [19] discovered that the fairness preference of innovative subject cooperative behavior can greatly affect the level of cooperation in BA network. Many scholars have begun to supplement and improve fairness preference theory in the context of a spatial public goods game on the network in three main ways. First, scholars seek to improve the investment process in a spatial public goods game and to study the influence of the investment fairness preference of innovators on the cooperation levels in the network. For example, some researchers have improved the investment fairness preference according to the degree value of the game subject[20–21] and have found that in the static rule network, a high-quality group preference can greatly enhance the cooperation level of the innovators. Other scholars have improved the investment fairness preference according to the previous income of the game subject[22] and have found that in the static BA network, the degree of investment differentiation increases, which can promote the cooperation level in the network. In addition, some studies have improved the investment fairness preference according to the cooperation proportion of the game subject in the neighborhood[23–25]. These studies that in the static rule network, a small increase in the investment heterogeneity can rapidly increase the cooperation level in the network. Second, studies have sought to improve the payoff allocation process in the spatial public goods game and have examined the impacts of payoff allocation fairness preferences on the cooperation levels in the network. For example, some researchers improved the payoff allocation fairness preferences according to the degree value of the game subject[26]. These researches found that in a static BA network, when the degree of differentiation in the payoff allocation is low, the level of cooperation in the network can be higher. Other scholars have improved the payoff allocation fairness preference according to the cooperation proportion in the neighborhood of the game subject[27]. These scholars found that in a static BA network, the greater the degree of differentiation in the payoff allocation is, the higher the level of cooperation in the network will be. In addition, some scholars improved the payoff allocation fairness preference according to the previous income of the players[28] and have found that in a static BA network, the level of cooperation in the network will increase significantly only when the degree of differentiation in the distribution of interests is above a certain threshold. Third, the existing research has improved the investment and payoff allocation process in the spatial public goods game, and it studied the impacts of the investment and payoff allocation fairness preference of innovators cooperative behavior on the cooperation level and cooperative benefit in a network. For example, some researchers have improved the investment and payoff allocation according to the degree value and the current investment the game subject[29]. They have found that in static BA networks, when the innovators’ neighbors allocate excessive benefits, the level and benefits of cooperation in the network can be significantly improved. Some scholars have improved the investment and payoff allocation according to the previous income and current investment[30]. These scholars found that in static regular networks, an increase in the investment differentiation can promote cooperation and increase the cooperative benefits in a network. In addition, other researchers improved the investment and payoff allocations according to the degree value, previous income, current investment and degree value[31]. These researchers found that in static BA networks, moderate enterprise degree can promote the formation of an interest community. Moreover, the improvement in the gain level is an important source of the increase in the average income and the emergence of cooperation.

In light of the existing research, the research on evolutionary games in cluster innovation networks based on the fairness preference has been substantial. Most studies are based on an established static network structure and analyze the evolution of innovators’ cooperative behavior under fairness preference in the spatial public goods game. However, the existing research still has the following shortcomings: (1) it has been under an established static network structure, and does not consider dynamic changes in the network structure; (2) because scholars mostly use weightless networks (such as rule networks, small world networks and BA scale-free networks) as the network model, weighted networks with a network relationship strength are seldom examined; (3) while existing research mainly improves the rules of payoff allocation from the degree value, current investment and cooperation proportions, it ignores the impact of the intensity of cooperation among innovators on the process of payoff allocation; and (4) last, scholars mostly aim to improve the level of cooperation in the network through the improvement of the fairness preferences for the investment and payoff allocation Thus, scholars have neglected to consider the return intensity and the cooperative benefits of innovators. In light of these limitations, the present paper takes the cluster innovation network constructed by the weighted evolutionary BBV model as the research object and, based on the spatial public goods game model and fairness preference theory, constructs an evolutionary game model of the cluster innovation network that combines the process of investment and payoff allocation. Using the MATLAB 2017b software, this research simulates and analyzes the evolution of cooperative behavior and the cooperative benefits of innovators in cluster innovation networks under a fairness preference and return intensity, which has important theoretical significance and practical relevance for revealing the evolution mechanism of cluster innovation networks and promoting their development.

The remainder of this paper is organized as follows. The model with network evolution analysis is presented in Section 2. Then, the model with heterogeneity of both the investment and payoff allocations is constructed in Section 3. Subsequently, the corresponding simulation results are given in Section 4. Finally, the conclusions are provided in Section 5.

2 Evolution analysis of the cluster innovation network under the fairness preference

Innovators in cluster innovation networks often show strong preferences for fairness in the process of cooperation[4], as they seek to maximize their own payoffs but also consider the fairness of the investment and payoff allocation[31]. The investment and payoff allocations are complementary processes that are independent and interrelated; that is, investment is an important prerequisite for the payoff allocation, and in turn, the payoff allocation is the main reference for the next round of investment. Therefore, from the perspective of the fairness preferences in the process of investment and payoff allocation, this paper analyzes the evolution process of cluster innovation networks.

The fairness preference of innovators for cooperative behavior is related to the scale of innovators and the intensity of their cooperative relationships. Among these factors, the strength and innovation abilities of innovators at different scales are different. The scale of the innovators greatly affects their investment fairness preferences, which can be reflected by the cooperation breadth of the nodes in cluster innovation networks. The cooperative R&D capability, trust and knowledge transfer efficiency of different cooperation intensity among innovators are also different. The cooperation intensity among innovators greatly affect the process of the payoff allocation of innovators, which can be reflected by the cooperation depth between the nodes in cluster innovation networks. Based on the relevant literature[31], to reflect the degree of differentiation in the fairness preference between the investment and payoff allocation and the importance degree of each index this paper uses the adjustment coefficient to reflect the different degree of fairness preference between the investment and payoff allocation in terms of the previous income, current investment, cooperation breadth and cooperation depth. Furthermore, the weight coefficient is used to reflect the degree of importance of the fairness preference between the investment and payoff allocation in the previous income, current investment, cooperation breadth and cooperation depth. In addition, since the return intensity is an important factor that affect the cooperative behavior and the cooperative income of the innovators in the process of the game, this paper uses the gain coefficient to adjust the return intensity from the investment cost to the income of the innovators in the process of the cooperative game [32].

In the process of the cooperative game, innovators in cluster innovation networks will adjust their cooperative strategies according to the Fermi rule [33], then change their cooperative behavior. At the same time, network nodes will adjust their cooperative goals according to the reconnection mechanism with preferred connections [34], which will change the network structure. As a result of the interaction between the network structure and innovators’ cooperative behavior, the cluster innovation network’s structure exhibits dynamic evolution.

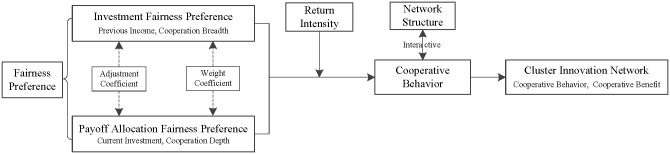
Accordingly, this paper constructs an evolutionary analysis framework of a cluster innovation network under the given fairness preferences, as shown in Fig 1. By embedding the fairness preference of innovators’ cooperative behavior into the game model of the process of investment and payoff allocation, and under the influence of the fairness preferences and return intensity, this paper reveals the evolution of cooperative behavior and the income of innovators in the dynamic change process of a cluster innovation network. It is of vital to promote the evolution and development of cluster innovation networks.

3 Evolutionary game model of a cluster innovation network based on fairness preferences

3.1 Basic hypothesis of the game model

In cluster innovation networks, nodes represent cluster enterprises, links represent the game relationships between innovators, and link weights represent the strength of the cooperative relationships between innovators. The innovators in the network update their own strategies according to the rules and adjust their relationships through the reconnection mechanism with preferential connections until the cooperative strategies of the innovators and the relationships between them reach a stable state. Based on the characteristics of the cluster innovation network structure and a realistic consideration of the game model, the following hypotheses are proposed:

Hypothesis 1: In the process of the game, the cooperative relationships between innovators are adjusted only according to the reconnection mechanism with preferential connections, the adjustments are made without considering the growth of nodes and edges in the network.
Hypothesis 2: In the process of the game, the innovators x with degree value k_x only participate in the game between the neighborhood centered on itself and neighborhood centered. Moreover, there is a total degree value of k_x + 1 in the neighborhood, and all of the nodes in the network have the same total investment C = 1.
Hypothesis 3: The innovators in the network are all limited rational individuals and can only choose two strategies: cooperation and noncooperation.

3.2 Construction of the game model

In the first round (t_n = 1) of the public goods game, the degree value of enterprise x is k_x, so if enterprise x chooses an uncooperative strategy (S_x = 0), the investment of enterprise x in its neighborhood is 0. However, if enterprise x chooses a cooperative strategy (S_x = 1), it participates in k_x + 1 neighborhoods centered on itself and neighbors, and its total investment is evenly distributed among all k_x + 1 neighborhoods. At this time, the investment in the neighborhood centered on enterprise y of x is as follows:

I_{x, \hat{y}} (t_{n}) = \frac{1}{k_{x} + 1}, if S_{x} = 1 and t_{n} = 1

(1)

In the process of the public goods game in round t_n (t_n ≥ 2), if enterprise x chooses cooperative strategy (S_x = 1), then it allocates the investment of one of its neighborhood $\hat{y}$ (the neighborhood composed of neighborhood enterprise y as the center and directly connected enterprises) according to Eqs (2) and (3):

I_{x, \hat{y}} (t_{n}) = C • {\bar{D}}_{x, \hat{y}} (t_{n})

(2)

D_{x, \hat{y}} (t_{n}) = (1 - w_{1}) \frac{m_{_{x, \hat{y}}}^{α_{1}} (t_{n - 1})}{\sum_{i = 0}^{k_{y}} m_{_{i, \hat{y}}}^{^{^{α_{1}}}} (t_{n - 1})} + w_{1} \frac{k_{x}^{α_{1}}}{\sum_{i = 0}^{k_{y}} k_{i}^{α_{1}}}, if S_{x} = 1 and t_{n} \geq 2

(3)

Among these variables, because that the total investment of each enterprise is 1, $D_{x, \hat{y}} (t_{n})$ is normalized according to the min-max normalization method. ${\bar{D}}_{x, \hat{y}} (t_{n})$ is the normalized value of $D_{x, \hat{y}} (t_{n})$ , t_n is the number of rounds of the public goods game (only if all of the nodes in the network have a specific round of the game to end the round of game), $I_{x, \hat{y}} (t_{n})$ is the input of enterprise x to neighborhood $\hat{y}$ in round the t_n of the public goods game, and $m_{i, \hat{y}} (t_{n - 1})$ is the revenue of enterprise i from neighborhood $\hat{y}$ after the first round t_n−1 of the public goods game. and $m_{x, \hat{y}} (t_{n - 1})$ is the revenue of enterprise x from neighborhood $\hat{y}$ after the first round t_n−1 of the public goods game. When i = 0 denotes enterprise y itself, k_y denotes the degree value of enterprise y. Eq (3) shows that the investment of enterprise x in neighborhood $\hat{y}$ is mainly measured by the previous income and degree value. Among these values, the profitability of neighborhood $\hat{y}$ is expressed by the previous income. If enterprise x can obtain more profits than other enterprises in neighborhood $\hat{y}$ , then enterprise x will invest more in neighborhood $\hat{y}$ . The degree value represents the social status of enterprise x in neighborhood $\hat{y}$ . Enterprises with higher degree value will earn more investment in the next round of the game. To measure the importance of the previous income and degree value in the process of enterprise investment, the weight coefficients 1-w₁ and w₁ are used, where 0 ≤ w₁ ≤ 1. Moreover, to reflect the degree of differentiation of the previous income and degree value in the process of enterprise investment in the network, this paper uses the adjustment coefficient α₁ [21]. When α₁ > 0, this implies greater prophase income and greater proportion of the degree value, hence more investment is made in the neighborhood. When α₁ = 0, the model is consistent with the classical public goods game, and the input is distributed equally according to the number of neighborhoods[35].

In round t_n of the game, when the input of enterprise x into its neighbor y is over, the profits from neighbor y are distributed according to Eq (4):

m_{x, \hat{y}} (t_{n}) = r [(1 - w_{2}) \frac{I_{_{x, \hat{y}}}^{α_{2}} (t_{n})}{\sum_{i = 0}^{k y} I_{_{i, \hat{y}}}^{α_{2}} (t_{n})} + w_{2} \frac{G_{x}^{α_{2}}}{\sum_{i = 0}^{k y} G_{i}^{α_{2}}}] • \sum_{i = 0}^{k y} I_{i, \hat{y}} (t_{n}) • S_{i} (t_{n}) - I_{x, \hat{y}} (t_{n}) • S_{x} (t_{n})

(4)

Among these variables, r is the gain coefficient that used to measure the return intensity of investment (r > 1), and $\sum_{i = 0}^{k y} I_{i, \hat{y}} (t_{n}) • S_{i} (t_{n})$ is used to represent the total investment of all enterprises i in neighborhood $\hat{y}$ . Eq (4) shows that the payoff allocation of enterprise x in neighborhood $\hat{y}$ is mainly measured by the current investment and the strength of the cooperative relationships. Among these factors, the current investment reflects the investment ability in neighborhood. The greater the investment of enterprise x in neighborhood $\hat{y}$ is, the more income enterprise x will earn from neighborhood $\hat{y}$ . The strength of the cooperative relationship indicates the degree of close cooperation in the relationship. The stronger the cooperative relationship between the enterprises and their neighbors is, the more profits they will earn from their neighbors. To measure the importance of the current investment and cooperation intensity in payoff allocation, the weight coefficients 1-w₂ and w₂ are used, respectively. In addition, α₂ is the adjustment coefficient, which is consistent with the meaning and function of α₁.

Thus, after the end of round t_n of the game, the total revenue obtained by enterprise x is the sum of its revenue obtained in neighborhood k_x + 1, that is:

M_{x} (t_{n}) = \sum_{\hat{y} = 0}^{k x} m_{x, \hat{y}} (t_{n})

(5)

3.3 Evolution rules

Node m in the cluster innovation network will randomly select a neighbor node n after each round of the game to compare strategies. If pr_n > pr_m, node m will imitate neighbor n’s game strategy in the next round of the game with probability W. According to the Fermi update rule [33], the imitation probability is as follows:

W_{m \to n} = \frac{1}{1 + exp [(p r_{n} - p r_{m}) / k]}

(6)

Here, k represents the intensity of the noise, that is, the interference of external factors on the strategy learning process. When k → 0, the external factors will not interfere with the node’s strategy learning; on the contrary, the node can only update its strategy randomly because of the external factors. Considering the impact of the node revenue and strategy, this paper selects a neutral noise factor K = 0.5 as the simulation parameter value.

When node m selects the strategy of learning neighbor node n with probability W, it will be reconnected with other non neighbor nodes in the network with probability ϒ_ms. In the process of reconnection, only one edge is broken at a time; that is, the weight of the edge is reduced by 1. Since the nodes have certain preferences when choosing partners, this paper uses the reconnection mechanism with preferential connections [34] to determine the outgoing connection s of node m, The random probability is as follows:

ϒ_{m s} = \sum_{m \in G} \frac{p_{s}^{β}}{p_{m}^{β}}

(7)

Here, p_s is the benefit of node s, G is the set where node m is located, β is the preference tendency, and β = 0 is the non preference connection tendency, that is, a random connection. Conversely, the preference connection tendency is greater. This paper utilizes a high preference of β = 1 for simulation.

4 Simulation analysis of a cluster innovation network evolution game

4.1 Simulation steps

Step 1: Initialize the evolutionary game parameters, and according to the cluster innovation network, randomly assign the two game strategies of "cooperation" and "noncooperation" to each node in the network, with an initial cooperation level of 50%; that is, the network cooperation density set at 0.5.
Step 2: In each round, all of the innovators play the game with their neighbors and accumulate the cooperative benefits of the innovators according to the game model.
Step 3: In each round of the game, all of the innovators update their strategies according to the Fermi strategy rule (Eq (6)) and adjust their partners based on the reconnection mechanism with preferential connections (Eq (7)).
Step 4: Repeat steps 2 and 3 until the number of Monte Carlo iterations is reached and the simulation is completed.

4.2 Setting and explaining of the simulation parameters

According to the evolutionary game model and the specific algorithm of cluster innovation networks, and using the simulation platform of MATLAB 2017b, we set the simulation parameters for the evolutionary game of the cluster innovation network. These parameters are given in Table 1.

Table 1. Parameter settings for the evolutionary game simulation of cluster innovation networks.

Number of games	Network Size	Average Degree	Maximum Node Degree	Minimum Node Degree	Maximum Cooperation Strength	Minimum Cooperation Strength
500	100	4	31	2	10	1

Open in a new tab

In this paper, we use the generation mechanism of the weighted evolution BBV model to produce a cluster innovation network with N = 100 nodes and an average degree of 4. The maximum node degree is 31, the minimum node degree is 2, the maximum cooperation intensity is 10, and the minimum cooperation intensity is 1. Each data point is the average of the simulation results after 200 independent experiments. To ensure the accuracy of the research results, this paper sets the number of game rounds to 500. After the system fully evolves to a stable stage, the average of the last 50 cooperation densities is taken as Fc. Since the investment rules and payoff allocations are complementary processes that promote each other, their consistency should be maintained in the game. This paper assumes that the adjustment coefficient α₁ of inputs and the adjustment coefficient α₂ of the payoff allocations have the same trend of change. Moreover, the weight coefficients w₁ and w₂ also have the same trend of change, i.e., α = α₁ = α₂ and w = w₁ = w₂. In addition, to facilitate the analysis of the effect of the weight coefficients of the fairness preferences on cooperative behavior and the cooperative benefits of the innovators in the network, this paper uses Ruguo [31] and Li [36]. That is, w = 0 represents the wealth preference mechanism, i.e., the processes of investment and payoff allocation are determined by the previous income and the current investment, respectively. w = 0.5 represents the mixed preference mechanism, that is, the processes of investment and payoff allocation are determined by the previous income, the degree value, the current investment and the intensity of the cooperation. and w = 1 represents the social preference mechanism, that is, the processes of investment and payoff allocation are determined by the degree value and the intensity of the cooperation, respectively.

4.3 Impact of the fairness preference and return intensity on the enterprise cooperation level in cluster innovation network evolution

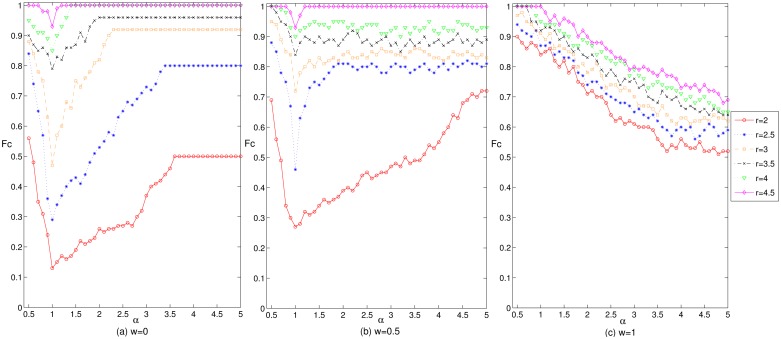
Fig 2 reflects the influence of the adjustment coefficient on the enterprise cooperation level in the cluster innovation network under three mechanisms and different gain coefficients. Observe in Fig 2 that under the wealth preference mechanism, with the increase in the adjustment coefficient, the level of enterprise cooperation in the network shows a trend of first decreasing, then rising, and finally stabilizing. When we have the adjustment coefficient α ≤ 1, along with the decrease of the difference degree of the previous income, degree value, current investment and cooperation intensity, the cooperation level of the enterprises in the network gradually decreases. Correspondingly, when we have the adjustment coefficient α > 1, with the increase of the difference degree of the previous income, degree value, current investment and cooperation intensity, the cooperation level of the enterprises in the network gradually increases. The increase in the degree of differentiation of the previous income and current investment can promote the level of enterprise cooperation. Compared with the wealth preference mechanism, the change of enterprise cooperation level under the mixed preference mechanism is more volatile. The reason is that under the mixed preference mechanism, the linked processes of investment and payoff allocation are affected by many factors, which makes enterprises more willing to change the existing cooperative relationship. Under the effects of the reconnection mechanism, the network structure will change greatly. When the cluster innovation network structure changes greatly, the changes will make the processes of the enterprise’s investment and payoff allocation more complex, which affects the choice of the enterprise cooperation strategy and leads to a greater fluctuation in the level of enterprise cooperation. Under the social preference mechanism, with the increase in the adjustment coefficient, the level of enterprise cooperation shows a gradual downward trend. This result is due to the increase in differentiation with regard to the breadth and depth of the enterprise cooperation, which renders more enterprises with less cooperation breadth and depth dissatisfied with the existing earnings. As a result, these enterprises change their partners, so the network structure changes. Whenever the network structure changes greatly, the profit margin of more enterprises is narrowed, which destroys the cooperative environment in the cluster. Thus cluster enterprises gradually withdraw from cooperation, which inhibits the improvement of the level of enterprise cooperation within the cluster [25]. In addition, the greater the differentiation is in terms of the breadth and depth of the enterprise cooperation, the more significant the interactions between the network structure and enterprise cooperative behaviors are, and the greater the inhibitory effect on the enterprise cooperation level is. In a the real cluster innovation network, the processes of enterprise investment and payoff allocation are affected by many factors. Furthermore, excessive profit-seeking of enterprises in the processes of investment and payoff allocation is not conducive to the maintenance of cooperative relationships among the enterprises in the network, which shows why it is difficult to have a high adjustment coefficient in the game model and in the mixed preference mechanism. Therefore, the appropriate return intensity is very important to maintaining the level of enterprise cooperation in the network and to promoting the healthy evolution and development of cluster innovation networks.

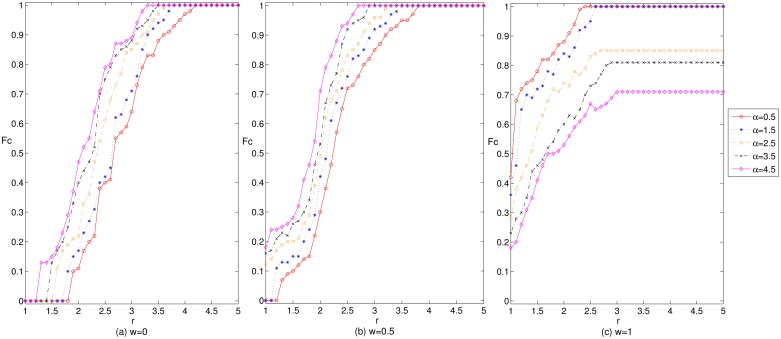
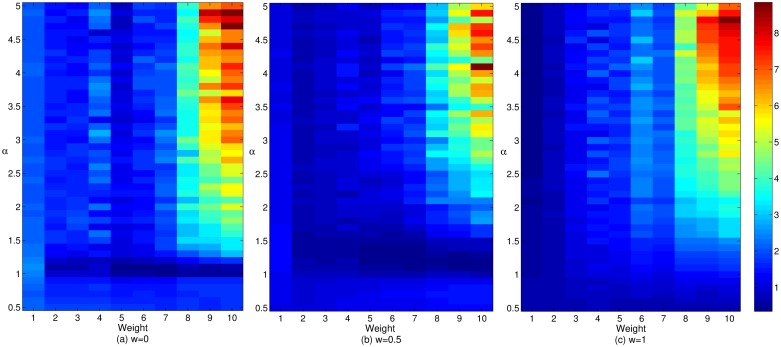
Fig 3 shows the effect of the gain coefficient on the enterprise cooperation level in cluster innovation networks under three mechanisms and different adjustment coefficients. Observe in Fig 3 that under the wealth preference mechanism, with an increase in the gain coefficient, the level of enterprise cooperation in the network first shows a stable trend, then the trend rises and finally stabilizes. This observation demonstrates that the level of enterprise cooperation in the network is only promoted when the return intensity exceeds a certain threshold, and the stronger the return intensity will be, the more obvious the promotion effect on the level of enterprise cooperation is. Under the mixed preference and social preference mechanisms, the level of enterprise cooperation shows a trend of first rising and then stabilizing. However, compared with the wealth preference mechanism, there is a lack of an initial stable development stage, and when the gain coefficient is relatively low, the level of enterprise cooperation can be stabilized. This result shows that the improvement of the preferences in terms of the breadth and depth of cooperation will enhance the ability of the investment and benefit allocation in cluster enterprises. Therefore, this improved preference will replace the role of returns to some extent. In addition, when the adjustment coefficient α is relatively low, with an increase of the weight coefficient w, the level of enterprise cooperation in the network gradually increases. This result may be due to the improvement of the preferences in terms of the breadth and depth of the enterprise cooperation and the increasing position of some enterprises in the network, whose partners are more willing to choose cooperation strategies to achieve greater benefits. At the same time, these enterprises will be dissatisfied because of the "speculative" and "free-rider" behavior of some partners and thereby change their own cooperative behavior and partners, which would cause the network structure to change greatly. When the network structure changes greatly, more enterprises will change their payoffs. Enterprises that employ non cooperative strategies will change their cooperative behavior for greater profits and, ultimately, improve the level of enterprise cooperation gradually. In addition, with an improvement of the preferences in terms of the breadth and depth of the enterprise cooperation, the interaction between cooperative behavior of innovators and network structure is stronger, and enterprise cooperation is more strongly promoted, which is more conducive to the evolution and development of the cluster innovation network. Therefore, to promote the emergence of cooperative behavior in cluster innovation networks, consider the return situation in the network in advance. When the return intensity is relatively low, the appropriate increase of the weight coefficient w can effectively maintain the level of enterprise cooperation at a higher level. Correspondingly, when the return intensity is relatively high, the lower weight coefficient w can ensure effective improvement in the enterprise cooperation.

4.4 Impact of the fairness preference and return intensity on the corporate cooperative benefit in cluster innovation networks

Figs 4 and 5 reflect the respective impacts of the adjustment and gain coefficients on the cooperative benefit of enterprises with different cooperative breadths in cluster innovation networks under three mechanisms. It can be seen from Figs 4 and 5 that with an increase in the weight coefficient, the profitability of enterprises with a large cooperation scale is gradually enhanced, while the cooperation income of enterprises with smaller cooperation breadth gradually decreases. The result is the phenomenon of “Care for this and lose that”, furthermore income imbalance among enterprises in the network becomes increasingly apparent. At the same time, the degree of enterprises with a wide range of cooperation is increasing, and the quantity is also increasing. This pattern occurs is because with the increase in the preference in terms of the breadth and depth of enterprise cooperation, the leading enterprises exhibiting broad cooperation have more substantial processes of profit distribution, which makes the cooperation income of larger enterprises increase continuously and reduce the profit margins of smaller enterprises. Therefore, the cooperation income of enterprises with smaller cooperation scope is declining continuously. In this case, the enterprises with smaller cooperation breadth will be dissatisfied because of their low income, hence, they will change their cooperative behavior. Under the effect of the reconnection mechanism, these enterprises are more inclined to R&D with the enterprises that have larger cooperation breadth to promote the increasing number of enterprises with larger cooperation scope, and their ability to benefit is also increasing gradually. In addition, with the changes in the network structure, the income of more enterprises are also changing. Increasing numbers of enterprises with smaller cooperation breadth will change their cooperative behavior because of dissatisfaction with their income. However, due to the unfavorable environment of cluster cooperation, under the interaction between cooperative behavior of innovators and the network structure, the benefits of enterprises with smaller cooperation breadth are gradually declining. Therefore, the increase in the preference in terms of the breadth and depth of the enterprise cooperation has a restraining effect on the increase in the incomes of enterprises with smaller cooperation breadth and a promoting effect on the increase in the incomes of enterprises with larger cooperation breadth, which is not conducive to the common development of all types of enterprises in cluster innovation network. The graph also reveals that with the increase in the gain coefficient r, the cooperative income has also increased. The enterprises with larger cooperation breadth have higher cooperative benefit. This result shows that the return intensity has a positive effect on the promotion of the corporate cooperation income, and this effect particularly significant for the promotion of enterprise cooperation income of enterprises with larger cooperation breadth. When the return intensity is continuously enhanced, this effect can effectively promote the enthusiasm of the cooperation among various types of the enterprises in the network, especially to enhance the cooperation incomes of enterprises with larger cooperation breadth to promote the benign evolution and development of cluster innovation network.

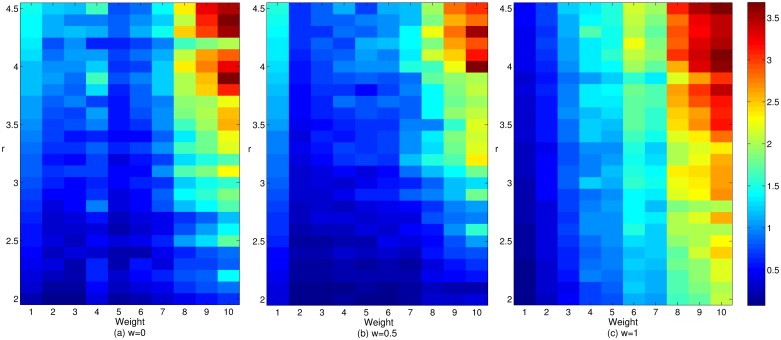
Figs 6 and 7 show the respective impacts of the adjustment coefficient and gain coefficient on the cooperation income of enterprises with different cooperation depths in cluster innovation network under three mechanisms. Figs 6 and 7 illustrate that among the three mechanisms, the cooperative benefit of enterprises with smaller cooperation depth under a wealth preference mechanism is relatively higher, and the corresponding benefit of enterprises with a larger cooperation depth is relatively lower. Under the social preference mechanism, the earnings of enterprises with smaller cooperation depth are relatively low, while those with larger cooperation depth are relatively high. This result may be due to the increase in the preference in terms of the breadth and depth of the enterprise cooperation, which enhances the enthusiasm of enterprises with larger cooperation depth for cooperation and innovation and reduces the same enthusiasm of enterprises with smaller cooperation depth. Under the effect of the reconnection mechanism, the same types of enterprises in cluster innovation network tend to cooperate, which makes the profits of enterprises with larger cooperation depth increase continuously, while those with smaller cooperation depth decrease gradually. The result is polarization, which is not conducive to the evolution and development of cluster innovation network. However, the change in the network structure will change many enterprises profits, and thereby aggravate the polarization phenomenon and increase the income gap between enterprises with larger cooperation depth and those with smaller cooperation depth. From the figure, we can also see that the cooperative benefit of both smaller and larger cooperation depth enterprises are rising in cooperation networks with the increase in the gain coefficient r. This result shows the increase of return can be promoted by improving the investment and profit ability of both smaller-depth and larger-depth cooperation enterprises, which will in turn prompt cooperative benefits in both smaller and larger depth cooperation enterprises. In addition, with the increase in the adjustment coefficient α, the earnings of enterprises with larger cooperation depth are gradually increasing. This result is due to the increase in the difference degree of the previous income, the current investment, the cooperation breadth and the cooperation depth, which enlarges the gap between the rich and the poor among the enterprises in the cluster. This difference in the degree can effectively enhance the position and power of enterprises with larger cooperation depth in the process of investment and payoff allocation to give full play to their knowledge transfer and cooperation innovation, this difference can also facilitate the promotion of enterprises cooperative benefit when they have larger cooperation depth. Therefore, the enhancement of the interenterprise cooperation relationship is conducive to the promotion of the corporate cooperative benefit, which is crucial for the benign evolution and development of cluster innovation network.

5 Conclusions

This paper takes the cluster innovation network constructed by the weighted evolutionary BBV model as the research subject. Based on network evolutionary game theory and fairness preference theory, this study constructs a cluster innovation network evolutionary game model that includes the investment index, benefit index, cooperation breadth index and cooperation depth index. Using simulation analysis, the cooperation level and cooperation income in the evolution process of the cluster innovation network under fair preference and return intensities are analyzed, and the following conclusions are drawn.

First, increases in the weight coefficient, the gain coefficient, the difference degree of the previous income and the current investment can promote the level of enterprise cooperation. The greater the degree of the difference of the weight coefficient, the gain coefficient, the previous income, and the current investment are, the more obvious the promotion effect of the enterprise cooperation level is. Among these factors, the level of enterprise cooperation can only be promoted if the gain coefficient reaches a certain threshold. In addition, the increase in the degree of the differentiation in the terms of the breadth and depth of enterprise cooperation has a restraining effect on the enterprises cooperative level. Moreover, the greater the differentiation is, the stronger the inhibitory effect will be.

Second, the increase in the adjustment coefficient and the gain coefficient can promote increases in the cooperative income of enterprises, and the larger the adjustment coefficient and the gain coefficient are, the more obvious the promotion of the cooperative income of enterprises will be. The increase in the weight coefficient has a restraining effect on the increase in the cooperation income of enterprises with smaller cooperation breadth and deeper cooperation depth and has a promoting effect on the increase in the cooperation income of enterprises with larger cooperation breadth and deeper cooperation depth. The result is an unbalanced development mode of "Care for this and lose that" that is not conducive to the common development of cluster enterprises. In addition, the increase in the enterprise cooperation breadth and the enhancement of the interenterprise cooperation relationship can effectively promote the improvement of the enterprise cooperative benefit.

Data Availability

All data needed to replicate all of the figures, graphs, tables, statistics, and other values are provided within the https://dx.doi.org/10.17504/protocols.io.8pdhvi6.

Funding Statement

This work was financially supported by the National Natural Science Foundation of China (Grant No. 71473055).

References

1.Iammarino S, Mccann P. The structure and evolution of industrial clusters: Transactions, technology and knowledge spillovers. Research Policy, 2006,35(7):1018–1036. 10.1016/j.respol.2006.05.004 [DOI] [Google Scholar]
2.Pouder R, John C H S. Hot Spots and Blind Spots: Geographical Clusters of Firms and Innovation. Academy of Management Review, 1996,21(4):1192–1225. 10.5465/amr.1996.9704071867 [DOI] [Google Scholar]
3.Dutta PK, Sundaram RK. The Tragedy of the Commons?. Economic Theory, 1993,3(3):413–426. 10.1007/BF01209694 [DOI] [Google Scholar]
4.Charness G, Rabin M. Understanding Social Preference with Simple Tests. Quarterly Journal of Economics, 2002(91):151–172. 10.1162/003355302760193904 [DOI] [Google Scholar]
5.Szolnoki A, Perc M. Group-size effects on the evolution of cooperation in the spatial public goods game. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2011,84(4):47102 10.1103/PhysRevE.84.047102 [DOI] [PubMed] [Google Scholar]
6.Melamed D, Simpson B. Strong ties promote the evolution of cooperation in dynamic networks. Social Networks, 2016,45:32–44. 10.1016/j.socnet.2015.11.001 [DOI] [Google Scholar]
7.Lin Z, Fu B B, Li Y X. Cascading Failure of Urban Weighted Public Transit Network under Single Station Happening Emergency. Procedia Engineering, 2016,137:259–266. 10.1016/j.proeng.2016.01.267 [DOI] [Google Scholar]
8.Barrat A, Barthélemy M, Vespignani A. Weighted evolving networks: coupling topology and weight dynamics. Physical Review Letters, 2004,92(22):228701 10.1103/PhysRevLett.92.228701 [DOI] [PubMed] [Google Scholar]
9.Dugatkin L A. The Evolution of Cooperation. Bioscience, 1997,47(6):355–362. 10.2307/1313150 [DOI] [Google Scholar]
10.Bauman Y, Klein G. The Tragedy of the Commons. Surgery, 2012,151(3):490–491. 10.1016/j.surg.2011.12.037 [DOI] [PubMed] [Google Scholar]
11.Kim J, Chae H, Yook SH, Kim Y. Spatial evolutionary public goods game on complete graph and dense complex networks. Scientific Reports, 2015,5:9381 10.1038/srep09381 [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Kamei K, Putterman L. Play It Again: Partner Choice, Reputation Building and Learning From Finitely repeated Dilemma Games. Economic Journal, 2017,127(602):1069–1095. 10.1111/ecoj.12320 [DOI] [Google Scholar]
13.Stoop J, van Soest D, Vyrastekova J. Rewards and cooperation in social dilemma games. Journal of Environmental Economics & Management, 2018,88:300–310. 10.1016/j.jeem.2017.12.007 [DOI] [Google Scholar]
14.Liu J, Meng H, Wei W, Tong L, Yong Y. Synergy punishment promotes cooperation in spatial public good game. Chaos Solitons & Fractals, 2018,109:214–218. 10.1016/j.chaos.2018.01.019 [DOI] [Google Scholar]
15.Szolnoki A, Perc M, Szabó G. Topology-independent impact of noise on cooperation in spatial public goods games. Phys Rev E Stat Nonlin Soft Matter Phys, 2009,80(2):56109 10.1103/PhysRevE.80.056109 [DOI] [PubMed] [Google Scholar]
16.Wu Z X, Xu X J, Chen Y, Wang Y H. Spatial prisoner’s dilemma game with volunteering in Newman-Watts small-world networks. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2005, 71(3 Pt 2B):037103 10.1103/PhysRevE.71.037103 [DOI] [PubMed] [Google Scholar]
17.Ichinose G, Sayama H. Invasion of Cooperation in Scale-Free Networks: Accumulated versus Average Payoffs. Artificial Life, 2017,23(1):25–33. 10.1162/ARTL_a_00220 [DOI] [PubMed] [Google Scholar]
18.Nowak M A, May R M. Evolutionary games and spatial chaos. Nature, 1992,359(6398):826–829. 10.1038/359826a0 [DOI] [Google Scholar]
19.Santos F C, Santos M D, Pacheco J M. Social diversity promotes the emergence of cooperation in public goods games. Nature, 2008,454(7201):213 10.1038/nature06940 [DOI] [PubMed] [Google Scholar]
20.Cao X B, Du W B, Rong Z H. The evolutionary public goods game on scale-free networks with heterogeneous investment. Physica A Statistical Mechanics & Its Applications, 2010,389(6):1273–1280. 10.1016/j.physa.2009.11.044 [DOI] [Google Scholar]
21.Huang K, Wang T, Cheng Y, Zheng X P. Effect of Heterogeneous Investments on the Evolution of Cooperation in Spatial Public Goods Game. Plos One, 2015,10(3):e120317 10.1371/journal.pone.0120317 [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Ding H, Zhang Y, Ren Y, Shi B Y, Choo K K. Heterogeneous investment in spatial public goods game with mixed strategy. Soft Computing, 2018,22(4):1287–1294. 10.1007/s00500-016-2415-4 [DOI] [Google Scholar]
23.Yuan W J, Xia C Y. Role of Investment Heterogeneity in the Cooperation on Spatial Public Goods Game. Plos One, 2014,9(3):e91012 10.1371/journal.pone.0091012 [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Zhang Y, Wang J, Ding C, Xia C Y. Impact of individual difference and investment heterogeneity on the collective cooperation in the spatial public goods game. Knowledge-Based Systems, 2017,136:150–158. 10.1016/j.knosys.2017.09.011 [DOI] [Google Scholar]
25.Wang Q, Wang H, Zhang Z, Li Y M, Liu Y, Perc M. Heterogeneous investments promote cooperation in evolutionary public goods games. Physica A Statistical Mechanics & Its Applications, 2018,502:570–575. 10.1016/j.physa.2018.02.140 [DOI] [Google Scholar]
26.Peng D, Yang H X, Wang W X, Chen G R, Wang B H. Promotion of cooperation induced by nonuniform payoff allocation in spatial public goods game. European Physical Journal B, 2010,73(3):455–459. 10.1140/epjb/e2010-00008-7 [DOI] [Google Scholar]
27.Zhang H, Yang H, Du W, Wang B H, Cao X B. Evolutionary public goods games on scale-free networks with unequal payoff allocation mechanism. Physica A Statistical Mechanics & Its Applications, 2010,389(5):1099–1104. 10.1016/j.physa.2009.11.029 [DOI] [Google Scholar]
28.Meloni S, Xia C Y, Moreno Y. Heterogeneous resource allocation can change social hierarchy in public goods games. Royal Society Open Science, 2017,4(3):170092 10.1098/rsos.170092 [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Lei C, Wu T, Jia JY, Cong R, Wang L. Heterogeneity of allocation promotes cooperation in public goods games. Physica A Statistical Mechanics & Its Applications, 2010,389(21):4708–4714. 10.1016/j.physa.2010.06.002 [DOI] [Google Scholar]
30.Zhang H, Shi D, Liu R, Wang B H. Dynamic allocation of investments promotes cooperation in spatial public goods game. Physica A Statistical Mechanics & Its Applications, 2012,391(8):2617–2622. 10.1016/j.physa.2011.12.005 [DOI] [Google Scholar]
31.Fan R, Zhang Y, Luo M, Zhang H J. Promotion of cooperation induced by heterogeneity of both investment and payoff allocation in spatial public goods game. Physica A Statistical Mechanics & Its Applications, 2017,465:454–463. 10.1016/j.physa.2016.08.039 [DOI] [Google Scholar]
32.Botelho A, Harrison G W, Pinto L M C, Rutström E E. Testing static game theory with dynamic experiments: A case study of public goods. Games & Economic Behavior, 2009,67(1):253–265. 10.1016/j.geb.2008.11.013 [DOI] [Google Scholar]
33.Vukov J, Szabó György. Evolutionary prisoner’s dilemma game on a square lattice. Physical Review E, 1998,58(1):69–73. 10.1103/PhysRevE.71.036133 [DOI] [Google Scholar]
34.Traulsen A, Nowak M A. Evolution of cooperation by multilevel selection. Proceedings of the National Academy of Sciences, 2006,103(29):10952–10955. 10.1073/pnas.0602530103 [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Szabó G, Hauert C. Phase transitions and volunteering in spatial public goods games. Physical Review Letters, 2002,89(11):118101 10.1103/PhysRevLett.89.118101 [DOI] [PubMed] [Google Scholar]
36.Li J, Wu T, Zeng G, Wang L. Selective investment promotes cooperation in public goods game. Physica A Statistical Mechanics & Its Applications, 2012,391(15):3924–3929. 10.1016/j.physa.2012.03.016 [DOI] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0226777.r001

Decision Letter 0

Luo-Luo Jiang

12 Sep 2019

PONE-D-19-22374

Research on an Evolutionary Game Model and Simulation of a Cluster Innovation Network Based on Fairness Preference

PLOS ONE

Dear Dr. Cao,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

We would appreciate receiving your revised manuscript by Oct 27 2019 11:59PM. When you are ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter.

To enhance the reproducibility of your results, we recommend that if applicable you deposit your laboratory protocols in protocols.io, where a protocol can be assigned its own identifier (DOI) such that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). This letter should be uploaded as separate file and labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. This file should be uploaded as separate file and labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. This file should be uploaded as separate file and labeled 'Manuscript'.

Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out.

We look forward to receiving your revised manuscript.

Kind regards,

Luo-Luo Jiang, Ph.D.

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

http://www.journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and http://www.journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

2. Please include captions for your Supporting Information files at the end of your manuscript, and update any in-text citations to match accordingly. Please see our Supporting Information guidelines for more information: http://journals.plos.org/plosone/s/supporting-information.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Partly

Reviewer #2: Partly

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: No

Reviewer #2: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: In this manuscript, the authors concern a cluster innovation network based on based on game theory and the fair preference theory, and investigate cooperation level and cooperation income in evolution process of cluster innovation network subjected to fair preference and return intensity. Although the numerical results are interesting, I do not recommend the manuscript for publication in its present form. I can reconsider my decision if a number of issues listed below are properly addressed.

1.What is the BBV model? This manuscript investigates cluster innovation network constructed by BBV model, but there is no introduction about the model in the INTRODUCTION.

2.The first sentence in 3.2 Construction of Game Model shows that whatever the strategy Sx chooses, the investment of enterprise x is always zero. Please check it.

3.Figure.2(b) shows a nonmonotonic behavior of fc vs. α at r=2, while there is a monotonic behavior in Figure.3(b) for r=2. The results are inconsistent. Please check the numerical results.

4.The manuscript is written very poorly, strongly lacking clarity in presentation. For example:

(1)In Page2, “....and have find that in...” → “....and have found that in...”.

(2)In Page9, “...the greater the inhibitory effect on enterprise cooperation level are...” → “...the greater the inhibitory effect on enterprise cooperation level is...”.

(3)In Page10, “...improvement of preference in the terms of the breadth...” → “...improvement of preference in terms of the breadth...”.

(4)There have some inaccurate subscripts in the Eqs.(8) and (9).

(5)Some sentences are repeated, i.e., “...Sx is the enterprise x game strategy ( Sx=1 means cooperation, Sx means non-cooperation). ..”, which has been mentioned in the first paragraph in Construction of Game Model.

Please check the full manuscript. A through improvement of English is necessary.

Reviewer #2: Review report for “Research on an Evolutionary Game Model and Simulation of a Cluster Innovation Network Based on Fairness Preference” by Li et al.

This paper studies an evolutionary game model of a cluster innovation network based on a spatial public goods game and the theory of fairness preference, where the network is constructed by the weighted evolutionary BBV model. Using network-based simulations, the authors found that an increase in the weight coefficient, gain coefficient and degree of differentiation between previous income and current investment can effectively promote improvements in the level of enterprise cooperation. Moreover, the increase in regulation and gain coefficients can promote enterprise cooperation while the increase in the differentiation in the breadth and depth of enterprise cooperation will hinder enterprise cooperation.

The cooperative environment of cluster innovation networks is an important issue that deserves further investigation. I found that this paper considers an interesting problem, the structure is well organized, and the paper is well written. However, there are some issues that hinder the acceptance of this paper in its current form. In the following, I would like to give some comments and suggestions, which may help the authors improve the quality of their paper.

1, In the abstract, the authors directly go the introduction of methods and results. However, I think some introduction of general background regarding this topic should be added. Moreover, the authors are suggested to introduce their motivations after the background introduction. Furthermore, at the end of the abstract, it would be better to highlight the implication and application of their results.

2, In the introduction section, the authors present that “cluster innovation networks have the characteristics of a weighted scale-free network[8], so a simulation network based on the weighted evolution BBV model can simulate the real cluster innovation network well[9]”. I think it is not clear enough to the readers that whether cluster innovation networks have the characteristics of a weighted scale-free network. It would be better if the authors can explain more regarding this point.

3, On page 2, the authors present that “Some scholars also find that fixed static network structures such as rule networks[16], world networks[17] and scale-free networks[18] can also promote cooperation under certain conditions[19]”. I think “world networks[17]” should be “small-world networks[17]”. Moreover, in the follow sentence, “Santos[20] also found that the fairness preference of innovative subject cooperative behavior can greatly affect the level of cooperation in BA network”. It should be written as “Santos et al. [20] also found that xxx”.

4, In Figure, the sentences “Previous Income、Cooperation Breadth” and “Current Investment、Cooperation Depth” should be revised. In English, there is no “、” but “,”. The authors should replace “、” by “,” in these two sentences.

5, In section 3.2 Construction of Game Model, the authors present that “it participates in $k_x + 1$ neighborhoods centered on itself and neighbors, and its total investment is 0”. I think the total investment is 1 instead of 0. The authors should check this.

6, Before Equation (6), the sentence “as the center and directly connected enterprises) according to formula (6)”. I think Equation is more usually used than formula, and formula (6) should be replaced by “Equation (6)”. The same applies to the following sections, such as “Formula (7) shows that” and “Formula (8) shows that”. The authors are suggested to go through the paper and fix this problem.

7, Below Equation (7), the sentence “Among these variables, $\\bar{D_{x,y}}(t_n)$is the normalized value of $D_{x,y}(t_n) $, $t_n$ is the number of rounds of the public goods game (only if all nodes in the network have a round of game to end the round of game)”. The readers may wonder which kind of normalization that the authors used. I thinks it would be better to add more details.

8, For the following sentences, “the revenue of enterprise x(i)” and “denotes the degree value of enterprise y(i)”, it would be better to separate them into two sentences. It would be hard to distinguish x(i) from x and i.

9, In section 4.1 Simulation steps, the authors set an initial cooperation level as of 50%, i.e., the network cooperation density being 0.5. The authors may wonder how this parameter affects the results, and what happens if the initial cooperation level is set as 40% or 60%. Moreover, the cluster innovation network is with N=100 nodes, where I wonder how the network size affects the results. Maybe the authors want to add one or more figures to show the network size effects.

10, In Figure 2 and Figure 3, I found a lot of fluctuations in the results. The authors present that “each data point is the average of simulation results after 50 independent experiments”. I think it would be better to increase the times of independent experiments. Maybe 500 is a better choice to avoid fluctuations and make the results more reliable. Moreover, the resolution of these two figures should be remarkably enhanced, and more detailed captions should be added to explain these figures.

11, For the sentence “this paper uses Ruguo Fan [34] and Li [39] as references for the study of the weight coefficient, and implements three mechanisms to correspond to the three weight coefficients”. I think it would be better to revise “Ruguo Fan [34] and Li [39]” because it is not a typical reference style.

12, In the reference section, many papers published in Chinese are referred, such as Refs [1],[7],[8],[17], [23],[33],and [35], however, these papers are usually invisible to the international community. I wonder if these works are follow ups of some very related international studies, and some of them can be replaced by references published in English journals. I will let the authors to decide.

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files to be viewed.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email us at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2020 Jan 13;15(1):e0226777. doi: 10.1371/journal.pone.0226777.r002

Author response to Decision Letter 0

26 Oct 2019

1.What is the BBV model? This manuscript investigates cluster innovation network constructed by BBV model, but there is no introduction about the model in the INTRODUCTION.

Answer: The evolution model of weighted network was first established by Barrat, Barthelemy and Vespignani in 2004. It is usually called BBV model. It is a simple weight driven dynamic model, and generates statistical properties very similar to the real weight network, such as the law of network weight evolution with time, and the scale-free characteristics of strength distribution. Since the weighted scale-free network constructed by the weighted evolutionary BBV model was proposed, just like the BA scale-free network, it is gradually known. So in the introduction, the author did not introduce the BBV model in detail. In order to explain more clearly why BBV model is used to build cluster innovation network, the author makes the following modifications to this part of the text:

In addition, in the actual network evolution game process, the cooperation behavior of innovators is not only influenced by the network structure but also closely related to the intensity of the cooperative relationship between innovators[6], that is, the connection in the real network has the weight attribute. According to the existing research, a real network with connected weights has both the power-law distribution characteristics of the degree distribution and the power-law distribution characteristics of the strength distribution[7].

2.The first sentence in 3.2 Construction of Game Model shows that whatever the strategy Sx chooses, the investment of enterprise x is always zero. Please check it.

Answer: according to the reviewer’s opinion, the author found the writing error here, and has modified the paragraph as follows:

In the first round (tn=1 ) of the public goods game, the degree value of enterprise s is kx , so if the enterprise x chooses uncooperative strategy (Sx=0 ), the investment of enterprise x in its neighborhood is 0; if enterprise x chooses a cooperative strategy (Sx=0), it participates in Kx+1 neighborhoods centered on itself and neighbors, and its total investment is evenly distributed among Kx+1 neighborhoods.

3.Figure.2(b) shows a nonmonotonic behavior of fc vs. a at r=2, while there is a monotonic behavior in Figure.3(b) for r=2. The results are inconsistent. Please check the numerical results.

Answer: according to the reviewer’s opinion, author remade the simulation, redraws Figure 2 and figure 3, and corrects Figure 2 (b). See the manuscripts Fig2 and Fig3 for the new simulation results

4.The manuscript is written very poorly, strongly lacking clarity in presentation. For example:

(1)In Page2, “....and have find that in...” → “....and have found that in...”.

(2)In Page9, “...the greater the inhibitory effect on enterprise cooperation level are...” → “...the greater the inhibitory effect on enterprise cooperation level is...”.

(3)In Page10, “...improvement of preference in the terms of the breadth...” → “...improvement of preference in terms of the breadth...”.

(4)There have some inaccurate subscripts in the Eqs.(8) and (9).

(5) Some sentences are repeated, i.e., “... is the enterprise x game strategy ( Sx=1 means cooperation, Sx=0 means non-cooperation)...”, which has been mentioned in the first paragraph in Construction of Game Model. Please check the full manuscript. A through improvement of English is necessary.

Answer: according to the reviewer’s opinion, the author revised (1)-(3) in the manuscript. For example: the previous income of the players[30] and have found that in a static BA network….

the more significant the interactions between network structure and enterprise cooperative behaviors are, and the greater the inhibitory effect on enterprise cooperation level is.

This result shows that the improvement of preference in terms of the breadth and depth of cooperation…

Comments on Revision (4), The author referred to several references and rechecked formulas (8) and (9). No editorial errors were found in the subscripts of formulas (8) and (9). Each subscript is described here. In formula (8), The author referred to several references and rechecked formulas (8) and (9). No editorial errors were found in the subscripts of formulas (8) and (9). Each subscript is described here. In formula (8), the subscript Mxy represents the income of x in neighborhood y , the subscript Ixy represents the input of x in neighborhood y, and the subscript y=0 in formula (9) represents the neighborhood centered on x (neighborhood y refers to the neighborhood composed of neighbor enterprise y and its directly connected enterprises). If you have any questions from the reviewer, please point out and I will revise it.

Comments on Revision (5), after careful comparison, the author has deleted similar sentences in the text and asked AJE to polish the full text, so as to improve the English level of the manuscript. Red font in English Revision

Reviewer #2: Review report for “Research on an Evolutionary Game Model and Simulation of a Cluster Innovation Network Based on Fairness Preference” by Li et al.

Answer: according to the reviewer’s opinion, the author added the background and purpose of the writing topic in the abstract, and added the significance of the paper research in the end. The added content is as follows:

At the beginning of the abstract: The cluster innovation network is an important part of regional economic development. In addition, the fairness preference of internal innovators in the processes of investment and benefit distribution are particularly important for curbing "free riding" and other speculative behaviors and for creating a good cooperation environment. Therefore, taking……

At the end of the abstract: Finally, we hope to improve the overall cooperation level and cooperation income of the network by deeply understanding the fair preferences of innovators in the processes of investment and benefit distribution, which is helpful for promoting the evolution and development of cluster innovation networks.

Answer: according to the reviewer’s opinion, in order to explain more clearly why BBV model is used to build cluster innovation network, the author makes the following modifications to this part of the text:

Answer: according to the reviewer’s opinion, The author found that he had made some mistakes in the translation process, and now he has made some modifications to these two problems. Amend to read: Some scholars also find that fixed static network structures such as rule networks[16], small-world networks[17] and scale-free networks[18] can also promote cooperation under certain conditions[19]. Santos et al[20] also found that the fairness preference of innovative subject cooperative behavior can greatly affect the level of cooperation in BA network.

Answer: according to the reviewer’s opinion, the author changed "、" in Fig1 to "," and modified some words in Figure 1. Figure 1 in the manuscript shows the modification result of the figure.

5, In section 3.2 Construction of Game Model, the authors present that “it participates in Kx+1 neighborhoods centered on itself and neighbors, and its total investment is 0”. I think the total investment is 1 instead of 0. The authors should check this.

Answer: after checking, the author found that there are some problems in this sentence, and has modified the paragraph as follows:

In the first round ( tx=1) of the public goods game, the degree value of enterprise x is Kx , so if the enterprise x chooses uncooperative strategy ( Sx=0), the investment of enterprise x in its neighborhood is 0; if enterprise chooses a cooperative strategy (Sx=1 ), it participates in Kx+1 neighborhoods centered on itself and neighbors, and its total investment is evenly distributed among Kx+1 neighborhoods.

Answer: according to the reviewer’s opinion, the author has modified the “formula” in the full text to Eqs. (Equation) Since formula 6-11 has a large span in the text, it is not listed here. The modified part has been marked with red font.

7, Below Equation (7), the sentence “Among these variables, Dxy(tn) is the normalized value of Dxy(tn) , tn is the number of rounds of the public goods game (only if all nodes in the network have a round of game to end the round of game)”. The readers may wonder which kind of normalization that the authors used. I thinks it would be better to add more details.

Answer: according to the reviewer’s opinion, The author considers that the total investment of each enterprise is 1. At the same time, in order to ensure the linear change of investment, the author uses min max normalization method to standardize. The content of this paper is modified as follows:

Among these variables, considering that the total investment of each enterprise is 1, Dxy(tn) is normalized according to the min-max normalization method. Dxy(tn) is the normalized value of Dxy(tn) , tn is the number of rounds of the public goods game (only if all nodes in the network have a round of game to end the round of game).

Answer: according to the reviewer’s opinion, according to the expert opinion, the author divides and adjusts the content of the sentence as follows:

…. and Mxy(tn-1) is the revenue of enterprise i from neighborhood y after the first round tn-1 of the public goods game. and Mxy(tn-1) is the revenue of enterprise x from neighborhood y after the first round t-1 of the public goods game.

Answer: according to the reviewer’s opinion, considering the below two reasons, the author decided not to increase the network cooperation density and network scale in this paper.

（1）before the experts put forward this opinion, the author has studied the influence of initial cooperation density and network scale on cooperation behavior, but found that the research conclusions are not innovative in this paper, so they are deleted and not reflected in the text. A. the emergence of cooperative behavior in the cluster innovation network is closely related to the game environment around the innovation subject. When adjusting the network cooperation density (0.4 or 0.6), it does not have a substantial impact on the change of cooperative behavior, only prolongs the network evolution time. B. before that, I have studied the network size of 50, 100, 200 and 500 under various influencing factors. It is found that the difference of the influence of network scale on cooperation behavior is only reflected in the number of iterations (evolution time). C. due to the figures 2.3 and 2.4 doesn’t reflect the trend of cooperation level over time. Therefore, the influence of network cooperation density and network scale on cooperation behavior can’t be reflected in this paper, so these two factors are put here, which makes the innovation slightly inadequate. Considering the actual simulation time and the dynamic evolution process of the network, the author finally selected the network scale of 100 for simulation research. However, according to the review experts, the research on the relationship between network scale and cooperation behavior over time has been reflected in another article "the game simulation research on knowledge transfer evolution of cluster innovation network under different network scales".

(2) this paper focuses on the impact of fair preferences of investment and payoff allocation on the cooperative behavior in the evolution process of cluster innovation network. In order to avoid too scattered research, the network cooperation density and network scale are not included in this study.

Answer: according to the reviewer’s opinion, and due to the limited simulation time, the author increased the number of independent experiments to 200 times, and took the average value of simulation results after 200 times. Therefore, the author re simulated, The new simulation results are shown in Fig2 and Fig3 in the manuscript.

Answer: according to the reviewer’s opinion, the author has deleted this part as required.

Answer: The author deleted the literature published in Chinese [1], [23], [33]. Chinese literature [5], [7], [8], [14], [17] and [35] are replaced by similar references published in some English journals, in order to meet the requirements of English journals.

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(218KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0226777.r003

Decision Letter 1

Luo-Luo Jiang

11 Nov 2019

PONE-D-19-22374R1

Research on an Evolutionary Game Model and Simulation of a Cluster Innovation Network Based on Fairness Preference

PLOS ONE

Dear Dr. Cao

We would appreciate receiving your revised manuscript by Dec 26 2019 11:59PM. When you are ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). This letter should be uploaded as separate file and labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. This file should be uploaded as separate file and labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. This file should be uploaded as separate file and labeled 'Manuscript'.

We look forward to receiving your revised manuscript.

Kind regards,

Luo-Luo Jiang, Ph.D.

Academic Editor

PLOS ONE

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

Reviewer #2: (No Response)

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #1: Yes

Reviewer #2: Yes

**********

6. Review Comments to the Author

Reviewer #1: The revised manuscript reads much better, is significantly improved and looks suitable for publication in Plos One.

Reviewer #2: Review report for “Research on an Evolutionary Game Model and Simulation of a Cluster Innovation Network Based on Fairness Preference”.

I would thank the authors for considering my previous comments and suggestions in revising their manuscript. I think the new version has been well improved. Before the consideration for publication, however, the authors are suggested to address the following two issues.

1. For all figures, the labels of axis (as well as titles) are currently so small that it is very hard for the readers to pick up the information. The authors are suggested to remarkably increase the font size in all figures.

2. Regarding my previous comment (9) “In section 4.1 Simulation steps, the authors set an initial cooperation level as of 50%, i.e., the network cooperation density being 0.5. The authors may wonder how this parameter affects the results, and what happens if the initial cooperation level is set as 40% or 60%. Moreover, the cluster innovation network is with N=100 nodes, where I wonder how the network size affects the results. Maybe the authors want to add one or more figures to show the network size effects”, I don’t think the authors tried their best to answer my question.

Firstly, in their reply, they presented that “When adjusting the network cooperation density (0.4 or 0.6), it does not have a substantial impact on the change of cooperative behavior, only prolongs the network evolution time”. However, I failed to find any figure in their reply that can support their claim.

Secondly, the authors presented that “due to the figures 2.3 and 2.4 doesn’t reflect the trend of cooperation level over time. Therefore, the influence of network cooperation density and network scale on cooperation behavior can’t be reflected in this paper”. However, I could not find “figures 2.3 and 2.4”, and I am curious about the effects of the network scale and cooperation density other than the trend of cooperation level over time.

Thirdly, the authors presented that “the relationship between network scale and cooperation behavior over time has been reflected in another article "the game simulation research on knowledge transfer evolution of cluster innovation network under different network scales".”. However, I failed to find this referred article in web of science or using Google Scholar. I wonder if there is really a paper, and if this paper should be cited in the main text.

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

PLoS One. 2020 Jan 13;15(1):e0226777. doi: 10.1371/journal.pone.0226777.r004

Author response to Decision Letter 1

22 Nov 2019

Since the image cannot be pasted in the reply, I hope the editor can help me to provide the reviewer 2 with the word “response to reviewer”，and the figure in it can help to explain my answer.

Reviewer #2: Review report for “Research on an Evolutionary Game Model and Simulation of a Cluster Innovation Network Based on Fairness Preference”.

Answer: according to the reviewer’s opinion, the author enlarges the label of axis (as well as the title) font of all Figure in the manuscript to ensure that readers can easily obtain information. Due to there are many Figure in manuscript, so I do not be displayed here. See the revised manuscript for details.

Answer: according to the reviewer’s opinion, the author put research on the influence of different network cooperation density on the evolution of cluster innovation network cooperation here to support the author's explanation. To ensure the scientific nature of the research, the author sets the weight coefficient w=0.5 (hybrid preference mechanism), the adjustment coefficient ( alpha=1，alpha=2 and alpha=3 ), three kinds of gain coefficient ( r=1,r=2 and r=3 ), and three kinds of network cooperation density (p=0.4, p=0.5 and p=0.6 ) to carry out simulation analysis, to illustrate the influence of the network cooperation density on the evolution of cluster innovation network under different adjustment coefficients and gain capabilities. The simulation times are set to 100. After the system fully evolves to the stable stage, the average value of the last 30 cooperation densities is taken as P .

Figure 1 show the effect of the network cooperation density on the enterprise cooperation level in cluster innovation network under different adjustment coefficients. It can be seen from Figure 1 that under the same adjustment coefficient, with the increase of network cooperation density, the time from network evolution to stability is gradually longer, and the network evolution speed is gradually reduced. In addition, in the three adjustment coefficients, the simulation results are similar. Figure 2 show the effects of the network cooperation density on the enterprise cooperation level in cluster innovation network under different gain coefficients. the simulation results in Figure 2 are similar to those in Figure 1. Therefore, we have the same result.

Because of the similar simulation results under different parameters, the author thinks that it is not enough to study the influence of network cooperation density on the evolution of cluster innovation network cooperation. Therefore, the author thinks over and over again, and does not put the research results in the manuscript, and hopes that the reviewers will understand.

(a) alpha=1 (b) alpha=2 (c) alpha=3

Fig. 1 The effect of the network cooperation density on the enterprise cooperation level in cluster innovation network under different adjustment coefficients

(a) r=2 (b) r=3 (c) r=4

Fig. 2 The effects of the network cooperation density on the enterprise cooperation level in cluster innovation network under different gain coefficients

Answer: Due to my writing mistakes, let you have misunderstanding figure 2.3 or 2.4, I apologize to you. What I want to explain is that in Figure 2, Figure 3, … and in Figure 7, the change trend of cooperation level over time is not reflected, and the influence of network cooperation density and network scale on cooperation behavior is not reflected in the manuscript. Therefore, it will be awkward to put these two factors here alone, and it will appear that innovation is a little inadequate.

Answer: first of all, here, the author apologizes to the reviewer. In the last reply to your opinion, I did not inform the reviewer of the relevant information of that manuscript. Here, Here, the author explains the manuscript to you.

The manuscript “Evolutionary Game Simulation of Knowledge Transfer in Industry-University-Research Cooperative Innovation Network under Different Network Scales” is currently under reviewed in 《scientific reports》. Due to it has not been uploaded, so it cannot be found in web of science or using Google Scholar. The manuscript was submitted at the end of August, and the overhaul comments were received on October 4st. On November 21st, the author submit the revised manuscript to 《scientific reports》. Among them, according to the reviewer’s opinion, in order to highlight the difference between enterprises and research institutions in knowledge transfer, the manuscript title has been slightly adjusted. The title “Evolutionary Game Simulation of Knowledge Transfer in Cluster Innovation Network under Different Network Scales” is modified to “Evolutionary Game Simulation of Knowledge Transfer in Industry-University-Research Cooperative Innovation Network under Different Network Scales”. Figure 3 is the proof of manuscript review in 《scientific reports》 after overhaul. Since the manuscript was revised before and after, the research on the relationship between the network scale and cooperative behavior has not changed much. Therefore, the conclusions of this study can be used for reference by reviewers. Considering that the manuscript is still in the process of review, the author will only present the relevant research contents about network scale and cooperation behavior in the manuscript “Evolutionary Game Simulation of Knowledge Transfer in Industry-University-Research Cooperative Innovation Network under Different Network Scales”, please understand. In the following text, red font is the conclusion of the study. There is a discussion about the influence of network structure on the evolution speed of knowledge transfer in cooperative behavior in the text.

Fig.3 Proof of manuscript review in scientific reports

Evolutionary Game Simulation of Knowledge Transfer in Industry-University-Research Cooperative Innovation Network under Different Network Scales

Abstract: This paper takes the industry-university-research cooperation innovation network constructed by the weighted evolutionary BBV model as the research object, which is based on bipartite graph and evolutionary game theory, and constructing the game model of knowledge transfer in the industry-university-research cooperation innovation network, by using the simulation analysis method and analyzing the evolution law of knowledge transfer in the industry-university-research cooperation innovation network under different network scales, three scenarios, the knowledge transfer coefficient and the knowledge reorganization coefficient. The results show that the increase of network size reduces the speed of knowledge transfer in the network. and the greater the average cooperation intensity of the nodes, the higher the evolution depth of knowledge transfer. Compared with university-research institutes, the evolution depth of knowledge transfer in enterprises is higher, and with the increase of network scale, the gap between the evolution depth of knowledge transfer between them is gradually increasing. Only when reward, punishment and synergistic innovation benefits are higher than the cost of knowledge transfer that can promote the benign evolution of industry-university-research cooperation innovation networks. Only when the knowledge transfer coefficient and the knowledge reorganization coefficient exceed a certain threshold will knowledge transfer behavior emerge in the network. With the increase of the knowledge transfer coefficient and the knowledge reorganization coefficient, the knowledge transfer evolutionary depth of the average cooperation intensity of all kinds of nodes is gradually deepening.

Key words: BBV model; Industry-University-Research Cooperative Innovation network; knowledge transfer; game model; simulation

4.3 Simulation Results Analysis

(1) The influence of the three scenarios on the knowledge transfer evolution of the industry-university-research cooperation innovation network under different network scales.

It can be found from Fig. 4 that the evolution simulation of knowledge transfer in the industry-university-research cooperation innovation network has similar evolution results under different network scales. In the same situation, along with the increase of network scale, the time of knowledge transfer evolving to a stable stage in the industry-university-research cooperation innovation network is gradually longer, and the evolution speed of knowledge transfer is gradually slower. This may be because the node degree, average weighted degree and shortest path in small-scale networks are relatively small, and the efficiency of information transmission is high. In large-scale networks, the more cooperative relationships there are among the nodes, the more uneven distribution and heterogeneity of the nodes, the more complex the process of revenue comparison and strategy learning among the nodes in the game process, the lower the efficiency of information transmission and the slower the speed of knowledge transfer 44.

(a) n=100 (b) n=200 (c) n=500

Figure 4 Evolution simulation results of knowledge transfer in the industry-university-research cooperation innovation network under different network scales and three scenarios

(2) The influence of the knowledge transfer coefficient on the knowledge transfer evolution of the industry-university-research cooperation innovation network under different network scales.

On the basis of the situation in which the evolutionary depth of knowledge transfer in the industry-university-research cooperation innovation network is 0, the knowledge transfer coefficients of advantage university-research institutes, advantage enterprise, general university-research institutes, and general enterprise obey the uniform distribution of (0.05,0.15) ,(0.10,0.20) ,(0.15,0.25) and (0.20,0.30) in turn. The values of i are 0.0, 0.2, 0.4 and 0.6, respectively, to adjust the knowledge transfer coefficient alpha of all kinds of innovators, expressed by P1, P2, P3 and P4, respectively. The simulation results of the knowledge transfer evolution in the industry-university-research cooperation innovation network under different network scales and knowledge transfer coefficients are obtained, as shown in Fig. 5. Among them, Fig. 5 (a, b and c) respectively shows the simulation results of knowledge transfer evolution under three network scales, P1, P2, P3 and P4 represent the simulation evolution curves under four knowledge transfer coefficients.

From Fig. 5, it can be found that when the final results of network evolution converge to 0 under the same network scale, with the increase of knowledge transfer coefficient, the time for the evolution of the industry-university-research cooperation innovation network to be stable gradually becomes longer. This is because the increase of the knowledge transfer coefficient enhances the knowledge transfer ability, the knowledge transfer willingness and the knowledge absorption ability of the innovators, and the innovators’ knowledge transfer behavior preference gradually strengthens, so that the innovators’ cooperative behavior preference changes from a "non transfer" dominant direction to a "transfer" dominant direction. Under the same knowledge transfer coefficient, along with the increase of the network scale, the time for the evolution of the industry-university-research cooperation innovation network to stability gradually becomes longer. This is due to the increase of the network scale, the average path between innovators increases gradually, and the efficiency of information transmission decreases gradually. In the process of network games, innovators are faced with more complex revenue comparison and strategy selection, which leads to the slow evolution of knowledge transfer and the time from the evolution of the industry-university-research cooperation innovation network to stabilization gradually becomes longer. In addition, it can be found that only when i is 0.6, that is, when the knowledge transfer coefficient is the maximum, the evolution result of knowledge transfer in the industry-university-research cooperation innovation network converges to 1. It shows that only when the knowledge transfer coefficient is higher than a certain threshold will the knowledge transfer behavior of innovators emerge in the network48.

(a) n=100 (b) n=200 (c) n=500

Figure 5 Evolution simulation results of knowledge transfer in the industry-university-research cooperation innovation network under different network scales and knowledge transfer coefficients

(3) The influence of the knowledge reorganization coefficient on the evolution of knowledge transfer in the industry-university-research cooperation innovation network under different network scales.

On the basis of the situation in which the evolutionary depth of knowledge transfer in the industry-university-research cooperation innovation network is 0, the knowledge reorganization coefficients of advantage university-research institutes, advantage enterprise, general university-research institutes, general enterprise obey the uniform distribution of (0.02,0.03),(0.015,0.025) , (0.01,0.02) and (0.005,0.015) in turn. The values of i are 0.01, 0.02, 0.03, and 0.04, respectively, to adjust the knowledge reorganization coefficients beta of all kinds of innovators, expressed by P1, P2, P3 and P4, respectively. The simulation results of the knowledge transfer evolution in the industry-university-research cooperation innovation network under different network scales and knowledge reorganization coefficients are obtained, as shown in Fig. 6. Among them, Fig. 6 (a, b and c) respectively shows the evolution results of knowledge transfer under three network scales. P1, P2, P3 and P4 represent the simulation evolution curves under four knowledge reorganization coefficients.

From Fig. 6, it can be found that when the final results of network evolution converge to 0 under the same network scale, with the increase of the knowledge reorganization coefficient, the time of knowledge transfer evolving to stability is gradually longer. However, when the final results of network evolution converge to 1, with the increase of the knowledge reorganization coefficient, the time of knowledge transfer evolving to stability is gradually shortened. This may be due to the increase of the knowledge reorganization coefficient, which makes the ability of innovators to understand, comprehend and apply knowledge gradually enhanced. The new knowledge acquired through digestion, absorption and reinnovation increases gradually, so that the knowledge transfer behavior preference of the innovator is gradually enhanced and then promotes the steady development of knowledge transfer in the industry-university-research cooperation innovation network. With the same knowledge reorganization coefficient, along with the increase of network scale, the time of knowledge transfer evolving to stability in the industry-university-research cooperation innovation network gradually becomes longer. This is because with the increase of the network scale, the level of knowledge application ability of innovators is not uniform, and the average path length between innovators is gradually increasing, which affects the transmission efficient knowledge information in the network, thus reducing the evolution speed of knowledge transfer and delaying the evolution time of knowledge transfer. In addition, it can be found from the graph that the final result of knowledge transfer evolution of the industry-university-research cooperation innovation network converges to 1 only when j is 0.03. This also shows that only when the knowledge reorganization coefficient is higher than a certain threshold, the innovator has a certain ability of understanding, comprehending and applying the knowledge, so that the knowledge transfer behavior will emerge in the network.

(a) n=100 (b) n=200 (c) n=500

Figure 6 Evolution simulation results of knowledge transfer in the industry-university-research cooperation innovation network under different network scales and knowledge reorganization coefficients

Attachment

Submitted filename: Response to Reviewers.doc

Click here for additional data file.^{(664KB, doc)}

PLoS One. doi: 10.1371/journal.pone.0226777.r005

Decision Letter 2

Luo-Luo Jiang

6 Dec 2019

Research on an Evolutionary Game Model and Simulation of a Cluster Innovation Network Based on Fairness Preference

PONE-D-19-22374R2

Dear Dr. Cao,

We are pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it complies with all outstanding technical requirements.

Within one week, you will receive an e-mail containing information on the amendments required prior to publication. When all required modifications have been addressed, you will receive a formal acceptance letter and your manuscript will proceed to our production department and be scheduled for publication.

Shortly after the formal acceptance letter is sent, an invoice for payment will follow. To ensure an efficient production and billing process, please log into Editorial Manager at https://www.editorialmanager.com/pone/, click the "Update My Information" link at the top of the page, and update your user information. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to enable them to help maximize its impact. If they will be preparing press materials for this manuscript, you must inform our press team as soon as possible and no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

With kind regards,

Luo-Luo Jiang, Ph.D.

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

PLoS One. doi: 10.1371/journal.pone.0226777.r006

Acceptance letter

Luo-Luo Jiang

27 Dec 2019

PONE-D-19-22374R2

Research on an Evolutionary Game Model and Simulation of a Cluster Innovation Network Based on Fairness Preference

Dear Dr. Cao:

I am pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please notify them about your upcoming paper at this point, to enable them to help maximize its impact. If they will be preparing press materials for this manuscript, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

For any other questions or concerns, please email plosone@plos.org.

Thank you for submitting your work to PLOS ONE.

With kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Dr. Luo-Luo Jiang

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(218KB, docx)}

Attachment

Submitted filename: Response to Reviewers.doc

Click here for additional data file.^{(664KB, doc)}

Data Availability Statement

All data needed to replicate all of the figures, graphs, tables, statistics, and other values are provided within the https://dx.doi.org/10.17504/protocols.io.8pdhvi6.

[pone.0226777.ref001] 1.Iammarino S, Mccann P. The structure and evolution of industrial clusters: Transactions, technology and knowledge spillovers. Research Policy, 2006,35(7):1018–1036. 10.1016/j.respol.2006.05.004 [DOI] [Google Scholar]

[pone.0226777.ref002] 2.Pouder R, John C H S. Hot Spots and Blind Spots: Geographical Clusters of Firms and Innovation. Academy of Management Review, 1996,21(4):1192–1225. 10.5465/amr.1996.9704071867 [DOI] [Google Scholar]

[pone.0226777.ref003] 3.Dutta PK, Sundaram RK. The Tragedy of the Commons?. Economic Theory, 1993,3(3):413–426. 10.1007/BF01209694 [DOI] [Google Scholar]

[pone.0226777.ref004] 4.Charness G, Rabin M. Understanding Social Preference with Simple Tests. Quarterly Journal of Economics, 2002(91):151–172. 10.1162/003355302760193904 [DOI] [Google Scholar]

[pone.0226777.ref005] 5.Szolnoki A, Perc M. Group-size effects on the evolution of cooperation in the spatial public goods game. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2011,84(4):47102 10.1103/PhysRevE.84.047102 [DOI] [PubMed] [Google Scholar]

[pone.0226777.ref006] 6.Melamed D, Simpson B. Strong ties promote the evolution of cooperation in dynamic networks. Social Networks, 2016,45:32–44. 10.1016/j.socnet.2015.11.001 [DOI] [Google Scholar]

[pone.0226777.ref007] 7.Lin Z, Fu B B, Li Y X. Cascading Failure of Urban Weighted Public Transit Network under Single Station Happening Emergency. Procedia Engineering, 2016,137:259–266. 10.1016/j.proeng.2016.01.267 [DOI] [Google Scholar]

[pone.0226777.ref008] 8.Barrat A, Barthélemy M, Vespignani A. Weighted evolving networks: coupling topology and weight dynamics. Physical Review Letters, 2004,92(22):228701 10.1103/PhysRevLett.92.228701 [DOI] [PubMed] [Google Scholar]

[pone.0226777.ref009] 9.Dugatkin L A. The Evolution of Cooperation. Bioscience, 1997,47(6):355–362. 10.2307/1313150 [DOI] [Google Scholar]

[pone.0226777.ref010] 10.Bauman Y, Klein G. The Tragedy of the Commons. Surgery, 2012,151(3):490–491. 10.1016/j.surg.2011.12.037 [DOI] [PubMed] [Google Scholar]

[pone.0226777.ref011] 11.Kim J, Chae H, Yook SH, Kim Y. Spatial evolutionary public goods game on complete graph and dense complex networks. Scientific Reports, 2015,5:9381 10.1038/srep09381 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0226777.ref012] 12.Kamei K, Putterman L. Play It Again: Partner Choice, Reputation Building and Learning From Finitely repeated Dilemma Games. Economic Journal, 2017,127(602):1069–1095. 10.1111/ecoj.12320 [DOI] [Google Scholar]

[pone.0226777.ref013] 13.Stoop J, van Soest D, Vyrastekova J. Rewards and cooperation in social dilemma games. Journal of Environmental Economics & Management, 2018,88:300–310. 10.1016/j.jeem.2017.12.007 [DOI] [Google Scholar]

[pone.0226777.ref014] 14.Liu J, Meng H, Wei W, Tong L, Yong Y. Synergy punishment promotes cooperation in spatial public good game. Chaos Solitons & Fractals, 2018,109:214–218. 10.1016/j.chaos.2018.01.019 [DOI] [Google Scholar]

[pone.0226777.ref015] 15.Szolnoki A, Perc M, Szabó G. Topology-independent impact of noise on cooperation in spatial public goods games. Phys Rev E Stat Nonlin Soft Matter Phys, 2009,80(2):56109 10.1103/PhysRevE.80.056109 [DOI] [PubMed] [Google Scholar]

[pone.0226777.ref016] 16.Wu Z X, Xu X J, Chen Y, Wang Y H. Spatial prisoner’s dilemma game with volunteering in Newman-Watts small-world networks. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2005, 71(3 Pt 2B):037103 10.1103/PhysRevE.71.037103 [DOI] [PubMed] [Google Scholar]

[pone.0226777.ref017] 17.Ichinose G, Sayama H. Invasion of Cooperation in Scale-Free Networks: Accumulated versus Average Payoffs. Artificial Life, 2017,23(1):25–33. 10.1162/ARTL_a_00220 [DOI] [PubMed] [Google Scholar]

[pone.0226777.ref018] 18.Nowak M A, May R M. Evolutionary games and spatial chaos. Nature, 1992,359(6398):826–829. 10.1038/359826a0 [DOI] [Google Scholar]

[pone.0226777.ref019] 19.Santos F C, Santos M D, Pacheco J M. Social diversity promotes the emergence of cooperation in public goods games. Nature, 2008,454(7201):213 10.1038/nature06940 [DOI] [PubMed] [Google Scholar]

[pone.0226777.ref020] 20.Cao X B, Du W B, Rong Z H. The evolutionary public goods game on scale-free networks with heterogeneous investment. Physica A Statistical Mechanics & Its Applications, 2010,389(6):1273–1280. 10.1016/j.physa.2009.11.044 [DOI] [Google Scholar]

[pone.0226777.ref021] 21.Huang K, Wang T, Cheng Y, Zheng X P. Effect of Heterogeneous Investments on the Evolution of Cooperation in Spatial Public Goods Game. Plos One, 2015,10(3):e120317 10.1371/journal.pone.0120317 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0226777.ref022] 22.Ding H, Zhang Y, Ren Y, Shi B Y, Choo K K. Heterogeneous investment in spatial public goods game with mixed strategy. Soft Computing, 2018,22(4):1287–1294. 10.1007/s00500-016-2415-4 [DOI] [Google Scholar]

[pone.0226777.ref023] 23.Yuan W J, Xia C Y. Role of Investment Heterogeneity in the Cooperation on Spatial Public Goods Game. Plos One, 2014,9(3):e91012 10.1371/journal.pone.0091012 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0226777.ref024] 24.Zhang Y, Wang J, Ding C, Xia C Y. Impact of individual difference and investment heterogeneity on the collective cooperation in the spatial public goods game. Knowledge-Based Systems, 2017,136:150–158. 10.1016/j.knosys.2017.09.011 [DOI] [Google Scholar]

[pone.0226777.ref025] 25.Wang Q, Wang H, Zhang Z, Li Y M, Liu Y, Perc M. Heterogeneous investments promote cooperation in evolutionary public goods games. Physica A Statistical Mechanics & Its Applications, 2018,502:570–575. 10.1016/j.physa.2018.02.140 [DOI] [Google Scholar]

[pone.0226777.ref026] 26.Peng D, Yang H X, Wang W X, Chen G R, Wang B H. Promotion of cooperation induced by nonuniform payoff allocation in spatial public goods game. European Physical Journal B, 2010,73(3):455–459. 10.1140/epjb/e2010-00008-7 [DOI] [Google Scholar]

[pone.0226777.ref027] 27.Zhang H, Yang H, Du W, Wang B H, Cao X B. Evolutionary public goods games on scale-free networks with unequal payoff allocation mechanism. Physica A Statistical Mechanics & Its Applications, 2010,389(5):1099–1104. 10.1016/j.physa.2009.11.029 [DOI] [Google Scholar]

[pone.0226777.ref028] 28.Meloni S, Xia C Y, Moreno Y. Heterogeneous resource allocation can change social hierarchy in public goods games. Royal Society Open Science, 2017,4(3):170092 10.1098/rsos.170092 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0226777.ref029] 29.Lei C, Wu T, Jia JY, Cong R, Wang L. Heterogeneity of allocation promotes cooperation in public goods games. Physica A Statistical Mechanics & Its Applications, 2010,389(21):4708–4714. 10.1016/j.physa.2010.06.002 [DOI] [Google Scholar]

[pone.0226777.ref030] 30.Zhang H, Shi D, Liu R, Wang B H. Dynamic allocation of investments promotes cooperation in spatial public goods game. Physica A Statistical Mechanics & Its Applications, 2012,391(8):2617–2622. 10.1016/j.physa.2011.12.005 [DOI] [Google Scholar]

[pone.0226777.ref031] 31.Fan R, Zhang Y, Luo M, Zhang H J. Promotion of cooperation induced by heterogeneity of both investment and payoff allocation in spatial public goods game. Physica A Statistical Mechanics & Its Applications, 2017,465:454–463. 10.1016/j.physa.2016.08.039 [DOI] [Google Scholar]

[pone.0226777.ref032] 32.Botelho A, Harrison G W, Pinto L M C, Rutström E E. Testing static game theory with dynamic experiments: A case study of public goods. Games & Economic Behavior, 2009,67(1):253–265. 10.1016/j.geb.2008.11.013 [DOI] [Google Scholar]

[pone.0226777.ref033] 33.Vukov J, Szabó György. Evolutionary prisoner’s dilemma game on a square lattice. Physical Review E, 1998,58(1):69–73. 10.1103/PhysRevE.71.036133 [DOI] [Google Scholar]

[pone.0226777.ref034] 34.Traulsen A, Nowak M A. Evolution of cooperation by multilevel selection. Proceedings of the National Academy of Sciences, 2006,103(29):10952–10955. 10.1073/pnas.0602530103 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0226777.ref035] 35.Szabó G, Hauert C. Phase transitions and volunteering in spatial public goods games. Physical Review Letters, 2002,89(11):118101 10.1103/PhysRevLett.89.118101 [DOI] [PubMed] [Google Scholar]

[pone.0226777.ref036] 36.Li J, Wu T, Zeng G, Wang L. Selective investment promotes cooperation in public goods game. Physica A Statistical Mechanics & Its Applications, 2012,391(15):3924–3929. 10.1016/j.physa.2012.03.016 [DOI] [Google Scholar]

PERMALINK

Research on an evolutionary game model and simulation of a cluster innovation network based on fairness preference

Chuanyun Li

Xia Cao

Ming Chi

Roles

Abstract

1 Introduction

2 Evolution analysis of the cluster innovation network under the fairness preference

Fig 1. Evolution analysis framework of cluster innovation networks under fairness preferences.

3 Evolutionary game model of a cluster innovation network based on fairness preferences

3.1 Basic hypothesis of the game model

3.2 Construction of the game model

3.3 Evolution rules

4 Simulation analysis of a cluster innovation network evolution game

4.1 Simulation steps

4.2 Setting and explaining of the simulation parameters

Table 1. Parameter settings for the evolutionary game simulation of cluster innovation networks.

4.3 Impact of the fairness preference and return intensity on the enterprise cooperation level in cluster innovation network evolution

Fig 2. The effect of the adjustment coefficient on the level of enterprise cooperation in cluster innovation network under three mechanisms and different gain coefficients.

Fig 3. The effect of the gain coefficient on the enterprise cooperation level in cluster innovation network under three mechanisms and different adjustment coefficients.

4.4 Impact of the fairness preference and return intensity on the corporate cooperative benefit in cluster innovation networks

Fig 4. The effect of the adjustment coefficient on the cooperative benefits of enterprises with different cooperative breadths in cluster innovation network under three mechanisms.

Fig 5. The effect of the gain coefficient on the cooperative benefits of enterprises with different cooperative widths in cluster innovation networks under three mechanisms.

Fig 6. The effect of the adjustment coefficient on the cooperative returns of enterprises with different cooperative depths in cluster innovation network under three mechanisms.

Fig 7. The effect of the gain coefficient on the cooperative benefits of enterprises with different cooperation depths in cluster innovation network under three mechanisms.

5 Conclusions

Data Availability

Funding Statement

References

Decision Letter 0

Luo-Luo Jiang

Roles

Author response to Decision Letter 0

Decision Letter 1

Luo-Luo Jiang

Roles

Author response to Decision Letter 1

Decision Letter 2

Luo-Luo Jiang

Roles

Acceptance letter

Luo-Luo Jiang

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases