On the choice of multiscale entropy algorithm for quantification of complexity in gait data

Abstract

The present study aimed at identifying a suitable multiscale entropy (MSE) algorithm for assessment of complexity in a stride-to-stride time interval time series. Five different algorithms were included (the original MSE, refine composite multiscale entropy (RCMSE), multiscale fuzzy entropy, generalized multiscale entropy and intrinsic mode entropy) and applied to twenty iterations of white noise, pink noise, or a sine wave with added white noise. Based on their ability to differentiate the level of complexity in the three different generated signal types, and their sensitivity and parameter consistency, MSE and RCMSE were deemed most appropriate. These two algorithms were applied to stride-to-stride time interval time series recorded from fourteen healthy subjects during one hour of overground and treadmill walking. In general, acceptable sensitivity and good parameter consistency were observed for both algorithms; however, they were not able to differentiate the complexity of the stride-to-stride time interval time series between the two walking conditions. Thus, the present study recommends the use of either MSE or RCMSE for quantification of complexity in stride-to-stride time interval time series.

Summary

Complexity of various physiological systems has been suggested to be linked to the health status of the system. In human walking, the dynamics of stride-to-stride time interval time series has been used to investigate the effect of neuromuscular diseases and injuries on motor control. Thus, the quantification of complexity in these time series could reveal relevant information of the dynamics of human walking. Multiscale entropy is based on the quantification of regularity on multiple scales of a given time series and has been suggested useful to assess complexity. Numerous competing versions of multiscale entropy have been proposed as improvements of the original algorithm. However, it remains unknown which algorithm is suitable to apply to stride-to-stride time interval time series. We applied different multiscale algorithms to both theoretical and biological time series and investigated their ability to differentiate signals with different temporal dynamics, their sensitivity and their parameter consistency. We observed that the original multiscale entropy and refined composite multiscale entropy algorithm outperformed the other algorithms. Thus, future studies should use these algorithms when quantifying complexity in stride-to-stride time interval time series during human walking.

Introduction

The ‘Loss of Complexity’ theory by Lipsitz and Goldberger proposes that the process of aging is associated with a decrease in the complexity of different physiological systems (e.g. cardiovascular, hormonal, and neurological) which leads to reduced adaptability in the functions of these systems [1]. As an elaboration of this theory, it has been suggested that changes in the complexity of the physiological system can be linked to different pathologies [2–5]. A variety of nonlinear tools have been applied to assess this complexity in physiological signals in humans (e.g. heart rhythms, blood pressure, breathing frequencies) [4, 6–9].

A key characteristic of the complex nonlinear behavior of human signals is predictability, which can be quantified by entropy [10–12]. Entropy has been applied to stride time intervals and joint kinematics during walking [13–20]. Sample entropy (SaEn) is the most popular method used to quantify predictability of a system and has been proven to be methodologically stable [14]. In the past, many have stated that increased entropy equates to an increase in complexity; however, it is questionable if this holds true. According to the description by Delignières and Marmelat, complexity and complication are very different concepts [21]. Complication refers to many uncorrelated components, where each component can be analyzed and eventually the entirety of the system has been analyzed. However, in a complex system, a large number of components are intricately related (“infinitely entangled”) and the system cannot be decomposed into individual components [21]. Thus, stating that SaEn calculated solely from one single time series, capturing information regarding the amount of complexity of the underlying system, is incorrect.

Based on the argument that complexity of biological systems originates from the particular interaction of components on multiple scales [4, 22], Costa and colleagues introduced in 2002 multiscale entropy (MSE) as a useful tool to quantify the complexity of biological signals [22]. MSE rescales the original time series by successively averaging an increasing number of consecutive data points into new, coarse-grained time series and calculates the SaEn of each coarse-grained time series. This enables quantification of the complexity of a time series on shorter and longer scales [4, 22]. In a series of studies, Costa and colleagues applied MSE to estimate the complexity of heart rate fluctuations in different populations [22–26]. Furthermore, MSE has been utilized to estimate the complexity of trunk kinematics, stride time intervals, and lower leg muscle activity during human gait [27–31]. In a recent study, Bizovska and colleagues applied MSE to the trunk acceleration of young and older women during treadmill and overground walking and observed that complexity differed between the two walking conditions in older but not younger individuals [32]. Using the same approach, Bisi and Stagni recently observed a maturation effect on trunk acceleration complexity during walking in children, adolescents, and young adults [33].

When applied to stride time intervals, MSE has revealed higher levels of complexity during walking at self-selected speed compared to slower and faster walking [27]. Thus, MSE applied to human locomotion can reveal important information regarding the complexity of gait dynamics.

Since the introduction of the original MSE algorithm, a number of ‘competing’ algorithms have been presented to overcome potential methodological drawbacks [34]. Refined composite multiscale entropy (RCME) was suggested by Wu and colleagues [35] to have lower probability of inducing undefined entropy of the different scales compared to previous suggested MSE versions [34, 35]. MSE has been criticized for not detecting the presence of high frequency in the signal in question and for a lack of adaptability to nonstationary/nonlinear signals [36]. To address these issues, intrinsic mode entropy (IME) computes intrinsic mode functions of the signal in question and calculates the SaEn of the cumulative sums of each of the intrinsic mode functions [36]. Most versions of MSE algorithms use the original SaEn algorithm by Richman and Moorman [12] for entropy calculations. However, one potential drawback of this algorithm is the Heaviside function used to measure the degree of match between two vectors, which presents a discontinuous and hard boundary. To overcome this, fuzzy entropy uses fuzzy membership functions instead of the Heaviside function, which was found to additionally improve parameter consistency and data length independence [37]. Fuzzy entropy was later incorporated into a multiscale framework (multiscale fuzzy entropy – MSFE) by Xiong and colleagues [38]. The authors of the original algorithm, Costa and Goldberger, introduced generalized multiscale entropy (GMSE) in 2015, which addresses the coarse-graining procedure [23]. Instead of using the average of consecutive data points when rescaling the original time series, the authors used the variance of each non-overlapping segment of the time series [23]. Thus, GMSE quantifies the dynamics of the volatility (variance) of a signal.

Although numerous studies have introduced new versions of the MSE algorithm, few studies have compared the performance of different versions [35, 38]. Several criteria could be posed for the evaluation of the performance of the MSE algorithm. When applied to both theoretical and biological signals, a useful algorithm should be able to distinguish between signals with different temporal structure. Furthermore, the algorithm should have relatively high parameter consistency when applied to both theoretical and biological signals.

The present study aimed at identifying a suitable MSE algorithm for assessment of complexity in stride-to-stride time interval time series. Five different versions of the MSE algorithm were included in the present study; the original MSE [22], RCMSE [35], IME [36], MSFE [38] and GMSE [23].

To identify an appropriate MSE algorithm(s), we proposed three criteria: First a suitable algorithm would be able distinguish between three theoretical signals with different temporal structure. Secondly, the algorithm(s) would have high sensitivity (i.e. consistently returning the correct level of complexity in accordance with the expected complexity of the theoretical time series in question). Thirdly, the algorithm(s) would possess relatively high parameter consistency.

In order to test the application of the identified algorithm(s) to gait data, the complexity in stride-to-stride time intervals obtained under two different walking conditions (overground and treadmill) was quantified. Additionally, the sensitivity and parameter consistency of the algorithm(s) were investigated.

Based on the results of the present study, it was possible to experimentally support the choice of a specific algorithm for assessment of complexity in stride-to-stride time intervals in future studies.

Methods

The present study included new analyses of both theoretical and biological data collected during the experimental part of a previous study [39]. The theoretical data consisted of 20 time series of three different theoretical signals of 2500 data points. The colored noise generator function in Matlab (Math Works R2011b) was used to create a pink noise signal (power spectrum of 1/f), considered to be chaotic, and a white Gaussian noise signal (constant power spectrum), considered to be random. A sine wave signal with added white noise, considered to be highly predictable, was created by the following equation:

$$y\left(x\right)=2\cdot \sin \left(x\right)+0.5\cdot whitenoise$$ Equation 1:

The three signals were selected to represent three different levels of complexity with the pink noise signal having the highest complexity, the white noise signal having an intermediate level of complexity, and the sine wave signal with added white noise having lowest level of complexity. The biological data consisted of stride-to-stride time interval time series obtained from healthy individuals during one-hour trials of overground and treadmill walking. The experimental setup is described below.

Subjects

Fourteen young healthy adults with no diagnosed lower limb injuries within the past year volunteered to participate in the present study. They had a mean (± SD) age of 25.0 years (± 4.2), height of 170.8 cm (± 11.9) and body mass of 69.4 kg (± 16.9). The subjects were informed of the experimental conditions and gave their written consent to participate in the study. The study was approved by the by the Institutional Review Board of the University of Nebraska Medical Center and the study was carried out in accordance with the approved guidelines.

Protocol

The subjects reported to the laboratory on two separate occasions. During the first visit, the subjects walked for one hour on a circular track (circumference 1/8 mile = 201.1m). During the second visit, the subjects completed one hour of treadmill walking. During both the overground and treadmill walking trials, the subject walked at their self-selected speed. During both walking trials, heel strikes were recorded at a sampling rate of 148 Hz by footswitches (Trigno™ 4-channel FSR Sensor, Delsys Inc., Natick, MA) placed under both heels.

Analysis

The theoretical signals were subjected to the original MSE algorithm and the four alternative versions following the procedures described below. The algorithms that met the expectation of returning the pink noise signal with the highest level of complexity, the white noise signal with the intermediate level of complexity, and the sine wave signal with added white noise having the lowest level of complexity, were also applied to the stride-to-stride time intervals signals. The heel strike data from both feet was transferred to Matlab (MathWorks R2011b) and stride time intervals of the right foot were calculated for both the treadmill and overground trial. After elimination of the first and last five minutes of the trial, each stride-to-stride time interval time series was cut to contain 2500 strides.

The original multiscale entropy algorithm

The MSE procedure rescaled the original time series by dividing it into non-overlapping windows of length τ and averaging the data points within each window, creating new time series [4, 27]. The k’th coarse-grained time series $y_k^{\tau }=\left\{y_{k,1}^{\tau }{y}_{k,2}^{\tau }\dots y_{k,p}^{\tau }\right\}$ of x was defined as equation 2:

$$y_{k,j}^{\tau }=\frac{1}{\tau }{\sum }_{i=\left(j-1\right)\tau +k}^{j\tau +k-1}{x}_i,\text{for}1\le \text{j}\le \frac{N}{j},1\le \text{k}\le \mathrm{\tau }$$ Equation 2:

According to this procedure, for a singular time series = [1 2 3 4 5 6 7 8 9 10 11 12], the first rescaled time series = [1.5 3.5 5.5 7.5 9.5 11.5], the second rescaled time series = [2 5 8 11] and the third rescaled time series = [2.5 6.5 10.5]. The theoretical time series were rescaled 20 times and the stride-to-stride time interval time series were rescaled 6 times. For each new rescaled time series and the original time series, SaEn was calculated using the method presented by Richman and Moorman [12]. For the time series x = {x₁ x₂ … x_N} of the length N, template vectors with dimension m were constructed as: $x_i^m=\left\{x_i{x}_{i+1}\dots x_{i+m-1}\right\}$, for 1 ≤ i ≤ N – m. Matches n^m were counted when the distance between two template vectors was smaller than a predefined critical limit r. The distance d was calculated by equation 3:

$$d_{ij}^m={\Vert x_i^m-x_j^m\Vert }_{\infty },\text{for}1\le \text{i},\text{j}\le \text{N}–\text{m},\text{j}\ne \text{i}.$$ Equation 3:

This procedure was repeated for m = m + 1 and matches n^{m + 1} were counted. SaEn was defined as the logarithm of the ratio between n^{m + 1} and n^m (equation 4):

$$SaEn=-\ln \frac{n^{m+1}}{n^m}$$ Equation 4:

Refined composite multiscale entropy

The coarse-grained procedure of RCMSE was the same as in MSE but the SaEn calculation is different [35]. The procedure consisted of two steps. First, at a scale factor of τ, the number of matched vector pairs, $n_{k,\tau }^{m+1}$ and $n_{k,\tau }^m$, was calculated for all τ coarse-grained series. Secondly, ${\overline{n}}_{k,\tau }^m$ and ${\overline{n}}_{k,\tau }^{m+1}$ represent the mean of $n_{k,\tau }^{m+1}$ and $n_{k,\tau }^m$ for 1 ≤ k ≤ τ. RCMSE, for each scale factor τ, was defined as the logarithm of the ratio between ${\overline{n}}_{k,\tau }^{m+1}$ and ${\overline{n}}_{k,\tau }^m$ (equation 5).

$$RCMSE=-\ln \frac{{\overline{n}}_{k,\tau }^{m+1}}{\overline{{\overline{n}}_{k,\tau }^m}},\text{where}{\overline{n}}_{k,\tau }^{m+1}=\frac{1}{\tau }{\sum }_{k=1}^{\tau }{n}_{k,\tau }^{m+1}\text{and}{\overline{n}}_{k,\tau }^m=\frac{1}{\tau }{\sum }_{k=1}^{\tau }{n}_{k,\tau }^m$$ Equation 5:

Intrinsic mode entropy

The coarse-grained procedure of MSE was replaced by multilevel filtering of the original signal in IME by using empirical mode decomposition to decompose the time series into waveforms modulated in amplitude and frequency [40]. The first iteration of the algorithm extracted the first intrinsic mode function (IMF). A residual was calculated as the difference between the original time series and the IMF time series. The second IMF was extracted by rerunning the empirical mode decomposition on the residual. This procedure was repeated to extract the subsequent IMFs. Thus, the original signal x(t) was represented as the sum of IMFs and the residual component. $x\left(t\right)={\sum }_{k=1}^K{d}_k\left(t\right)+r_K\left(t\right),$ where ${\left\{d_k\left(t\right)\right\}}_{k=1}^K$ denoted as the K extracted empirical modes and r_K(t) as the residual. IME was achieved by calculating SaEn of the cumulative sums ($C_{IMF}^k$) of the IMFs up to the order of k [36] (equation 6):

$$C_{IMF}^k(t)={\sum }_{j=1}^k{d}_j\left(t\right)$$ Equation 6:

Multiscale fuzzy entropy

MSFE used the same coarse-graining procedure as the original MSE algorithm. The function, which determined matches of vector pairs in the SaEn procedure, was a Heaviside step function (equation 7) that is discontinuous and makes a binary decision.

$$H=\{\begin{array}{c}1,d\le r,\\ 0,d>r,\end{array}$$ Equation 7:

In MSFE, this function was replaced by Gaussian function μ [38] (equation 8):

$$\mu (d,r,c)=\exp \left(-\frac{d^{\frac{\ln \left({ln2}^c\right)}{lnr}}}{c}\right)$$ Equation 8:

where r was a location parameter which determined the location of the function (at which point the function takes a value of 0.5) and c was the shape parameter deciding the steepness of the function (ranging from 0 to 1/ln2) [38].

Generalized multiscale entropy

GMSE introduced a family of coarse-graining procedures in which the averaging function can be substituted with other functions. In the study by Costa and Goldberger [23], they used a variance function which was adopted by the present study (equation 9):

$${\sigma }^2=\frac{1}{(N-1)}{\sum }_{i=1}^N{\left(x_i-x\right)}^2$$ Equation 9:

Following this coarse-graining procedure, SaEn was calculated for each rescaled time series.

Quantification of complexity

The five different versions of MSE were applied to the theoretical signals and their respective 20 rescaled time series. In accordance with Costa et al. 2003 [27], only 6 rescaled time series were used for the MSE algorithm(s) applied to the stride-to-stride time intervals time series. The entropy values for each algorithm were plotted as a function of the number of rescaled time series and the area below the curve was calculated as a quantification of complexity [4].

Choice of input parameters and parameter consistency

Our previous studies have shown SaEn calculations to be sensitive to the selection of the input parameters [14, 20]. To investigate parameter consistency, a range of values of each input parameter was included. The input parameter, m, was the length of the vectors being compared and r was the similarity criterion. For all algorithms, an m = 2 and 3 and r = 0.1, 0.15, 0.2, 0.25 and 0.3 were selected as input parameters. The results from the analyses using m=2 and r=0.2 are presented in the results paragraph. The results from the analyses using the other input parameters are presented in the supplementary material. For the MSE, RCMSE, MSFE, and GMSE, the coarse-graining procedure resulted in a successive reduction in the length of each new rescaled time series. The rescaled time series at scale 20 consisted of 125 data points for the theoretical signals and 416 data points at scale 6 for the stride-to-stride time interval time series. This was not the case for IME, where the length of time series was kept constant across all rescaled time series.

Statistics

The sample entropy measure was plotted as a function of scale for each theoretical signal and each algorithm (Figure 1) for visual inspection. For the first criteria, the difference in the estimation of complexity in the three theoretical signals between the five MSE algorithms, was assessed using a one-way, repeated measure ANOVA with signal type as the independent factor. In case of significant effect of signal, a Holm-Sidak post-hoc test was applied. To evaluate the second criteria, the sensitivity of the five MSE algorithms when applied to the theoretical signals, the percentage of correct estimates of complexity (i.e. the complexity of pink noise being the highest, white noise being intermediate, and the sine wave with added noise being the lowest) out of the 3 × 20 signal iterations was calculated. Furthermore, the consistency in the complexity estimation of each algorithm was calculated as the coefficient of variation across the 20 iterated signals of each type. The third criteria of parameter consistency for each of the five algorithms was qualitatively evaluated (figures are presented in the supplementary material).

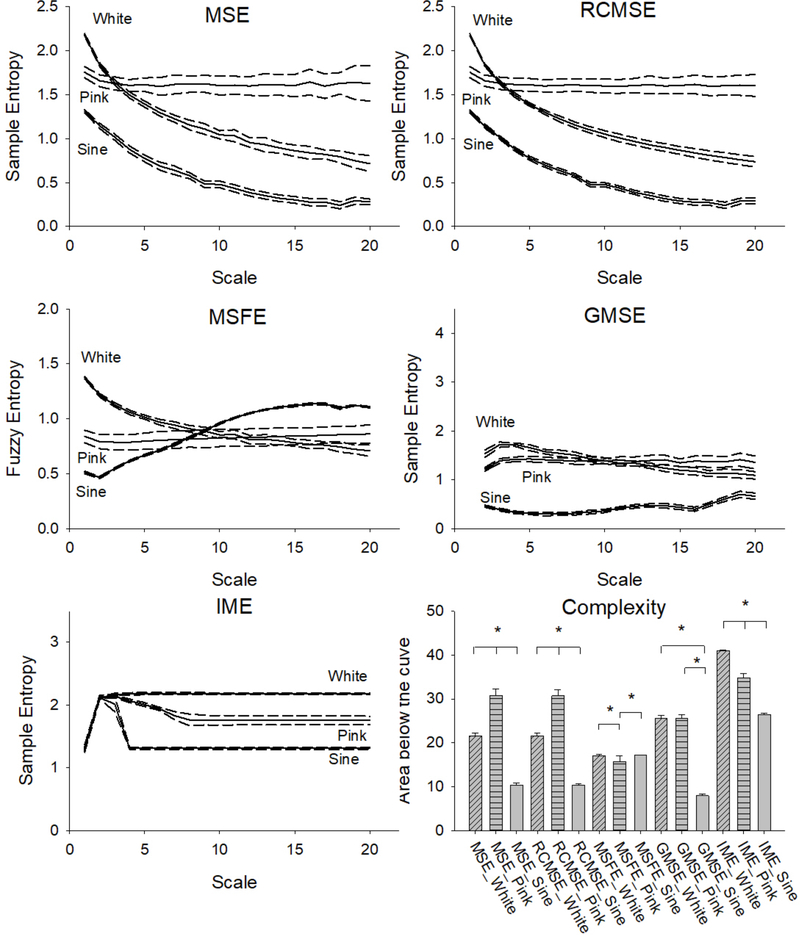
Figure 1: Multiscale entropy of theoretical signals.

MSE, RCMSE, MSFE, GMSE, IME and complexity for white and pink noise and a sine wave with added noise signals with m=2 and r=0.2. Asterisk indicates significant differences between the level of complexity.

Using the selected algorithms based on the differentiation of the theoretical signals, the difference in the estimation of complexity between the two walking conditions was established using a paired Student’s t-test. Furthermore, the sensitivity of the selected algorithms, when applied to the stride-to-stride time interval time series, was quantified by calculating the percentage of subjects that exhibited a difference in complexity between the two conditions when exceeding a critical limit. The critical limit was based on a modification of the Cohen’s d effect size equation and calculated as 0.8 multiplied by the pooled standard deviation of the complexity values from the two conditions [41]. Parameter consistency was qualitatively evaluated for the selected algorithms applied to the stride-to-stride time signals. In all cases, the level of significance was set to 5%. All statistical calculations were performed in Sigmaplot (Systat Software, Inc. 2014, version 13.0, Germany).

Results

Theoretical signals

The results from the five multiscale analyses with m=2 and r=0.2 applied to white noise, pink noise, and the sine wave with added noise are presented in Figure 1. For MSE and RCMSE, the entropy decreased with increasing scale for white noise and the sine wave with added noise, while entropy was relatively unchanged for pink noise. For MSFE, the entropy of white and pink noise showed the same tendency as for MSE and RCMSE; although, the values were lower. In contrast, the sine wave with added noise increased with increasing scale. The GMSE showed a similar pattern to MSFE; however, for the sine wave with added noise, the entropy remained relatively constant across scales. At lower scales, the entropy of white noise was higher compared to pink noise and vice versa at higher scales. For the IME, the entropy from all three signals increased from the first to the second scale. While the entropy of white noise did not change with an increase in scale, the entropy of pink noise decreased until scale 8, after which it remained constant. Entropy of the sine wave with added noise exhibited the same pattern but decreased even more until scale 4, after which it remained constant.

Complexity, calculated as the area below the multiscale curves, for the three signals and the five algorithms is presented in Figure 1. There was a significant effect of signal type (p < 0.001) for all five algorithms. Post-hoc tests revealed MSE, RCMSE and IME had significant differences between the complexities of the different signal types (p < 0.001 in all cases). The MSFE showed significant differences between pink noise and the two other signals, but no difference between white noise and the sine wave with added noise. The GMSE showed significant differences between the sine wave signal with added noise and the two other signal types (p < 0.001 in both cases), but no difference between pink and white noise (Figure 1). The results presented in the supplementary material showed, in general, the same tendencies when m=2 across different r values. However, when using m=3, the outcome of the MSFE and GMSE analyses changed compared to m=2 (see supplementary material for details).

The quantification of sensitivity demonstrated that MSE and RCMSE, in all cases, returned the expected ranking of complexity among the three signals (Table 1). In contrast, MSFE, GMSE and IME all returned white noise to have higher complexity compared to pink noise. While GMSE and IME confirmed the between-signal levels of complexity for white noise and pink noise versus sine wave with added noise, this was not the case for MSFE (Table 1). The coefficient of variation ranged between 2.2 and 4.5% for MSE, RCMSE, and GMSE and between 0.3 and 8.6% for MFSE and IME (Figure 2).

Table 1:

Sensitivity of the five MSE algorithms expressed as the percentage of corrected ranked signals (white noise, pink noise and sine wave with added noise) based on their estimated complexity for m=2 and r=0.2.

	MSE	RCMSE	MSFE	GMSE	IME
White < Pink	100	100	0	0	0
White > Sine wave	100	100	25	100	100
Pink > Sine wave	100	100	5	100	100
Mean	100	100	10	66.7	66.7

Figure 2: Complexity coefficient of variation of the theoretical signals.

Coefficient of variation of the estimated level of complexity of the three theoretical signals using the MSE, RCMSE, MSFE, GMSE and IME algorithms with m=2 and r=0.2. High coefficient of variation indicates low sensitivity of the algorithm in question.

The qualitative evaluation of parameter consistency was conducted of figures similar to Figure 1 for m=2 and 3 and r=0.1, 0.15, 0.2, 0.25 and 0.3, respectively. These figures are presented in the supplementary material. MSE, RCMSE and IME showed in general a good parameter consistency for both m=2 and m=3 and for r greater than 0.15. When applying different m-values to MFSE and GMSE, these algorithms showed less parameter consistency.

Stride-to-stride time interval time series

Based on the results from the analyses of the three theoretical signals, the MSE and RCMSE were applied to the stride-to-stride time interval time series from overground and treadmill walking with m=2 and r=0.2. The SaEn was plotted as a function of scale for the two conditions and presented in Figure 3. MSE and RCMSE revealed a similar pattern for both walking conditions, decreasing SaEn at increasing scales.

Figure 3: Multiscale entropy of stride time intervals.

MSE and RCMSE and complexity of the stride time intervals time series during overground and treadmill walking with m=2 and r=0.2.

The complexity of the stride-to-stride time interval time series did not differ between walking conditions for the two algorithms (Figure 3). The two algorithms estimated approximately the same level of complexity.

The quantification of sensitivity revealed that both MSE and RCMSE could differentiate the complexity of the stride-to-stride time intervals time series for more than 50% of the subjects (Table 2). However, both algorithms were inconsistent in their differentiation of conditions and returned between 21 and 28% of the subjects to have higher complexity during overground walking and between 28 and 36% to have higher complexity during treadmill walking. The coefficient of variation for the MSE applied to the stride-to-stride time interval time series was 8.0 and 10.9% for the overground and treadmill walking, respectively. For the RCMSE the coefficient of variation was 7.8 and 10.5%, respectively.

Table 2:

Sensitivity of the MSE and RCMSE algorithm applied to the stride-to-stride time interval time series from the overground (OG) and treadmill (TM) conditions and the percentage of subjects which return complexity during OG higher compared to TM, TM higher compared to OG and no differences between the two conditions.

	Sensitivity	OG > TM	OG < TM	OG ≈ TM
MSE	64.3 %	28.6 %	35.7 %	35.7 %
RCMSE	50.0 %	21.4 %	28.6 %	50.0 %

Figures similar to Figure 3 for m=2 and 3, and r=0.1, 0.15, 0.2, 0.25 and 0.3, respectively (presented in the supplementary material), were used for the qualitative evaluation of parameter consistency. Good parameter consistency was observed for both algorithms especially when r was above 0.15. Complexity appears to be more affected by changes in r compared to changes in m; however, both did not differ between walking conditions for any of the investigated parameter combinations.

Discussion

The present study aimed at identifying a suitable MSE algorithm for assessment of complexity in stride-to-stride time interval time series. Five different versions of the MSE algorithm were included. The performance of the five algorithms was evaluated based on three raised criteria related to their ability to differentiate the complexity, sensitivity, and parameter consistency of 20 iterations of white noise, pink noise and sine wave with added noise. The best performing algorithms were then applied to stride-to-stride time interval time series to investigate if the selected algorithm could differentiate the level of complexity between the two walking conditions.

Theoretical signals

The first criterion suggested that an appropriate algorithm should be able to separate the level of complexity in a time series. Based on the definition of complexity by Delignieres and Marmelat [21], it seemed reasonable to assume that theoretical signals with very different power spectrum (e.g. white and pink noise, and a sine wave with added noise) are expected to have distinguishable levels of complexity. Thus, any suitable algorithm would be able to differentiate between the three included signals based on the level of complexity. A pink noise-like behavior has been observed in many biological structures and in the behavior of biological systems and has been linked to a high complexity [8]. Furthermore, the presence of long range correlations in pink noise agrees well with the notion that components within a complex system are intricately related (“infinitely entangled”) [21]. The uncorrelated nature of white noise suggests a lower complexity, more likely increased complication, compared to the pink noise. Finally, the combination of a predictable sine wave with added white noise provides a signal with a strong presence of long range correlation. Thus, the quantified complexity should be highest in the pink noise, intermediate in white noise, and lowest in the sine wave with added noise. In the present study, only MSE and RCMSE fulfilled this prediction. Both MFSE and IME returned white noise with higher complexity compared to pink noise. GMSE was not able to distinguish between white and pink noise and return the sine wave with added noise with the lowest complexity. Based on these observations, MSE and RCMSE appeared to best quantify complexity. It is unknown why differences between algorithm’s outcome exist. In a previous study, Chen and colleagues [42] compared SaEn and fuzzi entropy applied to sine wave signal at 50 and 100 Hz. Both algorithms returned the high-frequency signal to have higher entropy values compared to the low-frequency. This observation was later confirmed and elaborated by the same group in 2009 [37] who found that both algorithms differentiated a high- and low-level complexity stochastic model according to the expectation. Furthermore, the authors observed an almost similar classification ability of the sample and fuzzy entropy algorithms. These studies would suggest a similar quantification of complexity by the MSE, RCMSE and MFSE which was not observed. Neither the study by Amound and colleagues [36] who introduced IME or the study by Costa and colleague [23] who introduced GMSE investigated the performance the algorithms on theoretical data with known different complexity.

The second criterion also supported that MSE and RCMSE were the most appropriate algorithms as they both returned a sensitivity of 100% for all signal comparisons. The coefficient of variation was below 5% for both algorithms regardless of the investigated signal. The range of coefficients of variation for the other algorithms was in general larger compared to MSE and RCMSE. This suggests that MSE and RCMSE have an acceptable precision regardless of the type of signal.

The third criterion addressed an important methodological aspect of the use of SaEn. Our previous studies have shown the importance of controlling SaEn for parameter consistency when applied to stride-to-stride time interval time series [14, 20]. Therefore, the present study applied a range of each input parameter. The results showed, in general, good parameter consistency for both m=2 and m=3 and for r greater than 0.15 for MSE, RCMSE and IME when applied to the theoretical signals. In contrast, MFSE and GMSE were observed to have less parameter consistency with different m-values. A low parameter consistency implies that minor changes in input parameters could lead to significant changes in the outcome values. Thus, the interpretation between-group or between-trial design studies could be biased by the selected input parameters. Furthermore, comparisons between studies using different input parameters would be compromised by this low parameter consistency. Thus, MSE, RCMSE and IME seemed to be the most appropriate algorithms.

Based on the evaluation of the three raised criteria, MSE and RCMSE were chosen as the most appropriate algorithms. While these two algorithms are closely related and perform similarly well, the other five algorithms are substantially different. The intrinsic mode function and subsequent summarizing of the signal in the IME algorithm introduces a smoothing effect which potentially removes information from the investigated signals related to the inherent complexity [36]. The MFSE uses a fuzzy membership functions instead of a Heaviside function in the SaEn calculations [37, 38]. The fuzzy membership functions appear to lower the calculated SaEn across all scales for white and pink noise, but increase it for sine wave with added noise across all scales. The latter seems contra intuitive as the rescaling procedure of averaging subsequent data points should remove unpredictability at higher scales for the sine wave with added noise. Apparently, the fuzzy membership functions identification of matching vectors in the time series was not able to assess this aspect. Finally, the GMSE differs from MSE and RCMSE by quantifying the dynamics of volatility (variance) of the signal in question and not the dynamics of mean [23]. It is unknown how this measure should be related to the definition of complexity proposed by Delignières and Marmelat [21].

Stride-to-stride time interval time series

To further verify the use of the MSE and RCMSE algorithms on biological data, the present study applied both algorithms on hour long stride-to-stride time interval time series recorded during overground and treadmill walking. Previous studies have observed differences in movement dynamics between overground and treadmill walking [39, 43], suggesting that the complexity in stride-to-stride time interval time series would differ between these two conditions. Furthermore, assuming that treadmill walking imposes a constraint condition related to the stride time, stride length and stride speed fluctuations, the unconstraint nature of overground walking would exhibit higher complexity [27, 44, 45]. However, neither MSE nor RCMSE could differentiate the level complexity between the two walking conditions. This was true for all input parameter combinations and confirmed by the sensitivity analysis, which showed very inconclusive results regarding a differentiation of the level of complexity in the time series from the two walking conditions.

These observations indicate that either the applied algorithms were not able to detect the difference in complexity between the two walking conditions, or that no difference in complexity between the two conditions exists. Similar to the present results, Lindsay and colleagues [46] did not observe differences when applying MSE to the stride-to-stride time interval time series recorded during overground and treadmill running at preferred running speed. However, when running speed was altered beyond or below the preferred speed, overground running exhibited higher levels of complexity. It is unknown if similar speed related alterations during walking would induce differences in complexity between the two conditions. In the original paper by Costa and colleagues [27], differences in complexity were observed between walking at preferred walking speed and slower and faster walking speeds. Thus, the complexity of stride-to-stride time intervals seems to be more sensitive to the constraints posed by changes in walking speed than the constraints posed by change in walking conditions (overground vs. treadmill). This could explain the lack of difference in complexity observed by the present study, since the subjects walked at their preferred walking speed, which was not expected to differ between conditions. However, the results of the present study do support the study by Bizovska and colleagues, where no effect of walking condition was observed when assessing MSE from trunk acceleration signals recorded during treadmill and overground walking in young women [32].

While several studies have applied nonlinear methods to demonstrate differences in the stride-to-stride time interval dynamics between different age groups and between individuals with various pathologies and healthy individuals [5, 13, 47, 48], to the best of our knowledge, no studies have used MSE algorithms. However, the lack of ability to differentiate between walking condition of the MSE algorithms should be kept in mind before conducting such studies in the future. Furthermore, the present study included 2500 stride recorded during hour long walking trials. While this is possible with young healthy subjects, it is an unrealistic protocol for most frail and pathological populations. It was beyond the scope of this study to address the required number of stride for a stable estimation of complexity using these algorithms. However, it is important to keep in mind that for both MSE and RCMSE the number of data points decreased significantly with each scale. In the present study, the sixth scale included 416 data points. In our previous study, we have observed that calculating SaEn on stride-to-stride time interval time series including less than 200 strides might be questionable [14]. Thus, including a minimum of 200 data points for the sixth scale would require 1200 stride in total. While lower than the number of strides used in the present study, this may not be feasible for frail or pathological populations.

Conclusion

Based on the results of the present study, MSE and RCMSE were able to distinguish between the three different theoretical signals in accordance with the prediction. Furthermore, both the sensitivity analysis and parameter consistency evaluation supported the use of these two algorithms. This advocated for the use of either MSE or RCMSE to quantify complexity in the biological time series. Finally, it is possible that the remaining three algorithms have inherent bias towards quantifying complexity in light of the definition by Delignières and Marmelat [21]. MSE and RCMSE were not able to differentiate the complexity in the stride-to-stride time interval time series during the two walking conditions. This is potentially due to 1) either the algorithms were not sensitive enough to detect differences or 2) simply, that no differences exist. Based on the body of literature thus far, it appears that speed may affect complexity of walking more so than walking condition (overground vs. treadmill). Future studies are needed to confirm or refute this hypothesis. If future studies are to use MSE or RCMSE on stride-to-stride time intervals, it is recommended that caution be given to the length of data, considering the coarse-graining procedure shortens the time series with each scale. We recommend that future studies use either MSE or RCMSE for quantification of complexity due to its ability to differentiate signals with different complexity and its acceptable sensitivity and high parameter consistency.