Large-scale state-dependent membrane remodeling by a transporter protein

Wenchang Zhou; Giacomo Fiorin; Claudio Anselmi; Hossein Ali Karimi-Varzaneh; Horacio Poblete; Lucy R Forrest; José D Faraldo-Gómez

doi:10.7554/eLife.50576

. 2019 Dec 19;8:e50576. doi: 10.7554/eLife.50576

Large-scale state-dependent membrane remodeling by a transporter protein

Wenchang Zhou ¹, Giacomo Fiorin ¹, Claudio Anselmi ^1,^†, Hossein Ali Karimi-Varzaneh ^2,^‡, Horacio Poblete ^1,^2,^§, Lucy R Forrest ^2,^✉, José D Faraldo-Gómez ^1,^✉

Editors: Nir Ben-Tal³, Richard W Aldrich⁴

PMCID: PMC6957315 PMID: 31855177

Abstract

That channels and transporters can influence the membrane morphology is increasingly recognized. Less appreciated is that the extent and free-energy cost of these deformations likely varies among different functional states of a protein, and thus, that they might contribute significantly to defining its mechanism. We consider the trimeric Na⁺-aspartate symporter Glt_Ph, a homolog of an important class of neurotransmitter transporters, whose mechanism entails one of the most drastic structural changes known. Molecular simulations indicate that when the protomers become inward-facing, they cause deep, long-ranged, and yet mutually-independent membrane deformations. Using a novel simulation methodology, we estimate that the free-energy cost of this membrane perturbation is in the order of 6–7 kcal/mol per protomer. Compensating free-energy contributions within the protein or its environment must thus stabilize this inward-facing conformation for the transporter to function. We discuss these striking results in the context of existing experimental observations for this and other transporters.

Research organism: None

Introduction

Integral membrane proteins can have a marked impact on the morphology of the surrounding bilayer. For example, they might alter its curvature or thickness, or foster the enrichment or depletion of specific types of lipid in their vicinity (Lee, 2004; Andersen and Koeppe, 2007; Marsh, 2008; Phillips et al., 2009). These perturbations develop to accommodate the amino-acid composition and specific structural features of the protein surface. For a broad range of systems of interest, however, these features are not static, but vary as the protein carries out its biological activity. Examples include channel proteins and their gating mechanisms, or the conformational cycles resulting in alternating access in active transporters. The protein-lipid interface also changes when membrane proteins form complexes or oligomers. Because most membrane perturbations entail an energetic or entropic cost, it seems reasonable to expect that the bilayer contributes to the thermodynamics and kinetics of these processes, favoring or disfavoring specific structural states. Such interdependence would help explain why changes in lipid bilayer composition, either resulting from natural regulatory mechanisms or induced artificially, can have a determining effect on protein function (Jensen and Mouritsen, 2004; Andersen and Koeppe, 2007; Denning and Beckstein, 2013; Cordero-Morales and Vásquez, 2018; Haselwandter and MacKinnon, 2018).

Here, we seek to gain insights into this interplay for a class of membrane proteins known to undergo a striking structural transformation, namely secondary-active transporters featuring the so-called elevator mechanism. We specifically focus on the Na⁺-aspartate symporter Glt_Ph from Pyrococcus horikoshii, a member and model system of the Excitatory Amino-Acid Transporter (EAAT) family, which includes the human SLC1 neurotransmitter transporters (Gether et al., 2006). Secondary-active transporters like Glt_Ph interconvert between two major conformational states that alternately expose binding sites for ions and substrate to either side of the membrane (Figure 1) (Jardetzky, 1966; Reyes et al., 2009; Boudker and Verdon, 2010; Forrest et al., 2011). In Glt_Ph, this conformational interconversion takes place only when Na⁺ and aspartate occupy the transporter or when the transporter is empty (Yernool et al., 2004; Boudker et al., 2007; Ryan et al., 2009), which defines this protein as a co-transporter. For either occupancy state, the exchange between outward- and inward-facing conformations is spontaneous, that is it does not require an extrinsic electrochemical driving force. However, the relative populations of these conformational states and the net directionality of the transport cycle do depend on the membrane potential and the relative concentrations of ions and substrates on either side of the membrane. This dependence is why downhill translocation of Na⁺ will power uphill transport of aspartate, and vice versa.

Figure 1. — (A) View from the extracellular space, with the three protomers in the outward-facing conformation (PDB 2NWL). The ‘scaffold’ (blue) mediates all protein-protein interactions between protomers. The ‘transport’ domains (orange) carry the bound substrates, moving relative to the scaffold perpendicularly to the membrane. Side-chains that might form hydrogen-bonds with lipid headgroups are highlighted (Tyr, Trp, Arg, Lys). (B) Same as (A), viewed along the membrane plane, with the approximate membrane region shown as a gray box. (C) Same view as (B), with all three protomers in the inward-facing conformation (PDB 3KBC).

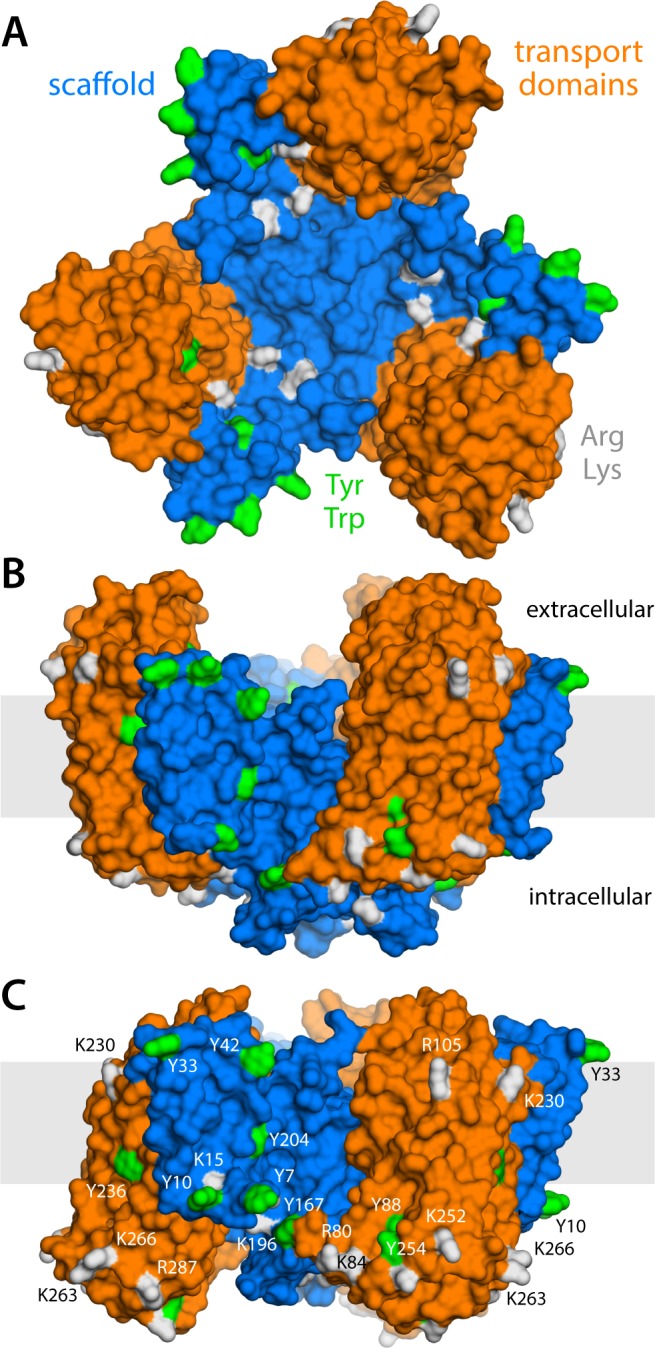
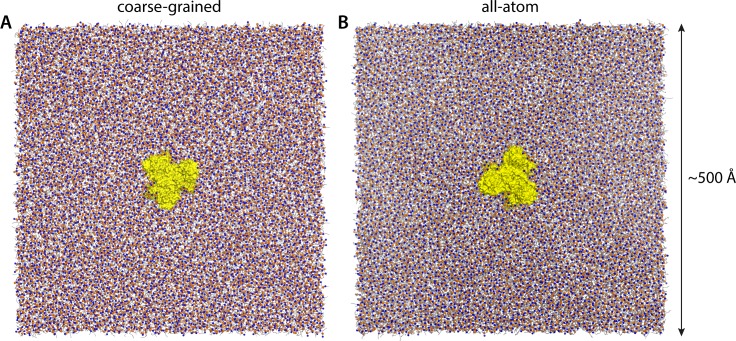
Figure 1—figure supplement 1. — (A) View from the extracellular space, with the three protomers in the outward-facing conformation (PDB 2NWL). The ‘scaffold’ (blue) mediates all protein-protein interactions between protomers. The ‘transport’ domains (orange) carry the bound substrates, moving relative to the scaffold perpendicularly to the membrane. Side-chains that might form hydrogen-bonds with lipid headgroups are highlighted (Tyr, Trp, Arg, Lys). (B) Same as (A), viewed along the membrane plane, with the approximate membrane region shown as a gray box. (C) Same view as (B), with all three protomers in the inward-facing conformation (PDB 3KBC).

Glt_Ph forms a homotrimer (Yernool et al., 2004); yet, each protomer works independently from its neighbors (Akyuz et al., 2013; Erkens et al., 2013; Akyuz et al., 2015; Ruan et al., 2017). The protomers consist of two distinct units: the scaffold domain, which provides a stable trimerization interface (Groeneveld and Slotboom, 2007; Verdon and Boudker, 2012; Georgieva et al., 2013; Hänelt et al., 2013), and the transport domain, which encapsulates the ion and aspartate binding sites (Yernool et al., 2004; Reyes et al., 2009). Both domains are exposed to the lipid bilayer, but structures of Glt_Ph in outward- and inward-facing states clearly reveal that it is the movement of the latter domain that results in alternating access (Yernool et al., 2004; Reyes et al., 2009). Specifically, if one assumes that the scaffold domains remain stationary relative to the membrane mid-plane, each transport domain would move perpendicularly to that plane by approximately 15 Å, that is about one-third of the total bilayer width. How this drastic structural change impacts the relationship between protein and membrane has, to our knowledge, not been previously evaluated. One might envisage that the transport domains simply traverse the membrane (like an elevator), moving polar sidechains on their surface into the bilayer interior and exposing hydrophobic ones to the solvent (Reyes et al., 2009). Alternatively, the morphology of the lipid bilayer could adapt to the conformational state of the protein, and match the amino-acid make-up of the protein surface throughout the transport cycle. Which of these two possibilities entails the least energetic cost is entirely unclear. The absence of functional cooperativity among protomers would appear to rule out the latter, as a pronounced membrane deformation induced by one protomer could impact the conformational dynamics of its two neighbors. On the other hand, the cumulative cost of dehydration of polar and charged sidechains could be exceedingly large. Experimental studies of the Glt_Ph homolog EAAT2 also appear to show that bilayer-facing regions in the outward-facing state are similarly solvent-accessible throughout the transport cycle (Silverstein et al., 2013).

Molecular dynamics simulations in principle provide a means to examine this interplay in great detail (Cui et al., 2013; Marrink et al., 2019). Current computing power makes it feasible to examine the morphology of simple phospholipid membranes around protein structures, for many cases of interest. Highly complex membranes remain beyond reach, however, if represented in atomic detail, as the relaxation time of an arbitrarily-configured multi-component lipid mixture is slower than typically attainable simulation times, thus imposing a starting-condition bias on any analysis. In such cases, so-called coarse-grained simulations are a viable approach despite their reduced level of detail (Corradi et al., 2018). By contrast, simulation methods that permit a direct quantification of the energetic footprint of a membrane morphological change have been lacking. Computational approaches in this area have typically relied on continuum-mechanics theories of membrane elasticity, which necessarily pre-suppose important parameters defining the bilayer energetics (Argudo et al., 2017). Although such approaches can be predictive and insightful in some cases (Mondal et al., 2011; Bethel and Grabe, 2016), it is unclear whether macroscopic models are generally transferable to the length-scales of individual membrane proteins (Lee et al., 2013; Fiorin et al., 2019). To circumvent this problem, we have recently developed a free-energy simulation method (Fiorin et al., 2019) with which the potential-of-mean-force of a membrane deformation can be probed directly from a simulation system, much in the same way processes such as ligand recognition or ion permeation are commonly characterized. Here, in addition to conventional simulations and structural bioinformatic approaches, we apply this new technology to obtain quantitative insights into the nature of the interplay between Glt_Ph and the surrounding membrane. The implications of the major conformational change required for transport are discussed in the light of available experimental observations.

Results

Alternating access causes major membrane deformations, long-ranged but non-cooperative

To examine how the transport cycle of Glt_Ph impacts the surrounding membrane, we carried out molecular dynamics simulations of phospholipid bilayers containing structures of Glt_Ph trimers in four different conformational states. Specifically, we examined states where all three protomers are in either the inward- or outward-facing states (Figure 1), as well as two intermediates where one protomer is inward-facing and the other two are outward-facing, or vice versa. To enable the calculations to reveal long-range perturbations, the simulated membranes are about 50 × 50 nm² in size, that is six-fold wider than the transporter (Figure 1—figure supplement 1). This area translates into ~7500 lipid molecules, much larger than typical simulation systems. In a first set of calculations, therefore, we opted for coarse-grained representation of the molecular system, using the MARTINI forcefield (Marrink et al., 2007; Monticelli et al., 2008). The conformational state of the trimer was preserved throughout each of the simulations, while the lipid bilayer was free to adjust to that state. It is worth noting that the elastic properties of lipid bilayers, as quantified by, for example, their macroscopic bending modulus, are well described by MARTINI, despite its inherent approximations (Marrink et al., 2004; Fiorin et al., 2019).

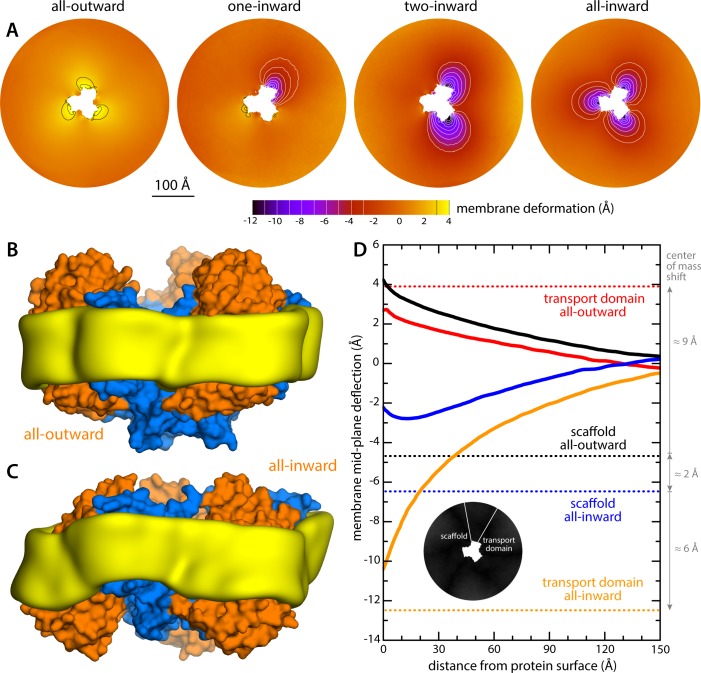
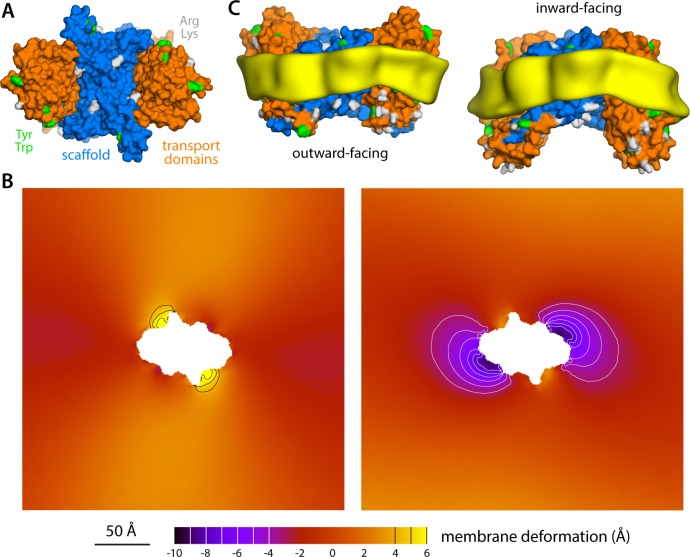
The results of this analysis are summarized in Figure 2. For the state with all three protomers in the outward-facing conformation, we found the membrane to be only modestly perturbed. This perturbation is maximal in the vicinity of the transport domains, where the membrane mid-plane is elevated by 3–4 Å; near the scaffold, however, the elevation is only ~2 Å. By contrast, for the cases in which one, two or all three transport domains are in the inward-facing state, we observe a major morphological impact on the surrounding membrane. Specifically, we observe that the displacement of the transport domain causes a ~ 10 Å depression in the lipid bilayer, that is, about 50% of the width of its hydrophobic core. This perturbation is also remarkably long-ranged, extending radially for nearly 100 Å from the protein surface (Figure 2D). Strikingly, however, along the perimeter of the protein, the perturbation is entirely confined to the interface with the transport domain, that is, it is abruptly terminated near the scaffold, where the membrane is again minimally depressed, by only about 1–2 Å. Indeed, comparison of intermediates with one or two protomers in the inward-facing state shows that each transport domain causes an independent perturbation, largely identical and seemingly additive to that caused by the other protomers, while in the vicinity of the scaffold domains the membrane remains largely unperturbed.

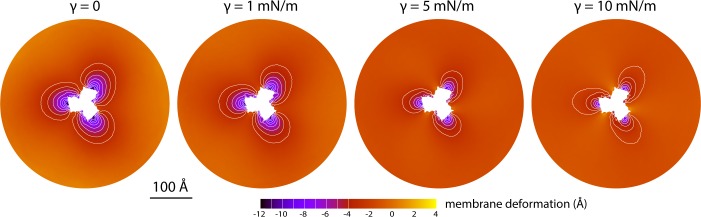
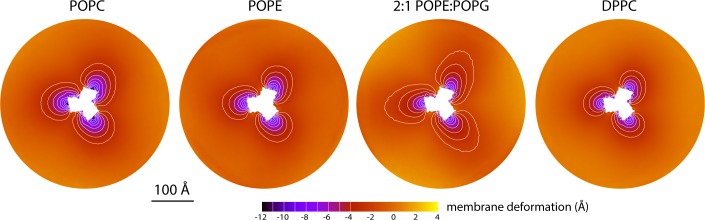
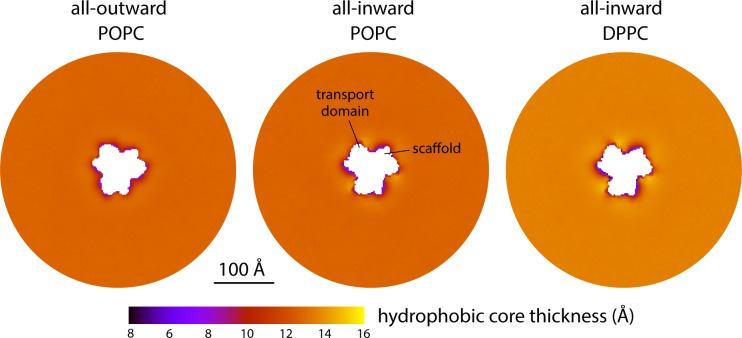
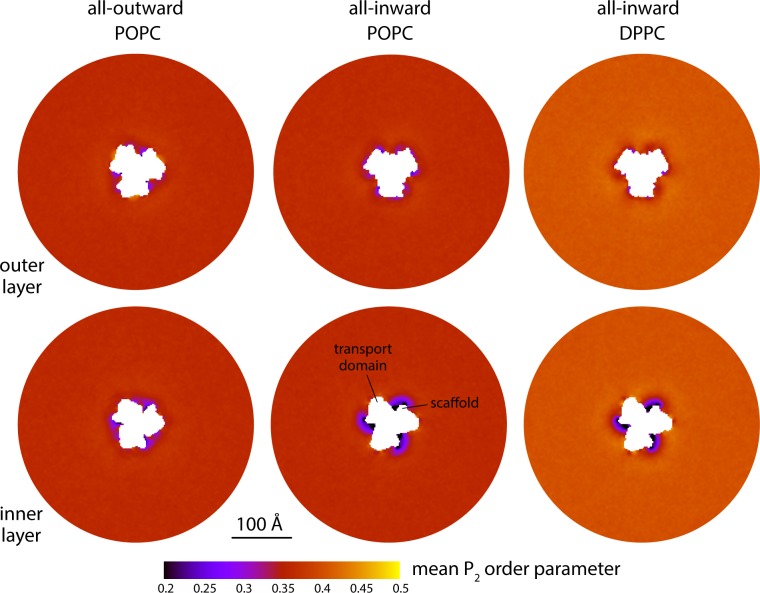
The data presented in Figure 2 were obtained for a POPC membrane under no tension (Materials and methods). Similar results were obtained in simulations with applied membrane tensions as high as 10 mN/m (Figure 3), and in simulations with bilayers of different composition, namely either POPE, a 2:1 mixture of POPE and POPG (both at 298 K), and DPPC (at 323 K) (Figure 4). It should also be noted that the observed deflections in the membrane mid-plane do not result from significant differences in lipid-bilayer thickness (Figure 4—figure supplement 1). Analysis of the second-rank order parameter of the lipid alkyl tails, which is a measure of their tilt relative to the membrane perpendicular, also shows little contrast between the outward- and inward-facing conformational states (Figure 4—figure supplement 2). The only significant difference is observed for the inner leaflet, at the point where the transport domain meets the scaffold, in the inward-facing state. Here, the lipids become significantly tilted, on average, seemingly to adapt to the abrupt changes in membrane curvature induced by the transport domains. This effect is, however, localized and does not propagate beyond the perimeter of the scaffold. We conclude, therefore, that the long-ranged deformations induced by Glt_Ph are most accurately described as bending, rather than other types of perturbation.

Figure 3. — The deflection of the membrane mid-plane was calculated and represented as in Figure 2A. From left to right, the standard error of the data (N = 3) across each map is, on average, 0.6 Å, 0.7 Å, 0.4 Å and 0.3 Å.

Figure 4. — The data for POPC, POPE, and 2:1 POPE:POPG were obtained at 298 K; the data for DPPC were obtained at 323 K. The deflection of the membrane mid-plane was calculated and represented as in Figure 2A. From left to right, the standard error of the data (N = 3) across each map is, on average, 0.6 Å, 0.6 Å, 0.4 Å and 1.0 Å.

Figure 4—figure supplement 1. — The data for POPC, POPE, and 2:1 POPE:POPG were obtained at 298 K; the data for DPPC were obtained at 323 K. The deflection of the membrane mid-plane was calculated and represented as in Figure 2A. From left to right, the standard error of the data (N = 3) across each map is, on average, 0.6 Å, 0.6 Å, 0.4 Å and 1.0 Å.

Finally, it is interesting to note that our simulations show that the trimerization domain is not completely static relative to the membrane throughout the alternating-access cycle; as indicated in Figure 2D, we observe that the scaffold shifts by about 2 Å when the all-outward and all-inward states are compared. Consequently, the vertical displacement of the transport domains relative to the membrane is slightly larger than the ~15 Å that would be deduced from an overlay of the structures.

Transport domains bend the membrane, while scaffold domains anchor it

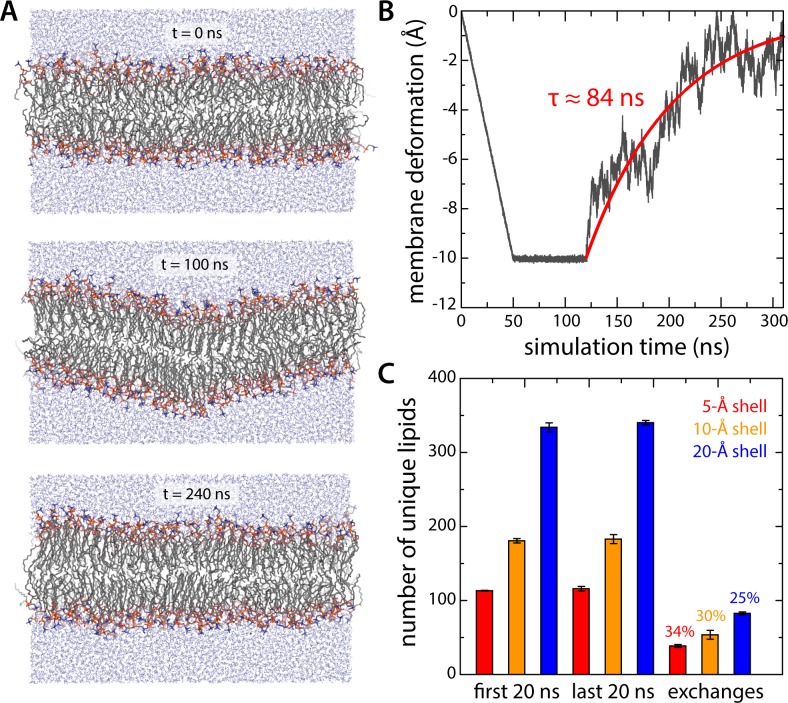
Although the coarse-grained MARTINI forcefield yields a reasonably accurate description of membrane elasticity (Marrink et al., 2004; Fiorin et al., 2019), the degree to which it also captures the specificity of bi-molecular interactions has been questioned (Javanainen et al., 2017). We thus considered the possibility that the nature of the membrane deformations observed for the inward-facing conformation of Glt_Ph results from the lack of sufficient detail in the representation of protein and lipid structures and their interactions. To address this concern, we carried out three independent simulations of the all-inward state, using the all-atom CHARMM forcefield (see Materials and methods). Each trajectory was initialized with a different starting condition, derived from the previous coarse-grained simulations. The simulation systems are therefore identical in size to those described above. Of course, the computational cost is much greater, as the simulation system now amounts to ~3,000,000 atoms (Figure 1—figure supplement 1B).

Reassuringly, the results obtained with the all-atom representation recapitulate those obtained with the coarse-grained forcefield (Figure 5). Even after a suitable relaxation time following the change in forcefield (Figure 5—figure supplement 1AB), and despite a significant number of exchanges between lipids in the bulk and near the protein surface (Figure 5—figure supplement 1C), the deformations induced by the transport domains were sustained in both magnitude and range; the abrupt restoration of membrane shape at the scaffold-domain interface also continued to be observed.

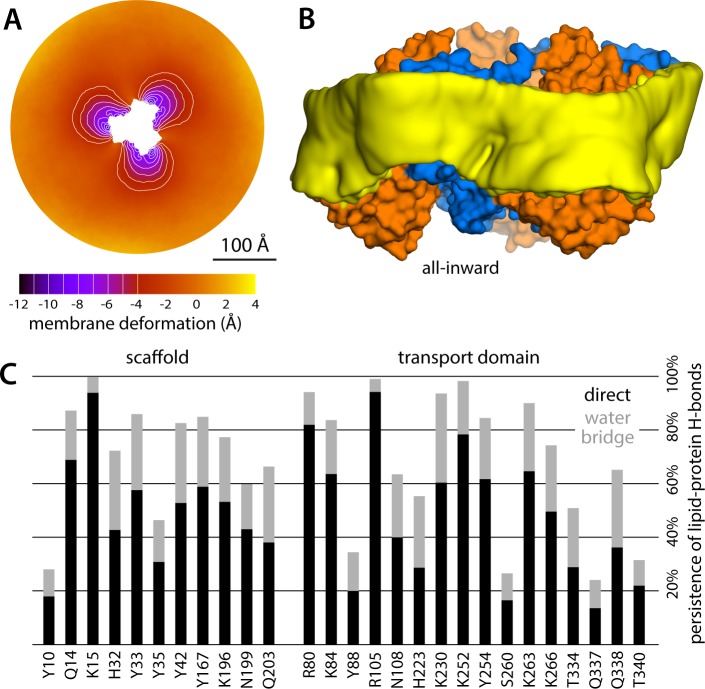
Figure 5—figure supplement 1. — (A) Deflection of the membrane mid-plane relative to a flat surface, calculated exactly as in Figure 2A. The standard error of the data (N = 3 trajectories, 150 ns each) across the deflection map is, on average, 1.5 Å. (B) Structure of all-inward Glt_Ph (as in Figure 1), alongside a calculated density map for the lipid bilayer alkyl chains within 10 Å from the protein surface (yellow), based on all simulation data gathered for this state. See also Figure 5—video 1. (C) Hydrogen-bonding lipid-protein interactions observed during the all-atom simulations of all-inward Glt_Ph. Direct donor-acceptor interactions are considered, as are interactions mediated by a water molecule. For each protein side chain, the plot quantifies the fraction of the simulation time during which an interaction with a lipid was observed. Figure 1C indicates the location of most of the side chains observed to have persistent lipid interactions.

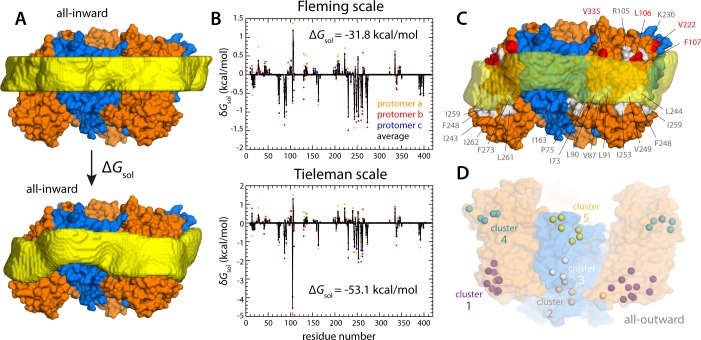
What might explain these striking effects? The complementary analyses described in Figure 5C and Figure 6 indicate that the membrane adapts to the conformational state of the protein to preclude strongly hydrophilic side chains from penetrating the core of the bilayer, while also avoiding exposure of hydrophobic portions of the protein surface to solvent. The deformed state of the bilayer also appears to be stabilized by numerous hydrogen-bonding interactions between polar and aromatic residues and lipid headgroups. For example, it is apparent that Arg105 and Lys230, which face the extracellular solution in the outward-facing state (Figure 1), would be fully dehydrated in the inward-facing conformation were it not for the fact that the membrane bends inwards (Figure 6C). Instead, these residues form highly persistent interactions with the phosphate and ester groups in the lipid bilayer (Figure 5C). Conversely, a large number of hydrophobic residues on the intracellular side of the transport domain would be exposed to solvent if the membrane was unchanged (Figure 6C). As illustrated in Figure 6B (and Figure 6—figure supplement 1B) individual per-residue preferences accumulated across the protein surface add up to very large energetic gains (which, as will be discussed later, are balanced by the resistance of the membrane to be deformed). Notably, this pattern of H-bonding interactions extends to the scaffold, where they appear to help anchor the bilayer in between adjacent transport domains, on both sides of the membrane (Figure 5C). Interestingly, clear co-evolutionary relationships can be detected across Glt_Ph homologs for several clusters of membrane-exposed residues that include those engaged in hydrogen-bonding with lipids in our simulations (Figure 6D). In summary, the changes in membrane morphology induced by the conformational cycle of Glt_Ph thus appear to be dictated by the displacement of protein interfaces that have evolved to be closely matched with the chemical features of the membrane and the surrounding solvent.

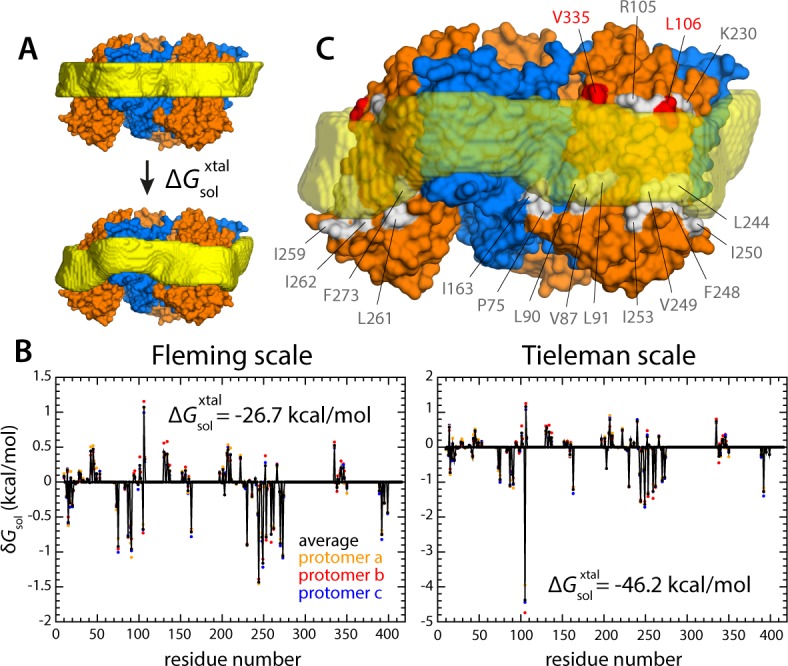
(A) Molecular systems used to evaluate the change in the free energy of polar/hydrophobic solvation that results from membrane bending, for all-inward Glt_Ph. The solvent-accessible surface area of each residue in the protein was calculated for either case (Materials and methods). (B) Per-residue change in the free-energy of polar/hydrophobic solvation, deduced from two alternative hydrophobicity scales (Materials and methods). Negative values of δG_sol indicate the deformed membrane state is favored; positive values favor the flat configuration instead. All residue contributions, in the three protomers, were summed to obtain the total value of ΔG_sol. (C) Residues for which the magnitude of δG_sol is 1 k_BT or greater (with both scales) are highlighted in the context of the proposed membrane deformation for all-inward Glt_Ph. Residues that favor the deformed state are shown in gray; those that favor the flat state are shown in red. The protein structure examined in panels (A, B) is an equilibrated snapshot of the all-atom simulation of all-inward Glt_Ph. An analogous analysis of the X-ray structure of all-inward Glt_Ph is shown in Figure 6—figure supplement 1. (D) Residues involved in H-bonds to lipid head groups (Figure 5C) that are also predicted to have co-evolved with neighboring residues at the protein-lipid interface (Materials and methods). The position of these residues in the outward-facing X-ray structure of Glt_Ph is indicated by their Cα atoms (spheres). On the cytoplasmic side of the protein, there are three main clusters: one on the transport domain (cluster 1, purple) comprising residues E80, K84 and Y88 (TM3), L250, Y254 (TM6), I411, V412, K414, T415, and E416 (TM8); and two mostly on the scaffold: one including A67 (TM3), A164, Y167 (TM4), K196, and G200 (TM5) (cluster 2, gray), and the other including K15 (TM1), Q203 and I207 (TM5) (cluster 3, white). On the periplasmic side, there are two clusters: one on the transport domain (cluster 4, cyan), comprising R105, N108 (TM3), F323 (TM7), V335, and Q338 (HP2a); and one on the scaffold (cluster 5, yellow) containing L30, H32, Y33 (TM1), T41, Y42, and V43 (TM2).

The inward-facing state incurs a major energetic penalty due to membrane bending

The data presented in Figures 2–5 shows each Glt_Ph protomer causes a membrane deflection of about 10 Å in an area of about 1,000 Å², that is, a very pronounced change in membrane curvature. This observation begs the question: what is the energetic cost of such a deformation? To answer this question precisely is very challenging. As we discuss in detail elsewhere (Fiorin et al., 2019), most computational strategies to examine the energetics of membrane bending are based upon the Helfrich-Canham theory, which predicts a relationship between curvature and energy dictated by the bending modulus of the bilayer (Canham, 1970; Helfrich, 1973). Although this theory is appropriate for mesoscopic perturbations, it can be inadequate on its own in the length scales that are relevant to membrane protein mechanistic studies (Goetz et al., 1999; Brannigan and Brown, 2006). Hence, a number of variations and extensions of the Helfrich-Canham function have been proposed to account for other possible contributions to the membrane energetics, based on more complex functions of the local bilayer curvature (Brannigan and Brown, 2006; Watson et al., 2012; Khelashvili et al., 2013). An alternative route to evaluate membrane perturbations would be to calculate the associated free-energy cost directly from a molecular dynamics simulation, using enhanced-sampling techniques. This type of model-free, microscopic approach has become state-of-the-art in computational studies of other molecular-scale processes such as ion permeation, ligand binding, or protein conformational change (Perez et al., 2016; Harpole and Delemotte, 2018; Flood et al., 2019), superseding other types of models and theories. The reason why microscopic enhanced-sampling approaches have lagged behind for membranes is the difficulty in formulating appropriate descriptors of the membrane shape and configuration – that is the so-called ‘collective variable’ problem.

In a recent development, we have reported a novel free-energy simulation strategy to address this problem, which we refer to as Multi-Map (Fiorin et al., 2019). The central element of this method is a collective variable that quantifies the similarity between the instantaneous configuration of the lipid membrane and a set of pre-defined density distributions mapped onto a 3D grid. Biased exploration of this Multi-Map variable, for example using umbrella-sampling simulations, not only transforms the bilayer shape as dictated by the set of target density distributions, but also permits derivation of the corresponding potential-of-mean-force. What, then, is the free-energy cost of the membrane deformations induced by inward-facing Glt_Ph?

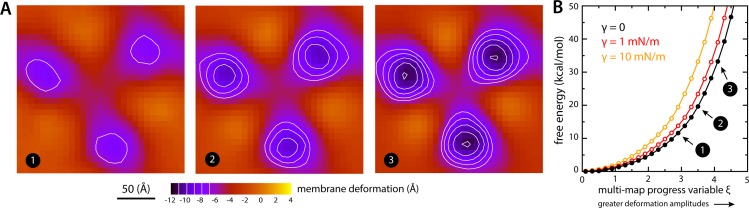
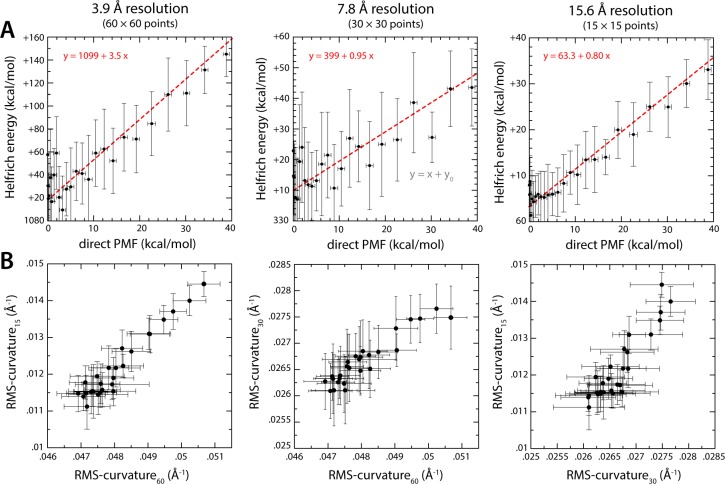
To evaluate this cost, we devised a Multi-Map calculation whereby a lipid membrane is driven to deform in a manner that mimics the perturbation caused by Glt_Ph, but in the absence of the protein. In Figure 7A, we show 2D representations of three membrane configurations sampled by this enhanced-simulation methodology. The simulations also sample configurations for which the amplitude of the membrane perturbations is greater and smaller than those shown in Figure 7A, that is larger and smaller values of the Multi-Map variable. The corresponding potential-of-mean-force curve, that is, the free-energy change as a function of the deformation amplitude, is shown in Figure 7B. From comparison of this data with the results shown in Figure 2A, it can be inferred that the cost of the membrane perturbation induced by all-inward Glt_Ph is on the order of 20 kcal/mol in total, or 6–7 kcal/mol per protomer. (This value was obtained in the absence of membrane tension; under membrane tension, the cost would be greater, as shown in Figure 7B, but the extent of the deformation is smaller, as shown in Figure 3.) Clearly, this energetic penalty is sizable; as noted above, however, energetic gains that result from polar and hydrophobic solvation of the protein surface when the membrane is deformed are comparable in magnitude, if not greater (Figure 6). At any rate, this analysis shows that the morphological preference of the membrane is a major contributor to the free-energy landscape of this transporter; it specifically and strongly opposes the inward-facing state, and so must be counterbalanced by other free-energy contributions for the transporter to carry out its structural mechanism. (For completeness, a comparative analysis with results obtained using the Helfrich-Canham macroscopic theory is presented and discussed in Figure 7—figure supplement 1.)

Figure 7. — (A) Simulated membrane deformation, in the absence of the protein, induced by application of the Multi-Map method in combination with umbrella sampling, for a coarse-grained POPC lipid bilayer at 298 K. The figure shows three deflection maps analogous to those shown in Figure 2A, that is calculated from trajectory data by averaging the Z coordinate of the bilayer mid-plane across the range of X and Y encompassed by the simulation box. The deflection maps shown correspond to three individual umbrella-sampling windows used in this free-energy calculation, differing in the amplitude of the perturbation that is induced in each case. Other trajectories/windows sample deformation amplitudes that are smaller or larger than those represented in the figure, that is, smaller or larger values of the Multi-Map variable. Each map reflects an average of 18 independent simulations of 1 μs each. (B) Potential-of-mean-force (PMF) curve for the morphological perturbation depicted in panel (A), as a function of the Multi-Map variable, that is, as a function of an increasing deformation amplitude. The free-energy values for the three configurations represented in panel (A) are indicated. PMF curves are also shown for two additional calculations based on umbrella-sampling simulations under an applied membrane tension, for the values indicated. Each of these PMF curves is an average of 18 independent calculations, each sampling 1 μs per window. Error bars for each curve average to about 0.6 kcal/mol.

Figure 7—figure supplement 1. — (A) Simulated membrane deformation, in the absence of the protein, induced by application of the Multi-Map method in combination with umbrella sampling, for a coarse-grained POPC lipid bilayer at 298 K. The figure shows three deflection maps analogous to those shown in Figure 2A, that is calculated from trajectory data by averaging the Z coordinate of the bilayer mid-plane across the range of X and Y encompassed by the simulation box. The deflection maps shown correspond to three individual umbrella-sampling windows used in this free-energy calculation, differing in the amplitude of the perturbation that is induced in each case. Other trajectories/windows sample deformation amplitudes that are smaller or larger than those represented in the figure, that is, smaller or larger values of the Multi-Map variable. Each map reflects an average of 18 independent simulations of 1 μs each. (B) Potential-of-mean-force (PMF) curve for the morphological perturbation depicted in panel (A), as a function of the Multi-Map variable, that is, as a function of an increasing deformation amplitude. The free-energy values for the three configurations represented in panel (A) are indicated. PMF curves are also shown for two additional calculations based on umbrella-sampling simulations under an applied membrane tension, for the values indicated. Each of these PMF curves is an average of 18 independent calculations, each sampling 1 μs per window. Error bars for each curve average to about 0.6 kcal/mol.

Discussion

Our simulations predict that the conformational cycle of Glt_Ph induces a long-ranged remodeling of the surrounding lipid membrane, as a result of the elevator-like motion of the transport domains, each of which displaces its protein-lipid interface by about one-half the width of the bilayer hydrophobic core. Strikingly, this perturbation is abruptly suppressed at the point where the bilayer meets the trimerization domain; therefore, each protomer induces an independent deformation, consistent with existing experimental evidence demonstrating no protomer-protomer cooperativity in this class of transporters (Grewer et al., 2005; Koch and Larsson, 2005; Koch et al., 2007; Leary et al., 2007; Akyuz et al., 2013; Erkens et al., 2013; Akyuz et al., 2015; Ruan et al., 2017). These results provide a working hypothesis and as such require experimental verification; while direct structural data confirming the drastic effects that we predict here are still lacking, such information is not beyond reach. As demonstrated by recent structural studies of Ca²⁺-dependent lipid scramblases, single-particle cryo-EM can reveal the morphological features of detergent micelles and lipid nanodiscs in considerable detail (Falzone et al., 2018; Falzone et al., 2019; Kalienkova et al., 2019); crystallographic studies can also reveal the contours of the lipid bilayer, as observed for stacked membrane crystals of the SERCA Ca²⁺-ATPase pump (Sonntag et al., 2011). Analogous data for alternate conformational states of Glt_Ph, or a close homolog thereof, ought to validate or refute the predicted impact of this transporter on the membrane morphology.

Single-molecule FRET measurements of substrate-loaded and substrate-free Glt_Ph in outside-out proteoliposomes have indicated that the intrinsic free-energy difference between the outward- and inward-facing states of the transporter is approximately zero, that is, both states are approximately equally populated (Akyuz et al., 2013; Erkens et al., 2013; Akyuz et al., 2015). Here, we have shown that the membrane deflection induced by inward-facing Glt_Ph translates into a substantial energetic penalty, which we estimate to be in the order of 6–7 kcal/mol per protomer, or about 20 kcal/mol in total. To balance out this cost, therefore, the inward-facing conformation must somehow recoup this energy, through distinct protein-protein, protein-lipid and/or protein-water interactions. Admittedly, at this point we can only infer the magnitude of free-energy penalty from simulations where the Multi-Map method mimics the impact of the protein on the membrane. While imperfect, it is worth underscoring the technical breakthrough made by this approach: it provides a means to estimate the membrane energetics directly from simulated molecular-dynamics trajectories, without a priori theoretical assumptions. Thus, we believe that further methodological developments and systematic applications of this methodology, in combination with other enhanced-sampling techniques, will result in increasingly precise estimates, and will also enable us to dissect the compensating interactions that must occur in this and other membrane-protein systems. These caveats notwithstanding, we believe our estimate of the free-energy penalty of membrane bending not to be at all unrealistic. For example, based on electrophysiological studies of the gating mechanism of the Shaker voltage-gated K⁺ channel, it has been deduced that at zero membrane potential the conformational free-energy of the open state is about 15 kcal/mol lower than that of the closed state (Chowdhury and Chanda, 2012). Similarly, a value of 16 kcal/mol was deduced for the Na⁺-channel Na_v1.4 (Chowdhury and Chanda, 2012). Regardless of the specifics, this study underscores that the configurational energetics of the lipid bilayer are non-negligible and must therefore be incorporated into the conceptual models and theories used to describe membrane-protein mechanisms – much in the same way one would consider, for example, the dehydration energetics of different ions (also in the order of tens of kcal/mol) when rationalizing the selectivity or conductance rates of a channel protein. It is hoped, therefore, that the calculations presented here will spur further biophysical studies designed to assess the impact of bilayer composition and morphology on the energetics of transporters – in analogy with research other membrane proteins such as receptors (Brown and Chawla, 2017) and channels (Phillips et al., 2009; Andersen, 2013). For example, it would be of interest to dissect how the functional dynamics of a transporter such as Glt_Ph are influenced by the amino-acid make-up of the protein-lipid interface, as well as by lipid bilayer composition. Indeed, functional studies have shown that subtle lipid modifications (methylation) and single-point mutations (Tyr33) have detectable effects on the rates of Glt_Ph transport (McIlwain et al., 2015). It is also intriguing that long-chain polyunsaturated fatty acids (PUFA) modulate the activity of neuronal EAAT transporters (Zerangue et al., 1995; Fairman et al., 1998; Tzingounis et al., 1998; Grintal et al., 2009) and are also known to influence the bending energetics of lipid bilayers (Cordero-Morales and Vásquez, 2018).

The aforementioned smFRET studies have also indicated that the balance of outward- and inward-facing states hardly differs when measured in liposomes (containing mostly PE, PG and PC lipids) or in DDM micelles (Akyuz et al., 2015). Taken together with our findings, this observation challenges the notion that detergent micelles have no distinct morphological preference and will comply to the conformation of a protein at little or no energetic cost. To the contrary, when a detergent solution is concentrated above a certain threshold, the micelles that form have an inherently preferred geometry and size (Lipfert et al., 2007; Oliver et al., 2013), that is, there exists a well-defined free-energy minimum of micelle formation. When a micelle assembles around a protein, one might expect that free-energy minimum to naturally shift, that is, the micelle morphology will adapt to the volume and surface of the protein. However, this adaption is not necessarily identical for all conformations of a protein; indeed, one might expect that different free-energy minima will exist for alternative structural states (both in magnitude and morphology), and that this difference in will be greater for some detergents than for others. The expectation that the deformation of a micelle entails little or no energetic cost is even less intuitive if one assumes that the micelle does not reassemble when a protein changes structure. Indeed, the above-mentioned cryo-EM data for nhTMEM16 shows that a highly localized feature of the protein surface causes nearly identical morphological changes in a lipid nanodisc and in a DDM micelle, namely a perturbation that gradually decays along the protein perimeter (Kalienkova et al., 2019). If the DDM micelle was indeed much softer or more compliant than the lipid nanodisc, the resulting curvature would be more localized. Thus, on this matter too we believe our data highlights the need for further work probing how the thermodynamics of micellar or lipid solvation might depend on the conformational state of a protein, or on its oligomerization state.

The dynamics of Glt_Ph at the single-molecule level have also been evaluated using high-speed AFM measurements in protein-dense 2D preparations (Ruan et al., 2017). These elegant measurements clearly confirmed that each protomer exchanges between outward- and inward-facing states stochastically (provided the adequate occupancy state) and independently from each other. Intriguingly, though, in these measurements the population ratio between outward- and inward-facing is shifted significantly against the latter, by about 5-fold (Ruan et al., 2017; Heath and Scheuring, 2019). A possible explanation for the discrepancy between the smFRET and AFM measurements is that the curvature of the outside-out proteoliposomes used in the former experiment favors the inward-facing state, while the flat membranes in the latter do not. However, our finding that the membrane perturbation caused by Glt_Ph projects away from the protein surface for several nanometers provides an alternative explanation: transition to the inward-facing state would be more energetically costly when this deformation must occur in a more confined space. In other words, it is conceivable that the aforementioned balance between large, competing energetic contributions is altered as a result of molecular crowding, in this case favoring the outward-facing conformation. Interestingly, some members of the EAAT family are expressed in the membranes of certain cell types at very high densities (in the order of thousands of transporters per square-micron [Danbolt, 2001]), raising the possibility that crowding effects occur in physiological settings. On a related, more technical note, it is worth noting that molecular simulation studies aiming to evaluate the alternating-access mechanism and protein-lipid interplay for cases such as Glt_Ph might be significantly skewed by finite-size effects if the lipid bilayer patch is not sufficiently large to accommodate the full range of the membrane perturbation created by the protein.

Large-scale structural changes are not exclusive to membrane proteins in the EAAT superfamily. Elevator-like secondary-active transporters are, however, appealing model systems to evaluate the interplay between proteins and the lipid bilayer, given the range of their motions and that these motions occur spontaneously and, in some cases, on time-scales amenable to single-molecule measurements like smFRET or high-speed AFM. As an example of another elevator-like mechanism, an initial analysis of the bacterial sodium-dicarboxylate symporter VcINDY is shown in Figure 8. VcINDY is a dimer, but is similar to Glt_Ph in that each of the constituent protomers features two distinct domains, one facilitating dimerization and the other responsible for substrate translocation (Mancusso et al., 2012; Mulligan et al., 2016). Our simulations show that upon transition from the (predicted) outward-facing state to the (experimentally determined) inward-facing conformation, the transport domains would induce a deformation in the membrane that is comparable to that observed for Glt_Ph. Again, this deformation is suppressed by the scaffold, suggesting that the protomers function independently. Despite the commonalities between Glt_Ph and VcINDY, however, it is important to note that other elevator-like transporters, perhaps even those in the same structural family, might influence the membrane differently, as this interplay is ultimately determined by the amino-acid make-up of the protein surface. For example, it is entirely possible that, in some cases, the outward-facing state perturbs the membrane the most. To document and dissect this variability is no doubt of interest and will be the focus of future studies.

Figure 8. — (A) Structure of the VcINDY dimer in the outward-facing state, viewed along the membrane perpendicular from the extracellular space. The protein is represented as Glt_Ph in Figure 1. (B) Deflection of the membrane mid-plane induced by VcINDY in the outward- and inward-facing states (left and right, respectively) based on three independent simulations for either state. The view is from the extracellular space. From left to right, the standard error of the data (N = 3) across each map is, on average, 1.0 Å and 0.8 Å. (C) Structures of outward- and inward-facing VcINDY (represented as in panel A), alongside calculated density maps for lipid alkyl chains within 10 Å from the protein surface (yellow), based on all the simulation data obtained for either state. Note the outward-facing state is a model, constructed on the basis of the experimental inward-facing structure through repeat-swapping (Mulligan et al., 2016).

Glt_Ph and VcINDY are stark examples of membrane proteins that cause large-scale morphological changes in the bilayer. Needless to say, numerous channels and transporters also undergo major conformational changes during function, which might impact the membrane to varying degrees. The computational analysis presented here makes it clear that the inherent configurational energetics of the lipid bilayer can be both non-negligible and markedly state-dependent, and must therefore be integrated in our conceptualizations of membrane protein mechanisms.

Materials and methods

Coarse-grained simulations of Glt_Ph trimers and VcINDY dimers

Four different conformational states of the Glt_Ph transporter were simulated using a coarse-grained (CG) representation of the protein and its environment, using the MARTINI 2.1 forcefield (Marrink et al., 2007). Symmetric trimers of outward- and inward-facing conformers were obtained from X-ray crystal structures (PDB 2NWL and 3KBC, respectively Boudker et al., 2007; Reyes et al., 2009). These differ primarily in the position of the transport domains (defined here as residues 74–129 and 223–416), relative to the central oligomerization domain, or scaffold (residues 6–73 and 120–222). Two asymmetric trimers were also considered, combining two outward- and one inward-facing protomer, or two inward- and one outward-facing protomer. These intermediates were constructed by superposing the scaffold domain of individual protomers from the inward-facing structure onto the trimer with all protomers outward-facing. All four states of the transporter were embedded in a hydrated bilayer of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) lipids, to evaluate the morphological adaption of the membrane to the protein conformation. The conformation of each state was maintained throughout the simulations by applying a network of harmonic distance restraints to a pre-defined set of pairs of non-bonded protein atoms. This set comprises all pairs of backbone atoms separated by a distance between 5 and 9 Å; the force constant of these elastic restraints is 1.2 kcal/mol Å⁻². The protein-membrane systems include ~7500 lipids and ~170,000 solvent molecules, for a total of ~260,000 particles. The dimensions of the simulation systems are approximately 500 × 500 × 120 Å. Counter-ions were added to the solvent to neutralize the total charge of all molecular systems.

All CG simulations were carried out using GROMACS 4.5.5 (Hess et al., 2008), with a 10-fs integration time-step. Temperature and pressure were maintained constant using the Berendsen barostat and thermostat (Berendsen et al., 1984). The pressure (one atm) was applied semi-isotropically, that is X and Y dimensions (the bilayer plane) fluctuate but at constant X/Y ratio, while fluctuations in Z are independent. Unless specified otherwise, the pressure components P_xx, P_yy and P_zz were such that the resulting membrane tension is zero. Periodic boundary conditions were used. Non-bonded interactions were described by a shifted Lennard-Jones potential, cut-off at 12 Å, and by a Coulombic potential with relative dielectric constant ε_r = 15.

For each Glt_Ph state, we calculated three independent trajectories of 600 ns. Analogous, triplicated simulations of 600 ns were also carried out for all-inward Glt_Ph in a bilayer of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) lipids at 323 K; in a mixed bilayer of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE) lipids and 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1'-rac-glycerol) (POPG) lipids in a 2:1 ratio, at 298K; and in a bilayer of POPE lipids, also at 298 K. Triplicated simulations of 600 ns were also carried out for all-inward Glt_Ph in POPC at 298 K under applied membrane tensions of 1, 5 and 10 mN/m. Finally, triplicated simulations of 600 ns each were carried out for the Na⁺-dicarboxylate transporter VcINDY, in POPC at 298 K, in both outward- and inward-facing conformations; the latter corresponds to the experimentally determined X-ray structure (PDB 5ULD, Nie et al., 2017 ) while the former is a computational model (Mulligan et al., 2016).

All-atom simulations in all-inward Glt_Ph

For the all-inward state (with all three Glt_Ph protomers inward-facing) we also calculated three independent trajectories of 150 ns each, using an all-atom representation of the molecular system. The starting coordinates for each of these simulations were obtained from selected snapshots of the three independent CG simulations carried out for the all-inward state in DPPC. Specifically, we chose those snapshots in which the instantaneous shape of the membrane mid-plane showed the lowest RMS deviation from the shape calculated by averaging all trajectory data for this all-inward state. Using an all-atom model of the protein derived from the crystal structure (PDB 3KBC), the surrounding (coarse-grained) membrane and solvent were transformed into an all-atom representation as prescribed elsewhere (Wassenaar et al., 2014), and equilibrated through a series of simulations implementing positional restraints. The final models comprise ~3,000,000 atoms. The all-atom simulations were carried out using NAMD version 2.9 (Phillips et al., 2005). The CHARMM36 force field (Klauda et al., 2010; Best et al., 2012) was used for the protein and the lipids, while the TIP3P model was adopted for the water (Jorgensen et al., 1983). To preserve the conformation of the protein, a restraint was applied to the RMSD of the C_α trace, relative to the experimental structure, of force constant 100 kcal/mol Å⁻². The simulations were carried out at constant temperature (323 K), using a Langevin thermostat, and constant semi-isotropic pressure (one atm), using the Nosé-Hoover-Langevin barostat, with periodic boundaries. The integration time-step was 2 fs. Electrostatic interactions were calculated using Particle-Mesh Ewald with a real space cut-off of 12 Å. The same cut-off was also used for the shifted Lennard-Jones potential describing van der Waals interactions.

Energetics of polar/hydrophobic solvation

The molecular systems depicted in Figure 6A show two membrane states: one deformed, and identical to that observed in our simulations (Figure 5A), and a hypothetical version thereof with the same thickness (16 Å) but flat; both membranes are aligned at the scaffold. (In this context, ‘membrane’ refers to the solvent-excluded region of the bilayer). For each of these two systems, we calculated the solvent-accessible surface area (SASA) for each of the protein residues i, denoted by A_bent(i) and A_flat(i), using PyMol (Schrödinger, Inc) and a probe radius of 1.4 Å. A SASA value denoted as A_max(i) was also calculated for each amino-acid type when fully solvent-exposed in a GXG tri-peptide. The per-residue change in the free-energy of polar/hydrophobic solvation (Figure 6B) was then calculated as δG_sol(i) = S_transfer(i) × [ A_flat(i) – A_bent(i) ] / A_max(i), where S_transfer(i) are identical for residues of the same type, and derive from two independent hydrophobicity scales: one based on experimental measurements of the stability of wild-type and mutagenized OMPLA, referred to as the Fleming scale (Moon and Fleming, 2011); and another based on PMF calculations of side-chain analog insertion in a DOPC bilayer, referred to as the Tieleman scale (MacCallum et al., 2007). For His, Gly and Pro, which lack values in the latter scale, values from the Fleming scale were used in both calculations.

Coevolutionary analysis

The Uniprot sequence GLT_PYRHO was used as input to the EVcouplings server (Marks et al., 2011) with default parameters. The results can be considered to be robust because the ratio of effective sequences in the alignment (9565 sequences obtained using a bit-score threshold of 0.3) to the length of the protein sequence is >20. To limit our search to reliable scores, we focused on pairs whose scores have coupling probabilities greater than 0.5, which comprises the top 0.8% of all possible pairs. To identify positions that co-evolved in order to maintain interactions with the lipid head groups, we focused on pairs involving at least one residue known to H-bond with lipids in the all-atom simulations of Glt_Ph (Figure 5C). Pairs were excluded if they contained buried residues, or residues exposed only to the central aqueous vestibule, or were less than eight residues apart in sequence, that is within two turns of a helix. The remaining pairs were assigned to a cluster if at least one residue was involved in more than one pair in that cluster.

Potential-of-mean-force (PMF) calculations

The recently developed Multi-Map method (Fiorin et al., 2019) was used to compute the free-energy cost of a membrane deformation that is similar to that induced by all-inward Glt_Ph, but in the absence of the protein. To this end, a set of 10 three-dimensional density maps that idealize this deformation but vary in its amplitude were generated and used to define the so-called Multi-Map coordinate ξ. This variable quantifies the similarity between any instantaneous configuration of the membrane and each of the density maps in the target set. Biased-sampling of the Multi-Map coordinate ξ thus perturbs the membrane as dictated by the set of target maps and permits a derivation of the corresponding free-energy cost as a function of the deformation amplitude, that is, the potential of mean force (Fiorin et al., 2019). This technique was applied to a CG bilayer of 1,800 POPC molecules (side length of approx. 230 Å), using a developmental version of NAMD (Phillips et al., 2005) and analogous pressure and temperature conditions as those specified above. Umbrella-sampling was employed as the biasing method; the target range in ξ was divided into 61 windows, and 18 simulations of 1 μs each were carried out to sample ξ in each window. The PMF was calculated on the basis of the resulting time-series of ξ, using the WHAM method (Kumar et al., 1992). To examine the effect of membrane tension, analogous umbrella-sampling simulations and PMF curves were calculated under applied tensions of 1 and 10 mN/m.

Acknowledgements

The authors are grateful to numerous colleagues and lab members for their commentary on different aspects of this work – too numerous to be listed here. Special thanks are owed to Janice L Robertson for useful discussions, and to Michael Grabe and co-workers for helping us to apply their continuum-mechanics method to examine the membrane deformations caused by elevator-like transporters. This research was initially supported by the Max Planck Society and The German Research Foundation, and subsequently by the Divisions of Intramural Research of the National Institute of Neurological Disorders and Stroke and of the National Heart, Lung and Blood Institute, National Institutes of Health (NIH). In part, this work utilized the computational resources of the NIH HPC facility Biowulf.

Funding Statement

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Contributor Information

Lucy R Forrest, Email: lucy.forrest@nih.gov.

José D Faraldo-Gómez, Email: jose.faraldo@nih.gov.

Nir Ben-Tal, Tel Aviv University, Israel.

Richard W Aldrich, The University of Texas at Austin, United States.

Funding Information

This paper was supported by the following grants:

National Heart, Lung, and Blood Institute to Wenchang Zhou, Giacomo Fiorin, Claudio Anselmi, José D Faraldo-Gómez.
National Institute of Neurological Disorders and Stroke to Hossein Ali Karimi-Varzaneh, Horacio Poblete, Lucy R Forrest.

Additional information

Competing interests

Senior editor, eLife.

Reviewing editor, eLife.

No competing interests declared.

Author contributions

Formal analysis, Investigation, Visualization.

Conceptualization, Supervision, Investigation, Visualization.

Additional files

Transparent reporting form

elife-50576-transrepform.pdf^{(122.4KB, pdf)}

Data availability

Input and output files for 1 (out of 3) replica of each simulation system/condition in our study have been uploaded to Zenodo, a public repository free of charge, and is available at the DOI: https://doi.org/10.5281/zenodo.3558957.

The following dataset was generated:

Zhou Wenchang, Fiorin Giacomo, Anselmi Claudio, Karimi-Varzaneh Hossein Ali, Poblete Horacio, Forrest Lucy Rachel, Faraldo-Gómez José Diego. 2019. Simulation files for "Large-scale state-dependent membrane remodeling by a transporter protein". Zenodo.

The following previously published datasets were used:

Gouaux E, Boudker O, Ryan R, Yernool D, Shimamoto K. 2007. Crystal structure of GltPh in complex with L-aspartate and sodium ions. Protein Data Bank. 2NWX

Reyes N, Ginter C, Boudker O. 2009. Crystal structure of GltPh K55C-A364C mutant crosslinked with divalent mercury. Protein Data Bank. 3KBC

Nie R, Stark S, Symersky J, Kaplan RS, Lu M. 2017. Structure and function of the divalent anion/Na+ symporter from Vibrio cholerae and a humanized variant. Protein Data Bank. 5ULD

Mulligan C, Fenollar-Ferrer C, Fitzgerald GA, Vergara-Jaque A, Kaufmann D, Li Y, Forrest LR, Mindell JA. 2016. Model of outward-facing VcINDY. Protein Model Data Base. PM0080216

References

Akyuz N, Altman RB, Blanchard SC, Boudker O. Transport dynamics in a glutamate transporter homologue. Nature. 2013;502:114–118. doi: 10.1038/nature12265. [DOI] [PMC free article] [PubMed] [Google Scholar]
Akyuz N, Georgieva ER, Zhou Z, Stolzenberg S, Cuendet MA, Khelashvili G, Altman RB, Terry DS, Freed JH, Weinstein H, Boudker O, Blanchard SC. Transport domain unlocking sets the uptake rate of an aspartate transporter. Nature. 2015;518:68–73. doi: 10.1038/nature14158. [DOI] [PMC free article] [PubMed] [Google Scholar]
Andersen OS. Membrane proteins: through thick and thin. Nature Chemical Biology. 2013;9:667. doi: 10.1038/nchembio.1368. [DOI] [PubMed] [Google Scholar]
Andersen OS, Koeppe RE. Bilayer thickness and membrane protein function: an energetic perspective. Annual Review of Biophysics and Biomolecular Structure. 2007;36:107–130. doi: 10.1146/annurev.biophys.36.040306.132643. [DOI] [PubMed] [Google Scholar]
Argudo D, Bethel NP, Marcoline FV, Wolgemuth CW, Grabe M. New continuum approaches for determining Protein-Induced membrane deformations. Biophysical Journal. 2017;112:2159–2172. doi: 10.1016/j.bpj.2017.03.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR. Molecular dynamics with coupling to an external bath. The Journal of Chemical Physics. 1984;81:3684–3690. doi: 10.1063/1.448118. [DOI] [Google Scholar]
Best RB, Zhu X, Shim J, Lopes PE, Mittal J, Feig M, Mackerell AD. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ (1) and χ(2) dihedral angles. Journal of Chemical Theory and Computation. 2012;8:3257–3273. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bethel NP, Grabe M. Atomistic insight into lipid translocation by a TMEM16 scramblase. PNAS. 2016;113:14049–14054. doi: 10.1073/pnas.1607574113. [DOI] [PMC free article] [PubMed] [Google Scholar]
Boudker O, Ryan RM, Yernool D, Shimamoto K, Gouaux E. Coupling substrate and ion binding to extracellular gate of a sodium-dependent aspartate transporter. Nature. 2007;445:387–393. doi: 10.1038/nature05455. [DOI] [PubMed] [Google Scholar]
Boudker O, Verdon G. Structural perspectives on secondary active transporters. Trends in Pharmacological Sciences. 2010;31:418–426. doi: 10.1016/j.tips.2010.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brannigan G, Brown FL. A consistent model for thermal fluctuations and protein-induced deformations in lipid bilayers. Biophysical Journal. 2006;90:1501–1520. doi: 10.1529/biophysj.105.075838. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brown MF, Chawla U. The Biophysics of Cell Membranes, Biological Consequences. Springer; 2017. [Google Scholar]
Canham PB. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. Journal of Theoretical Biology. 1970;26:61–81. doi: 10.1016/S0022-5193(70)80032-7. [DOI] [PubMed] [Google Scholar]
Chowdhury S, Chanda B. Estimating the voltage-dependent free energy change of ion channels using the median voltage for activation. The Journal of General Physiology. 2012;139:3–17. doi: 10.1085/jgp.201110722. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cordero-Morales JF, Vásquez V. How lipids contribute to ion channel function, a fat perspective on direct and indirect interactions. Current Opinion in Structural Biology. 2018;51:92–98. doi: 10.1016/j.sbi.2018.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
Corradi V, Mendez-Villuendas E, Ingólfsson HI, Gu RX, Siuda I, Melo MN, Moussatova A, DeGagné LJ, Sejdiu BI, Singh G, Wassenaar TA, Delgado Magnero K, Marrink SJ, Tieleman DP. Lipid-Protein interactions are unique fingerprints for membrane proteins. ACS Central Science. 2018;4:709–717. doi: 10.1021/acscentsci.8b00143. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cui Q, Zhang L, Wu Z, Yethiraj A. Generation and sensing of membrane curvature: where materials science and biophysics meet. Current Opinion in Solid State and Materials Science. 2013;17:164–174. doi: 10.1016/j.cossms.2013.06.002. [DOI] [Google Scholar]
Danbolt NC. Glutamate uptake. Progress in Neurobiology. 2001;65:1–105. doi: 10.1016/S0301-0082(00)00067-8. [DOI] [PubMed] [Google Scholar]
Denning EJ, Beckstein O. Influence of lipids on protein-mediated transmembrane transport. Chemistry and Physics of Lipids. 2013;169:57–71. doi: 10.1016/j.chemphyslip.2013.02.007. [DOI] [PubMed] [Google Scholar]
Erkens GB, Hänelt I, Goudsmits JM, Slotboom DJ, van Oijen AM. Unsynchronised subunit motion in single trimeric sodium-coupled aspartate transporters. Nature. 2013;502:119–123. doi: 10.1038/nature12538. [DOI] [PubMed] [Google Scholar]
Fairman WA, Sonders MS, Murdoch GH, Amara SG. Arachidonic acid elicits a substrate-gated proton current associated with the glutamate transporter EAAT4. Nature Neuroscience. 1998;1:105–113. doi: 10.1038/355. [DOI] [PubMed] [Google Scholar]
Falzone ME, Rheinberger J, Lee B-C, Peyear T, Sasset L, Raczkowski A, Eng E, Lorenzo AD, Andersen OS, Nimigean CM, Accardi A. Cryo-EM structures reveal bilayer remodeling during Ca2+ activation of a TMEM16 scramblase. bioRxiv. 2018 doi: 10.1101/420174. [DOI]
Falzone ME, Rheinberger J, Lee BC, Peyear T, Sasset L, Raczkowski AM, Eng ET, Di Lorenzo A, Andersen OS, Nimigean CM, Accardi A. Structural basis of Ca2+-dependent activation and lipid transport by a TMEM16 scramblase. eLife. 2019;8:e43229. doi: 10.7554/eLife.43229. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fiorin G, Marinelli F, Faraldo‐Gómez JD. Direct derivation of free energies of membrane deformation and other solvent density variations from enhanced sampling molecular dynamics. Journal of Computational Chemistry. 2019;118 doi: 10.1002/jcc.26075. [DOI] [PMC free article] [PubMed] [Google Scholar]
Flood E, Boiteux C, Lev B, Vorobyov I, Allen TW. Atomistic simulations of membrane ion channel conduction, gating, and modulation. Chemical Reviews. 2019;119:7737–7832. doi: 10.1021/acs.chemrev.8b00630. [DOI] [PubMed] [Google Scholar]
Forrest LR, Krämer R, Ziegler C. The structural basis of secondary active transport mechanisms. Biochimica Et Biophysica Acta (BBA) - Bioenergetics. 2011;1807:167–188. doi: 10.1016/j.bbabio.2010.10.014. [DOI] [PubMed] [Google Scholar]
Georgieva ER, Borbat PP, Ginter C, Freed JH, Boudker O. Conformational ensemble of the sodium-coupled aspartate transporter. Nature Structural & Molecular Biology. 2013;20:215–221. doi: 10.1038/nsmb.2494. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gether U, Andersen PH, Larsson OM, Schousboe A. Neurotransmitter transporters: molecular function of important drug targets. Trends in Pharmacological Sciences. 2006;27:375–383. doi: 10.1016/j.tips.2006.05.003. [DOI] [PubMed] [Google Scholar]
Goetz R, Gompper G, Lipowsky R. Mobility and elasticity of Self-Assembled membranes. Physical Review Letters. 1999;82:221–224. doi: 10.1103/PhysRevLett.82.221. [DOI] [Google Scholar]
Grewer C, Balani P, Weidenfeller C, Bartusel T, Tao Z, Rauen T. Individual subunits of the glutamate transporter EAAC1 homotrimer function independently of each other. Biochemistry. 2005;44:11913–11923. doi: 10.1021/bi050987n. [DOI] [PMC free article] [PubMed] [Google Scholar]
Grintal B, Champeil-Potokar G, Lavialle M, Vancassel S, Breton S, Denis I. Inhibition of astroglial glutamate transport by polyunsaturated fatty acids: evidence for a signalling role of docosahexaenoic acid. Neurochemistry International. 2009;54:535–543. doi: 10.1016/j.neuint.2009.02.018. [DOI] [PubMed] [Google Scholar]
Groeneveld M, Slotboom DJ. Rigidity of the subunit interfaces of the trimeric glutamate transporter GltT during translocation. Journal of Molecular Biology. 2007;372:565–570. doi: 10.1016/j.jmb.2007.06.067. [DOI] [PubMed] [Google Scholar]
Hänelt I, Wunnicke D, Bordignon E, Steinhoff HJ, Slotboom DJ. Conformational heterogeneity of the aspartate transporter glt(Ph) Nature Structural & Molecular Biology. 2013;20:210–214. doi: 10.1038/nsmb.2471. [DOI] [PubMed] [Google Scholar]
Harpole TJ, Delemotte L. Conformational landscapes of membrane proteins delineated by enhanced sampling molecular dynamics simulations. Biochimica Et Biophysica Acta (BBA) - Biomembranes. 2018;1860:909–926. doi: 10.1016/j.bbamem.2017.10.033. [DOI] [PubMed] [Google Scholar]
Haselwandter CA, MacKinnon R. Piezo's membrane footprint and its contribution to mechanosensitivity. eLife. 2018;7:e41968. doi: 10.7554/eLife.41968. [DOI] [PMC free article] [PubMed] [Google Scholar]
Heath GR, Scheuring S. Advances in high-speed atomic force microscopy (HS-AFM) reveal dynamics of transmembrane channels and transporters. Current Opinion in Structural Biology. 2019;57:93–102. doi: 10.1016/j.sbi.2019.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Zeitschrift Für Naturforschung C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
Hess B, Kutzner C, van der Spoel D, Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. Journal of Chemical Theory and Computation. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
Jardetzky O. Simple allosteric model for membrane pumps. Nature. 1966;211:969–970. doi: 10.1038/211969a0. [DOI] [PubMed] [Google Scholar]
Javanainen M, Martinez-Seara H, Vattulainen I. Excessive aggregation of membrane proteins in the martini model. PLOS ONE. 2017;12:e0187936. doi: 10.1371/journal.pone.0187936. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jensen Morten Ø., Mouritsen OG. Lipids do influence protein function—the hydrophobic matching hypothesis revisited. Biochimica Et Biophysica Acta (BBA) - Biomembranes. 2004;1666:205–226. doi: 10.1016/j.bbamem.2004.06.009. [DOI] [PubMed] [Google Scholar]
Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. The Journal of Chemical Physics. 1983;79:926–935. doi: 10.1063/1.445869. [DOI] [Google Scholar]
Kalienkova V, Clerico Mosina V, Bryner L, Oostergetel GT, Dutzler R, Paulino C. Stepwise activation mechanism of the scramblase nhTMEM16 revealed by cryo-EM. eLife. 2019;8:e44364. doi: 10.7554/eLife.44364. [DOI] [PMC free article] [PubMed] [Google Scholar]
Khelashvili G, Kollmitzer B, Heftberger P, Pabst G, Harries D. Calculating the bending Modulus for multicomponent lipid membranes in different thermodynamic phases. Journal of Chemical Theory and Computation. 2013;9:3866–3871. doi: 10.1021/ct400492e. [DOI] [PMC free article] [PubMed] [Google Scholar]
Klauda JB, Venable RM, Freites JA, O'Connor JW, Tobias DJ, Mondragon-Ramirez C, Vorobyov I, MacKerell AD, Pastor RW. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. The Journal of Physical Chemistry B. 2010;114:7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
Koch HP, Brown RL, Larsson HP. The glutamate-activated anion conductance in excitatory amino acid transporters is gated independently by the individual subunits. Journal of Neuroscience. 2007;27:2943–2947. doi: 10.1523/JNEUROSCI.0118-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
Koch HP, Larsson HP. Small-scale molecular motions accomplish glutamate uptake in human glutamate transporters. Journal of Neuroscience. 2005;25:1730–1736. doi: 10.1523/JNEUROSCI.4138-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. the method. Journal of Computational Chemistry. 1992;13:1011–1021. doi: 10.1002/jcc.540130812. [DOI] [Google Scholar]
Leary GP, Stone EF, Holley DC, Kavanaugh MP. The glutamate and chloride permeation pathways are colocalized in individual neuronal glutamate transporter subunits. Journal of Neuroscience. 2007;27:2938–2942. doi: 10.1523/JNEUROSCI.4851-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lee AG. How lipids affect the activities of integral membrane proteins. Biochimica Et Biophysica Acta (BBA) - Biomembranes. 2004;1666:62–87. doi: 10.1016/j.bbamem.2004.05.012. [DOI] [PubMed] [Google Scholar]
Lee KI, Pastor RW, Andersen OS, Im W. Assessing smectic liquid-crystal continuum models for elastic bilayer deformations. Chemistry and Physics of Lipids. 2013;169:19–26. doi: 10.1016/j.chemphyslip.2013.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lipfert J, Columbus L, Chu VB, Lesley SA, Doniach S. Size and shape of detergent micelles determined by small-angle X-ray scattering. The Journal of Physical Chemistry B. 2007;111:12427–12438. doi: 10.1021/jp073016l. [DOI] [PubMed] [Google Scholar]
MacCallum JL, Bennett WF, Tieleman DP. Partitioning of amino acid side chains into lipid bilayers: results from computer simulations and comparison to experiment. The Journal of General Physiology. 2007;129:371–377. doi: 10.1085/jgp.200709745. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mancusso R, Gregorio GG, Liu Q, Wang DN. Structure and mechanism of a bacterial sodium-dependent dicarboxylate transporter. Nature. 2012;491:622–626. doi: 10.1038/nature11542. [DOI] [PMC free article] [PubMed] [Google Scholar]
Marks DS, Colwell LJ, Sheridan R, Hopf TA, Pagnani A, Zecchina R, Sander C. Protein 3D structure computed from evolutionary sequence variation. PLOS ONE. 2011;6:e28766. doi: 10.1371/journal.pone.0028766. [DOI] [PMC free article] [PubMed] [Google Scholar]
Marrink SJ, de Vries AH, Mark AE. Coarse grained model for semiquantitative lipid simulations. The Journal of Physical Chemistry B. 2004;108:750–760. doi: 10.1021/jp036508g. [DOI] [Google Scholar]
Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, de Vries AH. The MARTINI force field: coarse grained model for biomolecular simulations. The Journal of Physical Chemistry B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
Marrink SJ, Corradi V, Souza PCT, Ingólfsson HI, Tieleman DP, Sansom MSP. Computational modeling of realistic cell membranes. Chemical Reviews. 2019;119:6184–6226. doi: 10.1021/acs.chemrev.8b00460. [DOI] [PMC free article] [PubMed] [Google Scholar]
Marsh D. Protein modulation of lipids, and vice-versa, in membranes. Biochimica Et Biophysica Acta (BBA) - Biomembranes. 2008;1778:1545–1575. doi: 10.1016/j.bbamem.2008.01.015. [DOI] [PubMed] [Google Scholar]
McIlwain BC, Vandenberg RJ, Ryan RM. Transport rates of a glutamate transporter homologue are influenced by the lipid bilayer. Journal of Biological Chemistry. 2015;290:9780–9788. doi: 10.1074/jbc.M114.630590. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mondal S, Khelashvili G, Shan J, Andersen OS, Weinstein H. Quantitative modeling of membrane deformations by multihelical membrane proteins: application to G-protein coupled receptors. Biophysical Journal. 2011;101:2092–2101. doi: 10.1016/j.bpj.2011.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
Monticelli L, Kandasamy SK, Periole X, Larson RG, Tieleman DP, Marrink SJ. The MARTINI Coarse-Grained force field: extension to proteins. Journal of Chemical Theory and Computation. 2008;4:819–834. doi: 10.1021/ct700324x. [DOI] [PubMed] [Google Scholar]
Moon CP, Fleming KG. Side-chain hydrophobicity scale derived from transmembrane protein folding into lipid bilayers. PNAS. 2011;108:10174–10177. doi: 10.1073/pnas.1103979108. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mulligan C, Fenollar-Ferrer C, Fitzgerald GA, Vergara-Jaque A, Kaufmann D, Li Y, Forrest LR, Mindell JA. The bacterial dicarboxylate transporter VcINDY uses a two-domain elevator-type mechanism. Nature Structural & Molecular Biology. 2016;23:256–263. doi: 10.1038/nsmb.3166. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nie R, Stark S, Symersky J, Kaplan RS, Lu M. Structure and function of the divalent anion/Na+ symporter from Vibrio cholerae and a humanized variant. Nature Communications. 2017;8:15009. doi: 10.1038/ncomms15009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Oliver RC, Lipfert J, Fox DA, Lo RH, Doniach S, Columbus L. Dependence of micelle size and shape on detergent alkyl chain length and head group. PLOS ONE. 2013;8:e62488. doi: 10.1371/journal.pone.0062488. [DOI] [PMC free article] [PubMed] [Google Scholar]
Perez A, Morrone JA, Simmerling C, Dill KA. Advances in free-energy-based simulations of protein folding and ligand binding. Current Opinion in Structural Biology. 2016;36:25–31. doi: 10.1016/j.sbi.2015.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kalé L, Schulten K. Scalable molecular dynamics with NAMD. Journal of Computational Chemistry. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
Phillips R, Ursell T, Wiggins P, Sens P. Emerging roles for lipids in shaping membrane-protein function. Nature. 2009;459:379–385. doi: 10.1038/nature08147. [DOI] [PMC free article] [PubMed] [Google Scholar]
Reyes N, Ginter C, Boudker O. Transport mechanism of a bacterial homologue of glutamate transporters. Nature. 2009;462:880–885. doi: 10.1038/nature08616. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ruan Y, Miyagi A, Wang X, Chami M, Boudker O, Scheuring S. Direct visualization of glutamate transporter elevator mechanism by high-speed AFM. PNAS. 2017;114:1584–1588. doi: 10.1073/pnas.1616413114. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ryan RM, Compton EL, Mindell JA. Functional characterization of a na+-dependent aspartate transporter from Pyrococcus horikoshii. The Journal of Biological Chemistry. 2009;284:17540–17548. doi: 10.1074/jbc.M109.005926. [DOI] [PMC free article] [PubMed] [Google Scholar]
Silverstein N, Crisman TJ, Forrest LR, Kanner BI. Cysteine scanning mutagenesis of transmembrane Helix 3 of a brain glutamate transporter reveals two conformationally sensitive positions. Journal of Biological Chemistry. 2013;288:964–973. doi: 10.1074/jbc.M112.403576. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sonntag Y, Musgaard M, Olesen C, Schiøtt B, Møller JV, Nissen P, Thøgersen L. Mutual adaptation of a membrane protein and its lipid bilayer during conformational changes. Nature Communications. 2011;2:304. doi: 10.1038/ncomms1307. [DOI] [PubMed] [Google Scholar]
Tzingounis AV, Lin CL, Rothstein JD, Kavanaugh MP. Arachidonic acid activates a proton current in the rat glutamate transporter EAAT4. Journal of Biological Chemistry. 1998;273:17315–17317. doi: 10.1074/jbc.273.28.17315. [DOI] [PubMed] [Google Scholar]
Verdon G, Boudker O. Crystal structure of an asymmetric trimer of a bacterial glutamate transporter homolog. Nature Structural & Molecular Biology. 2012;19:355–357. doi: 10.1038/nsmb.2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wassenaar TA, Pluhackova K, Böckmann RA, Marrink SJ, Tieleman DP. Going backward: a flexible geometric approach to reverse transformation from coarse grained to atomistic models. Journal of Chemical Theory and Computation. 2014;10:676–690. doi: 10.1021/ct400617g. [DOI] [PubMed] [Google Scholar]
Watson MC, Brandt EG, Welch PM, Brown FL. Determining biomembrane bending rigidities from simulations of modest size. Physical Review Letters. 2012;109:028102. doi: 10.1103/PhysRevLett.109.028102. [DOI] [PubMed] [Google Scholar]
Yernool D, Boudker O, Jin Y, Gouaux E. Structure of a glutamate transporter homologue from Pyrococcus horikoshii. Nature. 2004;431:811–818. doi: 10.1038/nature03018. [DOI] [PubMed] [Google Scholar]
Zerangue N, Arriza JL, Amara SG, Kavanaugh MP. Differential modulation of human glutamate transporter subtypes by arachidonic acid. Journal of Biological Chemistry. 1995;270:6433–6435. doi: 10.1074/jbc.270.12.6433. [DOI] [PubMed] [Google Scholar]

eLife. doi: 10.7554/eLife.50576.sa1

Decision letter

Editor: Nir Ben-Tal¹

Reviewed by: Nir Ben-Tal², Simon Scheuring³

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

Conventional molecular dynamics simulations and a new enhanced sampling method, presented in another paper (in J Comp Chem), were used to examine the extent of lipid perturbation due to conformational changes of the Na+-aspartate symporter GltPh. This transporter, which follows the 'elevator mechanism', undergoes particularly large conformational changes upon substrate transport; the transition between the outward-facing and inward-facing conformations involves a 15Ang motion of the transport domain with respect to the stationary domain of the protein. Their simulations suggested that this transition radically perturbs the lipid bilayer, which is expected. However, very surprisingly, it leads to a large free energy penalty of about 20 kcal/mol, which of course needs to be balanced by internal components of the free energy. The manuscript addresses a fundamental and very interesting question in membrane biophysics.

Decision letter after peer review:

Thank you for submitting your article "Large-scale state-dependent membrane remodeling by a transporter protein" for consideration by eLife. Your article has been reviewed by three peer reviewers, including Nir Ben-Tal as the Reviewing Editor and Reviewer #1, and the evaluation has been overseen by Richard Aldrich as the Senior Editor. The following individual involved in review of your submission has agreed to reveal their identity: Simon Scheuring (Reviewer #2).

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Summary:

A new enhanced sampling simulation method, presented in another paper (in review with J Comp Chem), is used to examine the extent of lipid perturbation due to conformational changes of the Na+-aspartate symporter GltPh. This transporter, that typifies the 'elevator mechanism', undergoes particularly large conformational changes upon substrate transport; the transition between the outward-facing and inward-facing conformations involves a 15 Ang motion of the transport domain with respect to the stationary domain of the protein. The simulations suggest that this transition radically perturbs the lipid bilayer, which is expected. However, very surprisingly, it leads to a large free energy penalty of about 20 kcal/mol (which of course needs to be balanced by internal components of the free energy).

Opinion:

The manuscript addresses a fundamental and very interesting question in membrane biophysics. In this respect it is very suitable for publication in eLife. The problem is that it is unclear how trustworthy this large estimate is. The following suggestions may increase the credibility of the manuscript.

Essential revisions:

1) The in-plane distributions of the membrane deformations predicted by the simulations are inaccessible for experimental verifications. Moreover, the character of these deformations (types of strains in the case of 3D description or bending/stretching/chain tilting for a 2D description of the membrane) is not determined.

2) "In a recent breakthrough, we have developed and validated a promising free-energy simulation strategy to address this problem, which we refer to as Multi-Map (Fiorin, 2019)". The Fiorin paper is not in review here so we will not comment about it in detail. However, the draft that is included does not consolidate this bold statement. To our understanding it shows that the new formalism converges to the Helfrich-Canham theory and agrees with measurements at long distances (100Ang and more), as it should. However, we did not see any comparison regarding short distances which are relevant here. This statement should be removed.

3) The authors dismiss the Helfrich-Canham theory and its extensions, arguing that they do not hold for short distances. And yet, it would be insightful for the reader to know what values this approximate model and its extensions give for GltPh. At the very least it would indicate how high the 20 kcal/mol value is compared to existing theory.

4) The derived energies of the membrane deformations, which could be indeed important for understanding the effects of the membrane lipid composition on the protein function, are not supported by any independent estimations and remain, therefore, completely dependent on the parameters of the computational model (forcefield parameters), and other details of the simulations. The authors should admit to it or provide experimental measurements.

5) No analysis is provided either of the effects of membrane tension, which may dramatically change the protein-mediated deformations and their distribution, or of the presence in the membrane of specific lipids such as cholesterol, PIPs, DAGs, etc, whose redistribution to the protein vicinity may moderate the elastic energy. This decreases the general impact of the results.

6) Evidently, the authors are aware of the exceedingly high energy penalty due to lipid perturbation and try to explain it in Discussion. However, the arguments raised are not compelling. Thus, the tune of the manuscript should reflect the fact that all we have here is a computation that may or may not be correct.

7) Introduction, third paragraph: The question is nicely set between (1) "moving polar sidechains on their surface into the bilayer interior and exposing hydrophobic ones to the solvent" and (2) "the morphology of the lipid bilayer could adapt to the conformational state of the protein, and match the amino-acid make-up of the protein surface". The authors obviously come to the conclusion that the latter (2) is the case. However, at a considerable (20kcal/mol) cost. Given that the structure of all conformations are known, the authors should provide an estimate of the energetic cost for the rejected hypothesis (1).

The simulations:

8) The boundary conditions imposed on the membrane fragment are not specified. At the same time, in the absence of membrane tension, which seems to be the case here, the effects of the boundary conditions might be substantial.

9) The method is based on combining coarse-grained and all-atom simulations, which can be tricky. In particular, for the all-atom simulations, the authors take the course-grained system they simulated and convert it to all-atom, while also (naturally) changing force-fields. Then they let the system relax and report that the trends observed are consistent with the course-grain simulations. It is theoretically possible that transitioning the system from the course-grained to the all-atom parameters is not that trivial, and maybe the fact that they start from an already equilibrated state introduces some bias. Could it be examined somehow?

10) It is unfortunate that DPPC (transition temperature 41C) was chosen for many simulations. Why? Also, simulations using POPC (transition temperature -2C) are shown. The fact that the results are quasi identical seems rather worrying than comforting. Why these choices? Why not using a mixture, it is not unthinkable that in a mixture the protein would recruit specific lipids on these interfaces between transporter and scaffold domains. Please comment. Or, better, examine in simulations.

Presentation:

11) Introduction: "These perturbations develop to accommodate the amino-acid composition and specific structural features of the protein surface.": This deserves a reference to the Piezo channel, the only protein that displays clear structural features that force the membrane into bending, and for which a theory and experiments about how membrane bending (and flattening / the physics of the membrane) is exploited to gate the channel was presented.

12) The general reader might not know what the second-rank order parameter of the lipid alkyl chains is.

13) Figure 2, Figure 3 and associated, in the context of "Transport domains bend the membrane, while scaffold domains anchor it": While we understand the measurements, the results and the importance of all these results, the presentation is unclear with respect to the setting of the 0-level. From the captions "2(A) The deflection is quantified by calculating the mean value of the Z coordinate of the bilayer across the X-Y plane." and "(A) Deflection of the membrane mid-plane relative to a flat surface". For example, the image in 3A), all the membrane has negative deformation. Wouldn't that correspond to creation of a net elastic and potential energy? Shouldn't the bilayer as a whole still go towards flat and as a result one has negative deformation next to the transporter domains and positive deformation next to the scaffold domain. This does not change anything to the results in terms of local deformation, right? Is the bilayer held in place at the periphery of the simulation box?

14) Further on this: Why is the scaffold domain considered the 'anchor'? Why does the membrane next to the transporter domains (that are in the inward (down) orientation) move down, rather than the scaffold domain moving upwards? Overall – after sufficiently long relaxation of the all-inward structure – shouldn't the overall level of the membrane remain 0 and the membrane next to the transporter domains shift downwards, but the membrane next to the scaffold domains shift upwards? Especially, in light of Figure 3C, which seems to show that there are many more key amino acids in the transporter than in the scaffold domain, one would expect that the transport domain dominates the relative motion. It is unclear how in panels like Figure 2A left, 2A right, Figure 3A, all membrane deformation values can be positive or negative? Is this the reason why such huge energy penalties result from the analysis?

15) Discussion section: The authors find a large energetic penalty for the inward facing state due to membrane deformation. They note that the smFRET studies displayed almost zero energy difference between the states. In contrast the HS-AFM study revealed that the inward facing state indeed was the high energy state (like here). The authors mention that the HS-AFM study was performed in rather densely packed membrane where no such long range lipid relaxations are possible as in the study here, yet it is a flat membrane. In this context, it is also noticeable that the smFRET studies are performed either in detergent or on transporters in small vesicles that are tethered in outside-out configuration only – which goes against the bowl-shaped structure of GltPh – of which the authors see the preference for membrane bending in Figure 1 (side view), which might favor the adoption of the inward-facing state in the smFRET experiments.

eLife. 2019 Dec 19;8:e50576. doi: 10.7554/eLife.50576.sa2

Author response

Opinion:

The manuscript addresses a fundamental and very interesting question in membrane biophysics. In this respect it is very suitable for publication in eLife. The problem is that it is unclear how trustworthy this large estimate is. The following suggestions may increase the credibility of the manuscript.

We appreciate the editor’s remarks in regard to the broad significance of the subject of our study, and are thankful to all reviewers for their suggestions and constructive criticisms. We trust that the new data and clarifications provided in the revised manuscript will address the reviewers’ concerns.

For the record, however, we believe it is important to clarify that our analysis of the extent of the membrane perturbations induced by Glt_Ph did not involve the use of a new enhanced sampling simulation method, as the Summary states. This component of the study, which has been substantially modified and expanded in the revision, entailed standard simulation methods, in different conditions and using both coarse-grained and all-atom forcefields – the latter being particularly challenging due to the very large size of the system. The new enhanced-sampling methodology mentioned in the Summary, now published in J Comp Chem, was used only to estimate the energetic cost of this perturbation. This second component has also been expanded in the revision.

Essential revisions:

1) The in-plane distributions of the membrane deformations predicted by the simulations are inaccessible for experimental verifications. Moreover, the character of these deformations (types of strains in the case of 3D description or bending/stretching/chain tilting for a 2D description of the membrane) is not determined.

We understand that by in-plane distributions the reviewer refers to the two-dimensional representations of the deflection (depression/elevation) of the membrane mid-plane. We believe this kind of representation is important as it quantifies what is observed in the simulations, which in turn permits comparison of different conditions and conformational states. In order to facilitate a direct comparison with experiment, however, we also provided three-dimensional distributions (Figure 2, Figure 5, Video 1 and Video 2, Figure 8) of the lipid density around the protein – for both Glt_Ph and VcINDY. We believe that in time it will be possible to directly contrast this data with three-dimensional density maps derived from single-particle cryo-EM imaging of these transporters reconstituted in lipid nanodiscs – as has been possible for other membrane proteins.

With regard to the character of the deformation induced by all-inward Glt_Ph, additional figures have been provided to underscore that the impact of the protein is primarily a change in the curvature of both membrane leaflets, as originally stated. Specifically, Figure 4—figure supplement 1 shows that the thickness of the membrane is, relatively speaking, influenced only minimally, both in terms of magnitude and range. Figure 4—figure supplement 2 reiterates the observation made in the original version that a significant change in alkyl-chain tilt (as quantified by the second-rank order parameter) is observed only in the inner leaflet, and only at the interface between the membrane and the scaffold. By contrast, the alkyl-chain tilt along the periphery of the transport domain, where the membrane is most significantly depressed, is essentially bulk-like. This data correlates with what can be inferred from the graphical 3D representations of lipid density in Figure 2, Figure 5, and Video 1and Video 2.

2) "In a recent breakthrough, we have developed and validated a promising free-energy simulation strategy to address this problem, which we refer to as Multi-Map (Fiorin, 2019)". The Fiorin paper is not in review here so we will not comment about it in detail. However, the draft that is included does not consolidate this bold statement. To our understanding it shows that the new formalism converges to the Helfrich-Canham theory and agrees with measurements at long distances (100Ang and more), as it should. However, we did not see any comparison regarding short distances which are relevant here. This statement should be removed.

We have no objection to rephrasing this statement to make it strictly factual: “In a recent development, we have reported a novel free-energy simulation strategy to address this problem, which we refer to as Multi-Map (Fiorin, 2019).”

We must note, however, that in this context the term “validation” refers to the fact we established the correctness of the enhanced-sampling algorithm, i.e., that it reproduces the expected thermodynamic ensemble, the target membrane morphology, and the mean forces along the biased collective variable from which the free energy is derived.

One way in which the proposed method was validated (as defined above) was by comparing it with unbiased-sampling simulations, for a problem that is fully quantifiable through both approaches (the free-energy of hydration of a hydrophobic cavity). In addition, the draft of Fiorin et al., enclosed with the original submission of the current article did include a comparison of calculated and measured bending moduli for small bilayers of different lipid types, in the presence and absence of cholesterol. Because experiments and computations probe very different length scales, what was evaluated is the relative change in this bending modulus upon addition of cholesterol. The results of this analysis were positive for the lipid types for which the experimental data is uncontroversial (POPC and DMPC). Thus, at least in regard to the effect of cholesterol on membrane rigidity of small lipid bilayers, the computational Multi-Map method performs no worse than existing experimental techniques.

3) The authors dismiss the Helfrich-Canham theory and its extensions, arguing that they do not hold for short distances. And yet, it would be insightful for the reader to know what values this approximate model and its extensions give for GltPh. At the very least it would indicate how high the 20 kcal/mol value is compared to existing theory.

We have not argued, here or elsewhere, that extensions to the Helfrich-Canham theory do not hold for small wave-length deformations, nor have we dismissed them. To the contrary, in Fiorin et al., we discuss how these extensions address the known limitations of the Helfrich-Canham model (described by us and others before us), in some cases quite elegantly. We have however argued that an alternative, direct PMF approach is advantageous as it does not entail important ad hoc assumptions (e.g. a bending modulus, a homogenous membrane, etc.) and avoids ill-defined methodological choices (as discussed below). In any case, it is beyond our specific expertise to carry out a systematic comparison of the multiple variations and extensions of the Helfrich-Canham functional that have been formulated over the years. As per eLife’s editorial policy, we believe this request is outside the scope of this revision.

Using our own simulation data, however, it is relatively straightforward to illustrate why an alternative to the Helfrich-Canham approach is advantageous. In the newly provided Figure 7—figure supplement 1A, we compare free-energy curves calculated with the direct PMF method (Figure 7) with 3 alternative results deduced from the Helfrich-Canham equation, for the same set of molecular configurations (i.e. for each of the umbrella-sampling simulations carried out to calculate the PMF). The two inputs for the calculation of the Helfrich-Canham energy are the assumed bending modulus (here we use k_c = 18 kcal/mol, standard for POPC) and the membrane curvature distribution across the bilayer plane, c(x,y). We evaluate this curvature distribution from analysis of the average mid-plane in from each umbrella-sampling simulation (18 μs per window) – see Materials and methods section. The Helfrich-Canham energy is then obtained by integrating the energy density [0.5 k_cc² (x,y)] over the area of the membrane. The three calculations in Figure 7—figure supplement 1A use the same value of the bending modulus, but differ in the level of resolution used to probe c(x,y). Linear regressions of the data in each case show that the Helfrich energy can be much larger, similar or somewhat smaller depending on the resolution with which the average local curvature of the membrane is evaluated. Needless to say, a smaller or larger value of the bending modulus might improve this correlation for a given resolution, but make it worse for another. Nevertheless, it seems clear that there is no reasonable choice of either k_c or the curvature-map resolution that would lead to Helfrich energies that are, say, 2-fold smaller than those we calculate with the Multi-Map method. The opposite is however true, i.e. Helfrich energies that are significantly larger than those deduced with a direct PMF method can be easily envisaged. In sum, going back to reviewers’ point, the 20 kcal/mol value reported in the manuscript is no larger than what would be reasonably inferred from non-microscopic theories of membrane energetics.

As illustrated in Figure 7—figure supplement 1B, a rigorous evaluation of the local membrane curvature c(x,y) is itself challenging and prone to large statistical errors despite extensive simulation time (18 μs per point, split in 1-μs fragments). Thus, when comparing RMS-curvatures across the bilayer obtained at different resolutions, the expected correlation is degraded at moderate to low curvature values. These ambiguities involved in extracting membrane curvature from molecular configurations further highlight the value of direct PMF calculations, of the kind now made possible by the Multi-Map method.

4) The derived energies of the membrane deformations, which could be indeed important for understanding the effects of the membrane lipid composition on the protein function, are not supported by any independent estimations and remain, therefore, completely dependent on the parameters of the computational model (forcefield parameters), and other details of the simulations. The authors should admit to it or provide experimental measurements.

The reviewer is right, evidently, that the results from any computer simulation or theoretical analysis are hypothetical until proven by experiment. This point has been clarified in the Discussion section.

5) No analysis is provided either of the effects of membrane tension, which may dramatically change the protein-mediated deformations and their distribution, or of the presence in the membrane of specific lipids such as cholesterol, PIPs, DAGs, etc, whose redistribution to the protein vicinity may moderate the elastic energy. This decreases the general impact of the results.

We appreciate the opportunity to discuss in detail the effect of membrane tension and membrane composition, as this is a recurrent question. As shown in the newly provided Figure 3, tensions of increasing magnitude do not dramatically change the nature of the deformations induced by all-inward Glt_Ph. At the structural level, the effect of increased membrane tension is to gradually reduce the magnitude of the depression induced by the transport domains. Nevertheless, this perturbation is discernable even when the applied membrane tension is as high as 10 mN/m. It is important to note, however, that the energetic cost of the membrane deformation induced by Glt_Ph increases under membrane tension, as we show in the revised version of Figure 7B. Thus, while the amplitude of the perturbation caused by the transporter would be somewhat diminished if the membrane was under tension, the resulting energetic cost might be comparable to (or greater than) a condition where the membrane is not under tension.

With regard to the effect of lipid composition, we now compare 4 different conditions, namely POPC, POPE and 2:1 POPE-POPG at 298 K and DPPC at 323 K. Albeit simplified, we would argue these model membranes are not entirely unlike the conditions that have been probed in published liposome reconstitutions. As shown in Figure 4, the nature of the deformations induced by all-inward Glt_Ph is not dramatically changed by different lipid compositions either.

The notion that the functional regulation of membrane proteins by specific lipids (PIP2, cholesterol, etc) might be in part due to changes in the energetics of membrane plasticity is indeed an intriguing possibility, which we are currently pursuing for other systems where systematic experimental analyses have been conducted. We are unaware of such data for Glt_Ph and thus we believe that addressing this question is beyond the scope of this study.

6) Evidently, the authors are aware of the exceedingly high energy penalty due to lipid perturbation and try to explain it in Discussion. However, the arguments raised are not compelling. Thus, the tune of the manuscript should reflect the fact that all we have here is a computation that may or may not be correct.

See our response to points 4 and point 7.

7) Introduction, third paragraph: The question is nicely set between (1) "moving polar sidechains on their surface into the bilayer interior and exposing hydrophobic ones to the solvent" and (2) "the morphology of the lipid bilayer could adapt to the conformational state of the protein, and match the amino-acid make-up of the protein surface". The authors obviously come to the conclusion that the latter (2) is the case. However, at a considerable (20kcal/mol) cost. Given that the structure of all conformations are known, the authors should provide an estimate of the energetic cost for the rejected hypothesis (1).

We thank the reviewers for this suggestion, as this analysis enables us to quantify our claim that the cost of membrane bending is considerable smaller than the cost of the alternative (rejected) hypothesis.

This analysis is summarized in the newly provided Figure 6, for an equilibrated simulation snapshot of all-inward Glt_Ph, and in Figure 6—figure supplement 1 for the crystal structure. The question that we pose is: what would be the hypothetical free-energy gain/cost of preserving a flat membrane when the transporter is in the all-inward state? To estimate this cost, we considered the two membrane configurations described in the figure – one deformed, as in our simulation, and a version thereof that has the same thickness but flat. (By ‘membrane’, we refer to the solvent-excluded region of the bilayer.) We then calculated the solvent-accessible surface area (SASA) for all protein residues in either case. The difference, i.e. ΔSASA, was then normalized by the SASA of each residue-type when fully solvent-exposed in a Gly-X-Gly peptide. The resulting ‘dehydration factor’ was then multiplied by the transfer free-energy of that residue type into the membrane, according to two independent hydrophobicity scales: one based on experimental measurements of the stability of WT and mutagenized OMPLA, published by Karen Fleming; and another published by Peter Tieleman, based on MD simulations.

Taken together, these results underscore how strikingly unfavorable it would be for the membrane to remain flat when the transport domains adopt the inward facing state. Small energy penalties from a large number of residues add up to very large totals – specifically about 30 kcal/mol for the Fleming scale and about 50 kcal/mol for the Tieleman scale. As originally stated, these penalties result from either exposing polar sidechains to the bilayer interior (R105, K230), or from exposing hydrophobic sidechains to the solvent; indeed, more than a dozen hydrophobic residues disfavor the flat membrane by 1 k_BT or more, each. As one might expect, the polar residues that contribute the most are on the extracellular side of the transport domains, while the hydrophobic groups are on the intracellular side. A few hydrophobic residues on the extracellular side favor the flat membrane, but their total contribution is comparatively much smaller than the energetic penalty that opposes it.

It should be noted that, by definition, this ‘transfer free-energy’ examines the energetics of hydration/dehydration, neglecting the stabilizing effect of the hydrogen-bonding interactions between polar sidechains and the lipid headgroups described in Figure 5; many of these lipid contacts would be unfeasible if the membrane was flat, and would be replaced by water, penalizing this hypothetical state further.

In summary, the adaptation of the membrane to the conformational state of the transporter, while clearly costly, is nevertheless much more favorable than the alternative.

The simulations:

8) The boundary conditions imposed on the membrane fragment are not specified. At the same time, in the absence of membrane tension, which seems to be the case here, the effects of the boundary conditions might be substantial.

The boundary conditions are now specified in the Materials and methods section, i.e., semi-isotropic pressure coupling and periodic boundary conditions. As mentioned, simulations are now presented with and without applied membrane tension. See Figure 3 and our response to point 5.

9) The method is based on combining coarse-grained and all-atom simulations, which can be tricky. In particular, for the all-atom simulations, the authors take the course-grained system they simulated and convert it to all-atom, while also (naturally) changing force-fields. Then they let the system relax and report that the trends observed are consistent with the course-grain simulations. It is theoretically possible that transitioning the system from the course-grained to the all-atom parameters is not that trivial, and maybe the fact that they start from an already equilibrated state introduces some bias. Could it be examined somehow?

This possibility was examined in the original submission, specifically in Figure 5—figure supplement 1AB (Formerly Figure 3—figure supplement 1). In this calculation, a perturbation of magnitude comparable to that induced by Glt_Ph is created in an all-atom lipid bilayer and allowed to relax over time. The perturbation dissipates well within 100 ns, which is shorter than the length of the Glt_Ph all-atom simulations.

In the revised version of the article, we further examine this question by quantifying the degree to which lipid molecules exchange between the first solvation shells around the protein and the rest of the membrane in the course of our 3 all-atom simulations of all-inward Glt_Ph. As shown in the newly-provided Figure 5—figure supplement 1C, we find that, by the end of the simulation, about 30% of the lipids that are initially in these first solvation shells are replaced by other lipid molecules from further away from the protein – with the overall lipid number in each shell approximately constant. These exchanges would permit a change in membrane morphology, if the such change was favorable. The fact that the membrane remains deformed, despite the results from these two control calculations, suggests that this deformation is the preferred state of the molecular system, and not an artifact of the coarse-grained forcefield, preserved at the all-atom level.

10) It is unfortunate that DPPC (transition temperature 41C) was chosen for many simulations. Why? Also, simulations using POPC (transition temperature -2C) are shown. The fact that the results are quasi identical seems rather worrying than comforting. Why these choices? Why not using a mixture, it is not unthinkable that in a mixture the protein would recruit specific lipids on these interfaces between transporter and scaffold domains. Please comment. Or, better, examine in simulations.

Although we did not observe a phase transition in any of our original simulations, we recognize that the use of DPPC near the (coarse-grained) transition temperature is a concern. To address this concern, we have repeated all the coarse-grained simulations using different conditions. Specifically, we repeated the triplicated simulations of all-outward, one-inward, two-inward, and all-inward Glt_Ph using POPC at 298 K, and show the results in Figure 2. We also carried out triplicated simulations of all-inward Glt_Ph in POPE and in a 2:1 POPE:POPG mixture at 298 K, as well as in DPPC at 323 K, i.e., well above the transition temperature. The results of these simulations are shown in Figure 4. The triplicated simulations of VcINDY, in all-outward and all-inward conformations were also repeated using POPC at 298 K, and the results shown in Figure 8. Taken together, these new simulation data convey that the effects we describe are not critically dependent on variations in the lipid composition of the membrane. Please see also our response to point 5.

Presentation:

11) Introduction: "These perturbations develop to accommodate the amino-acid composition and specific structural features of the protein surface.": This deserves a reference to the Piezo channel, the only protein that displays clear structural features that force the membrane into bending, and for which a theory and experiments about how membrane bending (and flattening / the physics of the membrane) is exploited to gate the channel was presented.

A reference has been added.

12) The general reader might not know what the second-rank order parameter of the lipid alkyl chains is.

An explanation has been added (see caption of Figure 4—figure supplement 2).

13) Figure 2, Figure 3 and associated, in the context of "Transport domains bend the membrane, while scaffold domains anchor it": While we understand the measurements, the results and the importance of all these results, the presentation is unclear with respect to the setting of the 0-level. From the captions "2(A) The deflection is quantified by calculating the mean value of the Z coordinate of the bilayer across the X-Y plane." and "(A) Deflection of the membrane mid-plane relative to a flat surface". For example, the image in 3a), all the membrane has negative deformation. Wouldn't that correspond to creation of a net elastic and potential energy? Shouldn't the bilayer as a whole still go towards flat and as a result one has negative deformation next to the transporter domains and positive deformation next to the scaffold domain. This does not change anything to the results in terms of local deformation, right? Is the bilayer held in place at the periphery of the simulation box?

We have clarified this point in the revised version.

The Z-coordinate of the membrane mid-plane is obtained from an average over all snapshots collected in a given simulation. The protein starts perfectly centered in the membrane, but in the course of a simulation it tumbles and rotates freely (and the membrane, which is initially flat, adapts accordingly). To analyze the simulation data, therefore, all snapshots must be first transformed so that the center-of-mass and orientation of the Glt_Ph trimer are consistent across the data set. To do so, all atomic coordinates (protein, membrane, solvent) are roto-translated equally, in a manner that results in an optimal (least-squares) fitting of the protein backbone. Note that this transformation does not alter in any way the relative coordinates of the atoms in the molecular system. Through this procedure, the membrane shape is defined with good precision in the vicinity of the protein. Conversely, at the edges of the simulated membrane patch, this procedure leads to large “apparent” fluctuations and an ill-defined average. Nevertheless, with extensive sampling it becomes possible to define a 0-level with confidence, i.e. a broad region far from the protein where the membrane is flat on average, and where the “apparent” fluctuations induced by the analysis process are small. In our case, that 0-level is about ~200 Å from the protein center.

The original version of Figure 5A (formerly 3A) was a close-up view of the membrane close to the protein – hence this 0-level wasn’t clear. To avoid confusion, in the new version we zoom out and present the data exactly as for the coarse-grained simulations in Figure 2. As mentioned, the 0-level becomes clear at about 200 Å from the protein center.

The membrane is not held in place, anywhere along the periphery of the system, or elsewhere. The perturbation caused by the transporter does however decay naturally away from the protein surface and so the membrane does indeed become flat, as it should. That is the region where the 0-level is set.

14) Further on this: Why is the scaffold domain considered the 'anchor'? Why does the membrane next to the transporter domains (that are in the inward (down) orientation) move down, rather than the scaffold domain moving upwards? Overall – after sufficiently long relaxation of the all-inward structure – shouldn't the overall level of the membrane remain 0 and the membrane next to the transporter domains shift downwards, but the membrane next to the scaffold domains shift upwards? Especially, in light of Figure 3C, which seems to show that there are many more key amino acids in the transporter than in the scaffold domain, one would expect that the transport domain dominates the relative motion. It is unclear how in panels like Figure 2A left, 2A right, Figure 3A, all membrane deformation values can be positive or negative? Is this the reason why such huge energy penalties result from the analysis?

As explained above, the 0-level can be defined reliably at about 200 Å from the center of the protein, which is about 150 Å from its surface. Relative to this 0-level, the change in the membrane mid-plane is much smaller at the interface with the scaffold domain than at the interface with the transport domains (see 1D profiles in Figure 2D, formerly Figure 3C). The relative change in this mid-plane when comparing all-outward to all-inward is also much larger for the transport domains. Therefore, it seems logical to think of the scaffold domain as the ‘anchor’. As noted, however, the scaffold isn’t entirely stationary. Comparing the all-outward with the all-inward state, we detect a small net displacement inwards and the transport domains move inwards too. However, we certainly do not observe an upwards displacement, relative to the 0-level. [Of course, one could arbitrarily redefine the 0-level so that the membrane mid-plane appears unperturbed at the transport domain, but that 0-level would not be consistent with the lipid bilayer further from the protein.]

Ultimately, the geometry of the membrane and the position of the protein therein is determined by a complex free-energy function that, as we argue, includes the conformational preference of the membrane itself and not only a protein-centric perspective. The geometry described by the reviewer for all-inward Glt_Ph seems entirely plausible a priori (i.e., the membrane is elevated near the scaffold domain and approximately balances out the opposite perturbation caused the transport domains), but in our view is not more intuitive than other alternatives. Arguably, the purpose of molecular simulations such as those presented in our article is precisely to investigate complex, multi-component problems such as this – notwithstanding the caveat in point 4.

15) Discussion section: The authors find a large energetic penalty for the inward facing state due to membrane deformation. They note that the smFRET studies displayed almost zero energy difference between the states. In contrast the HS-AFM study revealed that the inward facing state indeed was the high energy state (like here). The authors mention that the HS-AFM study was performed in rather densely packed membrane where no such long range lipid relaxations are possible as in the study here, yet it is a flat membrane. In this context, it is also noticeable that the smFRET studies are performed either in detergent or on transporters in small vesicles that are tethered in outside-out configuration only – which goes against the bowl-shaped structure of GltPh – of which the authors see the preference for membrane bending in Figure 1 (side view), which might favor the adoption of the inward-facing state in the smFRET experiments.

We thank the reviewers for pointing out this interesting possibility, which has been noted in the Discussion section.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Citations

Zhou Wenchang, Fiorin Giacomo, Anselmi Claudio, Karimi-Varzaneh Hossein Ali, Poblete Horacio, Forrest Lucy Rachel, Faraldo-Gómez José Diego. 2019. Simulation files for "Large-scale state-dependent membrane remodeling by a transporter protein". Zenodo. [DOI] [PMC free article] [PubMed]
Gouaux E, Boudker O, Ryan R, Yernool D, Shimamoto K. 2007. Crystal structure of GltPh in complex with L-aspartate and sodium ions. Protein Data Bank. 2NWX
Reyes N, Ginter C, Boudker O. 2009. Crystal structure of GltPh K55C-A364C mutant crosslinked with divalent mercury. Protein Data Bank. 3KBC
Nie R, Stark S, Symersky J, Kaplan RS, Lu M. 2017. Structure and function of the divalent anion/Na+ symporter from Vibrio cholerae and a humanized variant. Protein Data Bank. 5ULD [DOI] [PMC free article] [PubMed]
Mulligan C, Fenollar-Ferrer C, Fitzgerald GA, Vergara-Jaque A, Kaufmann D, Li Y, Forrest LR, Mindell JA. 2016. Model of outward-facing VcINDY. Protein Model Data Base. PM0080216

Supplementary Materials

Transparent reporting form

elife-50576-transrepform.pdf^{(122.4KB, pdf)}

Data Availability Statement

The following dataset was generated:

The following previously published datasets were used:

Gouaux E, Boudker O, Ryan R, Yernool D, Shimamoto K. 2007. Crystal structure of GltPh in complex with L-aspartate and sodium ions. Protein Data Bank. 2NWX

Reyes N, Ginter C, Boudker O. 2009. Crystal structure of GltPh K55C-A364C mutant crosslinked with divalent mercury. Protein Data Bank. 3KBC

Nie R, Stark S, Symersky J, Kaplan RS, Lu M. 2017. Structure and function of the divalent anion/Na+ symporter from Vibrio cholerae and a humanized variant. Protein Data Bank. 5ULD

Mulligan C, Fenollar-Ferrer C, Fitzgerald GA, Vergara-Jaque A, Kaufmann D, Li Y, Forrest LR, Mindell JA. 2016. Model of outward-facing VcINDY. Protein Model Data Base. PM0080216

[bib1] Akyuz N, Altman RB, Blanchard SC, Boudker O. Transport dynamics in a glutamate transporter homologue. Nature. 2013;502:114–118. doi: 10.1038/nature12265. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib2] Akyuz N, Georgieva ER, Zhou Z, Stolzenberg S, Cuendet MA, Khelashvili G, Altman RB, Terry DS, Freed JH, Weinstein H, Boudker O, Blanchard SC. Transport domain unlocking sets the uptake rate of an aspartate transporter. Nature. 2015;518:68–73. doi: 10.1038/nature14158. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib3] Andersen OS. Membrane proteins: through thick and thin. Nature Chemical Biology. 2013;9:667. doi: 10.1038/nchembio.1368. [DOI] [PubMed] [Google Scholar]

[bib4] Andersen OS, Koeppe RE. Bilayer thickness and membrane protein function: an energetic perspective. Annual Review of Biophysics and Biomolecular Structure. 2007;36:107–130. doi: 10.1146/annurev.biophys.36.040306.132643. [DOI] [PubMed] [Google Scholar]

[bib5] Argudo D, Bethel NP, Marcoline FV, Wolgemuth CW, Grabe M. New continuum approaches for determining Protein-Induced membrane deformations. Biophysical Journal. 2017;112:2159–2172. doi: 10.1016/j.bpj.2017.03.040. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib6] Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR. Molecular dynamics with coupling to an external bath. The Journal of Chemical Physics. 1984;81:3684–3690. doi: 10.1063/1.448118. [DOI] [Google Scholar]

[bib7] Best RB, Zhu X, Shim J, Lopes PE, Mittal J, Feig M, Mackerell AD. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ (1) and χ(2) dihedral angles. Journal of Chemical Theory and Computation. 2012;8:3257–3273. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib8] Bethel NP, Grabe M. Atomistic insight into lipid translocation by a TMEM16 scramblase. PNAS. 2016;113:14049–14054. doi: 10.1073/pnas.1607574113. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib9] Boudker O, Ryan RM, Yernool D, Shimamoto K, Gouaux E. Coupling substrate and ion binding to extracellular gate of a sodium-dependent aspartate transporter. Nature. 2007;445:387–393. doi: 10.1038/nature05455. [DOI] [PubMed] [Google Scholar]

[bib10] Boudker O, Verdon G. Structural perspectives on secondary active transporters. Trends in Pharmacological Sciences. 2010;31:418–426. doi: 10.1016/j.tips.2010.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib11] Brannigan G, Brown FL. A consistent model for thermal fluctuations and protein-induced deformations in lipid bilayers. Biophysical Journal. 2006;90:1501–1520. doi: 10.1529/biophysj.105.075838. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib12] Brown MF, Chawla U. The Biophysics of Cell Membranes, Biological Consequences. Springer; 2017. [Google Scholar]

[bib13] Canham PB. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. Journal of Theoretical Biology. 1970;26:61–81. doi: 10.1016/S0022-5193(70)80032-7. [DOI] [PubMed] [Google Scholar]

[bib14] Chowdhury S, Chanda B. Estimating the voltage-dependent free energy change of ion channels using the median voltage for activation. The Journal of General Physiology. 2012;139:3–17. doi: 10.1085/jgp.201110722. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib15] Cordero-Morales JF, Vásquez V. How lipids contribute to ion channel function, a fat perspective on direct and indirect interactions. Current Opinion in Structural Biology. 2018;51:92–98. doi: 10.1016/j.sbi.2018.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib16] Corradi V, Mendez-Villuendas E, Ingólfsson HI, Gu RX, Siuda I, Melo MN, Moussatova A, DeGagné LJ, Sejdiu BI, Singh G, Wassenaar TA, Delgado Magnero K, Marrink SJ, Tieleman DP. Lipid-Protein interactions are unique fingerprints for membrane proteins. ACS Central Science. 2018;4:709–717. doi: 10.1021/acscentsci.8b00143. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib17] Cui Q, Zhang L, Wu Z, Yethiraj A. Generation and sensing of membrane curvature: where materials science and biophysics meet. Current Opinion in Solid State and Materials Science. 2013;17:164–174. doi: 10.1016/j.cossms.2013.06.002. [DOI] [Google Scholar]

[bib18] Danbolt NC. Glutamate uptake. Progress in Neurobiology. 2001;65:1–105. doi: 10.1016/S0301-0082(00)00067-8. [DOI] [PubMed] [Google Scholar]

[bib19] Denning EJ, Beckstein O. Influence of lipids on protein-mediated transmembrane transport. Chemistry and Physics of Lipids. 2013;169:57–71. doi: 10.1016/j.chemphyslip.2013.02.007. [DOI] [PubMed] [Google Scholar]

[bib20] Erkens GB, Hänelt I, Goudsmits JM, Slotboom DJ, van Oijen AM. Unsynchronised subunit motion in single trimeric sodium-coupled aspartate transporters. Nature. 2013;502:119–123. doi: 10.1038/nature12538. [DOI] [PubMed] [Google Scholar]

[bib21] Fairman WA, Sonders MS, Murdoch GH, Amara SG. Arachidonic acid elicits a substrate-gated proton current associated with the glutamate transporter EAAT4. Nature Neuroscience. 1998;1:105–113. doi: 10.1038/355. [DOI] [PubMed] [Google Scholar]

[bib22] Falzone ME, Rheinberger J, Lee B-C, Peyear T, Sasset L, Raczkowski A, Eng E, Lorenzo AD, Andersen OS, Nimigean CM, Accardi A. Cryo-EM structures reveal bilayer remodeling during Ca2+ activation of a TMEM16 scramblase. bioRxiv. 2018 doi: 10.1101/420174. [DOI]

[bib23] Falzone ME, Rheinberger J, Lee BC, Peyear T, Sasset L, Raczkowski AM, Eng ET, Di Lorenzo A, Andersen OS, Nimigean CM, Accardi A. Structural basis of Ca2+-dependent activation and lipid transport by a TMEM16 scramblase. eLife. 2019;8:e43229. doi: 10.7554/eLife.43229. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib24] Fiorin G, Marinelli F, Faraldo‐Gómez JD. Direct derivation of free energies of membrane deformation and other solvent density variations from enhanced sampling molecular dynamics. Journal of Computational Chemistry. 2019;118 doi: 10.1002/jcc.26075. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib25] Flood E, Boiteux C, Lev B, Vorobyov I, Allen TW. Atomistic simulations of membrane ion channel conduction, gating, and modulation. Chemical Reviews. 2019;119:7737–7832. doi: 10.1021/acs.chemrev.8b00630. [DOI] [PubMed] [Google Scholar]

[bib26] Forrest LR, Krämer R, Ziegler C. The structural basis of secondary active transport mechanisms. Biochimica Et Biophysica Acta (BBA) - Bioenergetics. 2011;1807:167–188. doi: 10.1016/j.bbabio.2010.10.014. [DOI] [PubMed] [Google Scholar]

[bib27] Georgieva ER, Borbat PP, Ginter C, Freed JH, Boudker O. Conformational ensemble of the sodium-coupled aspartate transporter. Nature Structural & Molecular Biology. 2013;20:215–221. doi: 10.1038/nsmb.2494. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib28] Gether U, Andersen PH, Larsson OM, Schousboe A. Neurotransmitter transporters: molecular function of important drug targets. Trends in Pharmacological Sciences. 2006;27:375–383. doi: 10.1016/j.tips.2006.05.003. [DOI] [PubMed] [Google Scholar]

[bib29] Goetz R, Gompper G, Lipowsky R. Mobility and elasticity of Self-Assembled membranes. Physical Review Letters. 1999;82:221–224. doi: 10.1103/PhysRevLett.82.221. [DOI] [Google Scholar]

[bib30] Grewer C, Balani P, Weidenfeller C, Bartusel T, Tao Z, Rauen T. Individual subunits of the glutamate transporter EAAC1 homotrimer function independently of each other. Biochemistry. 2005;44:11913–11923. doi: 10.1021/bi050987n. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib31] Grintal B, Champeil-Potokar G, Lavialle M, Vancassel S, Breton S, Denis I. Inhibition of astroglial glutamate transport by polyunsaturated fatty acids: evidence for a signalling role of docosahexaenoic acid. Neurochemistry International. 2009;54:535–543. doi: 10.1016/j.neuint.2009.02.018. [DOI] [PubMed] [Google Scholar]

[bib32] Groeneveld M, Slotboom DJ. Rigidity of the subunit interfaces of the trimeric glutamate transporter GltT during translocation. Journal of Molecular Biology. 2007;372:565–570. doi: 10.1016/j.jmb.2007.06.067. [DOI] [PubMed] [Google Scholar]

[bib33] Hänelt I, Wunnicke D, Bordignon E, Steinhoff HJ, Slotboom DJ. Conformational heterogeneity of the aspartate transporter glt(Ph) Nature Structural & Molecular Biology. 2013;20:210–214. doi: 10.1038/nsmb.2471. [DOI] [PubMed] [Google Scholar]

[bib34] Harpole TJ, Delemotte L. Conformational landscapes of membrane proteins delineated by enhanced sampling molecular dynamics simulations. Biochimica Et Biophysica Acta (BBA) - Biomembranes. 2018;1860:909–926. doi: 10.1016/j.bbamem.2017.10.033. [DOI] [PubMed] [Google Scholar]

[bib35] Haselwandter CA, MacKinnon R. Piezo's membrane footprint and its contribution to mechanosensitivity. eLife. 2018;7:e41968. doi: 10.7554/eLife.41968. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib36] Heath GR, Scheuring S. Advances in high-speed atomic force microscopy (HS-AFM) reveal dynamics of transmembrane channels and transporters. Current Opinion in Structural Biology. 2019;57:93–102. doi: 10.1016/j.sbi.2019.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib37] Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Zeitschrift Für Naturforschung C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]

[bib38] Hess B, Kutzner C, van der Spoel D, Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. Journal of Chemical Theory and Computation. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]

[bib39] Jardetzky O. Simple allosteric model for membrane pumps. Nature. 1966;211:969–970. doi: 10.1038/211969a0. [DOI] [PubMed] [Google Scholar]

[bib40] Javanainen M, Martinez-Seara H, Vattulainen I. Excessive aggregation of membrane proteins in the martini model. PLOS ONE. 2017;12:e0187936. doi: 10.1371/journal.pone.0187936. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib41] Jensen Morten Ø., Mouritsen OG. Lipids do influence protein function—the hydrophobic matching hypothesis revisited. Biochimica Et Biophysica Acta (BBA) - Biomembranes. 2004;1666:205–226. doi: 10.1016/j.bbamem.2004.06.009. [DOI] [PubMed] [Google Scholar]

[bib42] Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. The Journal of Chemical Physics. 1983;79:926–935. doi: 10.1063/1.445869. [DOI] [Google Scholar]

[bib43] Kalienkova V, Clerico Mosina V, Bryner L, Oostergetel GT, Dutzler R, Paulino C. Stepwise activation mechanism of the scramblase nhTMEM16 revealed by cryo-EM. eLife. 2019;8:e44364. doi: 10.7554/eLife.44364. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib44] Khelashvili G, Kollmitzer B, Heftberger P, Pabst G, Harries D. Calculating the bending Modulus for multicomponent lipid membranes in different thermodynamic phases. Journal of Chemical Theory and Computation. 2013;9:3866–3871. doi: 10.1021/ct400492e. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib45] Klauda JB, Venable RM, Freites JA, O'Connor JW, Tobias DJ, Mondragon-Ramirez C, Vorobyov I, MacKerell AD, Pastor RW. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. The Journal of Physical Chemistry B. 2010;114:7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib46] Koch HP, Brown RL, Larsson HP. The glutamate-activated anion conductance in excitatory amino acid transporters is gated independently by the individual subunits. Journal of Neuroscience. 2007;27:2943–2947. doi: 10.1523/JNEUROSCI.0118-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib47] Koch HP, Larsson HP. Small-scale molecular motions accomplish glutamate uptake in human glutamate transporters. Journal of Neuroscience. 2005;25:1730–1736. doi: 10.1523/JNEUROSCI.4138-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib48] Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. the method. Journal of Computational Chemistry. 1992;13:1011–1021. doi: 10.1002/jcc.540130812. [DOI] [Google Scholar]

[bib49] Leary GP, Stone EF, Holley DC, Kavanaugh MP. The glutamate and chloride permeation pathways are colocalized in individual neuronal glutamate transporter subunits. Journal of Neuroscience. 2007;27:2938–2942. doi: 10.1523/JNEUROSCI.4851-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib50] Lee AG. How lipids affect the activities of integral membrane proteins. Biochimica Et Biophysica Acta (BBA) - Biomembranes. 2004;1666:62–87. doi: 10.1016/j.bbamem.2004.05.012. [DOI] [PubMed] [Google Scholar]

[bib51] Lee KI, Pastor RW, Andersen OS, Im W. Assessing smectic liquid-crystal continuum models for elastic bilayer deformations. Chemistry and Physics of Lipids. 2013;169:19–26. doi: 10.1016/j.chemphyslip.2013.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib52] Lipfert J, Columbus L, Chu VB, Lesley SA, Doniach S. Size and shape of detergent micelles determined by small-angle X-ray scattering. The Journal of Physical Chemistry B. 2007;111:12427–12438. doi: 10.1021/jp073016l. [DOI] [PubMed] [Google Scholar]

[bib53] MacCallum JL, Bennett WF, Tieleman DP. Partitioning of amino acid side chains into lipid bilayers: results from computer simulations and comparison to experiment. The Journal of General Physiology. 2007;129:371–377. doi: 10.1085/jgp.200709745. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib54] Mancusso R, Gregorio GG, Liu Q, Wang DN. Structure and mechanism of a bacterial sodium-dependent dicarboxylate transporter. Nature. 2012;491:622–626. doi: 10.1038/nature11542. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib55] Marks DS, Colwell LJ, Sheridan R, Hopf TA, Pagnani A, Zecchina R, Sander C. Protein 3D structure computed from evolutionary sequence variation. PLOS ONE. 2011;6:e28766. doi: 10.1371/journal.pone.0028766. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib56] Marrink SJ, de Vries AH, Mark AE. Coarse grained model for semiquantitative lipid simulations. The Journal of Physical Chemistry B. 2004;108:750–760. doi: 10.1021/jp036508g. [DOI] [Google Scholar]

[bib57] Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, de Vries AH. The MARTINI force field: coarse grained model for biomolecular simulations. The Journal of Physical Chemistry B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]

[bib58] Marrink SJ, Corradi V, Souza PCT, Ingólfsson HI, Tieleman DP, Sansom MSP. Computational modeling of realistic cell membranes. Chemical Reviews. 2019;119:6184–6226. doi: 10.1021/acs.chemrev.8b00460. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib59] Marsh D. Protein modulation of lipids, and vice-versa, in membranes. Biochimica Et Biophysica Acta (BBA) - Biomembranes. 2008;1778:1545–1575. doi: 10.1016/j.bbamem.2008.01.015. [DOI] [PubMed] [Google Scholar]

[bib60] McIlwain BC, Vandenberg RJ, Ryan RM. Transport rates of a glutamate transporter homologue are influenced by the lipid bilayer. Journal of Biological Chemistry. 2015;290:9780–9788. doi: 10.1074/jbc.M114.630590. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib61] Mondal S, Khelashvili G, Shan J, Andersen OS, Weinstein H. Quantitative modeling of membrane deformations by multihelical membrane proteins: application to G-protein coupled receptors. Biophysical Journal. 2011;101:2092–2101. doi: 10.1016/j.bpj.2011.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib62] Monticelli L, Kandasamy SK, Periole X, Larson RG, Tieleman DP, Marrink SJ. The MARTINI Coarse-Grained force field: extension to proteins. Journal of Chemical Theory and Computation. 2008;4:819–834. doi: 10.1021/ct700324x. [DOI] [PubMed] [Google Scholar]

[bib63] Moon CP, Fleming KG. Side-chain hydrophobicity scale derived from transmembrane protein folding into lipid bilayers. PNAS. 2011;108:10174–10177. doi: 10.1073/pnas.1103979108. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib64] Mulligan C, Fenollar-Ferrer C, Fitzgerald GA, Vergara-Jaque A, Kaufmann D, Li Y, Forrest LR, Mindell JA. The bacterial dicarboxylate transporter VcINDY uses a two-domain elevator-type mechanism. Nature Structural & Molecular Biology. 2016;23:256–263. doi: 10.1038/nsmb.3166. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib65] Nie R, Stark S, Symersky J, Kaplan RS, Lu M. Structure and function of the divalent anion/Na+ symporter from Vibrio cholerae and a humanized variant. Nature Communications. 2017;8:15009. doi: 10.1038/ncomms15009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib66] Oliver RC, Lipfert J, Fox DA, Lo RH, Doniach S, Columbus L. Dependence of micelle size and shape on detergent alkyl chain length and head group. PLOS ONE. 2013;8:e62488. doi: 10.1371/journal.pone.0062488. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib67] Perez A, Morrone JA, Simmerling C, Dill KA. Advances in free-energy-based simulations of protein folding and ligand binding. Current Opinion in Structural Biology. 2016;36:25–31. doi: 10.1016/j.sbi.2015.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib68] Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kalé L, Schulten K. Scalable molecular dynamics with NAMD. Journal of Computational Chemistry. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib69] Phillips R, Ursell T, Wiggins P, Sens P. Emerging roles for lipids in shaping membrane-protein function. Nature. 2009;459:379–385. doi: 10.1038/nature08147. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib70] Reyes N, Ginter C, Boudker O. Transport mechanism of a bacterial homologue of glutamate transporters. Nature. 2009;462:880–885. doi: 10.1038/nature08616. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib71] Ruan Y, Miyagi A, Wang X, Chami M, Boudker O, Scheuring S. Direct visualization of glutamate transporter elevator mechanism by high-speed AFM. PNAS. 2017;114:1584–1588. doi: 10.1073/pnas.1616413114. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib72] Ryan RM, Compton EL, Mindell JA. Functional characterization of a na+-dependent aspartate transporter from Pyrococcus horikoshii. The Journal of Biological Chemistry. 2009;284:17540–17548. doi: 10.1074/jbc.M109.005926. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib73] Silverstein N, Crisman TJ, Forrest LR, Kanner BI. Cysteine scanning mutagenesis of transmembrane Helix 3 of a brain glutamate transporter reveals two conformationally sensitive positions. Journal of Biological Chemistry. 2013;288:964–973. doi: 10.1074/jbc.M112.403576. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib74] Sonntag Y, Musgaard M, Olesen C, Schiøtt B, Møller JV, Nissen P, Thøgersen L. Mutual adaptation of a membrane protein and its lipid bilayer during conformational changes. Nature Communications. 2011;2:304. doi: 10.1038/ncomms1307. [DOI] [PubMed] [Google Scholar]

[bib75] Tzingounis AV, Lin CL, Rothstein JD, Kavanaugh MP. Arachidonic acid activates a proton current in the rat glutamate transporter EAAT4. Journal of Biological Chemistry. 1998;273:17315–17317. doi: 10.1074/jbc.273.28.17315. [DOI] [PubMed] [Google Scholar]

[bib76] Verdon G, Boudker O. Crystal structure of an asymmetric trimer of a bacterial glutamate transporter homolog. Nature Structural & Molecular Biology. 2012;19:355–357. doi: 10.1038/nsmb.2233. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib77] Wassenaar TA, Pluhackova K, Böckmann RA, Marrink SJ, Tieleman DP. Going backward: a flexible geometric approach to reverse transformation from coarse grained to atomistic models. Journal of Chemical Theory and Computation. 2014;10:676–690. doi: 10.1021/ct400617g. [DOI] [PubMed] [Google Scholar]

[bib78] Watson MC, Brandt EG, Welch PM, Brown FL. Determining biomembrane bending rigidities from simulations of modest size. Physical Review Letters. 2012;109:028102. doi: 10.1103/PhysRevLett.109.028102. [DOI] [PubMed] [Google Scholar]

[bib79] Yernool D, Boudker O, Jin Y, Gouaux E. Structure of a glutamate transporter homologue from Pyrococcus horikoshii. Nature. 2004;431:811–818. doi: 10.1038/nature03018. [DOI] [PubMed] [Google Scholar]

[bib80] Zerangue N, Arriza JL, Amara SG, Kavanaugh MP. Differential modulation of human glutamate transporter subtypes by arachidonic acid. Journal of Biological Chemistry. 1995;270:6433–6435. doi: 10.1074/jbc.270.12.6433. [DOI] [PubMed] [Google Scholar]

PERMALINK

Large-scale state-dependent membrane remodeling by a transporter protein

Wenchang Zhou

Giacomo Fiorin

Claudio Anselmi

Hossein Ali Karimi-Varzaneh

Horacio Poblete

Lucy R Forrest

José D Faraldo-Gómez

Roles

Abstract

Introduction

Figure 1. Structure of the GltPh trimer in the outward- and inward-facing states.

Figure 1—figure supplement 1. Molecular simulation systems.

Results

Alternating access causes major membrane deformations, long-ranged but non-cooperative

Figure 2. Changes in membrane morphology induced by the conformational cycle of GltPh.

Figure 2—video 1. Changes in membrane morphology induced by the conformational cycle of GltPh.

Figure 2—video 2. Changes in membrane morphology induced by the conformational cycle of GltPh.

Figure 3. Membrane deformation induced by all-inward GltPh in coarse-grained MD simulations in a POPC bilayer at 298 K, with and without an applied membrane tension of increasing magnitude (as indicated).

Figure 4. Membrane deformation induced by all-inward GltPh in coarse-grained MD simulations in different bilayers.

Figure 4—figure supplement 1. Changes in bilayer thickness induced by the conformational cycle of GltPh.

Figure 4—figure supplement 2. Changes in lipid-chain tilt induced by the conformational cycle of GltPh.

Transport domains bend the membrane, while scaffold domains anchor it

Figure 5. Membrane deformation induced by all-inward GltPh, based on large-scale all-atom simulations in DPPC at 323 K.

Figure 5—figure supplement 1. Evaluation of potential biases resulting from conversion of coarse-grained molecular configurations into an all-atom representation.

Figure 5—video 1. Membrane deformation induced by all-inward GltPh in large-scale all-atom simulations.

Figure 6. Energetics of solvation and evolutionary conservation of the GltPh lipid interface.

Figure 6—figure supplement 1. Energetics of polar and hydrophobic solvation of the GltPh lipid interface.

The inward-facing state incurs a major energetic penalty due to membrane bending

Figure 7. Estimate of the free-energy cost associated with the membrane deformation caused by all-inward GltPh, from direct potential-of-mean-force calculations.

Figure 7—figure supplement 1. Comparison of membrane-bending free-energy values calculated with the Multi-Map method and with the Helfrich-Canham theory, for the same ensembles of molecular configurations.

Discussion

Figure 8. Membrane deformation induced by the Na+-dicarboxylate symporter VcINDY, based on coarse-grained MD simulations in POPC at 298 K.

Materials and methods

Coarse-grained simulations of GltPh trimers and VcINDY dimers

All-atom simulations in all-inward GltPh

Energetics of polar/hydrophobic solvation

Coevolutionary analysis

Potential-of-mean-force (PMF) calculations

Acknowledgements

Funding Statement

Contributor Information

Funding Information

Additional information

Competing interests

Author contributions

Additional files

Data availability

References

Decision letter

Roles

Author response

Associated Data

Data Citations

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Figure 1. Structure of the Glt_Ph trimer in the outward- and inward-facing states.

Figure 2. Changes in membrane morphology induced by the conformational cycle of Glt_Ph.

Figure 2—video 1. Changes in membrane morphology induced by the conformational cycle of Glt_Ph.

Figure 2—video 2. Changes in membrane morphology induced by the conformational cycle of Glt_Ph.

Figure 3. Membrane deformation induced by all-inward Glt_Ph in coarse-grained MD simulations in a POPC bilayer at 298 K, with and without an applied membrane tension of increasing magnitude (as indicated).

Figure 4. Membrane deformation induced by all-inward Glt_Ph in coarse-grained MD simulations in different bilayers.

Figure 4—figure supplement 1. Changes in bilayer thickness induced by the conformational cycle of Glt_Ph.

Figure 4—figure supplement 2. Changes in lipid-chain tilt induced by the conformational cycle of Glt_Ph.

Figure 5. Membrane deformation induced by all-inward Glt_Ph, based on large-scale all-atom simulations in DPPC at 323 K.

Figure 5—video 1. Membrane deformation induced by all-inward Glt_Ph in large-scale all-atom simulations.

Figure 6. Energetics of solvation and evolutionary conservation of the Glt_Ph lipid interface.

Figure 6—figure supplement 1. Energetics of polar and hydrophobic solvation of the Glt_Ph lipid interface.

Figure 7. Estimate of the free-energy cost associated with the membrane deformation caused by all-inward Glt_Ph, from direct potential-of-mean-force calculations.

Figure 8. Membrane deformation induced by the Na⁺-dicarboxylate symporter VcINDY, based on coarse-grained MD simulations in POPC at 298 K.

Coarse-grained simulations of Glt_Ph trimers and VcINDY dimers

All-atom simulations in all-inward Glt_Ph