Photoacoustic spectroscopy for gas sensing: A comparison between piezoelectric and interferometric readout in custom quartz tuning forks

Abstract

We report on a comparison between piezoelectric and interferometric readouts of vibrations in quartz tuning forks (QTFs) when acting as sound wave transducers in a quartz-enhanced photoacoustic setup (QEPAS) for trace gas detection. A theoretical model relating the prong vibration amplitude with the QTF prong sizes and electrical resistance is proposed. To compare interferometric and piezoelectric readouts, two QTFs have been selected; a tuning fork with rectangular-shape of the prongs, having a resonance frequency of 3.4 kHz and a quality-factor of 4,000, and a QTF with prong having a T-shape characterized by a resonance frequency of 12.4 kHz with a quality-factor of 15,000. Comparison between the interferometric and piezoelectric readouts were performed by using both QTFs in a QEPAS sensor setup for water vapor detection. We demonstrated that the QTF geometry can be properly designed to enhance the signal from a specific readout mode.

1. Introduction

Laser-based trace-gas sensors have great potential for biological, medical and environmental applications, especially when long-term stability, real-time monitoring and maintenance-free conditions are required [1]. Photoacoustic spectroscopy (PAS) is a well-known technique for trace gas analysis that meets all these requirements, together with high sensitivity and selectivity, for single- or multi-gas detection [2]. In PAS, the gas is enclosed in a resonant acoustic cell and a highly sensitive microphone is used to detect optically-induced sound waves generated by the absorbing gas analyte. Quartz-enhanced PAS (QEPAS) is a variant of PAS in which the microphone is replaced by a quartz-tuning fork (QTF); when sound waves are generated between the prongs and one of in-plane anti-symmetrical flexural modes is excited, prong vibrations are converted in an electrical signal thanks to quartz piezoelectricity and properly designed gold contact patterns deposited on the prongs surfaces [3,4]. The advantages provided using QTFs are: high resonance quality-factor, small size of the sensing module, and insensitivity to ambient acoustic noise as well as their cost-effectiveness [[5], [6], [7]]. Usually, QTFs are acoustically coupled with a pair of resonator tubes positioned on both sides of QTFs, acting as an organ pipe resonator to probe and amplify the sound wave [6]. This coupling allows increasing the detection sensitivity up to a factor of 30 when standard 32.7 kHz-QTFs are used [8]. Starting from 2015, extensive theoretical and experimental investigations have been performed to study the acousto-electro properties of QTFs, the acoustic coupling between the QTF and the tube resonator system, the damping mechanisms occurring in a vibrating prong immersed in a gas, and the spatial distribution of the stress field when prongs are forced to vibrate, with the aim of identifying the prong geometry to optimize the sensing performance of a QEPAS gas sensor [[9], [10], [11], [12], [13], [14]]. These studies allowed to increase the QEPAS detection sensitivity and improve the optical coupling between the QTF and dual-tube resonator system [14]. These studies opened the way to the implementation of QTF first overtone mode in QEPAS, when its resonance frequency is lower than 40 kHz [9,10]. However, piezoelectric readout cannot be used in applications where high electromagnetic fields would affect the electric signal or for explosive detection, where electrical sparks may trigger gas deflagration. To overcome these limitations, deflections of the prongs in QEPAS can be measured by optical readout methods based on a laser interferometer, which adapts well to multiplexing. Laser interferometers have demonstrated to be able to measure displacements with accuracies to the level of the picometer [15,16]. Compact interferometric systems integrating near-infrared diode lasers and photodetectors are commercially available. If optical readout is adopted in a QEPAS sensor, no electrical contacts are needed for the acoustic detection module. In 2011, M. Kohring et al. employed an optical readout based on a Nomarski interferometer for QTF-based PAS sensing, exploiting quartz and silicon tuning fork for gas detection [[17], [18], [19]]. They demonstrated that the optical readout is limited by the QTF thermal noise. When compared with piezoelectric readout, the sensitivity and detection limits reached with the optical readout are similar. Although progresses in QTFs design identified the figures of merit to be optimized by playing on the prong geometry [11,14], there is no equivalent investigation in the literature focused on the optimization of the interferometric readout of prong vibrations.

In this work, we identified the vibration amplitude of the QTF prong as the figure of merit to be optimized for an efficient interferometric readout. We related the vibration amplitude of the prongs with their geometrical parameters and with the electrical resistance of the QTF. Hence, we selected two QTFs having different geometry: one optimized for the piezoelectric readout and the other one for the optical readout. A comparison between performances of PAS sensing exploiting interferometric and conventional piezoelectric readout have been performed by implementing both QTFs in a QEPAS sensor setup for water detection in the mid-infrared spectral range and evaluate the signals obtained using simultaneously both readout methods.

2. Optical and piezoelectric readout

The QEPAS signal is proportional to the product Q∙P∙α∙ε, where Q is the QTF resonance quality-factor, α is the gas target absorption coefficient, P is the laser power and ε is the conversion efficiency of the absorbed optical power into sound. A modulation of the laser intensity causes an alternation of optical absorption and non-radiative relaxation in the gas, i.e. generation of sound waves. When the laser beam is focused between prongs, sound waves deflect them. The QTF anti-symmetrical flexural mode is excited only if the laser modulation frequency match one of flexural modes (or its subharmonics) resonances. If the modulation frequency is too high, the gas might have not enough time to fully relax the absorbed energy and, as a consequence, the sound efficiency generation ε is reduced. Hence, the straightforward approach to design QTFs optimized for QEPAS sensing is to reduce the resonance frequency while keeping a high quality-factor. Both resonance parameters (resonance frequency and quality-factor) can be calculated from the geometrical features of the prongs. The resonance frequency of the fundamental in-plane flexural mode can be well predicted by using the Euler-Bernoulli equation for a single rectangular cantilever:

$$f=0.16\frac{T}{L^2}\sqrt{\frac{E}{\rho }}$$ (1)

where ρ =2,650 kg/m³ is the density of quartz, E =72 GPa is the component of the quartz Young’s modulus in the vibrating plane of the QTF, T is the prong thickness and L its length [11,20]. An experimental investigation described in [11] demonstrated that the overall quality-factor can be heuristically related to the prong sizes via:

$$Q=3.78\bullet {10}^5\frac{wT}{L}$$ (2)

where w is the quartz crystal thickness. The piezoelectric readout of the QTF is based on the detection of local polarization of quartz induced by the mechanical stress when QTF vibrates at one of flexural modes. The polarization charges can be collected by electrical contacts deposited on the QTF prongs surface and the polarization depends on the stress field via the quartz piezoelectric tensor. The stress field is mainly located at the junction between the prong base and the QTF support and extends across the support area. It has been shown that if some extra mass is added to the free end of the prong, an increase of the global stress field is obtained and the stress distribution along the internal prong surface is enhanced. Based on these arguments, have been realized QTFs with prongs having a T-shape geometry (T-QTF) and capable to provide a quality-factor as high as 15,000 while keeping the fundamental flexural mode at ∼12 kHz. T-shaped QTFs have shown the best performance for QEPAS sensing when compared with other prong geometries [14] and have been selected in this work as the QTF optimized for piezoelectric readout.

The optical readout is based on measurement of deflections of a cantilever via an optical interferometric system. If the QTF is excited via photoacoustic effect, very small deflections of the prongs, in the order of few nanometers or less, are produced. Obviously, the larger the vibration amplitude of the prong, the higher the optical readout signal. Assuming that the two prongs are equivalent, each prong stores an elasto-mechanical energy equal to ka²/2, where k is the spring constant and a is the motion amplitude, leading to a total energy of ka² stored by the fork. By considering the resonator time τ = Q/2πf, one can infer that the energy loss per unit time is 2πfka²/Q. Since the QTF can be modelled as an RLC series circuit, the generated electrical power P_e = V·I, where V is the voltage across the QTF and I the generated piezo-current. Assuming that the mechanical energy stored during each oscillation cycle is fully converted in electrical power, the amplitude of the motion can be related by the QTF resonance and electrical properties by the relation:

$$a=\sqrt{\frac{QVI}{2\pi fk}}$$ (3)

The spring constant $k$ of the fundamental mode of a rectangular prong is determined by its geometrical parameters and Young modulus as:

$$k=0.2575\frac{T^{3}w}{L^3}$$ (4)

At resonance, the impedance of an RLC circuit is equal to its electrical resistance R, thus V = RI, that together with Eqs. (1), (2) and (4), leads to the following dependence for the prong vibration amplitude by prong sizes and the electrical resistance:

$$a\propto \sqrt{R}\frac{L^2}{T^{3/2}}$$ (4)

The electrical resistance is hard to be modelled as a function of prong sizes. For this reason, when analysing the set of custom QTFs discussed in [11], the experimental values measured for $R$ have been used and the QTF showing the highest vibration amplitude is the one labelled as QTF#4 in Ref. [11]. Its fundamental resonance mode frequency is 3,442.5 Hz with a quality-factor of 4,000 at atmospheric pressure. This QTF is an excellent candidate for optical readout approach and will be labelled in this work as I-QTF. The main geometrical parameters of T- and I-QTF are show in Table 1.

Table 1.

Prongs length L, thickness T and spacing s for the investigated QTFs.

QTF Type	Prongs length L (mm)	Prongs thickness T (mm)	Prongs spacing s (mm)
T-QTF	9.4	2	0.8
I-QTF	11.0	0.5	0.6

3. Experimental setup

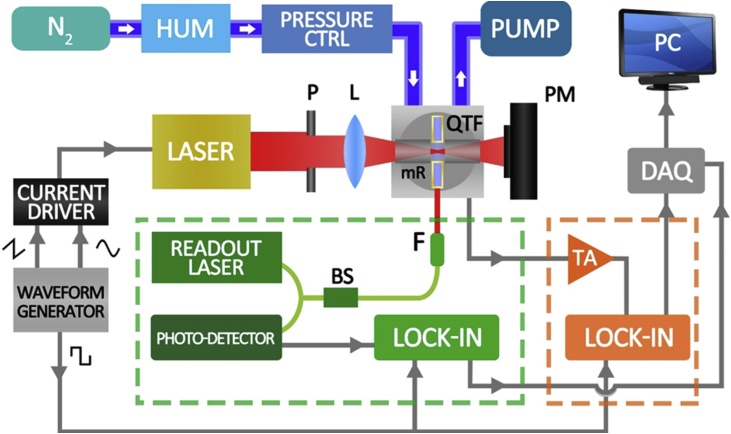
To compare the performance of the optical and piezoelectric readout methods for a vibrating QTF, a conventional QEPAS system shown in Fig. 1 was used.

Fig. 1.

Experimental setup for the simultaneous analysis of spectroscopic signals with QEPAS and interferometric PAS techniques. The instrumentation for interferometric readout is in green colour, while the instrumentation for the QEPAS readout is in orange colour. HUM: humidifier, P: pinhole, L: focusing Lens, mR: mini-Resonators, QTF: Quartz Tuning, Fork, BS: Beam Splitter, F: optical Fiber, TA: Transimpedance pre-Amplifier, DAQ: Data Acquisition card, PM: power meter, PC: personal computer.

A single-mode continuous-wave quantum cascade laser (QCL) was employed as excitation source to generate the photoacoustic signal. The collimated laser beam was spatially filtered by means of a pinhole and then focused between the QTF prongs using a ZnSe lens with a focal length of 50 mm. The platform allowed an easily interchange between T-QTF and I-QTF. The percentage of the laser intensity passing through the prongs of the bare QTFs was ∼99.5 %, this value drops by few percent when the QTFs are coupled with pairs of resonators in dual-tube configuration and slight increases of the noise levels of the PAS signal was observed, as a consequence of small fraction of the laser beam hitting the internal walls of tubes. At a temperature of 20 °C, the laser source is characterized by a central emission wavelength at 7.72 μm. By applying a low frequency ramp (f_ramp = 5 mHz) at the laser current driver, the wavelength emission was tuned to scan across two water absorption features peaked at 1,296.49 cm⁻¹ and 1,296.71 cm⁻¹ at atmospheric pressure. Both QEPAS and optical readout were operated in wavelength modulation and second harmonic detection configuration. The laser beam was sinusoidally modulated at half of the QTF resonance frequency by adding a sinusoidal dither to the current driver. Sound waves deflect the two prongs and the QTF anti-symmetrical flexural mode is excited, with electrical charges generated on prongs surfaces via direct piezoelectric effect. The electrical charges are collected by gold electrodes deposited on prong surfaces and a current signal proportional to prong deflection is generated. This is converted in a voltage signal by means of a transimpedance amplifier. The voltage signal is demodulated at the QTF resonance frequency by using a dedicated lock-in amplifier, set with a time constant of 100 ms.

While, for the optical readout, a commercial fiber coupled interferometer (OP1550 V3, Optics11) based on Fabry–Perot interference was employed. A C-band DFB laser with an output power of P = 10 mW hit the lateral surface of one prong through a cleaved optical fiber, at a distance of ∼ 500 μm. Gold layers deposited on the lateral surfaces of the QTF prongs allowed smooth and high reflective surfaces for an efficient optical readout. The laser beam pointed close to the top where the lateral displacement of the prong is largest. The back-reflected light beam from the prong surface and the fiber tip surface interfered with each other. The interference signal was sent to the detection unit to generate a voltage signal proportional to the interference light intensity. The voltage signal was demodulated at the QTF resonance frequency by using a dedicated lock-in amplifier, set with a time constant of 100 ms, the same as the QEPAS technique. When the QTF prongs vibrate, the voltage signal is modulated due to the modulation of optical path difference of the two interference light beams. Hence the optical readout output from the lock-in amplifier could be related to the QTF vibration. In this way, optical and electrical readout of water detection via QTF vibration can be performed simultaneously. All measurements were performed in air at atmospheric pressure, with a stable concentration of water vapor constantly monitored by an in-line hygrometer.

4. Results

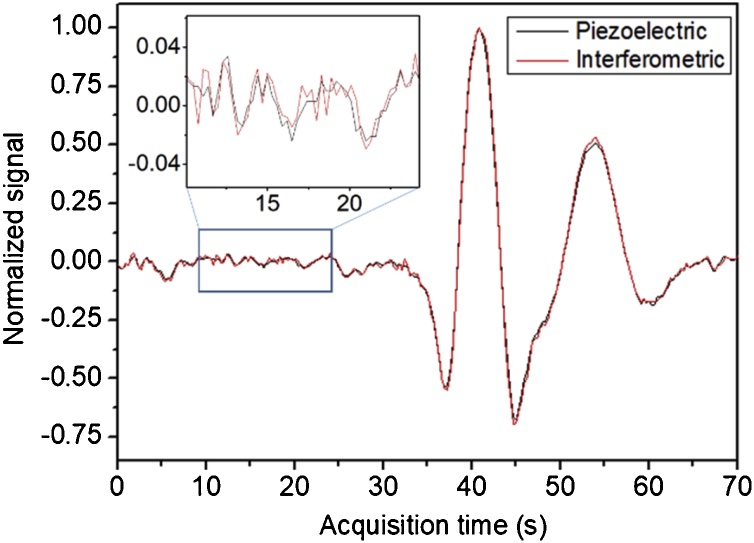
In order to exclude any mutual influence of the two readout methods, the piezoelectric and optical detection were performed both individually and simultaneously. The signals obtained by using only one readout method and by using both approaches simultaneously showed the same spectral intensity and profile. This result confirms that there is no cross-talking between the two readout methods and, therefore, that the use of one does not affect the performance of the other one. Hereafter, we will only describe the results obtained while the piezoelectric and optical readout were tested simultaneously. Fig. 2 shows the piezoelectric and the optical signal for T-QTF acquired while the laser wavelength was scanned across the two selected water absorption lines. To facilitate the comparison, both scans have been normalized to the relative peak value.

Fig. 2.

Piezoelectric (black curve) and interferometric (red curve) PAS signals normalized and superimposed, measured using the T-QTF. In the inset is show an enlarged view of the noise fluctuations.

The perfect overlap between the spectral scans suggests that both techniques are suitable to reconstruct absorption features. Far from the two strong absorption peaks, both interferometric and piezoelectric readouts are background-free. An enlarged view of the noise fluctuations is visible in the inset of Fig. 2. To compare the sensing performance, the signal-to-noise ratio has to be extracted. The piezoelectric peak signal is ∼30.15 mV with a 1σ-noise level of 0.36 mV, resulting in SNR ∼ 84. The optical readout has a peak signal of ∼230 μV, with a noise level of 3.8 μV leading to SNR ∼ 60. Hence, the piezoelectric readout results ∼40 % more sensitive than the interferometric one when employing T-QTF.

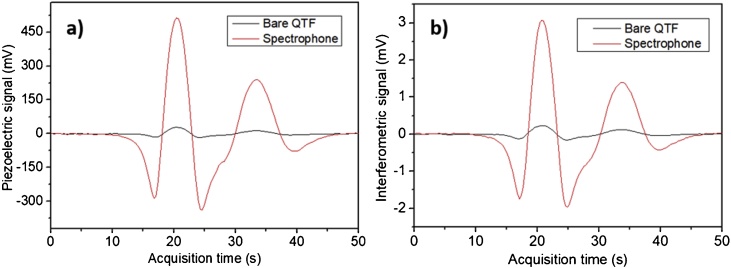
In QEPAS, a tuning fork is acoustically coupled with a pair of resonator tubes, acting as amplifiers for the sound wave. The system composed by the QTF and tubes is usually referred as spectrophone. The QTF is typically positioned between the tubes to probe the acoustic vibration excited in the absorbing gas contained inside the tubes. Tubes having length of 10 mm and an internal diameter of 1.59 mm were selected and both positioned about 200 μm far from the QTF surface. Spectral scans measured by the T-QTF spectrophone are shown in Fig. 3, together with the signal acquired with bare T-QTF, using piezoelectric and interferometric readouts.

Fig. 3.

(a) Bare T-QTF (black curve) and dual-tube on-beam piezoelectric signal (red curve). The SNR enhancement is ∼16. (b) Bare T-QTF interferometric (black curve) and dual-tube on-beam signal (red curve). The SNR enhancement is ∼13.

In the dual-tube configuration, the piezoelectric signal increases up to ∼503 mV with a 1σ-noise level equals to 0.37 mV, which lead to a SNR enhancement of ∼16 compared to the bare T-QTF. For the optical readout, an increase of the peak signal up to ∼3 mV with a noise equal to 4 μV is obtained, corresponding to a SNR enhancement of ∼13. Thereby, when implementing resonator tubes the T-QTF piezoelectric detection is ∼80 % more sensitive than the interferometric one. This can be ascribed to the fact that T-QTF was properly designed to offer high QEPAS performance for piezoelectric readout.

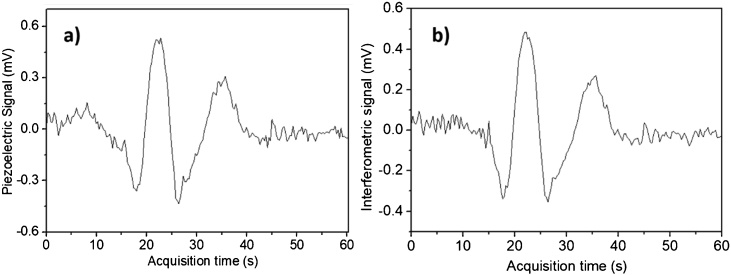
In order to confirm the hypothesis that by properly designing the prongs geometry it could be possible to selectively enhance the sensitivity of the piezoelectric or interferometric readout, the T-QTF has been replaced with a I-QTF. The spectral scans acquired with both techniques when the I-QTF is excited at the fundamental mode are shown in Fig. 4, at the same experimental conditions previously used.

Fig. 4.

(a) Bare I-QTF piezoelectric signal. The SNR is ∼23. (b) Bare I-QTF interferometric signal. The SNR is ∼35.

The peak value acquired with the piezoelectric readout is ∼0.55 mV with an estimated noise of 24 μV, resulting in a SNR ∼ 23, about 3.5 times lower than that obtained with T-QTF. This result was expected because T-QTF geometry has been properly optimized for piezoelectric readout, as already discussed. The peak value obtained with the interferometric technique is ∼490 μV with a noise of 14 μV, resulting in a SNR ∼ 35, i.e., about 50 % higher than the piezoelectric one. Thereby, I-QTF showed best performance when the optical readout was used. Implementing an optimal on-beam resonator for I-QTF requires the use of resonator tubes as long as 3,5 cm, which is unfeasible for QEPAS technique, thereby we did not investigate the piezoelectric and interferometric readout behaviors in this case.

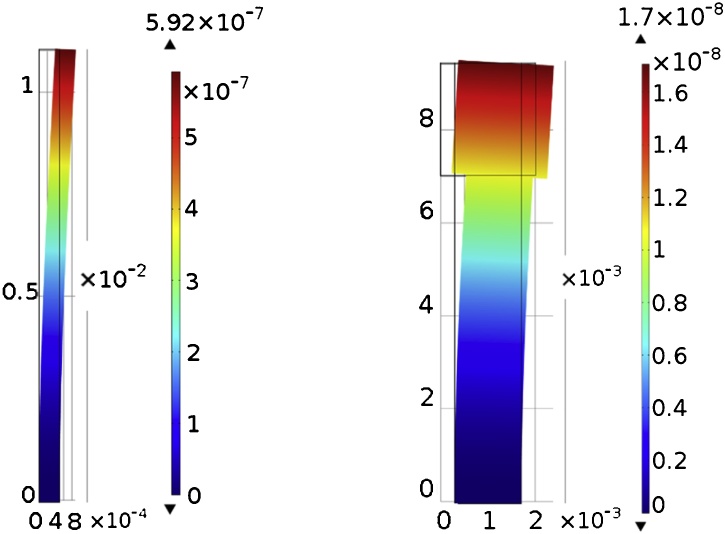
A direct comparison between T-QTF and I-QTF when optical readout is used can be done by estimating the vibration amplitude of both QTFs using Eq. (3). The spring constant was estimated by using a finite element analysis based on COMSOL Multiphysics. The simulation was set in order to apply a load on the prong free-end and evaluate the induced deformation in term of static displacement x. The elastic constant can be retrieved using the linear relation F = k · x. The analysis was performed for both the QTFs and the results are shown in Fig. 5.

Fig. 5.

(a) COMSOL simulation of a boundary load applied at the far end of I-QTF. (b) COMSOL simulation of a boundary load applied at the far end of T-QTF. The color scales gave the displacement from equilibrium position, in meters.

The applied load on the upper-left edge of the two tuning forks had an intensity of 1 N/m, resulting in a total applied force F = 0.25 mN. The static displacement induced on the I-QTF is equal to 592 nm and therefore the simulated elastic constant k turns out to be 422.3 N/m, in excellent agreement with the prediction by using Eq. (4) (422.19 N/m). The static displacement induced on the T-QTF instead is 17 nm, resulting in an elastic constant k = 14,695.5 N/m. By using the electrical resistance values of 157.5 kΩ and 843.1 kΩ measured for T-QTF and I-QTF, respectively, the ratio between the vibration amplitude for the QTFs results a_I-QTF/ a_T-QTF = 2.6, comparable with the ratio between peak interferometric readout signals S_I-QTF/ S_T-QTF = 2.13. Hence, the larger the vibration amplitude, the higher the optical readout signal. This proves that the QTF geometry could be optimized when interferometric measurement systems are to be adopted.

The I-QTF is capable to operate at its first overtone mode of ∼21.40 kHz, showing a quality-factor of ∼12,000 suitable for QEPAS operation Thereby, keeping the experimental conditions fixed, both piezoelectric and interferometric readouts were performed, while I-QTF is excited at the first overtone mode. The acquired spectral scans for both readout techniques are shown in Fig. 6.

Fig. 6.

(a) Piezoelectric signal acquired with bare I-QTF operating at its 1^st overtone mode. The SNR is equal to 51. (b) interferometric signal acquired with bare I-QTF operating at its 1^st overtone mode. The SNR is equal to 39.

The peak signal obtained from the piezoelectric readout is equal to ∼18 mV with a noise level of 0.35 mV, corresponding to a SNR ∼ 51, 2.2 times higher than that obtained when the I-QTF operated at the fundamental mode. This result is in agreement with that observed in [21] and demonstrates the possibility to increase the piezoelectric readout sensitivity through the use of QTFs optimized to operate at the first resonance overtone. The signal obtained with the interferometric technique is equal to ∼97 μV with an estimated noise of 2.5μV, showing a SNR ∼ 39, comparable with that measured when I-QTF vibrates at the fundamental mode. However, a signal 5 times lower with respect to the fundamental mode has been observed, caused by a lower vibration amplitude of the overtone mode with respect to the fundamental one. This proves that the interferometric technique is not influenced by the use of the flexural resonance mode of the I-QTF and thereby, any investigation when implementing resonator tubes is worthless.

In Table 2, all results obtained by using the piezoelectric or the optical readouts are summarized.

Table 2.

PAS signals, 1σ noise levels and signal-to-noise ratios (SNRs) measured for I-QTF (at the fundamental and first overtone mode) and T-QTF, when piezoelectric or interferometric readouts are selected.

	Frequency (kHz)	Piezoelectric readout			Interferometric readout
		Signal (mV)	Noise (mV)	SNR	Signal (μV)	Noise (μV)	SNR
I-QTF fund mode	3.44	0.55	0.024	23	490	14.0	35
T-QTF	12.45	30.15	0.36	84	230	3.8	60
I-QTF overt mode	21.40	18.0	0.35	51	97	2.5	39

Despite the highest PAS interferometric signal (490 μV) has been measured with the I-QTF, the highest interferometric SNR (60) has been achieved when using T-QTF. This is due to the 1/f dependence of the noise level, demonstrating that the optical readout is sensitive to the flicker noise of the acoustic source. Thus, even if the vibration amplitude is the figure of merit to be optimized to enhance the optical readout signal, moving to lower frequency negatively affects the noise level. For the piezoelectric readout, the ultimate noise level is dominated by the thermal noise of the QTF (which scales as the inverse of the root of the electrical resistance) and the electronic noise of the transimpedance amplifier, which usually scales linearly with the resonance frequency.

5. Conclusions

In this work, we reported on a comparison between the piezoelectric and interferometric readouts of vibrations in quartz tuning forks (QTFs) when used as sound wave transducers in QEPAS sensors. We demonstrated that by playing on the prongs geometry design it is possible to enhance interferometric readout signal with respect to the piezoelectric one or vice versa. For piezoelectric readout, the QTF showing the highest performance has a T-shape prong geometry and a resonance frequency of 12.45 kHz. Among custom QTFs employed so far in QEPAS, the one providing the largest vibration amplitude is the I-QTF, showing a resonance frequency of 3.44 kHz for the fundamental mode and ∼21.40 kHz for the 1st overtone mode. Both QTFs were implemented in a QEPAS sensor and tested for the detection of water vapor concentration in the room air. The signal-to-noise ratio of piezoelectric readout results ∼ 40 % higher than the interferometric one when the bare T-QTF was employed. This SNR difference increases up to 80 % when the QTF was acoustically coupled with a dual-tube resonator system. Conversely, an interferometric SNR ∼ 50 % times larger than the piezoelectric one has been measured when implementing the I-QTF, having a rectangular prong geometry. When operating at the 1st overtone mode, the I-QTF provide a piezoelectric SNR ∼2.2 times higher than when operating at the fundamental mode, while the interferometric SNR remains nearly unchanged (∼10 % increases).

Finally, with respect to QEPAS, optical readout PAS no longer require restriction on the use of piezoelectric materials. Consequently, keeping fixed the tuning fork geometry, materials showing a lower Young modulus such as KBr [22] or KCl [23] could provide higher sensitivity.

Funding

This work was supported by THORLABS GmbH, within the joint-research laboratory PolySense. We also acknowledge the support from European Research Council (ERC) (615170) and LASERLAB-EUROPE (654148).

Biographies

Stefano Dello Russo obtained his M.S. degree (cum laude) in Physics in 2018 from the University of Bari. From the same year, he is a PhD student at the Physics Department of the University of Bari, developing his research work at PolySense Lab, joint-research laboratory between Technical University of Bari and THORLABS GmbH. Currently, his research activities are focused on the development of custom tuning forks for Quartz-Enhanced Photoacoustic Spectroscopy and on the study of vibrational-translational dynamics of molecules in gaseous mixtures.

Sheng Zhou is a Ph.D. candidate at Vrije Universiteit Amsterdam, Faculty of Science. He received his B.Sc. degree in Material Processing and Control Engineering from Huazhong University of Science and Technology in 2012. Also, he received his Master degree in Material Processing Engineering from Huazhong University of Science and Technology in 2015. His current research interests include photoacoustic spectroscopy, gas sensing, fiber optic sensors, and instrument miniaturization.

Andrea Zifarelli obtained his M.S. degree (cum laude) in Physics in 2018 from the University of Bari. From the same year, he is a PhD student at the Physics Department of the University of Bari, developing his research work at PolySense Lab, joint-research laboratory between Technical University of Bari and THORLABS GmbH. Currently, his research activities are focused on the development of gas sensors based on Quartz-Enhanced Photoacoustic Spectroscopy for detection of gas mixtures and broadband absorbers, exploiting non-conventional laser sources.

Pietro Patimisco obtained the Master degree in Physics (cum laude) in 2009 and the PhD Degree in Physics in 2013 from the University of Bari. Since 2018, he is Assistant professor at the Technical University of Bari. He was a visiting scientist in the Laser Science Group at Rice University in 2013 and 2014. Dr. Patimisco’s scientific activity addressed both micro-probe optical characterization of semiconductor optoelectronic devices and optoacoustic gas sensors. Recently, his research activities included the study and applications of trace-gas sensors, such as quartz-enhanced photoacoustic spectroscopy and cavity enhanced absorption spectroscopy in the mid infrared and terahertz spectral region, leading to several publications, including a cover paper in Applied Physics Letter of the July 2013 issue.

Angelo Sampaolo obtained his Master degree in Physics in 2013 and the PhD Degree in Physics in 2017 from University of Bari. He was a visiting researcher in the Laser Science Group at Rice University from 2014 to 2016. Since May 2017, he is a Post-Doctoral Research associate at University of Bari. His research activity has included the study of the thermal properties of heterostructured devices via Raman spectroscopy. Most recently, his research interest has focused on the development of innovative techniques in trace gas sensing, based on Quartz-Enhanced Photoacoustic Spectroscopy and covering the full spectral range from near-IR to THz. His achieved results have been acknowledged by a cover paper in Applied Physics Letter of the July 2013 issue.

Marilena Giglio received the M.S. degree (cum laude) in Applied Physics in 2014, and the PhD Degree in Physics in 2018 from the University of Bari. In 2012 she’s been visiting the Academic Medical Center of Amsterdam as a trainee. In 2015 she was a Research Assistant with the Department of Physics, University of Bari. She was a visiting researcher in the Laser Science Group at Rice University from 2016 to 2017. Since 2018, she is a Post-Doc Research Assistant at the Physics Department of the Technical University of Bari. Her research activity is focused on the development of gas sensors based on Quartz-Enhanced Photoacoustic Spectroscopy and on the optical coupling of hollow-core waveguides with interband- and quantum-cascade lasers.

Davide Iannuzzi obtained his PhD at the University of Pavia in 2002. He then went to the USA, where he was postdoctoral fellow at Bell Labs and Harvard. In 2005, he moved to the Vrije Universiteit Amsterdam, where he is now Professor in Experimental Physics. He is one of the two the co-founders of Optics11 - a 40+ people company that designs, produces, and sells optical fiber sensors all across the world. In Amsterdam, he has also created a knowledge transfer and entrepreneurship laboratory, which he is still the director of. Iannuzzi, who also holds an MBA from TIAS School for Business and Society (2015), has received several international recognitions, published nearly 100 papers, collected more than 7 million euros of research funds (including 3 ERC grants), and has written the book “Entrepreneurship for Physicists”, which nowadays counts nearly 20,000 downloads (entire book and single chapters).

Vincenzo Spagnolo obtained the PhD in physics in 1994 from University of Bari. From 1997 to 1999, he was researcher of the National Institute of the Physics of Matter. Since 2004, he works at the Technical University of Bari, formerly as assistant and associate professor and, starting from 2018, as full Professor of Physics. He is the director of the joint-research lab PolySense between Technical University of Bari and THORLABS GmbH, fellow member of SPIE and senior member of OSA. His research interests include optoacoustic gas sensing and spectroscopic techniques for real-time monitoring. His research activity is documented by more than 190 publications and two filed patents. He has given more than 50 invited presentations at international conferences and workshops.