Abstract
We present fast functional optical-resolution photoacoustic microscopy (OR-PAM) that can simultaneously image hemoglobin concentration, blood flow speed, and oxygen saturation with three-pulse excitation. To instantaneously determine the blood flow speed, dual-pulse photoacoustic flowmetry is developed to determine the blood flow speed from photoacoustic signal decay in sub-microseconds. Grueneisen relaxation effect is compensated for in the oxygen saturation calculation. The blood flow imaging is validated in phantom and in vivo experiments. The results show that the flow speed can be measured accurately in sub-microseconds by comparing the dual-pulse flowmetric method with photoacoustic Doppler flowmetry. Wide-field OR-PAM of hemoglobin concentration, blood flow speed, and oxygen saturation are demonstrated in the mouse ear. This technical advance enables more biomedical applications for fast functional OR-PAM.
Keywords: Dual-pulse photoacoustic flowmetry, Grueneisen relaxation effect, Multi-functional, Sub-microseconds
1. Introduction
Hemoglobin concentration (CHb), oxygen saturation (sO2), and blood flow (vflow) are important functional parameters for diagnosing, staging, and study of many diseases, such as diabetes, stroke, cancer, and neural degenerative diseases [[1], [2], [3], [4], [5], [6], [7], [8], [9],45,47]. Taking advantage of high sensitivity to optical absorption and subcellular spatial resolution, optical-resolution photoacoustic microscopy (OR-PAM) has demonstrated superior imaging of these functional parameters in vivo [[10], [11], [12], [13], [14], [15], [16],46]. Simultaneous imaging of the three parameters even enables quantification of the regional metabolic rate of oxygen (MRO2). High imaging speed is of great interest for increasing throughput, mitigating motion artifacts, and enabling the study of temporal and spatial connectivity among functional parameters, tissue activities, and diseases progress.
OR-PAM measures hemoglobin concentration with a single laser pulse excitation at an isosbestic wavelength. In sO2 measurement, OR-PAM needs to acquire PA signals at two or more optical wavelengths. Pulse-by-pulse switching the excitation wavelengths has been employed for fast OR-PAM of sO2. OR-PAM can image blood flow speed using several different approaches, such as photoacoustic Doppler (PAD) [12,14,[17], [18], [19]], photoacoustic correlation spectroscopy (PACS) [[20], [21], [22]], and thermal diffusion flowmetry (TDF) [[23], [24], [25], [26]]. Although each method has its own advantages, they all need tens to hundreds of PA measurements to calculate the flow speed, which makes photoacoustic blood flow imaging time-consuming. Simultaneous imaging of hemoglobin concentration, oxygen saturation, and blood flow has not achieved a speed comparable with the A-line speed.
Here we present new fast functional OR-PAM that can simultaneously measure hemoglobin concentration, oxygen saturation, and blood flow based on only three A-lines. Using a nanosecond pulsed laser and two stimulated-Raman-scattering (SRS) shifters [[27], [28], [29], [30]], we develop a three-wavelength (532, 545, and 558 nm) OR-PAM system that switches among the three wavelengths pulse by pulse. At each pixel, the OR-PAM system acquires three temporally separated A-line signals at the three wavelengths. The time delay between two adjacent laser pulses is ∼260 ns. Then, we quantify the hemoglobin concentration, oxygen saturation, and blood flow based on the three A-lines. The hemoglobin concentration and oxygen saturation are determined based on system calibration and a conventional linear spectral unmixing method [30,31]. To determine the blood flow speed, we propose a hypothesis that the blood flow can change the Grueneison relaxation effect even within sub-microseconds [32,33]. We test this hypothesis in phantom and in vivo experiments. A strong correlation between the blood flow speed and Grueneison relaxation effect is observed. Based on this phenomenon, we develop a dual-pulse approach to measure the blood flow speed from two adjacent A-lines. We compare the dual-pulse approach with a conventional photoacoustic Doppler method [12,14,[17], [18], [19]] in blood flow imaging. Phantom and in vivo experimental results show that the dual-pulse method can measure blood flow accurately. Taking advantage of fast dual-pulse flow measurement, we observed periodic changes of blood flow speed in the artery caused by heart beating. Using the three-wavelength OR-PAM system, we demonstrate wide-field simultaneous imaging of hemoglobin concentration, oxygen saturation, and blood flow with a single raster scan.
2. Method
2.1. Dual-pulse photoacoustic flowmetry
To determine the blood flow speed, we develop a dual-pulse method based on the Grueneisen relaxation effect. In PA imaging, the Grueneisen parameter depends on the local temperature. The local temperature can change due to thermal diffusion and blood flow. This phenomenon has been explored in PA flowmetry mainly at milliseconds to seconds time scales [34,35]. In the existing methods, multiple PA measurements during a long period of time are employed to calculate the blood flow speed. Here we study the Grueneisen relaxation effect between two A-lines with only sub-microseconds delay. We hypothesize that the blood flow can significantly affect the Grueneisen relaxation effect in such a short time delay. We model the relationship between the dual-pulse Grueneisen relaxation effect and the blood flow speed as an exponential decay model. After calibration, we can measure the flow speed within sub-microseconds.
In the dual-pulse flowmetric method, we use two short-delayed nanosecond laser pulses to excite two PA signals. The time delay between the two laser pulses is . In linear range, the induced PA amplitudes and can be approximated as [36,37]
| (1) |
where k is the detection sensitivity, is the Grueneisen parameter at baseline temperature, is the increased Grueneisen parameter at the second PA excitation, is the light-to-heat conversion coefficient, and are the optical fluences, and and are the optical absorption coefficients at the two laser wavelengths. If we use two isosbestic wavelengths, i.e., 532 nm and 545 nm, the absorption coefficients at the two wavelengths are independent of oxygen saturation, and is a known constant. In the second PA excitation, the increased Grueneisen parameter is proportional to the local temperature rise . Here we model the increased Grueneisen parameter as [23,24,26,32]
| (2) |
where and are constant coefficients, is proportional to the initial local temperature rise caused by the first PA excitation, the exponential decay describes the thermal clearance related to thermal conduction and convection, is a time constant related to thermal conduction, is the flow speed.
We simplify the second photoacoustic amplitude as
| (3) |
where . The coefficients , , and are independent of the blood flow and can be determined via system calibration. In superficial tissue, we can approximate the ratio of to from the tissue surface fluences. To calibrate , , and , we set the flow speed and time delays to different values and then fit the three coefficients from the PA measurements. If a different equals to , other parameters (e.g. surface fluence) remain the same and flow speed is set to 0, then we can simplify Eq. (3) as = and = respectively for time delays and . We can obtain . After calibration, we can determine the blood flow speed from the two measured PA signals.
2.2. Compensation for Grueneisen relaxation effect in sO2 measurement
Without considering the Grueneisen relaxation effect, the sO2 can be determined from the PA signals at 532 nm and 558 nm as follows [30]
| (4) |
where , and are the PA amplitudes and optical fluences at λ1 = 532 nm and λ3 = 558 nm, and are the molar extinction coefficients of HbR and HbO2 at the two wavelengths [13,30,38].
In the three-pulse excitation, the temperature rise caused by the 1st and 2nd pulses may increase the Grueneisen parameter and the amplitude of the 3rd PA signal, leading to underestimated sO2. To compensate for this error, the elevated Grueneisen parameter is taken into consideration in the sO2 measurement.
| (5) |
where is the time delay between the 1st and 3rd pulses, and is the time delay between the 2nd and 3rd pulses. With the determined flow speed , we can calculate a modified as
| (6) |
Replacing the with in Eq. (4), we can compensate for the elevated Grueneison parameter in sO2 computation.
If the absorption coefficient is too high or the axial resolution Δz is too low, the PA signal may nonlinearly depend on the [31]. A nonlinear model can be used to compensate for the nonlinearity in sO2 imaging [31]. However, in this work, because we use three wavelengths to determine three parameters, i.e., hemoglobin concentration, oxygen saturation, and flow speed, we did not compensate for the nonlinearity and simply use a linear model in the oxygen saturation calculation. In the future, if we have four or more wavelengths, then we can compensate for the nonlinearity and determine the three parameters at the same time.
2.3. Three-wavelength OR-PAM system
We develop an OR-PAM system that can acquire three-wavelength PA signals in sub-microseconds. Fig. 1a shows a schematic of the imaging system. We use a nanosecond pulsed laser (532-nm wavelength, VPFL-G-20, Spectra-Physics) as a pump laser. Two optical fibers are pumped to generate two new wavelengths, i.e., 545 nm and 558 nm. The pulse repetition rate of the pump laser can reach up to 1 MHz and the pulse width is set to 7 ns. Two sets of halfwave plates (HWP1 and HWP2) and polarizing beamsplitters (PBS1 and PBS2) separate the pump beam into three paths: a 532-nm direct path, a 545-nm Raman path, and a 558-nm Raman path. The half-wave plates (WPH10E-532, Thorlabs Inc) in front of the two PBSs adjust the powers of the three paths. In this work, we didn’t compensate for the fluctuations of the laser pulse energy via photodiode, because the stability of the SRS laser is quite good. We test the average, standard deviation (SD) and drift of the pulsed light energy for these wavelengths during 66.7 min.. The normalized average and SD for 532-nm, 545-nm, and 558-nm wavelengths are 33,545 24.4, 33,887 36.5, and 34522 45.5. And the energy drifts for these 3 wavelengths after 66.7 min. are 8 %, 10 % and 9 %, which we think are quite stable.
Fig. 1.
(a) Schematic of the three-wavelength OR-PAM system. Amp: amplifier, BS: beam splitter R/T: 10/90, DM: dichroic mirror 550 nm long-pass, DAQ: data Acquisition, FC: fiber coupler, HWP: half-wave plate, LPF: 540 nm long-pass filter, MMF: multi-mode fiber, PBS: polarizing beam splitter, PM-SMF: polarization-maintain single-mode fiber, SPF: 570 nm short-pass filter, UST: ultrasonic transducer, NDF: neutral density filter, WT: water tank (b) The time delays among different pulses measured by a photodiode.
In the 545-nm Raman path, a 50-m polarization-maintaining single-mode fiber (PM-S405-XP, NUFERN) is used to generate the 545-nm wavelength through SRS effect and delay it by 260 ns measured by a photodiode in Fig. 1b. The theoretical time delay in a 50-m fiber is ∼243 ns. Due to the time delay in free space, the actual time delay increases. Via adjusting the incident pulse energy and polarization state, the 50-m fiber maximizes the pulse energy of the 545-nm wavelength and avoids generating other stokes wavelengths. Here we adjust the energy and polarization to generate only the 1st wavelength (545-nm) but not other higher order Stokes wavelengths. The beam combination is for 532-nm and 545-nm wavelengths. A long-pass filter (LPF, T540lpxr, CHROMA) is placed after the 50-m Raman fiber to pass the 545-nm wavelength and reflect the 532-nm wavelength. For system calibration, another 30-m polarization-maintaining single-mode fiber is used to generate and delay the 545-nm wavelength by 163 ns.
In the 558-nm Raman path, the pump beam is coupled into a 100-m graded-index multi-mode fiber (GIMMSC(50/125)HT, FIBERCORE) to generate 558-nm wavelength with a 512-ns time delay. Because the SRS threshold of a single-mode fiber is limited to its length, the highest 558-nm pulse energy generated by a 100-m single-mode fiber is not enough for sensitive PA imaging. A long fiber is easier to generate Stokes wavelength via SRS and makes the Raman threshold lower [30,48]. Here a 100-m graded-index multi-mode fiber is used to increase the SRS threshold [40]. Although the 100-m SRS fiber is multi-mode for the pump light, the generated 558-nm wavelength is nearly single mode due to the Raman beam clean-up effect [[39], [40], [41], [42]]. A half-wave plate adjusts the polarization of the incident light to maximize the 558-nm energy. A short pass filter (RPE570SP, OMEGA) after the 100-m fiber rejects other wavelengths longer than 570 nm.
A 550-nm long-pass dichroic mirror (T550lpxr-UF1, CHROMA) is used to combine the 545-nm and 558-nm wavelengths. A 10/90 beam splitter combines the direct 532-nm wavelength with the delayed 545-nm and 558-nm wavelengths. A variable neutral density filter (NDC-50C-2, Thorlabs Inc) is added to each path to adjust the output energy. At the last stage, the three wavelengths are coupled into an OR-PAM probe via a 2-meter single-mode fiber (P1-460B-FC-2, Thorlabs Inc).
The fiber coupling efficiencies for all the single-mode beams are higher than 50 %. When coupling the 558-nm beam to the 2-m single-mode fiber, because the 558-nm wavelength is not 100 % single mode, the coupling efficiency is ∼30 %. The pulse energy on the sample surface for each wavelength is higher than 100 nJ.
In the OR-PAM probe, the laser beam from the 2-m fiber is focused by a pair of achromatic doublets (AC064-013-A, Thorlabs). The focused optical beam is reflected on an optical/acoustic beam combiner, transmits through a plano-concave lens (45–697, Edmund optics), then illuminates the sample. Induced ultrasonic waves are collimated by the plano-concave lens, transmits through the optical/acoustic beam combiner, and detected by a 50-MHz broadband piezoelectric transducer (V214-BC-RM, Olympus). To optimize the detection sensitivity, the focused optical beam is coaxially and confocally aligned with the focused ultrasonic detection beam.
At each pump laser pulse, the laser system generates three temporally separated laser pulses at 532, 545, and 558 nm, and the OR-PAM system sequentially acquires three depth-resolved A-lines at the three wavelengths. Volumetric PA images are acquired by raster scanning the PA probe in the lateral plane. The lateral resolution is 3.4 μm. The time to acquire one set of three-wavelength PA signals is ∼500 ns. If the mechanical scanning or blood flow speed is less than 1 cm/s, the misalignment among the three A-lines would be smaller than 5 nm, which is negligible compared with the lateral resolution. Detailed information of the OR-PAM probe can be referred to in our previous work [11,13,30,31].
3. Results
3.1. Calibration of and validation of dual-pulse flowmetry
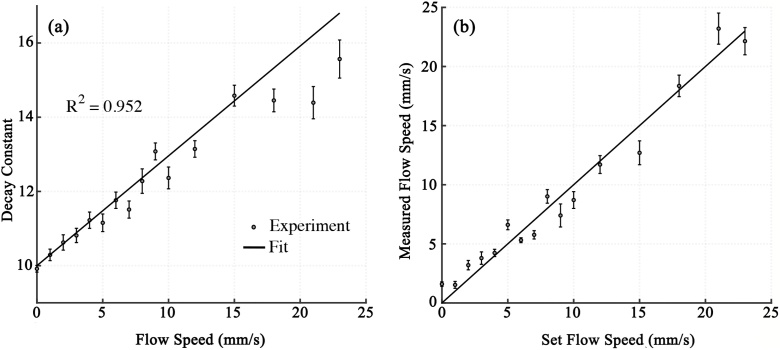
To valid the exponential model in Eq. (3), we measure the decay constants at different blood flow speeds ranging from 0 to 23 mm/s in a blood phantom. The phantom is anticoagulated bovine blood filled in transparent rubber tube (0.25-mm inner diameter, TYGON S-54- HL, Norton Performance Plastics, NJ). The blood flow speed is set by a syringe pump. The photoacoustic probe and the blood sample are immersed in a water tank for acoustic coupling. The laser repetition rate is 4 kHz. The pulse energy on the sample surface is 100 nJ for each wavelength. The exponential decay model is fitted with the least square criteria. The exponential decay constants at different set flow speeds are plotted in Fig. 2a. As expected, the decay constant is a linear function of the flow speed with a determination coefficient (R2) of 0.952, indicating the high dependence of the Grueneisen relaxation effect on the flow speed. , , and are fitted as 0.11 ± 0.01 (SD), 10.19 ± 0.85 (SD) and 0.30 ± 0.04 (SD). With the fitted coefficients, the flow speed can be determined from two PA signals. Using the same experimental setup, we validate the flow speed measurement in blood phantom. As shown in Fig. 2b, the measured flow speed is averaged by 100 times and compared with the set flow speed. The measured flow speed is proportional to the set flow speed, showing that the dual-pulse approach is applicable for measuring the blood flow speed.
Fig. 2.
(a) Exponential decay constant versus set flow speed. Error bars are standard deviations. (b) Measured flow speed versus set flow speed. Error bars are standard deviations.
3.2. In vivo blood flow imaging
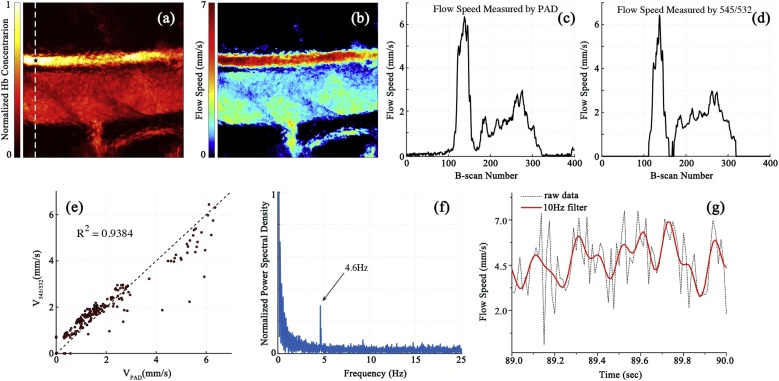
We use dual-pulse flowmetry to measure blood flow speed in the mouse ear. The in vivo experiment is carried out on anaesthetized female BALB/c mice (4 weeks), with permission from the animal ethical committee of the City University of Hong Kong. The region of interest (ROI) shown in Fig. 3a is . The raster scanning takes 40 s with a 10-Hz b-scan rate. The laser repetition rate is 4 kHz and the pulse energy for each wavelength is ∼80 nJ. Using the fitted model, the blood flow speed in the ROI is calculated at each pixel from the PA signals at 545 nm and 532 nm as shown in Fig. 3b. In the artery, the averaged flow speed is ∼6 mm/s. In the vein, the averaged flow speed is ∼3 mm/s.
Fig. 3.
(a) PA imaging of blood vessels in the mouse ear acquired with 532-nm wavelength. (b) Flow speed image measured by dual-pulse flowmetry. (c) and (d) flow speed profiles along with the dashed white line in (a) measured by the photoacoustic Doppler method and the dual-pulse method, respectively. (e) Linear relationship between the PA Doppler results and the dual-pulse results. A linear fitting gives the R2 of 0.9384. VPAD is the flow speed measured by PA Doppler method. V545/532 is the flow speed measured by the dual-pulse method. (f) Spectrum of the dual-pulse flow speed in the artery as labeled with a black star in figure a. A heartbeat rate of 4.6 Hz is observed. (g) Time-domain blood flow speed in the artery which is averaged by 100 times. The red line is a lowpass filtered result cut off at 10 Hz.
For comparison, both PA Doppler (PAD) flowmetry and dual-pulse flowmetry are used to measure the same blood flow speed in the mouse ear. Because PAD needs to use multiple A-lines to calculate flow speed, the scanning mode is changed to acquiring multiple successive A-lines at each point. We scan the PA probe along a dashed white line in Fig. 3a and measure the flow speed profile using the two methods. 200 successive A-lines at each point are used to do autocorrelation for PAD calculation. In the dual-pulse method, each pair of 545-nm and 532-nm PA data can calculate a flow speed. For comparison, we average the dual-pulse flow result over all A-line pairs. Flow results calculated by the two methods are shown in Fig. 3c and d. We further compare the two results by fitting them to a linear regression model, as shown in Fig. 3e. The determination coefficient R2 is 0.938, indicating that the flow results measured by the two methods match well.
To further demonstrate the high speed of dual-pulse flowmetry, we measure the mouse heartbeat in the artery. The measurement spot is labeled with a black star in Fig. 3a. We calculate the maximum amplitudes of multiple successive A-lines and determine the blood flow speeds by Eq. (3). Fourier transformation is applied to the blood flow speeds at multiple A-lines. The frequency spectrum shows a peak at ∼4.6 Hz in Fig. 3f, which matches with the heartbeat rate of the mouse under anesthesia [43,44]. The heart beating can also be visible in the time domain as shown in Fig. 3g. We average 100 times and then filter the data with a 10-Hz lowpass filter. The heartbeat cycles become obvious in the measured blood flow speeds. This result shows the dual-pulse method is advantageous in A-line based flow imaging.
3.3. Simultaneous imaging of multiple functional parameters
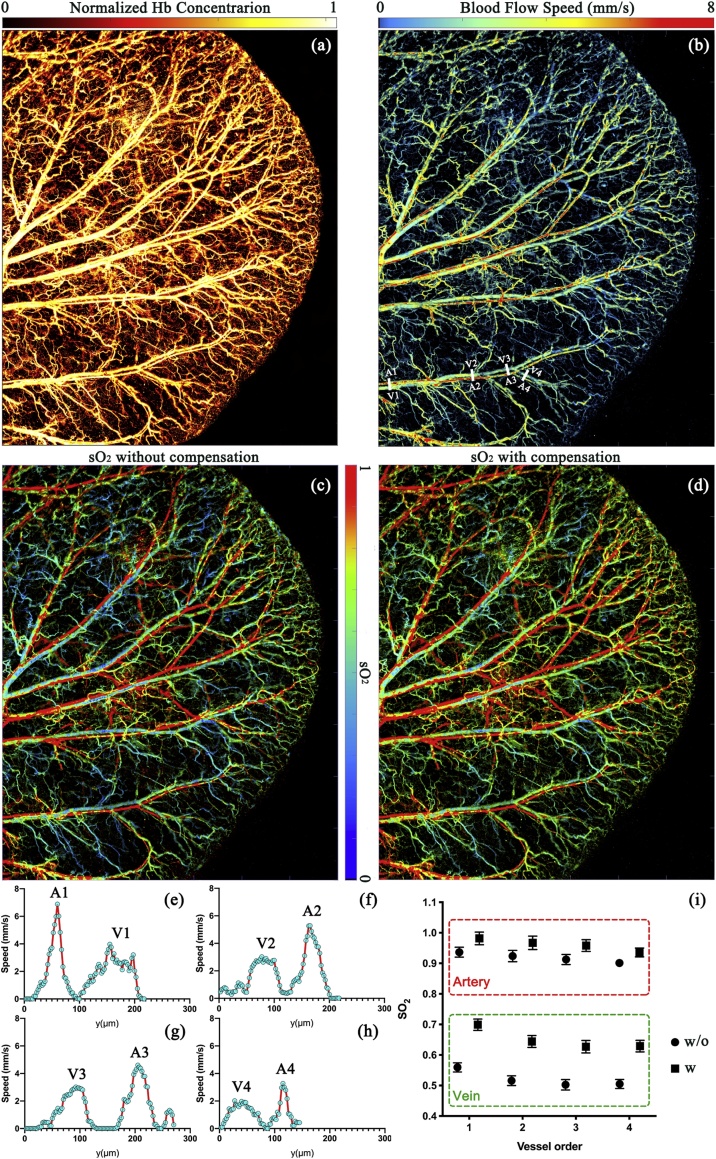
Using the three-wavelength OR-PAM system, we simultaneously quantify hemoglobin concentration, blood flow speed, and oxygen saturation in vivo. Due to the Grueneisen relaxation effect, one laser pulse may increase the PA amplitude generated by the following laser pulses. This may cause a systematic error in sO2 calculation. With system calibration, we show that we can compensate for the Grueneisen relaxation effect in the sO2 imaging. In vivo sO2 comparison results are shown in Fig. 4. The laser repetition rate is 4 kHz. Pulsed energy for each wavelength is ∼80 nJ. The imaging area is . Fig. 4a shows the normalized hemoglobin concentration imaged at 532 nm. The system has enough SNR (>20 dB) to show the capillaries. The blood flow speed calculated by the dual-pulse method is shown in Fig. 4b. Four artery-vein pairs of vessels labeled with white lines are selected to plot profiles of the blood flow speed, as shown in Fig. 4e–h. From the root to the tip of the ear, the blood flow speed in the artery decreases from ∼7 mm/s to ∼3.3 mm/s, and in the vein, the flow speed maintains ∼2 mm/s. sO2 images without and with compensation for Grueneisen relaxation effect are shown in Fig. 4c and d. Artery-vein pairs labeled with white lines are selected to compare the sO2 values. As shown in Fig. 4i, without compensation, the artery sO2 values at the 1st to the 4th spots are 0.94 ± 0.01 (SE), 0.92 ± 0.02 (SE), 0.91 ± 0.02 (SE) and 0.90 ± 0.02 (SE), and the vein sO2 values at the same spots are 0.56 ± 0.01 (SE), 0.52 ± 0.02 (SE), 0.50 ± 0.02 (SE), 0.50 ± 0.01 (SE). With compensation, the artery sO2 values increase to 0.98 ± 0.02 (SE), 0.96 ± 0.02 (SE), 0.95 ± 0.02 (SE), 0.94 ± 0.01 (SE), and the vein sO2 values become 0.69 ± 0.02 (SE), 0.64 ± 0.02 (SE), 0.63 ± 0.02 (SE), 0.63 ± 0.01 (SE).
Fig. 4.
(a) Microvascular structure of the mouse ear. (b) Blood flow speed measured by the dual-pulse method. (c) and (d) sO2 imaging without and with compensation for the Grueneisen relaxation effect. (e)-(h) Blood flow speed measured in selected artery-vein pairs labeled with white lines in (b). (i) Comparison of sO2 without and with compensation in selected artery-vein pairs labeled by white lines in (b). Error bars are standard errors.
4. Conclusion
In summary, we develop new functional OR-PAM that can simultaneously image hemoglobin concentration, blood flow speed, and oxygen saturation within sub-microseconds. A dual-pulse approach can measure the blood flow with only two short-delayed A-lines. An exponential model is developed to quantify the blood flow speed from two PA measurements. Based on the exponential model, the Grueneisen relaxation effect is compensated for in sO2 imaging. We develop a three-wavelength OR-PAM system to implement simultaneous multi-parameter imaging. Phantom experiments validate the linear relationship between the blood flow speed and the exponential decay constant. Blood flow speed up to 23 mm/s has been experimentally measured by dual-pulse flowmetry. In vivo experiments are conducted in the mouse ear. Via comparing the dual-pulse flowmetric results with existing photoacoustic Doppler results, we show that dual-pulse flowmetry can accurately measure blood flow speed and requires only two PA measurements in sub-microseconds. We also demonstrate simultaneous imaging of hemoglobin concentration, blood flow speed, and oxygen saturation in the mouse ear. The sO2 images without and with compensation for the Grueneisen relaxation effect show that the sO2 values in both arteries and veins can be compensated for. Unlike conventional functional OR-PAM, the dual-pulse flowmetry and three-wavelength OR-PAM do not need multiple repeated A-line imaging at one spot, which saves imaging time, increases throughput, and may mitigate potential motion artifacts. This technical advance enables dynamic functional imaging at the sub-microseconds scale.
Funding
This work is partially supported by the National Natural Science Foundation of China (NSFC) (81627805, 61805102); Research Grants Council of the Hong Kong Special Administrative Region (21205016, 11215817, 11101618); Shenzhen Basic Research Project (JCYJ20160329150236426, JCYJ20170413140519030).
Declaration of Competing Interest
The authors declare that there are no conflicts of interest related to this article.
Biographies

Chao Liu is a Ph.D. candidate student from Biomedical Engg Department in City University of Hong Kong. He received Bachelor degree from Xi'an Jiaotong University, and Master degree from Hong Kong University of Science and Technology. His research emphasis focuses on photoacoustic microscopy and biophotonics.

Yizhi Liang received the Bachelor degree from the Guangdong University of Technology, Guangzhou, China. and Ph.D. degree from the Jinan University, Guangzhou, China. He joined the Jinan University in 2017. His research focuses on fiber sensor, fiber laser, biophotonics, biomedical imaging, and their biomedical applications.

Lidai Wang received the Bachelor and Master degrees from the Tsinghua University, Beijing, and received the Ph.D. degree from the University of Toronto, Canada. After working as a postdoctoral research fellow in the Prof Lihong Wang's group, he joined the City University of Hong Kong in 2015. His research focuses on biophotonics, biomedical imaging, wavefront engineering, instrumentation and their biomedical applications. He has invented single-cell flowoxigraphy (FOG), ultrasonically encoded photoacoustic flowgraphy (UE-PAF) and nonlinear photoacoustic guided wavefront shaping (PAWS). He has published more 30 articles in peer-reviewed journals and has received four best paper awards from international conferences.
Contributor Information
Yizhi Liang, Email: lyz0528@jnu.edu.cn.
Lidai Wang, Email: lidawang@cityu.edu.hk.
References
- 1.Fagrell B., Intaglietta M. Microcirculation: its significance in clinical and molecular medicine. J. Intern. Med. 1997;241:349–362. doi: 10.1046/j.1365-2796.1997.125148000.x. [DOI] [PubMed] [Google Scholar]
- 2.Macé E., Montaldo G., Cohen I., Baulac M., Fink M., Tanter M. Functional ultrasound imaging of the brain. Nat. Methods. 2011;8:662. doi: 10.1038/nmeth.1641. [DOI] [PubMed] [Google Scholar]
- 3.Brizel D.M., Klitzman B., Cook J.M., Edwards J., Rosner G., Dewhirst M.W. A comparison of tumor and normal tissue microvascular hematocrits and red cell fluxes in a rat window chamber model. Int. J. Radiat. Oncol. 1993;25:269–276. doi: 10.1016/0360-3016(93)90348-y. [DOI] [PubMed] [Google Scholar]
- 4.Kamoun W.S., Chae S.-S., Lacorre D.A., Tyrrell J.A., Mitre M., Gillissen M.A., Fukumura D., Jain R.K., Munn L.L. Simultaneous measurement of RBC velocity, flux, hematocrit and shear rate in vascular networks. Nat. Methods. 2010;7:655. doi: 10.1038/nmeth.1475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kleinfeld D., Mitra P.P., Helmchen F., Denk W. Fluctuations and stimulus-induced changes in blood flow observed in individual capillaries in layers 2 through 4 of rat neocortex. Proc. Natl. Acad. Sci. U. S. A. 1998;95:15741–15746. doi: 10.1073/pnas.95.26.15741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Woolsey T.A., Rovainen C.M., Cox S.B., Henegar M.H., Liang G.E., Liu D., Moskalenko Y.E., Sui J., Wei L. Neuronal units linked to microvascular modules in cerebral cortex: response elements for imaging the brain. Cereb. Cortex. 1996;6:647–660. doi: 10.1093/cercor/6.5.647. [DOI] [PubMed] [Google Scholar]
- 7.McMillan D.E. The effect of diabetes on blood flow properties. Diabetes. 1983;32 doi: 10.2337/diab.32.2.s56. 56 LP – 63. [DOI] [PubMed] [Google Scholar]
- 8.Zhu X.-H., Chen J.M., Tu T.-W., Chen W., Song S.-K. Simultaneous and noninvasive imaging of cerebral oxygen metabolic rate, blood flow and oxygen extraction fraction in stroke mice. Neuroimage. 2013;64:437–447. doi: 10.1016/j.neuroimage.2012.09.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Matsuda H. Cerebral blood flow and metabolic abnormalities in Aizheimer’s disease. Ann. Nucl. Med. 2001;15:85–92. doi: 10.1007/BF02988596. [DOI] [PubMed] [Google Scholar]
- 10.Fang H., Maslov K., Wang L.V. Photoacoustic Doppler effect from flowing small light-absorbing particles. Phys. Rev. Lett. 2007;99:184501. doi: 10.1103/PhysRevLett.99.184501. [DOI] [PubMed] [Google Scholar]
- 11.Wang L., Maslov K., Yao J., Rao B., Wang L.V. Fast voice-coil scanning optical-resolution photoacoustic microscopy. Opt. Lett. 2011;36:139–141. doi: 10.1364/OL.36.000139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yao J., Maslov K.I., Shi Y., Taber L.A., Wang L.V. In vivo photoacoustic imaging of transverse blood flow by using Doppler broadening of bandwidth. Opt. Lett. 2010;35:1419–1421. doi: 10.1364/OL.35.001419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wang L., Maslov K., Wang L.V. Single-cell label-free photoacoustic flowoxigraphy in vivo. Proc. Natl. Acad. Sci. U. S. A. 2013;110:5759–5764. doi: 10.1073/pnas.1215578110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fang H., Maslov K., Wang L.V. Photoacoustic Doppler flow measurement in optically scattering media. Appl. Phys. Lett. 2007;91:264103. [Google Scholar]
- 15.Shi J., Wang L.V. Bessel-beam Grueneisen relaxation photoacoustic microscopy with extended depth of field. J. Biomed. Opt. 2015;20:116002. doi: 10.1117/1.JBO.20.11.116002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yao J., Gilson R., Maslov K.I., Wang L., Wang L.V. Calibration-free structured-illumination photoacoustic flowgraphy of transverse flow in scattering media. J. Biomed. Opt. 2014;19:46007. doi: 10.1117/1.JBO.19.4.046007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Brunker J., Beard P. Velocity measurements in whole blood using acoustic resolution photoacoustic Doppler. Biomed. Opt. Express. 2016;7:2789–2806. doi: 10.1364/BOE.7.002789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang R., Yao J., Maslov K.I., Wang L.V. Structured-illumination photoacoustic Doppler flowmetry of axial flow in homogeneous scattering media. Appl. Phys. Lett. 2013;103:94101. doi: 10.1063/1.4819735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yao J., Wang L.V. Transverse flow imaging based on photoacoustic Doppler bandwidth broadening. J. Biomed. Opt. 2010;15:021304. doi: 10.1117/1.3339953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chen S., Xie Z., Carson P.L., Wang X., Guo L.J. In vivo flow speed measurement of capillaries by photoacoustic correlation spectroscopy. Opt. Lett. 2011;36:4017–4019. doi: 10.1364/OL.36.004017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chen S.-L., Ling T., Huang S.-W., Baac H.W., Guo L.J. Photoacoustic correlation spectroscopy and its application to low-speed flow measurement. Opt. Lett. 2010;35:1200–1202. doi: 10.1364/OL.35.001200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ning B., Kennedy M.J., Dixon A.J., Sun N., Cao R., Soetikno B.T., Chen R., Zhou Q., Shung K.K., Hossack J.A. Simultaneous photoacoustic microscopy of microvascular anatomy, oxygen saturation, and blood flow. Opt. Lett. 2015;40:910–913. doi: 10.1364/OL.40.000910. [DOI] [PubMed] [Google Scholar]
- 23.Sheinfeld A., Eyal A. Photoacoustic thermal diffusion flowmetry. Biomed. Opt. Express. 2012;3:2610–2612. doi: 10.1364/BOE.3.000800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang L., Maslov K.I., Wang L.V. Ultrasound-heated photoacoustic flowmetry. J. Biomed. Opt. 2013;18:117003. doi: 10.1117/1.JBO.18.11.117003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang R., Wang L., Yao J., Yeh C.-H., Wang L.V. In vivo optically encoded photoacoustic flowgraphy. Opt. Lett. 2014;39:3814–3817. doi: 10.1364/OL.39.003814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Liu W., Lan B., Hu L., Chen R., Zhou Q., Yao J. Photoacoustic thermal flowmetry with a single light source. J. Biomed. Opt. 2017;22:96001. doi: 10.1117/1.JBO.22.9.096001. [DOI] [PubMed] [Google Scholar]
- 27.Hajireza P., Forbrich A., Zemp R.J. Multifocus optical-resolution photoacoustic microscopy using stimulated Raman scattering and chromatic aberration. Opt. Lett. 2013;38:2711–2713. doi: 10.1364/OL.38.002711. [DOI] [PubMed] [Google Scholar]
- 28.Hajireza P., Forbrich A., Zemp R. In-vivo functional optical-resolution photoacoustic microscopy with stimulated Raman scattering fiber-laser source. Biomed. Opt. Express. 2014;5:539. doi: 10.1364/BOE.5.000539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Xu L., Alam S., Kang Q., Shepherd D.P., Richardson D.J. Raman-shifted wavelength-selectable pulsed fiber laser with high repetition rate and high pulse energy in the visible. Opt. Express. 2017;25:351–356. doi: 10.1364/OE.25.000351. [DOI] [PubMed] [Google Scholar]
- 30.Liang Y., Jin L., Guan B.-O., Wang L. 2 MHz multi-wavelength pulsed laser for functional photoacoustic microscopy. Opt. Lett. 2017;42:1452. doi: 10.1364/OL.42.001452. [DOI] [PubMed] [Google Scholar]
- 31.Liu C., Liang Y., Wang L. Optical-resolution photoacoustic microscopy of oxygen saturation with nonlinear compensation. Biomed. Opt. Express. 2019;10:3061–3069. doi: 10.1364/BOE.10.003061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wang L., Zhang C., Wang L.V. Grueneisen relaxation photoacoustic microscopy. Phys. Rev. Lett. 2014;113:174301. doi: 10.1103/PhysRevLett.113.174301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ma J., Shi J., Hai P., Zhou Y., Wang L.V. Grueneisen relaxation photoacoustic microscopy in vivo. J. Biomed. Opt. 2016;21:66005. doi: 10.1117/1.JBO.21.6.066005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pramanik M., Wang L.V. Thermoacoustic and photoacoustic sensing of temperature. J. Biomed. Opt. 2009;14:54024. doi: 10.1117/1.3247155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shah J., Park S., Aglyamov S.R., Larson T., Ma L., Sokolov K.V., Johnston K.P., Milner T.E., Emelianov S.Y. Photoacoustic imaging and temperature measurement for photothermal cancer therapy. J. Biomed. Opt. 2008;13:34024. doi: 10.1117/1.294036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wang L.V., Hi Wu. Wiley-Interscience.xiv; Hoboken, N.J: 2007. Biomedical Optics: Principles and Imaging; p. 362. [Google Scholar]
- 37.Xu M., Wang L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006;77 [Google Scholar]
- 38.Maslov K., Zhang H.F., Wang L.V. Effects of wavelength-dependent fluence attenuation on the noninvasive photoacoustic imaging of hemoglobin oxygen saturation in subcutaneous vasculature in vivo. Inverse Probl. 2007;23 [Google Scholar]
- 39.Murray J.T., Austin W.L., Powell R.C. Intracavity Raman conversion and Raman beam cleanup. Opt. Mater. (Amst.) 1999;11:353–371. [Google Scholar]
- 40.Baek S.H., Roh W.B. Single-mode Raman fiber laser based on a multimode fiber. Opt. Lett. 2004;29:153–155. doi: 10.1364/ol.29.000153. [DOI] [PubMed] [Google Scholar]
- 41.Pourbeyram H., Agrawal G.P., Mafi A. CLEO Sci. Innov. Optical Society of America; 2013. SRS-mediated generation of new wavelengths from 523 nm to 1750 nm in a graded-index multimode optical fiber; p. CTu2E-7. [Google Scholar]
- 42.Chiang K.S. Stimulated Raman scattering in a multimode optical fiber: evolution of modes in Stokes waves. Opt. Lett. 1992;17:352–354. doi: 10.1364/ol.17.000352. [DOI] [PubMed] [Google Scholar]
- 43.Minderer M., Liu W., Sumanovski L.T., Kügler S., Helmchen F., Margolis D.J. Chronic imaging of cortical sensory map dynamics using a genetically encoded calcium indicator. J. Physiol. 2012;590:99–107. doi: 10.1113/jphysiol.2011.219014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.(a) Ho D., Zhao X., Gao S., Hong C., Vatner D.E., Vatner S.F. Heart rate and electrocardiography monitoring in mice. Curr. Protoc. Mouse Biol. 2011;1:123–139. doi: 10.1002/9780470942390.mo100159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Jeon S., Kim J., Lee D., Baik J.W., Kim C. Review on practical photoacoustic microscopy. Photoacoustics. 2019;15:100141. doi: 10.1016/j.pacs.2019.100141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Moore M.J., El-Rass S., Xiao Y., Wang Y., Wen X.-Y., Kolios M.C. Simultaneous ultra-high frequency photoacoustic microscopy and photoacoustic radiometry of zebrafish larvae in vivo. Photoacoustics. 2018;12:14–21. doi: 10.1016/j.pacs.2018.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Liu W., Yao J. Photoacoustic microscopy: principles and biomedical applications. Biomed. Eng. Lett. 2018;8:203–213. doi: 10.1007/s13534-018-0067-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Agrawal G. Chapter 8- stimulated Raman scattering. In: G.B.T.-N.F.O, Agrawal Fifth E., editors. Opt. Photonics. Academic Press; Boston: 2013. pp. 295–352. [Google Scholar]