CoSIMS: An Optimized Trajectory Based Collision Simulator for Ion Mobility Spectrometry

Abstract

A new, multi-threaded, trajectory method based software platform, CoSIMS, is revealed and compared to reference MOBCAL collision cross sections (CCS). CoSIMS employs various molecular mechanics algorithms to lessen the computational resources required to simulate thousands of buffer gas - ion collisions, including the neglect of London dispersion interactions at long distances and the removal of trajectories that insignificantly contribute to the total CCS via an ellipsoidal projection approximation. The showcased program is used to calculate the collision cross sections of carbon fullerenes, proteins, and DNA strands of various lengths, sizes, and molecular weights, and compared against the the CCSs calculated by MOBCAL. Through this analysis, it is shown that the application the aforementioned algorithms enables for both faster and more reasonable CCS calculations than MOBCAL for highly elongated molecules such as nucleic acids; for all other molecules, CoSIMS is able to reproduce the CCSs generated by MOBCAL’s trajectory method within a few percent. Overall, CoSIMS is able to calculate nearly identical CCSs as MOBCAL in nearly two orders of magnitude less CPU time due to the various numerical methods implemented into the software, even when run on a single CPU core.

Graphical Abstract

1. Introduction

Ion Mobility Spectrometry - Mass Spectrometry (IMS-MS) is an experimental technique used for structural characterization of ionic species. Charged molecules are displaced through a linear drift-tube, or mobility chamber, by an electric field in which the transfer of momentum between the analyte and a buffer gas establish a constant drift speed.^1,2 Collisions with the buffer gas increase the ion’s drift time depending on the ion’s topological surface, described by the momentum transfer or collision cross-section (CCS) integral.^3,4 Therefore, IMS-MS is an attractive tool for characterizing conformational changes of biomacromolecules - how- ever, this crucially requires an accurate method to predict the CCS for a given analyte conformation.

The conventional approach for computing CCSs, termed the trajectory method (TM), simulates thousands of buffer gas-ionic collisions governed by a suitable interaction potential.⁵ The ”gold standard” for computing such CCSs is a FORTRAN 77 program called MOBCAL, developed by the Jarrold and coworkers at Indiana University 1996.^6,7 MOBCAL was originally designed to study metal-ion clusters,^8,9 fullerenes (i.e. C₆₀,C₁₂₀),^6,7,10 and small globular proteins (Cytochrome C, BPTI),^11,12 which are all roughly spherical analytes, mostly composed of only 100’s of atoms. In recent times, IMS-MS has become a popular method to detect conformational changes in macromolecular complexes that are orders of magnitude larger (i.e. Bacteriophage HK97: molecular weight 1.8 × 10⁷ Daltons). Unfortunately, it becomes increasingly difficult to compute TM CCSs using MOBCAL for systems over 100 kilo-Daltons.¹³ Even more difficult are studies of dynamic complexes such as nucleic acids or intrinsically unstructured proteins, where the CCS must be calculated as an ensemble average over many different structures generated from molecular dynamic simulations, further increasing the computational complexity.^14–16

To this end, the work presented here introduces a novel collision engine that calculates trajectory method CCSs of both small and large molecules, applies common molecular mechanic algorithms when appropriate to save computational time, and is designed for both single and multi-threaded computer systems. A summary of the most common CCS calculation methods used in practice will be covered in section 2, while the details of the algorithm used in our proposed Collision Simulator for Ion Mobility Spectrometry (CoSIMS) will be described in section 3. The most noteworthy of these features is CoSIMS’ ability to dynamically adjust the geometrical space of interactions to the topology of the ionic analyte, improving the accuracy of the CCS for elongated molecules such as nucleic acids. Finally, section 4 compares the accuracy of our model is compared to MOBCAL for various proteins, carbon fullerenes, and nucleic acids (DNA) of assorted sizes. Our analysis reveals that MOBCAL can not reliably handle molecules with large, asymmetrical geometries, as it breaks central assumptions in the algorithms implementation. This becomes readily apparent when comparing CCSs of highly similar molecular dynamic snapshots (Figures 5b and 6 in section 4) and therefore, CoSIMS was built from the ground up to adjust it’s functionality based on the geometry of the analyte.

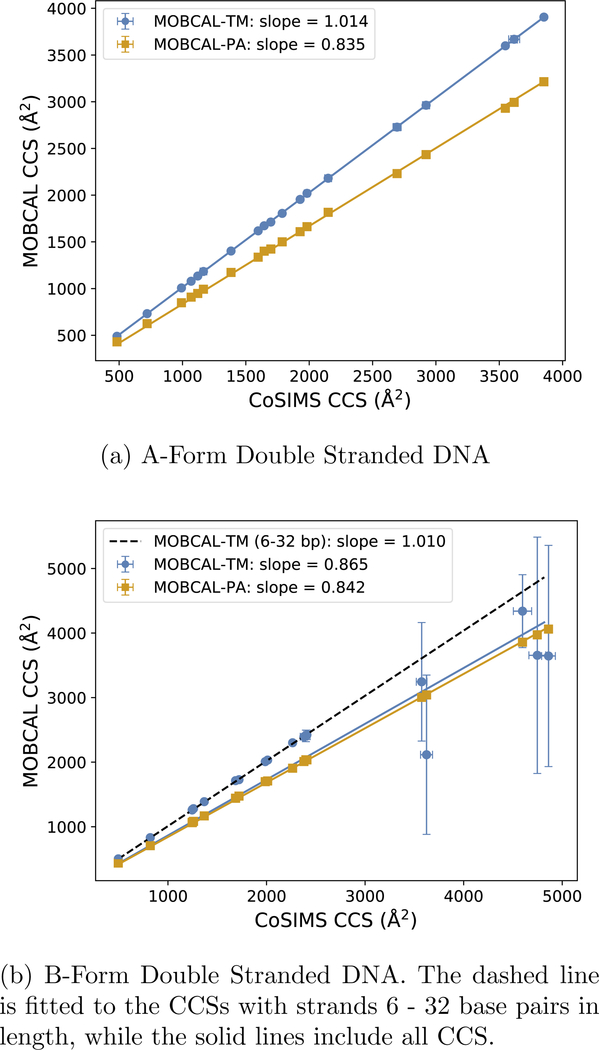
Figure 5:

Comparison between CCSs computed by CoSIMS and MOBCAL for (a) A-form ds DNA and (b) B-form ds DNA. Error bars are standard deviations from averaging over all 21 frames. PA results are also presented to show the relative change in CCS for individual structures.

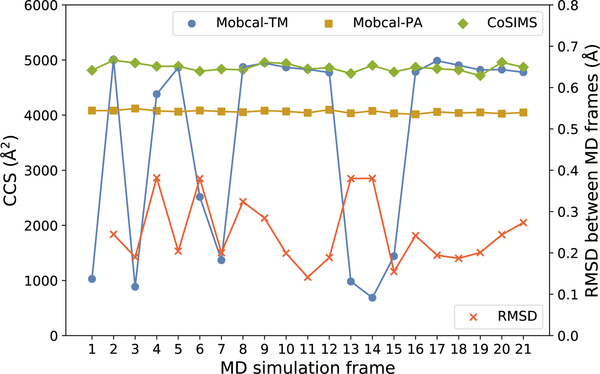
Figure 6:

CCS values for various MD frames of a 64 base pair, B-form, −14 charge state DNA. The RMSD on the right axis is between two consecutive frames and defined by Equation 12. Error bars for each of the CCS vales are smaller than the plot markers and are not shown in this figure. PA results are shown for comparison means only.

2. Theoretical Background

2.1. Ion Mobility and the Collision Cross Section Integrals

The majority of ion mobility experiments are conducted under low-field equilibrium conditions where the linear flux of ions with a total charge q along the direction of the field is balanced by the diffusion of ions against the field direction. The mass diffusion coefficient D of this experiment is related to the mobility K by the Nernst-Townsend-Einstein relation^1,2

$$K=\frac{qD}{k_{B}T}$$ (1)

The Chapman-Enskog description of diffusion allows us to write D, and thus K, in terms of momentum-transfer integrals Ω^(l,s) to first-order as^3,4

$$K=\frac{3}{16}\frac{q}{N}{\left(\frac{2\pi }{\mu k_{B}T}\right)}^{1/2}\frac{1}{{\Omega }^{(1,1)}}.$$ (2)

Here, N is the number density of the buffer gas and μ is the reduced mass of the ion species and a single gas atom. Ω^(1,1) is typically termed a collision cross-section (CCS), and although not technically the same as a momentum transfer integral as further pointed out in Gabelica and Marklund,¹⁷ it does reduce to a CCS under hard-sphere approximations and we will hereby refer to it as a cross-section. More specifically, Ω^(1,1) depends on the relative velocities v_r and scattering angles χ of the ion and the buffer gas,

$${\Omega }^{(1,1)}=\frac{1}{8}{\left(\frac{\mu }{k_{B}T}\right)}^3\int \text{d}{v}_r\int \text{d}b{v}_r^5{e}^{-m_1{v}_r^2/2kT}2\pi b(1-\cos \chi ).$$ (3)

Because this formulation of kinetic theory is written in terms of point-like particle collisions, we typically replace Ω^(1,1) by an orientally-averaged integral ${\Omega }_{avg}^{(1,1)}$ for describing polyatomic molecules that are anisotropic in their topologies:6,7,18,19

$${\Omega }_{avg}^{(1,1)}=\frac{1}{8\pi }{\int }_0^{2\pi }\text{d}\varphi {\int }_0^{\pi }\text{d}\theta \sin \theta {\int }_0^{2\pi }\text{d}\gamma {\Omega }^{(1,1)}$$ (4)

with Euler angles ϕ, θ, and γ. The scattering angle χ = χ(v_r , b, ϕ, θ, γ) depends on the interaction potential between the two species, and thus the integral must be solved numerically. As Ω depends on the size and shape of the ion, one of the major challenges of ion mobility is how to determine its value.

In order to lower the computational time of calculating CCSs, projection approximations^6,7,18,20 and elastic/diffusive hard sphere scattering^7,18,21 models have been developed along side trajectory methods. While some of these methods, specifically the projection approximations, are used in to study proteins, others require additional calibration curves and shape factors to accurately approximate the TM CCSs calculated by MOBCAL.^22–26 However, an implicit assumption of these methods is that the approximated CCS, calculated via hard sphere or projection methods, can be used in place of the momentum transfer integrals, provided that they are parameterized to replicate the CCSs from experimental data^7,24 or a TM such as MOBCAL.^22,26 Not only are these models approximate in nature, but demonstrating their accuracy through the comparison to MOBCAL, which is designed for studying smaller molecules a few hundred Daltons in size, could lead to the incorrect elucidation of an ion’s structural properties if used on larger biomolecules outside the realm of MOBCAL’s intended use. Nevertheless, it is important to understand the assumptions that go into these approximate methods in order to facilitate the development of a better TM method. A more detailed description of these algorithms can be found in Gabelica and Marklund,¹⁷ Shvartsburg and Jarrold,⁷ and in Bleiholder et al.²²

2.2. Current Methods for Calculating Collision Cross-Sections

The Exact Hard Sphere Scattering⁷ (EHSS) model, like the name suggests, represents every atom of the ion species by a rigid sphere with a constant radius. Trajectories of gas molecules are calculated through a ray tracing algorithm to save computational power as opposed to integrating equations of motion derived from an interaction Hamiltonian. Like EHHS, the Projection Approximation (PA)^6,7,26 also uses rigid spheres, in which these atoms are then projected onto a plane located behind or in front of the molecule and the total area of this projection is considered to be a good approximation of the CCS. Because the nature of the interactions describing a scattering process using PA or EHSS methods are only approximate, both of these models precludes the inclusion of individual interactions such as a surface charge distribution or the strength of Lennard-Jones forces. For example, PAs cannot directly account for the effects of concavity or disconnectivity. However, work of the Bowers group compensate for these effects through multiplicative ”shape factors” terming their algorithm the projected superposition approximation (PSA),^22–25 while those from Marklund et al introduce a power-law correction between TM and PA collision cross sections.²⁶

The most physically realistic method to overcome the approximations of the PA or EHSS models is by simulating a large collection of trajectories of colliding gas particles with the ion, which we will call the trajectory method (TM). Trajectory methods are a class of molecular mechanics models where the dynamics of buffer gas molecules are propagated using a classical interaction potential. Although these interactions are fundamentally quantum mechanical in nature, it is their computational efficiency that make them powerful tools for simulating dynamics of large molecules. It should also be noted that Equation 2 is only of first order accuracy, and a second order correction, for example, use l and s values not necessarily equal to 1.^3,4,27 In spite of the fact that this correction factor is also multiplicative to K, TM’s are the only model that can accurately account for higher order corrections to the mobility when the drift speed of the ion is not considered to be small relative to the mean speed of the buffer gas. Although TMs are commonly considered the gold standard for comparing CCSs to, both experimentally or for parameterizing PA and EHSS approximations, these trajectories are very computationally expensive to calculate. This is one of the primary motivations behind the development of the aforementioned approximations, especially for studying large macromolecular complexes with more than 10⁵ atoms. In the following sections, we will show that a properly tuned TM model implemented with modern computational methods can be nearly efficient as projection or hard sphere models.

3. Computational Method

3.1. Interaction Potential

For simplicity, we consider only Helium atoms as our buffer gas, although the framework employed here can further be extended to point-particle models for nitrogen. In this model, the total potential energy Φ(r) between the ion and the buffer gas include a repulsive electronic exchange (Pauli exclusion) term, an attractive induced dipole-induced dipole (London dispersion) term, and a repulsive ion-induced dipole term written as

$$\Phi (r)=4\sum _{i=1}^N{ϵ}_i\left[{\left(\frac{{\sigma }_i}{r_i}\right)}^{12}-{\left(\frac{{\sigma }_i}{r_i}\right)}^6\right]-\frac{\alpha }{2}{\left[\sum _{i=1}^M\frac{q_i{r}_i}{r_i^3}\right]}^2.$$ (5)

Here, r_i = r – R_i is the vector from the gas-atoms position r to the position R_i of an ith atom out of N total atoms in our ion, σ is the van der Waals radii, ϵ is the minimum of the Lennard-Jones energy, α is the polarizability of the gas atom, and M is the total number of atoms that contain a partial charge q, where N ≥ M. Collisions between the ion and the buffer gas are also considered to be fully elastic in nature; accounting for a small transfer of kinetic energy from the point-particle buffer gas to the ion through inelastic collisions seems to have little effect in the overall CCS as per the work of Shirirvastav and co-workers.²⁸

Because Φ(r) is only dependent on the position of the gas atoms, the Hamiltonian H of the system in a relative coordinate frame of reference is simply this potential term plus a momentum dependent kinetic term T(p), that is, H = T(p) + Φ(r). Therefore, Hamilton’s equations of motion can be integrated through the use of a symplectic integrator, specifically a Velocity Verlet algorithm.^29,30 Verlet methods are fourth order in local accuracy, which is necessary for collisions that occur under a twelfth power repulsive potential, and only requires one force evaluation per time step.^31,32 This choice of integrator is more accurate than commonly used first-order Euler methods¹⁹ and also significantly faster than a fourth order Runge-Kutta used in MOBCAL.⁶

The actual evaluation of the integral in Equation 4 is performed in an importance sampling Monte-Carlo fashion. Relative initial velocities, impact parameters, and orientations of the ion are chosen at random according to a probability distribution ρ(x) where x = (v_r, b, ϕ, θ, γ). If ω(x) is the integrand of Equation 4, then the CCS is approximated as

$${\Omega }_{avg}^{(1,1)}=\int {\text{d}}^{5}x\omega (x)={\displaystyle \int {\text{d}}^5}x\frac{\omega (x)}{\rho (x)}\rho (x)\approx \frac{1}{\mathcal{N}}{\displaystyle \sum _{i=1}^{\mathcal{N}}\frac{\omega \left(x_i\right)}{\rho \left(x_i\right)}}$$ (6)

for $\mathcal{N}$ integration points. This allows CoSIMS to sample a homogeneous distribution of orientations and collision points over the molecule’s surface. Each parameter is chosen independently of each other so that the probability distribution is of the form

$$\begin{array}{l}\rho (x)=\rho \left(v_r\right)\rho (b)\rho (\varphi )\rho (\theta )\rho (\gamma )\\ =\left[{\left(\frac{\mu }{2k_{B}T}\right)}^3{v}_r^5{e}^{-m_1{v}_r^2/2kT}\right]\left[\frac{2b}{b_{max}^2}\right]\left[\frac{1}{2\pi }\right]\left[\frac{\sin \theta }{2}\right]\left[\frac{1}{2\pi }\right].\end{array}$$ (7)

A fifth power velocity distribution is chosen rather than a Maxwellian so that the integral converges quickly to a lower error with fewer trajectories. Because the summation representation of the integral cannot practically use velocities equal to zero or infinity, a Monte-Carlo sampling allows for velocities at the extremes of the distribution to be chosen less frequently than those near the mean. This is opposed to evaluating the integral as a Riemann sum like MOBCAL or Collidoscope,¹⁹ a more recent CCS program. Instead of using an active rotation of the molecule itself, the need for computing thousands of matrix multiplications to rotate the molecule for each chosen x_i is eliminated by performing a passive rotation of the initial position of the incoming gas atom. A similar approach has also been used in Shvartsburg et al.³³

3.2. Ellipsoid Projection Approximation

Recall that the averaging over molecular orientations in Equation 4 is defined over a spherical coordinate system. This process would be well suited for ions that are spherical in shape, however, the many conformations taken by nucleic acids typically do not contain spherical symmetries. Molecules with a high aspect ratio will not equally fill this spherical volume, resulting in a vast amount of the calculated trajectories to terminate with a scattering angle close to zero. This means that many trajectories (e.g. equations of motion) are solved for in order to obtain a value of χ that contributes very little to the summation in Equation 6. To simplify our computational effort, we perform a pseudo-projection approximation as described below.

The CCS integral for the interaction of two point particles can be written as^2,27

$${\Omega }^{(1,1)}={\displaystyle {\int }_0^{\infty }2}\pi b\frac{\langle \delta p_r\rangle }{\langle p_r\rangle }\text{d}b,$$ (8)

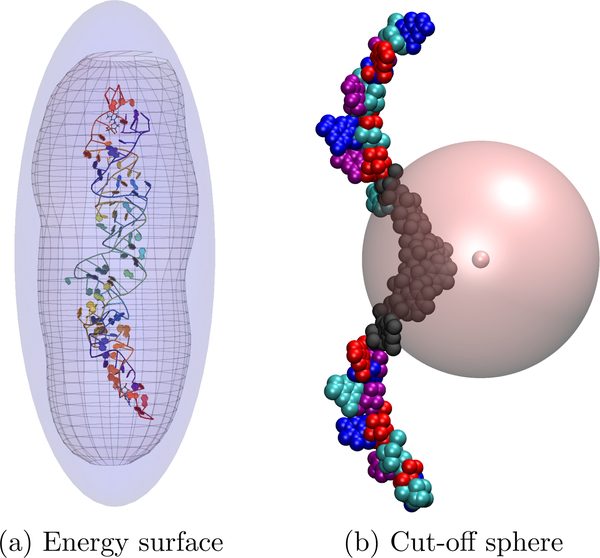
where the angled brackets denote an average over the probability of a collision occurring with a relative momentum p_r. This can be interpreted as defining the CCS of a molecule in terms of an interaction region such that the change in relative momentum δp of two colliding molecules is nonzero. Therefore, we define this interaction region by an approximate closed surface surrounding the molecule where the evaluation of V(r) at a position r on this surface is below some numerical tolerance. This is depicted in Figure 1.

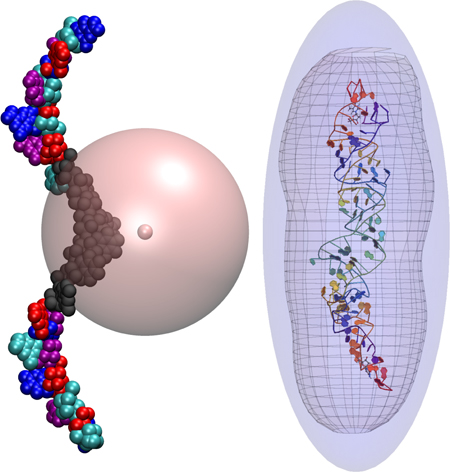
Figure 1:

(a) A surface of constant energy, represented by the transparent mesh, is chosen according to the method described in the text. An ellipsoid (the blue surface) is then fit to this surface and enlarged uniformly in each axis direction until the mesh fits completely inside the ellipsoid. (b) The cut-off sphere, represented by the large pink sphere, is centered at the gas atoms position. The multi-colored clusters each have an associated set of multipoles and any cluster intersecting the sphere (in black) use exact potentials.

First the surface is computed by uniformly searching for K points that meet this minimum energy requirement, and then approximated by an ellipsoid defined by the axes (a, b, c) = (A^−1/2, B^−1/2, C^−1/2) obtained by minimizing the (approximate) logarithm of a Student-t distribution $\mathcal{L}$ w.r.t. the axes lengths,

$$\mathcal{L}=C-\frac{K}{2}{\displaystyle \sum _{i=1}^K{\left(A{x}_i^2+B{y}_i^2+C{z}_i^2-1\right)}^2}.$$ (9)

Using the optimum axes lengths chosen, the ellipsoid is then enlarged uniformly along each principle axes until each of the K test points lie within this surface to ensure that any trajectory initiated on this surface has a negligible amount of potential energy. At the start of each trajectory, this ellipsoid is then projected onto a plane orthogonal to the gas molecules initial velocity vector. Any initial position of this gas molecule that does not lie within this projected area is assumed to have a scattering angle χ ≈ 0 and its trajectory is not computed, but still counted as a ”trajectory” used in the CCS summation. All other trajectories are considered to enter a region of non-zero potential. The initial position is then advanced to its point of intersection with this ellipsoid by assuming a constant velocity, and the trajectory continues as usual. In such a way, this approximation is analogous to some of the concepts of a projection or hard sphere models; an initial silhouette of the ion is selected by projecting away the trajectories that contribute very little to the CCS integral, while the curvature of each trajectory is neglected until reaching the interaction region defined by this ellipsoid.

3.3. Dispersion Cut-off and Multipole Approximations

The most expensive part of solving the equations of motion is the force evaluation, especially if the charge of the ion is explicitly specified for each of the atomic coordinates. For atoms distant from the gas molecule, the induced dipole due to the electric field of these charges will be quite small, and even more so for the Lennard-Jones induced dipoles. As such, the electric potential generated by these distant atoms can be approximated by a multipole approximation, and the repulsive dispersion interactions can be ignored.

In order to quickly determine their atomic positions, the ion is first clustered into P nearly uniform sized clusters through a principle component analysis. Each cluster that is smaller than a specified radius is continuously partitioned along its principle axes into equally smaller clusters until the radius of the cluster is below some specified size. For each cluster, its monopole, dipole and quadrupole is calculated with the cluster’s position a defined as their respective origin. A multipole expansion for the electric potential V^(m) is thus evaluated at the gas molecule’s position by expanding about a

$$V^{(m)}(r)={{\displaystyle \sum _{j=1}^P\left[\frac{Q^{(0)}}{d}+\frac{Q_{\alpha }^{(1)}{d}_{\alpha }}{d^3}+\frac{1}{2}\frac{Q_{\alpha \beta }^{(2)}{d}_{\alpha }{d}_{\beta }}{d^5}\right]}|}_{d=d_j,Q=Q_j}$$ (10)

with d_i = r – a_i, Q⁽ⁿ⁾ is the nth order multipole tensor, and a summation is implied over repeated tensor indices’s. The potential is then partitioned into an exactly calculated potential term V^(e) and the approximated term such that V = V^(e) + V^(m). From here, the electric field, and hence the ion-induced dipole energy, can be derived using this partition. Higher order terms in the expansion greater than the electric quadrupole are excluded for computational efficiency; higher order terms also require additional tensor contractions, resulting in the approximation being not much cheaper than evaluating the potential exactly.

At each time step of a trajectory, if a cluster is within or intersects a cut-off sphere centered at the gas molecules position, then the total energy for all atoms within that cluster are calculated exactly. Else, the ion-induced dipole energy is calculated through the multipole expansion and all Lennard-Jones interactions are ignored for all clusters that do not intersect the sphere. This process is depicted in Figure 1b and the exclusion of Lennard-Jones interactions will hereafter be called the dispersion cut-off (DC) approximation. The radius of the sphere for the dispersion approximation (which can, but not required to be the same for the multipole approximation) is chosen such that the ratio α of the LJ potential energy from the atoms within this sphere to the total LJ energy is roughly 99.5% by solving

$$\frac{4\pi {\displaystyle {\int }_{\sigma }^a{V}_{LJ}}(r)r^2{\text{d}}^{3}r}{4\pi {\displaystyle {\int }_{\sigma }^{\infty }{V}_{LJ}}(r)r^2{\text{d}}^{3}r}\approx 1-\frac{3}{2}{\left(\frac{\sigma }{a}\right)}^3=\alpha$$ (11)

for the cutoff radius a, where we have dropped (σ/a)⁹ terms, σ is the largest van der Waals radii used in the forcefield, and α is a tolerance parameter^†.

3.4. Program Details and Features

All IMS experiments are not identical and more exotic systems may benefit more or less from the approximation schemes implemented into this collision software. Although MOBCAL is also a compiled program like CoSIMS, many of the parameters that define a CCS calculation, such as the number of trajectories, number of integrals to perform, system temperature, and force-field parameters, are hard coded within the program source which must then be recompiled if adjustments are desired. Instead, CoSIMS is a modular program, where all of these parameters are externally adjustable through the use of an optional input file. This makes it possible for one to explore the use of alternate molecular models, such as using a different buffer gas or a coarse-grained representation of the ion. CoSIMS represents the gas molecule as as point-particle, and thus a point-particle model of nitrogen can also be used with this program, given the proper Lennard-Jones parameters and atomic polarizability. Furthermore, coarse-grained models for the ion can also be implemented with CoSIMS through the use of an additional forcefield file.

As mentioned in section 1, CCS calculators are commonly used on large biological molecules with thousands of atoms or more. Since Monte-Carlo methods are considered ”embarrassingly parallel” algorithms, our program also utilizes the OpenMP library to run CoSIMS as a multi-threaded program. This is in contrast to MOBCAL which is only a serial program, or PSA which runs off of a web-server and the user can not adjust the number of cores used.

4. Results and Discussion

4.1. Details of the CCS calculations

Because the most widely used program for trajectory method CCS calculations is MOBCAL, we will compare all results to MOBCAL’s trajectory method (MOBCAL-TM). We also include MOBCAL’s projection approximation, which we will refer to it as MOBCAL-PA, as a sanity check to identify instances where MOBCAL’s TM method produces unreliable results (i.e Figures 5b and 6). Both PA and EHSS calculations are calculated, simultaneously, in the MOBCAL program prior to invoking its trajectory method. All benchmark times for MOBCAL-TM are determined by subtracting out the CPU time used to calculate PA and EHSS CCSs, which we will hereby refer to as MOBCAL-EHSS+PA. Furthermore, we will use the abbreviation CoSIMS-DC to indicate that the dispersion cut-off approximation has been invoked.

Any new CCS algorithm requires rigorous testing against the TM ”gold standard” model, which has been shown in prior work for PA, EHSS, and other recently proposed models.^{6,7,10,19,24,28} In order to facilitate comparison, the results in this work also use the same Lennard-Jones parameters included in the MOBCAL suite. However, part of the motivation for developing CoSIMS was to disambiguate errors in the integration algorithm from inaccuracies in the underlying potential; the next logical step is improving the Lennard-Jones potential itself to better match quantum mechanical interaction energies and experimental data, though this is beyond the scope of the current work.

In order to ensure that CosIMS performs as expected, we tested our code on three distinct sets of molecular test systems: temperature dependent fullerenes, double stranded DNA, and assorted proteins of various sizes. Protein studies are prominent in the IMS community, while carbon fullerenes were used by MOBCAL for the initial parameterization of the program’s Lennard-Jones interaction and hard sphere radii. Because these types of structures are all roughly spherical in shape, a successful TM calculator should be able to reproduce the CCSs of MOBCAL using the same interaction parameters. Any differences in CCSs between the two algorithms should therefore be small and not due to the geometries of the molecules tested. Double stranded DNA then served as our test on asymmetrical molecules. The nucleic acids used in this work are flexible enough to provide a variance in CCS when ensembles of structures are generated from MD simulations, yet still rigid enough that individual structures from the ensemble should have similar CCSs. We will show in section 4.3 that MOBCAL does not give comparable CCSs for consecutive MD snapshots that are nearly identical in their geometries and that this comparison further emphasizes the stability of CoSIMS.

All CCS calculations were performed on a single core from an Intel Xeon E5–2670 processor at 2.60GHz on a single CPU socket, unless otherwise specified. MOBCAL is designed to compute n CCS integrals (the default value is n = 10), equally average each of the results, and then take a standard deviation σ to obtain a standard error ${\sigma }_0=\sigma /\sqrt{n}$. Although a full Monte-Carlo integrator such as CoSIMS can instead compute a weighted average and standard error using the uncertainty in each CCS integral, we chose to perform the same calculation as MOBCAL for consistency. For all calculations presented in this section, CoSIMS was run with a total of 2.5 × 10⁵ trajectories while MOBCAL-TM was run with the default 10⁵ trajectories. CoSIMS requires more trajectories in order to achieve a similar distribution of errors as MOBCAL-TM, however, sections 4.2 and 4.3 will show that the time it takes to execute the additional computations does not impact its performance. Since most of the error bars are smaller than the data points themselves, most of them are excluded in many of the following figures and no further discussion on either program’s accuracy, in this context, is needed.

4.2. Fullerenes and Proteins

The original publications of MOBCAL chose to use carbon fullerene ion mobility data of various sizes to determine the Lennard-Jones potential parameter for carbon, as well as ”carbon like” atoms such as nitrogen and oxygen. The assumption is that the averaged van der Waals radii and strength of the Lennard Jones interaction potential (σ and ϵ, respectfully, in Equation 5) between helium and carbon will be approximately close to that of oxygen and nitrogen with helium. Although using a single parameter to represent all heavy atoms may seem oversimplified and coarse-grained, MOBCAL has been rather successful in its application to ion mobility for a wide range of small molecules over the past two decades. Our program should necessarily replicate these small molecule results in order to be considered an improvement over the existing algorithms.

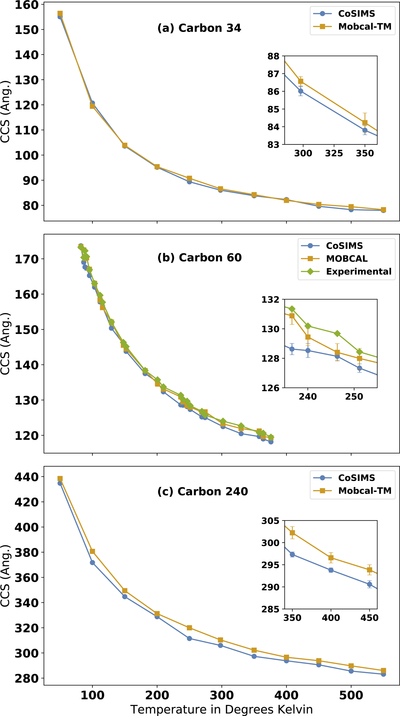
Data for the C₆₀ fullerene was graphically digitized from.⁶ Temperatures for each of these molecules ranged from 50 to 500 degrees Kelvin, and the initial structures were taken from the supplemental material of Tománek.³⁴ In order to compare to the original 1996 MOBCAL publications, each of these geometries were minimized according to Gustavo³⁵ at the Hartree-Fock level of theory with an STO-3G basis set using the Q-Chem software suite.³⁶ Although more advanced basis sets and quantum mechanical methods exist, the purpose is to re-create the fullerene structures used for the initial parameterization of MOBCAL. Each structure was given a positive charge of +1e distributed uniformly over each atom. Because of the fullerene’s relative sizes with respect to the programs default cut-off sphere radii of approximately 25 Å neither the LJ cut-off approximation nor multipole expansions were used here.

As shown in Figure 2, MOBCAL and CoSIMS have nearly identical CCSs. MOBCAL and CoSIMS differ on average by 0.77%, 0.86%, and 1.43%, for C₃₄, C₆₀, and C₂₄₀, respectfully. The experimental CCS for C₆₀ on average agrees with CoSIMS by 1.10% while it agrees with MOBCAL by 0.50%. Although both programs barely do not agree with the experimental data within their respective computational error, not much more can be said given the nature of how the data was obtained. Overall, CoSIMS tends to underestimate the CCSs predicted by MOBCAL, although less so for the smaller C₃₄ and C₆₀ fullerenes. Small variations between the two programs should be expected due the difference in how each program integrates over relative velocities. Because these are spherical structures, the differences between the CCSs is not due to the ellipsoid projection approximation used in CoSIMS, for the region that is chosen to integrate over is nearly a sphere.

Figure 2:

Temperature dependent CCS calculations by MOBCAL and CoSIMS for (a)C₃₄, (b)C₆₀, and (c)C₂₄₀. The inset plot demonstrates the relative size of the error bars to the CCS.

Although the CCSs predicted by the two program’s may seem to disagree with increasing fullerene size, this does not appear to be the case for the protein test sets, as depicted in Figure 3. A total of 50 protein structures were taken from the Protein Data Bank, and a complete list can be found in Tables S3 and S4 of the supplemental material. Half of these proteins were chosen to be be globally asymmetric, while the other half consisted of structures with either cyclic or dihedral symmetries. Because many of the proteins in the PDB are from NMR studies that include hydrogen atoms, these were not removed from the structures, which accounts for roughly half of all proteins used here. The additional hydrogens also require extra CPU time to calculate the CCS and will allow us to see differences in this aspect of the two programs. Charges were not included in calculating their CCSs, as this effect will be very small for most of the large proteins. As compared to the DNA’s in the next section, or nucleic acids in general, proteins are usually more spherically symmetric in shape. When using the LJ cut-off approximation, more of the molecule’s atoms will, on average, be included in the cutoff sphere as compared to the DNA structures and should prove the validity of this approximation

Figure 3:

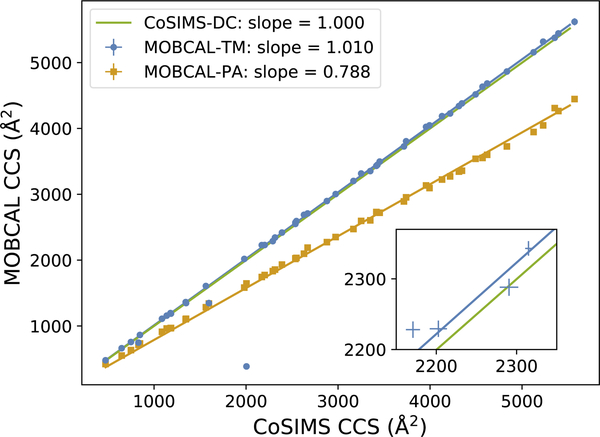
Comparison between CoSIMS and MOBCAL CCS results for 50 various proteins. MOBCAL-PA results are also presented here to demonstrate stability of both programs. Error bars are not shown in the main plot for they are smaller than the data points themselves, demonstrated by the inset plot.

Figure 3 compares the CCS as calculated by MOBCAL-TM and CoSIMS. For nearly all proteins studied here, both programs give nearly identical results with similarly-sized errors. CoSIMS, with and without the dispersion cut-off approximation invoked, and MOBCAL-TM all have a mean standard error less than 0.50%. When using the dispersion cut-off approximation, the mean percent difference between all protein CCSs is 0.038±0.034% with a maximum percent difference of 0.164%. All calculations using the cut-off approximation were well within the standard error of the calculated results. It should also be noted that CoSIMS is designed to only accept trajectories that conserve energy within 0.50%, while trajectories that have larger deviations are continuously recalculated with a smaller integration time-step until this condition is satisfied. Given the energy conservation constraint, and the slope of the fitted trend-line in Figure 3, invoking the dispersion cut-off approximation yields CCSs that are in good agreement with the exactly calculated results.

MOBCAL will periodically predict a CCS that is completely unreliable, as seen by the outlier data point in the bottom left of Figure 3. The MOBCAL-PA results are also shown here to demonstrate that CoSIMS does give an appropriate CCS for this protein, despite the CCS that MOBCAL-TM predicts. The best-fit line between CoSIMS and MOBCAL-TM excludes this data point. The slope of nearly 1.0 in Figure 3 further emphasizes that when using the same force-field parameters, CoSIMS will give the same CCS as MOBCAL-TM for larger, nearly spherically symmetric molecules, that is, when MOBCAL functions as expected.

As CoSIMS systematically gives slightly smaller CCSs than MOBCAL, as shown in Figures 2 and 3, a brief explanation is warranted. As described in section 3, CoSIMS uses a full Monte-Carlo integration over initial relative speeds while MOBCAL uses a Riemann sum. Obviously, one cannot numerically sample nearly infinite initial speeds as required by Equation 3. By instead using the velocity distribution specified in Equation 7, faster moving gas particles can be sampled less often, and the upper limit of such large speeds is set higher than that of MOBCAL. Since faster moving particles will, on average, have smaller scattering angles, we should expect a slightly smaller CCS than MOBCAL.

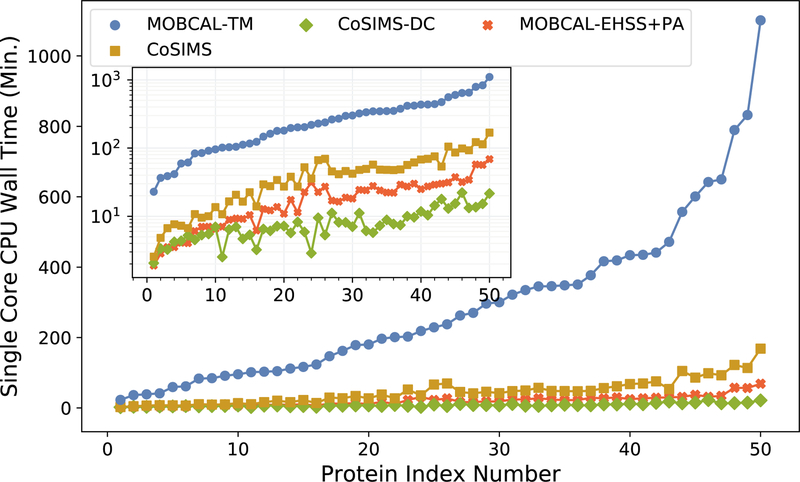
The computational time for MOBCAL-TM and CoSIMS are presented in Figure 4. Each data point is sorted according to increasing CPU runtime for MOBCAL-TM and the protein index number is simply used for sorting purposes. CoSIMS using the exact LJ potential takes only a few minutes to complete its calculations for the smaller proteins, and just over an hour for the largest structures used here. When the dispersion cut-off approximation is enabled, the largest protein CCS included here (9986 total atoms including hydrogens), takes just over 22 minutes to compute. As compared to MOBCAL-TM’s runtime, this brings the CCS trajectory method calculations for CoSIMS within the regime of acceptable calculation time for large proteins. It should also be mentioned that the majority of the CPU time for MOBCAL-EHSS+PS is due to the EHSS algorithm, meaning that CoSIMS-DC, for protein systems, is roughly comparable if not faster than MOBCAL-EHSS.

Figure 4:

CPU run times for MOBCAL-TM, CoSIMS using an exact potential, and CoSIMS using the dispersion cut-off approximation.

4.3. Double Stranded DNA

The nucleic acid data set consisted of 38 different DNA strands ranging from 6 to 64 base pairs in length. Multiple charge states were considered and the data set was divided into both A-form and B-form helices. The molecule files were generated according to Lippens and co-workers¹⁴ and generously provided to us by the authors. Because of their asymmetrical, elongated shape, many of the trajectories used here will generate glancing collisions with very small scattering angles. The use of the ellipsoidal projection approximation should therefore eliminate many of the equations of motion that need to be solved, and major differences between the CoSIMS and MOBCAL CCSs would serve as evidence that this approximation is invalid.

Nucleic acids can still be very flexible in their shape, even in a gas phase, and these slight deformations in their topologies will of course be noticeable in an actual IMS experiment. In order to generate these structural deformations, gas phase, all-atom molecular dynamic simulations were performed on each of the strands using GROMACS 4.6.3.³⁷ The simulations were performed in accordance with the computational methods of Lippens and co-workers.¹⁴ To briefly summarize their procedure, each of the simulations were 1 nanosecond in length and 21 conformations at 25 picosecond intervals were taken from the end of the simulations to generate an ensemble of structures to average their CCS over; a grand total of 798 structure files were generated.

The total charge of the ion is classically represented by partial charges placed at each of the atomic coordinates. Since the precise arrangement of these charges in actual molecular ions for an IMS experiment is unknown, the most unbiased distribution to choose is a uniform one. As each of these structures contain hundreds to thousands of atoms, the contribution to the potential energy between the helium buffer gas and a single atom in the ion due to the partial charge will be negligible and is usually ignored. Therefore, the CCS for only neutral molecules are highlighted here. When the correct amount of charge is uniformly distributed over the molecules surface, the CCSs calculated by MOBCAL and CoSIMS are nearly identical and generate plots identical to Figure 5. There are of course instances when the charge distribution will become important, and so the CPU runtimes for a uniform distribution are shown in the supplemental material.

Figure 5 shows the comparison between MOBCAL-TM and CoSIMS CCSs computed for neutral DNA. Each data point represents an average CCS taken over the ensemble of a particular charge state, while the error bars represent the standard deviation of their respective averages. The linear PA results are presented in Figure 5 to demonstrate that the molecular topology for each MD frame do not deviate from each other as much as MOBCAL predicts, and that the molecule has in fact not significantly changed its geometry between two molecular dynamics snapshots only by several picoseconds. As with the fullerene and protein results in the previous section, CoSIMS gives a CCS that is slightly smaller than MOBCAL, as seen by the slope of the best-fit lines being slightly greater than one.

What is most apparent in Figure 5 are the large standard deviations in MOBCAL-TM for the B-form strands greater than 30 base pairs in length. The source of these error bars is due to the variations in CCS for individual MD frames and an example of such occurrences is depicted in Figure 6^†. The nth RMSD between consecutive frames for N atoms in a molecule at time t_n reported in Figure 6 was calculated with GROMACS 2016³⁷ and defined as

$$RMSD\left(t_n\right)={\left[\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left(r_i\left(t_n\right)-r_i\left(t_{n-1}\right)\right)}^2}\right]}^{1/2}$$ (12)

With the maximum RMSD between two frames being approximately 0.38 Å, the geometries of each structure are very similar to that of an MD frame captured immediately before or after. Therefore, there is no particular reason why the difference in CCSs between consecutive frames should be much different, which is supported by the relatively stable CCS of CosIMS and MOBCAL-PA. Noting that the error bars for each frame are on average less than 1.2%, even for MD frames where MOBCAL-TM gives underestimated CCSs, the source of error is not due to a lack of trajectories invoked in either software. What can be most concerning is when MOBCAL-TM reports a plausible CCS that is actually incorrect. For example, frame 4 in Figure 6 depicts MOBCAL-TM reporting its CCS to be greater than MOBCAL-PA, which is to be expected given the nature of PA methods. However, if CoSIMS is presumed to give comparable CCSs as supported by the fullerene, protein, and A-form DNA results, then the actual CCS for frame 4 is much larger than what MOBCAL-TM predicts, as per CoSIMS’s calculation. MOBCAL thus gives a plausible, yet clearly incorrect CCS for a structure that, without the assistance of a secondary TM software, would otherwise be assumed to be correct.

Although A-form DNA has a different helical twist as compared to B-form DNA, their length is one of the only major differences between the two topologies of these structures. Like the example shown in Figure 6, each consecutive simulation frame from the structures reported in Figure 5 are not very different from the ones before it, and further examples can be found in the supplementary material. MOBCAL was originally designed to study smaller, spherically symmetric metal clusters, and as a result predicts acceptable CCS values for roughly spherical structures that are 6 to 30 base pairs in length. The original intent of this program implies the root cause of this error is geometrical in origin, and great care should be taken when interpreting CCSs for highly asymmetrical molecules. CoSIMS, by comparison, reports stable CCSs with smaller standard deviations between each MD frame for all lengths of nucleic acid helices studied here.

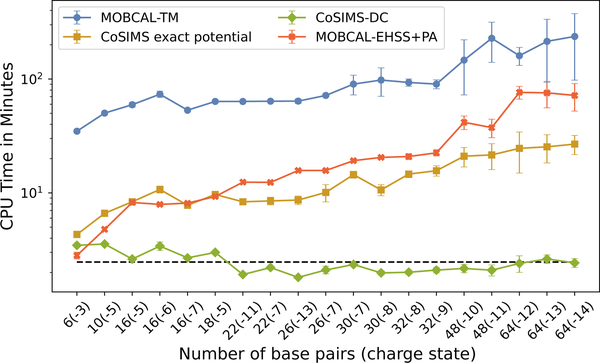
The computations using the dispersion-approximation as described in Section 3.2 in CoSIMS were also conducted, with the benchmark CPU times for B-form DNA shown in 7^†. Each calculation used the same initial random number seed to ensure that all trajectories produce identical orientation and initial velocity distributions. When executed using the DC approximated potential, CoSIMS shows a huge speedup in computational time as seen in Figure 7, making it nearly two orders of magnitude faster than MOBCAL. Because the ellipsoidal surface is chosen according to the overall shape of the molecule, which in return determines the number of trajectories exactly solved for, deviations in CPU time for longer, more flexible strands is expected. This is also evident in Figure 7 when comparing the error bars for strands 48 and 64 base pairs in length to the error bars for the shorter strands associated with the CoSIMS exact potential CPU times. The same cannot, however, be argued for the MOBCAL results, and this trend is surprisingly not seen in the A-form strands for either program^†.

Figure 7:

CPU run times for B-form DNA strands. The average computational time of 2.47 ± 0.52 minutes using the dispersion cut-off approximation is shown by the dashed line.

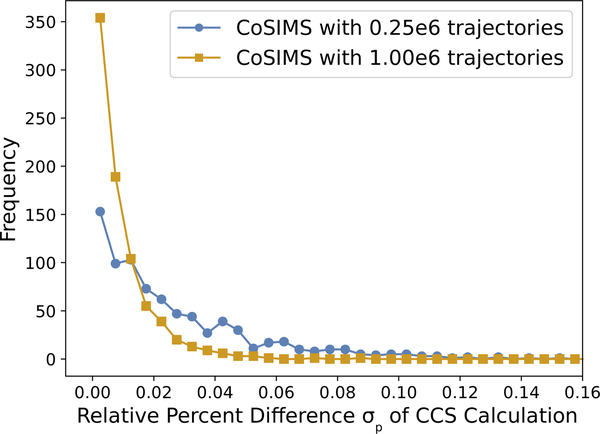
The addition of the dispersion-approximation allows for nearly constant runtime even for larger strands as evident in Figure 7. Because roughly the same number of atoms are used to compute the potential energy given a constant cut-off radius, longer strands should not affect the time to calculate most of the trajectories, hence the nearly constant runtime. To show the accuracy between the two methods, we will define the relative percent difference σ_p = 100|A–B|/A between two cross sections A and B. Distributions of σ_p for all 798 DNA calculations are shown in Figure 8. In addition to the set of calculations described above, the number of trajectories were also increased to 10⁶ in order to facilitate that the approximation converges to the correct CCS. Evidentially, the agreement between the two CCS improves with an increasing number of trajectories. Be it that this is a typical approximation used in many modern molecular dynamics simulators, it is highly encouraged to enable this approximation for all CoSIMS calculations, and the best efficiency is seen when used in conjunction with the EPA.

Figure 8:

Distribution of relative percent difference σ_p between neutral DNA CCS calculations with an exact LJ potential and with the dispersion approximation.

4.4. Comparison to Other CCS Programs and Final Remarks

The inaccuracies that arise in MOBCAL are, to our knowledge, geometric in nature and could not have easily been fixed with minor code revisions or patches. Creating a trajectory engine that is as efficient as projection or hard-sphere models while retaining the robustness of a traditional TM algorithm was therefore the primary focus of this work. It should be noted that MOBCAL is not the only alternative CCS calculator and other TM based programs do exist. Some models are still kept ”in house” unless requested from the authors, while other research groups have released their own form of softwares, such as IMoS¹⁸ and Collidoscope,¹⁹ that use their own mix of approximations and algorithms; Collidoscope uses a low order, yet faster, integrator for trajectories, while IMoS models slightly more computationally expensive inelastic, polyatomic collisions. Our work attempts to find a similar balance between accuracy and efficiency, for example, though the use of multipole and energy cut-off schemes. Coincidentally, Collidoscope and IMoS also use similar concepts of an energy barrier that are analogous to our ellipsoidal projection approximation, albeit with different geometries, and it is reassuring that this concept is well accepted in the IMS community. For a brief comparison of CoSIMS against Collidoscope, IMoS, and a more recent TM software, HPCCS,³⁸ please see the supporting information.

Trajectory methods, with the innate complexity of explicitly calculated buffer gas collisions, are unlikely to ever be as efficient as hard-sphere or projection based methods. Conversely, hard sphere or projection derived CCSs will never be as accurate as trajectory method derived CCSs as they do not consider either the molecular topology of the ion or the attractive dispersion interactions that are known to be important for describing the collisions of buffer molecules. Because of the steep computational resources previously required by TM calculations, PA or EHSS methods were the only alternative for CCS calculations of large molecules. From the CPU benchmarks presented in Figures 4 and 7, as well as the multipole approximation benchmarks presented in the supplemental material, excessive computational requirements should no longer require sacrificing accuracy for efficiency in CCS calculations. CoSIMS is able to reproduce nearly identical CCSs for both large proteins and nucleic acids in less time than that of MOBCAL-PA and MOBCAL-EHSS combined, while retaining its stability when studying the largest of molecular structures. Although CoSIMS is designed to use either a multipole or dispersion cut-off approximation for best performance, the simplification is in interaction potentials that dictate the trajectories of buffer gas particles, not in the method of calculating the ion’s CCS as a whole. As a result, the development of CoSIMS now allows the ion-mobility community to rely less on the approximate PA or EHSS based models for CCS calculations.

As with any of the CCS algorithms mentioned in this paper, the accuracy of the model will always be dependent upon the parameters given to the program. The next logical step for improving CoSIMS would be to investigate the quality of the Lennard-Jones parameters used for the underlying interaction potential. As mentioned in the beginning of section 4, the Lennard-Jones parameters from MOBCAL were borrowed for all CCS calculations in this paper and are currently the default values used in the software. This forcefield treats all heavy atoms with the same parameters as carbon, while modern forcefields typically assign different van der Waals parameters not only for atoms of different elements, but also based on the identity of neighboring bonded atoms. The process of creating such a forcefield would require the numerous calculation of CCSs for various molecular sizes, temperatures, and values of Lennard-Jones parameters, which is much more feasible with the advent of the CoSIMS platform presented here.

Now that we have developed a CCS engine that can perform trajectory method CCS calculations at greater speeds than the approximate PA or EHSS methods, we can now begin the development of such a gas phase forcefield for CCS prediction using CoSIMS. This feat would not have been possible with current TM softwares as we are limited in the amount of computational time and, as Figure 6 demonstrates, the stability on the software. With nitrogen buffer gases proving to provide better separability between IMS-MS spectra over traditional helium gas,,^13,39,40 the development of a point particle forcefield for nitrogen can also be studied, as the simulation of diatomic molecular collisions would be more complex and time consuming than the model currently invoked by CoSIMS. Furthermore, the degree to which a coarse-grained model of the atomic coordinates is warranted also requires the parameterization of such interaction potentials. CoSIMS was designed from the ground up to be a modular, easily customizable program (the details of which are described at the end of section 3) and the speed and stability of the program also opens the opportunity to develop improved coarse-grained models for trajectory based calculations. CoSIMS is freely available via a GitHub repository at https://github.com/ChristopherAMyers/CoSIMS under the GNU General Public License v3.0.

5. Conclusions

A novel trajectory based CCS engine, CoSIMS, is presented as a program that is both computationally efficient as projection and hard sphere based methods and more stable than MOBCAL’s trajectory based method when studying large biomolecules. The model proposed here uses well established molecular mechanics techniques for simplifying the interaction potentials used for calculating collisions of buffer gas particles with ionic analytes and for eliminating trajectories that insignificantly contribute to the total CCS. CoSIMS is applied to proteins, carbon fullerenes, and DNA strands of various sizes, lengths, and molecular weights and the CCS calculated with these structures are then compared to MOBCAL.

This comparison shows that CoSIMS is both a faster and more stable CCS engine than MOBCAL’s trajectory based method, and can also finish its calculations in less CPU time that MOBCAL’s projection and hard sphere methods combined. Furthermore, since the CCSs of the structures tested in this paper are nearly identical to CCSs given by MOBCAL, CoSIMS is a viable substitution to not only projection and hard sphere based models, but also other trajectory based methods as well. Additional features of the program include the ability to run on multiple CPU cores, change its forcefield and polarizability for both all-atom and coarse grained molecules, and adjust various parameters of the program to tailor the software to the specific system being studied. Further improvements to the forcefield used in CoSIMS, the development of a nitrogen buffer gas model, and the comparison to other CCS based models that demonstrate its efficiency will be presented in future work.