Summary
Nervous systems have evolved to combine environmental information with internal state to select and generate adaptive behavioral sequences. To better understand these computations and their implementation in neural circuits, natural behavior must be carefully measured and quantified. Here, we collect high spatial resolution video of single zebrafish larvae swimming in a naturalistic environment and develop models of their action selection across exploration and hunting. Zebrafish larvae swim in punctuated bouts separated by longer periods of rest called interbout intervals. We take advantage of this structure by categorizing bouts into discrete types and representing their behavior as labeled sequences of bout-types emitted over time. We then construct probabilistic models – specifically, marked renewal processes – to evaluate how bout-types and interbout intervals are selected by the fish as a function of its internal hunger state, behavioral history, and the locations and properties of nearby prey. Finally, we evaluate the models by their predictive likelihood and their ability to generate realistic trajectories of virtual fish swimming through simulated environments. Our simulations capture multiple timescales of structure in larval zebrafish behavior and expose many ways in which hunger state influences their action selection to promote food seeking during hunger and safety during satiety.
BLURB:
Johnson et al. use a moving camera system to observe naturalistic larval zebrafish behavior and develop probabilistic models to predict and simulate behavioral sequences. Their simulations capture behavioral dynamics spanning multiple timescales, from reactions to prey to hunger-dependent changes in action selection across hunting and exploration.
Introduction
Methods to quantify freely-moving animal behavior are quickly advancing as cameras, pose estimation algorithms, and behavioral models improve. Modern behavioral analysis pipelines [1] commonly involve: (1) acquiring behavioral video, (2) extracting low-dimensional time series representations of postural dynamics, and (3) annotating each image frame with a behavioral state label (e.g. “head-grooming”, “rearing”). Variations of this pipeline have been used to discover sets of stereotyped actions generated by worms [2, 3, 4, 5], flies [6, 7, 8], fish [9, 10, 11, 12, 13], and mice [14]. Importantly, these methods produce statistical behavioral summaries to facilitate comparison of nervous system function across animals.
Larval zebrafish are convenient to use in behavioral studies due to their simple body plan, temporally discrete behavior, and stereotyped locomotor repertoire. With their compact shape and limited flexibility, automatic posture tracking [15, 16, 17] of larval zebrafish is uncomplicated. Since larvae swim in punctuated bouts, temporal segmentation of their behavior into bout and interbout epochs is also straightforward. Together, the anatomy and movement of zebrafish larvae simplify behavioral analyses, allowing swim bouts to be represented as points in a high-dimensional posture or kinematic parameter space. Several studies have leveraged these properties to categorize swim bouts. The most comprehensive effort [13] identified 13 basic types used during hunting [18, 19], taxis behaviors [20, 21, 22, 23], escape maneuvers [24, 25, 26], social interactions [27], and spontaneous swimming in light and dark.
While larval zebrafish locomotor patterns have been well studied, much less is known about the complex generative processes underlying their natural behavioral sequences. How do external inputs (e.g. prey positions and properties) and internal inputs (e.g. behavioral history and hunger state) combine to influence action selection? To address this general problem, we use a moving camera system to collect high spatial resolution video of individual larvae swimming in a large arena with abundant prey. This approach eliminates a rigid trade-off between spatial resolution and arena size, allowing us to observe hundreds of consecutive swim bouts without interference from arena boundaries. We then use this data to construct probabilistic behavioral models – building on point process models with a long history in computational neuroscience [28, 29, 30, 31] – to evaluate how internal and external inputs shape behavior. By sampling from these models, we simulate larval trajectories capturing behavioral dynamics spanning multiple timescales, from reactions to prey (< 100 milliseconds), across stretches of hunting and exploration (seconds to minutes), and throughout changing hunger state (minutes to hours).
Results
Acquiring Behavioral Data with BEAST
We constructed BEAST (Behavioral Evaluation Across SpaceTime, Figure 1A, Video S1) to observe 7-8 days-post-fertilization nacre zebrafish larvae (n=130) one at a time. To evaluate how hunger influences behavior, each fish was given abundant paramecia (fed group, n=73) or deprived of food for 2.5-5 hours (starved group, n=57) prior to observation. Previous studies show that brief food deprivation robustly increases larval zebrafish food intake [32, 33] and that hunger increases their likelihood to approach, rather than avoid, prey-like visual stimuli [34, 35]. We therefore expect our fed and starved fish groups to display different behavioral patterns and aim to construct models to quantify these effects.
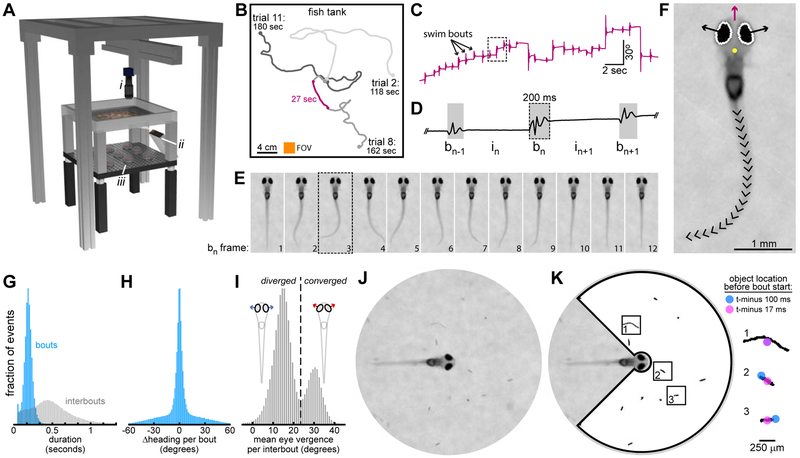
Figure 1: Acquiring Behavioral Data with BEAST.
A. BEAST Schematic. Infrared camera (i) moves on motorized gantry to stay above fish. Frame rate = 60 fps. Projector (ii) and IR-LEDs (iii) illuminate screen embedded in tank bottom. See Video S1 for animated schematic. B. Swim paths from 3 trials from 1 fish. Arena water volume = 300 × 300 × 4 mm. Camera field of view = 22 × 22 mm (orange square). C. Fish heading direction over time (from purple section in B). D. Expansion of box from C with bout and interbout epochs identified (notation indicated). E. One swim bout (from box in D) after image registration. F. Head position (yellow dot), heading direction (purple arrow), eye vergence angles (angles of black arrows above horizontal), and tail shape (20 tail tangent directions) extracted in every frame (frame 3 from E shown). See Figure S1 for details. G. Histograms of all bout and interbout durations. H. Histogram of heading direction change per bout (Δ heading). I. Histogram of mean eye vergence per interbout. Convergence threshold set at local minimum: 24°. J. Video dataset cropped to circular FOV (diameter = 8.12 mm). K. Locations, sizes, shapes, and relative velocities of putative prey are identified preceding initiation of every swim bout (here shown for objects in J). Box width = 820 μm. Identified objects are mostly edible (paramecia, rotifers), but include also algae, dust (box 1), and artefacts.
We place each fish in the arena and repeatedly recruit it to the center to initiate up to 18 observational trials. We leverage the optomotor response [23] to guide fish to the center by projecting optic flow stimuli onto a screen embedded in the tank bottom. Once at the center, a static natural scene replaces the gratings and the fish is recorded for up to 3 minutes or until it reaches the arena edge or tracking fails. Swim paths from 3 representative trials are shown (Figure 1B) and the fish’s heading direction throughout a portion of one trial is plotted (Figure 1C). Swim bouts are seen as brief fluctuations in heading direction over time and the timing of bout and interbout epochs is determined from this signal (Figure 1D). We translate and rotate each image frame to register the video to the fish’s reference frame (Figure 1E) and encode fish posture by estimating eye vergence angles [19] and tail shape [36] (Figures 1F, S1). Larvae can accelerate rapidly (e.g. during escape swims), sometimes causing online tracking failure. Offline pose estimation is also occasionally compromised due to motion blur (during very high speed swims) or body roll (causing one eye to occlude the other in the image). We retain only video segments in which all postural features are accurately extracted in every frame for further analysis.
The processed dataset contains 40 hours of behavioral data (4002 video segments) parsed into bout and interbout epochs (Figure 1G). Across all swim bouts (n=200,559), heading angle change per bout is narrowly and symmetrically distributed (Figure 1H). The arena contains abundant prey (mostly paramecia, some rotifers) and the fish tend to hunt prey near the water surface. Larvae converge their eyes during hunts to pursue prey with binocular vision. While not hunting, larvae keep their eyes more diverged, increasing visual coverage of the environment which should improve threat detection. Larvae therefore experience a natural trade-off between seeking food and seeking safety. These opposing states are seen in the bimodal distribution of eye position measurements during interbout intervals (Figure 1I). We maintain a large circular field of view centered around the fish head (Figure 1J) with sufficient image sharpness to extract positions, sizes, shapes, and motion patterns of objects near the water surface (Figure 1K). We later use this information to construct compressed representations of environmental state to predict the type of the next swim bout.
Exploring and Hunting Bout-Type Categorization
To quantify behavioral sequence structure and compare across fed and starved groups, we first aim to categorize swim bouts into discrete types. We represent each swim bout as a 10-frame (167 ms) postural sequence beginning at bout initiation, giving a 220-D egocentric representation of every bout (Figure 2A). We embed these observations in 2-D space with tSNE [37, 38] (Figure 2B) and use density-based clustering [7, 39] to isolate 5 major classes of swim bouts (Figure S2). These classes consist of hunting bouts (here called J-turn, pursuit, abort, strike) and non-hunting bouts (here called exploring). Zebrafish larvae typically initiate hunts by converging their eyes and orienting toward prey with a J-turn [19], close distance to prey while maintaining eye convergence with pursuits [40] (also called approach [13] swims), and end hunts with eye divergence during a strike (also called capture [13] swim) or abort [41].
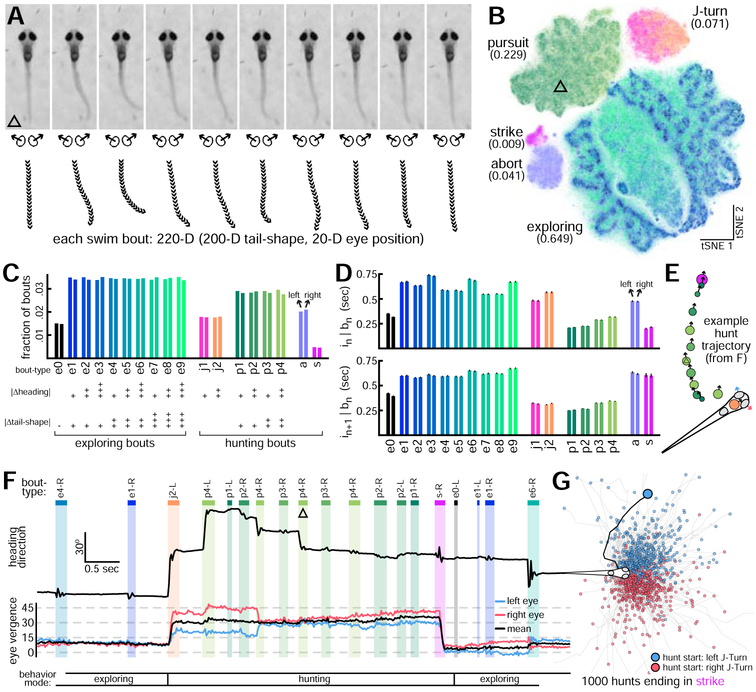
Figure 2: Exploring and Hunting Bout-Type Categorization.
A. Bouts are represented as 10-frame postural sequences beginning at bout initiation. Bout shown immediately follows image from Figure 1J. B. Bout dataset embedded in 2-D space with tSNE. 5 bout-classes (abundances in parentheses) identified with density-based clustering (see Figure S2). Location of bout from A indicated with triangle. Each bout is a point, colored by bout-type (see C for colormap). C. Large bout-classes are subdivided to get bout-types. Plus signs indicate kinematic parameter magnitude. D. Duration (mean ± SE) of interbout intervals preceding (top) and following (bottom) left and right versions of each bout-type. E. Trajectory of 13-bout hunt ending in strike. Circle locations and arrows indicate head position and heading direction preceding bout initiation. Circle colors indicate bout-type. Circle areas are proportional to ∣ Δ tail-shape∣. F. Hunt from E contained in a longer bout sequence. Heading direction and eye vergence angles shown over time with bout and interbout epochs indicated. Bout from A indicated (triangle). See Video S2 for corresponding video data. G. Trajectories from 1000 complete hunts ending in strike (black line: hunt from E).
To improve analytical sensitivity, we further subdivide the 3 largest bout-classes to yield 10 exploring and 8 hunting bout-types (Figure 2C). Each bout-type is symmetric with nearly equal numbers of leftward and rightward bouts. We use 2 scalar kinematic measurements to subdivide bout-classes: ∣ Δ heading∣ and ∣ Δ tail-shape∣. ∣ Δ heading∣ is the magnitude of heading angle change per bout, and ∣ Δ tail-shape∣ is the sum of the magnitudes of frame-to-frame changes in tail shape for each 10-frame bout representation (Methods), a metric correlating with distance traveled per bout and presumably energy expenditure. See Figure S2 for detailed bout-type descriptions.
With labels assigned, the distributions of interbout intervals preceding and following each bout-type are compared (Figures 2D). Larvae select longer intervals during exploration and shorter intervals during hunts. Distributions of intervals preceding (or following) left and right versions of each bout-type are approximately equal, showing how left-right symmetry organizes population-level behavior. Larvae alternate between exploring and hunting modes, as seen in an example bout sequence containing a successful hunt (Figure 2E-F, Video S2). We define a complete hunt as a bout sequence beginning with J-turn, ending with abort or strike, and padded with only pursuits (for hunts longer than 2 bouts). The full dataset contains 7230 complete hunts (19.6% end in strike). For comparison, the example hunt trajectory is shown with 999 other complete hunts ending in strike (Figure 2G).
Hunger Regulates Eye Position and Action Selection
Feeding state strongly regulates larval zebrafish behavior, seen by comparing eye position histograms (as in Figure 1I) across fed and starved fish groups in the first 10 minutes of testing (Figure 3A). The fraction of intervals during which eyes are converged (threshold: mean vergence angle = 24°) is increased 183% from 0.124 in fed fish to 0.351 in starved fish in this time window. Fed fish also maintain wider eye divergence during exploration, but not while actively hunting (Figure 3B).
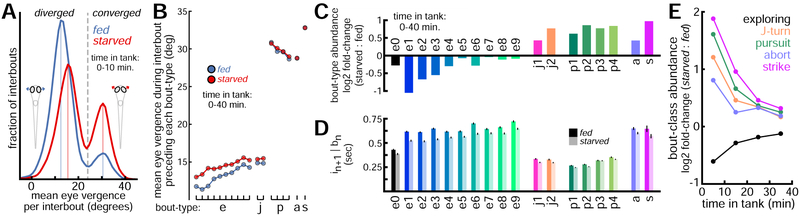
Figure 3: Hunger Regulates Eye Position and Action Selection.
A. Mean eye vergence per interbout (like Figure 1I) for observations in first 10 minutes of testing, shown separately for fed and starved groups. Solid vertical lines indicate local histogram peaks. B. Fed fish display wider eye divergence preceding exploring bouts and J-turns, but not pursuits, aborts, and strikes (bout-types ordered as in C). See Figure S3 for eye kinematics associated with each bout-type. C. Log2 of relative bout-type abundances (starved / fed) during first 40 minutes of testing. D. Interval durations (mean ± SE) following each bout-type for fed and starved groups (first 40 minutes of testing). E. Log2 of relative bout-class abundances (starved / fed) in 10-minute bins.
By comparing bout-type abundances and interbout intervals across fish groups in the first 40 minutes of testing, we find hunger affects larval zebrafish action selection in previously unreported ways. Fed fish upregulate use of low-energy exploring bouts (e1-3) relative to starved fish, with selection of the lowest-displacement forward swim e1 increased 107% (Figure 3C). Starved fish are more likely to start hunts, especially through high-angle J-turns (j1 up 35%, j2 up 70%), and increase use of pursuits (up 71%), aborts (up 34%), and strikes (up 96%). Fed fish also produce longer intervals than starved fish, especially following low-energy exploring bouts (Figure 3D). Over ~40 minutes, behavioral patterns of fed and starved fish converge (Figure 3E) as their feeding states shift from opposing initial conditions (high hunger or high satiety) toward an intermediate state near nutrient equilibrium. To better quantify the behavioral sequences observed in this study, we next construct probabilistic models to predict the timing and type of swim bouts.
Probabilistic Models to Predict Interbout Intervals
We model the data as a marked renewal process [31, 42], a stochastic process generating a sequence of discrete events in time, each characterized by an associated “mark” (Figure 4A). These statistical models specify the conditional distribution of the time and type of the next event in a sequence given the history of preceding events. First, we consider bout timing. Our key question for model construction is, “what features of the event history carry predictive information about the timing of the next event?” We choose five interpretable features to represent behavioral history on multiple timescales (Figure 4B). On the shortest timescale, we model the interbout interval (in) as a function of preceding bout-type (bn–1) and preceding interbout interval (in–1). On an intermediate timescale, we use hunt dwell-time (thunt) and explore dwell-time (texplore) features to encode how long the fish has been hunting or exploring immediately prior to in. On the longest timescale, we encode how long the fish has been in the tank (tank-time, ttank), relating how behavior changes with hunger. By comparing models composed from different features, we can learn how past actions predict future behavior.
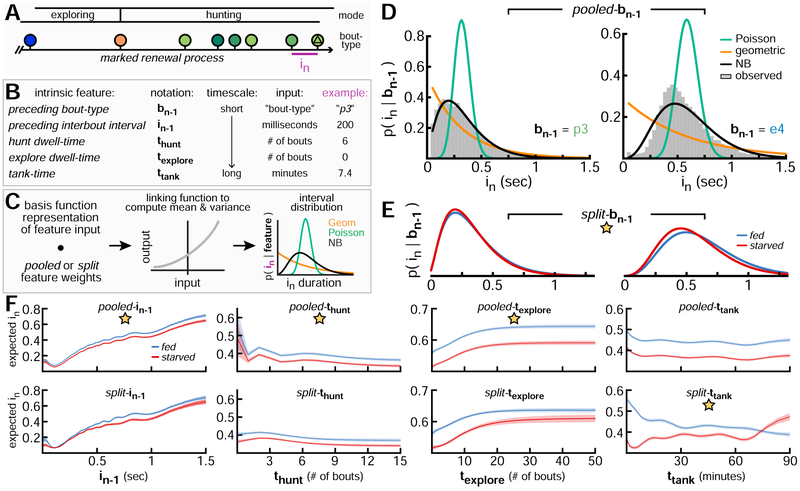
Figure 4: Probabilistic Models to Predict Interbout Intervals.
A. Behavioral data conceptualized as marked renewal process. Part of bout sequence from Figure 3F shown for example. B. Intrinsic features relate behavioral history and hunger to interval in. Example inputs to predict interval from A shown. C. Schematic of GLM to generate predictive probability distribution over in. Geometric and Poisson distributions are parameterized by just their mean, while the negative binomial distribution is also parameterized by variance. D. in probability distributions given 2 possible values for preceding bout-type. E. Similar to D, but for split-bn–1 (NB distribution only). F. Predicted in (mean with 95% credible intervals) given from pooled and split forms of single-feature NB models.
Starved fish select shorter intervals than fed fish, but how else do patterns of bout timing differ? To interpret how feeding state influences relationships between behavioral history and interval selection, we consider 2 forms for each predictive feature: pooled and split. In pooled form, data from fed and starved fish are pooled to fit one set of weights relating that feature to in. In split form, separate weight sets are fit for each fish group. We use a generalized linear model [43] (GLM) with an exponential inverse link function to generate a probability distribution over in (Figure 4C). Briefly, the dot product of a basis function representation of the feature input with corresponding feature weights is computed and passed through an inverse link function to give the mean of a probability distribution over in (Methods S1). We considered 3 types of probability distributions over nonnegative counts: geometric, Poisson, and negative binomial (NB). We find the NB distribution fits observed data best and consider this form throughout the paper.
For each model, we use an empirical Bayes [44] hyperparameter selection method (Methods S1) to choose an appropriate prior variance on weights, number of basis functions, and a preferred feature form (pooled or split, indicated with star). To model in given preceding bout-type, separate NB distributions are fit for each possible value of bn–1 (2 examples shown, Figure 4D). In split form, the bn–1 feature captures subtle differences in intervals produced by fed and starved fish (Figure 4E). For remaining features, we plot the predictive in mean for pooled and split models over a range of input values (Figure 4F). Each of these models include additional split-bias weights to capture overall differences in interval mean and variance across groups (2 extra free parameters per group: 1 for mean, 1 for variance). This design choice allows pooled feature models to capture basic group differences without using the more complex split features. On a short timescale, we find consecutive intervals are autocorrelated (column 1). On an intermediate timescale, intervals get shorter as hunt sequences get longer (column 2). By contrast, as exploring sequences get longer, intervals get longer (column 3). Aside from a shift in mean, the general relationship between these features and in is similar across groups. By contrast, fed and starved fish display opposing interval selection patterns on the longest timescale (column 4). Starved fish initially hunt more, producing shorter intervals. Fed fish initially explore more, producing longer intervals. As their hunger states converge, intervals selected by fed and starved fish become more similar. These opposing patterns require the split-ttank feature to be modeled appropriately.
Probabilistic Models to Predict Bout-Types
The second component of the marked renewal process is a model of how the next bout-type is selected depending on behavioral history, including the interval immediately preceding it. We add 4 extrinsic features to model how locations (νloc), sizes (νsize), and relative velocities (νx, νy) of local environmental objects relate to bout-type selection (Figure 5A). We construct an 868-D image (νloc) to encode putative prey object locations immediately preceding bout initiation. We modify νloc to construct the other extrinsic features by scaling pixel intensities representing each object (Figure S4). We take the dot product of a basis function representation of a feature input with its corresponding weights to produce a vector of bout-type “activations”, ψ (Figure 5B). This vector is passed through a softmax function to generate a valid probability distribution, π, over all 36 possible bout-types (Methods S1). As before, we select hyper-parameters and preferred feature forms, choosing pooled forms for all features except ttank. As before, we include split-bias weights to account for differences in baseline bout-type abundances across fed and starved fish groups (36 extra free parameters per fish group).
Figure 5: Probabilistic Models to Predict Bout-Types.
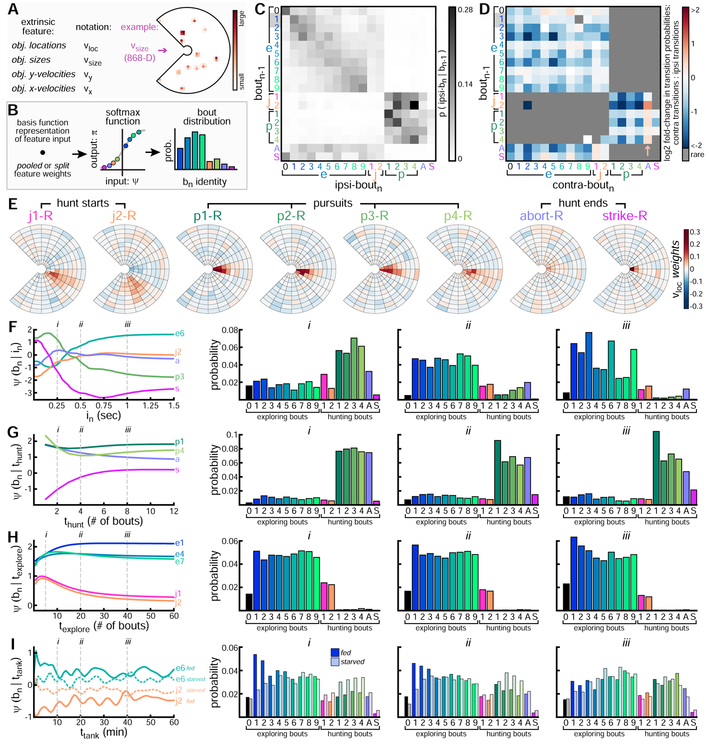
A. Extrinsic features encode surface object locations and properties (see Figure S4). For example, νsize encodes object sizes (here, for objects from Figure 1K). B. Schematic of GFM to generate predictive probability distribution over bn. C. Ipsilateral bout transition probabilities (i.e. left to left, or right to right) from pooled-bn–1 model. Each row shows bn probability given preceding boat-type. D. Contralateral bout transition probabilities (i.e. left to right, or right to left) from pooled-bn–1 model, reported relative to ipsilateral transition probabilities. Rare transitions not shown. Blue squares indicate transitions that are more likely to occur ipsilaterally. Transitions into abort are more likely to occur contralaterally. E. Weights from pooled-νloc model shown for each rightward hunting bout-type. F. pooled-in model summary. Activations of 5 bout-types shown given preceding interbont interval. Full bout-type probability distribution evaluated at 3 specific in values (indicated with i, ii, iii). G-I. Similar to F, but for hunt dwell-time, explore dwell-time, and tank-time. We choose the split architecture for tank-time, with separate distributions for fed and starved fish shown.
Bout transition probabilities are captured by the preceding bout-type feature (Figure 5C-D). While exploring, larvae link consecutive bouts of similar energy (note increased transition probability along diagonal in Figure 5C). This may help larvae maintain speed [45] over many seconds, especially in combination with autocorrelated intervals. Larvae enter hunting mode with a transition to J-turn, after which they are likely to emit pursuits before an abort or strike. Since behavior is symmetric at the population level, we enforce feature symmetry to simplify and improve models. For example, the preceding bout-type feature encodes ipsilateral (Figure 5C) and contralateral (Figure 5D) bout transition probabilities. Larvae are known to link bouts in the same direction while exploring featureless environments [46], and we too see ipsilateral transitions are more probable. We find this pattern extends also to hunting, except for transitions into abort (Figure 5D, arrow), during which fish are likely to switch left-right state.
Prey object locations influence bout-type selection, especially during hunts, and pooled-νloc weights associated with each hunting bout-type are shown (Figure 5E). Since νloc inputs are high-dimensional, we compress them by summing νloc pixels within spatial bins as shown (Figure S4). Objects located in red bins increase the probability that the corresponding bout-type will be selected next by the fish. Larvae typically select a J-turn to orient toward a laterally located object ( ~ 15-60 ° relative to heading) and the magnitude of heading angle change depends on prey location [18] (compare j1, j2). Energetic pursuits (p3-4) are more likely when prey are further away, while larger ∣ Δ heading∣ pursuits (p2, p4) are more likely when prey are located more laterally. Prey locations affect how hunts end, with strike becoming most likely with an object located directly in front of the mouth. By contrast, aborts are weakly related to prey location and may be selected to terminate unsuccessful hunts. When prey are absent, exploring bouts become more probable since their associated νloc weights are more spatially uniform with near-zero or negative values (not shown).
The generative process underlying bout-type selection depends nonlinearly on preceding interbout interval. We capture this dependency with the pooled-in model (Figure 5F). Activations (ψ) of several bout-types across the range of in input values are shown (left panel), with larger activations indicating higher bout-type probability. Full bout-type probability distributions evaluated at 3 specific in values are shown (panels i-iii), with probabilities across fed and starved fish averaged for display. At very short preceding interbout interval values (in < 0.25 sec), activations of p3, strike, and abort have different dynamics, indicating how timing is intricately involved in bout-type selection during hunts. As in extends from 0 to 0.25 seconds, strikes become less likely, aborts become more likely, and p3 probability peaks near 150 ms before decreasing again. As in reaches 0.5 seconds (panel ii), exploring bouts become more probable. As in reaches 1 second (panel iii), low-energy e1–3 and high-∣ Δ heading ∣ e3, e6, e9 bouts become most likely.
Longer timescale dependencies are captured with thunt, texplore, and ttank features. As hunts extend, aborts become less likely and strikes become more likely (Figure 5G). Pursuits are always likely when larvae are in hunting mode (i.e. thunt is non-zero), but the probability mass shifts toward the short straight p1 bout as hunts get longer and larvae approach a target. As explore dwell-time increases, larvae become more likely to select low-energy exploring bouts and to remain in exploring mode (Figure 5H). J-turn emission probability decreases ~46% as texplore increases from 5 to 40 bouts. This may be partly explained by decreased food density as fish navigate toward the arena edge. On the longest timescale, the ttank feature captures slow fluctuations in bout-type probabilities over the course of observation (Figure 5I). As with models of bout timing, the ttank feature must be split to capture opposing behavioral trends of fed and starved fish on this timescale. Separate bout-type probability distributions for fed and starved fish are shown. These distributions becomes similar across groups as their hunger states converge at ttank = 40 minutes.
Comparing and Combining Behavioral Models
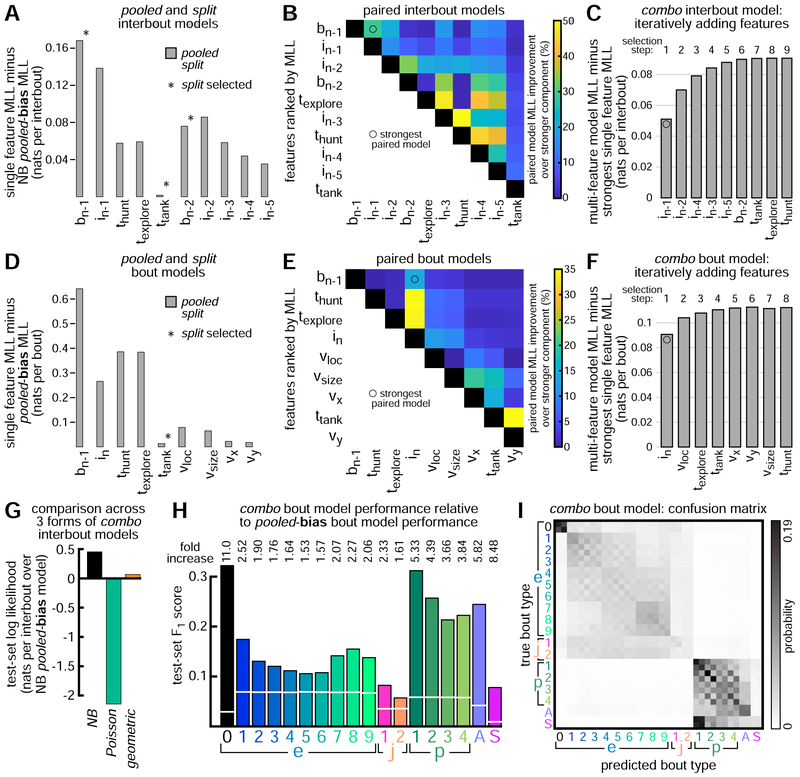
Having constructed several single-feature models, we next compare their quality. We compute the marginal log likelihood (MLL) of each model and report improvement over the simplest baseline model (pooled-bias). For interbout models, the baseline NB pooled-bias model has 2 parameters (1 for mean, 1 for variance). For model comparison, we plot MLL for pooled and split forms of each model (Figure 6A). We include also bn–2 as well as in–2, in–3, in–4, and in–5 to show how predictive information decays over time. We find preceding bout-type is best able to predict in, but that preceding interbout interval is a close second, and that more distant behavioral history also provides useful information to model intervals. In general, MLL is similar across pooled and split forms, except for ttank. We interpret this to suggest that any mild gains in predictive performance through use of split features may be offset by increased complexity and decreased training examples per split weight.
Figure 6: Comparing and Combining Behavioral Models.
A.Pooled and split single-feature NB interbout models compared by marginal log likelihood (MLL). MLL of simplest NB interbout model (pooled-bias) subtracted from each model’s MLL as baseline. For comparison, we include features similar to preceding bout-type and preceding interbout interval, but from further into behavioral history. Pooled forms selected unless indicated. B. All pairwise combinations of features (in selected form) are used to make 45 paired interbout models. Paired model MLL calculated as in A (i.e. baseline-subtracted) and divided by baseline-subtracted MLL of stronger feature component. C. All features combined to make combo GFM for intervals. Starting with strongest paired model, we add the feature at each selection step which increases MLL most, until all features are added. D-F. Same as A-C, but for bout-type models. See Figure S5 for information on extrinsic feature neural network models. G. NB combo interbout model compared to similarly constructed combo geometric or Poisson models to predict in. NB distribution fits the data best. H. Performance of combo bout model compared to baseline (pooled-bias model captures only overall bout-type abundances). F1-statistic computed for each bout-type on test-set data (combo model: bars; baseline: white lines). Fold increase shown for each bout-type. See Figure S6 for similar analyses of single-feature bout models. I. Combo bout model confusion matrix (separate rows for left and right versions of each bout-type). Each row sums to one, showing average model output for all bouts of that type in test-set.
While preceding bout-type is the best predictor of in, can we build stronger models by combining features? We approach this question by combining all pairs of features (in their selected forms) to produce 45 paired interbout GLMs (Figure 6B). For each paired model, we compute MLL and report improvement over the stronger component. Paired models showing large improvement should combine features that provide some unique information about interbout in. We find preceding bout-type and preceding interbout interval combine to produce the strongest paired interbout model. This paired [bn–1, in–1] model improves over bn–1 alone by 0.05 nats per interbout, or 29% relative to baseline. By contrast, the [bn–1, texplore] model improves over bn–1 by just 0.002 nats per interbout, or 1.4%. Since models can improve by combining features, we combine all features to construct a combo interbout model (Figure 6C). Features are added sequentially via greedy stepwise selection, adding the feature that increases MLL most at each step. Model quality improves and saturates during construction.
We repeat this procedure for bout-type models. We find preceding bout-type is by far the best predictor of bout-type bn, followed by hunt dwell-time and explore dwell-time, and then preceding interbout interval (Figure 6D). As constructed, our extrinsic feature GLMs fail to fully capture the complex relationship between environmental state and bout-type selection. This problem is challenging for several reasons. Identified objects include both prey and non-prey (e.g. dust, algae), which differentially influence behavior. Second, environmental objects are highly abundant in these experiments (mean # of identified objects per bout = 12), complicating the visual scenes experienced by the fish and also our environmental representations. Third, the locations, sizes, shapes, and motion patterns of objects are likely to interact in complex ways to influence larval zebrafish action selection. To improve our understanding of how sensory input relates to bout-type selection, we construct feed-forward neural networks that take extrinsic feature inputs (Figures S5) and combine them nonlinearly to form a prediction. We find this neural network model improves substantially over the νloc GLM, with predictions of all bout-types improving on held-out data, especially hunting bouts. However, bout-type bn is still far better predicted by preceding bout-type, indicating more sophisticated modeling approaches will be needed to better predict future behavior from complex environmental data, but also that bout-type selection depends strongly on the animal’s short-term behavioral history [1].
The strongest paired bout model again combines preceding bout-type with preceding interbout interval, even though preceding interbout interval is just the 4th strongest individual feature (Figure 6E). This paired [bn–1, in] model improves over bn–1 alone by 0.09 nats per bout, or 14%. By contrast, the paired [bn–1 texplore] model improves over bn–1 by just 0.005 nats per bout, or 0.8%. This result again indicates that distinct features of the fish’s short-term behavioral history (i.e. preceding bout-type and preceding interbout interval) encode non-redundant information about future action selection. As before, we construct a combo bout model through greedy stepwise selection (Figure 6F). The strongest 3-component bout model ([bn–1, in, νloc]) adds information about prey locations to the strongest paired bout model, combining internal and external information over a timescale of a second or less.
We next examine combo model quality. To confirm the NB distribution is warranted, we compare our NB combo interbout model to similar combo models constructed instead with Poisson or geometric distributions (Figure 6G). While requiring more free parameters, the NB model clearly outperforms the others on held-out data. For the combo bout model, we show its ability to predict each individual bout-type, as measured by the F1 score [47] of each one-vs-rest classifier, and compare this performance to baseline (Figure 6H). This shows us which bout-types are easiest to predict (e.g. pursuits, aborts, strikes, e0), and which are most challenging (e.g. e4-6, j2). We reproduce this analysis for several single-feature bout models as well as the strongest paired and 3-component bout models (Figure S6). The combo bout model distributes probability mass over similar bout-types (Figure 6I), which should be expected if the generative processes involved in producing similar bout-types are also similar.
Simulating Trajectories of Fed and Starved Fish
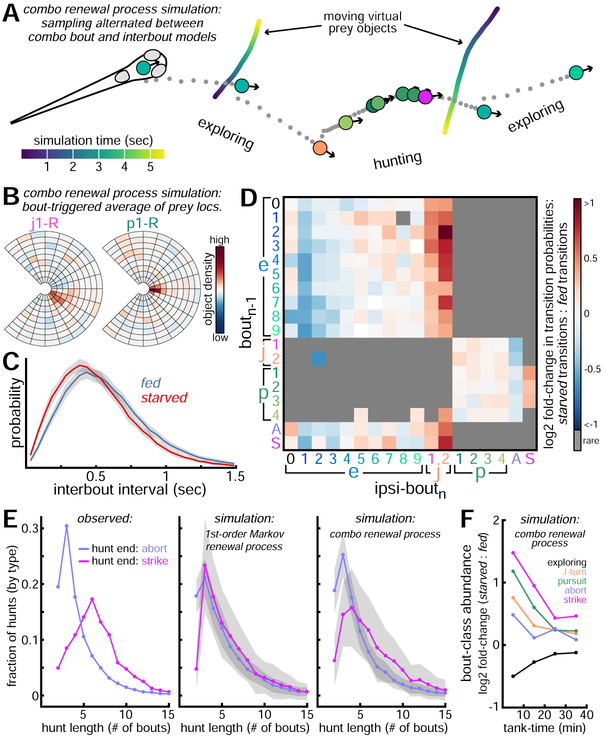
A strong test of a behavioral model is to evaluate its ability to generate realistic behavior in novel contexts. To that end, we alternate sampling from our combo bout and interbout models (here called a combo renewal process) to move a virtual fish through an artificial environment with abundant prey (Figure 7A, Videos S3-4). We simulated trajectories of fed and starved fish to capture multiple timescales of structure in larval zebrafish behavior. Prey object locations influence hunting bout selection in expected ways (Figure 7B) and fed fish select longer intervals (Figure 7C), as expected. The strong effects of hunger are seen by comparing bout transition probabilities of simulated fed and starved fish (Figure 7D). Fed fish are more likely to transition to low-energy exploring bouts, while starved fish are more likely to transition to high-energy exploring bouts. Starved fish also adjust their behavior in several ways to increase food intake. They are more likely to transition to J-turns (especially j2) and to extend hunt sequences by linking pursuits [41]. Starved fish are also less likely to transition to abort and more likely to transition to strike.
Figure 7: Simulating Trajectories of Fed and Starved Fish.
A. We simulate behavioral trajectories of 50 fed and 50 starved fish (40 minutes per fish) by alternating sampling from combo interbout and bout models (here called a combo renewal process). ~5 seconds of simulated behavior shown in which fish hunts and strikes at a virtual prey. See Video S3 for animation of this simulated sequence and Video S4 for visualization of how these bout-types and intervals were selected from conditional probability distributions evolving overtime. Fish move through the environment using bout-type trajectories shown in Figure S7. Virtual prey move through environment as biased random-walking particles with fixed sizes and speeds. B. Bout-type triggered averages of fish FOV preceding initiation of 2 bout-types. C. Histograms of simulated interval durations (mean ± SE). D. Ipsilateral bout transition probabilities of simulated fed and starved fish are compared. Red squares indicate increased transition probability for starved fish relative to fed fish. E. Hunt length distributions for complete hunts ending in strike or abort. Left panel: real data. Middle panel: data from simulations in which bout-types and intervals depend on only preceding bout-type (called a 1st-order Markov renewal process). Right panel: data from combo renewal process simulations. F. Relative bout-class abundances produced in combo renewal process simulations (similar to Figure 3E).
These simulations also capture longer timescale behavioral dependencies observed in our experiments. With real fish, we find hunts ending in strike are much longer than those ending in abort (Figure 7E). This trend is absent in simulations generated from a first-order Markov renewal process in which intervals and bout-types depend on just preceding bout-type (bn–1). By contrast, combo renewal process simulations do better to recover this higher-order hunting structure. Our simulations also capture non-Markovian dynamics during exploration (e.g. decreased J-turn probability as exploring sequences lengthen; not shown). Finally, our model reproduces slowly changing bout-type selection probabilities across fed and starved fish as their hunger states converge over 40 minutes (Figure 7F).
Discussion
Behavior is the principal output of the nervous system and is complex and high-dimensional [48, 49]. To make studying the brain more manageable, behavior is often constrained in neurobehavioral experiments. This reductionist approach has many benefits: it simplifies behavioral description, reduces experimental variability, and improves interpretability of neural data. However, an important frontier in neuroscience is to better understand how brains function in natural conditions [50]. The NIH BRAIN Initiative [51] has identified study of the “Brain In Action” [52] as a priority research area, stating that “a critical step ahead is to study more complex behavioral tasks and to use more sophisticated methods of quantifying behavioral, environmental, and internal state influences on individuals.” [53] Importantly, these methods should capture dynamics of minimal behavioral elements, scale to big datasets, and be compatible with modern techniques to record neural population activity. Here we describe such an approach to predict and simulate natural larval zebrafish behavior. Further, by constructing a model of how state influences action, we can make predictions about what types of signals must be present in the neural system driving this behavior.
Our study generates testable hypotheses about how neural mechanisms might give rise to observed behavioral patterns on multiple timescales. On a short timescale, we see larvae are likely to link consecutive exploring bouts through ipsilateral transitions, but also tend to begin hunts ipsilaterally. It has been shown that reciprocally connected circuits in the anterior hindbrain (anterior rhombencephalic turning region: ARTR) alternate between “leftward” and “rightward” states to mediate temporal correlations in turn direction during exploration [46], but how ARTR or related circuits may bias reactions to prey stimuli is unknown. We predict ARTR projections may asymmetrically modulate premotor systems (e.g. reticulospinal neurons [54], hunting command neurons [55], or premotor tectal assemblies [56]) such that, with the ARTR in a leftward state, leftward J-turns are generated preferentially to rightward J-turns. Alternatively, ARTR-state-dependant modulation could occur further upstream in the sensorimotor hierarchy through asymmetric modulation of retinorecipient areas processing prey stimuli (e.g. optic tectum, AF7) [56, 57]. If so, retinal output may be processed asymmetrically to promote ipsilateral transitions from exploring to hunting.
Following hunt initiation, several behavioral patterns interact to influence hunt outcome. As hunts extend, larvae select shorter intervals, pursuits become finer, and abort probability decreases while strike probability increases. By contrast, as intervals extend, abort probability increases, pursuit probability rises and falls, and strike probability decreases. These time-sensitive patterns likely depend on reciprocal connectivity between the nucleus isthmi (NI) and (pre)tectum. It has been shown that NI neurons become active following hunt initiation and that NI ablation leads to specific deficits in hunt sequence maintenance [41]. Henriques et al. [41] propose NI-mediated feedback facilitation of (pre)tectal prey responses increases hunt sequence extension probability. This mechanism may explain why abort probability decreases and strike probability increases as hunts elongate in our study. However, how hunting bout-type selection depends so precisely on bout timing is not well understood. We posit tectal prey representations may attenuate as intervals extend past a few hundred milliseconds, potentially through phasic bout-locked NI feedback that decreases as intervals elongate. Alternatively, premotor populations [34, 55, 56] involved in pursuit and strike generation may become increasingly inhibited as interbouts get longer, increasing hunt termination probability. Also, since larvae tend to abort hunts through contralateral transitions, we suspect abort generation may frequently coincide with a change in ARTR state. Such a mechanism could facilitate switches in spatial attention from one hemifield to the other, thereby inhibiting return [58] to a previously pursued object.
Hunger state affects larval zebrafish behavior in many ways. We see starved fish are more likely to initiate and extend hunts. They also upregulate transitions to strike and downregulate transitions to abort relative to fed fish. It has been shown that food deprivation modulates larval zebrafish tectal processing of prey-like and predator-like visual stimuli such that food-deprived larvae are more likely to approach small moving dots [35]. Specifically, hunger induces recruitment of additional prey-responsive tectal neurons and neuroendocrine and serotonergic signaling mediates this effect [35]. We posit this mechanism may increase tectal input to NI, thereby increasing NI-mediated feedback to facilitate hunt sequence extension and increased strike probability in starved fish. While not yet tested, direct hunger-state modulation of tectal-projecting NI neurons is also plausible. Other studies show that lateral hypothalamic neuron activity correlates positively with feeding rate [59] and that lateral hypothalamic neurons respond to both sensory and consummatory food cues [60]. This brain region is likely critically involved in sustaining increased hunting over tens of minutes through modulating visual responses to prey and/or facilitating hunting (pre)motor circuits.
While the above mechanisms can explain why fed fish initiate fewer hunts, we posit satiety signals affect additional circuits to further improve safety against predation during exploration. Fed fish select longer interbout intervals, lower-energy exploring bouts, and maintain wider eye divergence during exploration. These strategies could improve safety by decreasing their visibility to predators (by moving less) and increasing their ability to detect threats (by widening surveillance). To coordinate these behavioral patterns, satiety cues may separately modulate midbrain nuclei involved in regulating bout timing [61], nMLF neurons involved in regulating swim bout duration and tail-beat frequency [45], and oculomotor centers involved in controlling eye position [62, 63, 64]. It is clear that feeding state coordinates a complex array of behavioral modifications, likely through modulation of many circuits distributed across the larval zebrafish brain.
There are many avenues to extend this work. In future studies, moving camera systems should use faster camera frame rates, shorter exposure durations, and better tracking algorithms to improve raw behavioral data. These adjustments will allow for higher resolution pose estimation (e.g. by including pectoral fin dynamics, pitch and roll estimates, and tail half-beat analysis [13]), facilitate more comprehensive bout-type classification, and yield significantly longer continuous behavioral sequences. Richer datasets will enable future models to extract nuanced environmental dependencies, like prolonged attention to single prey amongst many distractors [65]. Future models may simultaneously infer discrete behavioral states and their dynamics [7, 14, 66, 67], though the non-Markovian dependencies on past behavior present new challenges [68]. Likewise, there are many other internal state variables governing action selection, and future models could seek to infer these latent states [68] rather than using proxy covariates like tank-time. Behavioral states and dynamics differ slightly from one individual larva to the next, and long-term behavioral recordings combined with hierarchical models [69, 70] will allow us to study how these behavioral differences emerge and change throughout early development. The contribution of particular neural populations in generating naturalistic behavioral patterns may also be probed by combining our behavioral models with experiments to activate, inhibit, or ablate specific neural cell-types in observed fish. Finally, our approach may be combined with new technologies to record large neural populations in freely swimming fish [71, 72, 73, 74, 75]. This will present opportunities to construct joint models of neural activity and natural behavior that are likely to improve the predictability of behavioral sequences while providing important new tools to study the brain in action [76, 77].
STAR Methods
Lead Contact and Materials Availability
Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Robert Evan Johnson (robertevanjohnson@gmail.com).
Materials Availability Statement
This study did not generate new unique reagents.
Experimental Model and Subject Details
All fish were 7-8 days post-fertilization (dpf) mitfa−/− (nacre) zebrafish raised at ~27C. Fish were given abundant live paramecia as food beginning at 5dpf. On test day, fish from the fed group remained in their Petri dish with abundant paramecia while fish from the starved group were placed in clean water for ~2.5-5 hours prior to testing. Testing was performed between 10 AM and 6 PM with 4-6 fish usually tested per day. All protocols and procedures were approved by the Harvard University/Faculty of Arts and Sciences Standing Committee on the Use of Animals in Research and Teaching (Institutional Animal Care and Use Committee).
Method Details
BEAST Design
The gantry was acquired from CNC Router Parts (CRP4848 4ft x 4ft CNC Router Kit; www.cncrouterparts.com) and was modified to run upside-down on top of a support structure constructed from aluminum T-slotted framing available through 80/20 Inc (www.8020.net). Three electric brushless servo motors (CPM-MCPV-3432P-ELN ClearPath Integrated Servo Motors) and 3 Amp DC Power Supply (E3PS12-75) were acquired from Teknic (www.teknic.com). The camera (EoSens 3CL) was acquired from Mikrotron (www.mikrotron.de) with a frame-grabber from National Instruments (NI PCIe-1433; www.ni.com). The camera lens was acquired from Nikon (AF-S VR Micro-Nikkor 105mm f/2.8G IF-ED; www.nikonusa.com). A long-pass infrared filter was placed over the lens (62 mm Hoya R72; www.hoyafilter.com) to block light from the projector and collect transmitted light from an array of 16 IR-LED security dome lights (850 nm Wide Angle Dome Illuminators) positioned on the air table below the fish tank. The projector was acquired from Optoma (Optoma GT1080; www.optoma.com) and mounted on the side of the air table to project onto a diffusive screen (Rosco Cinegel 3026 Tough White Diffusion (216); www.stagelightingstore.com) embedded in the bottom of the plexiglass tank.
Data Acquisition
The walls of the observation arena were assembled with light gray LEGO blocks to confine the fish to a water volume of 300 x 300 x 4 mm. Approximately 15 ml of water containing a high density of live paramecia were added near the center of the arena prior to testing each fish. This paramecia stock also contained some rotifers and algae particles. For testing, single fish were transferred to the arena where inwardly drifting concentric gratings were projected to bring the fish to the arena center. Zebrafish larvae tend to turn and swim in the direction of perceived whole-field motion, a reflexive behavior called the optomotor response, and we leverage this response to relocate the fish. Once the overhead camera detected the arrival of the fish, the first observational trial was initiated and the drifting gratings were replaced by a static color image of small pebbles, a natural image with reasonably high spatial contrast. Next, the camera moved automatically on the gantry to maintain position above the fish and capture video with a frame-rate of 60Hz and 2 millisecond exposure duration per frame. The fish was tracked for 3 minutes or until it reached the edge of the arena or tracking failed. The fish could evade the tracking camera with a high-speed escape maneuver, but these events were fairly rare. At the end of each trial, the camera returned to the arena center, video data was transferred from memory to hard disk, and concentric gratings were once again used to bring the fish back to the arena center to initiate another trial (up to 18 trials per fish). If the fish did not return to the center within 10-15 minutes, the experiment was terminated. The tracking algorithm was written to keep the darkest pixel in the image (usually contained within one of the eyes of the fish) within a small bounding box located at the image center. If the darkest pixel was located outside this bounding box, a command was sent to the motors to reposition the camera to the location of that darkest pixel. In this way, the camera moved smoothly from point to point to follow the fish, using the “Pulse Burst Positioning Mode” setting for the ClearPath motors. We run the ClearPath motors with Teknic’s jerk-limiting RAS technology engaged to generate smooth motion trajectories and minimize vibration during point to point movement. Experiments were run using PsychToolBox in Matlab.
Statistical Models
See Methods S1 for statistical modeling details.
Quantification and Statistical Analysis
Image Registration and Fish Pose Estimation
In every image frame, connected component pixel regions corresponding to the left eye, right eye, and swim bladder were identified. The fish head center was defined as the average position of the centers of these 3 regions of interest. Heading direction is defined as the direction of the vector from the swim bladder center to the midpoint between the two eye centers. This information is used to translate and rotate each image for subsequent pose estimation and environment analysis. Only image frames in which all postural features could be extracted were included for further analysis. One common issue with pose estimation was caused by body roll of the fish, usually during an attempt to strike at a prey object, in which the fish would roll (rotate around its rostro-caudal axis) enough for one eye to occlude the other from the view of the overhead camera. Rather than estimate eye vergence angles in these situations, these image frames were excluded. Another common issue was caused by high-speed maneuvers by the fish during which a 2 millisecond exposure was insufficient to capture a suitably sharp image, thus causing either image registration or pose estimation algorithms to be compromised. We included only image frames in which all postural features could be accurately extracted for further analysis. Video segments containing problematic frames were split into separate video segments.
Temporal Segmentation of Bout and Interbout Epochs
Bout and interbout epochs were identified by taking the absolute value of the frame to frame difference in heading angle and thresholding this time-series at 0.7 degrees. This binary signal was then dilated (radius = 2 elements) and eroded (radius = 1 element) with built-in Matlab functions (imdilate, imerode) to merge bout fragments and expand bout epochs to include one extra frame at the beginning and end of each bout. These operations set the minimal duration of both bout and interbout epochs to 3 frames (50 ms).
Bout Summary Statistics
Δ heading per bout: The change in heading angle per bout was calculated by averaging the heading direction of the fish over all frames in the preceding interbout epoch and subtracting this value from the average heading direction through all frames in the following interbout epoch. Positive values are assigned to leftward bouts.
∣ Δ heading∣ per bout: The absolute value of Δ heading per bout.
distance traveled per bout: The change in head position per bout was calculated by averaging the position of the fish head in the arena over all frames in the preceding interbout epoch (starting position) and also for the frames in the following interbout epoch (ending position). The distance between these two points is the distance traveled per bout.
∣ Δ tail-shape∣ per bout: This non-negative 1-dimensional quantity summarizes how much the tail changes shape during the 10 frames used to represent each swim bout (as in Figure 2A). To compute this quantity, let the 10-frame tail angle measurements be placed in an array T with shape 20 × 10. First, the magnitude of frame to frame changes in each tail segment angle are computed to give a new array with shape 20 × 9. ∣ Δ tail-shape∣ is the sum of the absolute values of these 180 array elements. This value is divided by 180 to give units: radians per segment per frame. In Matlab syntax, this is computed as: abs_delta_tail_shape = sum(sum(abs(diff(T, n=1, dim=2)))) / 180
Several additional summary statistics are used to describe the fish eyes during each bout. These metrics are computed from the 10-frame representations of each bout and are further described in Figure S3.
tSNE Input
Each swim bout is represented as a 220-dimensional vector encoding the posture of the fish through 10 image frames beginning at bout initiation with 20 tail vectors and 2 eye vergence angles per frame (see also Figure S1). All rightward bouts (Δ heading < 0) were mirror reflected prior to running tSNE by swapping the left and right eye measurements and multiplying all tail angle measurements by −1. Because tail measurements are tenfold more abundant than eye measurements and we sought to emphasize eye data in our clustering, we decreased the relative magnitude of the tail measurements by encoding tail measurements in radians and encoding eye measurements in degrees. In practice, we found that we could identify roughly the same bout-classes across a fairly wide range of scaling factors used to emphasize eye measurements relative to tail measurements. While it is common to preprocess data with PCA prior to running tSNE, we achieved qualitatively similar embedding results with and without this step, so we simply ran tSNE on the 220-D inputs.
Each of the 200,559 swim bouts are represented as 220-D vectors as described above and are embedded in a 2-D space with tSNE. We implement tSNE with Barnes-Hut approximations with CUDA to decrease tSNE runtime (https://github.com/georgedimitriadis/t_sne_bhcuda). Euclidean distance was used as a distance metric. Following embedding, 5 bout classes were identified with the routines described in Figure S2. The 3 largest clusters were then further subdivided by kinematic variables, ∣ Δ heading∣ and ∣ Δ tail-shape∣, as described in Figure S2 and above.
Identifying and Encoding Environmental Information
Objects near the water surface preceding each swim bout are identified with image processing routines. The focal plane of our camera was positioned near the water surface, so objects near the water surface are in focus while objects near tank bottom are blurry. We therefore wrote routines to isolate high spatial contrast objects. Following image translation and rotation, a stack of the 6 images preceding bout initiation are cropped as in Figure 1J. High spatial contrast objects are identified in Matlab by filtering each image in this stack with a Laplacian of Gaussian 2-D filter (size = 13 × 13 pixels, sigma = 1.6). Contiguous 3-D object volumes in this image stack are smoothed with 3-D dilation and erosion. The average position of each object in the image frame preceding bout initiation was used to encode object location with the extrinsic feature νloc. The number of pixels assigned to each object in this final frame was used to encode object size with the extrinsic feature νsize. The velocity of each object was computed by calculating the distance between the center of mass of each object in the 6th image frame preceding bout initiation (t-minus 100 ms) and the 1st frame preceding bout initiation (t-minus 17 ms) and dividing by the time elapsed. If an object was not properly segmented through all 6 frames, the velocity was calculated from fewer frames (with a minimum of 3 frames). The velocity vectors for each object were used to encode x-velocity and y-velocity in the extrinsic features νx and νy. While the image resolution is sufficient to extract additional features such as the orientation, eccentricity, and detailed shape of each of object, we have not yet included this information in our predictive models.
Intrinsic Features to Predict Interbout Intervals and Bout-types
preceding interbout interval: the duration of the preceding interbout interval in seconds. For models to predict interbout interval duration (in), this is the duration of interbout in–1. For models to predict bout-type (bn), this is the duration of interbout in.
preceding bout-type: the category (i.e. bout-type) of the preceding swim bout. There are 18 bout-types, each of which is composed of left and right versions, giving 36 categories in total. hunt dwell-time: the integer number of observed preceding consecutive hunting bouts (i.e. J-turn, pursuit, abort, strike). As hunt sequences extend, this value increases.
explore dwell-time: the integer number of observed preceding consecutive exploring bouts. For all predicted interbout intervals and bout-types, either hunt dwell-time or explore dwell-time will be zero, with the other being a positive integer. Only the contiguous bout sequence containing the predicted interbout interval (in) or bout-type (bn) is used to define these feature values.
tank-time: the amount of time (in minutes) elapsed since the first trial was initiated for that fish.
Extrinsic Features to Predict Bout-types
νloc: locations of potential prey in the local environment.
νsize: sizes of potential prey in the local environment..
νx: relative x-velocities of potential prey in the local environment.
νy: relative y-velocities of potential prey in the local environment.
See Figure S4 for more information on intrinsic and extrinsic feature encoding.
Simulations
For our combo renewal process simulations, we simulated an environment with prey objects that move as biased random walking particles. Each particle has a constant size and speed. These particles influence bout-type selection as their locations, sizes, and relative velocities are encoded with the extrinsic features νloc, νsize, νx, and νy. We simulated 50 fed and 50 starved fish for 40 minutes each (in 20 two-minute trials). Similar to our real experiments, prey are distributed with a centro-peripheral gradient, with the highest density of prey located near where trials begin. To simulate a behavioral sequence, an interbout interval duration is selected by randomly sampling from an interbout interval distribution generated from the combo interbout interval model. Next, a bout-type is selected by randomly sampling from a bout-type probability distribution generated from the combo bout model. Upon selection of a bout-type, we move the fish through its virtual world along the bout-type specific trajectories described in Figure S7. Since the combo bout model depends on the environment in addition to behavioral history and hunger state, the virtual prey objects influence the fish’s behavioral trajectory. We call this combined bout and interbout model a combo renewal process. For comparison, we simulate 50 fed and 50 starved fish with a simpler model in which interbout intervals and bout-types depend only on preceding bout-type (bn–1). In these simulations, interbout interval durations are sampled from a probability distribution generated by the selected form of the preceding bout-type feature (split-bn–1), and bout-types are sampled from a bout-type probability distribution generated from the selected form of the preceding bout-type feature (pooled-bn–1). This model is referred to as a first-order Markov renewal process, and has no environmental dependencies. For both the combo renewal process simulations and the first-order Markov renewal process simulations, model weights are set at the maximum a posteriori (MAP) estimate of the GLM weights from the trained models.
Data and Code Availability
Compressed behavioral data (https://data.mendeley.com/placeholder) and statistical models (https://github.com/slinderman/placeholder) are available online. Uncompressed data available upon request.
Supplementary Material
Methods S1: Technical Appendix for Statistical Models. Related to STAR Methods. This document describes our approach to constructing and evaluating statistical models presented in this paper.
Video S1: Data Acquisition with BEAST (Animated). Related to Figure 1. Animation of BEAST rig used to acquire data for this study. The larval zebrafish swims in an expansive arena and is tracked with a camera moving automatically overhead. The tank rests on an air table to isolate the fish from the vibration of the moving gantry. The camera has an infrared filter and collects light from the array of IR-LEDs positioned on the air table. The diffusive screen embedded in the tank bottom scatters the infrared light and helps to create even lighting for behavioral imaging. A projector is used to project inwardly drifting gratings (not shown) onto the screen in the tank bottom to bring the fish to the center of the arena, where the camera waits to detect the arrival of the fish. Once at the center, the projector delivers a static color image of pebbles (pictured in the video).
Video S2: Registered Behavioral Video Containing a Hunt Sequence. Related to Figure 2. This video shows the behavioral sequence described in Figure 2F. All behavioral video in this study is acquired at 60 frames per second, but this video is shown at half-speed (30 frames per second). The video contains 439 image frames (7.32 seconds in real time). The fish emits 2 exploring bouts, and then transitions into a 13-bout hunt sequence ending with a successful strike to capture a prey. The fish initiates the hunt by orienting toward a prey object with a high-∣ Δ heading∣ leftward J-turn (j2-L). However, upon orienting toward this prey object, another prey arrives in the same location, and the fish appears to switch to a separate isolated prey target using a high-∣ Δ heading∣, high-∣ Δ tail-shape∣ pursuit bout (p4-L). The fish then pursues this moving prey object, closing the distance to the target and aligning its heading direction with the heading direction of the target. During prey capture, the prey can be seen entering the mouth of the fish and then moving around inside the mouth before it is swallowed. Swallowing of the prey coincides with emission of an e0 bout. These subtle movements highlight a challenge in parsing larval zebrafish behavior into bouts and interbouts since swallowing behavior and other orofacial and pectoral fin movements are near our threshold for bout detection. In the right panel of the video, the 20 tail vectors used to define tail-shape are shown in each image frame, and the vergence angle of each eye is indicated by coloring the outline of each eye with the “cool” colormap from Matlab, ranging from blue (diverged) to magenta (converged). Prey objects are extracted from the movie for display with image processing routines similar to those used to encode environmental state preceding each swim bout.
Video S3: Animation of a Simulated Behavioral Trajectory. Related to Figure 7. The behavioral trajectory shown in Figure 7A is reproduced here in animated form. This excerpt is 411 frames (6.85 seconds of simulated time at 60 Hz), but is slowed down 3x for display in this video. This behavior is generated by sampling from our combo renewal process model. In this sequence, the virtual fish exits exploring mode to hunt a moving prey object, ending this virtual hunt with a strike toward the prey. This example captures many salient features of naturalistic larval zebrafish behavior observed in our study. That being said, we searched our simulated data to locate a behavioral sequence for display, and this example is not necessarily representative of an average simulated hunt. Also, when the fish strikes at the virtual prey object in this movie, we remove that prey from the video for display purposes. However, in our simulations, the environment runs in open-loop and prey are not affected by the behavior of the virtual fish.
Video S4: Visualizing Action Selection in Combo Renewal Process Simulations. Related to Figure 7. Here we show a full 2-minute behavioral trial simulated from our combo renewal process model. This video is slowed down 4x relative to simulated time. The behavioral sequence shown in Figure 7A and Video S3 is taken from this simulated trial (beginning with bout b161 at 6:14 in the video). Fish head position (colored circle) and heading direction (rightward) are held constant, and the virtual environment translates and rotates as the fish moves during swim bouts. Virtual prey are shown as black circles and the corresponding representation of prey locations with the νloc feature is shown (upper right panel). For simulation, an interbout interval duration is randomly sampled from a probability distribution generated from the combo interbout model (bottom right in video). Sampled interbout interval durations are indicated with a red bar, and the distribution from which it was sampled is shown in black. A gray bar moves rightward to indicate the passage of time during interbout intervals. As time passes, we update the bout-type probability distribution generated from our combo bout model (bottom left of video), evaluated for the currently displayed value of the ongoing interbout interval (this is the preceding interbout interval on which the next bout-type partially depends). In this way, the change in bout-type probabilities with increasing interbout interval can be observed. Once the sampled time for the interbout interval has elapsed, a bout-type is randomly sampled from the bout-type probability distribution (indicated with a star). The virtual fish then moves through its environment along the designated trajectory for that bout-type (see Figure S7).
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited Data | ||
| Compressed Behavioral Data | This paper | www.mendeley.com/placeholder |
| Experimental Models: Organisms/Strains | ||
|
7-8 days-post-fertilization Danio rerio: mitfa−/− (nacre) |
Harvard University; MCB Fish Facility |
N/A |
| Software and Algorithms | ||
| Statistical Modeling Code | This paper | www.github.com/slinderman/placeholder |
HIGHLIGHTS:
Naturalistic larval zebrafish behavior is observed with a moving camera system.
Probabilistic models are used to predict and simulate behavioral sequences.
Models combine environmental dynamics, behavioral history, and hunger state.
Simulations capture behavioral dynamics spanning multiple timescales.
Acknowledgements
Research was funded by NIH grant U19NS104653 and Simons Foundation grant SCGB-325207. S.L. was supported by a Simons Collaboration on the Global Brain postdoctoral fellowship (SCGB-418011) and the Siebel Scholarship. We thank Ed Soucy, Joel Greenwood, and Adam Bercu of the Harvard Center for Brain Science Neuroengineering Core for technical support. We thank Andrew Bolton for helpful discussions on pose estimation and prey quantification, George Dimitriadis and Adam Kampff for assistance with GPU implementation of tSNE, and Matthew Johnson for helpful modeling discussions.
Footnotes
Declaration of Interests
The authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Brown AE and De Bivort B (2018). Ethology as a physical science. Nature Physics. [Google Scholar]
- 2.Stephens GJ, Johnson-Kerner B, Bialek W, and Ryu WS (2008). Dimensionality and dynamics in the behavior of C. elegans. PLoS computational biology 4(4), e1000028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Swierczek NA, Giles AC, Rankin CH, and Kerr RA (2011). High-throughput behavioral analysis in C. elegans. Nature methods 8(7), 592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yemini E, Jucikas T, Grundy LJ, Brown AE, and Schafer WR (2013). A database of Caenorhabditis elegans behavioral phenotypes. Nature methods 10(9), 877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gyenes B and Brown AE (2016). Deriving shape-based features for C. elegans locomotion using dimensionality reduction methods. Frontiers in behavioral neuroscience 10, 159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Vogelstein JT, Park Y, Ohyama T, Kerr RA, Truman JW, Priebe CE, and Zlatic M (2014). Discovery of brainwide neural-behavioral maps via multiscale unsupervised structure learning. Science 344(6182), 386–392. [DOI] [PubMed] [Google Scholar]
- 7.Berman GJ, Choi DM, Bialek W, and Shaevitz JW (2014). Mapping the stereotyped behaviour of freely moving fruit flies. Journal of The Royal Society Interface 11(99), 20140672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Klibaite U, Berman GJ, Cande J, Stern DL, and Shaevitz JW (2017). An unsupervised method for quantifying the behavior of paired animals. Physical biology 14(1), 015006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Girdhar K, Gruebele M, and Chemla YR (2015). The behavioral space of zebrafish locomotion and its neural network analog. PloS one 10(7), e0128668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Burgess HA and Granato M (2007). Modulation of locomotor activity in larval zebrafish during light adaptation. Journal of Experimental Biology 210(14), 2526–2539. [DOI] [PubMed] [Google Scholar]
- 11.Mirat O, Sternberg JR, Severi KE, and Wyart C (2013). Zebrazoom: an automated program for high-throughput behavioral analysis and categorization. Frontiers in neural circuits 7, 107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jouary A and Sumbre G (2016). Automatic classification of behavior in zebrafish larvae. bioRxiv p. 052324. [Google Scholar]
- 13.Marques JC, Lackner S, Félix R, and Orger MB (2018). Structure of the zebrafish locomotor repertoire revealed with unsupervised behavioral clustering. Current Biology 28(2), 181–195. [DOI] [PubMed] [Google Scholar]
- 14.Wiltschko AB, Johnson MJ, Iurilli G, Peterson RE, Katon JM, Pashkovski SL, Abraira VE, Adams RP, and Datta SR (2015). Mapping sub-second structure in mouse behavior. Neuron 88(6), 1121–1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mathis A, Mamidanna P, Cury KM, Abe T, Murthy VN, Mathis MW, and Bethge M (2018). DeepLabCut: markerless pose estimation of user-defined body parts with deep learning. Nature Neuroscience 21(9), 1281–1289. 10.1038/s41593-018-0209-y. [DOI] [PubMed] [Google Scholar]
- 16.Pereira TD, Aldarondo DE, Willmore L, Kislin M, Wang SSH, Murthy M, and Shaevitz JW (2019). Fast animal pose estimation using deep neural networks. Nature methods 16(1), 117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Graving JM, Chae D, Naik H, Li L, Koger B, Costelloe BR, and Couzin ID (2019). Fast and robust animal pose estimation. bioRxiv p. 620245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Patterson BW, Abraham AO, MacIver MA, and McLean DL (2013). Visually guided gradation of prey capture movements in larval zebrafish. Journal of Experimental Biology 216(16), 3071–3083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bianco IH, Kampff AR, and Engert F (2011). Prey capture behavior evoked by simple visual stimuli in larval zebrafish. Frontiers in systems neuroscience 5, 101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Portugues R and Engert F (2011). Adaptive locomotor behavior in larval zebrafish. Frontiers in systems neuroscience 5, 72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Oteiza P, Odstrcil I, Fauder G, Portugues R, and Engert F (2017). A novel mechanism for mechanosensory-based rheotaxis in larval zebrafish. Nature 547(7664), 445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Haesemeyer M, Robson DN, Li JM, Schier AF, and Engert F (2015). The structure and timescales of heat perception in larval zebrafish. Cell systems 1(5), 338–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Naumann EA, Fitzgerald JE, Dunn TW, Rihel J, Sompolinsky H, and Engert F (2016). From whole-brain data to functional circuit models: the zebrafish optomotor response. Cell 167(4), 947–960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Colwill RM and Creton R (2011). Imaging escape and avoidance behavior in zebrafish larvae. Reviews in the Neurosciences 22(1), 63–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lacoste AM, Schoppik D, Robson DN, Haesemeyer M, Portugues R, Li JM, Randlett O, Wee CL, Engert F, and Schier AF (2015). A convergent and essential intemeuron pathway for Mauthner-cell-mediated escapes. Current Biology 25(11), 1526–1534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dunn TW, Gebhardt C, Naumann EA, Riegler C, Ahrens MB, Engert F, and Del Bene F (2016). Neural circuits underlying visually evoked escapes in larval zebrafish. Neuron 89(3), 613–628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dreosti E, Lopes G, Kampff AR, and Wilson SW (2015). Development of social behavior in young zebrafish. Frontiers in neural circuits 9, 39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Truccolo W, Eden UT, Fellows MR, Donoghue JP, and Brown EN (2005). A point process framework for relating neural spiking activity to spiking history, neural ensemble, and extrinsic covariate effects. Journal of Neurophysiology 93(2), 1074–1089. [DOI] [PubMed] [Google Scholar]
- 29.Cunningham JP, Yu BM, Sahani M, and Shenoy KV (2007). Inferring neural firing rates from spike trains using Gaussian processes. Advances in Neural Information Processing Systems pp. 329–336. [Google Scholar]
- 30.Pillow JW, Shlens J, Paninski L, Sher A, Litke AM, Chichilnisky E, and Simoncelli EP (2008). Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature 454(7207), 995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kass RE, Eden UT, and Brown EN (2014). Analysis of neural data, volume 491 (Springer; ). [Google Scholar]
- 32.Jordi J, Guggiana-Nilo D, Soucy E, Song EY, Lei Wee C, and Engert F (2015). A high-throughput assay for quantifying appetite and digestive dynamics. American Journal of Physiology-Regulatory, Integrative and Comparative Physiology 309(4), R345–R357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jordi J, Guggiana-Nilo D, Bolton AD, Prabha S, Ballotti K, Herrera K, Rennekamp AJ, Peterson RT, Lutz TA, and Engert F (2018). High-throughput screening for selective appetite modulators: A multibehavioral and translational drug discovery strategy. Science advances 4(10), eaav1966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Barker AJ and Baier H (2015). Sensorimotor decision making in the zebrafish tectum. Current Biology 25(21), 2804–2814. [DOI] [PubMed] [Google Scholar]
- 35.Filosa A, Barker AJ, Dal Maschio M, and Baier H (2016). Feeding state modulates behavioral choice and processing of prey stimuli in the zebrafish tectum. Neuron 90(3), 596–608. [DOI] [PubMed] [Google Scholar]
- 36.Huang KH, Ahrens MB, Dunn TW, and Engert F (2013). Spinal projection neurons control turning behaviors in zebrafish. Current Biology 23(16), 1566–1573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Maaten L.v.d. and Hinton G (2008). Visualizing data using t-SNE. Journal of machine learning research 9(Nov), 2579–2605. [Google Scholar]
- 38.Dimitriadis G, Neto JP, and Kampff AR (2018). T-SNE visualization of large-scale neural recordings. Neural computation 30(7), 1750–1774. [DOI] [PubMed] [Google Scholar]
- 39.Todd JG, Kain JS, and de Bivort BL (2017). Systematic exploration of unsupervised methods for mapping behavior. Physical biology 14(1), 015002. [DOI] [PubMed] [Google Scholar]
- 40.Gahtan E, Tanger P, and Baier H (2005). Visual prey capture in larval zebrafish is controlled by identified reticulospinal neurons downstream of the tectum. Journal of Neuroscience 25(40), 9294–9303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Henriques PM, Rahman N, Jackson SE, and Bianco IH (2019). Nucleus isthmi is required to sustain target pursuit during visually guided prey-catching. Current Biology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Daley DJ and Vere-Jones D (2003). An Introduction to the Theory of Point Processes. Vol. I Elementary Theory and Methods (New York: ). Springer-Verlag, New York,). [Google Scholar]
- 43.McCullagh P and Nelder J (1989). Generalized Linear Models, Second Edition. Chapman and Hall/CRC; Monographs on Statistics and Applied Probability Series (Chapman & Hall). [Google Scholar]
- 44.Carlin BP and Louis TA (2010). Bayes and empirical Bayes methods for data analysis (Chapman and Hall/CRC; ). [Google Scholar]
- 45.Severi KE, Portugues R, Marques JC, O’Malley DM, Orger MB, and Engert F (2014). Neural control and modulation of swimming speed in the larval zebrafish. Neuron 83(3), 692–707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dunn TW, Mu Y, Narayan S, Randlett O, Naumann EA, Yang CT, Schier AF, Freeman J, Engert F, and Ahrens MB (2016). Brain-wide mapping of neural activity controlling zebrafish exploratory locomotion. eLife 5, e12741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chinchor N (1992). MUC-4 evaluation metrics. In Proceedings of the 4th Conference on Message Understanding (Association for Computational Linguistics; ), pp. 22–29. [Google Scholar]
- 48.Anderson DJ and Perona P (2014). Toward a science of computational ethology. Neuron 84(1), 18–31. [DOI] [PubMed] [Google Scholar]
- 49.Gomez-Marin A, Paton JJ, Kampff AR, Costa RM, and Mainen ZF (2014). Big behavioral data: psychology, ethology and the foundations of neuroscience. Nature neuroscience 17(11), 1455. [DOI] [PubMed] [Google Scholar]
- 50.Krakauer JW, Ghazanfar AA, Gomez-Marin A, MacIver MA, and Poeppel D (2017). Neuroscience needs behavior: correcting a reductionist bias. Neuron 93(3), 480–490. [DOI] [PubMed] [Google Scholar]
- 51.Bargmann CI and Newsome WT (2014). The Brain Research through Advancing Innovative Neurotechnologies (BRAIN) initiative and neurology. JAMA neurology 71(6), 675–676. [DOI] [PubMed] [Google Scholar]
- 52.Mott MC, Gordon JA, and Koroshetz WJ (2018). The NIH BRAIN Initiative: Advancing neurotechnologies, integrating disciplines. PLoS biology 16(11), e3000066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Dulac C, Maunsell J, Anderson D, Anikeeva P, Arlotta P, Churchland A, Deisseroth K, Denison T, Deshler J, Dzirasa K, et al. (2019). The Brain Research through Advancing Innovative Neurotechnologies (BRAIN) initiative 2.0. [Google Scholar]
- 54.Orger MB, Kampff AR, Severi KE, Bollmann JH, and Engert F (2008). Control of visually guided behavior by distinct populations of spinal projection neurons. Nature neuroscience 11(3), 327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Antinucci P, Folgueira M, and Bianco IH (2019). A pretectal command system controls hunting behaviour. BioRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Bianco IH and Engert F (2015). Visuomotor transformations underlying hunting behavior in zebrafish. Current biology 25(7), 831–846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Semmelhack JL, Donovan JC, Thiele TR, Kuehn E, Laurell E, and Baier H (2014). A dedicated visual pathway for prey detection in larval zebrafish. eLife 3, e04878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Klein RM (2000). Inhibition of return. Trends in cognitive sciences 4(4), 138–147. [DOI] [PubMed] [Google Scholar]
- 59.Wee CL, Song EY, Johnson RE, Ailani D, Randlett O, Kim J, Nikitchenko M, Bahl A, Ahrens M, Kawakami K, et al. (2019). A bidirectional network for appetite control in zebrafish. bioRxiv p. 631341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Muto A, Lai P, Ailani D, Abe G, Itoh M, and Kawakami K (2017). Activation of the hypothalamic feeding centre upon visual prey detection. Nature communications 8, 15029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Abdelfattah AS, Kawashima T, Singh A, Novak O, Liu H, Shuai Y, Huang YC, Grimm JB, Patel R, Friedrich J, et al. (2018). Bright and photostable chemigenetic indicators for extended in vivo voltage imaging. bioRxiv p. 436840. [DOI] [PubMed] [Google Scholar]
- 62.Trivedi CA and Bollmann JH (2013). Visually driven chaining of elementary swim patterns into a goal-directed motor sequence: a virtual reality study of zebrafish prey capture. Frontiers in neural circuits 7, 86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Portugues R, Feierstein CE, Engert F, and Orger MB (2014). Whole-brain activity maps reveal stereotyped, distributed networks for visuomotor behavior. Neuron 81(6), 1328–1343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Bianco IH, Ma LH, Schoppik D, Robson DN, Orger MB, Beck JC, Li JM, Schier AF, Engert F, and Baker R (2012). The tangential nucleus controls a gravito-inertial vestibulo-ocular reflex. Current Biology 22(14), 1285–1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Bolton AD, Haesemeyer M, Jordi J, Schaechtle U, Saad FA, Mansinghka VK, Tenenbaum JB, and Engert F (2019). Elements of a stochastic 3d prediction engine in larval zebrafish prey capture. bioRxiv p. 755777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Harpaz R, Tkačik G, and Schneidman E (2017). Discrete modes of social information processing predict individual behavior of fish in a group. Proceedings of the National Academy of Sciences 114(38), 10149–10154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Bodóvá K, Mitchell GJ, Harpaz R, Schneidman E, and Tkačik G (2018). Probabilistic models of individual and collective animal behavior. PloS one 13(3), e0193049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Sharma A, Johnson R, Engert F, and Linderman S (2018). Point process latent variable models of larval zebrafish behavior. In Advances in Neural Information Processing Systems, pp. 10919–10930. [Google Scholar]
- 69.Gelman A and Hill J (2006). Data analysis using regression and multilevel/hierarchical models (Cambridge University Press; ). [Google Scholar]
- 70.Linderman SW, Nichols AL, Blei DM, Zimmer M, and Paninski L (2019). Hierarchical recurrent state space models reveal discrete and continuous dynamics of neural activity in C. elegans. bioRxiv p. 621540. [Google Scholar]
- 71.Kim DH, Kim J, Marques JC, Grama A, Hildebrand DG, Gu W, Li JM, and Robson DN (2017). Pan-neuronal calcium imaging with cellular resolution in freely swimming zebrafish. Nature methods 14(11), 1107. [DOI] [PubMed] [Google Scholar]
- 72.Cong L, Wang Z, Chai Y, Hang W, Shang C, Yang W, Bai L, Du J, Wang K, and Wen Q (2017). Rapid whole brain imaging of neural activity in freely behaving larval zebrafish (Danio rerio). eLife 6, e28158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Naumann EA, Kampff AR, Prober DA, Schier AF, and Engert F (2010). Monitoring neural activity with bioluminescence during natural behavior. Nature neuroscience 13(4), 513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Symvoulidis P, Lauri A, Stefanoiu A, Cappetta M, Schneider S, Jia H, Stelzl A, Koch M, Perez CC, Myklatun A, et al. (2017). Neubtracker-imaging neurobehavioral dynamics in freely behaving fish. Nature Methods 14(11), 1079. [DOI] [PubMed] [Google Scholar]
- 75.Muto A, Ohkura M, Abe G, Nakai J, and Kawakami K (2013). Real-time visualization of neuronal activity during perception. Current Biology 23(4), 307–311. [DOI] [PubMed] [Google Scholar]
- 76.Markowitz JE, Gillis WF, Beron CC, Neufeld SQ, Robertson K, Bhagat ND, Peterson RE, Peterson E, Hyun M, Linderman SW, et al. (2018). The striatum organizes 3d behavior via moment-to-moment action selection. Cell 174(1), 44–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Allen WE, Chen MZ, Pichamoorthy N, Tien RH, Pachitariu M, Luo L, and Deisseroth K (2019). Thirst regulates motivated behavior through modulation of brainwide neural population dynamics. Science 364(6437), 253. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Methods S1: Technical Appendix for Statistical Models. Related to STAR Methods. This document describes our approach to constructing and evaluating statistical models presented in this paper.
Video S1: Data Acquisition with BEAST (Animated). Related to Figure 1. Animation of BEAST rig used to acquire data for this study. The larval zebrafish swims in an expansive arena and is tracked with a camera moving automatically overhead. The tank rests on an air table to isolate the fish from the vibration of the moving gantry. The camera has an infrared filter and collects light from the array of IR-LEDs positioned on the air table. The diffusive screen embedded in the tank bottom scatters the infrared light and helps to create even lighting for behavioral imaging. A projector is used to project inwardly drifting gratings (not shown) onto the screen in the tank bottom to bring the fish to the center of the arena, where the camera waits to detect the arrival of the fish. Once at the center, the projector delivers a static color image of pebbles (pictured in the video).
Video S2: Registered Behavioral Video Containing a Hunt Sequence. Related to Figure 2. This video shows the behavioral sequence described in Figure 2F. All behavioral video in this study is acquired at 60 frames per second, but this video is shown at half-speed (30 frames per second). The video contains 439 image frames (7.32 seconds in real time). The fish emits 2 exploring bouts, and then transitions into a 13-bout hunt sequence ending with a successful strike to capture a prey. The fish initiates the hunt by orienting toward a prey object with a high-∣ Δ heading∣ leftward J-turn (j2-L). However, upon orienting toward this prey object, another prey arrives in the same location, and the fish appears to switch to a separate isolated prey target using a high-∣ Δ heading∣, high-∣ Δ tail-shape∣ pursuit bout (p4-L). The fish then pursues this moving prey object, closing the distance to the target and aligning its heading direction with the heading direction of the target. During prey capture, the prey can be seen entering the mouth of the fish and then moving around inside the mouth before it is swallowed. Swallowing of the prey coincides with emission of an e0 bout. These subtle movements highlight a challenge in parsing larval zebrafish behavior into bouts and interbouts since swallowing behavior and other orofacial and pectoral fin movements are near our threshold for bout detection. In the right panel of the video, the 20 tail vectors used to define tail-shape are shown in each image frame, and the vergence angle of each eye is indicated by coloring the outline of each eye with the “cool” colormap from Matlab, ranging from blue (diverged) to magenta (converged). Prey objects are extracted from the movie for display with image processing routines similar to those used to encode environmental state preceding each swim bout.
Video S3: Animation of a Simulated Behavioral Trajectory. Related to Figure 7. The behavioral trajectory shown in Figure 7A is reproduced here in animated form. This excerpt is 411 frames (6.85 seconds of simulated time at 60 Hz), but is slowed down 3x for display in this video. This behavior is generated by sampling from our combo renewal process model. In this sequence, the virtual fish exits exploring mode to hunt a moving prey object, ending this virtual hunt with a strike toward the prey. This example captures many salient features of naturalistic larval zebrafish behavior observed in our study. That being said, we searched our simulated data to locate a behavioral sequence for display, and this example is not necessarily representative of an average simulated hunt. Also, when the fish strikes at the virtual prey object in this movie, we remove that prey from the video for display purposes. However, in our simulations, the environment runs in open-loop and prey are not affected by the behavior of the virtual fish.
Video S4: Visualizing Action Selection in Combo Renewal Process Simulations. Related to Figure 7. Here we show a full 2-minute behavioral trial simulated from our combo renewal process model. This video is slowed down 4x relative to simulated time. The behavioral sequence shown in Figure 7A and Video S3 is taken from this simulated trial (beginning with bout b161 at 6:14 in the video). Fish head position (colored circle) and heading direction (rightward) are held constant, and the virtual environment translates and rotates as the fish moves during swim bouts. Virtual prey are shown as black circles and the corresponding representation of prey locations with the νloc feature is shown (upper right panel). For simulation, an interbout interval duration is randomly sampled from a probability distribution generated from the combo interbout model (bottom right in video). Sampled interbout interval durations are indicated with a red bar, and the distribution from which it was sampled is shown in black. A gray bar moves rightward to indicate the passage of time during interbout intervals. As time passes, we update the bout-type probability distribution generated from our combo bout model (bottom left of video), evaluated for the currently displayed value of the ongoing interbout interval (this is the preceding interbout interval on which the next bout-type partially depends). In this way, the change in bout-type probabilities with increasing interbout interval can be observed. Once the sampled time for the interbout interval has elapsed, a bout-type is randomly sampled from the bout-type probability distribution (indicated with a star). The virtual fish then moves through its environment along the designated trajectory for that bout-type (see Figure S7).
Data Availability Statement
Compressed behavioral data (https://data.mendeley.com/placeholder) and statistical models (https://github.com/slinderman/placeholder) are available online. Uncompressed data available upon request.