Population trends for two Malagasy fruit bats

Abstract

Madagascar is home to three endemic species of Old World Fruit Bat, which are important pollinators and seed dispersers. We aimed to quantitatively assess population trajectories for the two largest of these species, the IUCN-listed ‘Vulnerable’ Eidolon dupreanum and Pteropus rufus. To this end, we conducted a longitudinal field study, in which we live-captured E. dupreanum and P. rufus, estimated species-specific fecundity rates, and generated age-frequency data via histological analysis of cementum annuli layering in tooth samples extracted from a subset of individuals. We fit exponential models to resulting data to estimate annual survival probabilities for adult bats (s_A = .794 for E. dupreanum; s_A = .511 for P. rufus), then applied Lefkovitch modeling techniques to infer the minimum required juvenile survival rate needed to permit longterm population persistence. Given estimated adult survival, population persistence was only possible for E. dupreanum when field-based fecundity estimates were replaced by higher values reported in the literature for related species. For P. rufus, tooth-derived estimates of adult survival were so low that even assumptions of perfect (100%) juvenile annual survival would not permit stable population trajectories. Age-based survival analyses were further supported by longitudinal exit counts carried out from 2013–2018 at three local P. rufus roost sites, which demonstrated a statistically significant, faintly negative time trend, indicative of subtle regional population declines. These results suggest that Malagasy fruit bat species face significant threats to population viability, with P. rufus particularly imperiled. Immediate conservation interventions, including habitat restoration and cessation of legally sanctioned bat hunting, are needed to protect Madagascar’s fruit bats into the future.

1. INTRODUCTION

The International Union for the Conservation of Nature (IUCN) classifies 35% of Old World Fruit Bats (order: Chiroptera, family: Pteropodidae) as threatened, nearly three times the extent (12%) for all other bat species combined (IUCN 2018). Pteropodids are imperiled by land conversion and human hunting, and many are island endemics with small baseline populations inherently vulnerable to environmental stressors (Voigt and Kingston, 2016). Madagascar is home to three endemic pteropodids—the IUCN-listed ‘Vulnerable’ Madagascan fruit bat (Eidolon dupreanum) and the Madagascan flying fox (Pteropus rufus), as well as the ‘Near-threatened’ Madagascan rousette (Rousettus madagascariensis) (Goodman, 2011)—which offer important ecosystem services as pollinators and seed dispersers (Bollen and Elsacker, 2002; Picot et al., 2007). Extrapolated field survey results once proposed roughly 300,000 P. rufus to inhabit Madagascar (MacKinnon et al., 2003), though more recent surveys suggest this number may have declined by as much as 40% (Oleksy et al., 2015). No population estimates are available for E. dupreanum or R. madagascariensis.

Fruit bat hunting is legal during the Malagasy winter (1 May – 1 September), directly preceding the E. dupreanum and P. rufus birth pulse (Ranaivoson et al., 2019). Concentrated hunting immediately before the birth pulse can severely jeopardize population viability by truncating time for density-dependent reproductive compensation (Brook et al., 2018; Kokko and Lindström, 1998). Regardless of legality, all three Malagasy fruit bats are consumed during all months of the year, with peak harvest typically tracking local fruit abundance (Jenkins and Racey, 2008; Reuter et al., 2016). Of the three species, P. rufus is the largest, making it the most heavily hunted, and the only tree rooster, making it the most vulnerable to deforestation (MacKinnon et al., 2003).

Population viability analysis (PVA) employs mathematical modeling techniques to project future population trends from species- and age-specific demographic rates (Beissinger and McCullough, 2002). Historically, PVAs on bats have been limited to insectivorous species (O’Shea et al., 2004), though some recent efforts have evaluated the sustainability of flying fox culling for fruit crop protection in Australia (McIlwee and Martin, 2002) and hunting for food in Malaysia (Epstein et al., 2009). Only a few previous studies have attempted to estimate demographic parameters for fruit bats from field data, via recovery of banded bats post-mortem (Tidemann and Nelson, 2014) or via analysis of cementum annuli layers deposited in fruit bat teeth (for Pteropus conspicillatus: Fox et al., 2008; and for Eidolon helvum: Hayman et al., 2012; Hayman and Peel, 2016).

Broadly, we asked, what are the current conservation statuses and population trajectories for Madagascar’s two largest fruit bats, E. dupreanum and P. rufus? To address this question, we aimed to quantify (1) fecundity and (2) adult survival rates from field data, then (3) use Lefkovitch matrix modeling techniques to assess whether, given rates estimated in aims (1) and (2), it was possible to derive reasonable juvenile survival rates that would support stable population trajectories for both species. To this end, we carried out a 2013–2018 field study, in which we live-captured E. dupreanum and P. rufus, estimated adult annual fecundity rates, and established adult survival rates from age-frequency analysis of cementum layering in bat teeth. We then used matrix modeling techniques to infer juvenile survival rates assuming stable population trajectories and evaluate population viability given these probabilities. Finally, we compared tooth-derived P. rufus population trajectories with trends quantified from roost exit counts.

2. METHODS

Capture and sampling

We net-captured 470 cave-dwelling Eidolon dupreanum and 248 tree-roosting Pteropus rufus between November 2013 and September 2018 from eight Madagascar localities during all months of the year (Supplementary Information). Bats were captured every 4–6 weeks at established roost sites using 19mm, 2.4×18m nylon mist nets deployed from 6pm to midnight, then again from 3am to 8am across cave mouths (for E. dupreanum) and in roost-adjacent tree canopies (for P. rufus). Upon capture, bats were placed in cloth canvas bags to await processing the following dawn.

During processing, one researcher manually restrained bats while a second researcher collected biological samples (i.e. blood, feces, urine, saliva) for pathogen studies published elsewhere (Brook et al., 2015; Ranaivoson et al., 2019). All animals were weighed in their cloth bags with a Pesola scale, and standard measurements (forearm, tibia, ear, body length) were taken; sex and reproductive condition were assessed via measurement of testes/mammary glands and abdominal palpitation.

A randomly-selected subset of adult bats of both sexes (90 E. dupreanum; 90 P. rufus) underwent anesthesia via halothane vaporizer (4% halothane in oxygen at 0.7L/min) and extraction of the lower left premolar tooth. Tooth samples were processed histologically and aged by counting stained cementum annuli layers under microscope magnification at Matson’s Laboratory (Missoula, Montana); Matson’s exact procedures are proprietary, but see Divljan et al., 2006 for a description of comparable methodology. Because fruit bats birth in seasonal annual pulses, we obtained more precise age estimates by assuming a standard birth date for all E. dupreanum (November 1) and P. rufus (October 1) (Ranaivoson et al., 2019). We added the duration of time between capture and birth to the cementum integer to compute age to the nearest day; pups under one year with zero cementum layers (43 E. dupreanum; 65 P. rufus) were aged via the same method. In total, we calculated ages for 133 E. dupreanum (76 male, 56 female) and 155 P. rufus (85 male, 70 female).

All field work was conducted according to American Veterinary Medical Association guidelines, under permit authorization from the Madagascar Ministry for Water and Forests (166/14/MEF/SG/ DGF/DCB.SAP/SCB, 75/15/MEEMEF/SG/DGF/DCB.SAP/SCB, 92/16/MEEMEF/SG/DGF/DCB.SAP/SCB, 259/16/MEEF/SG/DGF/DSAP/SCB, 170/18/MEEMEF/SG/ DGF/DCB.SAP/SCB, 259/16/MEEF/SG/DGF/DSAP/SCB). Protocols were pre-approved by the Princeton University Institutional Animal Care and Use Committee (Protocol #1926) and UC Berkeley Animal Care and Use Committee (Protocol #AUP-2017-10-10393).

Annual fecundity estimates

We estimated maximum adult annual fecundity for both species by calculating the proportion of reproductively mature females observed as lactating in the months immediately following gestation (November-December for E. dupreanum and October-December for P. rufus) across all study years (Table 1). P. rufus and E. dupreanum first reproduce at the end of their second or third year (McIlwee and Martin, 2002; Ranaivoson et al., 2019); thus, when bat ages were known, we limited fecundity calculations to females aged 1.5 years or older. As witnessed in other systems, we anticipate that only a subset of first-year breeders will typically rear successful young, however (McIlwee and Martin, 2002). As such, incorporation of all 1–2-year-olds in fecundity analyses for a post-breeding census may produce underestimates. Because ages were known for only nine E. dupreanum and seven P. rufus adult females captured during reproductive months, we also included adult-size bats of unknown age in fecundity calculations, a practice that could additionally downward-bias estimates if some adult-sized individuals were still reproductively immature.

Table 1.

Annual fecundity estimates from capture data

Species	Month of Capture	Total adult females captured, #*	Total adult females lactating, # (%)*
Eidolon dupreanum	November	26	13 (50)
	December	11	4 (36.4)
	Estimated annual fecundity†	37	17 (45.9)
Pteropus rufus	October	1	1 (100)
	November	18	17 (89.5)
	December	11	8 (61.5)
	Estimated fecundity†	30	26 (86.7)

^*Monthly counts are combined across all years of the study (2013–2018)

^†Note that these annual fecundities include both male and female offspring. Assuming no sex biases in reproduction, we halve these rates (Table 2) to model population projections for females.

Because of these potential biases, we assigned field-derived annual fecundities as ‘worst’ case demographic parameters for both species, assuming first reproduction at age three, compared with near-perfect, ‘best’ case fecundities derived from the E. helvum literature, assuming first reproduction at age two (Hayman et al., 2012) (Table 2). Ultimately, ‘best’-case literature-derived annual fecundities offered the best recapitulation of our data (via AIC comparison; Table 2) and were adopted for final reporting (see ‘Results’). Previous studies of Australian fruit bats suggest that few flying foxes survive to achieve reproductive senescence (estimated to occur at >13 years in Pteropus conspicillatus and >15 years in Pteropus poliocephalus; Fox et al., 2008; McIlwee and Martin, 2002), supporting our assumption of constant fecundity across all reproductively mature ages. Because we modeled only females, we divided annual fecundity rates in half. If all reproductively-mature females produced exactly one offspring per year, this would correspond to a female annual fecundity (F_A) of 0.5, indicating that one daughter was produced, on average, every two years.

Table 2.

Demographic parameters

Species	Scenario	Age 1st Reprod.	Adult annual fecundity*	Adult ann. survival estimate |lci-uci]†	Juv ann. survival** estimate |uci-lci]†	Neg. Log-likelihood
Eidolon dupreanutn	Best	2	.48	0.794 [.717–.871]	.539 [.822–.307]	32.59
	Worst	3	.23	0.794 [.717–.871]	1.419 [2.39–.737]	42.31
Pteropus rufus	Best	2	.48	0.511 [.313–.719]	1.993 [4.57–.854]	28.17
	Worst	3	.433	0.511 [.313–.719]	4.320 [16.19–.1.33]	49.13

^*‘Best’ fecundity estimates derived from Hayman et al. 2012; ‘worst’ from capture data (Table 1). Note that these rates give the annual fecundity rate for production of female offspring.

^**Juvenile survival rates are inferred using Lefkovitch matrix techniques assuming stable age structure and constant population size (λ = 1). Survival rates >1 are not biologically plausible, meaning that the assumption of λ = 1 must be incorrect (in actuality, λ < 1) if specified adult fecundity and survival parameters are accurate.

^†lci and uci refer to lower and upper 95% confidence intervals (respectively) on estimated parameters. For adult survival rates, these were derived from the standard error of the slope estimated from the fitted exponential model. For juvenile survival rates, these are listed as uci-lci because they represent the derived juvenile response rate assuming λ = 1 if the lci and uci of adult survival are adopted.

Annual survival estimates

To estimate adult annual survival, we fit exponential models incorporating variable mortality hazards to species-specific age-frequency data for bats over one year in age. Following Siler (1979), we initially compared competing risk models allowing for reduced survival during maturation and/or senescence. Ultimately, model comparison by Akaike Information Criterion (AIC) offered strongest support for models incorporating constant survival rates across adult lifespan, consistent with the E. helvum literature (Hayman et al., 2012; Hayman and Peel, 2016) (Supplementary Information). We report only results for the simplest survival models here:

$$l_{x,2}=e^{-a_{2}x}$$ (1)

where l_x,2 indicates survivorship at age x and a₂ gives the constant annual adult mortality rate (Siler, 1979). Note that, because these analyses were restricted to adult-age bats only, survivorship refers to the proportion of the initial cohort beginning at age one (when bats enter adulthood) and surviving to age x.

We next inferred juvenile (bats ≤ 1 year) survival using Lefkovitch matrix techniques (Lefkovitch, 1965). Leslie and Lefkovitch matrices incorporate, respectively, age- or stage-structured demographic survival and fecundity rates into matrix form for population projection (Lefkovitch, 1965; Leslie, 1945). Calculation of stage-structured fecundity/survival rates and the intrinsic population growth rate (λ) are mutually co-dependent; one must be known or assumed in order to infer the other (Hayman et al., 2012). Thus, with female annual fecundity (F_A) and adult annual survival (s_A) already established, we followed previously published stability analyses (Brook et al., 2018; Dobson and Lyles, 1989; Lyles and Dobson, 1988) to infer the minimum juvenile annual survival (s_J) rate needed to recover assumptions of stable age structure and constant population size (λ = 1). We explored a range of ‘best’ and ‘worst’ case demographic scenarios assuming first reproduction at respective ages two or three (Supplementary Information). Our stage-based Lefkovitch transition matrices thus took on the following form, assuming a post-breeding census :

Age two first reproduction:

$$A=\begin{array}{c}\begin{array}{cc}juv& adult\end{array}\\ \left[\begin{array}{ll}o\hfill & s_A{F}_A\hfill \\ s_J\hfill & s_A\hfill \end{array}\right]\end{array}$$ (2)

Age three first reproduction:

$$\text{A}=\begin{array}{c}\begin{array}{ccc}juv& sub& adult\end{array}\\ \left[\begin{array}{lll}0\hfill & 0\hfill & s_A{F}_A\hfill \\ s_J\hfill & 0\hfill & 0\hfill \\ 0\hfill & s_A\hfill & s_A\hfill \end{array}\right]\end{array}$$ (3)

where F_A indicates adult annual fecundity, s_A represents adult annual survival (bats aged 1+ years) and s_J represents juvenile annual survival (bats aged 0–1 year). For ‘worst’ case scenarios assuming age three first reproduction (equation 3), the second column in the transition matrix (“sub”) corresponds to sub-adult bats (1–2 years), which we model as reproductively immature but with adult annual survival rates.

The dominant eigenvalue of the Leslie/Lefkovitch matrix (λ) represents the intrinsic growth rate for a population at stable age distribution; populations grow when λ > 1 and trend towards extinction when λ < 1. Assuming λ = 1, we next expressed s_J in terms of s_A (s_J = is_A) and derived an equation for i, the zero-growth isocline for each species (Brook et al., 2018; Dobson and Lyles, 1989; Lyles and Dobson, 1988):

$$i=\frac{1-s_A}{s_A^a{F}_A}$$ (4)

where α (in $s_A^a$) denotes age at first reproduction (Supplementary Information).

Roost exit counts

Finally, we assessed P. rufus population trajectories from longitudinal roost exit counts. Between July-September 2008 and September 2013-July 2018, we conducted 69 exit counts at three protected area P. rufus roosts in central Madagascar. Between one and seven people replicated each exit count at each site, recording the number of bats flying out of the roost at dusk using a clicker counter. For all sampling events except those in 2008, researchers also recorded the weather (“dry” vs. “not dry”) at the time of sampling. To examine time trends in these counts across the three sites, we first calculated the mean and standard deviation of all counts conducted at one site within the same month and year. Any replicate counts deviating from this mean by more than one standard deviation were discarded. Subsequently, we recalculated the mean and standard deviation of each unique month-year sampling event, using only these more consistent counts.

To explore longitudinal trends in P. rufus abundance at three roosting sites in the District of Ambatondrajaka, we next fit a generalized additive mixed model (‘GAMM’) in the Poisson family to the time series count data for 2013–2018; data from 2008 were not included in these models due to methodological inconsistencies (Supplementary Information). All models included a response variable of count (averaged among replicates) with a fixed predictor of year : site interaction, a monthly smoothing term (with the number of smoothing knots, k, fixed at 7, as recommended by the package author; Wood, 2001), and a random effect of weather of sampling. We originally also examined “quasipoisson” distributions for overdispersed. (variance > mean) data but found these models to yield much larger confidence intervals than the conventional Poisson family, so we ultimately adopted the latter.

3. RESULTS

Annual fecundity estimates

We captured 37 E. dupreanum and 30 P. rufus adult-size females during lactation months surveyed in our study (November-December for E. dupreanum and October-December for P. rufus). Of those captures, 17 (45.9%) E. dupreanum and 26 (86.7%) P. rufus were observed as lactating (Table 1), yielding respective female annual fecundity rates of F_A = .230 and .433. Cementum annuli tooth analysis identified 1–2-year-old pregnant or lactating females of both species, validating inclusion of these age classes in fecundity assessments. Due to concerns over underestimation of field fecundities, however (see ‘Methods’), we assigned these rates to ‘worst’ case demographic scenarios and adopted estimates from E. helvum literature (F_A = .48; Hayman et al. 2012) in ‘best’ case scenarios for both species (Table 2).

Annual survival estimates

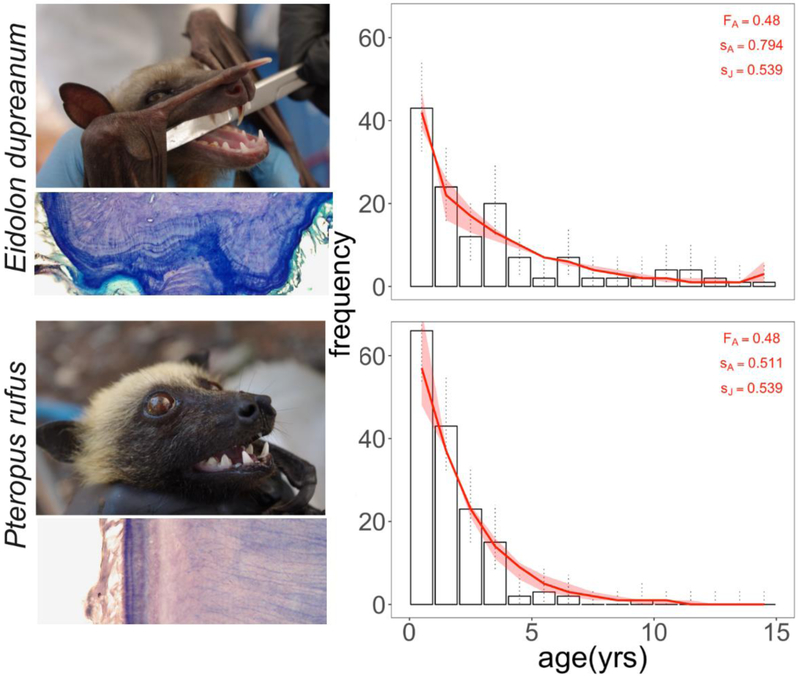
We plotted a raw age-frequency histogram for all aged E. dupreanum and P. rufus (Fig. 1). Exponential model fits to adult data (bats > 1 year) produced annual survival estimates of .794 [.717–.871] for E. dupreanum and .511 [.313–.719] for P. rufus (Table 2, where brackets indicate the 95% confidence intervals by standard error as derived from the fitted exponential models). Assuming constant population size (λ = 1), we inferred a biologically plausible juvenile survival rate under ‘best’ case demographic conditions for E. dupreanum (.539 [.822–.307]; note the lower confidence limit for adult survival is paired with the upper confidence limit for juvenile survival to maintain stable population size). We modeled the resulting age-frequency distribution in Fig. 1 (F_A = .48; s_A = .794; s_J = .539). In the case of P. rufus, assumptions of λ = 1 were only possible if juvenile survival rates exceeded 100%, or if we selected the upper confidence limit estimate for adult survival (s_{A_uci} = .719 which could be balanced by juvenile survival, s_{J_lci} = .854 or higher). Because survival rates in excess of 100% are biologically impossible, we instead paired ‘best’ case fecundity (F_A = .48) and adult survival rates for P. rufus (s_A = .511) with ‘best’ case juvenile survival rates for E. dupreanum (s_J = .539) to model P. rufus age-frequency distributions in Fig. 1. These fecundity and survival parameters produced a declining P. rufus population trajectory (λ = 0.825).

Figure 1. Age-frequency data and fitted survival models for Madagascar’s fruit bats.

Left-hand panels show images of Eidolon dupreanum (top) and Pteropus rufus (bottom), paired with cross-sectional images of cementum annuli layering in teeth for, respectively, a 14-year-old E. dupreanum and a 2-year-old P. rufus. Right-hand panels show age-frequency histograms from age analysis of tooth data for E. dupreanum (top) and P. rufus (bottom) with exponential survival model overlain as a solid line. Survival and fecundity parameters used for the demonstrated model are printed in the top righthand corner of each plot; note that juvenile survival rates for P. rufus were adopted from ‘best’ case scenarios for E. dupreanum (Table 2), since no biologically plausible values for P. rufus could maintain a constant population size (λ = 1). Shading is derived from 95% confidence intervals on s_A and s_J survival terms – see Table 2 for raw values).

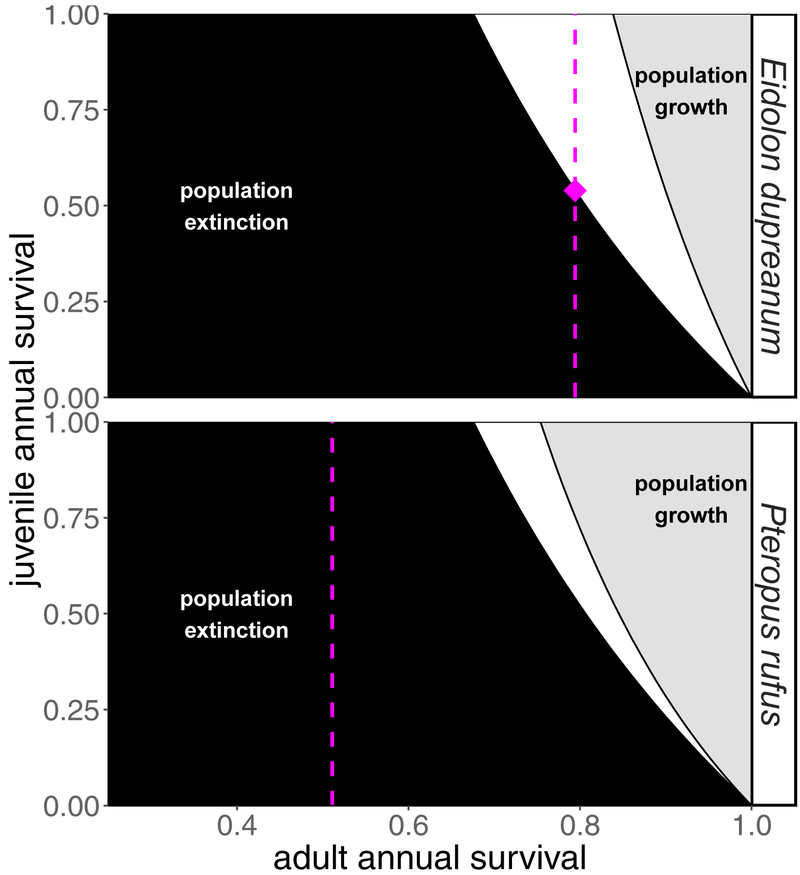
Using ‘best’ and ‘worst’ case fecundity estimates (F_A; Table 2) we next computed ‘best’ and ‘worst’ case zero-growth isoclines for each species (λ = 1), visualized as relative rates of adult versus juvenile annual survival (Fig. 2). We plotted adult survival estimates from tooth data as vertical dashed lines in survival parameter space.

Figure 2. Zero-growth isoclines for Madagascar’s fruit bats.

Species-specific zero-growth isoclines are here plotted in units of annual survival (adult annual survival = s_A; juvenile annual survival = s_J; Supplementary Information). Each species is represented by two isoclines: the bottom (left) isocline is generated by fecundity parameters most favorable to demographic growth (scenario ‘best’; Table 2) and the top (right) isocline by fecundity parameters least favorable to growth (scenario ‘worst’; Table 2). Regions shaded in gray correspond to survival parameter combinations yielding population growth (λ > 1), while regions shaded in black correspond to survival parameter combinations yielding population extinction (λ < 1). The white-shaded regions correspond to survival parameter combinations which result in uncertain population trajectories, dependent on the species-specific annual fecundity rate. The vertical dashed lines give the estimated rate of adult annual survival from analysis of cementum annuli layers in fruit bat teeth; the intersecting diamond in the E. dupreanum plot corresponds to the minimum juvenile annual survival needed to maintain a constant population size (λ = 1) at adult annual survival = .794 and fecundity = .48. The adult annual survival estimate from tooth data (.511) was too low for P. rufus to recover a stable population size, even at juvenile annual survival of 100%.

Roost exit counts

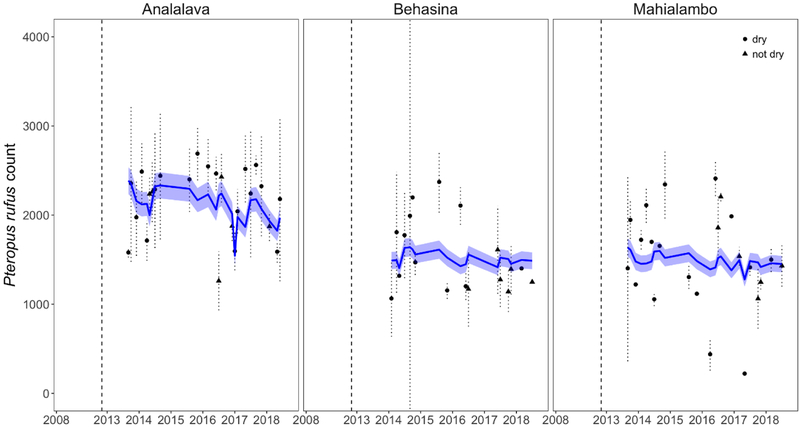
We report the average of P. rufus count replicates as solid points by site in Fig. 3, with the 95% confidence interval by standard deviation of each count shown as a dashed vertical line. Using generalized additive modeling techniques, we detected a statistically significant slightly negative time trend in P. rufus roost counts across all three regional sites monitored between 2013–2018 (Fig. 3; slope = −0.023, se − .0022; site-specific p-values: Analalava = 8.19×10⁻¹⁵, Behasina = 6.17×10⁻¹⁵, Mahialambo = 6.05×10⁻¹⁵). Local P. rufus populations appear to have slightly declined across the study period, while demonstrating significant seasonal dynamism, as captured in a significant monthly smoothing term (p<2×10⁻¹⁶) and a random effect of weather included in the fitted model (Supplementary Information).

Figure 3. Longitudinal exit counts for three Pteropus rufus roosts in the District of Amabatondrajaka, Madagascar.

Longitudinal raw exit counts for Pteropus rufus carried out by the conservation NGO, Madagasikara Voakajy, at three roost sites (Analava, Behasina, Mahialambo) in the District of Ambatondrajaka in 2008 (left of dashed vertical line) and from 2013–2018 (right of dashed vertical line). Points depict raw data, with surveys conducted on “dry” days represented as closed circles and surveys conducted on “shady”, “drizzly”, “overcast”, or “rainy” days (“not dry”) represented as closed triangles (though note that weather was not recorded for 2008 data, shown here as a closed circle). We fit a generalized additive mixed model (GAMM) in the Poisson family to the 2013–2018 count data; model output is shown as a solid blue line atop the raw data (shading=95% confidence interval by standard error), incorporating a response variable of count and a fixed predictor variable of year : site interaction. Predicted counts demonstrated a statistically significant slightly negative trend through time for all sites surveyed (slope = −0.023, se − .0022; site-specific p-values: Analalava = 8.19×10⁻¹⁵, Behasina = 6.17×10⁻¹⁵, Mahialambo = 6.05×10⁻¹⁵). A significant monthly smoothing term (p<2×10⁻¹⁶) and a random effect of weather were also included in the model.

4. DISCUSSION

Analysis of field-derived fecundity and survival data for Eidolon dupreanum and Pteropus rufus suggests that population viability is seriously threated for both species, with P. rufus particularly endangered. Estimated annual survival rates for E. dupreanum are only compatible with assumptions of long-term population persistence when capture-derived fecundities are exchanged with higher rates from the literature. Much lower estimated survival rates for P. rufus are incompatible with assumptions of stable population size under all fecundity assumptions, indicating that P. rufus populations may already be declining.

In reality, population trajectories for E. dupreanum and P. rufus are potentially more optimistic than those predicted here. For both species, ‘best’ case demographic scenarios using more favorable survival and fecundity parameters derived from the literature or from proxy species offered better fits to data than ‘worst’ case, field-derived scenarios, and 95% confidence intervals on adult-stage survival estimates for both species included parameters by which viable host populations can be sustained (Table 2). As mentioned, field-derived annual fecundities could be underestimates due to inclusion of reproductively immature adult-size bats of unknown age in calculations; it is additionally possible that we have underestimated P. rufus adult survival, as two of four P. rufus sampling sites were seasonal maternity colonies (Jenkins et al., 2007), which preferentially favor captures of mothers and juveniles that could downward-bias age-frequency distributions and yield below-accurate survival. Nonetheless, estimated adult survival estimates for P. rufus were so low that even considerable increases would be insufficient to alter projections of population decline; indeed, the upper 95% confidence limit on adult survival for P. rufus (s_{A_uci} = .719) necessitates juvenile survival rates to exceed those of adults (s_{J_lci} = .854) in order to preserve stable population size. These assumptions are unlikely to be met, though we currently possess no field-derived data for juvenile survival. Estimation of these rates for both E. dupreanum and P. rufus is thus a major conservation priority.

Future work will need to expand on the geographic extent of age-based survival analyses for island-wide, panmictic populations of E. dupreanum and P. rufus (Chan et al., 2011; Shi et al., 2014). Pairing of longitudinal exit counts with tooth-derived survival assessments across a wider geographic range would enable estimation of time-to-extinction or extirpation for species in decline. In keeping with population trends predicted from tooth data, we detected evidence of statistically significant (albeit subtle) declines in P. rufus counts at three longitudinally-monitored roosts in a central Madagascar protected area. Nonetheless, the difficulties inherent in distinguishing regional survival variations for panmictic species (Hayman and Peel, 2016) make us cautious of the extent to which single site population counts can be more broadly extrapolated. Island-wide roost occupancy surveys and more numerous longitudinal monitoring sites thus represent additional management priorities. Since tooth-derived age analysis is impossible for smaller-bodied R. madagascariensis, mark-recapture or telemetry studies assessing survival probabilities for this third species will also be important.

Eidolon dupreanum and Pteropus rufus are IUCN ‘Vulnerable’ species, a threatened status supported by our field-based population viability analyses. Our work suggests that P. rufus is more ‘Vulnerable’ than E. dupreanum and should undergo IUCN conservation status reassessment to evaluate whether it now meets criteria for classification as ‘Endangered.’ Habitat restoration efforts designed to augment P. rufus roosting territory are needed to offset land conversion threats to already-declining populations. Cessation of the legal hunt season for Malagasy fruit bats, currently ill-timed to coincide with peak bat gestation, is also critical. Flying foxes offer important pollination and seed dispersal services for Malagasy ecosystems (Bollen and Elsacker, 2002; Picot et al., 2007), and loss of these bats and their services would have devastating consequences.

The fate of Pteropus rufus epitomizes threats faced by flying fox populations everywhere. Like P. rufus, many pteropodid species are island endemics persecuted for bushmeat consumption or use in traditional medicine (Voigt and Kingston, 2016). As highlighted by our study, population trends are often difficult to assess in the absence of quantitative demographic data, the likes of which have only been previously compiled for a few Old World Fruit Bat species. Collection and compilation of survival and fecundity estimates for other pteropodids is desperately needed to assess population trends more broadly. A 2008 conservation reappraisal of the IUCN Red List status of bats resulted in reclassification of four new Pteropus spp. as ‘Extinct” (Voigt and Kingston, 2016). Detailed demographic analyses and appropriate conservation responses will be critical to preventing this statistic from growing.