Optimization of a saturated gas plant: Meticulous simulation-based optimization – A case study

Graphical abstract

Highlights

• •A viable optimization-simulation strategy by coupling Aspen HYSYS with MATLAB.
• •The optimization strategy has been applied to a complex complete saturated-gas plant.
• •Different stochastic algorithms have been applied.
• •The benefits and shortcoming of each method have been investigated.
• •The implemented strategy precisely reached the optimum operating conditions.

Abstract

An optimization-simulation strategy has been applied by coupling a commercial process simulator (Aspen HYSYS®) with a programming tool (MATLAB®) to produce a precise steady state simulation-based optimization of a whole green-field saturated gas plant as a real case study. The plant has more than 100-components and comprises interacting three-phase fractionation towers, pumps, compressors and exchangers. The literature predominantly uses this coupling to optimize individual units at small scales, while paying more attention to optimizing discrete design decisions. However, bridging the gap to scalable continuous design variables is indispensable for industry. The strategy adopted is a merge between sensitivity analysis and constrained bounding of the variables along with stochastic optimization algorithms from MATLAB® such as genetic algorithm (GA) and particle swarm optimization (PSO) techniques. The benefits and shortcomings of each optimization technique have been investigated in terms of defined inputs, performance, and finally the elapsed time for such highly complex case study. Although, both GA and PSO were satisfactory for the optimization, the GA provided greater confidence in optimization with wider ranges of constrained bounds. The implemented strategy precisely reached the best operating conditions, within the range covered, by minimizing the total annual cost while maintaining at least 92% butane recovery as a process guarantee for the whole plant. The optimization-simulation strategy applied in the current work is recommended to be used in brownfields to optimize the operating conditions since they are susceptible to continuous changes in feedstock conditions.

Introduction

Traditionally, surplus gases in refinery plants have been disposed of by flaring to the atmosphere. Currently, this type of disposal is becoming an inferior solution for reducing emissions to the atmosphere, while simultaneously conserving energy. Therefore, the pressing demand for processes that can safely and economically use these surplus gases is rapidly increasing. In this context, the “light ends” process is the only process in modern refinery plants that is designed to separate almost pure components from crude oil [1]. Light end processing units have several stages of separation and fractionation that are used to separate light fractions from heavier fractions and purify contaminants, mainly sulfur, from lighter fractions. Usually, at least two light end processing units, a saturated gas plant (SGP) and an un-saturated gas plant, exist in very large refinery plants. Both are open art technologies and have some similarities in the arrangement and sequence of the process. However, the main differences between these units mostly relate to the location of each separation unit, type of feed and, subsequently, type of products. In principle, un-saturated gas plants are usually adjacent to cracking units for producing olefin streams, whereas SGPs are usually located adjacent to isomerization, naphtha hydro-treating and atmospheric crude distillation units (CDUs) for producing paraffinic streams [2].

Optimization applications are frequently applied as prominent tasks in all areas of process systems engineering from model and process development to process synthesis and design, and finally to process operations control, process safety analysis, planning and scheduling [3], [4], [5], [6], [7], [8]. In essence, energy conservation is the most important rule of sustainable design optimization since it is considered a key part in saving money in the long term. Energy conservation concepts should be implemented on an ongoing basis at all stages of asset lifecycle development. In most chemical process plants, an enormous amount of energy of up to approximately 40% of the total energy consumption is consumed in an intensive way in separation and purification processes [9]. In many cases, separation processes are commonly conducted by using distillation towers that have a wide variety of uses throughout the industry because of their ability to split feed streams into pure components or mixtures of components with similar boiling points [10]. Undoubtedly, optimization of the operating conditions of distillation towers is the most crucial step to minimize energy consumption and consequently reduce the total annual cost (TAC) of the whole plant. This optimization is accentuated because it contributes, in turn, to the determination of the number of pumps and compressors stages, electricity consumption, and types/amount of heating and cooling sources that are used in any plant. Although the number of trays has the primary impact on the capital cost in terms of the total height of the tower, this number is also optimized based on energy consumption regarding the total duty.

Usually, a sophisticated simulation-based optimization is required to optimize distillation towers. Since sensitivity analysis provides good intuition about how various parameters affect the objective function, and to rank the parameters [11], this analysis is usually used as a part of the optimization process to minimize the calculation time of the optimization algorithm employed. In this regard, much attention has been paid to mathematical programming for optimization problems related to distillation columns. To reliably provide rigorous stage-by-stage equilibrium optimization models for distillation towers for finding the optimal feed locations and the optimum number of trays, mixed integer nonlinear programming (MINLP) [12], [13], [14], [15] or generalized disjunctive programming (GDP) [16], [17], [18] is usually used. The first reliable model used to obtain the optimum number of stages and optimum feed locations for an individual distillation tower was executed by using MINLP [19], [20]. However, there were some shortcomings and difficulties in these models that were solved by using a GDP representation [21]. These shortcomings were due to the enforcement of vapor-liquid equilibrium conditions on all trays of the tower, and this enforcement could produce numerical problems as a result of the convergence of the equilibrium equation. Many difficulties exist in using MINLP or GDP techniques related to the need for expert persons in the areas of programming, modelling and optimization to adapt to different types of problems such as initialization of models, debugging, and determining how to guarantee the accuracy of results and similar aspects [21], [22], [23]. All problems related to the initialization and convergence of distillation columns are nearly settled when a process simulator is integrated with an external optimizer. As an example, the first integrated model was developed by integrating of HYSYS with both MATLAB and GAMS-CPLEX [24].

Commercial process software, e.g., Aspen HYSYS®, is considered “modular architecture”, which means that any process plant or any complex systems can be built and divided into sub-components (modules) without affecting the rest of the system [25]. Flow sheets can be decomposed into blocks or modules (e.g., distillation column, absorption column, …, etc.) that can be interpreted, debugged, and coded by themselves [26]. Both debugging and initialization difficulties in the equation-based models are solved in HYSYS. HYSYS-Optimizer can be used for sensitivity analysis (what-if studies) or as a single-step optimization method to find the operating conditions that locally minimize or maximize an objective function. In addition, in the first integrated model, the decision variables sent from the solver at each time must converge; otherwise, the whole algorithm will fail. Therefore, the independent variables should be selected carefully to converge at any initial point [24]. In HYSYS-Optimizer, neither the embedded code nor derivative information is accessible to users since all existing processing units in commercial simulators are “black box” models [19]. This concern should be taken into consideration since gradient-based algorithms always depend on precise derivative information from the process simulator. In this regard, many attempts have been reported in the literature to couple a process simulator with an external optimization tool to overcome the simulator-optimizer limitations. In general, the literature predominantly uses this coupling to optimize a few individual units at small scales while paying more attention to optimizing discrete design decisions. However, bridging the gap to scalable continuous design variables is indispensable for industry. For example, to overcome the limitations related to derivative-optimization techniques, a genetic algorithm (GA) and particle swarm optimization (PSO) algorithm were used as stochastic algorithms [27], [28], [29]. Aspen HYSYS was linked with a GA built-in MATLAB code to externally optimize and control HYSYS in a successful way to minimize shaft power requirements for an LNG refrigeration cycle [30], [31]. The optimization was performed to optimize the refrigerant composition and the operating conditions for the whole loop based on the selected composition. In addition, HYSYS was linked with PSO to optimize a configuration of distillation towers in terms of the optimum number of stages and the optimum feed location, based on TAC, for three different distillation systems [32]. Moreover, Aspen HYSYS and a stochastic optimization strategy for simulation and optimization were linked to determine the design variables for a crude oil separation process to maximize profits [33].

The purpose of this work is to apply a simulation-based optimization strategy for optimizing operating conditions for a whole plant in an effective and reliable way through coupling Aspen HYSYS and MATLAB. The strategy adopted is a merge between sensitivity analysis and constrained bounding of the variables along with either GA or PSO stochastic optimization algorithms. As a real case study, the procedure has been applied to an entire SGP that will be established in Egypt to produce LPG and stabilized naphtha. The plant represents a highly non-linear case with more than 100-components and comprises interacting three-phase fractionation towers, pumps, compressors, and exchangers. The remarkable challenge is determining how to handle the large numbers of equipment, continuous constraints, and variables in a corrective way without deviation from the feasible solution. The performance and results of both GA and PSO optimization algorithms have been discussed.

Methodology

Simulation problem: the case study

The refinery plant that is studied in this work mainly consists of two crude distillation units (CDU 1 and 2), including an existing SGP unit that recovers the gases produced from CDU (1). In this refinery plant, a new SGP (green field) with a design capacity of 400,000 ton/year is planned to be installed in parallel to the existing one. This SGP will be flexible to serve one or both CDUs in addition to the naphtha complex effluent streams to finally produce LPG and stabilized naphtha. The naphtha complex effluent streams are the sour off-gas from naphtha hydro-treating, off-specification LPG from continuous catalytic regeneration, off-gas from continuous catalytic regeneration, and off-gas from isomerization.

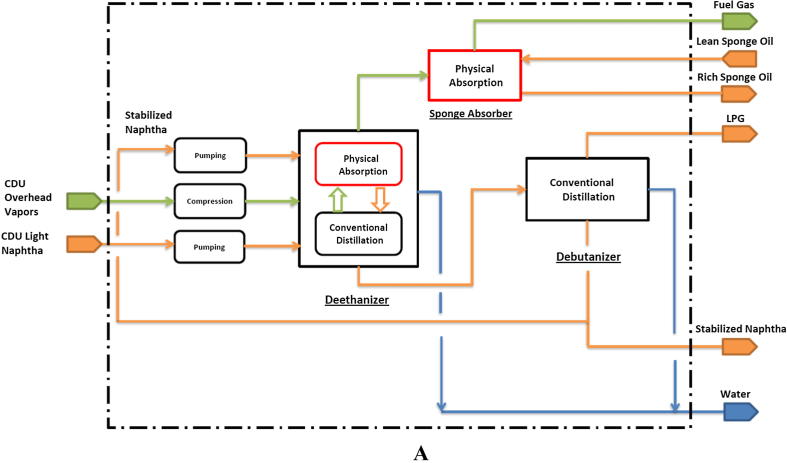
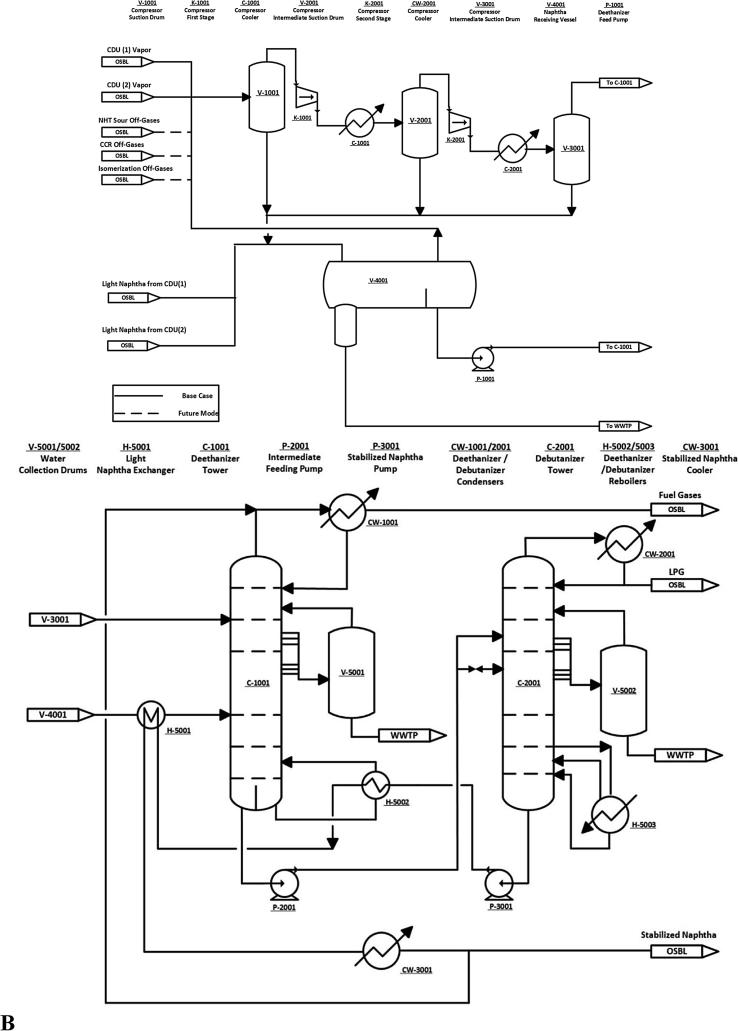
The new SGP is required to handle both design and future modes without any overdesign margin. In the design mode, two vapor streams and two liquid light naphtha streams from two different CDUs are directed to the new SGP. The vapor streams are combined and then compressed to the fractionation section and the two liquid light naphtha streams are mixed and then pumped to the same destination. In the future mode, the naphtha complex effluent streams will be routed to the new SGP with the same design capacity of 400,000 ton/year as the design mode without any overdesign margin. Fig. 1A shows a simple schematic block flow diagram with boundary limits for the process while Fig. 1B shows the detailed process flow diagram showing both the base and future modes.

Fig. 1.

A-Simple schematic block flow diagram with boundary limits; B- Overall detailed process flow diagram.

Aspen HYSYS simulation package v. 8.6 was used in developing the process model. The Peng-Robinson thermodynamic fluid property package [34] was used throughout the simulation.

Pretreatment facilities

The process starts by saturation of the feeds with water before entrance to the pretreatment facilities. In these facilities, further free-water separation and adjustment of the operating conditions are performed before sending these streams to the fractionation sections. Pretreatment facilities are required to alleviate the load of water-separation on the fractionation train, enhance the efficiency of separation, and adjust the operating conditions needed to meet the product specifications.

Compression station package

The pressure ratio across the two compression stages (with polytrophic efficiency of 75%) in the existing train is limited to 3.5. Thus, the maximum discharge pressure for the collated vapors after saturation with water is 0.9 MPa. The delivered pressure of the collated vapors from naphtha complex effluent streams in the future mode is also limited to 0.85 MPa as a design basis.

Naphtha-receiving three-phase separator

The collated water streams from the knock-out drums of compressors are sent to three-phase separator with the incoming light naphtha streams. The gas vapor stream is then recycled to the inlet vapor streams, the light naphtha is routed to the deethanizer tower for further separation, and the separated free water is sent to an existing sour water system.

Fractionation train

The fractionation train consists of two distillation towers (a deethanizer and debutanizer). A depropanizer does not exist since the LPG composition is fixed with a certain vapor pressure limit to be used in the local market. Some common practices and design criteria considered for the fractionation train are as follows:

• •The inlet feed temperature should match the tray temperature.
• •The internal temperature profile should be normal without any vertical or horizontal asymptote.
• •“HYSIM Inside-Out” is used as a built-in solving method for the three-phases (water, gas, and hydrocarbon liquid) distillation for extracting water from the trays expected to have water by having water withdrawal streams.

Deethanizer

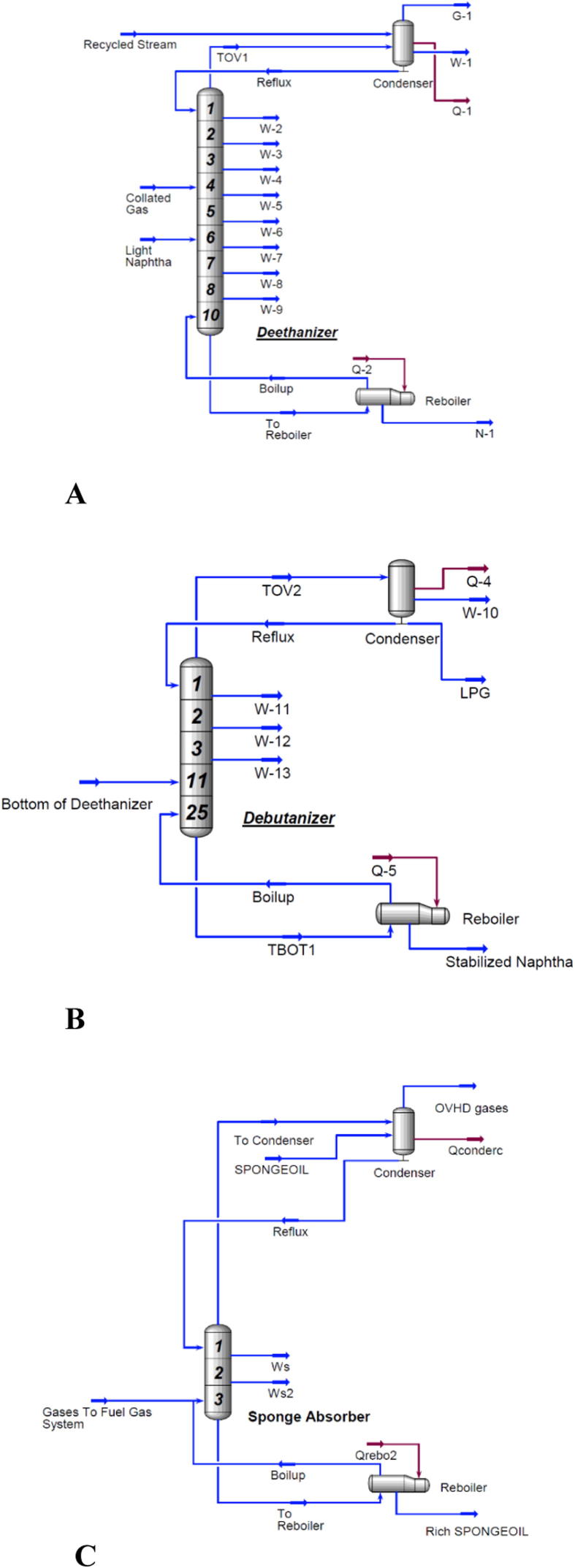
The deethanizer is simulated using the abovementioned criteria to recover C1 and C2 from the overhead, while the slipped C3 + is withdrawn from the bottom and then routed to the debutanizer, as shown in Fig. 2A. The deethanizer tower is considered to be a combination between two sections, an absorber in the top section and a conventional fractionation tower in the bottom section, rather than separating them into two standalone towers. The absorber section is considered to be a tray tower, not a packed tower, because higher flow rates of liquid and gases require larger diameters [35]. Stabilized naphtha is used as lean oil in the primary absorber due to the high absorption factor, which leads to a lower flow rate. However, some naphtha is lost to the off-gas due to equilibrium. An overhead full reflux condenser (shell and tube heat exchanger) utilizing sea water for condensation is used with a recommended minimum temperature approach of 10 °C as per common practice. The recycled stabilized naphtha is preferred to be routed to the overhead condenser to increase absorption efficiency.

Fig. 2.

A-Configuration of the deethanizer tower; B-Configuration of the debutanizer tower; C- Configuration of the sponge oil absorber.

Debutanizer

The debutanizer is simulated to recover commercial C3/C4 (LPG) from the overhead condensate, while the stabilized naphtha is from the reboiler, as shown in Fig. 2B. An overhead full reflux condenser (shell and tube heat exchanger), utilizing sea water for condensation with a temperature approach of 10 °C, was used.

Sponge absorber

To recover the lost stabilized naphtha escaping with the off-gas (fuel gas) from the deethanizer, heavier absorption oil (with a lower absorption factor than the stabilized naphtha) is used in the second stage (sponge absorber) to absorb the stabilized naphtha from the first stage of absorption (Fig. 2C). The sponge-oil rate is conventionally adjusted to control the C5 + in the off-gas to lower than 0.5% to reach an overall C5 + recovery of 99.8%. The overhead gases from the sponge oil absorber are directed to an existing fuel gas system, while the rich sponge oil is returned to the existing CDU (2). The exact amount of sponge oil should be determined by integrating the sponge absorber with CDU (2). In common practice, the number of theoretical stages of a sponge absorber ranges from approximately 3 to 5 theoretical stages with a tray efficiency of 20% [36].

Heat integration

Medium pressure steam is available at the plant. However, to minimize the amount of steam, it is used only for the reboiler of the debutanizer. On the other hand, the bottom of the deethanizer is reboiled by the hot outlet stream (stabilized naphtha) from the debutanizer reboiler. The stabilized naphtha is then routed to heat the light naphtha feed and, is finally cooled to 43 °C.

Sensitivity analysis

Sensitivity analysis was first performed on the HYSYS model as a single step optimization to identify the local optimum points before applying the optimization techniques to determine the influence of all parameters on the outcomes. Instead of using the GAMS solver, the sensitivity analysis technique was conservatively conducted on the fractionation section to provide the closest configuration to the optimum design by determining the optimum number of stages and the optimum feed locations.

Then, the HYSYS model was optimized by tuning the most influential design variables in the range of the constrained bounds for each design variable to be an input for the optimization stage. The optimization was implemented through a linkage between HYSYS and MATLAB. Finally, after implementation of the optimization techniques, sensitivity analysis was performed on the selected algorithm to test the robustness of the objective function to small changes in the values of the optimized parameters and/or small changes in the initial values.

Implicit-constraints and assumptions

The implicit constraints are imposed on HYSYS model through a large list of “column specification” that gives the possibility to select from different operating conditions as degrees of freedom for the tower. Thus, there was no need to add explicit constrains for the objective function. The implicit constraints were done based on surrounding environment conditions, process design guarantee, specifications, and common standard practice in the field. These implicit constraints are:

• •Since cooling water maximum temperature in summer is 33 °C, the overhead temperature of the deethanizer and debutanizer is not lower than 43 °C to keep the minimum temperature approach to 10 °C.
• •The recovery of C5 + in the bottom of the deethanizer is not less than 97% to decrease the amount of naphtha that may carry up with ascending vapor.
• •The overall recovery of n-C4 in each of the deethanizer and debutanizer is not less than 92% as a process guarantee for the whole plant.
• •The recovery of C3 in the bottom of the deethanizer is not less than 90% to avoid exceeding the maximum limit of LPG vapor pressure per Egyptian specification.
• •The maximum liquid volume percentage of C2 in LPG stream is 5% per Egyptian LPG specification.
• •The maximum liquid volume percentage of C5 + in LPG stream, equivalent to final boiling point test, is 5% per Egyptian LPG specification.
• •The available steam in the plant is medium pressure steam with maximum temperature around 160 °C within range of pressure of 7–8 bars.
• •The maximum shipping envelope length for distillation towers is 35 m. This is specified according to limit of feasible transport.
• •The tray spacing has been taken to be 0.9 m as a conservative space.
• •Absorber efficiency has been taken about 20%, whereas the normal distillation tower efficiency has been taken about 60% per common practice.

To develop a precise pressure profile across SGP, some realistic assumptions and calculations are made to determine the discharge pressure and the temperature required to flow the gas/liquid streams through the equipment until the boundary limits. The following assumptions were considered in the simulation:

• •Every heat transfer equipment has a pressure drop around 0.0345 MPa, except for deethanizer and debutanizer reboilers, and deethanizer feed preheater, in which the pressure drop has been around 0.0689 MPa.
• •The minimum temperature approach in all water cooler/condensers is 10 °C, as per common practice for shell and tube heat exchangers.

Finally, since feed gas compositions are available on a dry basis, water saturation utility tool in HYSYS has been used to get gas composition on a wet basis. It is important to note that HYSYS model assumes theoretical trays with vapor and liquid phases are in equilibrium on each tray. However, the economic costs have been calculated based on the actual number of trays and actual height.

Optimization-simulation methodology

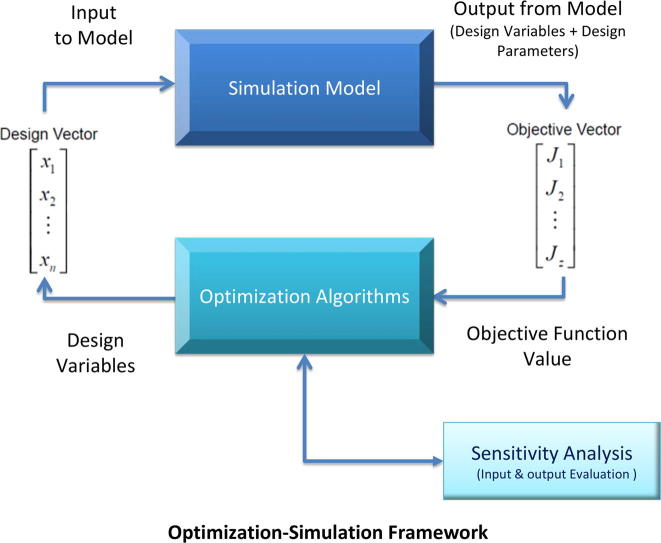
Aspen HYSYS [37] is automated by MATLAB (R2015a) as the external solver, which programmatically runs HYSYS as a front-end. All simulation calculations, thermodynamic properties, and physical properties calculations were done by HYSYS side. On the other hand, MATLAB programmatically controlled black-box functions inside HYSYS and took all relevant decisions to attain the optimum design with the appropriately selected algorithm (GA or PSO).

Objective function

Indeed, coupling HYSYS with external software for optimization such as MATLAB requires the objective function to be well-defined in terms of process design variables (input to HYSYS) and process design parameters (output from HYSYS). The objective function selected for the current work is the TAC, which comprises two main terms for operating cost and capital cost (Equation (1)) [38]:

$$\mathit{TAC}=F\times C_{\mathit{Cap}}+C_{\mathit{Op}}$$ (1)

where:

• TAC: Total annual cost

• F: Annualization factor

• C_Cap: Capital cost

• C_Op: Operating cost

The annualization factor (F) of the capital cost is calculated by (Equation (2)) [39]:

$$\mathrm{F}=\frac{i\ast {(1+i)}^n}{{\left(1+i\right)}^n-1}$$ (2)

where:

• i: fractional interest rate per year. A typical value for (i) is 10% per common practice.

• n: years over which the capital is to be annualized. A typical value for n is 5 years per common practice

For the current plant, distillation towers and heat exchangers (condensers and reboilers) have the main impact on the capital cost. Compressors and pumps are the only other equipment available in the plant. For compressors, per the current real case study, an old compression station with two compression stages with their accessories from the refinery plant was intended to be used. Accordingly, their power consumption only has been included as operating cost. For pumps, their capital cost change is trivial and negligible compared to that of the towers and heat exchangers. Accordingly, only their operating cost was included. In reality, pumps are usually designed based on the maximum flow rate with multi-impellers.

The capital cost of heat exchangers depends on the calculated areas of condensers and reboilers of towers. The area of exchangers is a function of heat duties and the logarithmic mean temperature difference. Similarly, the cost of a tower is a function of the diameter, height, and operating pressure of the tower. The capital cost of the towers was calculated based on the maximum diameter that is produced from the maximum vapor rate in the future mode as the worst-case scenario and the actual maximum height. After inserting the values of the diameter and actual height in the capital cost function of the towers, this function becomes a function of only the operating pressure [40]. On the other hand, the operating cost was estimated based on the cost of medium pressure steam, cooling water and electricity that are consumed in each tower for 330 days per year operation [38]. The details of the TAC calculations are in the supporting information.

Using sensitivity analysis, there are five process design variables (input to HYSYS) that are required to completely specify the simulated case study. To expedite the optimization process, the number of generations/iterations needed to find an optimum solution can be minimized by decreasing the number of design variables to only three design variables as follows:

• •Bottom pressure of the deethanizer (Peth).
• •Bottom pressure of the debutanizer (Pbut).
• •Split ratio (recycled flow rate of stabilized naphtha) (W).

The other two process design variables (top pressures of the deethanizer and debutanizer) were taken as 0.05 MPa lower than their corresponding tower bottom pressures. This helped in decreasing the time from HYSYS to MATLAB and decreasing the total computational time. Apart from the elapsed time as a result of the executed algorithm, the optimization process can be expedited by minimizing the maximum number of iterations that is adjusted by the HYSYS solver itself to be only 150 iterations for the distillation column.

The process design parameters (output from HYSYS) included in the objective function are:

• •Heat duty of deethanizer’s condenser (Qcond)
• •Heat duties of the debutanizer’s condenser and reboiler (Qconb and Qreb)
• •Power of the first and second stages of the compressor (PWa and PWb)
• •Power of the light naphtha pump, booster pump and stabilized naphtha pump (PWc, PWd, and PWe)
• •Overhead temperatures of the deethanizer and debutanizer (TOVa and TOVb)
• •Bottom temperatures of the deethanizer and debutanizer (TBOTa and TBOTb)

After accessing HYSYS through an ActiveX server and activating a HYSYS case from MATLAB, almost all unit operations in HYSYS become accessible as automated objects, which can be recalled and controlled externally with a certain interfacing code. In MATLAB, user can review the variables that are available for automations or from COM server, where all variables and type of each variable are listed. Moreover, user can reach the design variable or parameter by more than one way to select the easiest way to transfer the data directly from HYSYS to MATLAB and vice versa. The framework directly links to key parameters and looks live and interactive, in contrast to linking to a spreadsheet, as has been done in most previous endeavors. It is important to note that if information is sent to HYSYS from a client application, HYSYS does not return control to the calling program until calculations are complete [41]. All simulation runs and executed algorithms were performed by using a computer with a 2.10 GHzi3-2310 M processor and 3 GB of RAM.

Optimization algorithms

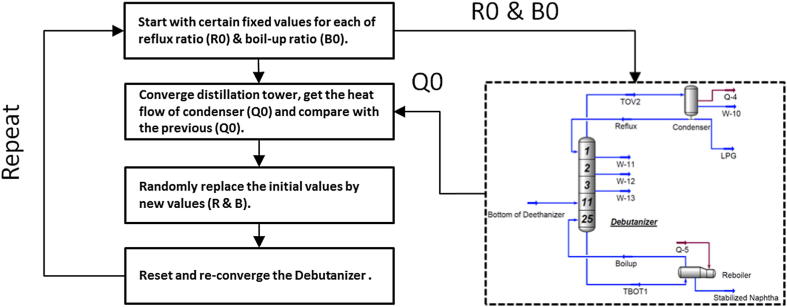
The most important step in the optimization process is to select a tailored algorithm that fits the problem to be optimized. In general, optimization algorithms are classified into two broad categories: gradient-based algorithms and algorithms that employ derivative-free optimization. When using the gradient-based algorithms, the only way to obtain the derivative information from HYSYS is to make a disturbance for the design variables. Fig. 3 shows a numerical experiment to clarify how the information is transferred from HYSYS to MATLAB and vice versa. The accuracy of the transferred data is of paramount importance for optimization.

Fig. 3.

Mechanism of getting derivative information from Aspen HYSYS “black box”

HYSYS-Optimizer only employs some gradient-based algorithms that need convex models to ensure local optima. On the other hand, MATLAB has both gradient-based and derivative-free optimization approaches. In HYSYS, small numerical noise usually arises when the initial values of the variables change and then recover. This numerical noise is large enough to prevent the calculation of accurate derivatives. This effect results in gradient-based optimization algorithms or finite difference methods that exist in MATLAB or in HYSYS itself being unreliable [42]. To minimize this numerical noise, the tolerance values should be less than 10^-6. However, these tolerance values make convergence of the flow sheet very difficult, especially when treating interrelated systems such as recycle streams. On the other hand, algorithms that employ stochastic optimization techniques provide an attractive option for optimization since these methods are derived from heuristics that depend on derivative-free optimization techniques. This means that the information can be transferred from/to HYSYS through a perturbation mechanism by making a disturbance to the design variables instead of derivative information. Therefore, these algorithms avoid the difficulties of the high level of numerical noise that is produced from deterministic techniques [43], [44]. In this work, Global Optimization Toolbox, a built-in MATLAB tool, was used to provide methods of optimization. Both GA [45] and PSO [46], [47] were selected for comparison.

The GA uses the principle of “survival of the fittest” in its search process to select and generate individuals (design solutions) that are adapted to their (design objectives/constraints). The GA will then apply one of three stochastic operators to each point in the population. It will either keep a point for the next generation (selection), combine two points to obtain a new point (crossover), or randomly perturb a candidate solution by changing the point completely (mutation) [45]. On the other hand, the GA shows poor performance.in highly constrained systems.

PSO is a relatively novel stochastic technique. This technique mimics the way a swarm of birds (particles) locates a best landing place applies the social interaction behavior of fish schooling or bird flocking [46]. Each particle is treated as a particle in N-dimensional space that adjusts its “flying” according to its own flying experience as well as the flying experience of other particles [47].

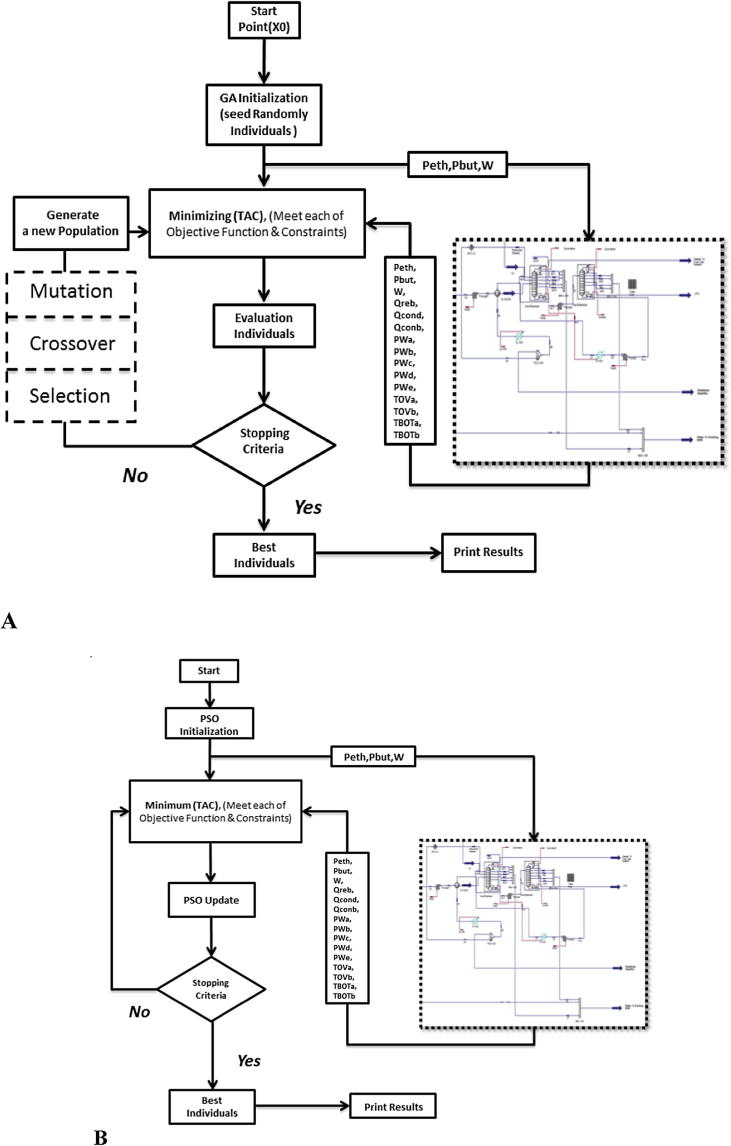
The default number of generations in MATLAB for the GA is (100 × number of variables) to guarantee the minimum objective function value [48]. Therefore, there is no need to re-execute the algorithm to guarantee the same solution. However, the GA needs some kind of sensitivity analysis after implementation with different initial values to guarantee the fittest solution. As shown in Fig. 4A, the algorithm starts by the converged steady-state simulation model, and then the objective function is evaluated for different design variables and design parameters to determine the best design variables. All newly populated design variables are reverted to evaluate objective function again for the next generation. This process is repeated until the stopping criterion is satisfied.

Fig. 4.

A-Logical flowchart for the proposed algorithm using the GA; B- Logical flowchart for the proposed algorithm using the PSO.

On the other hand, in PSO, the number of particles in the swarm (swarm size) is the minimum of 100 or (10 × number of variables) to guarantee the minimum objective function value [49]. Due to the random population of design variables, convergence to the same solution is not always guaranteed in the case of PSO. Thus, the algorithm is executed a certain number of times to assess the convergence of the proposed optimization approach and check to what extent the values are close to each other. As shown in Fig. 4B, the algorithm starts by the converged steady- state simulation model, and then the objective function is evaluated for different design variables and design parameters to determine the best design variables. All newly populated particles are reverted into the PSO as the next generation. This process is repeated until the stopping criterion is satisfied.

Results and discussion

Sensitivity analysis

Debutanizer

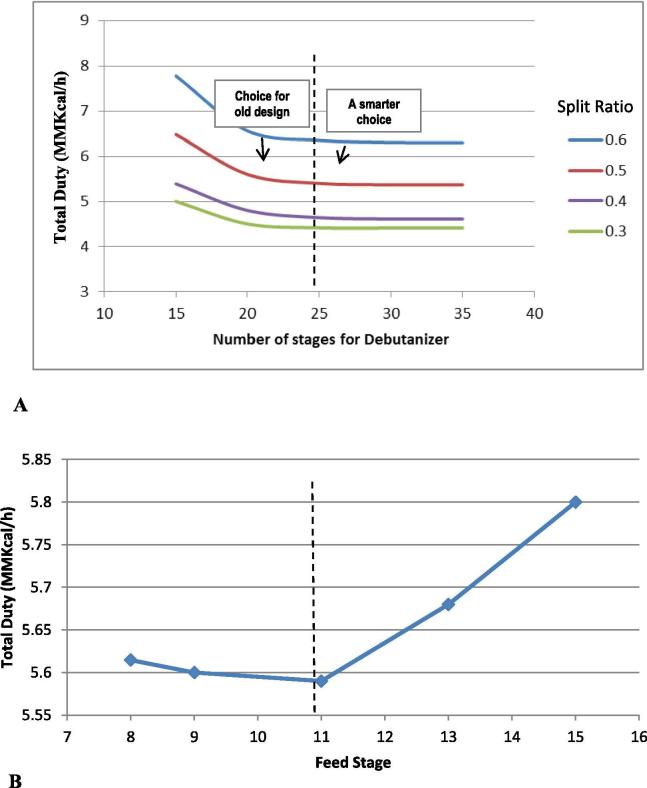
Since the optimum operating conditions are absent in the beginning of the design, the number of stages of the debutanizer against the total duty has been explored at different split ratios by changing the operating tower pressure (Fig. 5A). The lower number of trays reflects a lower capital cost, but at the expense of the operating cost.

Fig. 5.

Sensitivity analysis for the debutanizer (theoretical stages are excluding the reboiler and condenser stages). A- Number of stages; B- Feed location.

In the old design of the debutanizer, the number of stages was chosen closer to the focus point of the hyperbola (21 theoretical stages excluding the reboiler and condenser). However, the price of energy and its fluctuations greatly influence the optimum number of stages. Therefore, it is currently recommended to presume higher energy cost during the design phase to accommodate the fluctuations in the price of energy [39]. As shown in Fig. 5A, the curve flattens at approximately 25 theoretical stages (excluding the reboiler and condenser). Consequently, a smarter choice for the optimum number of stages for the debutanizer would be around this value to increase the flexibility of the operation.

The optimum feed location of the debutanizer should be selected based on the lowest total duty for the selected number of stages. In addition, the optimum feed location should be feeding to a tray with a similar composition to minimize the composition gradient between the feed and tray and consequently reduce the total duty. Hence, evaluating the feed location is an essential step for successful distillation unit optimization. Fig. 5B shows that the optimum feed location is around the 11th stage for the selected total number of stages.

Deethanizer

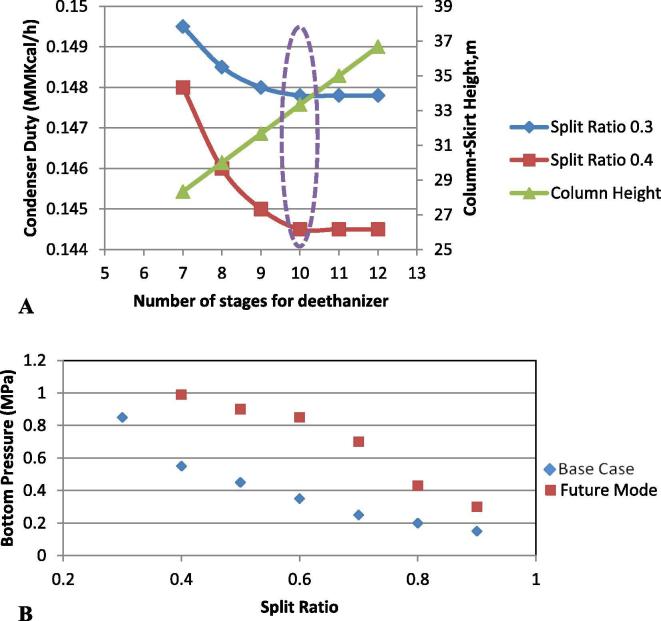
As mentioned before, the deethanizer tower consists of an absorber rectifying section and a conventional distillation stripping section. Since the duty of the reboiler is supplied by the hot stream of stabilized naphtha, the operating cost is a function of only the cooling duty of the condenser. A change in the number of stages of the deethanizer has a minor effect on the cooling duty of the condenser, although this effect decreases with increasing the number of stages (Fig. 6A). As per common practice, the absorber tray efficiencies run notoriously low. Therefore, the number of stages has to be selected carefully not to violate the maximum allowable equipment shipping length (35 m), while maintaining moderate duty and tuned temperature profile along the tower. As shown in Fig. 6A, the optimum is approximately 10–11 theoretical stages, which does not exceed the maximum length.

Fig. 6.

A-Sensitivity analysis for the number of stages of the deethanizer (theoretical stages are excluding the reboiler and condenser stages); B-Impact of lean oil recycle amount on the operating bottom pressure of the deethanizer in each of the base case and future mode.

Lean oil

The amount of recycled lean oil has a great impact on the operating pressure of the towers and the total duties. Table 1 (A and B) shows the effect of the split ratio for the base case and future mode, respectively.

Table 1.

Effect of split ratio for the lean oil: A-base case; B-future mode. Deethanizer and debutanizer theoretical stages are 25 and 10, respectively.

A (base case)	Split ratio
	0.9	0.8	0.7	0.6	0.5	0.4	0.3	0.25
Recycle flow (ton/day)	6912	2851	1840	1201	795	512	337	315
Bottom pressure of deethanizer (MPa)	0.15	0.2	0.25	0.35	0.45	0.55	0.85	0.85
Bottom pressure of debutanizer (MPa)	0.45	0.45	0.5	0.5	0.5	0.5	0.5	0.7
Bottom temperature of (deethanizer/debutanizer) (oC)	67/127	70/127	72/127	82/127	89/127	95/127	116/128	114/130
Total duty for deethanizer and debutanizer (MMKcal/h)	18.75	10	7.7	6.3	5.4	4.67	4.4	5.6
CAPEX/OPEX	Higher/Higher	Higher/Lower	Higher/Lower	Higher/Lower	Higher/Lower	Higher/Lower	Lower/Lower	Lower/Higher

B (future mode)	Split Ratio
	0.9	0.8	0.7	0.6	0.5	0.4
Recycle flow (ton/day)	4886	2150	1531	1064	820	809
Bottom pressure of deethanizer (MPa)	0.3	0.43	0.7	0.85	0.9	0.99
Bottom pressure of debutanizer (MPa)	0.5	0.5	0.55	0.6	0.8	0.85
Bottom temperature of (deethanizer/debutanizer) (oC)	89/140	90/140	110/140	114/140	111/150	125/155
Total duty for deethanizer and debutanizer (MMKcal/h)	14	9	7.5	6.2	9.7	9.61
CAPEX/OPEX	Higher/Higher	Higher/Lower	Higher/Lower	Higher/Lower	Higher/Lower	Higher/Higher

The operating pressure of the deethanizer in the future mode increases notably more than that in the base case (Fig. 6B). The feed mixture in the future mode is lighter than that in the baseline scenario. Accordingly, the vapor pressure of the overhead stream is higher. Therefore, to keep the constraint of the lowest overhead temperature of 43 °C, the operating pressure of the tower was increased. Similarly, the bottom temperature of the deethanizer tower notably increases with decreasing split ratio due to the increased operating pressure of the tower.

As for the debutanizer, its pressure should be compromised. The increase in the operating pressure of the debutanizer leads to violating the constraint of C4 specification. On the other hand, decreasing the operating pressure of the debutanizer decreases the bottom temperature of the debutanizer, and which this effect leads to the absence of thermal integration between the deethanizer and debutanizer reboilers.

Finally, at higher split ratios, the total duty and the area of condensers are higher. Thus, CAPEX and OPEX increase dramatically. Consequently, very high split ratios are excluded from upper bounds to reduce the execution time of the optimization algorithm. Similarly, much lower split ratios are also excluded for two reasons. First, an additional operating cost is needed due to utilizing high-pressure steam in each reboiler of the deethanizer and debutanizer. Second, heat integration for the feed preheater could not happen in the case of increasing the pressure of the deethanizer above a certain value or decreasing the pressure of the debutanizer under a certain value.

Constrained bounds for the base case and future mode

According to the implemented sensitivity analysis, constrained bounds for each design variable are deduced to be used as inputs for the optimization. Since the split ratio is the most effective design variable that affects the recovery of LPG and the other design parameters, a wider range was used. Table 2 shows the bounds used for the base case and future mode, respectively.

Table 2.

Constrained bounds for design variables for the base case and future mode.

		Recycle naphtha flow (kg/s)	Bottom operating pressure of deethanizer (MPaa)	Bottom operating pressure of debutanizer (MPaa)
Base case	Upper bound	45	0.85	0.70
	Lower bound	3.2	0.15	0.45
Future mode	Upper bound	25	0.9	0.85
	Lower bound	10	0.43	0.5

Optimization

Outputs of the GA

The initial values affect the results of the GA to a great extent. Therefore, these values should be selected based on a real understanding of the system and the objective function. If the selected initial values are very far from the optimum point, the whole algorithm will fail and produce infeasible solutions for the objective function. These infeasible solutions arise because the flow sheet does not converge at all points within the constraint bounds of the design variables through the objective function correlation. Nevertheless, the GA has the ability to move away from the infeasible regions and keep searching for the minimum real value as long as the initial values produce a feasible value in the initialization step.

Table 3 represents the outputs from the GA optimization including the optimum design values of the variables, the optimum objective function and the CPU times for the base case and future mode. Unlike the baseline scenario, the future mode suffered from instability issues. Due to this instability, the deethanizer was resettled at each generation of the design variables to guarantee convergence for the whole flow sheet. However, the CPU time increased tremendously.

Table 3.

Computational outputs from the GA for the base case and future mode.

	Initial values
	Base Case			Future Mode
	[Recycle amount (kg/s), Bottom operating pressure of deethanizer (MPaa), Bottom operating pressure of debutanizer (MPaa)]
	[20, 0.69, 0.45]	[7, 0.9, 0.7]	[3.9, 0.95, 0.6]	[12,0.85,0.6]	[17,0.7,0.55]
Optimum recycled flowrate (kg/s)	3.21	3.206	3.2	10.0011	10.0011
Optimum bottom operating pressure for deethanizer (MPaa)	0.848922	0.849922	0.8489375	0.8697659	0.8697659
Optimum bottom operating pressure for debutanizer (MPaa)	0.500124	0.50001	0.500	0.5500942	0.5500942
TAC (1000 USD/year)	826.300	826.300	825.760	1118.60	1118.80
CPU time (s)	25,610	25,609	10,000	35,503	40,951
Function evaluations	6650	6650	4900	1850	2600

Outputs of PSO

In some meta-heuristic algorithms such as PSO, there are two methods to guarantee producing feasible solutions of the whole algorithm and avoid any deviation from feasible regions. One of these methods is accompanying the algorithm with penalty functions, in which external constraints are placed into the objective function via penalty parameters to penalize any violation, in addition to broadening the ranges of the bound constraints for the design variables. However, due to the large number of constraints encountered in the optimization, it is advisable to avoid adding any penalty terms in the objective function to facilitate the problem and guarantee the robustness of the solution [50]. To remedy this problem without the adoption of penalty strategies, the constrained bounds were divided here to more than one interval. Each interval contained the constrained bounds that guaranteed the convergence of the simulator in the whole interval without deviation. The division of the intervals was determined by checking whether the objective function is valid by using the option “FunValCheck” in the syntax to stop the algorithm and display an error when the objective function returns a value that is infeasible and then identify the new interval. Thus, this second method depends on some intervention from the user to facilitate convergence and guarantee the feasibility of the solution. Moreover, in the PSO algorithm, the small variations that exist between the values of the objective function are usually a consequence of small numerical noise from the process simulator. Therefore, five consecutive executions were produced to determine the optimum operating conditions and are considered enough, especially since the design variables here are continuous, not discrete.

For the base case, the constrained bounds were divided into two intervals as shown in Table 4. For each interval, the results of five consecutive executions of the optimization algorithm coupled with CPU time and the minimum TAC are included. The lowest TAC is considered the best minimum for the whole range from PSO for the base case and is similar in value to that obtained previously from the GA optimization.

Table 4.

Computational outputs from the PSO for the base case (Two interval).

	[Recycle amount (kg/s), Bottom operating pressure of deethanizer (MPaa), Bottom operating pressure of debutanizer (MPaa)]
	First Interval [12–45, 0.45–0.85, 0.5–0.7]
	Execution number
	1	2	3	4	5
Optimum recycled flowrate (kg/s)	12	12	12	12	12
Optimum bottom operating pressure for deethanizer(MPaa)	0.85	0.85	0.85	0.85	0.85
Optimum bottom operating pressure for debutanizer (MPaa)	0.50	0.50	0.50	0.50	0.50
TAC (1000 USD/year)	1132.90	1132.92	1132.95	1132.90	1132.98
CPU time (s)	973	978	1026	950	1000
Function evaluations	690	690	690	690	690

	Second Interval [3.2–12, 0.8–0.85, 0.5–0.7]
	Execution number
	1	2	3	4	5
Optimum recycled flowrate (kg/s)	3.2	3.2	3.2	3.2	3.2
Optimum bottom operating pressure for deethanizer (MPaa)	0.85	0.85	0.85	0.85	0.85
Optimum bottom operating pressure for debutanizer (MPaa)	0.50	0.50	0.50	0.50	0.50
TAC (1000 USD/year)	821.420	821.465	821.452	821.420	821.420
CPU time (s)	493	480	490	490	490
Function evaluations	660	660	660	660	660

For the future mode, due to the instability, the intervals of constrained bounds were divided into three intervals as shown in Table 5. For each interval, the results of 5 consecutive executions of the optimization algorithm coupled with CPU time and the minimum TAC are included. The lowest TAC is considered the best minimum for the whole range from PSO for the future mode and is similar in value to that obtained previously from the GA optimization.

Table 5.

Computational outputs from the PSO for the future mode (Three intervals).

	[Recycle amount (kg/s), Bottom operating pressure of deethanizer (MPaa), Bottom operating pressure of debutanizer (MPaa)]
	First Interval [12.3–23, 0.43–0.85, 0.5–0.6]
	Execution number
	1	2	3	4	5
Optimum recycled flowrate (kg/s)	12.3	12.3	12.3	12.3	12.3
Optimum bottom operating pressure for deethanizer(MPaa)	0.85	0.85	0.85	0.85	0.85
Optimum bottom operating pressure for debutanizer (MPaa)	0.5	0.5	0.5	0.5	0.5
TAC (1000 USD/year)	1141.72	1141.65	1141.59	1141.70	1141.69
CPU time (s)	5489	5479	5480	5488	5488
Function evaluations	660	660	660	660	660

	Second Interval [10.2–12.3, 0.62–0.87, 0.5–0.55]
	Execution number
	1	2	3	4	5
Optimum recycled flowrate (kg/s)	10.2	10.2	10.2	10.2	10.2
Optimum bottom operating pressure for deethanizer (MPaa)	0.864	0.864	0.864	0.864	0.864
Optimum bottom operating pressure for debutanizer (MPaa)	0.55	0.55	0.55	0.55	0.55
TAC (1000 USD/year)	1130.37	1130.40	1130.45	1130.36	1130.37
CPU time (s)	2089	2080	2081	2089	2089
Function evaluations	660	660	660	660	660

	Third Interval [10–10.2, 0.86–0.87, 0.55–0.55]
	Execution number
	1	2	3	4	5
Optimum recycled flowrate (kg/s)	10	10	10	10	10
Optimum bottom operating pressure for deethanizer (MPaa)	0.866	0.866	0.866	0.866	0.866
Optimum bottom operating pressure for debutanizer (MPaa)	0.55	0.55	0.55	0.55	0.55
TAC (1000 USD/year)	1118.2	1118.2	1118.2	1118.2	1118.2
CPU time (s)	2268	2267	2268	2260	2268
Function evaluations	660	660	660	660	660

From the above tables, both the GA and PSO reached nearly the same best optimum for the base case and future case of 826,000 and 1,118,000 USD/year, respectively. In addition, the final produced optimum design variables from each algorithm are nearly the same. For the base case, the optimum operating pressure of the deethanizer, the optimum operating pressure of the debutanizer and the recycled stabilized naphtha were 0.85 MPa, 0.50 MPa and 3.2 kg/s, respectively. For the future mode, the optimum operating pressure of the deethanizer, the optimum operating pressure of the debutanizer, and the recycled stabilized naphtha were 0.87 MPa, 0.55 MPa and 10 kg/s, respectively. For ease of tower operation, the internal temperature profile along the distillation towers should be tuned according to the optimum operating conditions to align with the normal temperature profile.

The time taken by PSO in both of the base case and future mode (1500 s and 9850 s, respectively) was less than that taken by the GA in both the base case and future mode (25610 s and 40951 s, respectively). However, PSO needs more understanding of the system. This need is reflected in the intervals of the constrained bounds chosen to avoid using any additive penalty function terms in the objective function. On the other hand, the GA provides the best optimum within a wider range of bound constraints, as long as good intuition about the initial point is given to the algorithm. Finally, it is clear from the above that both the GA and PSO can be used as “fit-for-purpose” optimization algorithms according to the nature of the optimization problem.

The implemented strategy adopted in the current work shows how to optimize more complex systems and/or entire green- or brown-field plants. These systems require more constraints, design variables, and design parameters to couple the simulator with MATLAB in a rational and seamless way. The strategy sheds light on how to deal with alternative stochastic algorithms, i.e., the GA and PSO, in such a wide range of conditions. Moreover, this optimization-simulation strategy can be generalized to be used in dynamic simulations to optimize control parameters. Finally, the strategy can be very beneficial for brownfields to optimize the operating conditions, particularly, for CDUs and vacuum distillation units, which require periodic tuning to optimize operating conditions due to the continuous changes in the feedstock conditions.

Conclusions

A coupling between Aspen HYSYS and MATLAB to produce a precise steady state simulation-based optimization strategy was developed through a real case study. The coupling was demonstrated in optimization of a complex SGP in a certain refinery plant in Egypt to maximize the benefit from the produced off-gases. A merge between sensitivity analysis and stochastic optimization techniques such as GA and PSO was adopted in the optimization strategy. The implemented strategy reached the best operating conditions by minimizing the total annual cost while maintaining at least 92% butane recovery as a process guarantee for the whole plant.

The advantages and disadvantages of each method were discussed in detail. The elapsed time needed by PSO was less than that needed by the GA, but PSO needed more understanding of the system in terms of the well-defined bounds. This difference was reflected in the constrained bounds chosen to avoid using any additive penalty function terms in the objective function. Despite the large amount of time needed, the GA provides greater confidence than PSO in optimization with wider ranges of constrained bounds. In any case, both methods are fit-for-purpose algorithms.

The results show that the implemented strategy can provide viable and reliable operating conditions. This finding is reflected in obtaining essentially the same best conditions whether by using the GA or PSO within the bounds implemented for both algorithms. For ease of tower operation, the internal temperature profile along the distillation towers should be finally tuned corresponding to the best operating conditions to align with the normal temperature profile. The optimization-simulation strategy can be used in brownfields to optimize the operating conditions, which may be susceptible to continuous changes in feedstock conditions.

Compliance with Ethics Requirements

This article does not contain any studies with human or animal subjects.

Declaration of Competing Interest

The authors have declared no conflict of interest.

Appendix A. Supplementary material

The following are the Supplementary data to this article: