Robust differential microRNA targeting driven by supplementary interactions in vitro

Abstract

Complementarity to the microRNA (miRNA) seed region has long been recognized as the primary determinant in target recognition by the Argonaute-miRNA complex. Recently, we reported that pairing to miRNA 3′-supplementary region (nucleotides 13–16) can increase target affinity by more than an order of magnitude beyond seed-pairing alone. Here, we present biochemical evidence that supplementary interactions can drive robust differential targeting between equivalently seed-matched target RNAs in vitro. When mixed together, Ago2–miRNA complexes initially bind seed-matched targets equally but then redistribute between targets based on the strength of supplementary interactions. Thus, while initial target recognition was driven by seed-pairing, the distribution of Ago2–miRNA complexes between targets was determined by retention of Ago2 on target RNAs via supplementary interactions. Mathematical modeling and biochemical data predict that targets with strong supplementary interactions could be more strongly repressed than seed-only matched targets, even when vastly outnumbered by seed-only targets. The combined results raise the possibility that supplementary interactions could play a role in specifying specific miRNA targets for enhanced repression.

INTRODUCTION

MicroRNAs (miRNAs) are small (∼22 nt) regulatory RNAs that function as guides for Argonaute proteins. Argonautes bind miRNAs to form the core of the miRNA-induced silencing complex (miRISC), which uses the miRNA as a guide to identify RNA targets for posttranscriptional repression. Human Argonaute proteins, including Ago2, require only partial base-pairing complementary to their miRNA guides to bind and repress target mRNAs. Accordingly, individual miRNAs generally have hundreds of different binding sites throughout the transcriptome (Friedman et al. 2009; Agarwal et al. 2015).

Inspection of regulatory elements in Drosophila mRNAs first indicated that complementarity to the miRNA 5′ end, particularly nucleotides 2–8, is a key feature in target recognition (Lai 2002). Comparison of miRNA recognition sites in flies (Stark et al. 2003) and phylogenetic analyses of conserved 7-nt segments in vertebrate mRNAs (Lewis et al. 2003) defined complementarity to this 5′-region of miRNAs, termed the “seed region,” as the most evolutionarily conserved feature of miRNA targets in animals. Complementarity to the miRNA seed can be sufficient for target recognition and repression (Doench and Sharp 2004; Brennecke et al. 2005; Lai et al. 2005; Lim et al. 2005), and seed-pairing is the primary metric for miRNA target prediction (Agarwal et al. 2015). Biochemically, seed complementarity was found to provide nearly all the binding energy tethering mouse miRISC to its targets (Wee et al. 2012). miRNAs with the same seed sequence are therefore considered as members of a targeting family in which all members share the same predicted targets (Bartel 2009).

Early observations in worms suggested that regions toward the miRNA 3′ end might also be used for target recognition by miRISC (Lee et al. 1993; Wightman et al. 1993; Reinhart et al. 2000). Indeed, Grimson et al. (2007) found evidence for “supplementary” pairing, centered around miRNA nucleotides 13–16, that can enhance the efficacy of mammalian seed-matched target sites. Evaluation of supplementary interactions has since been used to better predict the efficacy of seed-matched targets, and this metric currently is as informative as the metric that evaluates site conservation (Agarwal et al. 2015). 3′-pairing, can also compensate for a seed mismatch and thereby create a functional recognition site (Vella et al. 2004; Brennecke et al. 2005; Broughton et al. 2016; Brancati and Großhans 2018). However, 3′-supplementary and 3′-compensatory sites appear to be rare, consisting of <5% of preferentially conserved target sites (Brennecke et al. 2005; Lewis et al. 2005; Friedman et al. 2009). Additionally, the typical influence of supplementary pairing on repression was found to be modest—less than the difference in repression levels between 7mer and 8mer seed-matched sites (Grimson et al. 2007; Bartel 2009), which differ in affinity for miRISC by about fourfold (Schirle et al. 2014, 2015; Klum et al. 2017). Supporting this view, biochemical characterization of mouse miRISC found that complementarity to the miRNA “3′ supplementary region” (nucleotides 13–16) increased target affinity less than twofold over seed-pairing alone (Wee et al. 2012). The combined results supported the conclusion that supplementary 3′ pairing plays a modest role in target recognition (Bartel 2009), and has little influence on-site affinity and efficacy (Bartel 2018).

Recently, we determined the structure of the Ago2–miRNA complex engaged with a target paired to the miRNA seed and supplementary regions (Sheu-Gruttadauria et al. 2019b). As seen in previous structures (Schirle et al. 2014), Ago2 creates a seed-chamber that encapsulates seed-paired miRNA-target duplexes up to 7 bp in length. Additionally, the new structure revealed that Ago2 also creates a supplementary chamber to house supplementary target interactions up to 5 bp in length. Binding measurements showed that optimal supplementary pairing can increase the affinity of the Ago2–miRNA complex for a seed-matched target more than 20-fold. These observations stand in contrast to the modest view of 3′-supplementary interactions, and suggest that miRISC has the capacity to use miRNA supplementary region to make substantial contributions toward target recognition.

Here, we further examine the potential of the miRNA 3′-supplementary region to influence target recognition by miRISC. Using purified Ago2–miRNA complexes, we show that supplementary interactions are sufficient to drive a strong selection between equivalently seed-matched target RNAs in a short period of time. We present a mathematical description of Ago2–miRNA targeting behavior between seed-only and seed + supplementary matched targets. Our results demonstrate that seed-matched targets with efficacious supplementary pairing can remain highly occupied by Ago2 even when vastly outnumbered by seed-only targets. These results raise the possibility that, in some biological contexts, miRISC may be able to use supplementary interactions to single out and more profoundly repress specific seed-matched target mRNAs.

RESULTS

Supplementary interactions can drive targeting specificity in vitro

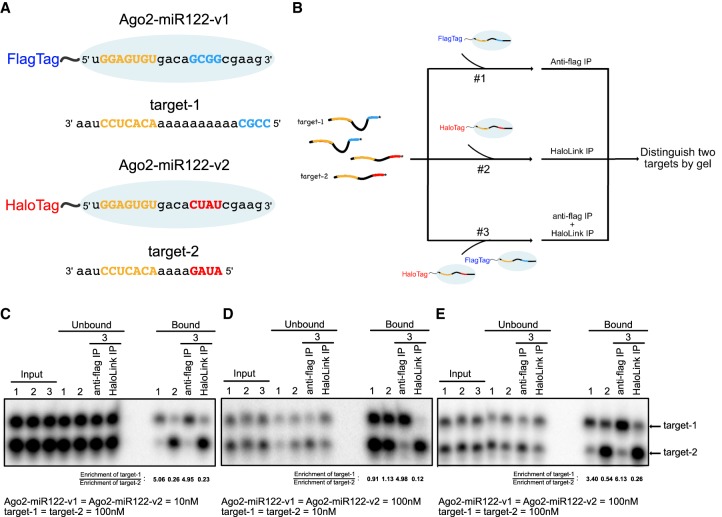
We recently demonstrated that the Ago2–miRNA complex can bind target RNAs with seed and supplementary pairing with an affinity >10-fold greater than target RNAs with complementarity limited to the seed region alone (Sheu-Gruttadauria et al. 2019b). This difference in affinity led us to hypothesize that interactions with the supplementary region may allow the Ago2–miR complex to distinguish between two different perfectly seed-matched target RNAs. To test this hypothesis experimentally, we generated samples of Ago2 bound to one of two variants of miR-122 (v1 and v2), which differ only in the sequence of the 3′-supplementary region (miRNA nucleotides 13–16) (Fig. 1A,B). miR122-v1 was designed to have a strong (4 G/C nucleotides) supplementary sequence, and miR122-v2 had a weaker (1 G/C + 3 A/U nucleotides) sequence. Care was also taken to design the pair of miR-122 variants such that recognized targets contain no predicted secondary structure, have no possibility of cross-variant supplementary target pairing, and have complementary restricted to the seed and supplementary regions of the two miR-122 variants. Ago2 proteins in the two preparations were differentially tagged such that Ago2 loaded with miR122-v1 contained an amino-terminal Flag-tag, and Ago2 loaded with miR122-v2 contained an amino-terminal Halo-tag. Importantly, once loaded into Ago2 miRNAs dissociate with a half-life on the order of days (De et al. 2013). Thus, pull down of Ago2–miR122 complexes using either α-Flag agarose or HaloLink resin allowed us to separate target RNAs associated with Ago2–miR122-v1 or Ago2–miR122-v2 from each other and from unbound target RNAs. Finally, we generated two miR-122 seed-matched target RNAs where target-1 and target-2 contained complementarity to the supplementary regions of miR122-v1 and miR122-v2, respectively. Target-1 contained an extended (10 nt) bridging region between seed and supplementary pairing sequences, while the bridging region of target-2 was 4 nt. This length difference allowed the two target RNAs to be readily distinguished from each other by denaturing PAGE.

FIGURE 1.

Supplementary interactions drive targeting specificity in vitro. (A) Schematic of Ago2 (blue oval) with miRNA and target sequences indicated. Seed (in miRNA) and seed-complementary (in targets) nucleotides are colored yellow. Supplementary (in miRNA) and supplementary-complementarity (in targets) nucleotides are colored red (v1) or blue (v2). (B) Flowchart of target pull-down assays. (C) Results from pull-down of 100 nM target RNAs by 10 nM Ago2–miR122 (each). (D) Results from pull-down of 10 nM target RNAs by 100 nM Ago2–miR122 (each). (E) Results from pull-down of 100 nM target RNAs by 100 nM Ago2–miR122 (each). Enrichment of target-1 (compared to input) for each pull-down is indicated in panels C–E.

We first monitored target selection under conditions in which Ago2–miR122 was limiting in the binding reaction (Fig. 1C). Reactions containing 10 nM Ago2–miR122 complex and 100 nM ³²P-labeled target RNAs were allowed to come to equilibrium at room temperature prior to pull down via the Flag or Halo tags on Ago2. Complementarity in the supplementary region correlated with selective pull down of the target RNAs, with Ago2–miR122-v1 precipitates enriched for target-1 and Ago2–miR122-v2 precipitates enriched for target-2 (Fig. 1C, binding reactions 1 and 2). Including both Ago2–miR122 variants in the same reaction mixture did not influence targeting selectivity under these conditions (Fig. 1C, binding reaction 3). Switching the bridging region sequences of target-1 and target-2 did not diminish target-1 enrichment in Ago2–miR122-v1 pull downs (Supplemental Fig. S1). In contrast, pull downs by Ago2–miR122-v2, which looses supplementary interactions with long bridging region lengths (Sheu-Gruttadauria et al. 2019b), showed diminished enrichment of target-2 (Supplemental Fig. S1). We conclude that, under conditions of excess target RNA, supplementary interactions allow the Ago2–miRNA complex to distinguish targets with both seed and supplementary pairing (seed + sup) from targets capable of seed pairing only (seed-only).

We next examined target selection under conditions in which target RNA was limiting (Fig. 1D). Ago2–miR122 complexes (100 nM) were allowed to come to equilibrium with target RNAs (10 nM). When either version of the Ago2–miR122 complex was used alone in the binding reaction both target RNAs were equally present in Flag and Halo precipitates (Fig. 1D). Thus, under conditions of limiting target RNA selective targeting was not observed. The loss of selectivity is likely connected to the high concentrations of Ago-miR122 and target RNA used in the reaction mixture—both were well above the K_D of the seed-only paired target RNA (∼0.2 nM, Schirle et al. 2014). Thus, under these conditions it is expected that the Ago2–miR122 complex would bind nearly all available target RNA molecules. Notably, selectivity was restored when both Ago2–miR122-v1 and Ago2–miR122-v2 were included in a single reaction mixture (Fig. 1D, binding reaction 3). This observation indicates that one Ago2–miRNA complex can out compete another for target binding using supplementary interactions.

We finally tested target selection under conditions in which the concentrations of Ago2–miR122, target-1, and target-2 were all equal to each other (Fig. 1E). Reactions containing 100 nM Ago2–miR122 and 100 nM target RNAs were allowed to come to equilibrium at room temperature. Targeting selectivity was observed when either version of the Ago2–miR122 complex was used alone in the binding reaction, with Ago2–miR122-v1 precipitates enriched for target-1 and Ago2–miR122-v2 precipitates enriched for target-2 (Fig. 1E, binding reactions 1 and 2). Notably, Ago2–miR122-v2 showed weaker selectivity than Ago2–miR122-v1. This observation likely reflects the weaker supplementary sequence in miR122-v2 (1G/C + 3 A/U) than in miR122-v1 (4 G/C). Including both Ago2–miR122 variants in the same reaction further increased selectivity (Fig. 1E, binding reaction 3). These results show that, when there are similar amounts of Ago-miRNA complexes and target RNAs present, the Ago2–miRNA complex can effectively distinguish between two targets using supplementary interactions.

The Ago2–miRNA complex distributes between targets over time

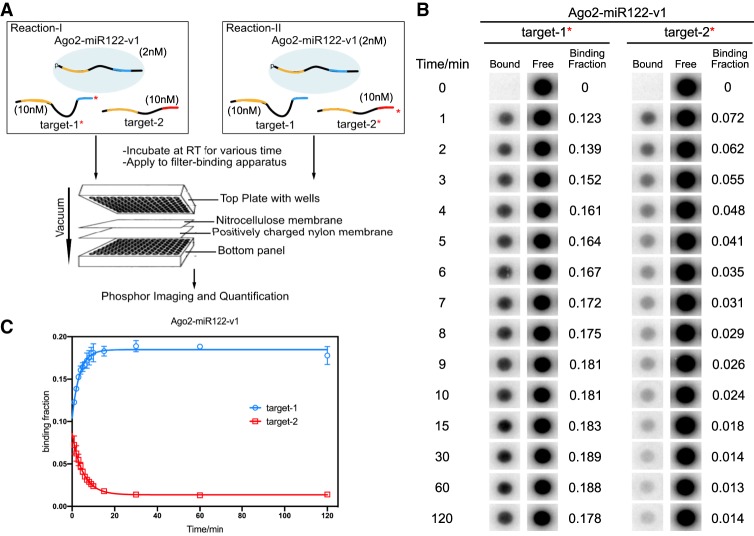
The experiments described above tested the effect of supplementary interactions on Ago2–miRNA distribution at equilibrium, but offered no insight into how target discrimination occurs over time. Because the pull-down step in the experiments described above is not amiable to making measurements over short incubation times, we devised a modified filter-binding assay to make target-binding measurements on a faster time scale (Fig. 2A; Supplemental Fig. S2A). In this experiment, the Ago2–miR122 complex (either v1 or v2) was incubated with both target-1 and target-2. For each incubation, two parallel reactions were set up, in which one reaction contained ³²P-radiolabeled target-1, and the other contained ³²P-radiolabeled target-2. At various time points, samples of each reaction were applied to a filter-binding apparatus that rapidly pulled the samples through a nitrocellulose membrane (which binds Ago2-associated RNAs), stacked on top of a positively charged nylon membrane (which binds free RNA). By analyzing the radioactivity on each membrane, the fraction of each ³²P-labeled target RNA associated with Ago2–miRNA at each time point was determined.

FIGURE 2.

Distribution of Ago2–miRNA-v1 between competing targets over time. (A) Flowchart schematic of the experimental setup. For each experiment two reactions were run in parallel (with either target-1 or target-2 ³²P-labeled). (B) Phosphorimages of ³²P-labeled target RNAs in bound (to Ago2–miR122-v1) or free fractions. Binding fractions are the means of three independent replicates. (C) Quantified binding data in panel B plotted as a function of incubation time. Data were fit into one-phase decay (Plateau of target-1 = 0.18; Plateau of target-2 = 0.014). All plotted data are the means of at least three independent replicates. Error bars indicate SD.

Our equilibrium experiments showed that targeting selectivity is most robust when Ago2–miRNA is limiting (Fig. 1C). Therefore, we monitored the distribution of Ago2–miR122-target complexes under this condition over time. Two nanomolars of Ago2–miR122 (v1 or v2) was incubated with 10 nM target RNAs (each) at room temperature. Samples of the binding reactions were applied to the filter-binding apparatus at various times over the course of 2 h. At the earliest time point (1 min), both Ago2–miR122 variants bound their respective seed + sup and seed-only targets at a ratio of roughly 2:1 (Fig. 2B; Supplemental Fig. S2B). Selectivity increased steadily over the following 10 min with increased binding of the seed + sup target and a corresponding decreased binding of the seed-only target (Fig. 2C; Supplemental Fig. S2C). Distribution changes became immeasurable after about 15 min, with Ago2–miR122-v1 binding its seed + sup and seed-only targets at a ratio of ∼13:1, and Ago2–miR122-v2 binding its seed + sup and seed only targets at a ratio of about ∼5:1.

The difference of the Ago2–miR122 distribution between two targets was larger for Ago2–miR122-v1 complex than Ago2–miR122-v2 complex (Fig. 2C; Supplemental Fig. S2C). This observation supports the notion that stronger supplementary interactions (4 G/C in miR122-v1 g13-g16 vs. 1 G/C + 3 A/U in miR122-v2 g13-g16) can enhance miRNA-targeting specificity. Moreover, this result indicates that Ago2–miR122 distribution among target RNAs follows the law of mass action and thus can be predicted by the relative strengths of interactions between Ago2–miRNA and the target RNAs.

Mathematical model for Ago2–miRNA time-course distribution of two competing targets

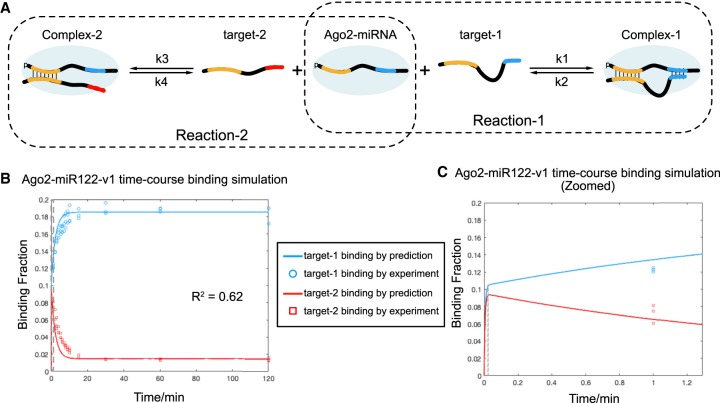
We noted that target selectivity by Ago2 was initially modest (approximately twofold at the earliest time point) and increased over time. This observation suggested to us that Ago2–miR122 initially bound both targets with a similar on-rate and then redistributed between seed-only and seed + sup targets over time. This idea is consistent with previous single-molecule data indicating Ago2 primarily searches for potential targets via seed pairing (Chandradoss et al. 2015; Salomon et al. 2015). To explore this possibility further and predict Ago2–miRNA distributions, we developed a mathematical model to describe how Ago2–miRNA behaves in this in vitro system (Fig. 3A). The model assumes two competing binding reactions, in which Ago2–miRNA can bind target-1 to form Complex-1, or target-2 to form Complex-2. Complex-1 and Complex-2 can also dissociate back into Ago2–miRNA and free target RNA. Thus, the change in concentration of Complex-1 and Complex-2 over time can be described by the following formulas:

$$\frac{d[C1]}{dt}=k1\ast ([Ago\mathrm{t}]-[C1]-[C2])\ast ([T1\mathrm{t}]-[C1])-k2\ast [C1](1)(\mathrm{reaction}-1)$$

and

$$\frac{d[C2]}{dt}=k3\ast ([Ago\mathrm{t}]-[C1]-[C2])\ast ([T2\mathrm{t}]-[C2])-k4\ast [C2],(2)(\mathrm{reaction}-2)$$

where [C1] = Complex-1 concentration, [C2] = Complex-2 concentration, [Agot] = total Ago2–miRNA concentration, [T1t] = total target-1 concentration, [T2t] = total target-2 concentration, k1 = k_on of reaction-1, k2 = k_off of reaction-1, k3 = k_on of reaction-2, k4 = k_off of reaction-2.

FIGURE 3.

Mathematical model for Ago2–miRNA time-course distribution of two competing targets. (A) Illustration of Ago2–miRNA binding two competing target RNAs. (B) Predicted fractions of target-1 (blue) and target-2 (red) bound by Ago2–miR122-v1 plotted as a function of time (solid lines). Experimental data from Figure 2 are included for comparison (open circles and squares). Dashed line indicates region shown in panel C. (C) Close up view of earliest time point in panel B. Solid lines indicate predicted fractions of target RNAs bound by Ago2–miR122-v1.

We next determined these constants experimentally. Dissociation constants (K_D) of target-1 and target-2 from Ago2–miR122-v1 were measured in equilibrium binding assays as 0.0056 ± 0.0005 nM and 0.085 ± 0.0022 nM, respectively (Supplemental Fig. S3A,C). Association rates (k_on) of target-1 and target-2 binding Ago2–miR122-v1 were measured by target association assays as 10.59 ± 0.72 nM⁻¹ min⁻¹ (k1) and 9.63 ± 0.90 nM⁻¹ min⁻¹ (k3), respectively (Supplemental Fig. S3B,D). These values are similar to those determined by single-molecule studies, which have reported k_on values ranging from 14 nm⁻¹ min⁻¹ to 0.7 nM⁻¹ min⁻¹ for seed-paired target RNAs (Chandradoss et al. 2015; Jo et al. 2015; Salomon et al. 2015; Schirle et al. 2015). The similar k_on between two targets is consistent with previous reports that target association rate is largely dependent on seed pairing (Chandradoss et al. 2015; Salomon et al. 2015). Therefore, dissociation rate (k_off) was calculated from the product of K_D and k_on as 0.059 min⁻¹ for target-1 (k2) and 0.81 min⁻¹ for target-2 (k2). Target affinities and binding rates were not substantially affected by increasing target length to extend 8 nt. beyond the supplementary-paired region (Supplemental Fig. S3).

The calculated change in the fraction of each target bound by Ago2–miR122-v1 (binding fraction: [C1]/T1 and [C2]/T2) over time was plotted by Matlab using the parameters described above. The prediction curves fit the experimental binding data with a R² value of 0.62 (Fig. 3B), suggesting that our mathematical model has predictive power for Ago2–miRNA complex distribution in vitro. Zooming in near the earliest time point shows binding of both targets increasing rapidly at the beginning of the reaction (<2 sec) until the bound fraction of each target reaches ∼0.1 (Fig. 3C). At this point, the free Ago2–miRNA complex is expected to be almost completely depleted. Target-1 then begins to sequester increasing amounts of Ago2–miR122-v1, at the expense of bound target-2, until the system reaches equilibrium at ∼15 min. Thus, both experimental data and theoretical modeling indicate that while seed pairing likely drives rapid target searching by Ago2, selectivity between two different seed-matched targets is dictated by the relative strength of supplementary interactions.

Prediction of Ago2–miRNA distribution between various amounts of competing targets

In the human transcriptome, miRNA target sites with supplementary interactions are thought to be relatively rare, making up <5% of predicted, functional seed-matched sites (Bartel 2009). We therefore wondered the extent to which supplementary interactions can drive targeting selectivity when seed-only targets vastly outnumber seed + sup targets, and how the ratio of seed-only to seed + sup target levels impacts the efficiency of selectivity. To explore this question we derived a mathematical model to calculate the distribution of Ago2–miRNA complexes at equilibrium in a two target competing system (Fig. 3A). Similarly to above, we used two equations to describe each reaction in the system:

$$\begin{array}{rl}& [C1e]=\\ & \frac{([T1\mathrm{t}]+[Ago\mathrm{t}]+Kd1-[C2e])-\sqrt{{([C2e]-[T1\mathrm{t}]-[Ago\mathrm{t}]-Kd1)}^2-4\ast ([Ago\mathrm{t}]-[C2e])\ast [T1\mathrm{t}]}}{2}\end{array}(3)(\mathrm{reaction}-1)$$

and,

$$\begin{array}{rl}& [\mathrm{C}2\mathrm{e}]=\\ & \frac{([T2\mathrm{t}]+[Ago\mathrm{t}]+\mathrm{Kd}2-[\mathrm{C}1\mathrm{e}])-\sqrt{{([\mathrm{C}1\mathrm{e}]-[T2\mathrm{t}]-[Ago\mathrm{t}]-\mathrm{Kd}2)}^2-4\ast ([Ago\mathrm{t}]-[\mathrm{C}1\mathrm{e}])\ast [T2\mathrm{t}]}}{2}\end{array},(4)(\mathrm{reaction}-2)$$

where [C1e] = the Ago2–miRNA-target-1 complex (Complex-1) concentration at equilibrium, [C2e] = the Ago2–miRNA-target-2 complex (Complex-2) concentration at equilibrium, [Agot] = total Ago2–miRNA concentration, [T1t] = total target-1 concentration, [T2t] = total target-2 concentration, Kd1 = k2/k1 (equilibrium dissociation constant of reaction-1), Kd2 = k4/k3 (equilibrium dissociation constant of reaction-2).

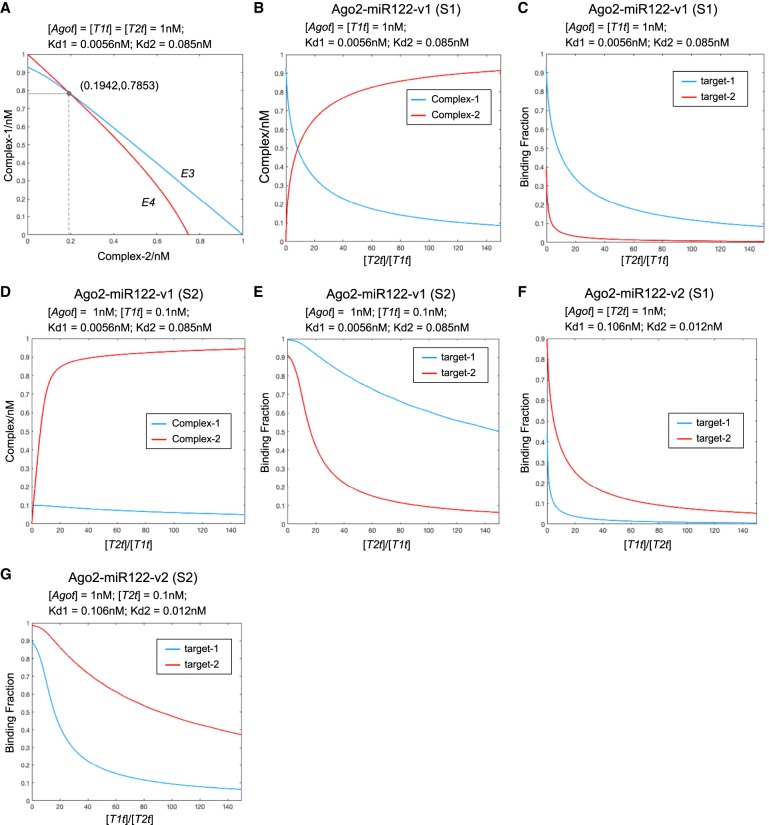
For any given [Agot], [T1t] and [T2t], E3 and E4 can be plotted as [C1e] versus [C2e]. The intersection point of these two curves is the solution that satisfies both equations (for example, see Fig. 4A). Thus, the coordinates of the intersection point provides the concentrations of Complex-1 and Complex-2 when the system is at equilibrium.

FIGURE 4.

Prediction of Ago2–miRNA complex distribution between various amounts of two competing targets. (A) Plot of E3 and E4 as [C1e] versus [C2e] when [Agot] = [T1t] = [T2t] = 1 nM, Kd1 = 0.0056 nM (binding affinity between Ago2–miR122-v1 and target-1), and Kd2 = 0.085 nM (binding affinity between Ago2–miR122-v1 and target-2). The intersection coordinate is (0.1942,0.7853), meaning that the calculated concentrations of Complex-1 and Complex-2 at equilibrium are 0.7853 and 0.1942 nM, respectively. (B) Predicted concentrations of Complex-1 (blue line) and Complex-2 (red line) plotted as a function of the target-2:target-1 ratio. In this simulation (S1) Ago2–miR122-v1 and target-1 were fixed at 1 nM, and target-2 was varied. (C) Fraction of total target-1 (blue) and target-2 (red) bound to Ago2–miR122-v1 plotted as a function of the target-2:target-1 ratio. In this simulation (S1) Ago2–miR122-v1 and target-1 concentrations were fixed at 1 nM, and target-2 concentration was varied. (D) Predicted concentrations of Complex-1 (blue line) and Complex-2 (red line) plotted as a function of the target-2:target-1 ratio. In this simulation (S2) Ago2–miR122-v1 and target-1 concentrations were fixed at 1 and 0.1 nM, respectively, and target-2 concentration was varied. (E) Fraction of total target-1 (blue) and target-2 (red) bound to Ago2–miR122-v1 plotted as a function of the target-2:target-1 ratio. In this simulation (S2) Ago2–miR122-v1 and target-1 concentrations were fixed at 1 and 0.1 nM, respectively, and target-2 concentration was varied. (F) Fraction of total target-1 (blue) and target-2 (red) bound to Ago2–miR122-v2 plotted as a function of the target-1:target-2 ratio. In this simulation (S1) Ago2–miR122-v2 and target-2 concentrations were fixed at 1nM, and target-1 concentration was varied. (G) Fraction of total target-1 (blue) and target-2 (red) bound to Ago2–miR122-v2 plotted as a function of the target-1:target-2 ratio. In this simulation (S2) Ago2–miR122-v2 and target-2 concentrations were fixed at 1 and 0.1 nM, respectively, and target-1 concentration was varied.

We first considered a situation (S1) in which seed + sup target (T1) and Ago2–miRNA (Ago) concentrations are equal to each other. We set [T1t] = [Agot] = 1 nM, and then calculated [C1e] and [C2e] at varying concentrations of the seed-only target (T2). Kd1 and Kd2 were set to 0.0056 and 0.085 nM, respectively, which correspond to the K_d values of Ago-miR122-v1 binding target-1 and target-2 (Supplemental Table S1). As expected, calculated [C1e] levels are high in the absence of T2 and decrease as [C2e] increases (Fig. 4B). [C1e] and [C2e] are equal at about 8 nM T2, and for all T2 values beyond this point the majority of Ago exists in Complex-2 (i.e., most of the Ago is bound to the seed-only target). Thus, at sufficiently high levels the seed-only target RNA is expected to effectively compete with the seed + sup target for binding Ago2.

Notably, for T2 (seed-only target) to effectively compete with T1 (seed + sup target), [T2t] had to be raised above the value of [Agot] used in the calculation. Thus, the vast majority (∼94%) of T2 molecules would not be bound by Ago2 in this condition. We expect that overall repression of the seed-only target would be very weak in this situation because repression of a target molecule requires Ago-binding. Therefore, prediction of target repression requires examining the fraction of the total amount of an RNA target that is in complex with Ago2 ([C1e]/[T1t] and [C2e]/[T2t]). Plotting [C1e]/[T1t] and [C2e]/[T2t] as a function of [T2t]/[T1t] (the ratio of seed-only to seed + sup target levels) reveals that, as expected, both values decrease as T2 increases (Fig. 4C). However, [C1e]/[T1t] is always greater than [C2e]/[T2t]. Indeed, the fold difference between [C1e]/[T1t] and [C2e]/[T2t] only increases as T2 increases, such that even when T2 is 50-times greater than T1 ([T2t]/[T1t] = 50), [C1e]/[T1t] maintains a value ∼0.2 while [C2e]/[T2t] is diminished to ∼0.016, (Fig.4C; Supplemental Fig. S4A). Thus, in situation S1 (Ago2 and seed + sup target at equivalent levels), seed + sup targets are expected to always be substantially more repressed than seed-only targets.

We next considered a situation (S2) in which the seed + sup target concentration is 10-fold less than Ago-miR122-v1. We set [T1t] = 0.1*[Agot] = 0.1 nM and calculated [C1e] and at varying concentrations of the seed-only target (T2). In this case, only ∼0.11 nM T2 is required to reach equivalent levels of Complex-1 and Complex-2 (Fig. 4D). Again, both [C1e]/[T1t] and [C2e]/[T2t] decrease with increasing T2, but the decrease of [C1e]/[T1t] is much slower than in situation 1 (where [T1t] = [Agot] ). In this case [C1e]/[T1t] remains above 0.6, while [C2e]/[T2t] is only 0.09 when T2 is 100-fold greater than T1 (Fig. 4E; Supplemental Fig. S4B). This indicates that the repression of seed + sup targets expressed at low levels is expected to be even more resistant to inhibition by the high levels of seed-only targets.

Repeating these calculations using K_d values of Ago2–miR122-v2 (Supplemental Table S1) led to similar disproportionate predicted repression of the seed + sup target (Fig. 4F,G; Supplemental Fig. S4C,D). Thus, we predict that, regardless of seed-only target levels, seed + sup targets will always be better recognized and more strongly repressed than equivalent seed-only target RNAs.

Experimental support for targeting discrimination mathematical model

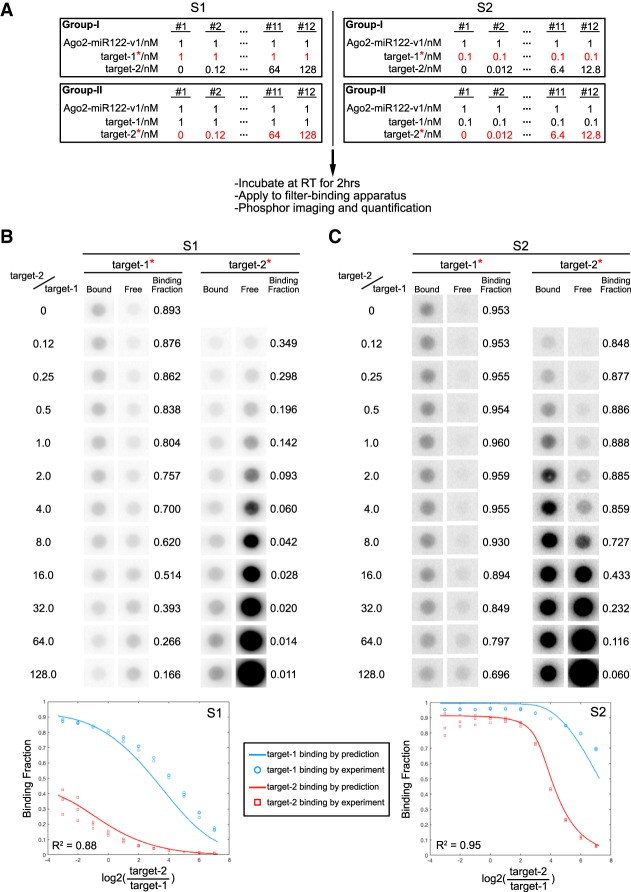
To test how well our mathematical model of Ago2–miRNA targeting predicts Ago2 behavior in vitro, we further modified our filter-binding assay to measure the binding of Ago2–miRNA to two different targets at different concentrations. In this experiment, fixed concentrations of seed + sup target (target-1) and Ago2–miRNA-v1 were incubated with various concentrations of seed-only target (target-2). As before, for each condition two reactions were set up in parallel with either target-1 or target-2 ³²P-labeled. Upon reaching equilibrium (2 h) the reactions were applied to a filter-binding apparatus, and the fraction of each target bound by Ago2–miR-122-v1 was determined by phosphor-imaging (Fig. 5A).

FIGURE 5.

Biochemical validation of predicted target discrimination by Ago2–miR122-v1. (A) Experimental parameters and flowchart. Two situations (S1 and S2) were examined in which target-1 concentration was either 1 nM (S1) or 0.1 nM (S2). Ago2–miR122-v1 concentration was fixed at 1 nM. The concentration of target-2 was varied between 0–128 nM. For each situation two reactions were run in parallel with either target-1 or target-2 ³²P-labeled. (B) Bound and free target RNAs in S1. (Top) Phosphorimages of bound and free ³²P-labeled target-1 or target-2 in S1. Note that binding fraction of target-1 (seed + sup target) is always higher than target-2 (seed-only). (Bottom) Theoretically predicted and experimentally measured data are plotted in the same graph for comparison. (C) Bound and free target RNAs in S2. (Top) Phosphorimages of bound and free ³²P-labeled target-1 or target-2 in S2. Note that the binding fraction of target-1 (seed + sup target) is relatively uninfluenced by increasing concentrations of target-2 (seed-only). (Bottom) Theoretically predicted and experimentally measured data are plotted in the same graph for comparison. X-axis in graphs in B and C is plotted as log₂(target − 2/target − 1) rather than target − 2/target − 1 in Figure 4E for even distribution of experimental data across the graph.

Binding experiments were set up to emulate the mathematical simulations described above. In the first experiment, we examined the binding of 1 nM Ago2–miR122-v1 to 1 nM target-1 and varying concentrations of target-2 (ranging from 0 to 128 nM) (Fig. 5B). Plotting the experimental data on the same graph as data calculated from the model shows a strong agreement. As predicted by the model, even though target-2 was able to compete with target-1 for Ago2–miR122-v1, the binding fraction of target-1 was always higher than the binding fraction of target-2. This effect was even stronger in the second experiment, where we measured binding of 1 nM Ago2–miR122-v1 to 0.1 nM target-1 at varying concentrations of target-2 (Fig. 5C). We also repeated these measurements using Ago2–miR122-v2, for which target-1 matches the seed-only and target-2 has seed + sup complementarity. Again, the experimental data were well aligned with those of the predicted model (Supplemental Fig. S5). Moreover, as predicted by our model, the seed-sup target of Ago2–miR122-v2 was less resistant to high levels of seed-only target than Ago2–miR122-v1. This observation further supports the notion that stronger supplementary interactions (4 G/C in miR122-v1 g13-g16 vs. 1 G/C + 3 A/U in miR122-v2 g13-g16) enhance miRNA-targeting specificity. The combined results experimentally demonstrate that, regardless of seed-only target levels, Ago2 always specifically and preferentially recognize seed + sup targets. When assuming that Ago2 targeting directly correlates with repression, this observation could lead to the prediction that seed + sup targets will be more repressed than seed-only targets.

DISCUSSION

Our results show that, in a simple in vitro system, supplementary interactions can drive robust differential targeting by the Ago2–miRNA complex. Thus, when provided with supplementary interactions, the Ago2–miRNA complex is fully capable of distinguishing between equivalently seed-matched target RNAs. Mathematical modeling indicates that even when vastly outnumbered by seed-only matched targets, the seed + sup targets will always be more highly occupied, and thereby could potentially be more strongly repressed. These observations may explain why, in some cases, supplementary interactions appear to have been necessary to observe target repression in vivo (Brennecke et al. 2005; Wahlquist et al. 2014).

Examination of 170 human miRNA families with multiple members reveals that more than half have at least one member with an alternate supplementary sequence (Supplemental Fig. S6). This observation raises the possibility of differential targeting within a large fraction of miRNA families. However, our data show that the degree of differential targeting potential of any given miRNA depends on the relative strengths of its seed and supplementary sequences. For example, let-7a has an exceptionally strong seed sequence (K_d of 20 ∼ 40 pM for seed-only targets) and supplementary interactions increase target affinity less than twofold above seed-pairing alone (Wee et al. 2012; Salomon et al. 2015; Becker et al. 2019; Sheu-Gruttadauria et al. 2019b). On the other hand, miR-21 has a weak seed (K_d of 20 ∼ 155 nM) and supplementary interactions can increase target affinity >10-fold (Salomon et al. 2015; Ziv et al. 2018; Becker et al. 2019). This may explain why lsy-6, which has an exceptionally weak seed sequence (Garcia et al. 2011), only silenced a target with strong supplementary complementary in vivo (Didiano and Hobert 2006). We have also found that extensive 3′ pairing can exceed the capacity of the supplementary chamber in Ago2, leading to an extremely stable Ago2–miRNA-target complex that could potentially be subject to exceptionally strong differential targeting (Sheu-Gruttadauria et al. 2019a). Finally, we recently found that supplementary interactions expand with increasing miRNA 3′ tail length (Sheu-Gruttadauria et al. 2019b). This observation suggests that longer 3′ isomiRs may have more differential targeting potential.

Notably, the level of differential targeting we can achieve in vitro is substantially greater than the typical modest effect supplementary interactions are reported to have on target repression in living cells (Grimson et al., 2007). The reason for this discrepancy is not yet known. One possibility we considered is that differential targeting is lost when miRNA levels exceed target levels (Fig. 1D), which can be the case for miRNA transfection experiments where the cells may be flooded with high concentrations of miRNA. However, comparison of endogenous miRNA and target site levels in a variety of human cells types suggests this is not often likely the case (Supplemental Fig. S7). A second possibility we considered is that repression steps following target recognition may be faster than dissociation of miRISC from the seed-paired target RNAs such that miRISC does not have the time necessary to distribute between targets based on the additional affinity offered by supplementary pairing (Figs. 2, 3). However, the findings that targets with 6mer and 8mer sites have similar kon rates (Chandradoss et al. 2015; Salomon et al. 2015) yet exhibit differential repression levels (Bartel 2009) argues against this. A final possibility is that by examining targets in aggregate, Grimson et al. (2007) may have diluted a small number of targets containing strong supplementary contributions with a larger number targets that are predicted to make supplementary interactions, but do so only weakly. This would suggest that factors in cellular environment, such as RNA-binding proteins or structure within target RNAs, disproportionately disfavor supplementary over seed pairing such that supplementary interactions reach their full repressive potential in only a limited number of specialized targets.

MATERIALS AND METHODS

Oligonucleotides

miR-122 variants

• miR122-v1: 5′-Phosphate-rUrGrGrArGrUrGrUrGrArCrArGr CrGrGrCrGrArArArG-3′

• miR122-v2: 5′-Phosphate-rUrGrGrArGrUrGrUrGrArCrArCr UrArUrCrGrArArArG-3′

miR-122 purification oligonucleotides

• Capture oligo: 5′-Biotin-mUmCmUmCmGmUmCmUmAm AmCmCmAmUmGmCmCmAmAmCmAmC mUmCm CmAmAmCmUmCmU-3′

• Competitor DNA: 5′-Biotin-GCAGAGATCAAGTGTTCGC ATGGTTAGCAGAGA-3′

miR-122 target RNAs

• target-1: 5′-rCrCrGrCrArArArArArArArArArArArCrArCrUrC rCrUrArA-3′

• target-2: 5′-rArUrArGrArArArArArCrArCrUrCrCrUrArA-3′

• target-1-A₈: 5′-rArArArArArArArArCrCrGrCrArArArArArAr ArArArArArCrArCrUrCrCrUrArA-3′

• target-2-A₈: 5′-rArArArArArArArArArUrArGrArArArArArCr ArCrUrCrCrUrArA-3′

Ago2 constructs

Coding sequence for an amino-terminal Flag tag was introduced into pFastbac HT A (Invitrogen) between the His₆ tag and TEV cleavage site through quick-change PCR to produce a vector named pFastbac-HFT. The HaloTag coding sequence was amplified from pENTR4-HaloTag (w876-1) (Addgene), and cloned into pFastbac-HFT after TEV cleavage site using NEBuilder HiFi DNA Assembly Master Mix kit (Cat. #E2621) to produce the vector pFastbac-HFT-Halo. Full-length human Ago2 was cloned into pFastBac-HFT and pFastbac-HFT-Halo for expression using the Bac-2-Bac (Invitrogen) baculovirus expression system.

Ago2–miRNA complex preparation

Human Ago2 loaded with miR-122 variants was purified as described previously (Schirle et al. 2014). Briefly, His₆-Flag-Tev-tagged and His₆-Flag-Tev-Halo-tagged Ago2 proteins were expressed in Sf9 cells using a baculovirus system (Invitrogen). 60-h cultured 750 mL 1.7 × 10⁶ cells/mL Sf9 cells were harvested by centrifugation and suspended in ∼30 mL Lysis Buffer (50 mM NaH₂PO₄, pH 8, 300 mM NaCl, 5% glycerol, 0.5 mM TCEP). Resuspended cells were lysed by passing twice pass through a M-110P lab homogenizer (Microfluidics). The resulting total cell lysate was clarified by centrifugation (30,000g for 25 min) and the soluble fraction was applied to 1.5 mL packed Ni-NTA resin (Qiagen) and incubated at 4°C for 1.5 h in 50 mL conical tubes. Resin was pelleted by brief centrifugation and the supernatant solution was discarded. The resin was washed with ∼50 mL ice cold Nickel Wash Buffer (300 mM NaCl, 15 mM imidazole, 0.5 mM TCEP, 50 mM Tris, pH 8). Centrifugation/wash steps were repeated a total of three times. Copurifying cellular RNAs were degraded by incubating with 100 U micrococcal nuclease (Clontech) on-resin in ∼15 mL of Nickel Wash Buffer supplemented with 5 mM CaCl₂ at room temperature for 45 min. The nuclease-treated resin was washed three times again with Nickel Wash Buffer and then eluted in four column volumes of Nickel Elution Buffer (300 mM NaCl, 300 mM imidazole, 0.5 mM TCEP, 50 mM Tris, pH 8). Eluted Ago2 was incubated with a synthetic miR-122 variant during an overnight dialysis against 1–2 liters of Dialysis Buffer (300 mM NaCl, 0.5 mM TCEP, 50 mM Tris, pH 8) at 4°C. For HaloTag-Ago2 preparations, 150 µg TEV protease was added prior to dialysis. The Ago2 molecules loaded with miR-122 were isolated using an immobilized capture oligo nucleotide with complementarity to the miR-122 seed region, via the Arpon method (Flores-Jasso et al. 2013). Loaded Ago2 protein was dialyzed into Tris pH 8 Crystal Buffer (10mM Tris pH 8, 100 mM NaCl, 0.5 mM TCEP), concentrated to ∼2 mg/mL, aliquoted and flash frozen and stored at −80°C. Samples were thawed slowly on ice for all experiments.

Pull-down assays

Corresponding amounts of HFT-Ago2–miR122-v1, HaloTag-Ago2–miR122-v2, target1 and target2 were incubated in reaction buffer (30 mM Tris, pH 8, 100 mM KOAc, 2 mM MgOAc, 0.5 mM TCEP) with 0.01 mg/mL tRNA at room temperature for 30 min. A small aliquot of the reaction was quenched by 2× FLB as Input sample, the rest of the reaction was incubated with either 5 µL ANTI-Flag M2 Affinity Gel (Cat. #A2220) or HaloLink Resin (Cat. #G1912) at room temperature for 30 min. After incubation, the resin was pelleted by brief centrifugation, and a small aliquot of the supernatant liquid was quenched by 2× FLB as Unbound sample. The resin was washed once with 500 µL prechilled reaction buffer, and quenched by 2× FLB. The samples were analyzed by denaturing (8 M urea) 15% PAGE.

Equilibrium target binding assays

Equilibrium dissociation constants were determined as described previously (Schirle et al., 2014). Briefly, various concentrations of the Ago2–miR-122 complex were incubated with 0.005 nM ³²P 5′-radiolabeled target RNA in binding reaction buffer (30 mM Tris pH 8, 100 mM KOAc, 2 mM MgOAc, 0.5 mM TCEP, 0.005% [v/v] NP-40, 0.01 mg/mL baker's yeast tRNA), in a reaction volume of 100 µL at room temperature for 45 min. Using a dot-blot apparatus (GE Healthcare Life Sciences), protein–RNA complexes were captured on Protran nitrocellulose membrane (0.45 µm pore size, Whatman, GE Healthcare Life Sciences) and unbound RNA on Hybond Nylon membrane (GE Healthcare Life Sciences). Samples were applied with vacuum and immediately washed once with 100 µL of ice-cold wash buffer (30 mM Tris pH 8.0, 0.1 M potassium acetate, 2 mM magnesium acetate, 0.5 mM TCEP). Membranes were air-dried and ³²P signal was visualized by phosphor-imaging. ImageQuant (GE Healthcare Life Sciences) was used to quantify data and dissociation constants calculated using Prism version 6.0g (GraphPad Software, Inc.), using the following formula, which accounts for potential ligand depletion (Wee et al. 2012):

$$\mathrm{F}={\mathrm{B}}_{\max }\frac{([\mathrm{ET}]+[\mathrm{ST}]+\mathrm{Kd})-\sqrt{{\left([\mathrm{ET}]+[\mathrm{ST}]+\mathrm{Kd}\right)}^2-4[\mathrm{ET}][\mathrm{ST}]}}{2[\mathrm{ST}]},$$

where F = fraction of target bound, B_max = calculated maximum number of binding sites, [E_T] = total enzyme concentration, [S_T] = total target concentration, and K_d = apparent equilibrium dissociation constant.

Target association assay

Five picomolars of ³²P 5′-radiolabeled target RNA was prepared in binding reaction buffer (30 mM tris pH 8.0, 100 mM potassium acetate, 2 mM magnesium acetate, 0.5 mM TCEP, 0.005% [v/v] NP-40, 0.01 mg/mL baker's yeast tRNA) in a final volume of 700 µL. The time point 0 aliquot (50 µL) was removed, and bound and free RNA were separated using a dot-blot apparatus. Ago2–miR122 samples were mixed with 5 pM 5′ ³²P-radiolabeled target RNA in binding reaction buffer to a final conc 50 pM. Further samples were immediately removed at various time points and separated as before. ³²P-labeled target RNA was visualized and quantified by phosphorimaging, as described above. The fraction of the ³²P-labeled target bound to Ago2 was plotted as a function of time, normalized to timepoint 0, and fit to one-phase association equation using Prism version 6.0g (GraphPad Software, Inc.):

$$\mathrm{Y}=\mathrm{Y}0+(\mathrm{Plateau}-\mathrm{Y}0)\ast (1-\exp (-K\ast x\left)\right),$$

where Y0 is the Y value when X (time) is zero, Plateau is the Y value at infinite times, K = [Ago2–miRNA]_t × k_on + k_on × K_d, [Ago2–miRNA]_t is concentration of total Ago2–miR122 added in reaction. k_on is association rate, k_d is dissociation constant.

Competition target binding assays

Ago2–miR complex was incubated with a combination of unlabeled target1 and ³²P 5′-radiolabeled target2 or ³²P 5′-radiolabeled target1 and unlabeled target2 in binding reaction buffer (30 mM Tris pH 8, 100 mM KOAc, 2 mM MgOAc, 0.5 mM TCEP, 0.005% [v/v] NP-40, 0.01 mg/mL baker's yeast tRNA) at room temperature. For time-course experiments, 100 µL reaction of the reaction was applied to dot-blot apparatus (as described above) at different time points. For equilibrium sequester assays, the reactions were incubated at room temperature for 2 h and then applied to dot-blot apparatus like described above.

Mathematical model derivations

Two competing targets time-course model:

For a very short period of time dt:

The change of complex-1 concentration = (generation from free Ago2–miRNA binding to free target-1) − (dissociation of complex-1):

$$\frac{d[C1]}{dt}=k1\ast [Ago\mathrm{f}]\ast [T1\mathrm{f}]-k2\ast [C1].$$

Because free Ago2–miRNA concentration is difficult to know, it is substituted total Ago2–miRNA concentration. Total Ago2–miRNA includes both free Ago2–miRNA and Ago2–miRNA within complex1 and complex2:

$$[Ago\mathrm{f}]=[Ago\mathrm{t}]-[C1]-[C2].$$

Similarly, total target-1 includes both free target-1 and target-1 within complex1:

$$[T1\mathrm{f}]=[T1\mathrm{t}]-[C1].$$

Substitute 1.2 and 1.3 into 1.1:

$$\frac{d[C1]}{dt}=k1\ast ([Ago\mathrm{t}]-[C1]-[C2])\ast ([T1\mathrm{t}]-[C1])-k2\ast [C1].$$

Similarly, the change of complex-2 concentration can be written as:

$$\frac{d[C2]}{dt}=k3\ast ([Ago\mathrm{t}]-[C1]-[C2])\ast ([T2\mathrm{t}]-[C2])-k4\ast [C2].$$

These two equations were solved by Matlab ode45 function with [C1]_{t = 0} = 0, [C2]_{t = 0} = 0. Matlab code can be downloaded from https://github.com/Kikou33/Robust-differential-microRNA-targeting-driven-by-supplementary-interactions.git.

Two competing targets at equilibrium model

When the system reaches to equilibrium, the concentrations of every component should be remain unchanged over time.

Thus, for complex-1: d[C1]/dt = 0. Substitute into 1:

$$k1\ast \left([Ago\mathrm{t}]-[C1]-[C2]\right)\ast \left([T1\mathrm{t}]-[C1]\right)-k2\ast [C1]=0.$$

Organize 3.1 as a function of [C1]:

$$\begin{array}{rl}[C1{]}^2& +\left([C2]-[Ago\mathrm{t}]-[T1\mathrm{t}]-\frac{k2}{k1}\right)\ast [C1]+[Ago\mathrm{t}]\ast [T1\mathrm{t}]\\ & -[T1\mathrm{t}]\ast [C2]=0.\end{array}$$

3.2 is a quadratic function of [C1], leading to two roots of [C1]:

$$\begin{array}{rl}& [C1]=\\ & \frac{\left([T1\mathrm{t}]+[Ago\mathrm{t}]+{\displaystyle \frac{k2}{k1}-[C2]}\right)+\sqrt{{\left([C2]-[T1\mathrm{t}]-[Ago\mathrm{t}]-{\displaystyle \frac{k2}{k1}}\right)}^2-4\ast \left([Ago\mathrm{t}]-[C2]\right)\ast [T1\mathrm{t}]}}{2}.\end{array}$$

$$\begin{array}{rl}& [C1]=\\ & \frac{\left([T1\mathrm{t}]+[Ago\mathrm{t}]+{\displaystyle \frac{k2}{k1}-[C2]}\right)-\sqrt{{\left([C2]-[T1\mathrm{t}]-[Ago\mathrm{t}]-{\displaystyle \frac{k2}{k1}}\right)}^2-4\ast \left([Ago\mathrm{t}]-[C2]\right)\ast [T1\mathrm{t}]}}{2}\end{array}.$$

When $[C2]=0,\mathrm{we}\mathrm{have}0\le [C1]\le min\left([Ago\mathrm{t}],[T1\mathrm{t}]\right)$, we can narrow down the solution to 3.4.

Also because k2/k1 = Kd1 (dissociation constant between target-1 and Ago2–miRNA-v1), we can express 3.4 as:

$$\begin{array}{rl}& [C1]=\\ & \frac{\left([T1\mathrm{t}]+[Ago\mathrm{t}]+Kd1-[C2]\right)-\sqrt{{\left([C2]-[T1\mathrm{t}]-[Ago\mathrm{t}]-Kd1\right)}^2-4\ast \left([Ago\mathrm{t}]-[C2]\right)\ast [T1\mathrm{t}])}}{2}.\end{array}$$

Similarly, for complex-2 at equilibrium: d[C2]/dt = 0. Through the approach described above we derive:

$$\begin{array}{rl}& [C2]\\ & =\frac{\left([T2\mathrm{t}]+[Ago\mathrm{t}]+Kd2-[C1]\right)-\sqrt{{\left([C1]-[T2\mathrm{t}]-[Ago\mathrm{t}]-Kd2\right)}^2-4\ast \left([Ago\mathrm{t}]-[C1]\right)\ast [T2\mathrm{t}]}}{2}\end{array}.$$

When the system reaches equilibrium, both 3 and 4 should be satisfied. For any given [Agot], [T1t] and [T2t], there are only two unknown variables ([C1] and [C2]) in 3 and 4. Thus, 3 and 4 can be plotted as [C1]versus[C2] on a single graph (Fig. 4A), in which the intersection point is the solution that satisfies both equations. The coordinates at the intersection point are the concentrations of complex-1 and complex-2 at equilibrium. This process was done by a Matlab program, Matlab code can be downloaded from https://github.com/Kikou33/Robust-differential-microRNA-targeting-driven-by-supplementary-interactions.git.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.