Transcriptome-Based Prediction of Complex Traits in Maize

Transcript level-based genomic prediction models can be used to predict trait values in maize with performance comparable to genetic marker-based models.

Abstract

The ability to predict traits from genome-wide sequence information (i.e., genomic prediction) has improved our understanding of the genetic basis of complex traits and transformed breeding practices. Transcriptome data may also be useful for genomic prediction. However, it remains unclear how well transcript levels can predict traits, particularly when traits are scored at different development stages. Using maize (Zea mays) genetic markers and transcript levels from seedlings to predict mature plant traits, we found that transcript and genetic marker models have similar performance. When the transcripts and genetic markers with the greatest weights (i.e., the most important) in those models were used in one joint model, performance increased. Furthermore, genetic markers important for predictions were not close to or identified as regulatory variants for important transcripts. These findings demonstrate that transcript levels are useful for predicting traits and that their predictive power is not simply due to genetic variation in the transcribed genomic regions. Finally, genetic marker models identified only 1 of 14 benchmark flowering-time genes, while transcript models identified 5. These data highlight that, in addition to being useful for genomic prediction, transcriptome data can provide a link between traits and variation that cannot be readily captured at the sequence level.

INTRODUCTION

The prediction of complex traits from genetic data is a grand challenge in biology, and the outcome of such prediction has become increasingly useful for plant and animal breeding (Heffner et al., 2009; Jonas and de Koning, 2013). Among the different approaches for connecting genotypes to phenotypes, genomic prediction (or genomic selection) using all available markers was developed to overcome the limitations of marker-assisted selection, which uses only significant quantitative trait loci (QTLs), for breeding traits that are controlled by many small-effect alleles (Meuwissen et al., 2001; Ribaut and Ragot, 2007). Using genomic prediction, breeders are able to make data-driven decisions about what lines to include in their programs, speeding up and reducing the cost of developing the next generation of crops (Endelman et al., 2014; Spindel et al., 2015). Furthermore, because genomic prediction models associate genetic signatures with phenotypes, untangling genomic prediction models has the potential to improve our understanding of the genetic basis of complex traits. However, as with related approaches such as genome-wide association studies and QTL mapping, it remains difficult to go from associated genetic markers to the molecular basis for a trait (Drinkwater and Gould, 2012; Solberg Woods, 2014).

A number of factors contribute to this difficulty. The variation in markers associated with phenotypes may not be the causal variants but are linked to the genes that control the trait in question. Considering that linkage disequilibrium distance can range from 1 kb in diverse maize (Zea mays) populations (Tenaillon et al., 2001) to ∼250 kb in Arabidopsis (Arabidopsis thaliana; Nordborg et al., 2002), the linked candidate genes can range from a few to a few hundreds. Even if the associated genetic variant controls the underlying phenotype, most variants associated with complex traits have small effect sizes. Furthermore, associated variants may be located in a distal regulatory region (Albert and Kruglyak, 2015); thus, these variants may not be closely linked to the genes they regulate. Furthermore, multiple regulatory variants that have indiscernible effects on their own could interact epistatically to influence gene and ultimately trait expression. However, even with sufficient statistical power to detect genetic variants with small effect sizes and interactions between them, genetic information is connected to traits through multiple intermediate processes, including, for example, transcription, translation, epigenetic modification, and metabolism. Each of these intermediate processes represents an additional level of complexity that obscures the association between genetic information and a trait.

One solution is to account for these intermediate processes by integrating relevant omics data in addition to genetic variation. This approach has led to promising, but often mixed, results in plants. Current efforts have focused primarily on predicting hybrid performance using transcriptional information from the parental lines. For example, transcript level-based distance measures generated from transcripts associated with the trait were better than genetic markers in predicting hybrid performance in maize (Frisch et al., 2010; Fu et al., 2012). However, when all transcripts were used (instead of a subset of preselected transcripts), model performance decreased (Zenke-Philippi et al., 2016). The performance of models based on transcript levels can be better or worse compared with those based on genetic markers depending on the trait. For example, transcriptome data performed better for predicting grain yield in hybrid maize populations, but genetic marker data performed better for predicting grain dry matter content in the same population (Schrag et al., 2018). Similarly, in a maize diversity panel, genomic prediction models that combined transcript and marker data only outperformed models using markers alone for certain traits (Guo et al., 2016). Finally, efforts to integrate additional omics information to predict various traits in Drosophila melanogaster (Li et al., 2019) and human diseases, such as breast cancer (González-Reymúndez et al., 2017), and responses to treatment interventions, including acute kidney rejection and response to infliximab in ulcerative colitis (Kang et al., 2017; Zarringhalam et al., 2018), have demonstrated the potential usefulness of transcriptome data in the field of precision medicine.

Overall, these efforts provide reasonable evidence that transcriptome data could be useful for trait prediction. However, genomic prediction-based approaches trained on the entire transcriptome data have not been used to better understand the genetic mechanisms for a trait. In addition, it is not known the degree to which transcriptomes obtained at a particular developmental stage can be informative for predicting phenotypes scored at a different stage. To address these questions, we used transcriptome data derived from maize whole seedlings (Hirsch et al., 2014) to predict phenotypes (flowering time, height, and grain yield) at much later developmental stages. In addition to comparing prediction performance between genetic marker- and transcriptome-based models, we also looked at whether transcripts and genetic markers that were important for the prediction models were located in the same or adjacent regions. Finally, we determined how well our models were able to identify a benchmark set of flowering-time genes to explore the potential of using genomic prediction to better understand the mechanistic basis of complex traits.

RESULTS AND DISCUSSION

Relationships between Transcript Levels, Kinship, and Phenotypes among Maize Lines

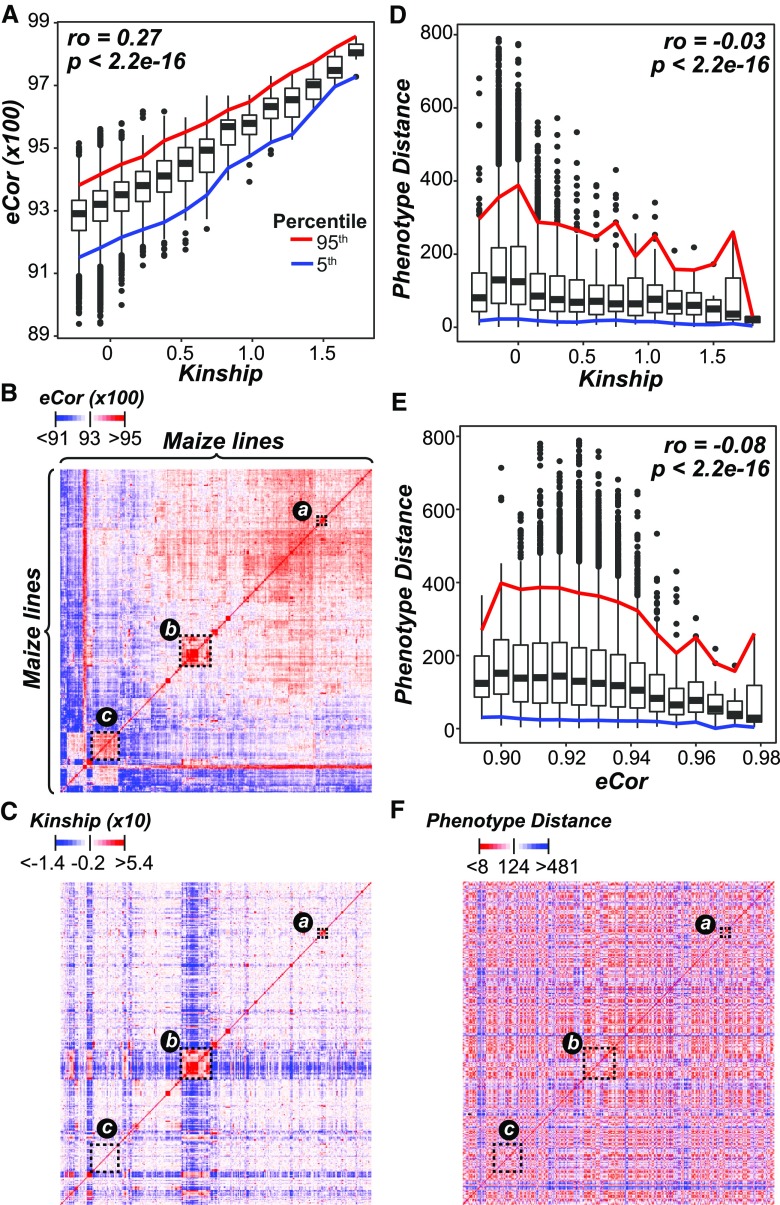
Before using the transcriptome data for genomic prediction, we first assessed properties of the transcriptome data in three areas: (1) the quantity and distribution of transcript information across the genome, (2) the amount of variation in transcript levels, and (3) the similarity in the transcriptome profile between maize lines, with an emphasis on how these properties compared with those based on the genotype data. After filtering out 16,898 transcripts that did not map to the B73 reference genome or had zero or nearly zero variance across lines (see Methods), we had 31,238 transcripts. While the number of transcripts was <10% of the number of genetic markers used in this study (332,178), the distribution of transcripts along the genome was similar to the genetic marker distribution (Supplemental Figure 1). The log₂-transformed median transcript level across lines ranged from 0 to 12.4 (median = 2.2) and the variance ranged from 3 × 10⁻³⁰ to 14.5 (median = 0.13), highlighting that a subset of transcripts had relatively high variation in transcript levels across maize lines at the seedling stage. To determine how similar transcript levels were between lines, we calculated the expression correlation (eCor) between all pairs of lines using Pearson’s correlation coefficient (PCC). The eCor values ranged from 0.84 to 0.99 (mean = 0.93). As expected, lines with similar transcriptome profiles were also genetically similar, as there was a significant correlation between eCor values and values in the kinship matrix generated from the genetic marker data (Spearman’s rank ρ = 0.27, P < 2.2 × 10⁻¹⁶; Figure 1A). As a result, we were able to find clusters of lines that had both high transcript and genetic similarities (e.g., clusters a and b; Figures 1B and 1C). However, most of the variation in eCor was not explained by kinship, which explained why we identified other clusters that had similar transcriptome profiles but were not genetically similar (e.g., cluster c; Figures 1B and 1C).

Figure 1.

Relationships between Lines from Transcript and Genetic Marker Data.

(A) Relationship between kinship based on genetic marker data (x axis) and eCor (in PCC) based on transcript data (y axis). Boxplots show the median y axis value for each x axis bin (bin size = 0.15), with the 5th (blue) and 95th (red) percentile ranges shown. The correlation between kinship and eCor was calculated using Spearman’s rank coefficient (ρ).

(B) and (C) The relationships between lines based on eCor (B) or kinship (C) for all pairs of maize lines. Lines are sorted based on hierarchical clustering results using the eCor values. The blue, white, and red color scales indicate negative, no, and positive correlations, respectively. Dotted rectangles indicate clusters of lines discussed in the text.

(D) and (E) The relationships between the Euclidean distance calculated with phenotype values (phenotype distance; y axis) and kinship (D) and eCor (E). Colored lines follow those in (A).

(F) The relationships between lines based on phenotype distance, where the lines were sorted as in (B). Red indicates smaller distance (more similar) and blue indicates greater distances (less similar).

Because the basis of genomic prediction is to predict a phenotype from genetic data, we next asked if kinship or eCor was anticorrelated with the phenotypic distances between lines (see Methods). While both kinship (ρ = −0.03, P < 2.2 × 10⁻¹⁶; Figure 1D) and eCor (ρ = −0.08, P < 2.2 × 10⁻¹⁶; Figure 1E) were significantly negatively correlated with the phenotype distance, the degree of correlation was minor. Furthermore, the groups of lines that clustered together based on their eCor (e.g., clusters a and b; Figures 1B and 1C) did not have lower phenotypic distance (Figure 1F). Taken together, these findings suggest that transcriptome data may be similarly informative as genotype data but capture different aspects of phenotypic variation. We tested both of these interpretations further in subsequent sections.

Predicting Complex Traits from Transcript or Genetic Marker Data

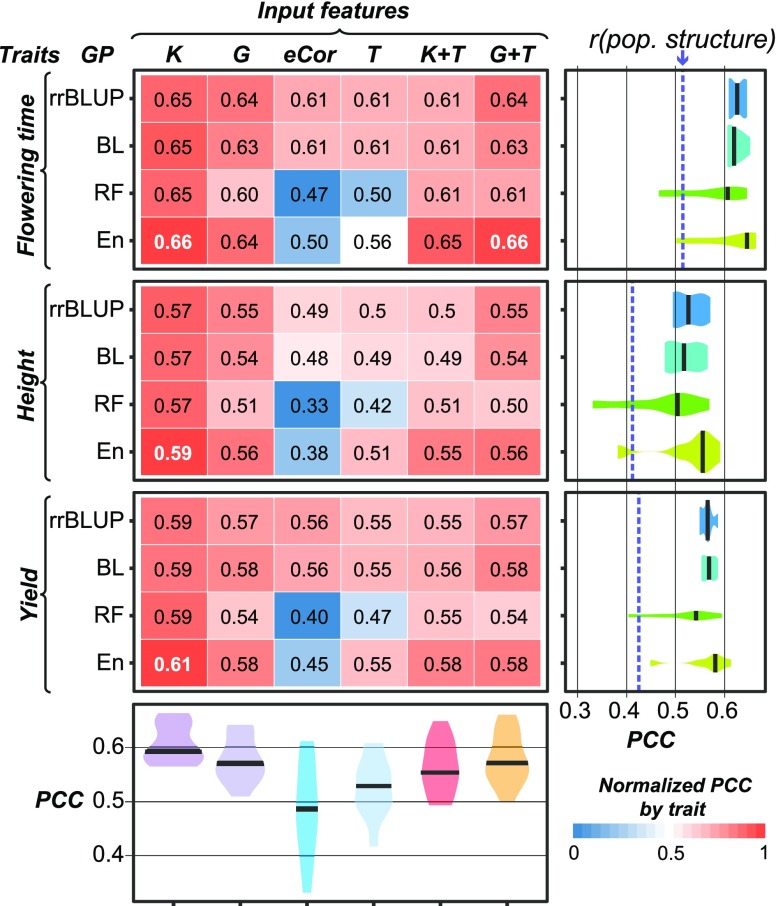
To test how useful transcriptome data were for genomic prediction compared with genetic marker data, we applied four approaches to predict three agronomically important traits in maize: flowering time, height, and grain yield. Because no one genomic prediction algorithm always performs best (Heslot et al., 2012; Spindel et al., 2015), we tested two linear algorithms (ridge regression Best Linear Unbiased Predictor [rrBLUP] and Bayesian-Least Absolute Shrinkage and Selection Operator [BL]), one nonlinear algorithm (Random Forest [RF]), and one Ensemble approach (En; see Methods). To establish a baseline for our genomic prediction models, we determined the amount of the phenotypic signal that could be predicted using population structure alone, defined as the first five principal components from the genetic marker data. Then we built models for each trait using genetic marker data (G), kinship (K) derived from G, transcript levels (T), or eCor derived from T (Figure 2). Model performance was measured using PCC between the actual and the predicted phenotypic values.

Figure 2.

Genomic Prediction Model Performance.

PCCs between predicted and true values for three traits and four algorithms using six different input features are shown. The text in each box represents the absolute PCC, with the best performing model for each trait in white. The box color represents the PCC normalized by trait, where the brightest red (1) corresponds to the algorithm/input feature combination that performed the best for the trait and the brightest blue (0) corresponds to the combination that performed the worst. Violin plots at right show the PCC distributions among different input features for each algorithm. The median PCCs are indicated with black bars. The model performance PCCs based on only population structure (first 75 principal components) are indicated with blue dashed lines. Violin plots at bottom show the PCC distributions among different algorithms for each input feature.

Across algorithms and traits, the K data resulted in models with the best predictive performance, while models built using the eCor data performed the worst (Figure 2; Supplemental Table 1). Furthermore, models built using G always outperformed models using T. Regardless, eCor- and T-based models were significantly better than the baseline predictions (dotted blue lines, Figure 2), indicating that transcriptome data can be informative in genomic prediction. Considering that the transcriptome data are from seedlings, it is particularly surprising that mature plant phenotypes can be predicted. Next, we asked if using only the most informative (i.e., the largest absolute coefficients) transcripts or genetic markers as input into our models would improve trait predictions (see Methods). We also tested differently sized subsets of transcripts with the greatest degrees of line-specific expression to test if they could better predict traits. However, using rrBLUP to predict flowering time as an example, none of these subsets performed better than the full T data (Supplemental Table 2). We also tested setting the most variable transcripts as fixed effects in our rrBLUP models, but this also did not improve performance (Supplemental Table 2). Finally, consistent with earlier findings (Shen and Chou, 2006; Jia et al., 2015), combining the predictions from multiple algorithms, known as an En approach, resulted in the best predictive models (Figure 2) and is therefore used to illustrate most of our findings in the following sections.

Predicting Complex Traits Using Both Transcript and Genetic Marker Data

Because the genetic marker and transcriptome data represented different types of molecular information that could be associated with the traits of interest, we hypothesized that their combination would be more informative and next built models that used combined data, either K+T or G+T. However, adding the transcript data did not substantially improve performance over K or G alone (Figure 2). One possible reason for this lack of improvement could be overfitting. This is most common when there is only a small amount of training data (i.e., few maize lines) but a very large number of predictor variables (i.e., many genetic markers/transcripts). To test this hypothesis, we trained rrBLUP models (referred to as G₂₀₀+T₂₀₀) to predict flowering time using only the 200 genetic markers and the 200 transcripts with the largest absolute coefficients from the G and T rrBLUP models, respectively (see Methods). These genetic markers and transcripts are referred to as “features.” To avoid overfitting during feature selection (Bermingham et al., 2015), we first separated the data set into training and testing sets. The top features were selected using the training data only. The testing data were never used to select the top features. Using the independent testing data to evaluate performance, our ability to predict flowering time improved using G₂₀₀+T₂₀₀ (PCC = 0.68 ± 0.06) compared with the full G+T model (PCC = 0.64 ± 0.01) and with the individual G and T models (PCC = 0.64 ± 0.01 and 0.61 ± 0.01, respectively). One explanation for this improvement could be that using only the top features of each data type reduced noise from the model. If this is the case, the G₂₀₀ and T₂₀₀ models would be expected to outperform the G and T models, respectively. However, we see the opposite results (see previous section; Supplemental Table 2), suggesting that this improvement was due to a reduction in overfitting.

To assess if G or T data features tend to be more informative in predicting traits, we further quantified the importance score of each genetic marker and transcript feature for models using G+T data. The importance score represents the influence that each feature had on model performance defined according to the algorithm used (see Methods). Because the G and T data features may contain overlapping information and, thus, are not independent, the importance scores from the G+T model may be effects by issues caused by collinearity. However, given that the importance scores assigned to transcripts in the G+T models were correlated with the scores from the T-only models (Supplemental Figure 2A), the addition of the genetic marker features into the model did not affect the relative importance of transcript features. The only exception was a subset of Ts that were important for the G+T but not the T-only BL models. Because RF importance measures tend to be biased toward continuous features (Strobl et al., 2007), we focused on rrBLUP and BL importance scores. For all three traits, the top 1000 most important features were enriched for genetic markers relative to transcript features (odds ratio = 0.17∼0.44, all P < 1 × 10⁻¹⁶; Supplemental Figure 2B; Supplemental Table 3). However, the top 20 most important features tended to be enriched for transcript relative to genetic marker features (odds ratio = 2.66∼13.0, P = 0.087∼<1 × 10⁻¹⁶; Supplemental Table 3), with transcript features making up the top two most important feature in all cases (Supplemental Figure 2B). The consistency with which transcript features were the most important for the models suggests that transcript information is useful for genomic prediction.

Comparison of the Importance of Transcripts Versus Genetic Markers for Model Predictions

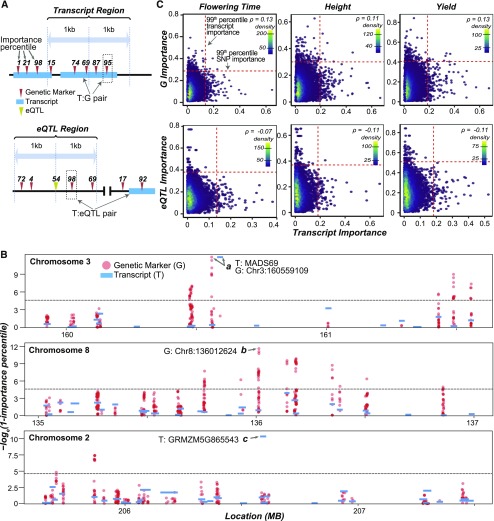
Because models built using transcript features outperformed baseline models based solely on population structure, we know that transcriptome data contained information useful for explaining phenotypic variation. Furthermore, using feature selection to combine both data sets into one predictive model (G₂₀₀+T₂₀₀) improved our ability to predict flowering time (Supplemental Table 2). Therefore, we hypothesized that these two data types capture different aspects of phenotypic variation. To address this, we assessed the extent to which the important genetic markers (from G-based models) overlapped with or neighbored the genes where the important transcripts (from T-based models) originated from (Figure 3A, top). We did not use the importance values from the G+T model due to concern regarding feature dependence. The genic region and flanking sequences within a defined window of an important transcript is referred to as the transcript region (see Methods). For each trait and algorithm, we compared the importance assigned to the transcript with that of the genetic marker with the highest average importance in the transcript region (T:G pair).

Figure 3.

Correlation between Genetic Marker and Transcript Importance for Flowering Time.

(A) Illustration of how T:G (top graph) and T:eQTL (bottom graph) pairs were determined. Genetic marker importance percentiles are shown above the genetic markers (red triangles) and eQTL (yellow triangle). A T:G pair was defined as the transcript and the most important genetic marker within the transcript region (top graph). A T:eQTL pair was defined as the transcript and the most important genetic marker within the eQTL region (bottom graph).

(B) Manhattan plots of the transcript (blue bar) and genetic marker (red dot) importance scores [−log_e(1−importance percentile)] in a 2-Mb window surrounding top two genetic markers (top and middle plots) and transcripts (top and bottom plots) based on the T-based and G-based En models for predicting flowering time, respectively. All genetic markers (i.e., not just the T:G pair) are shown. The threshold (gray dotted lines) is set at the 99th percentile importance.

(C) Density scatterplot of the importance scores (see Methods) of the genetic marker (y axis) and transcript (x axis) for T:G pairs (top graphs) and of the eQTL genetic marker (y axis) and transcript (x axis) for the T:eQTL pairs (bottom graphs) for three traits derived from the G-based and T-based En models, respectively. The threshold (red dotted line) was set at the 99th percentile importance score for each trait and input feature type. The correlation between importance scores between transcript and genetic marker/eQTL pairs was calculated using Spearman’s rank (ρ). SNP, single nucleotide polymorphism.

Multiple window sizes were explored (see Methods), and we used 2 kb (±1 kb from the center of a gene) where the feature importance correlation between transcripts and genetic markers was maximized (Supplemental Figure 3A). Using this window size, 15,049 T:G pairs were identified. At the whole-genome level, there appeared to be regions where both genetic markers and transcripts were identified as important (Supplemental Figure 4). However, when we look closer, those regions mostly do not overlap. In some cases, the important genetic markers and transcripts were in linkage disequilibrium. Using the flowering-time model as an example, we found that the most important genetic marker was within a gene upstream of the most important transcript (GRMZM2G171650: MADS69; Figure 3B, arrow a), but the two are in linkage disequilibrium (Hirsch et al., 2014). In most cases, there were no important genetic markers that were located nearby to important transcripts, and if we extend the window size to 80 kb, we see that MADS69 is the exception rather than the rule (Supplemental Figure 3B). For example, the second most important flowering-time genetic marker was not located near important transcript regions (Figure 3B, arrow b). Similarly, the second most important flowering-time transcript (GRMZM5G865543) was over 0.6 Mb from an important genetic marker (Figure 3B, arrow c). Across all traits and algorithms, T:G pairs were only moderately correlated (ρ = 0.09–0.13; Figure 3C; Supplemental Figure 5A).

This lack of correlation is notable for the most important genetic markers and transcripts. For example, across the three traits, only four to seven T:G pairs were in the top 1% most important features from the En models, and those pairs were never the top ranked genetic markers or transcripts from the model (Figure 3B). These findings argue against the notion that these two data types capture similar aspects of phenotypic variation, as we hypothesized earlier. One concern was that the lack of correlation was due to the genetic marker data being derived from RNA-seq experiments and thus limited to the transcribed regions. However, when the experiment was repeated using ∼1 million genome-wide genetic markers (G_GW) derived from whole-genome sequencing (Bukowski et al., 2018) as input features (Supplemental Figure 6A), the correlation between T:G_GW pairs did not increase (Supplemental Figures 6B and 6C).

In light of this, we hypothesized that the lack of correlation was because important transcripts tend to be regulated by important trans-factors located far beyond the transcript region. To test this, we assessed the degree to which important genetic markers identified as expression QTL (eQTLs) were associated with important transcripts. We identified 62 cis- and 58,299 trans- eQTLs, a total of 58,361 eQTLs, associated with 7052 transcripts and defined T:eQTL pairs for each of these transcripts by selecting the genetic marker within ±1 kb of an eQTL for that transcript (i.e., eQTL region) with the highest average importance. Across all traits and algorithms, the importance of transcripts and eQTLs in T:eQTL pairs was actually negatively correlated (ρ = -0.15 ∼ -0.06; Figure 3C; Supplemental Figure 5B).

The lack of correlation between importance scores for T:G and T:eQTL pairs was in contrast to the relatively high correlation observed in feature importance between algorithms (ρ = 0.31–0.98), with rrBLUP and BL importance scores being the most correlated (ρ = 0.87–0.98) and the average correlation between genetic markers (ρ = 0.75) being higher than for transcripts (ρ = 0.55; correlation between algorithms; Supplemental Figure 7). Together with the findings that important genetic markers were not colocated and eQTLs were not associated with genes that gave rise to the important transcripts for any of the three traits, these findings may suggest that transcriptome data are capturing layers of information, such as epigenetic signals, that are not captured by genome sequences. However, we cannot rule of the possibility that the eQTL approach using RNA-seq-based genetic markers is not sufficiently sensitive in identifying important trans-factors. Further study with more trait and high-quality genome-wide genetic marker data is needed to resolve these possibilities.

Assessment of Benchmark Flowering-Time Genes

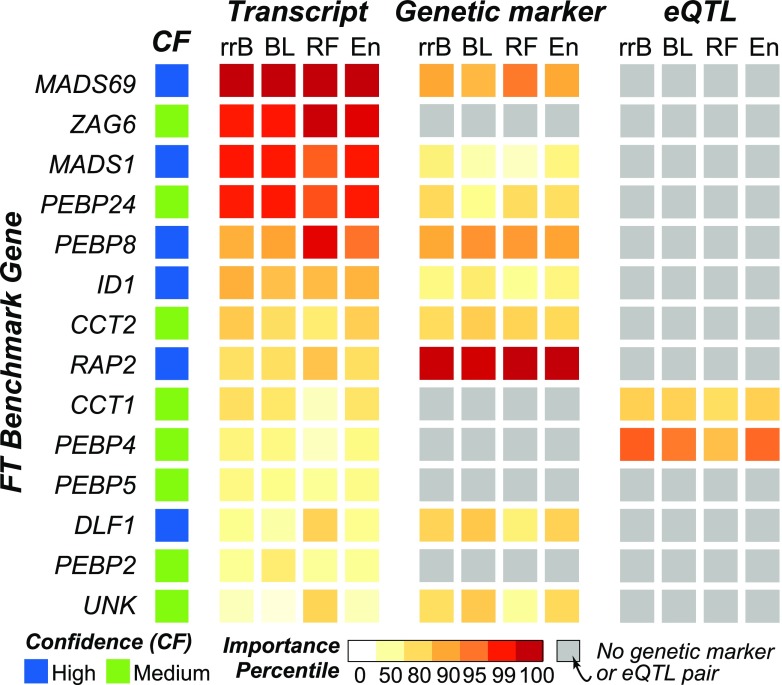
Because the genetic basis for flowering time is well studied (Muszynski et al., 2006; Danilevskaya et al., 2010; Lazakis et al., 2011; Meng et al., 2011), we identified a set of 14 known flowering-time genes (Supplemental Table 4). To assess the extent to which these benchmark genes can predict flowering time, we trained an rrBLUP model where we set these 14 genes as fixed, rather than random, effects, and our model performance increased (PCC = 0.64 ± 0.01; Supplemental Table 2) compared with when they were not fixed (PCC = 0.61). Then we compared the ability of genetic marker- and transcript-based models to identify these benchmark genes as important using the T:G and T:eQTL pairs described earlier. Of the 14 benchmark genes, 4 had corresponding genetic markers in our T:G pair data. When we increased the flanking region threshold to 20 kb from the center of the transcript for defining T:G pairs, corresponding genetic markers were found for five additional benchmark genes. Two benchmark genes, CCT1 and PEBP4, neither of which was a member of a T:G pair, were associated with eQTLs. To account for differences in distribution and range of importance scores generated by different algorithms and numbers of features, the importance scores were converted to percentiles for comparison purposes.

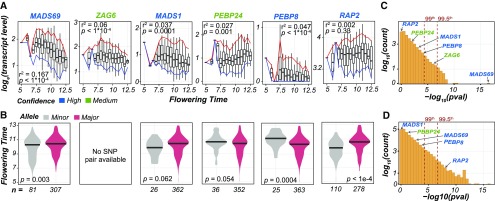
Different benchmark genes were important (>95th percentile) for models using the two different data types, with one and five benchmark genes considered important by the genetic marker-based and the transcript-based models, respectively (Figure 4; Supplemental Data Set 1). For example, the genetic marker located within the RAP2 gene, which has been shown to be associated with flowering time in multiple studies (Buckler et al., 2009; Hirsch et al., 2014), was identified as important based on genetic marker (99.7th to 99.9th percentile) but not transcript (59th to 79th percentile) data. By contrast, MADS69, MADS1, PEBP24, and PEBP8 were identified as important using transcript data (95th to 100th percentile) but not using genetic marker data (16th to 93th percentile). Furthermore, with transcript data, we were able to assess the importance of three genes (ZAG6, PEBP5, and PEBP2) that were not located near genetic markers or associated with eQTLs. For example, there were no eQTLs associated with genetic markers within the 40-bp window of ZAG6, but ZAG6 was identified as important (98th to 99.9th percentile) in the transcript-based models (Figure 4). For some of these benchmark genes, the region most closely linked to trait variation could be outside the ±20-kb window. For example, as described above, the important genetic marker for MADS69 (Chr3: 160559109) is ∼32 kb upstream (Figure 3B, a arrows). However, when we plotted the correlation between importance scores between T:G pairs using the largest window size (80 kb), we found that MADS69 was the only gene for which this was the case (Supplemental Figure 3B). Taken together, these finding further highlight the usefulness of transcript data for identifying the genetic basis for variation in a trait.

Figure 4.

Comparison of Transcript and Genetic Marker Importance Scores for Benchmark Flowering-Time Genes.

Importance percentile of each transcript and genetic marker pair as determined by each of the four algorithms (x axis) is shown. Genes are sorted based on hierarchical clustering of their importance percentiles. Gray boxes designate benchmark genes that did not have genetic markers within a 40-kb window. Confidence levels (high or medium) were assigned based on the type of evidence available for the benchmark gene (see Methods). rrB, rrBLUP.

Improving Our Understanding of the Genetic Basis of Flowering Time Using Transcriptome Data

An open question was why transcript-based models were able to identify as important five benchmark flowering-time genes that were not identified by genetic marker-based models and if transcriptome data could be used to better understand the genetic basis of flowering time. To understand why benchmark genes were not uniformly identified as important for flowering time when using both genetic marker and transcript data, we determined the extent to which transcript levels and the genetic marker allele (i.e., major or minor) were related to flowering time. As expected, we observed the most significant differences in flowering time for the transcripts (Figure 5A; Supplemental Figure 8A) and genetic markers (Figure 5B; Supplemental Figure 8B) that were identified as important by our models. For example, MADS1 was important only in the transcript-based models and transcript level was significantly correlated with flowering time (P = 0.0001; Figure 5A). By contrast, lines with the major allele for the genetic marker that paired with the MADS1 transcript (Chr9: 156980141) did not flower at a significantly different time than lines with the minor allele (P = 0.062; Figure 5B). Another example was RAP2, which was important only in the genetic marker-based models. Lines with the major allele in RAP2 were more likely to flower late (P < 1 × 10⁻⁴), but RAP2 transcript levels did not significantly correlate with changes in flowering time (P = 0.33). Overall, benchmark genes were more likely to have transcript levels associated with flowering time (Figure 5C) than genetic marker alleles associated with flowering time (Figure 5D).

Figure 5.

Relationship between Transcript Level/Allele Type and Flowering Time for Benchmark Genes.

(A) Boxplots show the transcript levels [log_e(fold change)] over the flowering-time bin with the 5th (blue) and 95th (red) percentile ranges shown. Flowering time was defined as the growing degree days/100. Linear models were fit, and adjusted R² and P values are shown. Confidence levels of benchmark genes are designated as in Figure 4.

(B) Distributions of flowering time for lines with the major (red) or minor (gray) alleles for the genetic marker paired with each benchmark gene as indicated in (A). Differences in flowering time by allele were tested using t tests.

(C) Number of transcripts (y axis) for which transcript levels were associated with flowering time in linear models within P value bins [−log₁₀(P value); x axis]. Benchmark genes are labeled as in (A).

(D) Number of genetic markers (y axis) for which differences in flowering time by allele from t tests were within P value bins [−log₁₀(P value); x axis]. Benchmark genes are labeled as in (A).

Importantly, using the transcriptome data, we were also able to understand in more detail the influence of the benchmark genes on flowering time. For example, variation in transcript levels of MADS69 accounted for 16.7% of the variation in flowering time, more than any other transcript, where lines with lower levels of transcription flowered later. Modulation of MADS69 expression levels has recently been patented as an approach to controlling flowering time (Kaeppler et al., 2014). Similarly, MADS1 transcript levels explained 3.7% of the variation in flowering time, with lines with lower levels of transcription flowering later. This is consistent with what has been observed experimentally, where downregulation of MADS1 results in delayed flowering time (Alter et al., 2016). For medium-confidence benchmark genes (i.e., identified through association studies), the specific roles of the genes in flowering time are not well understood, but by finding positive or negative correlations between transcript levels and the underlying phenotypes, more mechanistic details can be inferred. For example, transcript levels of ZAG6 had the second largest influence on flowering time, accounting for 6% of variation, with increased transcript levels associated with earlier flowering. Another example is PEBP24, with transcript levels of PEBP24 accounting for 2.7% of the variation in flowering time. Unlike many of the other benchmark genes, increased PEBP24 transcript levels were associated with later flowering time. Overall, the identification of these medium-confidence benchmark genes as important transcripts indicates the relevance of transcriptional regulation in their flowering-time functions.

While using the benchmark genes allowed us to assess the usefulness of transcript levels compared with genetic marker information for identifying genes involved in flowering time, we should note that many nonbenchmark genes were also identified by our models as important. For example, from the En model, there were 154 important, nonbenchmark transcripts with importance scores falling between the two most important benchmark genes (MADS69, 100th percentile and ZAG6, 99.5th percentile; yellow, Supplemental Data Set 2). While seven of those in between transcripts were annotated with the Gene Ontology (GO) term “flower development” (GO:0009908; green, Supplemental Data Set 2), these 154 nonbenchmark transcripts were not enriched for this GO term (q = 1.0). In fact, neither these transcripts nor any other set of important transcripts from models based on other algorithms (see Methods) were enriched for any GO terms. Therefore, from our transcript-based genomic prediction models, we have identified 147 high-ranking transcripts, many of which have unknown functions, that are among the most important in predicting flowering time in maize but do not play known roles in this process. For example, GRMZM5G865543 and GRMZM2G023520 (the second and third most important transcripts, respectively, from the En model) do not have annotated functions in maize. While they do have homologs in Arabidopsis and rice (Oryza sativa), those homologs do not have known functions in flowering time (see Supplemental Table 5 for similar information about the top 10 transcripts). Note that the transcriptome data are from the seedling stage. It is possible that genes of these important transcripts influence biological processes in earlier stages of development that influence flowering time later. To further our understanding of the genetic basis of flowering-time control and the connections between juvenile and adult phenotypes, these important transcripts are prime candidates for future genetic studies.

CONCLUSIONS

We have generated predictive models that use genetic markers, transcripts, and their combination to predict flowering time, height, and yield in a diverse maize population. While models built using transcriptome data did not outperform models that used genotype data, transcript-based models performed well above random expectation, and in many cases, performance was similar to that of genotype-based models. We found that transcripts and genetic markers from different genomic regions were identified as important for model predictions. Furthermore, by assessing the relative importance of the features used to build the models, we found that transcript-based models identified more known flowering time-associated genes than genetic marker-based models. These findings underscore the usefulness of transcript data for improving our understanding of the genetic mechanisms responsible for complex traits.

There are four possible mechanistic explanations for why transcript levels could have a similar predictive power to genetic markers. First, cis-regulatory variants that affect transcript levels are all more likely to be similar between closely related individuals. Therefore, the ability of transcript data to predict phenotypes is simply a reflection of that dependency. However, we demonstrated that the most informative transcript features for predicting maize phenotypes are distinct from the most informative genetic marker features found in the transcript regions. While for some important transcripts the associated important genetic marker could be in linkage disequilibrium but outside of the 2-kb window used in our study (e.g., ∼32 kb away in the case of MADS69), overall, as we increased the transcript region window size, the correlation between the importance scores assigned to T:G pairs decreased, suggesting that this is not generally the case. Thus, the second explanation is that there are trans-regulatory variants (e.g., due to transposon polymorphisms or transcriptional regulators) that play a major role. However, we found that the importance of eQTLs (99.9% trans) and their associated transcripts were not positively correlated, suggesting that the trans-regulatory variation we identified cannot explain why transcript variation is predictive of phenotypic variation either. However, considering the challenges in identifying eQTLs due to the mixed tissues used (Wills et al., 2013), in modeling epistatic interactions (Becker et al., 2012), and in our limited ability to find cis-eQTLs, we cannot conclusively rule out this possibility. The third explanation is that transcription is a molecular phenotype caused by the integration of multiple genetic marker signals, both cis and trans, that may not have had strong signals individually. The fourth explanation is that there are epigenetic variants contributing to expression variation. It remains to be determined what the contribution of epigenetic variation is on our ability to use transcript data to predict phenotypes.

One surprise is that the transcript data generated using V1 seedling tissues can predict adult plant phenotypes. We reason that complex traits, such as flowering time, are influenced by more than just canonical genes that act immediately prior to the growth and developmental sequences leading to flowering. For example, early developmental events such as cotyledon damage (Hanley and May, 2006), root restriction (Keever et al., 2015), and photoperiod and temperature changes (Song et al., 2013) can influence flowering time in mature plants. Therefore, early development transcript differences could eventually result in different flowering times. There were three limitations of this study that made our ability to predict adult plant phenotypes and identify known important transcripts even more surprising. First, transcript-level data were derived from whole V1 seedling tissue, which should limit the predictive power of our genomic prediction models for mature plant traits. We expect that transcript information taken from tissues and time points more relevant to the phenotype of interest are more likely to be predictive. For example, coexpression networks derived from maize root tissues are more predictive of the accumulation of 17 different elements (e.g., Al, Fe, K, and Zn) in maize seeds than coexpression networks derived from tissues not involved in element uptake and transport (Schaefer et al., 2018). Second, transcript levels were calculated by mapping reads to the B73 reference genome without considering that structural and fragmental variations exist between diverse maize lines. Having only a B73 reference genome to map to likely results in bias or noise in our transcriptome data set. In future studies, it will be informative to determine if correcting for such structural and fragmental variation would improve genomic prediction. Finally, a third limitation of our study is that no environmental component is considered. An area of active research in genomic prediction is the incorporation of genotype-by-environment interactions into predictive models (Burgueño et al., 2012; Cuevas et al., 2017; Granato et al., 2018). Thus, a potential benefit of using transcript information for genomic prediction could be that genotype-by-environment interactions would be picked up by transcript-level signals. Because the transcriptome and phenotype data used in our study were derived from different individual plants at different developmental stages, this could not be tested.

Our findings highlight an important benefit of using transcript data to better understand the genetic basis of a trait. While it can be difficult to associate signals from a number of small-effect genetic markers or even a single large-effect genetic marker back to a specific gene, transcript-level information is inherently associated with genes. Because of the importance of regulatory variation on complex traits (Albert and Kruglyak, 2015), the use of transcript information in genomic prediction could be crucial for deciphering the contribution of regulatory variation to the genetic basis of traits. Therefore, while we observed that in terms of predictive ability, genetic marker data outperformed transcript data, expression differences are more straightforward to interpret than sequence polymorphisms. In practice, this meant that transcript-based models identified five benchmark flowering-time genes while genetic marker-based models only identified one, and it highlighted our finding that more insight into the genetic basis of complex traits can be gained when transcriptome data are considered.

METHODS

Genotypic, Transcriptomic, and Phenotypic Data Processing

The phenotypic (Hansey et al., 2011) and genotypic and transcriptomic (Hirsch et al., 2014) data used in this study were generated from the pan-genome population consisting of diverse inbred maize (Zea mays) lines. Genotype, transcriptome, flowering time, height, and yield data were all available for 388 lines out of the 503 maize pan-genome panel and were used for the study (Supplemental Data Set 3). Genetic marker scores derived from RNA-seq reads were converted to a [−1,0,1] format corresponding to [aa,Aa,AA] with the more common allele (AA) designated as 1. The genetic marker positions were converted from maize B73 reference genome A Golden Path v2 (AGPv2) to AGPv4.37. The AGPv2 genetic markers that did not map to AGPv4.37 and genetic markers with a minor allele frequency less than 5% were removed, resulting in 332,178 genetic markers. To determine if the use of RNA-seq-derived genetic markers biased our results, we also tested a set of genome-wide markers (G_GW). These markers were downloaded already processed and uplifted to AGPv4 from Bukowski et al. (2018). Data were available for 149 maize lines included in the study. After removing G_GW with minor allele frequency less than 5% and duplicate patterns of allele calls across the 149 lines (i.e., the same criteria used for the G data set), ∼1.08 million markers were available for this analysis.

RNA-seq-derived transcriptomic data from whole-seedling tissue (i.e., root and shoot) at the V1 stage from Hirsch et al. (2014) were processed to remove loci that did not map to AGPv4.37. The remaining maize B73 genes were filtered with default settings of the nearZeroVar function from the R caret package to remove genes with zero or nearly zero variance (>95% of the lines sharing the same transcript level) across lines. After the filtering steps, transcript counts for 31,238 genes were retained in the final data set. The raw transcripts per million count data were transformed with a log_e + 1 transformation before the data were used in subsequent analyses. Mapping rates to the B73 genome assembly were also downloaded from Hirsch et al. (2014). To assess if transcriptome data had predictive power beyond random expectation, transcriptome data were permuted by gene, so that each gene had the same distribution of transcript values, but the values were randomly assigned to different maize lines for building the transcriptome-shuffled models. To compare important transcripts and genetic markers from genomic prediction models, transcripts were converted from AGPv2 to AGPv4, and only genes with one-to-one correspondence between AGPv3 and AGPv4 were included in this analysis. To assess the effect uplifting had on expression levels, we remapped transcript data from B73 to AGPv4 using Bowtie2 (version 2.3.2) and performed read counting using Cufflinks (version 2.2.1). The correlation between uplifted and remapped gene expression levels for B73 was 0.94 (PCC, P < 2 × 10⁻¹⁶).

Comparison of Transcript and Genetic Marker Data

Three different approaches were used to determine the similarity between lines based on the three different data types. For the genotype data, a kinship matrix was generated using the centered Identity By State method (Endelman and Jannink, 2012) implemented in TASSEL v5.20180517 (Bradbury et al., 2007). The PCC between RNA-seq mapping rates and kinship with B73 was calculated using the cor.test function in R. For the transcript data, we generated an eCor matrix by calculating the PCCs of transcript values between lines using the cor.test function in R. The eCor matrix was normalized between 0 and 1, and the diagonal was set as 1. Finally, for phenotype data, we calculated the Euclidean distance between lines using the distances package in the R environment. The correlation between kinship, eCor, and phenotype distance between pairs of lines was calculated using PCC.

Genomic Prediction Models and Model Performance

Because part of the phenotypic signal observed in genomic prediction models may be due to population structure/family relatedness within the breeding population, we established a baseline for our genomic prediction models by using the principal components (PCs) generated using the marker data alone to predict phenotypic values for each trait. Because the relationship between the population structure and traits can vary by trait and by population, we tested the top 5, 10, 15, 20, 50, 75, and 100 PCs and selected the top 75 PCs to use as our baseline because accuracy plateaued after this point. Four methods were used for each trait, two linear-parametric methods, rrBLUP (Endelman, 2011) and BL (Pérez and de los Campos, 2014), one nonlinear and nonparametric method, RF (Breiman, 2001), and one En approach (Dietterich, 2000). The rrBLUP models used the mixed.solve function in the rrBLUP package implemented in R. The BL models were also implemented in R using the BGLR package. RF was implemented in Python using Scikit-Learn (Pedregosa et al., 2011). En predictions were generated by taking the mean of the predicted trait values from rrBLUP, BL, and RF. A grid search was performed on the first 10 of the 100 cross-validation replicates to find the best combination of parameters for the RF model. Parameters tested included max tree depth (3, 5, 10, and 50) and max number of features included in each tree (10, 50, and 100%, square root, and log₂).

The predictive performance of the models was compared using the PCC. The PCC between the predicted (Ŷ) and the true trait value (Y) was computed using the cor() function in R for rrBLUP and BL or the NumPy corrcoef function in Python for RF. One hundred replicates of a fivefold cross-validation approach were applied to maximize the data available for model training without resulting in overfitting. For each replicate, the lines were randomly divided into five subsets, where each subset is used as the testing set once and the other four subsets were combined to train the model, resulting in a total of 500 cross-validated runs. PCC was calculated using only the predicted values from the testing set for each run.

For the top 10 most important transcripts from the En model, leave-one-feature-out analysis was performed using rrBLUP with 100 replicates to get a score for how much the model performance (PCC) changes when that one transcript is removed from training (Supplemental Table 5). Information about top BLAST matches was collected from maizeGDB (https://www.maizegdb.org/).

Selecting Subsets of T or G for Input to Genomic Prediction Models

To determine if using smaller subsets of T or G as input to the genomic prediction models would improve our ability to predict traits, we used rrBLUP and flowering time as an example to select features. For transcript data, features were selected in three ways. First, 10, 20, 100, and 1000 transcripts with the greatest variance across the maize lines were selected and used as input to the rrBLUP models. Second, the 14 benchmark flowering-time genes (see Benchmark Flowering-Time Genes below) were used. Finally, 14 and 200 transcripts with the greatest absolute coefficient (i.e., weight) assigned by rrBLUP during training were selected. For this analysis, the models were rerun without cross-validation so that feature selection and model training were performed on the training data and the testing data were only used to measure model performance, thus ensuring against overfitting. This was done for each of the 100 replicates.

Genetic Marker/Transcript Importance Analysis

To identify features important for building the genomic prediction models, feature importance information was extracted from each model established with one of four methods: rrBLUP, BL, RF, and En. For rrBLUP, the importance metric was the marker effect calculated by mixed.solve in the R rrBLUP package. For BL, the importance metric was the estimated posterior mean calculated using the R BGLR package. The absolute values of marker effect and estimated posterior mean were used, since the features are categorical with no particular meaning for the sign of importance metrics. For RF, the importance metric was the Gini importance, collected using the _importance_score function built into the Scikit-Learn implementation of RF. The Gini importance is the total decrease in node impurity (i.e., the homogeneity of classes in a node) after a particular feature is used to split a node. Node impurity decreases as instances from one of the classes are removed from the node, leaving a greater proportion of instances from the other class. Importance metrics from rrBLUP, BL, and RF were averaged over the 100 cross-validation replicates. En importance scores were calculated by normalizing the average importance scores from each model and each method between 0 and 1, then taking the mean of normalized importance scores across the three algorithms. Enrichment for transcript compared with genetic marker features within the top 1000 or top 20 features was done using Fisher’s exact test, where the number of transcript features in and not in the top X features were compared with the number of genetic marker features in and not in the top X features.

To determine the degree to which the importance of a transcript correlates with the importance of nearby genetic markers, the genetic marker G with the greatest mean importance score within a fixed window from the center of a genomic region R where a transcript T mapped to was selected among genetic markers in region R, referred to as a T:G pair (Figure 3A). To identify the effect of window size, a series of window sizes ranging from 1 to 80 kb were tested. For each window size, the Spearman’s correlation was calculated between the importance scores of T:G pairs. The window size with the highest correlation (2 kb) was chosen (Supplemental Figure 3A). For this analysis, transcripts without location information or without one-to-one mapping between AGPv3 and AGPv4 were removed, leaving 24,412 transcripts. With a window size of 2 kb, additional transcripts were dropped because there was not a genetic marker within that window, resulting in 15,049 transcripts to be included in the downstream analysis. This analysis was repeated for the genome-wide genetic markers (G_GW) from Bukowski et al. (2018).

To determine the degree to which the importance of a transcript correlated with the importance of trans-regulatory variants, significant eQTLs (multiple testing corrected P < 0.05) were identified for each transcript using the linear regression (modelLINEAR) approach from MatrixeQTL implemented in R. Benjamini-Hochberg false discovery rate correction was used to adjust P for multiple testing, and eQTLs were considered significant if adjusted P < 0.05. The distance for considering eQTL as cis was 1 Mb (Zan et al., 2016); however, because <0.1% of eQTLs identified were cis, all eQTLs were analyzed together. The importance of an eQTL or the neighboring genetic marker located within a 2-kb window of the eQTL with the greatest average importance score was compared with the importance of the transcript with the eQTL in question (T:eQTL pair).

Enrichment of GO terms associated with important transcripts compared with the reference genome was tested using agriGO v2 (Tian et al., 2017). The enrichment P values are corrected for multiple testing by agriGO v2 using false discovery rate. The top 10, 25, and 100 transcripts from each algorithm, excluding the benchmark flowering-time genes, were tested against the reference genome. The top 153 transcripts excluding benchmark genes (i.e., the top transcripts between the best two benchmark genes) from the En algorithm and the union of the top 10, 25, and 100 transcripts from all four algorithms were tested.

Benchmark Flowering-Time Genes

We compiled a list of genes known to be involved in flowering time based on evidence from knockdown experiments (Muszynski et al., 2006; Danilevskaya et al., 2010; Lazakis et al., 2011; Meng et al., 2011; Alter et al., 2016) and/or association studies (Salvi et al., 2007; Hirsch et al., 2014). Genes were assigned confidence levels based on the type of evidence available, with experimental evidence considered high confidence and association study evidence and significant similarity with known flowering-time genes from other species considered medium confidence (Supplemental Table 4). Because some of these genes did not have genetic markers located within the 2-kb window of the center of the transcript, progressively larger windows were used to identify the most important nearby genetic marker up to 40 kb. To compare importance scores across algorithms and between models using G or T data as input, percentiles were used. To determine if transcripts or genetic markers assigned to flowering-time benchmark genes were associated with flowering time in this study, linear models and t tests, respectively, implemented in R were used.

Accession Numbers

All data and code needed to reproduce the results from this study are available on GitHub (https://github.com/ShiuLab/Manuscript_Code/tree/master/2019_expression_GP/data): DLF1 (GRMZM2G067921), ID1 (GRMZM2G011357), MADS1 (GRMZM2G171365), PEBP8 (GRMZM2G179264), RAP2 (GRMZM2G700665), CCT1 (GRMZM2G381691), CCT2 (GRMZM2G004483), MADS69 (GRMZM2G171650), PEBP2 (GRMZM2G156079), PEBP24 (GRMZM2G440005), PEBP4 (GRMZM2G075081), PEBP5 (AC217051.3_FG006), ZAG6 (GRMZM2G026223), and unknown (GRMZM2G106903).

Supplemental Data

• Supplemental Figure 1. Distribution of genetic marker and transcript data across maize chromosomes.

• Supplemental Figure 2. Feature importance analysis for G+T models.

• Supplemental Figure 3. Influence of transcript region sizes on importance correlation between transcript:genetic marker pairs.

• Supplemental Figure 4. Manhattan plot of importance scores from Genomic Prediction models.

• Supplemental Figure 5. Correlation between genetic marker/eQTL and transcript importance.

• Supplemental Figure 6. Genomic prediction and genetic marker:transcript pairs using genome-wide genetic markers (G_GW).

• Supplemental Figure 7. Correlation of feature importance between algorithms.

• Supplemental Figure 8. Relationship between transcript levels and alleles and flowering time for benchmark genes.

• Supplemental Table 1. Model performance by feature input type and algorithm.

• Supplemental Table 2. Effect of feature selection and setting select features as fixed effects on ability to predict flowering time using rrBLUP.

• Supplemental Table 3. Enrichment of transcript vs. genotype features among the top most important features from G+T models.

• Supplemental Table 4. Description of benchmark flowering-time genes, including evidence for flowering-time association and T:Gs and T:eQTL pair information.

• Supplemental Table 5. In silico analysis of top 10 most important transcripts for predicting flowering time from the Ensemble model.

• Supplemental Data Set 1. Importance scores and percentiles for benchmark gene transcripts, and genetic marker and eQTL pairs.

• Supplemental Data Set 2. Top 1000 most important transcripts for each trait from the transcript-based Ensemble models.

• Supplemental Data Set 3. Account of data (Genetic Marker, Transcript, Phenotype) availability for maize lines and decision to include line in the study.

DIVE Curated Terms

The following phenotypic, genotypic, and functional terms are of significance to the work described in this paper:

• DLF1 Gramene: GRMZM2G067921

• DLF1 Araport: GRMZM2G067921

• ID1 Gramene: GRMZM2G011357

• ID1 Araport: GRMZM2G011357

• MADS1 Gramene: GRMZM2G171365

• MADS1 Araport: GRMZM2G171365

• PEBP8 Gramene: GRMZM2G179264

• PEBP8 Araport: GRMZM2G179264

• RAP2 Gramene: GRMZM2G700665

• RAP2 Araport: GRMZM2G700665

• CCT1 Gramene: GRMZM2G381691

• CCT1 Araport: GRMZM2G381691

• CCT2 Gramene: GRMZM2G004483

• CCT2 Araport: GRMZM2G004483

• MADS69 Gramene: GRMZM2G171650

• MADS69 Araport: GRMZM2G171650

• PEBP2 Gramene: GRMZM2G156079

• PEBP2 Araport: GRMZM2G156079

• PEBP24 Gramene: GRMZM2G440005

• PEBP24 Araport: GRMZM2G440005

• PEBP4 Gramene: GRMZM2G075081

• PEBP4 Araport: GRMZM2G075081

• PEBP5 Gramene: AC217051.3_FG006

• PEBP5 Araport: AC217051.3_FG006

• ZAG6 Gramene: GRMZM2G026223

• ZAG6 Araport: GRMZM2G026223

• unknown Gramene: GRMZM2G106903

• unknown Araport: GRMZM2G106903