Attenuation‐based size metric for estimating organ dose to patients undergoing tube current modulated CT exams

Abstract

Purpose:

Task Group 204 introduced effective diameter (ED) as the patient size metric used to correlate size‐specific‐dose‐estimates. However, this size metric fails to account for patient attenuation properties and has been suggested to be replaced by an attenuation‐based size metric, water equivalent diameter (D_W). The purpose of this study is to investigate different size metrics, effective diameter, and water equivalent diameter, in combination with regional descriptions of scanner output to establish the most appropriate size metric to be used as a predictor for organ dose in tube current modulated CT exams.

Methods:

101 thoracic and 82 abdomen/pelvis scans from clinically indicated CT exams were collected retrospectively from a multidetector row CT (Sensation 64, Siemens Healthcare) with Institutional Review Board approval to generate voxelized patient models. Fully irradiated organs (lung and breasts in thoracic scans and liver, kidneys, and spleen in abdominal scans) were segmented and used as tally regions in Monte Carlo simulations for reporting organ dose. Along with image data, raw projection data were collected to obtain tube current information for simulating tube current modulation scans using Monte Carlo methods. Additionally, previously described patient size metrics [ED, D_W, and approximated water equivalent diameter (D _Wa)] were calculated for each patient and reported in three different ways: a single value averaged over the entire scan, a single value averaged over the region of interest, and a single value from a location in the middle of the scan volume. Organ doses were normalized by an appropriate mAs weighted CTDI_vol to reflect regional variation of tube current. Linear regression analysis was used to evaluate the correlations between normalized organ doses and each size metric.

Results:

For the abdominal organs, the correlations between normalized organ dose and size metric were overall slightly higher for all three differently (global, regional, and middle slice) reported D_W and D _Wa than they were for ED, but the differences were not statistically significant. However, for lung dose, computed correlations using water equivalent diameter calculated in the middle of the image data (D _W,middle) and averaged over the low attenuating region of lung (D _W,regional) were statistically significantly higher than correlations of normalized lung dose with ED.

Conclusions:

To conclude, effective diameter and water equivalent diameter are very similar in abdominal regions; however, their difference becomes noticeable in lungs. Water equivalent diameter, specifically reported as a regional average and middle of scan volume, was shown to be better predictors of lung dose. Therefore, an attenuation‐based size metric (water equivalent diameter) is recommended because it is more robust across different anatomic regions. Additionally, it was observed that the regional size metric reported as a single value averaged over a region of interest and the size metric calculated from a single slice/image chosen from the middle of the scan volume are highly correlated for these specific patient models and scan types.

1. INTRODUCTION

Turner et al. ¹ showed the value of using CTDI_vol as a normalization factor, resulting in scanner‐independent organ dose coefficients that are size dependent. Using patient's perimeter as the size metric along with scanner‐reported CTDI_vol and scanner‐independent organ dose coefficients, dose to abdominal organs from fixed tube current (FTC) CT exams could be estimated. Hence, a measure of patient size is essential in obtaining accurate estimates of organ dose from CT exams.

AAPM Task Group 204 (Ref. 2) extended this and used effective diameter (ED) as patient size descriptor to adjust scanner‐reported CTDI_vol for size. Effective diameter is the diameter of a circle that has the same cross sectional area as the patient at a given z‐axis or longitudinal location. This was used to obtain the size‐specific dose estimates (SSDE). Effective diameter can be estimated using measured lateral and anterior–posterior distance of the patient using either the projectional radiograph used as a localizer or axial CT images. These measurements can be either performed on work stations using electronic measuring tools or physical devices such as calipers.

Effective diameter is a simple physical measure of the patient's outer diameter, and therefore, does not account for patient's composition and attenuation properties. Knowing that it is not solely the physical dimensions of the patient but also patient's attenuation properties that affect the amount of energy absorbed, it is reasonable to hypothesize an improved dose estimate if an attenuation‐based metric is utilized to describe the differences among patients instead of measures of physical dimensions such as effective diameter. As an example, the measured effective diameter of a patient taken in the thoracic area and abdominal region can be the same, but due to lung's lower density and different compositions as compared to abdomen, for the same amount of CT output, thorax would attenuate fewer photons and therefore have a higher absorbed dose than abdomen. Hence, results from TG 204 may underestimate actual dose to the thoracic region, i.e., lungs. Corrections factors generated by TG 204 resulted from measurements and simulations performed in phantoms with composition and density close to water; hence, the relationship between effective diameter and water equivalent diameter (D_W) for all of the phantoms and models that were included in the TG 204 analysis is close to unity.

In addition to the need for a more appropriate patient size metric for accurate dose estimation, knowledge of regional tube current variation in tube current modulation (TCM) scans is also necessary, which was not considered in either of the previously cited efforts. The organ dose coefficients published by Turner et al. and TG 204 conversion factors were both based on fixed tube current simulations and measurements. As shown in earlier papers on TCM, ³ , ⁴ , ⁵ tube current variations along the scan length can be significant and result in lower and even sometimes higher organ doses as compared to fixed tube current exams. Therefore, accurate estimates of organ dose from TCM scans, which are used in the vast majority of scans performed clinically, require the knowledge of both, the TCM function, regional description of scanner output, as well as description of patient size. Additionally, since tube current variation in TCM is a direct result of patient's attenuation and composition, a regional description of both TCM and patient size may result in more accurate organ dose estimates.

Although, water equivalent diameter has been previously explored ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ as an alternative size metric and compared to different body size parameters, ¹² its role in estimating organ dose and specifically, its correlation with patient‐specific organ dose, has not yet been investigated. Additionally, none of the previously published studies considered the effects of tube current modulation and how this will impact the correlation between patient size and organ dose.

Therefore, the purpose of this study is to investigate different size metrics in combination with regional descriptions of scanner output to establish the most appropriate size metric to be used as a predictor for organ dose in tube current modulated CT exams. To do this, three different size metrics, ED, D_W, and approximated water equivalent diameter (D _Wa), were investigated and specifically characterized in terms of their correlation with CTDI_vol,regional normalized organ doses.

2. METHODS

To investigate the performance of different size metrics as organ dose predictors, the exponential form of the relationship between normalized organ dose and size as described by TG 204 was explored for each size metric [Eq. (1)]. However, to account for local variations in tube current and scanner output, a previously introduced regional descriptor of scanner output, ⁵ CTDI_vol,regional, was used as the normalizing quantity in Eq. (1). As described below, the organ doses were determined from detailed Monte Carlo simulations. Then, the A and B coefficients for each size metric were determined based on relationship described by Eq. (1),

$${\displaystyle \text{Normalized}\hspace{0.17em}\text{Organ}\hspace{0.17em}\text{Dose}=\frac{\text{Organ}\hspace{0.17em}\text{Dose}}{{\text{CTDI}}_{\text{vol}},\hspace{0.17em}\text{regional}}=A\times e^{-B\times \text{Size}\hspace{0.17em}\text{Metric}}.}$$ (1)

2.A. Voxelized models and Monte Carlo simulations

101 thoracic (51 females and 50 males) and 82 abdomen/pelvis (41 females and 41 males) scans were collected retrospectively from clinically indicated CT exams with Institutional Review Board (IRB) approval. All scans were acquired on Siemens Sensation 64 MDCT and were used to generate voxelized models for use in Monte Carlo simulations. All voxelized models were generated from images reconstructed at 500 mm DFOV to ensure coverage of the entire body. The data set consisted of a large range of sizes from pediatric to very large adult patients. Thoracic models included 30 pediatric patients and the abdomen/pelvis models included 20 pediatric patients. Liver, spleen, and kidneys were identified and segmented on the abdomen/pelvis CT images, while thoracic images were used to identify and segment lungs and glandular breast tissue, which was only segmented on female models. ³ , ⁴ , ¹³ , ¹⁴

2.B. Monte Carlo‐based organ dose simulations

A previously developed and validated Monte Carlo based CT dosimetry package was used to estimate organ doses from tube current modulated thoracic and abdomen/pelvis CT exams. ³ , ⁴ , ⁵ , ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ The default source code of mcnpx (Monte Carlo N‐Particle eXtended v2.6.0) ¹⁹ , ²⁰ was modified to enable simulation of various protocols and scan modes such as helical scan. All simulations were performed in photon transport mode with a low‐energy cutoff of 1 keV.

For each simulated photon, mcnpx tally type *F4 was used to track energy fluence in organs of interest and multiplied by mass energy‐absorption coefficients (μ _en/ρ) to convert to collision kerma. The resulting dose per simulated photon for each organ was converted to dose per tube current (mA) by multiplying the Monte Carlo output by a normalization factor, which is scanner, collimation, and kVp dependent and is used to take into account the fluence changes from varying the beam collimation. Absolute organ doses were obtained by multiplying dose per mAs (tube current times rotation time) by the product of maximum tube current value obtained from each patient's TCM data, the exam's number of rotations, and rotation time. ³ , ⁴ , ⁵

2.C. Regional‐specific CTDI_vol

For each patient, calculated regional CTDI_vol, using scanner‐reported CTDI_vol, which in Siemens is calculated using the global averaged mAs along with regional averaged tube current values, was used as normalization factors for Monte Carlo simulated organ doses. As previously shown, ⁵ CTDI_vol,regional values are better normalization quantities in tube current modulated CT scans compared to global CTDI_vol. In this study, CTDI_vol,regional was used to investigate the most appropriate size metric as an organ dose predictor. Table I summarizes the definition of regional CTDI_vol values in abdomen/pelvis and chest CT exams.

Table I.

Tabular description and abbreviation of regional CTDI_vol.

Exam	Definition	Abbreviation
Abdomen/pelvis	Top of liver to the iliac crest	CTDIvol,abd
Chest	Inferior edge of the scapula and superior boundary of the liver	CTDIvol,Low Att

2.D. Size metrics

A semiautomated segmentation tool based on a combination of Otsu thresholding and 3D region growing ²¹ was utilized to segment out the whole body from the surrounding air and the table for calculating effective diameter, as defined in TG 204, and D_W, water equivalent diameter, on each axial image. D_W is defined as ⁶ , ⁷ , ¹¹ , ¹²

$${\displaystyle D_W=\rho \times 2\sqrt{\frac{A_{\text{Patient}}}{\pi }},}$$ (2)

where ρ is the average attenuation of the patient defined as

$${\displaystyle \rho =\sum \frac{\left[\left(\frac{I\left(x,y\right)}{1000}\right]+1\right)}{N}.}$$ (3)

With N being the number of voxels within the patient, and A _Patient the area of the patient defined as

$${\displaystyle A_{\text{Patient}}=N\times A_{\text{Pixel}}}$$ (4)

with A _Pixel being the area of each pixel.

A second attenuation based size metric, the D _Wa is defined similarly with the exception of the average attenuation being inside the radical, ¹¹ , ¹² as shown in Eq. (5). This simplifies the calculation of water equivalent diameter, in which no contouring is required and the entire image can be used to calculate A _Patient, A _Pixel, and ρ. However, this method is expected to be less accurate since it is using a square root of average attenuation instead of average attenuation to keep the overall water‐equivalent area (A_W) unchanged

$${\displaystyle D_{\mathrm{Wa}}=2\sqrt{\frac{A_W}{\pi }},}$$ (5)

$${\displaystyle A_W=\rho \times A_{\text{image}}.}$$ (6)

Although this method includes the surrounding air in the calculation, which can vary from one patient to another, it does not dramatically affect the value of A_W. For instance, if less surrounding air is included in the calculation of D _Wa, the mean CT number (ρ) increases but the area of the image, A _image, decreases proportionally so that the product A_W remains relatively unchanged. Hence, for calculating D _Wa, the average density or mean CT number ρ is taken inside the radical to keep A_W unchanged. This approach was explored by Wang et al. ⁷ and it was established that inclusion of table and hence the surrounding air results in overestimation of D_W, especially for smaller patients.

The tool was applied on each set of patient images to segment out the body from the surrounding air and the table; the segmented region was used to calculate an ED and D_W per image. Additionally, pixel values of entire axial image (including the surrounding air) within a series were used to calculate a D _Wa, per image, reconstructed at 500 mm FOV.

For each patient, each size metric was reported in three different ways

• 1.As a global average size metric, calculated over all images within each scan (either abdomen/pelvis scan or chest scan): ED_global, D _W,global, D _Wa,global.
• 2.As a regional average size metric, calculated using images within abdomen region for abdomen/pelvis models and low attenuating region for thoracic models (i.e., ED_Low Att, D _{W,Low Att}, D _{Wa,Low Att}, ED_abd, D _W,abd, D _Wa,abd).
• 3.As a single value measured approximately in the middle of the scan (abdomen/pelvis and chest scan), e.g., ED_middle, D _W,middle, D _Wa,middle.

The definition of “regional” in both, abdomen/pelvis and thorax, is given in Table I and corresponds to the same regions for which regional CTDI_vol values were calculated.

2.E. Statistical analysis

Linear regressions were used to investigate the effect of different size metrics on normalized organ doses. The log‐transformation of normalized organ dose was used to fit a linear regression with the covariate of different metrics. The coefficient of determination (R ²) was reported to quantify the proportion of variation explained by different size metrics and to evaluate the benefit of using each size metric. A scatter diagram with a fitted exponential curve, as described by Eq. (1), is used to demonstrate the relationship between normalized organ dose and individual size metrics for each organ. Pearson correlation coefficients and 95% confidence intervals (CI) were reported from the log‐transformed linear regression. The 95% confidence intervals of different size metrics were compared to each other and a p‐value smaller than 0.05 was considered to be significant. All data were analyzed using Stata 12.0 (StataCorp; College Station, TX).

3. RESULTS

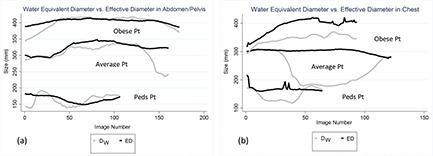
In the abdominal region, the various tissues can be approximated as water with a density close to 1 g/cm³. Therefore, in the abdominal region, the mean CT number ρ is close to unity and so D_W is almost equal to ED. However, in the thoracic area, due to low attenuating lungs and density lower than water, the mean CT number is smaller than unity, and therefore, D_W is smaller than ED. Figure 1 illustrates the difference between D_W and ED in thoracic and abdomen/pelvis regions. The difference between ED and D_W is not as profound in abdomen/pelvis as it is in thorax; in particular, the difference becomes significant in the low attenuating region of the thorax, which contains most of the lung and is defined as the region between the inferior edge of the scapula and superior boundary of the liver. As shown in Fig. 1, all abdomen/pelvic CT scans include a portion of the thoracic region, encompassing some section of the lungs. Hence, the difference between ED and D_W increases in this specific region, represented here with a dashed ellipse in Fig. 1.

Figure 1.

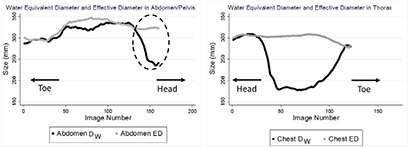
Left: The difference between ED and D_W in an abdomen/pelvis scan, showing almost no difference except toward the end of the scan which includes some sections of the thorax, illustrated with an enclosed ellipse on the figure. Right: The difference between ED and D_W in thorax, indicating a visible difference between these metrics in the thoracic area.

The difference between ED and D_W was statistically not significant in the abdominal region, while in the low attenuating region of the thoracic area, the difference was observed to be statistically significant.

For D _Wa, no statistically significant difference was observed compared to ED and D_W. Figure 2 shows the difference between global and regional D _Wa and D_W in the thorax and abdomen. In abdomen, both regional and global D _Wa slightly overestimate regional and global D_W in a linear fashion. Additionally, no difference is observed between regional and global averaged of the size metric, i.e., in the abdominal scans, size can be reported either as a regional average or global. Meanwhile, the difference between D_W and D _Wa in thoracic scans is more noticeable. Furthermore, a distinct difference is seen between regional and global average of both D_W and D _Wa.

Figure 2.

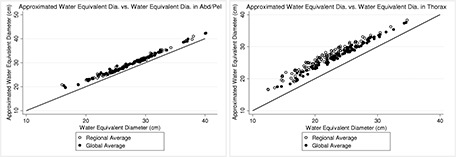
Left: The difference between regional and global D _Wa and D_W in abdomen/pelvis scans, showing small overestimation of D_W by D _Wa and almost no difference between regional and global average. Right: The difference between D _Wa and D_W in chest scans, indicating a visible difference between these metrics in the thoracic area, and also a noticeable difference between differently reporting them, i.e., as a regional versus global average.

The relationship between organ dose normalized by CTDI_vol,regional and size was investigated and compared across all metrics. Tables II, III, IV, V, VI  summarize these results for all five organs, while Fig. 3 shows the exponentially fitted data for normalized kidney and lung dose. For the abdominal/pelvic organs, Tables II, III, IV, report the R ², Pearson correlation coefficients, and the 95% confidence interval of normalized abdominal organ doses for each combination of the size metrics. Although the R ² value slightly increases for D_W and D _Wa compared to ED, this increase is not statistically significant. Furthermore, the different variations of measuring size (i.e., global average, regional average, and single value from approximately the middle of the scan volume) do not result in statistically significant differences.

Table II.

R ², Pearson correlation, and 95% confidence interval of normalized liver dose by CTDI_vol,regional and size metrics. ^a

			CTDIvol,abd
			Size metricglobal		Size metricregional		Size metricmiddle
Organ	Metric	n	r (95% CI)	R 2	r (95% CI)	R 2	r (95% CI)	R 2
	ED	82	−0.9181(−0.947, −0.876)	0.84	−0.9261(−0.952, −0.887)	0.86	−0.9085(−0.940, −0.861)	0.83
Liver	DW	82	−0.9365(−0.959, −0.903)	0.88	−0.9452(−0.964, −0.916)	0.89	−0.9198(−0.948, −0.878)	0.85
	D Wa	82	−0.9434(−0.963, −0.913)	0.89	−0.9507(−0.968, −0.924)	0.90	−0.9298(−0.954, −0.893)	0.86

^aLog transformation is applied for Pearson correlation and 95% confidence interval.

Table III.

R ², Pearson correlation, and 95% confidence interval of normalized spleen dose by CTDI_vol,regional and size metrics. ^a

			CTDIvol,abd
			Size metricglobal		Size metricregional		Size metricmiddle
Organ	Metric	n	r (95% CI)	R 2	r (95% CI)	R 2	r (95% CI)	R 2
	ED	82	−0.8686(−0.913, −0.803)	0.75	−0.8732(−0.917, −0.810)	0.76	−0.8543(−0.904, −0.782)	0.73
Spleen	DW	82	−0.8658(−0.912, −0.799)	0.75	−0.8688(−0.914, −0.803)	0.75	−0.8433(−0.896, −0.767)	0.71
	D Wa	82	−0.8713(−0.915, −0.807)	0.76	−0.8694(−0.914, −0.804)	0.76	−0.8507(−0.901, −0.777)	0.72

^aLog transformation is applied for Pearson correlation and 95% confidence interval.

Table IV.

R ², Pearson correlation, and 95% confidence interval of normalized kidney dose by CTDI_vol,regional and size metrics. ^a

			CTDIvol,abd
			Size metricglobal		Size metricregional		Size metricmiddle
Organ	Metric	n	r (95% CI)	R 2	r (95% CI)	R 2	r (95% CI)	R 2
	ED	82	−0.8560(−0.905, −0.785)	0.73	−0.8626(−0.909, −0.794)	0.73	−0.8512(−0.902, −0.778)	0.72
Kidney	DW	82	−0.8557(−0.905, −0.784)	0.73	−0.8702(−0.915, −0.805)	0.76	−0.8618(−0.909, −0.793)	0.74
	D Wa	82	−0.8678(−0.913, −0.802)	0.75	−0.8760(−0.918, −0.814)	0.77	−0.8678(−0.913, −0.802)	0.75

^aLog transformation is applied for Pearson correlation and 95% confidence interval.

Table V.

R ², Pearson correlation, and 95% confidence interval of normalized lung dose by CTDI_vol,regional and size metrics. ^a

			CTDIvol,Low Att
			Size metricglobal		Size metricregional		Size metricmiddle
Organ	Metric	n	r (95% CI)	R 2	r (95% CI)	R 2	r (95% CI)	R 2
	ED	101	−0.6498(−0.750, −0.520)	0.42	−0.6579(−0.756, −0.531)	0.43	−0.6647(−0.761, −0.539)	0.44
Lung	DW	101	−0.7148(−0.799, −0.604)	0.51	−0.8311 b (−0.883, −0.759)	0.70	−0.8350 b (−0.886, −0.764)	0.70
	D Wa	101	−0.6858(−0.777, −0.566)	0.47	−0.7751(−0.843, −0.683)	0.60	−0.7833(−0.849, −0.694)	0.61

^aLog transformation is applied for Pearson correlation and 95% confidence interval.

^bStatistically significant improvement (p‐value <0.05) compared to effective diameter by using log transformation.

Table VI.

R ², Pearson correlation, and 95% confidence interval of normalized breast dose by CTDI_vol,regional and size metrics. ^a

			CTDIvol,Low Att
			Size metricglobal		Size metricregional		Size metricmiddle
Organ	Metric	n	r (95% CI)	R 2	r (95% CI)	R 2	r (95% CI)	R 2
	ED	51	−0.8100(−0.887, −0.688)	0.66	−0.8385(−0.905, −0.732)	0.70	−0.8464(−0.910, −0.744)	0.72
Breasts	DW	51	−0.7860(−0.873, −0.652)	0.62	−0.8302(−0.900, −0.719)	0.69	−0.8329(−0.902, −0.723)	0.69
	D Wa	51	−0.7917(−0.876, −0.660)	0.63	−0.8341(−0.902, −0.725)	0.70	−0.8404(−0.906, −0.735)	0.71

^aLog transformation is applied for Pearson correlation and 95% confidence interval.

Figure 3.

Illustration of normalized kidney and lung dose versus regional average ED, D_W, and D _Wa. The improvement of fitted normalized lung dose with D_W is evident compared to ED.

Table V summarizes the statistical analysis for different size metrics investigated for the normalized lung dose, showing 70% of the variation of size being explained by D_W, while only 42% is explained by ED. Similarly the R ² increases for D _Wa; however, it is not statistically significantly different from D_W. The only statistically significant improvement of using D_W over ED is observed in regional average (low attenuating region of thorax) D _{W,Low Att} and D _W,middle. Additionally, for lungs, there was no significant difference between D _{W,Low Att} and D _W,middle.

Similar to the abdominal organs, no significant improvement in correlation between normalized breast dose and size was observed when attenuation‐based metrics (D_W and D _Wa) were employed (Table VI) as compared to results obtained with effective diameter. Also, no significant difference was observed among differently reported size metrics, global, regional, and single value measured in the middle of the scan volume.

Figure 3 illustrates the exponential fit of normalized kidney and lung dose by CTDI_vol,regional versus three different regional average size metrics.

Exponential regression equations, as described by Eq. (1), were obtained for all five organs. The coefficients (A and B), along with the correlation coefficient of the exponential regression analysis (R ²), are displayed in Table VII for D_W and D _Wa. Each model was used to estimate dose to each organ and compared to simulated organ doses. Table VII lists percent minimum, maximum, and average for this comparison.

Table VII.

Results of the exponential regression analysis describing normalized organ dose by regional CTDI_vol as a function of D_W and D _Wa.

		Size metricregional						Size metricmiddle
Organ		A	B	R 2	%Max	%Min	%Ave	A	B	R 2	%Max	%Min	%Ave
Liver	DW	3.60	−0.040	0.89	21.7	0.2	5.4	3.04	−0.034	0.85	27.0	0.06	6.5
	D Wa	4.20	−0.043	0.90	17.7	0.01	4.8	3.47	−0.036	0.86	26.8	0.02	6.1
Spleen	DW	2.70	−0.030	0.75	36.9	0.2	6.2	2.39	−0.025	0.71	39.8	0.2	6.8
	D Wa	2.96	−0.031	0.76	34.7	0.01	6.2	2.59	−0.026	0.72	38.1	0.2	6.7
Kidneys	DW	2.79	−0.031	0.76	22.7	0.02	7.1	2.50	−0.027	0.74	22.8	0.3	7.5
	D Wa	3.09	−0.032	0.77	27.2	0.09	7.1	2.72	−0.028	0.75	24.8	0.2	7.5
Lungs	DW	4.81	−0.048	0.69	38.5	0.07	12.0	4.86	−0.049	0.70	40.0	0.4	11.58
	D Wa	5.27	−0.042	0.60	44.5	0.1	14.3	5.37	−0.043	0.61	39.7	0.01	13.6
Breasts	DW	3.44	−0.045	0.69	31.7	0.3	10.1	3.40	−0.045	0.69	33.7	0.6	10.0
	D Wa	4.80	−0.049	0.70	31.8	0.04	9.9	4.80	−0.049	0.71	34.4	0.6	9.8

4. DISCUSSION

Simulated organ doses were normalized by CTDI_vol,regional and their correlation with different size metrics was investigated. As expected for the abdominal organs, no significant improvement was observed when D_W and D _Wa were used as patient size metrics compared to previously recommended metric, ED. Furthermore, no statistically significant difference was observed between global, regional, and middle of the scan volume measures of a size metric.

For lungs and breasts, although the hypothesis was an improvement in the exponential relationship between normalized dose and size metric, the improvements were only statistically significant in lungs for D _W,regional and D _W,middle. This indicates that there is no difference between the different regions over which D_W is calculated, i.e., either as an average over a specific region or from a single image chosen from the middle of the scan length.

For three out of five organs, the R ² value increased with the use of an attenuation based metric; however, the increase in R ² was only statistically significant for lung dose once D _W,regional and D _W,middle were employed. These results suggest that overall there is no statistically significant difference between investigated size metrics along the z‐axis of the patient except for lower attenuating regions of thorax.

A scatter plot with identity line demonstrating ED_regional versus D _W,regional was used to understand the relationship between these size metrics and the importance of the low attenuating region within thorax [Fig. 4(b)]. As illustrated, ED overestimates D_W across all patients. However, there seem to be a varying degree of overestimation which is very patient dependent. In Fig. 4(b), the depicted obese patient has a larger ratio of soft tissue (fat and muscle) to lung tissue and ED overestimates D _W,regional only by 5 cm. In addition to being obese, this specific patient has one arm in the scan field of view, which further increases the ratio of soft tissue (and bone) to lung tissue. For a more average looking patient, ED overestimates D _W,regional by 13 cm. For the pediatric patient, the overestimation is only by 4.5 cm. This varying degree of difference between ED and D_W is more extreme once the D_W is averaged over the low attenuating region compared to the global average, which artificially decreases the difference between ED and D_W [Fig. 5(b)]. Compared to abdominal regions, ED and D_W are very similar in magnitude as shown in Fig. 5(a). And there is no difference between regional versus global average of the size metrics [Fig. 5(a)]. Figure 6(b) shows the difference between ED and D_W for three different sizes, illustrating a large difference between ED and D_W for average sized patient, while demonstrating a smaller difference for the pediatric and obese patient. It is also evident that a regionally measured D_W will enhance the difference between ED and D_W. Similarly, the difference is enhanced if a single image in the middle of a typical thoracic scan is chosen to represent patient's size. However, the performance of the chosen image, in terms of predicting dose, can depend on the scan length and if middle happens to be in the low attenuating region of the lungs. Similarly, there is almost no statistically significant difference observed between regional and global average of both ED and D_W in the abdominal regions [Fig. 6(a)].

Figure 4.

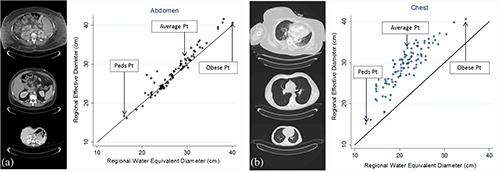
Scatter plot of ED_regional versus D _W,regional in abdomen (a) and chest (b) along with the identity line illustrating ED overestimating D_W in chest, while the difference between ED and D_W in abdomen is minor.

Figure 5.

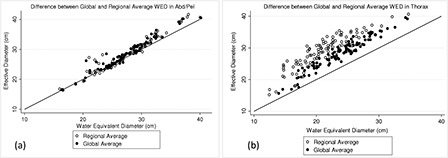
Scatter plot of ED versus D_W for two differently averaged values (regional versus global) in abdomen (a) and chest (b) along with the identity. While there is almost no difference between regionally and globally averaged size metric in abdomen, in chest, the value of both ED and D_W depends highly on how it was calculated, as a regional average or global.

Figure 6.

Difference between ED and D_W shown for three different patient sizes in abdomen (a) and chest (b).

As shown, the value of D_W and D _Wa varies significantly along the patient's long axis. Hence, if an averaged value is used as a size descriptor, it needs to reflect the averaged value of the region of interest for which organ doses are estimated. Similarly, if a single image is chosen to calculate D_W from, the selection of the image should be based on the organ of interest and not randomly such as the middle image within the series. A more educated selection will result in better organ dose estimation, especially in instances where the exam is not a typical thorax or abdomen/pelvis scan in terms of anatomical start and end location of the scan.

Before normalizing simulated organ doses by CTDI_vol,regional, a not before seen trend was observed between organ dose and patient size. As it was previously observed, ³ , ⁵ in TCM, organ dose increases with patient size; however, for some of the larger patients, a rather decrease in organ dose was observed. This was also noticed for all the other size metrics across all studied organs (liver, spleen, and breasts). Figure 7 demonstrates the relationship between absolute organ dose and one of the size metrics (D _W,global) for kidneys (from abd/pel scans) and lungs (from thoracic scans). To investigate this sudden decrease in dose for larger patients, they were identified and their TCM functions were studied.

Figure 7.

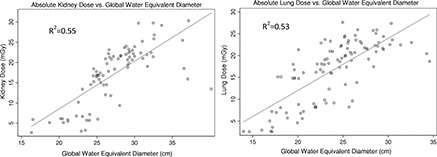
Illustration of kidney (left) and lung dose (right) versus D _W,global, both showing an increase in magnitude with increased size, except for few larger patients.

Once the corresponding TCM function of each of these patients was studied, it was established that the studied TCM functions were maxed out due to reaching the generator's instantaneous power limit caused by larger patient size. Figure 8 demonstrates the TCM function of one of these patients. Comparing the illustrated TCM function with a typical abdomen/pelvis TCM function, it is apparent that the z‐axis modulation portion of the TCM is lost due to tube current reaching its maximum value. Once the tube current reaches a maximum, the expected relationship between dose and size in TCM mode no longer holds and patient dose starts decreasing with increasing size; acting as if the scan was performed using fixed tube current.

Figure 8.

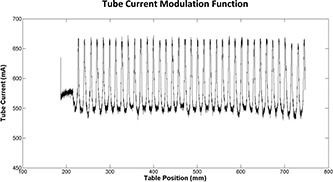
Illustration of a maxed out TCM function resulting in loss of z‐axis modulation and behaving as a fixed tube current examination.

To illustrate the transition from TCM to fixed tube current mode for large patients, for each patient, fixed tube current simulations were performed and results were plotted versus D _W,global along with doses from TCM simulations (Fig. 9). As seen in this figure, results from fixed tube current simulations overlap with the TCM simulation results for these specific patients with maxed out tube current (showed in an enclosed ellipse).

Figure 9.

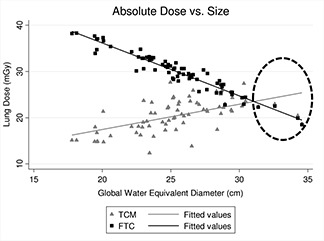
Lung doses resulting from FTC and TCM simulations versus D _W,global. At larger patient sizes, the TCM is compromised due to generator's limit and patient dose starts decreasing with increasing size as if the scan was a fixed tube current scan.

There are possible solutions to prevent scans from reaching the limit of scanner's output. In Siemens scanners, when the peak exposure demand exceeds system's limit, the operator is given the option to still load and proceed with the exposure or change parameters such as kVp, rotation time, and pitch to avoid maxing out the tube current. For instance, increasing the rotation time (e.g., from 0.5 to 1 s/rotation) and decreasing the pitch (e.g., from 1.0 to 0.8) can result in lower instantaneous mA for the same effective mAs however, these have other clinical implications such as increasing the time length of the scan and so may not always be practical.

Another finding, unveiled by graphically representing absolute organ doses versus size, was a distinct separation between pediatric and adult patient models. As illustrated by Fig. 10, kidney doses from pediatric and adult patient models result in two distinctive linear fits. This could be due to two different Siemens scanner's reference sizes (child vs adult) utilized during TCM scans. Nevertheless, neither one of these findings seem to have been carried on once organ doses are normalized by CTDI_vol,regional, as shown in Fig. 3.

Figure 10.

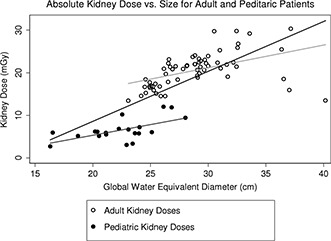
Graphically separated kidney dose for adult and pediatric patient models, demonstrating two distinct set of data with different linear fits.

Although the demonstrated results are promising and the developed models may be used to estimate organ dose from tube current modulated CT examinations, these models have some limitations in terms of their ability to estimate dose to all organs. These mathematical models are based on actual patient scans and images, which were used to generate the patient models. In this work, our focus was on estimating dose to fully irradiated organs; that is, organs fully contained within the image data. Because the patient scans did not contain all radiosensitive organs—that is, they were clinical scans that focused on either the abdominal/pelvic region or the thoracic region—this limited the ability to determine the location of organs that were only partially represented in the scan data or were not present at all (e.g., the thyroid or brain for an abdominal/pelvic scan). Therefore, dose to partially irradiated and nondirectly irradiated organs cannot be evaluated using these models. However, as long as the organs of interest are contained within the scan volume, then the developed estimation models can be used to estimate dose regardless of scan length, assuming the region used to calculate the size metric was appropriately selected.

It should also be noted that, for the same reasons as above, these models do not include any dose contributed from scatter from the rest of the body; for example, from the overscan region where there is radiation but not image data to model the patient's anatomy. For the fully irradiated organs, we assume this contribution to be negligible compared to the doses received from being fully irradiated in the scan. Another limitation of this study is the absent of a test set. The generated models need to be tested on a separate test set to accurately assess their performance.

5. CONCLUSION

Although the value of R ² increased for most organs, once D_W and D _Wa were used compared to ED, no statistically significant difference was observed between ED and attenuation‐based size metric in the abdomen. The only statistically significant improvement was observed for normalized lung dose and D _W,regional and D _W,middle, compared to ED; 70% of the variation of size is explained by D_W, while only 42% is explained by ED.

Overall, for abdominal organs, any of the size metrics discussed in this paper (ED, D_W, and D _Wa) can be used as a predictor of organ dose. However, D_W showed improved statistically significant correlation with normalized lung dose compared to D _Wa and ED. Hence, as a single size metric robust enough to be used in any anatomical region, i.e., chest, abdomen, and pelvis, D_W is recommended; however, D _Wa also resulted in improved correlations (higher R ² values) as compared to ED, just not statistically significant. As compared to D_W, for which segmentations are required, calculation of D _Wa is much effortless and straightforward.

As seen in Fig. 10, there might be some categorical factors which might impact organ dose; in this case, the model might behave differently if the dose is estimate to a pediatric versus an adult patient. Future studies will incorporate categorical variables to generate a more population‐specific model in or der to improve dose estimates.

None of the studied metrics are capable of representing patient's shape, which may significantly affect the x − y modulation of the TCM function. Specifically, the x − y modulation for a patient with an extreme circular shape would be very different from one with an extreme elliptical shape. Further studies need to focus on how a shape component can be included into the attenuation of the patient to better describe patient size for the purpose of dose estimation.

ACKNOWLEDGMENT

The authors would like to acknowledge grant support from Siemens Healthcare through the Master Research Agreement with UCLA Radiological Sciences.