Accuracy of UTE‐MRI‐based patient setup for brain cancer radiation therapy

Abstract

Purpose:

Radiation therapy simulations solely based on MRI have advantages compared to CT‐based approaches. One feature readily available from computed tomography (CT) that would need to be reproduced with MR is the ability to compute digitally reconstructed radiographs (DRRs) for comparison against on‐board radiographs commonly used for patient positioning. In this study, the authors generate MR‐based bone images using a single ultrashort echo time (UTE) pulse sequence and quantify their 3D and 2D image registration accuracy to CT and radiographic images for treatments in the cranium.

Methods:

Seven brain cancer patients were scanned at 1.5 T using a radial UTE sequence. The sequence acquired two images at two different echo times. The two images were processed using an in‐house software to generate the UTE bone images. The resultant bone images were rigidly registered to simulation CT data and the registration error was determined using manually annotated landmarks as references. DRRs were created based on UTE‐MRI and registered to simulated on‐board images (OBIs) and actual clinical 2D oblique images from ExacTrac™.

Results:

UTE‐MRI resulted in well visualized cranial, facial, and vertebral bones that quantitatively matched the bones in the CT images with geometric measurement errors of less than 1 mm. The registration error between DRRs generated from 3D UTE‐MRI and the simulated 2D OBIs or the clinical oblique x‐ray images was also less than 1 mm for all patients.

Conclusions:

UTE‐MRI‐based DRRs appear to be promising for daily patient setup of brain cancer radiotherapy with kV on‐board imaging.

1. INTRODUCTION

Traditional radiation therapy relies on computed tomography (CT) for dose calculation, treatment simulation, and patient setup. Recently, MRI is increasingly used in the workflow of radiation therapy for improved tumor delineation due to its superior soft tissue contrast. However, a number of challenges remain to be addressed before MRI‐based simulation and patient setup can be widely accepted in clinical practices. One important issue is that, unlike CT, traditional MRI techniques cannot image the bones well because of the extremely short T2 relaxation time of cortical bones. As a result, the bony structures in traditional T1 or T2 weighted MRI techniques appear dark. This lack of bone signal creates issues not only in treatment planning or radiation dose calculation but also in the use of the MR image set for validation of patient setup on a fraction‐to‐fraction basis. In a traditional CT‐based workflow, patients are often positioned in each fraction using radiographic imaging (such as kV image pairs), which is registered to a digitally reconstructed radiograph (DRR) that is generated by projecting through the simulation CT datasets. Because bony anatomy has low signal in MR images, using conventional MR images to generate a DRR is difficult, despite several previously described approaches. ¹ , ² , ³ It is possible to acquire both a simulation CT and an MRI dataset before the therapy and register the MRI dataset to the simulation CT. However, MR‐CT registration can carry significant uncertainties even in the simple cranial rigid registration ⁴ due to the lack of bone signals in the MR images. The uncertainty may negatively impact the treatment accuracy based on MR‐CT registration with traditional MRI techniques. Therefore, there are growing interests in the use of MR alone for simulation. This strategy provides better tumor conspicuity, removes the need for MR‐CT registration, and may be more cost effective because only one image dataset is needed for simulation.

There are several existing methods for generating MR images with high signal intensities for the bones. In postprocessing‐based methods, different tissue types (air, bone, fat, soft tissue, and fluid) are segmented, either manually or automated, and electron densities are assigned to the segmented structures. Manual segmentation‐based methods, which either assign electron densities to the contoured structures as bulk assignments ⁵ or use a learning algorithm for pixel‐by‐pixel assignments, ⁶ are labor intensive because the bone contour is manually drawn. The automated segmentation‐based methods either use atlas‐based segmentation algorithms, ⁷ which are automatic but often inaccurate when handling patient anatomies that deviate from the standard atlas, or voxel‐based automated segmentation, which cannot differentiate bone from air and therefore require manual contouring of airways. ⁸ In addition to the above methods based on image postprocessing, a more direct way of generating brighter bone signals in MR is to capture the short T2 signals of the bones using ultrashort echo time (UTE) MRI, a pulse sequence that samples the free induction decay immediately after the radio frequency pulse as opposed to a spin or gradient echo. ⁹ UTE‐MRI has been successfully used to generate simulated CT images via MR‐CT registration and to generate DRRs. ¹⁰ , ¹¹ However, to our best knowledge, the accuracy of UTE‐MRI derived DRR‐radiograph registration for patient setup has not been quantified. We present a study to investigate the accuracy of UTE‐MRI‐based DRRs for patient setup of intracranial tumors.

2. METHODS AND MATERIALS

2.A. Data acquisition

Seven patients diagnosed with brain tumors referred for radiation therapy were included in this study, which was approved by the Institutional Review Board. In addition to the routine MRI protocols on a 1.5 T MR scanner (Avanto, Siemens Medical Solutions, Erlangen, Germany), the patients also underwent a 3D radial UTE‐MRI scan using a head coil. The UTE sequence, which is available as a “work‐in‐progress” (WIP) sequence on Siemens systems, used a nonselective radio frequency excitation pulse and an asymmetrical readout to sample the k‐space using 3D radial trajectory. Two echoes were acquired (TE1 = 0.07 ms and TE2 = 4.28 ms) from each excitation (flip angle = 18°) with a readout bandwidth of 511 Hz/pixel. The repetition time (TR) was 6.32 ms. The images were reconstructed to a 192 × 192 × 192 matrix, with isotropic resolution of 1.6 mm and the images were subsequently interpolated to 0.4 mm isotropic resolution using zero‐padding in k‐space to mimic the resolution of CT. A total of 15 000 radial spokes were sampled to cover the 3D k‐space and the image was reconstructed using a standard regridding algorithm using a Kaiser–Bessel window. ¹² The total scan time of the dual‐echo UTE sequence was approximately 1.5 min.

An automated algorithm was applied to the two images acquired at different TEs to generate a bone image. An initial bone image was calculated by performing pixel‐by‐pixel magnitude subtraction of the two images (TE1 – TE2). The two images had different T2* weighting because they were acquired at different echo times. As the cortical bone has shorter T2* compared with other tissues, it is brighter in the subtracted images than other tissues. Further image postprocessing was performed on the subtracted image in order to remove the background noise, and to remove the signal from interface between the scalp and air, which also has short T2 values due to the local magnetic susceptibility gradient and would therefore appear bright as well in the subtracted image. To remove the noise, a hard intensity threshold of 100 was used to differentiate the bone pixels from nonbone‐pixels (including background air). To find the pixels that correspond to skin, a multislice 2D region growing algorithm ¹³ was performed on the TE2 images with initial seed point set to the center of each image. The region growing process will find the boundary of the head and any pixels that were less than 2 pixels away from the boundary were defined as skin. The signal intensity of the identified skin pixels was subsequently set to 0 in the subtracted images. The final processed bone images were loaded into commercial software packages (mim software™, VARIAN Eclipse™ Treatment Planning System, Novalis ExacTrac™ Patient Positioning System) for further processing as follows.

2.B. Image registration

The UTE‐MRI bone images for each of the seven patients were rigidly registered to the patient's simulation CT using the mim software™ so that the clinical treatment plan could be transferred to the UTE‐MRI for generation of DRRs and further registration studies. To evaluate geometrical differences of bony structure representations between the UTE‐MRI bone images and CT images, we measured the thickness of the skull bone based on UTE‐MRI and CT, respectively. For each patient, the thickness at ten arbitrarily selected locations in two different slices of the 3D volume was measured and compared.

To evaluate the registration accuracy between CT and UTE‐MRI bone image, a radiation oncologist (evaluator) selected 100 bony anatomical landmarks within the image volumes of UTE‐MRI and CT for each of the seven patients, and an in‐house image registration evaluation software was used to evaluate image registration accuracy by calculating the Euclidean distance between each pair of anatomical landmarks based on UTE‐MRI and CT, respectively. The UTE‐MRI‐based bone image was considered the source (or reference) image and the CT was considered the target image. For each of the landmarks the evaluator selected in the reference image, the corresponding landmark in the target image was located using the image registration vector. Crosshairs were visually displayed in the target image at the corresponding location. The evaluator was able to either accept the registration results as correct or click on the point in the target image that the evaluator felt correctly corresponded to the landmark in the source image. The target registration error (TRE), defined as the root mean squared difference between the ground truth displacement and the displacement computed from the registration process, was computed for each of the landmarks to quantify the error and standard deviation of the registration accuracy, as shown in the following equation:

$${\displaystyle \text{TRE}=\sqrt{{(X_i-x_i)}^2+{(Y_i-y_i)}^2}.}$$

X_i and Y_i are the coordinates of ground truth displacement of the i‐th landmark and x_i and y_i are the coordinates of displacement computed from the registration process.

2.C. Orthogonal kV image pair simulation

To evaluate the accuracy of using UTE‐MRI‐based DRRs for 2D patient setup based on orthogonal image pairs, on‐board kV image pairs were simulated using each patient's simulation CT. The pair of the simulation CT and the aligned secondary UTE‐MRI bone image for each patient were imported into the VARIAN Eclipse™ treatment planning system. Anterior–posterior (AP) and left lateral (LLAT) DRR pairs were generated from both CT and UTE‐MRI bone images, respectively. The ray tracing algorithm for DRR calculation ¹⁴ was used for both CT and UTE‐MRI data sets. The CT Hounsfield unit window for CT DRR generation was set as −100 to 1200 to best simulate on‐board kV image quality. By manually modifying image DICOM file headers, the CT DRR pairs were reidentified as on‐board orthogonal kV imaging (OBI) pairs. Randomly assigned translational shifts between −10 and 10 cm were applied to these simulated OBIs via DICOM header modification. The resultant simulated kV pairs were loaded into the VARIAN ARIA™ image registration to perform autoregistration between the simulated kV pair and the UTE‐MRI‐based DRR for each patient with no manual interference. The calculated shifts then were compared with the assigned shifts.

2.D. Oblique kV image pair study

To evaluate the accuracy of using UTE‐MRI‐based DRRs for 2D patient setup based on oblique image pairs, the clinical treatment plan for each of the seven patients was copied onto the aligned UTE‐MRI bone image sets in VARIAN ARIA™ to ensure a common isocenter location. Among the seven patients in this study, three patients were treated using single‐fraction stereotactic radiosurgery (SRS) and the rest received fractionated treatments ranging from 28 to 31 fractions. One patient had two isocenters treated. Clinical setup images of the single‐fraction patients and the first ten fractions of the fractionated patients were automatched to the UTE‐MRI DRRs using a BrainLab ExacTrac system with no manual interference. In this work, the patients' teeth and any dental fillings/crowns were excluded in our automatching process. The teeth were excluded because of patient jaw motion from fraction to fraction. The metallic dental fillings/crowns were excluded because they have high signal intensity in CT images but do not have any MRI signal. The resultant shifts and rotations calculated from the automatching were compared with automatching between the clinical setup images and the patient's simulation CT.

3. RESULTS

For all seven patients, the anatomic features of cranial, facial, and vertebral bones were well visualized in the patients' UTE‐MRI bone image. Figure 1 shows a representative CT and UTE‐MRI bone image pair as well as DRRs generated from the two imaging modalities. Excellent agreement of bone depiction between CT and MRI was observed and this allowed us to generate a good quality DRR solely based on UTE‐MRI.

Figure 1.

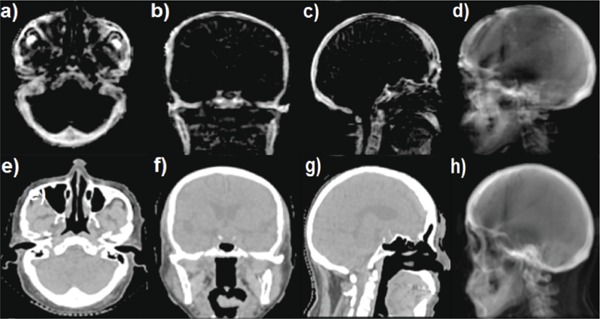
[(a)–(d)] Three orthogonal planes [(a)–(c)] of UTE‐MRI‐based bone image and an UTE‐MRI DRR (d) generated from a left lateral beam from a patient. [(e)–(g)] Three planes of CT image [(e)–(g)] and a CT‐based DRR (h) generated from a left lateral beam from the same patient.

Mean TREs between the UTE‐MRI and simulation CT are listed in Table I. The mean TRE for all the patients was in the range of 0.3–0.6 mm. Scalp bone thickness measurements from CT and UTE‐MRI, shown in Fig. 2, had excellent agreement with Lin's concordance correlation coefficient ¹⁵ of 0.9715 and the difference was <1 mm at 117 out of the 140 measured locations and the maximum difference was 2.9 mm.

Table I.

TRE (mean ± standard deviation) between UTE‐MRI and simulation CT evaluated using a landmark tool for seven patients.

	Pt. 1	Pt. 2	Pt. 3	Pt. 4	Pt. 5	Pt. 6	Pt. 7
TRE (mm)	0.3 ± 0.5	0.7 ± 0.7	0.4 ± 0.7	0.3 ± 0.5	0.4 ± 0.6	0.3 ± 0.6	0.6 ± 0.8

Figure 2.

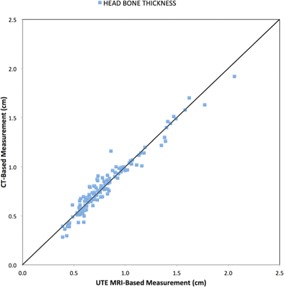
A comparison of head bone thickness measurements based on UTE‐MRI and CT plotted on a unit slope.

In our simulated patient setup study of the seven patients with orthogonal image pairs, the registration errors measured using UTE‐MRI DRR were all within 1 mm. Figure 3 shows the automatching results between the simulated kV imaging and the UTE‐MRI DRR in the LLAT and AP orientations. Autoregistration results between UTE‐MRI DRR and orthogonal kV imaging pair for all the seven patients are listed in Table II.

Figure 3.

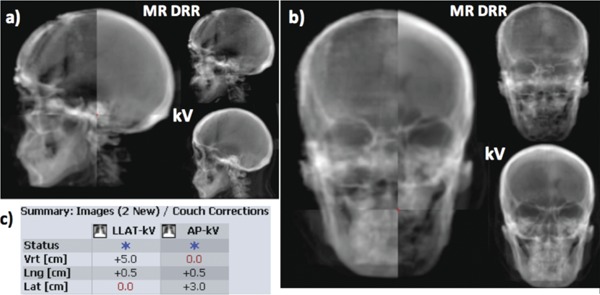
Automatching between UTE‐MRI bone DRR and simulated kV imaging pair for one patient. (a) Automatching result between LLAT kV and LLAT DRR; (b) automatching result between AP kV and AP DRR; (c) after automatching simulated kV pair to UTE‐MRI DRRs, the resultant translational couch shifts in vertical, longitudinal, and lateral directions match the known shifts we applied to the simulated kV pairs within clinical tolerance of 1 mm.

Table II.

Automatching results between UTE‐MRI DRR and orthogonal kV imaging pair (LLAT and AP) for all seven patients.

	Calculated shifts (cm)			Known shifts (cm)			Error (cm)
Patient no.	Vertical	Longi‐tudinal	Lateral	Vertical	Longi‐tudinal	Lateral	Vertical	Longi‐tudinal	Lateral
Pt. 1	1.0	−1.5	1.0	1.0	−1.5	1.0	0.0	0.0	0.0
Pt. 2	0.8	−0.9	0.5	0.7	−1.0	0.5	0.1	0.1	0.0
Pt. 3	5.0	0.5	3.0	5.0	0.5	3.0	0.0	0.0	0.0
Pt. 4	0.5	0.5	1.0	0.5	0.5	1.0	0.0	0.0	0.0
Pt. 5	−0.1	0.3	0.1	−0.1	0.3	0.1	0.0	0.0	0.0
Pt. 6	−0.2	0.4	0.4	−0.2	0.4	0.4	0.0	0.0	0.0
Pt. 7	−2.0	−0.9	2.0	−2.0	−0.8	2.0	0.0	−0.1	0.0

In our retrospective study for 2D patient setup based on the actual oblique image pairs, registration differences between UTE‐MRI DRR and CT DRR were all within 1 mm for shifts and 1° for rotations, which was within clinical tolerances. Analysis results for all the seven patients are listed in Table III. Figure 4 shows the autoregistration results in the ExacTrac system based on patient simulation CT and UTE‐MRI DRRs, demonstrating excellent agreement.

Table III.

Retrospective automatching results between clinical oblique setup images on the ExacTrac system and the UTE‐MRI DRR. The numbers are difference in translation and rotation between UTE‐MRI‐based and CT‐based automatching results.

	Vertical		Longitudinal		Lateral
Patient	Translational error (mm)	Angular error (deg)	Translational error (mm)	Angular error (deg)	Translational error (mm)	Angular error (deg)
Pt. 1	−0.33 ± 0.46	−0.22 ± 0.56	0.33 ± 0.43	−0.47 ± 0.33	−0.15 ± 0.47	−0.11 ± 0.41
Pt. 2	0.16 ± 0.14	0.10 ± 0.36	−0.09 ± 0.22	−0.30 ± 0.15	−0.12 ± 0.19	1.56 ± 0.49
Pt. 3	−0.25 ± 0.44	0.11 ± 0.17	0.05 ± 0.42	0.34 ± 0.27	−0.06 ± 0.30	0.45 ± 0.49
Pt. 4	−0.01 ± 0.35	−0.07 ± 0.37	−0.39 ± 0.34	0.16 ± 0.32	−0.19 ± 0.32	0.30 ± 0.32
Pt. 5	0.10 ± 0.36	−0.39 ± 0.39	−0.74 ± 0.16	0.31 ± 0.33	0.18 ± 0.58	0.00 ± 0.19
Pt. 6—tumor1	0.52 ± 0.38	0.48 ± 0.30	0.44 ± 0.26	−0.07 ± 0.30	−0.01 ± 0.43	−0.42 ± 0.29
Pt. 6—tumor2	−0.31 ± 0.23	0.58 ± 0.16	0.15 ± 0.28	0.00 ± 0.16	−0.67 ± 0.14	0.13 ± 0.18
Pt. 7	0.39 ± 0.66	−0.44 ± 0.32	−0.41 ± 0.42	0.01 ± 0.23	0.06 ± 0.30	1.28 ± 0.46

Figure 4.

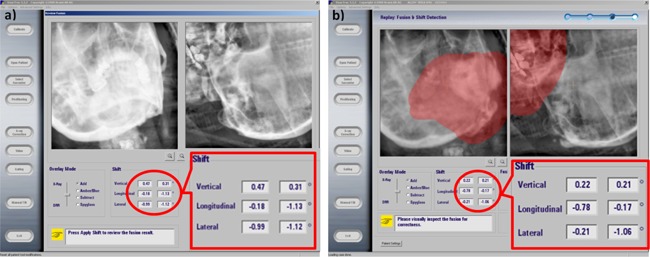
Patient setup example based on oblique image pairs. (a) 2D patient clinical setup result based on patient's simulation CT; (b) retrospective patient setup result by using patient's clinical ExacTrac images and the UTE‐MRI bone image. The calculated shifts in vertical, longitudinal, and laterals directions matched well between UTE‐MRI and simulation CT.

4. DISCUSSION

MRI plays an increasingly important role in radiotherapy due to its unique advantages in tissue contrast and its lack of ionizing radiation. However, incorporating MRI in the radiotherapy treatment workflow requires modification of the MR images to be better compatible with x‐ray dominant planning and radiation therapy treatment processes. A critically important goal is to image bony anatomy in MRI so that the accuracy in MR‐CT registration can be improved and, in the case of MR only simulation, useful DRRs can be generated for patient positioning on a daily basis. In this work, we prospectively acquired UTE‐MRI for brain patients and registered these images to their CT simulation scans. DRRs generated from the MR images were then registered to the radiograph images (both simulated orthogonal kV imaging pairs and oblique kV imaging pairs acquired during treatment). Unlike previous studies that emphasized the use of UTE‐MRI for electron density assignments in treatment planning, ⁵ , ¹¹ the current work provides a quantification of the geometrical accuracy of UTE‐generated bone images. Our results show that by adding the bone information in MR, MR‐CT registration accuracy can be reduced to submillimeter. This is a remarkable improvement compared to a recent study which showed an inherent uncertainty of 2 mm when registering traditional T1‐weighted MRI to CT images. ⁴ The uncertainty of 2 mm would be considered unacceptable for clinical intracranial SRS protocols. Furthermore, UTE‐MRI enables the generation of useful DRRs for stereo tactic radiograph guided radiotherapy, which is the standard of practice for intracranial treatments. Our results suggest that for the intracranial treatments, elimination of the simulation CT is feasible.

The UTE‐MRI sequence used in the current study was a 3D dual‐echo gradient recalled echo (GRE) 3D radial sequence covering 300 × 300 × 300 mm³ field of view. Johansson et al. ¹⁶ previously proposed a protocol of two UTE‐MRI scans with flip angles of 10° and 60° to help differentiate the cortical bone, which has short T2, from the air–tissue interfaces, which has shorter T2* but long T1. In our study, we only used a single UTE‐MRI data set with 18° flip angle. Compared to the UTE‐MRI protocol proposed by Johansson et al., ¹⁰ , ¹⁶ our total imaging time was approximately 50% shorter. Although we demonstrated that our UTE‐MRI provides sufficiently accurate DRR image registrations with 2D on‐board imaging, further study is warranted to evaluate registration accuracy with other on‐board imaging (such as cone beam CT) and the efficacy of treatment planning and dose calculation based on our UTE‐MRI data. Furthermore, recent developments in image acceleration methods such as parallel imaging and compressed sensing ¹⁷ , ¹⁸ may be applied to our sequence to further reduce the total MRI scan time. ¹⁹

MRI is known to have geometric distortions either due to gradient nonlinearity or due to B ₀ field inhomogeneity, depending on pulse sequences used. The UTE‐MRI sequence in this work is not sensitive to B ₀ field inhomogeneity related distortions due to its short TE. The MRI system used in this work passed the American College of Radiology (ACR) phantom testing with <1 mm error in the diameter measurement of the ACR phantom. Therefore, we do not expect geometric distortion to be a major contributor in the registration errors presented in this work.

5. CONCLUSION

An UTE‐MRI sequence was implemented and tested in brain cancer patients to obtain bony anatomies for 3D and 2D image registration. The resultant images provided accurate bone thicknesses measurements using the CT images as the ground truth. Quantification using manually annotated landmarks showed submillimeter registration error between the UTE‐MRI and the simulation CT. The same accuracy level was also observed when registering the DRRs generated from UTE‐MRI to the radiograph images simulated from planning CT and the ExacTrac oblique kV images acquired during treatment of these patients.