Topography and pachymetry maps for mouse corneas using optical coherence tomography

Abstract

The majority of the eye’s refractive power lies in the cornea, and pathological changes in its shape can affect vision. Small animal models offer an unparalleled degree of control over genetic and environmental factors that can help elucidate mechanisms of diseases affecting corneal shape. However, there is not currently a method to characterize the corneal shape of small animal eyes with topography or pachymetry maps, as is done clinically for humans. We bridge this gap by demonstrating methods using optical coherence tomography (OCT) to generate the first topography and pachymetry (thickness) maps of mouse corneas. Radii of curvature acquired using OCT were validated using calibration spheres as well as in vivo mouse corneas with a mouse keratometer. The resulting topography and pachymetry maps are analogous to those used diagnostically in clinic and potentially allow for characterization of genetically modified mice that replicate key features of human corneal disease.

1. Introduction

The cornea contributes the majority of the eye’s refractive power, and diseases that affect its shape such as astigmatism and keratoconus can profoundly affect one’s vision (Yu and Jackson, 1999; US National Library of Medicine, 2019; Wolffsohn et al., 2011). To better understand ocular disease including corneal diseases, researchers have used small animal models such as mice. Transgenic mouse lines are widely used in research and provide unparalleled opportunities for genetic manipulation and intervention assessment to elucidate disease mechanisms (Huberman and Niell, 2011; Chang, 2013).

A barrier to studying mouse corneal shape is the lack of diagnostics analogous to those used to study human corneas. In humans, corneal shape is characterized using clinical diagnostics such as topography and pachymetry maps. Topography maps display localized curvatures and allow for easy detection of localized corneal aberrations (Klyce and Wilson, 1989; Bruce, 2018), while pachymetry maps characterize the thickness profile of a cornea. Both of these maps aid in identifying corneal ectasias such as keratoconus that lead to significant refractive errors (Li et al., 2008). There are presently no analogous methods for characterizing the mouse cornea; current methods to analyze mouse corneas, such as histology, confocal microscopy, and keratometry, all have limitations. Histology’s sacrificial nature prevents longitudinal studies, and samples are subject to swelling, shrinking, and fixation distortions that affect the thickness and native curvature of the cornea (Hanlon et al., 2011). Confocal microscopy has demonstrated its utility for imaging cellular-level detail in vivo, but its limited imaging depth and narrow field-of-view are not suited for analyzing overall shape of the cornea (Petroll and Robertson, 2015). While mouse keratometers are able to measure corneal curvature, they represent a single-position measurement of a small area of the cornea, are sensitive to alignment errors, can change significantly in response to tear film and hydration status, and are currently unable to quantify localized irregularities (Wang and Swartz, 2008). Hence, these limitations hinder our ability to fully phenotype murine models of human corneal diseases.

In contrast, images acquired using optical coherence tomography (OCT) are not subject to these same limitations. These high-resolution images are noninvasive, relatively insensitive to alignment, and provide sufficient imaging depth to capture the entire mouse cornea. OCT has been used to measure mouse corneas including calculating biometrics within single B-scans (Chou et al., 2011; Ruggeri et al., 2010). Here, we expand this by developing and validating an accurate, in vivo OCT-based method to analyze anterior and posterior corneal shape in 3-D via corneal topography and pachymetry in murine models. We then utilized these new maps to provide the first detailed description of mouse corneal morphometry in a 29–301 day old cohort of ten mice.

2. Materials and supplies

2.1. Imaging samples

Calibration spheres to validate our program were purchased from McMaster (McMaster-Carr, 2019). Three spheres were used with diameters that were closest to a typical mouse cornea, which ranges2.3–2.6 mm across several strains of adult mice (Henriksson et al., 2009). The spheres included a 3/32-inch diameter (2.381 mm) silicon-nitride ceramic ball, a 1/8-inch diameter (3.175 mm) silicon-nitride ceramic ball, and a 3-mm diameter tungsten carbide ball. Manufacturer tolerance was within 0.02% of all respective diameters.

Nine male C57BI/6J mice (Jackson Laboratory, Bar Harbor, ME) and one D4R wild-type mouse all spanning 29–301 days old were anesthetized with a ketamine-xylazine solution (ketamine 80 mg/kg; xylazine 16 mg/kg). Each mouse was analyzed first with a keratometer and then with the OCT in order to minimize the effects of corneal dehydration. Steps to prevent dehydration such as eye drops were not used because adding an artificial, irregular film over the cornea may affect the keratometric reflections and lead to inaccurate keratometer readings. Keratometer measurements were carried out as swiftly as reasonably possible to minimize dehydration, and then followed with OCT imaging, which is relatively unaffected by the cornea’s hydration state as it depends on backscatter from corneal surfaces rather than Purkinje reflections.

2.2. Materials for imaging and processing

The anesthetized mice were placed on an elevated imaging stage before the mouse keratometer (Fig. 1A), which consisted of a ~300 mm diameter ring with 8 infrared light emitting diodes (IR LEDs) (Schaeffel, 2008). Because keratometer imaging of each mouse lasted approximately 1 min, a heating pad was not used to control for body temperature. Rather, the flat stage was used to allow maximum maneuverability of each mouse subject.

Figure 1. Keratometer (A) and OCT (B) imaging setup as viewed from above.

A) To obtain keratometer measurements, anesthetized mice were placed on an imaging platform in front of the keratometer (white arrow), which consisted of 8 infrared light emitting diodes. B) To acquire OCT images, anesthetized mice were placed within an imaging stage that provided a bite bar for stabilization and rotational capabilities for alignment. The mouse and stage were then oriented in front of a spectral-domain OCT (white arrow) system fixed on a translation mount with a 12 mm anterior segment imaging bore.

A small animal OCT device (Envisu R4300; Leica Microsystems, Inc.) was used to acquire tomographic images of the mouse cornea. The OCT was attached with a 12 mm anterior segment imaging bore and fixed on a translation mount. Anesthetized mice were placed in front of the OCT within an imaging stage that provided a bite bar for stabilization and rotational capabilities for alignment. Due to the OCT’s longer imaging duration, the imaging stage was equipped with a holding tube and heating pad to maintain mouse body temperature during image acquisition and intersession mouse repositioning. Pixel-to-mm conversions were calculated using the Edmund Optics Dual Axis Linear Scale Micrometer (Part #58608) using steps detailed in the “OCT Calibration” section of the Supplemental Material.

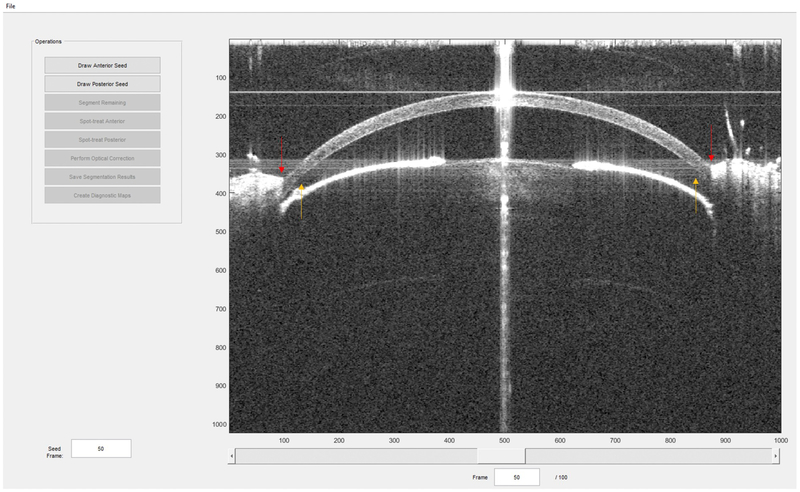
The Mouse Corneal Analysis Program (MCAP, Fig. 2) was used to process OCT images. From these images, the program extracts corneal biometrics, outputs the distortion-corrected corneal surfaces as data points, and generates thickness and curvature maps.

Figure 2. A sample screen capture of the MCAP (Mouse Corneal Analysis Program) with sample OCT data.

Program commands for image segmentation, optical dewarping, and map creation are located on the left. During processing, text will appear in lower left panel to display program status and corneal biometrics. Interactive pachymetry and topography maps (such as those in Fig. 6) on which the user can click to retrieve localized thickness and curvature measurements will be displayed in the main window, where the OCT image is currently displayed. Red arrows point out eyelids that may obscure the cornea. Orange arrows indicate areas of signal attenuation due to deviation from the center of depth of focus and system roll-off.

3. Detailed methods

As an overview, corneal measurements were made using both OCT and a dedicated mouse keratometer (Schaeffel, 2008) for comparison. Both imaging techniques were first validated using calibration spheres of known radii. After validation, mouse corneas were imaged with both techniques. Measurements shared between both techniques were compared.

We imaged a total of eleven eyes from ten mice. The OCT images were processed using MCAP (which has a typical processing time of about 1 min for image segmentation and 1 min for map creation and exportation, assuming initial OCT images have a high signal-to-noise ratio) to generate corneal biometrics and diagnostic topography and pachymetry maps. The detailed methodology follows:

3.1. Keratometer imaging protocol

Anesthetized mice were placed on a platform approximately 15 cm in front of the keratometer. Mice sedated with ketamine/xylazine naturally kept their eyes open, so no steps were taken to support their eyelids during imaging with either modality. The IR LEDs created reflections on the corneal surface that were fitted to a circle. The circle’s diameter is known to be nearly linearly proportional to the curvature of the cornea (Schaeffel, 2008). The proportionality constant relating the circle diameter to the actual R_C was obtained by measuring the diameter of reflections from a separate set of ball bearings with known radii. By plotting several spheres’ known R_C against the reflection diameters, one can find the proportionality constant, which is the slope. However, because the diameter - R_C relationship is not exactly linearly proportional over all values, one must use multiple ball bearings spanning the approximate sizes of interest in finding this constant. We used 4 ball bearings with radii spanning 1.19–2.38 mm (3/32–3/16 inch ball bearings), yielding a proportionality constant of 2.458.

3.2. OCT imaging protocol

Imaging was performed using a spectral domain OCT (SD-OCT) system fixed on a translation mount with a 12 mm anterior segment imaging bore. The OCT engine utilized a light source with a central wavelength of 870 ± 50 nm, giving a theoretical axial optical resolution in tissue of 2.4 μm. Maximum image depth was 5.4 mm in tissue. Lateral optical resolution of the 12 mm telecentric lens was 8.5 μm over a 10 mm maximum diameter, from which a 3.5 mm nominal imaging diameter was selected. The axial resolution of the OCT system was4.1 μm in air and 2.9 μm in corneal tissue. A-scan rate was 20 kHz with scan time of 5.4 s for each 2048 × 1000 × 100 (depth × A-scan × B-scan) radial volume used in this study, although MCAP is able to analyze other volume sizes (such as smaller scan densities to decrease scan times). To test repeatability, each eye was imaged three times per position (intrasession) with five re-positions (intersession), which produced a total of fifteen volumes per eye. Each session produced a single corneal volume, which consisted of 100 radial images (B-scans), where each B-scan was centered on a rotational axis.

3.3. Mouse Corneal Analysis Program components

3.3.1. Image segmentation

OCT images were first preprocessed through 2-D median filtering and pixel intensity remapping such that the bottom and top 1% of pixels in each B-scan were saturated to enhance signal. We then used a custom semi-automatic, gradient-based segmentation algorithm that utilizes a user-drawn seed segmentation in the first frame to identify the approximate corneal epithelium and endothelium boundaries. This seed is then processed and used to automatically segment all remaining frames.

Signal attenuation was observed on the left and right sides of OCT images due to system rolloff and deviation from the center of depth of focus (Fig. 2). Corneal boundaries were blurry in these regions, often leading to localized segmentation error. To minimize these effects downstream, segmentations in these peripheral regions were excluded from subsequent steps.

3.3.2. Motion correction and resampling to Cartesian space

This study utilized a radial scanning pattern to ensure that every B-scan had an area of high signal to noise ratio from the central cornea, to allow for axial motion-correction since all scans share a common pivot point, and to utilize the radial symmetry to aid our segmentation algorithms. However, radial scans are not evenly distributed in Cartesian space across the cornea (denser sampling centrally and lower sampling peripherally). Thus, radial corneal data was first converted to physical distances, corrected for axial motion, and then evenly resampled in order to obtain a uniform Cartesian distribution for subsequent 3D refraction correction. Segmentations were multiplied by pixel-to-mm conversions in the X, Y, and Z directions to obtain corneal dimensions in physical space. We also corrected all segmentations for 1.73 pixels of spatial delay per meridian due to the galvanometer mirror inertia and control circuit loop delay.

Then, segmentations were corrected for axial motion by assuming all B-scans in the data set shared a common physical axis along the OCT scan rotational axis, ideally located incident to the corneal vertex. The intersection of the epithelial segmentation with the axis in the first frame was used as a reference point. The offset of each epithelial segmentation intersection in subsequent frames was then used to axially re-align all segmentations in each B-scan. Finally, Zernike interpolation (6th order Zernike polynomial expansion) was used to fit the sampled points and create a regularly sampled 3D representation of the imaged corneal surfaces.

3.3.3. Optical distortion correction

Due to the optical nature of OCT, data below the air-epithelial interface are distorted, and it is therefore necessary to correct corneal surfaces for optical distortions (Zhao et al., 2010; Westphal et al., 2002; Ortiz et al., 2010; Borja et al., 2010). These distortions primarily manifest as optical path length distortions due to group delay of the material and due to refraction. First, to correct for optical path length distortions, we transformed optical into physical path lengths between the epithelium and endothelium. Optical modeling software (OpticStudio, Zemax; Kirkland, WA) was used to extrapolate the mouse corneal phase index of refraction for our OCT source centered at 870 nm. Specifically, the Conrady formula (OpticStudio Manual, 2018) was used to fit refractive indices previously measured in mice between the wavelengths 488–655 nm (Remtulla and Hallett, 1985). Once determined, this best-fit equation was utilized to extrapolate the desired index of refraction at the target wavelength of 870 nm and then converted to the group refractive index (Rogers and Hopler, 1988). Using these methods, the group refractive index of the mouse cornea was calculated to be n = 1.3987.

Refraction correction of the reconstructed surface was performed using a modified vector form of Snell’s law that required three inputs – the refracted vector, incident vector, and surface normal vector:

$$r\widehat{e}f=\sqrt{(1-{\left(\frac{{\text{n}}_1}{{\text{n}}_2}\right)}^2{\left(\left|i\widehat{n}c\times -\widehat{N}\right|\right)}^2}*\left(-\widehat{N}\right)+\frac{n_1}{n_2}\cdot \left|i\widehat{n}c\times -\widehat{N}\right|*\frac{\left(i\widehat{n}c\times -\widehat{N}\right)\times \widehat{N}}{\left|\left(i\widehat{n}c\times -\widehat{N}\right)\times \widehat{N}\right|}$$ (1)

Where $r\widehat{e}f$ is the unit refracted vector, $i\widehat{n}c$ is unit incident vector (assuming telecentric rays from the OCT), $\widehat{N}$ is unit surface normal vector, and n₁, n₂ are indices of refraction for air and cornea, respectively (derivation of this equation can be found under “Derivation of Vector Snell’s Law” in the Supplemental Material). This dewarping method was validated using a software phantom cornea with known dimensions. The phantom’s epithelial and endothelial surfaces consisted of two concentric spheres. To simulate refractive warping, meridians in the endothelium were distorted using the standard, 2D form of Snell’s Law. A Zernike polynomial was fit to the warped meridians to create the full, optically distorted endothelial surface that was then corrected using Equation (1) and validated against the original, dewarped cornea. To calculate percent error, the root mean square error (RMSE) between the known and calculated surfaces was divided by the phantom surfaces’ radii. Our method yielded 0.0475% error, while previously published dewarping methods yielded 0.0476% error (Zhao et al., 2010). Given its comparable accuracy and relative simplicity of input arguments, this method was utilized to refraction-correct surfaces. The corrected endothelial surfaces were resampled again to a 6th-order Zernike polynomial to create an evenly distributed data set.

Finally, the epithelial and corrected endothelial corneal surfaces may be exported from MCAP as multiple file formats for the user’s convenience. This data can be used for a myriad of subsequent analyses, such as applying Zernike decompositions, fitting other mathematical models, and creating elevation maps. As an example, representative elevation maps are demonstrated in Fig. 6D–E for an abnormal mouse cornea.

3.3.4. Keratometry calculations using OCT data

Keratometry values were calculated from OCT data based on methods previously described in McNabb et al. (2013) and Kuo et al. (2012). The anterior corneal surface was fitted to a sphere by least squared error (Jennings, 2013). We acquired fifteen corneal OCT volumes per eye for intrasession repeatability in in vivo corneas and three volumes per calibration sphere for validation. The R_C from all corresponding volumes were averaged to produce the overall R_C measurement for that specific cornea or calibration sphere.

3.3.5. Validation using calibration spheres of known radii

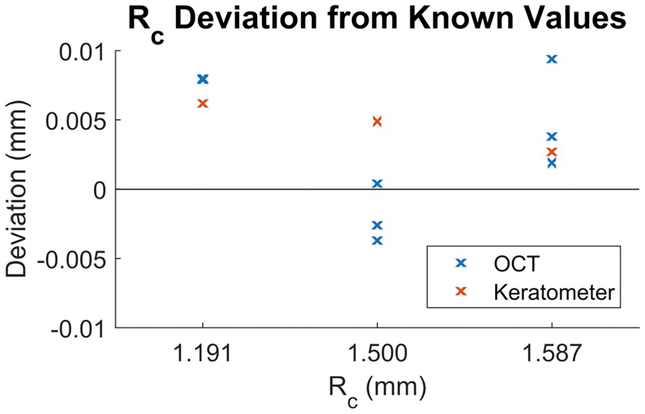
Validation of our method was based on techniques described in previous work (Kuo et al., 2012). Calibration spheres had dimensions that spanned a typical mouse cornea. A custom mount was used to secure calibration balls on the mouse keratometer and OCT imaging stages. Calibration spheres were imaged three times each to characterize repeatability. OCT imaging used scan parameters identical to those for in vivo imaging, and images were segmented and put through the same processing pipeline as in vivo corneas. R_C of the calibration spheres calculated using our OCT-based method were all within 1% of the manufacturer specified dimensions (Fig. 3). Paired differences between the reference calibration spheres and OCT-generated R_C for the calibration spheres were evaluated using the Wilcoxon Signed-Rank test and found to be not statistically significant (p = 0.25). The paired differences between keratometer and OCT R_C measurements of these calibration spheres were also not significant (p = 0.25). Variations in their average percent error corresponded to a 2–8 μm (1–3 pixel) difference, which was on the order of our OCT imaging resolution. Mean absolute bias was 0.005 mm for OCT and 0.004 mm for the mouse keratometer.

Figure 3. Deviation of R_c (in mm) from our OCT-based method (blue) versus keratometer (red) compared to known values of calibration spheres.

We measured accuracy and repeatability of our OCT-based method by imaging three calibration spheres from each dimension, for a total of nine data points in blue. Keratometer accuracy was also evaluated for each of the three sphere dimensions, giving a total of three data points in red. Average absolute bias was 0.005 mm for OCT and 0.004 mm for the keratometer. All values were within 1% of the manufacturer reported dimensions.

3.3.6. Validation of in vivo mouse corneas

Anesthetized mice were imaged in a heated holding tube located on an imaging stage in front of the OCT. This experiment was under compliance with the ARRIVE guidelines, and animals were handled according to the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

Averaged anterior and posterior R_C measured using the MCAP were1.473 ± 0.007 mm and 1.374 ± 0.008 mm, respectively. Average intrasession repeatability was 9 μm for MCAP (calculated by averaging the standard deviations of R_C from volumes imaged in the same position) and 8.4 μm for the mouse keratometer (calculated by averaging standard deviations of the keratometer measurements, which automatically measures Purkinje reflections multiple times while the mouse is in the same position). The mean paired difference between epithelial radii of curvature obtained using OCT versus a dedicated mouse keratometer was 0.020 mm. Paired differences were not statistically significant (p = 0.12, Table 1 and Fig. 4B), despite one eye (subject 3 OD) having a tear film disturbance and another eye (subject 3 OS) having a corneal abnormality. The tear film error likely distorted keratometer reflections and contributed to higher variability in right eye R_C measurements. Fitting a perfect sphere or circle to the left cornea, which inherently has abnormal shape due to corneal thinning, may have also increased R_C variability measured by both imaging modalities. The corneal diameter used in OCT-based calculations averaged 2.08 mm (ranging from 1.55 to 2.42 mm) after excluding areas obscured by eyelid or blurred by signal rolloff (the typical C57BL/6 mouse corneal diameter is 2.6 mm (Henriksson et al., 2009)).

Table 1. Radii of curvatures for eleven experimental corneas from ten mice spanning 29–301 days old.

All subjects with the exception of subject 3 (D4RWT) were C57BL/6J mice (subjects were numbered according to age and not the order in which they were imaged). OCT analysis diameters were chosen to minimize segmentation error due to eyelid and image signal attenuation (a sample frame shown in Fig. 2).

Age (days)	Mouse subject (eye)	Keratometer Anterior Rc (mm)	OCT Anterior Rc (mm)	OCT Posterior Rc (mm)	OCT – Keratometer Anterior Rc (μm)	OCT Analysis Diameter (mm)
29	1 (OD)	1.347 ± 0.004	1.337 ± 0.008	1.208 ± 0.006	11	1.548
29	2 (OD)	1.360 ± 0.002	1.389 ± 0.006	1.285 ± 0.004	−29	1.885
30	3 (OD)	1.427 ± 0.013	1.377 ± 0.016	1.251 ± 0.009	50	1.728
30	3 (OS)	1.363 ± 0.031	1.368 ± 0.027	1.240 ± 0.015	−5	1.588
56	4 (OD)	1.452 ± 0.019	1.506 ± 0.011	1.402 ± 0.007	−53	2.138
65	5 (OD)	1.459 ± 0.004	1.468 ± 0.006	1.393 ± 0.012	−9	2.336
65	6 (OD)	1.421 ± 0.004	1.475 ± 0.005	1.400 ± 0.011	−54	2.340
105	7 (OD)	1.580 ± 0.003	1.559 ± 0.005	1.484 ± 0.008	21	2.416
287	8 (OS)	1.579 ± 0.008	1.618 ± 0.011	1.527 ± 0.011	−38	2.349
301	9 (OD)	1.572 ± 0.002	1.615 ± 0.007	1.525 ± 0.009	−43	2.144
301	10 (OD)	1.510 ± 0.002	1.576 ± 0.007	1.506 ± 0.008	−66	2.420

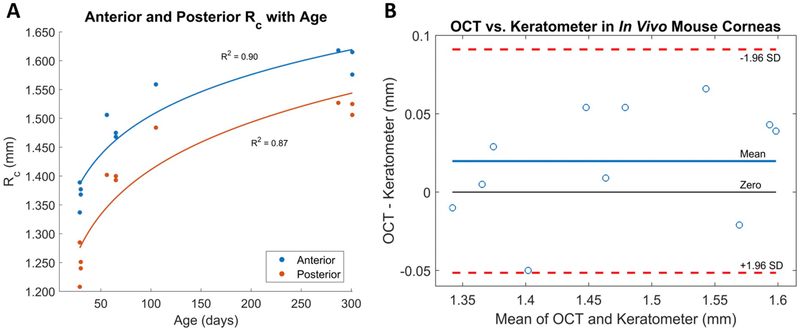
Figure 4. A) OCT-based R_C in eleven eyes from differently aged mice and B) Bland-Altman plot comparing RC obtained using both measurement techniques.

A) Corneal flattening (increase in R_c) was observed in both the anterior and posterior corneal surfaces as mice age increased. B) The limits of agreement (LoA), or the mean difference ± 1.96 SD, in our Bland-Altman plot was −0.313–0.911 mm. The line of equality (zero) was within the 95% confidence interval of mean difference. The mean paired difference between anterior radii of curvature measured by OCT and keratometer was 20 μm, which was not statistically significant (p = 0.12).

Corneal flattening with age was observed in both the anterior and posterior surfaces (Fig. 4A), which is consistent with previously published literature (Chakraborty et al., 2017; Chou et al., 2011). This flattening was found to be associated with larger OCT analysis diameters in older mice (Table 1). A power regression analysis revealed that changes in R_C calculated using the OCT-based method were positively correlated with changes in age (anterior corneal R_C vs. age R² = 0.90; posterior corneal R_C vs. age R² = 0.87). Analysis using the dedicated mouse keratometer showed similarly strong correlations (anterior corneal R_C vs. age R² = 0.87).

3.3.7. Topographic and pachymetric mapping

We based our methods for calculating axial curvature on formulas outlined in the ANSI Z80.23–2007 standard for corneal topography (A.N.S.I., 2007). Curvatures were calculated at 100 points along each meridian. This process was repeated for 100 meridians in both the epithelium and the endothelium, generating curvature data for 10,000 points across the nominal optical zone. R_C was calculated by taking the multiplicative inverse of curvature.

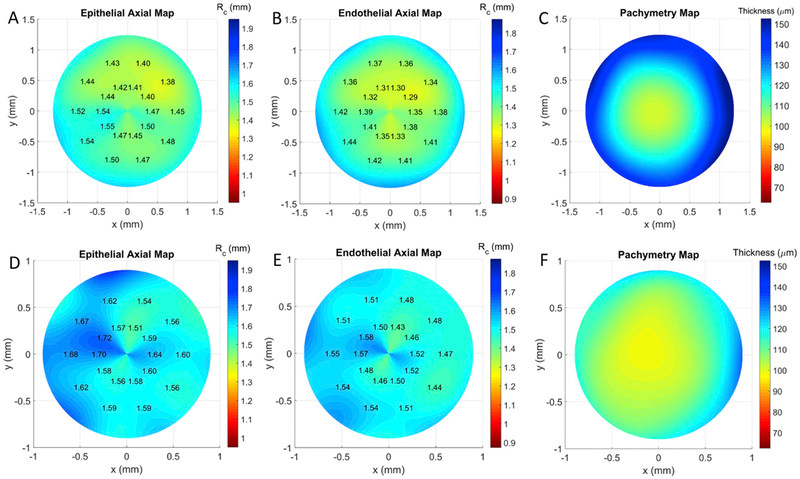
A subset of these localized R_C values is displayed on the topography maps. The maps indicate steep areas in warm colors and flat areas in cool colors with the numerical R_C shown on the right of the plot (e.g. Fig. 5A and B). The age at which animal models are most commonly used in research is 8–12 weeks (Jackson et al., 2017), so we took the average R_C of mice at 10 weeks as the normal anterior R_C. This age is also within the phase of slowest expansion in the mouse eye observed using small-animal magnetic resonance imaging (Tkatchenko et al., 2010). The average anterior R_C for C57BL/6J adult mice at 10 weeks has been reported to be 1.45 ± 0.01 mm using keratometer measurements (Chakraborty et al., 2017) – R_C measurements have also been obtained using OCT and MRI, but explicit numbers were very similar(1.483 ± 0.016 mm for 67 day-old mice, Tkatchenko et al., 2010) or not provided (Chou et al., 2011). However, the reported standard deviation of 0.01 mm was only for mice in this age range and does not represent a larger C57BL/6J mice population. Therefore, we defined our anterior topography map color bar using the standard deviation calculated from our population of mice (0.103 mm), whose ages spanned approximately 4–43 weeks. The color bar spanned approximately five standard deviations above and below 1.450 mm (± 0.500 mm).

Figure 5. Representative anterior curvature maps (A,D), posterior curvature maps (B,E), and pachymetry map (B,F) maps from C57Bl/6J at 65 (A–C) and 301 days (D–F) of age.

The older mouse (D–F) demonstrates a characteristic bow-tie pattern of astigmatism. The smaller diameter in the older mouse is due to more of the cornea masked by eyelid.

Color map limits for the posterior topography map spanned approximately five standard deviations above and below to the average posterior R_C of our mice population (1.374 ± 0.500 mm), which was similar to previously reported posterior R_C values in mice obtained using single OCT scans (Chou et al., 2011).

Regular corneas should exhibit relatively uniform colors around the circumference of its topography maps (Fig. 5A and B). Regular astigmatism, on the other hand, manifests on topography maps as a symmetric “bow-tie” pattern along a single meridian with a straight axis on both sides of center (American Academy of Ophthalmology, 2019). One can see this characteristic bowtie pattern on an astigmatic mouse cornea in Fig. 5D and E. This condition was present in several of our animals.

Our program has the added option to produce individualized topography maps with color limits centered around the anterior or posterior R_C specific to that corneal volume rather than a standardized population average. This helps detection of irregularities within the context of that particular eye.

The central corneal thickness (CCT) of the mice was calculated as the thickness at the corneal vertex as defined by ANSI (A.N.S.I., 2007). Thickness maps were obtained through direct subtraction of corrected endothelial and epithelial surfaces. Cooler colors (blue) are thicker and warmer colors (red) are thinner with numerical values on the right side of plot (e.g. Fig. 5C). Color maps were based on averaging murine CCT values measured across several mouse strains (Lively et al., 2010) and spanned ± 5 of the reported standard deviations (107.6 ± 45 μm). The sub-micrometer digit was due to averaging and not a reflection of the pachymeter resolution.

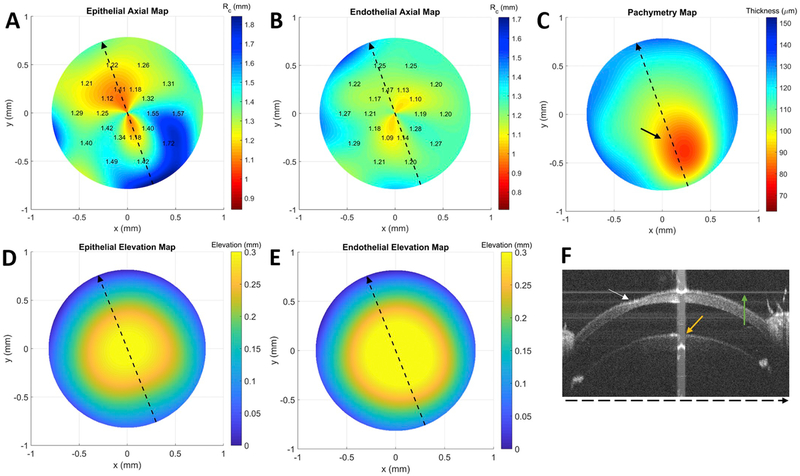
The average CCT in ten mice was 100 ± 3 μm, which is consistent with previously published results of 91–105 μm using optical low coherence reflectometry (Nissirios et al., 2007). One mouse exhibited corneal thinning, which was not immediately noticed during initial review of the OCT volume (Fig. 6D). However, this abnormality was readily detectable in its pachymetry map (Fig. 6C).

Fig. 6. Anterior (A) and posterior (B) curvature map, pachymetry map (C), anterior (D) and posterior (E) elevation maps, and sample OCT B-scan (F) for mouse (subject 3 OS) with corneal thinning.

The dotted lines in A-E represent the lateral location of the OCT scan (F). The area of corneal thinning is indicated by the black (C) or white arrow (F) and its subtle epithelial elevation abnormality can be seen in (D) near the coordinates (x,y) = (0.25,−0.3), especially when compared to the same location in its endothelial counterpart (E). Axial map limits are centered about mean R_C specific to this cornea. The orange and green arrows in (F) correspond to saturation and background subtraction artifacts, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

4. Potential pitfalls and troubleshooting

Our murine topography and pachymetry maps are analogous to those used clinically to characterize localized corneal aberrations and assess general health of the human cornea. We were able to analyze anterior and posterior murine corneal shape in detail for the first time using these maps, and biometric values such as R_C and CCT obtained using our method were consistent with literature. Although we analyzed only one eye from each mouse (with the exception of one mouse that exhibited a corneal abnormality), MCAP is capable of measuring both left and right eyes. Researchers will thus be able to use this program to analyze both eyes scanned in the same session if desired.

This study utilized a Leica OCT system, but MCAP can theoretically be applied to radial OCT images acquired using any system. It should be noted that in order to use MCAP, an OCT system must first be properly calibrated. The pixel-to-mm conversions should be obtained in order to accurately portray the cornea. Additionally, the motors for the galvanometer scanning mirrors in the OCT imaging system may exhibit hysteresis, meaning the galvanometer may lag in expected position for a given input scanning pattern. This results in B-scans that may be translationally offset in physical space. We detail how to obtain this calibration information for any OCT system in the “OCT Calibration” section of the Supplemental Material.

Although our OCT-based method has been validated against calibration spheres for accuracy, there are a few limitations to consider. First, this was a cross-sectional study that primarily demonstrates the utility of MCAP as a tool for researchers. Longitudinal data was not acquired in this study, but it will be useful to evaluate longitudinal reproducibility of this program when imaging mice days or weeks later for further validation. Second, our sample subjects primarily consisted of C57BI/6J mice and only one D4R mouse. This mouse was included due to observations that D4R mice often presented with corneal aberrations, whereas the C57 do not. Thus, the results from our D4R mouse suggest that MCAP can identify these aberrations and analyze other strains as well. Further analysis with greater sample size across multiple strains would be useful to confirm this.

Additionally, it is important to note that while changes in mouse positioning theoretically should not affect R_C and pachymetry maps, mouse positioning may influence CCT and curvature maps. R_C and thickness are biometrics that are relatively independent of orientation since a sphere’s radius should be the same regardless of the sphere’s orientation, and the tomographic nature of OCT should allow for the same thicknesses after optical correction despite repositioning. However, because axial curvature involves calculating distances relative to the corneal topographer axis (as defined by the ANSI standards), differences in mouse positioning can lead to different curvature maps. CCT is also calculated at the corneal vertex, which can change with cornea position (for instance, center of the cornea not being in the center of the scan). Future investigation would be useful to study ways to standardize curvature maps and CCT measurements across different mouse corneal positions.

Since MCAP relies on OCT data, poor OCT image quality can affect the resulting analysis. It is important to optimize the OCT system dispersion settings to prevent corneal surfaces from being blurred. This blurring can affect the accuracy of the corneal segmentations, which likely contributed to higher standard deviations in R_C for the first three mice that we imaged (we first imaged subjects 3, 4, and 8 – subjects were numbered according to age and not the order in which they were imaged). Once dispersion was optimized and the remaining mice were imaged, there was a decrease in R_C standard deviations. However, this decrease may also be partially due to the user familiarity and expertise improving over the course of this study, which would explain the slight decrease in corresponding keratometer standard deviations in the second imaging session as well (subjects 1–2, 5–7, and 9–10). Despite this limitation, overall differences in R_C between OCT and keratometer were not significant. Many OCT images may also experience saturation and background subtraction artifacts, which are lines on the images caused by specular reflections in the sample saturating the camera (Fig. 6D). This saturation is a loss of information in a small center region of the cornea. While it is currently not possible to remove these artifacts completely, methods were implemented in MCAP to interpolate across these regions, which is similar to correction methods used in human corneal OCT segmentation algorithms (Larocca et al., 2011; Huang and Kang, 2012; Rabbani et al., 2016). Our validation results support that we were able to properly address these saturation artifacts.

In conclusion, we presented and validated a method called MCAP that generates key corneal biometrics from mouse OCT volumes. These biometrics include CCT, R_C, anterior and posterior topography maps, and pachymetry (corneal thickness) maps and were previously unavailable to the small animal community. Previously available mouse keratometers are cheaper and take images more quickly, reducing the effects of animal movement. However, our OCT-based method takes advantage of the OCT’s high-resolution images to describe corneal shape in greater detail and generates metrics such as thickness and topography maps of the anterior and posterior surfaces that are not attainable through other methods such as keratometers. Furthermore, we demonstrated that MCAP is capable of accentuating subtle abnormalities in corneal shape, such as corneal thinning, that may otherwise be difficult to detect. The MCAP software package has been made publicly available as part of this manuscript at https://sites.duke.edu/akuolab/mouse-corneal-analysis-program. The ability to measure these biometrics may allow researchers using mouse models of corneal disease to create and noninvasively analyze transgenic mouse lines that replicate human diseases of corneal shape such as keratoconus and astigmatism. These biometrics are analogous diagnostics to those used to characterize human corneal disease and should provide a valuable quantitative tool, especially for laboratories that already have an OCT system, for phenotyping corneas in mouse models of corneal diseases.