Abstract
Rapidly expanding road networks have been a key driver of the fragmentation and isolation of many wildlife species, and are a source of significant mortality due to collisions with vehicles. But not all animals are affected equally by transportation infrastructure, and in most cases little is known about the population-scale consequences of roads for wildlife. Even less information is available to characterize species’ behavioral responses to roads. Although research shows that maned wolves (Chrysocyon brachyurus) in Brazil are experiencing considerable fragmentation and road mortality, the degree to which these disturbances are impacting the species’ viability is unknown. The goal of this study was to analyze the potential effects of roads on maned wolf population size and structure. We used a simulation model to evaluate the population-scale consequences of individual maned wolf interactions with roads, which can result in road crossing, avoidance, or mortality due to a collision with a vehicle. We also forecasted where in Brazil these impacts might be most significant. Our model incorporated species demographic and movement parameters, plus habitat quality and a map of the road network. We found that even moderate rates of road mortality led to severe declines in population size, and that four specific locations accounted for a disproportionate fraction of roadkill events. Our approach will be generally useful for evaluating the relative importance of road effects on species conservation in many ecological systems, for prioritizing data collection efforts, and for informing conservation policies and mitigation strategies.
1. Introduction
The expansion of road networks over the past few decades has been an important mechanism leading to the fragmentation and isolation of many wildlife species, and is responsible for extensive mortality due to collisions with vehicles (Borda-de-Água, Grilo, & Pereira, 2014; van der Ree, Smith, & Grilo, 2015). Existing literature shows that not all fauna are equally affected by road infrastructure (Benítez-López, Alkemade, & Verweij, 2010), and species’ traits and behaviors influence the effects that roads have on a population (Fahrig & Rytwinski, 2009). In general, species with high vagility, low reproductive rates, and that exhibit minimal avoidance of automobiles tend to be more susceptible to road impacts (Jaeger et al., 2005; Rytwinski & Fahrig, 2013). Although there is some literature describing species behavior towards roads (Grilo et al., 2018, 2012; Riley et al., 2006) and quantifying road impacts on populations (Ceia-Hasse, Borda-de-Água, Grilo, & Pereira, 2017), a lack of data for most species (Beaudry, deMaynadier, & Hunter, 2008; Cullen et al., 2016) underscores the value of insights that can be gained through simulation modeling.
Mechanistic predictive models that scale up from individuals to populations are essential tools for forecasting the consequences of road networks on population viability (Borda-de-Água et al., 2014; Jaeger et al., 2005). Models can also address a lack of quantitative data describing behavioral responses to roads by examining the implications of a range of plausible outcomes. While this utility is widely appreciated, few simulation-based assessments (e.g. Huber et al. 2014) have, to our knowledge, explored the consequences that individual behaviors towards roads have for population viability at large spatial scales. Even fewer studies have examined how uncertainty in wildlife-road interaction outcomes propagates through spatial demographic processes to affect conservation-relevant endpoints such as the number and distribution of individuals.
Existing research provides evidence that the maned wolf (Chrysocyon brachyurus) in Brazil is highly impacted by both habitat fragmentation and mortality due to collisions with vehicles. Maned wolf roadkill rates can be as high as 0.083 ind./km/year (Carvalho, 2014), which when coupled with the species’ low population densities (Rodrigues, 2002; Trolle, Noss, De S. Lima, & Dalponte, 2006), likely represents a significant annual loss of individuals. And in Brazil, as for many emerging economies, road networks and traffic volumes are growing rapidly (Laurance et al., 2014; Meijer, Huijbregts, Kees C G, & Schipper, 2018), so the associated impacts on wildlife can be expected to increase with time. For example, Paula & Desbiez (2013) estimated that ongoing habitat loss and fragmentation will cause a reduction of up to 56% of the maned wolf population in Brazil over the next 100 years.
Our principal goal is to evaluate the impacts roads may be having on maned wolf population dynamics. To this end, we employ an individual-based model to measure the potential effects of roads on maned wolf population size and structure. Our model tracks individual interactions with roads, which can result in one of three possible outcomes: road crossing, avoidance, or mortality due to a collision with a vehicle. Because the relative frequencies of maned wolf-road interaction outcomes are poorly known, we perform a sensitivity analysis to explore the population-scale consequences of this uncertainty. Our novel methodology is capable of identifying portions of the Brazilian road network that may qualify as high priority candidates for detailed empirical studies, and ultimately for mitigation efforts such as the installation of fencing and safe passages corridors (Huijser et al., 2016).
2. Methods
2.1. Study area
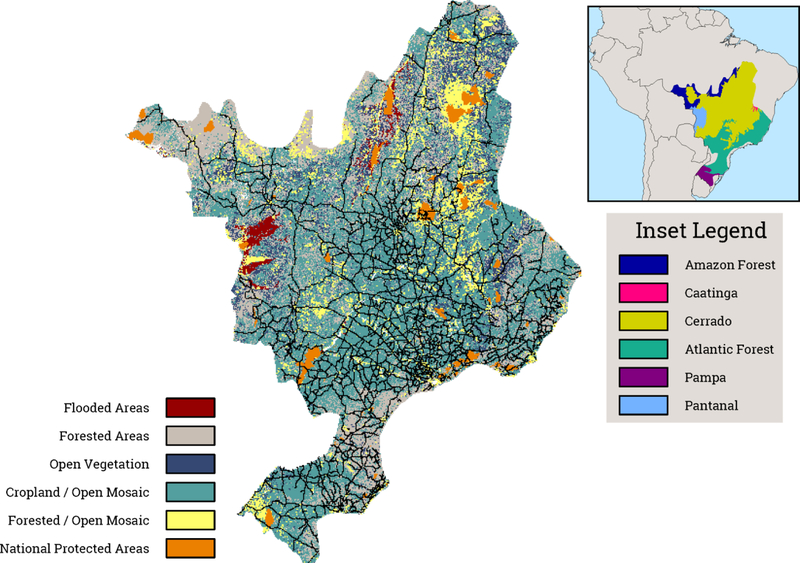
Our study area includes the maned wolf’s current range in Brazil (Fig. 1), which encompasses >3 million km2 comprised mainly of the Cerrado biome (savannah and grasslands), but that also includes small areas of Atlantic Forest, Amazonia Forest, Pantanal (tropical wetlands), Pampas lowlands, and Caatinga (xeric shrubland). Road information was extracted from the ArcGIS road map OpenStreetMap (https://www.geofabrik.de). We considered only paved roads with at least two lanes.
Figure 1.
The study area, road network (black lines), and land cover categories, including regional context (inset). Regional biomes are indicated in the upper-left legend, which corresponds to the inset map.
A map of maned wolf habitat quality was not available for our study area, thus we developed one following an expert-based process known as the Delphi method (MacMillan & Marshall, 2006; Store & Kangas, 2001; Thorn et al., 2018) derived from multi-criteria decision making (Roszkowska & Białymstoku, 2013) and frequently used in land use planning (Kangas et al., 2016), ecosystem services research (Campagne, Sylvie Campagne, & Roche, 2018; Martínez-Harms & Balvanera, 2012), ecology, and conservation (Aizpurua et al., 2015; Krueger, Page, Hubacek, Smith, & Hiscock, 2012; Laniak et al., 2013). We obtained spatial data on land cover from the Global Land Cover Map (http://due.esrin.esa.int/page_globcover.php) and used this information to identify five cover categories occurring throughout the study area (Queirolo et al., 2011; Torres, Pablo Jayat, & Pacheco, 2013): flooded areas, forested areas, mosaic cropland/open vegetation, mosaic forested/open vegetation, and open vegetation. Each category’s importance to maned wolves was ranked from 0 – 100 by five species experts, with 0 indicating non-habitat and 100 indicating very desirable habitat. As described in Holey et al. (2007) and Thorn et al. (2018), the median of each set of five expert-supplied values was taken to represent the importance of the land cover classes (Table 1), and used to assemble a map of habitat quality.
Table 1.
Resource values supplied by species experts that were used to construct the habitat quality map.
| Land Cover Class | Mosaic Cropland / Open Vegetation | Flooded Areas | Forest Area | Mosaic Forest / Open Vegetation | Open Vegetation | Water Bodies and Surroundings | Urban Areas and Surroundings |
|---|---|---|---|---|---|---|---|
| Reviewer 1 | 80 | 75 | 50 | 95 | 100 | 55 | 10 |
| Reviewer 2 | 80 | 10 | 60 | 90 | 100 | 80 | 50 |
| Reviewer 3 | 70 | 30 | 50 | 80 | 100 | 60 | 20 |
| Reviewer 4 | 95 | 2 | 5 | 85 | 95 | 1 | 45 |
| Reviewer 5 | 55 | 15 | 5 | 55 | 80 | 15 | 2 |
| Median Value | 80 | 15 | 50 | 85 | 100 | 55 | 20 |
2.2. Study design
We used HexSim 4.0 (Schumaker & Brookes, 2018) to develop a spatially-explicit, individual-based life history model of the maned wolf. While other simulation models might have been adopted for this study – for example Vortex (www.vortex10.org), RAMAS (www.ramas.com), or NetLogo (https://ccl.northwestern.edu/netlogo) – we selected HexSim because it is spatially-explicit and individual-based, and because it contains features designed specifically for evaluating the consequences of individual interactions with roads. Our model tracked females only, included stage-specific vital rates scaled by resource acquisition, and exhibited density-dependent effects on survival and reproduction. Our “baseline model” incorporated demographic but not environmental stochasticity, and we used it to develop ten separate simulations which were identical except for properties exhibited by our road map (Table 2). We also developed a companion model that included both demographic and environmental stochasticity, but was otherwise identical to the baseline model. To add environmental stochasticity, this model assigned each year a numeric quality coefficient by drawing a random value from a uniform distribution bounded by 0.9 and 1.1. Every individual’s fecundity and survival values were then multiplied by this year-quality coefficient, thus producing a ±10% correlated annual variation in all vital rates.
Table 2.
Road properties used in the study. Simulations 0, 6, and 7 were run for 150 time steps because they took longer to reach steady state.
| Simulation ID | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Transmission | 0.50 | 0.45 | 0.40 | 0.35 | 0.30 | 0.25 | 0.00 | 1.00 | 0.00 | 0.50 |
| Deflection | 0.50 | 0.45 | 0.40 | 0.35 | 0.30 | 0.25 | 1.00 | 0.00 | 0.50 | 0.00 |
| Mortality | 0.00 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.00 | 0.00 | 0.50 | 0.50 |
| Time steps | 150 | 100 | 100 | 100 | 100 | 100 | 150 | 150 | 100 | 100 |
Our study considered three possible wolf-road interaction outcomes: successful road crossing (hereafter transmission), road avoidance (hereafter deflection), and death due to a collision with an automobile (hereafter mortality). Road transmission, deflection, and mortality rates necessarily summed to 1.0; and in any given simulation, a single set of rates were applied to the entire road map (Table 2). For clarity, we distinguish between our two parameterized HexSim computer models, with and without environmental stochasticity, and the replicated studies we conducted using them. We use the term “simulation” to indicate a replicated application of one of the maned wolf models run with a specific set of road transmission, deflection, and mortality rates. In this context, each simulation can be thought of as one component of a sensitivity analysis of the uncertainty in the frequency of maned wolf-road interaction outcomes. The model time step was one year, and ten replicates were performed for each baseline model simulation, as initial experimentation illustrated that number was quite adequate in the absence of environmental stochasticity. We gathered data from 50 replicates to characterize simulations that included environmental stochasticity.
Six baseline model simulations evaluated the consequences of increasing road mortality rates from 0.0 to 0.5 per encounter. While the limits of this range may be unrealistic, our intent was to characterize population responses to a wide spectrum of road properties. Two additional baseline model simulations examined zero-mortality assumptions in which roads were purely transmitting or purely deflecting. In two final baseline model simulations, either road transmission or deflection rates were set to zero (Table 2).
Our land cover and road maps were static, and long model runs were used to gather large amounts of data at steady-state, not to forecast population size far into the future. Simulations with zero road mortality were slow to reach steady state because they produced relatively large population sizes. We therefore ran our simulations for 150 time steps in the absence of road mortality, and 100 time steps otherwise (Table 2). With the exception of population size, model outputs were compiled only after steady state had been reached – which was always considered to be the final 50 time steps of a simulation.
2.3. HexSim model
HexSim tessellates space using a hexagonal grid, and it converted our habitat map into an array of approximately 15M hexagonal cells. Each of these cells was 21.65 ha in area and had a diameter (the distance separating parallel edges) of 500 meters. Each hexagonal cell’s habitat value was set to the mean of the rankings assigned to the raster land cover pixels it intersected. Our road layer was imported as an ESRI polyline Shapefile, and in this process HexSim snapped road polylines to the nearest hexagon vertices. After import, our road layer consisted of approximately 385K separate hexagonal edge segments, each roughly 289 meters in length. Simulated maned wolves experienced a probabilistic barrier interaction when they moved between two adjacent hexagons if a barrier was located at the shared edge.
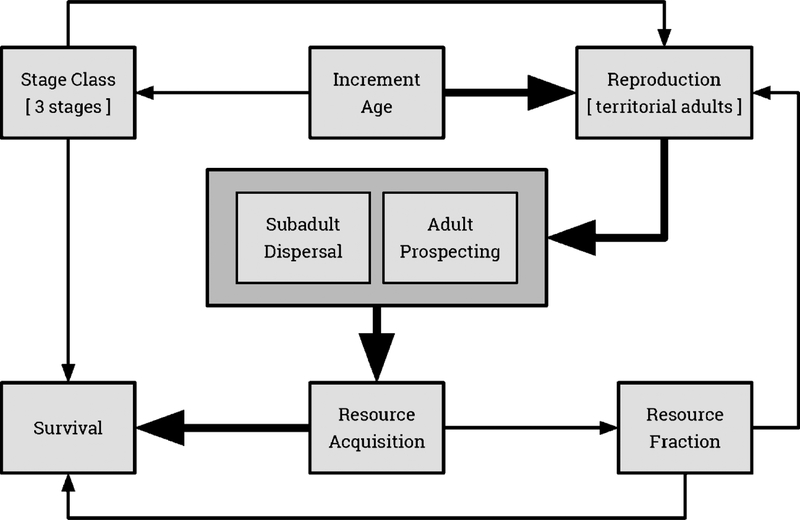
Our models (Table 3, Fig. 2) divided maned wolves into three stage classes labeled juvenile, subadult, and adult. The juvenile and subadult stages lasted a single year. Maned wolves dispersed as subadults (Paula & Desbiez, 2013), and prospected for territories as adults (Amboni, 2007; Azevedo, 2008; Coelho et al., 2008). Adults who failed to obtain a breeding territory continued to search for one. Individuals became reproductive in their third year of life (IUCN, 2008; Paula et al., 2008; Paula & Desbiez, 2013) and litter sizes ranged between 0 – 3 (Dietz, 1984; Paula et al., 2008; Silveira, 1999). Annual mortality not attributed to roads (Paula et al., 2008; Paula & Desbiez, 2013) included senescence once a maximum estimated lifespan of 13 years was reached (IUCN, 2008; Paula et al., 2008). During movement, all individuals encountering a road could either (a) avoid it, (b) cross it successfully, or (c) die trying to cross due to an assumed roadkill event. Simulated maned wolves could encounter roads multiple times per movement event.
Table 3.
Model parameters used to simulate key demographic processes. The calculation of survival outcomes and litter sizes were influenced by resource acquisition rates, and involved drawing random values from uniform and normal distributions, respectively. Realized territory sizes varied depending on landscape quality, road properties, and conspecific competition.
| Demographic Parameter | Value | References |
|---|---|---|
| Maximum Territory Size | 13.64 km2 or 63 Hexagons | Amboni 2007 |
| Azevedo 2008 | ||
| Coelho et al. 2008 | ||
| Maximum Lifespan | 156 Months | Rodden et al. 2004 |
| Paula et al. 2008 | ||
| Litter Size (mean, maximum) | 1.5, 3.0 | Dietz 1984 |
| Paula et al. 2008 | ||
| Silveira 1999 | ||
| Age at First Birth | 24 Months | Paula et al. 2008 |
| Annual Survival Rate (juvenile, subadult, adult) | 0.40, 0.76, 0.90 | Paula et al. 2008 |
| Paula & Desbiez 2013 |
Figure 2.
A simplified schematic of the model life cycle. Thick lines connect the principal events taking place within a year, beginning with wolves getting older, and ending with a survival decision. Consequences of these events for individual state variables (e.g. stage and resource class) are indicated with thin lines.
Realized survival and reproductive rates were stochastic and influenced by resource availability evaluated at the scale of the individual territory. Survival outcomes were determined by drawing random values from a uniform distribution, while litter sizes were drawn from a normal distribution (Table 3). Territories were non-overlapping, and access to resources could be constrained by the presence of neighboring maned wolves. Only territorial adults were allowed to reproduce, and established territories were never abandoned. Prospecting adults assembled territories from hexagons with a minimum habitat value of 50 on a scale of 0 – 100, which prevented individuals from settling in exceptionally poor locations.
Subadult dispersers took a sequence of steps between adjacent hexagons, and were influenced by both habitat quality (a tendency to move towards better habitat) and a moderately-high degree of autocorrelation (a tendency to move in a forward direction). Rodrigues (2002) observed dispersal distances varying between 47 – 86 km, while the equation published by Bowman, Jaeger, & Fahrig (2002) suggests that dispersers move between 3 – 106 km. We used the broader Bowman et al. bounds to parameterize simulated maned wolf dispersal distances. Dispersers stopped if they encountered a high-quality habitat patch after moving at least 10 km from their natal site.
2.4. Simulation outputs
For each baseline model simulation, we combined the results from all ten replicates to track population size, the frequency with which maned wolves encountered individual road segments, occupancy rates, and source-sink properties. Building on the approach articulated in Schumaker et al. (2014) and Schumaker & Brookes (2018), we sampled occupancy and source-sink value using multi-hexagon patches. This sampling was performed simultaneously at five spatial scales (Table 4) in order to eliminate artifacts generated by the patch edges. We describe this map-generation process in greater detail below.
Table 4.
Spatial sampling scheme details. The patches used to sample occupancy rate and source-sink quality were themselves hexagonal in shape. Original and split patch numbers refer to the total count before and after patches were intersected and split by roads.
| Sampling Scales | |||||
|---|---|---|---|---|---|
| Patch Diameter (hexagons) | 51 | 73 | 89 | 101 | 113 |
| Patch Area (hexagons) | 1951 | 3997 | 5941 | 7651 | 9577 |
| Number Original Patches | 7966 | 3956 | 2698 | 2123 | 1710 |
| Number Split Patches | 10,520 | 5827 | 4296 | 3560 | 3235 |
Occupancy rates and source-sink values could be gathered for each individual hexagon, but that spatial scale is too fine to meaningfully resolve landscape-wide patterns. Instead, we collected occupancy and source-sink information by aggregating information within larger multi-hexagon patches. These patches ranged in area from 1951 to 9577 hexagons (Table 4), were themselves hexagonal in shape, and were arranged in space-filling arrays. Each patch was assigned an occupancy or source-sink value equal to the sum of the individual contributions observed for each hexagon it contained. For organisms like the maned wolf that are wide-ranging relative to the size of a hexagon, this mapping technique effectively illustrates emergent model properties. But the method also introduces two artifacts: mapped occupancy and source-sink values will often change abruptly at patch edges, and no single spatial scale will be optimal landscape-wide. We addressed both concerns by sampling occupancy and source-sink data at five spatial scales simultaneously (Table 4) – a process greatly facilitated by HexSim’s design. The results were then normalized by linearly transforming each single-scale occupancy map to the range [0, 100], and each source-sink map to the range [−100, 100]. Final multi-scale output maps were developed by assigning each hexagon the mean of the normalized occupancy rates or source-sink values observed at each of the five sampling scales. The patch maps used in the sampling process were only employed for data collection, and had no effect on the simulated maned wolves. Every replicate simulation gathered data at all five scales simultaneously.
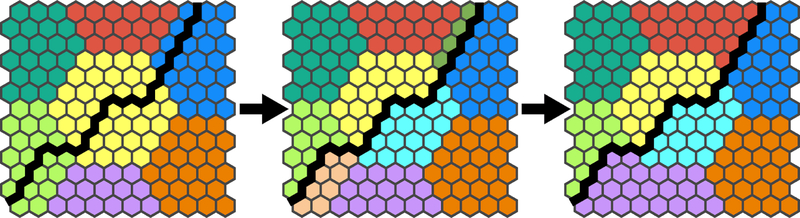
Before the sampling maps (Table 4) could be used, we first had to intersect them with the road network, thus subdividing many of the patches they contained. The need for this can be illustrated by considering a sampling patch divided by a road into left and right halves. If the road could not be crossed, a situation could arise in which the left half of the patch was frequently used, while the right half was never visited. If occupancy rate or source-sink value were compiled for the patch as a whole, then the impact of the road would be obscured. We therefore split all sampling patches that were divided by roads, and computed each fragment’s occupancy and source-sink value separately (Figure 3).
Figure 3.
A hypothetical illustration of the process involved in splitting patches along roads (left, center), and merging resulting small fragments (right). A road is indicated by the thick black line.
Our occupancy rates were tallies of the number of individuals that remained in a patch for a full year. Source-sink data were gathered as the number of individuals emigrating from a patch minus the number immigrating. Patches that exported more individuals than they imported were sources, and net importers were sinks. While occupancy rates were always non-negative, source-sink values could be negative (sinks) or positive (sources). Both source-sink and occupancy data were gathered at steady-state, and we confirmed that source-sink maps made by tracking births – deaths were identical to those made by tracking emigration – immigration (Schumaker et. al., 2018). Occupancy rates and source or sink values were bounded only by the number of observations, but we standardized the data collection effort across all simulations. Further, the maps of occupancy rates and source-sink values we developed illustrate relative, not absolute quantities.
2.5. Model availability and usability
The HexSim models used in this study, including all maps and related data, are available for download at www.hexsim.net. We ran all simulations on a laptop computer having a 2.8 GHz processor and 16 GB of RAM. Individual simulation replicates with a road mortality rate of 0.3 (simulation ID 3) took four to five hours to complete, and each produced roughly 1.6 GB worth of model output. However, the simulations can run considerably more rapidly if HexSim is instructed not to write out its “log file”, which accounts for the vast majority of disk space consumed. Simulations producing larger population sizes took longer to complete, and visa-versa. Two simulations of the maned wolf model could be run simultaneously without exceeding the computer’s available memory.
3. Results
3.1. Population dynamics
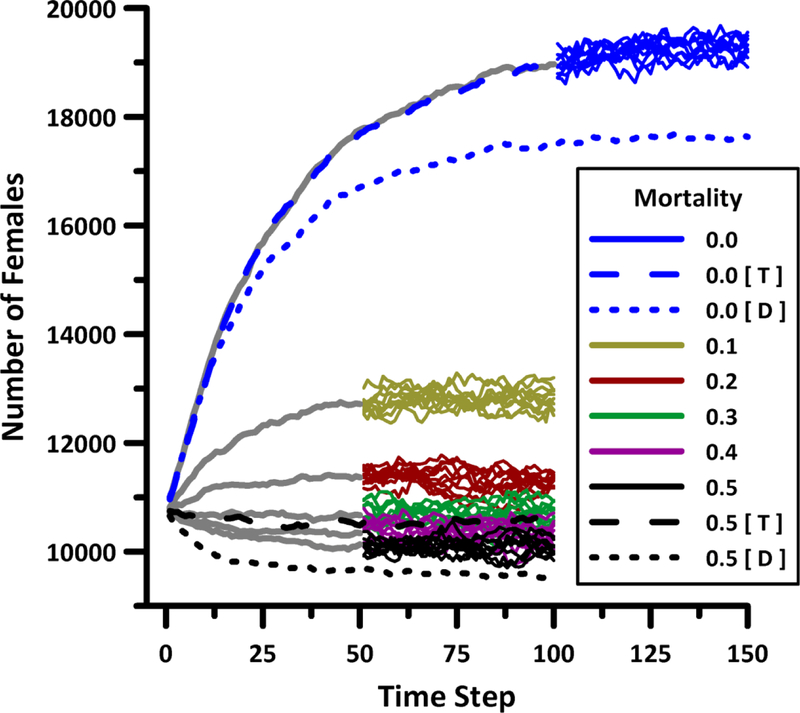
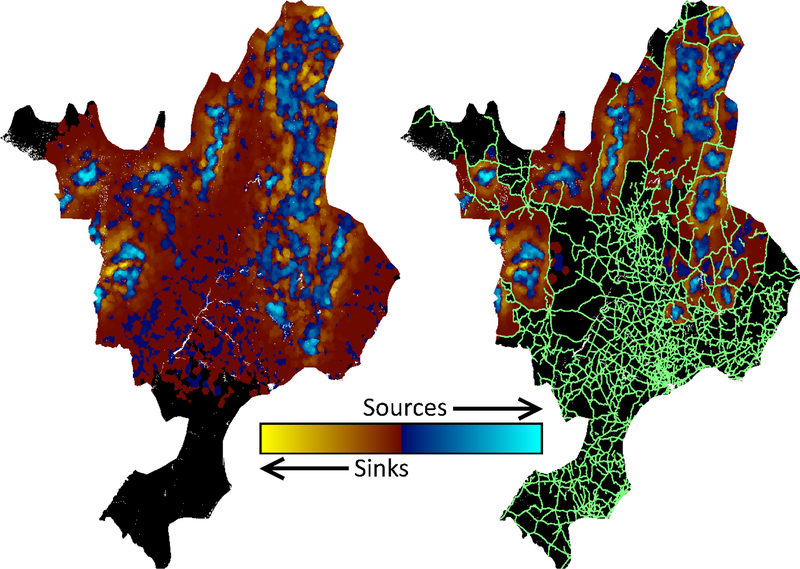
Variability between simulation replicates was low (Fig. 4) because our baseline model did not include environmental stochasticity. In the absence of road mortality (simulation IDs 0, 6, 7 in Table 2), we observed population sizes in excess of 17K females (full deflection) or 19K females (partial or no deflection). Population size decreased as road mortality increased, but the relationship linking this driver (road mortality) and its response (population size) was nonlinear. In the absence of road mortality, the maned wolf population declined by roughly 1.5K females as road attributes were shifted from being fully permeable (simulation ID 7, Fig. 4 upper dashed blue line) to fully deflective (simulation ID 6, Fig. 4 lower dashed blue line). The imposition of just 10% road mortality (simulation ID 1, Figure 4 yellow line) caused the mean population size to drop below 13K females, and as road mortality was increased to a maximum of 50% (simulation IDs 5, 8, 9), the observed mean population size dropped to about 10K females. The lowest mean population sizes were observed when road mortality was highest and the probability of crossing a road was lowest (simulation ID 8). The maned wolf’s effective range and the distribution of demographic source and sink areas also exhibited a strong response to road properties (Fig. 5). Demographic sources were primarily observed in portions of Brazil’s Pantanal and Cerrado.
Figure 4.
Observed population sizes. Solid colored lines illustrate the steady-state results collected from groups of 10 replicates having the indicated mortality rate, (simulation ID 0–5 in Table 2). Gray lines represent corresponding mean values prior to steady-state. Dashed lines illustrate mean values for replicate simulations in which all non-lethal encounters resulted exclusively in transmission [T] or deflection [D] (simulation ID 6–9 in Table 2).
Figure 5.
The observed source-sink distribution resulting from two simulations: ID 7 (no impacts, left) and ID 8 (this study’s maximum impacts, right). Each map was assembled using data from all ten replicates. Demographic sinks trend in color from yellow (strong) to red (weak), while sources trend from blue (weak) to cyan (strong). Neutral areas are showed in black, and the road network is displayed in green.
For comparison, we ran 50 replicates of our model incorporating environmental stochasticity and a road mortality rate of 0.3 (simulation ID 3). Collectively, these results exhibited a population size varying between 5.6K and 17.5K females, with a mean of 10.5K. Our ten baseline model replicates run with identical road properties produced population sizes that ranged from 10.1K to 11.1K females and a mean of 10.7K (Fig. 4). The mean observed population size therefore increased by roughly 2.7% with the inclusion of environmental stochasticity. We also used the results from the 10 replicate baseline model simulations imposing a road mortality rate of 0.3 (simulation ID 3) to examine the emergent frequency distribution of maned wolf dispersal distances. This distribution (not shown) was roughly lognormal, as might be expected for a wide-ranging vertebrate species prospecting for resources within a highly disturbed landscape. The mean observed dispersal distance was 63km.
When road mortality was nonzero, we clearly gathered simulation outputs at steady-state (Fig. 4). We may have slightly underestimated the maximum population size when both road mortality and deflection rates were zero; however, this no-impact limiting case is only employed here as a frame of reference for evaluating other results. Trade-offs between transmission and deflection captured in our results illustrate the negative consequences of the latter (Fig. 4, black and blue dashed lines). When mortality was highest, increasing road permeability boosted population sizes, and vice-versa. When mortality was absent, population size decreased substantially as permeability fell from 100% to zero.
3.2. Road impacts
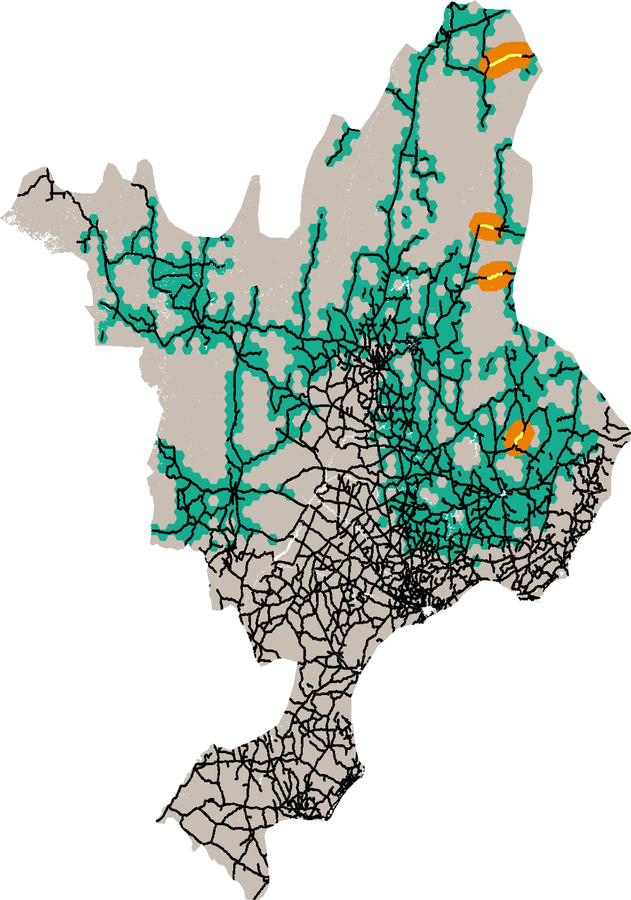
Our results exhibited a non-uniform spatial distribution of road impacts, with the majority of road segments responsible for unusually large roadkill frequencies clustered into four specific locations (Fig. 6). These high impact road segments account for just 0.3% of our total road network, but were responsible for 7, 9, and 10% (respectively) of all roadkill events observed in simulations with IDs 1, 2 & 3, and, 4 & 5 (Table 2). The high impact roads fell along a north-south axis in the western portion of the study area, and were observed to occur in the spaces separating significant demographic sources (q.v. Fig. 5 right and Fig. 6).
Figure 6.
Road impacts observed across the study area. The stretches of road responsible for the greatest mortality are displayed in yellow and highlighted in orange. Roads highlighted in green resulted in at least one mortality in one or more simulations.
As indicated above, the baseline model with a road mortality rate of 0.3 (simulation ID 3) produced a cumulative mortality of 9.0% for the 0.3% of the road network we characterized as high impact. For comparison purposes, we used the 50 replicates simulations conducted using our model incorporating environmental stochasticity to gauge the sensitivity of our results to the addition of annual variability. When the road impacts assessment was repeated with the results from the model incorporating environmental stochasticity, the cumulative mortality attributable to the same high impact road segments increased slightly to 9.2%.
4. Discussion
In this study, we provided an example showing how recent developments in ecological modeling can help scientists leverage existing data to inform policy. Our results help validate the common contention (Ceia-Hasse et al., 2017; Paula & Desbiez, 2013) that mortality due to collisions with vehicles is a major contributor to the negative effects of roads on maned wolves. A comparison of our findings to available estimates of population size and distribution across the study area (IUCN, 2008; Paula & Desbiez, 2013; Queirolo et al., 2011; Trolle et al., 2006), indicates that road mortality rates may now be approximately 20 – 30% on average, and we assert that the available literature (Grilo, Ascensão, Santos-Reis, & Bissonette, 2010; Grilo et al., 2012; Santos, Lourenço, Mira, & Beja, 2013) suggests these values are plausible.
We found that emergent demographic sources represent a small portion of species’ current range, and observed that these areas correspond well to the locations of the principal maned wolf subpopulations, as defined by canid specialists in Brazil (see Paula & Desbiez 2013 for detailed information). The spatial distribution of demographic source areas was mostly invariant to changes in simulated road properties. Our model indicated that four specific stretches of road were responsible for a disproportionate number of roadkill events, and that these high-impact roadways were situated between adjacent demographic sources.
For any given simulation, all of the roads were assigned identical properties. Observed roadkill rates must therefore correspond directly to encounter frequency, which is in turn dictated by dispersal and prospecting behavior, and the distribution of roads. But the demographic and behavioral feedbacks (e.g. density dependence, landscape influences on movement behavior) that complicate the inference of source-sink attributes based strictly upon habitat quality also make it difficult to anticipate which roads will realize the most crossing attempts. Thus while the likelihood of being killed when crossing a road was the same everywhere, the emergent roadkill patterns were highly non-uniform. Our results suggest this emergent spatial distribution of roadkill rates was influenced by large dispersal fluxes that became established between highly productive source areas (e.g. Schumaker et. al., 2014). Our simulations also illustrate that the character of road impacts is robust to the addition of environmental stochasticity.
Finally we observed that even if they impart zero mortality, roads can significantly reduce population size (Fig. 4) by constraining maned wolf dispersal. Large portions of the maned wolf’s range are highly fragmented by roads (Fig. 5). When these roads could not be crossed, subpopulations falling within their bounds frequently became completely isolated. These population fragments were impacted by higher rates of stochastic extinction, and had no possibility of demographic rescue. Compounding this dynamic, simulated maned wolf home ranges and territories were also not allowed to span fully-impermeable roads, thus constraining the carrying capacity and resources available to occupants of isolated habitat areas. Our results thus reinforce the concern that the benefit of lowered roadkill rates gained from the construction of fencing may be somewhat offset by the costs attributable to additional resulting landscape fragmentation.
Naturally, our model has limitations that might be evaluated and possibly corrected prior to any attempt at informing management or policy decisions. One goal of this study was to illustrate that spatial IBMs need not be so data-hungry that their application is limited to the best studied systems. Data is clearly a constraint in the maned wolf system; and our model would be improved if we, for example, had access to better habitat maps, relationships tying resources and disturbance to vital rates, or a richer understanding of movement behavior. More idiosyncratic limitations also warrant consideration. While actual road properties will change from place to place, the quality of our road map prevented us from discriminating between road types. Thus, for a given simulation, we assigned all of our roads identical properties. We did not have maps projecting how the road network or traffic volumes would change through time, nor did we have range-wide data sufficient for developing disturbance models for other stressors. These limitations necessitated constructing a relatively simple model, which as a consequence is easy to understand. We note that none of these constraints were imposed by HexSim; were new data to become available, relaxing them would not be difficult.
5. Conclusion
Our study illustrates how, in spite of significant data limitations, a spatial life history simulator can be developed and put into service in support of conservation goals. This is broadly relevant since empirical data, and our understanding of species’ ecology and disturbance regimes, are often quite limited. As is the case for many species, the maned wolf’s extensive remaining geographic distribution makes prioritization of conservation and mitigation measures both scientifically and logistically complex. Because these efforts will be costly and difficult to implement, attempts must be made to inform planning and decision-making using the best available information and research. By identifying four specific stretches of road exhibiting high apparent roadkill frequencies, we have illustrated how an individual-based simulation model can assist the prioritization of future empirical research and eventually conservation actions.
The challenge of protecting maned wolves has much in common with efforts to assist other species of concern. And insights gleaned from our mechanistic demographic model complement those obtained from methodologies that cannot evaluate the full costs of roads for wildlife. Popular tools employing graph theory, circuit theory, or least cost path analysis will measure road impacts to connectivity, but must stop short of inferring consequences for population size or viability. We hope readers inspired by our work will make use of the methods described here to evaluate potential road impacts on other species of concern, and to continue bringing biological detail and realism to landscape connectivity assessments.
Acknowledgements
This study was part of the project “Road Macroecology: analysis tools to assess impacts on biodiversity and landscape structure” funded by CNPq (N° 401171/2014-0). PB was supported by FAPEMIG grant (Process PAPG-11686) and CG by CNPq (AJT N° 300021/2015-1). Thanks are also due for the financial support to CESAM (UID/AMB/50017/2019), to FCT/MCTES through national funds. We thank Anthony P. Clevenger for early comments on the manuscript. Special thanks to all the Canid specialists that responded to our enquiries, including Flávio H. G. Rodrigues, André G. Chiarello, Eleonore Setz, Eliana F. Santos and José C. Motta-Júnior. We also greatly appreciate the thoughtful and insightful comments provided by two anonymous reviewers. The information in this document has been funded in part by the U.S. Environmental Protection Agency. It has been subjected to review by the National Health and Environmental Effects Research Laboratory’s Western Ecology Division and approved for publication. Approval does not signify that the contents reflect the views of the Agency.
Literature Cited
- Aizpurua O, Cantú-Salazar L, Martin GS, Biver G, Brotons L, & Titeux N (2015). Reconciling expert judgement and habitat suitability models as tools for guiding sampling of threatened species. The Journal of Applied Ecology, 52(6), 1608–1616. [Google Scholar]
- Amboni MPM (2007). Dieta, disponibilidade alimentar e padrão de movimentação de loboguará, Chrysocyon brachyurus, no Parque Nacional da Serra da Canastra (MS) Universidade Federal de Minas Gerais, Belo Horizonte, Minas Gerais. [Google Scholar]
- Azevedo FC (2008). Área de vida e organização espacial de lobos-guará (Chrysocyon rachyurus) na região do Parque Nacional da Serra da Canastra (MS) Universidade Federal de Minas Gerais, Belo Horizonte, Minas Gerais. [Google Scholar]
- Beaudry F, deMaynadier PG, & Hunter ML (2008). Identifying road mortality threat at multiple spatial scales for semi-aquatic turtles. Biological Conservation, 141(10), 2550–2563. [Google Scholar]
- Benítez-López A, Alkemade R, & Verweij PA (2010). The impacts of roads and other infrastructure on mammal and bird populations: A meta-analysis. Biological Conservation, 143(6), 1307–1316. [Google Scholar]
- Borda-de-Água L, Grilo C, & Pereira HM (2014). Modeling the impact of road mortality on barn owl (Tyto alba) populations using age-structured models. Ecological Modelling, 276, 29–37. [Google Scholar]
- Bowman J, Jaeger JAG, & Fahrig L (2002). Dispersal Distance of Mammals Is Proportional to Home Range Size. Ecology, 83(7), 2049. [Google Scholar]
- Campagne CS, Sylvie Campagne C, & Roche P (2018). May the matrix be with you! Guidelines for the application of expert-based matrix approach for ecosystem services assessment and mapping. One Ecosystem, 3, e24134. [Google Scholar]
- Carvalho CF (2014). Atropelamento de vertebrados, hotspots de atropelamentos e parâmetros associados, BR-050, trecho Uberlândia-Uberaba (MS) Universidade Federal de Uberlândia, Uberlândia, Minas Gerais. [Google Scholar]
- Ceia-Hasse A, Borda-de-Água L, Grilo C, & Pereira HM (2017). Global exposure of carnivores to roads. Global Ecology and Biogeography: A Journal of Macroecology, 26(5), 592–600. [Google Scholar]
- Coelho CM, De Melo LFB, Sábato MAL, Vaz Magni EM, Hirsch A, & Young RJ (2008). Habitat Use by Wild Maned Wolves (Chrysocyon brachyurus) in a Transition Zone Environment. Journal of Mammalogy, 89(1), 97–104. [Google Scholar]
- Cullen L Jr, Stanton JC, Lima F, Uezu A, Perilli MLL, & Akçakaya HR (2016). Implications of Fine-Grained Habitat Fragmentation and Road Mortality for Jaguar Conservation in the Atlantic Forest, Brazil. PloS One, 11(12), e0167372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dietz JM (1984). Ecology and social organization of the maned wolf (Chrysocyon brachyurus). Smithsonian Contributions to Zoology, (392), 1–51. [Google Scholar]
- Fahrig L, & Rytwinski T (2009). Effects of Roads on Animal Abundance: an Empirical Review and Synthesis. Ecology and Society, 14(1). 10.5751/es-02815-140121 [DOI] [Google Scholar]
- Grilo C, Ascensão F, Santos-Reis M, & Bissonette JA (2010). Do well-connected landscapes promote road-related mortality? European Journal of Wildlife Research, 57(4), 707–716. [Google Scholar]
- Grilo C, Molina-Vacas G, Fernández-Aguilar X, Rodriguez-Ruiz J, Ramiro V, Porto-Peter F, … Revilla E (2018). Species-specific movement traits and specialization determine the spatial responses of small mammals towards roads. Landscape and Urban Planning, 169, 199–207. [Google Scholar]
- Grilo C, Sousa J, Ascensão F, Matos H, Leitão I, Pinheiro P, … Revilla E (2012). Individual spatial responses towards roads: implications for mortality risk. PloS One, 7(9), e43811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holey EA, Feeley JL, Dixon J, & Whittaker VJ (2007). An exploration of the use of simple statistics to measure consensus and stability in Delphi studies. BMC Medical Research Methodology, 7, 52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber PR, Greco SE, Schumaker NH, Hobbs J (2014). A priori assessment of reintroduction strategies for a native ungulate: using HexSim to guide release site selection. Landscape Ecology, 29, 689–701. [Google Scholar]
- Huijser MP, Fairbank ER, Camel-Means W, Graham J, Watson V, Basting P, & Becker D (2016). Effectiveness of short sections of wildlife fencing and crossing structures along highways in reducing wildlife–vehicle collisions and providing safe crossing opportunities for large mammals. Biological Conservation, 197, 61–68. [Google Scholar]
- IUCN. (2008). Chrysocyon brachyurus: Rodden M, Rodrigues F & Bestelmeyer S IUCN Red List of Threatened Species. 10.2305/iucn.uk.2008.rlts.t4819a11097908.en [DOI] [Google Scholar]
- Jaeger JAG, Bowman J, Brennan J, Fahrig L, Bert D, Bouchard J, … von Toschanowitz KT (2005). Predicting when animal populations are at risk from roads: an interactive model of road avoidance behavior. Ecological Modelling, 185(2–4), 329–348. [Google Scholar]
- Kangas KM, Tolvanen A, Tarvainen O, Nikula A, Nivala V, Huhta E, & Jäkäläniemi A (2016). A method for assessing ecological values to reconcile multiple land use needs. Ecology and Society, 21(3). 10.5751/es-08590-210305 [DOI] [Google Scholar]
- Krueger T, Page T, Hubacek K, Smith L, & Hiscock K (2012). The role of expert opinion in environmental modelling. Environmental Modelling & Software, 36, 4–18. [Google Scholar]
- Laniak GF, Olchin G, Goodall J, Voinov A, Hill M, Glynn P, … Hughes A (2013). Integrated environmental modeling: A vision and roadmap for the future. Environmental Modelling & Software, 39, 3–23. [Google Scholar]
- Laurance WF, Clements GR, Sloan S, O’Connell CS, Mueller ND, Goosem M, … Arrea IB (2014). A global strategy for road building. Nature, 513(7517), 229–232. [DOI] [PubMed] [Google Scholar]
- MacMillan DC, & Marshall K (2006). The Delphi process - an expert-based approach to ecological modelling in data-poor environments. Animal Conservation, 9(1), 11–19. [Google Scholar]
- Martínez-Harms MJ, & Balvanera P (2012). Methods for mapping ecosystem service supply: a review. International Journal of Biodiversity Science, Ecosystems Services & Management, 8(1–2), 17–25. [Google Scholar]
- Meijer JR, Huijbregts MAJ, Kees CG, & Schipper AM (2018). Global patterns of current and future road infrastructure. Environmental Research Letters: ERL [Web Site], 13(6), 064006. [Google Scholar]
- Paula RC, Medici P, & Morato RG (2008). Plano de Ação para a Conservação do LoboGuará - Análise de Viabilidade Populacional e de Hábitat (PHVA). Instituto Brasileiro de Meio Ambiente e Recursos Naturais Renováveis (IBAMA). [Google Scholar]
- Paula R, & Desbiez A (2013). Maned Wolf Population Viability. In Ecology and Conservation of the Maned Wolf (pp. 15–34). [Google Scholar]
- Queirolo D, Moreira JR, Soler L, Emmons LH, Rodrigues FHG, Pautasso AA, … Salvatori V (2011). Historical and current range of the Near Threatened maned wolf Chrysocyon brachyurus in South America. Oryx: The Journal of the Fauna Preservation Society, 45(02), 296–303. [Google Scholar]
- Riley SPD, Pollinger JP, Sauvajot RM, York EC, Bromley C, Fuller TK, & Wayne RK (2006). A southern California freeway is a physical and social barrier to gene flow in carnivores. Molecular Ecology, 15(7), 1733–1741. [DOI] [PubMed] [Google Scholar]
- Rodrigues FHG (2002). Biologia e conservação do lobo-guará na estação ecológica de Águas Emendadas, DF (Ph.D.). University of Campinas, São Paulo. [Google Scholar]
- Roszkowska E, & Białymstoku U. w. (2013). Rank Ordering Criteria Weighting Methods – a Comparative Overview. Optimum. Studia Ekonomiczne, 5(65), 14–33. [Google Scholar]
- Rytwinski T, & Fahrig L (2013). Why are some animal populations unaffected or positively affected by roads? Oecologia, 173(3), 1143–1156. [DOI] [PubMed] [Google Scholar]
- Santos SM, Lourenço R, Mira A, & Beja P (2013). Relative effects of road risk, habitat suitability, and connectivity on wildlife roadkills: the case of tawny owls (Strix aluco). PloS One, 8(11), e79967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schumaker NH, & Brookes A (2018). HexSim: a modeling environment for ecology and conservation. Landscape Ecology, 33, 197–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schumaker NH, Brookes A, Dunk JR, Woodbridge B, Heinrichs JA, Lawler JJ, … LaPlante D (2014). Mapping sources, sinks, and connectivity using a simulation model of northern spotted owls. Landscape Ecology, 29(4), 579–592. [Google Scholar]
- Silveira L (1999). Ecologia e conservação dos mamíferos carnívoros do Parque Nacional das Emas, Goiás (MS) Universidade Federal de Goiânia, Goiânia, Goiás. [Google Scholar]
- Store R, & Kangas J (2001). Integrating spatial multi-criteria evaluation and expert knowledge for GIS-based habitat suitability modelling. Landscape and Urban Planning, 55(2), 79–93. [Google Scholar]
- Thorn JC, Brookes ST, Ridyard C, Riley R, Hughes DA, Wordsworth S, … Hollingworth W (2018). Core Items for a Standardized Resource Use Measure: Expert Delphi Consensus Survey. Value in Health: The Journal of the International Society for Pharmacoeconomics and Outcomes Research, 21(6), 640–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torres R, Pablo Jayat J, & Pacheco S (2013). Modelling potential impacts of climate change on the bioclimatic envelope and conservation of the Maned Wolf (Chrysocyon brachyurus). Mammalian Biology = Zeitschrift Fur Saugetierkunde, 78(1), 41–49. [Google Scholar]
- Trolle M, Noss AJ, De S Lima E, & Dalponte JC (2006). Camera-trap studies of maned wolf density in the Cerrado and the Pantanal of Brazil. Biodiversity and Conservation, 16(4), 1197–1204. [Google Scholar]
- van der Ree R, Smith DJ, & Grilo C (2015). Handbook of Road Ecology. John Wiley & Sons. [Google Scholar]