A primer on model selection using the Akaike Information Criterion

Abstract

A powerful investigative tool in biology is to consider not a single mathematical model but a collection of models designed to explore different working hypotheses and select the best model in that collection. In these lecture notes, the usual workflow of the use of mathematical models to investigate a biological problem is described and the use of a collection of model is motivated. Models depend on parameters that must be estimated using observations; and when a collection of models is considered, the best model has then to be identified based on available observations. Hence, model calibration and selection, which are intrinsically linked, are essential steps of the workflow. Here, some procedures for model calibration and a criterion, the Akaike Information Criterion, of model selection based on experimental data are described. Rough derivation, practical technique of computation and use of this criterion are detailed.

1. Motivation

Richard Casement wrote (Casement, 1984) “It is a common fallacy to confuse scientists’ models of reality with reality itself. A model is a map. A map is not the territory it describes”. For instance, if we wanted to cross Canada by bike, we would need a road map of Canada with the elevation and inclination to be able to select the shortest route with the least difference in elevations. A political map of Canada representing the provinces, which is another model of Canada, will however be useless for the purpose of crossing Canada by bike. Hence, before writing a mathematical model, the question to be investigated has to be carefully defined, since a good answer to a poor question is still a poor answer (Burnham & Anderson, 2002).

Once the question is determined, the modelling process comprises several steps that can be organized in a recursive way. Based on experimental data available, the model variables and parameters are defined. To make the model as simple as possible, assumptions have to be made, identifying the important processes governing the problem investigated in the perspective of the question considered. Then, using basics principles governing the variables considered, such as physical laws or types of interactions, equations of the model can be written using the appropriate mathematical formalism. The well-posedness of the model such as the consistency of units, existence and uniqueness of solutions and non-negativity of solutions (if needed) have to be verified.

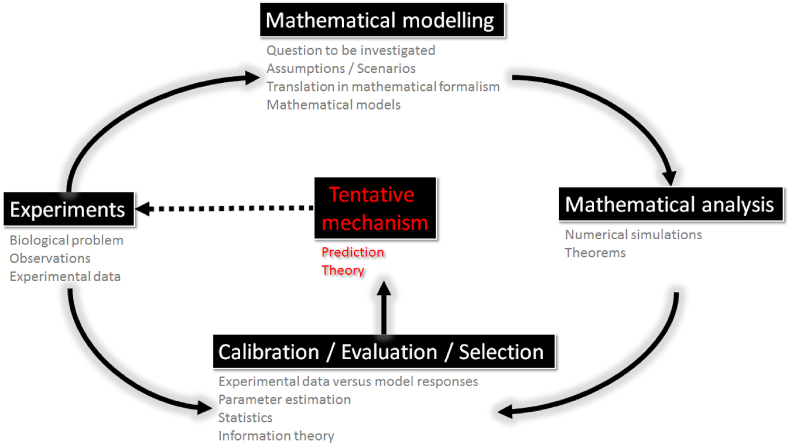
Once the model is written, its mathematical analysis has to be conducted to characterize its behaviour using the appropriate mathematical techniques and theories. Numerical experiments then need to be conducted. Adequate numerical methods have to be carefully chosen to ensure the accuracy of numerical solutions of the model. Numerical experiments require the choice of values for model parameters. These values can be chosen from published work or estimated by calibrating the model responses to experimental data. Sensitivity analysis can help to understand the effects of model inputs (parameters or initial conditions) on model outputs and identify parameters that are the key drivers of the model responses. Finally, the model must represent accurately the observed process, it must reproduce known states of the real process. If several models are considered, model selection has to be used to identify the best model to represent the data. Ultimately, the proposed mechanism identified by the (best) model has to be validated by further experiments. The typical workflow used in mathematical biology is represented in Fig. 1.

Fig. 1.

Mathematical biology workflow; adapted from (Portet, 2015).

The next example, adapted from (Zhang, Cao, & J Carroll, 2015), motivates the use of a collection of models and gives an illustration of its design.

Example 1.1

If we want to investigate the interactions between a population of rabbits and a population of foxes on a specific territory in which it is known that the foxes are specialist predators (foxes feed only on rabbits), we can propose a mathematical model using the formalism of ordinary differential equations. To do so, the following mechanisms have to be described:

• •dynamics of predators in absence of preys,
• •dynamics of preys in absence of predators,
• •interactions between preys and predators.

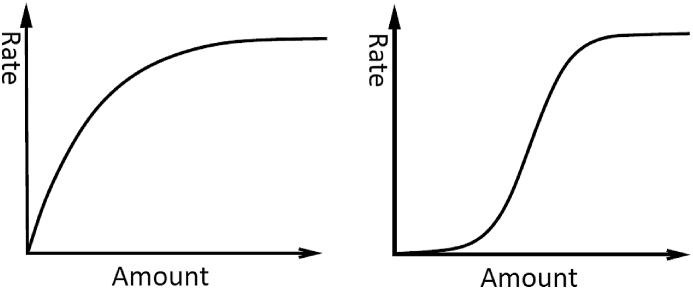
For the dynamics of predators in absence of preys, the assumptions are pretty specific and allow us to write that the dynamics shows exponential decay. However, for the rabbit population, we have no specification. Hence, we could describe the dynamics of rabbits in absence of predators as an exponential growth, to translate an unlimited growth of the rabbit population, or as a logistic term to specify the limitation of the rabbit population due to the environmental supply. Similarly, for the interactions between the two populations, the predator-prey link can be described by different functional responses; a mass action type term or a saturating rate could be hypothesized. The saturating rate would describe the fact that even if the amount of rabbit is infinite, foxes cannot consume rabbits faster than some maximal rate. Different translations of the saturating process can be used; see for instance Fig. 2. Here, to write the model, we use a Michaelis-Menten type or Holling type II saturating term (left panel of Fig. 2).

Fig. 2.

Different translations of saturating rates. (Left) Hyperbolic saturation: as the amount increases the rate increases but slowing down (Michaelis-Menten dynamics or Holling type II function). (Right) Sigmoidal saturation: from a slow to rapid rate, “switch-like” rise toward to the limiting value or Holling type III function (Cooperativity).

The different assumptions yield different terms and then different models. Here, we consider three candidate models.

$$\begin{array}{ccc}\text{Model}\text{I}& \text{Model}\text{II}& \text{Model}\text{III}\\ \frac{dR}{dt}=aR-bRF& \frac{dR}{dt}=a\left(1-\frac{R}{k}\right)R-bRF& \frac{dR}{dt}=aR-\frac{bRF}{1+fR}\\ \frac{dF}{dt}=-cF+eRF& \frac{dF}{dt}=-cF+eRF& \frac{dF}{dt}=-cF+\frac{eRF}{1+fR}\end{array}$$

Model I is the famous Lotka-Volterra model in which the rabbits grow exponentially. Model II describes a limitation of the rabbit population due to environmental factors. Model III is characterized by a saturating rate in the functional response. These three models are non-nested, as, for instance, Model II cannot be obtained from any other models. However, we can also define a general model

$$\begin{array}{l}\frac{dR}{dt}=aR-v{R}^2-\frac{bRF}{1+fR}\\ \frac{dF}{dt}=-cF+\frac{eRF}{1+fR}.\end{array}$$

Each of the three models is a particular case of the general model obtained by setting some parameters to zero:

• •$v=f=0\Rightarrow$ Model I (Lotka-Volterra model),
• •$f=0\Rightarrow$ Model II (with logistic dynamics for preys),
• •$v=0\Rightarrow$ Model III (with saturating rate in functional response).

The three models are therefore nested models of the general model. Note that from the general model, more nested models can be defined by setting other subsets of parameters to zero.

In Example 1.1, due to lack of knowledge of the processes, we had to consider different assumptions for a given mechanism. Furthermore, we could have used different translations for the saturating rate; that yields the definition of a collection of models. The design of a collection of models can be also used to mimic the well known positive and negative control experimental protocol used in experimental sciences. Considering a collection of models will allow the identification of a most plausible scenario for the defined problem. Systematic modelling of all possible scenarios is a powerful approach; see, for instance, (Gotoh et al., 2016).

Once we have a collection of models depending on unknown parameters, two questions have to be addressed. What are the parameter values? What is the best model to represent the experimental data? The first question will be solved using parameter estimation or model calibration methods. The second question can be addressed by model selection methods, which can be divided into two types:

• •information theory criteria,
• •statistical tests.

Here, only information theory based selection model methods are presented.

2. Model calibration

A mathematical model depends on independent variable(s), dependent variable(s) or state variable(s) and parameters p. Parameters of the model have (biological) interpretations and their values are unknown. Hence, we need to estimate the model parameters (find appropriate values) from measurements (the experimental data) in presence of errors in measurements. Here, two general (optimal) methods for parameter estimation are presented:

• •Least Squares (LS), in which an objective function (sum of squared residuals of all measurements) is minimized.
• •Maximum Likelihood (ML), in which the likelihood function is maximized.

Both LS and ML methods are optimization problems and provide point estimates. Other types of methods such as Bayesian inferences use the likelihood combined with priors on parameters to provide posterior distributions of parameters (Coelho, Codeço, & Gomes, 2011; Friston, 2002).

After presenting LS and ML methods, we will show that if the measurement errors are independent and normally distributed with a common variance, both methods are equivalent and give the same estimate for the mathematical model parameters.

2.1. A few words on optimization

When an analytic expression of the function to be optimized $f\left(p\right)$ is known and has appropriate properties, the following well known result can be used to find local extrema.

Theorem 2.1

A smooth function $f\left(p\right)$ attains a local minimum (resp. maximum) at $\hat{p}$ if the following two conditions hold

• •the gradient $\frac{\partial f\left(p\right)}{\partial p}$ vanishes at $\hat{p}$
• •the Hessian $H\left(p\right)$ with $\left(i,j\right)th$ entry $\frac{{\partial }^{2}f\left(p\right)}{\partial p_i\partial p_j}$ is positive definite (resp. negative definite) at $\hat{p}$, or

$$z^{T}H\left(p\right)z>0(resp.<0)\text{,}$$

where z is any real non-zero vector.

If $f\left(p\right)$ is non-smooth, the local extrema are at the discontinuity of $f\left(p\right)$ or where the gradient $\frac{\partial f\left(p\right)}{\partial p}$ is discontinuous or vanishes.

However, when the analytic expression of the function to be optimized $f\left(p\right)$ is unknown or lacks appropriate properties, search methods have to be used. These methods can be categorized as local or global optimization methods (Pitt & Banga, 2019; Sagar, LeCover, Shoemaker, & Varner, 2018). Local optimization methods are faster but might converge to local optima that are suboptimal solutions or only find a global optimum for appropriate starting points. Gradient descent-based methods such as Levenberg-Marquardt or Gauss-Newton or derivative-free local search methods such as simplex or Nelder-Mead are local optimization methods. Global optimization methods, which are heuristic or meta-heuristic methods, are more time consuming. Some examples of global optimization methods are the simulated annealing, genetic algorithms or particle swarm methods.

2.2. Least squares

The aim of the LS method is to find parameter values of the model that minimize the distance between data and model output. First, a simple case of the problem to solve is described.

• •Observation: we have n data points $\left(t_i,y_i\right)$ with $i=1,\dots ,n,$ where $t_i$ are the values of the independent variable t.
• •Model: the model is a differentiable function $f\left(t,p\right)$ that depends on t and p, the latter being a $k-$vector of parameters (k parameters).
• •Criterion: the total error between the model and data is defined as the residual sum of squares ($RSS$), the sum of squared residuals,

$$RSS\left(p\right)=\stackrel{n}{\sum _{i=1}}{\left(y_i-f\left(t_i,p\right)\right)}^2$$ (1)

and depends on p. The residual is the difference between the actual value $y_i$ (data) and the predicted value $f\left(t_i,p\right)$ at a value of the independent variable $t_i$.

• •Solution: the solution is the $k-$vector of parameter values ${\hat{p}}_{lsq}$ (the LS Estimate) that minimizes the sum of squares of vertical distances between data points and model points,

$$RSS\left({\hat{p}}_{lsq}\right)=\underset{p}{\text{min}}RSS\left(p\right)\text{.}$$

Hence, based on Theorem 2.1, possible solutions for ${\hat{p}}_{lsq}$ can be obtained by setting the gradient equal to zero

$$\frac{\partial RSS}{\partial p_j}=0,j=1,\dots ,k\text{,}$$

yielding

$$-2\stackrel{n}{\sum _{i=1}}\left(y_i-f\left(t_i,p\right)\right)\frac{\partial f\left(t_i,p\right)}{\partial p_j}=0,j=1,\dots ,k\text{.}$$ (2)

Then, solve the k equations for $p_j$ with $j=1,\dots ,k$.

Example 2.1

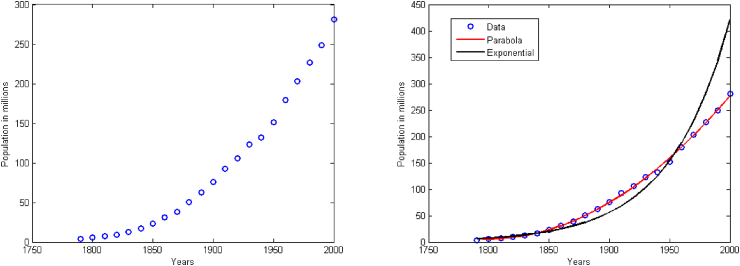
To illustrate, we consider the temporal evolution of the US population from 1790 to 2000; data are obtained from the US census (Fig. 3). Observations consist of $n=22$ data points $\left(t_i,y_i\right)=$ (year, population) with $i=1,\dots ,22$. Based on the trend of data, we can hypothesize different forms for the model f, such as

• •A quadratic function in t (years, the independent variable),

$$f\left(t,a,b,c\right)=y=a{t}^2+bt+c\text{;}$$

then $k=3$ parameters are to be estimated and $p=\left(a,b,c\right)$.

• •An exponential function in t (years),

$$f\left(t,a,b\right)=y=a{e}^{bt}\text{.}$$

Using the change of variable $\text{ln}y=Y$, we obtain

$$\ln y=Y=\ln a+bt=A+bt\text{.}$$

Here, $k=2$ parameters are to be estimated and $p=\left(A,b\right)$.

Notice that both models are linear in the parameters; hence, equation (2) to be solved to estimate parameter values is a linear system in p. Here, we only explicitate the solution of the problem when the exponential function is used.

When the exponential form is considered, the change of variable $\ln y=Y$ is used to make the model linear in the parameters; hence, the analytic expression of the RSS (1) takes the following form:

$$RSS\left(A,b\right)=\sum _{i=1}^n{\left(\ln y_i-\left(A+b{t}_i\right)\right)}^2\text{.}$$

We want to find values of A and b that minimize $RSS\left(A,b\right)$. By setting its gradient to zero to find critical points of $RSS\left(A,b\right)$, (2) is then

$$\begin{array}{l}\stackrel{n}{\sum _{i=1}}\left(\ln y_i-\left(A+b{t}_i\right)\right)\frac{\partial \left(A+b{t}_i\right)}{\partial A}=\stackrel{n}{\sum _{i=1}}\left(\ln y_i-\left(A+b{t}_i\right)\right)=0\text{,}\\ \stackrel{n}{\sum _{i=1}}\left(\ln y_i-\left(A+b{t}_i\right)\right)\frac{\partial \left(A+b{t}_i\right)}{\partial b}=\stackrel{n}{\sum _{i=1}}\left(\ln y_i-\left(A+b{t}_i\right)\right)t_i=0\text{.}\end{array}$$

These two necessary conditions for the existence of a local extremum can be rewritten in matrix form as follows

$$\left[\begin{array}{cc}n& \sum _{i=1}^n{t}_i\\ \sum _{i=1}^n{t}_i& \sum _{i=1}^n{t}_i^2\end{array}\right]\left[\begin{array}{c}\hat{A}\\ \hat{b}\end{array}\right]=\left[\begin{array}{c}\sum _{i=1}^n\ln y_i\\ \sum _{i=1}^n{t}_i\ln y_i\end{array}\right]\text{,}$$

where $\hat{A}$ and $\hat{b}$ (LS estimates of A and b) are the unique solutions if the matrix is non-singular. In such a case, using Cramer’s rule, the unique solution that minimizes $RSS$ is

$$\begin{array}{l}\hat{A}=\frac{{\sum }_{i=1}^n\ln y_i{\sum }_{i=1}^n{t}_i^2-{\sum }_{i=1}^n{t}_i\ln y_i{\sum }_{i=1}^n{t}_i}{n{\sum }_{i=1}^n{t}_i^2-{\left({\sum }_{i=1}^n{t}_i\right)}^2}\text{,}\\ \hat{b}=\frac{n{\sum }_{i=1}^n{t}_i\ln y_i-{\sum }_{i=1}^n\ln y_i{\sum }_{i=1}^n{t}_i}{n{\sum }_{i=1}^n{t}_i^2-{\left({\sum }_{i=1}^n{t}_i\right)}^2}\text{.}\end{array}$$

Results are given on the right panel of Fig. 3.

Note that the two models considered in Example 2.1 are not explanatory models but descriptive models. They have a strong predictive power but they cannot encode any underlying process to explain the trend in data. For instance, with these two models, we cannot decide if the increase of the population is due to either an increase in fertility, a decrease in the death rate or the contribution of immigration. To unravel the processes responsible for the trend in data, a mechanistic approach needs to be followed and explanatory models need to be designed by modelling the hypothesized underlying mechanisms such as, for instance, in Example 1.1. Hence, when the ODE formalism is used, explanatory models can be expressed as follows

$$\frac{dx}{dt}=m\left(x,p,t\right),x\left(t_0\right)=x_0\left(p\right),\text{with }h\left(x,p,t\right)=\tilde{y}\text{,}$$ (3)

where t is the independent variable, $x\left(t\right)$ is the vector of state variables, $x_0$ is the vector of initial conditions and p is the vector of unknown constant parameters. The observable function h depends on model inputs and outputs.

Now, the LS method detailed above is generalized. To find the vector of parameter values p that minimizes the distance between measured and simulated observations, the scalar objective function (cost function), $F_{ls}\left(p\right)$, is defined:

$$F_{ls}\left(p\right)=\stackrel{n_e}{\sum _{e=1}}\stackrel{n_o^e}{\sum _{o=1}}\stackrel{n_i^{e,o}}{\sum _{i=1}}{\omega }_i^{e,o}{\left(y_e^o\left(t_i\right)-{\tilde{y}}_o^e\left(t_i,p\right)\right)}^2\text{,}$$ (4)

with $n_e$ the number of experiments, $n_o^e$ the number of observables per experiments and $n_i^{e,o}$ the number of samples per observable per experiment. Also, $y_e^o\left(t_i\right)$ are measured data, ${\omega }_i^{e,o}$ are weights and ${\tilde{y}}_o^e\left(t_i,p\right)$ are simulated observable outputs. Then, an optimization method to minimize $F_{ls}\left(p\right)$ has to be chosen to find ${\hat{p}}_{LSE}$ (the LS Estimate) such that

$$F_{ls}\left({\hat{p}}_{LSE}\right)=\underset{p}{\text{min}}{F}_{ls}\left(p\right)\text{.}$$

Note that when models as defined in (3) are considered, analytic expressions of observables $\tilde{y}$ might not exist; in this case, only their numerical approximations can be used to compute (4). Hence, prior to any model calibration, the mathematical analysis of the ODE model (3) has to be carried out to characterize the model behaviour in as much detail as possible. For instance, if the model (3) presents an oscillatory regime, specific search methods will have to be used (Pitt & Banga, 2019).

Fig. 3.

(Left) US population (in millions) from 1790 to 2000; data from the US census, https://www.u-s-history.com/pages/h980.html. (Right) Data and best fits of the quadratic function $f\left(t\right)=0.0067t^2-24.0358t+21620.47$ and exponential function $f\left(t\right)=1.2162\times {10}^{-15}{e}^{0.0202t}$.

2.3. Maximum likelihood

Experimental data $y=\left(y_1,\dots ,y_n\right)$ can be interpreted as a random sample generated from an unknown probability distribution function (pdf) depending on parameters $p=\left(p_1,\dots ,p_k\right)$. Then, a model is defined as a family of probability distributions indexed by the model’s parameters,

$$f\left(y|p\right)=\text{probability}\text{of}\text{observing}\text{data}y\text{given}\text{the}\text{parameter}p\text{.}$$

If the observations $y_i$ are statistically independent of one another, the pdf of observing the data $y=\left(y_1,\dots ,y_n\right)$ given the parameter vector p is the multiplication of the pdfs for individual observations

$$f\left(\left(y_1,\dots ,y_n\right)|\left(p_1,\dots ,p_k\right)\right)=f\left(y_1|\left(p_1,\dots ,p_k\right)\right)f\left(y_2|\left(p_1,\dots ,p_k\right)\right)$$

$$\cdots f\left(y_n|\left(p_1,\dots ,p_k\right)\right)\text{.}$$

The function $f\left(\left(y_1,\dots ,y_n\right)|\left(p_1,\dots ,p_k\right)\right)$ is the probability of observing data y for a given value of p and is a function of data y. Varying the parameter p across its range defines a family of pdfs that makes up the model.

Hence, the inverse problem to solve is to find the pdf among all the pdfs of the family that is the most “likely” to have produced the data y. To attack the problem, a function of parameters p needs to be defined. Hence, the likelihood function $\mathcal{L}$ is the density function regarded as a function of p

$$\mathcal{L}(p|y)=f(y|p)\text{.}$$

The role of data y and parameters p is reversed. The likelihood of a particular value for a parameter is the probability of obtaining the observed data y if the parameter had that value. It measures how well the data supports that particular value of parameters. The density function f (function of y, data scale) gives the probability of observing y given the parameter p and sums to 1 over all the possible values of y. The likelihood function $\mathcal{L}$ is a function of p (parameter scale) given the data and does NOT sum to 1 over the possible values of p.

The inverse problem to solve is equivalent to seeking the value ${\hat{p}}_{MLE}=\left({\hat{p}}_{1,MLE},\dots ,{\hat{p}}_{k,MLE}\right)$ of the parameter vector p that maximizes the likelihood function $\mathcal{L}\left(p|y\right)$. In practice, the log-likelihood $\ln \mathcal{L}\left(p|y\right)$ will be considered. As the logarithm is a monotonically increasing function, maximizing $\mathcal{L}\left(p|y\right)$ is equivalent to maximizing the log-likelihood $\text{ln}\mathcal{L}\left(p|y\right)$ to find the Maximum Likelihood Estimator ${\hat{p}}_{MLE}$. A ${\hat{p}}_{MLE}$ satisfies the following conditions based on Theorem 2.1:

• •Necessary condition of existence of a ${\hat{p}}_{MLE}$,

$$\frac{\partial \ln \mathcal{L}\left(p|y\right)}{\partial p_i}=0,i=1,\dots ,k\text{.}$$

• •Convexity condition: consider the Hessian matrix $H\left(p\right)$, $H_{i,j}\left(p\right)=\frac{{\partial }^2\ln \mathcal{L}\left(p|y\right)}{\partial p_i\partial p_j}$ with $i,j\in \left\{1,\dots ,k\right\}$. Then there must hold that

$$z^{T}H\left(p\right)z<0\text{,}$$

where z is any real non-zero $k-$vector.

Example 2.2

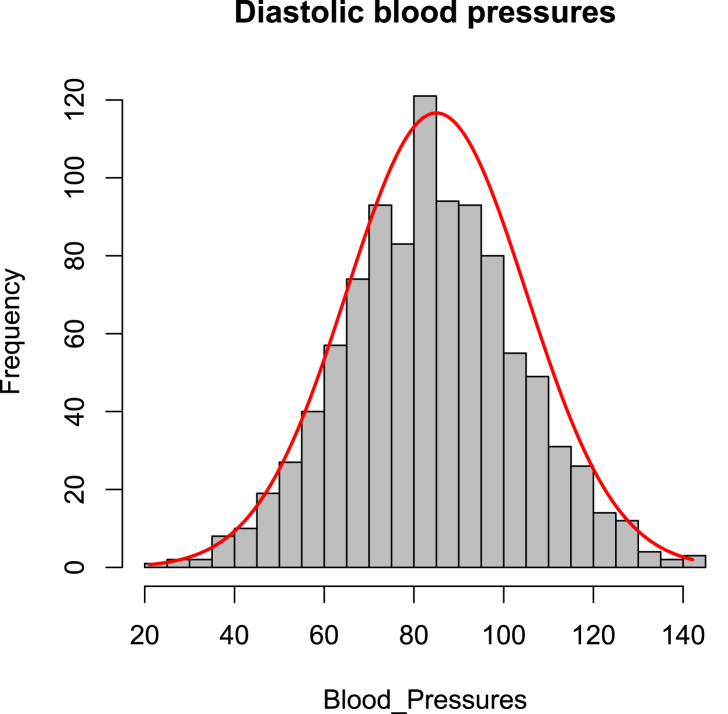
Suppose the blood pressure of 1000 patients is recorded with observations given in gray in Fig. 4. Seeing the shape of the data in Fig. 4, we assume that experimental data $y_1,\dots ,y_n$ ($y_i$ is the blood pressure of the patient i with $i\in \left\{1,\dots 1000\right\}$) are drawn from a normal distribution $\mathcal{N}\left(\mu ,{\sigma }^2\right)$ with μ and σ unknown ($k=2$, $p=\left(\mu ,\sigma \right)$).

Let $Y_1,\dots ,Y_n$ be n i.i.d.1 $\mathcal{N}\left(\mu ,{\sigma }^2\right)$ random variables,

$$f_{Y_i}\left(y_i|\mu ,\sigma \right)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{\left(y_i-\mu \right)}^2}{2{\sigma }^2}}\text{.}$$

The joint probability distribution function is

$$f\left(y_1,\dots ,y_n|\mu ,\sigma \right)={\left(\frac{1}{\sqrt{2\pi }\sigma }\right)}^n{e}^{-{\sum }_{i=1}^n\frac{{\left(y_i-\mu \right)}^2}{2{\sigma }^2}}\text{.}$$

Hence, for a fixed data set $y_1,\dots ,y_n$, the likelihood function is

$$\mathcal{L}\left(\mu ,\sigma |y_1,\dots ,y_n\right)={\left(\frac{1}{\sqrt{2\pi }\sigma }\right)}^n{e}^{-{\sum }_{i=1}^n\frac{{\left(y_i-\mu \right)}^2}{2{\sigma }^2}}$$

and the log-likelihood function is

$$\text{ln}\mathcal{L}\left(\mu ,\sigma |y_1,\dots ,y_n\right)=-n\left(\ln \left(\sqrt{2\pi }\right)+\text{ln}\left(\sigma \right)\right)-\sum _{i=1}^n\frac{{\left(y_i-\mu \right)}^2}{2{\sigma }^2}\text{.}$$

To find the Maximum Likelihood Estimate of μ, ${\hat{\mu }}_{MLE}$, we differentiate the log-likelihood function with respect to μ,

$$\frac{\partial \ln \mathcal{L}\left(p|y\right)}{\partial \mu }=\sum _{i=1}^n\frac{\left(y_i-\mu \right)}{{\sigma }^2}=0\Rightarrow \sum _{i=1}^n{y}_i=n{\hat{\mu }}_{MLE}\Rightarrow {\hat{\mu }}_{MLE}=\frac{1}{n}\sum _{i=1}^n{y}_i=\bar{y}\text{.}$$

To find the Maximum Likelihood Estimate of σ, ${\hat{\sigma }}_{MLE}$, we differentiate the log-likelihood function with respect to σ,

$$\frac{\partial \ln \mathcal{L}\left(p|y\right)}{\partial \sigma }=-\frac{n}{\sigma }+\sum _{i=1}^n\frac{{\left(y_i-\mu \right)}^2}{{\sigma }^3}=0\Rightarrow {\hat{\sigma }}_{MLE}^2=\frac{1}{n}\sum _{i=1}^n{\left(y_i-\mu \right)}^2\text{.}$$

Using $\mu ={\hat{\mu }}_{MLE}$ we obtain ${\hat{\sigma }}_{MLE}^2=\frac{1}{n}{\sum }_{i=1}^n{\left(y_i-{\hat{\mu }}_{MLE}\right)}^2.$ Maximum Likelihood Estimates are ${\hat{\mu }}_{MLE}$ (the mean of data) and ${\hat{\sigma }}_{MLE}^2$ (the variance of data). Using the data, we compute ${\hat{\mu }}_{MLE}=85$ and ${\hat{\sigma }}_{MLE}^2={20}^2$ and we plot in red the normal distribution function $\mathcal{N}\left(85,{20}^2\right)$ in Fig. 4. Furthermore, the maximum log-likelihood can be computed by replacing μ and σ by their estimates as follows:

$$\ln \mathcal{L}({\hat{\mu }}_{MLE},{\hat{\sigma }}_{MLE}|y_1,\dots ,y_n)=\underset{\mu ,\sigma }{\text{max}}\ln \mathcal{L}(\mu ,\sigma |y_1,\dots ,y_n)\text{.}$$

For many problems, even computational evaluation of the likelihood is infeasible. A relationship between the negative of the log-likelihood function and the residual sum of squares (or the cost function used in least squares method) is now derived under some condition.

Fig. 4.

Blood pressures of 1000 patients (data generated in R). In gray, observations that looks normally distributed. In red, the normal distribution $\mathcal{N}\left({\hat{\mu }}_{MLE},{\hat{\sigma }}_{MLE}^2\right)=\mathcal{N}\left(85,{20}^2\right)$.

2.4. Relationship between least squares estimate and maximum likelihood estimate

Define the statistical model

$$Y_e^o={\tilde{y}}_o^e\left(t_i,p\right)+{\epsilon }_e^o\text{,}$$

where the measured data $y_e^o\left(t_i\right)$ is a realization of the random variable $Y_e^o$, ${\tilde{y}}_o^e\left(t_i,p\right)$ is the (algebraic, ODE or PDE) mathematical model output and the random variable ${\epsilon }_e^o$ represents measurement errors or noise (Miao, Dykes, Demeter, & Wu, 2009; Zhang et al., 2015). Assuming independent and normally distributed additive measurement errors with standard deviation ${\sigma }_i^{e,o}$, the probability of observing the data y given the parameters p and ${\sigma }_i^{e,o}$ is

$$f\left(y|\theta \right)=\prod _{e=1}^{n_e}\prod _{o=1}^{n_o^e}\prod _{i=1}^{n_i^{e,o}}\frac{1}{\sqrt{2\pi }{\sigma }_i^{e,o}}exp\left(-\frac{1}{2}{\left(\frac{y_e^o\left(t_i\right)-{\tilde{y}}_o^e\left(t_i,p\right)}{{\sigma }_i^{e,o}}\right)}^2\right)\text{,}$$

where $y_e^o\left(t_i\right)$ are measured data, ${\tilde{y}}_o^e\left(t_i,p\right)$ model output and θ includes the mathematical model parameters p and the statistical model parameters ${\sigma }_i^{e,o}$. As previously defined, $n_e$ is the number of experiments, $n_o^e$ is the number of observables per experiment and $n_i^{e,o}$ is the number of samples per observable per experiments. Hence, the likelihood function is

$$\mathcal{L}\left(\theta |y\right)=\prod _{e=1}^{n_e}\prod _{o=1}^{n_o^e}\prod _{i=1}^{n_i^{e,o}}\frac{1}{\sqrt{2\pi }{\sigma }_i^{e,o}}exp\left(-\frac{1}{2}{\left(\frac{y_e^o\left(t_i\right)-{\tilde{y}}_o^e\left(t_i,p\right)}{{\sigma }_i^{e,o}}\right)}^2\right)\text{.}$$

Maximizing the likelihood is equivalent to minimizing the negative of the log-likelihood function, so we consider the negative of the log-likelihood function, defined as

$$-\ln \mathcal{L}\left(\theta |y\right)=\frac{1}{2}\sum _{e=1}^{n_e}\sum _{o=1}^{n_o^e}\sum _{i=1}^{n_i^{e,o}}[\text{ln}\left(2\pi {\left({\sigma }_i^{e,o}\right)}^2\right)+{\left(\frac{y_e^o\left(t_i\right)-{\tilde{y}}_o^e\left(t_i,p\right)}{{\sigma }_i^{e,o}}\right)}^2]\text{.}$$

Recall the cost function, $F_{ls}\left(p\right)$, defined in the least squares method by (4). Hence, there is the following relationships between the negative log-likelihood $-\text{ln}\mathcal{L}\left(\theta |y\right)$ and least squares cost function $F_{ls}\left(p\right)$ (Baker, Bocharov, Paul, & Rihan, 2005).

• •For ${\omega }_i^{e,o}=1/{\left({\sigma }_i^{e,o}\right)}^2$ (weighted LS),

$$-\ln \mathcal{L}\left(\theta |y\right)=\frac{1}{2}\stackrel{n_e}{\sum _{e=1}}\stackrel{n_o^e}{\sum _{o=1}}\stackrel{n_i^{e,o}}{\sum _{i=1}}\text{ln}\left(2\pi {\left({\sigma }_i^{e,o}\right)}^2\right)+\frac{1}{2}{F}_{ls}\left(p\right)=n_e{n}_o^e{n}_i^{e,o}\text{ln}\left(\sqrt{2\pi }\right)+\text{ln}\left(\stackrel{n_e}{\prod _{e=1}}\stackrel{n_o^e}{\prod _{o=1}}\stackrel{n_i^{e,o}}{\prod _{i=1}}{\sigma }_i^{e,o}\right)+\frac{1}{2}{F}_{ls}\left(p\right)\text{.}$$

Hence, $-\text{ln}\mathcal{L}\left(\theta |y\right)$ and $F_{ls}\left(p\right)$ have the same optimal mathematical model parameters p ($\hat{p}={\hat{p}}_{MLE}={\hat{p}}_{LSE}$).

• •For ${\sigma }_i^{e,o}=\sigma$ (weighted LS) and ${\omega }_i^{e,o}=1$ (ordinary LS),

$$-\ln \mathcal{L}\left(\theta |y\right)=n_e{n}_o^e{n}_i^{e,o}\left(\ln \left(\sqrt{2\pi }\right)+\text{ln}\left(\sigma \right)\right)+\frac{1}{2{\sigma }^2}{F}_{ls}\left(p\right)\text{.}$$

Hence, $-\text{ln}\mathcal{L}\left(\theta |y\right)$ and $F_{ls}\left(p\right)$ have the same optimal parameters for the mathematical model parameters p ($\hat{p}={\hat{p}}_{MLE}={\hat{p}}_{LSE}$) and from $\frac{\partial \text{ln}\mathcal{L}\left(\theta |y\right)}{\partial \sigma }=0$,

$${\hat{\sigma }}^2=\frac{1}{n_e{n}_o^e{n}_i^{e,o}}{F}_{ls}\left(\hat{p}\right)\text{.}$$

Thus, the minimum of the negative of the log-likelihood function is

$$-\ln \mathcal{L}\left({\hat{\theta }}_{MLE}|y\right)=\frac{n_e{n}_o^e{n}_i^{e,o}}{2}\text{ln}\left(2\pi \right)+\frac{n_e{n}_o^e{n}_i^{e,o}}{2}+\frac{n_e{n}_o^e{n}_i^{e,o}}{2}\text{ln}\left(\underset{\text{MLE of variance}}{\underbrace{\frac{F_{ls}\left(\hat{p}\right)}{n_e{n}_o^e{n}_i^{e,o}}}}\right)\text{,}$$ (5)

where $\hat{p}={\hat{p}}_{MLE}={\hat{p}}_{LSE}$.

Therefore, under the assumption of independent, normally distributed additive measurement errors with constant variance, the Least Squares Estimates and Maximum Likelihood Estimates of the mathematical model parameters are the same.

2.5. Problems in model calibration

The use of optimal methods for model calibration (LS or ML) for non-linear models have inherent problems that can be categorized as follows.

• •Lack of prior knowledge about parameters.
• •
  Lack of identifiability (non-uniqueness of optimal solutions for parameter estimation) (Miao et al.,2009). There exist two types of identifiability:

  • 1
    (Practical identifiability) The larger the number of unknown parameters in a model, the larger the amount of quantitative data necessary to determine meaningful values for these parameters.
  • 2
    (Structural identifiability) Even if appropriate experimental data are available, model parameters may not be uniquely identifiable.
• •Convergence to local optima (ill-conditioning and non-convexity).
• •Overfitting (fitting the noise instead of the signal).

Example 2.3

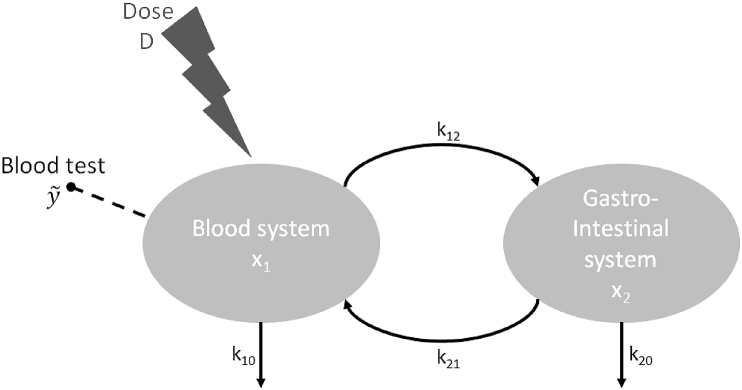
A famous example illustrates the problem of structural identifiability (Janzén et al., 2016; Yates, 2006). A two compartment model describing the temporal evolution of the amount of drug injected in the blood system is considered (Fig. 5):

$$\begin{array}{l}\frac{d{x}_1}{dt}=-\left(k_{12}+k_{10}\right)x_1+k_{21}{x}_2,x_1\left(0\right)=D\text{,}\\ \frac{d{x}_2}{dt}=k_{12}{x}_1-\left(k_{21}+k_{20}\right)x_2,x_2\left(0\right)=0\text{,}\\ \tilde{y}=\frac{x_1}{V_1}\text{,}\end{array}$$

where $x_1$ (variable) is mass of drug in compartment 1 (blood system), $x_2$ (variable) mass of drug in compartment 2 (gastro-intestinal system), $\tilde{y}$ (variable) is the observable concentration of drug in the blood test with $V_1$ (parameter) the volume of the observed compartment (blood system). The parameters $k_{ij}$ are rates of transfer from i to j. The dose D of drug injected in the blood system is a known parameter. Hence, there are five parameters to estimate.

The model is a homogeneous linear system that can be solved explicitly; closed forms of $x_1\left(t\right)$ and $x_2\left(t\right)$ can be obtained. Hence, the time solution $\tilde{y}\left(t\right)$ can be expressed as follows:

$$\tilde{y}\left(t\right)=C_1{e}^{-{\lambda }_{1}t}+C_2{e}^{-{\lambda }_{2}t}\text{.}$$

As seen in Example 2.1, functions of the form $C_i{e}^{-{\lambda }_{i}t}$ can be linearised by a change of variables; then, $C_1$, $C_2$, ${\lambda }_1$, and ${\lambda }_2$ can be determined from the observed concentration curve in a unique way. However, their knowledge results in only four conditions/equations that depend on the five unknown parameters $k_{ij}$ and $V_1$. Hence, we cannot find a unique solution for the five parameters to estimate. Therefore, the model is structurally unidentifiable.

Fig. 5.

Pharmacokinetics model: evolution of the amount of drug in the blood system $x_1$, the gastro-intestinal system $x_2$ and the blood test, which is the only observable outputs of the model.

3. Model selection

When a collection of models is considered to investigate a problem, after calibrating each model to the available experimental data, a model selection method can be employed to discriminate between the different candidate models of the collection in terms of the representation of experimental data considered.

3.1. Naive approach

For linear models, a naive approach to compare models is to used the $R^2$ or adjusted $R^2$. They are a measure of the goodness of fit; the best fit is selected but the model complexity is neglected. The $R^2$ is defined as

$$R^2=1-\frac{RSS/n}{{\sum }_{i=1}^n{\left(y_i-\bar{y}\right)}^2/n}$$

or by replacing the two variances with their unbiased estimates, the adjusted $R^2$ is obtained,

$$R_{adj}^2=1-\frac{RSS/\left(n-k-1\right)}{{\sum }_{i=1}^n{\left(y_i-\bar{y}\right)}^2/\left(n-1\right)}\text{,}$$

where $RSS$ is the residual sum of squares as defined in (1), n is the sample size, y are the data, $\bar{y}$ is the average of the data and k is the number of parameters. These criteria select the model that maximizes $R^2$ or $R_{adj}^2$; the most parameter rich model is selected.

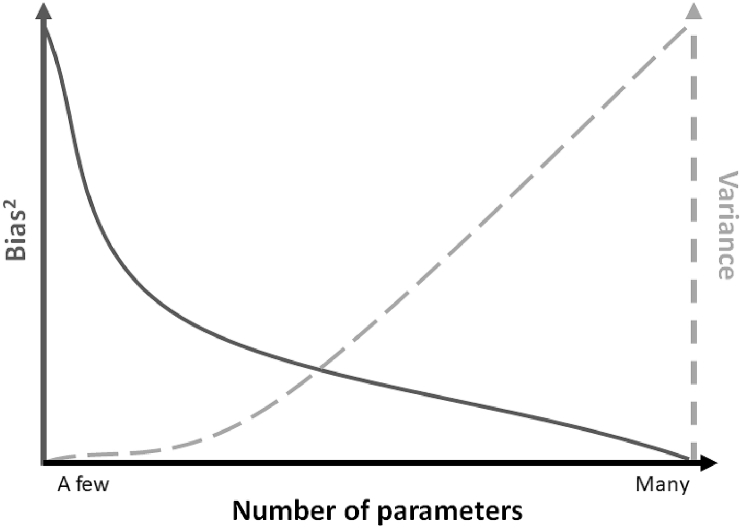
However, in selecting the best model, the principle of parsimony, which states that a model should be as simple as possible, should be employed (Fig. 6). A good model is a proper balance between underfitting and overfitting. Johnson and Omland (Johnson & Omland, 2004) state the following: “Parsimony is, in statistics, a trade-off between bias and variance. Too few parameters results in high bias in parameter estimators and an underfit model (relative to the best model) that fails to identify all factors of importance. Too many parameters results in high variance in parameter estimators and an overfit model that risks identifying spurious factors as important, and that cannot be generalized beyond the observed sample data”.

Fig. 6.

Principle of parsimony.

Here a model selection method is introduced, the Akaike Information Criterion, which accounts for the goodness of the fit and parsimony principle.

3.2. Sketch of Akaike Information Criterion derivation

First we need to define the Kullback-Leibler (KL) divergence, which is used to measure the difference between two probability distributions $f\left(x\right)$ and $g\left(x\right)$ defined over the same probability space (Kullback & Leibler, 1951). The KL divergence of $g\left(x\right)$ from $f\left(x\right)$ is

$$I\left(f,g\right)=\sum _{x\in X}f\left(x\right)\text{ln}\left(\frac{f\left(x\right)}{g\left(x\right)}\right)\text{,}$$

if $f\left(x\right)$ and $g\left(x\right)$ are pdfs of a discrete random variable X and

$$I\left(f,g\right)=\underset{X}{\int }f\left(x\right)\text{ln}\left(\frac{f\left(x\right)}{g\left(x\right)}\right)dx\text{,}$$

if $f\left(x\right)$ and $g\left(x\right)$ are pdfs of a continuous random variable X.

The KL divergence can be interpreted as the distance between two probability distributions; however, it is not really a distance as the KL divergence is not symmetrical. Here are some properties of the KL divergence:

• •$I\left(f,g\right)\ne I\left(g,f\right)$ (not symmetric),
• •$I\left(f,g\right)\ge 0\text{,}$
• •$I\left(f,g\right)=0$ if and only if $f=g$.

In 1973, Akaike (AkaikePetrov and Csaki, 1973) found a relationship between the maximum likelihood (statistical analysis) and Kullback-Leibler divergence (information theory) and, based on that, defined a model selection criterion, now called Akaike Information Criterion (AIC). A sketch of the AIC derivation is given here.

As no single model includes the whole truth or the complete information about the phenomena under investigation, the quantity of information loss has to be determined. The Kullback-Leibler divergence can be used as a measure to quantify the information lost when approximating the full reality $f\left(x\right)$ by a model $g\left(x|\theta \right)$, where the model $g\left(x|\theta \right)$ depends on parameters θ,

$$I\left(f,g\right)=\int f\left(x\right)\text{ln}\left(\frac{f\left(x\right)}{g\left(x|\theta \right)}\right)dx\text{.}$$

However, the reality/truth f is unknown and the parameters θ must be estimated from data y (generated from f).

Measurement of the information lost when approximating the full reality $f\left(x\right)$ by a model $g\left(x|\theta \right)$, $I\left(f,g\right)$, can be rewritten as the difference between two expectations with respect to the true distribution f as follows:

$$\begin{array}{cc}I\left(f,g\right)& =\int f\left(x\right)\text{ln}\left(\frac{f\left(x\right)}{g\left(x|\theta \right)}\right)dx\\ & =\int f\left(x\right)\text{ln}\left(f\left(x\right)\right)dx-\int f\left(x\right)\text{ln}\left(g\left(x|\theta \right)\right)dx\\ & =E_f\left[\text{ln}\left(f\left(x\right)\right)\right]-E_f\left[\text{ln}\left(g\left(x|\theta \right)\right)\right]\text{,}\end{array}$$

where the first term $E_f\left[\text{ln}\left(f\left(x\right)\right)\right]=C$, which depends only on the unknown true distribution f, is unknown and constant. The second term is the relative KL divergence between f and g and is defined as

$$I\left(f,g\right)-C=-E_f\left[\text{ln}\left(g\left(x|\theta \right)\right)\right]\text{.}$$

Consider two models $g_1$ and $g_2$. If $I\left(f,g_1\right)<I\left(f,g_2\right)$ then model $g_1$ is better than model $g_2$. In other words,

$$\begin{array}{c}I\left(f,g_1\right)<I\left(f,g_2\right)\\ I\left(f,g_1\right)-C<I\left(f,g_2\right)-C\\ -E_f[\text{ln}\left(g_1(x|\theta ))\right]<-E_f\left[\text{ln}(g_2(x|\theta )\right)]\text{.}\end{array}$$

Thus, without knowing C, we know how much better $g_1$ is than $g_2$ (comparison between 2 models),

$$I\left(f,g_2\right)-I\left(f,g_1\right)=-E_f[\text{ln}\left(g_2(x|\theta ))\right]+E_f\left[\text{ln}(g_1(x|\theta )\right)]\text{.}$$

Hence, the use of the relative KL divergences between f and the models $g_i$ (instead of the KL divergence between f and $g_i$ that compares the model $g_i$ to the unknown truth f) allows the comparison of the candidate models $g_i$.

The models depend on parameters that have to be estimated using the data y. Let us define $\hat{\theta }\left(y\right)$, the estimator of θ, as a random variable. Consequently, $I(f,g(\cdot |\hat{\theta }\left(y\right)))$ is also a random variable. Hence, its expectation can be estimated,

$$E_y[I(f,g(\cdot \left|\hat{\theta }\left(y\right)\right))]=C-E_y[E_x[\text{ln}\left(g\left(x\right|\hat{\theta }\left(y\right)\right))]]\text{,}$$

where x and y are two independent random samples from the same distribution f and both statistical expectations are taken with respect to the truth f.

As we want to minimize the information loss by approximating the full reality f by models, we want to minimize the estimated expected KL divergence $E_y\left[I(f,g(\cdot |\hat{\theta }\left(y\right)))\right]$ over the set of models considered. That is equivalent to maximizing the estimated expected relative KL divergence. Hence, a model selection criterion can be defined as follows:

$$\underset{g\in G}{\text{max}}{E}_y\left[E_x\left[\text{ln}\left(g\left(x|\hat{\theta }\left(y\right)\right)\right)\right]\right]\text{,}$$

where G is the collection of models in terms of probability density functions.

In 1973, Akaike (AkaikePetrov and Csaki, 1973) found an asymptotically (for a large sample) unbiased estimator of the expected relative Kullback-Leibler divergence $E_y\left[E_x\left[\text{ln}\left(g\left(x|\hat{\theta }\left(y\right)\right)\right)\right]\right]$, given by

$$\ln \mathcal{L}\left({\hat{\theta }}_{MLE}|y\right)-K\text{,}$$

where $\mathcal{L}$ is the likelihood function (previously defined in the section on model calibration), ${\hat{\theta }}_{MLE}$ is the maximum likelihood estimate of θ ($\text{ln}\mathcal{L}\left({\hat{\theta }}_{MLE}|y\right)$ is the maximum log-likelihood value) and K is the number of estimated parameters including the variance (the bias correction term). Akaike multiplied this estimator by −2. Thus, the Akaike Information Criterion for each model considered with the same data set is defined as

$$AIC=-2\text{ln}\left(\mathcal{L}\left({\hat{\theta }}_{MLE}|y\right)\right)+2K\text{.}$$ (6)

Therefore, the best model within the collection of models considered given the data is the one with the minimum AIC value. More details on the derivation of AIC can be found in (Burnham & Anderson, 2002).

3.3. Model selection using AIC

Consider a collection of R models. Which model of the collection would best represent reality given the data we have recorded? To answer this question, we can compute the information criterion for each model of the collection.

If the number of observations is large enough, $K<\left(N/40\right)$, use AIC

$$AIC=-2\ln \left(\mathcal{L}\left({\hat{\theta }}_{MLE}|y\right)\right)+2K\text{.}$$

For a small number of observations, $K>\left(N/40\right)$, Sigiura (Hurvich & Tsai, 1989; Sugiura, 1978) developed the corrected AIC (AICc),

$$AICc=-2\ln \left(\mathcal{L}\left({\hat{\theta }}_{MLE}|y\right)\right)+\frac{2KN}{N-K-1}=AIC+\frac{2K\left(K+1\right)}{N-K-1}\text{,}$$

where K is the number of estimated parameters in the mathematical and statistical model and N is the number of observations. As $N\to \infty$, $AICc\to AIC$. Other extensions of the AIC have been derived to accommodate other specific cases (Burnham & Anderson, 2002).

In practice, except for some simple models, computing the minimum of the negative of the log-likelihood $-\text{ln}\left(\mathcal{L}\left({\hat{\theta }}_{MLE}|y\right)\right)$ for a model is difficult, in particular when dealing with an ODE or PDE model. However, under some assumptions, we have previously derived a relationship between the negative of the log-likelihood and least squares cost function, which can be used to easily compute AIC and AICc.

Recall that when the measurement errors are independent, identically and normally distributed with the same variance, the minimum of the negative of the log-likelihood function can be expressed as follows (see (5)),

$$-\ln \mathcal{L}\left({\hat{\theta }}_{MLE}|y\right)=\frac{N}{2}\text{ln}\left(2\pi \right)+\frac{N}{2}+\frac{N}{2}\text{ln}\left(\frac{F_{ls}\left(\hat{p}\right)}{N}\right)\text{,}$$

with $\hat{p}={\hat{p}}_{MLE}={\hat{p}}_{LSE}$ and the number of observations $N=n_e{n}_o^e{n}_i^{e,o}$. Hence, under this assumption and as the AIC or AICc are used to compare the models with each other and that the same data are used to estimate the parameters for all the models, the first term of (6) can be expressed as $-2\ln \left(\mathcal{L}\left({\hat{\theta }}_{MLE}|y\right)\right)\approx N\ln \left(\frac{F_{ls}\left(\hat{p}\right)}{N}\right)$. Therefore, $AIC$ and $AICs$ can be computed as follows:

$$AIC=N\ln \left(\frac{F_{ls}\left(\hat{p}\right)}{N}\right)+2K=N\ln \left(\frac{RSS}{N}\right)+2K$$

and

$$AICc=N\ln \left(\frac{F_{ls}\left(\hat{p}\right)}{N}\right)+\frac{2KN}{N-K-1}=N\ln \left(\frac{RSS}{N}\right)+\frac{2KN}{N-K-1}\text{,}$$

where K is the number of estimated parameters (numbers of mathematical model estimated parameters + 1 for the variance) and N is the number of observations.

Due to this approximation, interpreting the actual values of AIC and AICc has no real meaning. Furthermore, as only the estimates of the expected relative KL divergences between f and $g_i\left(x|\theta \right)$ are known with the information criteria, it is convenient to scale them with respect to the minimum AIC value among all models. Compute $AI{C}_i$ of each model i with $i\in \left\{1,\dots ,R\right\}$ and then compute the AIC differences ${\text{Δ}}_i$ as follows (Akaike, 1974):

$${\text{Δ}}_i=AI{C}_i-\underset{i}{\text{min}}AI{C}_i\text{,}$$

where ${\text{min}}_{i}AI{C}_i$ is the AIC value of the best model in the collection. The AIC difference ${\text{Δ}}_i$ estimates the information loss when using model i rather than the estimated best model. Hence, the larger ${\text{Δ}}_i$, the less plausible is model i.

Some guidelines for the interpretation of AIC difference ${\text{Δ}}_i$ in the case of nested models are given in (Burnham & Anderson, 2002):

• •${\text{Δ}}_i\in \left[\mathrm{1,2}\right],$ model i has substantial support and should be considered,
• •${\text{Δ}}_i\in [4,\dots ,7],$ model i has less support,
• •${\text{Δ}}_i>10,$ model i has no support and can be omitted.

However, these rules might be different for non-nested models or when a very large number of models is present.

Going further, for an easier interpretation, ${\text{Δ}}_i$ can be rescaled. The likelihood of model $g_i$ given the data y can be defined as

$$\mathcal{L}\left(g_i|y\right)\propto \text{exp}\left(-\frac{{\text{Δ}}_i}{2}\right)\text{.}$$

The model likelihoods can be normalized so that they sum to 1. This normalization yields the definition of the Akaike weight or “weight of evidence” of model i for being the best model (in terms of KL) of the collection given the data recorded,

$$w_i=\frac{\text{exp}\left(-{\text{Δ}}_i/2\right)}{{\sum }_{r=1}^R\text{exp}\left(-{\text{Δ}}_r/2\right)}\text{.}$$ (7)

The Akaike weight $w_i$ of model i can be interpreted as the probability that model i is the best (approximating) model given the experimental data and the collection of models considered. Hence, the smaller the weight $w_i$, the less plausible is model i. We can consider a single best model i if $w_i>0.9$.

Moreover, by using Akaike weights, the evidence ratio of model i versus model j can be defined as

$$\frac{w_i}{w_j}=\frac{\mathcal{L}(g_i|y)}{\mathcal{L}\left(g_j|y\right)}\text{.}$$

This evidence ratio quantifies the strength of evidence in favour of model i over model j.

Furthermore, using Akaike weights, the confidence set of models can be also defined. Rank models in order of Akaike weights (from the largest to smallest); then, compute the cumulative sum of their weights. The minimal subset of models whose the cumulative sum is larger than 0.95 constitutes the $95\text{\%}$ confidence set of models (in terms of KL) (Symonds & Moussalli, 2011): there is $95\text{\%}$ confidence that the best approximating model is in this subset.

Last but not least, Akaike weights can also be used to determine the relative importance of a process. The sum of Akaike weights over all models in which the process of interest appears gives a measure of the relative importance of the process of interest.

If the aim of the study is parameter estimation and when several models are well supported by the experimental data or when there is no model i with $w_i>0.9$, we can use model averaging. If θ is a parameter common to all models well supported by the data, the weighted average of parameter estimate $\hat{\theta }$ is

$$\widehat{\stackrel{‾}{\theta }}=\sum _{i=1}^R{w}_i{\hat{\theta }}_i\text{,}$$

where ${\hat{\theta }}_i$ is the MLE ${\hat{\theta }}_{MLE}$ from model i. If θ is only common to a subset of models, rescale the $w_i$ of the subset to have $\sum w_i=1$.

Example 3.1

In Jacquier et al. (2018) (Jacquier et al., 2018), using a collection of mathematical models, the regulation of NMT1 by mTOR is investigated. mTOR is a kinase (enzyme that phosphorylates other molecules) that regulates cell growth, proliferation, survival and migration. mTOR exists in two forms: the inactive form (mTOR) and the active form (pmTOR). Cancer cells exploit mTOR to enhance their capacity to grow. Rapamycin is a drug used in cancer therapy that targets mTOR and prevents its activation by preventing mTOR phosphorylation. Strong expression of NMT1 has been reported in malignant breast tissues compared with normal breast cells.

Experimental data used in (Jacquier et al., 2018) shows that Rapamycin treatment decreases phosphorylation of mTOR (pmTOR) and augments total NMT1 levels over time. However, there is no significant change in the total mTOR levels (mTOR + pmTOR). Four dataset are recorded for this study. For each of the four datasets, three quantities are measured at $m=9$ time points: total mTOR ($T_{total}^{exp}$), pmTOR ($T_p^{exp}$) and total NMT1 ($N_{total}^{exp}$).

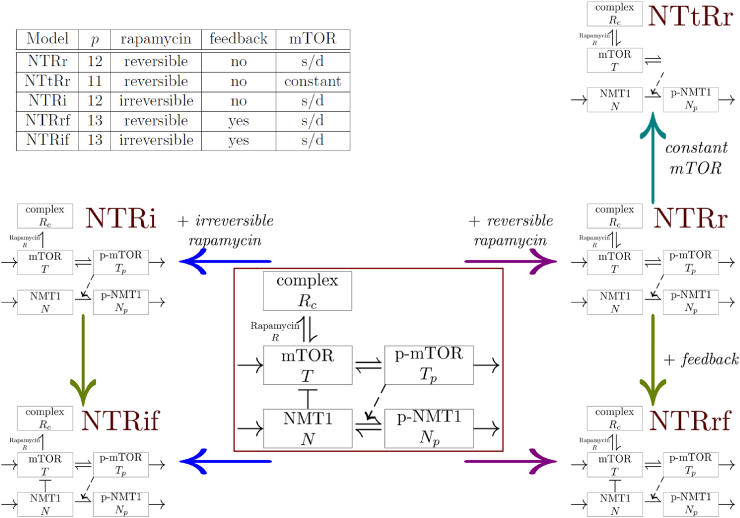
The core assumption of the work is that the NMT1 phosphorylation is regulated by pmTOR; the general model described in the framed diagram of Fig. 7 is

$$\begin{array}{l}\frac{\text{d}T}{\text{d}t}=\stackrel{\text{phosphorylation}}{\overbrace{\frac{-{\alpha }_{T}T}{K_T+T}}}+\stackrel{\text{dephosphorylation}}{\overbrace{\frac{{\alpha }_{T_p}{T}_p}{K_{T_p}+T_p}}}+{\stackrel{\text{synthesis}}{\overbrace{\text{Π}}}}_T-\stackrel{\text{feedback}}{\overbrace{\beta TN}}+\stackrel{\text{rapamycin effect}}{\overbrace{g(T,R_c)}}\text{,}\\ \frac{\text{d}{T}_p}{\text{d}t}=\stackrel{\text{phosphorylation}}{\overbrace{\frac{{\alpha }_{T}T}{K_T+T}}}-\stackrel{\text{dephosphorylation}}{\overbrace{\frac{{\alpha }_{T_p}{T}_p}{K_{T_p}+T_p}}}-\stackrel{\text{degradation}}{\overbrace{{\delta }_{T_p}{T}_p}}\text{,}\\ \frac{\text{d}N}{\text{d}t}=-\stackrel{\text{phosphorylation}}{\overbrace{\frac{{\alpha }_N{T}_{p}N}{K_N+N}}}+\stackrel{\text{synthesis}}{\overbrace{{\text{Π}}_N}}\text{,}\\ \frac{\text{d}{N}_p}{\text{d}t}=\stackrel{\text{phosphorylation}}{\overbrace{\frac{{\alpha }_N{T}_{p}N}{K_N+N}}}-\stackrel{\text{degradation}}{\overbrace{{\delta }_{N_p}{N}_p}}\text{,}\\ \frac{\text{d}{R}_c}{\text{d}t}=\stackrel{\text{rapamycin effect}}{\overbrace{h(T,R_c)}},\end{array}$$

where T is the inactive form of mTOR, $T_p$ is (pmTOR) the active form of mTOR, N is the active form of NMT1, $N_p$ is the phosphorylated form of NMT1 (pNMT1) and $R_c$ is the complex formed by Rapamycin and mTOR. In presence of Rapamycin, five models are considered to test alternative hypotheses difficult to test experimentally.

• •Does the regulation of endogenous levels of mTOR components impact the dynamics? Two cases are described:
• –synthesis and degradation of the relevant forms of mTOR,
• –the total mTOR (mTOR + pmTOR) is assumed to be constant.
• •Does NMT1 have a negative feedback effect on mTOR? Two cases are considered:
• –no feedback, $\beta =0$,
• –presence of feedback, $\beta >0$.
• •Is the effect of rapamycin on mTOR reversible or irreversible? Two cases are considered:
• –a reversible binding with $g\left(T,R_C\right)=-\gamma RT+\kappa R_C$ and $h\left(T,R_C\right)=-g\left(T,R_C\right)$,
• –an irreversible binding following $g\left(T,R_C\right)=-\gamma RT$ and $h\left(T,R_C\right)=\gamma RT-{\delta }_{R_C}{R}_C$.

Fig. 7.

General model and collection of models considered for the interactions between NMT1 and mTOR in breast cancer cells in Jacquier et al. (2018) (Jacquier et al., 2018). In the centre, the framed diagram is the general model. The non-framed diagrams represent the five models of the collection. At the top left corner, the table lists the collection of models studied with their number of parameters p, assumptions on rapamycin binding, feedback regulation of mTOR by NMT1 and mTOR dynamics (s/d meaning an explicit synthesis and degradation of mTOR). Figure adapted from (Jacquier et al., 2018).

The five models in the collection resulting from the general model, their assumptions and number of parameters are given in Fig. 7.

The five models are calibrated to each of the four datasets. For the four datasets, the residual sum of squares between experimental and simulated data for model $i\in \left\{1,\dots ,5\right\}$ is minimized using a genetic algorithm. For each dataset, the residual sum of squares is defined as

$${\text{RSS}}_i=\sum _{j=1}^m\left[{\left(T_p^{exp}\left(t_j\right)-T_p^i\left(t_j\right)\right)}^2+{\left(T_{total}^{exp}\left(t_j\right)-T_{total}^i\left(t_j\right)\right)}^2+{\left(N_{total}^{exp}\left(t_j\right)-N_{total}^i\left(t_j\right)\right)}^2\right]\text{,}$$ (8)

where $t_j$ are the $m=9$ time points, $T_{total}^i\left(t_j\right)=T^i\left(t_j\right)+T_p^i\left(t_j\right)$ and $N_{total}^i\left(t_j\right)=N^i\left(t_j\right)+N_p^i\left(t_j\right)$ are the responses in model i. Hence, for a given dataset, a model is associated with a nominal set of parameters.

To identify the best model and characterize the required mechanisms for each of the four dataset, the corrected AIC are used as the number of observations is small ($n=3m=27$, for each dataset) in comparison to the number of parameters $p+1$ (see table in Fig. 7). For each dataset and each model $i\in \left\{1,\dots ,5\right\}$, $AIC{c}_i$ is computed as previously shown:

$${\text{AICc}}_i=n\ln \left(\frac{{\text{RSS}}_i}{n}\right)+\frac{2k_{i}n}{n-k_i-1}\text{.}$$ (9)

$k_i$ is the number of estimated parameters for model i (p in the table displayed in Fig. 7), including the estimation of the variance by ${\text{RSS}}_i/n$. Using (7) with (9), the Akaike weights are computed for an easier interpretation of results (Table 1).

Table 1.

${\text{AICc}}_i$ and Akaike weights $w_i$ for the five models for datasets 1 to 4, with $k_i=p+1$ the number of parameters considered to compute the ${\text{AICc}}_i$, with i denoting the model considered. The weights corresponding to each assumption are obtained by summing the weights of the models verifying the assumption (see the table in Figure 7). Thus, the weight of models with reversible (resp. irreversible) rapamycin effect is obtained by summing the weights of models including this assumption namely NTRr, NTtRr and NTRrf (resp. NTRi and NTRif). The weight of the feedback assumption corresponds to the sum of the weights of models NTRrf and NTRif.

Models		Dataset 1		Dataset 2		Dataset 3		Dataset 4
	$k_i$	${\text{AICc}}_i$	$w_i$	${\text{AICc}}_i$	$w_i$	${\text{AICc}}_i$	$w_i$	${\text{AICc}}_i$	$w_i$
NTRr	13	-2.3	0.393	-107.1	${10}^{-4}$	-75.9	0.025	-58.8	0.407
NTtRr	12	-1.4	0.248	-124.9	0.997	-83.1	0.929	-58.2	0.305
NTRi	13	-2.0	0.351	-113.5	0.003	-76.7	0.039	-58.1	0.282
NTRrf	14	7.0	0.004	-91.6	${10}^{-8}$	-73.2	0.007	-48.0	0.002
NTRif	14	6.6	0.005	-102.4	${10}^{-5}$	-66.6	${10}^{-4}$	-49.4	0.004
Assumptions
Reversible			0.64		0.9967		0.961		0.714
Irreversible			0.36		0.0033		0.039		0.286
Feedback			0.008		${10}^{-5}$		0.007		0.006
No feedback			0.992		0.99999		0.993		0.994

This example highlights that conclusions depend strongly on experimental data. For dataset 2 and 3, the Akaike weight of model NTtRr is found to be larger than 0.9; for dataset 2 and 3, model NTtRr is the best model. However, for dataset 1 and 4, none of models obtains a high Akaike weight. Model selection to find the best model is not conclusive when using dataset 1 and 4. However, discriminating between feedback and no feedback is conclusive for all the four datasets. There is strong evidence that there does not exist a negative feedback regulation of mTOR by NMT1. The reversible binding assumption is more likely to occur when dataset 2 and 3 are used; however, discriminating between reversible and irreversible binding is not conclusive when dataset 1 and 4 are considered.

In summary, the Akaike Information Criterion, valid to compare nested and non-nested models, can be used as a powerful tool for model selection. AIC or AICc allows the ranking of the candidate models and might select a best model within the collection given the experimental data considered. The best model has the lowest AIC or AICc values; however, the actual values of AIC or AICc have no meaning. The use of Akaike weights computed from AIC or AICc allows the interpretation of results by providing the probability that a model is the best model given the experimental data and the set of models considered. Furthermore, the Akaike weights allow the quantification of the likelihood of diverse assumptions considered within the model collection. The model selection method is specific to a given set of data; neither AIC nor AICc can be used to compare models based on different datasets. Information criteria are not statistical tests. Finally, never forget that the best model cannot be considered as the “truth”.

4. Conclusion

The principle of multiple working hypotheses is important in Science as it permits to confront different mechanisms; when considered with appropriate selection criteria, it allows the culling of hypotheses and the unimportant and required mechanisms can be identified. The use of a collection of models coupled with a model selection method instead of a single model makes the mathematical modelling approach more powerful and helps convince experimental scientists of the use and power of theoretical approaches. For instance, in (Kirmse et al., 2007), the use of a collection of models allows the identification of the longitudinal annealing of filaments as a required mechanism for the filament elongation of in vitro intermediate filaments. This mechanism was experimentally confirmed a few years later in (Colakoglu & Brown, 2009) and (Winheim et al., 2011). In (Portet, Madzvamuse, Chung, Leube, & Windoffer, 2015), the use of a collection of models combined with Akaike Information Criterion model selection allows to demonstrate that the directed transport of assembled intermediate filament proteins in cells was required to explain the spatial distributions of intermediate filaments.

Summing up, investigating a question in Biology by combining experimental data and mathematical modelling could follow the different steps (Baker et al., 2005; Burnham & Anderson, 2002; Miao et al.,2009 Symonds & Moussalli, 2011):

• •a systematic modelling of possible scenarios based on biological hypotheses and first principles to design a collection of models;
• •once the collection of models is formed, each model has to be calibrated using the same data set or data sets;
• •once parameter estimates are known for each model, compute their AIC or AICc and associated Akaike weights; rank models and identify the best model or the 95% confidence set of models;
• •partition the collection of models in subsets of models based on their underlying hypotheses and using Akaive weights, evaluate the importance of different processes.

Declaration of competing interest

• No conflict of interest

Handling editor: Dr. J Wu