Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Dec 3;16(1):443–452. doi: 10.1021/acs.jctc.9b00981

The Electron Affinity as the Highest Occupied Anion Orbital Energy with a Sufficiently Accurate Approximation of the Exact Kohn–Sham Potential

M Amati †,*, S Stoia †, E J Baerends ‡,*
PMCID: PMC6964414  PMID: 31794657

Abstract

graphic file with name ct9b00981_0001.jpg

Negative ions are not accurately represented in density functional approximations (DFAs) such as (semi)local density functionals (LDA or GGA or meta-GGA). This is caused by the much too high orbital energies (not negative enough) with these DFAs compared to the exact Kohn–Sham values. Negative ions very often have positive DFA HOMO energies, hence they are unstable. These problems do not occur with the exact Kohn–Sham potential, the anion HOMO energy then being equal to minus the electron affinity. It is therefore desirable to develop sufficiently accurate approximations to the exact Kohn–Sham potential. There are further beneficial effects on the orbital shapes and the density of using a good approximation to the exact KS potential. Notably the unoccupied orbitals are not unduly diffuse, as they are in the Hartree–Fock model, with hybrid functionals, and even with (semi)local density functional approximations (LDFAs). We show that the recently developed B-GLLB-VWN approximation [Gritsenko et al. J. Chem. Phys.2016, 144, 204114] to the exact KS potential affords stable negative ions with HOMO orbital energy close to minus the electron affinity.

I. Introduction

The ionization energy and electron affinity of molecules are a subject of continuing interest.1−5 So-called Δ methods (e.g., ΔSCF or ΔMP2) calculate these properties as differences of total energies from separate calculations on neutral and charged species. The disadvantage is that a small quantity is obtained as difference of two large numbers. Direct methods2,5 compute the desired quantities as (orbital) energies of suitable one-electron Hamiltonians, or as linear combinations of orbital energies at some intermediate points between the neutral and ionic systems (integration methods, see below). Best known is of course the Hartree–Fock (HF) model, where the HOMO orbital energy is a frozen orbital approximation (Koopmans) to minus the ionization energy (IP) and the LUMO orbital energy is a Koopmans approximation to minus the electron affinity (EA). These HF orbital energy estimates entail considerable error; for instance, the HF HOMO orbital energy has the typical Koopmans’ error of ca. 1 eV, while the LUMO orbital energy has a larger error and is (in particular in small molecules) much above −EA, often even positive (cf. ref (6) and references therein). The Kohn–Sham (KS) model has the HOMO energy exactly equal to minus the IP.7,8 The KS LUMO orbital has physically a different meaning than the HF LUMO orbital. It describes approximately an excited electron, not an added electron.6,9 The KS LUMO orbital energy is not close at all to minus the EA, but the HOMO–LUMO gap of the KS model approximates the first excitation energy. It is an optical gap rather than the fundamental gap (the IP – EA difference; see for a recent review, ref (10)). With hybrid functionals, one may follow the optimized effective potential (OEP) route, trying to minimize the total energy using a local potential. This has been pioneered for atoms with grid-based methods for the Hartree–Fock exchange case by Talman and Shadwick11 and Krieger et al.12 The HOMO orbital energy then is close to (or identical to) the Hartree–Fock value, and no special problem with the stability of anions will be encountered. But the HOMO orbital energy of the exact-exchange OEP methods will still have the same error (in the order of 1 eV) with respect to the experimental IP as Hartree–Fock itself. OEP calculations for (large) molecules require the use of finite basis sets, with ensuing uniqueness problems as highlighted by Staroverov et al.13 Solving the latter involves a balancing act between basis set quality for orbital expansion and potential expansion,14,15 which may affect the numerical precision with which orbital energies are obtained. One may also use the so-called generalized KS (GKS)16 strategy of performing an orbital optimization in the same way as in HF theory, which will result in a one-electron Hamiltonian with certain percentages of the DFA exchange-correlation potential and the nonlocal HF exchange operator. Orbital energies will be in between the Hartree–Fock and DFA values. Being strongly dependent on the percentage of exact exchange in the functional, unoccupied orbital energies may be anywhere between the low KS like value and the high HF value.

One may introduce orbital occupation numbers in the total energy expression such that the derivative ∂Emodel/∂ni = ϵi, a relation derived a long time ago for the HF energy expression and exchange-only LDA (Xα) by Slater et al.17,18 and others.19 Care must be taken that this equality is obeyed by a suitable introduction of occupation numbers. It is possible to introduce dependence on occupation numbers for which the relation would not hold.10 If the relation holds, it is possible to reproduce total energy based ΔE numbers by a numerical integration, e.g., for the ionization potential (ionization from the HOMO)

I. 1

Even if the derivative with respect to occupation number is not an orbital energy, one may use this numerical integration if just ∂E/∂ni can be determined. If the total energy is a quadratic function of the occupation numbers (usually a very good approximation), i.e., if the ϵi or just the ∂E/∂ni derivative is a linear function of nH, a single point approximation (e.g., ϵ(nH = 1/2)) gives an excellent result.5 This is in fact the Slater transition state method. More accurate results can be obtained in this integration method2,5,19 with more points and weights in the numerical integration. All these “direct” methods circumvent the subtraction of two large numbers and determine the IP and/or EA from just the relatively small orbital energy (or ∂E/∂ni) directly.

A related approach is one in which the functional is tuned, i.e. by varying the amount of exact exchange, such that the HOMO and LUMO orbital energies are close to −IP and −EA, respectively. This has been advocated by Yang and co-workers.4,20,21 The development of such density functional approximations has been motivated by the proposal by Perdew, Parr, Levy, and Balduz (PPLB)22 that the total energy for fractional electron numbers behaves as a set of straight line segments between the integer N values. The slope of these lines then obviously is −IP for N – δ and −EA for N + δ electrons. Equating [∂E/∂N]+ with ∂E/∂nLUMO = ϵLUMO, one can observe that the LUMO orbital energy should be −EA in order to obey the PPLB behavior. Irrespective of the question whether such straight-line behavior is a necessary requirement in DFT or just a possible choice,23 this approach would clearly also lead to a direct determination (approximation) of the EA (and IP) values from orbital energies.

In the same vein it is possible to construct range-separated hybrid functionals that provide good approximations to the fundamental gap by optimal tuning (system dependent) of the range separation parameter.24−27 This can be perfected3 for the electron affinity by performing the optimal tuning for just the anion HOMO orbital energy, minimizing the error J2(μ) = [ϵHOMOμ(N + 1) + EAμ(N)]2. The anion HOMO orbital energies then yield good approximations to the EAs.

A related strategy is the development of so-called Koopmans-compliant functionals, where additional terms are introduced in the functional with the explicit purpose to obtain HOMO and LUMO orbital energies close to −I and −A.28−30

It is a disadvantage of these methods that the LUMO is not only high-lying but will also be rather diffuse, in particular in small molecules. The physical meaning of (shape of) the LUMO is no longer clear, and it precludes the transparent assignment of many electronic excitations as just single orbital–orbital transitions, which is a great virtue of the (exact) KS orbital basis.9

Maybe the most simple and straightforward method to obtain IPs and the EA from orbital energies is by modeling the exact KS potential directly. For neutral systems, this should yield the first IP as the HOMO orbital energy, while the negative anion will provide the EA from its HOMO orbital energy. Recently, a proposal has been made31 for a reasonably accurate approximation to the exact KS potential. It is based on a breakdown of the total KS potential into various parts, such as the exchange-correlation hole potential and the so-called response potential. It has been argued that in the LDA and GGA approximations the exchange-correlation hole potential is fairly accurate, but the response part of the potential is erroneous in these approximations. The LDA exchange response potential is much too repulsive. It causes the anomalous upshift of ca. 5 eV of the orbital energies of the LDA/GGA models. A much better approximation to the KS potential is obtained when the exchange part of the response potential is replaced by the approximation proposed a long time ago by Gritsenko et al. (GLLB).32 The exchange-correlation hole potential is approximated by the LDA exchange hole (the same as the original Slater exchange hole approximation) plus Becke’s correction of the exchange hole potential, while the LDA correlation hole and correlation response potentials (in the VWN parametrization) are retained. This so-called B-GLLB-VWN potential proved to remedy the erroneous upshift of the orbitals of the LDA/GGA models and to yield orbital energies in much better agreement with “exact” (very accurate) KS orbital energies.31 It is well-known that the KS HOMO orbital energy is exactly equal to the first IP, but also the other exact KS orbital energies are rather good approximations of the higher ionization potentials (see refs (33−35) and see further illustration at the end of the present paper (section III)). The B-GLLB-VWN potential therefore provided very good estimates of the first and also the higher IPs by way of the HOMO and lower occupied orbital energies.31

In the present paper, we investigate the performance of the B-GLLB-VWN potential for anions and the electron affinity. There is the notorious problem with the usual DFAs for anions that they are often unbound (positive orbital energy for the anion HOMO). This was noted in the early days of LDA calculations36,37 and caused some concern later.38,39 It has been clear, however, that the problem was caused by the deficiency of the DFA KS potential mentioned above, namely, the erroneous upshift of ca. 5 eV. Given the generally small EAs (a few electronvolts at best), this tends to move the anion HOMO to positive energy, i.e., make the anion unbound. This error can be remedied by correcting the potential, e.g., with the Perdew–Zunger SIC correction40 or by asymptotic and other corrections41 (the F– anion that caused some concern was bound in the so-called LB94 potential41). This problem of the DFAs, and hybrid functionals as well, has continued to generate interest.42−45 Obviously, if we have a good approximation to the exact KS potential, and therefore a HOMO orbital energy of the anion close to minus the EA, the anion does not suffer from the problem of unboundedness. It is the purpose of this work to investigate whether the B-GLLB-VWN approximation31 to the exact KS potential is able to describe anions, and to establish the accuracy with which the anion HOMO orbital energy approximates minus the EA.

The B-GLLB-VWN potential is based on the partitioning of vxc, which naturally emerges from its definition in the Kohn–Sham (KS) theory as a functional derivative of Exc with respect to the electron density ρ(r)46,47

I. 2

In eq 2, g̅(r2, r3) is the pair-correlation function integrated over the coupling parameter λ of the electron–electron interaction λ/r12. Then, the derivatives of the densities ρ(r2) and ρ(r3) in the numerator of eq 2 yield identical results, adding up to the full potential of the xc hole v̅xchole (the coupling constant integration of the hole and its potential are indicated with an overbar)

I. 3

The term in the potential coming from the derivative of g̅ produces the so-called response potential v̅resp

I. 4

The total vxc is the sum of eqs 3 and 4

I. 5

The hole potential is approximated with the original Slater ρ1/3 form (practically identical to the LDA exchange only form, see ref.31), to which the Becke88 correction48 is added. The response potential is approximated with the step potential derived in ref.32 and is denoted GLLB

I. 6

No optimization or parameter variation is applied. The only parameter is the Kg factor in eq 6 which in the derivation of ref (32) was determined at K = 0.382 for the uniform electron gas (in which case the GLLB response potential becomes exact). We refer to ref (31) for a comprehensive discussion of this approximation and examples of its use. As a brief explanation of how the B-GLLB-VWN potential improves upon (semi)local DFAs, we note here that it has been observed31 that the DFA orbital energies are too high lying (too destabilized, not negative enough) for the following reason. The LDA exchange potential (which is the main part of almost all DFA potentials) consists of a hole potential which is adequately stabilizing (practically the Slater ρ1/3 potential), −3[3/(8π)]1/3ρ(r)1/3, plus a response part. The LDA exchange response part is destabilizing, +[3/(8π)]1/3ρ(r)1/3. This destabilization is much too strong. This is evident from pictures of the LDA or GGA potentials compared to exact KS potentials: the DFA potentials run in the bulk atomic or molecular region usually rather parallel to the exact KS potential, but on the order of 5 eV destabilized. The B-GLLB-VWN does not use the too strongly repulsive LDA exchange response potential but replaces it with the much less repulsive GLLB approximation of eq 6. It has been found that the occupied orbital energies are then suitably stabilized compared to DFAs, the HOMO energy for a series of neutral benchmark molecules only deviating from the IP by a few tenths of an electronvolt at most. We here investigate whether this is also true for negative ions.

We note in passing that the same GLLB response potential approximation offers a cheap method of correcting the KS one-electron energy band gap to the total energy based fundamental gap in solids.49−51

II. B-GLLB-VWN Orbital Energies and Electron Affinities of Molecules

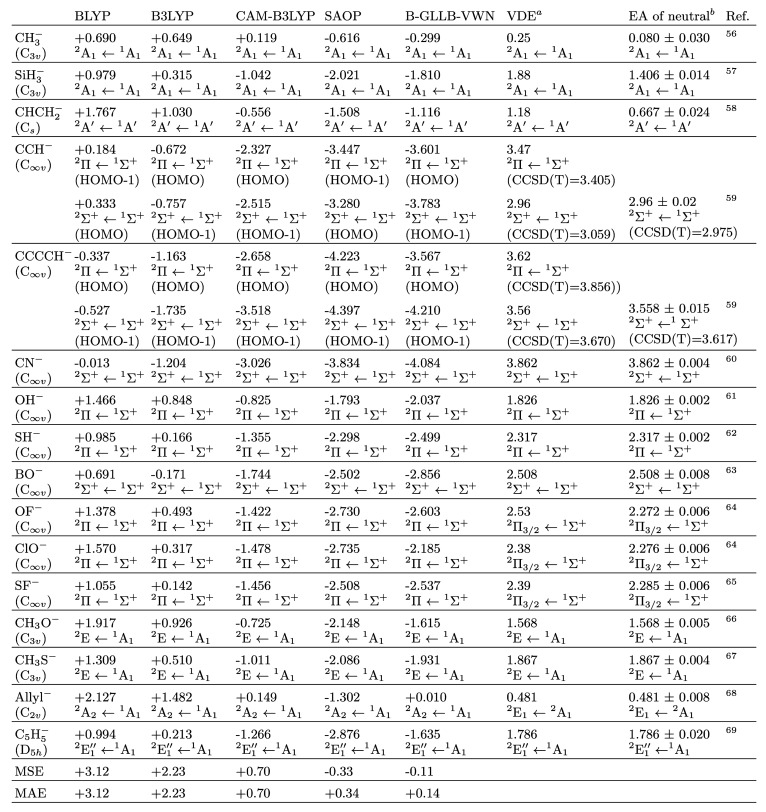
Table 2 collects the HOMO energies of a series of closed-shell anions computed with various potentials, to be compared to vertical electron detachment energies (VDE). The DFT calculations have been performed with the ADF code52−54 using an even-tempered STO basis denoted ET/TEST/ET-QZ+5PALT in the ADF2017.113 documentation. It consists of an all electron quadruple-ζ basis set (s- and p-functions) plus five polarization functions (three d- and two f-type functions), two diffuse functions (s- and p-functions), and two tight functions of s- and p-type. This basis set is very generous, since STO bases converge rapidly for diffuse systems like these anions. In Table 1, we demonstrate this convergence for a few examples from our series of molecules. A straightforward TZP basis (triple-ζ 2s, 2p basis plus a 3d polarization function) is inadequate since it lacks diffuse functions. Augmentation with one diffuse function of type s, p, and d to form the AUG/ATZP basis brings the basis close to completeness. Further addition of a polarization function has no effect, and the further extension to ET/TEST/ET-QZ+5PALT makes hardly any change (a few hundredths electronvolts at most). The equilibrium geometries of all the anions used in these calculations were determined with CCSD(T) calculations using the Gaussian 09 software55 with an aug-cc-pvtz Gaussian basis set and default options for the SCF, CCSD(T), and geometry optimization thresholds. Hessian evaluations were performed on all the equilibrium structures to check the nature of minima points on the potential energy surface. A few benchmark theoretical values for the VDE were obtained from CCSD(T) calculations on both anion and neutral systems when the experimental numbers required verification or clarification, see discussion below.

Table 2. HOMO Energies (eV) of Closed-Shell Molecular Anions Obtained through Several xc Functionalsa−69.

II.

Open in a new tab
a

The state resulting from electron detachment from the HOMO is given (as well as the starting ground state of the negative ion).

b

Vertical detachment energy, the frozen-geometry energy gap between anion and neutral species. The opposite of VDE is used in this paper as an experimental value of the HOMO for the evaluation of the MAE and MSE. VDE values were evaluated from the referenced experimental photoelectron spectrum; CCSD(T) benchmark values for the VDE are provided if verification or clarification of the experimental numbers is required, see text.

c

Electron affinities, the zero-point energy difference between the anion and neutral molecules.

Table 1. Dependency of the Computed (B-GLLB-VWN) HOMO Energies (eV) on the Basis Set Size.

  TZP ATZP ATZ2P ET-QZ+5 Palt
CH3– +0.131 –0.273 –0.272 –0.299
LiH– –0.409 –0.564 –0.564 –0.564
Li2– –0.621 –0.631 –0.631 –0.639
NO– –0.041 –0.312 –0.330 –0.350
Open in a new tab

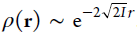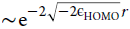The asymptotic decay of the electron density at a fixed geometry is known to be exponential according to the vertical ionization energy I at that geometry, Inline graphic. The Kohn–Sham calculation provides an electron density that decays as the slowest decaying orbital density, the HOMO density, with exponential decay Inline graphic (assuming the KS potential to go to zero at infinity). So strictly speaking, we should compare the calculated HOMO orbital energy to the vertical ionization energy of the anion, i.e., the energy difference between the anion at its equilibrium geometry and the neutral molecule at exactly the same geometry. The experimental so-called vertical (electron) dissociation energy (VDE)80 measures the vertical ionization energy from the ground vibrational state rather than from the bottom of the potential energy well. Given the level of accuracy that the various DFAs are reaching, we can make a meaningful comparison of the HOMO orbital energies to these VDEs without correcting for the zero point vibrational energy. In fact, in all the studied compounds, zero point energy corrections to VDE can be considered negligible, being lower than 0.06 eV.

The experimental EA represent the energy differences between the vibrational ground states of anions and neutral molecules, with negligible (for our goals) corrections associated with the rotational motions. As can be seen from the table, in a few cases (CH3–, SiH3, and CHCH2–) the difference of the experimental EA with the experimental VDE is large, several tenths of an electronvolt, up to 0.5 eV. These are cases where the anions exhibit considerable geometry relaxation compared to the neutral molecule. In these cases, VDEs were evaluated by us from the referenced (in the table) experimental photoelectron spectrum, by taking the energy value of the most intense peak in the spectrum. In cases where the geometry relaxation is very small, the EA and VDE values may not be distinguishable, and in the table we then use the same numerical value. In fact, in those cases, the zero point energies of the anion and neutral species are expected to almost cancel each other out.

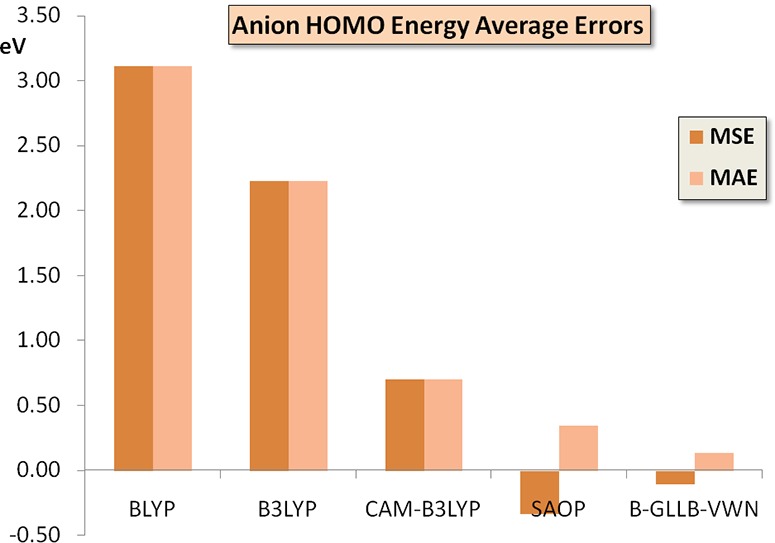
The first columns of Table 2 demonstrate the well-known fact that, in many cases, the anion HOMO orbital energy is at positive energy for typical DFAs like the GGA BLYP and hybrid B3LYP, and still in some cases for the long-range corrected CAM-B3LYP. These positive orbital energies are arbitrary, being determined completely by the finite extent of the basis functions. If one would extend the basis set to completeness, including also infinitely extended basis functions (plane waves), the orbital energy will go down to zero,6 describing a free electron with zero kinetic energy. The HOMO orbital energy turns negative for most anions with the CAM-B3LYP functional, but still the HOMO level is much too high lying, the orbital energies are considerably above the negatives of the VDE values. The consistently too high lying HOMO levels with the BLYP, B3LYP, and CAM-B3LYP functionals lead to a positive mean signed error (MSE) almost identical to the mean absolute error (MAE) with respect to the VDE. These positive errors diminish in the order BLYP, B3LYP, and CAM-B3LYP but are all large. This behavior is visible in the error bars for these functionals in Figure 1.

Figure 1.

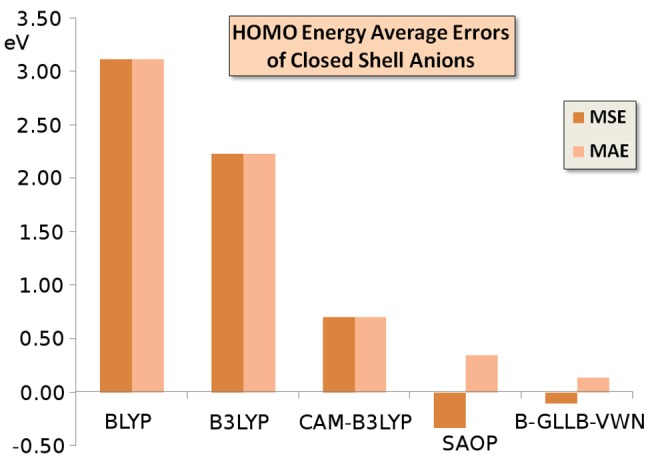
Figure 1

Open in a new tab

Mean signed error (MSE) and mean absolute error (MAE) of the HOMO orbital energy of the closed shell anions of Table 2 with respect to the experimental VDEs (vertical electron dissociation energies), according to the various GGA and hybrid functionals, and from the model potentials SAOP and B-GLLB-VWN.

In contrast, the B-GLLB-VWN anion HOMO orbital energies are always negative, hence the anions are stable, except for the case of allyl (+0.01 eV). In many cases, the HOMO orbital energies are very close to (minus) the VDE values, often 0.1 eV or less, and only some molecules have larger errors of ca. 0.2 eV. The MAE is only 0.14 eV, the MSE a bit lower at −0.11 eV. The performance of B-GLLB-VWN for this set of molecules is excellent. For comparison, the results of an earlier approximation of the exact KS potential, the statistical average of orbital dependent potentials (SAOP), are also displayed. The performance of the SAOP potential is also good, but the MSE and MAE are, with −0.39 eV and +0.40 eV, distinctly worse than for B-GLLB-VWN.

We note that CCH– and CCCCH– are special cases. The determination of the VDE is complicated by the presence of two close-in-energy states of the neutral molecule (2∑+ and 2Π) and, consequently, overlapping features and high levels of anisotropy in the photoelectron spectrum.75 The low-lying 2∑+ and 2Π states of the neutral molecule being so close (for CCCCH almost degenerate), there is considerable vibronic coupling between them. Such vibronic coupling effects are absent from the straightforward Born–Oppenheimer (clamped nuclei) KS calculations. Thus, CCSD(T)/aug-ccpVTZ calculations were performed, obtaining VDE values based on the Δ method. In CCH, the CCSD(T) calculations find the ground state to be the 2∑+ state, ca. 0.5 eV below the excited 2Π state, while for CCCCH the near degeneracy of the 2∑+ and 2Π states is confirmed. In these cases, the EA was also computed (including geometry relaxation effects) at the same level of theory, as a test of the used post-HF method. These CCSD(T) values for the EA (for the 2∑+ states) are included in the table in parentheses and compare very well to the experimental values.

We observe that, in these cases, the HOMO is calculated to be a π orbital for all functionals, with the single exception of SAOP in case of CCH (and BLYP for CCH, which is left out of consideration because the orbital energies are unrealistic anyway). The π HOMO orbital energy has to be associated with the 2Π ← 1Σ+ experimental VDE and shows very good agreement with it for B-GLLB-VWN for both CCH– and CCCCH–. However, this is the second VDE in these molecules (clearly so for CCH–, but almost equal to the first VDE in CCCCH–). On the other hand, the HOMO–1 σ orbital energy, which is to be associated with the first VDE (2Σ+ ← 1Σ+) is clearly inaccurate. If we limit the evaluation of the B-GLLB-VWN errors to the HOMO energies, that is, we exclude the HOMO–1 evaluation of CCH– and CCCCH–, the MAE and MSE errors fall to the really low values of +0.14 and −0.08 eV. However, the fact remains that B-GLLB-VWN is not able to predict the correct HOMO in both these molecules (or the near degeneracy in CCCCH–).

The picture for SAOP is mixed, with good results for CCH–, notably its π orbital energy, but remarkably poor for CCCCH–.

The allyl anion case shows an unusually large discrepancy between the SAOP and B-GLLB-VWN potentials which cannot be easily explained. The B-GLLB-VWN orbital energy is a puzzling (barely) positive +0.010, in error by a significant but not excessive +0.47 eV, while the negative SAOP value of −1.302 eV has a much larger error in the opposite direction.

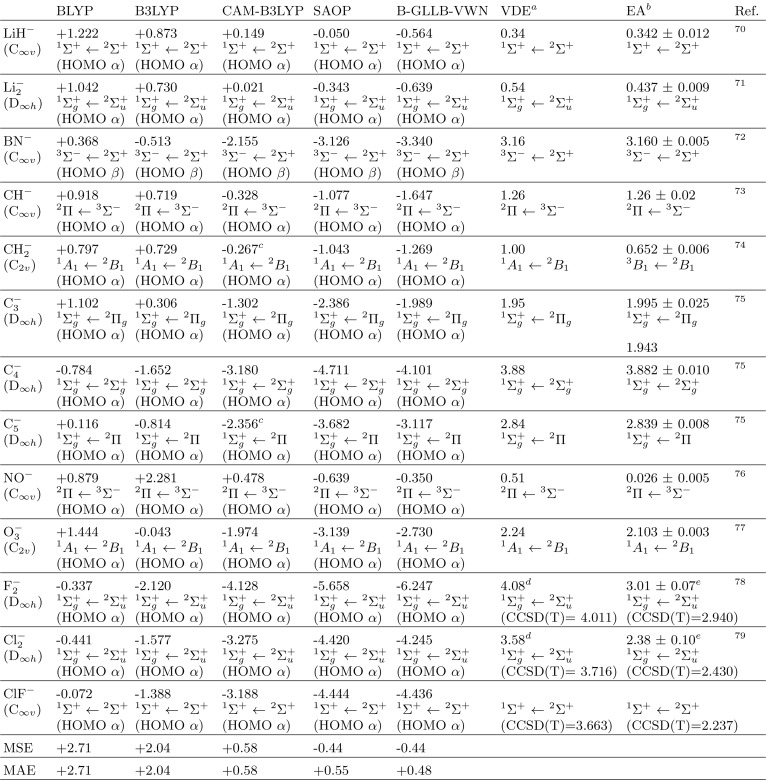
Most molecules are closed-shell and yield open-shell anions. In Table 3, we present a sample of open-shell anions, which have been calculated with the unrestricted version of the B-GLLB-VWN potential. In the unrestricted case, we have separate manifolds of α and β spin orbitals and orbital energies. In this case, we compute different response potentials for the orbitals of different spins, using the different energies of the highest occupied spin orbital in the spin-adapted version of eq 6:

II. 7

Table 3. HOMO Energies (eV) of Open-Shell Molecular Anions from Unrestricted SCF Computations Obtained through Several xc Functionals−77.

II.

Open in a new tab
a

Vertical Detachment Energy, the frozen-geometry energy gap between anion and neutral species. The opposite of VDE is used in this paper as experimental value of the HOMO for the evaluation of the MAE and MSE. VDE values were evaluated from the referenced experimental photoelectron spectrum; CCSD(T) benchmark values for the VDE are provided if verification or clarification of the experimental numbers is required, see text.

b

Electron Affinities, the zero-point energy difference between the anion and neutral molecules.

c

Due to SCF convergence problems, the ET/ET-QZ3P-1DIFFUSE basis set (ADF.2017.113) was used in this case.

d

Estimated in this paper by adding the expermental EA to the computed (CCSD(T)/aug-pVTZ) relaxation energy of the neutral molecule.

e

The assignment of the anion and neutral states is not experimentally available.

Again, we note the much too high lying HOMO (actually a singly occupied highest molecular orbital or SOMO) with BLYP, B3LYP, and CAM-B3LYP, see also Figure 2.

Figure 2.

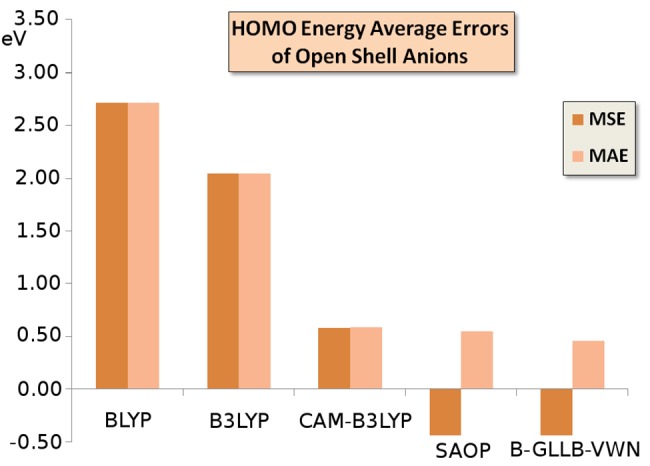
Figure 2

Open in a new tab

Mean signed error (MSE) and mean absolute error (MAE) of the orbital energies of the highest (singly) occupied orbital (HOMO) of the open shell anions of Table 3 with respect to the experimental VDEs (vertical electron dissociation energies), according to the various GGA and hybrid functionals, and from the model potentials SAOP and B-GLLB-VWN.

Many of the B-GLLB-VWN and SAOP HOMO levels are excellent. The opposite signs of MSE and MAE imply that the HOMO energies have a systematic error, being consistently too negative. CH2– has an unpaired electron in the π orbital perpendicular to the molecular plane. The vertical ionization is to the singlet state of CH2 at the same geometry, but geometry relaxation and singlet–triplet intersystem crossing bring the neutral CH2 molecule to its triplet ground state, on which the EA is based. The B-GLLB-VWN orbital energy of the π SOMO is in excellent agreement with the VDE.

There appears to be a problem with the dihalogens: the result for F2– is a remarkable outlier, and also Cl2– and ClF– are poor, when compared to the theoretical (CCSD(T)) VDE values.

Overall, the SOMO orbital energies are in worse agreement with the VDE than with the closed shell anions. Much of this increased error is coming from the dihalogens: if we omit these three cases, the MSE and MAE drop to −0.20 and +0.23 eV. It is nevertheless true that these poorer results for the unrestricted cases invite a further scrutiny of the possible causes, which will be the subject of further work.

III. B-GLLB-VWN Orbital Energies and Electron Affinities for Closed Shell Atomic Anions and Neutral Atoms

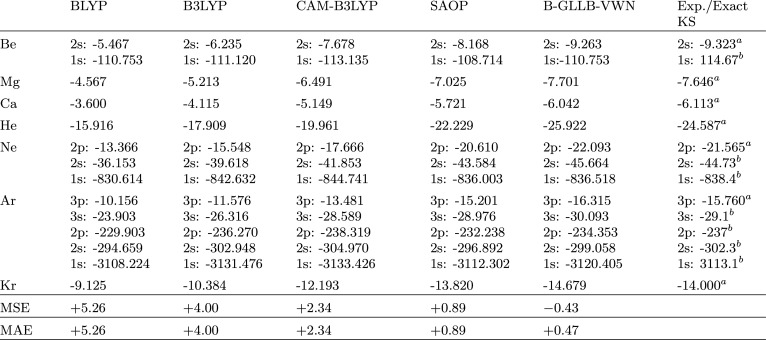
In Table 4, results for atomic anions are presented. The HOMO eigenvalues obtained with the GGAs BLYP, B3LYP, and CAM-B3LYP are positive and therefore not meaningful. They should be zero in a complete basis but are positive due to the finite range of the basis functions. The atomic results for B-GLLB-VWN and SAOP are somewhat inferior to the molecular ones. The response potential has a very small contribution in the HOMO region, the repulsive jump behavior of this potential only starting in the sub-HOMO region. The atoms ((ns)k or (np)k configuration) have relatively many electrons in the outer shell. Apparently, the repulsive behavior of the GLLB model response potential is not strong enough in that region. This is particularly manifest in the poor result of the hydrogen anion, where the GLLB potential is zero by construction. We note that for these atomic anions the SAOP and GLLB results in most cases straddle the experimental EA values of the neutral atom, SAOP putting the HOMO level too high, and B-GLLB-VWN too low. The halogen results are the poorest, with much too deep lying HOMOs, behavior which we have also seen for the molecular dihalogens. For completeness, we also make a comparison of the HOMO energies of a series of closed shell neutral atoms with B-GLLB-VWN (and other DFA potentials; Table 5). Here, we also check on the deeper lying levels. Looking at the HOMO energies first, it can be noted that again GGA, hybrid, and range-separated functionals yield poor (much too high lying) HOMO levels. Clearly, B-GLLB-VWN has the best performance, with errors of only a few tenths of an electronvolt. It is considerably better in these cases than SAOP. These observations can be extended to the lower valence levels. It should be kept in mind that for the levels below the HOMO, we should (and do) compare to the exact KS orbital energies rather than to the experimental IPs. In particular for the core levels we can no longer compare to IPs, since the differences between the exact KS orbital energies and IPs become significant (on the order of 10 eV), see ref (33). For semicore levels like Ne 2s and Ar 3s, B-GLLB-VWN and SAOP are still good, while the conventional DFAs again have too high lying levels. For the deep core levels, the picture becomes mixed. In fact, the important observation is that all DFAs perform pretty well. Maybe B-GLLB-VWN is the best overall, but notably CAM-B3LYP is rather accurate for a number of core levels.

Table 4. HOMO Energies (eV) of Several Closed-Shell Atomic Anions and the Opposite of the Experimental EA As Reference Value.

  BLYP B3LYP CAM-B3LYP SAOP B-GLLB-VWN −EA
H– +1.387 +0.886 –0.340 –0.517 –1.520 –0.754
Li– +0.539 +0.577 –0.109 –0.329 –0.830 –0.618
Na– +0.473 +0.282 –0.176 –0.347 –0.791 –0.549
K– +0.621 +0.433 –0.073 –0.360 –0.696 –0.497
F– +1.289 +0.021 –1.876 –2.626 –3.706 –3.401
Cl– +0.306 –0.722 –2.408 –3.463 –4.306 –3.613
Br– –0.100 –1.062 –2.700 –3.812 –4.327 –3.364
MSE +2.47 +1.89 +0.73 +0.19 –0.48  
MAE +2.47 +1.89 +0.73 +0.32 +0.48  
Open in a new tab

Table 5. HOMO Energies (eV) of Several Closed-Shell Neutral Atoms and the Opposite of the Experimental IPs As Reference Value.

III.

Open in a new tab
a

Experimental – IP.

b

Exact KS value from ref.81

IV. Conclusions

We conclude that the use of a good approximation to the exact KS potential solves the problem of the instability of anions that has been noted with approximations like LDA and GGAs. It is not necessary to have recourse to hybrids. In fact, the occupied orbitals of hybrids still lie too high. The occupied orbital energies of the Hartree–Fock model are typically too low (ca. 1 eV), so this model offers, in general, stable anions. But Hartree–Fock also has the problem that its orbital shapes and hence the one-electron density is not particularly good. In cases where there is significant electron correlation, notably at elongated bond lengths and when there is multiple bonding,47,82 the Hartree–Fock densities are deficient. For negative ions, Hartree–Fock densities are better than LDA, GGA, and hybrid densities. Then, a possible strategy to obtain reliable total energies is to perform a HF SCF calculation and feed the HF density into a GGA or hybrid energy expression, as for instance practiced in density-corrected DFT calculations.45,83,84 A similar approach can of course be followed with accurate KS potentials like B-GLLB-VWN and SAOP.

Hybrids, and in particular Hartree–Fock, also have the problem that the unoccupied orbitals lie much higher than the exact KS ones, making them an unphysical basis for excited state calculations. They describe approximately the diffuse orbital for an added electron, while the (exact) unoccupied KS orbitals describe approximately (actually rather accurately) excited electrons. This is why many excitations have energies close to an unoccupied–occupied orbital energy difference ϵa – ϵi and are described in a KS orbital basis as simple orbital-to-orbital transitions, while they are comprised of several (often many) orbital–orbital transitions in the HF or in hybrid MO bases.9

In the special case of charge-transfer transitions from a donor molecule or fragment D to acceptor A, the KS unoccupied orbital energies do not provide a good estimate of an excitation energy ϕi → ϕa as orbital energy difference Δϵ = ϵa(A) – ϵi(D). Such transitions approach the difference IPD – EAA between the ionization energy IPD of the donor D and the electron affinity EAA of the acceptor A if the acceptor and donor are spatially widely separated. The KS orbital energy ϵi(D) of the orbital on the donor then is a good approximation of an ionization energy of D but the KS orbital energy ϵa(A) does not approximate the electron affinity of the acceptor. In the calculation of charge-transfer excitation energies, we should use for the orbital energy of the acceptor that of the negative ion.85 We have demonstrated in this paper that the B-GLLB-VWN approximation to the KS potential is providing this anion orbital energy with the same accuracy as the orbital energies (close to ionization energies) of neutral molecules. It therefore offers an avenue to correction of TDDFT calculations in such a way that they can also be used for charge transfer excitations.

The authors declare no competing financial interest.

References

  1. Teke N. K.; Pavošević F.; Peng C.; Valeev E. Explicitly correlated renormalized second-order Green’s function for accurate ionization potentials of closed shell molecules. J. Chem. Phys. 2019, 150, 214103. 10.1063/1.5090983. [DOI] [PubMed] [Google Scholar]
  2. Su N. Q.; Xu X. Insights into direct methods for predictions of ionization potential and electron affinity in density functional theory. J. Phys. Chem. Lett. 2019, 10, 2692–2699. 10.1021/acs.jpclett.9b01052. [DOI] [PubMed] [Google Scholar]
  3. Anderson L. N.; Oviedo M. B.; Wong B. M. Accurate electron affinities and orbital energies of anions from a nonempirically tuned range-separated density functional theory approach. J. Chem. Theory Comput. 2017, 13, 1656–1666. 10.1021/acs.jctc.6b01249. [DOI] [PubMed] [Google Scholar]
  4. Zhang D. D.; Zheng X.; Li C.; Yang W. T. Orbital relaxation effects on Kohn-Sham frontier orbital energies in density functional theory. J. Chem. Phys. 2015, 142, 154113. 10.1063/1.4918347. [DOI] [PubMed] [Google Scholar]
  5. Beste A.; Vázquez-Mayagoitia A.; Ortiz J. V. Direct ΔMBPT(2) method for ionization potentials, electron affinities and excitation energies using fractional occupation numbers. J. Chem. Phys. 2013, 138, 074101. 10.1063/1.4790626. [DOI] [PubMed] [Google Scholar]
  6. Baerends E. J.; Gritsenko O. V.; van Meer R. The Kohn-Sham gap, the fundamental gap and the optical gap: the physical meaning of occupied and virtual Kohn-Sham orbital energies. Phys. Chem. Chem. Phys. 2013, 15, 16408–16425. 10.1039/c3cp52547c. [DOI] [PubMed] [Google Scholar]
  7. Levy M.; Perdew J. P.; Sahni V. Exact differential equation for the density and ionization energy of a many-particle system. Phys. Rev. A: At., Mol., Opt. Phys. 1984, 30, 2745. 10.1103/PhysRevA.30.2745. [DOI] [Google Scholar]
  8. Almbladh C.-O.; von Barth U. Exact results for the charge and spin densities, exchange-correlation potentials, and density-functional eigenvalues. Phys. Rev. B: Condens. Matter Mater. Phys. 1985, 31, 3231–3244. 10.1103/PhysRevB.31.3231. [DOI] [PubMed] [Google Scholar]
  9. van Meer R.; Gritsenko O. V.; Baerends E. J. Physical meaning of virtual Kohn-Sham orbitals and orbital energies: an ideal basis for the description of molecular excitations. J. Chem. Theory Comput. 2014, 10, 4432–4441. 10.1021/ct500727c. [DOI] [PubMed] [Google Scholar]
  10. Baerends E. J. Density functional approximations for the orbital energies and total energies of molecules and solids. J. Chem. Phys. 2018, 149, 054105. 10.1063/1.5026951. [DOI] [PubMed] [Google Scholar]
  11. Talman J.; Shadwick W. Optimized effective atomic central potential. Phys. Rev. A: At., Mol., Opt. Phys. 1976, 14, 36. 10.1103/PhysRevA.14.36. [DOI] [Google Scholar]
  12. Krieger J. B.; Li U.; Iafrate G. J. Construction and application of an accurate local spin-polarized Kohn-Sham potential with integer discontinuity: exchange-only theory. Phys. Rev. A: At., Mol., Opt. Phys. 1992, 45, 101–126. 10.1103/PhysRevA.45.101. [DOI] [PubMed] [Google Scholar]
  13. Staroverov V. N.; Scuseria G. E.; Davidson E. R. Optimized effective potentials yielding Hartree-Fock energies and densities. J. Chem. Phys. 2006, 124, 141103. 10.1063/1.2194546. [DOI] [PubMed] [Google Scholar]
  14. Hesselmann A.; Götz A.; Della Sala F.; Görling A. Numerically stable optimized effective potential method with balanced Gaussian basis sets. J. Chem. Phys. 2007, 127, 054102. 10.1063/1.2751159. [DOI] [PubMed] [Google Scholar]
  15. Heaton-Burgess T.; Yang W. T. Optimized effective potentials from arbitrary basis sets. J. Chem. Phys. 2008, 129, 194102. 10.1063/1.2982799. [DOI] [PubMed] [Google Scholar]
  16. Seidl A.; Görling A.; Vogl P.; Majewski J. A.; Levy M. Generalized Kohn-Sham schemes and the band gap problem. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 53, 3764. 10.1103/PhysRevB.53.3764. [DOI] [PubMed] [Google Scholar]
  17. Slater J. C.; Mann J. B.; Wilson T. M.; Wood J. H. Nonintegral occupation numbers in transition atoms in crystals. Phys. Rev. 1969, 184, 672. 10.1103/PhysRev.184.672. [DOI] [Google Scholar]
  18. Slater J. C.The Self-Consistent Field for Molecules and Solids: Quantum Theory of Molecules and Solids, Vol. 4; McGraw-Hill, Inc.: New York, 1974. [Google Scholar]
  19. Williams A. R.; de Groot R.; Sommers C. B. Generalization of Slater’s transition state concept. J. Chem. Phys. 1975, 63, 628. 10.1063/1.431382. [DOI] [Google Scholar]
  20. Zheng X.; Cohen A. J.; Mori-Sánchez P.; Hu X.; Yang W. T. Improving band gap prediction in density functional theory from molecules to solids. Phys. Rev. Lett. 2011, 107, 026403. 10.1103/PhysRevLett.107.026403. [DOI] [PubMed] [Google Scholar]
  21. Yang W. T.; Cohen A. J.; Mori-Sánchez P. Derivative discontinuity, bandgap and lowest unoccupied molecular orbital. J. Chem. Phys. 2012, 136, 204111. 10.1063/1.3702391. [DOI] [PubMed] [Google Scholar]
  22. Perdew J. P.; Parr R. G.; Levy M.; Balduz J. L. Density functional theory for fractional particle number: derivative discontinuities of the energy. Phys. Rev. Lett. 1982, 49, 1691–1694. 10.1103/PhysRevLett.49.1691. [DOI] [Google Scholar]
  23. Baerends E. J.On derivatives of the energy with respect to total electron number and orbital occupation numbers. A critique of Janak’s theorem. Mol. Phys. 2019, 117. 10.1080/00268976.2019.1612955 [DOI]
  24. Baer R.; Neuhauser D. Density functional theory with correct long-range asymptotic behavior. Phys. Rev. Lett. 2005, 94, 043002. 10.1103/PhysRevLett.94.043002. [DOI] [PubMed] [Google Scholar]
  25. Salzner U.; Baer R. Koopmans springs to life. J. Chem. Phys. 2009, 131, 231101. 10.1063/1.3269030. [DOI] [PubMed] [Google Scholar]
  26. Baer R.; Livshits E.; Salzner U. Tuned range separated hybrids in density functional theory. Annu. Rev. Phys. Chem. 2010, 61, 85. 10.1146/annurev.physchem.012809.103321. [DOI] [PubMed] [Google Scholar]
  27. Stein T.; Eisenberg H.; Kronik L.; Baer R. Fundamental gaps in finite systems from eigenvalues of a generalized Kohn-Sham method. Phys. Rev. Lett. 2010, 105, 266802. 10.1103/PhysRevLett.105.266802. [DOI] [PubMed] [Google Scholar]
  28. Dabo I.; Ferretti A.; Poilvert N.; Li Y.; Marzari N.; Cococcioni M. Koopmans’ condition for density functional theory. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 115121. 10.1103/PhysRevB.82.115121. [DOI] [Google Scholar]
  29. Dabo I.; Ferretti A.; Park C. H.; Poilvert N.; Li Y.; Cococcioni M.; Marzari N. Donor and acceptor levels of organic photovoltaic compounds from first principles. Phys. Chem. Chem. Phys. 2013, 15, 685–695. 10.1039/C2CP43491A. [DOI] [PubMed] [Google Scholar]
  30. Borghi G.; Ferretti A.; Nguyen N. L.; Dabo I.; Marzari N. Koopmans-compliant functionals and their performance against reference molecular data. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 075135. 10.1103/PhysRevB.90.075135. [DOI] [Google Scholar]
  31. Gritsenko O. V.; Mentel L.; Baerends E. J. On the errors of local density (LDA) and generalized gradient (GGA) approximations to the Kohn-Sham potential and orbital energies. J. Chem. Phys. 2016, 144, 204114. 10.1063/1.4950877. [DOI] [PubMed] [Google Scholar]
  32. Gritsenko O. V.; van Leeuwen R.; van Lenthe E.; Baerends E. J. Self-consistent approximation to the Kohn-Sham exchange potential. Phys. Rev. A: At., Mol., Opt. Phys. 1995, 51, 1944. 10.1103/PhysRevA.51.1944. [DOI] [PubMed] [Google Scholar]
  33. Chong D. P.; Gritsenko O. V.; Baerends E. J. Interpretation of the Kohn–Sham orbital energies as approximate vertical ionization potentials. J. Chem. Phys. 2002, 116, 1760. 10.1063/1.1430255. [DOI] [Google Scholar]
  34. Gritsenko O. V.; Baerends E. J. The analog of Koopman’s theorem in spin-density functional theory. J. Chem. Phys. 2002, 117, 9154–9159. 10.1063/1.1516800. [DOI] [Google Scholar]
  35. Gritsenko O. V.; Braïda B.; Baerends E. J. Physical interpretation and evaluation of the Kohn-Sham and Dyson components of the ϵ – I relations between the Kohn-Sham orbital energies and the ionization potentials. J. Chem. Phys. 2003, 119, 1937. 10.1063/1.1582839. [DOI] [Google Scholar]
  36. Schwarz K. Instability of stable negative ions in the Xα method or other local density functional schemes. Chem. Phys. Lett. 1978, 57, 605–607. 10.1016/0009-2614(78)85330-5. [DOI] [Google Scholar]
  37. Sen K. D. Instability of negative ions in Xα method. Chem. Phys. Lett. 1980, 74, 201–202. 10.1016/0009-2614(80)85044-5. [DOI] [Google Scholar]
  38. Galbraith J. M.; Schaefer H. F. III Concerning the applicabilityof density functional methods in atomic and molecular negative ions. J. Chem. Phys. 1996, 105, 862–864. 10.1063/1.471933. [DOI] [Google Scholar]
  39. Jarecki A. A.; Davidson E. R. Density functional theory calculations for F–. Chem. Phys. Lett. 1999, 300, 44–52. 10.1016/S0009-2614(98)01367-0. [DOI] [Google Scholar]
  40. Cole L. A.; Perdew J. P. Calculated electron affinities of the elements. Phys. Rev. A: At., Mol., Opt. Phys. 1982, 25, 1265–1271. 10.1103/PhysRevA.25.1265. [DOI] [Google Scholar]
  41. van Leeuwen R.; Baerends E. J. Exchange-correlation potential with correct asymptotic behavior. Phys. Rev. A: At., Mol., Opt. Phys. 1994, 49, 2421. 10.1103/PhysRevA.49.2421. [DOI] [PubMed] [Google Scholar]
  42. Vydrov O. A.; Scuseria G. E. Ionization potentials and electron affinities in the Perdew-Zunger self-interaction corrected density-functional theory. J. Chem. Phys. 2005, 122, 184107. 10.1063/1.1897378. [DOI] [PubMed] [Google Scholar]
  43. Jensen F. Describing anions by density functional theory: fractional electron affinity. J. Chem. Theory Comput. 2010, 6, 2726–2735. 10.1021/ct1003324. [DOI] [PubMed] [Google Scholar]
  44. Lee D. H.; Furche F.; Burke K. Accuracy of electron affinities of atoms in approximate density functional theory. J. Phys. Chem. Lett. 2010, 1, 2124–2129. 10.1021/jz1007033. [DOI] [Google Scholar]
  45. Kim M. C.; Sim E. J.; Burke K. Communication: avoiding unbound anions in density functional calculations. J. Chem. Phys. 2011, 134, 171103. 10.1063/1.3590364. [DOI] [PubMed] [Google Scholar]
  46. Buijse M. A.; Baerends E. J.; Snijders J. G. Phys. Rev. A: At., Mol., Opt. Phys. 1989, 40, 4190. 10.1103/PhysRevA.40.4190. [DOI] [PubMed] [Google Scholar]
  47. Baerends E. J.; Gritsenko O. V. A Quantum Chemical view of Density Functional Theory. J. Phys. Chem. A 1997, 101, 5383. 10.1021/jp9703768. [DOI] [Google Scholar]
  48. Becke A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A: At., Mol., Opt. Phys. 1988, 38, 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  49. Kuisma M.; Ojanen J.; Enkovaara J.; Rantala T. T. Kohn-Sham potential with discontinuity for band gap materials. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 115106. 10.1103/PhysRevB.82.115106. [DOI] [Google Scholar]
  50. Baerends E. J. From the Kohn-Sham band gap to the fundamental gap in solids. An integer electron approach. Phys. Chem. Chem. Phys. 2017, 19, 15639–15656. 10.1039/C7CP02123B. [DOI] [PubMed] [Google Scholar]
  51. Tran F.; Ehsan S.; Blaha P. Assessment of the GLLB-SC potential for solid state properties and attempts for improvement. Phys. Rev. Materials 2018, 2, 023802. 10.1103/PhysRevMaterials.2.023802. [DOI] [Google Scholar]
  52. te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931. 10.1002/jcc.1056. [DOI] [Google Scholar]
  53. Fonseca Guerra C.; Snijders J. G.; te Velde G.; Baerends E. J. Towards an order-N DFT method. Theor. Chem. Acc. 1998, 99, 391–403. 10.1007/s002140050353. [DOI] [Google Scholar]
  54. Amsterdam Density-Functional Program; SCM, Department of Theoretical Chemistry, Vrije Universiteit: Amsterdam, 2017. URL: http://www.scm.com. [Google Scholar]
  55. Frisch M. J., et al. Gaussian 09, revision C.01; Gaussian Inc.: Wallingford, CT, 2009.
  56. Ellison G. B.; Engelking P. C.; Lineberger W. C. An experimental determination of the geometry and electron affinity of methyl radical. J. Am. Chem. Soc. 1978, 100, 2556–2558. 10.1021/ja00476a054. [DOI] [Google Scholar]
  57. Nimlos M. R.; Ellison G. B. Photoelectron spectroscopy of silicon trihydride and trideuteride anions. J. Am. Chem. Soc. 1986, 108, 6522–6529. 10.1021/ja00281a013. [DOI] [Google Scholar]
  58. Ervin K. M.; Gronert S.; Barlow S. E.; Gilles M. K.; Harrison A. G.; Bierbaum V. M.; DePuy C. H.; Lineberger W. C.; Ellison G. B. Bond strengths of ethylene and acetylene. J. Am. Chem. Soc. 1990, 112, 5750–5759. 10.1021/ja00171a013. [DOI] [Google Scholar]
  59. Taylor T. R.; Xu C.; Neumark D. M. Photoelectron spectra of the C2nH– (n = 1–4) and C2nD– (n = 1–3) anions. J. Chem. Phys. 1998, 108, 10018–10026. 10.1063/1.476462. [DOI] [Google Scholar]
  60. Bradforth S. E.; Kim E. H.; Arnold D. W.; Neumark D. M. Photoelectron spectroscopy of CN–, NCO–, and NCS–. J. Chem. Phys. 1993, 98, 800–810. 10.1063/1.464244. [DOI] [Google Scholar]
  61. Celotta R. J.; Bennett R. A.; Hall J. L. Laser photodetachment determination of the electron affinities of OH, NH2, NH, SO2, and S2. J. Chem. Phys. 1974, 60, 1740–1745. 10.1063/1.1681268. [DOI] [Google Scholar]
  62. Breyer F.; Frey P.; Hotop H. High resolution photoelectron spectrometry of negative ions: Rotational transitions in laser-photodetachment of OH–, SH–, SD–. Z. Phys. A: At. Nucl. 1981, 300, 7–24. 10.1007/BF01412609. [DOI] [Google Scholar]
  63. Wenthold P. G.; Kim J. B.; Jonas K.-L.; Lineberger W. C. An experimental and computational study of the electron affinity of boron oxide. J. Phys. Chem. A 1997, 101, 4472–4474. 10.1021/jp970645u. [DOI] [Google Scholar]
  64. Gilles M. K.; Polak M. L.; Lineberger W. C. Photoelectron spectroscopy of the halogen oxide anions FO–, ClO–, BrO–, IO–, OClO–, and OIO–. J. Chem. Phys. 1992, 96, 8012–8020. 10.1063/1.462352. [DOI] [Google Scholar]
  65. Polak M. L.; Gilles M. K.; Lineberger W. C. Photoelectron spectroscopy of SF–. J. Chem. Phys. 1992, 96, 7191–7192. 10.1063/1.462526. [DOI] [Google Scholar]
  66. Celotta R. J.; Bennett R. A.; Hall J. L. Laser photodetachment determination of the electron affinities of OH, NH2, NH, SO2, and S2. J. Chem. Phys. 1974, 60, 1740–1745. 10.1063/1.1681268. [DOI] [Google Scholar]
  67. Schwartz R. L.; Davico G. E.; Lineberger W. C. Negative-ion photoelectron spectroscopy of CH3S–. J. Electron Spectrosc. Relat. Phenom. 2000, 108, 163–168. 10.1016/S0368-2048(00)00125-0. [DOI] [Google Scholar]
  68. Wenthold P. G.; Polak M. L.; Lineberger W. C. Photoelectron spectroscopy of the allyl and 2-methylallyl anions. J. Phys. Chem. 1996, 100, 6920–6926. 10.1021/jp953401n. [DOI] [Google Scholar]
  69. Engelking P. C.; Lineberger W. C. Laser photoelectron spectrometry of C5H5: A determination of the electron affinity and Jahn–Teller coupling in cyclopentadienyl. J. Chem. Phys. 1977, 67, 1412–1417. 10.1063/1.435014. [DOI] [Google Scholar]
  70. Sarkas H. W.; Hendricks J. H.; Arnold S. T.; Bowen K. H. Photoelectron spectroscopy of lithium hydride anion. J. Chem. Phys. 1994, 100, 1884–1888. 10.1063/1.466540. [DOI] [Google Scholar]
  71. Sarkas H. W.; Arnold S. T.; Hendricks J. H.; Slager V. L.; Bowen K. H. Characterization of the X 2Σu+ state of Li2 via negative ion photoelectron spectroscopy. Z. Phys. D: At., Mol. Clusters 1994, 29, 209–212. 10.1007/BF01437139. [DOI] [Google Scholar]
  72. Asmis K. R.; Taylor T. R.; Neumark D. M. Anion photoelectron spectroscopy of BN–. Chem. Phys. Lett. 1998, 295, 75–81. 10.1016/S0009-2614(98)00943-9. [DOI] [Google Scholar]
  73. Goebbert D. J. Photoelectron imaging of CH–. Chem. Phys. Lett. 2012, 551, 19–25. 10.1016/j.cplett.2012.08.065. [DOI] [Google Scholar]
  74. Leopold D. G.; Murray K. K.; Miller A. E. S.; Lineberger W. C. Methylene: A study of the X̃3B1 and ã1A1 states by photoelectron spectroscopy of CH2 and CD2. J. Chem. Phys. 1985, 83, 4849–4865. 10.1063/1.449746. [DOI] [Google Scholar]
  75. Arnold D. W.; Bradforth S. E.; Kitsopoulos T. N.; Neumark D. M. Vibrationally resolved spectra of C2–C11 by anion photoelectron spectroscopy. J. Chem. Phys. 1991, 95, 8753–8764. 10.1063/1.461211. [DOI] [Google Scholar]
  76. Travers M. J.; Cowles D. C.; Ellison G. Reinvestigation of the electron affinities of O2 and NO. Chem. Phys. Lett. 1989, 164, 449–455. 10.1016/0009-2614(89)85237-6. [DOI] [Google Scholar]
  77. Arnold D. W.; Xu C.; Kim E. H.; Neumark D. M. Study of lowlying electronic states of ozone by anion photoelectron spectroscopy of O3. J. Chem. Phys. 1994, 101, 912–922. 10.1063/1.467745. [DOI] [Google Scholar]
  78. Wenthold P. G.; Squires R. R. Bond Dissociation Energies of F2– and HF2–. A Gas-Phase Experimental and G2 Theoretical Study. J. Phys. Chem. 1995, 99, 2002–2005. 10.1021/j100007a034. [DOI] [Google Scholar]
  79. Chupka W. A.; Berkowitz J.; Gutman D. Electron affinities of halogen diatomic molecules as determined by endoergic charge transfer. J. Chem. Phys. 1971, 55, 2724–2733. 10.1063/1.1676487. [DOI] [Google Scholar]
  80. Rienstra-Kiracofe J. C.; Tschumper G. S.; Schaefer H. F.; Nandi S.; Ellison G. B. Atomic and molecular electron affinities: photoelectron experiments and theoretical computations. Chem. Rev. 2002, 102, 231–282. 10.1021/cr990044u. [DOI] [PubMed] [Google Scholar]
  81. Zhao Q.; Morrison R. C.; Parr R. G. From electron densities to Kohn-Sham kinetic energies, orbital energies, exchange-correlation potentials, and exchange-correlation energies. Phys. Rev. A: At., Mol., Opt. Phys. 1994, 50, 2138–2142. 10.1103/PhysRevA.50.2138. [DOI] [PubMed] [Google Scholar]
  82. Gritsenko O. V.; Schipper P. R. T.; Baerends E. J. Exchange and correlation energy in density functional theory: comparison of accurate density functional theory quantities with traditional Hartree-Fock based ones and generalized gradiemt approximations for the molecules Li2, N2, F2. J. Chem. Phys. 1997, 107, 5007–5015. 10.1063/1.474864. [DOI] [Google Scholar]
  83. Kim M. C.; Sim E. J.; Burke K. Reducing errors in density functional calculations. Phys. Rev. Lett. 2013, 111, 073003. 10.1103/PhysRevLett.111.073003. [DOI] [PubMed] [Google Scholar]
  84. Kim M. C.; Sim E. J.; Burke K. Ions in solution: density corrected density functional theory (DC-DFT). J. Chem. Phys. 2014, 140, 18A528. 10.1063/1.4869189. [DOI] [PubMed] [Google Scholar]
  85. Gritsenko O.; Baerends E. J. Asymptotic correction of the exchange-correlation kernel of time-dependent density functional theory for long-range charge-transfer excitations. J. Chem. Phys. 2004, 121, 655. 10.1063/1.1759320. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES