Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2019 Dec 30;5(1):864–870. doi: 10.1021/acsomega.9b03779

Robust Net Magnetic Moment in Janus V-Based Nitride MXenes: Insight from First-Principles Calculations

Shulin Zhong 1, Bo Xu 1,*, Ao Cui 1, Siyu Li 1, Susu Liao 1, Guoqing Wang 1, Gang Liu 1, Baozhen Sun 1
PMCID: PMC6964525  PMID: 31956838

Abstract

graphic file with name ao9b03779_0007.jpg

Two-dimensional materials with robust magnetic moments are of great interest to explore the exciting physics and applications of nanoscale spintronic devices. However, the antiferromagnetic (AFM) ground states often restrict the applications of symmetric MXenes. Herein, we proposed a kind of Janus structure for the V-based nitride MXene V2N with one V layer replaced by the Ti/Cr layer. In this work, we demonstrated from the first-principles calculations that although the AFM ground states are formed, the Janus TiVN and CrVN monolayers possess net magnetic moments of 1.97 and 0.28 μB per formula unit, respectively. Moreover, the net magnetic moments of TiVN and CrVN monolayers are robust even if considerable strains (−8 to 8%) are applied. Our results also show that TiVN and CrVN exhibit half-metallic and metallic features, respectively. These properties widen the potential applications of Janus V-based MXenes in spintronic or other electronic devices.

1. Introduction

Two-dimensional (2D) electronic materials have been of great interest to researchers since the discovery of graphene.1−3 Recently, a new class of 2D transition-metal carbides, nitrides, or carbon nitrides, that is, MXenes, with the general formula of Mn+1XnTx (M = transition metals, X = C and/or N, T = O, OH, F, n = 1–3), has received more and more attention since its synthesis. Their structures and properties are extensively predicted from the theoretical point of view.4−8 Studies have shown that MXenes, as an important layered material, have excellent electrical properties, optical properties, thermal stability, and mechanical properties, and have been well applied in the fields of energy storage, catalysis, etc.4,9−13 Among the various MXene materials, the research on 2D transition-metal carbides has been relatively abundant. Theoretical investigations show that different carbide MXenes, such as Ti3C2,14−16 Ti2C,17 and Cr2C,6 could exhibit different magnetic properties. Compared with the carbide MXenes, nitride-based MXenes possess several potential advantages, such as a higher electronic conductivity than their carbide counterparts18 and higher magnetic moments,19 and may be suitable candidates for electrodes in electrochemical capacitors or metamaterial devices.20,21

Previous studies of symmetric MXene materials show that most of them have been predicted to have an antiferromagnetic (AFM) ground state, such as Cr2N22 as well as the Ti2N monolayer.21 As a result of the same spin-polarized ability and antiparallel alignment of transition-metal atoms in the symmetric structures, the total magnetic moment of the whole system would remain zero. Considering that the MXenes, M2X, are composed of two transition-metal layers, we could replace one layer with another transition-metal layer, forming the so-called Janus structure. If the asymmetric factor is taken into account, the net magnetic moments are extremely possible to be found due to the different atomic magnetic moments in the different transition-metal layers. In this situation, a considerable magnetic moment could be observed for the systems even if they are in antiferromagnetic ground states. It indicates that on the basis of the pristine state, an asymmetrical alignment of the transition-metal ions on each layer can result in a different chemical environment, which may regulate the physical and chemical properties of the material itself. Recently, first-principles calculations have predicted that Janus Cr2I3X3 (X = Br, Cl) monolayers are indirect-bandgap semiconductors with good stability, intrinsic ferromagnetism, and electric polarization.23 A previous study on a Janus VSSe monolayer shows that it has room-temperature ferromagnetic ordering with piezoelectricity, ferroelasticity, and a large valley polarization.24 Therefore, it is meaningful to search for the Janus MXenes with robust net magnetic moments.

In this work, we studied the structural, magnetic, and electronic properties and the dynamic stability of two V-based Janus nitride MXenes, TiVN and CrVN monolayers, by means of first-principles calculations. Our results show that considerable net magnetic moments can be found in both TiVN and CrVN with antiferromagnetic ground states. TiVN and CrVN exhibit half-metallic and metallic features, respectively. Furthermore, strain application demonstrates that both TiVN and CrVN have robust net magnetic moments with the strain ranging from −8 to 8%. These properties make V-based Janus MXenes have potential applications in spintronic or other electronic devices.

2. Results and Discussion

2.1. Magnetic Structures of Symmetric V2N and Janus TiVN and CrVN Monolayers

The structures of MXenes were built from their corresponding MAX phases by removing the A-group (mostly IIIA and IVA) element atomic layer.6 The structure of the V2N monolayer is shown in Figure 1. The middle N layer is sandwiched by two V layers. Each V atom is bonded with three N atoms with the same bond lengths. An interlayer vacuum space of 15 Å was imposed on the neighboring slabs to eliminate possible interactions of individual layers.

Figure 1.

Figure 1

Open in a new tab

(a) Top view and (b) side view of monolayer V2N, TiVN, and CrVN. Gray balls and red balls represent the N atoms and V atoms, while blue balls represent the Ti/V/Cr atoms.

Before calculating the electronic structures and magnetic properties of the V2N monolayer, we performed the geometry optimization by relaxing both lattice constants and atomic positions. Considering the magnetism of the V element, we employed both ferromagnetic (FM) and antiferromagnetic (AFM) orders for the unit cell of the V2N monolayer. For the AFM magnetic state, the initial magnetic moments of the top V atom and the bottom V atom are antiparallel. After structural optimization, it is found that the total energy of the V2N monolayer with AFM order is 398 meV lower than that with FM order. Therefore, the V2N monolayer with AFM order is more stable when compared with FM order. Table 1 lists the structural parameters and magnetic moments of the V2N monolayer with AFM order. The optimized lattice constant and the corresponding bond lengths between V and N atoms are 3.193 and 2.141 Å, respectively. The atomic magnetic moment of V is 2.63 μB. Due to the AFM order, the total magnetic moment for the V2N monolayer is 0 μB. To further confirm that the AFM order with an antiparallel alignment of the top V atom and the bottom V atom in the unit cell is the ground state, we considered other different AFM orders within a 2 × 1 × 1 V2N supercell. Figure 2 shows the V2N monolayer with FM order and three different AFM orders, which are labeled as AFM1, AFM2, and AFM3. It is noted that the AFM1 magnetic order corresponds to the AFM order in a unit cell. Total energy calculations show that the energy of AFM1 is significantly lower than that of the other three magnetic orders (FM, AFM2, and AFM3). The energy differences between AFM1 and the other magnetic states are listed in Table 2, which indicate that the energy of the AFM1 order is at least 346 meV lower than that of the other magnetic states. As a result, the magnetic order with the parallel alignment in the intralayer and antiparallel alignment in the interlayer is the ground state for the V2N monolayer.

Table 1. Optimized Lattice Constants with the AFM Order (a0), Bond Lengths between the Transition Metal and N Atoms (dV–N and dTi/Cr–N), Total and Atomic Magnetic Moments (Mtot, MV, and MV/Ti/Cr), and Energy Differences between FM and AFM (EFM – EAFM).

  a0 (Å) dV–N (Å) dTi/Cr–N (Å) Mtot (μB) MV (μB) MV/Ti/Cr (μB) EFM – EAFM (meV)
V2N 3.193 2.141   0 –2.63 2.63 398
TiVN 3.071 2.167 2.097 –1.97 –2.73 0.97 205
CrVN 3.116 2.225 2.015 0.28 –2.81 3.45 398
Open in a new tab

Figure 2.

Figure 2

Open in a new tab

Atomic structures of (a) FM, (b) AFM1, (c) AFM2, and (d) AFM3 magnetic orders of the MVN (M = V, Ti, and Cr) monolayer within a 2 × 1 × 1 supercell. The blue-colored balls represent Cr/Ti/V, gray balls represent N atoms, and red balls represent V atoms. “+” represents an up-spin and “–” represents a down-spin.

Table 2. Energy Differences between AFM1 and the Other Magnetic States for the MVN (M = V, Ti, and Cr) Monolayer.

  EFM – EAFM1 (meV) EAFM2 – EAFM1 (meV) EAFM3 – EAFM1 (meV)
V2N 801 503 346
TiVN 407 72 497
CrVN 792 362 213
Open in a new tab

However, strangely, it is noted that the previous results reported by Gao et al.25 demonstrated the nonmagnetic (NM) state of the V2N monolayer with zero magnetic moment of the V atom, regardless of the FM and AFM initial magnetic settings. Further analysis indicates that Gao et al. used the GGA method in their calculations without adding the Hubbard model. To confirm the effect of the Hubbard model, we reoptimized the structures of the V2N monolayer with the GGA method. Our results show that both FM and AFM magnetic orders would result in the NM states, which is consistent with the results of Gao et al. Obviously, the correlation effect of electrons essentially affects the magnetic ground state. Furthermore, by applying the GGA + U method, we compared the energy of AFM V2N with that of the NM state. It is found that the V2N monolayer with AFM order remains at a lower energy with respect to the NM state.

Based on the V2N monolayer structure, we replaced the top V atom with one Ti or Cr atom to obtain the asymmetric layer structure, labeled as Janus V-based MXenes. Figure 1a,b presents the top and side views of Janus TiVN and CrVN monolayers.

We first optimized the structural parameters of the TiVN and CrVN monolayers. In our calculations, the GGA + U method is used not only for the V atom but also for Ti and Cr atoms. The optimized results are presented in Table 1. Similar to the case of V2N, both FM and AFM orders for the unit cell of TiVN and CrVN monolayers were considered. Table 1 shows that the AFM order is more stable than the FM order. The total energies of AFM orders are 205 and 398 meV lower than those of FM orders for TiVN and CrVN monolayers, respectively. Therefore, the ground states of Janus TiVN and CrVN monolayers retain the AFM orders. It is also noted that the considerable magnetic moments of the whole AFM systems for TiVN and CrVN monolayers are −1.97 and 0.28 μB per unit cell, respectively. Further analysis indicates that the non-zero net magnetic moments originate from the unequal local magnetic moments of Ti/Cr and V atoms (Table 1). We also considered the FM order and the three AFM orders that are shown in Figure 2 to identify the most stable magnetic configuration. Total energy calculations demonstrate that either TiVN or CrVN has an AFM1 ground state, which is an in-plane FM coupling, whereas an AFM coupling for interlayers. The differences in the total energy between AFM1 and the other magnetic structures are also listed in Table 2. Based on the AFM order, it is found that the optimized lattice constants of TiVN and CrVN are 3.071 and 3.116 Å, respectively. The lattice constants of Janus TiVN and CrVN are slightly smaller than that of V2N. The bond lengths between Ti/Cr and N are 2.097/2.015 Å in the TiVN/CrVN monolayer. The bond lengths between V and N are 2.167 and 2.225 Å for TiVN and CrVN, respectively.

2.2. Dynamical Stability of Janus TiVN and CrVN

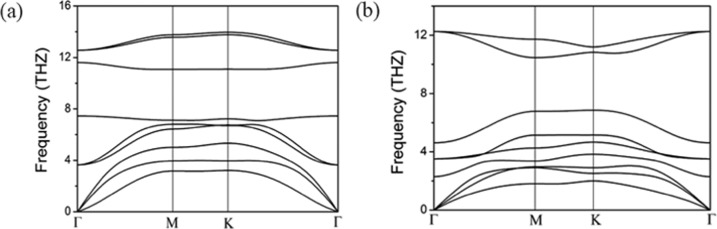
Considering that the Janus TiVN and CrVN monolayers have not been experimentally synthesized, their vibrational property needs to be investigated to examine the dynamical stability. The phonon spectra of these two Janus monolayers are shown in Figure 3. A primitive cell of the Janus MXene monolayer contains three atoms. Therefore, nine phonon branches are included in the phonon spectra. It is significant to find that there is no imaginary frequency at any wave vector for the phonon dispersion curves, which demonstrates that the given structures of the Janus V-based MXene monolayers are dynamically stable. Besides the experimental pristine structure of V2N, thus, Janus TiVN and CrVN monolayers would be likely realized in the future. It is surely interesting to study their magnetic, electronic, and other physical or chemical properties.

Figure 3.

Figure 3

Open in a new tab

Phonon spectra of (a) TiVN and (b) CrVN monolayers.

2.3. Electronic Structures of Symmetric V2N and Janus TiVN and CrVN Monolayers

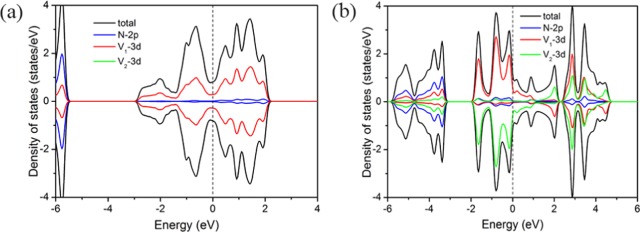
To further understand the correlation effects of electrons on the electronic structures, we plotted the density of states (DOS) of the V2N monolayer with the GGA and GGA + U methods. Figure 4 shows the total density of states (TDOS) and projected density of states (PDOS) of N-2p and V-3d orbitals. As we know, the spin magnetic moments originate from the difference between the number of up-spin and down-spin electrons. From Figure 4, it is found that the occupied states of N atoms are equal for the up-spin and down-spin channels. Therefore, the contribution of N atoms to the magnetic moments is less, regardless of the GGA or GGA + U methods. When the GGA + U method is applied, a strong spin polarization of V-3d orbitals is observed. For the V atom in the top layer, the occupied up-spin states (V1-3d) are significantly larger than the down-spin ones, which results in a large local magnetic moment, as shown in Figure 4b. Similarly, the V atom in the bottom layer (V2-3d) produces an opposite magnetic moment with respect to the V atom in the top layer. Therefore, despite the non-zero local magnetic moment of V atoms, the total magnetic moment of the whole system is zero, which corresponds to the AFM order. However, when the GGA method is applied, the occupied down-spin states of the V atom in the top layer evidently increase, while the occupied up-spin states decrease, as shown in Figure 4a. Such a change ultimately results in the zero magnetic moment of the V atom in the top layer. A similar situation is also found for the V atom in the bottom layer. Obviously, the magnetic moment of the entire system is zero.

Figure 4.

Figure 4

Open in a new tab

Total and projected densities of states of the V2N monolayer with (a) the GGA and (b) the GGA + U methods.

The comparison of the results from the GGA and GGA + U methods shows that the interaction between strongly localized electrons has a great influence on the electronic structures of the V2N monolayer. Such a strong correlation is mainly reflected in the 3d electrons of the transition-metal atoms. At the GGA + U level, this Coulomb repulsion increases the difference between the number of electrons occupying the up-spin and down-spin channels, thus leading to the increase of the atomic magnetic moment.26,27 In contrast, the GGA method underestimates the correlation interaction between electrons. Considering the local 3d-orbital of V atoms, thus, we used the GGA + U method for the V-based MXenes materials in our calculations.

Figure 5a,b shows the TDOS and PDOS of TiVN and CrVN monolayers with AFM order. It can be seen that the DOSs of the two systems share similar characteristics. The states near the Fermi level are contributed by the transition-metal atoms Ti/Cr and V. In the TiVN/CrVN monolayer, the occupied up-spin states near the Fermi level are from Ti-3d/Cr-3d orbitals, while the down-spin ones are from V-3d orbitals. Therefore, distinct spin polarization is observed for these transition-metal atoms, which ultimately results in the local magnetic moments. On the other hand, the occupied up-spin states are inequal to the down-spin ones, regardless of the TiVN or CrVN monolayer, thus making the entire system process the net magnetic moments. As shown in Figure 5c,d, the spin-polarized energy band structures for both spins also imply the magnetism. As a result, the net magnetic moments are easy to be found in the asymmetric Janus V-based MXenes due to the different spin-polarized abilities of the transition-metal atoms in the top and bottom layers.

Figure 5.

Figure 5

Open in a new tab

(a) Density of states and (c) band structure of the TiVN monolayer with AFM order. (b) Density of states and (d) band structure of the CrVN monolayer with AFM order. The Fermi levels are all set to 0 eV.

The energy band structure of CrVN exhibits a metallic characteristic as the bands in both spin channels cross the Fermi level, as shown in Figure 5d. In contrast, the calculated energy band structure reveals that TiVN with AFM order is half-metallic with the existence of a metallic transport behavior for one spin channel and a semiconducting behavior for the other, as shown in Figure 5c. Such a half-metallicity with a small band gap for the up-spin channel leads to 100% spin polarization of the conduction electrons, and the conductivity is dominated by single-spin charge carriers. Materials with such a behavior are highly desired for next-generation spintronic devices, such as spin filters, spin injectors, and magnetic sensors.28,29

2.4. Effect of Strain on the Magnetic Moments of Janus TiVN and CrVN

As existing studies have indicated that the electronic and magnetic properties could be tunable by strain for 2D materials from the experimental and theoretical points of view,30−32 it is meaningful to search for robust, highly desirable magnetic properties in 2D materials. As mentioned above, despite the AFM ground states of Janus TiVN and CrVN, net magnetic moments of TiVN and CrVN monolayers still remain the same. To study the magnetism of TiVN and CrVN against external stress, we apply biaxial strains from −8 to 8% to the AFM TiVN and CrVN monolayers. Here, the strain (ε) is defined as the ratio between the change of lattice constant (Δa) and the equilibrium lattice constant (a), namely ε = Δa/a. A positive value means tensile strain, while a negative value means compressive strain. Generally, the lattice mismatch, coefficient of thermal expansion mismatch, and substrate compression can be used to generate wrinkling and realize the strain in 2D materials. Despite this, a strain as large as 8% is indeed hard to be realized for 2D materials in the experiments. However, our study aims to prove the total magnetic moments of CrVN and TiVN being insensitive to the strain. As a result, the wide range of strain (−8 to 8%) is considered in our calculations. Our results reveal that either TiVN or CrVN maintains strong antiferromagnetism, and the magnetic moment remains very powerful under the different biaxial strains, indicating that the AFM characteristic of TiVN and CrVN monolayers is robust under a large strain (up to 8% biaxial strain). Furthermore, Figure 6a gives the calculated magnetic moments of TiVN and CrVN as a function of strain. One can see that the variation in the total magnetic moment of the TiVN monolayer is always maintained at a very small value, which is no more than 0.5 μB. When it comes to CrVN, similar to TiVN, its total magnetic moment varies slightly. When the strains (−8 to 8%) are applied, the total magnetic moments range from 0.542 to 0.144μB.

Figure 6.

Figure 6

Open in a new tab

(a) Calculated total magnetic moments of TiVN and CrVN monolayers under different strains. AFM orders are applied for both TiVN and CrVN. (b) Calculated local magnetic moments of V, Ti, and Cr atoms in TiVN and CrVN monolayers under different strains.

Further understanding of the detailed change of total magnetic moments with different strains for TiVN and CrVN could be achieved from Figure 6b, which provides the local magnetic moments of V, Ti, and Cr atoms in TiVN and CrVN monolayers under different strains. With the increase of compressive strains, the local magnetic moments undergo little change for Ti and Cr atoms but decrease for V atoms in TiVN and CrVN cases. On the other hand, with the increase of tensile strains, the local magnetic moments increase for Ti and Cr atoms and also slightly increase for V atoms. Considering the opposite directions of magnetic moments for Ti/Cr and V atoms, the trend of total magnetic moments in Figure 6a could be easily obtained.

To elucidate the trivial effect of strain on the magnetic moments of Janus V-based MXenes, we plotted the TDOS and PDOS of the TiVN monolayer under different strains as an example, which are shown in Figure 7. It is found that the changes of magnetic moments of TiVN under strains are almost dominated by Ti and V atoms. The contribution of N is negligible. With the strain changing from −5 to 5%, namely from compressive to tensile, the expansion of the occupied states near the Fermi level decreases, which is clearly observed from the increase of the energy gap around −3 eV. This is due to the increase of the distance between Ti/V and N atoms with the strain changing from compressive to tensile, thus reducing the interaction between atoms as well as the orbital overlap. Despite this, it can also be seen from Figure 7 that the occupied states near the Fermi level from Ti and V atoms have no distinct change within the whole strain range. Obviously, the magnetic moments originating from Ti and V atoms almost remain unchanged. Therefore, robust net magnetic moments could be found in the TiVN and CrVN monolayers, which is strongly against the external stress.

Figure 7.

Figure 7

Open in a new tab

Density of states of the TiVN monolayer under (a) −5%, (b) −2%, (c) 2%, and (d) 5% biaxial strains.

3. Conclusions

In conclusion, we have studied the structural, dynamical, electronic, and magnetic properties of Janus V-based nitride MXenes, TiVN and CrVN, using the first-principles calculations based on the density functional theory. Phonon spectra calculations show that the TiVN and CrVN monolayers are dynamically stable. The TiVN and CrVN monolayers still prefer the AFM order with the parallel arrangement of magnetic moments in the intralayer and the antiparallel arrangement of magnetic moments in the interlayer, which is the same as the symmetric MXene V2N. Despite this, non-zero net magnetic moments could be observed for the Janus TiVN and CrVN, which are −1.97 and 0.28 μB per formula unit, respectively. When strains are applied, the net magnetic moments of TiVN and CrVN monolayers remain stable, indicating that the magnetism of TiVN and CrVN is robust. Density of states and energy band structures show that TiVN exhibits a half-metallic behavior while CrVN is metallic. Our results demonstrate the potential for the utilization of Janus MXenes in innovative spintronic and electronic devices.

4. Computational Methods

All calculations were performed using first-principles calculations based on the density functional theory as implemented in the Vienna ab initio simulation package (VASP).33,34 The projector augmented-wave (PAW) pseudopotentials and the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional were adopted with a cutoff energy of 500 eV for plane-wave expansions.35 The valence electron configurations of Ti, V, and Cr are 3s23p63d24s2, 3s23p63d44s1, and 3s23p63d54s1, respectively. The convergence criteria of total energy and atomic force for each atom were set to 10–6 eV per unit cell and 10–3 eV/Å, respectively. A Monkhorst–Pack sampling method with 12 × 12 × 1 and 32 × 32 × 1 k-point meshes in the Brillouin zone integration were used for the calculations of structure optimization and density of states. Because of the magnetism of transition-metal atoms, spin polarization was taken into account in our calculations. As the correlation effect is important in determining the electronic and magnetic properties of 3d transition-metal atoms, the GGA + U method (with the Hubbard U interaction) was employed with the effective onsite Coulomb term Ueff = U – J. The Ueff values are chosen from previous studies, with 4.2, 4.0, and 3.0 eV for Ti, V, and Cr, respectively.19,36,37 Moreover, different Ueff values for each element are tested. The results show that the energy differences between AFM and FM orders are basically independent of the selected Ueff. To investigate the dynamical stability of Janus nitride MXenes, the phonon spectra were calculated by PHONOPY software.38

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11664012, 11664013), the Excellent Youth Foundation of Jiangxi Province (Grant No. 20171BCB23035), and the Natural Science Foundation of Jiangxi Province (Grant No. 2017BAB211008).

The authors declare no competing financial interest.

References

  1. Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Zhang Y.; Dubonos S. V.; Grigorieva I. V.; Firsov A. A. Electric Field Effect in Atomically thin Carbon Films. Science 2004, 306, 666–669. 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
  2. Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Katsnelson M. I.; Grigorieva I. V.; Dubonos S. V.; Firsov A. A. Two-Dimensional Gas of Massless Dirac Fermions in Graphene. Nature 2005, 438, 197–200. 10.1038/nature04233. [DOI] [PubMed] [Google Scholar]
  3. Zhang Y.; Tan Y.-W.; Stormer H. L.; Kim P. Experimental Observation of the Quantum Hall Effect and Berry’s Phase in Graphene. Nature 2005, 438, 201–204. 10.1038/nature04235. [DOI] [PubMed] [Google Scholar]
  4. Naguib M.; Kurtoglu M.; Presser V.; Lu J.; Niu J.; Heon M.; Hultman L.; Gogotsi Y.; Barsoum M. W. Two Dimensional Nanocrystals Produced by Exfoliation of Ti3AlC2. Adv. Mater. 2011, 23, 4248–4253. 10.1002/adma.201102306. [DOI] [PubMed] [Google Scholar]
  5. Anasori B.; Xie Y.; Beidaghi M.; Lu J.; Barsoum M. W.; et al. Two-Dimensional, Ordered, Double Transition Metals Carbides (MXenes). ACS Nano 2015, 9, 9507–9516. 10.1021/acsnano.5b03591. [DOI] [PubMed] [Google Scholar]
  6. Khazaei M.; Arai M.; Sasaki T.; Chung C.-Y.; Venkataramanan N. S.; Estili M.; Sakka Y.; Kawazoe Y. Novel Electronic and Magnetic Properties of Two Dimensional Transition Metal Carbides and Nitrides. Adv. Funct. Mater. 2013, 23, 2185–2192. 10.1002/adfm.201202502. [DOI] [Google Scholar]
  7. Kurtoglu M.; Naguib M.; Gogotsi Y.; Barsoum M. W. First Principles Study of Two-Dimensional Early Transition Metal Carbides. MRS Commun. 2012, 2, 133–137. 10.1557/mrc.2012.25. [DOI] [Google Scholar]
  8. Khazaei M.; Arai M.; Sasaki T.; Estili M.; Sakka Y. Two-Dimensional Molybdenum Carbides: Potential Thermoelectric Materials of the MXene Family. Phys. Chem. Chem. Phys. 2014, 16, 7841–7849. 10.1039/C4CP00467A. [DOI] [PubMed] [Google Scholar]
  9. Nicolosi V.; Chhowalla M.; Kanatzidis M. G.; Strano M. S.; Coleman J. N. Liquid Exfoliation of Layered Materials. Science 2013, 340, 1226419 10.1126/science.1226419. [DOI] [Google Scholar]
  10. Fiori G.; Bonaccorso F.; Iannaccone G.; Palacios T.; Neumaier D.; Seabaugh A.; Banerjee S. K.; Colombo L. Electronics Based on Two-Dimensional Materials. Nat. Nanotechnol. 2014, 9, 768–779. 10.1038/nnano.2014.207. [DOI] [PubMed] [Google Scholar]
  11. Xia F.; Wang H.; Xiao D.; Dubey M.; Ramasubramaniam A. Two-Dimensional Material Nanophotonics. Nat. Photonics 2014, 8, 899–907. 10.1038/nphoton.2014.271. [DOI] [Google Scholar]
  12. Koppens F. H. L.; Mueller T.; Avouris P.; Ferrari A. C.; Vitiello M. S.; Polini M. Photodetectors Based on Graphene, Other Two-Dimensional Materials and Hybrid Systems. Nat. Nanotechnol. 2014, 9, 780–793. 10.1038/nnano.2014.215. [DOI] [PubMed] [Google Scholar]
  13. Akinwande D.; Petrone N.; Hone J. Two-Dimensional Flexible Nanoelectronics. Nat. Commun. 2014, 5, 5678 10.1038/ncomms6678. [DOI] [PubMed] [Google Scholar]
  14. Shein I. R.; Ivanovskii A. L. Graphene-Like Titanium Carbides and Nitrides Tin+1Cn, Tin+1Nn (n = 1, 2, and 3) from De-Intercalated MAX Phases: First-Principles Probing of Their Structural, Electronic Properties and Relative Stability. Comput. Mater. Sci. 2012, 65, 104–114. 10.1016/j.commatsci.2012.07.011. [DOI] [Google Scholar]
  15. Tang Q.; Zhou Z.; Shen P. Are MXenes Promising Anode Materials for Li Ion Batteries? Computational Studies on Electronic Properties and Li Storage Capability of Ti3C2 and Ti3C2X2 (X = F, OH) Monolayer. J. Am. Chem. Soc. 2012, 134, 16909–16916. 10.1021/ja308463r. [DOI] [PubMed] [Google Scholar]
  16. Wu F.; Luo K.; Huang C.; Wu W.; Meng P.; Liu Y.; Kan E. Theoretical Understanding of Magnetic and Electronic Structures of Ti3C2 Monolayer and Its Derivatives. Solid State Commun. 2015, 222, 9–13. 10.1016/j.ssc.2015.08.023. [DOI] [Google Scholar]
  17. Xie Y.; Kent P. R. C. Hybrid Density Functional Study of Structural and Electronic Properties of Functionalized Tin+1Xn (X = C, N) Monolayers. Phys. Rev. B 2013, 87, 235441 10.1103/PhysRevB.87.235441. [DOI] [Google Scholar]
  18. Zhong Y.; Xia X.; Shi F.; Zhan J.; Tu J.; Fan H. J. Transition Metal Carbides and Nitrides in Energy Storage and Conversion. Adv. Sci. 2016, 3, 1500286 10.1002/advs.201500286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kumar H.; Frey N. C.; Dong L.; Anasori B.; Gogotsi Y.; Shenoy V. B. Tunable Magnetism and Transport Properties in Nitride MXenes. ACS Nano 2017, 11, 7648–7655. 10.1021/acsnano.7b02578. [DOI] [PubMed] [Google Scholar]
  20. Morel A.; Borjon-Piron Y.; Porto R. L.; Brousse T.; Bélanger D. Suitable Conditions for the Use of Vanadium Nitride as an Electrode for Electrochemical Capacitor. J. Electrochem. Soc. 2016, 163, A1077–A1082. 10.1149/2.1221606jes. [DOI] [Google Scholar]
  21. Wang D.; Gao Y.; Liu Y.; Jin D.; Gogotsi Y.; Meng X.; Du F.; Chen G.; Wei Y. First-Principles Calculations of Ti2N and Ti2NT2 (T = O, F, OH) Monolayers as Potential Anode Materials for Lithium-Ion Batteries and Beyond. J. Phys. Chem. C 2017, 121, 13025–13034. 10.1021/acs.jpcc.7b03057. [DOI] [Google Scholar]
  22. Wang G. Theoretical Prediction of the Intrinsic Half-Metallicity in Surface Oxygen-Passivated Cr2N MXene. J. Phys. Chem. C 2016, 120, 18850–18857. 10.1021/acs.jpcc.6b05224. [DOI] [Google Scholar]
  23. Zhang F.; Mi W.; Wang X. Spin-Dependent Electronic Structure and Magnetic Anisotropy of 2D Ferromagnetic Janus Cr2I3X3 (X = Br, Cl) Monolayers. Adv. Electron. Mater. 2019, 1900778 10.1002/aelm.201900778. [DOI] [Google Scholar]
  24. Zhang C.; Nie Y.; Sanvito S.; Du A. First-Principles Prediction of a Room-Temperature Ferromagnetic Janus VSSe Monolayer with Piezoelectricity, Ferroelasticity, and Large Valley Polarization. Nano Lett. 2019, 19, 1366–1370. 10.1021/acs.nanolett.8b05050. [DOI] [PubMed] [Google Scholar]
  25. Gao G.; Ding G.; Li J.; Yao K.; Wu M.; Qian M. Monolayer MXenes: Promising Half-Metals and Spin Gapless Semiconductors. Nanoscale 2016, 8, 8986–8994. 10.1039/C6NR01333C. [DOI] [PubMed] [Google Scholar]
  26. Ali M. E.; Sanyal B.; Oppeneer P. M. Electronic Structure, Spin-States, and Spin-Crossover Reaction of Heme-Related Fe-Porphyrins: A Theoretical Perspective. J. Phys. Chem. B 2012, 116, 5849–5859. 10.1021/jp3021563. [DOI] [PubMed] [Google Scholar]
  27. Wei-Hua W.; Guo-Zhong Z.; Xi-Xia L. GGA + U Study of the Electronic Energy Bands and State Density of the Wurtzite In1-xGaxN. Chin. Phys. B 2013, 22, 120205 10.1088/1674-1056/22/12/120205. [DOI] [Google Scholar]
  28. Wolf S. A.; Awschalom D. D.; Buhrman R. A.; Daughton J. M.; von Molnár S.; Roukes M. L.; Chtchelkanova A. Y.; Treger D. M. Spintronics: A Spin-Based Electronics Vision for the Future. Science 2001, 294, 1488–1495. 10.1126/science.1065389. [DOI] [PubMed] [Google Scholar]
  29. Katsnelson M. I.; Irkhin V. Y.; Chioncel L.; Lichtenstein A. I.; de Groot R. A. Half-Metallic Ferromagnets: From Band Structure to Many-Body Effects. Rev. Mod. Phys. 2008, 80, 315–378. 10.1103/RevModPhys.80.315. [DOI] [Google Scholar]
  30. Ferralis N.; Maboudian R.; Carraro C. Evidence of Structural Strain in Epitaxial Graphene Layers on 6H-SiC (0001). Phys. Rev. Lett. 2008, 101, 156801 10.1103/PhysRevLett.101.156801. [DOI] [PubMed] [Google Scholar]
  31. Kou L.; Du A.; Chen C.; Frauenheim T. Strain Engineering of Selective Chemical Adsorption on Monolayer MoS2. Nanoscale 2014, 6, 5156–5161. 10.1039/C3NR06670C. [DOI] [PubMed] [Google Scholar]
  32. Conley H. J.; Wang B.; Ziegler J. I.; Haglund R. F.; Pantelides S. T.; Bolotin K. I. Bandgap Engineering of Strained Monolayer and Bilayer MoS2. Nano Lett. 2013, 13, 3626–3630. 10.1021/nl4014748. [DOI] [PubMed] [Google Scholar]
  33. Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab-initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  34. Kresse G.; Furthmuller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  35. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  36. Frey N. C.; Bandyopadhyay A.; Kumar H.; Anasori B.; Gogotsi Y.; Shenoy V. B. Surface-Engineered MXenes: Electric Field Control of Magnetism and Enhanced Magnetic Anisotropy. ACS Nano 2019, 13, 2831–2839. 10.1021/acsnano.8b09201. [DOI] [PubMed] [Google Scholar]
  37. Wang D.; Gao Y.; Liu Y.; Gogotsi Y.; Meng X.; Chen G.; Wei Y. Investigation of Chloride Ion Adsorption onto Ti2C MXene Monolayers by First-Principles Calculations. J. Mater. Chem. A 2017, 5, 24720–24727. 10.1039/C7TA09057A. [DOI] [Google Scholar]
  38. Togo A.; Tanaka I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1–5. 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES