Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2019 Dec 31;5(1):914–917. doi: 10.1021/acsomega.9b03940

Introducing Kolmogorov–Smirnov Tests under Uncertainty: An Application to Radioactive Data

Muhammad Aslam 1,*
PMCID: PMC6964527  PMID: 31956845

Abstract

graphic file with name ao9b03940_0001.jpg

The Kolmogorov–Smirnov (K–S) tests based on the assumptions of determined observations in the sample have been popularly applied for the analysis of the data. The existing K–S tests for one sample and two samples cannot be applied when the data contains neutrosophic observations measured from the complex system or under uncertainty. In this paper, we propose the generalization of the existing K–S tests under the neutrosophic statistics. The proposed tests are known as neutrosophic Kolmogorov–Smirnov (NK–S) tests. We present the necessary measures and procedures to perform the proposed tests. An example and advantages of the proposed NK–S tests are given in the paper.

1. Introduction

The statistical methods/techniques have been commonly used in all fields for the analysis of the data, estimation, and forecasting purposes. The data obtained from the system always follows some statistical distribution, which is unknown in advance. Usually, it is assumed that the data follows the normal distribution. However, in practice, it is not always necessary that the data in hand follows the normal distribution. Therefore, statisticians designed several tests to test some hypotheses about the distribution of the data under investigation; see ref (1). As mentioned by Massey,1 “Attempts have been made to find test statistics whose sampling distribution does not depend upon either the explicit form of or the value of certain parameters in, the distribution of the population. Such tests have been called non-parametric or distribution-free tests.” The Kolmogorov–Smirnov (K–S) test is an alternative non-parametric test, which uses the cumulative distribution to decide about the specific distribution of the data. The K–S test is found to be efficient for goodness of fit purposes. Many authors worked on the K–S test; see, for example, refs (1−8).

The K–S test under classical statistics is applied when all observations in the data are determined, precise, and sure. However, in real situations, it may happen that the data cannot be represented by statistical terms or the data may be in an interval or imprecise data. For example, the ecology data, soil data, ocean data, and censored data may be fuzzy data rather than exact data. Therefore, several authors developed the K–S test for the analysis of fuzzy data; see, for example, refs (9−16).

The fuzzy logic is a special case of neutrosophic logic. The neutrosophic logic is considered the measure of indeterminacy in addition to the fuzzy logic; see ref (17). More applications of the neutrosophic logic can be seen in refs (18−23). The neutrosophic statistics was developed by Smarandache24 using the neutrosophic logic. The neutrosophic statistics is an extension of classical statistics, which considers the measure of indeterminacy. The neutrosophic statistics is applied when the observations in the data are neutrosophic numbers. Chen et al.25,26 discussed the advantages of methods based on neutrosophic numbers. Previous work27,28 introduced several basic concepts for the neutrosophic statistics. Recently, another previous work29 proposed the neutrosophic ANOVA test.

The existing K–S test under classical statistics and a fuzzy approach cannot be applied when the measure of indeterminacy is needed. By exploring the literature on classical statistics and the fuzzy approach, we did not find any work on the K–S test under the neutrosophic statistics. In this paper, we propose neutrosophic Kolmogorov–Smirnov (NK–S) tests for a single sample and two samples. It is expected that the proposed NK–S tests will effectively analyze the imprecise, vague, and uncertain data compared to the existing K–S test under classical statistics.

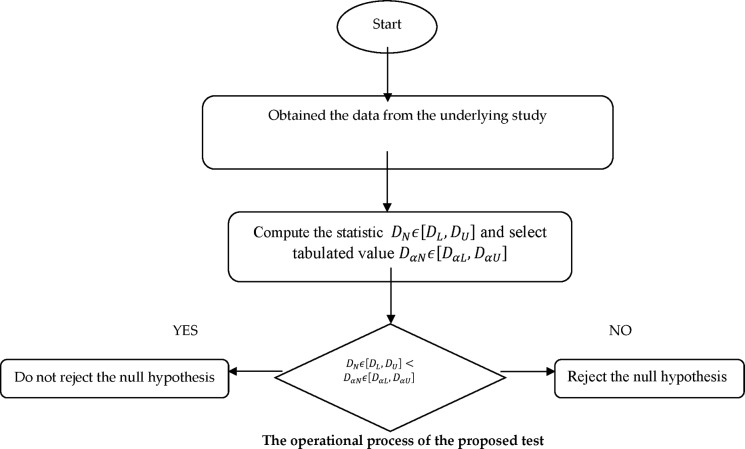
2. Results

For a radioactive source model, radioactive engineering is interested in testing the assumption that the count rate per second follows a neutrosophic Poisson distribution. The count rate per second has the neutrosophic mean [5,7] counts per second. To test the assumption, radioactive engineering collected a large number of count data. The neutrosophic Poisson distribution from ref (18) is given by

2.

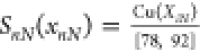and Inline graphic where Cu(XiN) is the neutrosophic commutative values, λNϵ[5,7] and nNϵ[78,92].

The neutrosophic count data and neutrosophic statistics are shown in Table 1. Suppose the level of significance for this test is 0.01. The critical neutrosophic value from ref (32) is 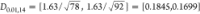Inline graphic. According to eq 4, the statistic in the indeterminacy interval can be written as 0.1594 + 0.4032I; INϵ[0,0.6046]. The neutrosophic statistic from Table 1 is DNϵ[0.4032,0.1594]. Note here that the lower value of the indeterminacy interval denotes the determined part. By comparing the values of DN with D0.01,14, we note that the determinate part follows the Poisson distribution, but the indeterminate part of the data does not follow the Poisson distribution.

Table 1. Necessary Computations for the NK–S Test.

no. XiN Cu(XiN) SnN(xnN) F0N(xn) DN
1 [1,4] [1,4] [0.0128,0.0435] [0.0404,0.1730] [0.0276,0.1295]
2 [1,4] [2,8] [0.0256,0.0870] [0.0404,0.1730] [0.0148,0.0860]
3 [3,5] [5,13] [0.0641,0.1413] [0.2650,0.3007] [0.2009,0.1594]
4 [3,5] [8,18] [0.1026,0.1957] [0.2650,0.3007] [0.1625,0.1051]
5 [4,5] [12,23] [0.1538,0.2500] [0.4405,0.3007] [0.2866,0.0507]
6 [5,6] [17,29] [0.2179,0.3152] [0.6160,0.4497] [0.3980,0.1345]
7 [5,6] [22,35] [0.2821,0.3804] [0.6160,0.4497] [0.3339,0.0693]
8 [6,6] [28,41] [0.3590,0.4457] [0.7622,0.4497] [0.4032,0.0041]
9 [6,6] [34,47] [0.4359,0.5109] [0.7622,0.4497] [0.3263,0.0612]
10 [6,7] [40,54] [0.5128,0.5870] [0.7622,0.5987] [0.2494,0.0118]
11 [8,8] [48,62] [0.6154,0.6739] [0.9319,0.7291] [0.3165,0.0552]
12 [8,9] [56,71] [0.7179,0.7717] [0.9319,0.8305] [0.2141,0.0588]
13 [10,9] [66,80] [0.8462,0.8696] [0.9863,0.8305] [0.1402,0.0391]
14 [12,12] [78,92] [1.0000,1.0000] [0.9980,0.9730] [0.0020,0.0270]
Open in a new tab

3. Discussion

In this section, we compare the performance of the proposed NK–S test over the K–S test under classical statistics. According to refs (25) and (26), a method that provides the results in the indeterminacy interval when the data have the neutrosophic numbers is said to be more adequate and effective than the method that provides the results in the determined form. To compare the proposed NK–S test with the existing NK test, we will use the same data that are given in Table 1. Note here that the data given in Table 1 reduces to the determined part under classical statistics if no observations of uncertainty are recorded. For example, for sample 1, the first value, which is 1, represents the indeterminate part of the indeterminacy interval. The second value of this sample represents the determinate part of the interval. From Table 1, we note that the proposed test provides the results in the indeterminacy interval rather than the determined values. Using eq 4, the values of the statistic in the indeterminacy form can be written as 0.1594 + 0.4032I; INϵ[0,0.6046]. Note here that the proposed test provides a good measure of indeterminacy. At a level of significance 0.01, the probability that the null hypothesis will be accepted is 0.99, the probability of rejecting the null hypothesis when it is true is 0.01, and the probability of indeterminacy is 0.60. For example, in the statistic DNϵ[0.4032,0.1594], the value DL = 0.1594 presents the determined part under the classical statistics, and the value DU = 0.4032 shows the indeterminate part under the uncertainty. By comparing both tests, we note that DL < 0.1845, which shows that the existing NK test indicates that the sample belongs to the Poisson distribution. However, the indeterminate part shows that under uncertainty, the sample does not come from the Poisson distribution. From this comparison, we conclude that the values of the statistic DN can be from 0.1594 to 0.4032 under uncertainty. Hence, the theory of the proposed NK–S test concurs with the theories of refs (25) and (26).

4. Concluding Remarks

In this paper, we presented the modifications of the Kolmogorov–Smirnov (K–S) test under the neutrosophic statistics. We proposed the neutrosophic Kolmogorov–Smirnov (NK–S) tests, which are the generalization of the K–S tests. The proposed NK–S test under the neutrosophic statistical interval method is more adequate, informative, and effective to be applied when the data have neutrosophic numbers. The proposed test provides the results in the indeterminacy interval, which is desirable under uncertainty or when the data is measured from the complex system. We presented an example and found that the proposed test is better than the existing K–S test. We recommend applying the proposed NK–S tests for the analysis of the data in biomedical sciences, big data analysis, engineering, and statistics. More properties using the simulation data and/or the development of software for the analysis of the proposed NK–S tests can be considered for future research.

5. Computational Methods

Assume that XN = aN + bNIN be a neutrosophic number (NN) where aN is the determinate part and bNIN; INϵ[IL, IU] is the indeterminate part of the NN. Let XN = X + INX; XNϵ[XL, XU] be a random variable based on the NN where XL and XU are lower and upper values of the indeterminacy interval. Note here that the NN and XNϵ[XL, XU] reduce to a number and a variable under classical statistics if IL = 0 or XL = XU, respectively. The neutrosophic variable XNϵ[XL, XU] presented the NNs in a sample selected from the population having imprecise, uncertain, and indeterminate values or parameters. More details about neutrosophic statistics can be seen in ref (17). The main aim is to propose the K–S tests under the neutrosophic statistics to determine the specific distribution of the data in the presence of neutrosophy.

5.1. Neutrosophic Kolmogorov–Smirnov Tests

The Kolmogorov–Smirnov (K–S) test was originally derived by Kolmogorov30 and Smirnov31 and has been used in nonparametric testing of the hypothesis. In classical statistics, the K–S test has been commonly used to test whether the sample under study belongs to a specific distribution or not. In other words, the K–S test is applied to decide whether the observed distribution significantly differs from the specified population distribution.32 The existing K–S test is applied under the assumption that all observations/parameters in the observed sample and in the population are determined and precise. The data that came from complex systems such as the ocean, the human brain data, and power grid or under uncertainty may not have all determined observations. In these situations, the K–S test under classical statistics cannot be applied for testing whether the data belong to a specific distribution. We modify the existing K–S test under classical statistics using the neutrosophic statistics. The proposed neutrosophic Kolmogorov–Smirnov (NK–S) test is the generalization of the existing K–S test proposed by Kolmogorov30 and Smirnov.31 The proposed NK–S test will be applicable under the following assumptions:

  • 1.

    The data consists of uncertain, imprecise, and indeterminate values.

  • 2.

    The two neutrosophic samples should be mutually independent.

The K–S test can be applied independent of the cumulative distribution function. Woodruff et al.33 used it for the Weibull distribution. Papadopolous and Qiao34 and Frey35 presented the K–S test for the Poisson distribution.

Suppose that X1N, X2N, ..., XnN be a neutrosophic random sample from a neutrosophic population having a neutrosophic cumulative frequency distribution function, say F0N(xn). By following ref (1), the null hypothesis that the neutrosophic sample came from the specified neutrosophic distribution is rejected if the neutrosophic cumulative frequency distribution function is not close to the specified neutrosophic distribution function. Suppose now that F0N(xn); F0N(xnN)ϵ[F0L(xnL), F0N(xnU)] and SnN(xnN); SnN(xnN)ϵ[SnL(xnL), SnU(xnU)] be the neutrosophic population cumulative distribution function and the observed neutrosophic sample distribution function, respectively. Then, the neutrosophic maximum difference statistic based on F0N(xn); F0N(xnN)ϵ[F0L(xnL), F0N(xnU)] and SnN(xnN)ϵ[SnL(xnL), SnU(xnU)] is given by

5.1. 1

The proposed test in the indeterminacy interval can be written as

5.1. 2

Note here that AN and BNIN are the determined and indeterminate parts of the test. The proposed test reduces to the tests in refs (30) and (31) if no indeterminacy is found in the data. Also, note here that the proposed NK–S test reduces to the tests in refs (30) and (31) when DL = DU. The neutrosophic null hypothesis that the sample came from the neutrosophic specified population is accepted if DNϵ[DL, DU] > DαN where DαNϵ[DαL, DαU] is a neutrosophic critical value and can be selected from ref (32).

5.2. NK–S Test for Comparing Two Populations

Kolmogorov30 and Smirnov31 also extended the K–S test for comparing two populations. Like the K–S test for a single population, this test is also based on the assumption that the observations/parameters of two populations should be determined and precise. In this section, we present the NK–S test for comparing two neutrosophic populations. Let X1N, X2N, ..., Xn1N and Y1N, Y2N, ..., Yn2N be two neutrosophic independent samples of sizes n1Nϵ[n1L, n1U] and n2Nϵ[n1L, n1U] from a specified population, respectively. Let Sn1N(xn1N)ϵ[SnL(xn1L), SnU(xn1U)] and Sn2N(yn2N)ϵ[SnL(yn2L), SnU(yn2U)] be neutrosophic sample cumulative distribution functions. Then, the neutrosophic maximum difference statistic based on Sn1N(xn1N)ϵ[SnL(xn1L), SnU(xn1U)] and Sn2N(yn2N)ϵ[SnL(yn2L), SnU(yn2U)] is given by

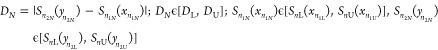5.2. 3

The proposed test for two populations in the form of indeterminacy can be written as

5.2. 4

Note here that CN and ENIN are the determined and indeterminate parts of the test. The proposed test reduces to the tests in refs (30) and (31) if no indeterminacy is found in the data. Note also here that the proposed NK–S test reduces to the tests in refs (30) and (31) when SnL(xn1L) = SnU(xn1U) and SnL(yn2L) = SnU(yn2U). The neutrosophic null hypothesis that two samples came from the same neutrosophic specified population is accepted if DNϵ[DL, DU] > DαN where DαNϵ[DαL, DαU] is a neutrosophic critical value.

Acknowledgments

The author is deeply thankful to the editor and the reviewers for their valuable suggestions to improve the quality of this manuscript. This work was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant no. 130-132-D1441. The author, therefore, gratefully acknowledges the DSR technical and financial support.

The author declares no competing financial interest.

References

  1. Massey F. J. Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. 10.1080/01621459.1951.10500769. [DOI] [Google Scholar]
  2. Fleming T. R.; O’Fallon J. R.; O’Brien P. C.; Harrington D. P. Modified Kolmogorov-Smirnov test procedures with application to arbitrarily right-censored data. Biometrics 1980, 607–625. 10.2307/2556114. [DOI] [Google Scholar]
  3. Steinskog D. J.; Tjøstheim D. B.; Kvamstø N. G. A cautionary note on the use of the Kolmogorov–Smirnov test for normality. Mon. Weather Rev. 2007, 135, 1151–1157. 10.1175/MWR3326.1. [DOI] [Google Scholar]
  4. Wang C.; Zeng B.; Shao J.. Application of bootstrap method in Kolmogorov-Smirnov test. In 2011 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering; IEEE: 2011, pp 287–291.
  5. Van Zyl J. M. Application of the kolmogorov–smirnov test to estimate the threshold when estimating the extreme value index. Commun. Stat. – Simul. Comput. 2011, 40, 199–207. 10.1080/03610918.2010.533227. [DOI] [Google Scholar]
  6. Næss S. K. Application of the Kolmogorov-Smirnov test to CMB data: Is the universe really weakly random?. Astron. Astrophys. 2012, 538, A17. 10.1051/0004-6361/201117344. [DOI] [Google Scholar]
  7. Noughabi H. A. A Comprehensive Study on Power of Tests for Normality. J. Stat. Theory Appl. 2018, 17, 647–660. 10.2991/jsta.2018.17.4.7. [DOI] [Google Scholar]
  8. Antoneli F.; Passos F. M.; Lopes L. R.; Briones M. R. S. A Kolmogorov-Smirnov test for the molecular clock based on Bayesian ensembles of phylogenies. PLoS One 2018, 13, e0190826 10.1371/journal.pone.0190826. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Lin P.-C.; Wu B.; Watada J.. Kolmogorov-Smirnov two sample test with continuous fuzzy data. In Integrated Uncertainty Management and Applications; Springer: 2010; 175–186. [Google Scholar]
  10. Huynh V.-N.; Nakamori Y.; Lawry J.; Inuiguchi M.. Integrated uncertainty management and applications; Springer Science & Business Media: 2010, 68. [Google Scholar]
  11. Xiang G.; Kreinovich V. Towards fast and accurate algorithms for processing fuzzy data: interval computations revisited. Int. J. Gen. Syst. 2013, 42, 197–223. 10.1080/03081079.2012.745243. [DOI] [Google Scholar]
  12. Destercke S.; Strauss O.. Kolmogorov-Smirnov test for interval data. In International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems; Springer: 2014; 416–425.
  13. Laurent A.; Strauss O.; Bouchon-Meunier B.; Yager R. R.. Information Processing and Management of Uncertainty in Knowledge-Based Systems. In 16th International Conference, IPMU; Springer: 2014, 442.
  14. Hesamian G.; Chachi J. Two-sample Kolmogorov–Smirnov fuzzy test for fuzzy random variables. Stat. Pap. 2015, 56, 61–82. 10.1007/s00362-013-0566-2. [DOI] [Google Scholar]
  15. Momeni F.; Gildeh B. S.; Hesamian G. Kolmogorov-Smirnov two-sample test in fuzzy environment. J Hyperstructures 2017, 6, 147–155. [Google Scholar]
  16. Liu X.; Li Z.; Zhang G.; Xie N. Measures of uncertainty for a distributed fully fuzzy information system. Int. J. Gen. Syst. 2019, 625–655. 10.1080/03081079.2019.1609954. [DOI] [Google Scholar]
  17. Smarandache F.Neutrosophic Logic-A Generalization of the Intuitionistic Fuzzy Logic. In Multispace & Multistructure. Neutrosophic Transdisciplinarity (100 Collected Papers of Science); Infinite Study: 2010,4, 396. [Google Scholar]
  18. Alhabib R.; Ranna M. M.; Farah H.; Salama A.. Some Neutrosophic Probability Distributions. In Neutrosophic Sets and Systems; Infinite Study: 2018, 22. [Google Scholar]
  19. Broumi S.; Bakali A.; Talea M.; Smarandache F.. Bipolar neutrosophic minimum spanning tree; Infinite Study: 2018. [Google Scholar]
  20. Abdel-Basset M.; Atef A.; Smarandache F. A hybrid Neutrosophic multiple criteria group decision making approach for project selection. Cognit. Syst. Res. 2019, 57, 216–227. 10.1016/j.cogsys.2018.10.023. [DOI] [Google Scholar]
  21. Abdel-Baset M.; Chang V.; Gamal A. Evaluation of the green supply chain management practices: A novel neutrosophic approach. Comput. Ind. 2019, 108, 210–220. 10.1016/j.compind.2019.02.013. [DOI] [Google Scholar]
  22. Abdel-Basset M.; Nabeeh N. A.; El-Ghareeb H. A.; Aboelfetouh A. Utilising neutrosophic theory to solve transition difficulties of IoT-based enterprises. Enterp. Inf. Syst. 2019, 1–21. 10.1080/17517575.2019.1633690. [DOI] [Google Scholar]
  23. Nabeeh N. A.; Abdel-Basset M.; El-Ghareeb H. A.; Aboelfetouh A. Neutrosophic multi-criteria decision making approach for iot-based enterprises. IEEE Access 2019, 7, 59559–59574. 10.1109/ACCESS.2019.2908919. [DOI] [Google Scholar]
  24. Smarandache F.Introduction to neutrosophic statistics; Infinite Study: 2014. [Google Scholar]
  25. Chen J.; Ye J.; Du S. Scale effect and anisotropy analyzed for neutrosophic numbers of rock joint roughness coefficient based on neutrosophic statistics. Symmetry 2017, 9, 208. 10.3390/sym9100208. [DOI] [Google Scholar]
  26. Chen J.; Ye J.; Du S.; Yong R. Expressions of rock joint roughness coefficient using neutrosophic interval statistical numbers. Symmetry 2017, 9, 123. 10.3390/sym9070123. [DOI] [Google Scholar]
  27. Aslam M. A New Sampling Plan Using Neutrosophic Process Loss Consideration. Symmetry 2018, 10, 132. 10.3390/sym10050132. [DOI] [Google Scholar]
  28. Aslam M. Attribute Control Chart Using the Repetitive Sampling under Neutrosophic System. IEEE Access 2019, 7, 15367–15374. 10.1109/ACCESS.2019.2895162. [DOI] [Google Scholar]
  29. Aslam M. Neutrosophic analysis of variance: application to university students. Complex Intell. Syst. 2019, 5, 403–407. 10.1007/s40747-019-0107-2. [DOI] [Google Scholar]
  30. Kolmogorov A. Sulla determinazione empirica di una lgge di distribuzione. Inst. Ital. Attuari, Giorn. 1933, 4, 83–91. [Google Scholar]
  31. Smirnov N. Table for estimating the goodness of fit of empirical distributions. Ann. Math. Stat. 1948, 19, 279–281. 10.1214/aoms/1177730256. [DOI] [Google Scholar]
  32. Kanji G. K.100 statistical tests; Sage Publications, Inc.: 2006. [Google Scholar]
  33. Woodruff B. W.; Moore A. H.; Dunne E. J.; Cortes R. A modified Kolmogorov-Smirnov test for Weibull distributions with unknown location and scale parameters. IEEE Trans. Reliab. 1983, R-32, 209–213. 10.1109/TR.1983.5221536. [DOI] [Google Scholar]
  34. Papadopoulos A. S.; Qiao N. On the Kolmogorov-Smirnov test for the Poisson distribution with unknown parameter. J. Interdiscip. Math. 2003, 6, 65–82. 10.1080/09720502.2003.10700331. [DOI] [Google Scholar]
  35. Frey J. An exact Kolmogorov–Smirnov test for the Poisson distribution with unknown mean. J. Stat. Comput. Stimul. 2012, 82, 1023–1033. 10.1080/00949655.2011.563740. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES