Assessing the information content of ERP signals in schizophrenia using multivariate decoding methods

Highlights

• •This study took multivariate decoding methods that are widely used to assess the nature of neural representations in neurotypical people and applied them to a comparison of people with schizophrenia and matched control subjects.
• •Participants performed a visual working memory task that required remembering 1–5 items from one side of the display and ignoring an equal number of items on the other side of the display.
• •We attempted to decode which side was being held in working memory from the scalp distribution of the ERP activity during the delay period of the working memory task, and we found greater decoding accuracy in people with schizophrenia than in control subjects when a single item was being held in memory.
• •These results support the hyperfocusing hypothesis of cognitive dysfunction in schizophrenia, and they provide an important proof of concept for applying multivariate decoding methods to comparisons of neural representations in psychiatric and non-psychiatric populations.

Abstract

Multivariate pattern classification (decoding) methods are commonly employed to study mechanisms of neurocognitive processing in typical individuals, where they can be used to quantify the information that is present in single-participant neural signals. These decoding methods are also potentially valuable in determining how the representation of information differs between psychiatric and non-psychiatric populations. Here, we examined ERPs from people with schizophrenia (PSZ) and healthy control subjects (HCS) in a working memory task that involved remembering 1, 3, or 5 items from one side of the display and ignoring the other side. We used the spatial pattern of ERPs to decode which side of the display was being held in working memory. One might expect that decoding accuracy would be inevitably lower in PSZ as a result of increased noise (i.e., greater trial-to-trial variability). However, we found that decoding accuracy was greater in PSZ than in HCS at memory load 1, consistent with previous research in which memory-related ERP signals were larger in PSZ than in HCS at memory load 1. We also observed that decoding accuracy was strongly related to the ratio of the memory-related ERP activity and the noise level. In addition, we found similar noise levels in PSZ and HCS, counter to the expectation that PSZ would exhibit greater trial-to-trial variability. Together, these results demonstrate that multivariate decoding methods can be validly applied at the individual-participant level to understand the nature of impaired cognitive function in a psychiatric population.

1. Introduction

The present study had two related goals. The main goal was to determine whether multivariate pattern classification (decoding) methods can be validly used to compare neural representations in psychiatric and non-psychiatric populations given that the data may be noisier in the psychiatric population (Yang et al., 2014). Addressing this issue required a careful assessment of the strength of the working memory-related signals, the noise level, and the ratio of signal to noise in each group.

A secondary goal was to provide converging evidence for the hyperfocusing hypothesis of cognitive impairment in schizophrenia (Luck et al., 2019), which proposes that people with schizophrenia (PSZ) tend to focus their processing resources more narrowly and more intensely than healthy control subjects (HCS). Consistent with this hypothesis, we have previously shown that univariate measures of ERP and fMRI activity in posterior brain regions during working memory tasks are actually greater in PSZ than in HCS when a single object is being maintained in memory (Hahn et al., 2018; Leonard et al., 2013). The present study asked whether applying multivariate pattern classification (decoding) methods to the ERP data would also yield greater decoding accuracy in PSZ than in HCS for this condition. We also asked whether the ERP signals are actually noisier in PSZ than in HCS.

We will begin by describing why multivariate decoding methods may be particularly useful for understanding schizophrenia (and other neuropsychiatric disorders), and we will then turn to the specific questions about working memory addressed by the present study.

1.1. The potential value of decoding methods for studying neuropsychiatric disorders

Basic cognitive neuroscience research has increasingly embraced multivariate analyses that examine fine-grained patterns of neural activity instead of overall response magnitudes. In fMRI research, for example, the pattern of activity over a set of voxels within a region can provide more precise information about neural representations than the average activity level of the region (Kriegeskorte et al., 2008; Norman et al., 2006; Poldrack, 2011). One common multivariate approach involves classifying the stimuli or experimental conditions from the pattern of activity over the voxels within a region, which can be thought of as decoding the neural signal. For example, instead of asking whether overall activity in the fusiform face area is greater for faces than for non-face stimuli (Kanwisher et al., 1997), decoding methods can ask whether the specific face being viewed can be reliably determined from the pattern of activity across voxels in this area (Anzellotti et al., 2014; Axelrod and Yovel, 2015). This makes it possible to go beyond asking whether a given area is more responsive to faces than to other stimuli and instead ask whether that area contains information (as classically defined by information theory) about the identity of individual faces. Thus, decoding methods can be used to assess the amount of information represented in specific brain regions and how the amount of information varies across experimental conditions.

Decoding methods can also be applied to ERPs and other electromagnetic signals, making it possible to assess how the information content of the neural signal varies from moment to moment following the onset of a stimulus (see review by Grootswagers et al., 2017). In principle, ERP decoding could reveal how PSZ and HCS differ in terms of the information they represent at each moment in time following the onset of a stimulus. ERP decoding is often conducted by classifying the stimuli on the basis of the pattern of voltage (or frequency-specific power) across the entire set of electrode sites, providing an overall measure of the information present in the signal rather than assessing the information present in specific brain regions. For many questions about psychiatric disorders—especially in the domains of perception, attention, and working memory—temporal resolution may be just as important as spatial resolution (Erickson et al., 2018).

Decoding methods can detect subtle aspects of neural representations that cannot be detected by conventional univariate ERP methods. For example, by applying decoding to the ERP scalp distributions of individual subjects, it is possible to determine which one of 16 orientations is being maintained in working memory at each moment of the retention period (Bae and Luck, 2018), and it is even possible to detect the automatic reactivation of this information when the next trial begins (Bae and Luck, 2019a). We call this the information-based decoding approach, because it seeks to quantify the information present in the neural signals of each individual participant.

A distinctly different decoding approach has been applied in several previous studies of schizophrenia (e.g., Bleich-Cohen et al., 2014; Du et al., 2012; Koch et al., 2015). In this approach, the decoder attempts to classify the group membership (PSZ vs. HCS) of each individual subject on the basis of the pattern of brain activity observed under a given set of conditions. That is, in this group classification approach, the decoder is given data from many participants and learns to classify the group membership of the individual participants. This contrasts with the information-based approach, in which a separate decoder is trained for each participant and the goal is to assess the information content of the neural signal. Although the group classification approach can be valuable, especially when developing diagnostic tools, it is not designed to characterize how each group represents and processes information. That is, the group classification approach aims to predict whether or not someone has schizophrenia on the basis of the pattern of brain activity, not the information content of the brain activity in each group. Consequently, this approach may show that PSZ and HCS reliably differ in terms of the pattern of neural activity without revealing how the information content of the neural representations differs across groups. Both decoding approaches are potentially valuable, but they serve different goals (reflecting two distinct streams of research in computational psychiatry; see Bennett et al., 2019). In the group classification approach, the main goal is to achieve high levels of decoding accuracy, whereas in the information-based approach the main goal is to gain insight into the nature of the neural representations, which can often be achieved with only modest levels of decoding accuracy (Hebart and Baker, 2018).

In the present study, we applied the information-based decoding approach that is typically used in basic cognitive neuroscience, but we asked how decoding accuracy (as a measure of information content) differs between PSZ and HCS. This approach has been used only rarely in schizophrenia research (e.g., Schmack et al., 2017).

1.2. The role of variability in comparing decoding accuracy across groups

Comparisons of decoding accuracy across groups of participants must address the fact that decoding is impacted by trial-to-trial variability, which may differ across groups for reasons unrelated to the neurocognitive process of interest. Data from one subset of trials is typically used to train the decoder, and then the decoder attempts to classify the data from a different set of trials that were not used in training. Trial-to-trial variability in the signal will cause these two sets of trials to differ from each other, decreasing decoding accuracy. It is quite plausible that trial-to-trial variability would be greater in PSZ than in HCS, owing to greater variability in neural activity (including neural activity that is unrelated to the processes of interest) and/or greater contamination by nonneural artifacts. During the resting state, for example, PSZ have been found to exhibit greater moment-to-moment variability than HCS in both global signal strength and local voxel activity (Yang et al., 2014). PSZ have also been found to exhibit greater intraindividual variability in manual and saccadic reaction times (Smyrnis et al., 2009; Vinogradov et al., 1998). Note, however, that this is an issue of trial-to-trial variability rather than subject-to-subject variability, and the information-based decoding approach does not require that the populations being compared have equivalent subject-to-subject variability.

In general, decoding accuracy for a given participant is related to (a) the magnitude of the differences in neural activity between the conditions being classified in that participant, and (b) the trial-to-trial variability of the measured activity in that participant. We can combine these into a contrast-to-noise ratio (CNR), where the difference in the pattern of activity between conditions is the contrast and the trial-to-trial variability is the noise (see Welvaert and Rosseel, 2013 for a discussion of CNRs in the context of fMRI). This is analogous to a signal-to-noise ratio (SNR), but the numerator reflects differences in the signal among the conditions rather than reflecting the raw signal magnitude, and the denominator reflects trial-to-trial variability in the differences among conditions rather than variability in the raw signal.

Differences in decoding accuracy between groups could reflect differences in the task-related neural activity (i.e., the contrast between the stimuli or conditions being classified) or differences in the noise (i.e., the trial-to-trial variability). To draw inferences about differences in neural representations between two groups, it is necessary to exclude the possibility that the observed differences in decoding accuracy reflect differences in the noise. In the present study, we therefore quantified these two sources of variance as well as their ratio (the CNR). Note that an analogous issue arises in fMRI studies that compare decoding accuracy for different brain regions rather than for different groups of participants, and CNR analyses are used to ensure that any differences in decoding accuracy between regions are not a result of differences in noise (Haynes, 2015).

1.3. Hyperfocusing and working memory in people with schizophrenia

On the basis of experimental evidence gathered over the last decade, we have proposed a hyperfocusing hypothesis that is designed to explain many aspects of cognitive impairment in schizophrenia (reviewed by Luck et al., 2019). According to this hypothesis, schizophrenia involves an abnormally narrow but intense focusing of processing resources. This is thought to reduce the ability of PSZ to distribute attention among multiple locations in space (Hahn et al., 2012; Kreither et al., 2017), decrease the number of representations they can simultaneously maintain in working memory (Leonard et al., 2013), and cause their attention to be abnormally captured by irrelevant inputs that share features with active representations (Luck et al., 2014; Sawaki et al., 2017).

The hyperfocusing hypothesis makes a specific prediction about neural activity in working memory tasks: When only a single item is being stored in working memory, PSZ should focus their resources unusually intensely on this item, leading to greater neural activity in PSZ than in HCS; however, PSZ should be impaired at distributing their resources when a larger set of items must be stored, leading to greater neural activity in HCS than in PSZ. Consistent with this prediction, both ERP and fMRI studies have found that PSZ exhibit greater WM storage-related neural activity than HCS in posterior brain regions when the task requires maintaining a single object in working memory, but PSZ exhibit reduced activity relative to HCS when multiple objects must be maintained in memory (Hahn et al., 2018, 2017; Leonard et al., 2013).

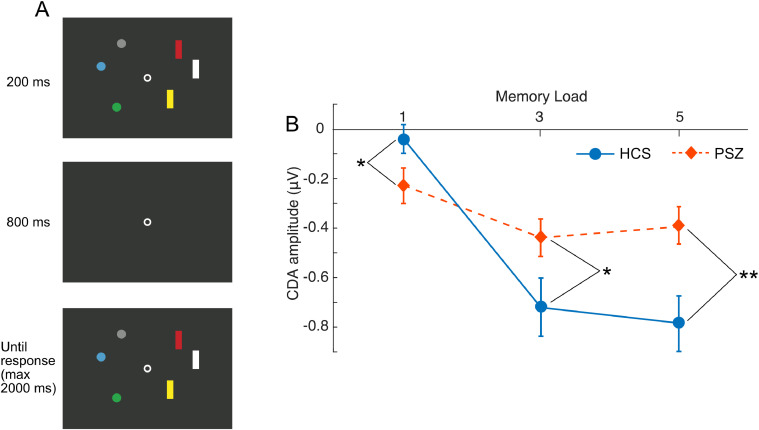
The ERP study (Leonard et al., 2013) took advantage of contralateral delay activity (CDA), a sustained ERP signal that is observed during the delay period of WM tasks and is strongly linked to individual differences in WM capacity (Vogel and Machizawa, 2004; Vogel et al., 2005). As illustrated in Fig. 1A, each display in this experiment contained rectangles on one side of the display and circles on the other, and the participants were instructed to remember the colors of the rectangles and filter out the circles (or vice versa). The side containing the to-be-remembered items varied unpredictably from trial to trial.

Fig. 1.

Procedure and results from the study of Leonard et al. (2013). (A) Example of a single trial. Participants were instructed to remember the colors of the target shapes in the first display (either the circles or the rectangles) and report whether a color of target shape changed between the two displays. Shown here is a ‘no change’ trial at memory load 3 when the circles were the to-be-remembered targets. (B) Average CDA amplitude at each memory load for healthy control subjects (HCS) and people with schizophrenia (PSZ), averaged across the time period of interest (i.e., 400–1000 ms after the onset of the first array). Error bars indicate ± 1 S.E. * = p < .05, ** = p< .01. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

As can be seen in Fig. 1B, CDA amplitude was significantly greater in PSZ than in HCS when each side contained only one item, providing evidence that PSZ were focusing their WM resources more intensely than HCS on the to-be-remembered object (a result that was replicated by Reinhart et al., 2018). However, CDA amplitude was smaller in PSZ than in HCS when each side contained 3 or 5 items, consistent with the proposal that PSZ were impaired at spreading their processing resources over multiple items. Analogous results in fMRI experiments have sometimes been explained as being a side effect of reduced WM capacity in PSZ (Manoach, 2003), but greater CDA amplitude in PSZ than in HCS for a single item was also found in subjects who were matched on behaviorally measured WM storage capacity.

1.4. Application of decoding methods to the CDA data

The present paper provides a re-analysis of the CDA data reported by Leonard et al. (2013), using decoding methods instead of standard univariate ERP amplitude measures. We focused on decoding which side of the stimulus display was being held in WM,1 and we contrasted two opposite predictions. First, one might expect that neural data would be much more variable in PSZ than in HCS—either because of greater intrinsic variability in neurocognitive processes (Smyrnis et al., 2009; Vinogradov et al., 1998; Yang et al., 2014) or greater nonneural noise—which might lead to lower decoding accuracy in PSZ than in HCS. Alternatively, given that CDA amplitude was greater for PSZ than for HCS, we might expect that decoding accuracy would be higher in PSZ than in HCS (consistent with the hyperfocusing hypothesis). A third possibility is that a larger CDA in PSZ and lower noise in HCS might lead to equivalent decoding accuracy in the two groups.

It might seem that decoding accuracy would be isomorphic with CDA amplitude in this paradigm and that decoding accuracy would inevitably be greater for the group with greater CDA amplitude. However, decoding accuracy in multivariate pattern analyses is not actually isomorphic with differences in amplitude in standard univariate analyses. First, the decoding approach employed in the present study used the fine-grained scalp distribution of the ERPs to predict which side contained the to-be-remembered information, whereas fine-grained scalp distribution information usually plays a secondary role in the standard approach and can be difficult to interpret (Urbach and Kutas, 2006, 2002). Second, the standard approach examines commonalities in scalp patterns across participants and loses power when scalp distributions vary across individuals, whereas the decoding approach finds the optimal scalp patterns for each individual participant and is not hindered by individual differences in scalp topography.

Third, the decoding approach is designed to answer a different question than the standard approach: Rather than asking whether a neural signal with a known meaning differs across groups or conditions (which can lead to the problem of reverse inference; Poldrack, 2006), the decoding approach asks how much information is present in the pattern of neural signals and how the information content differs across conditions or groups (Hebart and Baker, 2018; Poldrack, 2011). This is important because the magnitude of the neural response can be dissociated from the decodable information content (Emrich et al., 2013), and it is even possible to decode the content of the neural representation when the overall response does not exceed baseline levels (Serences et al., 2009). Thus, whereas the previous finding of greater CDA amplitude in PSZ than in HCS provides evidence that PSZ devote more neural activity to WM-related processes than do HCS (when storing a single item in memory), a finding of greater decoding accuracy in PSZ than in HCS would allow us to conclude that the neural signals contain more information about which side is being maintained in memory in PSZ than in HCS. Although such a finding would provide only a modest increment in knowledge about WM abnormalities in schizophrenia, it would provide an important proof of concept for using information-based decoding methods to compare psychiatric and non-psychiatric populations. This could then set the stage for studies that attempt to decode more subtle information in these populations (e.g., facial expressions).

Because trial-to-trial variability plays a major role in decoding accuracy, we also provided separate measures of the strength of the task-related signal (the brain activity that differed as a function of which side was being remembered) and the noise (the trial-to-trial variability in this signal, as will be defined more precisely in Section 2.5) for the two groups.

2. Materials and methods

This paper reports new analyses of previously published data (Leonard et al., 2013). Additional details of the stimuli, task, and analyses can be found in that paper. Here, we provide a summary of the key methodological details.

2.1. Participants

Usable data were available from 24 PSZ (including cases of both schizophrenia and schizoaffective disorder) and 21 HCS. The PSZ were chronic outpatients who were receiving stable levels of antipsychotic medications, and the HCS were matched for age, gender, ethnicity, and parental education. Details of recruiting, diagnosis, demographics, medications, and symptom scores can be found in Leonard et al. (2013).

2.2. Stimuli & task

The stimuli and task are depicted in Fig. 1. Stimuli were presented on a CRT monitor with a gray background. On each trial, one, three, or five objects (0.65° each) were presented on each side of a central fixation point, with equal numbers of objects on each side. The items on one side were circles and the items on the other side were rectangles. The objects were randomly positioned within two invisible rectangular regions (4° wide and 7.3° tall) that were centered 3.5° to the left or the right of fixation. The colors of the objects in the encoding display were randomly selected without replacement from a set of 12 categorically distinct colors. The encoding array was presented for 200 ms and was followed by an 800-ms delay interval in which only fixation was presented. A test array was then presented and remained on the screen until response (maximum of 2000 ms).

Participants performed a color change-detection task. They were instructed to remember the colors of the circles in half of the trial blocks and the colors of the rectangles in the remaining half. On no-change trials, the test array was identical to the encoding array. On change trials, the color of one randomly selected object in the test array was changed to a new color; the changed object was always one of the attended-shape items. Participants reported whether or not a color change occurred by pressing one of two buttons on a gamepad. The test array contained a new color on 50% of the trials and no change on the remaining 50%.

The test array was followed by 1000-ms intertrial interval. The side containing the to-be-remembered items and the number of items presented (the memory load) varied unpredictably from trial to trial. The relevant shape (circle or rectangle) alternated between blocks. To ensure that participants remembered which shape was relevant on each block, an outline of the relevant shape in the current block was visible at fixation throughout the block. There were 12 blocks of 75 trials, yielding a total of 150 remember-left trials and 150 remember-right trials at each memory load (1, 3, or 5). Participants completed a set of practice trials prior to the start of data collection.

2.3. EEG recording & preprocessing

The EEG was recorded using a Neuroscan Synamps 2 system (500 Hz sampling rate, half-amplitude bandpass filter from .05–100 Hz with a 60 Hz notch filter). Scalp electrodes were located at a subset of the International 10/20 system sites (O1, O2, Oz, P3, P4, Pz, P7, P8, T7, T8, TP7, TP8, CP3, CP4, CPz, C3, C4, Cz, F3, F4, Fz, and right mastoid) with a left mastoid reference. Bipolar horizontal and vertical electrooculogram (HEOG and VEOG) signals were also recorded. Signal processing and analysis was performed in Matlab using EEGLAB Toolbox (Delorme & Makeig, 2004), ERPLAB Toolbox (Lopez-Calderon & Luck, 2014), and custom Matlab code (available online at http://osf.io/6uv42). The data were bandpass filtered offline (non-causal Butterworth impulse response function, half-amplitude cutoffs at 0.1 and 80 Hz, 12 dB/oct roll-off) and resampled at 256 Hz. Note that the 0.1 Hz high-pass cutoff tends to be ideal for slow ERP components, reducing slow drifts but producing minimal time-domain distortion (Kappenman and Luck, 2010; Tanner et al., 2015). EEG segments with extreme artifacts (e.g., movement artifacts during breaks) were removed. Independent component analysis (ICA) was then performed to remove components associated with blinks (Jung et al., 2000) and eye movements (Drisdelle et al., 2017).

The ICA-corrected EEG data were segmented to include a 500-ms pre-stimulus period (which was used to perform subtractive baseline correction), the 200-ms duration of the encoding array, and 1300 ms following the encoding array. To ensure that our decoding analyses were not contaminated by ocular activity, we removed epochs that contained step-like voltage changes larger than 25 μV in the HEOG signal (see Luck, 2014), equivalent to saccades >1.5° (Lins et al. 1993). We also removed epochs with potentials exceeding 200 μV in any electrode and epochs with peak-to-peak deflections within any 200-ms window exceeding 150 μV. Overall, these removal procedures excluded an average of 2.7% of epochs in HCS and 5.1% of epochs in PSZ, yielding 145.1 ± 8.17 and 145.3 ± 6.67 usable trials for the left and right sides at memory load 1, 144.2 ± 8.25 and 145.0±8.36 usable trials for the left and right sides at memory load 3, and 144.4 ± 7.88 and 143.7 ± 8.94 usable trials for the left and right sides at memory load 5. As in most CDA studies, trials were included independent of whether the behavioral response was correct.

2.4. Decoding analyses

All analyses were performed in Matlab (The Mathworks, Natick, MA). The data and analysis scripts are available online at http://osf.io/6uv42.

2.4.1. Decoding procedure

We attempted to decode the side of the display that contained the to-be-remembered shapes on the basis of the scalp distribution of the phase-locked (averaged) ERPs during the delay period, separately for each memory load. We made an a priori decision to analyze the same time window used for CDA measurements in the original study (Leonard et al., 2013), namely 400–1000 ms after the onset of the encoding array. This window avoids both the initial sensory response and the neural activity related to focusing attention during perception of the array (e.g., the N2pc component). In the primary decoding analysis, we computed the mean voltage across the time window of interest at each electrode and decoded the side being maintained in memory from this time-averaged signal (which we will call time-averaged decoding). In additional analyses that are presented in online supplementary materials, we decoded the data separately at each time point during the window (which we will call point-by-point decoding).

We used a binary support vector machine (SVM) classifier to decode the side of the display (left vs. right) being maintained in memory on the basis of the spatial pattern of the averaged ERP activity across the 22 scalp electrodes. For each participant, the procedure was conducted separately for each of the three memory loads. The data from a given memory load were divided into remember-left and remember-right trials according to which side contained the to-be-remembered shape on a given trial. As in previous decoding studies (Bae and Luck, 2019b, 2019a, 2018), we used a 3-fold cross-validation procedure in which the remember-left and remember-right trials from the current memory load were each randomly divided into 3 sets. The data from a given set were averaged together. The averaged data from two of the three sets for a given remembered side were used to train the classifier, and then the performance of the classifier was assessed with the averaged data from the third set. This procedure was iterated multiple times with different randomly chosen trials in the training and test waveforms, which provides a more robust estimate of decoding accuracy.

More specifically, for each iteration the data from each stimulus side were averaged across the pre-defined time points (400–1000 ms) in each single-trial epoch and then randomly divided into three equal-sized sets of approximately 50 trials for the current memory load (this number varied slightly from participant to participant because of the exclusion of trials with artifacts). The trials in each set were then averaged together, producing a separate scalp distribution for each stimulus side (a matrix of 3 averages × 2 stimulus sides × 22 electrodes) for the current memory load. The averaged data from two of the three sets for each stimulus side served as the training dataset for the SVM classifier. The trained SVM classifier was then used to predict the stimulus side of the left-side and right-side averages that were not used for training. Decoding accuracy was computed by comparing the labels for the true to-be-remembered side in the testing dataset and the labels for the predicted side. The training and testing were accomplished using the fitcecoc() and predict() Matlab functions. Because the classification was binary, and the two alternatives were equally probable, chance performance was 0.5.

This procedure was repeated three times, with each of the three sets of trials for each stimulus side serving as the testing set and the other two sets serving as the training sets, and the entire procedure was iterated 50 times with new random assignments of trials to the three sets. Decoding accuracy was computed by averaging across the two stimulus sides, the 3 cross validations, and the 50 iterations (a total of 300 decoding attempts). This process was repeated for each of the three memory loads, separately for each participant.

One might be concerned that only four observations (two averages for remember-left and two for remember-right) were used to train the SVM, which is much smaller than the number of features (electrodes) used for the classification. In many situations, this would lead to overfitting and spurious results. However, our cross-validation approach rules out overfitting as an explanation for above-chance decoding. That is, if the hyperplane chosen by the SVM from the training data solely reflected noise in the data, the SVM would not perform above chance for the test data, because the noise in the training and test data on a given iteration were independent.

2.4.2. Statistical analysis of decoding accuracy

The dependent variable for the statistical analysis was the average decoding accuracy at each memory load for each participant. These values were analyzed using a 3 × 2 ANOVA with memory load (1, 3, 5) as a within-subjects factor and group (HCS, PSZ) as a between-subjects factor. We also conducted independent-samples t tests comparing decoding accuracy between HCS and PSZ at each memory load.

When the accuracy within a group was compared to chance, we used one-tailed tests (because below-chance accuracy is not meaningful with the present decoding procedures).

2.5. Relationship between contrast-to-noise ratio and decoding accuracy

Because decoding accuracy is impacted by the amount of trial-to-trial variability in the pattern of the neural response, we conducted additional analyses that quantified the contrast-to-noise ratio (CNR) in each participant. Although CNR is a simple concept, it is important to define the contrast and the noise so that they reflect the information that is relevant for a given classification task.

Our main goal was to determine whether we could predict which side of the display was being maintained in WM from the spatial pattern of voltages across the electrodes on the remember-left and remember-right trials. This is analogous to an interaction between stimulus and electrodes in a conventional two-way ANOVA, which asks whether the distribution of voltages is reliably different for the remember-left and remember-right trials. An ANOVA is analogous to a CNR insofar as it reflects variance due to condition divided by error variance. However, a traditional ANOVA is applied to the data from all participants in a study and therefore reflects subject-to-subject variability. We therefore applied our ANOVA-inspired approach to the single-trial epochs from an individual participant rather than applying it to the averaged ERPs from the entire set of participants. This gave us a separate measure of CNR for each participant in each group.2

Specifically, for each participant we decomposed the total ERP variance into 4 sum-of-squares (SS) values: (1) SS reflecting variance due to which side was to-be-remembered (SS_Side); (2) SS reflecting variance due to electrodes (SS_Electrode); (3) SS reflecting variance due to the interaction between to-be-remembered side and electrodes (SS_Interaction); and (4) SS reflecting variance across trials within each cell of the design (SS_Noise). The total SS (SS_Total) is equal to the sum of these four SS terms:

$$S{S}_{Total}=S{S}_{Side}+S{S}_{Electrode}+S{S}_{Interaction}+S{S}_{Noise}$$

To convert this from squared values into the original units of µV, which minimizes extreme values, we computed the root mean square (RMS) corresponding to each SS by dividing the SS value by the corresponding degrees of freedom (creating a mean squared value) and then taking the square root. RMS_Side reflects the overall voltage difference between the remember-left and remember-right trials irrespective of electrode site (corresponding to the main effect of the to-be-remembered side). RMS_Electrode reflects the overall voltage differences among the 22 electrode sites irrespective of the to-be-remembered side (corresponding to the main effect of electrode). RMS_Interaction reflects differences in scalp distribution between the remember-left and remember-right trials (corresponding to the interaction between to-be-remembered side and electrode), which is the information used for decoding. Finally, RMS_Noise reflects trial-to-trial differences that cannot be explained by to-be-remembered side, electrode site, or the interaction between them (corresponding to the error term in ANOVA). In other words, RMS_Noise represents the trial-to-trial variability within an average cell of the design. We used the ratio between RMS_Interaction and RMS_Noise to quantify the relevant CNR for decoding which side was being remembered. This was computed from the mean voltage from 400–1000 ms separately for each memory load and participant.

3. Results

3.1. Scalp distributions

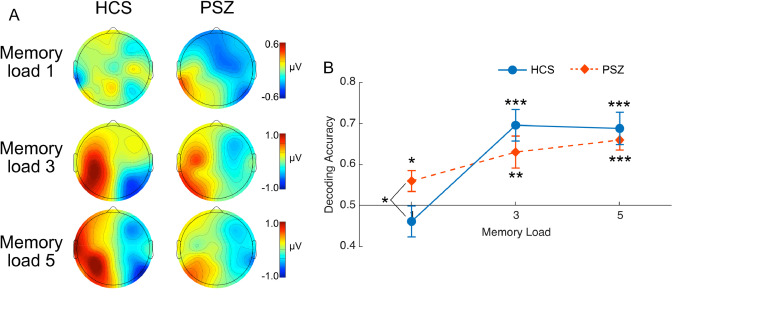
Our approach used differences in ERP scalp distributions to decode which side of the display was being maintained in WM. Fig. 2A shows scalp maps of the difference between remember-left and remember-right trials, averaged across the 400–1000 ms time window. At memory load 1, the voltage was positive at left posterior scalp sites and negative at right posterior scalp sites in PSZ, reflecting a negative voltage contralateral to the side being stored in memory. This effect was not clearly visible in the HCS scalp maps for memory load 1. Both groups exhibited this left-positive/right-negative pattern for memory loads 3 and 5, but this effect was larger for HCS than for PSZ. Note, however, that these maps were created by averaging across all participants, whereas the decoding was performed for each participant separately. Given that the scalp distribution likely varies across individuals as a result of biophysical factors, these maps are only an approximate representation of the single-participant differences in scalp distribution between the remember-left and remember-right conditions.

Fig. 2.

(A) Grand average ERP scalp maps (mean voltage from 400–1000 ms) of the remember-right minus remember-left difference in HCS and PSZ. In these difference maps, a negative value indicates greater negativity when attending to the left visual field, and a positive value indicates greater negativity when attending to the right visual field. (B) Decoding accuracy based on the average voltage from 400–1000 ms at each memory load for HCS (solid blue line) and PSZ (broken red line). Chance decoding would be 0.5. Error bars indicate ± 1 S.E. Blue and orange asterisks indicate significant above-chance decoding for a given group and memory load. The black asterisk at memory load one indicates a significant difference between HCS and PSZ. * = p < .05, * = p < .01, *** = p < .001. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.2. Decoding of time-averaged ERPs

Fig. 2B shows average decoding accuracy, separately for each memory load in each group. At memory load one, decoding accuracy was greater for PSZ than for HCS. At memory loads three and five, however, decoding accuracy was greater in HCS than in PSZ. These results are consistent with the prior finding (Leonard et al., 2013) that CDA amplitude (which reflects the left-right difference) was larger for PSZ than for HCS at memory load one but was smaller in PSZ than for HCS at memory loads three and five.

Our first statistical analyses used one-sample t tests to ask whether decoding accuracy was significantly greater than chance (0.5) for each combination of memory load and group (using one-tailed tests). We found that mean decoding accuracy was significantly greater than chance for all memory loads in PSZ (memory load one: t(23) = 2.22, p = .018; memory load three: t(23) = 3.22, p = .002; memory load five: t(23) = 6.33, p < .001) and for memory loads three and five in HCS (memory load one: t(20) = -1.05, p = .848; memory load three: t(20) = 4.90, p < .001; memory load five: t(20) = 4.62, p < .001).

To assess differences across groups and memory loads, we conducted a 3 × 2 ANOVA with memory load (1, 3, and 5) as a within-subject factor and group (HCS, PSZ) as a between-subject factor. The main effect of group was not significant (F(1,43) = .002, p = .97), providing no evidence of an overall difference in decoding accuracy between PSZ and HCS. The main effect of memory load was significant (F(2,86) = 17.62, p < .001, η_p² = .29), indicating greater decoding accuracy at higher memory loads. Most importantly, the interaction between memory load and group was significant (F(2,86) = 4.13, p = .019, η_p² = .09), consistent with the observation of greater accuracy for PSZ than for HCS at memory load one but greater accuracy for HCS than for PSZ at the higher loads.

To test our a priori hypothesis that decoding accuracy should be greater for PSZ than for HCS at memory load one but not at other memory loads, we compared PSZ and HCS at each memory load. We found that decoding accuracy was indeed significantly greater for PSZ than for HCS at memory load one (t(43) = -2.16, p = .036), but we found no significant group differences at memory load three (t(43) = 1.16, p = .253) or memory load five t(43) = 0.61, p = .543).

The present results were based on the mean voltage from 400–1000 ms, and because EEG signals are transmitted to the scalp with millisecond-level resolution and no delay, we can be confident that these results reflect neural activity during this precise time period. However, even more fine-grained information is possible from EEG signals, and a more detailed examination of the time course of decoding is provided in the Supplementary Materials. As shown in Supplementary Figure S1, decoding accuracy for memory load one was significantly above chance for most of the retention interval in PSZ but did not exceed chance at any time point in HCS. For memory loads three and five, decoding accuracy was above chance in both groups but tended to be greater in HCS than in PSZ (although this difference did not reach significance at memory load five).

Together, these results demonstrate that the scalp distribution of the sustained ERP activity contained information about which side was being maintained in working memory. Moreover, decoding accuracy was significantly greater in PSZ than HCS when a single object had to be remembered. Thus, EEG signals can contain more task-related information in PSZ than in HCS under some conditions.

3.3. Relationship between decoding accuracy and contrast-to-noise ratio

So far, we have demonstrated that the ERP scalp distribution contained information about which side of the display was being maintained in WM, with more information for PSZ than for HCS when a single object was being remembered. This result might seem as if it was inevitable given that the CDA was larger in PSZ than in HCS at memory load one in the original analyses of Leonard et al (2013). However, a larger signal does not necessarily lead to greater decoding accuracy, especially when assessed with a cross-validation procedure in which one subset of trials is used to train the decoder and a different subset is used to assess decoding accuracy. That is, when the trials were subdivided to create separate averaged ERP waveforms for training and testing, increased trial-by-trial variability would lead the training and testing waveforms to be more different from each other, decreasing decoding accuracy. Consequently, if the neural signals were more variable in PSZ than in HCS (owing to greater cognitive variability, greater variability in concurrent neural activity, or increased non-neural artifacts), decoding accuracy could actually be poorer in PSZ than in HCS even though the average CDA voltage was larger in PSZ than in HCS. Thus, the greater decoding accuracy observed for PSZ at memory load one implies that the single-participant contrast-to-noise ratio (CNR) was, on average, greater in PSZ than in HCS at this memory load.

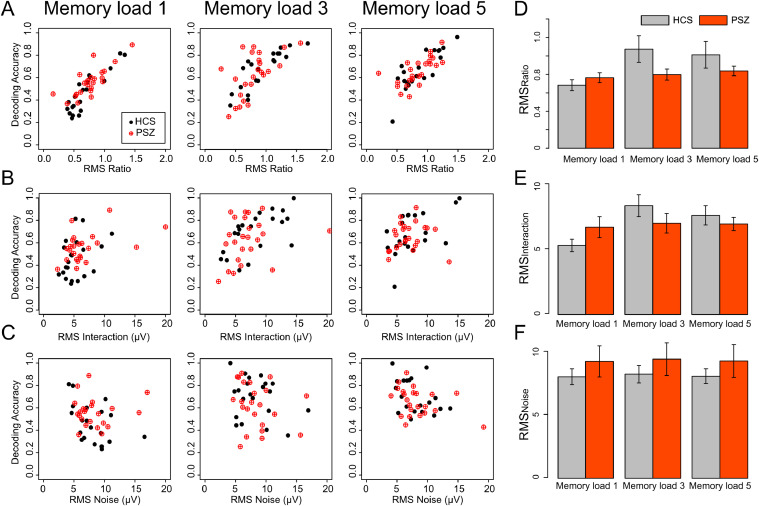
To assess this directly, we asked whether the greater decoding accuracy for PSZ than for HCS at memory load one was associated with a stronger contrast signal (i.e., a larger difference in scalp distribution between remember-left and remember-right trials, which was quantified as RMS_Interaction), reduced noise (quantified as RMS_Noise), and/or an increase in the ratio of the contrast signal to the noise (i.e., a larger CNR, quantified as RMS_Ratio = RMS_Interaction ÷ RMS_Noise). We computed each of these measures for each participant, and we asked how well each of these measures was correlated with decoding accuracy (using Pearson's r).

As can be seen in Fig. 3A, our measure of CNR (RMS_Ratio) was strongly correlated with decoding accuracy, accounting for a large proportion of the variance in decoding accuracy for both HCS and PSZ at all memory loads. These strong correlations demonstrate that RMS_Ratio was a very good predictor of decodability. Our measure of the contrast signal (RMS_Interaction) also exhibited a positive correlation with decoding accuracy (Fig. 3B), and our measure of the corresponding noise (RMS_Noise) exhibited a modest negative correlation (Fig. 3C). Table 1 summarizes these results.

Fig. 3.

Relationship between decoding accuracy and (A) RMS_Ratio, (B) RMS_Interaction, and (C) RMS_Noise at each memory load. Each dot represents a single participant. Average RMS_Ratio (D) RMS_Interaction (E) and RMS_Noise (F) for PSZ and HCS at each memory load. Error bars represent ± 1 S.E.

Table 1.

Correlation between decoding accuracy and RMS_Ratio, RMS_Interaction,and RMS_Noise for each group at each memory load.

Group	Memory load	Type	r	df	p
HCS	1	RMSratio	0.89	19	<.001
	3		0.73	19	<.001
	5		0.68	19	0.001
	1	RMSInteraction	0.34	19	0.126
	3		0.62	19	0.003
	5		0.53	19	0.012
	1	RMSNoise	−0.46	19	0.038
	3		−0.27	19	0.242
	5		−0.46	19	0.036
PSZ	1	RMSratio	0.78	22	<.001
	3		0.60	22	0.002
	5		0.68	22	<.001
	1	RMSInteraction	0.45	22	0.027
	3		0.23	22	0.277
	5		0.10	22	0.649
	1	RMSNoise	−0.13	22	0.549
	3		−0.05	22	0.804
	5		−0.22	22	0.311

These results show that individual differences in decoding accuracy are well explained by individual differences in CNR (RMS_Ratio), as might be expected. Interestingly, the magnitude of the task-related signal (i.e., the numerator in the CNR) was only modestly correlated with decoding accuracy, and the associated noise (i.e., the denominator in the CNR) exhibited even weaker correlations (especially in PSZ). It appears to be the ratio of these two factors that primarily predicts decoding accuracy.

Fig. 3D shows how RMS_Ratio varied across each combination of group and memory load. Mirroring the decoding accuracy results, RMS_Ratio was greater for PSZ than for HCS at memory load one but smaller for PSZ than for HCS at memory loads three and five. To test this statistically, we conducted a 3 × 2 ANOVA with memory load (1, 3, 5) as a within-subject factor and group (HCS, PSZ) as a between-subject factor. The two-way interaction was significant (F(2,86) = 4.742, p = .011, η_p²= .09). However, follow-up t tests comparing PSZ and HCS at each memory load did not yield a significant difference in RMS_Ratio at any individual memory load (memory load 1: t(43) = -1.036, p = .306; memory load 3: t(43) = 1.861, p = .070; memory load 5: t(43) = 1.196, p = .238). These results suggest that our CNR measure is not as sensitive as decoding accuracy, perhaps because the SVM finds the optimal hyperplane for separating the remember-left and remember-right trials.

We also found that RMS_Interaction was greater for PSZ than for HCS at memory load one but was lower for PSZ than for HCS at higher memory loads (Figure 3E). In a 3 × 2 way ANOVA with factors of memory load and group, the two-way interaction was significant (F(2,86) = 5.068, p = .008, η_p² = .11), supporting the idea of stronger signal strength for PSZ than for HCS at memory load one. Again, however, follow-up t tests comparing PSZ and HCS at each memory load did not yield a significant difference at any individual memory load (memory load 1: t(43) = −1.450, p = .154; memory load 3: t(43) = 1.211, p = .233; memory load 5: t(43) = .755, p = .454).

RMS_Noise was somewhat greater for PSZ than for HCS at all memory loads (Fig. 3F). However, in a two-way ANOVA with factors of memory load and group, the main effect of group was not significant (F(1,43) = .874, p = .355, η_p² = .02), nor was the interaction (F(2,86) = .229, p = .796, η_p² = .01). Thus, it is mainly the WM-related signal (RMS_Interaction) rather than the noise (RMS_Noise) that differentiated the groups. However, the lack of a significant difference between groups in RMS_Noise should not be taken as evidence that noise levels will be the same in PSZ and HCS in all experimental paradigms.

4. Discussion

The present results provide a proof of concept for taking the information-based decoding approach that is widely used in basic cognitive neuroscience and applying it to the study of schizophrenia and other neuropsychiatric disorders. One might expect that decoding would inevitably be less accurate in almost any clinical group compared to a matched control group as a result of differences in noise, making it problematic to compare decoding accuracy across groups. Indeed, subject-to-subject variability is greater among PSZ than among HCS for many measures (Alnæs et al., 2019; Joyce and Roiser, 2007), and there is some evidence of greater moment-to-moment variability of neural activity and response times in PSZ than in HCS (Smyrnis et al., 2009; Vinogradov et al., 1998; Yang et al., 2014). However, we found that decoding accuracy was actually greater in PSZ than in HCS at memory load one, mirroring the pattern observed for CDA amplitude. Thus, it is not the case that decoding accuracy will inevitably be lower in psychiatric populations than in non-psychiatric control groups. Moreover, when we carefully examined the WM-related signal (RMS_Interaction) and the trial-to-trial variability in that signal (RMS_Noise), we did not find that the ERP data were substantially noisier in PSZ than in HCS.

It might also seem inevitable that decoding accuracy would be greater for PSZ than for HCS at memory load one of the present experiment given that CDA amplitude was significantly greater for PSZ than for HCS in the original univariate analyses of Leonard et al. (2013). However, the univariate analyses are based on the mean voltage across trials for each participant, and they reflect the consistency of the effect across individuals rather than the consistency across trials. In contrast, the decoding analysis was performed separately for each participant, using averages of different subsets of trials for training and testing, and decoding accuracy for a given participant reflects the ability of the neural signal to reliably predict the to-be-remembered side in that participant. Indeed, decoding accuracy was predicted very strongly by the ratio of the WM-related signal to the variability in that signal (i.e., by the CNR). Thus, the decoding analysis makes it possible to draw a conclusion that would not be warranted from the univariate CDA analysis: the ERP signals contained more information about which side was to be remembered in PSZ than in HCS at memory load one.

In the present case, where we simply examined whether the left or right side of the display was being maintained in WM, the primary advantage of the decoding approach over the univariate approach is that the decoding results can be expressed in terms of the information contained in the neural signal rather than the magnitude of the signal. Consequently, in the present case, the decoding results provide only a small increment in knowledge over the prior univariate findings. Thus, the present results serve mainly as a proof of concept, demonstrating that information-based decoding can be used to compare psychiatric and non-psychiatric populations when the potential for group differences in noise is carefully considered.

This proof of concept is important, however, because the application of decoding methods to future studies could potentially reveal differences that would be difficult to detect with traditional univariate measures. For example, research with typical adults using fMRI has decoded face identity (Anzellotti et al., 2014; Axelrod and Yovel, 2015), the contents of working memory (Ester et al., 2015), the current focus of attention (Kamitani and Tong, 2005), visual features rendered invisible by masking (Haynes and Rees, 2005), and the contents of mental images (Reddy et al., 2010). Decoding of ERP signals has only recently become common outside the brain-computer interface literature, but already it is possible to decode—with a temporal resolution on the order of milliseconds—face identity (Nemrodov et al., 2016), semantic categories of words and pictures (Chan et al., 2011; Murphy et al., 2011), the direction of attention (Bae and Luck, 2018; Fahrenfort et al., 2017), and the contents of working memory (Bae and Luck, 2019a, 2018; Foster et al., 2016, 2020). The application of these techniques to neuropsychiatric populations could provide important new insights into how these individuals differ from typical individuals in the neural representation of information.

Thus, the present results should embolden researchers to use information-based decoding methods in future studies comparing neuropsychiatric populations with matched control populations. The results of such analyses will be especially compelling when decoding accuracy is found to be greater in the neuropsychiatric population, as in the present study. Findings of less accurate decoding can also be meaningful as long as CNR analyses demonstrate that the decreased accuracy cannot be explained by greater noise.

However, it is essential that the CNR quantifies the portion of the overall noise that actually impacts the decoding and not some generic measure of noise. In the present study, for example, the primary decoding analysis was performed on the scalp topography of the mean voltage from 400–1000 ms, and we quantified the noise as the trial-to-trial variation in this voltage topography (after factoring out consistent sources of variation, such as the to-be-remembered side). This excludes sources of noise that would not impact decoding accuracy. For example, high-frequency noise would be expected to have very little impact on either the time-averaged voltage that we used for decoding or our measures of contrast, noise, and CNR. However, such noise could have a large impact on generic measures of the noise level (e.g., the RMS voltage during the prestimulus period).

Although we did not find that the WM-related signals were substantially more variable in PSZ than in HCS, the present results should not be taken to indicate that neural signals will always have approximately the same level of noise in PSZ and in HCS (or across other diagnostic groups). The present study examined stable, medicated outpatients, who may exhibit less trial-to-trial variability than acutely psychotic individuals. In addition, the data were recorded by well trained and highly skilled personnel, and the EEG preprocessing pipeline was designed to minimize the effects of non-neural artifacts. Nonetheless, the present results suggest that comparable levels of noise can be obtained in psychiatric and non-psychiatric populations under these conditions.

Because EEG-based decoding can be influenced by the EOG voltages produced by eye movements (Mostert et al., 2018), it is important to show that our decoding results were not driven by systematic differences between groups in the EOG signals. To assess whether these signals differed systematically between PSZ and HCS, we applied our CNR analysis to the EOG data. As detailed in the online supplementary materials, we found no differences between groups that approached significance (all ps > .24), and Bayes factors indicated that the data were more consistent with the null hypothesis than with a difference between the two groups at all set sizes. Thus, it is unlikely that our main results were driven by eye movements. However, it is difficult to rule out the possibility of secondary consequences from very small eye movements, and this is an issue that requires caution and further methodological development.

In summary, information-based decoding methods can provide very useful evidence about the neural representations of information in a given group of people as they perform a task, and differences in decoding accuracy between groups can be meaningfully interpreted as long as care is taken to assess noise levels. Although the present study focused on a simple decoding of remember-left versus remember-right, future research can apply these methods to much more subtle aspects of neurocognitive processing.

CRediT authorship contribution statement

Gi-Yeul Bae: Conceptualization, Methodology, Formal analysis, Writing - original draft. Carly J. Leonard: Conceptualization, Writing - review & editing. Britta Hahn: Conceptualization, Writing - review & editing. James M. Gold: Conceptualization, Writing - review & editing, Funding acquisition. Steven J. Luck: Conceptualization, Supervision, Writing - original draft, Funding acquisition.

Declaration of Competing Interest

The authors declare no competing interests.