Abstract
Harmonic complex tones (HCTs) found in speech, music, and animal vocalizations evoke strong pitch percepts at their fundamental frequencies. The strongest pitches are produced by HCTs that contain harmonics resolved by cochlear frequency analysis, but HCTs containing solely unresolved harmonics also evoke a weaker pitch at their envelope repetition rate (ERR). In the auditory periphery, neurons phase lock to the stimulus envelope, but this temporal representation of ERR degrades and gives way to rate codes along the ascending auditory pathway. To assess the role of the inferior colliculus (IC) in such transformations, we recorded IC neuron responses to HCT and sinusoidally modulated broadband noise (SAMN) with varying ERR from unanesthetized rabbits. Different interharmonic phase relationships of HCT were used to manipulate the temporal envelope without changing the power spectrum. Many IC neurons demonstrated band-pass rate tuning to ERR between 60 and 1,600 Hz for HCT and between 40 and 500 Hz for SAMN. The tuning was not related to the pure-tone best frequency of neurons but was dependent on the shape of the stimulus envelope, indicating a temporal rather than spectral origin. A phenomenological model suggests that the tuning may arise from peripheral temporal response patterns via synaptic inhibition. We also characterized temporal coding to ERR. Some IC neurons could phase lock to the stimulus envelope up to 900 Hz for either HCT or SAMN, but phase locking was weaker with SAMN. Together, the rate code and the temporal code represent a wide range of ERR, providing strong cues for the pitch of unresolved harmonics.
NEW & NOTEWORTHY Envelope repetition rate (ERR) provides crucial cues for pitch perception of frequency components that are not individually resolved by the cochlea, but the neural representation of ERR for stimuli containing many harmonics is poorly characterized. Here we show that the pitch of stimuli with unresolved harmonics is represented by both a rate code and a temporal code for ERR in auditory midbrain neurons and propose possible underlying neural mechanisms with a computational model.
Keywords: inferior colliculus, pitch, rate code, temporal code, unanesthetized rabbits
INTRODUCTION
Harmonic complex tones (HCTs), in which all frequency components are multiples of a common fundamental frequency (F0), are ubiquitous in speech, music, and animal vocalizations. HCTs evoke a pitch percept matched to the pitch of a pure tone at F0, even when the F0 component is missing or masked [“missing fundamental phenomenon” (Licklider 1956; Schouten 1938)]. The pitch of HCT plays key roles in everyday listening including the perception of speech and music as well as in auditory scene analysis (Bregman 1994; Plack and Oxenham 2005a). The pitch of HCT can be inferred either from the spatial pattern of neural activity produced by low-frequency harmonics that are individually resolved by cochlear frequency analysis or through neural phase locking to the periodic envelope created by the beating of high-numbered, unresolved harmonics (Oxenham 2018; Plack and Oxenham 2005b). In general, the pitch produced by unresolved harmonics is less salient and more dependent on the phase relationship among harmonics than the pitch of resolved harmonics (Houtsma and Smurzynski 1990; Shackleton and Carlyon 1994). For example, an HCT consisting of unresolved harmonics in alternating sine-cosine phase complex produces a pitch percept at its envelope repetition rate 2 × F0, rather than at F0. Although pitch perception of HCT has been extensively studied in human listeners (see Oxenham 2018 for review), the neural mechanisms underlying behavior results are still poorly understood. The present report focuses on how the pitch of HCT with unresolved harmonics is encoded in the auditory midbrain. Recent behavioral studies (Osmanski et al. 2013; Shofner and Chaney 2013; Walker et al. 2019) suggest that small mammals may rely more on the pitch created by unresolved harmonics compared with humans because of their broader cochlear tuning (Sumner et al. 2018). A companion paper focuses on the coding of resolved harmonics (Su and Delgutte 2019).
In the auditory periphery, multiple neural codes to pitch cues of HCT are available, including a rate-place code for resolved harmonics, temporal codes based on the distribution of interspike intervals, and spatiotemporal codes that depend on both cochlear frequency selectivity and neural phase locking (Cariani and Delgutte 1996; Cedolin and Delgutte 2005, 2010; Rhode 1995; Winter et al. 2003). However, which of these codes are actually used to infer pitch is unknown. Pitch-selective neurons have been identified in a circumscribed region of marmoset auditory cortex (Bendor and Wang 2005). These neurons respond strongly to missing fundamental tones at a specific F0 but not to individual harmonics of this F0. How the central pitch selectivity arises from peripheral cues is unclear. Neural phase locking is known to degrade along the ascending pathway (Joris et al. 2004), so that the peripheral temporal code is likely converted at least partly to a rate code. On the other hand, phase locking to the stimulus envelope at low frequencies can be stronger in the midbrain than at lower processing stages (Delgutte et al. 1998; Joris et al. 2004; Krishna and Semple 2000). Understanding the conversion from a peripheral temporal code to a rate code may be crucial for unraveling pitch mechanisms.
The inferior colliculus (IC), the principal auditory center in the mammalian midbrain, is a logical target for this goal. It receives convergent excitatory and inhibitory inputs from multiple nuclei at lower processing stages (Adams 1979; Malmierca et al. 2005) and is the site of a nearly obligatory synapse (Winer and Schreiner 2005). IC neurons are sensitive to fluctuations in the amplitude of acoustic signals and can represent the amplitude modulation (AM) rate via both average firing rate and temporal phase locking (Batra et al. 1989; Joris et al. 2004; Krishna and Semple 2000; Langner and Schreiner 1988; Nelson and Carney 2007). However, studies of AM coding shed limited light on pitch processing in the IC, because AM sounds usually evoke weak pitch sensations (Burns and Viemeister 1981; Shackleton and Carlyon 1994). The few previous studies of the coding of HCTs containing many harmonics in the IC were focused on temporal coding (Peng et al. 2018; Shackleton et al. 2009; Sinex et al. 2002b; Sinex and Li 2007) or limited to low F0s within the range of the human voice (Peng et al. 2018; Shackleton et al. 2009). An exception is the study of Schnupp et al. (2015), which compared responses of IC multiunits to sinusoidally modulated (SAM) noise and click trains (which are harmonic complexes) over a wide frequency range. All of the above-mentioned studies using HCT stimuli were performed under anesthesia, which is known to alter neural activity in the IC (Bock and Webster 1974; Chung et al. 2014; Kuwada et al. 1989).
In this study, we investigated the neural representation of pitch cues in the IC of unanesthetized rabbits by measuring single-unit responses to both HCTs with different phase relationships among harmonics and sinusoidally amplitude‐modulated noise (SAMN), the latter of which evokes a weak pitch sensation at the modulation frequency. Rabbits have good low-frequency hearing similar to humans (Heffner and Heffner 2007), and preliminary behavioral results show that they can discriminate the F0 of HCTs with a missing fundamental (Delgutte et al. 2018). We identified a rate code for the envelope periodicity that is unrelated to pure-tone frequency tuning and also characterized temporal coding of the envelope repetition rate (ERR). A computational model that simulated aspects of the rate tuning to ERR suggests a role for inhibition in implementing a temporal-to-rate transformation.
A preliminary report of this work based on a subset of the present data and including less detailed analyses has been published as part of a conference proceedings (Su and Delgutte 2018).
METHODS
Four female and one male adult Dutch belted rabbits were used for the experiments. Single-unit extracellular activities were recorded during passive listening without anesthesia. For each rabbit, the recording period lasted 6–18 mo. The auditory brain stem response was measured at various points throughout the recording period to verify normal hearing (threshold <30 dB SPL). All procedures were approved by the animal care and use committee of Massachusetts Eye and Ear.
Surgical Preparation
Surgical procedures were adapted from Kuwada and colleagues (Kuwada et al. 1987) and have been described in previous publications from our laboratory (Day et al. 2012; Devore and Delgutte 2010). Each rabbit underwent two aseptic surgeries before the first electrophysiological recording session: a head bar and cylinder implantation and a craniotomy. In both surgeries, anesthesia was induced with xylazine (6 mg/kg) followed by ketamine (35–44 mg/kg) and maintained by either of two methods: 1) injection of one-third of the initial dose of xylazine-ketamine mix when the animal showed a withdrawal reflex or 2) face mask delivery of isoflurane gas mixed with oxygen (0.8 L/min, isoflurane concentration gradually increased to 2.5%).
Head bar and cylinder implantation.
A brass head bar and a stainless steel cylinder were affixed to the skull with stainless steel screws and dental acrylic. At the end of the surgery, the exposed skull was covered with topical antibiotic ointment (bacitracin) and the cylinder was filled with vinyl polysiloxane (Reprosil). This covering procedure was also applied after the craniotomy and at the end of every electrophysiological recording session.
Craniotomy.
Once fully recovered from the initial surgery, the rabbit was first accustomed to the experimental setup over the following 8–10 days. A small craniotomy (2- to 3-mm diameter) was then made within the cylinder at 10.5 mm posterior and 3 mm lateral to bregma to allow access to the IC. Immediately after the craniotomy, and while the animal was still under anesthesia, custom ear inserts were cast with Reprosil. Occasionally, the craniotomy was enlarged or moved to the contralateral side with the same procedure.
Single-Unit Recording
Each recording session lasted 1.5–2.5 h, during which the rabbit was wrapped in a spandex sleeve with its head fixed via the brass bar in a double-walled, electrically shielded, and sound-proof chamber. At the beginning of each session, the acoustic pressure inside the ear canal in response to a broadband chirp stimulus was measured with a probe-tube microphone (Etymotic ER-7C) to calibrate the acoustic assembly. An inverse digital filter was then created from the calibration over 0.05–18 kHz. The animal was monitored via closed-circuit video throughout the session, and the recording session was terminated if the animal showed signs of distress or moved excessively.
The majority of single-neuron recordings were made with polyimide-insulated platinum-iridium linear microelectrode arrays (MicroProbes) with four to six contacts spaced 150 μm apart, 0.2–1 MΩ impedance each. Some early recordings were made with epoxy-insulated tungsten electrodes (A-M Systems) with 2–4 MΩ impedance. During recording, the electrode was advanced through the occipital cortex toward the IC by a remote-controlled hydraulic micropositioner (David Kopf Instruments model 650). The IC was identified by audiovisual cues of entrainment to a search stimulus consisting of 200-ms broadband noise bursts presented diotically at 60 dB SPL. The signals recorded from the microelectrode array were first amplified and band-pass filtered from 300 to 5,000 Hz (Plexon, PBX2) and then sampled at 100 kHz (National Instruments, PXI-6123). Spike times were identified by the crossing of a manually set voltage threshold and recorded for later analysis. The signal recorded from tungsten electrodes was amplified (Axon Instruments, Axoprobe-1A) and filtered (Ithaco 1201) and then processed in the same way. Isolation of a single unit was determined based on the stable shape and amplitude of the spike waveform. Measurements with low spike quality (e.g., inconsistent spike shape, low signal-to-noise ratio) or containing short interspike intervals (<1 ms) that likely resulted from multiunit activity were excluded.
Stimuli
Acoustic stimuli were first created in MATLAB (The MathWorks) and passed through the digital filter created from the acoustic calibration to equalize the frequency response of the acoustic assembly. The filtered signals were then converted to analog by a 24-bit digital-to-analog converter (National Instruments, PXI-4461) and delivered to the animal ear by a pair of speakers (Beyer-Dynamic, DT48) via plastic tubes fitted through the ear inserts. Once a neuron was isolated, we first characterized its frequency tuning with pure tones and measured a rate-level function for broadband noise, and then we measured responses to HCT and SAMN stimuli.
Pure-tone frequency tuning.
In half of the neurons, we measured the frequency response area (FRA) to characterize pure-tone tuning. Tone bursts (100 ms on, 100 ms off) varying in frequency from 200 Hz to 18 kHz (0.25-octave step or finer) and in level from 5 dB SPL to 70 dB SPL were presented in random order, and each was repeated three times. The evoked firing rate was measured for each tone and plotted as a heat map on the log frequency vs. intensity plane. The heat map was then interpolated 10× on both the frequency and intensity axes to increase the resolution. Contours on the interpolated map were identified with the MATLAB image processing toolbox. The characteristic frequency (CF) was determined as the frequency corresponding to the lowest sound level on the longest contour (see Fig. 3 for examples). When the FRA included multiple, disjoint areas (e.g., Fig. 3C), the algorithm occasionally identified an incorrect CF. All these instances were manually corrected for statistical analysis.
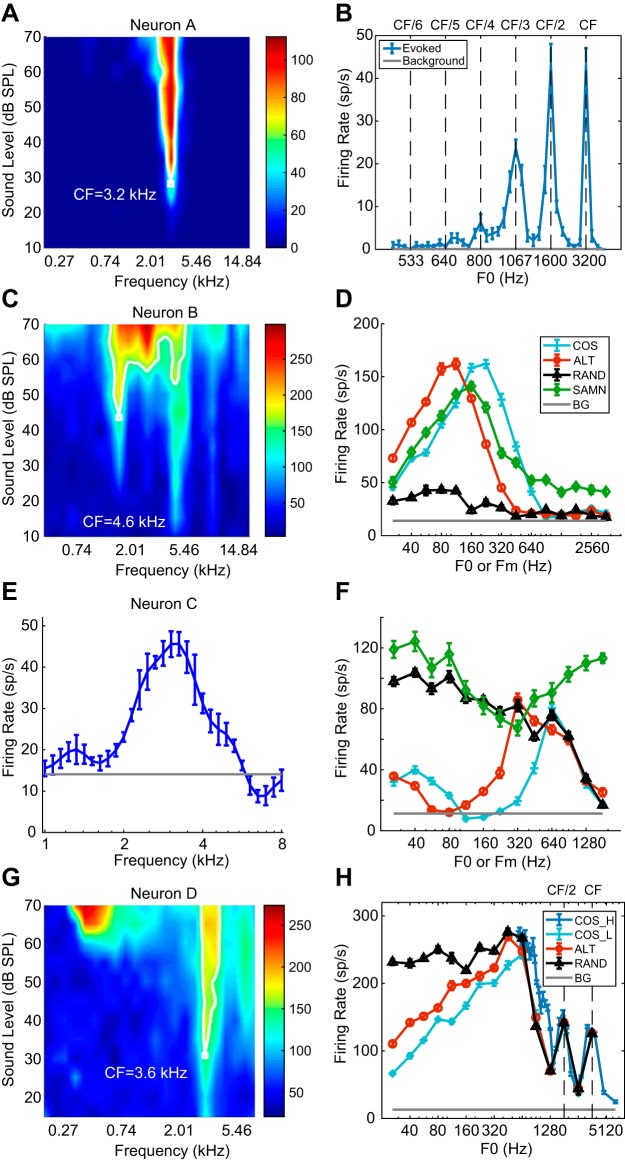
Fig. 3.
Pure-tone and complex-tone responses of 4 example neurons. A: frequency response area (FRA) of neuron A. The neuron is sharply tuned at 3.2 kHz. CF, characteristic frequency. B: rate-fundamental frequency (F0) profile of neuron A for all harmonics in cosine phase (COS) harmonic complex tone (HCT). Error bars represent ±1 SE. C: FRA of neuron B. The neuron has a complex response area, best frequency (BF) = 1.6 kHz. D: rate profiles of neuron B for HCT and sinusoidally modulated noise (SAMN). ALT, even harmonics in cosine phase and odd harmonics in sine phase; BG, background; Fm, modulation frequency; RAND, phase of each harmonic randomized for each neuron. E: isolevel tuning curve of neuron C measured at 40 dB SPL. BF = 3,062 Hz. F: rate-F0 profile of neuron C. G: FRA of neuron D. BF = 3.6 kHz. H: rate-F0 profiles of neuron D in response to complex tone with different phase configurations (COS_L, ALT, RAND) and COS phase at a different range of F0 (COS_H) designed to densely sample the region of resolved harmonics.
Before the FRA measurement was implemented, pure-tone tuning properties were characterized with either an automatic threshold tracking algorithm or an isolevel method. In the tracking method (Kiang and Moxon 1974), tone bursts (125 ms on, 125 ms off) were presented from high (18 kHz) to low (50 Hz) frequencies in 0.1-octave steps, and an automatic algorithm determined the threshold level at each frequency. This method often failed for neurons with irregular frequency responses. When the tracking method failed, we used an isolevel method in which tone bursts varying in frequency from 0.5 to 18 kHz (200 ms on, 300 ms off) were presented in random order at a fixed level (~10 dB above the threshold obtained from the noise rate-level function) with three repetitions. The best frequency was determined as the frequency that evoked the highest firing rate during tone presentation.
Most pure-tone responses were measured for monaural stimulation of the contralateral ear. In the rare cases when a neuron responded more strongly to ipsilateral sounds, frequency tuning was characterized for monaural stimulation of the ipsilateral ear. For brevity, we refer to both the characteristic frequency measured from the FRA or the tracking method and the best frequency measured by the isolevel method as “CF” in this report.
Harmonic complex tones.
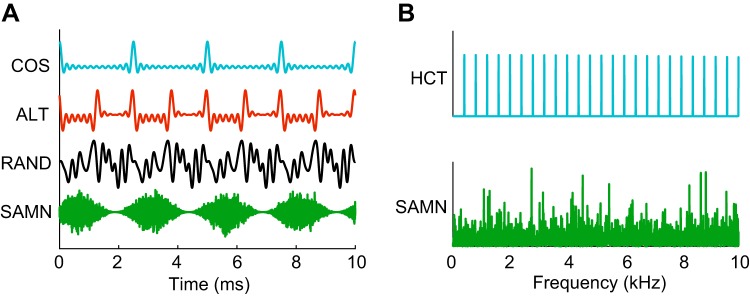
HCTs with F0s ranging from 26 to at least 2,560 Hz with 0.5-octave steps were used as stimuli. Each HCT consisted of equal-amplitude harmonics up to 18 kHz presented at an overall level of 40–60 dB SPL (so that the level per component increased with F0). For every F0, three different interharmonic phase relationships were applied to manipulate the temporal envelope of the tone (Fig. 1A) without changing the power spectrum (Fig. 1B): 1) COS: all harmonics in cosine phase, 2) ALT: even harmonics in cosine phase and odd harmonics in sine phase, and 3) RAND: the phase of each harmonic was randomized for each neuron and F0, and only signals with peak factor (maximum amplitude/root mean square amplitude) <2 were used in order to minimize envelope modulation. For all three phase relationships, the temporal periodicity of the waveform was equal to 1/F0. The COS and ALT stimuli have prominent periodic envelope modulations, whereas the RAND stimulus has a flatter envelope. When HCTs consist entirely of unresolved harmonics, COS and ALT stimuli evoke a stronger pitch than RAND (Bernstein and Oxenham 2003; Shackleton and Carlyon 1994). In this case, the pitch evoked by an ALT stimulus is perceived at twice the frequency of the pitch evoked by a COS stimulus with the same F0, reflecting the fact that the ERR of ALT is twice the ERR of COS and the common F0 of COS and ALT. In some neurons, we measured responses to COS HCTs over the same range of F0s at three different sound levels: low (30–44 dB SPL), medium (45–60 dB SPL), and high (61–85 dB SPL).
Fig. 1.
Temporal waveforms and power spectra of the stimuli. A: temporal waveforms of harmonic complex tones at fundamental frequency F0 = 400 Hz with 3 different phase relationships and sinusoidally modulated noise (SAMN) at modulation frequency (Fm) = 400 Hz. COS (all harmonics in cosine phase), RAND (phase of each harmonic randomized for each neuron), and SAMN stimuli have the same envelope repetition rate at 400 Hz but different shape (COS—sharp, pulselike, RAND—flat, SAMN—sinusoidal). ALT (even harmonics in cosine phase and odd harmonics in sine phase) has envelope morphology similar to COS but twice the envelope repetition rate (800 Hz). B: power spectra of harmonic complex tones (HCTs) and SAMN. The frequency axis is truncated at 10 kHz to show detail.
In each measurement, HCTs of different F0s, phase conditions (or sound levels) were randomly interleaved for a total of 10 repetitions each. Each complex tone was presented diotically for 200 ms with a 10-ms raised-cosine ramp at onset and offset and followed by a 300-ms silent interval.
Sinusoidally amplitude-modulated noise.
In two-thirds of the neurons, SAM broadband noise (SAMN) was interleaved with HCTs of different interharmonic phase relationships at the same overall sound level, duration, and interstimulus interval. The noise carrier was randomly generated for each measurement and fixed (“frozen”) for the 10 repetitions within the measurement. Modulation frequencies (Fm) matched the F0s of the HCTs. The modulation depth was always 1. The waveform and power spectrum of an example SAMN are shown in Fig. 1.
Histology
In the last recording session from two of the five rabbits, an electrolytic lesion was made to mark the recording site while the rabbit was under anesthesia (xylazine 6 mg/kg, ketamine 44 mg/kg). The animal was then injected with pentobarbital sodium (200 mg/kg) and immediately perfused transcardially with paraformaldehyde and glutaraldehyde in buffer solution. The brain was kept in fixative for 24 h before being transferred to 25% sucrose solution for ~3 days. Azure-thionin staining of cell bodies was made on coronal sections for the identification of lesion traces. All lesions were located in the central nucleus of IC.
Data Analysis
For all stimulus paradigms, the firing rate was averaged over the stimulus duration, excluding the 10-ms onset response, and plotted as a function of F0 or Fm to form a “rate profile.” Standard errors of the mean firing rates were also calculated and plotted as a function of F0 or Fm. For each measurement, the neuron’s background firing rate was calculated as the average firing rate during the last 200 ms of the 300-ms interstimulus interval across all stimuli. Because standard errors of the background firing rates were usually very small (<1 spike/s) because of the large number of trials, we do not show them in the figures.
Vector strength and upper limit of phase locking.
Neural synchronization to stimulus periodicities was quantified by the vector strength:
| (1) |
where N is the number of spikes and θi is the phase of the ith spike relative to the stimulus cycle. The statistical significance of VS was tested by the Rayleigh statistic (P = 0.01). VS values from measurements with <1 spike/trial (<10 spikes) were considered unreliable and were excluded from further analysis. For neurons with significant VS at two or more adjacent frequencies, the upper limit of phase locking Flim was defined as the highest frequency where VS was significant for both Flim and the next lower frequency.
Signal-to-total variance ratio.
We computed the signal-to-total variance ratio (STVR) (Hancock et al. 2010, 2012) to characterize neural sensitivity to F0 or Fm independent of the shape of tuning. STVR is an ANOVA metric derived from raw spike counts on each trial that represents the ratio of the variance in firing rates attributable to their dependence on F0 (or Fm) to the total variance, which is the sum of the variance in firing rates attributable to changes in F0 (or Fm) and the variance across multiple trials of the stimulus at a given F0 (or Fm):
| (2) |
STVR = 1 implies perfectly reliable sensitivity to F0 or Fm, i.e., all the response variability can be explained by changes in stimulus F0 or Fm, and STVR = 0 implies no sensitivity (flat tuning curve).
Classification of rate-frequency profiles.
Rate-frequency (F0 or Fm) profiles were classified into six different shapes with an automated algorithm: band pass (BP), band reject (BR), high pass (HP), low pass (LP), flat (FL), and complex (CPLX). Peaks in the rate profile that exceeded 60% of the maximum firing rate were first identified. If the dip between two peaks did not fall below 70% of the firing rate at the lower peak, the peak with a lower amplitude was excluded. For profiles with only one true peak, the classification was based on whether the firing rate on either side of the peak fell below 70% of the peak firing rate: BP—both sides crossed the 70% threshold; LP—only the high-frequency side crossed the threshold; HP—only the low-frequency side crossed the threshold; FL—neither side crossed the threshold. In the case of multiple peaks, the rate profile was first flipped by subtracting it from the maximum firing rate and then processed by the same classifier as described above. The original profile was classified as BR if the flipped profile was BP or as CPLX otherwise.
Experimental Design and Statistical Analysis
Each neuron’s responses to different stimulus conditions (interharmonic phase relationships or sound levels) were obtained by using randomly interleaved presentations to minimize the effect of possible fluctuations in overall neural responsiveness. Whenever possible, we used nonparametric statistical tests to compare neural response metrics (e.g., the STVR) between stimulus conditions across the neuronal population. When comparing two conditions, we used the Wilcoxon signed-rank test (for related variables) or the rank sum test (for independent variables) and the Kolmogorov–Smirnov test (KS test) for comparing the distributions. All tests were two sided, and P < 0.05 was considered statistically significant. For three or more conditions, we used Bonferroni correction for multiple comparisons. We used the chi-square test for comparing distributions of categorical data. Significance of the correlation between two quantities was determined by the Kendall’s τ test (Kendall and Gibbons 1990).
Computational Model
We implemented a three-stage same-frequency inhibition and excitation (SFIE) model (Carney et al. 2015; Nelson and Carney 2004) to explore possible mechanisms underlying the physiological results (Fig. 2A).
Fig. 2.
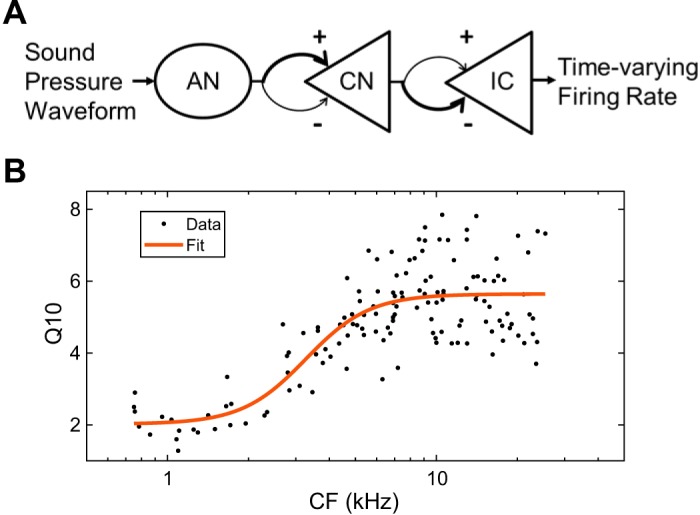
Same-frequency inhibition and excitation model with rabbit parameters. A: model diagram. B: sigmoidal fit (red curve) for rabbit Q10-characteristic frequency (CF) relationship measured by Borg et al. (1988). AN, auditory nerve; CN, cochlear nucleus; IC, inferior colliculus.
The first stage of the SFIE model is a physiologically based auditory nerve (AN) model (Zilany et al. 2009, 2014) that was modified for the rabbit as described below. The model transforms sound pressure in the ear canal into the instantaneous firing rate of an AN fiber. It has been thoroughly tested against a wide variety of physiological data in response to complex stimuli. The second and third stages model a cochlear nucleus (CN) neuron and an IC neuron, respectively. The CN and IC model neurons each receive one excitatory and one inhibitory input from the previous stage, in the form of excitatory (E) postsynaptic potentials (PSPs) and delayed inhibitory (I) PSPs (IPSPs) from the same upstream neuron. PSPs are implemented by convolving the input time-varying firing rate with an alpha function, p(t) = te−t/τ, where τ is the PSP time constant. The CN and IC model neurons have identical structure but different parameters: Mainly, inhibition is weaker than excitation at the CN stage but stronger than excitation at the IC stage. The ranges of model parameters and typical values used for simulations are shown in Table 1.
Table 1.
Parameters of SFIE model
| EPSP Time Constant τex, ms | IPSP Time Constant τinh, ms | Inhibition Delay re Excitation, ms | Inhibition Strength re Excitation inh_str | ||
|---|---|---|---|---|---|
| CN stage | Typical (Fig. 9B–9F) | 0.5 | 2 | 1 | 0.6 |
| IC stage | Range | 0.1–2 | 0.1–5 | 2 | 0.8–2 |
| Typical (Fig. 9C) | 0.5 | 1 | 2 | 1.5 |
CN, cochlear nucleus; EPSP, excitatory postsynaptic potential; IC, inferior colliculus; inh_str, inhibition strength; IPSP, inhibitory postsynaptic potential; SFIE, same-frequency inhibition and excitation.
Adjustments for Rabbit Periphery
The original AN model was developed for cat AN data and later extended to humans. The models for the two species differ in the middle ear transfer function and Q10 values of the cochlear filters. These two parameters were modified to simulate the rabbit periphery.
The dependence of rabbit Q10 on CF (in kHz) was modeled by fitting a sigmoidal function to the auditory nerve Q10 data of Borg et al. (1988) (Fig. 2B):
| (3) |
Because no direct measurements of middle ear transmission are available in rabbits, we used the cat middle ear filter that was implemented in the original model and applied a prefilter to the input acoustic signal to compensate for the expected difference between rabbit and cat middle ears. The prefilter is the cascade of a first-order high-pass Butterworth filter with a cutoff frequency of 0.8 kHz and a second-order low-pass Butterworth filter with a cutoff frequency of 18 kHz and a passband gain of –4 dB. This filter was designed to fit the magnitude difference (in dB) between cat (Heffner and Heffner 1985) and rabbit (Heffner and Masterton 1980) audiograms, based on the assumptions that thresholds of hearing are largely determined by the outer and middle ear (Rosowski 1994; Ruggero and Temchin 2002). Simulations performed with the rabbit AN model showed only minor differences from those obtained with the original cat model with respect to the points of interest in this report.
RESULTS
We measured single-unit activity from the IC of unanesthetized rabbits in response to HCT stimuli with different phase configurations in 186 IC neurons; 115 of these neurons were also tested with SAMN stimuli, and 53 were tested with COS HCT at three different sound levels. Pure-tone CFs of the neurons ranged from 0.4 to 24.3 kHz, with a median of 4.31 kHz.
Rate Tuning to Envelope Repetition Rate
Figure 3 shows the pure-tone tuning characteristics and rate-F0 profiles for HCT stimuli of four IC neurons. For neuron A (Fig. 3, A and B; CF = 3,200 Hz), the response to HCT in COS phase showed local maxima when F0 was a small-integer submultiple of the CF (CF, CF/2, CF/3,…). Similar response patterns have also been identified in the AN (Cedolin and Delgutte 2005, 2010), where local maxima in the rate-F0 profile occurred when a low-number, resolved harmonic coincided with the neuron’s CF, demonstrating a “rate-place” code to resolved harmonics. As the ratio CF/F0 increases, the frequency spacing between harmonics becomes narrower than the cochlear filter bandwidth, so that individual harmonics are no longer resolved and no longer produce peaks and troughs in the rate profile. Rate-place coding of resolved harmonics, which is dependent on cochlear frequency selectivity and tonotopic mapping, is described in a companion paper (Su and Delgutte 2019) and is not the focus of the present paper. Therefore, 15 neurons similar to neuron A that demonstrated peaks in firing rates only at resolved harmonics were excluded from the analysis in the present study.
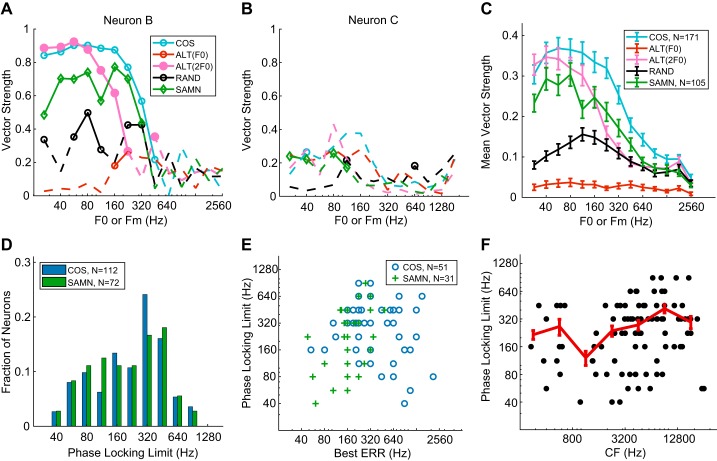
The FRA of neuron B (Fig. 3C) demonstrated a complex pattern with multiple response zones. Although the neuron’s CF was identified by the algorithm as 1.6 kHz (white contour; see methods), we manually set the CF to 4.6 kHz, at the tip of the lowest-threshold zone. For COS HCT, this neuron shows a single peak in firing rate at 224 Hz. Regardless of how CF is defined, the ratio of CF to peak F0 was >7, in a range in which harmonics are unlikely to be resolved in rabbits, and no peak corresponding to lower harmonics (i.e., higher F0s) was observed. Therefore, band-pass rate tuning to F0 of COS HCT in this neuron was not related to cochlear frequency selectivity. In contrast to COS HCT, the neuron’s response to RAND HCT showed a weak response with no tuning to F0, indicating that the tuning was dependent of the presence of envelope modulation. Furthermore, the response to ALT HCT showed band-pass tuning similar to that for COS HCT but shifted 1 octave toward lower F0s. Because the ERR of ALT HCT is 1 octave above its F0 (Fig. 1A), this octave shift suggests that this neuron was tuned to the ERR rather than to F0. Since HCTs in the three phase conditions have identical power spectra, the clear differences in rate-F0 profiles indicate that the band-pass rate tuning is not determined by the stimulus frequency composition, further justifying that it is not related to cochlear frequency selectivity.
Neuron C (CF = 3.1 kHz; Fig. 3, E and F) is another example of rate tuning to ERR. As in neuron B, the rate-F0 profile for COS HCT shows a single peak at 640 Hz. Although the peak frequency was close to CF/5, there were no peaks at other submultiples of F0 (CF/4, CF/3,…), suggesting that the main peak was not created by a resolved harmonic. This was verified by measuring the neuron’s response to HCTs with higher F0s near the CF (not shown). As in neuron B, the response of neuron C to ALT HCT showed a peak 1 octave below the peak for COS HCT, suggesting that tuning was governed by ERR. However, unlike neuron B, neuron C responded strongly to RAND HCT at low F0s, suggesting that there may be different forms of ERR rate tuning.
Finally, neuron D (CF = 3.6 kHz; Fig. 3, G and H) demonstrates that rate-place coding of resolved harmonics and band-pass rate tuning to ERR can coexist in the same neuron. This neuron’s response to COS HCT showed a main peak at 640 Hz and two small peaks at 1,792 and 3,584 Hz. The main peak occurred 1 octave below the COS peak for ALT HCT, but the smaller peaks at higher F0s were invariant to phase manipulations, indicating that they are governed by the power spectrum, not the temporal envelope. To further test whether these peaks correspond to resolved harmonics, we measured the neuron’s response to COS HCT in fine steps of F0 to specifically test submultiples of the neuron’s CF. This measurement confirmed that the neuron was able to resolve the fundamental and second harmonic but not higher-order harmonics. Thus the two small, high-F0 peaks in response to COS HCT arise from resolved harmonics, whereas the main peak at 640 Hz represents rate tuning to ERR. Despite showing multiple peaks, the profile of neuron D was classified as band pass because the two peaks at high F0s were very small and thus ignored by the algorithm. Such co-occurrence of band-pass ERR tuning and rate-place coding of resolved harmonics in the same neuron was rare in our neuronal sample.
We classified IC neurons according to the shape of their rate-F0 profiles in response to COS HCT. Fifteen neurons showing peaks in firing rate at one or more submultiples of the CF were excluded from further analysis, because their band-pass rate tuning could be due to resolved harmonics. The distribution of profile shapes among the remaining 171 neurons are shown in Table 2. The most common profile shape was band pass (BP, 40%) followed by complex (31%), and high pass (12%). Only a few neurons had low-pass (8%), band-reject (BR, 5%) or flat (4%) profiles.
Table 2.
Number of neurons with different rate profile shapes
| Band Pass | Band Reject | High Pass | Low Pass | Flat | Complex | Total | |
|---|---|---|---|---|---|---|---|
| COS HCT | 68 (40%) | 8 (5%) | 21 (12%) | 13 (8%) | 7 (4%) | 54 (31%) | 171 |
| SAMN | 19 (18%) | 22 (21%) | 20 (19%) | 2 (2%) | 19 (18%) | 23 (22%) | 105 |
COS, all harmonics in cosine phase; HCT, harmonic complex tone; SAMN, sinusoidally modulated noise.
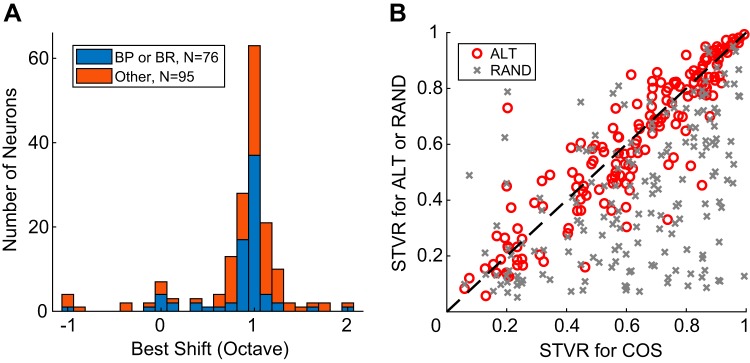
To test whether IC neurons were tuned to ERR or to F0 across the population, we computed the “best shift” between rate-F0 profiles in response to ALT and COS HCT as the F0 shift (in octaves) that minimized the city block distance (sum of absolute differences) between the two profiles. The distribution of best shifts (Fig. 4A) was centered at 1 octave for both tuned (BP or BR, n = 76) and nontuned (all other types, n = 95) groups, suggesting that the rate responses of IC neurons were largely governed by the ERR regardless of profile shape. A few neurons classified as band pass had a best shift of 0 octave. Further examination revealed that these neurons were similar to either neuron C (Fig. 3F), where the ALT and COS profiles were 1 octave apart at low F0s but aligned at high F0s, or neuron D (Fig. 3H), which demonstrated resolved harmonics at high F0s and a peak in the region of unresolved harmonics at low F0s.
Fig. 4.
Neurons are tuned to envelope repetition rate, not fundamental frequency (F0). A: best shift between rate-F0 profiles for COS (all harmonics in cosine phase) and ALT (even harmonics in cosine phase and odd harmonics in sine phase) harmonic complex tone. BP, band pass; BR band reject. B: comparison of signal-to-total variance ratio (STVR) between ALT and COS and RAND (phase of each harmonic randomized for each neuron) and COS across the neuronal sample (n = 171).
Figure 4B compares the strength of F0 coding for HCT with different phase conditions across the neuronal population using the STVR metric, which ranges from 0 (no sensitivity to F0) to 1 (perfectly reliable F0 coding); the x-axis represents the STVR for COS phase and the y-axis the STVRs for ALT or RAND phase for each neuron. ALT-COS pairs are distributed along the equality line, whereas RAND-COS pairs are scattered below. This indicates trends similar to those in the individual rate profiles in Fig. 3: comparable coding strengths for COS and ALT and minimal F0 coding for RAND. The median STVRs differed significantly between COS and RAND (P < 0.0001, Wilcoxon signed-rank test) and between ALT and RAND (P < 0.0001) but not between COS and ALT (P = 0.63). Although a minority of neurons in Fig. 4B have similar STVR values for COS and RAND, this does not necessarily indicate similar neural responses, e.g., for neuron C in Fig. 3F, STVR = 0.90 for COS and 0.87 for RAND because both response profiles varied strongly with F0. We did not observe neurons with similar response patterns in all three phase conditions, except when the neuron responded minimally to all stimuli or when it showed peaks in the rate profile at resolved harmonics.
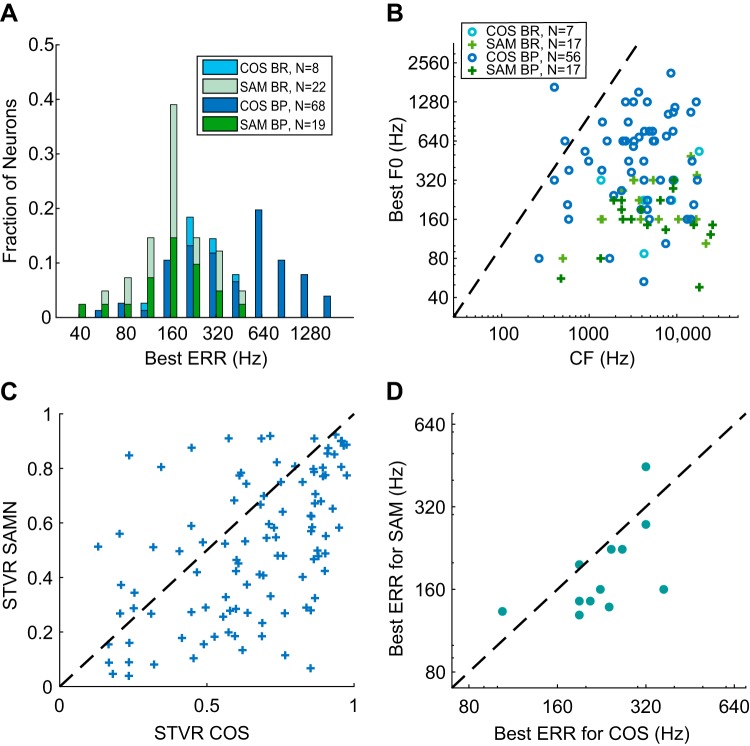
For BP and BR neurons, we defined the “best ERR” as the ERR (or F0) that evoked the maximum firing rate for BP or the minimum firing rate for BR in response to COS HCT. The distribution of best ERR (Fig. 5A) extended over a wide range of frequencies between 56 and 1,792 Hz. The limiting frequencies might be affected somewhat by the range of F0 we tested as well as the algorithm for classifying ERR tuning shape, but likely only slightly given the small tails on both ends of the best ERR distribution. Figure 5B shows a scatterplot of best ERR against pure-tone CF for neurons with BP/BR rate profiles across the neuronal sample. The best ERR was smaller than CF for most of the neurons, often much smaller, and there was no correlation between the two measures (Kendall’s τ = 0.051, P = 0.57). This lack of correlation is additional evidence that rate tuning to ERR is not related to cochlear frequency tuning.
Fig. 5.
Best envelope repetition rate (ERR) for neurons with band-pass (BP) or band-reject (BR) tuning to COS (all harmonics in cosine phase) or sinusoidally modulated (SAM) noise (SAMN) stimuli. A: distribution of best ERRs for COS and SAMN. B: best ERR of individual neurons in response to COS and SAMN showed no correlation with pure-tone characteristic frequency (CF). The dashed line indicates equality (best ERR = CF). The number of neurons included is smaller than in A because CF could not be clearly identified for some neurons. F0, fundamental frequency. C: comparison of signal-to-total variance ratio (STVR) between COS harmonic complex tone (HCT) and SAMN across the neuronal sample (n = 105). D: best ERR for COS HCT against best ERR for SAMN of neurons showing BP tuning to both stimuli (n = 12).
Dependence of ERR Tuning on Envelope Shape
The range of best ERR for COS HCT extends to higher frequencies than the best modulation frequencies in response to SAM stimuli reported in a previous study of rabbit IC (Nelson and Carney 2007) as well as studies in other species (Krishna and Semple 2000; Langner and Schreiner 1988; Rees and Møller 1983; Schnupp et al. 2015; Zheng and Escabí 2008). Therefore, we hypothesized that the rate tuning is dependent not only on ERR but also on the shape of the envelope. To directly test this hypothesis, we compared the responses to SAMN and COS HCT in 115 neurons. Ten of these neurons were also among the 15 neurons excluded from the HCT analysis because their responses showed resolved harmonics. Although SAMN stimuli do not have a harmonic spectrum, we still excluded these neurons from the following analysis to compare ERR tuning in response to SAMN and HCT in the same set of neurons. As a result, SAMN responses were analyzed in 105 neurons.
The rate-Fm profile of neuron B (Fig. 3D) demonstrates band-pass tuning to both SAMN and COS HCT. However, the maximum firing rate for SAMN was evoked at Fm = 160 Hz, lower than the best ERR for COS HCT at 224 Hz. Neuron C (Fig. 3F) showed band-reject tuning to SAMN with the minimum firing rate at Fm = 320 Hz, contrasting with the band-pass tuning for COS HCT. Across the neuronal sample, all six shapes of rate profiles were observed in response to SAMN, but the proportions of neurons in each type differed significantly from those for COS HCT (Table 2; P < 0.0001, chi-square test). Whereas band-pass tuning was the most common shape and band-reject tuning was rare for COS HCT, band-pass and band-reject shapes were almost equally common for SAMN. The proportion of flat responses was also higher for SAMN than for COS HCT, whereas the proportion of complex responses was lower for SAMN.
For SAMN responses, the best ERR (the best Fm) of neurons with band-pass and band-reject tuning was defined in the same way as for COS HCT. There was no correlation between the pure-tone CF and the best ERR for SAMN (Fig. 5B; Kendall’s τ = −0.0057, P = 0.98). This result was expected because SAMN has a flat long-term power spectrum regardless of Fm (Fig. 1B). The distribution of best ERR for SAMN (Fig. 5A) extended over a lower frequency range, mostly below 500 Hz, compared with the distribution for COS HCT. The median best ERR was 160 Hz for SAMN versus 415 Hz for COS HCT, and the difference was significant (P < 0.0001, Wilcoxon rank sum test). As noted above, a greater proportion of neurons showed band-reject tuning for SAMN compared with COS HCT (22/41 neurons for SAMN, 8/76 for COS). For the 12 neurons that showed band-pass tuning to both COS HCT and SAMN, the best ERR was usually lower for SAMN than for COS HCT (Fig. 5D) and the correlation between the two best ERRs was statistically significant (Kendall’s τ = 0.56, P = 0.018).
Figure 5C shows a scatterplot of the STVR for ERR in response to SAMN against the STVR in response to COS HCT for the 105 neurons that were tested with both stimuli. Although both cover a wide range of values, the majority of neurons had lower STVRs for SAMN than for COS HCT, indicating somewhat weaker strength of ERR coding with SAMN. The STVR distributions for the two stimuli were significantly different (P = 1.5 × 10−4, KS test), as were their medians (P < 0.0001, Wilcoxon signed-rank test).
In summary, rate tuning to ERR in IC is dependent on the shape of the stimulus envelope with respect to tuning shape, range of best ERR, and strength of coding.
Temporal Coding of ERR
In the auditory periphery, neurons can convey temporal information about the stimulus via phase locking to the envelope, the temporal fine structure, or both (see Winter 2005 for review). These temporal cues may play a crucial role in pitch perception. We therefore characterized temporal coding of F0 or Fm in IC neurons for both HCT and SAMN to test whether the codes present in the periphery are preserved or possibly enhanced.
The vector strength (VS) of neuron B is shown as a function of F0 or Fm in Fig. 6A. For COS, RAND, and SAMN, VS was computed with a period of 1/F0 or 1/Fm. For ALT, we additionally computed VS with a period of 1/2F0, i.e., 1/ERR, to test whether neurons were synchronized to F0 or ERR. The neuron showed significant phase locking to the ERR of COS and ALT but no significant phase locking to the F0 of RAND or ALT. Therefore, like rate tuning, temporal coding by this neuron was governed by the stimulus envelope, not F0. For SAMN, the neuron showed significant phase locking over a range of ERRs similar to COS HCT, but the VS values were lower. The Fourier transforms of the neuron’s peristimulus time histograms for both HCT and SAMN stimuli (not shown) showed no peak near the CF, indicating no phase locking to the temporal fine structure. Overall, phase locking to the temporal fine structure was rare in our neuronal sample, likely because most neurons had relatively high CF (>1 kHz), which is above the limit of phase locking of most IC neurons (Liu et al. 2006). Unlike neuron B, neuron C (Fig. 6B) showed little phase locking to any stimulus, despite its clear rate tuning to ERR. Overall, 59 of 171 neurons (35%) tested with COS HCT did not have significant phase locking at two or more consecutive frequencies and were therefore considered not to provide temporal coding.
Fig. 6.
Temporal coding in inferior colliculus (IC) neurons. A: vector strength as a function of fundamental frequency (F0) or modulation frequency (Fm) for neuron B. Dashed lines indicate insignificant vector strengths (Rayleigh’s test, P > 0.01). ALT, even harmonics in cosine phase and odd harmonics in sine phase; COS, all harmonics in cosine phase; RAND, phase of each harmonic randomized for each neuron; SAMN, sinusoidally modulated noise. B: vector strength against F0 for neuron C. C: average vector strength across all IC neurons. Both significant and insignificant values were included in the average. Error bars represent ±1 SE. D: distribution of the frequency limit of phase locking to envelope repetition rate (ERR) for COS and SAMN. E: phase-locking limit vs. best ERR across the neuronal sample (COS; SAMN). F: upper frequency limit of phase locking vs. characteristic frequency (CF) across the neuronal sample (black dots, n = 98). The curve is a moving average of limiting frequencies in 1-octave frequency bins (red line). Error bars represent ±1 SE.
The average VS across the entire neuronal sample (Fig. 6C) resembled the trends observed in the example of Fig. 6A. For both COS and SAMN, the average VS gently rolled off at ~224 Hz, but the mean VS values were smaller for SAMN than for COS. The VS-F0 curve for ALT (2F0) was similar to the COS curve but shifted 1 octave toward lower F0s, in line with phase locking to ERR. The upper frequency limit of phase locking of individual neurons for both COS and SAMN (Fig. 6D) ranged from 40 Hz to ~900 Hz. Neither the median limits (224 Hz for both, P = 0.18, Wilcoxon signed-rank test on the 72 neurons tested with both stimuli) nor the distributions of frequency limits differed statistically between the two stimuli (P = 0.94, KS test).
Across the neuronal sample, the limiting frequency of phase locking to ERR was not correlated with the best ERR for rate tuning to COS HCT (Fig. 6E; Kendall’s τ = −0.087, P = 0.41). However, the limiting frequency for SAMN showed a small correlation with the best ERR (Fig. 6E; τ = 0.30, P = 0.03). The phase locking limit was also not strongly related to the pure-tone CF (Fig. 6F; Kendall’s τ = 0.16, P = 0.025), although there may be a small trend for the phase-locking limit to increase with CF above 1,000 Hz. The lack of a clear relationship between pure-tone CF and phase-locking limit in our data contrasts with the finding by Middlebrooks and Snyder (2010) that the limit of phase locking to electric pulse trains in the IC of anesthetized cats is higher in low-CF (<1.5 kHz) neurons. In our data, the phase-locking limits did not significantly differ between low-CF (≤1.6 kHz, n = 18) and high-CF (>1.6 kHz, n = 80) neurons (Wilcoxon rank sum test, P = 0.057). We return to this point in discussion.
Two Subgroups Emerge Within Band Pass-Tuned Neurons
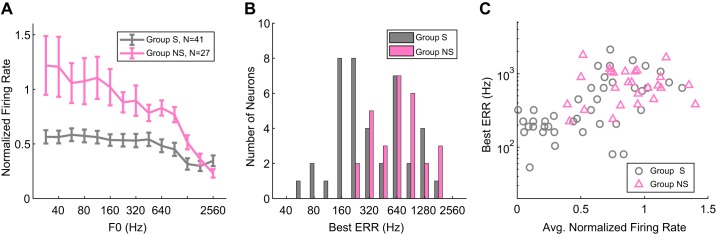
Neurons showing band-pass tuning to ERR for COS HCT could be divided into two subgroups depending on their ability to phase lock to the temporal envelope of COS HCT, and the grouping was related to their rate responses to RAND HCT. Neurons B and C in Fig. 3 and Fig. 6 are representative of the two subgroups: neuron B represents “group S” (synchronized) neurons that had significant phase locking to COS HCT at low to medium ERR (Fig. 6A) and minimal rate response to RAND HCT over the entire frequency range (Fig. 3D). In contrast, neuron C represents “group NS” (nonsynchronized) neurons that demonstrated minimal phase locking to COS HCT at all frequencies (Fig 6B) and a high firing rate for RAND HCT at low to medium F0s (Fig. 3F). A neuron with band-pass rate tuning was classified as S if it showed significant phase locking to COS HCT at two or more consecutive F0s and as NS otherwise. Figure 7A shows the average normalized rate profiles (firing rate normalized by the maximum firing rate for COS HCT) for RAND HCT in group S (n = 41) and group NS (n = 27) neurons. The average profiles are consistent with the individual examples in Fig. 3, D and F: S neurons had a flat, low firing rate across the entire frequency range, whereas NS neurons usually showed a two-segment pattern: a shallow decrease from a high firing rate at low to medium F0s followed by a sharp decline at higher F0s. Neurons in the two subgroups also differed with respect to the distribution of their best ERRs (Fig. 7B). Whereas the best ERR of group S neurons covered a wide range between 56 and 1,792 Hz (median 293 Hz), group NS neurons were tuned to relatively high ERRs between 448 and 1,792 Hz (median = 692 Hz). Figure 7C shows a scatterplot of best ERR against the normalized firing rate for RAND HCT averaged across F0s ≤ 320 Hz for group S and group NS neurons. Within group S, about half of the neurons had low firing rates (≤0.4) or small best ERR (≤224 Hz), and they formed a distinguishable cluster from NS neurons. However, the other half of group S neurons were not separated from NS on this display. The existence of at least two subgroups of band-pass tuned neurons suggests that the rate tuning to ERR may be generated by multiple mechanisms.
Fig. 7.
Two subgroups of neurons showing band-pass envelope repetition rate (ERR) tuning. A: average normalized rate profile for RAND (phase of each harmonic randomized for each neuron) harmonic complex tone (HCT) in synchronized (S) and nonsynchronized (NS) neurons. Firing rate was normalized by the neuron’s maximum firing rate in response to COS (all harmonics in cosine phase) HCT, i.e., the firing rate at the best ERR. F0, fundamental frequency. B: distribution of best ERRs in S and NS neurons. C: best ERR vs. normalized firing rate averaged over F0 ≤ 320 Hz for individual group S and NS neurons.
Effects of Stimulus Level on Rate and Temporal Coding of ERR
Because pitch perception is relatively invariant over a wide range of sound levels, a neural code for pitch should also be robust to variations in stimulus levels. We therefore tested a subset of 53 neurons with COS HCT at low (30–44 dB SPL), medium (45–60 dB SPL), and high (61–85 dB SPL) sound levels. The three sound levels used for each neuron were initially chosen in 15-dB increments (n = 10), but the increment was later increased to 20 dB (n = 43) in order to sample higher levels.
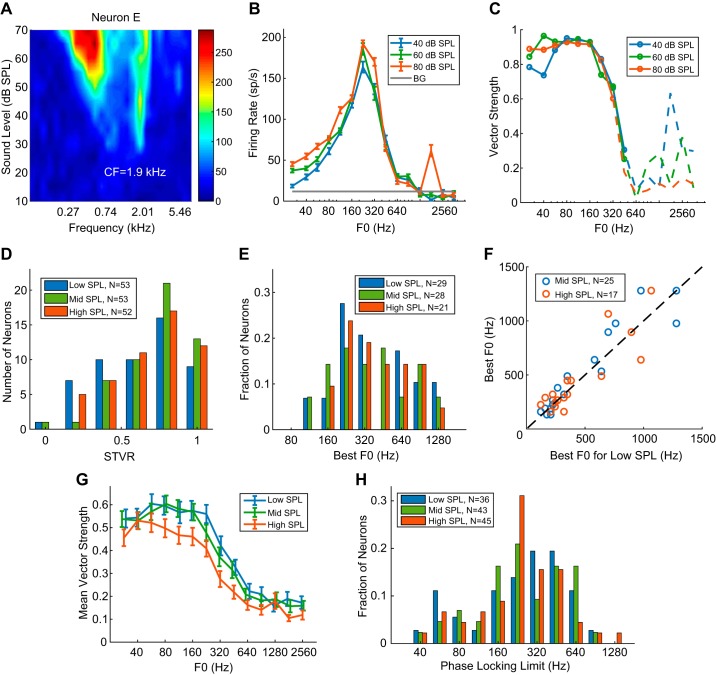
Figure 8, A–C, show the pure-tone receptive field, rate-F0 profile, and vector strength (VS), respectively, from neuron E at three sound pressure levels. The rate profiles at 40 and 60 dB SPL were almost identical, with a best F0 at 224 Hz. When the sound level was increased to 80 dB SPL, the rate profile retained a similar shape but showed a small peak at 1,792 Hz, possibly reflecting a response to the resolved fundamental near the CF. The VSs were almost identical at 40 and 60 dB SPL, showing strong phase locking to the stimulus envelope up to 448 Hz. At 80 dB the VS remained similar to the VS at lower SPLs up to 320 Hz but dropped below statistical significance at 448 Hz.
Fig. 8.
Effect of stimulus level on rate and temporal coding of envelope repetition rate ERR for COS (all harmonics in cosine phase) harmonic complex tone. A: frequency response area of example neuron E with characteristic frequency (CF) = 1.9 kHz. B: rate-fundamental frequency (F0) profiles of the neuron in A at 3 sound levels. BG, background. C: vector strength of the neuron in A at 3 sound levels. D: distribution of signal-to-total variance ratio (STVR) for all neurons tested at 3 levels (median = 0.68 for low SPL, 0.81 for mid SPL, and 0.79 for high SPL). E: distribution of best F0s at low, medium, and high sound levels for neurons showing band-pass/band-reject tuning. F: comparison of best F0s at different sound levels across the neuronal sample (blue circle, low vs. mid sound level; red circle, low vs. high sound level). G: mean vector strength as a function of F0 across all neurons at 3 sound levels. x-Coordinates for low- and mid-SPL were jittered to separate the error bars (±1 SE). H: distributions of the upper frequency limits of phase locking at 3 sound levels.
Figure 8D compares the distribution of F0 STVR at different intensities across the neuronal sample. The STVR distributions did not significantly differ between any pair of sound levels (KS tests; Table 3). The median STVR was significantly higher for mid SPLs than for low SPLs, but the differences were not significant when low versus high and mid versus high SPLs were compared (Wilcoxon signed-rank tests; Table 4). Among the 53 neurons tested at three sound levels, 29 showed band-pass or band-reject tuning to F0 for at least one level. [In all of these neurons, we verified that the rate tuning was governed by ERR using HCTs in ALT phase at one sound level, usually the lowest one. Therefore, the tuning was also likely governed by ERRs at the other SPLs. However, because we did not test tuning to ALT HCT at all levels, we still refer to the frequency to which these neurons are tuned as the best F0 rather than the best ERR.] The distributions of best F0s were similar across the three SPL ranges (Fig. 8E; see Table 3 for KS test results from pairwise comparisons), and the median best F0s were also similar (Wilcoxon signed-rank tests; Table 4), but the total number of band-pass and band-reject neurons slightly decreased at the highest sound level. For neurons demonstrating band-pass or band-reject tuning at the lowest sound level, best F0s at the medium and high sound levels were strongly correlated with the best F0 at the lowest level (Fig. 8F; Kendall’s τ = 0.81, P < 0.0001 for mid SPL, τ = 0.69, P = 1.9 × 10−4 for high SPL). Although some neurons did not have the same tuning shape for all three sound levels according to our criteria, morphologies of their rate profiles only changed gradually and remained similar across levels. For example, a band-pass neuron could transition into high pass because the high-frequency flank no longer fell below 70% of maximum firing rate. Together, the stable distributions of STVR and best ERR indicate that the rate code is robust over a 40-dB range of sound levels.
Table 3.
KS test P values comparing ERR or temporal coding across sound levels
| Low vs. Mid | Low vs. High | Mid vs. High | |
|---|---|---|---|
| Best ERR | 1 | 1 | 1 |
| STVR | 0.54 | 1 | 1 |
| Phase locking limit | 1 | 1 | 1 |
Values are Kolmogorov–Smirnov (KS) test P values comparing envelope repetition rate (ERR) or temporal coding across sound levels. STVR, signal-to-total variance ratio.
Table 4.
Signed-rank test P values comparing ERR rate or temporal coding across sound levels
| Low vs. Mid | Low vs. High | Mid vs. High | |
|---|---|---|---|
| Best ERR | 0.57 | 1 | 1 |
| STVR | 0.003 | 0.18 | 0.22 |
| Phase locking limit | 1 | 1 | 1 |
Values are signed-rank test P values comparing envelope repetition rate (ERR) or temporal coding across sound levels. STVR, signal-to-total variance ratio.
Figure 8, G and H, compare temporal coding for COS HCT across sound levels in the same way as Fig. 6, C and D, respectively. Across F0s, average VSs were almost identical for low- and medium-SPL stimuli but were lower for the high-SPL stimuli. The distributions of phase locking limits were similar over the SPL range (Table 3; KS tests), and the median limits did not significantly differ across levels (Table 4; Wilcoxon signed-rank tests). Although the average VS was higher in the low-SPL condition (Fig. 8G) than in the high-SPL condition (Fig. 8G), the number of neurons with significant phase locking was larger for high-SPL stimuli (n = 45) than for low-SPL stimuli (n = 36). In other words, some neurons only synchronized to ERR of HCT at the higher sound level. Overall, the temporal coding of ERR by the IC neuron population was fairly robust over the range of sound levels investigated.
Model Suggests Temporal Interaction Between Inhibition and Excitation
We implemented the SFIE model (Nelson and Carney 2004) using HCT and SAMN stimuli as inputs to simulate rate tuning to ERR. The SFIE model was originally designed to predict rate and temporal modulation transfer functions of IC neurons in response to SAM tones (Carney et al. 2015; Henry et al. 2017; Nelson and Carney 2004) but has not been systematically tested for HCT with various phase relationships among harmonics. In this three-stage model (Fig. 2), CN and IC cells receive one excitatory and one inhibitory input from the previous stage in the form of PSPs, and their output instantaneous firing rates are nonzero only when the EPSP exceeds the IPSP. Rate-F0 profiles for each model stage were obtained by averaging firing rates over 100 simulated stimulus trials. Model parameters are listed in Table 1.
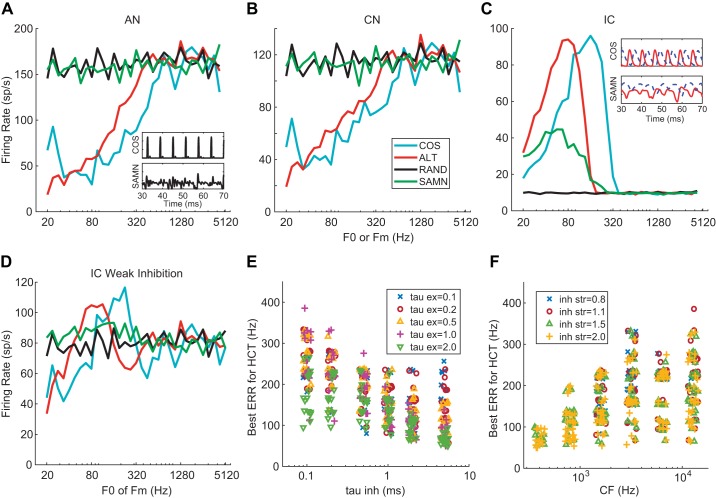
Rate profiles at the three SFIE model stages with CF = 6,400 Hz are shown in Fig. 9, A–C for HCT and SAMN stimuli presented at 60 dB SPL. At the AN stage (Fig. 9A), firing rates for COS and ALT HCT increased linearly with ERR (i.e., entrained to the ERR) up to 640 Hz and then plateaued at higher frequencies. In contrast, the rate profiles for RAND and SAMN were nearly flat across all F0s. Model CN responses (Fig. 9B) were almost identical to AN responses except for lower firing rates. Model IC responses (Fig. 9C) resembled the data for neuron B in Fig. 3D: band-pass tuning to ERR for COS and ALT with best ERR = 160 Hz and a flat, weak response to RAND. Importantly, the peak response to ALT occurred 1 octave below the peak for COS, consistent with the data and indicating that the model’s tuning was governed by the envelope. Also consistent with the data, the model showed band-pass tuning for SAMN, with a lower best ERR (57 Hz) than for COS.
Fig. 9.
Simulated rate profiles of the same-frequency inhibition and excitation (SFIE) model in response to stimuli at 60 dB SPL. A–C: output of SFIE model auditory nerve (AN; A), cochlear nucleus (CN; B), and inferior colliculus (IC; C) stages. See Table 1 for model parameters. Inset in A: instantaneous firing rate of AN stage for COS (all harmonics in cosine phase) harmonic complex tone (HCT) and sinusoidally modulated noise (SAMN) with envelope repetition rate (ERR) = 160 Hz. Inset in C: excitatory postsynaptic potential (solid) and inhibitory postsynaptic potential (dashed) at input to IC stage for ERR = 160 Hz. D: output of a model SFIE IC cell with inhibition strength (inh_str) = 0.8. Stimuli and other model parameters as in C. E: relationship between best ERR for COS HCT and time constants [excitatory (τex) and inhibitory (τinh)] of model IC cells. F: relationship between best ERR for COS HCT and characteristic frequencies (CFs) of the model and inh_str of model IC cells. In E and F, the x- and y-coordinates were jittered by up to ±5% to visually separate the data points.
We implemented the model with a wide range of parameter combinations and found that band-pass responses at the IC stage mainly occurred when the strength of inhibition exceeded that of excitation. Figure 9D shows the response of a model IC cell with the same inputs and parameters as in Fig. 9C but with an inhibition strength of 0.8 (inhibition weaker than excitation) instead of 1.5. The band-pass pattern was much less pronounced, and the rate profile did not resemble experimental data. Thus the SFIE model suggests that band-pass rate tuning to ERR can arise in the IC from interactions between weak excitation and strong inhibition.
The SFIE model could also account for the difference in tuning between SAMN and COS HCT observed in the data. The insets in Fig. 9, A and C, show the time-varying firing rates of the AN model and the PSPs at the IC stage for COS HCT and SAMN stimuli at 160 Hz (the best ERR). At the AN stage, the time-varying firing rates followed the envelopes of the stimuli: impulselike for COS and more graded for SAMN. As explained by Nelson and Carney (2004), at the IC stage the PSPs transform from phasic to tonic when the input envelope fluctuates faster than the time constant of the cell’s unitary PSP, resulting in degraded phase locking. Because inhibition has a longer time constant, this transformation occurs at a lower ERR for IPSP than for EPSP. For a COS HCT at 160 Hz, the EPSP and IPSP occur out of phase, resulting in strong, phase-locked firing. In contrast, for SAMN at the same ERR the EPSP has modest amplitude fluctuations inherited from the previous stages, whereas the IPSP has minimal fluctuations but a higher average amplitude compared with the EPSP, resulting in weak firing. Thus the dynamics of excitation and inhibition at the IC stage interact with the envelope shapes of the stimuli to yield a lower best ERR for SAMN.
To further understand the dependence of the best ERR on model parameters, we independently varied key model parameters (CF, IC excitatory and inhibitory time constants, and relative inhibition strength) over a wide range (600 parameter combinations). Figure 9E shows the relationship between best ERR and the PSP time constants (τinh on the x-axis, τex coded by colors and symbols) for model IC cells that demonstrated band-pass tuning to COS HCT at 60 dB SPL (524 combinations out of 600, tuning types classified with the same algorithm as for the neural data). Although the best ERRs covered a wide range for each τinh value on the x-axis, there was a clear trend of decreasing best ERR with both increasing inhibition and excitation time constants. In Fig. 9F, best ERR is plotted as a function of the CF of the AN stage (x-axis) with inhibition strength as a parameter (coded by colors and symbols). Because the two parameters were varied independently, the numbers of neurons showing band-pass rate tuning should be the same across all CF if there were no interaction between the two parameters. However, for CF <1 kHz, band-pass tuning was only observed when the inhibition strength was >1.5, indicating that band-pass tuning was more likely to occur for neurons with high CF and strong inhibition. In addition, the upper limit of the range of best ERRs increased systematically with increasing CF. In contrast, the inhibition strength seemed to have no effect on the best ERR for CF > 1 kHz. A small number of model IC cells with 0.8 inhibition strength were classified as band pass, but their tuning was less pronounced and the firing rate showed a plateau at high frequencies, as in the model cell of Fig. 9D.
Overall, the range of best ERR that could be simulated by the model for COS HCT was narrower (40–385 Hz; Fig. 9, E and F) compared with the range in the neural data (56–1,600 Hz). Thus the SFIE model can account for some aspects of the data but also has limitations.
DISCUSSION
Using single-neuron recordings from the IC of unanesthetized rabbits in response to HCT and SAMN stimuli, we characterized a rate code for ERR that was not related to pure-tone frequency tuning created in the cochlea. By comparing responses to HCT having the same power spectrum but different interharmonic phase relationships, we showed that tuning is governed by ERR rather than F0. This rate code was robust across a wide range of sound levels and depended on the shape of the stimulus envelope. We also characterized a temporal code that spanned a similar range of ERR (up to ~900 Hz) for both HCT and SAMN but was generally stronger for COS HCT. Computational modeling suggests that excitation-inhibition interactions can implement the temporal-to-rate code transformation necessary to create band-pass rate tuning to ERR.
Our conclusion that the rate tuning observed with HCT is governed by ERR rather than F0 is consistent with results from multiunit clusters in the IC of anesthetized guinea pigs (Shackleton et al. 2009), which compared responses to HCT in sine and ALT phase. However, the range of best ERR they reported (70–280 Hz) was much narrower than the range in our data (56–1,600 Hz). This difference arises in part because Shackleton et al. only tested F0s up to 400 Hz, and perhaps also because their animals were anesthetized. They also found that F0 tuning in a dichotic condition where even and odd harmonics were presented to opposite ears was shifted 1 octave below the tuning when all harmonics were presented to both ears. Because dichotic presentation doubles interharmonic spacing (and therefore the ERR) in each ear, their finding provides additional evidence that ERR determines the apparent rate tuning to F0. The present results extend those of Shackleton et al. (2009) to single units in unanesthetized preparations, to a wider range of F0s, and by directly comparing ERR tuning for HCT and SAMN.
We distinguished two subtypes among IC neurons showing band-pass tuning to ERR for COS HCT: synchronized and nonsynchronized. A parallel distinction has previously been established for neurons in the auditory cortex (Lu et al. 2001) and thalamus (Bartlett and Wang 2007) of awake marmosets with click train stimuli, although most of their responses would be classified as showing high-pass rate tuning rather than band-pass tuning on the basis of our criteria. Bartlett and Wang (2007) suggested that nonsynchronized neurons either only emerge in the thalamus or are unique to primates. Here we show that a form of nonsynchronized neurons is found in the IC of awake rabbits.
Rate and Temporal Coding of ERR Depend on Envelope Shape
In both our physiological and modeling results, rate tuning to ERR differed between HCT and SAMN with respect to tuning shape and range of best ERR, indicating that the tuning is dependent on envelope shape. Band-pass rate tuning to the modulation frequency of SAM stimuli has long been documented in IC neurons (Batra et al. 1989; Joris et al. 2004; Krishna and Semple 2000; Langner and Schreiner 1988; Nelson and Carney 2007; Rees and Møller 1983; Schnupp et al. 2015). The best modulation frequencies (BMFs) in these studies were mostly distributed below 300 Hz, with a tendency for higher BMFs in unanesthetized preparations (Nelson and Carney 2007) and when recordings were from multiunits compared with single units (Langner and Schreiner 1988; Schnupp et al. 2015). In general, this range of BMFs is in line with the range of best ERR for SAMN observed in the present study but lower than the range for COS HCT. Previous studies of IC neurons in anesthetized animals have also reported differences in rate tuning to ERR between pulse trains and sinusoidal modulations (Schnupp et al. 2015; Zheng and Escabí 2008) and between sinusoidal and triangular or trapezoidal modulations (Sinex et al. 2002a). As in our study, Schnupp et al. (2015) found only weak correlation between best ERR for SAMN versus periodic pulse trains (which are harmonic complexes) across the IC neuronal population. Envelope shape is perceptually important, e.g., it contributes to the timbre of musical instruments (Siedenburg 2019) and to phonetic distinctions in speech (Cutting and Rosner 1974). Our observation that the firing rates of single IC neurons are sensitive to both ERR and envelope shape is in line with results from Bizley et al. (2009), in which a majority of neurons in ferret A1 demonstrated sensitivity to two or more attributes of pitch, timbre, or sound localization cues and the interaction between pitch and timbre cues was particularly pronounced. How the envelope shape information is separated from ERR and extracted by downstream neurons needs further investigation. Although the discussion has focused on envelope shape, we cannot rule out the possibility that the inherent random fluctuations in the noise carrier of SAMN stimuli also contribute to the differences in neural responses between COS HCT and SAMN (Zheng and Escabí 2013) .
The effect of envelope shape on temporal coding of ERR was less pronounced. For the majority of IC neurons, the precision of phase locking to the envelope was poorer for SAMN than for COS HCT at the same ERR. Zheng and Escabí (2013) also reported higher vector strengths for trains of brief noise bursts than for SAM tones in the IC of anesthetized cats. However, the upper frequency limits of phase locking were comparable between the two stimuli and also similar to the results obtained with SAM tones in earlier studies (Batra et al. 1989; Joris et al. 2004; Krishna and Semple 2000; Langner and Schreiner 1988; Nelson and Carney 2007). The upper limit of phase locking to SAMN and COS HCT in the present study at ~900 Hz is in line with maximum frequency represented in the frequency-following response (FFR) measured at the scalp (e.g., Bidelman and Powers 2018), consistent with an upper brain stem origin of the FFR.
Mechanisms for Rate Tuning to ERR
Using the SFIE model, we explored one possible mechanism for creating band-pass rate tuning to ERR: the interaction between fast excitation and delayed, slower inhibition. Several in vivo studies (Kuwada et al. 1997; LeBeau et al. 2001; Nataraj and Wenstrup 2006; Rodríguez et al. 2010; Zhang and Kelly 2003) have demonstrated inhibitory interactions in the IC that could, in principle, provide a substrate for the SFIE model. However, the interaction between excitation and inhibition at the core of the SFIE model could also occur partly or wholly at lower stages along the auditory pathway.
The model predicted the differences in best ERR between SAMN and COS HCT observed in the data. However, it has two major limitations: 1) only band-pass tuning could be simulated and 2) the range of simulated best ERR (40–385 Hz) was much smaller than the neural data (56–1,600 Hz). Although the SFIE model was not designed to predict the band-reject tuning to ERR that was frequently observed with SAMN, band-reject tuning can be created through interaction between a broadly tuned excitatory input and inhibition from a band-pass-tuned neuron (Carney et al. 2015; Henry et al. 2017).
Because the best ERR of the model IC neuron’s band-pass tuning is dependent on the frequency at which envelope phase locking in the EPSP and IPSP starts to degrade, a neural mechanism that sharpens phase locking at higher frequencies, such as coincidence detection, might be able to expand the range of best ERR. Therefore, we also briefly explored an across-frequency coincidence detection model (Krips and Furst 2009) that received multiple excitatory inputs with different CFs from the same AN model as in the SFIE. For certain choices of parameters, the model was able to simulate band-pass tuning to COS HCT with much higher best ERRs (>1,000 Hz) than the SFIE model, as well as high-pass and complex tuning shapes. However, the range of best ERR was limited within 1 octave, and the model’s ability to generate band-pass tuning was very sensitive to the combination of parameters. Therefore, we do not include detailed results in this report. Other models based on coincidence detection can also predict band-pass rate tuning to ERR in the IC (Hewitt and Meddis 1994; Langner and Schreiner 1988) or at an equivalent stage along the auditory pathway (Huang and Rinzel 2016). These models need to be evaluated in detail against a broad set of neural data including responses to stimuli with different envelope shapes.
In summary, the temporal-to-rate code transformation yielding rate tuning to ERR might be implemented by several mechanisms, including excitatory-inhibitory interactions, coincidence detection, and additional mechanisms that were not explored, such as membrane resonances resulting from the interplay between conductances with different dynamics (Hutcheon and Yarom 2000; Laudanski et al. 2014). A plurality of mechanisms is consistent with the diversity of tuning patterns and wide range of best ERR observed in IC neurons.
CF Dependence of Temporal Coding of ERR in IC Neurons
We observed no evidence for a systematic dependence of the upper limit of phase locking to COS HCT on the CF of IC neurons (Fig. 6F). This finding contrasts with those of a study of the response of IC neurons to electric stimulation of the auditory nerve in deafened, anesthetized cats (Middlebrooks and Snyder 2010), in which the upper limit of phase locking to periodic electric pulse trains was clearly higher in low-CF neurons (<1.5 kHz). The different observations, however, do not contradict each other because electric pulse trains and COS HCT (which resemble click trains) produce very different spatiotemporal patterns of activity in low-CF AN fibers. Whereas each electric pulse usually produces a unimodal response pattern in AN fibers (Miller et al. 2001; Shepherd and Javel 1999; van den Honert and Stypulkowski 1987), each acoustic click produces multimodal response patterns with peaks at intervals of 1/CF (Kiang et al. 1965). Moreover, the lack of a cochlear traveling wave (Robles and Ruggero 2001) with electric stimulation will alter the pattern of across-fiber synchrony along the tonotopic axis of the AN. These differences in both single-fiber temporal response patterns and across-fiber synchrony between acoustic and electric stimulation are likely to translate downstream into differences in the temporal response patterns of IC neurons. Middlebrooks and Snyder (2010) also found that low-CF neurons had shorter first spike latencies than high-CF neurons, which is opposite to results from acoustical stimulation (Joris et al. 2006; Langner et al. 1987; Langner and Schreiner 1988; Liu et al. 2006). In addition to these differences in patterns of peripheral activation, there are also differences in species and preparation between the Middlebrooks and Snyder (2010) study and the present one. In particular, anesthesia has been shown to alter temporal response patterns in IC neurons of both normal-hearing (Bock and Webster 1974; Kuwada et al. 1989) and cochlear-implanted (Chung et al. 2014) animals.
Implications for Pitch Perception and Hearing Impairment
Although the pitch of HCT can be produced by stimuli with either resolved or unresolved harmonics, the temporal and rate codes we characterized are primarily relevant to the pitch of unresolved harmonics. Specifically, the pitch of ALT HCT matches the F0 when the stimulus contains resolved harmonics but matches the ERR when the stimulus contains only unresolved harmonics (Houtsma and Smurzynski 1990; Shackleton and Carlyon 1994). The pitch strength of RAND HCT is similar to that of COS HCT for stimuli with resolved harmonics but is weaker than COS HCT for unresolved harmonics (Bernstein and Oxenham 2003; Houtsma and Smurzynski 1990). Both the rate code and the temporal code consistently followed the ERR rather than the F0 for ALT HCT, and the representation of ERR by both codes was weaker for RAND HCT than for COS or ALT HCT. Thus these codes represent the pitch of unresolved harmonics.
Together, the ranges of best ERR for HCT (56–1,600 Hz) and the range of phase locking to ERR (up to ~900 Hz) in rabbit IC cover the range of human pitch perception for unresolved harmonics, which extends from ~30 Hz (Krumbholz et al. 2000; Pressnitzer et al. 2001) to 600–1,000 Hz (Burns and Viemeister 1976, 1981; Carlyon and Deeks 2002; Macherey and Carlyon 2014). Both the rate and temporal codes for ERR in IC are ultimately derived from temporal cues in the AN because rate tuning to ERR is lacking in the AN. Although there are no direct physiological data comparing the frequency ranges of phase locking in rabbits and humans, the study of Verschooten et al. (2018) suggests that the upper limit of phase locking in the human AN nerve is likely similar to or somewhat lower than that in laboratory animals. If so, the frequency ranges of ERR rate coding and temporal coding in humans would also be similar to or lower than in rabbits. Whether both the rate code and the temporal code are actually used to extract the pitch of unresolved harmonics is unclear.
The rate code and temporal code we observed in IC can robustly represent the ERR, which is crucial for the pitch perception of unresolved spectral components that is especially relevant for small mammals (Osmanski et al. 2013; Shofner and Chaney 2013; Walker et al. 2019), but cannot account for the pitch of resolved harmonics, which is more important for speech and music perception by normal hearing human listeners. Still, unresolved harmonics are likely to be particularly important in sensorineural hearing loss (SNHL), where place cues from resolved harmonics may no longer be available because of the degraded cochlear frequency selectivity (Moore 2008), while peripheral phase locking to ERR might be even strengthened with SNHL (Henry et al. 2014; Kale and Heinz 2010). The rate and temporal codes to ERR are also critical with cochlear implants because the spatial selectivity of present devices is inadequate to provide place information about individual harmonics (Oxenham 2008; Rodríguez et al. 2010).
GRANTS
This work was supported by NIH Grant R01 DC-002258.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
Y.S. and B.D. conceived and designed research; Y.S. performed experiments; Y.S. analyzed data; Y.S. and B.D. interpreted results of experiments; Y.S. and B.D. prepared figures; Y.S. drafted manuscript; Y.S. and B.D. edited and revised manuscript; Y.S. and B.D. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Yoojin Chung for help with experimental procedures, Ken Hancock for technical support, Oded Barzelay for providing the algorithm for estimating characteristic frequency, Kameron Clayton for fitting the rabbit auditory nerve data, and Camille Shaw, Alice Gelman, and Joseph Wagner for assisting with surgeries.
REFERENCES
- Adams JC. Ascending projections to the inferior colliculus. J Comp Neurol 183: 519–538, 1979. doi: 10.1002/cne.901830305. [DOI] [PubMed] [Google Scholar]
- Bartlett EL, Wang X. Neural representations of temporally modulated signals in the auditory thalamus of awake primates. J Neurophysiol 97: 1005–1017, 2007. doi: 10.1152/jn.00593.2006. [DOI] [PubMed] [Google Scholar]
- Batra R, Kuwada S, Stanford TR. Temporal coding of envelopes and their interaural delays in the inferior colliculus of the unanesthetized rabbit. J Neurophysiol 61: 257–268, 1989. doi: 10.1152/jn.1989.61.2.257. [DOI] [PubMed] [Google Scholar]
- Bendor D, Wang X. The neuronal representation of pitch in primate auditory cortex. Nature 436: 1161–1165, 2005. doi: 10.1038/nature03867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein JG, Oxenham AJ. Pitch discrimination of diotic and dichotic tone complexes: harmonic resolvability or harmonic number? J Acoust Soc Am 113: 3323–3334, 2003. doi: 10.1121/1.1572146. [DOI] [PubMed] [Google Scholar]
- Bidelman G, Powers L. Response properties of the human frequency-following response (FFR) to speech and non-speech sounds: level dependence, adaptation and phase-locking limits. Int J Audiol 57: 665–672, 2018. doi: 10.1080/14992027.2018.1470338. [DOI] [PubMed] [Google Scholar]
- Bizley JK, Walker KM, Silverman BW, King AJ, Schnupp JW. Interdependent encoding of pitch, timbre, and spatial location in auditory cortex. J Neurosci 29: 2064–2075, 2009. doi: 10.1523/JNEUROSCI.4755-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bock GR, Webster WR. Spontaneous activity of single units in the inferior colliculus of anesthetized and unanesthetized cats. Brain Res 76: 150–154, 1974. doi: 10.1016/0006-8993(74)90521-6. [DOI] [PubMed] [Google Scholar]
- Borg E, Engström B, Linde G, Marklund K. Eighth nerve fiber firing features in normal-hearing rabbits. Hear Res 36: 191–201, 1988. doi: 10.1016/0378-5955(88)90061-5. [DOI] [PubMed] [Google Scholar]
- Bregman AS. Auditory Scene Analysis: The Perceptual Organization of Sound. Cambridge, MA: MIT Press, 1994. [Google Scholar]
- Burns EM, Viemeister NF. Nonspectral pitch. J Acoust Soc Am 60: 863, 1976. doi: 10.1121/1.381166. [DOI] [Google Scholar]
- Burns EM, Viemeister NF. Played‐again SAM: further observations on the pitch of amplitude‐modulated noise. J Acoust Soc Am 70: 1655, 1981. doi: 10.1121/1.387220. [DOI] [Google Scholar]
- Cariani PA, Delgutte B. Neural correlates of the pitch of complex tones. I. Pitch and pitch salience. J Neurophysiol 76: 1698–1716, 1996. doi: 10.1152/jn.1996.76.3.1698. [DOI] [PubMed] [Google Scholar]
- Carlyon RP, Deeks JM. Limitations on rate discrimination. J Acoust Soc Am 112: 1009–1025, 2002. doi: 10.1121/1.1496766. [DOI] [PubMed] [Google Scholar]
- Carney LH, Li T, McDonough JM. Speech coding in the brain: representation of vowel formants by midbrain neurons tuned to sound fluctuations. eNeuro 2: ENEURO.0004-15.2015, 2015. doi: 10.1523/ENEURO.0004-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cedolin L, Delgutte B. Pitch of complex tones: rate-place and interspike interval representations in the auditory nerve. J Neurophysiol 94: 347–362, 2005. doi: 10.1152/jn.01114.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cedolin L, Delgutte B. Spatiotemporal representation of the pitch of harmonic complex tones in the auditory nerve. J Neurosci 30: 12712–12724, 2010. doi: 10.1523/JNEUROSCI.6365-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung Y, Hancock KE, Nam SI, Delgutte B. Coding of electric pulse trains presented through cochlear implants in the auditory midbrain of awake rabbit: comparison with anesthetized preparations. J Neurosci 34: 218–231, 2014. doi: 10.1523/JNEUROSCI.2084-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cutting JE, Rosner BS. Categories and boundaries in speech and music. Percept Psychophys 16: 564–570, 1974. doi: 10.3758/BF03198588. [DOI] [Google Scholar]
- Day ML, Koka K, Delgutte B. Neural encoding of sound source location in the presence of a concurrent, spatially separated source. J Neurophysiol 108: 2612–2628, 2012. doi: 10.1152/jn.00303.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delgutte B, Gelman A, Chung Y. Rabbits can discriminate harmonic complexes with missing fundamentals (Abstract). Association for Research in Otolaryngology Annual Midwinter Meeting San Diego, CA, February 10–14 2018, p. 797. [Google Scholar]
- Delgutte B, Hammond B, Cariani P. Neural coding of the temporal envelope of speech: relation to modulation transfer functions. In: Psychophysical and physiological advances in hearing, edited by Palmer AR, Rees A, Summerfield AQ, Meddis R. London: Whurr, 1998, p. 595–603. [Google Scholar]
- Devore S, Delgutte B. Effects of reverberation on the directional sensitivity of auditory neurons across the tonotopic axis: influences of interaural time and level differences. J Neurosci 30: 7826–7837, 2010. doi: 10.1523/JNEUROSCI.5517-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock KE, Chung Y, Delgutte B. Neural ITD coding with bilateral cochlear implants: effect of binaurally coherent jitter. J Neurophysiol 108: 714–728, 2012. doi: 10.1152/jn.00269.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock KE, Noel V, Ryugo DK, Delgutte B. Neural coding of interaural time differences with bilateral cochlear implants: effects of congenital deafness. J Neurosci 30: 14068–14079, 2010. doi: 10.1523/JNEUROSCI.3213-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heffner H, Masterton B. Hearing in glires: domestic rabbit, cotton rat, feral house mouse, and kangaroo rat. J Acoust Soc Am 68: 1584, 1980. doi: 10.1121/1.385213. [DOI] [Google Scholar]
- Heffner HE, Heffner RS. Hearing ranges of laboratory animals. J Am Assoc Lab Anim Sci 46: 20–22, 2007. [PubMed] [Google Scholar]
- Heffner RS, Heffner HE. Hearing range of the domestic cat. Hear Res 19: 85–88, 1985. doi: 10.1016/0378-5955(85)90100-5. [DOI] [PubMed] [Google Scholar]
- Henry KS, Abrams KS, Forst J, Mender MJ, Neilans EG, Idrobo F, Carney LH. Midbrain synchrony to envelope structure supports behavioral sensitivity to single-formant vowel-like sounds in noise. J Assoc Res Otolaryngol 18: 165–181, 2017. doi: 10.1007/s10162-016-0594-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henry KS, Kale S, Heinz MG. Noise-induced hearing loss increases the temporal precision of complex envelope coding by auditory-nerve fibers. Front Syst Neurosci 8: 20, 2014. doi: 10.3389/fnsys.2014.00020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hewitt MJ, Meddis R. A computer model of amplitude-modulation sensitivity of single units in the inferior colliculus. J Acoust Soc Am 95: 2145–2159, 1994. doi: 10.1121/1.408676. [DOI] [PubMed] [Google Scholar]
- Houtsma AJ, Smurzynski J. Pitch identification and discrimination for complex tones with many harmonics. J Acoust Soc Am 87: 304, 1990. doi: 10.1121/1.399297. [DOI] [Google Scholar]
- Huang C, Rinzel J. A neuronal network model for pitch selectivity and representation. Front Comput Neurosci 10: 57, 2016. doi: 10.3389/fncom.2016.00057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutcheon B, Yarom Y. Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci 23: 216–222, 2000. doi: 10.1016/S0166-2236(00)01547-2. [DOI] [PubMed] [Google Scholar]
- Joris PX, Schreiner CE, Rees A. Neural processing of amplitude-modulated sounds. Physiol Rev 84: 541–577, 2004. doi: 10.1152/physrev.00029.2003. [DOI] [PubMed] [Google Scholar]
- Joris PX, van de Sande B, Recio-Spinoso A, van der Heijden M. Auditory midbrain and nerve responses to sinusoidal variations in interaural correlation. J Neurosci 26: 279–289, 2006. doi: 10.1523/JNEUROSCI.2285-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kale S, Heinz MG. Envelope coding in auditory nerve fibers following noise-induced hearing loss. J Assoc Res Otolaryngol 11: 657–673, 2010. doi: 10.1007/s10162-010-0223-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kendall MG, Gibbons JD. Rank Correlation Methods. Oxford, UK: Oxford Univ. Press, 1990. [Google Scholar]
- Kiang NY, Moxon EC. Tails of tuning curves of auditory-nerve fibers. J Acoust Soc Am 55: 620–630, 1974. doi: 10.1121/1.1914572. [DOI] [PubMed] [Google Scholar]
- Kiang NY, Watanabe T, Thomas EC, Clark LF. Discharge Patterns of Single Fibers in the Cat’s Auditory Nerve. Cambridge, MA: MIT Press, 1965. [Google Scholar]
- Krips R, Furst M. Stochastic properties of coincidence-detector neural cells. Neural Comput 21: 2524–2553, 2009. doi: 10.1162/neco.2009.07-07-563. [DOI] [PubMed] [Google Scholar]
- Krishna BS, Semple MN. Auditory temporal processing: responses to sinusoidally amplitude-modulated tones in the inferior colliculus. J Neurophysiol 84: 255–273, 2000. doi: 10.1152/jn.2000.84.1.255. [DOI] [PubMed] [Google Scholar]
- Krumbholz K, Patterson RD, Pressnitzer D. The lower limit of pitch as determined by rate discrimination. J Acoust Soc Am 108: 1170–1180, 2000. doi: 10.1121/1.1287843. [DOI] [PubMed] [Google Scholar]
- Kuwada S, Batra R, Stanford TR. Monaural and binaural response properties of neurons in the inferior colliculus of the rabbit: effects of sodium pentobarbital. J Neurophysiol 61: 269–282, 1989. doi: 10.1152/jn.1989.61.2.269. [DOI] [PubMed] [Google Scholar]
- Kuwada S, Batra R, Yin TC, Oliver DL, Haberly LB, Stanford TR. Intracellular recordings in response to monaural and binaural stimulation of neurons in the inferior colliculus of the cat. J Neurosci 17: 7565–7581, 1997. doi: 10.1523/JNEUROSCI.17-19-07565.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuwada S, Stanford TR, Batra R. Interaural phase-sensitive units in the inferior colliculus of the unanesthetized rabbit: effects of changing frequency. J Neurophysiol 57: 1338–1360, 1987. doi: 10.1152/jn.1987.57.5.1338. [DOI] [PubMed] [Google Scholar]
- Langner G, Schreiner C, Merzenich MM. Covariation of latency and temporal resolution in the inferior colliculus of the cat. Hear Res 31: 197–201, 1987. doi: 10.1016/0378-5955(87)90127-4. [DOI] [PubMed] [Google Scholar]
- Langner G, Schreiner CE. Periodicity coding in the inferior colliculus of the cat. I. Neuronal mechanisms. J Neurophysiol 60: 1799–1822, 1988. doi: 10.1152/jn.1988.60.6.1799. [DOI] [PubMed] [Google Scholar]
- Laudanski J, Torben-Nielsen B, Segev I, Shamma S. Spatially distributed dendritic resonance selectively filters synaptic input. PLoS Comput Biol 10: e1003775, 2014. doi: 10.1371/journal.pcbi.1003775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeBeau FE, Malmierca MS, Rees A. Iontophoresis in vivo demonstrates a key role for GABAA and glycinergic inhibition in shaping frequency response areas in the inferior colliculus of guinea pig. J Neurosci 21: 7303–7312, 2001. doi: 10.1523/JNEUROSCI.21-18-07303.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Licklider J. Audio frequency analysis. In: Information Theory, edited by Cherry C. London: Butterworth, 1956, p. 253–268. [Google Scholar]
- Liu LF, Palmer AR, Wallace MN. Phase-locked responses to pure tones in the inferior colliculus. J Neurophysiol 95: 1926–1935, 2006. doi: 10.1152/jn.00497.2005. [DOI] [PubMed] [Google Scholar]
- Lu T, Liang L, Wang X. Temporal and rate representations of time-varying signals in the auditory cortex of awake primates. Nat Neurosci 4: 1131–1138, 2001. doi: 10.1038/nn737. [DOI] [PubMed] [Google Scholar]
- Macherey O, Carlyon RP. Re-examining the upper limit of temporal pitch. J Acoust Soc Am 136: 3186–3199, 2014. doi: 10.1121/1.4900917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malmierca MS, Saint Marie RL, Merchan MA, Oliver DL. Laminar inputs from dorsal cochlear nucleus and ventral cochlear nucleus to the central nucleus of the inferior colliculus: two patterns of convergence. Neuroscience 136: 883–894, 2005. doi: 10.1016/j.neuroscience.2005.04.040. [DOI] [PubMed] [Google Scholar]
- Middlebrooks JC, Snyder RL. Selective electrical stimulation of the auditory nerve activates a pathway specialized for high temporal acuity. J Neurosci 30: 1937–1946, 2010. doi: 10.1523/JNEUROSCI.4949-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller CA, Robinson BK, Rubinstein JT, Abbas PJ, Runge-Samuelson CL. Auditory nerve responses to monophasic and biphasic electric stimuli. Hear Res 151: 79–94, 2001. doi: 10.1016/s0300-2977(00)00082-6. [DOI] [PubMed] [Google Scholar]
- Moore BC. The role of temporal fine structure processing in pitch perception, masking, and speech perception for normal-hearing and hearing-impaired people. J Assoc Res Otolaryngol 9: 399–406, 2008. doi: 10.1007/s10162-008-0143-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nataraj K, Wenstrup JJ. Roles of inhibition in complex auditory responses in the inferior colliculus: inhibited combination-sensitive neurons. J Neurophysiol 95: 2179–2192, 2006. doi: 10.1152/jn.01148.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson PC, Carney LH. A phenomenological model of peripheral and central neural responses to amplitude-modulated tones. J Acoust Soc Am 116: 2173–2186, 2004. doi: 10.1121/1.1784442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson PC, Carney LH. Neural rate and timing cues for detection and discrimination of amplitude-modulated tones in the awake rabbit inferior colliculus. J Neurophysiol 97: 522–539, 2007. doi: 10.1152/jn.00776.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osmanski MS, Song X, Wang X. The role of harmonic resolvability in pitch perception in a vocal nonhuman primate, the common marmoset (Callithrix jacchus). J Neurosci 33: 9161–9168, 2013. doi: 10.1523/JNEUROSCI.0066-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oxenham AJ. Pitch perception and auditory stream segregation: implications for hearing loss and cochlear implants. Trends Amplif 12: 316–331, 2008. doi: 10.1177/1084713808325881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oxenham AJ. How we hear: the perception and neural coding of sound. Annu Rev Psychol 69: 27–50, 2018. doi: 10.1146/annurev-psych-122216-011635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng F, Innes-Brown H, McKay CM, Fallon JB, Zhou Y, Wang X, Hu N, Hou W. Temporal coding of voice pitch contours in mandarin tones. Front Neural Circuits 12: 55, 2018. doi: 10.3389/fncir.2018.00055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plack CJ, Oxenham AJ. Overview: the present and future of pitch. In: Pitch, edited by Plack CJ, Oxenham AJ, Fay RR, Popper AN. New York: Springer, 2005a, p. 1–6. [Google Scholar]
- Plack CJ, Oxenham AJ. The psychophysics of pitch. In: Pitch, edited by Plack CJ, Oxenham AJ, Fay RR, Popper AN. New York: Springer, 2005b, p. 7–55. [Google Scholar]
- Pressnitzer D, Patterson RD, Krumbholz K. The lower limit of melodic pitch. J Acoust Soc Am 109: 2074–2084, 2001. doi: 10.1121/1.1359797. [DOI] [PubMed] [Google Scholar]
- Rees A, Møller AR. Responses of neurons in the inferior colliculus of the rat to AM and FM tones. Hear Res 10: 301–330, 1983. doi: 10.1016/0378-5955(83)90095-3. [DOI] [PubMed] [Google Scholar]
- Rhode WS. Interspike intervals as a correlate of periodicity pitch in cat cochlear nucleus. J Acoust Soc Am 97: 2414–2429, 1995. doi: 10.1121/1.411963. [DOI] [PubMed] [Google Scholar]
- Robles L, Ruggero MA. Mechanics of the mammalian cochlea. Physiol Rev 81: 1305–1352, 2001. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodríguez FA, Read HL, Escabí MA. Spectral and temporal modulation tradeoff in the inferior colliculus. J Neurophysiol 103: 887–903, 2010. doi: 10.1152/jn.00813.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosowski JJ. Outer and middle ears. In: Comparative Hearing: Mammals, edited by Fay RR, Popper AN. New York: Springer, 1994, p. 172–247. [Google Scholar]
- Ruggero MA, Temchin AN. The roles of the external, middle, and inner ears in determining the bandwidth of hearing. Proc Natl Acad Sci USA 99: 13206–13210, 2002. doi: 10.1073/pnas.202492699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnupp JW, Garcia-Lazaro JA, Lesica NA. Periodotopy in the gerbil inferior colliculus: local clustering rather than a gradient map. Front Neural Circuits 9: 37, 2015. doi: 10.3389/fncir.2015.00037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schouten JF. The perception of subjective tones. Proc Koninklijke Nederlandse Akademie Wetenschappen 41: 1086–1093, 1938. [Google Scholar]
- Shepherd RK, Javel E. Electrical stimulation of the auditory nerve: II. Effect of stimulus waveshape on single fibre response properties. Hear Res 130: 171–188, 1999. doi: 10.1016/s0378-5955(99)00011-8. [DOI] [PubMed] [Google Scholar]
- Shackleton TM, Carlyon RP. The role of resolved and unresolved harmonics in pitch perception and frequency modulation discrimination. J Acoust Soc Am 95: 3529–3540, 1994. doi: 10.1121/1.409970. [DOI] [PubMed] [Google Scholar]
- Shackleton TM, Liu LF, Palmer AR. Responses to diotic, dichotic, and alternating phase harmonic stimuli in the inferior colliculus of guinea pigs. J Assoc Res Otolaryngol 10: 76–90, 2009. doi: 10.1007/s10162-008-0149-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shofner WP, Chaney M. Processing pitch in a nonhuman mammal (Chinchilla laniger). J Comp Psychol 127: 142–153, 2013. doi: 10.1037/a0029734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siedenburg K. Specifying the perceptual relevance of onset transients for musical instrument identification. J Acoust Soc Am 145: 1078–1087, 2019. doi: 10.1121/1.5091778. [DOI] [PubMed] [Google Scholar]
- Sinex DG, Henderson J, Li H, Chen GD. Responses of chinchilla inferior colliculus neurons to amplitude-modulated tones with different envelopes. J Assoc Res Otolaryngol 3: 390–402, 2002a. doi: 10.1007/s101620020026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinex DG, Li H. Responses of inferior colliculus neurons to double harmonic tones. J Neurophysiol 98: 3171–3184, 2007. doi: 10.1152/jn.00516.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinex DG, Sabes JH, Li H. Responses of inferior colliculus neurons to harmonic and mistuned complex tones. Hear Res 168: 150–162, 2002b. doi: 10.1016/S0378-5955(02)00366-0. [DOI] [PubMed] [Google Scholar]
- Su Y, Delgutte B. Pitch of harmonic complex tones: rate coding of envelope repetition rate in the auditory midbrain. Acta Acust United Acust 104: 860–864, 2018. doi: 10.3813/AAA.919239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su Y, Delgutte B. Pitch of harmonic complex tones: rate-place coding of resolved components in harmonic and inharmonic complex tones in auditory midbrain (Preprint). bioRxiv 802827, 2019. doi: 10.1101/8027 [DOI] [PMC free article] [PubMed]
- Sumner CJ, Wells TT, Bergevin C, Sollini J, Kreft HA, Palmer AR, Oxenham AJ, Shera CA. Mammalian behavior and physiology converge to confirm sharper cochlear tuning in humans. Proc Natl Acad Sci USA 115: 11322–11326, 2018. doi: 10.1073/pnas.1810766115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Honert C, Stypulkowski PH. Single fiber mapping of spatial excitation patterns in the electrically stimulated auditory nerve. Hear Res 29: 195–206, 1987. doi: 10.1016/0378-5955(87)90167-5. [DOI] [PubMed] [Google Scholar]
- Verschooten E, Desloovere C, Joris PX. High-resolution frequency tuning but not temporal coding in the human cochlea. PLoS Biol 16: e2005164, 2018. doi: 10.1371/journal.pbio.2005164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker KM, Gonzalez R, Kang JZ, McDermott JH, King AJ. Across-species differences in pitch perception are consistent with differences in cochlear filtering. eLife 8: e41626, 2019. doi: 10.7554/eLife.41626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winer JA, Schreiner CE (Editors). The central auditory system: a functional analysis. In: The Inferior Colliculus. New York: Springer, 2005, p. 1–68. [Google Scholar]
- Winter IM. The neurophysiology of pitch. In: Pitch, edited by Plack CJ, Oxenham AJ, Fay RR, Popper AN. New York: Springer, 2005, p. 99–146. [Google Scholar]
- Winter IM, Palmer AR, Wiegrebe L, Patterson RD. Temporal coding of the pitch of complex sounds by presumed multipolar cells in the ventral cochlear nucleus. Speech Commun 41: 135–149, 2003. doi: 10.1016/S0167-6393(02)00098-5. [DOI] [Google Scholar]
- Zhang H, Kelly JB. Glutamatergic and GABAergic regulation of neural responses in inferior colliculus to amplitude-modulated sounds. J Neurophysiol 90: 477–490, 2003. doi: 10.1152/jn.01084.2002. [DOI] [PubMed] [Google Scholar]
- Zheng Y, Escabí MA. Distinct roles for onset and sustained activity in the neuronal code for temporal periodicity and acoustic envelope shape. J Neurosci 28: 14230–14244, 2008. doi: 10.1523/JNEUROSCI.2882-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y, Escabí MA. Proportional spike-timing precision and firing reliability underlie efficient temporal processing of periodicity and envelope shape cues. J Neurophysiol 110: 587–606, 2013. doi: 10.1152/jn.01080.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zilany MS, Bruce IC, Carney LH. Updated parameters and expanded simulation options for a model of the auditory periphery. J Acoust Soc Am 135: 283–286, 2014. doi: 10.1121/1.4837815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zilany MS, Bruce IC, Nelson PC, Carney LH. A phenomenological model of the synapse between the inner hair cell and auditory nerve: long-term adaptation with power-law dynamics. J Acoust Soc Am 126: 2390–2412, 2009. doi: 10.1121/1.3238250. [DOI] [PMC free article] [PubMed] [Google Scholar]