Abstract
Nitrogen-vacancy (NV) centers in diamond are reliable single-photon emitters, with applications in quantum technologies and metrology. Two charge states are known for NV centers, NV0 and NV–, with the latter being mostly studied due to its long electron spin coherence time. Therefore, control over the charge state of the NV centers is essential. However, an understanding of the dynamics between the different states still remains challenging. Here, conversion from NV– to NV0 due to electron-induced carrier generation is shown. Ultrafast pump–probe cathodoluminescence spectroscopy is presented for the first time, with electron pulses as pump and laser pulses as probe, to prepare and read out the NV states. The experimental data are explained with a model considering carrier dynamics (0.8 ns), NV0 spontaneous emission (20 ns), and NV0 → NV– back transfer (500 ms). The results provide new insights into the NV– → NV0 conversion dynamics and into the use of pump–probe cathodoluminescence as a nanoscale NV characterization tool.
Keywords: nitrogen-vacancy centers, cathodoluminescence, carrier dynamics, ultrafast electron microscopy, state conversion
Nitrogen-vacancy (NV) centers in diamond are promising elements for quantum optical systems since they are single-photon emitters1,2 with high photostability, quantum yield, and brightness, even at room temperature.3−6 Moreover, they are integrated inside a wide-bandgap solid-state host, the diamond lattice, making them robust against decoherence and allowing device scalability.7−9 NV centers exhibit two different configurational states, the NV0 state, with a zero-phonon line (ZPL) at 2.156 eV (λ = 575 nm), and the NV– state, with a ZPL at 1.945 eV (λ = 637 nm).2 NV centers in the NV– state have received most of the attention in the past years since they exhibit a long electron spin coherence time that can be optically manipulated and read out,9,10 which, together with the characteristics mentioned previously, make them suitable as building blocks for quantum technologies,9,11,12 nanoscale magnetometry,13,14 and other applications.15,16 Typically, synthetically prepared diamonds with NV centers contain both NV0 and NV– states. Previous work has shown that the state of an NV center can be converted from NV– to NV0 (ionization) and vice versa (recombination). For example, the state of the NV centers can be changed by laser irradiation,17−19 as well as by shifting the Fermi level, either chemically20−22 or by applying an external voltage.23,24 Overall, the control and understanding of NV state dynamics is key to the development of efficient quantum optical systems based on NV centers.
So far, most work on NV characterization and state conversion dynamics has focused on optical excitation and readout of the NV state. However, NV centers can also be excited by high-energy (1–200 keV) electrons, using either a scanning or transmission electron microscope (SEM or TEM), while the emitted cathodoluminescence (CL) is collected. Given the small electron beam spot size, the study of NV centers with electron excitation allows for a spatial resolution only limited by the diffusion of carriers, which can be down to the nanometer scale.25 This opens the possibility to directly excite NV centers in nanodiamonds with high spatial resolution26 and study the coupling of locally excited nanostructures to NV centers,27,28 among others. Furthermore, NV centers are good platforms to study the fundamentals of quantum optics with electrons, in contrast to optical measurements. Electron-beam excitation of NV centers involves a multistep process, in which the primary electron beam inelastically interacts with the diamond lattice, creating bulk plasmons that decay by generating charge carriers.29−31 These carriers then diffuse through the diamond and recombine, partially through the excitation of NV centers. Single-photon emission of individual NV centers excited with electrons has already been demonstrated using measurements of the CL photon autocorrelation function (g(2)).26 Interestingly, in CL experiments typically only emission from the NV0 state is observed,25,26,32−37 with one exception,32 in which a very small NV– CL signal was observed at low temperature (16 K). This raises the question whether (1) the electron beam does not excite NV centers in the NV– state, (2) the electron beam quenches the NV– transition, or (3) the electron beam converts NV centers from the NV– to the NV0 state. Answering this question is essential to understand the NV state dynamics in general and to further exploit the use of CL in nanoscale characterization of atomic defects acting as single-photon emitters.
In this paper we study the interaction of electrons with NV centers, and in particular their state conversion dynamics. We perform the experiments using pump–probe CL spectroscopy, a novel technique that allows studying excited-state dynamics at ultrafast time scales. Previous works combining electron and light excitations in a TEM include photon-induced near-field electron microscopy (PINEM),38,39 in which the electron gains or loses energy when interacting with the optically-induced near-field, and femtosecond Lorentz microscopy,40 in which the laser-induced magnetization dynamics are probed with the electrons. Similarly, photoinduced carrier dynamics have been studied in an SEM by analyzing the secondary electron yield after laser excitation.41 However, in these configurations the electron acts as a probe, since the signal is either transmitted or secondary electrons. In contrast, in pump–probe CL the final signal is the emitted light, either CL or photoluminescence (PL); therefore, the electron can also act as a pump. In this work, we use an ultrafast SEM in which picosecond electron pulses are used to pump the diamond sample, while synchronously we optically probe the NV state. The electron pulses are generated using a laser-driven cathode configuration, a technique initially demonstrated by Merano et al. using a gold cathode42 and further developed in combination with field-emission guns (FEGs) to improve the spatial and temporal resolution.43,44 After ultrafast excitation of the NV centers, the CL and PL spectra are collected for spectral and temporal characterization. We find that repeated pulsed electron excitation (5.04 MHz) causes a state conversion from NV– to NV0, until a steady state is achieved in which the electron-induced NV– → NV0 conversion is balanced by the reverse NV0 → NV– back transfer. The steady-state NV0 population under electron irradiation can be controlled by the number of electrons per pulse. We describe the results with a model that includes electron-induced carrier generation and diffusion, with the NV centers acting as carrier traps and electrons converting NV centers from the NV– to the NV0 state. The time dynamics of carrier diffusion (∼0.8 ns), NV0 decay (∼20 ns), and NV0 → NV– back transfer (∼500 ms) are clearly observed from the pump–probe transients.
Pump–Probe CL Setup
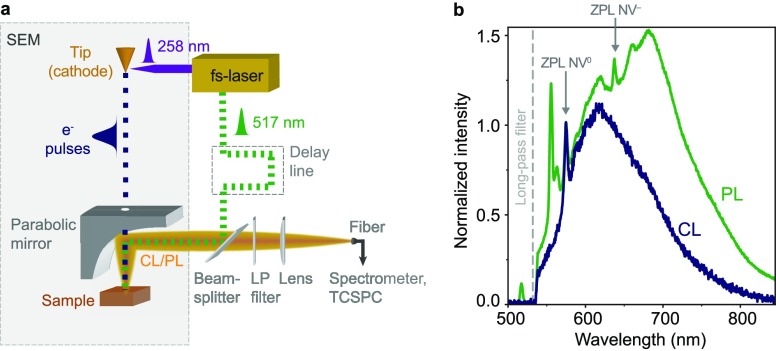
The pump–probe CL experiments are performed inside a SEM. We focus the fourth harmonic (λ = 258 nm) of an Yb-doped fiber fs laser on the electron gun to generate electron pulses by photoemission42,45 (Figure 1a). Photoemission of electron pulses using this setup was characterized previously,46 showing that the generated electron pulses are in the picosecond regime, similar to other work.44,47 The electron beam is focused on a single spot on the sample, corresponding to the center of the area irradiated by the laser beam. We synchronously excite the sample at the electron-irradiated region with second-harmonic (λ = 517 nm) pulses generated by the same fs laser, which are focused inside the SEM chamber to a ∼10 μm diameter spot on the sample using an Al parabolic mirror. The second harmonic path length can be tuned within a ±2 ns time window, such that the optical excitation pulse on the sample is delayed (or advanced) with respect to the electron pulse. CL and PL are collected by the parabolic mirror and directed to either a spectrometer or a time-correlated single photon counting (TCSPC) module. We use a 300 μm thick single-crystal diamond sample (obtained from Element 6 Inc.), grown by chemical-vapor deposition (<1 ppm nitrogen concentration, <0.05 ppm boron concentration), containing an approximate NV concentration of [NVtot] = 1.2 ppb (200 μm–3). The sample is coated with a thin charge dissipation layer (E-spacer 300) to avoid charging when exciting with the electron pulses.
Figure 1.
Pump–probe CL setup and NV center spectra. (a) Schematic of the pump–probe CL setup. The fourth harmonic (λ = 258 nm) of a fs laser is focused on the electron cathode to induce photoemission of electron pulses (0–400 electrons/pulse, picosecond temporal spread). The second harmonic (λ = 517 nm) of the same laser synchronously excites the sample to read out the NV state. The light pulse is delayed 1.3 ns with respect to the electron pulse. The emitted light, CL, PL, or both, is collected using a parabolic mirror and analyzed with a spectrometer or TCSPC module. A long-pass (LP, λ > 532 nm) filter is used to remove the light from the excitation laser. (b) Photoluminescence (green) and cathodoluminescence (blue) spectra obtained independently when exciting a bulk diamond sample with either a 517 nm pulsed laser beam (0.9 nJ/pulse) or a 5 keV pulsed electron beam (400 electrons/pulse), respectively. Both spectra are obtained when exciting with a repetition rate of 5.04 MHz and at the same position on the sample. CL and PL spectra have been normalized by the amplitude of the NV0 ZPL at 575 nm.
CL, PL, and Pump–Probe Measurements
Using the pump–probe CL setup, we acquire first PL and CL spectra, shown in Figure 1b. The PL spectrum shows emission from the ZPL of NV– (λ = 637 nm) and NV0 (λ = 575 nm), with both ZPL transitions accompanied by phonon replicas, forming a broadband spectrum in the 575–800 nm spectral range. A Raman peak at λ = 555 nm is also observed,48 as well as a peak around 563 nm, which has been observed in previous work and preliminarily attributed to a divacancy defect.37,49,50 The CL spectrum, obtained when exciting with a 5 keV pulsed electron beam, clearly shows the ZPL of the NV0 state, with phonon sideband, but no emission from the NV– state is observed, similar to previous work.25,26,32−37 The relative contribution of NV– and NV0 states to the PL spectrum is obtained by a fitting procedure, with the CL spectrum as a reference for the spectral shape of the NV0 emission (see Supporting Information). Using estimated optical absorption cross sections at the laser excitation wavelength (see Supporting Information) we derive the NV– and NV0 fractions: [NV–]/[NVtot] ≈ 0.4 and [NV0]/[NVtot] ≈ 0.6.
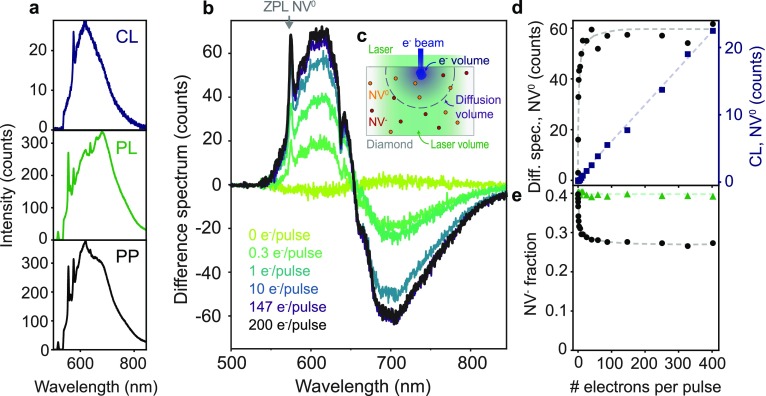
Our pump–probe measurements consist of the independent acquisition of a set of spectra: only CL, only PL, and pump–probe (PP). The latter is obtained under simultaneous electron and light excitation, with the light pulse arriving 1.3 ns after each electron pulse. A set of spectra is shown in Figure 2a. All measurements were performed at the same spot on the sample, to avoid effects due to concentration inhomogeneities. In addition to the differences in the PL and CL spectra mentioned above, we also observe that the PL signal is an order of magnitude higher than the CL one. Even though a detailed comparison between both magnitudes is complex due to the different incident powers and excitation mechanisms, we can estimate the number of NVs excited in each case. The laser spot size has a diameter of around 10 μm and large penetration depth, due to the low absorption of diamond and low NV concentration. Therefore, the volume is mostly determined by the collection volume of the setup (see Methods). The primary interaction volume of the 5 keV electron beam is around 0.4 μm3, as calculated from Monte Carlo-based simulations using the software Casino.51 Even though the effective volume is enlarged due to carrier diffusion, as will be shown below, it is still smaller than the volume excited by the laser. A sketch of both volumes is shown in Figure 2c. Taking into account the optical cross sections and collection geometry, we estimate that we collect PL from around 1.4 × 104 NVs per pulse for an incident power of 0.9 nJ (per pulse). Comparing the magnitude of the PL and CL signals, we can also extract that an average of 900 NV centers in the NV0 state are excited per electron pulse, in the steady-state situation, as will be discussed further on. In this case, each electron pulse contained 400 electrons with 5 keV energy (corresponding to 0.32 pJ per pulse).
Figure 2.
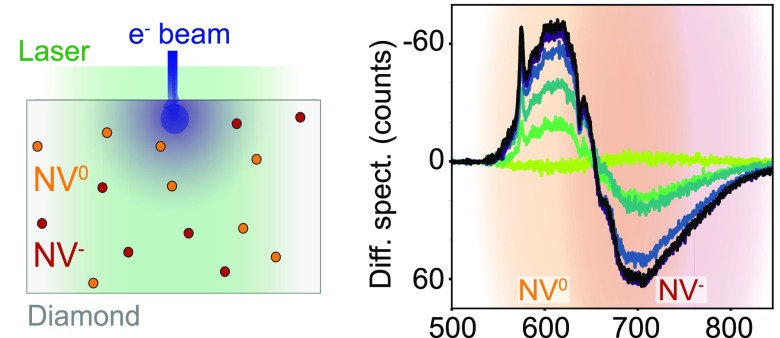
NV– → NV0 conversion under electron excitation (a) Top: CL spectrum (5 keV, 400 electrons/pulse), middle: PL spectrum (λ = 517 nm, 0.9 nJ/pulse), bottom: pump–probe (PP) spectrum obtained when both electrons and light (same conditions as before) excite the sample (5.04 MHz). The acquisition time was 1 min in all cases. (b) Difference spectrum, obtained by subtracting CL and PL spectra from the PP spectrum. (c) Sketch of the laser and electron excitation on the sample, representing the different volumes of primary electron interaction, diffusion of carriers, and laser volume. (d) NV0 ZPL intensity (λ = 575 nm) of the difference spectrum (black circles) and from the CL-only spectrum (blue squares) as a function of the average number of electrons per pulse. The NV0 ZPL of the difference spectrum shows saturation at around 20 electrons/pulse, while in the case of CL the dependence is linear. Dashed lines are shown as guides for the eye. (e) NV– fraction obtained from the PP as a function of the number of electrons per pulse (black circles). The green triangles indicate the NV– fraction derived from the PL spectra (all at the same PL pump power). Dashed lines are guides for the eye.
Using the PL, CL, and PP spectra shown above, we can analyze the effect of electron irradiation on NV centers. We define the quantity of a difference spectrum, obtained when subtracting CL and PL spectra from the PP spectrum. This analysis allows to study the correlation between electron and light excitation of the NV centers. Therefore, no correlation would lead to a flat difference spectrum. Instead, the difference spectrum obtained from the data in Figure 2a exhibits clear features, as shown in Figure 2b (black curve). We observe an increase of the signal (positive counts) in the lower-wavelength spectral band, corresponding to the NV0 emission. As a reference, we observe a clear peak corresponding to the NV0 ZPL. We also observe a concomitant decrease in the longer-wavelength band, corresponding to NV– emission. In this case, the NV– ZPL is visible as a dip. This implies that after electron excitation the number of emitting NV0 centers is increased, while the number of NV– centers is decreased. The results suggest that centers in the NV– states are converted into NV0 states under electron irradiation, corresponding to hypothesis (3) exposed earlier in the text. Difference spectra derived for different sets of measurements at 0.3, 1, 10, and 147 electrons per pulse are also shown in Figure 2b, as well as a reference measurement (no electron irradiation). Each set of measurements corresponds to the acquisition of independent CL, PL, and PP spectra, in which the number of electrons per pulse is varied, while keeping the laser excitation power constant at 0.9 nJ per pulse. We again observe NV– → NV0 conversion, with the number of converted centers rising for increasing average number of electrons per pulse. This behavior in the difference spectra was consistently observed in other measurements at different areas of the sample and also with other electron energies (30 keV, Figure S1).
To further investigate the electron-induced NV– → NV0 conversion trend, we plot the amplitude of the NV0 ZPL as a function of the number of electrons per pulse (Figure 2d). Saturation of the signal from the NV0 ZPL is observed above ∼20 electrons per pulse, suggesting that this is the required electron flux (at 5.04 MHz) to induce the saturation of the NV– conversion in the volume of the sample excited by electrons. For reference, Figure 2d also shows the CL intensity for the NV0 ZPL as a function of the number of electrons per pulse. The plot shows a linear trend, indicating that the NV0 CL signal is not saturating with increasing electron dose; that is, there is no strong depletion of the ground-state population. Therefore, from these results we derive that electrons can either excite NV centers in the NV0 state, which leads to a linear dependence on the electron flux, or convert NV– into NV0, which saturates with increasing number of electrons per pulse.
From the data in Figure 2b we can also derive the NV– population as a function of the number of electrons per pulse, as plotted in Figure 2e. This derivation is done by fitting the NV0 and NV– contributions from the PP measurements (see Supporting Information). Starting from the initial NV– fraction of 0.4 for the reference measurement, as already derived before, the population of centers in the NV– state rapidly decreases with increasing number of electrons per pulse, reaching a saturation level corresponding to a 0.26 NV– fraction. We attribute this saturation level to the full conversion of NV– centers into NV0 centers within the volume excited by the electrons, as will be discussed further on. The fact that the NV– fraction does not reach zero at saturation is attributed to the difference between excitation and collection volumes of electron and laser beam, as sketched in Figure 2c. For completeness, in Figure 2e we also show the NV– fraction derived from the PL measurements taken in each set of measurements from Figure 2b. We observe that the NV– fraction under only laser irradiation remains approximately constant, meaning that the NV– population before each set of measurements is identical. The fact that the NV– population is unchanged also implies that the electron-induced NV– → NV0 conversion is reversible, i.e., there is an NV0 → NV– back transfer process, and that damage induced by the electron to the sample is negligible. Given that NV– ↔ NV0 conversion has also been observed due only to laser irradiation,17−19 we also acquired PL spectra at different incident powers. The results are presented in Figure S2 and show that the NV– fraction remains constant for increasing laser power, therefore proving that NV conversion due to only laser irradiation is negligible in our experiment. Pump–probe measurements with different delays between electron and light were also acquired (Figure S3), but no significant differences are observed. This is attributed to the fact that the NV0 → NV– back transfer is on the order of milliseconds, as will be demonstrated below, larger than the time between pulses (198 ns at 5.04 MHz).
Excitation, Emission, and Conversion Dynamics
In order to further describe the interaction of electrons with NV centers, we study the excitation and emission dynamics of NV centers at the nanosecond time scale, as well as the NV0 → NV– back transfer that occurs in the millisecond scale. The time-dependent CL emission from NV centers upon electron excitation is shown in Figure 3a, which has been measured using the TCSPC technique. Notice that the CL intensity corresponds only to emission from excited NV0 centers, given that NV– emission is not probed with CL. The CL signal exhibits a gradual increase in the first 2 ns, reaching a maximum emission at around 2.2 ns (see inset). We ascribe this initial increase to the diffusion of carriers beyond the primary electron-excited volume, which increases the excited NV0 population well after the initial ps-electron pulse excitation. After the first 2 ns we observe a decay of the CL intensity, from which we extract a characteristic decay time of ∼20 ns, in agreement with the typical radiative decay time of excited NV0 centers.26,52 We also observe a ∼100 ps spike at 0 ns, which accounts for around 1% of the total intensity. The origin of this fast decay is unknown. The intensity of this peak depends on the position on the sample, as well as electron energy. Nevertheless, the amplitude of this peak does not show any correlation with the magnitude of the NV– → NV0 conversion, from which we infer that both effects are unrelated.
Figure 3.
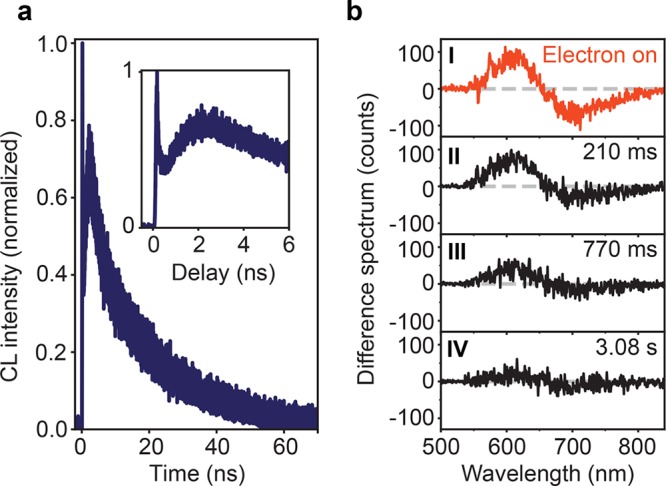
Carrier diffusion, excitation, and back transfer dynamics. (a) Peak-normalized CL intensity upon pulsed electron excitation (5 keV, ∼450 electrons/pulse, 5.04 MHz) at t = 0 ns, measured with time-correlated single-photon counting. Data are taken in the NV0 575–725 nm spectral band. Inset: enlarged early time scale. (b) Difference spectrum (defined as PP–CL–PL) obtained with the electron beam on (I) and 210 ms, 770 ms, and 3.08 s after the electron beam was blanked (II–IV, respectively). The NV0 → NV– back transfer takes around 500 ms. The time resolution of this experiment is 70 ms.
In contrast to the fast carrier diffusion and NV0 emission dynamics, previous studies of optically induced NV0 ↔ NV– conversion suggest that the NV0 → NV– back transfer is in the millisecond regime.17 To study this, we performed time-resolved spectral measurements over a millisecond time scale. We used the minimum exposure time possible in our spectrometer, acquiring a spectrum every 70 ms. The repetition rate is kept at 5.04 MHz, as in the previous experiments. We performed a spectral acquisition sequence in which initially both the electron and laser beam were irradiating the sample (PP spectrum). At some point during the acquisition, the electron beam was blanked, while the laser continued exciting the sample, and spectra kept being collected every 70 ms. In this way, the NV population can be probed immediately after the electron beam is switched off. Afterward, we also acquired CL and PL spectra with the same exposure time, such that a difference spectrum can be derived, similar to Figure 2b. An example of the obtained difference spectrum is shown in Figure 3b-I, which again reflects the NV– → NV0 conversion by the electron-excited carriers. In this case, the electron beam was still irradiating the sample. Figure 3b-II shows the difference spectrum obtained 210 ms after switching off the electron beam. Notice that here the difference spectrum is obtained by subtracting only PL from the PP measurement, given that there is no CL. We observe a 30% decrease of the intensity of the difference spectrum, indicating that most of the converted NV– centers still remain in the NV0 state, and only some have converted back into NV–. Results after 770 ms and 3.08 s are also plotted (Figure 3b-III,IV), in which we observe a progressive decay of the signal, indicating that NV0 centers are converted back to the NV– state. A complete transient of the average signal in the difference spectrum as a function of time is provided in Figure S4. These data indicate that the electron-induced NV– → NV0 state conversion is reversible, with the back transfer taking place within a characteristic time of ∼500 ms. This time scale is in agreement with earlier work, in which back transfer of optically induced NV– → NV0 conversion was found to occur with a characteristic time of 465 ms.17
Discussion and Phenomenological Model
Optically induced state conversion from NV– to NV0 has been previously explained to take place by the release of an electron from the NV– center to the conduction band of diamond.19,52−54 Literature values for the difference in energy between the NV– ground state and the conduction band range from 2.6 to 4.3 eV,17,19,52 and the NV–/NV0 optical conversion typically requires a two-photon absorption process. In our experiment, we propose a model in which electron–hole pairs generated from the electron cascade can recombine, thus providing the energy to induce the release of the bound electron from the NV– center, given that the bandgap of diamond is 5.5 eV. This conversion mechanism is similar to that in optical experiments, with the difference that the energy is provided by a carrier recombination event instead of two pump photons. This model is in agreement with previous work in which emission only from the NV0 state was observed when exciting with far-UV photons (λ = 170 nm, above the bandgap of diamond)55 and in electroluminescence.56,57 In both cases, charge carriers are generated and NV centers are excited through the recombination of carriers, similar to CL. In addition to this, the energy provided by a single carrier recombination event is larger than the energy needed to induce the NV– → NV0 conversion, suggesting that a single carrier recombination event could already release the electron, without the need to first excite the NV– center as in the case of optical experiments.19,52−54 The latter suggestion requires further studies in the mechanism of NV– → NV0 conversion by carrier recombination, which are beyond the scope of this paper.
To qualitatively analyze the data shown above, we model the electron-induced NV– → NV0 state conversion by means of a three-dimensional model, considering carrier diffusion and NV center conversion and excitation. We start by modeling the dynamics in the nanosecond regime, corresponding to carrier diffusion and NV0 decay. We use Monte Carlo simulations, using the software Casino,51 to obtain the three-dimensional spatial distribution of inelastic scattering events of the primary 5 keV electron beam. Most of the energy lost by the electron corresponds to the generation of bulk plasmons, described as excitations of the outer-shell electrons,29 with an energy corresponding to 31 eV for diamond.30 We then model the initial carrier distribution with a 3D Gaussian distribution, with standard deviation σ = 0.185 μm estimated from the plasmon distribution derived from Casino simulations and amplitude proportional to the number of electrons per pulse. We assume that each bulk plasmon effectively generates an average of two electron–hole pairs.30 The concentration of charge carriers as a function of time and space (ρeh(r, t)) is then obtained by solving the diffusion equation, with carrier recombination described with a lifetime τR.
Taking into account carrier diffusion, we model the concentration of NV– in the ground state (ρ–) and NV0 in the ground (ρ0g) and excited (ρ0) states by means of a rate equation model:
| 1a |
| 1b |
| 1c |
where vth is the thermal velocity of carriers, σ0eh is the cross-section to excite NV0 states by carriers, σc is the NV– → NV0 conversion cross-section, τ0 is the lifetime of the excited NV0 state, τback accounts for the NV0 → NV– back transfer, and ρ–i is the initial uniform concentration of NV–. In this model we assume that NV0 states can be excited by carriers, but NV– states cannot, given that we do not observe NV– signal in the CL measurements. Moreover, the interaction of the primary electron beam (picosecond temporal spread) with the sample, including generation of bulk plasmons and decay into carriers, is treated as instantaneous, given that it is much shorter than the characteristic time scale of the dynamics in eqs 1a–1c.
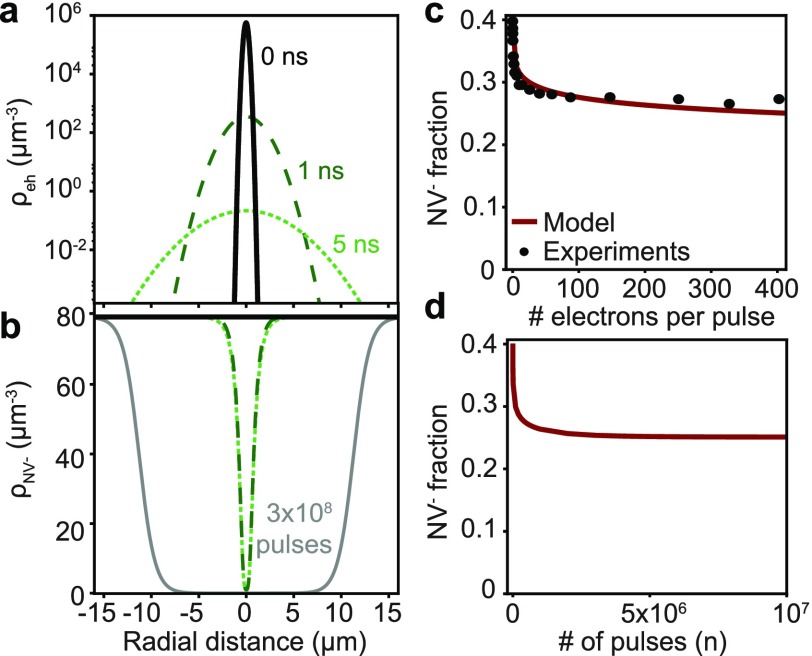
Numerically solving the system of differential equations over time, and integrating ρ0e(r, t) over the collection volume, allows to fit the trend in the first 2 ns of the time-dependent CL intensity shown in Figure 3a. The carrier lifetime derived from the fit is τR = 0.8 ns, corresponding to a diffusion length of 0.9 μm, which is in agreement with values reported for samples with a similar concentration of NV centers.58 From the model we also find that excitation with 400 electrons (5 keV) leads to about 740 NV0 centers excited per pulse, close to the value independently derived from the comparison of PL and CL intensities in Figure 2a,b. Taking into account the obtained carrier lifetime, in Figure 4a we plot the spatial distribution of the carrier concentration at t = 0 ns (solid black) and after 1 and 5 ns (dashed dark green and dotted light green, respectively), obtained from the expression of ρeh(r, t) (eq S1). The carrier distribution rapidly spreads out due to diffusion, with the total amount of carriers decreasing as a result of carrier recombination.
Figure 4.
Carrier diffusion and rate equation models. (a) Spatial distribution of the concentration of carriers at t = 0, 1, and 5 ns (solid black, dashed dark green, and dotted light green, respectively). (b) Initial spatial distribution of the concentration of NV– states (solid black) and after 1 and 5 ns (dashed dark and dotted light green) after a single electron pulse. The spatial distribution of NV– states after 3 × 108 pulses, corresponding to a typical acquisition time (∼1 min), is also plotted (solid gray). (c) Modeled NV– fraction as a function of the number of electrons per pulse (dark red curve), together with the experimental data (black circles). (d) NV– fraction as a function of the number of pulses (400 electrons/pulse), obtained using the discrete rate equation model.
The calculated spatial distribution of the NV– concentration is shown in Figure 4b, again at t = 0, 1, and 5 ns, obtained by solving eqs 1a–1c. Given that the electron excitation cross-sections for NV0 excitation and NV– → NV0 conversion are unknown, we estimate them by considering the known exciton capture cross-section of a nitrogen impurity in diamond,59 σ0eh = σc = 3 × 10–6 μm2. We consider vth = 100 μm/ns, τback = 500 ms, as obtained from the experimental data in Figure 3b, and an initial homogeneous NV– fraction of 0.4 (black line in Figure 4b for t = 0 ns), corresponding to the experimental data in Figure 2e. We observe that 1 ns after the first pulse NV centers in the NV– state that are located within a 1 μm range from the initial electron cascade have been converted to NV0 due to the interaction with carriers. For larger times (5 ns) the distribution of converted NV– centers is nearly the same as for t = 1 ns, as nearly all carriers have recombined.
In order to account for longer time scales, corresponding to the back transfer from NV0 to NV– and the time of acquisition of our experiments (typically 1 min, ∼3 × 108 pulses), we developed a discrete rate equation model. In this case, the concentration of NV– centers is modeled as a function of the pulse number (n):
| 2 |
where
| 3 |
is the probability of carrier-induced conversion of centers in the NV– states between subsequent pulses, with T being the time between pulses (198 ns at 5.04 MHz), and
| 4 |
is the probability that an NV0 center transfers back to the NV– state, again between subsequent pulses (see Supporting Information). Using this model, in Figure 4b we plot the spatial distribution of NV– centers after 3 × 108 pulses (solid gray), corresponding to a typical acquisition time (1 min), in which the steady state has been reached. The calculated steady-state NV– fraction as a function of the number of electrons per pulse is shown in Figure 4c, which is overlaid with the experimental data from Figure 2e (black circles). Each point in the plot corresponds to the steady-state value calculated using eq 2 and integrated over the excitation and collection volume (see Supporting Information). In our model, taking the parameters discussed above, the only fit parameter is the collection depth of the CL system, which is 23 μm for the best fit. This is a reasonable value given the confocal geometry of the CL/PL collection system (see Methods). Figure 4d shows the calculated NV– fraction as a function of the number of pulses. We observe that the NV– fraction saturates for ∼5 × 106 pulses (1 s), consistent with the fact that the steady state is reached for a time longer than the NV0 → NV– back transfer time. Overall, the model qualitatively describes properly the experimental data, therefore giving further proof for the proposed electron-induced mechanism for NV– → NV0 conversion dynamics.
Conclusions
In conclusion, we have used pump–probe CL spectroscopy to show that high-energy (5 keV) electron irradiation of NV centers induces a state conversion from the NV– to the NV0 state. We show that the NV– population decreases when increasing the number of electrons per pulse that excite the sample, until saturation is reached, which is attributed to the full conversion of the NV– centers in the volume excited through the electrons. Experiments also show that the NV– → NV0 conversion is reversible, with a typical back transfer time of 500 ms. We present a three-dimensional rate equation model, considering diffusion of electron-generated charge carriers and taking into account the integrated effect of subsequent pulses, which qualitatively describes the experimental results. This work shows that NV– centers are effectively converted to NV0 centers by electron irradiation and explains why NV– emission is not observed in CL measurements. We envision that the pump–probe CL approach presented in this work can be applied to other complex solid-state emitter systems, to obtain further insight in their complex dynamical behavior.
Methods
Ultrafast SEM
A schematic of the setup is shown in Figure 1a. The pump–probe CL experiments are performed inside an SEM (Thermo Fisher Scientific/XL30 FEI) containing a Schottky field-emission electron cathode consisting of a ZrO-coated W tip. The conditions used to generate the electron pulses are discussed in ref (46). We use a diode-pumped Yb-doped fiber system (IMPULSE Clark-MXR) providing 250 fs light pulses at a wavelength of λ = 1035 nm and repetition rate of 5.04 MHz. The primary laser beam is guided through a harmonic generator to create second, third, and fourth harmonics (517, 345, and 258 nm, respectively). The fourth harmonic is guided to the electron column and focused with an f = 15 cm lens onto the electron cathode, which is accessible through a vacuum window. Earlier work using the same setup has shown that this photoemission process results in electron pulses with a temporal spread in the picosecond range.46 We use a gradient neutral-density filter to change the fourth-harmonic pulse energy from 0 to 1.5 nJ/pulse, which results in an average number of electrons per pulse up to 400. The corresponding time-averaged beam current on the sample was 0–325 pA measured with a Faraday cup. The error in the current measurement is ∼25%, limited by the stability in the laser power and measurement method. In the experiments, the electron spot size has a diameter of ∼600 nm. Using the same setup, a higher spatial resolution can be achieved at the expense of lower current on the sample.46 All the experiments are performed at room temperature and at a pressure of 10–6 mbar.
Laser–Electron Beam Overlap
The second harmonic (λ = 517 nm) of the same primary laser beam is passed through a linear stage (Newport M-IMS600PP) with motor controller (Newport ESP301-1G), after which it is sent through a pellicle beam splitter (8:92), guided into the SEM sample chamber through a vacuum window, and focused onto the sample to a ∼10 μm diameter spot using an Al parabolic mirror (1.46π sr acceptance angle, 0.1 parabola parameter, and 0.5 mm focal distance). In the pump–probe measurements the second-harmonic path length was tuned such that the light pulse was delayed 1.3 ns with respect to the electron pulse. The second- and fourth-harmonic laser powers were independently controlled such that measurements with varying number of electrons per pulse could be done for constant second-harmonic PL power.
CL and PL Collection
Luminescence from the sample is collected using the Al parabolic mirror and directed to a light collection and analysis system. Light collected by the mirror is focused (f = 16 cm) onto the entrance facet of a multimode fiber (550 μm core diameter), creating a confocal collection geometry, which limits the PL and CL collection depth in the sample. The fiber guides the light to a Czerny–Turner spectrometer equipped with a CCD array detector (Princeton Spec10) and grating containing 150 lines/mm and blaze wavelength corresponding to 500 nm. A long-pass filter (λ > 532 nm) is used to suppress scattered pump laser light in the detection path. TCSPC measurements are performed by sending the CL signal to a single-photon avalanche photodiode (MPD PD-100) analyzed by time correlation (Picoquant PicoHarp 300), which builds a delay histogram. In this case, an additional bandpass filter (λ = 650 ± 75 nm) is used, corresponding to the spectral range within which NV emission occurs. We use the third-harmonic laser pulse measured with a photodiode as the trigger for the time-correlated measurements. The PL, CL, and PP data in Figure 1b and Figure 2a are collected over a time of 1 min each. The light collection geometry in this setup typically allows the collection of light within a 20 × 20 μm2 area. Only light emitted in this area, and within the escape cone of diamond, can be collected efficiently. Given the critical angle for diamond (θc < 24.6°), we can estimate that light emitted at a depth down to 20 μm inside the diamond can still be collected. Nevertheless, emission beyond this 20 μm depth might reach the surface at a position outside of the collection area; thus the collection efficiency decreases at larger depths.
Acknowledgments
This work is part of the research program of AMOLF, which is partly financed by the Dutch Research Council (NWO). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement no. 695343). We gratefully acknowledge the technical support of Erik Kieft, Hans Zeijlemaker, and Dion Ursem. We also gratefully acknowledge discussions with Mayeul Chipaux in the initial phase of this project, Patrick Maletinksy and Elke Neu for providing the bulk diamond sample, and Kévin Cognée for careful reading of the manuscript.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.9b01463.
Additional experimental data and description of the model (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Brouri R.; Beveratos A.; Poizat J.-P.; Grangier P. Photon Antibunching in the Fluorescence of Individual Color Centers in Diamond. Opt. Lett. 2000, 25 (17), 1294–1296. 10.1364/OL.25.001294. [DOI] [PubMed] [Google Scholar]
- Doherty M. W.; Manson N. B.; Delaney P.; Jelezko F.; Wrachtrup J.; Hollenberg L. C. L. The Nitrogen-Vacancy Colour Centre in Diamond. Phys. Rep. 2013, 528 (1), 1–45. 10.1016/j.physrep.2013.02.001. [DOI] [Google Scholar]
- Gruber A.; Dräbenstedt A.; Tietz C.; Fleury L.; Wrachtrup J.; von Borczyskowski C. Scanning Confocal Optical Microscopy and Magnetic Resonance on Single Defect Centers. Science (Washington, DC, U. S.) 2012, 276, 2012–2015. 10.1126/science.276.5321.2012. [DOI] [Google Scholar]
- Wee T.-L.; Tzeng Y.-K.; Han C.-C.; Chang H.-C.; Fann W.; Hsu J.-H.; Chen K.-M.; Yu Y.-C. Two-Photon Excited Fluorescence of Nitrogen-Vacancy Centers in Proton-Irradiated Type Ib Diamond. J. Phys. Chem. A 2007, 111 (38), 9379–9386. 10.1021/jp073938o. [DOI] [PubMed] [Google Scholar]
- Berthel M.; Mollet O.; Dantelle G.; Gacoin T.; Huant S.; Drezet A. Photophysics of Single Nitrogen-Vacancy Centers in Diamond Nanocrystals. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 035308. 10.1103/PhysRevB.91.035308. [DOI] [Google Scholar]
- Kurtsiefer C.; Mayer S.; Zarda P.; Weinfurter H. Stable Solid-State Source of Single Photons. Phys. Rev. Lett. 2000, 85 (2), 290–293. 10.1103/PhysRevLett.85.290. [DOI] [PubMed] [Google Scholar]
- Hausmann B. J. M.; Shields B.; Quan Q.; Maletinsky P.; McCutcheon M.; Choy J. T.; Babinec T. M.; Kubanek A.; Yacoby A.; Lukin M. D.; et al. Integrated Diamond Networks for Quantum Nanophotonics. Nano Lett. 2012, 12, 1578–1582. 10.1021/nl204449n. [DOI] [PubMed] [Google Scholar]
- Aharonovich I.; Englund D.; Toth M. Solid-State Single-Photon Emitters. Nat. Photonics 2016, 10 (10), 631–641. 10.1038/nphoton.2016.186. [DOI] [Google Scholar]
- Awschalom D. D.; Hanson R.; Wrachtrup J.; Zhou B. B. Quantum Technologies with Optically Interfaced Solid-State Spins. Nat. Photonics 2018, 12 (9), 516–527. 10.1038/s41566-018-0232-2. [DOI] [Google Scholar]
- Balasubramanian G.; Neumann P.; Twitchen D.; Markham M.; Kolesov R.; Mizuochi N.; Isoya J.; Achard J.; Beck J.; Tissler J.; et al. Ultralong Spin Coherence Time in Isotopically Engineered Diamond. Nat. Mater. 2009, 8 (5), 383–387. 10.1038/nmat2420. [DOI] [PubMed] [Google Scholar]
- Nemoto K.; Trupke M.; Devitt S. J.; Scharfenberger B.; Buczak K.; Schmiedmayer J.; Munro W. J. Photonic Quantum Networks Formed from NV– Centers. Sci. Rep. 2016, 6 (May), 26284. 10.1038/srep26284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hensen B.; Bernien H.; Dréau A. E.; Reiserer A.; Kalb N.; Blok M. S.; Ruitenberg J.; Vermeulen R. F. L.; Schouten R. N.; Abellán C.; et al. Loophole-Free Bell Inequality Violation Using Electron Spins Separated by 1.3 Kilometres. Nature 2015, 526, 682–686. 10.1038/nature15759. [DOI] [PubMed] [Google Scholar]
- Taylor J. M.; Cappellaro P.; Childress L.; Jiang L.; Budker D.; Hemmer P. R.; Yacoby A.; Walsworth R.; Lukin M. D. High-Sensitivity Diamond Magnetometer with Nanoscale Resolution. Nat. Phys. 2008, 4 (10), 810–816. 10.1038/nphys1075. [DOI] [Google Scholar]
- Mamin H. J.; Kim M.; Sherwood M. H.; Rettner C. T.; Ohno K.; Awschalom D. D.; Rugar D. Nanoscale Nuclear Magnetic Resonance with a Nitrogen-Vacancy Spin Sensor. Science (Washington, DC, U. S.) 2013, 339, 557–561. 10.1126/science.1231540. [DOI] [PubMed] [Google Scholar]
- Kucsko G.; Maurer P. C.; Yao N. Y.; Kubo M.; Noh H. J.; Lo P. K.; Park H.; Lukin M. D. Nanometre-Scale Thermometry in a Living Cell. Nature 2013, 500 (7460), 54–58. 10.1038/nature12373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolesov R.; Grotz B.; Balasubramanian G.; Stöhr R. J.; Nicolet A. A. L.; Hemmer P. R.; Jelezko F.; Wrachtrup J. Wave-Particle Duality of Single Surface Plasmon Polaritons. Nat. Phys. 2009, 5 (7), 470–474. 10.1038/nphys1278. [DOI] [Google Scholar]
- Aslam N.; Waldherr G.; Neumann P.; Jelezko F.; Wrachtrup J. Photo-Induced Ionization Dynamics of the Nitrogen Vacancy Defect in Diamond Investigated by Single-Shot Charge State Detection. New J. Phys. 2013, 15, 013064. 10.1088/1367-2630/15/1/013064. [DOI] [Google Scholar]
- Hacquebard L.; Childress L. Charge-State Dynamics during Excitation and Depletion of the Nitrogen-Vacancy Center in Diamond. Phys. Rev. A: At., Mol., Opt. Phys. 2018, 97 (June), 063408. 10.1103/PhysRevA.97.063408. [DOI] [Google Scholar]
- Siyushev P.; Pinto H.; Vörös M.; Gali A.; Jelezko F.; Wrachtrup J. Optically Controlled Switching of the Charge State of a Single Nitrogen-Vacancy Center in Diamond at Cryogenic Temperatures. Phys. Rev. Lett. 2013, 110 (16), 167402. 10.1103/PhysRevLett.110.167402. [DOI] [PubMed] [Google Scholar]
- Fu K.-M. C.; Santori C.; Barclay P. E.; Beausoleil R. G. Conversion of Neutral Nitrogen-Vacancy Centers to Negatively Charged Nitrogen-Vacancy Centers through Selective Oxidation. Appl. Phys. Lett. 2010, 96, 121907. 10.1063/1.3364135. [DOI] [Google Scholar]
- Hauf M. V.; Grotz B.; Naydenov B.; Dankerl M.; Pezzagna S.; Meijer J.; Jelezko F.; Wrachtrup J.; Stutzmann M.; Reinhard F.; et al. Chemical Control of the Charge State of Nitrogen-Vacancy Centers in Diamond. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 081304. 10.1103/PhysRevB.83.081304. [DOI] [Google Scholar]
- Rondin L.; Dantelle G.; Slablab A.; Grosshans F.; Treussart F.; Bergonzo P.; Perruchas S.; Gacoin T.; Chaigneau M.; Chang H.; et al. Surface-Induced Charge State Conversion of Nitrogen-Vacancy Defects in Nanodiamonds. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 115449. 10.1103/PhysRevB.82.115449. [DOI] [Google Scholar]
- Grotz B.; Hauf M. V.; Dankerl M.; Naydenov B.; Pezzagna S.; Meijer J.; Jelezko F.; Wrachtrup J.; Stutzmann M.; Reinhard F.; et al. Charge State Manipulation of Qubits in Diamond. Nat. Commun. 2012, 3, 729. 10.1038/ncomms1729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kato H.; Wolfer M.; Schreyvogel C.; Kunzer M.; Müller-sebert W.; Obloh H.; Yamasaki S.; Nebel C.. Tunable Light Emission from Nitrogen- Vacancy Centers in Single Crystal Diamond PIN Diodes. Appl. Phys. Lett. 2013, 102, 151101. 10.1063/1.4801871. [DOI] [Google Scholar]
- Tizei L. H. G.; Kociak M. Spectrally and Spatially Resolved Cathodoluminescence of Nanodiamonds: Local Variations of the NV0 Emission Properties. Nanotechnology 2012, 23, 175702. 10.1088/0957-4484/23/17/175702. [DOI] [PubMed] [Google Scholar]
- Tizei L. H. G.; Kociak M. Spatially Resolved Quantum Nano-Optics of Single Photons Using an Electron Microscope. Phys. Rev. Lett. 2013, 110 (15), 153604. 10.1103/PhysRevLett.110.153604. [DOI] [PubMed] [Google Scholar]
- Lourenço-Martins H.; Kociak M.; Meuret S.; Treussart F.; Lee Y. H.; Ling X. Y.; Chang H.-C.; Galvão Tizei L. H. Probing Plasmon-NV0 Coupling at the Nanometer Scale with Photons and Fast Electrons. ACS Photonics 2018, 5, 324–328. 10.1021/acsphotonics.7b01093. [DOI] [Google Scholar]
- Kumar S.; Huck A.; Andersen U. L. Efficient Coupling of a Single Diamond Color Center to Propagating Plasmonic Gap Modes. Nano Lett. 2013, 13, 1221–1225. 10.1021/nl304682r. [DOI] [PubMed] [Google Scholar]
- Egerton R. F. Electron Energy-Loss Spectroscopy in the TEM. Rep. Prog. Phys. 2009, 72 (1), 016502. 10.1088/0034-4885/72/1/016502. [DOI] [Google Scholar]
- Klein C. A. Radiation Ionization Energies in Semiconductors: Speculations about the Role of Plasmons. Proc. Int. Conf. Phys. Semicond. 1966, 21, 307–311. [Google Scholar]
- Kociak M.; Zagonel L. F. Cathodoluminescence in the Scanning Transmission Electron Microscope. Ultramicroscopy 2017, 174, 50–69. 10.1016/j.ultramic.2016.11.018. [DOI] [PubMed] [Google Scholar]
- Watanabe H.; Kitamura T.; Nakashima S.; Shikata S. Cathodoluminescence Characterization of a Nitrogen-Doped Homoepitaxial Diamond Thin Film. J. Appl. Phys. 2009, 105 (2009), 093529. 10.1063/1.3117214. [DOI] [Google Scholar]
- Zhang H.; Glenn D. R.; Schalek R.; Lichtman J. W.; Walsworth R. L. Efficiency of Cathodoluminescence Emission by Nitrogen-Vacancy Color Centers in Nanodiamonds. Small 2017, 13, 1700543. 10.1002/smll.201700543. [DOI] [PubMed] [Google Scholar]
- Davies G. Dynamic Jahn-Teller Distortions at Trigonal Optical Centres in Diamond. J. Phys. C: Solid State Phys. 1979, 12 (13), 2551–2566. 10.1088/0022-3719/12/13/019. [DOI] [Google Scholar]
- Tallaire A.; Collins A. T.; Charles D.; Achard J.; Sussmann R.; Gicquel A.; Newton M. E.; Edmonds A. M.; Cruddace R. J. Characterisation of High-Quality Thick Single-Crystal Diamond Grown by CVD with a Low Nitrogen Addition. Diamond Relat. Mater. 2006, 15, 1700–1707. 10.1016/j.diamond.2006.02.005. [DOI] [Google Scholar]
- Robins L. H.; Cook L. P.; Farabaugh E. N.; Feldman A. Cathodoluminescence of Defects in Diamond Films and Particles Grown by Hot-Filament Chemical-Vapor Deposition. Phys. Rev. B: Condens. Matter Mater. Phys. 1989, 39 (18), 368–377. 10.1103/PhysRevB.39.13367. [DOI] [PubMed] [Google Scholar]
- Malykhin S. A.; Houard J.; Ismagilov R. R.; Orekhov A. S.; Vella A.; Obraztsov A. N. Luminescent Characteristics of Needle-Like Single Crystal Diamonds. Phys. Status Solidi B 2018, 255, 1700189. 10.1002/pssb.201700189. [DOI] [Google Scholar]
- Barwick B.; Flannigan D. J.; Zewail A. H. Photon-Induced near-Field Electron Microscopy. Nature 2009, 462 (7275), 902–906. 10.1038/nature08662. [DOI] [PubMed] [Google Scholar]
- Feist A.; Echternkamp K. E.; Schauss J.; Yalunin S. V.; Schäfer S.; Ropers C. Quantum Coherent Optical Phase Modulation in an Ultrafast Transmission Electron Microscope. Nature 2015, 521 (7551), 200–203. 10.1038/nature14463. [DOI] [PubMed] [Google Scholar]
- Rubiano Da Silva N.; Möller M.; Feist A.; Ulrichs H.; Ropers C.; Schäfer S. Nanoscale Mapping of Ultrafast Magnetization Dynamics with Femtosecond Lorentz Microscopy. Phys. Rev. X 2018, 8 (3), 31052. 10.1103/PhysRevX.8.031052. [DOI] [Google Scholar]
- Liao B.; Najafi E. Scanning Ultrafast Electron Microscopy: A Novel Technique to Probe Photocarrier Dynamics with High Spatial and Temporal Resolutions. Mater. Today Phys. 2017, 2, 46–53. 10.1016/j.mtphys.2017.07.003. [DOI] [Google Scholar]
- Merano M.; Sonderegger S.; Crottini A.; Collin S.; Renucci P.; Pelucchi E.; Malko A.; Baier M. H.; Kapon E.; Deveaud B.; et al. Probing Carrier Dynamics in Nanostructures by Picosecond Cathodoluminescence. Nature 2005, 438 (7067), 479–482. 10.1038/nature04298. [DOI] [PubMed] [Google Scholar]
- Feist A.; Bach N.; Rubiano da Silva N.; Danz T.; Möller M.; Priebe K. E.; Domröse T.; Gatzmann J. G.; Rost S.; Schauss J.; et al. Ultrafast Transmission Electron Microscopy Using a Laser-Driven Fi Eld Emitter: Femtosecond Resolution with a High Coherence Electron Beam. Ultramicroscopy 2017, 176, 63–73. 10.1016/j.ultramic.2016.12.005. [DOI] [PubMed] [Google Scholar]
- Shahmohammadi M.; Ganière J.-D.; Zhang H.; Ciechonski R.; Vescovi G.; Kryliouk O.; Tchernycheva M.; Jacopin G. Excitonic Diffusion in InGaN/GaN Core–Shell Nanowires. Nano Lett. 2016, 16, 243–249. 10.1021/acs.nanolett.5b03611. [DOI] [PubMed] [Google Scholar]
- Carbone F.; Barwick B.; Kwon O.-H.; Park H. S.; Baskin J. S.; Zewail A. H. EELS Femtosecond Resolved in 4D Ultrafast Electron Microscopy. Chem. Phys. Lett. 2009, 468, 107–111. 10.1016/j.cplett.2008.12.027. [DOI] [Google Scholar]
- Meuret S.; Solà Garcia M.; Coenen T.; Kieft E.; Zeijlemaker H.; Lätzel M.; Christiansen S.; Woo S. Y.; Ra Y. H.; Mi Z.; et al. Complementary Cathodoluminescence Lifetime Imaging Configurations in Scanning Electron Microscopy. Ultramicroscopy 2019, 197, 28–38. 10.1016/j.ultramic.2018.11.006. [DOI] [PubMed] [Google Scholar]
- Sun J.; Melnikov V. A.; Khan J. I.; Mohammed O. F. Real-Space Imaging of Carrier Dynamics of Materials Surfaces by Second-Generation Four-Dimensional Scanning Ultrafast Electron Microscopy. J. Phys. Chem. Lett. 2015, 6, 3884–3890. 10.1021/acs.jpclett.5b01867. [DOI] [PubMed] [Google Scholar]
- Krishnamurti D. The Raman Spectrum of Diamond. Proc. - Indian Acad. Sci., Sect. A 1954, 40 (5), 211–216. 10.1007/BF03047399. [DOI] [Google Scholar]
- Zaitsev A. M.Optical Properties of Diamond: A Data Handbook; Springer, 2001. [Google Scholar]
- Iakoubovskii K.; Adriaenssens G. J. Luminescence Excitation Spectra in Diamond. Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 61 (15), 10174–10182. 10.1103/PhysRevB.61.10174. [DOI] [Google Scholar]
- Demers H.; Poirier-Demers N.; Couture A. R.; Joly D.; Guilmain M.; de Jonge N.; Drouin D. Three-Dimensional Electron Microscopy Simulation with the CASINO Monte Carlo Software. Scanning 2011, 33 (April), 135–146. 10.1002/sca.20262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beha K.; Batalov A.; Manson N. B.; Bratschitsch R.; Leitenstorfer A. Optimum Photoluminescence Excitation and Recharging Cycle of Single Nitrogen-Vacancy Centers in Ultrapure Diamond. Phys. Rev. Lett. 2012, 109 (9), 097404. 10.1103/PhysRevLett.109.097404. [DOI] [PubMed] [Google Scholar]
- Manson N. B.; Harrison J. P. Photo-Ionization of the Nitrogen-Vacancy Center in Diamond. Diamond Relat. Mater. 2005, 14 (10), 1705–1710. 10.1016/j.diamond.2005.06.027. [DOI] [Google Scholar]
- Hopper D. A.; Grote R. R.; Exarhos A. L.; Bassett L. C. Near-Infrared-Assisted Charge Control and Spin Readout of the Nitrogen-Vacancy Center in Diamond. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94, 241201. 10.1103/PhysRevB.94.241201. [DOI] [Google Scholar]
- Lu H.-C.; Peng Y.-C.; Chou S.-L.; Lo J.-I.; Cheng B.-M.; Chang H.-C. Far-UV-Excited Luminescence of Nitrogen-Vacancy Centers: Evidence for Diamonds in Space. Angew. Chem., Int. Ed. 2017, 56 (46), 14469–14473. 10.1002/anie.201707389. [DOI] [PubMed] [Google Scholar]
- Mizuochi N.; Makino T.; Kato H.; Takeuchi D.; Ogura M.; Okushi H.; Nothaft M.; Neumann P.; Gali A.; Jelezko F.; et al. Electrically Driven Single-Photon Source at Room Temperature in Diamond. Nat. Photonics 2012, 6 (May), 299–303. 10.1038/nphoton.2012.75. [DOI] [Google Scholar]
- Lohrmann A.; Pezzagna S.; Dobrinets I.; Spinicelli P.; Jacques V.; Roch J.-F.; Meijer J.; Zaitsev A. M. Diamond Based Light-Emitting Diode for Visible Single-Photon Emission at Room Temperature. Appl. Phys. Lett. 2011, 99, 251106. 10.1063/1.3670332. [DOI] [Google Scholar]
- Malinauskas T.; Jarasiunas K.; Ivakin E.; Ralchenko V.; Gontar A.; Ivakhnenko S. Optical Evaluation of Carrier Lifetime and Diffusion Length in Synthetic Diamonds. Diamond Relat. Mater. 2008, 17, 1212–1215. 10.1016/j.diamond.2008.01.005. [DOI] [Google Scholar]
- Shimomura T.; Kubo Y.; Barjon J.; Tokuda N.; Akimoto I.; Naka N. Quantitative Relevance of Substitutional Impurities to Carrier Dynamics in Diamond. Phys. Rev. Mater. 2018, 2, 1–7. 10.1103/PhysRevMaterials.2.094601. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.