Computational absorption and reflection studies of normal human skin at 0.45 THz

Abstract

Applications using terahertz (THz) frequency radiation will inevitably lead to increased human exposure. The power density and specific absorption rate (SAR) simulations of thin skin at 0.45 THz show the bulk of the energy being absorbed in the upper stratum spinosum, and the maximal temperature rise is in the lower stratum spinosum. There are regions of SAR increase of 100% above the local average at the stratum spinosum/stratum basale boundary. The dead Stratum Corneum layer protects underlying tissues in thick skin. Reflection studies suggest that acute angles and the use of polarised incident radiation may enhance the assessment of diabetic neuropathy.

1. Introduction

The terahertz frequency band (THz) of electromagnetic radiation is generally defined as being 0.1 to 10.0 × 10¹² Hz (corresponding to a wavelength (λ) of 3 mm to 0.03 mm in empty space). There are no significant natural sources of THz radiation that would impact on the human skin. THz radiation is absorbed readily by water, with an absorption coefficient in the order of 8000-35000 m^-1 (80-350 cm^-1) [1,2]. This property of THz results in the Earth’s atmosphere absorbing most of this radiation from the Sun and other celestial sources. The THz band has been poorly explored in the past due to the difficulties in producing and detecting the radiation [3]. Recent advances in THz production and spectroscopy methods have led to THz deployment in security screening, quality control of manufacturing processes [4,5] and analysis of chemical mixtures [6]. The higher frequency of THz radiation promises greater data carrying capacity when compared to the present mobile communication band around 1 GHz. This has led to proposals for telecommunication systems using frequencies up to 0.30 THz [7,8].

The free (bulk) water content of most normal body tissues, including the living skin, is 70% to 72%. The high absorption coefficient of water at THz frequencies results in an effective tissue penetration of 0.2-0.3 mm at body temperature. It follows that only the skin, cornea of the eye and the tympanic membrane of the ear can receive significant incidental or purposeful radiation from external sources. The thickness of the skin layers is the same order of magnitude as wavelengths of THz radiation. The outermost skin layer is the epidermis. It is morphologically divided into the inner Stratum Basale (SB), a cell monolayer, the Stratum Spinosum (SS), which is 0.05-0.10 mm thick, and an outer dead layer, the Stratum Corneum (SC) [9]. The SB contains the keratinocyte progenitor cells, the melanin producing melanocytes, the Merkel touch receptor cells and the immune mediating Langerhans cells. Since the SB is the most active skin cell proliferation layer, it is the site of cell mutations producing cancers such as Basal Cell Carcinoma (BCC) and Melanoma. The SB is, thus, the most important layer to consider regarding the potential for adverse THz effects. The keratinocyte progenitor cells divide to form successive layers of the SS. The cells progressively fill with keratin, and eventually undergo apoptosis (programmed cell death) to form the outer dead layer, the Stratum Corneum (SC).

The deepest layer of the skin is the Dermis. It contains nerve endings, blood vessels, lymphatic channels, and skin appendages such as the hair follicles, sebaceous glands and the eccrine and apocrine sweat glands. The thickness of the dermis is between 2 and 4 mm. The junction between the Dermis and the Epidermis is wavelike, and, depending on the perspective, the epidermis projects inward to form the rete ridges, or the Dermis projects outward as dermal papillae. Human skin is divided morphologically into thin and thick skin. The thick skin is found on the palm of the hand and the sole of the foot. The chief differentiating factor is the thickness of the Stratum Corneum (SC). The SC is 0.01–0.03 mm deep in thin skin [10] and 0.15–0.50 mm in thick skin [11]. There is no hair on the thick skin. The thick skin has 0.01-0.02 mm transitional layers between the SS and the SC, the Stratum Granulosum and Stratum Lucidum. The outer 0.1 mm of thick skin SC has 15-40% hydration [10,12] rising to 70-72% free water in the deeper skin layers [12].

Imaging of skin and skin pathology has been undertaken using confocal reflectance microscopy [13], high frequency ultrasound [14], optical coherence tomography [15] and photoacoustic imaging [16]. None of these methods are primarily dependent on water concentration as a contrast modality. The high absorption of liquid water by THz opens the possibility of using the difference between the water content of normal skin and skin pathology for imaging [17–19], making THz imaging a qualitatively novel method which can offer perspectives unachievable by other means. The contrast between the layers of the epidermis and pathological lesions can be enhanced by techniques such as nanoparticle insertion [20].The recent observations by Hernandez-Cardoso [21,22] that diabetic vasculopathy causes changes in the skin detectable by THz forms the basis for one of the most promising applications under development.

The International Commission on Non-Ionizing Radiation Protection (ICNIRP) utilises incident power flux density (PD) to set standards for exposure to THz radiation. The exposure to <0.3 THz is covered by the ICNIRP (1998) guidelines for 100 KHz - 300 GHz, which are currently being revised [23,24]. For exposure of >0.3 THz, the standards are set by the ICNIRP (2013) guidelines for laser radiation of wavelengths between 180 nm and 1,000 µm [25]. There is a significant divergence between the guidelines, with the >0.3 THz guidelines allowing for 20-100 times the intensity of exposure compared to <0.3 THz. For durations of >10 s, the >0.3 THz maximum PD is 1kWm^-2, whilst for <0.3 THz, the general public exposure limit is two orders of magnitude less at 10 Wm^-2. The ICNIRP (2013) guidelines give the skin injury temperature threshold of 45° C. There are no data on the non-thermal effects of long term exposure of humans to THz radiation [26,27] and thus only indirect inferences can be made from studies at other frequencies.

Whilst the PD and total energy density is used for exposure standards, the detailed assessment interaction of skin layers and appendages with THz radiation also requires the estimation of SAR and thermal effects within the structures of the skin. No direct information exists on the spatial distribution of radiation absorption, nor have there been any studies of the detail of the specific absorption rate (SAR) or thermal impact within the individual skin layers.

Given the high absorption coefficient of THz in tissues, the electric fields and exposure levels may vary significantly over distances of less than 0.1 mm, thus SAR needs to be considered in a novel way, over very small volumes. The concept of “micro” SAR is introduced to describe SAR variation at sub-millimeter distances. Any tissue heating in such small regions will dissipate over short time periods, thus SAR is likely to be more significant when considering the likelihood of the impact of any non-thermal effects.

A review of 32 papers dealing with the interaction of skin and THz [28] showed that most data on the dielectric properties of tissues are available in the 0.2-1.2 THz range. The 0.3 THz frequency is the upper range of proposed communication applications. The 0.30-0.70 THz band (λ in empty space of 1.0 to 0.43 mm) is also the most promising range for imaging, hydration sensing and industrial applications and is noted to be the optimal range when considering the compromise between sensitivity to water concentration, scattering and attenuation, and maximising spatial resolution [29–31].

The dielectric properties of skin tissue are influenced by not only water, but also major skin components such as keratin, collagen and melanin. These factors mean that the dielectric properties change in a non-linear way. For this reason, the FDTD simulations are best conducted with single frequencies. The 0.45 THz frequency (0.667 mm wavelength in empty space, 15 waves cm^-1) was chosen for the simulations as it is the approximate geometric mean between 0.30-0.70 THz and is thus the most useful single frequency for investigating the range. If the appropriate dielectric properties are used, and the meshing is of the suitable size, the technique outlined in the paper is capable of simulations at other frequencies.

For the estimations to be useful, the resolution needs to be capable of discerning the skin structures, and given the dimensions of the skin layers, a minimum resolution in the order of 0.01 mm is desirable. In empty space, this is λ/67 at 0.45 THz; when the refractive index of ∼2.0 for living tissues is considered, the resolution becomes ∼λ/33 at 0.45 THz.

The best THz imaging resolution presently available is 0.05 mm [32], thus computational modelling becomes an attractive option for the preliminary exploration of the sub-wavelength effects of 0.45 THz on skin. Computational modelling at high resolution extends knowledge to capabilities beyond current imaging technology, revealing patterns of absorption, as well as phenomena which may confound image production. Computational modelling tests concepts for future applications which can then be explored in-vivo as the technology improves.

Any modelling is limited by the accuracy of the inputs. The rendering of accurate anatomical models is important, but, in the case of skin interaction with THz, specifying reliable dielectric properties of tissues is paramount. These dielectric properties are incompletely understood in the THz band, however it is possible to make reasonable assumptions by the use of available data, extrapolation from other frequencies and data from cell and tissue components using mixing formulae.

2. Method

2.1. Transmission, absorption and thermal characteristics

A Finite Difference Time Domain (FDTD) solver, XFdtd Bio-Pro, (version 7.6.0.5.r48456, Remcom, State College, PA), was used for the anatomical design and the computational implementation of the simulations. The FDTD method was first defined by Kane Yee, [33] and is employed as described in Sullivan [34]. The simulation was performed using variable geometry to adequately explore the skin within the computational limitations. The problem space, minimum and maximum size of cells, time step duration and total number, and the total simulation time are outlined in Table 1 . Given that the refractive index (n) of tissues of the living skin is about 2.1, the λ of 0.45 THz radiation within living skin is in the order of 0.32 mm. The n of the dead SC is about 1.8 and varies with hydration, giving a λ of ∼0.37 mm.

Table 1. Simulation parameters, 0.45 THz (λ = 0.667 mm in free space, ∼0.32 mm in living tissues). The minimum resolution, problem space, number of time steps, time step duration, and total simulation time. Since the refractive index of skin tissues is in the order of 2.1, the indicative λ within skin is in the order of 0.32 mm at 0.45 THz.

Model	Thin Skin	Thick Skin
Problem Space (Yee cells)	841 × 552 × 454	875 × 587 × 375
Maximum cell dimension	λ/82	λ/26
Minimum cell dimension	λ/2392	λ/335
Step Size	0.499 fs	1.322 fs
Timesteps	30000	30000
Simulated time	14.1 ps	21.7 ps

The rendering of the anatomical detail of the skin was inhibited by the capability of the computer hardware; the random-access memory available limited models to 20-25 gigabytes in size. Separate models for thick skin and thin skin were employed. The design and dimensions of the thin skin and thick skin models, with representation of the skin layers, are presented in Fig. 1 . and Fig. 2 . respectively.

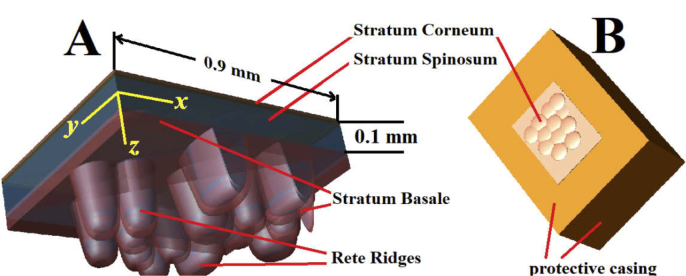
Fig. 1.

(A) The x, y, z orientation in the thin skin model, the Stratum Corneum (SC, light tan) and layers of the living epidermis. The thin skin SC was modelled with an irregular upper surface, with three layers of 0.01 mm that could be set at 15% to 40% hydration. The Stratum Spinosum (SS, blue) is 0.1 mm thick with the rete ridge extensions adding a further 0.17 mm in maximum depth. The Stratum Basale (SB, brown) was modelled as a 0.01 to 0.045 mm layer between the underlying Dermis and the SS. (B) The model is encased in the Dermis inferiorly and laterally, to prevent interference from stray excitation. The total depth of the model was 0.6 mm.

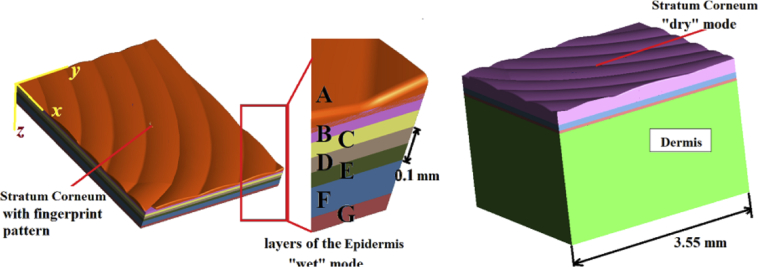
Fig. 2.

Left: The x, y, z orientation in the thick skin model (left), with a “fingerprint pattern” Stratum Corneum (SC), and the living layers of the Epidermis. The Dermis is rendered invisible. Centre: (A-D) Layers of the SC (each 0.05 mm in thickness, A-D), (E) represents the Stratum Granulosum and Stratum Lucidum (0.05 mm), (F) Stratum Spinosum (SS, 0.1 mm), and (G) Stratum Basale (SB, 0.05 mm). The dielectric properties of each layer can be individually altered to simulate varied states of hydration. Right: The model showing the thick Dermis (2.0 mm) to prevent interference from lateral excitation leakage.

To maximize resolution, the thin skin model cell sizes ranged from λ/82 for less important areas to λ/2392 for the detail around rete ridges. The thermal simulations required the prevention of unwanted lateral and inferior radiation intrusion on timescales allowing thermal equilibrium to be reached. This resulted in a larger, less detailed model. Skin exposure has peculiar features which can be used to simplify the model. Given that the entire layer at a particular depth is equally exposed to any incoming plane-wave radiation, the thermal losses in the epidermis will only be either outwards to the air or inwards to the deeper structures, thus the system can be modelled with large lateral padding to prevent interference from stray artifact radiation from the side of the simulation.

To accommodate the larger dimensions of the SC in the thick skin, the model was limited to a maximum of λ/26 and a minimum of λ/335. In practice, little 0.45 THz radiation penetrated past the dead layer of the SC in the thick skin simulations and the grainier method proved adequate.

Skin appendages such as hair, apocrine glands and sweat ducts were not considered in this simulation, nor were any differences in melanin content, nevi or any other anomalies. The lateral dimensions of the thin skin model were x = 0.90 mm, y = 0.65 mm. To prevent interference from stray or reflected radiation, the model was embedded in a laterally extended Dermis. (Figure 1B). This resulted in total dimensions of x = 1.80 mm, y = 1.20 mm, z = 1.00 mm. The thermal simulations of thin skin required a Dermis region around the model to be increased to x = 4.2 mm, y = 4.2 mm and z = 2.4 mm, and a longer time step to accommodate a stable thermal state endpoint. This necessitated the reduction in the resolution to a maximum of λ/27.

The dimensions of the layers in the thin skin model were SC 0.025 to 0.030 mm, SS 0.10 mm, with extensions into the rete ridges, SB 0.01 to 0.045 mm, and the Dermis filling the lower region of the limits of the model. To accommodate the change in the Stratum Corneum (SC) hydration profile with depth, the thin skin model had three individually defined layers for SC. Since the upper layer of the SC was modelled with a series of oblate spheroids to give an irregular surface, the thickness of this feature varied between 0.05 and 0.10 mm (Fig. 1B). The two deeper SC layers were each set at 0.01 mm in thickness.

In the thick skin model (Fig. 2), the dimensions were x = 3.55 mm, y = 2.40 mm, z = 2.30 mm. The thick skin model SC of 0.20 to 0.25 mm was arranged in four individually variable layers of 0.05 mm each. The upper SC layer had curving 0.7 mm wide ridges to represent the outer fingerprint pattern, giving it a variable thickness of 0.05 to 0.10 mm. A further 0.05mm layer was added to simulate the Stratum Granulosum and Stratum Lucidum (Fig. 2, center, layer E). Each layer could be set with dielectric properties representing a given hydration. In line with reference data on SC hydration in thick skin [10,12], a range of modes could be simulated to explore the penetration and reflection characteristics, from a completely “wet” mode, with all the SC layers (layers A to D) set at 40% hydration, to a very “dry” mode, which set the five outer layers (including the Stratum Granulosum and Stratum Lucidum) of the thick skin to a hydration of 15%.

The simulation used the real (ɛ′) and imaginary (ɛ′′) parts of the complex permittivity to specify the tissue dielectric properties. The ɛ’ and ɛ” for the skin components are based on available published data [35–44]. The lack of direct data necessitated use of data for tissue components rather than whole tissues and applying mixing formulae based on water content [37,45,46] to determine dielectric values. The ɛ′ and ɛ′′, conductivity (σ_t, Sm^-1), refractive index (n_t) the tissue density (ρt, kgm^-3), heat capacity (c_t, Jkg^-1K^-1) and the thermal conductivity (k_t,Wm^-1K^-1) for the skin layers are set out in Table 2 . The thermal properties of blood are also included. These were used to calculate SAR, PD and the associated temperature rise. Any melanin content as a contributor to THz absorption was not considered.

Table 2. Dielectric properties of skin tissues at 0.45 THz. The dielectric values are derived from data from refs. [35–44] and the analysis of tissue component and water mixing formulae [37,45,46]. The tissue densities, heat capacity and thermal conductivity are based on Hasgall [47] and for Stratum Corneum based on Dias [48]. The Stratum Granulosum and Strum Lucidum were considered to be equivalent to the 40% hydrated Stratum Corneum.

	ɛ’	ɛ"	Electrica Cond.(σt)	Ref. Index (n)	Tissue Density(ρt)	Heat Cap. (ct)	Therm. Cond. (kt)
Model Layer			Sm-1		kgm-3	Jkg-1K-1	Wm-1K-1
SC hydrated 15%, “dry”	3.0	1.0	25.0	1.76	1300	1800
SC hydrated 23%	3.2	1.3	32.5	1.82	1260	2200
SC hydrated 30%	3.4	1.5	37.6	1.89	1230	2500
SC hydrated 40% “wet”	3.7	1.8	45.1	1.98	1200	2800
Stratum Spinosum	4.1	2.3	57.6	2.10	1060	3600
Stratum Basale	4.4	3.2	80.1	2.22	1060	3600
Dermis	4.0	3.1	77.6	2.21	1080	3430
Blood					1057	3600

The SAR calculation employed the equation:

$$SAR=\frac{{\mathit{\sigma }}_t{E}^2}{{\mathit{\rho }}_t}$$ (1)

where E, σ_t and ρ_t are the maximum electric field (E-field) strength, electrical conductivity and the tissue density respectively of the relevant skin layer tissue type. Here we assume that the maximum electric field achieved in response to a pulse would be the same as that in response to a continuous incident sine wave of 1.0 Vm^-1. The equation used for incident power density in free space (PD) was:

$$PD=\frac{E^2}{377}$$ (2)

where impedance of free space is equal to 377 Ω.

The PD within the skin layers was calculated using the formula:

$$PD=\frac{{\mathit{n}}_t{E}^2}{377}$$ (3)

where n_t is the refractive index of the relevant tissue.

The temperature rise was calculated using two methods. For the brief periods of <100 ns, the contribution from blood flow, diffusion and radiative loss are neglected. It this situation it is sufficient to use the temperature rise formula:

$$\Delta T_t=(SAR/{\mathit{c}}_t)\Delta t$$ (4)

where ΔT_t, c_t and Δt are the temperature rise and heat capacity and the length of time under consideration respectively. The ICNIRP (2013) [25] guidelines specify a total energy of 100 Jm^-2. This is equivalent to the temperature rise produced by SAR from a 1000 Wm^-2 excitation, with a Δt = 0.1s. The thermal model [49,50] and the equation from Wang and Fujiwara [51] can deliver temperature rise estimations within the FDTD simulation, albeit at a reduced resolution when compared to the radiation and transmission studies. The extended time temperature elevation calculations use the bioheat equation [50] in a modified format:

$$\Delta T_t=\frac{k_t{\mathrm{\nabla }}^2{T}_t+{\rho }_{t}SAR-b(T_t-T_b)}{{\rho }_t{c}_t}\Delta t$$ (5)

where T_b is the blood temperature and b is a constant (Wm^-3C^-1) related to blood flow:

$$\mathit{b}={\mathit{\rho }}_b{\mathit{c}}_{b}BP$$ (6)

where ρ_b c_b and BP are the blood tissue density, heat capacity of blood (Table 2) and blood perfusion rate in the tissues respectively.

The blood perfusion rate was set at zero for SC, SS and SB, as they do not contain blood vessels, and was averaged for the Dermis from reported values [52] at 50 mlkg^-1 min^-1 (8.3 x10⁻⁷ m³kg^-1s^-1). The metabolic production of heat can be neglected as heat production in resting humans is relatively low [53], and the SC is composed of dead tissue. The proximity of the skin layers to the outside air results in the heat loss to the environment becoming the most important factor, even at relatively short exposure times. The heat loss to the environment, however, will vary according to the ambient temperature, sweat production, clothing and air flow [54] and thus is difficult to model in a “typical” way. The boundary condition for heat loss to the environment was considered in two scenarios: one based on “room temperature” air of 22° C, and an air temperature of 35° C, simulating a hot, clothed environment. In both cases, the temperature in the skin layers was set at 35° C and blood temperature at 37° C. The thick skin thermal studies were conducted using an “intermediate” mode, in which the outer two layers of the SC are set at 15% hydration and a cascade to 40% hydration just above the SS.

For the radiation penetration and exposure studies, the electric field (E-field), SAR, PD and thermal data was gathered using a polarised, far-field, sinusoidal waveform at exactly 0.45 THz, with an amplitude of 1.0 Vm^-1. The E-field polarisation was in the y direction. The thermal studies for thick and thin skin were conducted using an incident excitation amplitude of 614 Vm^-1, at 4.1 ms for thin skin and 3.6 ms for thick skin.

In thin skin, the simulations yielded SAR results in cut-planes of 669, 381 and 361 (x, y, z orientation). The cut-planes were separated by 0.0037mm, 0.0051mm and 0.001 mm respectively. Thick skin SAR simulations had 717, 570 and 302 (x, y, z) cut-planes, at 0.0014 mm, 0.0023 mm and 0.0040 mm intervals respectively. The SAR sensor output was a false colour image of the absolute values (Wkg^-1). In addition, 7 planar sensors were placed to directly demonstrate the E-field and estimate the resultant PD in all models. These sensors yielded false colour images, either decibel (dB) or linear scale, with a sampling interval of 100 time steps. An amplitude of 1.0 Vm^-1 produces an incident PD of 0.0027 Wm^-2. To bring the exposure to the >0.3 THz, ICNIRP (2013), maximum exposure guideline of 1kWm^-2, the simulation results need to be adjusted to a notional incident excitation amplitude of 614 Vm^-1, and for the < 0.3 THz, ICNIRP (1998), guidelines, the notional incident excitation amplitude is 61.4 Vm^-1.

2.2. Reflection studies

The simulations for the surface reflection studies were conducted using a polarised, far-field, 0.5 ps Gaussian waveform cantered at 0.45 THz, and sampled only at 0.45 THz, with an amplitude of 1.0 Vm^-1. The short pulse was necessary to differentiate the incoming from the reflected excitation. Thin skin reflection studies were conducted at an angle of incidence (θi) of 0° (orthogonal-right angle to the skin) and 50°. These studies were aimed at exploring the usefulness of using variation in the angle of polarised radiation in the hydration estimation within the thin skin epidermis.

The incident excitation for thick skin was varied from θi of 0° (orthogonal), 12.5° (the angle used by Hernandez-Cardoso [21], 25°, and 50° to evaluate the reflection geometry for diabetic neuropathy studies. Separate simulations were run with E-field polarisations oriented in the x (p-polarised) and y (s-polarised) axes within the thick skin models. Given that the simulated time was in the order of 10-24 ps, the dissipation of generated heat within the tissues was not considered in the reflection studies. To evaluate the reflected radiation, 3 E-field point sensors were placed 2.2 mm above the thick skin model, separated horizontally by 0.5 mm.

As noted, the surface of the thick skin has a series of fingerprint ridges and troughs, in which the nominal θi of 0°, 12.5°, 25°, and 50° do not hold for the entirety of the surface, rather they are an indication of the average excitation angle in relation to the x/y co-ordinates. For small areas, a fingerprint pattern in thick skin has the ridges running in a particular direction, thus, the ridges and troughs may give preference for the reflection of a particular polarisation. The thick skin model in Fig. 2. has the fingerprint ridges running generally in the x direction.

The Fresnel equations for reflection and transmission of polarized light are:

$$\begin{array}{l}{\mathit{r}}_s=\frac{n_i\mathrm{Cos}{\theta }_i-n_t\mathrm{Cos}{\theta }_t}{n_i\mathrm{Cos}{\theta }_i+n_t\mathrm{Cos}{\theta }_t}\\ {\mathit{t}}_s=\frac{2n_i\mathrm{Cos}{\theta }_i}{n_i\mathrm{Cos}{\theta }_i+n_t\mathrm{Cos}{\theta }_t}\\ {\mathit{r}}_p=\frac{n_i\mathrm{Cos}{\theta }_t-n_t\mathrm{Cos}{\theta }_i}{n_i\mathrm{Cos}{\theta }_t+n_t\mathrm{Cos}{\theta }_i}\\ {\mathit{t}}_p=\frac{2n_i\mathrm{Cos}{\theta }_i}{n_i\mathrm{Cos}{\theta }_t+n_t\mathrm{Cos}{\theta }_i}\end{array}$$ (7-10)

where r_s, t_s, r_p and t_p are the expressions for reflection and transmission of the S-polarised (perpendicular) and P-polarised (parallel) radiation respectively, and n_i, n_t, θ_i and θ_t denote the refractive indexes of the incident and transmitted media, and the incident and transmitted angles respectively. Contrast (K) is an indication of the capacity to discern between the two hydration states based on the magnitude of the reflected E-field, where K between the “dry” and “wet” configurations is expressed as:

$$\mathit{K}=1-(E_{Dry}/E_{Wet})$$ (11)

where “Dry” and “Wet” refer to 15% and 40% hydrated SC respectively, and E_Dry and E_Wet are the magnitude of the reflected E-field in each configuration. K = 0 represents no difference in the reflected signal (i.e. E_Dry = E_Wet) and K = 1 represents an asymptotic maximum difference. The Fresnel equations specify that K reduces with increasing θ with S-polarised radiation but increases with P-polarised radiation.

The refractive index in the SC changes with hydration from n = 1.76 at 15% (“dry” SC) to n = 1.98 at 40% (“wet” SC). The theoretical changes in reflected radiation with incident angle and refractive index are presented in Table 3 . The best theoretical K (largest difference between n = 1.76 and n = 1.98 is with P-polarised (y direction of the model) radiation at 50°, but under these conditions the total reflected E-field intensities are low.

Table 3. Theoretical reflection E-field magnitudes with a 1.0 Vm^-1 incident excitation. The estimation of the variability of reflected radiation using the Fresnel equations at “dry” 15% (n=1.76) and “wet” 40% (n=1.98) SC hydration, at θ of 12.5°, 25° and 50°, as a proportion of the total incident radiation. The best theoretical contrast (largest difference) is with 50°, P-polarised radiation, but at low total intensities.

	S-polarised (y axis)		S-polarised Contrast (K)	P-polarised (x axis)		P-polarised Contrast (K)
	EDry	EWet	1- EDry/EWet	EDry	EDry	1- EDry/EWet
Angle of incidence	n = 1.76	n = 1.98		n = 1.76	n = 1.98
12.5°	0.080	0.113	0.292	0.072	0.103	0.304
25.0°	0.094	0.131	0.282	0.059	0.087	0.320
50.0°	0.179	0.230	0.222	0.013	0.026	0.494

3. Results

3.1. Transmission, absorption and thermal simulations

A lateral cross section of a typical E-field penetration in thin skin at 6.9 ps into the simulation is presented in Fig. 3A . There is significant penetration of radiation into the region of the rete ridges and the SB. A typical cut-plane of the thin skin “micro SAR” distribution following an excitation of 1.0 Vm^-1 (equivalent to an incident PD in free space of 2.7 mWm^-2) is presented in Figs. 3B and 3C.

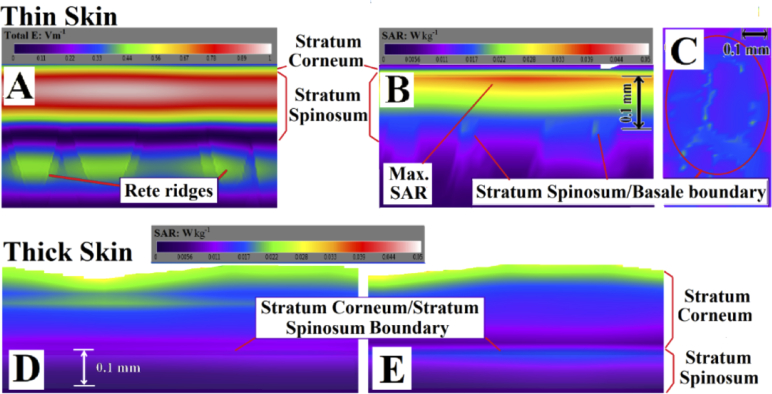
Fig. 3.

(A) Lateral cross section of a typical E-field distribution in thin skin following an excitation of 1.0 Vm^-1. The rete ridges are visualized. (B) The thin skin SAR distribution. The maximal SAR is in the upper SS and there are anomalous regions at the SS/SB boundary. (C) Horizontal section of the distribution of SAR at the SS/SB boundary at 0.13 mm below the skin surface, with regions of up to 100% higher absorption compared to the average. (D) Thick skin SAR with an intermediate mode in which the outer two layers are set at 15% hydration and a cascade to 40% hydration just above the SS. The energy is deposited in the upper regions of the dead SC. (E) The “dry” mode of thick skin, with more radiation surviving to the upper regions of the SS.

The effective SAR spatial resolution is 0.01 mm³ (λ/33³ in the SS). The maximal SAR at 0.45 THz occurs in the upper SS, at 0.03 to 0.05 mm under the skin surface. The SAR drops to 10% of the maximal levels in the SB. The three dimensional FDTD simulations allowed for effects of lensing and internal reflections from irregular surfaces and delivered direct results for SAR values. There were 0.01-0.02 mm³ regions of SAR increase of 100% over the surrounding tissues at the SS/SB boundary. In practice the variation in the hydration of the thin skin SC layers between 15% and 40% had negligible impact on the penetration of the orthogonal excitation in thin skin.

Thick skin SAR simulations in the “wet” mode (top SC layers at 40% hydration) show most of the energy is deposited in the upper layer of the dead SC, with variation following the pattern of the ridges and troughs of the fingerprint above. An “intermediate” mode, in which the outer two layers are set at 15% hydration and a cascade to 40% hydration just above the SS, produces a deeper radiation penetration to the wetter, deeper, SC (Fig. 3D). In simulations using the “dry” mode of thick skin, where the SC layers and the Stratum Granulosum/Stratum Lucidum are set at 15%, more radiation survived to the upper regions of the SS, but with no impact on the SB layer (Fig. 3E).

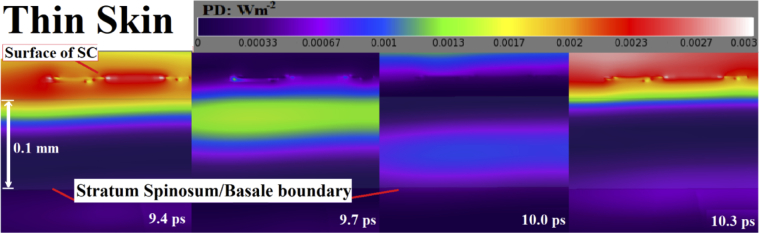
Living tissue n is approximately 2.0-2.2, thus the PD in the living tissues reaches higher values than in an equivalent electric field in free space. The local variations in the PD in thin skin are presented in a time series in Fig. 4 , from 9.4 ps to 10.3 ps into the simulation. The PD is shown to fall rapidly after passage through the upper SS with a PD of 0.0005-0.0007 Wm^-2 at the SS/SB boundary, which is ∼10% of the intensity of the incident excitation. The SS/SB boundary regions of higher SAR absorption were not discernable in the PD simulations.

Fig. 4.

Lateral cross section of a typical wave progression in thin skin following an excitation of 1.0 Vm^-1, (equivalent to a PD of 0.0027 Wm^-2 in free space). The thin skin PD progression is shown. The PD falls rapidly after passage through the upper SS, with a PD of ∼0.0005 Wm^-2 at the SS/SB boundary.

The results for the PD, “micro” SAR and temperature rise are outlined in Table 4 . The values for the PD calculations was taken from the simulations. The data are also adjusted to take account of the maximum recommended incident PD in the ICNIRP, (2013) guidelines of 1 kWm^-2 for exposures of >10 s [25]. The thermal rise is presented with three scenarios; a long-term exposure simulations with the ambient air temperatures of 22° C, and 35° C with an incident excitation of 614 Vm^-1 (corresponding to a PD of 1 kWm^-2), and an analytically calculated temperature rise with a total dose for short term (1-100 ns) radiation of 100 Jm^-2 [25] with the “micro” SAR values for the temperature calculations are taken from the simulation.

Table 4. Adjusted PD, micro SAR and temperature rise in thin and thick skin. PD, “micro” SAR and temperature rise in thin skin in the region of maximal absorption in the upper SS, the high SAR regions at the SS/SB boundary and the maximal absorption layer of the dead SC in the thick skin. The PD, SAR was adjusted for the maximum incident PD in the ICNIRP, (2013) [25] guidelines of 1 kWm^-2. Temperature rise assumed ambient air temperatures of 22° and 35° C.

	Simulation		Adj. 1 kWm-2		Temperature Rise
	PD	SAR	PD	SAR	22°C	35°C
Thin Skin	Wm-2	Wkg-1	Wm-2	Wkg-1	°C	°C
Upper Stratum Spinosum	0.0054	0.045	2010	16980	0.010	0.012
Lower Stratum Spinosum					0.020	0.020
Spinosum/Basale boundary	0.0015	0.015	565	7540	0.018	0.020
Thick Skin
Stratum Corneum	0.0027	0.0032	1000	12060	0.025	0.031

The thick skin was modelled in the “intermediate” mode as per Fig. 3D. When the ICNIRP, (2013) [25] recommendation of maximal exposure PD of 1 kWm^-2 is applied, the PD in the upper SS reached ∼2 kWm^-1; more importantly, the high exposure regions at the SS/SB boundary reached exposures of >500 Wm^-1. With the exposure adjusted to a PD of 1 kWm^-2, the SAR at the SS/SB boundary reached >7500 Wkg^-1 in high exposure regions.

As noted, the thermal studies for thick and thin skin were conducted with a using larger cell size and using a sinusoidal incident excitation amplitude of 614 Vm^-1 producing an incident PD of 1.0 kWm^-2. Thermal equilibrium was achieved at 4.1 ms and 3.6 ms for thin and thick skin respectively. The thermal studies with both the 22° and 35° C air temperature showed the highest temperature rise in the inner region of the SS, the region most distant from both the air and the blood circulation. The analytically calculated short pulse energy of 100 Jm^-2 used the assumption that it was equivalent to the temperature rise produced by SAR from a 1000 Wm^-2 excitation over 0.1s.

3.2. Reflection simulations

The maximum reflected E-field values at 50° for thin skin and 12.5°, 25° and 50° in thick skin are shown in Table 5 . There are significant differences in the S-Polarised and P-polarised values at 50°, with both skin types, with the greatest contrast at 50°.

Table 5. Maximum reflection E-field with a 1.0 Vm^-1 incident excitation. The maximum reflected E-field values at 50° for thin skin and 12.5°, 25° and 50° in thick skin 2.0 mm above the skin model. There are significant differences in the S-Polarised and P-polarised values at 50°, with both skin types, with the maximal K at 50°, with P-polarised excitation, in line with the theoretical predictions. K is reduced from the theoretical in all modes due to skin surface topology.

		S-polarised (y axis)		S-polarised Contrast (K)	P-polarised (x axis)		P-polarised Contrast (K)
		EDry	EWet	1- EDry/EWet	EDry	EWet	1- EDry/EWet
		n = 1.76	n = 1.98		n = 1.76	n = 1.98
Thin skin
Angle of incidence	50.0°	0.417	0.461	0.095	0.135	0.176	0.233
Thick skin
Angle of incidence	12.5°	0.178	0.214	0.168	0.174	0.212	0.179
	25.0°	0.182	0.219	0.169	0.175	0.216	0.190
	50.0°	0.195	0.225	0.133	0.070	0.094	0.255

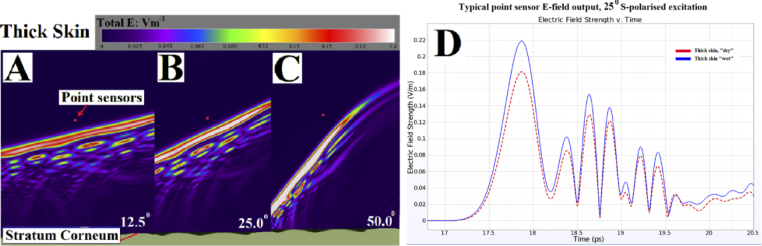
The thin skin reflection studies demonstrated that the outermost layer of the SC is responsible for most of the detected reflection. Given that the thin skin surface was modelled as a series of oblate spheroids, an angle of 50° from the orthogonal was required for the difference between the S-polarised and P-polarised excitation to become significant. The reflection studies of thick skin also illustrate that the bulk of the reflection comes from the outermost layer of the SC. The thick skin reflection of the E-field at 12.5°, 25° and 50° and the location of the point sensors 2 mm above the surface is shown in Fig. 5A-C . The time domain output of an E-field point sensor with the “dry” and “wet” settings using the 25°, S-polarised excitation is shown in Fig. 5D. Although the absolute values vary, the time domain change of the E-field value is similar for both the “dry” and “wet” settings, with only minor variations.

Fig. 5.

(A-C) A typical thick skin reflection pattern output of the E-field with S-polarised radiation at 12.5°, 25° and 50°, using a vertical planar sensor in the center of the model aligned with the x direction. Most of the reflection forms a single wave-front reflecting from the surface of the SC. The location of the point sensors 2.0 mm above the surface is marked. (D) Typical E-field time domain outputs of a point sensor with the “dry” (15% SC hydration, red dashed line) and “wet” (40% SC hydration, blue solid line) settings with 25°, S-polarised excitation.

The insertion of a high-density polyethylene (HDPE) window between the foot and the incoming radiation as used in the diabetic vasculopathy studies [21] introduces several new factors, making the direct comparison between the direct air and HDPE sheet reflection measurements difficult. At 0.45 THz the refractive index of HDP is 1.52 and the absorption coefficient is very low, in the order of 0.01 cm^-1 [55]. This translates to an ɛ’ of 2.31 and an ɛ” of 0.02. Given the refractive index of 1.52, the presence of a HDPE sheet produces a significant additional reflection at the air/HDPE interface and changes the incident angle at the HDPE/SC interface (an incident angle of 12.5° at the air/HDPE interface produces an incident angle of 8.2° at the HDPE/SC interface).

The capacity of a detection system to separate the air/HDPE interface reflection from the HDPE/SC interface reflection depends on the speed of the detector and the thickness of HDPE sheet. A thick HDPE sheet would delay passage of the radiation to and from the HDPE/SC interface, producing a temporal separation of the air/HDPE interface reflection from the HDPE/SC interface reflection. A further issue is the flattening of the surface of the skin at the HDPE/SC interface. This reduces any advantage that polarised incident radiation may have as there is a loss of any preferred orientation of the “fingerprint” pattern.

4. Conclusion and discussion

At 0.45 THz, the simulations suggest that the bulk of the energy in thin skin is absorbed in the upper region of the Stratum Spinosum (SS). Given that the cells in this region are undergoing the end stages of keratinocyte differentiation leading to apoptosis (programmed cell death), the only consideration is short term damage to the cells leading to premature death and shedding. The Stratum Basale (SB) is of greater long-term importance, given that the layer is responsible for the majority of cell proliferation. At 0.45 THz, when adjusted for the ICNIRP (2013) guidelines of a maximal PD of 1kWm^-2, the simulated exposures produced localised SAR levels at the SS/SB boundary of >5600 Wkg^-1. The simulations confirm that there is a negligible thermal impact of exposure at the maximal levels recommended in the ICNIRP (2013) guidelines, with sustained temperature rises in the order of 0.02° C at the SS/SB boundary using the PD of 1kWm^-2. Other studies of the thermal rise [56] at the skin surface suggest that the thermal impact at the surface may be higher, in the order of .018° C at 0.45 THz for a PD of 10 Wm^-2. It follows that if the skin was already under heat stress, and there were multiple sources of radiation (each within the ICNIRP guidelines), a temperature rise beyond the injury threshold of 45° within the skin could not be excluded.

The electric field (E-field) studies in thin skin suggest that the radiation penetrates to the level of the rete ridges in thin skin at an intensity of 0.3-0.4 Vm^-1, (using a 1.0 Vm^-1 excitation), which leaves open the possibility of imaging the thin skin rete ridge region using THz radiation. The reflection studies of thin skin suggest that the thin skin Stratum Corneum (SC) layer may provide information regarding hydration.

In thick skin, the SAR, PD and E-field studies show that the thicker SC layer protects the underlying tissues, with little penetration of radiation or absorption past the SC/SS boundary. Simulations of thick skin suggest that only the uppermost Stratum Corneum layer is sampled in reflection studies. The high-density polyethylene (HDPE) window as used in the existing diabetic vasculopathy studies [21] makes the direct comparison between the direct air and HDPE sheet reflection measurements difficult, however, given the relatively poor contrast in the simulations studies at an angle of 12.5°, the reported changes in the reflective properties of thick skin in diabetic neuropathy may not be due to hydration differences within the SC alone and may indicate changes in the nature of the SC itself or altered sweat duct activity. Polarisation studies suggest that measurements at several orientations with polarised radiation may improve hydration estimation by improving the measured change in the refractive index.

Since the wavelength of THz radiation is in same the order of magnitude as the scale of skin structures such hair and sweat ducts, there is possibility of interaction with these structures that may confound the findings and need to be explored.

Given that the non-thermal consequences of THz radiation are poorly understood and the inconsistency between the ICNIRP (2013) [25], >0.3 THz and the <0.3 THz (ICNIRP (1998) [23] guidelines, there may be anxiety generated regarding the discrepancy between the standards. The authors urge that a greater consistency be applied at the 0.3 THz boundary between the >0.3 THz ICNIRP (2013) [25] and the <0.3 THz (ICNIRP (1998) [23] guidelines.

Funding

National Health and Medical Research Council10.13039/501100000925 (1042464).

Disclosures

The authors declare no conflicts of interest.