How to define and optimize axial resolution in light-sheet microscopy: a simulation-based approach

Abstract

“How thick is your light sheet?” is a question that has been asked frequently after talks showing impressive renderings of 3D data acquired by a light-sheet microscope. This question is motivated by the fact that most of the time the thickness of the light-sheet is uniquely associated to the axial resolution of the microscope. However, the link between light-sheet thickness and axial resolution has never been systematically assessed and it is still unclear how both are connected. The question is not trivial because commonly employed measures cannot readily be applied or do not lead to easily interpretable results for the many different types of light sheet. Here, we introduce a set of intuitive measures that helps to define the relationship between light sheet thickness and axial resolution by using simulation data. Unexpectedly, our analysis revealed a trade-off between better axial resolution and thinner light-sheet thickness. Our results are surprising because thicker light-sheets that provide lower image contrast have previously not been associated with better axial resolution. We conclude that classical Gaussian illumination beams should be used when image contrast is most important, and more advanced types of illumination represent a way to optimize axial resolution at the expense of image contrast.

1. Introduction

Light sheet microscopy [1] has proven to be an enabling technology for a number of research fields including developmental biology [2], cell biology [3], neuroscience [4] and many more [5]. Applications benefit from the low photodamage [6] and high image acquisition speed [7,8] enabled by efficient use of light and high degree of parallelization. The purpose of the light sheet is to optically slice the sample to generate images with high contrast of thickly fluorescent samples. The thickness of the slice depends on the thickness of the light sheet. In other words, the light sheet fully determines optical sectioning. Illumination by a thicker light sheet results in the projection of a thicker section of the sample into a single image. If the light sheet is thicker than the depth of focus of the detection lens, the image contrast drops due to blurred information from object regions illuminated by the light sheet but out-of-focus of the detection lens. In thickly fluorescent three-dimensional samples, optical sectioning (OS) is required to generate image contrast. Because resolution depends on contrast, i.e. the separation of individual features is only possible for a sufficient drop in signal in between two features, optical sectioning should be seen as one of the fundamental parameters of a light sheet microscope.

The length of the light sheet determines the field of view that can be illuminated evenly – with nearly equal optical sectioning and axial resolution. Due to diffraction the thickness depends on the length of the light sheet: A conventional Gaussian-beam light sheet created at a higher NA is thinner at its waist but the distance over which it remains thin is also shorter. In commonly used microscopes that illuminate and detect light using a single objective resolution is anisotropic. In a light sheet microscope, lateral resolution is determined by the NA of the detection objective alone and axial resolution is additionally influenced by the intensity profile of the light sheet, hence by the illumination objective. A quantitative comparison of the resolution of light sheet microscopes and other fluorescence microscopy techniques can be found in [9].

Many researchers put a lot of effort into improving the properties of the light sheet because of its strong influence on image quality. The static light sheet was replaced by a scanned light sheet [10] and holographic beam shaping was employed to generate Bessel beams [11] to reduce scattering artefacts building on their self-reconstruction properties [12,13]. Since Bessel beams were also found to be non-diffracting, which means that their profile does not change over significant distances, attempts were undertaken to use them to provide higher resolution over larger fields of view, which required additional efforts, such as structured illumination or two-photon excitation [14], confocal detection [15] or application of the STED principle [16] to recuperate image contrast. Other non-diffracting beams like the scanned Airy beams [17] or the scanned Sectioned Bessel beam [18] but also Static Line Bessel sheets [19] and static Airy sheets [20] were also employed. Coherent super-position of Bessel beams, termed lattice light sheet was reported to be especially beneficial [3] by providing high spatiotemporal resolution. In summary, many different light sheet types have been proposed promising benefits particularly in terms of achievable image quality.

Considering the abundance of illumination schemes a general measure for comparison of the benefits of the methods is desirable. So far, measures used for the comparison are different across publications and range from image contrast [21], or measures of resolution such as the profile through the image of a bead [3,9] or the modulation transfer function (MTF) [3,17,18]. The lack of a uniform measure or application of measures used in other types of microscopes is a problem for two reasons: Firstly, the properties of the light sheets are very different, and some measures cannot account for these differences. An obvious example concerns the intensity profile of some light sheets decaying monotonically while others show side-lobes. Second, and more importantly, these measures may not be adequate to reflect the influence of parameters that control the ratio of axial resolution and image contrast that they provide. For example, in a confocal microscope, axial resolution and image contrast are linked unambiguously, i.e. they cannot be influenced independently. But in a light sheet microscope the light sheet can largely affect resolution and contrast independently. Accounting for this additional degree of freedom, we aim to provide measures to quantitatively analyze and compare light sheets in this publication.

Here, we establish a set of versatile and accurate measures that take the special properties of light sheet design into account and allow to quantify properties that are directly relevant for the image quality: axial resolution and optical sectioning. The measures were applied to a selection of different light sheets. Through this comprehensive assessment we gained understanding of the trade-offs between different illumination approaches. The question to be answered in this paper is not primarily which beam is better than the other because we found a simple binary answer to be inadequate. Rather, this study provides the reader with measures and a framework applied to a neutral and rigorous comparison between the trade-offs that exist between different illumination concepts in light sheet microscopes, enabling an informed decision. This endeavor is supported by the Matlab code we provide with this publication for the user to simulate various existing light sheets as well as new ones and quantitatively compare them to each other.

We apply our measures to simulated data of the 3D intensity distribution of the different light sheets for linear and two-photon excitation. The choice in our analysis was made according to the following rules: We limited our analysis to light sheet types that depend on the NA and up to one additional parameter. The beams differ in the order of the polynomial that describes the phase of the beams: A linear function (ϕ(r) ∼ r) for the Bessel beam, the Bessel beam lattice and the Double beam (ϕ(x,y) ∼ x), a quadratic function (ϕ(r) ∼ r²) for the Focused flat-top and the Gaussian beam, a cubic function (ϕ(x,y) ∼ x³ + y³) for the Airy beam, and a quartic function (ϕ(r) ∼ r⁴) for the Spherically aberrated beams. Light-sheets can be generated with these beams either by scanning across the field of view or by shaping the beam directly into a sheet, for example by a slit aperture in the back aperture of the illumination objective. The Line Bessel Sheet [19] is generated like a Bessel beam but with a slit aperture cropping the ring in the back focal plane. In principle, lattice sheets can be generated by a periodic structure of slits in the back focal plane for any kind of beam, not only the Bessel beam. When formed into a sheet by a slit aperture in the back focal plane, the profile of the Double beam, the Focused flat-top beam, the Gaussian beam, the Spherically aberrated beam remains unaffected.

Our simulation is based on the scalar propagator approach [22] which considers monochromatic, coherent light. The propagator itself represents an analytical solution to the Helmholtz-equation and does not use approximations. The accuracy of the simulation was validated [23,24]. We ensured that apodization and polarization effects can be neglected for light sheets.

2. Optical performance parameters of light sheet microscopes

We present different types of commonly employed light sheets and introduce three measures: Two for thickness and one for length. Most importantly, we use two separate measures to quantify different aspects related to the thickness of the light sheet that have different meanings for the performance of the microscope. This separation is both necessary and suitable to characterize a wide range of light sheets.

3. Characterization of light sheets

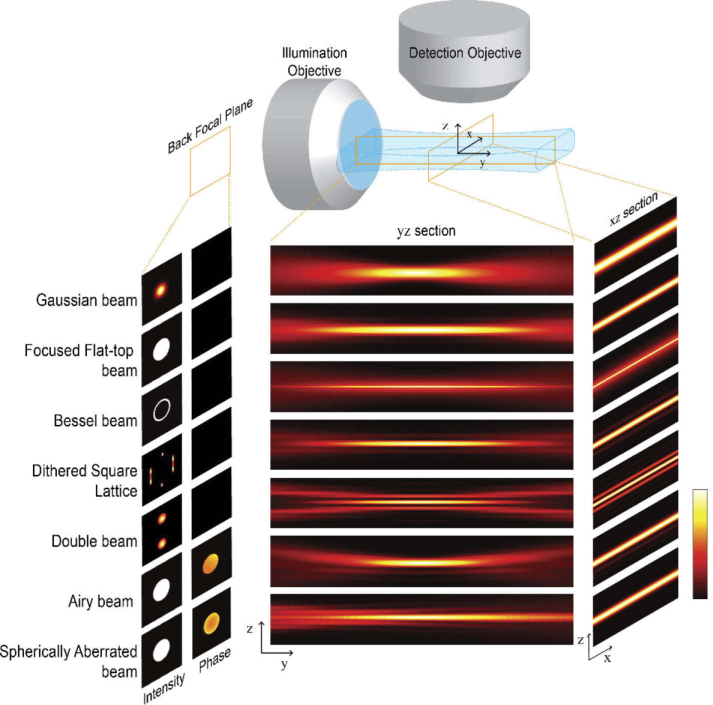
In this paragraph we give a short introduction to illumination beams that have been employed for sample illumination in light sheet microscopes. An overview of the different light sheets is shown in Fig. 1. The beams are described in more detail in Appendix A. Conceptually, a division into two major categories is helpful:

• •Single-lobe beams: These beams can be described by a single parameter: the focusing NA. The most commonly used light sheet has a Gaussian profile [1,10]. The intensity profile decays monotonically from the peak following a Gaussian distribution. The profile of Focused flat-top beams is often referred to as Airy disk. It exhibits a strong peak and very weak sidelobes and the ratio of their respective magnitudes is fixed.
• •Multi-lobe beams: These beams are determined by two parameters: The NA and a second parameter that is different for each beam. Examples constitute the Bessel beam [13,14], the Bessel beam lattice [3], Airy Beams, [17,20], Spherically aberrated beams and the Double beam [19]. The intensity profile of multi-lobe beams does not decay monotonically with the distance from the main lobe but shows a socket (e.g. for Spherically aberrated beams) or exhibits side lobes or side sheets (e.g. for the other three types). The side lobes carry a large proportion of the total power of these beams.

Fig. 1.

Illustration of the six light sheet types included in the comparison. The amplitude and phase of the electrical field in the back focal plane of the illumination objective is used to simulate the intensity distribution of the beams in the sample volume. Cross section along the illumination and detection axis (YZ) and along the scan axis and detection (XZ) of the sheets resulting from beam scanning or sheet dithering.

The light-sheets can be formed statically, e.g. by a cylindrical lens in the beam path, by dithering the lattice or by scanning the beam in the focal plane of the detection lens.

3.1. Quantitative analysis of light sheets

In this section we explain the measures we establish in this manuscript and explain their practical meaning and relevance to the performance of the microscope.

3.1.1. How thick is a light sheet? Main lobe thickness vs optical sectioning

When assessing the thickness of the light sheet it is important to keep in mind the two image quality parameters that the light sheet affects: axial resolution and image contrast. We base our analysis on the facts that:

• •axial resolution depends on the width of the profile of the microscope’s point-spread function (PSF) along the detection axis, and
• •image contrast depends on the overall thickness of the light sheet.

For the comparison purpose we develop here, both parameters are reflected by measures enabling to compare the performance of different light sheets. The measure for axial resolution is based on the width of the light sheet’s intensity profile along the detection axis. The measure for the thickness of the light sheet quantifies the range along the detection axis over which a significant portion of the total detected fluorescence originates.

For a conventional light sheet created by a Gaussian beam the two parameters are closely related and can be assessed with one existing measure. For example, the waist of a Gaussian beam is defined as the range around the peak where the intensity is larger than 1/e2 = 13.5% of its value at the peak. The beam carries 1-1/e2 = 86.5% of the power within a circle of that radius. Both measures are inseparably linked. For other beams, the measure needs to be generalized to reflect both the drop in intensity around the peak and the region carrying a substantial fraction of the power.

Looking at a light sheet formed by a scanned beam the relevant quantities are

• •the distance along the detection axis where intensity first drops to a fraction of the peak intensity and
• •the total fluorescence generated by the light sheet within a certain distance from the detection focal plane.

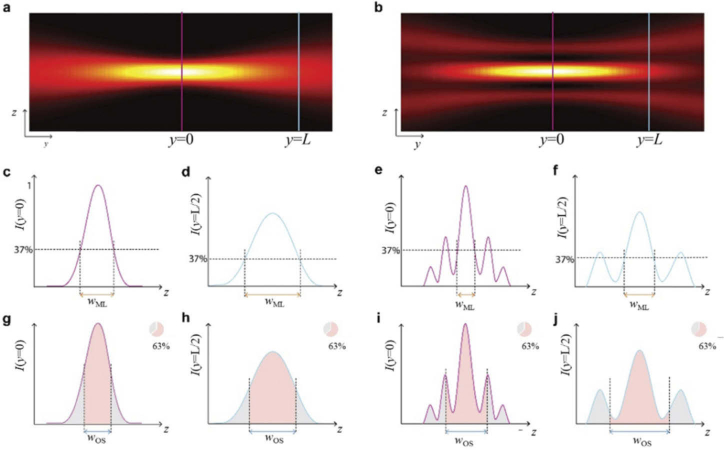
The first measure yields axial resolution while the second yields contrast. Axial resolution is the minimum distance at which two objects along the detection z-axis can be separated. Contrast is the difference in signal of an in-focus feature against background signal, mainly from out-of-focus features. Figure 2a shows an example for a light sheet formed by a single lobe beam. The width of the profile measured at 1/e = 37% of the peak intensity is shown in Fig. 2c, d for two positions along the beam’s propagation axis and the integral under the profile that marks 1-1/e = 63% of the total power of the beam in shown in Fig. 2g, h. Within the range where the intensity is larger than 37% of the peak intensity, the light sheet with a Gaussian intensity profile carries a higher fraction of 84% of its total power. The reason is that the light sheet is not a circularly symmetric beam but essentially spreads in only one direction, along the detection axis. For the purpose of comparing different light sheets the exact ratio is not essential, but the fact that this ratio does not depend on whether FWHM, 1/e or 1/e2 measures are used. Most importantly the ratio is independent of the length of the light sheet. The ratio between the first measure (drop in intensity) and the second measure (power contained within a region) are independent from the numerical value of the ratio for any length of the single-lobe light sheet.

Fig. 2.

Definition of Main Lobe Thickness and Optical Sectioning. yz-cross sections of the intensity of a single-lobe beam (a) and a multi-lobe beam (b) are shown. The respective profiles at the focus (purple line) and at a distance y = L, where the thickness has doubled (blue line) are shown in c-j. c, d and e, f illustrate the main-lobe thickness, defined as the range where the intensity is higher than 37% of the maximum intensity in the focus, in focus (c, e) and at distance y = L (d, f) for single-lobe beam (c, d) and multi-lobe beam, respectively. Sub-figures g-j correspondingly illustrate Optical Sectioning w_OS, defined as the range that contains 63% of the beam’s power.

For multi-lobe light sheets, however, the values obtained for the first and the second measure may be substantially different because they exhibit a more complex structure. As indicated in Fig. 2 on the right side, the distance over which the intensity profile drops to 1/e of its peak reflects only the thickness of the main lobe (Fig. 2e, f). Therefore, we introduce the term “main lobe thickness” for this measure. Optical Sectioning wOS, indicated in Fig. 2i, j, considers that the main lobe may not carry sufficient power to contribute 63% of the total detected signal. This measure gives a substantially larger value than the main-lobe thickness and more closely reflects the true light sheet thickness.

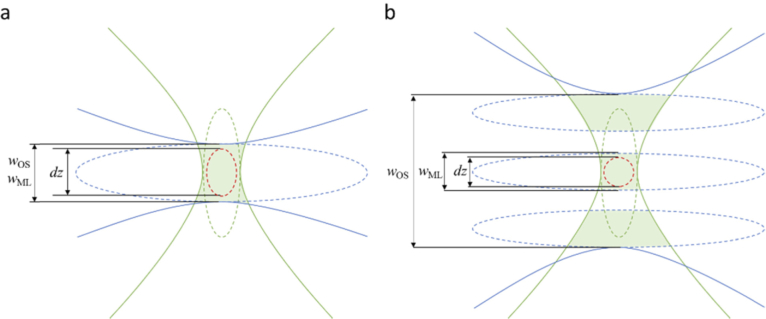
In many previous publications a missing distinction between light sheet thickness and thickness of the main lobe could cause confusion, e.g. when referring to „ultrathin planar illumination produced by scanned Bessel beams” or “Ultrathin Bessel Light Sheets” although only the main lobe is thinner than a conventional Gaussian light-sheet of equal length [19,25]. For the most frequently used light sheet with a Gaussian profile there is only one sheet and the measure of main lobe thickness and light sheet thickness are strictly proportional. But as illustrated in Fig. 3 this is not true for multilobe beams, that exhibit an auxiliary structure, such as side lobes or multiple parallel sheets. For multilobe beams a significant fraction of the total illumination power which the sample is exposed to is ignored when only the thickness of the main lobe is considered. This additional exposure contributes to the detected fluorescence signal in a light sheet microscope, potentially decreasing the image contrast. It is thus very important to consider the following: The slices through the PSF along the detection axis that are usually shown can be used to infer axial resolution. However, they make it impossible for the observer to estimate the optical sectioning performance or light-sheet thickness.

Fig. 3.

Schematic illustration of the effect of different beam shapes on axial resolution dz and optical sectioning OS in a light sheet microscope. The illumination PSF (blue) indicates the intensity of the illumination light. The detection PSF (green) indicates the location-dependent detection probability for fluorescence photons. The dotted lines indicate iso-intensity surfaces, e.g. at 37% of the peak value. The dotted red line indicates the iso-surface of the combined illumination and detection PSF (product of illumination intensity and detection probability). Its extent along the detection axis is proportional to the axial resolution of the system. The green shaded area indicates the volume where fluorophores are illuminated, and fluorescence is collected. The optical sectioning measures the extent of this volume along the detection axis. In a), where a single lobe illumination beam is shown, resolution is anisotropic, i.e. lateral resolution is better than axial resolution, but optical sectioning is close to axial resolution. In b), where a multi-lobe illumination beam is sketched, resolution is isotropic, but additional fluorescence signal is collected from the areas illuminated by the side lobes. Optical sectioning is inferior to axial resolution. The side lobes illuminate out-of-focus planes that blur the resulting image.

3.1.2. How long is a light sheet? Generalized Rayleigh range

Having established a measure for the light sheet thickness, it is sensible to base the definition of the light sheet length on it. This corresponds to a generalization of the concept of the Rayleigh range so that it can be applied to all the beam types included in our analysis. We choose to define the length of a light sheet as the distance over which the light sheet thickness, which we measure in terms of optical sectioning, doubles. This measure yields values equivalent to the Rayleigh range for Gaussian beams (except the Rayleigh range is based on an increase by a factor of √2) but better reflects loss in contrast by the spreading of beams with a non-monotonically decaying profile, a broader base or side-lobes. The measure quantifies the minimum extent along the detection axis that contains 67% of the light sheet’s energy regardless of the position of the light sheet’s peak along the detection axis. Even though it would be conceptually easier and more straight-forward to calculate, a measure based on the extent of the on-axis intensity is not useful for the comparison of different light sheets. For single lobe beams, both measures are strictly proportional to each other, but not for the other beams used in light sheet microscopy. In thickly fluorescent samples image contrast is essential and the optical sectioning is the parameter that best reflects the microscope’s ability to generate images with high contrast.

3.2. Comparative analysis

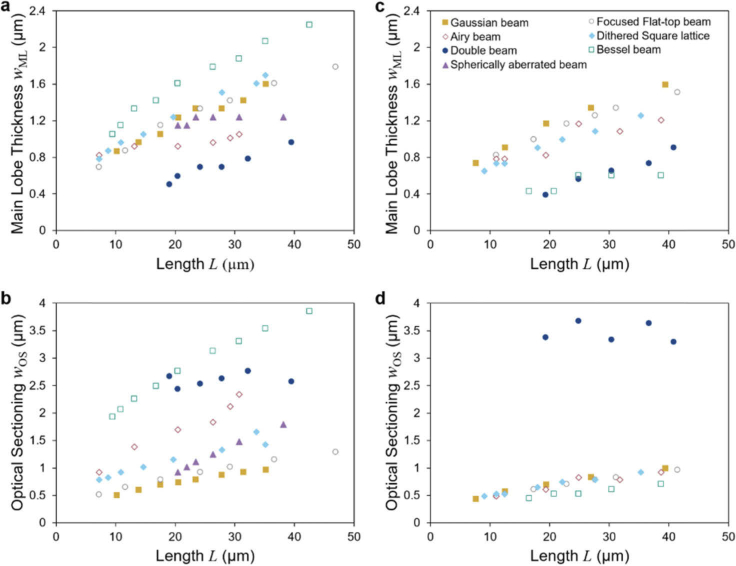
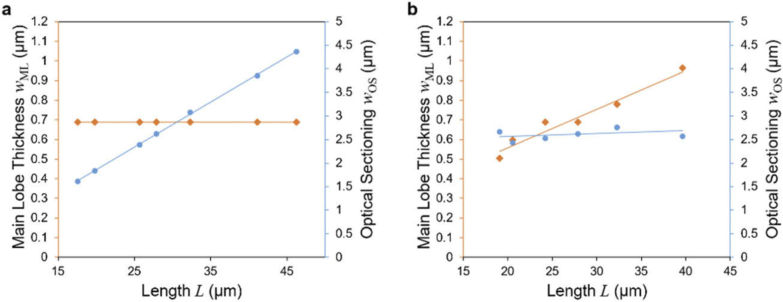
We used numerical simulations to generate the seven different light sheets shown in Fig. 1 for both linear and two-photon excitation. We used a wavelength of 488nm for linear excitation and 920nm for two-photon excitation. Figure 4 shows the main lobe thickness and full light sheet thickness / OS (see Fig. 3) as function of the light sheet length. Details on the simulation are explained in Appendix B.

Fig. 4.

Measurements of main lobe thickness and optical sectioning from simulated data. Main lobe thickness (a, c) and optical sectioning (c, d) are shown as a function of length for linear (a, b) and two-photon excitation (c, d). Parameters used in the simulations are NA = 0.14 to 0.26 for Gaussian beams; NA = 0.16 to 0.40 Focused flat-top beams; NA = 0.05 and separation NA = 0.14 to 0.3 for Double beams; NA = 0.5 and phase parameter a = 4 to 12 radians for Airy beams; NA = 0.32 to 0.6 with ring thickness parameter ɛ = 0.7 for the Bessel beam, NA = 0.25 with quartic phase amplitude a = 0.04 to 0.09 radians for the Spherically aberrated beam; and NA = 0.3 to 0.55 for ɛ = 0.7 for the dithered Square Bessel beam lattice.

To tune the length L of the light sheet, we varied the Numerical Aperture NA for the Gaussian and Focused flat-top beam. For the Double beam we adapted the separation between the two sub-beams in the back focal plane, NA_sep and held the NA of the sub-beams constant. For the Airy beam, the amplitude of the cubic phase was altered for a constant NA of the beam. For the Spherically aberrated beam, we varied the magnitude of the spherical aberrations at a constant NA. For the Bessel beam and the Bessel beam lattice we varied the NA for constant relative ring thickness parameter. Details on the generation and the beam parameters are given in Appendix B.

We find the expected square-root dependency of both the light sheet thickness and the main lobe thickness on the length for the Gaussian beam and the Focused flat-top beam. For these beams the width depends linearly on the NA and length scales inversely with the square of the NA.

Surprisingly, both the thickness of the main lobe and the optical sectioning of the dithered Square Bessel beam lattice, which was previously identified to provide best confinement of the excitation [3], were found to be a little worse than for the conventional beams. One explanation is based on the composition of the angular spectrum: there are two side bands and a split central band (see Fig. 1 where the intensity in the back focal plane is shown). The side bands and the central bands each generate beams that propagate at equal angles with respect to the optical axis. They also have equal depth of field which can be derived directly from the fact that the propagation invariant distance (the depth of focus or length of the light sheet) is given by the radial width of the angular spectrum [26]. However, the light-sheets created by the side bands provide less confinement along the detection axis. The angular spectra of these two sheets is less confined along k_z, the direction of the detection axis. The side-bands provide lateral structuring of the light sheet which is useful when structured illumination is used to recuperate image contrast and resolution in a post-processing step, but by dithering the light sheet the lateral structure of the light sheet blurs and the sidebands only increase the overall thickness of the light sheet. The dithered lattice can also be understood by relying on the Field Synthesis Theorem [27]: It is an incoherent superposition of three light sheets: A Line Bessel sheet [19] and two Focused flat-top light sheets. The Line Bessel sheet alone, like the Double beam, would provide a narrow main lobe but poor optical sectioning due to the side lobes. Through the incoherent superposition with the broad Focused flat-top beams the fine structure of the Line Bessel Sheet is washed out.

We also analyzed the hexagonal lattice. It features an additional degree of freedom: The period of the stripe pattern in the back focal plane. A more detailed description and results are shown in Appendix B. In summary, for the hexagonal lattice as for all other multi-lobe beams, a thinner main lobe comes at the cost of inferior optical sectioning.

For the Spherically aberrated (SA) light sheet an increase in depth of focus (light sheet length L) is obtained for equal NA by increasing the magnitude of the aberrations. In practice, these can arise whenever a microscope objective designed for one refractive index is used for another. This is often the case when optically cleared samples are examined. Due to their usually large dimensions, light sheets with low NA are used. In these cases, the effect of SA is small since they scale with NA⁴. In Fig. 4 it can be seen that at L∼15 µm, where the SA is weak, both w_OS and w_ML of the SA beam are similar to the diffraction-limited Gaussian beam. For stronger SA the length of the light sheet increases. While the associated increase in main lobe thickness w_ML is smaller than for the Gaussian beam, the increase in thickness w_OS is larger. Thus we conclude that a thicker light-sheet is the price to pay to maintain a thinner main lobe over a larger distance.

Similarly, for the Airy beam w_OS increases more strongly than for the Gaussian beam while w_ML increases less. However, w_OS showed a linear dependency on length L. We account this fact to the asymmetrical shape of the beam where all side lobes lie on one side of the main lobe.

The Double beam shows almost no dependency of optical sectioning on length. This effect can be explained by the fact that the Double beam light sheet is the product of the interference of two beams (or ‘sub-beams’) where the length L is increased by reducing the angle between the two sub-beams. As a consequence, the range along the optical axis where the sub-beams interfere stretches. However, because the NA of the sub-beams are not changed, the cross-section of the interference pattern changes only weakly.

For two-photon excitation the results show some interesting differences. We expected that the nonlinear fluorescence excitation leads to a suppression of the side lobes and thereby improves optical sectioning. We found that the Gaussian and Focused flat-top beams yield very similar results for linear and two-photon excitation. Here, the longer wavelength is almost completely compensated by the nonlinear response. The Bessel beam, which performs poorly for linear excitation outperforms all other beams in our selection for two-photon excitation. In contrast, the optical sectioning of the Double beam is surprisingly poor for two-photon excitation. This caused by the main lobe and the side lobes having very similar intensity. In comparison to Gaussian beams, Airy beams feature better optical sectioning and slightly thinner main lobes.

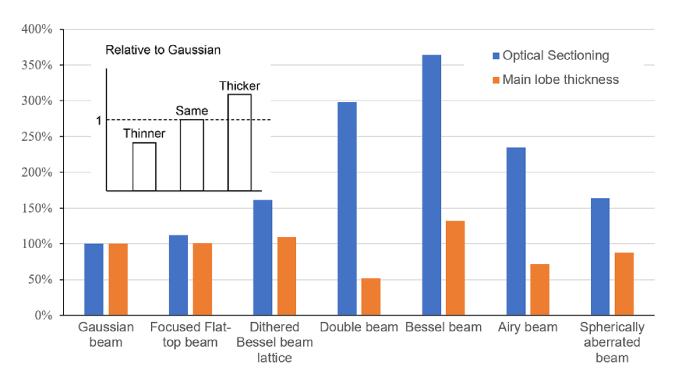
For all types of light-sheet the optical sectioning and axial resolution depends on their length. Therefore, it is essential to compare light sheet properties only for equal length. In most cases length is the parameter determined by the sample or the field of view that the researcher aims to observe in a single frame. Therefore, we chose the approach to define a light sheet length first and then compare the light sheets according to the axial resolution and optical sectioning they provide. Setting the Gaussian beam as the reference value, we compute the relative gain or loss in thickness and optical sectioning for all the different beam types for the same beam length. Figure 5 shows the results for a length of the light-sheets of 30 µm. Values above 100% indicate that the light sheet thickness w_OS or main lobe width w_ML is larger than for the Gaussian beam. Overall, we found that for all beam types there is a trade-off between the two properties: Making a thin light sheet comes at the expense of either length for Gaussian beams or at the expense of optical sectioning for other light sheet types.

Fig. 5.

Ratio of Optical Sectioning (blue) and Main Lobe Thickness (orange) for each beam type with respect to the Gaussian beam. All values are computed for beams with length L∼30 µm. The insert shows a scheme to interpret the graph. Values larger than 100% mean that the main lobe or optical section is thicker than for the Gaussian beam.

To further illustrate the possibility of tuning w_OS and w_ML for the multi lobe beams we analyzed the Double beam. The length of the double beam light-sheet can be tuned either by the angle between the two beams or by the thickness of the beams. When the angle is varied, the overall width of the interference region changes only very little because the cross-section of the sub-beams in the plane perpendicular to the optical axis is approximately constant for small angles between the optical axis and the propagation of the sub-beam whereas the range along which the sub-beams intersect along the optical axis changes. However, the smaller angle between the beams results in a larger period of the interference pattern (Fig. 6a). It is possible to obtain opposite trends, i.e. almost constant main lobe width and increasing light sheet thickness, if the NA of the interfering beams was altered instead of their interference angle (Fig. 6b). Note that while we used the Double beam similar tuning is possible for the dithered square Bessel beam lattice, the Spherically aberrated beam and the Airy beam likewise because they depend on two degrees of freedom (Appendix A & B).

Fig. 6.

The Main Lobe Thickness (orange) and Light Sheet Thickness / Optical Sectioning (blue) is shown for the double beam. The figure illustrates how the two parameters of multi lobe beams can be used to control beam length at the expense of a thicker light sheet or a thicker main lobe (a) To change the length of the light-sheet the NA of the two sub-beams is varied (NA = 0.2 to NA = 0.05) while the angle of interference is held constant (NAsep = 0.3) (b) the sub-beams NA is held constant while the angle of interference in varied (NAsep = 0.45 to NAsep = 0.15 and NA = 0.05).

4. Discussion

We analyzed the effect of different light sheets on image quality by using three parameters to represent properties which act as the major contributors: the thickness of the main lobe, the overall thickness of the light sheet and the length. Fundamental to our comparison of different light sheets is the insight that it must be performed for light sheets that have equal length. Based on the insight that most advanced light sheets like the Square Bessel beam lattice or the Airy beam feature two parameters that influence the shape of the light sheet we also implemented two measures: thickness of the main lobe which contributes to the axial resolution and the overall thickness which determines the optical sectioning.

In our analysis we neglected the effect of the detection objective, i.e. its point-spread function. The reasoning for this approach is the following: The detection NA by itself does not affect optical sectioning: Regardless of detection NA the integral collection efficiency of the signal out of any plane along the optical axis of the detection objective is the same. Optical sectioning therefore only arises from light sheet thickness. To get an idea of the influence of the light sheet on axial resolution it is insightful to approximate both the main lobe thickness of the light sheet and the axial profile of the detection PSF by Gaussian profiles: the detection profile is given by h_det(z) = Exp{-(z/dz)²}and the main lobe of the illumination profile by h_det(z) = Exp{-(z/w_LS)²}. The profile of the resulting point-spread function of the microscope is then h_sys(z) = Exp{-(z/w)²} where 1/w² = 1/dz²+1/w_LS². Thus, the light sheet always improves axial resolution in comparison to epi-fluorescence illumination. But there is only a significant effect on resolution when the light sheet’s main lobe thickness is smaller than the depth of focus of the detection lens. Some light sheet with thin main lobes may therefore provide higher axial resolution: For example, for equal depth of field and light sheet thickness, the resolution is increased by 30% (for w_LS = dz: w = 0.7 dz) but only by 10% for a light sheet that is twice as thick than the detection objectives depth of field (for w_LS = 2 dz: w = 0.90 dz), a case that occurs regularly, such as for detection NA_det=1.0 and a light sheet created at NA_ill=0.1, which is necessary for a field of view of dy_LS = 2nλ/NA² ≈130 µm. However, one important parameter that depends on the detection PSF is image contrast: The relationship between the optical section provided by the light-sheet and the depth of focus of the detection objective determines image contrast (see Fig. 3). If the light sheet thickness is larger than the detection depth of focus, out-of-focus planes within the sample are illuminated and detection and image quality is reduced. In conclusion, taking the detection NA into account is not required for a comprehensive comparison between different light sheets even though it influences image quality.

Image post-processing plays an increasingly important role in microscopy. Any light sheet where the optical sectioning is larger than the main lobe thickness will benefit from post-processing. When the depth of focus of the detection lens is shorter than the optical sectioning, raw images are blurred by out-of-focus signal. Deconvolution, which allows to computationally reassign the detected photons to their original position, is especially useful in these cases to improve image contrast. Amongst light-sheets, the option of post-processing means the following: When the quality of raw data matters, beams with good optical sectioning are preferable. When deconvolution is employed, it may be preferable to use light-sheets with thinner main lobes even if they have inferior optical sectioning because the high resolution provided by the main lobe can be recuperated. However, there are limitations to the amount of background that deconvolution can handle. For example, the signal generated by the main lobe should not be covered in the noise of the background signal generated by the side lobes of the light sheet. Also, a multi-lobe light sheet can be generated to be both very long and have a thin main lobe, but the strong background from poor optical sectioning will make deconvolution impossible. Finally, when multi-lobe beams are used to increase axial resolution the sample is always exposed to additional light due to the thicker light sheet. As a consequence, additional photodamage has also to be considered. To this end, our method offers guidance for the choice of ideal imaging conditions: which parameters can be used to generate light sheets for a given sample size that provide images with ideal axial resolution without too much background for deconvolution.

The analysis of the light sheet could also be based on the MTF or OTF as in previous publications [3,18]. MTF-based analysis is also helpful to evaluate the chances of successful deconvolution: The Bessel beam with a generally weak MTF is expected to be limited by signal-to-noise while the light sheets with a periodic pattern exhibit gaps in the MTF which is prone to artifacts. A similar approach, but based on images, has been used previously [21] but its use to quantify the axial resolution is not straightforward. To the trained eye, the MTF reveals at first glance the maximum spatial frequency representing smallest details that can be resolved. The contrast that these details will hold in the image is visually less easy to quantify because it is proportional to the quotient of the area under the MTF curve at high-frequencies to the area at low frequencies. The MTF is a well-established standard measure for the optical quality of a system to those comfortable thinking in k-space. Our set of measures is meant to provide a complementary approach in real space. We expect it to be a more intuitive method to quantify and compare the optical performance of light-sheets, especially for the many users of microscopy with a background in biology and bio-medical research rather than optics.

We used simulated data to compare the different light sheets. Since new light sheet types are continuously introduced in the field the simulation software we provide can be used as a tool to assess performance of emerging light sheets by comparison to the existing ones. The simulation method itself has been validated several times e.g. by [23,24]. An alternative simulation method that uses Debye theory is presented in [28]. The beam propagation method (BPM) represents an extension to the propagator approach which uses approximations but works in optically inhomogeneous media. The BPM has been used in a software package termed BioBeam that simulates light propagation through optically inhomogeneous media both in the illumination and detection path for different light sheet types at greatly improved speed by relying on a GPU [29]. In principle, our analysis can be readily applied to BioBeam results as well as to assess performance in inhomogeneous media.

The benefits of the two-photon excitation (TPE) for light-sheet microscopy with Bessel beams were already demonstrated in practice [30]. Nevertheless, we show here that while TPE generates much better optical sectioning without compromising axial resolution for many light-sheet types, the improvement is strongest for the Bessel beam. In contrast, TPE with the Double beam did not lead to an improvement over linear excitation. In all multi-lobe beams, even though TPE reduces the fluorescence excited by the side lobes relative to the main lobe due to their lower intensity, the side lobes may still contain a substantial fraction of the total power of the light sheet. Light-sheet microscopy with two-photon excitation by multi-lobe beams requires especially strong lasers and exposes the sample to a much larger total light dose than by Gaussian beams.

Other, more complex, illumination and detection schemes are suitable to improve axial resolution and optical sectioning at the same time. Examples include structured illumination [14], confocal slit detection [15], STED [16], RESOLFT [31], tiling [32,33], axially scanned light sheets [34] and computational reconstruction of images acquired with complementary light sheets [35,36]. However, the improved performance comes at a cost such as, for example, excess light exposure or reduction in achievable imaging speed. Image quality is controlled by additional parameters and degrees of freedom like the slit width for confocal slit detection or axially scanned light sheets or the power of the de-excitation beam for STED and would therefore require the extension of our model. We limited the selection of light-sheets to those that depend on only two parameters and see an extension of our method to more parameters as a very interesting direction for further development, potentially building on the Matlab code (see Appendix C) that we provide which is simple, easy to use and enables interested readers to simulate and analyze not only the light sheets used in this publication but also arbitrary ones.

5. Conclusion

In conclusion, we assess the optical performance for seven different light sheet types for linear and two-photon excitation by quantifying three different parameters. We distinguish between the main lobe thickness that controls axial resolution and the optical sectioning which determines image contrast. Surprisingly our comparison does not identify a clear winner: none of the light-sheets we analyzed is suitable improve axial resolution and optical sectioning at the same time. Thicker multi-lobe light sheets that expose the sample to more light are required for to improve axial resolution. To outperform the Gaussian beam, the use of these sheets must be combined with means for contrast enhancement, either by hardware, such as more complex image acquisition modes, or by software postprocessing such as deconvolution. A useful multi-lobe light sheet should exhibit a thin main lobe, the signal from this main lobe should stand out from the noise of the background generated by the side lobes of the sheet and the sample needs to tolerate the additional light-dose. The choice of light sheet should depend on whether axial resolution provided by a thin main lobe of the light sheet or image contrast and efficient use of light provided by better optical sectioning is more important, for example in localization microscopy [37]. Our publication is intended to offer guidance on the choice of light sheet and parameters. Based on the results from our analysis we suggest using Gaussian illumination beams for large FOVs, light-sensitive or thickly labelled samples where efficient use of light is key and therefore best optical sectioning is most important. For high flexibility and resolution in sparsely labelled samples we recommend the Double beam which we found to offer the best trade-of between optical sectioning and axial resolution that can be generated efficiently and where the trade-off between main-lobe thickness and light sheet thickness can be easily controlled.

Appendix A: Details on the light sheets

Gaussian beam:

Lasers ideally emit Gaussian beams. Gaussian beams are characterized by having an intensity profile along the radial direction following a Gaussian distribution. This profile is conserved along the propagation direction where only the beam radius changes. Light sheets with a Gaussian profile can be generated by a cylindrical lens [1] or scanning a Gaussian beam in focal plane of the detection objective [10]. This type of light sheet is by far the most common.

Focused flat-top beam:

A Focused flat-top beam is generated by homogeneously illuminating the back focal plane of an objective lens. The resulting intensity distribution in the focal plane is termed “Airy Disc” which is not to be confounded with the Airy beam and characterized by a main lobe with a very weak ring structure. Contrary to Gaussian beams, the shape of the intensity profile is not conserved along propagation. In practice a Focused flat-top beam is generated by expanding a Gaussian beam by a large factor so that its diameter is much larger than that of the back focal plane (BFP) of the objective lens. The profile is then approximately even across the BFP. In contrast to Gaussian beam, a larger fraction of the light is sent into the focus at a large angle with respect to the optical axis thereby leading to a tighter focus, at the expense of an additional ring structure. Focused flat-top beams can be used in confocal microscopy to increase lateral resolution because the fluorescence excited by the ring structure is suppressed on the detection side by the pinhole.

Bessel beam lattice:

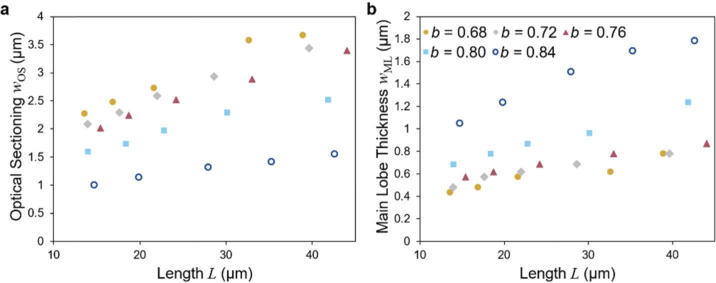
The lattice light sheet is a coherent superposition of equidistantly spaced Bessel beams. Depending on the distance at which the beams are separated different interference patterns are created. The main two are called square lattice and hexagonal lattice, names that stem from the light distribution in the back focal plane. For the hexagonal lattice the period b represents a third free parameter. Altering this parameter allows to trade main lobe thickness against optical sectioning as can be seen in Fig. 7.

Fig. 7.

The main lobe thickness and optical sectioning for different values of parameter b that determines the period of the lattice.

Airy beam:

Airy beams have a very characteristic “banana-like” bent shape. Experimentally, they can be generated by imposing a cubic phase to a Gaussian beam. This can be done, for example using a spatial light modulator. They are self-reconstructing, which means that they can recover their initial intensity profile behind scattering or absorbing obstacles. They were introduced to light-sheet microscopy for biological research by [17]. They can be used in two different orientations with different advantages and disadvantages. In one configuration, the beam’s main lobe is curved within the detection focal plane, but the beam’s side lobes lie on either side of the main lobe. The advantage is that the main lobe illuminates a flat plane and the disadvantage is that the side lobes on either side of the main lobe lead to a thicker overall light sheet. If the beam is rotated by 45° around the propagation axis, the main lobe of the sheet is bent with respect to the detection objective’s focal plane, but some lobes are situated next to the main lobe along the scan direction, i.e. they illuminate the same volume as the main lobe and thereby do not decrease optical sectioning. We included the latter version in our analysis because it provides better values in terms of optical sectioning. However, this approach requires a detection lens with sufficient depth of field (low NA leading to low lateral resolution) and/or postprocessing such a deconvolution to correct for the curvature of the illuminated volume.

Spherically aberrated beam:

Spherical aberrated beams occur when an objective lens designed to focus collimated light is used with defocused or focused light generating a focus away from the objective’s native focal plane. Most commonly, spherical aberrations occur in the presence of refractive index mismatch, i.e. an objective designed to focus into a medium with a refractive index is used to focus into a another medium with a different refractive index. Differential refraction of the rays depending on their radial position translates in an elongation of the beam’s peak and the formation of a socket around it. This type of beams has not been explicitly demonstrated for illumination purposes in a light-sheet microscope before, but mismatched illumination objectives such as air objectives to focus in water have been used, albeit at low NAs (NA < 0.4) [11]. The concept of focus elongation by spherical aberration has been used to increase the depth of focus, especially of detection objectives [38]. We model it by imposing a radially dependent biquadratic phase mask. Note that this beam is the only beam in our selection where the profile along the illumination axis is asymmetrical.

Double beam:

The Double beam is an interference pattern created by two beams (“sub-beams”) focused by an objective which then propagate at an angle relative to each other and to the objectives optical axis and interfere in the focal plane of the objective. The beams thereby generate an interference pattern consisting of alternating stripes of maximum and minimum intensity like Cosine Gauss beams [19]. Effectively the double beam generates a stack of light sheets. For light-sheet microscopy the central, and strongest light-sheet is placed in the focal plane of the detection lens. The auxiliary light sheets illuminate parallel planes [39]. The period of the interference pattern is equal to the separation of the light-sheets and depends on the angle of propagation between the beams. The depth of field on the diameter of the beams and the angle. Double beams can be generated by splitting a laser beam, e.g. a Gaussian beam, and sending the two sub-beams it into the back focal plane symmetrically around the center. The distance between the beams in the back focal plane determines the angle of propagation of the sub-beam and the diameter determines the sub-beams depth of field, i.e. the length of the interference pattern along the objective’s optical axis.

Appendix B: Details on simulation method

We performed simulations of the propagation of light using the Beam-Propagator Method. The intensity distribution of a light sheet is expressed by the illumination point spread function (PSF) h_ill. In combination with the detection PSF h_det, h_ill gives the response of an imaging system to an infinitely small point source. The illumination PSF h_ill can be calculated from the electric field E(x,y,z) as:

$$h_{\text{ill}}(x,y,z)={|E(x,y,z)|}^2.$$

At dy from the focus as:

$$E(x,y_0+dy,z)=\text{FT}\left\{\tilde{E}(k_{x,}{y}_0,k_z)\cdot \exp \{i\cdot {({(k_0\cdot n)}^2-{k_r}^2)}^{1/2}\cdot dy\}\right\}$$

Where k₀=2π/λ is the vacuum wavenumber and k_r² = k²-k_x²-k_z² is the radial component of the wave vector k. Here we assume that the light is propagating in water and therefore the refractive index n is constant and equal to 1.33. An important aspect of the simulation is the choice of discretization. It must be ensured that the sampling $\tilde{E}$ in k-space, dk, and E in real space, dx, are smaller than the relevant features. Because both values are inversely proportional to one another (dx = 2 π / N dk) where N is the length of the array, the simulation of beams with either a very narrow spectrum (low NA) or small foci (high NA) requires large arrays. The method works most effectively for medium NAs where both the spectrum and the beam are broad enough to be sampled well without the need for large arrays (large N).

The electric field at position of the focus, y₀, can be in turn computed as the Fourier Transform of the field in the Back Focal Plane (BFP) as:

$$E(x,y_0,z)=\text{FT}\left\{{\tilde{E}}_{\text{BFP}}(k_x,k_z)\right\}.$$

In our simulations, we defined the amplitude and phase of the field in BFP depending on the type of beam used, calculated the electric field at position y₀ and propagated the field. Due to sampling requirements, very long light sheets that require very large arrays were not considered.

Apodization and polarization can also be considered by multiplication ${\tilde{E}}_{\text{BFP}}$ with pupil functions [23,24]. However, both effects don’t lead to significant changes in the shape of the PSF for NA < 1.0 (n = 1.33) and illumination beams with such high NAs are not employed in light-sheet microscopy. Even for the beams with the highest NA shown in this manuscript (focused flat top beam at NA = 0.44 and Square Bessel beam lattice at NA = 0.6) we did not measure changes to the measured quantities by considering the sine condition and performing a vectorial computation.

Short pulses used for two-photon excitation have partial coherence which the simulation does not cover. Therefore, aspects depending on pulse the length such as the quantitative relationship between pulse energy and fluorescence excitation cannot be evaluated but do not affect the analysis of different light sheet shapes.

Depending on the number of parameters needed to define the amplitude and phase of the field we can classify the beams in one-parameter or two-parameter beams.

One-parameter beams:

• •Gaussian beam:
  In the BFP, the amplitude follows a gaussian distribution along radial profile. The phase is constant throughout the aperture.

  $${\tilde{E}}_{\text{BFP}}(k_r)=\exp \left\{-{(k_r/(k_0\cdot \text{NA}))}^2\right\}$$
• •Focused flat-top beam:
  Amplitude and phase are constant over the aperture.

  $${\tilde{E}}_{\text{BFP}}(k_r)=\text{circ}\left\{k_r/(k_0\cdot \text{NA})\right\}$$

Two-parameter beams:

• •Bessel beam lattice:
  The lattice is generated by the product of a ring-shaped intensity with a grid structure with period δk_x. The ratio between thickness of the ring and its radius is 1-√ɛ. The field in the back focal plane is given by:

  $${\tilde{E}}_{\text{BFP}}(k_x,k_z)=\text{comb}(k_x/\delta k_x)\cdot \exp \left\{-{((k_r-k_c)/k_t)}^2\right\}$$

  With k_c = k₀ NA (1+√ɛ) / 2 and k_t = k₀ NA (1-√ɛ) / 2

  Square lattice results from δk_x = √ɛ k₀ NA, hexagonal lattice from δk_x = b √ɛ k₀ NA

• •Airy beam:
  A cubic phase mask is superimposed on a homogeneous illumination in the BFP with

  $${\tilde{E}}_{\text{BFP}}(k_r)=\text{circ}\{k_r/(k_0\cdot \text{NA})\}\cdot \exp \{i\cdot a\cdot ({k_y}^3+{k_z}^3)/({k_0}^3\cdot \text{N}{\text{A}}^3)\}$$

  where the amplitude of cubic phase is controlled by a.
• •Spherically aberrated beam:
  The amplitude is constant on the aperture. The phase follows a biquadratic function.

  $${\tilde{E}}_{\text{BFP}}(k_r)=\text{circ}\left\{k_r/(k_0\cdot \text{NA})\right\}\cdot \exp \left\{i\cdot a\cdot {k_r}^4\right\}$$

  where the exponential term gives the phase modulation, and a stands for the amplitude of the phase difference.
• •Double beam:
  The double beam is generated by two gaussian beams determined by NA in the back focal plane centered at positions +δk_z and -δk_z where δk_z = k₀ NA_sep with

  $${\tilde{E}}_{\text{BFP}}(k_x,k_z)=\exp \left\{-{(k_{r1}/(k_0\cdot \text{NA}))}^2\right\}+\exp \left\{-{(k_{r2}/(k_0\cdot \text{NA}))}^2\right\}$$

  where k_r1² = kx² + (k_z-δk_z)² and k_r2² = kx² + (k_z+δk_z)².

Appendix C: Manual to the simulation software

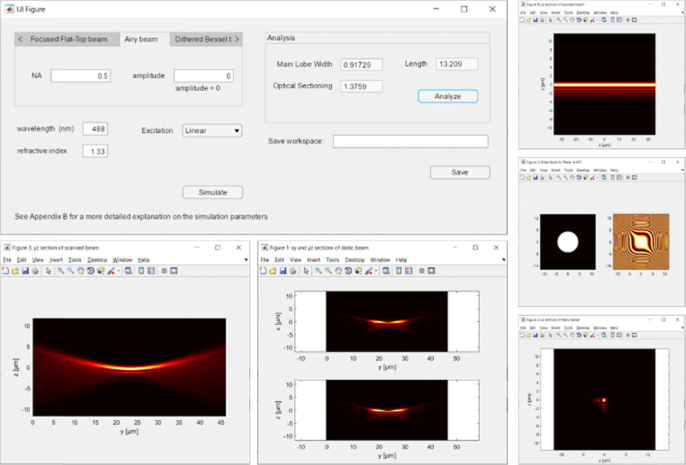
Our light sheet simulator app (Code 1, [40]) numerically computes the 3D intensity distribution of light sheets and quantifies its dimensions. It can generate Gaussian beam, Focused Flat Top beam, Airy beam, Bessel beam, Bessel beam lattices, Double beams and Spherically aberrated beams, as well as arbitrary types of light sheet introduced by the user. The algorithm takes as initial conditions the amplitude and phase of the electric field of the beam in the back focal plane and calculates its propagation around the focal plane using the beam propagation method.

To operate it, run LightSheet_Simulator.mlapp in Matlab environment. An example of the GUI is shown in Fig. 8. There are three possible actions:

• •Simulation: Allows visualization of cross-sections of the light sheet as well as the intensity and phase in the back focal plane. To simulate the light sheet discussed in this work, select the beam type in the tab panel and type in the required parameters. To simulate a custom light sheet, select the Create Light sheet tab. Type in the paths to the files containing the amplitude and the phase in the back focal plane. The files must be provided in tiff format.
• •Analysis: After simulation of the light sheet, press “Analyze” to obtain the values for Main Lobe Width w_ML, Optical Sectioning w_OS and Length L as defined in this work.
• •Saving: Creates the file simulated_ligthsheet.m in the directory indicated under Save workspace. The file contains a 3D intensity matrix and the numerical and physical parameters used in the calculations.

Fig. 8.

User interface of the beam simulator.

Funding

Horizon 2020 Framework Programme10.13039/100010661 (722427); European Research Council10.13039/501100000781 (682939).

Disclosures

The authors declare that there are no conflicts of interest related to this article.