Intensity-based registration of bright-field and second-harmonic generation images of histopathology tissue sections

Abstract

The use of second-harmonic generation (SHG) microscopy in biomedical research is rapidly increasing. This is due in large part to the wide spread interest of using this imaging technique to examine the role of fibrillar collagen organization in diseases such as cancer. The co-examination of SHG images and traditional bright-field (BF) images of hematoxylin and eosin (H&E) stained tissue as a gold standard clinical validation is usually required. However, image registration of these two modalities has been mostly done by manually selecting corresponding landmarks which is labor intensive and error prone. We designed, implemented, and validated the first image intensity-based registration method capable of automatically aligning SHG images and BF images. In our algorithmic approach, a feature extractor is used to pre-process the BF image to block the content features not visible in SHG images and the output image is then aligned with the SHG image by maximizing the common image features. An alignment matrix maximizing the image mutual information is found by evolutionary optimization and the optimization is facilitated using a hierarchical multiresolution framework. The automatic registration results were compared to traditional manual registration to assess the performance of the algorithm. The proposed algorithm has been successfully used in several biomedical studies such as pancreatic and kidney cancer studies and shown great efficacy.

1. Introduction

Alterations of stromal organization are commonly observed in the development of tumors such as breast cancer and pancreatic ductal adenocarcinoma [1–5]. It has been recognized that the extracellular matrix (ECM) in the tumor microenvironment can regulate tumor cell behavior and tissue tension homeostasis [6,7]. Collagen, as the major stromal component, constitutes the scaffold of tumor microenvironment and affects tumor development such as infiltration, angiogenesis, invasion, and migration. Second harmonic generation (SHG) imaging has been recognized as a powerful tool for revealing material non-linear optical response [8–10]. To achieve detectable SHG signal, a population of parallel molecules that are non-centrosymmetric or in other words contain a permanent dipole moment that must be present. Collagen fibers are the most abundant proteins in mammals that meet that requirement. Thus, SHG imaging has been used to examine collagen molecular and structural reorganizations in diseases such as cancer, fibrosis, and connective tissue disorders as it is highly sensitive to the collagen structure alternations that occur in these diseases. [11–15].

SHG images of collagen are location agnostic and have to be aligned with bright-field (BF) images of traditional Hematoxylin-Eosin (H&E) stained tissue to study the interactions between collagen fibers, cells and other components of the tissue in appropriate biological or pathological context [2,5,16]. For more than one hundred years, H&E staining has remained the gold standard staining technique in histopathology due to a combination of the two dyes that render different shades of pink and blue to a variety of tissue components for visualization using microscopic tools.

Over the last two decades, collagen fiber characteristics such as collagen fiber density and alignment have been widely studied along with cell morphology to identify image biomarkers for diagnosis and prognosis in a variety of cancer types [5,16–18]. Despite the fact that in most of these studies, BF images of H&E stained tissues have been used as a guide map for locating every collagen fiber, to the best of our knowledge, there has not been any report on automatic registration of the SHG images and BF images of H&E stained tissues. Additionally, registration is still largely done by manually aligning two images based on human observed markers that is both labor intensive and impossible for large image datasets. Image registration between the two modalities is cumbersome and one must have good knowledge of sources of contrast in both modalities as they represent different information related to the tissue. H&E staining protocol paints the nuclei dark blue using hematoxylin, while eosin stains the cytoplasm and other structures, including extracellular matrix components such as collagen, in up to five shades of pink and red blood cells as intensely red, while SHG imaging is only sensitive to the non-centrosymmetric molecules and mainly collagen fibers in tissue sections and the imaging requires laser scanning with femtosecond pulse width [8–10]. The collagen fibers are mixed with other extracellular components and are hard to resolve in H&E stained images but significantly highlighted in SHG images.

Landmark-based approaches such as SIFT rely on the matching of locally extracted descriptors that are scale-invariant but mostly created based on the same contrast mechanism. The image pair is often pre-processed to produce descriptors that represent the local features in the images, and a registration transformation is determined by matching similar descriptors in two images [19–22]. These methods have very limited cross-modality microscopic image registration capability especially on histology samples, since these different modalities usually have different optical contrast mechanisms such as absorption for fluorescent imaging, diffraction for BF imaging and second order scattering for SHG. These imaging contrast changes can be quite pronounced such that even visualizing the same tissue component in BF and SHG images can result in edge and texture distortion. In our presented case, SHG imaging mainly visualizes phase matched collagen fibers in tissue samples and other structures such as cells are not presented. In BF images they are both visible, and the collagen fibers are mixed with other ECM component with altered geometrical features and no phase matching is needed [8,10,13]. Secondly, BF histology images are dominated by low-level features with high co-occurrence such as cellular and stromal textures which can make the matching of the descriptors with a sparse image such as SHG image of fibrillar collagen very difficult [23,24]. Thus, extrinsic features such as fiducial markers or distinguishing outlines of the samples often need to be present in order to apply this family of approaches to cross-modality image registration [25–27]. On the other hand, intensity-based approaches widely applied to medical image registration [28–33] are free from the above limitations because they do not deal with the identification of local geometrical landmarks and instead, find a transformation that maximizes the global measurement of similarity. But these methods also tend to fail in our case due to the large amount of different information presented in two modalities. However, we notice that, the isolation of collagen fibers from BF images of H&E stained tissue can significantly increase the correlation of information between the two modalities. Once the collagen fibers are extracted, the transformation model between the two modalities can be reduced to a linear transform with no local deformations and an intensity-based method can potentially achieve satisfactory results with few modifications.

Although collagen fibers are hard to be directly extracted from H&E stained images, the ECM hosting the collagen fibers can be effectively isolated from other tissue components using image segmentation techniques. Thus, we first developed a feature extractor that extracts the ECM in the H&E stained images using Hue-Saturation-Value (HSV) space thresholding and Otsu’s method [34,35]. The extracted ECM image is then registered with the SHG image by finding the transform matrix that maximizes the mutual information of the two images [30,36]. We used a multi-resolution registration strategy that undergoes hierarchical optimization of an evolutionary optimizer to increase the registration speed and accuracy [31,37,38]. The performance of the automatic registration algorithm is evaluated by quantitative comparison to human registration and we have provided an experimental comparison between our method and three other recent and/or widely used registration methods. The proposed approach has been applied and shown great efficacy in several published studies that co-examined the H&E stained images and SHG images of tissue sections [5,16,39].

2. Methodology

2.1. Problem formulation

Registration is the process of aligning two images according to a given metric. We define the problem of registration between SHG and H&E image as follows. Given a BF image of a H&E stained tissue and an SHG image of the collagen in the same tissue section, the goal is to find a transformation $\mathcal{T}$ that maps the points set ${\mathit{C}}_{\mathit{s}}$ in the source image to the points set ${\mathit{C}}_{\mathit{t}}$ in the target image such that for each point ${\mathit{x}}_{\mathit{s}}\mathbf{\in }{\mathit{C}}_{\mathit{s}}\mathbf{,}{\mathit{x}}_{\mathit{t}}\mathbf{\in }{\mathit{C}}_{\mathit{t}}$ has the same histopathological location. Here we denote the BF image as the source image and the SHG image as the target image.

The direct registration between BF and SHG images is challenging because of the information difference contained in each modality. Due to the nonlinear property of SHG, only collagen fibers in the tissue section can be observed in SHG image, while all components stained with H&E dye are visualized in the BF image. Collagen fibers are hard to be directly extracted in BF images, however, they mostly exist in the extracellular matrix (ECM) which can be separated in H&E stained images by segmenting out the regions containing the cells. Thus, we first design a feature extractor $\mathcal{F}$ operating on the BF image to extract the ECM image, and then try to register only the ECM image to the SHG image so that the information difference between the two modalities is reduced before the optimization starts. Considering that for fixed tissue sections, there is no local deformation in the transformation model, we express the general form of the registration transformation as an affine transform with a homogeneous rotation matrix R, a translation matrix T, a scaling matrix S and a feature extractor $\mathcal{F}$ as:

$$\mathcal{T}(C_s\mathbf{;}\mathit{\mu })\mathbf{=}\mathit{T}\mathbf{\cdot }\mathit{R}\mathbf{\cdot }\mathit{S}\mathbf{\cdot }\mathcal{F}(C_s)$$ (1)

The transformation matrices are parameterized by $\mathit{\mu }\mathbf{=}\mathbf{\{}\mathit{\theta }\mathbf{,}{\mathit{t}}_{\mathit{x}}\mathbf{,}{\mathit{t}}_{\mathit{y}}\mathbf{,}{\mathit{s}}_{\mathit{x}}\mathbf{,}{\mathit{s}}_{\mathit{y}}\mathbf{\}}$, where $\theta$ is the rotation angle, $t_x$ and $t_y$ are the translations in x and y axis, $s_x$ and $s_y$ are scaling factors in x and y axis.

For each transformed source image ${\mathit{I}}_{\mathit{s}}\mathbf{(}\mathcal{T}\mathbf{(}{\mathit{C}}_{\mathit{S}}\mathbf{)}\mathbf{)}$ and the corresponding target image ${\mathit{I}}_{\mathit{t}}$, we use a function $\mathcal{M}$ that measures the intensity-based similarity between these two images. Thus, the problem of intensity-based registration between BF and SHG images can be posed as an optimization problem where we seek an optimal set of parameters $\mathbf{\{}\mathit{\mu }\mathbf{\}}$ that maximizes the similarity of the target image and the transformed source image:

$${\mathit{\mu }}_{opt}\mathbf{=}\mathbf{arg}\underset{\mathit{\mu }}{\mathbf{max}}\mathcal{M}\mathbf{(}{\mathit{I}}_{\mathit{s}}\mathbf{(}\mathcal{T}\mathbf{(}{\mathit{C}}_{\mathit{s}}\mathbf{)}\mathbf{)}\mathbf{,}{\mathit{I}}_{\mathit{t}}\mathbf{(}{\mathit{C}}_{\mathit{t}}\mathbf{)}\mathbf{)}$$ (2)

2.2. HSV colorspace segmentation of BF images

H&E staining renders color to both the cells and the ECM while SHG imaging is only sensitive to the collagen fiber presenting in the ECM. In order to decrease the amount of information difference between the two modalities, we used a HSV colorspace thresholding combined with Otsu’s thresholding method [34] to segment the region containing ECM in the BF images of H&E stained tissue before the registration.

BF images usually have several kinds of specimen preparation artifacts such as uneven staining and variation of dye concentration [40]. Thus, we first normalized the H&E images by stretching the dynamic range of RGB channel based on the mean value and standard deviation so that all BF images can be adjusted to have approximately the same dynamic range. Due to color specificity Hematoxylin and Eosin dye which stains cells dark blue, and ECM with color differentiated shades of pink, the pixels can be roughly classified based on the hue value [41]. Due to these differentiating properties, we converted the image colorspace to HSV and then applied empirical thresholding in the hue channel which categorizes the image pixels into cell pixels and ECM pixels.

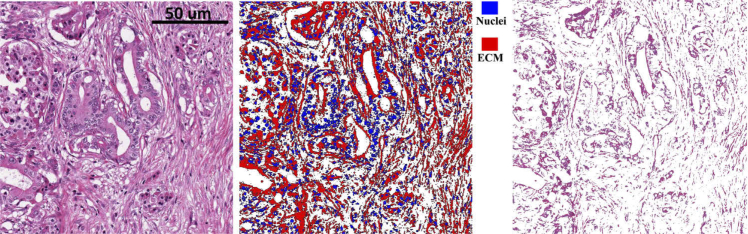
The hue channel thresholding does not separate the tissue section from its background in the H&E image since the colors of the background pixels are close to white and differs only slightly from pure white which can have hue values distributed in the whole hue space. In order to separate the background and the tissue, we applied Otsu’s method on the saturation channel which groups the pixels into foreground and background. Otsu’s method assumes that the image contains two classes of pixels and seeks a partition that minimizes the intra-class variance. Pixels belonging to the class with a smaller mean value are labeled as background pixels. Pixels belonging to the foreground are made into a logic mask applied to the segments outputted by hue channel thresholding of the previous step, disregarding the pixels that do not belong to the tissue. Pixels labeled as both foreground and ECM are considered as mask, which is further smoothed using a Gaussian filter. A representative segmentation result is shown in Fig. 1.

Fig. 1.

Bright-field image segmentation. Left: BF image of an H&E stained pancreas tissue section, scanned by an Aperio slide scanner. Middle:segmentation output (blue: nuclei, red: ECM). Right: segmented image of ECM. Scale bar is 50 microns.

2.3. Mutual information based registration

Instead of identification matching geometrical landmarks, intensity-based registration techniques seek an optimal solution that maximizes the overall measurement of similarity between the target image and the transformed source image. This family of methods is favored in medical image registration since there is no need for designing other object-specific feature extractors [32,42]. We chose to use random variable intensity values, mutual information measurement (function M) as the main criterion when measuring similarity between two tissues. The function M measures the amount of information can be obtained about one random variable through observing another random variable [43]. Mutual information of target image ${\mathit{I}}_{\mathit{t}}\mathbf{(}{\mathit{C}}_{\mathit{t}}\mathbf{)}$ and the transformed source image ${\mathit{I}}_{\mathit{s}}\mathbf{(}\mathcal{T}\mathbf{(}{\mathit{C}}_{\mathit{s}}\mathbf{)}\mathbf{)}$ is calculated based on the entropies of the two random variables:

$$\mathcal{M}\mathbf{(}{\mathit{I}}_{\mathit{s}}\mathbf{(}\mathcal{T}\mathbf{(}{\mathit{C}}_{\mathit{s}}\mathbf{)}\mathbf{,}{\mathit{I}}_{\mathit{t}}\mathbf{(}{\mathit{C}}_{\mathit{t}}\mathbf{)}\mathbf{)}\mathbf{=}\mathbf{\sum }_{\mathit{y}\mathbf{\in }\mathcal{Y}}\mathbf{\sum }_{\mathit{x}\mathbf{\in }\mathcal{X}}\mathit{p}\mathbf{(}x,y\mathbf{;}\mathit{\mu }\mathbf{)}\mathit{l}\mathit{o}\mathit{g}\frac{\mathit{p}\mathbf{(}x,y\mathbf{;}\mathit{\mu }\mathbf{)}}{\mathit{p}\mathbf{(}x\mathbf{)}\mathit{p}\mathbf{(}y\mathbf{;}\mathit{\mu }\mathbf{)}}$$ (3)

Where p(x, y) is the joint probability mass function of ${\mathit{I}}_{\mathit{t}}\mathbf{(}{\mathit{C}}_{\mathit{t}}\mathbf{)}$ and ${\mathit{I}}_{\mathit{s}}\mathbf{(}\mathcal{T}\mathbf{(}{\mathit{C}}_{\mathit{s}}\mathbf{)}\mathbf{)}$. p(x) and p(y) are the marginal probability mass functions of ${\mathit{I}}_{\mathit{t}}\mathbf{(}{\mathit{C}}_{\mathit{t}}\mathbf{)}$ and ${\mathit{I}}_{\mathit{s}}\mathbf{(}\mathcal{T}\mathbf{(}{\mathit{C}}_{\mathit{s}}\mathbf{)}\mathbf{)}$, respectively. $\mathcal{X}$ and $\mathcal{Y}$ are the sets of pixel values of ${\mathit{I}}_{\mathit{t}}\mathbf{(}{\mathit{C}}_{\mathit{t}}\mathbf{)}$ and ${\mathit{I}}_{\mathit{s}}\mathbf{(}\mathcal{T}\mathbf{(}{\mathit{C}}_{\mathit{s}}\mathbf{)}\mathbf{)}$, respectively. The marginal and joint probability densities of the image intensities are estimated using Parzen Windows [44]. In this approach, each data point ${\mathit{x}}_{\mathit{i}}$ from the image I is superimposed by a window such as Gaussian window with a bandwidth value of h. Thus, the mass function of the random variable I representing an image can be estimated as:

$$\mathit{p}\mathbf{(}\mathit{x}\mathbf{)}\mathbf{=}\frac{\mathbf{1}}{\mathit{n}\mathit{h}}\mathbf{\sum }_{\mathit{i}\mathbf{=}\mathbf{1}}^{\mathit{n}}\mathit{K}\mathbf{(}\frac{\mathit{x}\mathbf{-}{\mathit{x}}_{\mathit{i}}}{\mathit{h}}\mathbf{)}$$ (4)

Where n is the number of data points in image I, K is the Gaussian distribution.

2.4. Multi-resolution one-plus-one evolutionary optimization

The registration algorithm evaluates the similarity measurement function and adjusts the transformation parameters iteratively. At each iteration, the ECM image extracted from the H&E stained image is rotated, translated or scaled according to the transformation parameters and the mutual information with respect to the target image is computed. The process terminates when the convergence criterion is met such that the mutual information is considered maximized.

We choose the widely utilized one-plus-one evolutionary optimizer to drive the optimization [37,45]. The one-plus-one optimizer can adaptively adjust the search direction and step size and provides a fast convergence speed. In the one-plus-one optimizer, the population size and new individual size are both equal to one. The initial population of an individual $\mathit{\mu }$ is generated randomly and the fitness of the individual is calculated using a fitness function $\mathit{f}$. A new individual (child) is generated by adding mutations and the population is reduced to one as the fittest individual survive. The mutation is a random vector of the multidimensional normal distribution with mean $\mathit{\tau }\mathbf{=}{\mathit{p}}_{\mathit{p}\mathit{a}\mathit{r}\mathit{e}\mathit{n}\mathit{t}}$ and covariance matrix ${\mathbf{\Omega }}^{\mathbf{2}}$. The covariance matrix is adapted at each step such that it is increased when the new population consists of fitter individuals and it is reduced otherwise. The iteration terminates and returns the optimal $\mathbf{\{}{\mathit{\mu }}_{\mathit{o}\mathit{p}\mathit{t}}\mathbf{\}}$ when the convergence criterion is met. In our case, the individual is a candidate of the optimal set of parameters $\mathbf{\{}{\mathit{\mu }}_{\mathit{o}\mathit{p}\mathit{t}}\mathbf{\}}$ that characterizes the transformation $\mathcal{T}$ for the registration and the fitness function is the mutual information measurement between the transformed H&E stained image after the feature extractor $\mathcal{F}$ and the SHG image. The algorithm is summarized in Algorithm 1

Algorithm 1: One-plus-one evolution.

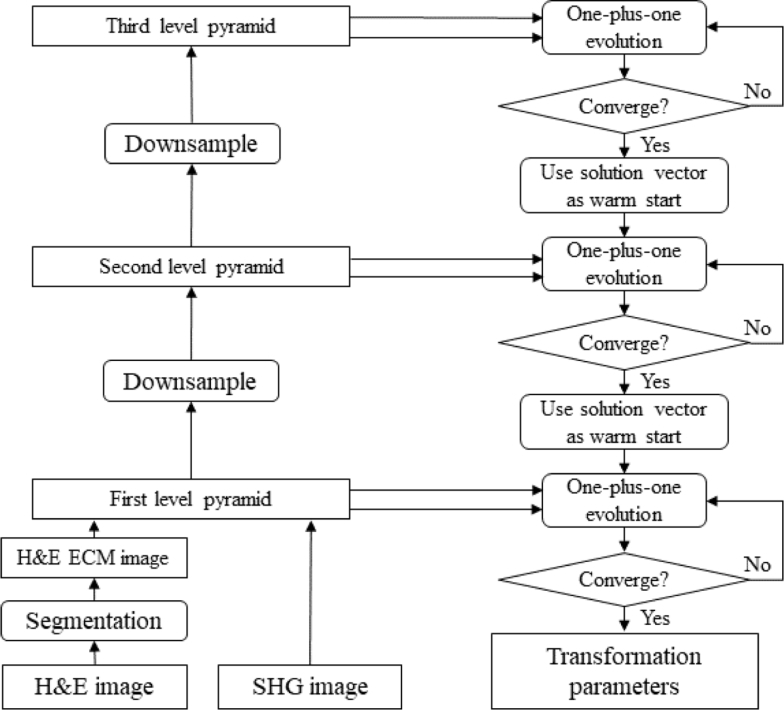
Whole slides or tissue micro-arrays (TMA) usually yield images with very big size, leading to long computation time. The efficiency of the registration of big images can be improved by using multi-resolution approaches. In the MATLAB (MathWorks, Natick MA) implementation, function imregtform constructs 3-level image Gaussian pyramids for hierarchical registration of two input images [29]. The registration starts from the lowest resolution level and the solution vector of transformation parameters returned by one-plus-one optimizer at each lower resolution level is passed to the higher resolution level. The computation cost for low resolution levels is much less than the high resolution levels due to smaller image sizes. The optimal vector for the higher resolution level can be found with fewer iterations using the vector returned by the previous level as a warm start, since it must lie within a neighborhood of the optimal vector returned by the previous level. Additionally, the solution vector found at the lowest resolution level can indicate a convergence basin of the global optima of the mutual information, which decreases the chance of being trapped in local optimal when searching the optimal vectors for higher resolution levels [46]. The flow of the registration between H&E stained images and SHG images using the image pyramid-based multi-resolution optimization is shown in Fig. 2.

Fig. 2.

Multi-resolution registration using image pyramid strategy.

3. Data

The H&E stained tissue section slides used for the validation are part of previously published breast cancer, pancreatic cancer, and kidney cancer studies at the University of Wisconsin at Madison [2,5,16]. BF images are acquired using an Aperio CS2 Digital Pathology Scanner (Leica Biosystems, Wetzlar, Germany) at 40x magnification. Additional H&E stained images of some slides were also acquired using a custom-built integrated SHG/bright-field imaging system at 20x magnification.

All SHG images were acquired using this SHG/bright-field imaging system. A MIRA 900 Ti: Sapphire laser (Coherent, Santa Clara, CA) tuned to 780 nm, with a pulse length of approximately 100 fs, was directed through a Pockel’s Cell (ConOptics, Danbury, CT), half and quarter waveplates (ThorLabs, Newton, NJ, USA), beam expander (ThorLabs, Newton, NJ), a 3 mm galvanometer driven mirror pair (Cambridge, Bedford, MA), a scan/tube lens pair (ThorLabs), through a dichroic beam splitter (Semrock, Rochester, NY), and focused by either a 40X/1.25NA water-immersion or 20X/0.75NA air objective lens (Nikon, Melville, NY). SHG light was collected in the forward direction with a 1.25 NA Abbe condenser (Olympus, Tokyo, Japan) and filtered with an interference filter centered at 390 nm with a full width at half maximum bandwidth of 22.4 nm (Semrock). The back aperture of the condenser lens was imaged onto the 5 mm aperture of a 7422-40P photomultiplier tube (Hamamatsu, Hamamatsu, Japan) the signal from which was amplified with a C7319 integrating amplifier (Hamamatsu) and sampled with an analog to digital converter (Innovative Integration, Simi Valley, CA). The controlling of the SHG/bright-field imaging system was done by our custom software called WiscScan https://loci.wisc.edu/software/wiscscan. Utilizing the intrinsic optical sectioning property of SHG imaging, each SHG image contains a stack of images sampled through the tissue section plane in the z direction. Thus, the image stacks were projected to single-plane images using maximum intensity projection before the registration.

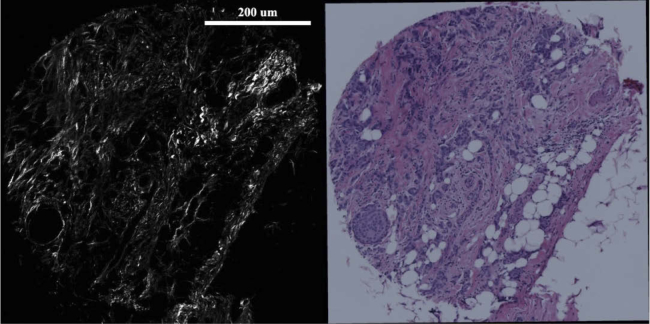
BF images were coarsely pre-cropped to have approximately the same field-of-view as the SHG images. For the validation of our method, the algorithm is used to perform registration between SHG and BF images from both slide scanner and bright-field microscope that have various light conditions, which in turn results in a slight change in image hue spectrum. A set of representative BF image and SHG image used for the registration algorithm are shown in Fig. 3.

Fig. 3.

A set of SHG and BF images. Left: SHG image of a TMA core from a breast tissue section, Right: BF image of the same TMA core. Scale bar is 200 microns.

4. Validation and results

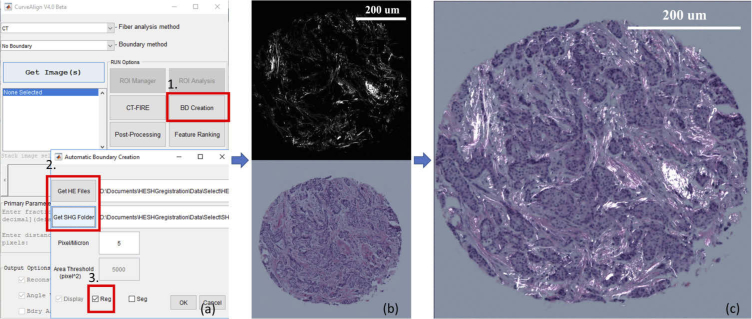
Validation of the registration algorithm for BF to SHG images is challenging due to the lack of literature investigations on this topic and the number of images that needed to be assessed to prove efficacy. Thus, we evaluated the performance of the registration algorithm by comparing the results to manual registration based on landmark correspondence. We selected 206 images from the dataset, and for each image, a number of landmark pairs distributed across the image were selected by an observer. The registration was performed based on the correspondence of the selected landmarks using the Landmark Correspondences plugin in ImageJ [47,48]. The same image pairs were fed to the algorithm for automatic registration. A difference map between the manual registration output and algorithm registration output was produced and the pixel mean absolute error (MAE) between the outputs was computed for each pair of images. Sample registration results are shown in Fig. 6. A graphical user interface was developed with MATLAB which allows users to select batch of images and check the registration results [49]. The MATLAB program as well as the user guide can be downloaded at https://loci.wisc.edu/software/curvealign. The workflow of the registration task is shown in Fig. 5.

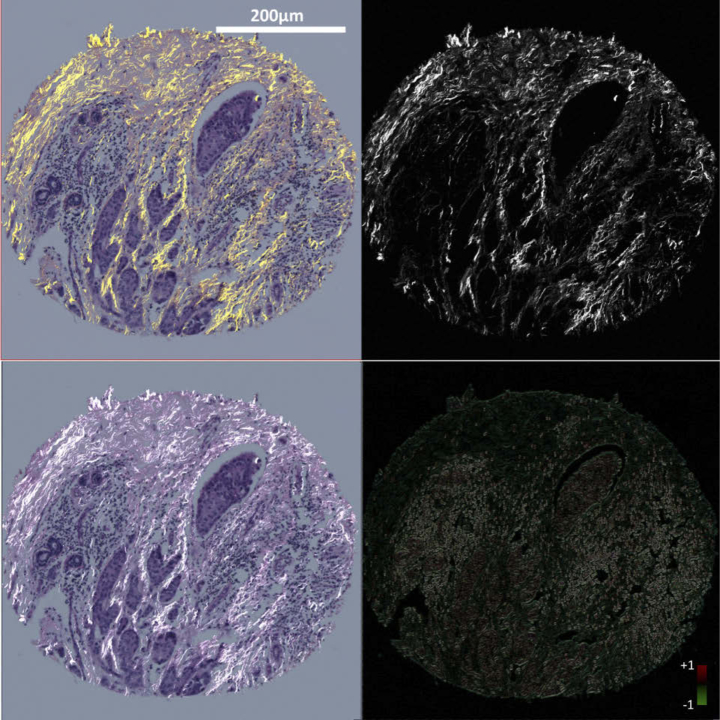
Fig. 6.

Sample registration results. left column: H&E stained image of a TMA core from a breast tissue section, right column: SHG image of the same core. Top left: manual registration using landmarks correspondence; Bottom left: automatic registration using proposed method; Top right: template SHG image; Bottom right: difference map between manual and automatic registration. Scale bar is 200 microns

Fig. 5.

Workflow of a registration task, program can be downloaded from Code 1 (Ref. [50]). (a): CurveAlign user interface. (1) select BD Creation. (2) select all BF images of H&E stained tissue and SHG image folder. (3) select registration mode; (b): program loads and feeds the images to the algorithm. top: SHG image of a TMA core from a breast tissue section, bottom: BF image of the same TMA core; (c): overlaid images of registration output. Scale bar is 200 um

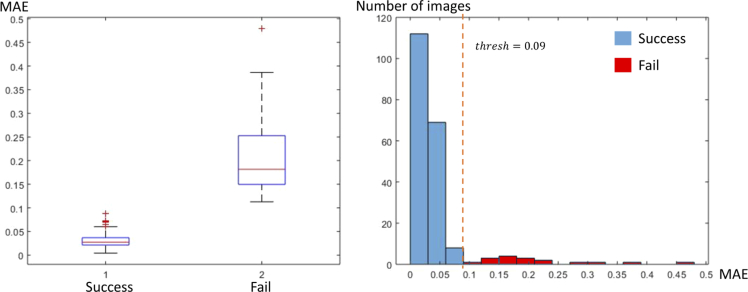
Image pairs are considered to be successfully registered if the MAE of the image pair is smaller than 0.09. Among the 206 images, 189 images are successfully registered (successful rate 92.2%). The average MAE between manual registration and automatic registration of the successfully registered images is 0.023 per pixel, and the average running time of each image with a resolution of 2048x2048 is 95 seconds. 17 of the 206 images are not correctly registered by our algorithm due to several reasons which will be discussed in the next section. The distributions of MAE results are shown in Fig. 4. As can be seen in this figure, a threshold of 0.09 (dashed line) for MAE separates successful (blue bars) and failed (red bars) registration results of our proposed method. Although the presented algorithm has already been used in several of our published biological studies such as breast, pancreatic and kidney cancer studies and the performance has been critical to their success [5,16,39], but the mechanics of the algorithm has never been published and there is a chance for other developers to use and improve upon.

Fig. 4.

Left: box plot of success MAE and fail MAE. The center red line represents the median, the lower and upper blue line represent the 25th and 75th percentiles, respectively, the dashed lines and black lines indicate the lower and upper limits of the inliers data points, and the red crosses represent outliers. Right: histogram of MAE.

We have compared the results of the proposed method to three other recently and/or widely used registration methods, in which the first two are landmark based and the third method is an intensity-based approach for image registration. The first method is the widely used SIFT-RANSAC [51–53] that uses SIFT features and finds the affine transform using random sample consensus to minimize the effect of outlier features [54]. The second method is PSO-SIFT-RANSAC that uses a gradient computation method that is more robust to complex nonlinear intensity transform in the images, and in addition, a robust point matching algorithm that combines the position, scale, and orientation of each key point to increase the number of correct correspondences is used in this method [21,55]. The two methods are implemented in MATLAB (MathWorks, Natick MA). The third method is called SimpleElastix [32,33], which is an open source software, based on Insight Segmentation and Registration Toolkit (ITK) [56] which is a widely used intensity-based medical image registration library. We randomly sampled 31 BF and SHG image pairs from the whole datasets of previous biological studies and tested the performance of these methods by applying them directly to the BF and SHG images. We also tested their performance on the ECM images extracted from the first step of our proposed method. The evaluation code can be found at https://github.com/uw-loci/shg_he_registration. The registration results were compared to manual registrations described above. Success rate and pixel MAE for successful cases are tabulated in Table 1.

Table 1. Performance comparison of other image registration techniques to the proposed method. A registration is considered successful if the MAE between the algorithm output and manual registration is less than 0.09.

	SIFT-RANSAC		PSOSIFT-RANSAC		Elastix-affine		Proposed
Input	SHG and BF	SHG and BF-ECM	SHG and BF	SHG and BF-ECM	SHG and BF	SHG and BF-ECM
Success rate	0%	32.3%	19.4%	32.3%	71.0%	74.2%	87.1%
Mean success MAE	NaN	0.061	0.057	0.065	0.05	0.059	0.047

The classic SIFT-RANSAC method has very limited efficacy on the SHG and BF dataset we tested. Although the accuracy was improved by registering SHG and ECM images compared to SHG and BF, both landmark-based methods failed in achieving a high accuracy in registering these images. However, SimpleElastix showed a better performance than SIFT, especially in registering SHG and ECM images, but still yielded much lower accuracy than our proposed method.

5. Discussion

The registration algorithm presented in this paper first extracts the ECM in the BF image to decrease the information difference between the source (BF) and target (SHG) image and then iteratively determines an optimal transform matrix that maximizes the mutual information between the source and target images using a multi-resolution strategy. The algorithm has been demonstrated to achieve high accuracy for automatic registration between BF and SHG images on a variety of histopathological samples with high accuracy and affordable running time.

However, we note below several conditions where the registration could fail. The feature extractor that extracts the ECM components in the BF image uses hue-based segmentation which is susceptible to the artifacts introduced in the staining and imaging procedures. Staining artifacts caused by nonuniform dye concentration or uneven propagation of the solvent can lead to hue bias in the BF images of H&E stained tissue [40,57]. Uneven illumination in the optical path can generate intensity bias in the BF images. Hue and intensity bias could affect the performance of the segmentation of the ECM region and cell region in the H&E images. The algorithm can also fail if the intensity signal level in the SHG images is too low. The amount of SHG signal presented in the slide is tissue type dependent [9,58,59]. Collagen fibers are the major non-centrosymmetric molecules in tissue that produce detectable SHG signal. If the tissue section does not contain enough concentration of non-centrosymmetric molecules such as fibrillar collagen, it cannot produce detectable SHG signals, which further confounds the registration between the SHG and BF images. Representative instances of these cases where the proposed method fail to register the images are shown in Fig. 7

Fig. 7.

Representative cases where the algorithm fails. Scale bar is 200 microns

The performance of the algorithm is also affected by the amount of overlapped field-of-view (FOV) presented in the two images. Empirically, we found that the failure rate increases significantly if the FOV difference in the SHG and BF images is greater than 20%.

Future work will be developing a normalization approach that corrects the artifacts introduced in the staining and illumination in the BF images and improve the signal-to-noise ratio in the SHG image by applying Poisson denoising. The hue bias and intensity bias can be corrected by training an image-to-image translation deep network that maps the biased BF dataset to a standard dataset [60]. Poisson denoising of the SHG images can be conducted by sparse coding using a learned dictionary from the SHG image dataset [61]. The presented method could potentially be extended to work on the registration of other imaging modalities that might be used with histopathology studies, such as polarization microscopy [62] and fluorescence imaging [63].

6. Conclusion

SHG microscopy has emerged as a powerful tool for biomedical imaging. It has been frequently used together with traditional histopathology techniques such as H&E staining to visualize collagen fibers in the tissue microenvironment. H&E staining renders different colors to different types of tissue components while SHG imaging is particularly sensitive to the collagen fibers in human tissue, which exist mostly in the ECM. The combination of the two modalities facilitates the interpretation of the role of collagen fibers in tissue microenvironment.

To our knowledge, the automatic registration of SHG and BF images was not available, and the method presented in the paper is the first to discuss the automatic registration between SHG and BF images of H&E stained tissues. Due to the fact that there is a large information difference between BF and SHG images, existing registration methods fail to readily register the images from these two modalities. For this reason, our intensity-based registration method begins with a segmentation step. Based on the colors rendered to different tissue components in the H&E staining and the capability of the SHG imaging to visualize the collagen fibers, we designed a feature extractor that segments the region containing ECM in the BF images using HSV space thresholding which decreases the amount of different information in the two modalities. Then, the registration transform matrix is found iteratively in a multi-scale strategy by maximizing the mutual information measurement using evolutionary optimization. We evaluated the effectiveness of our approach by comparing the results to human registered images. Our proposed method has been used and validated in several of our biomedical studies that involve histopathology examination of tissue sections from different organs [5,16,39]. The experiment results and validation studies show that our approach is capable of automatic registration of the SHG and BF images of histology slides with excellent performance.

Funding

Semiconductor Research Corporation10.13039/100000028; Morgridge Institute for Research.

Disclosures

The authors declare no conflicts of interest.