Abstract
We demonstrate a 3×3 coupler-based fiber-optic interferometric system to detect the local initial photoacoustic pressure. In contrast with the existing interferometric photoacoustic microscopy (PAM) relying on the measurement of the phase change of the probe light caused by the sample surface vibration, the present method measures the intensity change of the probe light caused by the initial photoacoustic pressure. Compared with the conventional interferometric PAMs, this method has the advantages: (1) it is free from the influence of the rough tissue surface, achieving complete noncontact in vivo imaging; (2) the probe light and the excitation light are focused at a same point below the sample surface, and the confocal configuration makes it more convenient for in vivo imaging; and (3) there is no need for phase stabilization, allowing a high imaging speed. These advantages show that the method will be a promising technique for in vivo imaging. This method is verified by imaging of a resolution test target and in vivo imaging of the blood vessels in a mouse ear.
1. Introduction
Photoacoustic microscopy (PAM), combining the advantages of optical imaging and acoustic detection, is capable of imaging of biological tissues with high resolution and high contrast [1–10]. PAM has developed to be an important tool for structural and functional imaging of a variety of tissues. Most PAMs rely on the measurement of the acoustic pressure with an acoustic detector, such as an ultrasound transducer [11–13], Fabry–Perot polymer film ultrasound sensor [14], optical fiber detector [15,16] or microring resonator [17]. In these PAMs, acoustic coupling media (water or oil) are usually required to reduce the high reflection loss of ultrasonic waves at the boundaries with an acoustic mismatch. This requirement is often difficult for in vivo imaging. The techniques of optical detection of ultrasound have the potential to detect ultrasound in noncontact mode, which is especially attractive for in vivo imaging. Besides, due to the strong scattering of light in tissues, PAMs are limited to superficial imaging with a penetration depth of ∼1 mm. Therefore, an endoscopy version is required to expand the clinical applications. For imaging of internal organs, the photoacoustic endomicroscopy (PAEM) probe head must be small. However, most reported PAEMs use an ultrasound transducer [18–20], leading to a difficult challenge to integrate both optical and acoustic components in a small space. The technique of optical detection of ultrasound is desirable for endomicroscopy imaging since it could dramatically simplify the structure of the probe head.
In recent years, a great variety of interferometric methods for photoacoustic imaging have been demonstrated, such as using a two-wave mixing interferometer [21], heterodyne interferometer [22,23], confocal Fabry–Perot interferometer [24], or homodyne interferometer [25–31]. These interferometric methods remotely measure the sample surface vibration caused by the photoacoustic wave that reaches the sample surface. Most of them were demonstrated by imaging of phantoms. These methods still have several significant technical limitations that need to be addressed. First, the rough tissue surface has a crucial influence on the optical interferometric measurement of the tissue surface vibration, such as the laser speckle, heterogeneous reflectivity, and complex interference caused by the probe light reflected from the subsurface of tissues. Our previous paper showed that the image quality is deteriorated when directly measuring the vibration of the tissue surface [3]. In the few reports of in vivo imaging, a water layer covered on the sample was usually used to provide a smooth reflective surface for the probe light [3,28–31]. So, these methods are quasi-noncontact. The water layer, just as the ultrasonic coupling medium used in the transducer-based PAMs, limits the clinical applications. Second, in these methods, the probe light is focused on the sample surface (or water surface), while the excitation light is focused below the sample surface. Such detection configuration needs to be elaborately adjusted, and it is difficult for in vivo imaging due to the uneven tissue surface. Finally, the stabilization of the phase is usually required to maintain the interferometric system at its highest sensitivity [3,25–31]. This will slow down the imaging speed. Park et al. demonstrated noncontact photoacoustic imaging of hair phantoms based on optical quadrature detection [32]. They used the two channels of a 3×3 fiber coupler to measure the sample surface vibration. By utilizing the intrinsic phase differences of the 3×3 coupler, the photoacoustic signals were reconstructed without suffering from the influence of the initial phase drift that usually occurs in a conventional interferometric system. However, this method also suffers from the first and second limitations.
Hajireza et al. recently demonstrated that the initial photoacoustic pressure (at the position where the pulsed ultrasound is excited) generates a local refractive index rise and subsequently results in a significant local reflectivity change [33]. They reported an optical non-interferometric PAM by detection of the intensity change of the probe light caused by the initial photoacoustic pressure. To achieve high sensitivity, they employed a free-space system to detect the quasi-ballistic photons [33–35] because the free-space configuration can significantly increase the amount of the quasi-ballistic photons entering the photodetector. Compared with the free-space system, a fiber optic system has the advantages of easy miniaturization and a high degree of flexibility. When an optical fiber is used to transmit the probe light, the small-core fiber limits the probe light entering the system, which reduces the system sensitivity. Kevan L et al. reported a non-interferometric fiber system for measurement of the initial photoacoustic pressure [36]. Up to now, various interferometric techniques have been developed for the measurement of the weak light backscattered from within biological tissues with high sensitivity. Here, we aim to measure the initial photoacoustic pressure with an interferometric fiber system. The major challenge of this work is to eliminate the random interference caused by the light backscattered from the surface and subsurface of scattering tissues.
In the conventional interferometric PAMs relying on the measurement of the sample surface vibration [3,25–31], the intensity of the probe light is considered as a constant and the phase change of the probe light caused by the surface vibration is detected. The light backscattered from the surface and subsurface of a scattering sample results in a complex interference, leading to a random influence on the sensitivity and stability. Such complex interference can be eliminated by using low-coherence interferometry (LCI) [27,31]. However, the interference sensitivity of LCI decreases with the increase of the optical path difference between the reference and probe beams, and the sensitivity will change to zero when the optical path difference is larger than the coherence length of the light source. It is difficult to maintain the interferometer at its highest sensitivity during in vivo imaging.
To address the above problems, we demonstrated a 3×3 coupler-based fiber-optic interferometric system to detect the local initial photoacoustic pressure. In contrast with the conventional interferometric PAMs relying on the measurement of the phase change of the probe light caused by the sample surface vibration, we measured the intensity change of the probe light caused by the local initial photoacoustic pressure. This method overcomes the limitations as mentioned above of the conventional interferometric PAMs and allows a complete-noncontact confocal PAM (cnccPAM). The proposed cnccPAM has the advantages: (1) there’s no need to cover a water layer on the sample surface, (2) the probe light and the excitation light are focused at a same point below the sample surface, which makes it more convenient for in vivo imaging, and (3) there’s no need for the phase stabilization, allowing a high imaging speed.
2. Setup and methods
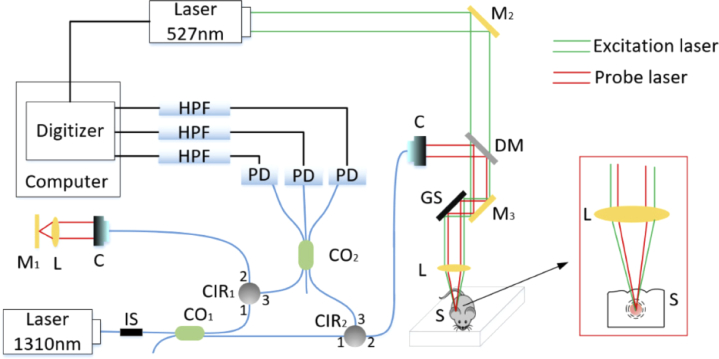
The schematic of the experimental setup is shown in Fig. 1, which is mainly a fiber-optic Mach-Zehnder homodyne interferometer with a single wavelength source. A solid-state laser (DTL-319QT, Laser-export. Co. Ltd.) with a wavelength of 527 nm and a pulse width of 7 ns was selected as the excitation light source due to its strong optical absorption by red blood cells. A laser diode (LSDLD131, Beijing Light Sensing Technology Co. Ltd.) with a wavelength of 1310 nm was used as the detection light source owing to its deep penetration depth in tissues. The coherence length of the detection light was more than several hundred millimeters. The detection light was divided into the reference and probe arms with an intensity ratio of 1:9 by a 2×2 fiber coupler (SSMC-2×2-1310-10, Shanghai Hanyu Technology Co. Ltd.). The probe beam passed through a fiber circulator (CIR-1310-3-P-FA, Shanghai Hanyu Technology Co. Ltd.). The collimated probe beam and the parallel excitation beam were combined with a dichroic mirror, and then they were focused at a same point below the sample surface. The enlarged confocal configuration is shown in the red box. The reference beam passed through a fiber circulator (CIR-1310-3-P-FA, Shanghai Hanyu Technology Co. Ltd.), and then the collimated reference beam was focused onto a mirror by a lens with a focal length of 30 mm. The light reflected from the reference and sample arms, passing through circulators CIR1 and CIR2, entered a 3×3 fiber coupler (SSMC-3 3-1310-1, Shanghai Hanyu Technology Co. Ltd.), respectively. The coupling ratio of the 3×3 fiber coupler was 1:1:1. The light from the 3×3 coupler was measured by three photodetectors (PDB410C, Thorlabs), respectively. The three electrical signals were filtered by a high-pass filter with a cutoff frequency of 130 kHz and then were acquired by a high-speed digitizer (PCI 5105, NI). When the excitation laser source was triggered to emit a pulsed laser for exciting an ultrasonic wave, a synchronization signal from the excitation laser source simultaneously triggered the digitizer for detection of photoacoustic signals. Two-dimensional scanning was performed using a two-dimensional galvanometer scanner (S-8107M, Beijing Century Sunny Technology Co. Ltd.).
Fig. 1.
Schematic of cnccPAM. GS, two-dimensional galvanometer scanner; CIR1-2, circulator; CO1-2, coupler; L, lens; M1−3, mirror; DM, dichroic mirror; IS, isolator; HPF, high-pass filter; PD, photodetectors; S, sample; C, collimator.
When a single-wavelength light source is used in the interferometric system, the light backscattered from the different depths within the sample results in a complex interference signal, which can be represented as:
| (1) |
where denotes the light intensity from the reference arm; denotes the light intensity from the sample at th depth; and denote the intensity change and phase change of the probe beam caused by the initial pressure, respectively; represents the sum of the initial phase and the phase perturbation of the environment; and are the time-varying phase differences between and , and between and , respectively. Compared with the short-pulse intensity change , the other terms in Eq. (1) are slowly varying and can be excluded by a high-pass filter. So, can be rewritten as:
| (2) |
Owing to that is much less than , and thus the measured interference signal is approximated as:
| (3) |
Equation (3) shows that the measured interference signal is modulated by and Here, we used a 3×3 fiber coupler-based method to calculate the intensity change and phase change. For 3×3 coupler-based demodulation shown in Fig. 1, according to Eq. (3), the measured interference signals , and from the three channels can be expressed as:
| (4) |
where is the sum of and , and denote the phase shift caused by the 3×3 coupler. , and are determined by the coupling ratio, and they are 0, and when the coupling ratio is 1:1:1, respectively. From Eq. (4), we get:
| (5) |
and
| (6) |
So, can be calculated as:
| (7) |
and can be expressed as [37]:
| (8) |
3. Results and discussion
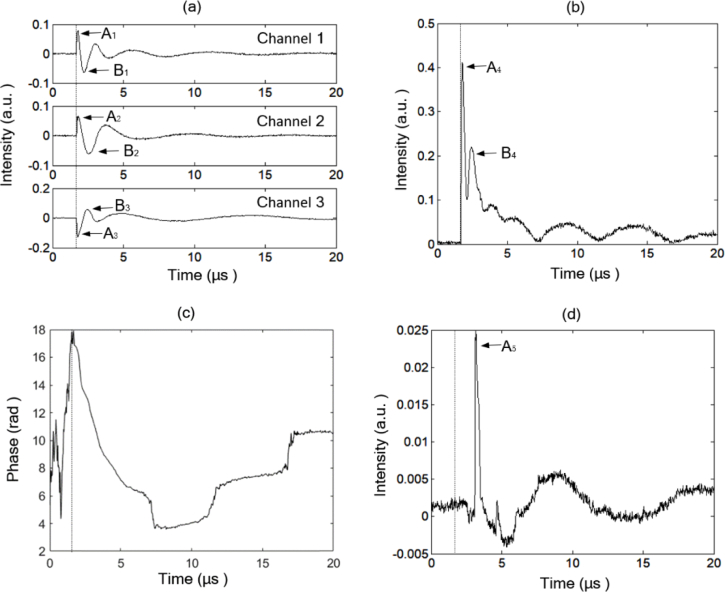
Representative interference signals from the three channels measured from a blood vessel in a mouse ear are shown in Fig. 2(a). In Fig. 2(a)–(d), the dotted vertical lines denote the trigger position. The demodulated and are shown in Fig. 2(b) and (c), respectively. is the sum of the phase change of the probe light caused by the initial photoacoustic pressure, the initial phase and the phase perturbation from the environment. Equation (8) indicates that the phase demodulation contains a denominator term . Due to the use of a high-pass filter, the denominator is close to zero when the filtered signals , and are close to zero, as shown in Fig. 2(a), which may lead to wrong phase demodulation. Equation (7) indicates that the intensity change is free from the influence of the initial phase and the phase perturbation from the environment. Therefore, we selected the intensity change to reconstruct the photoacoustic images. For comparing with the conventional interferometric PAM, we also measured the photoacoustic signal at the same position by the zero-crossing trigger method, as shown in Ref. [3]. The mouse ear was covered with a thin water layer to provide a smooth reflective surface for the probe light, and the probe light was focused on the water surface. The measured water surface vibration is shown in Fig. 2(d). Compared with Fig. 2(d), Fig. 2(b) shows a higher signal to noise ratio (SNR).
Fig. 2.
Demodulation of the phase change and intensity change of the probe light by the present method: (a) measured interference signals; (b) demodulated intensity change and (c) phase change; (d) measured photoacoustic signal by the zero-crossing trigger method.
In Fig. 2, the time interval between the trigger position and the measured pulse signal is equal to the travel time of the pulsed photoacoustic pressure between the position where the initial pressure occurs and the position where the pressure is measured. In Fig. 2(a) and (b), the peaks A1-3 and A4 appear close to the trigger position. So, the travel time of the pulsed photoacoustic pressures is close to zero, which means it is the detection of the initial pressures. In Fig. 2(d), the time interval between the trigger position and the peak A5 is about 1.5 µs, corresponding to 2.25 mm (calculated with an ultrasonic velocity of 1.5 mm/µs). The thickness of the mouse ear is less than 1 mm, and so it is sure that the signal is measured from the water surface.
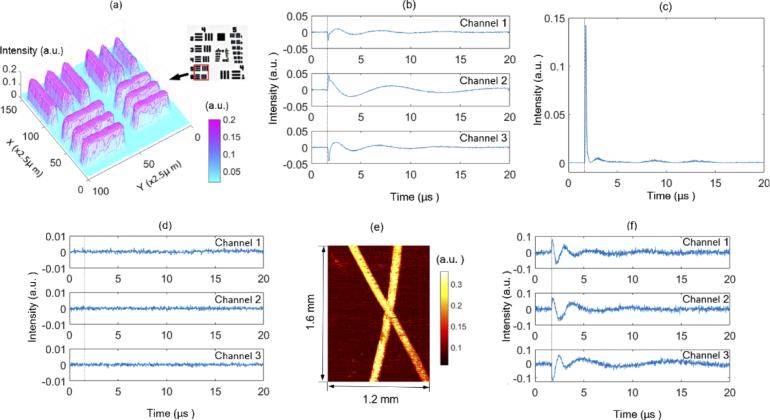
Next, we performed photoacoustic imaging of a chrome-on-glass 1951 USAF resolution target. To avoid possible damage to the chrome coating, the resolution target was immersed in water at a depth of about 1 cm. Both the excitation light and the probe light were focused at the surface of the resolution target by an achromatic lens with a focal length of 30 mm. Figure 3 is the photoacoustic maximum amplitude projection (MAP) image of the element 5 and 6 of group 4. The photograph of the resolution target is shown in the up-right corner. The steps in both the X-direction and Y-direction were 2.5 µm. The reconstructed bars show homogeneous intensity distribution, which shows that the system has a stable sensitivity. In contrast with the conventional interferometric PAMs, in which a water layer is used to provide a smooth reflective surface for the probe light, here, the water layer was employed to avoid the possible damage to the chrome coating and it is not necessary for the measurement of the intensity change. Figure 3(b) shows the raw interference signals measured from the chrome coating, and the calculated intensity change is plotted in Fig. 3(c). As a comparison, Fig. 3(d) shows the raw interference signals measured from the non-chrome part, and there is no observable intensity change due to its very weak optical absorption. Figure 3(d) clearly shows that the high-pass filter can effectively exclude the slowly varying signals. Figure 3(e) shows the photoacoustic MAP image of a thick tissue-mimicking phantom. The steps in both the X-direction and Y-direction are 4 µm. The phantom consists of two human hairs embedded in a scattering gel. The scattering gel is made of agar mixed with 1% intralipid, which gives a scattering background similar to tissues [3]. The distance between the hairs and the phantom surface is about 1 mm. Figure 3(f) shows representative signals generated by the hair. If the signals are from the phantom surface, the time delays of the signals should be about 0.67 µs. Moreover, Fig. 3(b) shows the signals from the chrome coating located below the water surface about 1 cm. So, the corresponding time delay will be about 6.7 µs if the signals are measured from the water surface. However, the time intervals between the trigger position and the first peaks of the signals (Fig. 3(b) and (f)) are about 0.1 us. Therefore, it can be concluded that the signals are measured from or very close to the position where the initial photoacoustic pressure is excited.
Fig. 3.
Results of a chrome-on-glass 1951 USAF resolution target and a tissue-mimicking phantom: (a) photoacoustic MAP image of a resolution target; (b) raw interference signals measured from the chrome coating and (c) the calculated intensity change; (d) raw interference signals measured from the non-chrome part; (e) photoacoustic MAP image of a thick tissue-mimicking phantom; (f) representative signals generated by a hair.
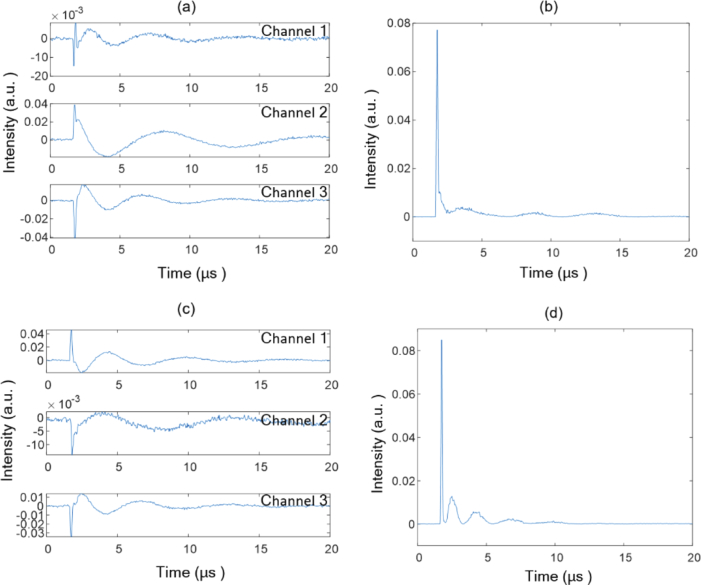
To test the influence of large phase changes on the systematic sensitivity, we measured photoacoustic signals at a point of the resolution target when manually disturbing the water surface. The water surface generated an observable fluctuation. Figure 4(a) and (c) show the measured raw signals, and the corresponding calculated intensity changes of the probe light are plotted in Fig. 4(b) and (d), respectively. Due to the influence of the phase disturbance, the raw signals exhibit random large intensity fluctuation. However, the calculated intensity changes of the probe light are similar. This indicates that the proposed system has a stable sensitivity.
Fig. 4.
Measured photoacoustic signals at a point of the resolution target when manually disturbing the water surface: (a) and (c) measured raw signals, and the corresponding calculated intensity changes of the probe light are plotted in (b) and (d), respectively.
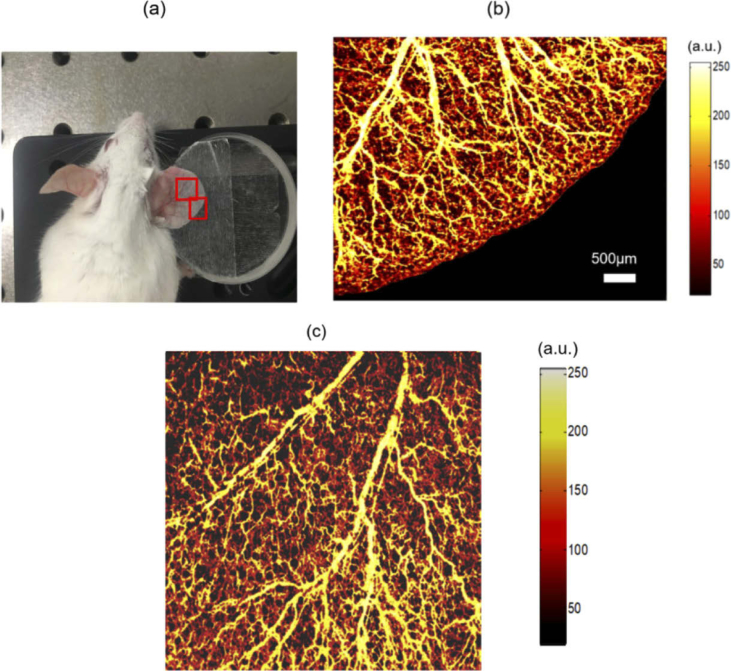
To verify the imaging capability of the cnccPAM system in biological tissues, we conducted in vivo photoacoustic imaging of blood vessels in a mouse ear. A nine weeks old mouse (female) was chosen for the experiment. The experiment was approved by the Animal Ethics Committee of Northeastern University (Shenyang, China), and the operation process was carried out according to the National Institutes of Health Laboratory Animal Care and Use Guidelines. The mouse was anesthetized using a mixture (ketamine, 80 mg/kg; xylazine, 6 mg/kg) through intraperitoneal injection. After the mouse was anesthetized, the right ear was pasted on a glass block shown in Fig. 5(a), and the hair was carefully removed. The excitation light and probe light were focused at a same point below the sample surface by an achromatic lens with a focal length of 30 mm. The photoacoustic MAP images of the regions in the red boxes are plotted in Fig. 5(b) and (c), respectively. The steps in both the X-direction and Y-direction were 7.5 µm. The imaging areas are 5.2mm×4mm (700×520 pixels) and 5.2mm×5.2mm (700×700 pixels), respectively. The scanning times are about 22 minutes and 30 minutes. Figure 5(b) and (c) have the same scale bar. The microvasculature of the mouse ear is visible with relatively high contrast.
Fig. 5.
In vivo photoacoustic imaging of the blood vessels in a mouse ear. (a) Photograph of the mouse ear. Photoacoustic MAP images of the regions inside the red boxes are plotted in (b) and (c), respectively.
The lateral resolution was measured to be about 11 µm by photoacoustic imaging of a sharp blade as demonstrated in Ref. [3], and the full width at half maximum (FWHM) of the lateral line spread function was considered as the lateral resolution. The imaging speed is mainly limited by the pulse repetition rate of the excitation laser (less than 1000 Hz in this study). The lateral resolution and imaging speed can be improved by using an objective lens with a larger numerical aperture (NA) and by using an excitation laser with a higher repetition rate, respectively. The power of the probe light incident on the sample is 3 mW, which is well below the American National Standards Institute (ANSI) standards (Z136.1) for the safe use of near-infrared light at 1310 nm [34,38,39]. The single pulse energy of the excitation beam for in vivo imaging is 1.2 µJ, corresponding to a surface fluence of about calculated according to Ref. [34]. The surface fluence is less than the single pulse limit of set by the ANSI [38]. In our previous paper [3], similar photoacoustic images of the blood vessels in a mouse ear were obtained by measurement of the tissue surface vibration, and a water layer was covered on the sample to eliminate the influence of the rough tissue surface. And the laser fluence of the excitation laser incident on the ear surface was , which is slightly higher than the single pulse limit set by the ANSI. The surface fluence used in this work is , which is nearly half of the previous surface fluence. This indicates the present method has a higher sensitivity than the conventional methods.
Unlike the conventional interferometric PAMs relying on the measurement of the tissue surface vibration, the proposed method measures the intensity change of the probe light. When an object absorbs light energy, the absorbed energy causes a temperature rise. And then, thermoelastic expansion occurs and generates ultrasonic waves. The changed pressure or temperature cause the variation of the refractive index, and consequently resulting in the changes of the reflectivity and optical path length. The intensity change and phase change shown in Fig. 2(b) and (c) are mainly attributed to the pressure-induced effect owing to that the thermal effect is negligible [33]. The intensity change is dependent on the change of the refractive index, while the phase change is determined by both the change of the refractive index and the change of the absorber size caused by the thermoelastic expansion.
In Fig. 2(b), the peaks A4 and B4 result from the pulses A1-3 and B1-3 shown in Fig. 2(a), respectively. These bipolar photoacoustic signals have been widely reported before [40–42], and the distances between the peaks A1-3 and peaks B1-3 are proportional to the axial size of the absorber illuminated by the excitation light [40–42]. In Fig. 3(c), the second peak disappears. This may because the second pulse superposes to the initial pulse due to the very thin optical absorption layer of the chrome coating (about 100 nm). The reconstructed photoacoustic images indicate that such superposition does not affect photoacoustic imaging.
The above results confirm that the present method can be successfully utilized for in vivo photoacoustic imaging of biological tissues. In contrast with the conventional interferometric PAMs, the proposed cnccPAM measures the intensity change of the probe light caused by the initial photoacoustic pressure. Such intensity change cannot be measured by using a 2×2 coupler and a balanced detector that is usually used in conventional interferometric systems. The 2×2 coupler-based methods measure the phase change of the probe light, and the intensity of the probe light is considered as a constant. In these methods, the phase stabilization is usually required to eliminate the influence of the random initial phase and environmental perturbation. However, such phase stabilization cannot be used to measure the initial photoacoustic pressure because the probe light backscattered from the surface and subsurface of scattering tissues results in a complex interference.
3×3 fiber-optic couplers have been widely used for extraction of the phase information of various interferometric systems [32,43]. Huang et al. reported a similar method to obtain phase information using three optical signals having phase shifts of [37]. We used the 3×3 coupler to calculate the intensity change. The coupling ratio of the 3×3 coupler used in this study is approximated as 1:1:1, which corresponding to a phase shift of among any two output ports of the coupler. Therefore, Eq. (5)–(8) were derived with phase shifts of . In fact, it’s not necessary to use ideal phase shifts of to calculate the intensity change. For a non-ideal 3×3 coupler, the quadrature components, as shown in Eq. (5) and (6), can also be calculated from the three interferometric signals with non-ideal phase shifts. Choma et al. reported an instantaneous quadrature low-coherence interferometry with a 3×3 fiber optic coupler, and they demonstrated the calculation of the quadrature components of the complex interferometric signals of a non-ideal 3×3 fiber optic coupler [43].
Park et al. used two channels of a 3×3 fiber coupler to measure the phase change of the probe light caused by the sample surface vibration [32], while the present method measures the intensity change of the probe light caused by the initial photoacoustic pressure. Both methods eliminate the need of the phase stability process. In Ref. [32], a low-coherence source was used to eliminate the influence of the complex interference caused by the probe light backscattered from the subsurface of a scattering sample. However, the interferometric sensitivity is dependent on the optical path difference between the reference and probe beams. The rough tissue surface could change the optical path difference, leading to a spatially varying sensitivity. Moreover, the sensitivity will change to zero when the optical path difference is larger than the coherence length of the light source. In contrast, we used a high-coherence source with a coherence length of more than several hundred millimeters. We eliminated the influence of the complex interference by using a high-pass filter. Only the short-pulse signals caused by the initial pulse pressure can pass through the filter.
Equation (4) shows the measured interference signal is mainly dependent on the term because (the intensity of the reference light) is much larger than (the intensity change of the probe light). The signals contain both the phase modulation and the amplitude modulation . In contrast, in the conventional interferometric PAMs, the intensity of the probe light is considered as a constant. Although only the intensity change is extracted to form photoacoustic images, the interferometric acquisition is necessary for achieving a high SNR. If acquisition of the signals without the reference beam, the acquired signal . In interferometric acquisition, the acquired signal . The interferometric acquisition has much higher SNR because is much larger than .
In a fiber-optic interferometer, the sensitivity suffers from the polarization fading due to the misalignment of the polarization states between the reference and probe arms. In this study, we bent the fiber to align the polarization states. For practical applications, an automated polarization controller can be used to improve the system sensitivity.
The proposed cnccPAM overcomes the limitations of the conventional interferometric PAMs and is especially attractive for in vivo imaging. First, it’s well known that the rough tissue surface has a crucial influence on the optical interferometric measurement of the tissue surface vibration, and therefore a water layer is usually required to reduce such influence. cnccPAM is free from the influence of the rough tissue surface, achieving complete noncontact in vivo imaging. In addition, the probe light and excitation light are focused at a same point below the sample surface. The confocal configuration makes it more convenient for in vivo imaging. Finally, the proposed demodulation method is free from the influence of the environment and initial phase, and thus there’s no need for phase stabilization, allowing a high imaging speed.
In the conventional interferometric PAM relying on the measurement of the sample surface vibration, the delay time of the measured PA waves is proportional to the depth of the absorber under imaging. However, for measurement of initial photoacoustic pressures, the intensity change and phase change of the probe light generated close to the absorber, and the delay time of the measured PA signal is independent of the depth of the absorber. So, the proposed method is not depth-resolved. This disadvantage may be overcome by using low-coherence interferometry.
The proposed method is only suitable for calculating the intensity change of the probe light generated from a thin optical absorption layer. Equation (7) and (8) were derived by neglecting the thickness of the absorber. For an absorber with a non-negligible thickness, the photoacoustic pressure is excited at different depths. Thus, Eq. (3) changes to , where and denote the intensity change and phase change generated at th depth, respectively, and represents the sum of the corresponding initial phase and the phase perturbation of the environment. The multiple intensity change generated at different depths cannot be extracted from the complex interferometric signals . In fact, in PAM, only the absorber close to the focus of the excitation laser can be excited, which means only a thin layer can be excited for a thick absorber. In PAM of blood vessels, it always needs to move the focus of the excitation laser to image the blood vessels at different depths [34,44].
4. Conclusions
In conclusion, we have demonstrated that the 3×3 coupler-based fiber-optic interferometric system can be used to detect the local initial photoacoustic pressures. The experimental results show that the intensity change is optimal for the detection of the local initial photoacoustic pressure. By combining a 3×3 coupler and a high-pass filter, we measured the intensity change of the probe light caused by the initial photoacoustic pressures. Compared with the conventional interferometric PAMs, the proposed complete-noncontact confocal PAM has the advantages such as complete-noncontact, confocal configuration, and without the need for phase stabilization. These advantages show that the proposed PAM will be a promising technique for in vivo imaging, especially for endoscopic imaging. Compared with the conventional methods relying on the measurement of the sample surface vibration, the major disadvantage of the present method is that it’s not depth-resolved, and this method is suitable for the case that the depth information is not required.
Funding
National Natural Science Foundation of China10.13039/501100001809 (31170956, 61275214, 61771119); Natural Science Foundation of Hebei Province10.13039/501100003787 (A2015501065, F2019501132, H2015501133); Fundamental Research Funds for the Central Universities10.13039/501100012226 (N172304034).
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References
- 1.Wang L. V., “Multiscale photoacoustic microscopy and computed tomography,” Nat. Photonics 3(9), 503–509 (2009). 10.1038/nphoton.2009.157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Beard P., “Biomedical photoacoustic imaging,” Interface Focus 1(4), 602–631 (2011). 10.1098/rsfs.2011.0028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lu J., Gao Y., Ma Z., Zhou H., Wang R. K., Wang Y., “In vivo photoacoustic imaging of blood vessels using a homodyne interferometer with zero-crossing triggering,” J. Biomed. Opt. 22(3), 036002 (2017). 10.1117/1.JBO.22.3.036002 [DOI] [PubMed] [Google Scholar]
- 4.Yang J., Favazza C., Chen R., Yao J., Cai S., Maslov K., Zhou Q., Shung K., Wang L. V., “Simultaneous functional photoacoustic and ultrasonic endoscopy of internal organs in vivo,” Nat. Med. 18(8), 1297–1302 (2012). 10.1038/nm.2823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang H. F., Maslov K., Stoica G., Wang L. V., “Functional photoacoustic microscopy for high-resolution and noninvasive in vivo imaging,” Nat. Biotechnol. 24(7), 848–851 (2006). 10.1038/nbt1220 [DOI] [PubMed] [Google Scholar]
- 6.Paproski R. J., Heinmiller A., Wachowicz K., Zemp R. J., “Multiwavelength photoacoustic imaging of inducible tyrosinase reporter gene expression in xenograft tumors,” Sci. Rep. 4(1), 5329 (2015). 10.1038/srep05329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wu D., Huang L., Jiang M. S., Jiang H., “Contrast agents for photoacoustic and thermoacoustic imaging: a review,” Int. J. Mol. Sci. 15(12), 23616–23639 (2014). 10.3390/ijms151223616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Strohm E. M., Moore M. J., Kolios M. C., “Single cell photoacoustic microscopy: a review,” IEEE J. Sel. Top. Quantum Electron. 22(3), 137–151 (2016). 10.1109/JSTQE.2015.2497323 [DOI] [Google Scholar]
- 9.Rousseau G., Blouin A., Monchalin J. P., “Non-contact photoacoustic tomography and ultrasonography for tissue imaging,” Biomed. Opt. Express 3(1), 16–25 (2012). 10.1364/BOE.3.000016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hajireza P., Sorge J., Brett M., Zemp R. J., “In vivo optical resolution photoacoustic microscopy using glancing angle-deposited nanostructured Fabry-Perot etalons,” Opt. Lett. 40(7), 1350–1353 (2015). 10.1364/OL.40.001350 [DOI] [PubMed] [Google Scholar]
- 11.Kim C., Erpelding T. N., Jankovic L., Pashley M. D., Wang L. V., “Deeply penetrating in vivo photoacoustic imaging using a clinical ultrasound array system,” Biomed. Opt. Express 1(1), 278–284 (2010). 10.1364/BOE.1.000278 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Maslov K., Zhang H. F., Hu S., Wang L. V., “Optical-resolution photoacoustic microscopy for in vivo imaging of single capillaries,” Opt. Lett. 33(9), 929–931 (2008). 10.1364/OL.33.000929 [DOI] [PubMed] [Google Scholar]
- 13.Hu S., Maslov K., Wang L. V., “Second-generation optical-resolution photoacoustic microscopy with improved sensitivity and speed,” Opt. Lett. 36(7), 1134–1136 (2011). 10.1364/OL.36.001134 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhang E., Laufer J., Beard P., “Backward-mode multiwavelength photoacoustic scanner using a planar Fabry-Perot polymer film ultrasound sensor for high-resolution three-dimensional imaging of biological tissues,” Appl. Opt. 47(4), 561–577 (2008). 10.1364/AO.47.000561 [DOI] [PubMed] [Google Scholar]
- 15.Paltauf G., Nuster R., Haltmeier M., Burgholzer P., “Photoacoustic tomography using a Mach-Zehnder interferometer as an acoustic line detector,” Appl. Opt. 46(16), 3352–3358 (2007). 10.1364/AO.46.003352 [DOI] [PubMed] [Google Scholar]
- 16.Allen T. J., Ogunlade O., Zhang E., Beard P. C., “Large area laser scanning optical resolution photoacoustic microscopy using a fibre optic sensor,” Biomed. Opt. Express 9(2), 650 (2018). 10.1364/BOE.9.000650 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xie Z., Chen S., Ling T., Guo L. J., Carson P. L., Wang X., “Pure optical photoacoustic microscopy,” Opt. Express 19(10), 9027–9034 (2011). 10.1364/OE.19.009027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yang J. M., Li C., Chen R., Rao B., Yao J., Yeh C. H., Wang L. V., “Optical-resolution photoacoustic endomicroscopy in vivo,” Biomed. Opt. Express 6(3), 918–932 (2015). 10.1364/BOE.6.000918 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yang J. M., Li C., Chen R., Zhou Q., Shuang K. K., Wang L. V., “Catheter-based photoacoustic endoscope,” J. Biomed. Opt. 19(6), 066001 (2014). 10.1117/1.JBO.19.6.066001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yuan Y., Yang S., Xing D., “Preclinical photoacoustic imaging endoscope based on acousto-optic coaxial system using ring transducer array,” Opt. Lett. 35(13), 2266 (2010). 10.1364/OL.35.002266 [DOI] [PubMed] [Google Scholar]
- 21.Berer T., Hochreiner A., Zamiri S., Burgholzer P., “Remote photoacoustic imaging on solid material using a two-wave mixing interferometer,” Opt. Lett. 35(24), 4151–4153 (2010). 10.1364/OL.35.004151 [DOI] [PubMed] [Google Scholar]
- 22.Carp S. A., Guerra A., Duque S. Q., Venugopalan V., “Optoacoustic imaging using interferometric measurement of surface displacement,” Appl. Phys. Lett. 85(23), 5772–5774 (2004). 10.1063/1.1831569 [DOI] [Google Scholar]
- 23.Park S. J., Eom J., Kim Y. H., Lee C. S., Lee B. H., “Noncontact photoacoustic imaging based on all-fiber heterodyne interferometer,” Opt. Lett. 39(16), 4903 (2014). 10.1364/OL.39.004903 [DOI] [PubMed] [Google Scholar]
- 24.Rousseau G., Gauthier B., Blouin A., Monchalin J. P., “Non-contact biomedical photoacoustic and ultrasound imaging,” J. Biomed. Opt. 17(6), 061217 (2012). 10.1117/1.JBO.17.6.061217 [DOI] [PubMed] [Google Scholar]
- 25.Hochreiner A., Bauer-Marschallinger J., Burgholzer P., Jakoby B., Berer T., “Non-contact photoacoustic imaging using a fiber based interferometer with optical amplification,” Biomed. Opt. Express 4(11), 2322–2331 (2013). 10.1364/BOE.4.002322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Berer T., Leiss-Holzinger E., Hochreiner A., Bauer-Marschallinger J., Buchsbaum A., “Multimodal noncontact photoacoustic and optical coherence tomography imaging using wavelength-division multiplexing,” J. Biomed. Opt. 20(4), 046013 (2015). 10.1117/1.JBO.20.4.046013 [DOI] [PubMed] [Google Scholar]
- 27.Wang Y., Li C., Wang R. K., “Noncontact photoacoustic imaging achieved by using a low-coherence interferometer as the acoustic detector,” Opt. Lett. 36(20), 3975–3977 (2011). 10.1364/OL.36.003975 [DOI] [PubMed] [Google Scholar]
- 28.Chen Z., Yang S., Wang Y., Xing D., “All-optically integrated photo-acoustic microscopy and optical coherence tomography based on a single Michelson detector,” Opt. Lett. 40(12), 2838–2841 (2015). 10.1364/OL.40.002838 [DOI] [PubMed] [Google Scholar]
- 29.Liu J., Tang Z., Wu Y., Wang Y., “Rapid and noncontact photoacoustic tomography imaging system using an interferometer with high-speed phase modulation technique,” Rev. Sci. Instrum. 86(4), 044904 (2015). 10.1063/1.4918801 [DOI] [PubMed] [Google Scholar]
- 30.Ma Z., Luo S., Yu M., Wang Y., “Assessment of microvasculature flow state with a high speed all-optic dual-modal system of optical coherence tomography and photoacoustic imaging,” Biomed. Opt. Express 9(12), 6103–6115 (2018). 10.1364/BOE.9.006103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chen Z., Yang S., Wang Y., Xing D., “Noncontact broadband all-optical photoacoustic microscopy based on a low-coherence interferometer,” Appl. Phys. Lett. 106(4), 043701 (2015). 10.1063/1.4906748 [DOI] [Google Scholar]
- 32.Park S., Rim S., Kim Y., Lee B. H., “Noncontact photoacoustic imaging based on optical quadrature detection with a multiport interferometer,” Opt. Lett. 44(10), 2590–2593 (2019). 10.1364/OL.44.002590 [DOI] [PubMed] [Google Scholar]
- 33.Hajireza P., Shi W., Bell K., Paproski R. J., Zemp R. J., “Non-interferometric photoacoustic remote sensing microscopy,” Light: Sci. Appl. 6(6), e16278 (2017). 10.1038/lsa.2016.278 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hajireza P., Bell K., Shi W., Shapiro J., Zemp R. J., “Deep non-contact photoacoustic initial pressure imaging,” Optica 5(7), 814 (2018). 10.1364/OPTICA.5.000814 [DOI] [Google Scholar]
- 35.Bell K., Hajireza P., Shi W., Zemp R., “Temporal evolution of low-coherence reflectrometry signals in photoacoustic remote sensing microscopy,” Appl. Opt. 56(18), 5172 (2017). 10.1364/AO.56.005172 [DOI] [PubMed] [Google Scholar]
- 36.Bell K., Hajireza P., Zemp R., “Real-time functional photoacoustic remote sensing microscopy,” Opt. Lett. 44(14), 3466–3469 (2019). 10.1364/OL.44.003466 [DOI] [PubMed] [Google Scholar]
- 37.Huang P. S., Zhang S., “Fast three-step phase-shifting algorithm,” Appl. Opt. 45(21), 5086–5091 (2006). 10.1364/AO.45.005086 [DOI] [PubMed] [Google Scholar]
- 38.Laser Institute of America , American National Standard for Safe Use of Lasers ANSI Z136.1–2007 (American National Standards Institute, 2007). [Google Scholar]
- 39.Choi W., Wang R., “Volumetric cutaneous microangiography of human skin in vivo by VCSEL swept-source optical coherence tomography,” Quantum Electron. 44(8), 740–745 (2014). 10.1070/QE2014v044n08ABEH015542 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Jun X., Yao J., Wang L. V., “Photoacoustic Tomography: Principles and Advances,” Prog. Electromagn. Res. 147, 1–22 (2014). 10.2528/PIER14032303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Calasso I. G., “Photoacoustic Point Source,” Phys. Rev. Lett. 86(16), 3550–3553 (2001). 10.1103/PhysRevLett.86.3550 [DOI] [PubMed] [Google Scholar]
- 42.Wang Y., Xing D., Zeng Y., Chen Q., “Photoacoustic imaging with deconvolution algorithm,” Phys. Med. Biol. 49(14), 3117–3124 (2004). 10.1088/0031-9155/49/14/006 [DOI] [PubMed] [Google Scholar]
- 43.Choma M. A., Yang C., Izatt J. A., “Instantaneous quadrature low-coherence interferometry with 3×3 fiber-optic couplers,” Opt. Lett. 28(22), 2162–2164 (2003). 10.1364/OL.28.002162 [DOI] [PubMed] [Google Scholar]
- 44.Yao J., Wang L., Yang J. M., Maslov K. I., Wong T. T. W., Li L., Huang C. H., Zou J., Wang L. V., “High-speed label-free functional photoacoustic microscopy of mouse brain in action,” Nat. Med. 12(5), 407–410 (2015). 10.1038/nmeth.3336 [DOI] [PMC free article] [PubMed] [Google Scholar]