Abstract
Understanding the meaning of abstract mathematical symbols is a cornerstone of arithmetic learning in children. Studies have long focused on the role of spatial intuitions in the processing of numerals. However, it has been argued that such intuitions may also underlie symbols that convey fundamental arithmetic concepts, such as arithmetic operators. In the present cross-sectional study, we used fMRI to investigate how and when associations between arithmetic operators and brain regions processing spatial information emerge in children from 3rd to 10th grade. We found that the mere perception of a ‘+’ sign elicited grade-related increases of spatial activity in the right hippocampus. That is, merely perceiving ‘+’ signs – without any operands – elicited enhanced hippocampal activity after around 7th grade (12–13 years old). In these children, hippocampal activity in response to a ‘+’ sign was further correlated with the degree to which calculation performance was facilitated by the preview of that sign before an addition problem, an effect termed operator-priming. Grade-related increases of hippocampal spatial activity were operation-specific because they were not observed with ‘×’ signs, which might evoke rote retrieval rather than numerical manipulation. Our study raises the possibility that hippocampal spatial mechanisms help build associations between some arithmetic operators and space throughout age and/or education.
Keywords: Arithmetic, Development, Attention, Space, fMRI, Hippocampus
1. Introduction
Humans are unique in their ability to represent abstract mathematical concepts by culturally invented symbols, such as Arabic numerals and arithmetic signs. Because these symbols are arbitrary, learning the relationship between their identity and the concept they represent is a challenge during early math education in children. Most prior studies have focused on the mechanisms supporting the acquisition of symbols representing numerical quantities (Piazza et al., 2007, Ansari, 2008, Holloway and Ansari, 2009, Lyons and Ansari, 2009, Mundy and Gilmore, 2009). However, efficient processing of symbols that convey fundamental arithmetic concepts (i.e., operators) may be an important and largely neglected aspect of arithmetic skills. This is suggested by the operator-priming effect (Roussel et al., 2002, Fayol and Thevenot, 2012, Mathieu et al., 2017), whereby the anticipated presentation of a ‘+’ or ‘-’ sign 150 ms before a single-digit addition or subtraction problem facilitates problem-solving in adults.
What aspect of the processing of an operator may cause the operator-priming effect in adults? A first possibility is that an arithmetic sign may automatically evoke a network of facts. For example, the perception of a ‘+’ or ‘-’ sign might pre-activate a network of additive or subtractive facts that would have been built in declarative memory after years of practice (Campbell and Xue, 2001, Ashcraft, 1992). Pre-activating such a network would facilitate the retrieval of the answer from memory when operands are presented. A second possibility is that an arithmetic sign may prime a specific procedure that would have been “automatized” after its repeated practice during arithmetic learning. For instance, Fayol and Thevenot argued that perceiving a ‘+’ or ‘-’ sign might trigger an automatized procedure that could be “linked to the convocation of the mental number line and could correspond to a preparation for a quick left-to-right or right-to-left browsing of this mental line” (Fayol and Thevenot, 2012). This proposal echoes the idea that adding or subtracting numbers involves rightward and leftward shifts of attention from a source to a target number along a mental map of numbers oriented from left to right, i.e., the mental number line (MNL) (Hubbard et al., 2005, Masson and Pesenti, 2014, Mathieu et al., 2016, Pinheiro-Chagas et al., 2017). Pre-activating such a procedure would result in a facilitation of subsequent calculation when operands are presented, thereby explaining the operator-priming effect.
Interestingly, two lines of evidence favor the procedural over the declarative interpretation of the operator-priming effect. First, the effect is not observed with the ‘×’ sign and multiplication problems (Roussel et al., 2002, Mathieu et al., 2017). Multiplication problems, however, are explicitly learned by rote in school and multiplication is unanimously viewed as the operation having the strongest association with a network of facts in memory (Campbell and Xue, 2001, Galfano et al., 2003, Thibodeau et al., 1996). Therefore, the lack of operator-priming effect for multiplication problems is difficult to reconcile with the idea that the effect is due to associations between operators and networks of stored facts. Second, in line with Fayol and Thevenot’s proposal that ‘+’ and ‘−’ signs may prime a spatial scanning of the MNL, a recent study suggests that ‘+’ and ‘−’ signs do evoke spatial intuitions. Specifically, Pinhas et al. (2014) found that, when instructed to categorize ‘+’ and ‘−’ signs with left-hand or right-hand responses, adults tend to respond faster to ‘+’ signs with the right hand than with the left hand, whereas they tend to respond faster to ‘-’ signs with the left hand than with the right hand (Pinhas et al., 2014). Thus, ‘+’ and ‘−’ signs appear to have some automatic associations with the right and left sides of space, respectively.
Using fMRI, we recently found that such spatial associations may stem from the fact that some arithmetic operators are automatically processed in brain regions involved in spatial attention in adults. We showed that the mere perception of a ‘+’ sign elicits greater activity than the mere perception of a ‘×’ sign in brain regions underlying overt spatial attention. These included the frontal eye fields (FEF) and the posterior superior parietal lobule (PSPL) (Mathieu et al., 2017). Thus, perceiving a ‘+’ sign (but not a ‘×’ sign) may be associated with a deployment of spatial attention in educated adults. Therefore, the rightward shifts of attention that have been posited to underlie addition problem-solving (Hubbard et al., 2005, Masson and Pesenti, 2014, Mathieu et al., 2016) might be primed by the mere preview of the addition sign (but not by the preview of a multiplication sign because multiplication is typically learned by rote and unlikely to be associated with movements along the MNL). Overall, there is mounting evidence that at least some arithmetic operators (e.g., ‘+’ but not ‘×’ signs) evoke spatial intuitions in adults, and that these intuitions may relate to the operator-priming effect.
However, associations between operators and space are arguably not innate. Therefore, a fundamental outstanding question is how and when such associations emerge in the developing brain. To answer that question, we studied 34 children from 3rd to 10th grade while they performed 3 tasks. First, fMRI activity was measured while children were instructed to make eye saccades towards visually presented targets. This allowed us to precisely localize several regions of interest (ROIs) involved in spatial attention across children. Second, fMRI activity was measured in these spatial attention ROIs while children were presented with trials in which a ‘+’ sign was displayed without any operands (hereafter addition sign-only trials). As in our previous study in adults (Mathieu et al., accepted), activity during the perception of addition sign-only trials was compared to activity associated with trials in which a ‘×’ sign was displayed without any operands (hereafter multiplication sign-only trials) because these do not appear to evoke any specific intuitions in adults (Fayol and Thevenot 2012). This allowed us to identify the spatial attention ROIs in which activity in response to a ‘+’ sign (as compared to a ‘×’ sign) increases with age and/or education, as well as the developmental time course of these effects.1 Third, outside of the scanner, we asked subjects to perform an operator-priming task and measured the correlation between inter-individual differences in the size of the operator-priming effect and inter-individual differences in sign-related activity in spatial attention ROIs as a function of grade. This allowed us to evaluate when sign-related activity in spatial attention ROIs leads to an operator-priming effect in children.
2. Material and methods
2.1. Participants
Forty-two right-handed children from 3rd to 10th grade participated in the study. All were native French speakers. Participants did not have prior history of neurological disease, psychiatric disorders, learning disabilities or attention deficits. All children and parents provided written informed consent to participate in the study, which was approved by the local ethics committee (CPP Sud-Est-II). Families received 80€ for their participation. Data from 8 subjects were excluded because of excessive head-movement in the scanner (see criteria in the Section 2.7., n = 3), poor whole-brain coverage (i.e. susceptibility artefacts from dental braces, n = 3) and unacceptably low performance during the task (i.e., lower than 50% accuracy on the sign-plus-operand trials, n = 2). Therefore, the final sample consisted of 34 children (20 males) from 3rd to 10th grade (age range: 8–15, mean age = 11.37, SD = 1.84). For each child, a continuous measure of grade was calculated by taking into account the specific date within the grade year when that child was scanned. The whole sample (n = 34) was evenly split into three groups as a function of grade: 11 children were from the ‘lower grades’ group (grade 3.2–5.4; mean = 4.4), 11 children were from the ‘intermediate grades’ group (grade 5.6–6.9; mean = 6.2), and 12 children were from the ‘higher grades’ group (grade 7.6–10.2; mean = 8.5).
2.2. Standardized measures
Children were administered standardized tests of intellectual and arithmetic abilities to ensure that there were no age differences with respect to those measures. Full-scale IQ was measured using the NEMI-2 (Cognet, 2006). Basic arithmetic knowledge was evaluated with the Math-Fluency subtest of the Woodcock-Johnson-III Tests of Achievement (WJ-III) (Woodcock et al., 2001). Across all participants, standardized (i.e., age-normalized) scores on IQ (mean = 112; SD = 10) and Math Fluency (mean = 106; SD = 16) tests were within the normal range. One-way ANOVAs with the between-subject factor group (lower, intermediate, higher grades) revealed no main effect of group on IQ (F(2,31) = 0.591, p = 0.560, BF10 = 0.29), indicating that age-normalized intellectual abilities were similar across groups. However, there was a main effect of group on Math Fluency (F(2,31) = 5.867, p = 0.007, BF10 = 7.24): Children from intermediate grades had a higher age-normalized score (mean = 118; SD = 18) than children from lower (mean = 100; SD = 11) and higher grades (mean = 100; SD = 13). Therefore, we included standardized Math-Fluency scores as nuisance covariate in all of our analyses.
2.3. Behavioral session
After standardized testing, children participated in a behavioral session during which they performed an operator-priming task adapted from Fayol and Thevenot (2012) and Roussel et al. (2002). Children were asked to evaluate 56 single-digit addition and 56 multiplication problems composed of operands between 2 and 9. Problems were presented in both commutative orders. Tie problems were excluded. Problems with a sum smaller than or equal to 11 and a product smaller or equal to 24 were considered small. Other problems were considered large.
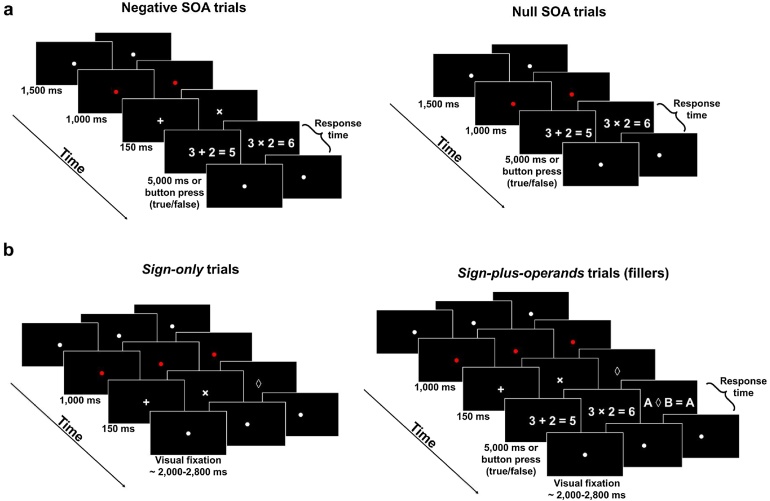
In each trial, a problem was presented with an answer (Fig. 1a). The arithmetic sign was presented either 150 ms before (Negative SOA condition) or at the same time (Null SOA condition) as the operands (Fig. 1a). All problems were presented once in both SOA condition with a valid answer. Twenty-eight addition and 28 multiplication problems were also presented in both SOA condition with an invalid answer (obtained by adding or subtracting 1 to or from the valid answer). Trials were pseudorandomly ordered so that no more than three problems of the same type appeared consecutively. Problems with an invalid answer were randomly chosen across subjects and the order of blocks was counter-balanced between subjects. The experiment started with 8 practice trials.
Fig. 1.
Experimental design. (a) During the behavioral session, children (n = 34) were asked to evaluate the result of single-digit addition and multiplication problems. For both operations, the arithmetic sign was presented either 150 ms before (negative SOA trials), or at the same time as the operands (null SOA trials). (b) In the scanner, children (n = 34) performed an arithmetic task during which they were presented with sign-only (left) and sign-plus-operands (right) addition, multiplication and baseline trials. In each trial, a sign (‘+’, ‘×’ or ‘◊’) was presented at the center of the screen for 150 ms. In sign-only trials, the trial ended with the presentation of the sign and was simply followed by the inter-trial period of fixation. In sign-plus-operands trials (filler trials), the ‘+’ or ‘×’ sign was immediately followed by a single-digit addition or multiplication problem (respectively) presented along an answer and the ‘◊’ sign was followed by 3 letters. In those cases, children had 5000 ms to evaluate whether the answer of the problem was true or false or to indicate whether one of the 3 letters was a B.
The experiment was controlled by Presentation software (Neurobehavioral Systems, Albany, CA). Problems were displayed in white Arial 60-point font on a black background. All trials started with the presentation of a white central fixation dot for 1500 ms, immediately followed by a red central fixation dot for 1000 ms signaling that the problem was about to be presented, either in the negative SOA condition or in the null SOA condition (Fig. 1a). Subjects had a maximum of 5000 ms to evaluate whether the response was valid or invalid as quickly as possible by pressing one of two keys on the computer keyboard.
2.4. fMRI session
During fMRI scanning, children performed a spatial attention localizer task and an arithmetic task. The spatial attention localizer task consisted in alternating blocks of fixation and saccades. During saccade blocks (n = 9), participants were asked to make saccades towards several successive target dots. Each saccade block contained 16 target dots (0.2° visual angle) that appeared at random positions with an eccentricity of 3°, 3.5°, 4°, 4.5°, 5° or 5.5° in the left or right visual field for an average of 800 ms (with a jitter of ±200 ms). During fixation blocks (n = 9), participants were asked to maintain fixation on a central dot for 12,800 ms. Block order was counterbalanced across children.
During the arithmetic task, children were presented with sign-only and sign-plus-operands versions of addition and multiplication trials (Fig. 1b). Each trial started with the presentation of either a ‘+’ or a ‘×’ sign at the center of the screen for 150 ms. In sign-only trials (n = 30), the trial ended with the presentation of the sign and was simply followed by the inter-trial period of fixation (see below). These sign-only trials were our trials of interest and allowed us to isolate neural activity due to the presentation of a sign alone. We also included in the experiment sign-plus-operands trials (n = 50). In those filler trials, the ‘+’ or ‘×’ sign was immediately followed by a single-digit addition or multiplication problem (respectively) presented with an answer. Participants were asked to indicate whether the answer was true or false. The goal of these filler trials (for which associated activity would be difficult to interpret because any effects could be attributable to the anticipatory presentation of the operator, the appearance of the operands, or a combination of both of these factors) was only to keep children engaged and attentive in the scanner. They also induced an arithmetic context, thereby ensuring that the ‘+’ and ‘×’ signs presented in sign-only trials were perceived as arithmetic signs. Problems in sign-plus-operand trials were constructed following the same criteria as in the behavioral session. Finally, the baseline consisted in trials in which the arithmetic sign was replaced by an abstract non-arithmetic sign (i.e., ‘◊’). We included 30 baseline sign-only trials (in which the ‘◊’ sign was presented in isolation) and 50 baseline sign-plus-operand trials (in which the ‘◊’ sign was followed by 3 letters and participants had to indicate whether one of these letters was a B). All trials were followed by a variable period of visual fixation ranging from 3000 ms to 3800 ms. That period consisted in a central white fixation dot that turned red 1000 ms before the onset of the next trial. The arithmetic task was decomposed in 4 functional runs. All trials were intermixed and the timing and order of trial presentation within each run was optimized for estimation efficiency using optseq2 (http://surfer.nmr.mgh.harvard.edu/optseq/). Behavioral responses were recorded using an MR-compatible response device.
Stimuli were generated using Presentation software (Neurobehavioral Systems, Albany, CA). Prior scanning, children were familiarized with the fMRI environment during a practice session that took place after the standardized testing and the behavioral session. During this practice session, children learned to minimize head movement in a mock fMRI scanner. The actual scanning session took place no more than 3 weeks after the practice session.
2.5. Behavioral analyses
RT data associated with the operator-priming task were normalized using a logarithmic transformation prior all analyses to improve the conformity of the data to the standard assumptions of parametric testing. Following Fayol and Thevenot (2012), mean RT was analyzed using planned comparisons that followed from a within-subject ANOVA with the factors Operation (Addition/Multiplication) and SOA (Negative/Null), conducted separately for each group. We report for all effects the corresponding Bayes factors (BF10), indicating the strength of evidence for the alternative hypothesis (H1) relative to the null hypothesis (H0). Substantial evidence in favor of the alternative hypothesis is typically suggested by a BF10 greater than 3 (Jeffreys, 1961, Dienes, 2011).
2.6. fMRI data acquisition
Images were collected with a Siemens Prisma 3T MRI scanner (Siemens Healthcare, Erlangen, Germany) at the CERMEP Imagerie du vivant in Lyon, France. The BOLD signal was measured with a susceptibility weighted single-shot EPI sequence. Imaging parameters were as follows: TR = 2000 ms, TE = 24 ms, flip angle = 80°, matrix size = 128 × 120, field of view = 220 × 206 mm, slice thickness = 3 mm (0.48 mm gap), number of slices = 32. A high-resolution T1-weighted whole-brain anatomical volume was also collected for each participant. Parameters were as follows: TR = 3500 ms, TE = 2.24 ms, flip angle = 8°, matrix size = 256 × 256, field of view = 224 × 224 mm, slice thickness = 0.9 mm, number of slices = 192.
2.7. fMRI preprocessing
Data analysis was performed using SPM12 (http://www.fil.ion.ucl.ac.uk/spm). Functional images were corrected for slice acquisition delays and spatially realigned to the first image of the first run. Images were then spatially smoothed with a Gaussian filter equal to twice the voxel size. ArtRepair was used to help remove motion from the functional images prior to normalization (Mazaika et al., 2009). Volumes with rapid scan-to-scan movements of greater than 1.5 mm were repaired by interpolation of the two nearest non-repaired scans. Each run with more than 5% of the total number of volumes replaced was removed from the analyses. A subject was excluded from further analysis if more than one run was removed. The number of volumes replaced did not differ between grade groups (F(2,31) = 2.20; p = 0.13). Finally, functional images were normalized into the standard MNI space (normalized voxel size, 2 × 2 × 3.5 mm3).
2.8. fMRI processing
Event-related statistical analysis was performed according to the general linear model (GLM). For the localizer task, brain activity associated with saccades and fixation blocks was modeled as epochs with onsets and offsets time-locked to the beginning and the end of each block. Each epoch was convolved with a canonical hemodynamic response function (HRF) and the time series data from each run were high-pass filtered (1/128 Hz). Finally, serial correlations were corrected using an autoregressive AR(1) model. Following our previous study using the same task in adults (Mathieu et al., 2017), brain activity associated with sign-only trials during the arithmetic task was estimated using a finite impulse response (FIR) model. We modeled 8 time points with an interval of 2 s (corresponding to one TR) ranging from the onset of the sign to 16 s after the sign. The magnitude of the fMRI response for each type of sign-only trial was calculated by subtracting activity at the onset of the sign (i.e., 1st bin, or 0 s after the onset) from the peak activity (i.e., 4th bin, or ∼8 s after the onset). The time series data from each run were high-pass filtered (1/128 Hz), and serial correlations were corrected using an autoregressive AR(1) model.
2.9. Region of interest (ROI) definition and analyses
The present study used a Region-of-Interest (ROI) approach to analyze brain activity associated with sign-only trials in brain regions involved in the orienting of spatial attention in children. All ROIs were independently defined using the contrast of saccades versus fixation blocks in the spatial attention localizer task. All subject-specific contrasts were entered into a random effect (RFX) one-sample t-test across subjects. The RFX contrast map was then thresholded across the whole-brain using an uncorrected voxel-level threshold of p < 0.001 and a false-discovery-rate (FDR) corrected cluster-level threshold of p < 0.05 (Chumbley and Friston 2009). Using the SPM toolbox Marsbar (http://marsbar.sourceforge.net/), ROIs were defined as 6-mm radius spheres around the peak coordinate of each region.
Within each ROI and for each participant, we calculated the average response (parameter estimates) for ‘+’ signs using the contrast of addition sign-only trials versus baseline sign-only trials. Similarly, we calculated the average response for ‘×’ signs using the contrast of multiplication sign-only trials versus baseline sign-only trials. Two analyses were performed in each ROI. First, we identified the ROI(s) in which a difference in fMRI activity between ‘+’ and ‘×’ signs emerged throughout age and/or education, using a 3 × 2 ANOVA with the between-subject factor group (lower/intermediate/higher grades) and the within-subject factor sign (‘+’/‘×’). Second, we tested in these ROIs whether inter-individual differences in the fMRI response to an arithmetic sign were correlated with inter-individual differences in the size of the operator-priming effect (measured in the behavioral session) for each group. In all analyses, we report uncorrected P values as well as P values corrected for multiple comparisons across all identified ROIs using the Bonferroni procedure. Bayes factor are also reported.
3. Results
3.1. The spatial localizer task activates a brain network encompassing frontal, parietal, occipital and hippocampal regions
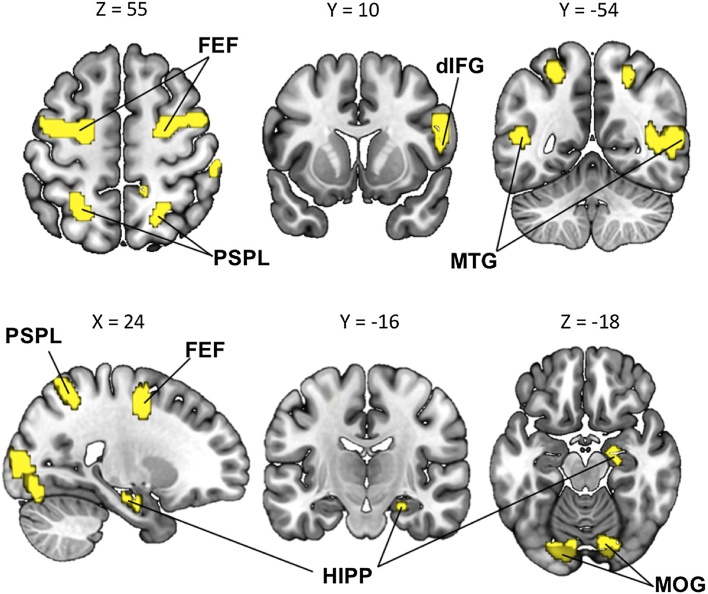
Contrasting saccades to fixation blocks in the spatial attention localizer task, we first identified 10 clusters supporting the orienting of spatial attention across subjects: the bilateral Frontal Eye Field (FEF), bilateral Posterior Superior Parietal Lobule (PSPL), bilateral Middle Temporal Gyri (MTG), bilateral Middle Occipital Gyri (MOG), right dorsal Inferior Frontal Gyrus (dIFG), and right Hippocampus (see Table 1 and Fig. 2). Therefore, a large brain network was involved in the orienting of spatial attention across subjects. Each of these regions served as an ROI in subsequent analyses.
Table 1.
Brain regions that were activated during the spatial attention localizer task. Each of these regions constituted an ROI.
| Anatomical location | ∼BA | Cluster size (mm3) |
MNI coordinates |
Z-score | ||
|---|---|---|---|---|---|---|
| X | Y | Z | ||||
| L. Middle Occipital Gyrus | 17 | 24640 | −24 | −96 | 10 | 5.37 |
| R. Middle Occipital Gyrus/Calcarine | 18 | – | 14 | −92 | 2 | 4.77 |
| L. Frontal Eye Field | 6 | 5824 | −34 | −8 | 55 | 5.34 |
| R. Middle Temporal Gyrus | 21 | 9534 | 54 | −52 | 13 | 4.68 |
| R. Frontal Eye Field | 6 | 5166 | 28 | −4 | 48 | 4.65 |
| R. Posterior Superior Parietal Lobule | 7 | 5250 | 18 | −66 | 66 | 4.61 |
| L. Posterior Superior Parietal Lobule | 7 | 3178 | −22 | −64 | 66 | 4.58 |
| L. dorsal Inferior Frontal Gyrus | 6/44 | 1316 | 56 | 10 | 20 | 4.52 |
| L. Middle Temporal Gyrus | 21 | 3626 | −50 | −54 | 13 | 4.33 |
| R. Hippocampus | – | 630 | 24 | −16 | −18 | 3.48 |
L. = left; R. = right; ∼BA = approximate Brodmannʼs area; MNI = Montreal Neurological Institute.
Fig. 2.
Brain regions activated in the spatial attention localizer task. Brain regions that were more activated during saccades than fixation blocks. Activations are overlaid on slices of the MNI-normalized anatomical brain. PSPL, Posterior Superior Parietal Lobule; FEF, Frontal Eye Field; MTG, Middle Temporal Gyrus; dIFG, dorsal Inferior Frontal Gyrus; MOG, Middle Occipital Gyrus.; HIPP, Hippocampus.
3.2. The right hippocampus region identified by the spatial localizer task is increasingly activated in response to a ‘+’ sign but not to a ‘×’ sign throughout age and/or education
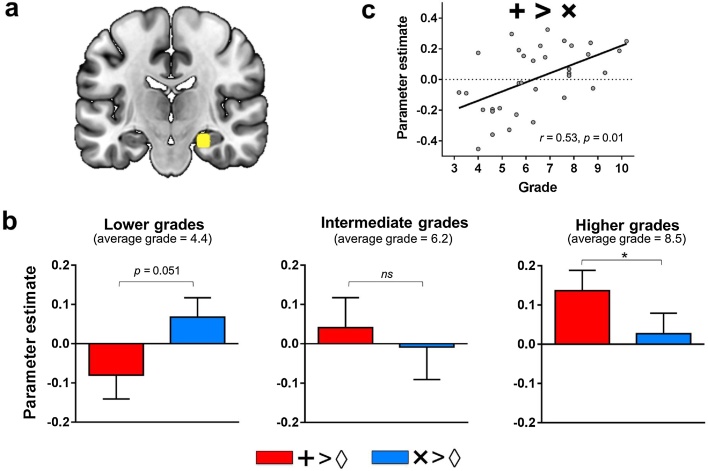
A 3 × 2 ANOVA with the between-subject factor group (lower/intermediate/higher grades) and the within-subject factor sign (‘+’/‘×’) was then conducted in each of the 10 ROIs identified by the spatial attention localizer. We found an interaction between group and sign in the right hippocampus (F(2.30) = 6.75, p = 0.0038, pcorr = 0.038; Fig. 3a and b), but not in any other ROIs (all Fs < 3.44, all ps > 0.046, all pscorr > 0.46). Bayes Factor analysis indicated substantial evidence for this interaction in the right hippocampus (BF10 = 11.53), while no or anecdotal evidence for such an interaction was found in the other ROIs (BF10 < 1.63). Follow-up t-tests in the hippocampus ROI revealed that children from higher grades (average grade = 8.5) exhibited greater activity for addition than multiplication sign-only trials (t11 = 3.02, p = 0.012), whereas there was no difference between signs in children from intermediate grades (average grade = 6.2) (t10 = 0.87, p = 0.41) and even a trend for less activity for addition than multiplication sign-only trials in children from lower grades (average grade = 4.4) (t10 = 2.22, p = 0.051). Bayes Factor analysis indicated substantial evidence for a difference of activity between addition and multiplication sign-only trials in children from higher grades (BF10 = 5.21), but evidence for this difference was absent in intermediate grades (BF10 = 0.41) and anecdotal in lower grades (BF10 = 1.69). Finally, across all groups, addition sign-only trials were associated with greater activity than baseline sign-only trials in children from higher grades (t11 = 2.63, p = 0.023), but not in any other groups (all ts < 1.32, all ps > 0.21). Multiplication sign-only trials were associated with greater activity than baseline sign-only trials in none of the groups (all ts < 1.38, all ps > 0.20). Bayes Factor analysis indicated substantial evidence for a difference between addition sign-only trials and baseline sign-only trials in children from higher grades (BF10 = 3.00), but no or anecdotal evidence in the other groups (all BF10s < 0.60) and for multiplication sign-only trials (all BF10s < 0.63). Overall, then, a difference in fMRI response to a ‘+’ and a ‘×’ sign emerged throughout age and/or education in the right hippocampus.
Fig. 3.
Grade-related changes of activity in the right hippocampus.
(a) Location of the right hippocampus ROI overlaid on a coronal slice of the MNI-normalized anatomical brain. (b) Activity in the right Hippocampus for addition versus baseline sign-only trials (red) and multiplication versus baseline sign-only trials (blue) in children from lower (n = 11; grade 3.2–5.4; mean grade = 4.4; mean age = 9.4), intermediate (n = 11; grade 5.6–6.9; mean grade = 6.2; mean age = 11.1) and higher grades (n = 12; grade 7.6–10.2; mean grade = 8.5; mean age = 13.4). (c) Difference in activity between addition and multiplication sign-only trials over grade in the right Hippocampus. *p < 0.05; r represents the Pearson correlation coefficient.
The findings above were confirmed by an additional correlation analysis in which grade was treated as a continuous predictor across all subjects. The difference in activity between addition and multiplication sign-only trials was positively correlated with grade in the right hippocampus (r = 0.53, p = 0.001, pcorr = 0.01; Fig. 3c). No other significant grade-related changes were found in any other regions (all rs < 0.38, all ps > 0.03, all pscorr > 0.30). Bayes Factor analysis indicated substantial evidence for this correlation in the right hippocampus (BF10 = 20.97), but no or anecdotal evidence in any other ROIs (all BF10s < 2.03). In the right hippocampus, the correlation between grade and the contrast of addition sign-only trials versus baseline sign-only trials, was also near significance (r = 0.33, p = 0.056; BF10 = 1.22).2 The correlation between grade and the contrast of multiplication sign-only trials versus baseline sign-only trials, however, was not significant (r = −0.18, p = 0.32; BF10 = 0.35).
3.3. Spatial hippocampal activity in response to a ‘+’ sign relates to an addition-priming effect in children from higher grades
We then tested whether the hippocampal response to a ‘+’ sign observed in children from higher grades was related to the operator-priming effect. To this aim, each child performed a version of the operator-priming task outside of the scanner (see Fig. 1a).
First, we tested whether the results obtained by Fayol and Thevenot (2012) in adults (i.e., an operator-priming effect for addition but not for multiplication across subjects) could be extended to our children participants. Because children from lower grades had a performance close to chance on large problems (58%), we exclusively focused our analyses on small problems for which accuracy was significantly above chance in all groups (lower grades: 80%, intermediate grades: 92%, higher grades: 96%). Planned comparisons revealed an operator-priming effect for addition in children from higher grades (1491 ms versus 1577 ms; F(1,11) = 8.11, p = 0.016), but not in children from lower grades (2289 ms versus 2417 ms; F(1,10) = 2.66, p = 0.134) and intermediate grades (1530 versus 1509 ms; F(1,10) = 0.01, p = 0.941). No operator-priming effect for multiplication was observed in any groups (lower grades: F(1,10) = 3.50, p = 0.091; intermediate grades: F(1,10) = 1.52, p = 0.246; higher grades: F(1,11) = 0.14, p = 0.715). Bayes Factor analysis indicated substantial evidence for an operator-priming effect with addition problems in children from higher grades (BF10 = 4.08), but no evidence in children from intermediate (BF10 = 0.30) and lower (BF10 = 0.83) grades. There was also no or anecdotal evidence for an operator-priming effect with multiplication problems in any group (higher grades: BF10 = 0.31; intermediate grades: BF10 = 0.55; lower grades: BF10 = 1.09).
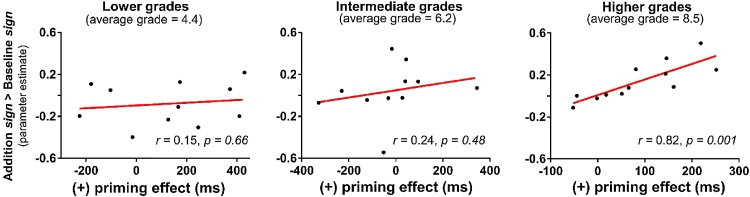
Second, we tested whether the size of the operator-priming effect in children (measured on small problems) was correlated to the magnitude of the response for addition sign-only trials versus baseline sign-only trials in the right hippocampus. Such a correlation was found to be highly significant in children from higher grades (r = 0.82, p = 0.0012, Fig. 4), surviving Bonferroni correction for multiple comparisons between the two conditions and across the three groups (pcorr = 0.007). That is, children from higher grades who show greater responses to ‘+’ signs in the right hippocampus are those who show larger operator-priming effect with addition problems. No significant correlation was found in children from lower (r = 0.15, p = 0.66 Fig. 4) and intermediate (r = 0.24, p = 0.48, Fig. 4) grades. Bayes Factor analysis indicated substantial evidence for the correlation in children from higher grades (BF10 = 38.15), but no evidence in children from lower (BF10 = 0.40) and intermediate (BF10 = 0.46) grades. There was also no significant (and anecdotal evidence for a) correlation between the operator-priming effect for addition problems and the fMRI response to multiplication sign-only trials (compared to baseline sign-only trials) in the right hippocampus, in any of the groups (lower grades: r = 0.06, p = 0.87, BF10 = 0.37; intermediate grades: r = 0.32, p = 0.34, BF10 = 0.56; higher grades: r = 0.51, p = 0.09, BF10 = 1.28). Therefore, not only did we observe an operator-priming effect for addition in the only group in which we also observed a greater hippocampal response to ‘+’ than ‘×’ signs (i.e., children from higher grades), but inter-individual differences in the size of the operator-priming effect in that group was also related to hippocampal activity.
Fig. 4.
Hippocampus brain-behavior correlation over grade.
Activity in the right hippocampus in response to addition sign-only trials versus baseline sign-only trials as a function of the operator-priming effect calculated in the behavioral session for addition problems in children from lower (n = 11; grade 3.2–5.4; mean grade = 4.4; mean age = 9.4), intermediate (n = 11; grade 5.6–6.9; mean grade = 6.2; mean age = 11.1) and higher grades (n = 12; grade 7.6–10.2; mean grade = 8.5; mean age = 13.4). r represents the Pearson correlation coefficient.
Third, we tested whether the correlation between the operator-priming effect and the contrast of addition sign-only trials versus baseline sign-only trials increased over grade. This was done by transforming the correlation coefficient in each group to a Fischer’s z score before comparing the groups using the cocor package (Diedenhofen and Musch, 2015). Although the correlation was not greater in children from intermediate than lower grades (z = 0.19, p = 0.43, one-tailed), it was significantly greater in children from higher than lower grades (z = 2.07, p = 0.019, one-tailed) and in children from higher than intermediate grades (z = 1.88, p = 0.030, one-tailed). Therefore, this brain-behavior correlation increased over grade.
4. Discussion
In the present study, we used fMRI and a cross-sectional design to investigate (i) how and when spatial processing related to the perception of an addition sign emerges in the developing brain, and (ii) to what extent it contributes to the emergence of an operator-priming effect.
4.1. The mere perception of a ‘+’ sign is associated with increased hippocampal spatial activity throughout age and/or education
It has been shown that the processing of a ‘+’ sign is associated with the right side of space (Pinhas et al., 2014) and activates brain regions involved in overt spatial attention in adults (Mathieu et al., 2017). Therefore, we expected arithmetic learning to be associated with increased recruitment of brain regions involved in spatial attention in response to the perception of a ‘+’ sign throughout age and/or education in children. This was the case in a region of the right hippocampus that we identified in our spatial attention localizer task. Therefore, it is possible that hippocampal spatial mechanisms may scaffold the progressive association between an arithmetic operator (i.e., a ‘+’ sign) and spatial intuitions throughout age and/or education. There is increasing evidence that the hippocampal formation, and particularly the right hippocampus, may house a ‘sense of space’ (Buffalo, 2015). Specifically, the right hippocampus has been extensively reported to support spatial representation and navigation in humans (Maguire et al., 1998, Burgess et al., 2002) as well as in non-human primates and rodents (O'keefe and Nadel, 1978, Bird and Burgess, 2008). For example, the hippocampus is typically activated when human participants learn to navigate through a mental representation of space (i.e., mental scanning) (Mellet et al., 2002, Spiers and Maguire, 2006). Interestingly, a recent study in monkeys demonstrated that neurons in the hippocampal formation may encode the direction of overt (Killian et al., 2015) as well as covert (Wilming et al., 2015) shifts of attention. Therefore, the hippocampal formation is likely a critical region for both representing a mental map of space and navigating along that map (Killian et al., 2012, Meister and Buffalo, 2016).
Why would such a hippocampal spatial navigation mechanism be increasingly recruited by the mere perception of a’+’ sign throughout age and/or education? One possibility is that this mechanism might enable children to construct a detailed representation of numbers in mental space, as well as to navigate along that mental representation. Indeed, there is overwhelming evidence that numbers of increasing size are organized along a left-to-right mental map (i.e., the MNL) in adults (Fischer and Shaki 2014). This spatial representation may enable individuals to add or subtract numbers by navigating from a source to a target number to the left or right of that MNL. This is supported by behavioral studies showing that addition and subtraction problem-solving is associated with rightward and leftward shifts of attention (Masson and Pesenti, 2014, Mathieu et al., 2016), as well as by a neuroimaging study indicating an overlap between the brain regions involved in overt shifts of attention and those involved in arithmetic calculation in adults (Knops et al., 2009). Such strategies may be acquired early by children, sometimes even explicitly in the classroom where addition and subtraction is often demonstrated on visual number lines. Yet, it is only with practice that they might become progressively attached to and evoked by an arithmetic operator such as a ‘+’, which might explain the grade-related increases of activity in this region in response to the ‘+’ sign (and the fact that it is only by 7th grade that children exhibit significant activity in response to that sign).
4.2. Hippocampal spatial activity in response to a ‘+’ sign relates to the operator-priming effect in children from higher grades
A critical question is to what extent this automatic processing of a ‘+’ sign in hippocampal spatial mechanisms is associated with children’s behavior. To answer this question, we asked all children to perform a version of the operator-priming task developed by Fayol and Thevenot (2012) and Roussel et al. (2002). First, we replicated the operator-priming effect observed in adults with addition problems (i.e., a facilitation of problem-solving when the operator is presented 150 ms before the operands), but only in children from higher grades (after around 7th grade). Like in adults, this effect was specific to addition problems and not observed with multiplication problems. Thus, the perception of a ‘+’ sign (but not that of a ‘×’ sign) appears to pre-activate a process that is likely used to solve the subsequent problem in children from higher grades. More central to our current interest, we found that the size of the operator-priming effect in these children was highly correlated with the degree of activation of hippocampal spatial mechanisms in response to a ‘+’ sign. This indicates that hippocampal spatial activity may be at the source of the operator priming-effect in older children, perhaps because these children might prepare for an attentional movement along the MNL as soon as a ‘+’ sign is presented. Because no brain-behavior correlation was observed in younger children, extensive practice might be needed before such mechanisms are triggered by the mere perception of the sign.
4.3. Hippocampal spatial activity in response to a ‘+’ sign is transient in development
Strikingly, the spatial brain mechanisms that respond to the mere perception of a ‘+’ sign appear to be different in children and adults. That is, albeit we found increased hippocampal spatial activity throughout age and/or education in the present study, we did not identify these mechanisms in our previous study in adult participants using the exact same task (Mathieu et al., 2017). Rather, we found increased activity in response to a ‘+’ sign in neocortical regions of the FEF and PSPL in adults. Therefore, the contribution of the hippocampus to the automatic processing of a ‘+’ sign is likely transient. Such a transient involvement of the hippocampus is consistent with a wealth of studies that have demonstrated that the spatial representations initially supported by the hippocampus during learning become independent from this brain structure over experience and transferred to neocortical regions (Rosenbaum et al., 2004, Hirshhorn et al., 2012b). For example, longitudinal studies demonstrate that right hippocampal activity associated with learning to mentally navigate through a new environment disappears and is replaced by neocortical activity when individuals become familiar with that environment (Spiers and Maguire, 2007, Hirshhorn et al., 2012a). It is possible that the same phenomenon is at play here: The hippocampus may be involved in the early representation of (and navigation along) the MNL before that representation is transferred to neocortical regions of the fronto-parietal cortex. Future investigations with a wider age sample than in the present study are needed to test this hypothesis.
4.4. Can right hippocampal involvement in the present study reflect mnemonic operations involved in learning arithmetic?
Although there is no doubt that the hippocampus supports spatial processing (Burgess et al., 2002, Spiers and Maguire, 2007), this brain structure is also well known to support the encoding and consolidation of verbal declarative knowledge into long-term memory (Eichenbaum, 2004). In fact, previous developmental studies have largely explained the involvement of the hippocampus during arithmetic learning by referring to its role in declarative memory rather than spatial processing (Rivera et al., 2005, De Smedt et al., 2011, Cho et al., 2011, Cho et al., 2012, Qin et al., 2014). This interpretation relies on the claim that results of well-practiced arithmetic facts (e.g., 2 + 3 or 4 × 2) might become progressively retrieved from memory (rather than calculated) over the course of learning and development (Campbell and Xue, 2001). The hippocampus might thus support the encoding and consolidation of networks of arithmetic facts in children.
Can the role of the hippocampus in declarative memory explain the operator-specific activity over grade (and correlation with the operator-priming effect) observed in the region of the right hippocampus identified by our spatial localizer task? We acknowledge that we did not have a task identifying processes involved in declarative memory. Thus, even if the right hippocampus is usually more associated with spatial than mnemonic processes (Burgess et al., 2002), it is possible that the hippocampal cluster that we identified as being involved in spatial processing may also be involved in some aspects of declarative memory. One might thus argue that grade-related increases of activity in relation to ‘+’ signs reflect the progressive association between a ‘+’ and a network of additive facts. This explanation, however, can be ruled out by an examination of activity related to ‘×’ signs. Because single-digit multiplication problems are almost exclusively learned by rote in school, multiplication is the operation that is perhaps the most associated with a network of stored facts in the literature (Campbell and Xue, 2001). Thus, if increased hippocampal activity in relation to ‘+’ signs were due to the progressive building of a network of additive facts, increased activity in that same region should have been observed during the perception of ‘×’ signs (perhaps even more so for the perception of ‘+’ signs). Yet, this is not the case. Not only did we not find any grade-related increase of activity for ‘×’ signs in the hippocampal cluster identified by our spatial localizer task, but activity was significantly greater for ‘+’ than ‘×’ signs in higher graders (who are as proficient in single-digit multiplication as addition). Similarly, no operator-priming effect was observed for multiplication problems in higher graders, indicating that the operator-priming effect observed for addition is likely to have little to do with the pre-activation of a network of stored facts (because this should be also observed for multiplication). Therefore, the specificity of our results to ‘+’ signs (as compared to ‘×’ signs) in the right hippocampus ROI makes it very unlikely that our results are related to mnemonic operations. In our view, emerging associations between ‘+’ signs and spatial intuitions related to the MNL are the best explanation of the effects reported here.
Of course, the fact that the role of the hippocampus in declarative memory is unlikely to explain our operator-specific findings in the right hippocampus ROI does not mean that hippocampal mechanisms supporting mnemonic operations do not contribute to arithmetic learning. Instead, they indicate that the hippocampus might contribute to arithmetic learning through its role in both declarative memory and spatial processing. Interestingly, the operator-specific activity observed in our (spatially localized) right hippocampal cluster is not observed in a mirror (left lateralized) cluster that is not activated in the localizer contrast (see Supplementary information). In that mirror region, no difference was observed between activity related to ‘+’ and ‘×’ signs in any group of children (and left hippocampal activity was not related to the operator-priming effect). Thus, the developmental effect reported here appears to be restricted to the right hippocampus. This specificity suggests that the observed developmental changes in the right hippocampus may not simply reflect general brain maturation but rather mechanisms that are specific to arithmetic learning.
4.5. Limitations
It is worth acknowledging here 2 potential limitations of the present work. First, as is the case for any cross-sectional fMRI studies, our study is correlational in nature. Thus, although our findings are consistent with the idea that the right hippocampus might scaffold the progressive association between (at least some) arithmetic operators and space throughout age and/or education, future studies might specifically investigate the causal role of these hippocampal mechanisms. Second, our finding of a correlation between grade and the processing of an addition sign in the right hippocampus (see Fig. 3C) relies on a relatively large sample size of 34 children. However, other findings involve subgroups of participants and therefore rely on smaller sample sizes. In particular, null findings in relation to these subgroups might be difficult to interpret because of potential lack of power. For example, whereas we found an operator-priming effect in children from higher grades and no effect in children from intermediate grades, there was no significant difference between these groups in terms of response times in negative SOA trials (1491 ms versus 1530 ms; t21 = 0.21; p = 0.84; BF10 = 0.39). Behavioral studies focusing on the operator-priming effect in children might test whether this difference emerges with larger sample sizes. More generally, future studies are needed to improve our understanding of the present results.
5. Conclusion
In sum, our findings suggest that the right hippocampus might contribute to the progressive association between (at least some) arithmetic operators and space throughout age and/or education. Therefore, our study raises the possibility that increased hippocampal activity during arithmetic learning in children may be explained by the role of this structure in spatial representations as well as in declarative memory.
Conflict of interest
The authors declare no competing financial interests.
Acknowledgments
This research was supported by a grant from the European Union (Marie Curie Career Integration Grant n° PCIG12-GA-2012-333602) to J.P. and a grant from the French Ministry of Higher Education and Research to R.M. We thank the Hospices Civils de Lyon for sponsoring the research, as well as Flora Schwartz and the MRI engineers (Franck Lamberton and Danielle Ibarrola) at the CERMEP-Lyon platform for their assistance in collecting the fMRI data. Finally, we are grateful to Pr. Christian Scheiber for his help with the pre-MRI medical exams.
Footnotes
Note that to induce an arithmetic context and disguise the goal of the experiment, we also included trials in which a ‘ + ’ or a ‘ × ’ sign was followed 150 ms later by operands and participants were asked to solve the problem. The low temporal resolution of fMRI, however, makes it impossible to dissociate activity associated with the sign from activity associated with operands in these problems. Therefore, they were simply designed to be filler trials.
There was a tendency for a correlation between grade and activity associated with addition sign-only trials (versus fixation) in the right hippocampus (r = 0.29, p = 0.09; BF10 = 0.82), but no correlation for baseline sign-only trials (versus fixation) (r = −0.10, p = 0.58; BF10 = 0.25). Thus, the correlation between grade and the contrast of addition sign-only trials versus baseline sign-only trials was more likely driven by changes of activity in addition sign-only trials than in baseline sign-only trials.
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.dcn.2017.06.001.
Contributor Information
Romain Mathieu, Email: rmathieu@isc.cnrs.fr.
Jérôme Prado, Email: jprado@isc.cnrs.fr.
Appendix A. Supplementary data
The following is Supplementary data to this article:
References
- Ansari D. Effects of development and enculturation on number representation in the brain. Nat. Rev. Neurosci. 2008;9:278–291. doi: 10.1038/nrn2334. [DOI] [PubMed] [Google Scholar]
- Ashcraft M.H. Cognitive arithmetic: a review of data and theory. Cognition. 1992;44:75–106. doi: 10.1016/0010-0277(92)90051-i. [DOI] [PubMed] [Google Scholar]
- Bird C.M., Burgess N. The hippocampus and memory: insights from spatial processing. Nat. Rev. Neurosci. 2008;9:182–194. doi: 10.1038/nrn2335. [DOI] [PubMed] [Google Scholar]
- Buffalo E.A. Bridging the gap between spatial and mnemonic views of the hippocampal formation. Hippocampus. 2015;25:713–718. doi: 10.1002/hipo.22444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess N., Maguire E.A., O'Keefe J. The human hippocampus and spatial and episodic memory. Neuron. 2002;35:625–641. doi: 10.1016/s0896-6273(02)00830-9. [DOI] [PubMed] [Google Scholar]
- Campbell J.I., Xue Q. Cognitive arithmetic across cultures. J. Exp. Psychol. Gen. 2001;130:299–315. doi: 10.1037//0096-3445.130.2.299. [DOI] [PubMed] [Google Scholar]
- Cho S., Ryali S., Geary D.C., Menon V. How does a child solve 7+ 8− decoding brain activity patterns associated with counting and retrieval strategies. Dev. Sci. 2011;14:989–1001. doi: 10.1111/j.1467-7687.2011.01055.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho S., Metcalfe A.W., Young C.B., Ryali S., Geary D.C., Menon V. Hippocampal–prefrontal engagement and dynamic causal interactions in the maturation of children's fact retrieval. J. Cogn. Neurosci. 2012;24:1849–1866. doi: 10.1162/jocn_a_00246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chumbley J.R., Friston K.J. False discovery rate revisited: FDR and topological inference using Gaussian random fields. Neuroimage. 2009;44:62–70. doi: 10.1016/j.neuroimage.2008.05.021. [DOI] [PubMed] [Google Scholar]
- Cognet G. Editions du Centre de Psychologie Appliquée; Paris: 2006. Nouvelle Echelle Métrique de l’Intelligence. [Google Scholar]
- De Smedt B., Holloway I.D., Ansari D. Effects of problem size and arithmetic operation on brain activation during calculation in children with varying levels of arithmetical fluency. Neuroimage. 2011;57:771–781. doi: 10.1016/j.neuroimage.2010.12.037. [DOI] [PubMed] [Google Scholar]
- Diedenhofen B., Musch J. Cocor: a comprehensive solution for the statistical comparison of correlations. PLoS One. 2015;10:e0121945. doi: 10.1371/journal.pone.0121945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dienes Z. Bayesian versus orthodox statistics: which side are you on? Perspect. Psychol. Sci. 2011;6:274–290. doi: 10.1177/1745691611406920. [DOI] [PubMed] [Google Scholar]
- Eichenbaum H. Hippocampus: cognitive processes and neural representations that underlie declarative memory. Neuron. 2004;44(1):109–120. doi: 10.1016/j.neuron.2004.08.028. [DOI] [PubMed] [Google Scholar]
- Fayol M., Thevenot C. The use of procedural knowledge in simple addition and subtraction problems. Cognition. 2012;123:392–403. doi: 10.1016/j.cognition.2012.02.008. [DOI] [PubMed] [Google Scholar]
- Fischer M.H., Shaki S. Spatial associations in numerical cognition—from single digits to arithmetic. Q. J. Exp. Psychol. 2014;67:1461–1483. doi: 10.1080/17470218.2014.927515. [DOI] [PubMed] [Google Scholar]
- Galfano G., Rusconi E., Umiltà C. Automatic activation of multiplication facts: evidence from the nodes adjacent to the product. Q. J. Exp. Psychol.: Sect. A. 2003;56:31–61. doi: 10.1080/02724980244000332. [DOI] [PubMed] [Google Scholar]
- Hirshhorn M., Grady C., Rosenbaum R.S., Winocur G., Moscovitch M. The hippocampus is involved in mental navigation for a recently learned, but not a highly familiar environment: a longitudinal fMRI study. Hippocampus. 2012;22:842–852. doi: 10.1002/hipo.20944. [DOI] [PubMed] [Google Scholar]
- Hirshhorn M., Grady C., Rosenbaum R.S., Winocur G., Moscovitch M. Brain regions involved in the retrieval of spatial and episodic details associated with a familiar environment: an fMRI study. Neuropsychologia. 2012;50:3094–3106. doi: 10.1016/j.neuropsychologia.2012.08.008. [DOI] [PubMed] [Google Scholar]
- Holloway I.D., Ansari D. Mapping numerical magnitudes onto symbols: the numerical distance effect and individual differences in children’s mathematics achievement. J. Exp. Child Psychol. 2009;103:17–29. doi: 10.1016/j.jecp.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Hubbard E.M., Piazza M., Pinel P., Dehaene S. Interactions between number and space in parietal cortex. Nat. Rev. Neurosci. 2005;6:435–448. doi: 10.1038/nrn1684. [DOI] [PubMed] [Google Scholar]
- Jeffreys H. 3rd ed. Oxford University Press; Oxford: 1961. Theory of Probability. [Google Scholar]
- Killian N.J., Jutras M.J., Buffalo E.A. A map of visual space in the primate entorhinal cortex. Nature. 2012;491:761–764. doi: 10.1038/nature11587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killian N.J., Potter S.M., Buffalo E.A. Saccade direction encoding in the primate entorhinal cortex during visual exploration. Proc. Natl. Acad. Sci. 2015;112:15743–15748. doi: 10.1073/pnas.1417059112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knops A., Thirion B., Hubbard E.M., Michel V., Dehaene S. Recruitment of an area involved in eye movements during mental arithmetic. Science. 2009;324:1583–1585. doi: 10.1126/science.1171599. [DOI] [PubMed] [Google Scholar]
- Lyons I.M., Ansari D. The cerebral basis of mapping nonsymbolic numerical quantities onto abstract symbols: an fMRI training study. J. Cogn. Neurosci. 2009;21:1720–1735. doi: 10.1162/jocn.2009.21124. [DOI] [PubMed] [Google Scholar]
- Maguire E.A., Burgess N., Donnett J.G., Frackowiak R.S., Frith C.D., O'Keefe J. Knowing where and getting there: a human navigation network. Science. 1998;280:921–924. doi: 10.1126/science.280.5365.921. [DOI] [PubMed] [Google Scholar]
- Masson N., Pesenti M. Attentional bias induced by solving simple and complex addition and subtraction problems. Q. J. Exp. Psychol. 2014;67:1514–1526. doi: 10.1080/17470218.2014.903985. [DOI] [PubMed] [Google Scholar]
- Mathieu R., Gourjon A., Couderc A., Thevenot C., Prado J. Running the number line: rapid shifts of attention in single-digit arithmetic. Cognition. 2016;146:229–239. doi: 10.1016/j.cognition.2015.10.002. [DOI] [PubMed] [Google Scholar]
- Mathieu R., Epinat-Duclos J., Sigovan M., Breton A., Cheylus A., Fayol M., Thevenot C., Prado J. What’s behind a ‘ + ’ sign? Perceiving an arithmetic operator recruits brain circuits for spatial orienting. Cereb. Cortex. 2017:1–12. doi: 10.1093/cercor/bhx064. [DOI] [PubMed] [Google Scholar]
- Mazaika P.K., Hoeft F., Glover G.H., Reiss A.L. Methods and software for fMRI analysis of clinical subjects. Neuroimage. 2009;47:S58. [Google Scholar]
- Meister M.L., Buffalo E.A. Getting directions from the hippocampus: the neural connection between looking and memory. Neurobiol. Learn. Mem. 2016;134:135–144. doi: 10.1016/j.nlm.2015.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mellet E., Bricogne S., Crivello F., Mazoyer B., Denis M., Tzourio-Mazoyer N. Neural basis of mental scanning of a topographic representation built from a text. Cereb. Cortex. 2002;12:1322–1330. doi: 10.1093/cercor/12.12.1322. [DOI] [PubMed] [Google Scholar]
- Mundy E., Gilmore C.K. Children’s mapping between symbolic and nonsymbolic representations of number. J. Exp. Child Psychol. 2009;103:490–502. doi: 10.1016/j.jecp.2009.02.003. [DOI] [PubMed] [Google Scholar]
- O'keefe J., Nadel L. Oxford University Press; USA: 1978. The Hippocampus as a Cognitive Map. [Google Scholar]
- Piazza M., Pinel P., Le Bihan D., Dehaene S. A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron. 2007;53:293–305. doi: 10.1016/j.neuron.2006.11.022. [DOI] [PubMed] [Google Scholar]
- Pinhas M., Shaki S., Fischer M.H. Heed the signs: operation signs have spatial associations. Q. J. Exp. Psychol. 2014;67:1527–1540. doi: 10.1080/17470218.2014.892516. [DOI] [PubMed] [Google Scholar]
- Pinheiro-Chagas P., Dotan D., Piazza M., Dehaene S. Finger tracking reveals the covert stages of mental arithmetic. Open Mind. 2017;1:30–41. doi: 10.1162/OPMI_a_00003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin S., Cho S., Chen T., Rosenberg-Lee M., Geary D.C., Menon V. Hippocampal-neocortical functional reorganization underlies children's cognitive development. Nat. Neurosci. 2014;17:1263–1269. doi: 10.1038/nn.3788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivera S.M., Reiss A., Eckert M.A., Menon V. Developmental changes in mental arithmetic: evidence for increased functional specialization in the left inferior parietal cortex. Cereb. Cortex. 2005;15:1779–1790. doi: 10.1093/cercor/bhi055. [DOI] [PubMed] [Google Scholar]
- Rosenbaum R.S., Ziegler M., Winocur G., Grady C.L., Moscovitch M. I have often walked down this street before: fMRI studies on the hippocampus and other structures during mental navigation of an old environment. Hippocampus. 2004;14:826–835. doi: 10.1002/hipo.10218. [DOI] [PubMed] [Google Scholar]
- Roussel J.-L., Fayol M., Barrouillet P. Procedural vs. direct retrieval strategies in arithmetic: a comparison between additive and multiplicative problem solving. Eur. J. Cognit. Psychol. 2002;14:61–104. [Google Scholar]
- Spiers H., Maguire E.A. Thoughts, behaviour, and brain dynamics during navigation in the real world. Neuroimage. 2006;31:1826–1840. doi: 10.1016/j.neuroimage.2006.01.037. [DOI] [PubMed] [Google Scholar]
- Spiers H., Maguire E.A. The neuroscience of remote spatial memory: a tale of two cities. Neuroscience. 2007;149:7–27. doi: 10.1016/j.neuroscience.2007.06.056. [DOI] [PubMed] [Google Scholar]
- Thibodeau M.H., Lefevre J.A., Bisanz J. The extension of the interference effect to multiplication. Can. J. Exp. Psychol. 1996;50:393–396. doi: 10.1037/1196-1961.50.4.393. [DOI] [PubMed] [Google Scholar]
- Wilming N., König P., Buffalo E.A. Grid cells reflect the locus of attention, even in the absence of movement. In Cosyne 2015 Main Meeting Program. 2015 p. 33. [Google Scholar]
- Woodcock R.W., McGrew K., Mather N. Riverside Publishing; Itasca IL: 2001. Woodcock-Johnson Tests of Achievement. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.