Making an unknown unknown a known unknown: Missing data in longitudinal neuroimaging studies

Abstract

The analysis of longitudinal neuroimaging data within the massively univariate framework provides the opportunity to study empirical questions about neurodevelopment. Missing outcome data are an all-to-common feature of any longitudinal study, a feature that, if handled improperly, can reduce statistical power and lead to biased parameter estimates. The goal of this paper is to provide conceptual clarity of the issues and non-issues that arise from analyzing incomplete data in longitudinal studies with particular focus on neuroimaging data. This paper begins with a review of the hierarchy of missing data mechanisms and their relationship to likelihood-based methods, a review that is necessary not just for likelihood-based methods, but also for multiple-imputation methods. Next, the paper provides a series of simulation studies with designs common in longitudinal neuroimaging studies to help illustrate missing data concepts regardless of interpretation. Finally, two applied examples are used to demonstrate the sensitivity of inferences under different missing data assumptions and how this may change the substantive interpretation. The paper concludes with a set of guidelines for analyzing incomplete longitudinal data that can improve the validity of research findings in developmental neuroimaging research.

1. Introduction

A number of neuroimaging techniques, including structural and functional magnetic resonance imaging (s/fMRI), have been employed to collect data that enable researchers to study the relation between neurobiology, cognition, and behavior. These techniques result in thousands of voxels per experimental unit, or participant, and are typically analyzed in a massively univariate framework, that is, by fitting the same statistical model to each voxel (Friston et al., 1995). More recently, neuroimaging data has been collected under repeated measures study designs, providing researchers with the opportunity to study empirical questions about neurodevelopment. The analysis of longitudinal neuroimaging data remains within the massively univariate framework where a growth model is fit to the repeated measures of each voxel. Thus, while the analysis of longitudinal neuroimaging data is relatively new, the field has the opportunity to exploit decades of methodological developments in longitudinal data analysis. One advantage of a longitudinal study designs over cross-sectional designs is that by collecting measures from study participants over multiple occasions, or waves, the analyst can test theories about development that do not conflate cohort effects with temporal effects (Skrondal and Rabe-Hesketh, 2004, Diggle et al., 2002). An all-to-common feature of longitudinal studies, regardless of the substantive area, is that some measures for some participants will go uncollected. That is, some participants may miss one or more waves of data collection intermittently throughout the study while others may dropout of the study altogether. How to obtain valid inferences for key model parameters in the presence of missing data has been a major focus in statistics for more than 40 years. The statistical literature uses the term incomplete data interchangeably with missing data in the context of longitudinal studies. The pioneering work of Rubin (1976) and Little (1976) introduced the issues associated with analyzing incomplete data and their impact on parameter estimates. More than forty years later, the analysis of incomplete data has grown into a prolific, currently active literature in statistics (e.g.,Mealli and Rubin, 2015, Seaman et al., 2013). When presented with missing data, the researcher must make assumptions about the reason(s) why the data went uncollected and realize that valid inferences rest on how those assumptions are operationalized. However, as we will make clear later in this paper, the nature of the missing data depends on the data that went uncollected, leaving the researcher unable to explicitly test the validity of those assumptions. As a result, there is no empirical way to determine which missing data assumption is correct (Molenberghs et al., 2008), making the assessment of multiple assumptions, often referred to as sensitivity analysis, even more critical. While attention to missing data and an awareness of appropriate methods analyzing incomplete data are critical for valid inferences, its import may not be fully understood across the developmental psychology field. Jelicić et al. (2009) conducted a systematic review of studies with developmental samples and showed that 82% used methods that place overly strict assumptions about the missing data. For example, many of those studies chose to omit subjects with missing data completely (i.e., list-wise deletion or complete case analysis), which may result in unacceptable levels of bias when generalizing to the intended population and reduces statistical power. These deletion methods also negate the effort from both researchers and study participants in collecting the available data. Indeed, opting to discard collected data when best practice indicates their use would very likely contravene our obligations under ethical guidelines for the use of human subjects. Misunderstanding and/or ignorance of the statistical issues associated with analyzing missing data could also contribute to discrepancies observed between datasets acquired across different laboratories and prevent replication efforts — a problem that has recently received noticeable attention and concern in the fields of neuroscience and psychology more broadly (Gorgolewski and Poldrack, 2016). Initial intuition often suggests it is better to remove those study participants who have missing data because there is no way of knowing what the missing values could have been. To many researchers, the treatment of missing data is seen as “making up” data, akin to waving a magic wand. And we agree that missing data is a theoretically challenging aspect of applied data analysis. With that, given that the analysis of longitudinal neuroimaging data is relatively new, we believe that it is much more difficult to reverse misconceptions than it is to properly introduce concepts from the beginning. Therefore, rather than rush through the statistical aspects of missing data and simply provide a list of tools that a researcher might employ when presented with missing data, the goal of this paper is to provide conceptual clarity of the issues (and non-issues) that arise from analyzing incomplete data in longitudinal studies. Although there are three general methods for analyzing incomplete data undergoing active development, (a) likelihood-based (including Bayesian), (b) multiple imputation, and (c) weighting, we focus on likelihood-based methods because (a) we believe it illustrates the issues of analyzing incomplete data clearly and (b) it is embodied in multiple imputation techniques. At the end of the paper, we offer further explanation for our choice of focusing on likelihood-based methods. Furthermore, we limit the paper to issues with missing outcome data (e.g., missing f/sMRI scans). To achieve this goal, the paper proceeds as follows. In Section 2, we review key contributions in the statistical literature on the relationship between likelihood-based inference and missing data. While notationally intensive and general, this section is required to foster an understanding of the statistical underpinnings that enable us to obtain valid inferences in the presence of incomplete data. We do not assume the reader is already familiar with this notation and devote space to translating much of the notation into plain English. In Section 3, we provide a set of simple simulations in an effort illustrate the statistical concepts covered in the previous section, focusing on how estimates change as a function of the missing data mechanism and how the data are analyzed. For Section 4, we re-analyze two longitudinal neuroimaging datasets, one fMRI and one sMRI, to demonstrate the sensitivity of inferences under different missing data assumptions and how this may change the substantive interpretation. Finally, in Section 5, we provide a discussion of the results and present three guidelines for analyzing incomplete longitudinal neuroimaging data.

2. Missing data

In order to review the concepts of missing data, particularly as they relate to longitudinal studies, some notation must be introduced. Recent literature (e.g., Mealli and Rubin, 2015, Seaman et al., 2013) has observed that the notation used to express concepts about missing data has shifted from that which was introduced by Rubin (1976) into something less precise, possibly creating confusion for readers. Given this, we do our best to adhere the notation of Rubin (1976) and Mealli and Rubin (2015) to review key concepts of analyzing longitudinal data with dropout. For simplicity, we consider the balanced repeated measures study. For participant i = 1, 2, …, N, there is an intent to collect j = 1, 2, …, n repeated measurements of the response variable of interest. Thus, let Y_i be a vector for participant i's n longitudinal outcomes, and $\text{Y}={({\text{Y}}_1^{\prime },{\text{Y}}_2^{\prime },\dots ,{\text{Y}}_N^{\prime })}^{\prime }$ be a vector for n · N observations of all outcomes in the sample.1 Let us assume (again for simplicity) that each observation Y_ij in Y_i is a continuous unknown real number that can take a value from the range of possible values (as defined by the sampling and measurement instrument) known as the sample space Ω. Finally, let X_i be an n × p matrix containing fixed covariates and the variable or variables that define how observations relate to the passage of time, where p is the number of covariates and time-defining variables. The goal of such a hypothetical study is to obtain correct inferences for the vector of unknown parameters θ that govern the conditional multivariate density f_Y(Y|X, θ) — that is, we estimate θ in order to learn something about how time, and our covariates in X relate to the outcome Y. Although the study intends to collect n repeated measures from the N participants, there will be those participants in the study who fail to provide all n responses. Therefore, let R_i be participant i's length n vector of observed-data indicators where R_ij = 1 if Y_ij is observed (i.e., taking a valid value in the sampling space Ω) and R_ij = 0 if Y_ij is missing (and so has the potential to take any value in Ω). The vector $\text{R}={({\text{R}}_1^{\prime },{\text{R}}_2^{\prime },\dots ,{\text{R}}_N^{\prime })}^{\prime }$ is the pattern of observed and missing measurements for each participant at each measurement occasion. Given the vector of observed-data indicators R_i, the vector Y_i can be partitioned into two ordered subvectors: those responses that are observed and those responses that are missing, denoted as Y_i,(1) and Y_i,(0), respectively. This partitioning enables us to be explicit about our handling of the observed outcomes and the unobserved outcomes. The missing data mechanism is the statistical model for the observed-data indicators, f_R(R|Y, X, Z, α). That is, missing data, R, may depend on the outcome of interest Y, the covariates of interest X, as well as a distinct set of covariates not related to Y, indicated by Z. Additionally α is the set of parameters that govern this relation, a set of parameters that are distinct from the parameters that govern the relation between Y and X (that is, θ). In the broad context of a statistical analysis, this means we now have a probability statement governing the outcome of interest Y as well as a probability statement governing the pattern of missing data indicators, R. Still following the notation of Rubin (1976), let r_i be a generic value of R_i and ${\tilde{\text{r}}}_i$ be a particular sample realization of R_i. Likewise, let y_i,(1) be a generic value for Y_i,(1) and ${\tilde{\text{y}}}_{i,(1)}$ be a sample realization of Y_i,(1). Clearly, there is no sample realization of Y_i,(0) as it contains the data that went unobserved for this particular sample so we only speak of the generic version, y_i,(0). Whether or not we can obtain correct inferences for θ using only Y_i,(1), that is, ignoring R_i, depends upon the nature of the missing data mechanism. The remainder of this section provides an overview of the hierarchy of missing data mechanisms and their association with likelihood-based methods.

2.1. Missing data hierarchy

2.1.1. Missing completely at random

One can think of missing responses that are missing completely at random, or MCAR, to be a random sample of the outcome vector Y_i, or equivalently, those who complete the study without any missing data are a random sample of the complete data vector. Stated more technically, missing data are MCAR when the probability that responses are missing, ${\text{R}}_i={\tilde{\text{r}}}_i$, is independent of the observed responses obtained, ${\text{Y}}_{i,(1)}={\tilde{\text{y}}}_{i,(1)}$, the responses that were intended to be obtained but were not, Y_i,(0) = y_i,(0), and the set of covariates, X_i. In other words, missing data are MCAR when R_i is independent of Y₍₁₎, Y₍₀₎, and X_i, stated probabilistically as:

$$\mathbb{P}({\text{R}}_i={\tilde{\text{r}}}_i|{\text{Y}}_{i,(1)}={\tilde{\text{y}}}_{i,(1)},{\text{Y}}_{i,(0)}={\text{y}}_{i,(0)},{\text{X}}_i,{\text{Z}}_i,\alpha )=\mathbb{P}({\text{R}}_i={\tilde{\text{r}}}_i|{\text{Z}}_i,\alpha ).$$ (1)

Note that Eq. (1) is a statement about the realized missing data, not about the missing data mechanism itself. Mealli and Rubin (2015) introduced the term missing always completely at random, or MACAR, which provides specific language for a missing data mechanism that will always produce missing data that are missing completely at random.

$$\mathbb{P}({\text{R}}_i={\text{r}}_i|{\text{Y}}_{i,(1)}={\text{y}}_{i,(1)},{\text{Y}}_{i,(0)}={\text{y}}_{i,(0)},{\text{X}}_i,{\text{Z}}_i,\alpha )=\mathbb{P}({\text{R}}_i={\text{r}}_i|{\text{Z}}_i,\alpha ).$$ (2)

Notice that ${\tilde{\text{r}}}_i$ and ${\tilde{\text{y}}}_{i,(1)}$ in Eq. (1) are replaced by r_i and y_i,(1) in Eq. (2) to signify that any realization of R_i will be missing completely at random. Thus, Eq. (1) defines data that are MCAR and Eq. (2) defines the MACAR missing data mechanism.

2.1.1.1. Covariate-dependent missingness

Little (1995) distinguished between MCAR as stated above and missingness that is conditionally independent of Y_i given some set of covariates X_i, which he referred to as covariate-dependent missingness. Covariate-dependent missingness can be stated probabilistically as

$$\mathbb{P}({\text{R}}_i={\tilde{\text{r}}}_i|{\text{Y}}_{i,(1)}={\tilde{\text{y}}}_{i,(1)},{\text{Y}}_{i,(0)}={\text{y}}_{i,(0)},{\text{X}}_i,{\text{Z}}_i,\alpha )=\mathbb{P}({\text{R}}_i={\tilde{\text{r}}}_i|{\text{X}}_i,{\text{Z}}_i,\alpha ).$$ (3)

This is to say, if data are missing because of a covariate associated with Y, if that covariate is included in the model for Y_i, then the parameter estimates based on Y_i,(1) will be unbiased. It is important to note that the subset of covariates that R_i depends on must be included in the model for Y_i. If those covariates are not included in the model then Y_i remains dependent on R_i. Equally important to consider is that the model fit without the covariate (or covariates) would also suffer from omitted variable bias.

2.1.2. Missing at random

Compared to MCAR, the assumption of missing at random, or MAR, is a less restrictive assumption in that the missing data can depend on Y_i,(1). Given the realized available data, ${\text{Y}}_{i,(1)}={\tilde{\text{y}}}_{i,(1)}$ and X_i, the probability of obtaining the missing data ${\text{R}}_i={\tilde{\text{r}}}_i$ does not vary with possible values of y_i,(0) or with possible values of the parameter vector α (Rubin, 1976, Mealli and Rubin, 2015). The MAR assumption may be stated probabilistically as

$$\begin{array}{c}\hfill \mathbb{P}({\text{R}}_i={\tilde{\text{r}}}_i|{\text{Y}}_{i,(1)}={\tilde{\text{y}}}_{i,(1)},{\text{Y}}_{i,(0)}={\text{y}}_{i,(0)},{\text{X}}_i,{\text{Z}}_i,\alpha )=\hfill \\ \hfill \mathbb{P}({\text{R}}_i={\tilde{\text{r}}}_i|{\text{Y}}_{i,(1)}={\tilde{\text{y}}}_{i,(1)},{\text{Y}}_{i,(0)}={\text{y}}_{i,(0)}^{\prime },{\text{X}}_i,{\text{Z}}_i,\alpha )\hfill \end{array}$$ (4)

for all α, y_i,(0) and ${\text{y}}_{i,(0)}^{\prime }$. This equality says that the realized missing data may depend on the set of observed responses Y_i,(1) and covariates X_i, but is free of dependence on the unobserved responses Y_i,(0). The missing data mechanism is missing always at random, or MAAR, if we replace ${\text{R}}_i={\tilde{\text{r}}}_i$ in Eq. (4) with R_i = r_i and ${\text{Y}}_{i,(1)}={\tilde{\text{y}}}_{i,(1)}$ with Y_i,(1) = y_i,(1) (Mealli and Rubin, 2015).

2.1.3. Missing not at random

Finally, when missing data depend on the data that went uncollected, Y_i,(0), the data are said to be missing not at random, or MNAR. Data that are missing not at random can be defined probabilistically if we replace the equality in Eq. (4) with an inequality,

$$\begin{array}{c}\hfill \mathbb{P}({\text{R}}_i={\tilde{\text{r}}}_i|{\text{Y}}_{i,(1)}={\tilde{\text{y}}}_{i,(1)},{\text{Y}}_{i,(0)}={\text{y}}_{i,(0)},{\text{X}}_i,{\text{Z}}_i,\alpha )\ne \hfill \\ \hfill \mathbb{P}({\text{R}}_i={\tilde{\text{r}}}_i|{\text{Y}}_{i,(1)}={\tilde{\text{y}}}_{i,(1)},{\text{Y}}_{i,(0)}={\text{y}}_{i,(0)}^{\prime },{\text{X}}_i,{\text{Z}}_i,\alpha )\hfill \end{array}$$ (5)

for some α, and some ${\text{y}}_{i,(0)}\ne {\text{y}}_{i,(0)}^{\prime }$. Like the definitions above, substituting ${\text{R}}_i={\tilde{\text{r}}}_i$ in Eq. (5) for R_i = r_i and ${\text{Y}}_i={\tilde{\text{y}}}_i$ with Y_i = y_i defines the missing not always at random mechanism, or MNAAR (Mealli and Rubin, 2015).

2.2. Likelihood-based inference

Remaining in the context of longitudinal studies, recall that we seek to obtain correct inferences for the vector of unknown parameters θ that govern the conditional multivariate density f_Y(Y|X, θ). This is often done by finding the values of θ with the maximum likelihood L_θ(θ|y, X) or its logarithm, ℓ_θ(θ|y, X). When missing data are present, however, ${\tilde{\text{y}}}_{(1)}$ may not provide sufficient information about Y to obtain valid estimates of θ. Thus, we would be naive to only consider $\tilde{\text{y}}$ without also considering $\tilde{\text{r}}$, which may provide necessary information about Y. That is, when presented with incomplete data, we must consider the joint distribution of the available data, ${\tilde{\text{y}}}_{(1)}$, and the missing data indicators, $\tilde{\text{r}}$, $f_{Y,R}({\tilde{\text{y}}}_{(1)},\tilde{\text{r}}|\text{X},\text{Z},\theta ,\alpha )$ and the log-likelihood ${\ell }_{\theta ,\alpha }(\theta ,\alpha |{\tilde{\text{y}}}_{(1)},\tilde{\text{r}},\text{X})$ (Rubin, 1976, Kenward and Molenberghs, 1998) — in other words, it may be the case that valid estimates of θ can only be obtained by estimating θ and α jointly. How we specify the likelihood, using ℓ_θ or ℓ_θ,α depends on our assumptions about the missing data mechanism. Rubin (1976) showed that when the missing data are MAR (with MCAR as a special case), the missing data mechanism is non-informative or ignorable. When missing data are MNAR, however, the missing data mechanism is informative or nonignorable.

2.2.1. Ignorable mechanisms

2.2.1.1. Missing completely at random

When missing data is assumed to be the result of an MACAR mechanism, the missing data indicator is (conditionally) independent of the responses. Thus, the joint distribution of the observed data can be factorized as

$$f_{Y,R}({\tilde{\text{y}}}_{(1)},\tilde{\text{r}}|\text{X},\text{Z},\theta ,\alpha )=f_Y({\tilde{\text{y}}}_{(1)}|\text{X},\theta )f_R(\tilde{\text{r}}|\text{X},\text{Z},\alpha )$$ (6)

with log-likelihood

$${\ell }_{\theta ,\alpha }(\theta ,\alpha |{\tilde{\text{y}}}_{(1)},\tilde{\text{r}},\text{X},\text{Z})={\ell }_{\theta }(\theta |{\tilde{\text{y}}}_{(1)},\text{X})+{\ell }_{\alpha }(\alpha |\tilde{\text{r}},\text{X},\text{Z}).$$ (7)

Thus, when interest is in values of θ and α is merely a vector of nuisance parameters, we can obtain valid inferences of θ by working with ℓ_θ exclusively, and no longer need to worry about α or ℓ_α. Furthermore, when missing data are missing completely at random, analysis using the data from just the set of participants who completed the study, ${\tilde{\text{y}}}_{(c)}$, and dropping all observations from participants who did not complete the study (commonly referred to as complete-case analysis) is suitable, although this approach is inefficient and so has reduced statistical power (Jennrich and Schluchter, 1986, Kenward and Molenberghs, 1998, Laird, 1988).

2.2.1.2. Missing at random

When missing data are assumed to be the result of an MAAR mechanism, we can still ignore the model for R. Unlike MCAR, however, ${\tilde{\text{y}}}_{(1)}$ and $\tilde{\text{r}}$ are not independent (Rubin, 1976, Mealli and Rubin, 2015). That is, the joint distribution of the observed data under MAR cannot be reduced beyond

$$f_{Y,R}({\tilde{\text{y}}}_{(1)},\tilde{\text{r}}|\text{X},\text{Z},\theta ,\alpha )=f_Y({\tilde{\text{y}}}_{(1)}|\text{X},\theta )f_R(\tilde{\text{r}}|{\tilde{\text{y}}}_{(1)},\text{X},\text{Z},\alpha ).$$ (8)

To conceptualize this issue, consider stratifying our sample based on observed outcomes up to, but not including occasion t. The unrealized cross-sectional distribution of outcomes at occasion t for those in a given stratum who are missing the observation at occasion t, $f({\mathrm{y}}_{j=t,(0)}|{\tilde{\text{y}}}_{j<t,(1)})$, is assumed to equal to the realized cross-sectional distribution of outcomes at occasion t for those in the stratum who have an observed outcome at occasion t, $f({\tilde{\mathrm{y}}}_{j=t,(1)}|{\tilde{\text{y}}}_{j<t,(1)})$ (Molenberghs and Fitzmaurice, 2009). This further suggests that when missing data are the result of a MAAR mechanism, those individuals with a complete set of responses, ${\tilde{\text{y}}}_{(c)}$ do not make up a representative sample of the population. Thus, when missing data are MAR, unlike the MCAR case above, any analysis conducted with only those participants with complete data may results in biased parameter estimates (Wang-Clow et al., 1995). Although the marginal distribution of ${\tilde{\text{y}}}_{(1)}$ may not equal the marginal distribution of Y under MAR, we can partition the log-likelihood for Eq. (8) as

$${\ell }_{\theta ,\alpha }(\theta ,\alpha |{\tilde{\text{y}}}_{(1)},\tilde{\text{r}},\text{X},\text{Z})={\ell }_{\theta }(\theta |{\tilde{\text{y}}}_{(1)},\text{X})+{\ell }_{\alpha }(\alpha |{\tilde{\text{y}}}_{(1)},\tilde{\text{r}},\text{X},\text{Z}).$$ (9)

Note that Eq. (9) is distinct from the MCAR log-likelihood Eq. (7) in that α is conditional on ${\tilde{\text{y}}}_{(1)}$. Again, though, if our interest is in θ, ℓ_α need not concern us. We can then make correct inferences about θ from ℓ_θ when the asymptotic covariance matrix for θ is computed from the observed information matrix rather than the expected information matrix (Jennrich and Schluchter, 1986, Kenward and Molenberghs, 1998, Laird, 1988). It is important to realize that the assumption of a MAR rests on the data that were unobserved and therefore cannot be empirically verified.

2.2.2. Nonignorable mechanisms

When missing data are the result of a missing not always at random, (nonignorable) mechanism, the probability of nonresponse depends on the outcomes that were not collected. This means that likelihood-based inference regarding θ that ignores the model for R when missing data are MNAR will be biased (Wang-Clow et al., 1995). When the missing data are assumed MNAR, nearly all standard methods of longitudinal analysis using only ℓ_θ are invalid. To obtain valid estimates of θ, one must model the response vector ${\tilde{\text{y}}}_{(1)}$ and the missing-data mechanism $\tilde{\text{r}}$ jointly. There are three main families of MNAR models that differ based on how this joint distribution is factorized, (a) pattern-mixture models, (b) selection models, and (c) shared-parameter models. Each approach has a particular set of assumptions and theoretical strengths.

2.2.2.1. Pattern-mixture models

The pattern-mixture model (Little, 1993, Little, 1994) specifies the marginal distribution of $\tilde{\text{r}}$ and the conditional distribution of ${\tilde{\text{y}}}_{(1)}$,

$$f_{Y,R}({\tilde{\text{y}}}_{(1)},\tilde{\text{r}}|\text{X},\text{Z},\theta ,\alpha )=f_R(\tilde{\text{r}}|\text{X},\text{Z},\alpha )f_Y({\tilde{\text{y}}}_{(1)}|\tilde{\text{r}},\text{X},\text{Z},\theta ,\alpha ).$$ (10)

That is, the pattern-mixture model stratifies the population based on the pattern of missing data and separate models are fit for each stratum. Stratification may be of substantive interest if it is not meaningful to consider non-response as missing data. For example, in the biostatistics literature, Y may be a quality of life measure and R = 0 for survivors and R = 1 for individuals who died before time j (Little, 2009).

2.2.2.2. Selection models

While the selection model has led to substantial development in the statistical literature to deal with attrition, the model's roots (and name) can be traced back to the econometrics literature for dealing with selection bias in non-randomized studies (e.g., Heckman, 1976). The selection model factorizes the joint distribution between $\tilde{\text{r}}$ and ${\tilde{\text{y}}}_{(1)}$ through models for the marginal distribution of ${\tilde{\text{y}}}_{(1)}$ and conditional distribution of $\tilde{\text{r}}$ given ${\tilde{\text{y}}}_{(1)}$:

$$f_{Y,R}({\tilde{\text{y}}}_{(1)},\tilde{\text{r}}|\text{X},\text{Z},\theta ,\alpha )=f_Y({\tilde{\text{y}}}_{(1)}|\text{X},\text{Z},\theta ,\alpha )f_R(\tilde{\text{r}}|{\tilde{\text{y}}}_{(1)},\text{X},\text{Z},\alpha ).$$ (11)

Selection models provide a natural way of factoring the model where f_Y is the model for the data in the absence of missing responses and f_R is the model for the missing data mechanism that determines what part of Y are observed. Because f_Y is unconditional, model parameters in θ may be interpreted in the same fashion as a model for f_Y with an ignorable missing data mechanism; an element of great appeal when θ contains the substantive parameters of interest to the researcher.

2.2.2.3. Shared-parameter models

Introduced by Wu and Carroll (1988), the shared-parameter model assumes the missing data are subject to random-coefficient-based missingness (Little, 1995). That is, the missing data are a function of one or more random coefficients such as a random intercept or slope rather than a function of the unrealized measures. The shared parameter model assumes $\tilde{\text{r}}$ and ${\tilde{\text{y}}}_{(1)}$ are independent conditional on those shared parameters. Consider the set of random coefficients ν with a given parametric form,

$$f_{Y,R}({\tilde{\text{y}}}_{(1)},\tilde{\text{r}}|\text{X},\text{Z},\theta ,\nu ,\alpha )=f_Y({\tilde{\text{y}}}_{(1)}|\text{X},\text{Z},\theta ,\nu ,)f_R(\tilde{\text{r}}|\text{X},\text{Z},\alpha ,\nu ).$$ (12)

Here, both f_Y and f_R are unconditional given the random effects ν.

3. Illustrations

To help connect the concepts of missing data reviewed in the previous section, consider a hypothetical study that was designed to understand if rates of cortical thinning in regions associated with impulse control from ages 12 to 17 differed for those children who had been diagnosed with ADHD before age 12 from those who had not been diagnosed. The study was able to recruit 200 12-year-old children to be followed for 5 years. At baseline, half of the 200 participants had been diagnosed with ADHD whereas the other half had not been diagnosed with ADHD. Furthermore, 50 children in each of the two groups had one or more siblings at the time of recruitment while the other 50 children in each group had no siblings by age 12. The study design included three waves of data collection, at ages 12, 14.5, and 17. For each study participant, define the following data elements:

• •CT_i = (CT_i1, CT_i2, CT_i3)′ is the cortical thinning complete-data vector for child i (one can think of this as the data that is possible to observe, though elements are sometimes missing).
• •AGE_i = (12, 14.5, 17)′ is the age vector that corresponds to CT_i.
• •WAVE_i = (0, 1, 2)′ is the wave vector that corresponds to the data collection wave.
• •ADHD_i is a baseline binary variable where ADHD_i = 1 for ADHD diagnosis before age 12 and 0 otherwise.
• •SIB_i is a baseline binary variable where SIB_i = 1 for children who have siblings by age 12 and 0 otherwise.

Using this hypothetical study, we simulated longitudinal data from a known cortical thinning population model and a variety of known missing data mechanisms. While the cortical thinning population model was the same for all simulations, we considered four missing data mechanisms that span MCAR, MAR, and MNAR. Elements of the generated data were used to highlight when complete-case analysis and available data analysis result in correct inference about the population parameters for cortical thinning. It is important to note that the examples provided here are not exhaustive but are meant to highlight the following key issues:

• 1.When missing data are covariate-dependent, both the complete-case analysis and available data analysis are unbiased when the correct analytical model is specified.
• 2.When missing data are covariate-dependent, omission of that covariate in the analytical model results in two forms of bias, (a) bias due to the non-independence of the missing data indicator and the outcome, and (b) omitted variable biased.
• 3.When missing data are due to, in part, a variable unrelated to the outcome, that variable is not required to be included in the analytical model.
• 4.When missing data are due to the observed outcomes, complete-case analysis produces biased point estimates.
• 5.When missing data are due to unobserved outcomes, neither complete-case analysis nor available data analysis produce unbiased estimates.

3.1. Population model for cortical thinning

For these illustrations, we define cortical thinning (in mm) between age 12 and 17 to differ based on ADHD diagnosis but not based on having or not having siblings. Let the participant-level population model for the repeated measures outcome CT_i be expressed using mixed-effects model notation (Laird and Ware, 1982),

$${\text{CT}}_i={\beta }_1+{\zeta }_{1i}+({\beta }_2+{\beta }_3{\mathrm{ADHD}}_i+{\zeta }_{2i}){\text{WAVE}}_i+{ϵ}_i.$$ (13)

with generating values: β₁ = 5.5 ; β₂ =−1.75 ; β₃ = 0.75 ;. This model indicates that the average level of the cortical thickness at age 12 is 5.5 mm and decreases by 1.75 mm every 2.5 years for the non-ADHD group, and by 1 mm every 2.5 years for the ADHD group. Because this is a mixed-effect model, participants are able to deviate from these population averages. The participant-specific deviation in the intercept is indicated by ζ_1i and participant-specific deviation in the slope is indicated by ζ_2i. The terms (ζ_1i, ζ_2i) are generated from a mean-zero multivariate normal distribution where ψ₁₁ = 1.25 defines the variation in the participant-specific intercepts around the population intercept (in standard deviates), ψ₂₂ = 0.5 defines the variation in participant-specific slopes around the population slope (in standard deviates), and ρ₂₁ =− .3 defines the correlation between the participant-specific intercepts and slopes (i.e., participants with thicker initial cortical measurements tend to decrease in thickness faster). The term ϵ_i is a vector of residuals distributed from a mean-zero normal distribution with standard deviation σ = 1. Note that all of the parameters in Eq. (13) were contained in θ in Section 2.

Now that we have defined the population model, we focus on a general model for the missing data mechanisms. We define additional elements for participant i:

• •r_i is the vector of observed-data indicators where r_ij = 1 indicates CT_ij is observed and r_ij = 0 indicates CT_ij is missing.
• •CT_i,(1) is the subvector of observed elements of CT_i.
• •CT_i,(0) is the subvector of missing elements of CT_i.

For simplicity (and without loss of generality) we constrain the possible patterns of r_i to be patterns that describe dropout: (1, 1, 1)′, (1, 1, 0)′, and (1, 0, 0)′. Given this constraint, let d be a discrete random variable whose values, d_i = k indicate the wave of dropout with d_i = C for those participants who completed the study. Thus, possible realizations for CT_i,(1), CT_i,(0), r_i and d_i are defined in Table 1. We now illustrate how the nature of the missing data mechanism determines what information must be included in the analysis and what information may be ignored to obtain unbiased population parameters. Because the illustration assumes data are collected in waves, or at discrete times, a convenient model for a missing data mechanism that describes dropout is the discrete-time survival model,

$$\mathbb{P}(d_i=k|d_i\ge k)=\frac{1}{1+\exp (-(\alpha w_i^{\prime }))}$$ (14)

where the probability of participant i dropping out after wave k given they did not drop out prior to wave k is governed by $\alpha w_i^{\prime }$. The vector $w_i$ includes discrete elements of time/wave and other characteristics that define the missing data mechanism. Whether the missing data mechanism is MCAR, MAR, or MNAR depends on what those other characteristics are. Note that the parameter vector α is the same α from Section 2.

Table 1.

Missing data patterns.

CTi,(1)	CTi,(0)	ri	di
(CTi1, CTi2, CTi3)′	–	(1, 1, 1)′	C
(CTi1, CTi2)′	(CTi3)	(1, 1, 0)′	2
(CTi1)	(CTi2, CTi3)′	(1, 0, 0)′	1

Notes: CT_i,(1) is the vector of participant i's observed cortical thickness measures. CT_i,(0) is the vector of participant i's missing cortical thickness measures. r_i is the vector of participant i's observed score indicators. d_i is an indicator for when participant i dropped out where d_i = C indicates study completion.

3.2. Independent mechanisms

As explained in Section 2.1.1, MACAR mechanisms are the only mechanisms where independence between y and the dropout pattern, r, is assumed. We provide two examples from the MACAR family: (a) covariate dependent missingness and (b) auxiliary variable-based missingness. For each example, we consider estimation bias and efficiency. Bias is assessed by comparing the average parameter estimates over 1000 replications to the generating values. Efficiency is evaluated based on the 95% coverage rate of the estimates of the 1000 replications — the rate at which the 95% confidence intervals contain the generating value.

3.2.1. Covariate-dependent dropout

The first missing data mechanism we specify is a covariate-dependent one where the probability of dropping out at a given wave is determined by a parameter for that wave as well as a parameter for the probability specific to those participants who had been diagnosed with ADHD by age 12. The missing data mechanism is defined as:

$$\mathbb{P}(d_i=k|d_i\ge k)=\frac{1}{1+\exp (-({\alpha }_1{\mathrm{WAVE}}_2+{\alpha }_2{\mathrm{WAVE}}_3+{\alpha }_3{\mathrm{ADHD}}_i))}$$ (15)

where α₁ is the log odds of dropping out between waves 1 and 2 for participants who had not been diagnosed with ADHD before age 12; α₂ is the log odds of dropping out between waves 2 and 3 for those participants who had not been diagnosed with ADHD before age 12 given they did not drop out previously; and α₃ is the increase of the log odds of dropping out at each wave for participants who had been diagnosed with ADHD before age 12. This model describes the probability of dropping out to be not only a function of time, but of ADHD diagnosis. To illustrate the impact of this dropout process, we simulated missing data under Eq. (15) using three sets of parameters. The generating values α₁ =−2.197 and α₂ = 1.735 were consistent across all three sets of parameters. The parameter α₁ =−2.197 results in 10% of participants in the non-ADHD dropping out after wave 1 and α₂ = 1.735 results in 15% of the remaining 90% of participants dropping out after wave 2, leaving 75% of the non-ADHD group with complete cases. The generating values for α₃ increased for each set of parameters (referred to as M1, M2, and M3) so that participants diagnosed with ADHD would have incrementally higher probabilities of dropping out after each wave as compared to those participants who were not diagnosed with ADHD: (0.201, 0.620, 1.100). That is, the three values of α₃ were set so that participants in the ADHD group would be 5%, 15% and 25% more likely to drop out after each wave than participants in the non-ADAD group.

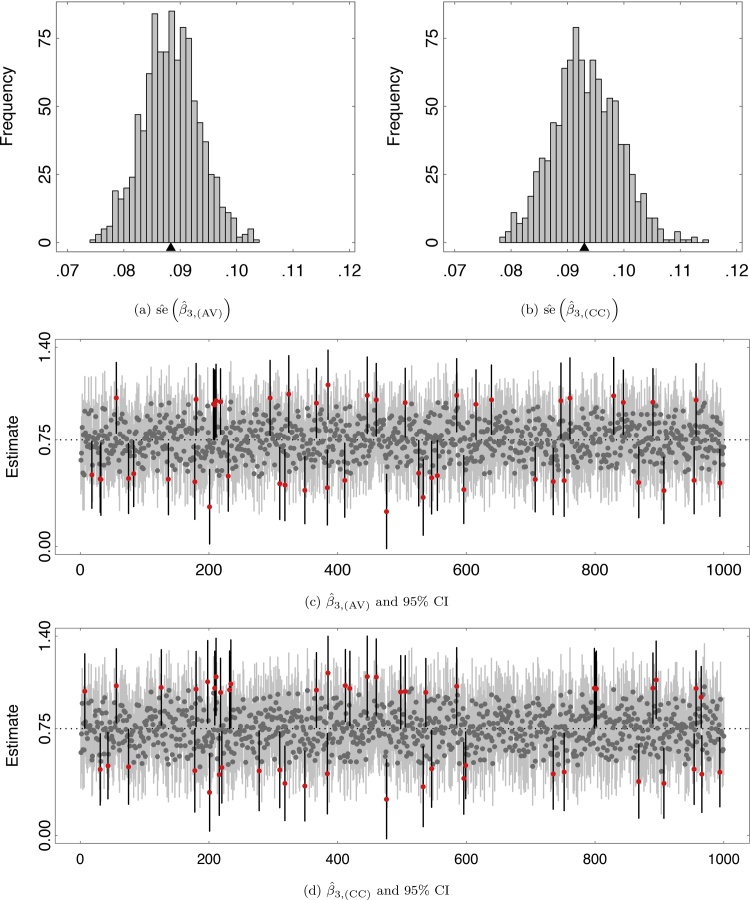
Table 2 provides the average percent observed data for both ADHD groups at each wave over 1000 replications. Notice that the percentage of observed data from those who were not diagnosed with ADHD, ADHD = 0, is the same for each of the three sets of missing data parameters. This is because α₁ and α₂ did not change between M1 and M3. The effect of α₃ becomes apparent looking to the percentage of observed data for those who had been diagnosed with ADHD before age 12. Two analyses were performed for each set of missing data parameters. The first analysis relied on only those participants who had not dropped out, referred to as complete-case analysis. The second analysis utilized the available data from every participant regardless of when they dropped out. Not shown here for space considerations, both approaches were unbiased under the three missing data mechanisms. Fig. 1a and b plot the estimated standard errors for β₃ — the difference in linear change for the ADHD group — under M3 revealing that, on average, the standard errors for the complete-case analysis were slightly higher than the standard errors estimated using the available data. Fig. 1c and d plot the 1000 point estimates for β₃ and their 95% confidence intervals for the available data analysis and complete-case analysis under M3, respectively. The red points and black line segments indicate those replicates where the 95% CI did not contain the generating value. Despite the complete-case analysis producing higher standard errors, the 95% coverage rate for both analyses were 0.95 meaning that the complete-case and available data standard errors were well estimated.

Table 2.

Average percent of observed data at each wave over 1000 replications, by ADHD.

Missing data mechanism	ADHD = 0			ADHD = 1
	WAVE1	WAVE2	WAVE3	WAVE1	WAVE2	WAVE3
M1, α3 = 0.201	100	90	76	100	88	72
M2, α3 = 0.620	100	90	77	100	83	62
M3, α3 = 1.100	100	90	76	100	75	50

Fig. 1.

Standard errors, point estimates, and 95% confidence intervals (CI) for β₃ under M3 over 1000 replications: (a) available data standard errors, (b) complete-case standard errors, (c) available data point estimates and 95% confidence intervals, and (d) complete-case point estimates and 95% confidence intervals. Red points and black segments indicate those 95% CIs that did not contain the generating value of 0.75.

A follow-up simulation was conducted to illustrate the consequence of omitting a covariate from the analytical model for which the missing data depends. For this, we generated data under the population model, Eq. (13), and imposed the missing data mechanism from the previous example. Instead of fitting the correct model, a knowingly misspecified model for CT was fit to the available data, one that omits ADHD_i.

$${\text{CT}}_i={\beta }_1+{\zeta }_{1i}+({\beta }_2+{\zeta }_{2i}){\text{WAVE}}_i+{ϵ}_i.$$ (16)

Table 3 reveals bias in the slope parameter, β₂, the slope variance ψ₂₂, and the correlation between the random intercepts and slopes, ρ₂₁, compared to their generating values. However, much of this bias should not be attributed to the dependence between CT_i and r_i, but instead, attributed to the omission of ADHD, often referred to as omitted variable bias. Because we ignore ADHD_i, β₂ under the misspecified model is the completely pooled linear change for the entire sample, (−1.75 +−1)/2 =1.375. This pooling extends to the linear slope variance component and the covariance, resulting in a standard deviation of 0.625 and correlation of 0.22. Given these pooled estimates, only the slope parameter exhibits bias due to the missing data under M2 and M3. Analysis of the available data under the most extreme missing data mechanism, M3, where the overall proportion of completers for the ADHD participants was half that of the non-ADHD group, resulted in 4.2% bias due to the dependence between CT and r. The bias for M3 is closer to the generating value of β₂ because there were fewer participants in the ADHD group resulting in less information to pool towards the generating value of β₃.

Table 3.

Misspecified ADHD-dropout model simulation results, average point estimates 1000 replications.

	β1	β2	β3	ψ11	ψ22	ρ21
Average point estimate
Generating value	5.50	−1.75	0.75	1.25	0.50	−0.30
M1, α3 = 0.201	5.50	−1.38	–	1.24	0.62	−0.22
M2, α3 = 0.620	5.51	−1.40	–	1.24	0.62	−0.22
M3, α3 = 1.100	5.50	−1.44	–	1.25	0.61	−0.22

3.2.2. Auxiliary variable dropout

Another potential missing data mechanism is one where dropout is determined by an auxiliary variable — a variable that is not associated with the outcome measure. For this example, the probability of dropping out increased for those participants with one or more siblings at the start of the study, perhaps due to scheduling difficulties for parents with larger families. That is, the auxiliary variable is SIB_i because it is independent of the population model for CT_i. Using the discrete-time survival model from above, we define the dropout process as

$$\mathbb{P}(d_i=k|d_i\ge k)=\frac{1}{1+\exp (-({\alpha }_1{\mathrm{WAVE}}_2+{\alpha }_2{\mathrm{WAVE}}_3+{\alpha }_3{\mathrm{SIB}}_i))}$$ (17)

where the values for α₁, α₂, and α₃ are the same as in Section 3.2.1. What is different is that instead of α₃ corresponding from ADHD_i, it now corresponds to SIB_i. Because of our study design, the proportion of missing data at each wave by group is equivalent (within replication variance) to that of Table 2. Note that this is not quite an example of a MACAR mechanism as defined in Eq. (2) because dropout is still dependent on time (WAVE). We know cortical thinning is independent of having one or more siblings but the probability of dropout is not. As seen in Table 4, because CT_i and SIB_i are independent, we can ignore SIB in our model for CT_i and obtain the corrected point estimates. Although the rate of attrition varies, at times drastically, between the two groups, Table 4 confirms that (a) ignoring SIB_i in the model for CT_i resulted in correct point estimates for parameters for CT_i, and (b) both available data and complete-case approaches worked equally well for obtaining those point estimates. Furthermore, with the the most severe missing data condition, coverage rates for both analyses were within 1%.

Table 4.

SIB-dropout simulation results for α₃ = 1.1, average point estimates and 95% coverage rates over 1000 replications.

	β1	β2	β3	ψ11	ψ22	ρ21
Average point estimate
Generating value	5.50	−1.75	0.75	1.25	0.50	−0.30
Complete-cases	5.50	−1.75	0.75	1.24	0.48	−0.26
Available data	5.50	−1.75	0.75	1.24	0.48	−0.27
95% Coverage rate
Complete-cases	0.96	0.95	0.94	–	–	–
Available data	0.95	0.96	0.94	–	–	–

3.3. Ignorable and non-ignorable mechanisms

Like the two examples above, we use Eq. (14) to simulate a MAAR and a MNAAR missing data mechanism. The MAAR and MANAR missing data mechanisms are inherently different from the two MACAR-family missing data processes used above, however, as they specify the probability of missing to be a function of CT_i. For the remaining two examples, rather than use CT_ij directly, we use ${\mathrm{CT}}_{\mathrm{ij}}^{★}={\mathrm{CT}}_{\mathrm{ij}}-{\overline{\mathrm{CT}}}_j$, a mean-centered transformation at each wave. A missing data mechanism that produces data that are missing at random is one that depends on the observed cortical thinning measures, CT_i,(1). We specify a rather simple MAAR mechanism that generates the probability of dropping out after each wave to depend on, in part, the measure of cortical thickness at that wave. That is, the measure of cortical thickness collected at time k influences whether or not that participant will return at the next wave.

$$\mathbb{P}(d_i=k|d_i\ge k)=\frac{1}{1+\exp (-({\alpha }_1{\mathrm{WAVE}}_2+{\alpha }_2{\mathrm{WAVE}}_3+{\alpha }_3{\mathrm{CT}}_{\mathrm{ik}}^{★}))}$$ (18)

The MNAAR mechanism is setup just as the MAAR mechanism, only instead of specifying the probability of dropping out after wave k to depend on ${\mathrm{CT}}_{\mathrm{ik}}^{★}$, we use ${\mathrm{CT}}_{i,k+1}^{★}$, or the measure that would have been collected at the following wave. This formulation results in missing data due to the cortical thinning measures we do not have.

$$\mathbb{P}(d_i=k|d_i\ge k)=\frac{1}{1+\exp (-({\alpha }_1{\mathrm{WAVE}}_2+{\alpha }_2{\mathrm{WAVE}}_3+{\alpha }_3{\mathrm{CT}}_{i,k+1}^{★}))}$$ (19)

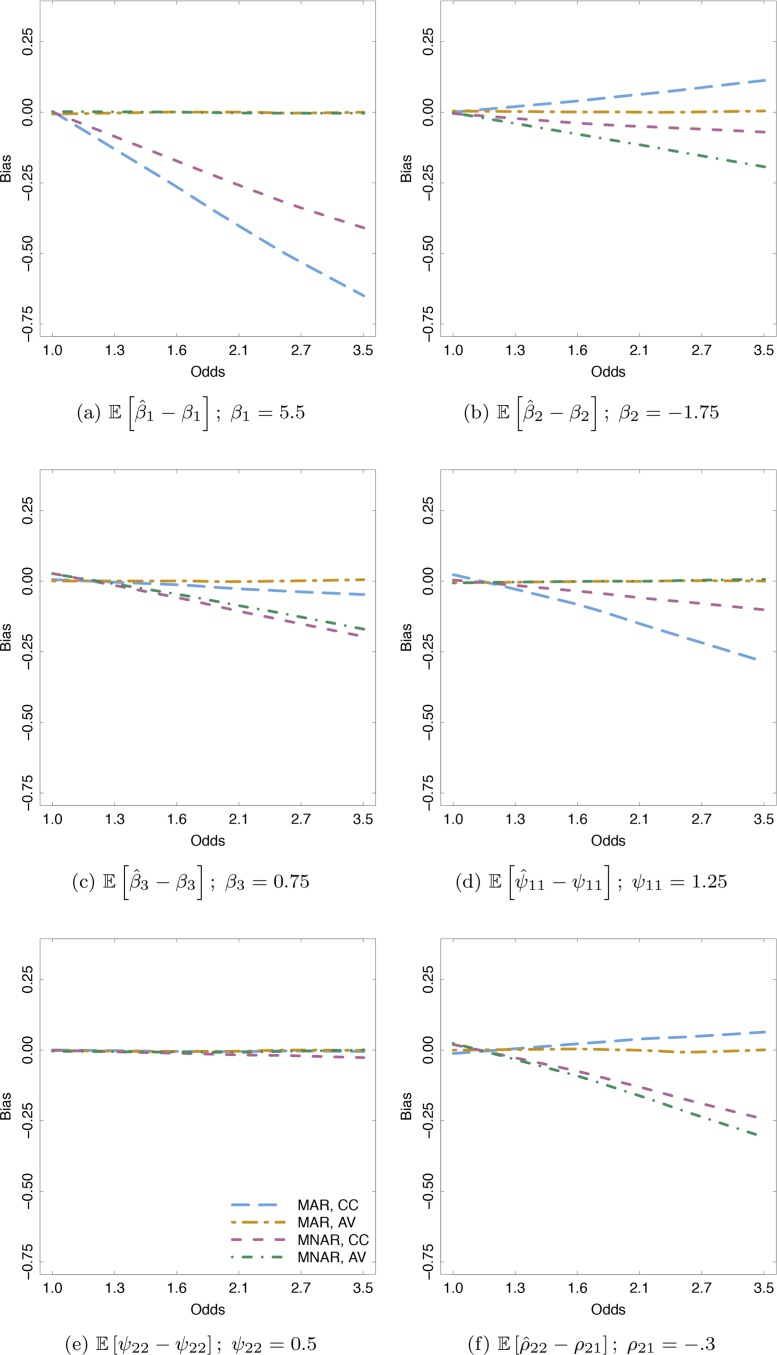
This model describes the probability of dropping out after wave k (given that the participant did not drop out prior to wave k) as increasing due to growth in cortical thickness after ${\mathrm{CT}}_{\mathrm{ik}}^{★}$ is collected. In order to enhance our understanding of the impact of ignorable and non-ignorable mechanisms on parameter estimates, both the MAAR and MNAAR simulations were setup differently than the simulations in Sections 3.2.1 and 3.2.2. The generating values for α₁ and α₂ in both models were −2.197 and −1.735, respectively, whereas the generating value for α₃ in both models was randomly sampled from a uniform distribution between 0 and 1.25 over 5000 replications. This strategy enables us to understand the impact of ${\mathrm{CT}}_{i,k+1}^{★}$ on parameter estimates as a smooth function rather than at select discrete values.

As was done for the examples above, the data was analyzed using (a) only the participants who had complete cases and (b) the available data from every subject. Fig. 2 plots a Loess curve of the bias for six parameters of the growth model estimated using complete-cases and available data when missing data are MAR and MNAR. Lines that depart from zero bias as the odds of dropout increase indicates that the parameter estimate under the given analysis is biased. Bias is present for five of the six parameters when the missing data are MAR and data from those participants who completed the study was used (orange lines). Fig. 2a and d indicate that for this particular simulation, the intercept, β₁ and the intercept variance, ψ₁₁, are most biased when only the complete cases are used and the missing data are MAR. All six parameters are unbiased when the missing data are MAR and the available data are used (green lines), even as α₃ increases. When missing data are MNAR, however, both the complete-case analysis (blue lines) and the available data analysis (purple lines) result in biased parameter estimates. Fig. 2e shows that the linear growth variance component was unbiased for all missing data mechanisms and analysis types. Average parameter estimates for certain values of α₃ are available in the supplemental information.

Fig. 2.

Loess curves fit to the bias of growth model parameters subject to MAR and MNAR missing data using complete-case analysis (CC) and available data analysis (AV). Odds = e^α₃. (For interpretation of the references to color in text near the reference citation, the reader is referred to the web version of this article.)

4. Longitudinal neuroimaging illustrations

The previous section analyzed simulated data from known missing data mechanisms to demonstrate some of the issues that arise when analyzing incomplete data. Whereas simulations rely on known missing data mechanisms, we can never be sure of the missing data mechanism that underlies data collected during a study. Therefore, we transition to the reanalysis of two existing longitudinal neuroimaging datasets, one functional and one structural. Specifically, we focus on the sensitivity of parameter estimates under various missing data assumptions. For both datasets, the first analysis exploited the available measures from all participants, an operationalization of the MAR assumption, while the second analysis employed the data from only those participants who were measured at all waves, an operationalization of the MCAR assumption. Our aim was to compare the sensitivity of estimates between available and complete data, which has not yet been done with longitudinal neuroimaging data. This is critical at this stage of the field because illustrating these differences may have a profound impact on how developmental cognitive neuroscientists analyze and interpret longitudinal neuroimaging data. For both datasets, we assessed the sensitivity of the parameter estimates to missing data assumptions by examining the number and extent of statistically significant clusters in the first example, and the number of statistically significant parcels in the second example. Because we are focused on the difference between available and complete-case data analyses, we are assessing the sensitivity of potential ignorable missing data mechanisms. Recall that MCAR is a special case of MAR, and complete-case analysis is only valid when missing data are MCAR. That is, if the missing data are MCAR, both analysis of the available data and analysis of the complete cases will produce similar point estimates while the available data analysis is sure to have greater statistical power. The difference in statistical power may result in different findings under null hypothesis significance testing. If, however, the missing data are not MCAR, the estimates produced by the two approaches will show substantial differences. It is important to emphasize that the analyses within this paper do not assess the sensitivity of parameter estimates to nonignorable missing data mechanisms, which will be taken up in the discussion.

4.1. Task-based functional MRI

4.1.1. Study design

The first example is from a study of the development of self-referential processing between the ages of 10 and 16. Study participants (N = 81) underwent functional magnetic resonance imaging (fMRI) while thinking about trait words related to the self, or a familiar other, in either a social, or an academic context over three waves (ages 10, 13, and 16). Further details of the study design and findings can be found in previously published work (Pfeifer et al., 2013, Pfeifer et al., 2007). Table 5 provides counts for each available data pattern where the data was unavailable for two possible reasons: a) a study participant did not arrive for a scan at a given wave, referred to as missing, or b) the scan was collected but later excluded due to data quality exclusion criteria, referred to as excluded. The first row (1, 1, 1), indicates the number of participants with data at all three time points. Of the 81 study participants, only 30 participants were present for all three waves. Regarding dropout, 30 participants dropped out after the first wave (1, 0, 0) and 16 participants dropped out after the second wave (1, 1, 0). Furthermore, three participants missed only the first wave (0, 1, 1) and two participants missed only the second wave (1, 0, 1). When data exclusion criteria are incorporated, only 22 participants ended up with three waves of usable data (complete cases) and 12 participants provided two waves of usable data — 10 of whom provided data for waves 1 and 2 and two who provided data for waves 1 and 3. In all, there were 58 observations at wave 1, 46 observations at wave 2, and 34 observations at wave 3.

Table 5.

Available data patterns.

Missing data pattern	Missing	Missing + Exclusion
(1, 1, 1)	30	22
(1, 0, 0)	30	24
(1, 1, 0)	16	10
(1, 0, 1)	2	2
(0, 1, 1)	3	7
(0, 1, 0)	–	7
(0, 0, 1)	–	3
(0, 0, 0)	–	6

1 indicates available data and 0 indicates unavailable data.

For this example, we need to consider two missing data mechanisms, one that governs whether or not a study participant arrives for a scan, the missing data; and one that governs whether or not the scan meets the quality criteria, the excluded data. If the missing data are assumed MCAR, participant i's blood-oxygen level dependent response has no relationship to their missing a scan. In other words, to assume MCAR, is to assume that the participant's BOLD responses, past, present, or future, during a social processing task is unrelated to whether or not a participant will miss a scan. The same consideration holds for the probability of excluding participant i's scan due to quality issues. This is the assumption we make when we use the complete-case analysis. Formalizing assumptions for missing BOLD responses that are MAR and MNAR are less straightforward as the causal relationship between BOLD responses and behavior is less well developed. If the missing data are assumed MAR, we assume that participant i's probability of missing a scan is related to those BOLD responses that have been collected. If the missing data are assumed MNAR, we assume that participant i's probability of missing a scan is related to those BOLD responses that went uncollected. The distinction between the two assumptions is whether or not those scans that went uncollected are systematically different from those scans that were collected. Although there is currently not enough evidence to suggest one assumption is more valid than another, and because modeling MNAR mechanisms is theory dependent, we only consider that the missing data may be MAR. Importantly, it is quite plausible that the probability of missing a scan, or having a scan excluded, is related to the BOLD response. Consider that the purpose of a developmentally focused analysis such as those in this section is to measure a maturation effect in neural correlates that we hope, a priori, are related to developing cognitive and behavioral capacities. It is not difficult to imagine that the maturational causes of missing or excluded data, e.g., inability to remain still for long periods of time, or increased involvement in extracurricular school activities, could be correlated with the maturation of those capacities (in this case, self-referential processing) that are the focus of the observation. If we take this correlation as a strong possibility, the assumption of MCAR in this example is nearly unsupportable — that is, it seems very possible that those participants excluded for excessive motion would have also evinced a less developmentally progressed pattern of BOLD signal in response to self-referential stimuli. As the field continues to grow and more evidence becomes available, future research may need to re-consider this assumption.2 The model used for both the available data and the complete-case data was specified as

$$\begin{array}{cc}\hfill {\text{BOLD}}_i=& {\beta }_1+{\zeta }_{1i}+({\beta }_2+{\zeta }_{2i}){\text{AGE}}_i+{\beta }_3{\text{AGE}}_i^3+{\beta }_4\text{TAR}+{\beta }_5{\text{DOM}}_i+\hfill \\ \hfill & {\beta }_6({\text{TAR}}_i{\text{DOM}}_i)+{\text{AGE}}_i({\beta }_7{\text{TAR}}_i+{\beta }_8{\text{DOM}}_i)+\hfill \\ \hfill & {\text{AGE}}_i^2({\beta }_9{\text{TAR}}_i+{\beta }_{10}{\text{DOM}}_i)+{ϵ}_i\hfill \end{array}$$ (20)

where BOLD_i is participant i's vector of blood-oxygen level dependent responses for a particular voxel for each level of target (self or other) and domain (academic or social) at each wave. AGE_i and ${\text{AGE}}_i^2$ are corresponding vectors of participant i's age and squared age (centered at 13). DOM_i and TAR_i are contrast-coded vectors for the levels of the domain and target factors at which the BOLD_i responses had been measured. The random effect terms for the intercept and age effect $\left({\zeta }_{1i},{\zeta }_{2i}\right)$ are assumed to be distributed multivariate normal with zero mean and unstructured covariance matrix Psi. The residual term ϵ_i is assumed to be normally distributed with zero mean and constant variance σ The data were analyzed using 3dLME in AFNI (Chen et al., 2013, version 17.0.16;][) and cluster-level significance (p_c < .05) was determined using spatial smoothness estimates across all ϵ calculated by 3dFWHMx (using the acf flag) and Monte-Carlo simulation as implemented in 3dClustSim. Whereas the model for the available data uses all 138 observations across three waves, only 66 observations from the 22 complete cases were used for the complete-case analysis. The results below focus on the sensitivity of β₄, the difference in BOLD while thinking about one's self verses a familiar other at age 13, at the average of the domain effect. Although this parameter carries an age-specific interpretation, its estimate is influenced by the longitudinal data. Furthermore, this estimate would be used for calculations of the average and subject-specific BOLD responses across the entire time horizon, so its sensitivity to missing data is just as important as those parameters that characterize, or interact with, time-specific variables.

4.1.2. Results

Regarding the number and extent of clusters in the two analyses, α = .05 was the probability that one or more clusters as big or bigger than the cut-off would be produced by random spatial noise. For both the complete-case analysis and the available data analysis, the cluster-defining threshold was p < 0.005. To be considered a significant finding (i.e., p_c < α) under the complete-case analysis, a cluster had to comprise 270 or more contiguous voxels. For the available data, a cluster had to comprise 274 or more contiguous voxels.

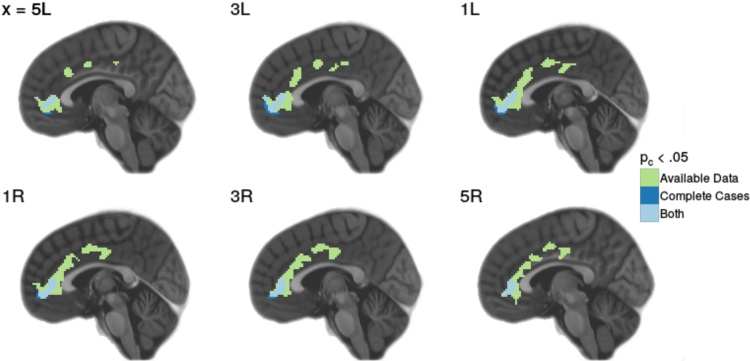
Table 6 indicates that analysis of the available data resulted in the identification of three clusters, with extents of 1043 voxels (cluster 1), 696 voxels (cluster 2), and 280 voxels (cluster 3). In the complete-case analysis, we reject the null hypothesis for a single, 312-voxel cluster. The single complete-case cluster shared 274 voxels with cluster 1 from the available data analysis. The two remaining clusters identified by the available data analysis, one consisting of 696 voxels and the other consisting of 280 voxels, went unidentified in the complete-case analysis. Fig. 3 visualizes those significant clusters pertaining to where β₄ was statistically significant for the available data analysis and the complete-case analysis.

Table 6.

Number of voxels contributing to each cluster estimated from the available data and complete-case analyses.

Cluster	Available data	Complete-cases	Both
1	1043	312	274
2	696	0	0
3	280	0	0

Both indicate the number of voxels that were part of a given cluster for both the available data analysis and the complete-case analysis.

Fig. 3.

Significant clusters identified in both available data and complete case analysis is indicated in blue, while significant clusters identified in the available data analysis only are indicated in green. Slice labels indicate the MNI coordinate along which the slice was acquired. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

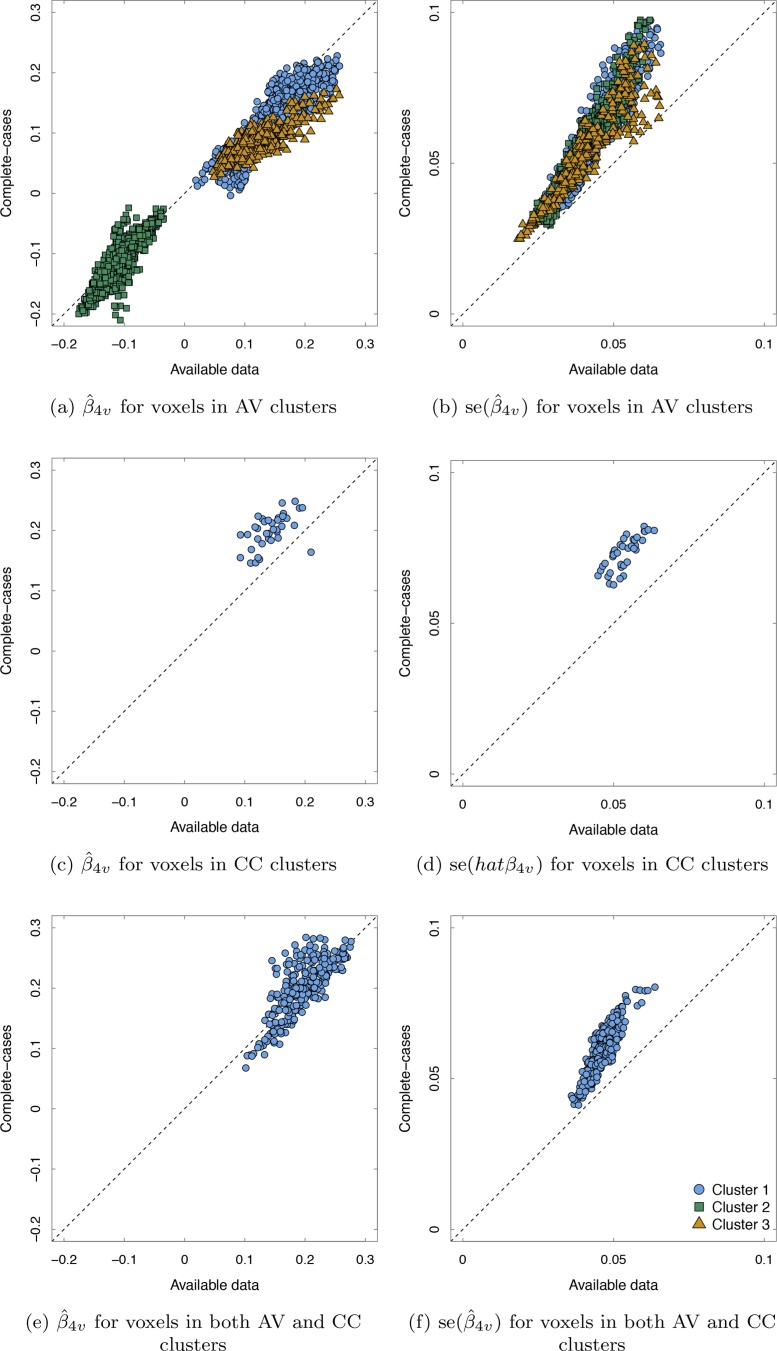
Fig. 4 contains six plots. The first column of plots plot the pairs of point estimates, $\left({\hat{\beta }}_{4v,(\mathrm{CC})},{\hat{\beta }}_{4v,(\mathrm{AV})}\right)$ for those voxels that contributed to the significant clusters based on (a) the available data only, (c) the complete-cases only, and (e) both the available data and complete-cases. The second column of plots plot the pairs of standard errors, $\left(\mathrm{se}\left({\hat{\beta }}_{4v,(\mathrm{CC})}\right),\mathrm{se}\left({\hat{\beta }}_{4v,(\mathrm{AV})}\right)\right)$ for those voxels that contributed to the significant clusters in the (b) available data analysis only, (d) complete-case analysis only, and (f) both analyses. Along the y-axis for each plot are the estimates from the complete-case analysis and along the x-axis are the estimates from the available data analysis. A point that fall on the 45-degree line indicates no difference in a voxel's estimate between the two analyses; a point that falls above the line indicates that the voxel's estimate was larger for the complete-case analysis; and a point that falls below the line indicates that the voxel's estimate was be larger for the available data analysis.

Fig. 4.

Pairs of complete-case and available data point estimates and pairs of complete-case and available data standard errors of ${\beta }_{4v}$ for those voxels that corresponded to significant clusters for the available data analysis, complete-case analysis, and both.

Fig. 4a shows that there was an increase in the available data estimates ${\hat{\beta }}_{4v,(\mathrm{CC})}$, compared to the complete-case estimates, ${\hat{\beta }}_{4v,(\mathrm{CC})}$, for a majority of the voxels the comprised cluster 1 as identified by the available data analysis. Furthermore, Fig. 4b shows that the standard errors for those voxels under the complete-case analysis were, in total, larger than the standard errors produced by the available data analysis. Fig. 4a further indicates that many of the voxel identified in cluster 2 were similar in size for the complete-case analysis and available data analysis. The standard errors for the cluster 2 voxels were larger under the complete-case analysis, likely being the reason the cluster went unidentified in the complete-case analysis. The third cluster under the available data had similar characteristics as the first cluster, many of the point estimates were larger under the available data analysis and the available data standard errors were smaller. Fig. 4c indicates that those 38 voxels identified by the complete case analysis had larger point estimates and Fig. 4d indicates they also had larger standard errors. The increase in the standard error was not great enough to counter the increase in the point estimates. Similarly, Fig. 4c shows that the point estimates of the voxels that were contributed to cluster 1 for the available data and the complete-case analysis, were similar in size or larger in size for the complete-case analysis while Fig. 4d indicates the standard errors were larger for the complete case-analysis. Because these were the voxels with the largest cluster 1 point estimates, the increased standard error, even when there was no change between analyses, enabled them to be identified by the complete-case analysis.

4.2. Surface-based structural MRI

4.2.1. Study design

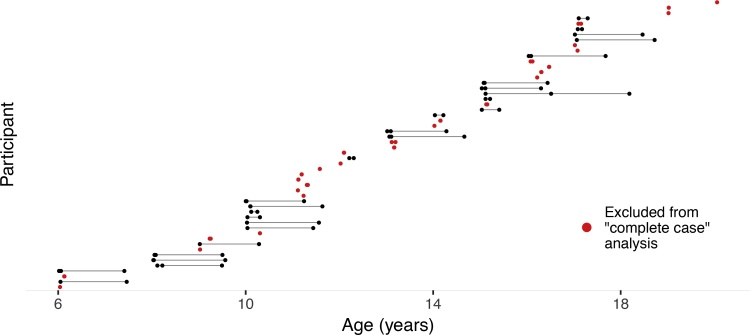
The enhanced Nathan Kline Institute-Rockland Sample (NKI-RS) is an ongoing study with the goal of creating a large-scale, community lifespan sample (details specified by Nooner et al., 2012). The study employs a cohort-sequential design where the repeated measures from multiple age cohorts are linked to create a common developmental trend. The present analysis utilizes those subjects that make up a developmental trend from ages 6 through 22, inclusive. The resulting data pattern can be seen in Fig. 5. Since this study is an accelerated longitudinal design, we compared the available date analysis (using all data) to an analysis that discards any participant with fewer than two measurements taken at least 30 days apart, which mimics the misconception that participants with data at just a single wave do not meaningfully contribute to estimates in longitudinal designs. For consistency, we refer to this reduced sample again as the complete-case analysis.

Fig. 5.

Age at which data was collected from each of 54 participants. Close or overlapping points indicate reliability acquisitions closely spaced in time.

For this example, the missing data mechanism governs the probability that a participant will contribute fewer than two measurements taken at least 30 days apart. In many respects, these subjects may have entered the study later than the other participants, and can be considered “missing by design.” While such a process would typically be the result of an MACAR mechanism, the nature of an accelerated longitudinal design complicates this. Here, because participants from different age-cohorts are entering the study at differing rates, and because each cohort provides weight to different portions of the developmental trend, including or excluding these participants will likely alter the estimates. If the missing data mechanism is MACAR, we should expect the estimates from the complete-case analysis to be similar to the available data analysis. For each participant, at each wave, cortical thickness measures were extracted using the ‘Destrieux’ cortical atlas (Fischl et al., 2004). To extract reliable cortical thickness estimates, images were processed with the longitudinal stream (Reuter et al., 2012) in FreeSurfer as implemented by the Freesurfer recon-all BIDS app (https://github.com/BIDS-Apps/freesurfer). Specifically an unbiased within-subject template space and image (Reuter and Fischl, 2011) is created using robust, inverse consistent registration (Reuter et al., 2010). Several processing steps are then initialized with common information from the within-subject template, significantly increasing reliability and statistical power (Reuter et al., 2012). To understand the functional form of change in cortical thickness, a series of nested models were fit for each parcel. The first model was a random intercepts model, followed by the inclusion of a linear slope, with the third step including a quadratic slope,

$$\mathrm{M}1:{\text{CT}}_i={\beta }_1+{\zeta }_{1i}+{ϵ}_i$$ (21)

$$\mathrm{M}2:{\text{CT}}_i={\beta }_1+{\zeta }_{1i}+{\beta }_2{\text{AGE}}_i+{ϵ}_i$$ (22)

$$\mathrm{M}3:{\text{CT}}_i={\beta }_1+{\zeta }_{1i}+{\beta }_2{\text{AGE}}_i+{\beta }_3{\text{AGE}}_i^2+{ϵ}_i$$ (23)

where CT_i is a vector of cortical thickness measures for participant i, AGE_i and ${\text{AGE}}_i^2$ are the vectors of participant i's age and squared age at each wave. The fixed effects β₁, β₂, and β₃ describe the intercept, linear growth, and quadratic growth, respectively. The random intercept ζ_1i is the participant-specific deviation from the average intercept β₁, and is assumed to be normally distributed with zero mean and variance ψ. The residual term ϵ_i is assumed to be normally distributed with zero mean and constant variance σ. The model for each parcel was estimated using the lme4 package version 1.1.12 (Bates et al., 2015) in R version 3.3.2 (R Core Team, 2016). The step-wise model building procedure enabled single-parameter tests of statistical significance using likelihood-ratio tests. After each step, a likelihood-ratio test was performed, comparing the change in deviance values to a χ² distribution with degrees of freedom equal to the number number of additional parameters. The FWER was set equal to.05 resulting in a Bonferroni correction of.05/108 = 0.0046. Furthermore, the p-values were divided by 2 as the likelihood ratio test is known to be conservative (Berkhof and Snijders, 2001).

4.2.2. Results

Table 7 provides the counts of parcels with statistically significant parameters by analysis type as determine by the likelihood-ratio tests. Of the 108 linear change parameters estimated, 47 were statistically significant under the available data analysis while 40 were statistically significant under the complete-case analysis. Of the 40 parcels with significant linear change parameters under the complete-case analysis, 35 were statistically significant for the available data analysis as well. There was no evidence of quadratic change in any of the 108 parcels for either the complete-case analysis or the available data analysis.

Table 7.

Counts of statistically significant parameters.

	Available data	Complete-cases	Both
β2	47	40	35
β3	0	0	0

Parameter significance was tested using deviance tests with a Bonferroni correction for FWER = 0.05.

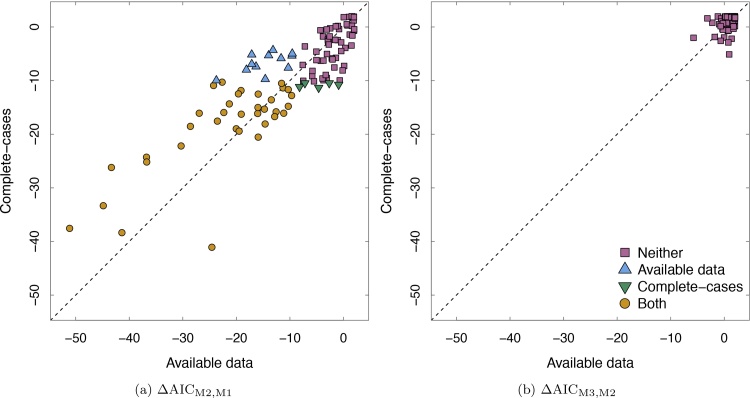
The AIC was also used to aid model selection, with a smaller AIC being suggestive of better model fit. Fig. 6 plots the change in AIC for two models using the complete-cases and change in AIC using the available data for β₂ and β₃. Because smaller AICs suggest better model fit, points with the greater (absolute) changes in AIC provide stronger evidence for the least restrictive model (e.g., the quadratic model is less restrictive than the linear). Points that fall above the diagonal line indicate the change in AIC was greater for the available data analyses while the points below the diagonal indicate the change in AIC was greater for the complete-cases analyses. The points are colored to indicate which parameters were found to be statistically significant based on Table 7.

Fig. 6.

Difference in AIC from complete-case analysis and available data analysis for β₂ and β₃. ΔAIC_Mj,Mk = AIC_Mj − AIC_Mk, is the difference in AICs between two models. Here, k is considered the restricted model and k is nested within j. M1 is Eq. (21), M2 is Eq. (22), M3 is Eq. (23). The leftmost plot describes the test of the linear versus the intercept-only model; the rightmost describes the test of the quadratic versus the linear model. Individual points are coded by color and shape to indicate if a given parameter was statistically significant using a likelihood ratio test.

5. Discussion

Missing data will always be a factor in longitudinal studies. While the analysis of longitudinal neuroimaging data is relatively new, it is built upon decades of methodological developments in longitudinal data analysis. One area that is particularly important in longitudinal studies is the analysis of longitudinal data when some outcome measures for some participants go uncollected. This article reviewed the taxonomy of missing data mechanisms and their relationship to likelihood-based statistics, a review that is necessary not just for likelihood-based methods, but also for multiple-imputation methods. Next, a series of simulations were analyzed to help make statistical concepts more concrete. Simulations prove effective for illustrating concepts of missing data because the missing data mechanism and missing data are known. Finally, two longitudinal neuroimaging datasets, one fMRI and one sMRI, were re-analyzed to demonstrate the sensitivity of inferences based on using the complete-case analysis and available data analysis — the former an operationalization of MCAR and the latter an operationalization of MAR.

5.1. Simulations

Simulation studies provide a valuable tool for understanding the impact of various missing data mechanisms on parameter estimation as the missing data mechanisms are known. The simulations presented in this paper were designed to be expository, illustrating many of the statistical concepts introduced in Section 2. The examples were divided into two parts, independent missing data mechanisms and non-independent mechanisms. The simulations focused on the limitations of both complete-case analysis and available data analysis as well as the non-issues related to covariate- and auxiliary variable-dependent missingness. The fact that many neuroimaging studies are based on only those participants who complete the study suggests that there is a fear that those participants with missing data will somehow corrupt their findings. In fact, we designed two simulations to show the opposite to be true! Basing one's analysis on the available data, including those subject who have incomplete data, will produce valid results for more types of missing data. We didn’t want readers to develop any unrealistic exceptions of available data analysis, that it will rescue their inferences from all types of missing data. As we showed with the MNAR example, using only the available data when data are missing based on the measures that went uncollected will result in biased estimates. The simulations were also designed to help researchers understand what missing not at random means from a statistical perspective. Often is the case that a researcher will claim that data is missing not at random because missing data is related to one or more variables in their dataset. The simulations in Section 3.2.1 were designed to show that if a covariate is associated with both the outcome of interest and the missing data indicator, by including that covariate in the model absolves the analysis of any problem. Leaving such a variable out of the model, we went on to show, will result in two sources of bias, bias due to missing data and omitted variable bias, the later having a potentially greater impact on the parameter estimates. Furthermore, we demonstrated the non-issue of missingness associated with an auxiliary variable — a variable that is not related to the outcome of interest.

5.2. Applied examples

The simulations were designed to be quite general, and did not address issues specific to longitudinal neuroimaging data. To make these issues relevant for longitudinal neuroimaging data, we presented the re-analysis of two datasets, one fMRI and one sMRI. These longitudinal neuroimaging illustrations demonstrated how neuroimaging findings can be sensitive to the assumptions we make about missing data. Although we are unable to empirically determine the true missing data mechanism, we can evaluate the extent to which inferences are sensitive to different assumptions about the missing data mechanism. In this paper, we only considered ignorable missing data mechanisms (MCAR and MAR), and stressed how sensitivity the parameter estimates were to these assumptions. The fMRI example demonstrated that the number of, and size of clusters identified can differ considerably based on one's missing data assumptions. Assuming that the missing data are MCAR, operationalized by using only the complete-cases, resulted in the identification of only one, relatively small cluster where there were differences in levels of activity in self vs. other social cognition. The less restrictive assumption of MAR, operationalized by using all the available data, resulted in the identification of three clusters, one of which completely subsumed the cluster identified using the complete cases. It is likely a combination of the smaller standard errors and the general increase in point estimates that enabled the available data analysis to identify 769 additional voxels as part of cluster 1. Overall, the voxel-specific change in this fMRI study was not negligible and was sensitive to missing data treatment. Therefore, because using the available data covers both MACAR and MAAR missing data mechanisms, as long as the missing data were not MNAR, the inferences drawn from the available data analysis had greater validity. These findings from the fMRI example are especially relevant for future research because they provide a more realistic idea of missing data in developmental longitudinal samples especially, where the data goes missing for two reasons: due to participants not arriving for their scan at a given time, or due to data quality issues (e.g., movement during the scan). Theoretically, these sources of missing data may be driven by different missing data mechanisms. If, however, both mechanisms are considered ignorable, as we assumed in our analyses, researchers can move forward with analysis using the available outcomes they have collected. In the sMRI example, the functional form of cortical thinning was estimated over a developmental period of age 6 through 22 using an accelerated longitudinal design. We considered the sensitivity of inferences when those participants who contributed only one measure (or two measures less than 30 days apart) were removed from the study, compared to using their data in the estimation. For both the complete-case analysis and the available data analysis, 35 parcels were found to show linear decline in cortical thickness between the ages of 6 and 22. The available data analysis resulted in an additional 12 parcels that showed significant decline while the complete-case analysis resulted in 5 additional parcels that showed significant decline. Those parcels that differed between the available data analysis and the complete-cases analysis did so because those participants who were removed were not a random subset of the sample. Like the sMRI example, because the available data are suitable for all ignorable mechanisms — the inferences from the available data were more valid than the complete-case analysis. In our two applied examples, it was clear that limiting data to only the complete cases restricted the findings. Of course, the specter of an MNAAR mechanism means that we cannot guarantee that our MAR assumption is more valid than the mcar assumption. Recall Fig. 2, where the estimated slope using the available data had greater bias when the missing data were MNAR than the estimated slope using the complete cases. The simulated findings were a product of the specific missing data mechanisms, and they should not suggest that had the missing data mechanisms in the applied examples been MNAAR that the complete-case analysis would be more accurate. Instead, we are saying that under the assumption that the missing data mechanism is ignorable, the available data analysis will be more valid. Furthermore, these examples demonstrate how critical it is for research teams in this field to be transparent about how they treat missing longitudinal neuroimaging data, as inconsistencies can adversely affect reproducibility efforts.

5.3. Guidelines

As more developmental neuroimaging studies adopt longitudinal designs, the field's understanding of the issues associated with analyzing incomplete data is paramount for fostering quality, reproducible research. Such an understanding is evident based on one's ability to theorize why the missing data went uncollected and relating those theories to an appropriate missing data mechanism. Furthermore, when the missing data mechanism is assumed to be ignorable, understanding is evident through one's use of the available data rather than just those study participants with complete data. Finally, understanding is evident by acknowledging that a missing data mechanism based on factors other than the outcome is largely benign. Given this, we have come up with three guidelines that should enable developmental neuroscientists to demonstrate understanding of the issues related to missing data.

5.3.1. Consider the missing data mechanism

While MCAR mechanisms can be explicitly tested, they are tested against the assumption that the data are MAR, an assumption that cannot be verified. Thus, even tests for MCAR rest on unverifiable assumptions. Given this, we believe part of the neurodevelopment research enterprise should consist of time spent considering why some participants in a particular study miss one or more waves of data collection, why others participants drop out altogether, and why some measures do not meet quality criteria. As we did in the applied example, researchers should fit multiple models that vary these assumptions about the missing data mechanism to understand how sensitive estimates are to a given assumption. For example, if an MCAR mechanism is assumed, the available data analysis and the complete-case analysis should result in very similar estimates.

5.3.2. Exploit the available data

A missing data mechanism that produces data that are MCAR is the only mechanism where using the subset of subjects who complete the study result in valid inferences. However, the use of the available data produces valid (and more precise) estimates when missing data are MCAR or MAR. Thus, removing participants from the analysis because they have missing data is only going to hurt the analysis, if not because of bias, because of the loss of information resulting in larger standard errors. Although the available data is insufficient when assumptions about the missing data tend toward non-ignorability, it provides the best solution without specifying a model for the joint distribution of the available repeated measures outcome and the observed data indicator. Furthermore, including all participants’ data in analyses is the most responsible research practice, given the cost and effort of participant and researcher time during data collection.

5.3.3. Focus on the analysis model

Intuition might lead us to think that estimates will be biased if missing data are related to one or more participant characteristics. As we saw in the simulations, however, if those characteristics are related to our outcome, we can indeed obtain unbiased estimates if we include those variables it in our analytical model. The threat of omitted variable bias should make us keen on including those variables just as much as any threat stemming from covariate-dependent missingness. If the variables related to the missing data process do not also relate to the outcome, it does not help our estimates to include them in the analytical model. Reasoning that one or more variables have been included in the analytical model purely because they may be related to missingness in the outcome is a misguided decision.

5.3.4. One mechanism for all voxels

Operating within the massively univariate framework, that is, fitting the same statistical model to each voxel/parcel, means we also must specify one missing data mechanism for all voxels/parcels. For example, in the context of sMRI, some parcels may show evidence of one missing data mechanism (e.g., MCAR) while others show evidence of another (e.g., MAR). It would be advantageous to specify the model to include the least conservative missing data assumption. For example, Fig. 6a shows the change in AIC for some parcels to be equal for the complete-case analysis and the available data analysis, while for other parcels, the change in AIC based on the complete-cases and available data suggest different substantive results. If a single model must be chosen, it would be advantageous to choose the model the makes the least restrictive assumption (in this case, MAR, the available data analysis).

5.4. Limitations and future directions

It is important to note that this article has not covered the entire field of missing data. Although we covered the general missing data hierarchy, we placed a majority of emphasis on likelihood-based methods for ignorable missing data mechanisms. As a result, we only touched on the issues related to data that are missing not at random. This leads to two topics worthy of future study, (a) the fitting of longitudinal neuroimaging models for non-ignorable missing data (e.g., Little, 1995 and (b) conducting sensitivity analyses for missing not at random assumptions within a massively univariate framework. Finally, a note on why we chose to focus on likelihood-based methods for missing data. Our first consideration was pedagogical, likelihood-based methods have an unambiguous relationship to the missing data hierarchy. Second, multiple imputation was originally developed for missing data problems in survey research where missing data exists on many variables (Andridge and Little, 2010, Belin and Song, 2014). In lab settings with tight protocols, where neuroimaging data is being originated, it is more likely to encounter a person with missing data for an entire wave rather than partial missing data at a given wave. Thus, although multiple imputation has proven effective for missing data problems outside of survey research, any advantage over maximum likelihood in such settings would be negligible. Third, although multiple imputation has become a popular tool for handling missing data, longitudinal neuroimaging data in a massively univariate framework creates many complexities. The first complexity is computational, with hundreds of thousands of models being estimated, using, say 10 imputed datasets would mean estimating ten times an already huge number of models. The second complexity is statistical, that is, a valid imputation model must considers the this structure of the longitudinal data — something not so straight forward (Goldstein and Carpenter, 2014). That said, we recommend the review by Harel and Zhou (2007) to those readers interested in multiple imputation as a general framework for handling missing data.

6. Conclusion

While the guidelines are not exhaustive, we believe adherence to them will elevate the quality of research in the field. That is, if future longitudinal neuroimaging studies exploit all of the available data and focus on properly specifying their analytical model, they will have fit a model that provides valid inferences under MCAR and MAR missing data processes. Reporting these practices transparently will result in higher rates of reproducibility and overall greater understanding of brain development. We hope that as longitudinal studies in developmental neuroscience continues to grow, the field does not stop here, but embraces the study of missing data as it relates to neuroimaging data.

Conflict of interest

None.