Does repeat synthesis in materials chemistry obey a power law?

Significance

A key goal of much chemistry and materials research is the creation of new chemicals or materials. Understanding how readily the synthesis of a material can be repeated gives important insight into how a material can be adopted by a technical community or used in practical applications. Surprisingly, little is known about how often the synthesis of new materials gets repeated. In this paper, an extensive analysis of published literature for a specific class of materials, metal-organic frameworks, is used to quantitatively address this issue.

Abstract

Finding examples where experimental measurements have been repeated is a powerful strategy for assessing reproducibility of scientific data. Here, we collect quantitative data to assess how often synthesis of a newly reported material is repeated in the scientific literature. We present a simple power-law model for the frequency of repeat syntheses and assess the validity of this model using a specific class of materials, metal-organic frameworks (MOFs). Our data suggest that a power law describes the frequency of repeat synthesis of many MOFs but that a small number of “supermaterials” exist that have been replicated many times more than a power law would predict. Our results also hint that there are many repeat syntheses that have been performed but not reported in the literature, which suggests simple steps that could be taken to greatly increase the number of reports of replicate experiments in materials chemistry.

Replicability is a core concept in the scientific method. At a fundamental level, accepting an experimentally derived observation as factual implies that carefully repeating the experiments under the same conditions would yield the same outcome. From an applied point of view, developing a new material for a practical application cannot occur unless the material’s properties are routinely repeatable. Systematic studies in fields including social psychology and biomedicine have raised concerns about repeatability of published studies (1–5).

Although recommendations for improving repeatability in research have been developed (6–9), it is not clear if they apply in a simple way to all fields. Before attempting to form recommendations appropriate for materials chemistry, or to decide if they are even needed, it is valuable to gather quantitative data related to experimental replicability. Mark Twain reputedly said “Everyone talks about the weather, but nobody does anything about it.” The situation for repeatability in materials chemistry may be similar. Any experienced investigator can share “war stories” of days (or weeks or more) spent in futile efforts to repeat reported experiments. Moving beyond this anecdotal level, however, requires a more systematic approach.

The most powerful way to examine repeatability is to systematically repeat experiments (7, 10). An obvious disadvantage of this approach is that is requires substantial resources. A less obvious disadvantage is that reporting results that contradict an earlier study is fraught with challenges. An alternative is to find repeated experiments that have already been performed via literature metaanalysis. In areas of great topical interest, it is not unusual for multiple investigators to study the same or similar materials, even though none of these efforts are performed specifically to study repeatability.

Park et al. (11) used literature metaanalysis to assess repeatability of CO₂ adsorption in metal-organic frameworks (MOFs). This work was only possible because of extensive work at the US National Institute of Standards (NIST) to exhaustively collate reported adsorption isotherms from the open literature (12). Although thousands of papers related to CO₂ adsorption exist, Park et al. (11) only found a small number of isotherms for which multiple independent experiments have been reported. Among all isotherms of this kind, ∼20% were identified as outliers, that is, as inconsistent with other available measurements.

Focusing literature metaanalysis on a highly specific property (e.g., CO₂ uptake) may underestimate what can be learned from published data about how repeatable synthesis of a material is. It is possible, for example, that a series of reports of different but related properties of a single material give useful information regarding the material’s reproducibility. This observation motivates the key question addressed in this paper: After a new material or molecule is synthesized for the first time, how often is the synthesis repeated? Below, we describe a simple power-law model for the frequency of repeat syntheses of materials, then compare this model to data from the synthesis of a particular class of materials, MOFs. In addition to studying a large number of example materials from the literature, we examine the 6 most widely studied MOFs to comment on the replicability of their material properties.

Power-Law Model for Repeat Synthesis of Materials

For a well-defined class of materials or chemicals, we define $\theta \left(n\right)$ as the fraction of materials whose synthesis has been independently reported exactly n times. We hypothesize that this quantity follows a power law:

$$\theta \left(n\right)=f{n}^{-\alpha }.$$ [1]

Power laws have been found to describe a wide range of phenomena, including the word distributions in many languages, the size of cities, wealth distributions, and the number of citations received by academic papers (13). Eq. 1 is a hypothesis, not a result we are attempting to derive or infer from prior reasoning. An interesting property of Eq. 1 is that it has only 1 free parameter because it must satisfy the normalization condition

$${\displaystyle \sum _{n=1}^{\infty }\theta \left(n\right)=1}.$$ [2]

This implies that $\zeta \left(\alpha \right)=1/f$, where $\zeta$ is the Riemann zeta function. Thus, if f is estimated or measured, the power law in Eq. 1 is fully specified. This is helpful because f has a simple physical interpretation: it is the fraction of materials than have been synthesized exactly once. Said differently, f is the fraction of materials that have been reported but have never been synthesized again. To give an example of the connection between f and $\alpha$ in Eq. 1, if f = 0.5 (i.e., 50% of materials are only synthesized once), then $\alpha =1.729$ and Eq. 1 implies that the probability that a randomly chosen material has been synthesized in 5 independent reports is 0.031.

Using the parameter f in Eq. 1 focuses attention on materials that have only been synthesized once. There are multiple reasons that synthesis of a material might not be repeated in later reports. At one extreme, it may be that repeat syntheses have been attempted but have failed and that these experiments have not been reported. Another situation that is perhaps more common is that no one has attempted a repeat synthesis because the first report indicated the material is not “useful” for some reason or simply because of lack of interest. Whatever the root cause, if a material has only been synthesized once, then no conclusions can be drawn about the repeatability of any of the material’s properties.

Another quantity of interest is the number of times that the most repeated material has been synthesized, which we denote $N_{max}$. Assuming that only one material has been synthesized $N_{max}$ times, Eq. 1 gives a simple expression for the total number of materials, $N_{total}$:

$$N_{total}=N_{max}^{\alpha }/f.$$ [3]

For example, if f = 0.5 and the most popular material has been synthesized 100 times then the power law predicts that the total number of materials in the group described by the power law is 5,741.

Testing whether an observed dataset can be described by a power law is a nontrivial issue. We use the principled statistical framework recommended by Clauset et al. (13), which uses a Kolmogorov–Smirnov (KS) test to quantify the distance between cumulative distributions of empirical data and a power-law model. In this approach, a power law is fitted to the observed experimental data and then a large number of synthetic datasets corresponding to this power law are generated. The distance, D, between a dataset and a power-law model is defined by

$$D=\underset{1\le i\le N}{\max }\left(\left|{\mathrm{F}}^{\ast }\left({\mathrm{n}}_i\right)-\mathrm{S}\left({\mathrm{n}}_i\right)\right|\right),$$ [4]

where F*(n) is the cumulative value of the fitted power law and S(n) is the cumulative value of an empirical dataset. Before D is calculated for any synthetic dataset, a power-law model is fitted to that dataset. The KS statistic is calculated for each dataset relative to its own model. In this way the same calculations are performed for each synthetic dataset as for experimental data. The P value of the power law is defined as the fraction of synthetic data sets that have D larger than the experimental data. Clauset et al. (13) recommended that the hypothesis of a power-law distribution be rejected if the P value is less than 0.1.

Assessing Repeat Synthesis of MOFs Using Literature Metaanalysis

To determine if Eq. 1 has any validity, we studied the synthesis of MOFs. MOFs have several characteristics that are typical of topical areas in materials chemistry: thousands or tens of thousands of distinct materials can be made (14, 15), their physical properties create potential applications in multiple different areas, and the potential of creating intellectual property and academic prestige creates strong incentives to introduce new materials. Intense interest in these materials has led to thousands of publications, dedicated conferences, and so on. Because MOFs are crystalline, the concept of synthesizing a new material can be concisely defined as reporting the crystal structure of a previously unknown material. Crucially for our purposes, systematic efforts have been made to catalog the MOFs that have been reported (14, 15). We focused on materials from the CoRE MOF database (15), a collection of >4,700 crystal structures from experimental reports.

For this study, we selected 130 materials (∼2.7% of the total) from the CoRE MOF database as listed in SI Appendix, Table S1. To select these MOFs, we first listed all materials that were first published between 2007 and 2013 and excluded examples in which the original report described more than one CoRE MOF structure. The latter choice simplified the following literature metaanalysis. The 130 MOFs we analyze below were randomly selected from the resulting list. In cases where the original paper identified an isoreticular family of structures but only a single material was entered into the CoRE MOF database, we looked for citations that resynthesized any variant reported by the original paper. Restricting our choice to materials reported before 2014 means that opportunities to resynthesize each material have existed for at least 5 y. We examined every paper listed by Google Scholar as citing one of the original reports. Citation statistics for these papers are shown in SI Appendix, Table S2. The original papers had been cited between 8 and 168 times, with an average of 34 citations. The correlation coefficient between the year of publication and the number of citations for these papers is 0.027, so these 2 quantities are not correlated (SI Appendix, Fig. S1).

Some of the citing papers we examined described synthesis of variations of the original materials, for example, with different metal centers or different linkers. Here, however, we focus on direct replication in which the original and later syntheses produced exactly the same material. We did not attempt to assess whether any of these syntheses were “successful” or “correct”: if a paper states that a specific material was synthesized then we counted this synthesis in our analysis. In addition to counting repeat syntheses, it is interesting to consider who reports each repeat synthesis. If a citing paper and the original paper included one or more common authors, we labeled a repeat synthesis as coming from the original research group.

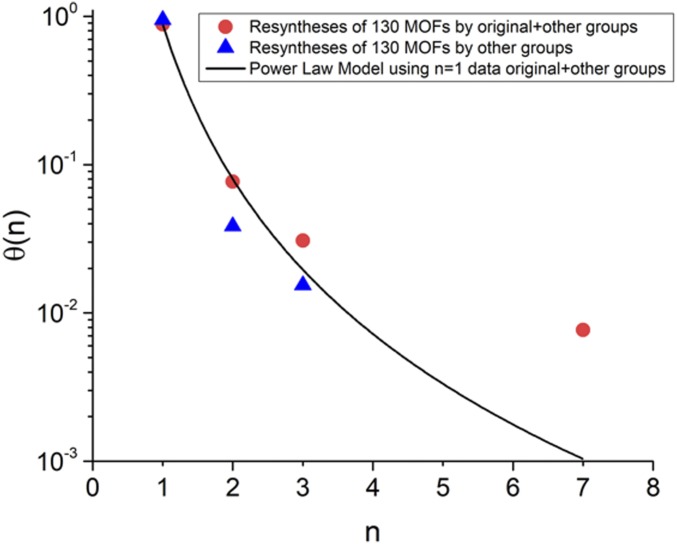
The repeat syntheses of the 130 MOFs we considered are described in SI Appendix, Table S1. Only 1 material was synthesized more than 3 times: a Zn-based MOF first produced by An et al. (16) with structure code SAPBIW (common name Bio-MOF-100) has been synthesized 7 times, including 2 instances by groups distinct from the original authors. Seven of the 130 MOFs have been resynthesized by a group distinct from the original authors, and 15 of the MOFs have been synthesized more than once by anyone. In the notation above, f = 115/130 = 0.8846, so if Eq. 1 applies then α = 3.46. Among the 4 original papers that have received the most citations [corresponding to the materials SAPBIW (16), MUVJIX (17), XUNGUJ (18), and IJOMOJ06 (19)], 3 materials have been synthesized more than once but in one case we did not find any reports of repeat synthesis.

Fig. 1 compares the power law with f = 0.8846 to the data from our literature metaanalysis. There is some discrepancy between the model and the data for n = 7, but because our data came from 130 materials, accurately resolving values of $\theta \left(n\right)<0.01$ is difficult. We performed a goodness-of-fit test with the KS statistic using 1,000 synthetic datasets generated from the power law shown in Fig. 1. SI Appendix, Fig. S2 shows an example of a small number of synthetic datasets compared with a power-law model. This gave a P value of 0.82, considerably higher than the threshold of 0.1 suggested by Clauset et al. (13) Using 10,000 synthetic datasets gave a P value of 0.81. A statistical test of this kind cannot prove that the underlying data come from a power law, but we can conclude that the observed data are not inconsistent with power-law behavior.

Fig. 1.

Fraction of MOFs whose synthesis has been reported exactly n times among the group of 130 MOFs described in the text. Blue (red) symbols show results for all reports (results when only resynthesis by authors distinct from the original paper are counted). The solid curve shows the power law described in the text with f = 0.8846.

If only repeat syntheses by groups distinct from the original authors are considered, a power law with f = 0.9461 and α = 4.45 is obtained. Only 2 of the 130 materials we examined had been resynthesized more than once by this metric (SI Appendix, Table S4). We are not arguing that repeat synthesis by the original authors should be devalued; reports of this kind are surely valuable. Nevertheless, looking at our data in this way highlights the low frequency with which materials synthesis has been repeated by investigators separate from those involved in the original discovery of a material.

The discussion above focuses on direct replicates, that is, work that reports the synthesis of exactly the same material as a previous report. We also found many examples of modified synthesis in which a new material is made based upon a previously reported material. We examined all papers citing the original reports of the 130 materials and defined a paper as reporting a modified synthesis if a crystal structure with a different stoichiometry than the original materials or a crystal polymorph was synthesized but no data were given describing (re)synthesis of the original material. Each paper was classified as either replicating the original material or reporting a modified synthesis of a new material or neither of these options. The numbers of modified syntheses for all 130 materials are given in SI Appendix, Tables S1 and S5. The prevalence of modified synthesis is very different from direct replication; for 65% of the 130 MOFs we studied a modified synthesis was reported at least once. Of the materials that have been synthesized with modifications at least once, 51% have been reported by a research group distinct from the authors of the original report. It seems likely that in many studies that created a modified material the authors also repeated the synthesis of an original material as part of their work. If this supposition is correct, there are many replications of MOF synthesis that have been performed in laboratories around the world but not reported in the literature. This points to a simple idea that would greatly enhance the materials chemistry community’s ability to assess (and enhance) data reproducibility: When an experiment from a previous report is repeated, the outcome should be reported even when this replication was a precursor to the main aim of the published work.

Replicability of Most-Synthesized MOFs in the Literature

A sensible objection to the analysis above is that the random sampling of materials used above is unlikely to include any of the small number of MOFs that have received the most attention. We used other methods to identify these materials. Specifically, we ranked materials by their frequency of appearance in the NIST Adsorption Database (12), by the frequency of their mention in the abstracts of a recent international conference dedicated to MOFs, and by the number of citations received by the original literature report for each MOF in common between these 2 rankings (SI Appendix, Table S6). These 3 approaches gave consistent results, and we selected UiO-66(Zr) (20), ZIF-8(Zn) (21), HKUST-1(Cu) (22) (also known as Cu-BTC or MOF-199), MIL-101(Cr) (23), IRMOF-1(Zn) (24) (also known as MOF-5), and MOF-177(Zn) (25) for further analysis. For each of these materials, 500 papers that cited the original synthesis report were randomly selected from all citing papers. These 3,000 papers were examined in the same way as described above for the materials selected from the CoRE MOF database. The total number of repeat syntheses that have been reported was estimated by scaling the number of replicates found among these 500 reports by the total number of citations a material had received (SI Appendix, Table S7). With this approach, we estimate that the number of times the synthesis of these materials has been reported in the literature varies from 61 (MOF-177) to almost 1,000 (Cu-BTC) and that 4 of the materials [Cu-BTC, UiO-66, ZIF-8, and MIL-101(Cr)] have been synthesized in more than 700 reports.

The existence of MOFs that have been replicated hundreds of times is inconsistent with the power law shown in Fig. 1 being valid for large values of n. We noted above that Eq. 1 predicts the total number of different materials that have been synthesized, N_total, if the number of reported syntheses for the most replicated material, N_max, is known. If we take N_max to be 1,000 (the value estimated for Cu-BTC to 1 significant digit), the power law implies that N_total = 2.7 × 10¹⁰. Even using a much lower estimate of N_max = 100, which is lower than the estimated values for 5 of the 6 materials in SI Appendix, Table S7, gives N_total = 9.4 × 10⁶. The CoRE MOF database and related collections of MOF materials (14, 15) clearly demonstrate that tens of thousands of distinct MOFs have been made, but not even the most optimistic proponents of the versatility of these materials would claim that millions or billions of different materials have been made. For comparison, it has been estimated that worldwide, around 6 × 10⁵ new chemical species per year are reported (26).

Anecdotal descriptions of power-law distributions often invoke the Pareto effect (also known as the 80/20 rule or the Matthew effect). In the context of Eq. 1, these effects would predict that a small handful of materials would receive a significant majority of all replications. The analysis in SI Appendix, Table S7, however, indicates a more extreme situation in which a very small number of materials account for almost all reported replications. If we assume that the actual value of N_total for MOFs is 20,000, a reasonable estimate based on efforts to catalog these materials (14, 15), and that Eq. 1 is only valid for n = 1–10, then Eq. 1 predicts that there are ∼3,600 reported replicate syntheses. Our independent estimates for the 6 most-studied materials in SI Appendix, Table S7 indicate that ∼3,600 replicate syntheses of these materials alone have been reported. With these estimates, 0.03% of known MOFs account for ∼50% of all replications that have been reported.

The discussion above leads to our tentative conclusion regarding the frequency with which the synthesis of MOFs has been replicated and reported: for most materials this frequency approximately follows a power law, but a small number of “supermaterials” exist that have been replicated many times more than most materials. It would be interesting to know whether similar observations apply to other classes of materials. The description we have just given seems consistent with common perceptions of how research in the materials chemistry community is pursued, but without quantitative analysis of other materials classes extending our conclusions to all materials would be speculative.

It is natural to ask what factors lead to a new material becoming what we have described as a supermaterial. We cannot offer a definitive answer, and it is likely that issues of timing and the sociology of scientific culture are important. Nevertheless, looking at common factors among the 6 materials listed in SI Appendix, Table S7 is interesting. All of these materials can be synthesized using chemicals that are readily available commercially, and all but one (MOF-177) involve only chemicals that are cheap. This suggests that at least in the MOF research community, materials in which chemical synthesis of component chemicals is required before materials synthesis from these components are unlikely to be supermaterials. It is encouraging to see that the materials in SI Appendix, Table S7 came from work at a geographically and internationally diverse group of institutions.

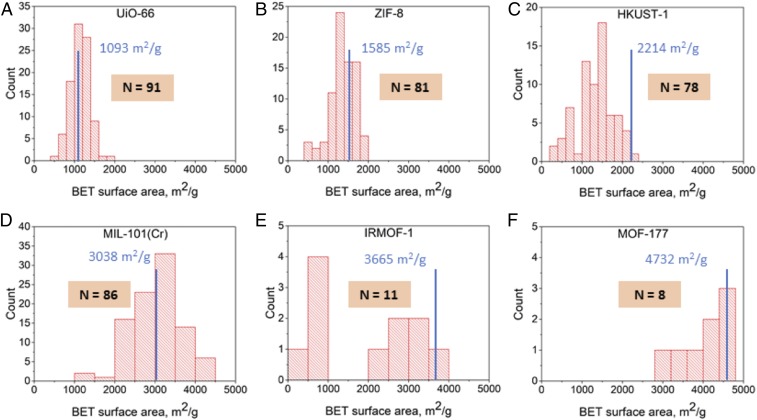
All of the results above have examined whether replicate syntheses of MOFs exist but not what can be deduced about reproducibility from these replicates. For the materials shown in Fig. 1 it is challenging to discuss reproducibility because the small number of replicates that have been reported did not always report the same quantitative properties as the original synthesis report (27). Among the materials listed in SI Appendix, Table S7, however, there are many replicate measurements of MOF surface areas, a quantity that can be readily compared between experiments. We focus below on the Brunauer–Emmett–Teller (BET) surface area, since well-established protocols exist for measuring and interpreting the data for this quantity (28). The BET surface area is strongly correlated with pore volume, another commonly reported property (SI Appendix, Fig. S3). Fig. 2 shows the reported BET surface areas for the 6 MOFs listed above. Among the 528 replicate syntheses listed in SI Appendix, Table S7, 355 reported BET surface areas. The figure also shows the surface area predicted computationally using a defect-free crystal structure using the Zeo++ software with a probe radius size of 1.8 Å to represent N₂ adsorption (29).

Fig. 2.

Histograms of experimentally reported BET surface areas for (A) UiO-66, (B) ZIF-8, (C) HKUST-1, (D) MIL-101(Cr), (E) IRMOF-1, and (F) MOF-177. The number of reported surface areas (N) for each material is indicated in each figure. Blue text and vertical lines show the calculated theoretical values from defect-free and solvent-free crystal structures.

In Fig. 2, HKUST-1 and IRMOF-1 show bimodal distributions of surface area observations. These materials are known to be sensitive to moisture (30), so it is likely that this variation is related to differences in materials handling and history among the replicate experiments. UiO-66, ZIF-8, and MIL-101(Cr) are known to be relatively stable toward moisture (30) and they show less variation in surface area among replicates. It is notable that for each material there are examples for which the surface area is much smaller than the theoretical value and examples for which the surface area is larger. In addition to materials degradation, incomplete removal of solvent from materials can lead to reduced surface areas (31, 32). The presence of local defects in MOFs can lead to higher surface areas than in an ideal crystal (33–36). It is therefore not surprising that each material in Fig. 2 shows a range of observed surface areas. These data suggest, however, that there are systematic variations in the materials properties among many replicate syntheses of these materials, implying that efforts to understand the phenomena that lead to these variations and more precisely describe the materials that are made would be useful. Careful comparison of the precise synthesis conditions and experimental details among many replicates would be helpful to begin to address these issues, but this is beyond the scope of our current work.

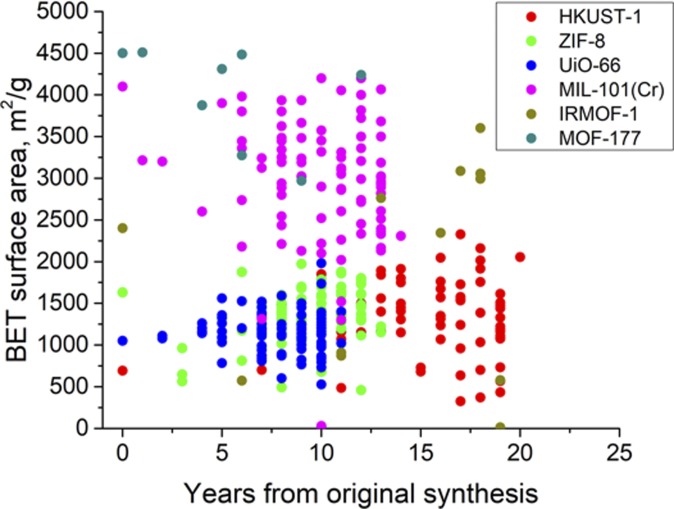
Because activation of MOFs can be a nontrivial issue (37, 38), it is conceivable that measured surface areas might improve over time as techniques for activating specific materials are improved. To see if there is evidence for this effect, we show in Fig. 3 the observed surface areas for each material as a function of years elapsed since their original synthesis. The same data using the actual date of each report of synthesis is shown in SI Appendix, Fig. S4. These data offer no support for the idea that the measured surface areas systematically improve over time during many replicate measurements. A caveat in considering these data are that unlike efforts to make high-precision measurements of physical constants (38), the measurement of surface area in the majority of these reports is not the central aim of the work, instead it is a characterization technique used in support of some other scientific goal.

Fig. 3.

Variation in BET surface areas of resynthesized MOFs from the year of their original synthesis.

Conclusion

We have collected data on how often the synthesis of new materials is replicated by analyzing the >4,300 papers that cite the original reports of 130 MOFs that were first made between 2007 and 2013. Among these materials, less than 12% have been replicated in a published report, and less than 6% have been replicated by a group of authors distinct from those of the original paper. The synthesis of 1 of these materials has been reported more than 3 times, but for every other material less information than this is available in published reports. We showed that the frequency of replications for these 130 materials can be described with a simple power-law model. This power-law model, however, does not appear to describe the most frequently replicated MOFs in the literature. We identified 6 MOFs that could be described as supermaterials in the sense that they have been made far more frequently than a power-law model would predict. The synthesis of these materials has been replicated hundreds of times, an observation that creates opportunities to consider factors underlying experimental reproducibility and variability that cannot be assessed for materials that have only been synthesized a few times.

Although replicate syntheses have been reported for only a small fraction of the 130 materials we studied, we found many instances where later work produced modified versions of these materials. These modified materials have a different chemical composition or crystal structure from the original material. For 65% of the 130 materials, a modified synthesis has been reported without any information being provided about replicate synthesis of the original material. It may be that in many of these studies, a replicate synthesis of the original material was performed but the authors chose not to report the results. If this is correct, this practice means that many opportunities for the scientific community to learn about the repeatability of materials synthesis are being missed.

Our study focused on MOFs, because the existence of curated libraries of these materials made it possible to select materials to analyze in an unbiased way. We do not know of any similar analysis for other classes of materials, so any discussion of how directly our findings will extend to other materials is speculative. Our methods, however, could readily be applied to other areas within materials chemistry. We hope that the work described here motivates future efforts of this kind.

Data Availability Statement.

All data relevant to the article is available in the SI Appendix.